- 1Scuola Internazionale Superiore di Studi Avanzati, Trieste, Italy
- 2Centre Nacional d'Anàlisi Genòmica-Centre de Regulació Genòmica, Barcelona, Spain
1. Introduction
From viruses to eukaryotes, genomic DNA filaments are confined in spaces of linear dimension much smaller than their contour lengths. In bacteriophages, the μm-long genome is stored in 50 nm-wide viral capsids and the corresponding packing density is so high that viral DNA filaments that have little chance to be entangled in solution (knotting probability <3%) become almost certainly knotted (>95% probability) once confined inside the capsid (Rybenkov et al., 1993; Arsuaga et al., 2002; Marenduzzo et al., 2009, 2010). In humans, instead, the various cm-long chromosomes that make up the genome are kept inside 10 μm-wide nuclei (Alberts et al., 2014). Despite the major change of scale with respect to viruses, the volume fraction occupied by this eukaryotic genome is still large, about 10% (Rosa and Everaers, 2008).
These considerations pose several conundrums: How can chromosomal DNA be at the same time packed and yet accessible to the regulatory and transcriptional machineries? What is its typical degree of genomic entanglement and how much does it interfere with DNA transactions? To what extent are these aspects shaped by general passive physical mechanisms vs. active ones, e.g., involving topoisomerase enzymes?
2. Intra- and Inter-Chromosome Architecture
2.1. Phenomenology
Addressing these questions has proved challenging because of the wide range of length and time scales involved in genome architecture. Classical experimental tools provide details of chromosome architecture at two opposite scales (Marti-Renom and Mirny, 2011). At the smallest one (10 − 100 nm) X-ray crystallography revealed that DNA achieves local packing by wrapping around histones, while at the largest one (1 − 10 μm) fluorescence in situ hybridization (FISH) showed that each chromosome occupies a compact region of the nucleus, termed territory (Cremer and Cremer, 2001, 2010).
More recently, experimental breakthroughs such as super-resolution imaging, electron microscopy tomography plus selective labeling, and chromosome conformational capture (Hi-C) techniques have significantly extended our multiscale knowledge of genome architecture (Dekker et al., 2002; Lieberman-Aiden et al., 2009; Boettiger et al., 2016; Ou et al., 2017; Bintu et al., 2018; Nir et al., 2018).
These and other advancements helped establish various results that foster the present discussion of genomic entanglement.
Regarding inter-chromosome organization we recall that:
(i) the positioning of chromosome territories correlates significantly with sequence-dependent properties of the underlying DNA [most notably, gene density (Bolzer et al., 2005)];
(ii) the intermingling of different chromosomes is minimal and mostly restricted to the boundaries of the territories (Cremer and Cremer, 2001; Branco and Pombo, 2006).
For intra-chromosome aspects we instead know that:
(iii) on the scale of a few kilo-basepairs up to about 1 mega-basepair, chromosomes are organized into self-interacting regions, called topologically-associating domains or TADs (Dixon et al., 2012; Nora et al., 2012). On the tens of mega-basepairs scale, chromatin is organized into compartments of varying compactness depending on their functional and epigenomic state (Lieberman-Aiden et al., 2009; Wang et al., 2016);
(iv) despite this variability, when averaged over chromosomes and experimental realizations, the mean contact probability of two chromosomal loci at genomic distance ℓ scales approximately as 〈pc(ℓ)〉 ~ ℓ−1 (Lieberman-Aiden et al., 2009), and the mean square separation scales as 〈R2(ℓ)〉 ~ ℓ2/3 (Sachs et al., 1995; Münkel et al., 1999).
2.2. Relating Genomic Architecture and Relaxation Dynamics With Polymer Physics
The interpretation of these experimental results has been aided by an intense theoretical and computational activity that demonstrated how salient genomic architecture properties can be reproduced by a broad range of polymer models, and hence are likely governed by general physical mechanisms (Mirny, 2011; Rosa and Zimmer, 2014; Bianco et al., 2017; Haddad et al., 2017; Jost et al., 2017; Tiana and Giorgetti, 2018). This applies in particular to the aforementioned properties (i–iv) which can be rationalized as manifestations of the topological constraints that rule the behavior of semi-dilute or dense polymer systems, particularly their relaxation time scales (Doi and Edwards, 1986).
In fact, a solution of initially disentangled chains of contour length Lc can reach the fully-mixed, homogeneous equilibrium state only via reptation, a slow and stochastic slithering-like motion with characteristic time scale equal to , where τe is a microscopic collision time and Le is the typical contour length between entanglement points (De Gennes, 1971; Doi and Edwards, 1986).
Thus, based on this fundamental polymer physics result, it was estimated that the characteristic relaxation, or equilibration, time of mammalian chromosomes exceeds 100 years (Rosa and Everaers, 2008). The orders-of-magnitude difference between this time scale and the typical duration of the cell cycle (≈ 1 day) has several implications for genome organization, as it was realized even before Hi-C probing methods became available (Rosa and Everaers, 2008). It is clear, in fact, that mammalian chromosomes are never fully relaxed as they undergo the cyclic structural rearrangements from the separate compact rod-like mitotic architecture to the decondensed interphase one (Grosberg et al., 1993; Rosa and Everaers, 2008).
2.3. Implications for (Minimal) Intra- and Inter-chromosome Entanglement
From this standpoint, the emergence of chromosome territories is quantitatively explained as due to the kinetically trapped decondensation of the compact mitotic chromatin (Rosa and Everaers, 2008): interphase chromosomes retain the memory and limited mutual overlap of the earlier mitotic state, consistent with experimental results (Cremer and Cremer, 2001, 2010; Branco and Pombo, 2006). In addition, the ordered linear organization of the mitotic rods should also inform the intra-chromosomal architecture, making it more local than equilibrated polymers. This is consistent with the experimental fact that the effective scaling behavior of the contact probability with the genomic separation ℓ in interphase chromosomes has a more local character (~ℓ−1) than the one expected (~ℓ−3/2) for equilibrated polymers (Lieberman-Aiden et al., 2009). Intuitively, the same memory mechanism ought to facilitate the subsequent separation of interphase chromosomes and their recondensation upon re-entering the mitotic phase in the cell cycle (Rosa and Everaers, 2008).
For the present discussion, we stress that these out-of-equilibrium effects should impact not only the architecture but also the physical entanglement of eukaryotic genomes. In fact, mammalian chromosomes should be more unlinked (for the limited inter-chromosomal intermingling) and unknotted (for the enhanced intra-chromosomal local contacts) than at equilibrium. These heuristic conclusions are supported by various studies showing that the aforementioned scaling relationships obtained by FISH and Hi-C experiments can be ascribed to the topological constraints at play in solutions of unknotted and unlinked polymers (Khokhlov and Nechaev, 1985; Vettorel et al., 2009; Halverson et al., 2014;Rosa and Everaers, 2014).
2.4. Implications for Genomic Structural Modeling and Its Improvement
These considerations appear particularly relevant for the structural modeling of eukaryotic genomes based on phenomenological data, such as spatial proximity constraints, which are typically too sparse to pin down even coarse-grained models of interphase chromosomes (Lieberman-Aiden et al., 2009).
A key question is whether such structural models should additionally be informed by the notion that interphase chromosomes must originate and eventually return to the separate and condensed mitotic state.
Evidence presented in our earlier work help shed some light on the matter. With our co-workers, we considered a model system of six copies of human chromosome 19 in a cubic simulation box with periodic boundary conditions to explore the connection between coregulation and colocalization of genes (Di Stefano et al., 2013). Each copy was initially prepared as a mitotic-like conformation (Rosa and Everaers, 2008), consisting of a polymer filament forming a solenoidal pattern with rosette-like cross-section featuring chromatin loops of about 50 kilo-basepairs, see Figure 1A. We then used a molecular-dynamics steering protocol to bring in proximity pairs of intra-chromosomal loci that were known to be significantly co-regulated. Importantly, topological constraints were accounted for by avoiding unphysical chain crossings during the steering process.
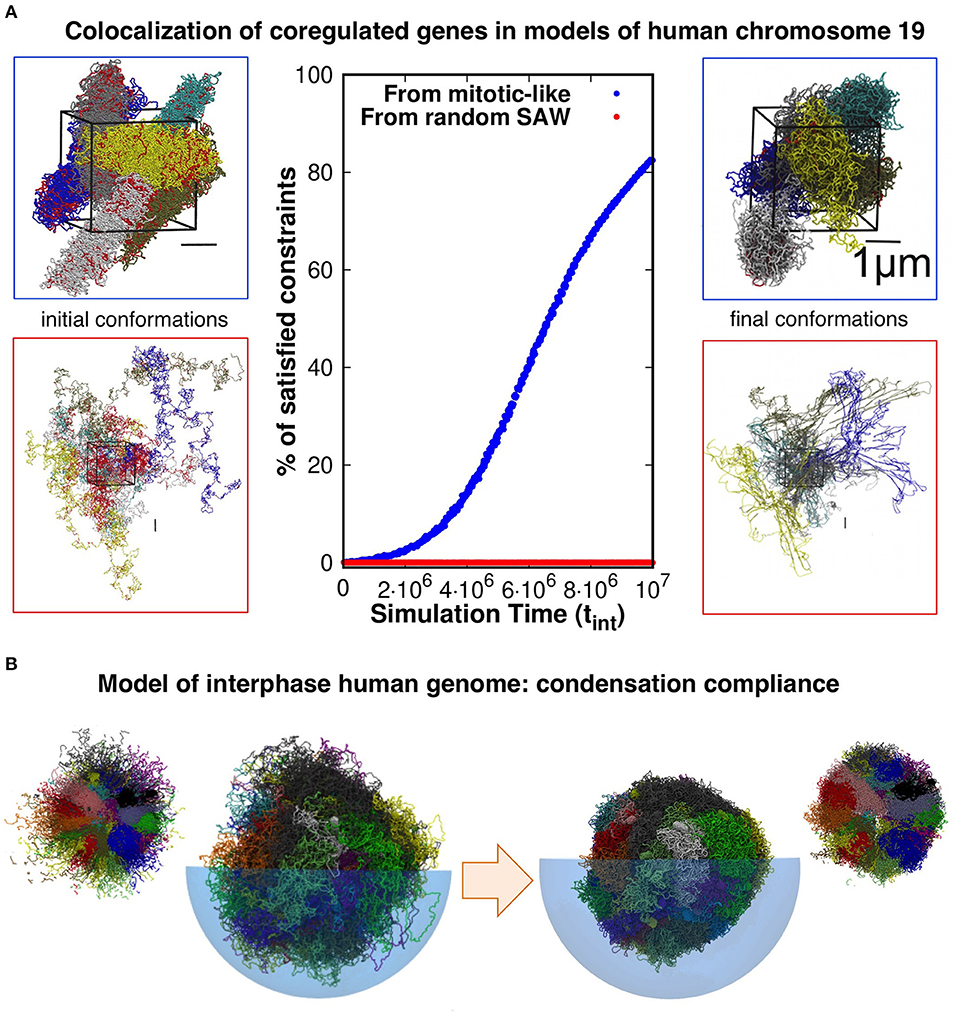
Figure 1. (A) Model conformations of human chromosome 19 (six copies, arranged in a periodic simulation box), described as self-avoiding chains of beads were reshaped by steered molecular dynamics (MD) simulations to promote the colocalization of pairs of loci that are significantly coregulated. Most (>80%) of the coregulated pairs were successfully brought into spatial proximity in simulations that started from relaxed solenoidal mitotic-like arrangements, while virtually no successful colocalization was observed for trajectories started from equilibrated, fully mixed, chromosomal arrangements. Adapted with permission from Di Stefano et al. (2013). (B) Model conformations of the entire-human genome, obtained by steered-MD colocalization of loci based on Hi-C data in Dixon et al. (2012) and Rao et al. (2014) could be successfully condensed with minimal hindrance from intra- or inter-chromosomal constraints, consistently with the expected reconfiguration compliance necessary for the interphase→mitotic transition. The smaller side pictures are cut-through views. Adapted with permission from Di Stefano et al. (2016).
Remarkably, and consistently with the gene kissing hypothesis (Cavalli, 2007), we found that most (>80%) pairs of significantly coregulated genes could indeed be colocalized in space within the contact range of 120nm and further showed that this colocalization compliance followed from the presence of gene cliques in the coregulatory network (Di Stefano et al., 2013).
Conversely, the same protocol applied to the same set of chains but initially prepared as generic self-avoiding random walks failed to give colocalization (Di Stefano et al., 2013). Physically, this happens because the intra- and inter-chain entanglements present in this system, which mimicks an artificial set of equilibrated chromosomes, were too numerous and conflicting to be successfully negotiated on a viable simulation time scale (see Figure 1A).
Further elements come from the genome-wide structural modeling of human chromosomes of Di Stefano et al. (2016). In this study too, the model chromosomes were initially prepared in mitotic-like states and were then steered to bring in proximity those pairs of loci that corresponded to significantly enhanced entries of two independent Hi-C datasets (Dixon et al., 2012; Rao et al., 2014). The architecture of the final conformations were, as expected, significantly changed by the steering protocol. Yet, as illustrated in Figure 1B, we verified that each model chromosome could be brought to a condensed compact shape as needed for the interphase-mitotic transition without significant hindrance from intra- or inter-chromosomal topological constraints (Di Stefano et al., 2016).
We note that the limitedly-entangled architecture of models of long eukaryotic chromosomes has emerged lately (Di Pierro et al., 2016) as the consequence of microphase separation of regions of different chromatin types (Jost et al., 2014) in a block co-polymer model with pair interactions tuned to reproduce the contact propensities of point (iv). The point is reinforced by studies on the yeast genome showing that knots and links have a generally low incidence especially in comparison to equivalent systems of equilibrated chains (Duan et al., 2010; Segal et al., 2014; Pouokam et al., 2019). Finally, besides the indication from structural models, other mechanisms such as loop extrusion have been advocated to be instrumental for maintaining a low degree of chromosomal entanglement (Racko et al., 2018; Orlandini et al., 2019).
To some inevitable extent though, physical entanglements are still expected to arise in eukaryotic chromosomes.
The recent work of Roca's lab showed that knots do occur in eukaryotic minichromosomes in vivo, for instance during transcription, due to transient accumulation of entanglement (Valdés et al., 2017, 2019). On broader scales, various knots (Siebert et al., 2017), and even links (Niewieczerzal et al., 2019), were found in model mouse chromosomes obtained from single cell Hi-C (Stevens et al., 2017). The genuineness of the entangled states was suggested by the systematic recurrence of certain knot types in independent instances of the reconstructed chromosomal structures (Siebert et al., 2017). These were obtained by imposing phenomenological constraints on an initially disconnected set of effective monomers, so we expect that a more defined knot spectrum could be obtained by using disentangled self-avoiding chains as the reference model.
3. Conclusions
To conclude, we have discussed experimental evidence and general physical mechanisms based on polymer theory that consistently point to an unusually low degree of entanglement expected in long eukaryotic chromosomes. Such property, which is arguably essential for the capability of chromosomes to reconfigure as needed at various stages of the cell cycle, appears important for genomic modeling too.
We argued that the structural modeling of long chromosomes can benefit, both for realism and computational efficiency, by starting off with disentangled self-avoiding chains, e.g., mitotic-like ones, because their plasticity makes it possible to accommodate a large number of phenomenological constraints in a physically-viable manner, i.e., without deformations involving intra- or inter-chain crossings.
The latter are, of course, possible in in vivo systems thanks to the action of topoisomerase enzymes. An important open question regards the extent to which these active mechanisms are involved in the shaping the overall intra- and inter-chromosome architecture. This point, we believe, can be significantly advanced in future studies with a tight synergy of experiments and models (Goloborodko et al., 2016; Jost et al., 2017; Valdés et al., 2019).
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
The authors acknowledge support from the Italian Ministry of Education, MIUR. The authors would like to acknowledge networking support by the COST Action CA17139.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Alberts, B., Johnson, A. D., Lewis, J., Morgan, D., Raff, M., Roberts, K., et al. (2014). Molecular Biology of the Cell, 6 th Edn. New York, NY: Garland Science.
Arsuaga, J., Vázquez, M., Trigueros, S., Sumners, D. W. L., and Roca, J. (2002). Knotting probability of DNA molecules confined in restricted volumes: DNA knotting in phage capsids. Proc. Natl. Acad. Sci. U.S.A. 99, 5373–5377. doi: 10.1073/pnas.032095099
Bianco, S., Chiariello, A. M., Annunziatella, C., Esposito, A., and Nicodemi, M. (2017). Predicting chromatin architecture from models of polymer physics. Chromosome Res. 25, 25–34. doi: 10.1007/s10577-016-9545-5
Bintu, B., Mateo, L. J., Su, J.-H., Sinnott-Armstrong, N. A., Parker, M., Kinrot, S., et al. (2018). Super-resolution chromatin tracing reveals domains and cooperative interactions in single cells. Science 362:419. doi: 10.1126/science.aau1783
Boettiger, A. N., Bintu, B., Moffitt, J. R., Wang, S., Beliveau, B. J., Fudenberg, G., et al. (2016). Super-resolution imaging reveals distinct chromatin folding for different epigenetic states. Nature 529, 418–422. doi: 10.1038/nature16496
Bolzer, A., Kreth, G., Solovei, I., Koehler, D., Saracoglu, K., Fauth, C., et al. (2005). Three-dimensional maps of all chromosomes in human male fibroblast nuclei and prometaphase rosettes. PLoS Biol. 3:e157. doi: 10.1371/journal.pbio.0030157
Branco, M. R., and Pombo, A. (2006). Intermingling of chromosome territories in interphase suggests role in translocations and transcription-dependent associations. PLoS Biol. 4:e138. doi: 10.1371/journal.pbio.0040138
Cavalli, G. (2007). Chromosome kissing. Curr. Opin. Genet. Dev. 17, 443–450. doi: 10.1016/j.gde.2007.08.013
Cremer, T., and Cremer, C. (2001). Chromosome territories, nuclear architecture and gene regulation in mammalian cells. Nat. Rev. Genet. 2, 292–301. doi: 10.1038/35066075
Cremer, T., and Cremer, M. (2010). Chromosome territories. CSH Perspect. Biol. 2:a003889. doi: 10.1101/cshperspect.a003889
De Gennes, P.-G. (1971). Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 55, 572–579. doi: 10.1063/1.1675789
Dekker, J., Rippe, K., Dekker, M., and Kleckner, N. (2002). Capturing chromosome conformation. Science 295:1306. doi: 10.1126/science.1067799
Di Pierro, M., Zhang, B., Lieberman-Aiden, E., Wolynes, P. G., and Onuchic, J. (2016). Transferable model for chromosome architecture. Proc. Natl. Acad. Sci. U.S.A. 113, 12168–12173. doi: 10.1073/pnas.1613607113
Di Stefano, M., Paulsen, J., Lien, T. G., Hovig, E., and Micheletti, C. (2016). Hi-c-constrained physical models of human chromosomes recover functionally-related properties of genome organization. Sci. Rep. 6:35985. doi: 10.1038/srep35985
Di Stefano, M., Rosa, A., Belcastro, V., di Bernardo, D., and Micheletti, C. (2013). Colocalization of coregulated genes: a steered molecular dynamics study of human chromosome 19. PLoS Comput. Biol. 9:e1003019. doi: 10.1371/journal.pcbi.1003019
Dixon, J. R., Selvaraj, S., Yue, F., Kim, A., Li, Y., Shen, Y., et al. (2012). Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature 485, 376–380. doi: 10.1038/nature11082
Doi, M., and Edwards, S. F. (1986). The Theory of Polymer Dynamics. New York, NY: Oxford University Press.
Duan, Z., Andronescu, M., Schutz, K., McIlwain, S., Kim, Y. J., Lee, C., et al. (2010). A three-dimensional model of the yeast genome. Nature 465:363. doi: 10.1038/nature08973
Goloborodko, A., Imakaev, M. V., Marko, J. F., and Mirny, L. (2016). Compaction and segregation of sister chromatids via active loop extrusion. Elife 5:e14864. doi: 10.7554/eLife.14864
Grosberg, A., Rabin, Y., Havlin, S., and Neer, A. (1993). Crumpled globule model of the three-dimensional structure of DNA. Europhys. Lett. 23, 373–378. doi: 10.1209/0295-5075/23/5/012
Haddad, N., Jost, D., and Vaillant, C. (2017). Perspectives: using polymer modeling to understand the formation and function of nuclear compartments. Chromosome Res. 25, 35–50. doi: 10.1007/s10577-016-9548-2
Halverson, J. D., Smrek, J., Kremer, K., and Grosberg, A. Y. (2014). From a melt of rings to chromosome territories: the role of topological constraints in genome folding. Rep. Prog. Phys. 77:022601. doi: 10.1088/0034-4885/77/2/022601
Jost, D., Carrivain, P., Cavalli, G., and Vaillant, C. (2014). Modeling epigenome folding: formation and dynamics of topologically associated chromatin domains. Nucleic Acids Res. 42, 9553–9561. doi: 10.1093/nar/gku698
Jost, D., Rosa, A., Vaillant, C., and Everaers, R. (2017). “A polymer physics view on universal and sequence-specific aspects of chromosome folding,” in Nuclear Architecture and Dynamics, Vol. 2, eds C. Lavelle and J.-M. Victor (London, UK Academic Press), 149.
Khokhlov, A. R., and Nechaev, S. K. (1985). Polymer chain in an array of obstacles. Phys. Lett. 112A:156–160. doi: 10.1016/0375-9601(85)90678-4
Lieberman-Aiden, E., van Berkum, N. L., Williams, L., Imakaev, M., Ragoczy, T., Telling, A., et al. (2009). Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science 326:289–293. doi: 10.1126/science.1181369
Marenduzzo, D., Micheletti, C., and Orlandini, E. (2010). Biopolymer organization upon confinement. J. Phys. Condens. Matter. 22:283102. doi: 10.1088/0953-8984/22/28/283102
Marenduzzo, D., Orlandini, E., Stasiak, A., Sumners, D. W., Tubiana, L., and Micheletti, C. (2009). DNA-DNA interactions in bacteriophage capsids are responsible for the observed DNA knotting. Proc. Natl. Acad. Sci. U.S.A. 106, 22269–22274. doi: 10.1073/pnas.0907524106
Marti-Renom, M. A., and Mirny, L. A. (2011). Bridging the resolution gap in structural modeling of 3d genome organization. PLoS Comput. Biol. 7:e1002125. doi: 10.1371/journal.pcbi.1002125
Mirny, L. A. (2011). The fractal globule as a model of chromatin architecture in the cell. Chromosome Res. 19, 37–51. doi: 10.1007/s10577-010-9177-0
Münkel, C., Eils, R., Dietzel, S., Zink, D., Mehring, C., Wedemann, G., et al. (1999). Compartmentalization of interphase chromosomes observed in simulation and experiment. J. Mol. Biol. 285, 1053–1065. doi: 10.1006/jmbi.1998.2361
Niewieczerzal, S., Niemyska, W., and Sulkowska, J. I. (2019). Defining and detecting links in chromosomes. Sci. Rep. 9:11753. doi: 10.1038/s41598-019-47999-4
Nir, G., Farabella, I., Prez Estrada, C., Ebeling, C. G., Beliveau, B. J., Sasaki, H. M., et al. (2018). Walking along chromosomes with super-resolution imaging, contact maps, and integrative modeling. PLoS Genet. 14:e1007872. doi: 10.1371/journal.pgen.1007872
Nora, E. P., Lajoie, B. R., Schulz, E. G., Giorgetti, L., Okamoto, I., Servant, N., et al. (2012). Spatial partitioning of the regulatory landscape of the x-inactivation centre. Nature 485:381. doi: 10.1038/nature11049
Orlandini, E., Marenduzzo, D., and Michieletto, D. (2019). Synergy of topoisomerase and structural-maintenance-of-chromosomes proteins creates a universal pathway to simplify genome topology. Proc. Natl. Acad. Sci. U.S.A. 116:8149. doi: 10.1073/pnas.1815394116
Ou, H. D., Phan, S., Deerinck, T. J., Thor, A., Ellisman, M. H., and O'Shea, C. C. (2017). Chromemt: visualizing 3d chromatin structure and compaction in interphase and mitotic cells. Science 357:eaag0025. doi: 10.1126/science.aag0025
Pouokam, M., Cruz, B., Burgess, S., Segal, M. R., Vazquez, M., and Arsuaga, J. (2019). The rabl configuration limits topological entanglement of chromosomes in budding yeast. Sci. Rep. 9:6795. doi: 10.1038/s41598-019-42967-4
Racko, D., Benedetti, F., Goundaroulis, D., and Stasiak, A. (2018). Chromatin loop extrusion and chromatin unknotting. Polymers 10:1126. doi: 10.3390/polym10101126
Rao, S. S. P., Huntley, M. H., Durand, N. C., Stamenova, E. K., Bochkov, I. D., Robinson, J. T., et al. (2014). A 3d map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell 159:1665–1680. doi: 10.1016/j.cell.2014.11.021
Rosa, A., and Everaers, R. (2008). Structure and dynamics of interphase chromosomes. PLoS Comput. Biol. 4:e1000153. doi: 10.1371/journal.pcbi.1000153
Rosa, A., and Everaers, R. (2014). Ring polymers in the melt state: the physics of crumpling. Phys. Rev. Lett. 112:118302. doi: 10.1103/PhysRevLett.112.118302
Rosa, A., and Zimmer, C. (2014). Computational models of large-scale genome architecture. Int. Rev. Cell Mol. Biol. 307, 275–349. doi: 10.1016/B978-0-12-800046-5.00009-6
Rybenkov, V. V., Cozzarelli, N. R., and Vologodskii, A. V. (1993). Probability of DNA knotting and the effective diameter of the DNA double helix. Proc. Natl. Acad. Sci. U.S.A. 90, 5307–5311. doi: 10.1073/pnas.90.11.5307
Sachs, R. K., van den Engh, G., Trask, B., Yokota, H., and Hearst, J. E. (1995). A random-walk/giant-loop model for interphase chromosomes. Proc. Natl. Acad. Sci. U.S.A. 92, 2710–2714. doi: 10.1073/pnas.92.7.2710
Segal, M. R., Xiong, H., Capurso, D., Vazquez, M., and Arsuaga, J. (2014). Reproducibility of 3d chromatin configuration reconstructions. Biostatistics 15, 442–456. doi: 10.1093/biostatistics/kxu003
Siebert, J. T., Kivel, A. N., Atkinson, L. P., Stevens, T. J., Laue, E. D., and Virnau, P. (2017). Are there knots in chromosomes? Polymers 9:317. doi: 10.3390/polym9080317
Stevens, T. J., Lando, D., Basu, S., Atkinson, L. P., Cao, Y., Lee, S. F., et al. (2017). 3d structures of individual mammalian genomes studied by single-cell hi-c. Nature 544, 59–64. doi: 10.1038/nature21429
Tiana, G., and Giorgetti, L. (2018). Integrating experiment, theory and simulation to determine the structure and dynamics of mammalian chromosomes. Curr. Opin. Struct. Biol. 49, 11–17. doi: 10.1016/j.sbi.2017.10.016
Valdés, A., Coronel, L., Martínez-García, B., Segura, J., Dyson, S., Díaz-Ingelmo, O., et al. (2019). Transcriptional supercoiling boosts topoisomerase ii-mediated knotting of intracellular DNA. Nucleic Acids Res. 47, 6946–6955. doi: 10.1093/nar/gkz491
Valdés, A., Segura, J., Dyson, S., Martínez-García, B., and Roca, J. (2017). DNA knots occur in intracellular chromatin. Nucleic Acids Res. 46, 650–660. doi: 10.1093/nar/gkx1137
Vettorel, T., Grosberg, A. Y., and Kremer, K. (2009). Territorial polymers. Phys. Today 62:72. doi: 10.1063/1.3206103
Keywords: DNA and chromosomes, structural models, genomic entanglement, topological constraints, physical knots and links
Citation: Rosa A, Di Stefano M and Micheletti C (2019) Topological Constraints in Eukaryotic Genomes and How They Can Be Exploited to Improve Spatial Models of Chromosomes. Front. Mol. Biosci. 6:127. doi: 10.3389/fmolb.2019.00127
Received: 12 September 2019; Accepted: 28 October 2019;
Published: 15 November 2019.
Edited by:
Valentina Tozzini, National Research Council, ItalyReviewed by:
Stephen Daniel Levene, The University of Texas at Dallas, United StatesCopyright © 2019 Rosa, Di Stefano and Micheletti. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Angelo Rosa, YW5yb3NhQHNpc3NhLml0; Marco Di Stefano, bWFyY28uZGlzdGVmYW5vQGNuYWcuY3JnLmV1; Cristian Micheletti, bWljaGVsZXRAc2lzc2EuaXQ=
 Angelo Rosa
Angelo Rosa Marco Di Stefano
Marco Di Stefano Cristian Micheletti
Cristian Micheletti