NNAN: Nearest Neighbor Attention Network to Predict Drug–Microbe Associations

Many drugs can be metabolized by human microbes; the drug metabolites would significantly alter pharmacological effects and result in low therapeutic efficacy for patients. Hence, it is crucial to identify potential drug–microbe associations (DMAs) before the drug administrations. Nevertheless, traditional DMA determination cannot be applied in a wide range due to the tremendous number of microbe species, high costs, and the fact that it is time-consuming. Thus, predicting possible DMAs in computer technology is an essential topic. Inspired by other issues addressed by deep learning, we designed a deep learning-based model named Nearest Neighbor Attention Network (NNAN). The proposed model consists of four components, namely, a similarity network constructor, a nearest-neighbor aggregator, a feature attention block, and a predictor. In brief, the similarity block contains a microbe similarity network and a drug similarity network. The nearest-neighbor aggregator generates the embedding representations of drug–microbe pairs by integrating drug neighbors and microbe neighbors of each drug–microbe pair in the network. The feature attention block evaluates the importance of each dimension of drug–microbe pair embedding by a set of ordinary multi-layer neural networks. The predictor is an ordinary fully-connected deep neural network that functions as a binary classifier to distinguish potential DMAs among unlabeled drug–microbe pairs. Several experiments on two benchmark databases are performed to evaluate the performance of NNAN. First, the comparison with state-of-the-art baseline approaches demonstrates the superiority of NNAN under cross-validation in terms of predicting performance. Moreover, the interpretability inspection reveals that a drug tends to associate with a microbe if it finds its top-l most similar neighbors that associate with the microbe.

Introduction

The human microbiome refers to all the microbes associated with a human body, including bacteriophages, archaea, bacteria, eukaryotes, and fungi (Lynch and Pedersen, 2016). To assess the diversity and functions of the human microbiome, the Human Microbiome Project (HMP) was supported by the National Institutes of Health (NIH) from 2007 to 2016 (Turnbaugh et al., 2007). HMP provided a complete description of the microbiome in five tissues of the human body, including skin, gut, nostrils, vagina, and mouth (Aagaard et al., 2013). Human microbes have been verified for their close associations with human health by cell experiments, animal experiments, epidemiological studies, clinical case studies (Schwabe and Jobin, 2013; Lynch and Pedersen, 2016), etc. Previous works have revealed that abnormal microbe communities lead to metabolic disorders [e.g., non-alcoholic fatty liver disease (Younossi et al., 2016), obesity, and diabetes mellitus (Jaacks et al., 2019; Zheng et al., 2018)]. Oral drug administration is a typical treatment. Many drugs, however, can be metabolized by human microbes, and the drug metabolites would significantly alter pharmacological effects and result in low therapeutic efficacy for patients. For example, after being modified by gut microbes, the compounds can lead to their activation [e.g., salicylazosulfapyridine (Sousa et al., 2014)] or inactivation [e.g., inactivation of the cardiac drug digoxin by the intestinal actinomycete Eggerthella lenta (Haiser et al., 2013)], or induce toxicity [e.g., 70% toxicity of Brivudine may be attributed to intestinal microorganisms (Zimmermann et al., 2019b)]. The persistent findings of microbiome-induced individual pathogenesis, phenotypes, and treatment responses boost the microbiome to be an integral part of precision medicine (Kashyap et al., 2017). Therefore, drug–microbe association (DMA) prediction is of great significance for therapy and medicine development. However, the acquisition of DMAs needs a large scale of assays with high costs, low efficiency, and culturing limitations, and that are time-consuming. To identify DMAs rapidly and effectively, machine learning methods, especially deep learning-based methods, have attracted many scientists due to their inspiring applications in other areas [e.g., predicting microbe–disease associations (He et al., 2018; Peng et al., 2018), drug–drug interactions (Yu et al., 2021a), lncRNA–miRNA interactions (Zhang L. et al., 2021), and lncRNA–protein interactions (Lihong et al., 2021; Zhou et al., 2021)].

In recent years, researchers have applied Graph Attention Network [GAT (Velickovic et al., 2018)] to bioinformatics with remarkable results. For instance, Zhang Z. et al. (2021) used fragments containing functional groups to represent molecular maps for molecular property prediction through a fragment-oriented multi-scale graph attention model. Bang et al. (2021) made the prediction of polypharmacy side effects with enhanced interpretability based on graph feature attention network. Constructing a bipartite network is the most popular approach to represent associations between two types of nodes. The prediction problem of DMA can then be transformed into a link prediction problem in a bipartite graph network. However, few models predict DMAs through bipartite graph networks. For example, EGATMDA (Long et al., 2020b) used the drug–disease–microbe perspective to predict the DMAs, which does not show a direct relationship between drugs and microbes and may contain noise. HMDAKATZ (Zhu et al., 2019) predicted the interactions between drugs and microbes based on the Katz (1953); the disadvantage of this method in the node’s information transmission (i.e., a node with a high central value transmits its high influence to all its neighbors) may not be appropriate in real life. GCNMDA (Long et al., 2020a) used GCN, random walk with restart, and GAT to learn node features, which relies on the parameter “step size” when using the restart random walk algorithm. HNERMDA (Long and Luo, 2020) learned the drug–microbe heterogeneous network information by metapath2vec measure, which considered the type of nodes in the meta-path-based random walk but the skip-gram does not treat them differently during training.

In the field of drug–target interaction prediction, there is a widely accepted assumption that structurally similar drugs tend to interact with the same target (Khalili et al., 2012). Analogously, we anticipate that if a drug (d_x) can associate with a microbe (b_p), the other drugs associated with the same microbe (b_p) are usually the first l nearest neighbors of the drug (d_x). Therefore, we propose a new model, Nearest Neighbor Attention Network (NNAN), which aggregates the information from nodes’ neighbors according to their entity types and maps them into a unified embedding space for further predicting potential DMAs. The comparison with state-of-the-art methods on two different databases demonstrates the superiority of our NNAN. Moreover, its interpretability is illustrated and validates our assumption. Finally, the case study assesses its ability to find potential associations between drugs and microbes. In general, our contribution is as follows:

• We make use of three networks: drug–drug similarity network, microbe–microbe similarity network, and a drug–microbe bipartite graph network. Imitate the idea of KNN [K-Nearest-Neighbor (Cover and Hart, 1967)] to learn the substructures of the bipartite graph network, which can promote the accuracy of link prediction.

• We follow the idea of GAT and use multiple DNNs to learn the weights of embedding features to improve the screening efficiency of potential associations.

• In a quantitative way, we verify the hypothesis that “If a drug can associate with a microbe, the other drugs that associate with the microbe are usually the first l nearest neighbors to the drug.”

Materials and Methods

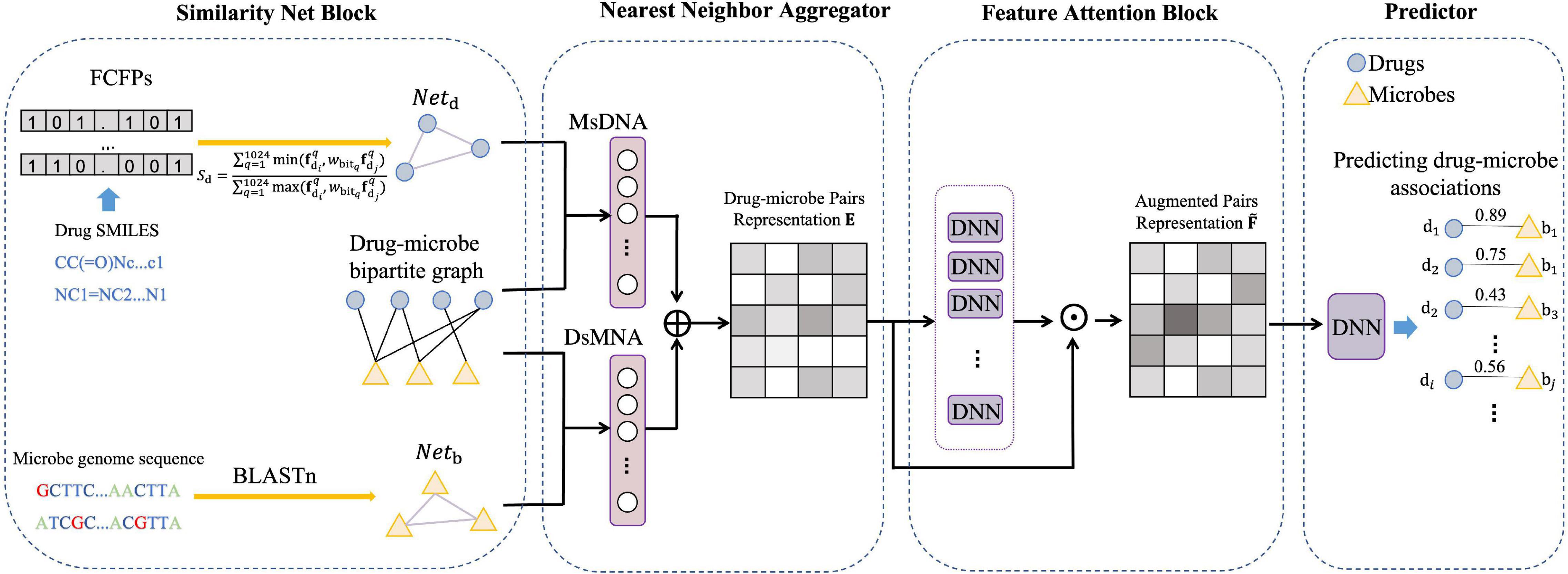
In this section, we describe a model for predicting DMAs in a bipartite graph network, named NNAN as shown in Figure 1. It consists of four components: a similarity network constructor, a nearest-neighbor aggregator, a feature attention block, and a predictor. Firstly, the similarity network constructor is mainly used to build a drug similarity network and a microbe similarity network (section “Similarity Networks” for details). Secondly, the nearest-neighbor aggregator generates the embedding representations of drug–microbe pairs by integrating drug neighbors and microbe neighbors of each drug–microbe pair in the network (section “Nearest-Neighbor Aggregator for Drug–Microbe Pair Embeddings” for details). Thirdly, the feature attention block evaluates the importance of each dimension of drug–microbe pair embedding by a set of ordinary multi-layer neural networks (section “Feature Attention Block” for details). Finally, we make use of a fully-connected deep neural network as a binary classifier to predict potential DMAs.

FIGURE 1

Figure 1. The overall framework of NNAN for drug–microbe association prediction.

Similarity Networks

Drug Similarity Network

We calculate drug similarities by the following steps. First, drugs are represented by Functional-Class Fingerprints [FCFPs (Rogers and Hahn, 2010)], which is the generalized version of Extended-Connectivity Fingerprints [ECFPs (Rogers and Hahn, 2010)] with more attention to atom functions. The FCFPs is implemented by RDKit (Landrum, 2010). Second, the similarity between drug d_i and drug d_j is calculated by the Tanimoto coefficient (Rogers and Tanimoto, 1960) as follows:

$S({\text{d}}_i,{\text{d}}_j)=\frac{{\mathbf{\text{f}}}_{{\text{d}}_i}\cdot {\mathbf{\text{f}}}_{{\text{d}}_j}}{||{\mathbf{\text{f}}}_{{\text{d}}_i}||+||{\mathbf{\text{f}}}_{{\text{d}}_j}||-{\mathbf{\text{f}}}_{{\text{d}}_i}\cdot {\mathbf{\text{f}}}_{{\text{d}}_j}}(1)$

where f_di and f_dj represent the FCFPs vector of drug d_i and drug d_j, respectively, ||⋅|| indicates the norm of the vector.

Fingerprint similarity provides intuitive results: why the two molecules have been determined to be similar, but this transparency tends to vanish completely when molecular fingerprints are used as input to machine learning models. Inspired by the similarity maps (Riniker and Landrum, 2013), we calculate the contribution of each atom to the similarity between two molecules. To make it easier to distinguish the drugs, we regard d_i as a reference drug, d_j as a comparison drug, and S(d_i,d_j) as the base similarity of this drug pair. The RDKit will automatically number each atom of the comparison drug d_j (K = {0,1,…,t−1}). Then, we remove the atoms of the comparison drug one by one in the order of the atomic numbers to form multiple new comparing drugs (${\text{d}}_j^k,k\in \mathrm{K},\mathrm{K}=\{0,1,\mathrm{\dots },t-1\}$). We calculate the new similarity between the reference drug (d_i) and the new comparison drug (${\text{d}}_j^k$), and regard the difference between the new similarity and the base similarity as the weight ($w{}_j^k$) of each removed atom. The weight $w{}_j^k$ is formulated as:

$w{}_j{}^k=|S({\text{d}}_i,{\text{d}}_j)-S({\text{d}}_i,{\text{d}}_j^k)|(2)$

We set the dimension of the FCFPs vector to 1,024 bits, of which the non-zero bits indicate the occurrences of drug feature substructures. To obtain the weight of each non-zero bit, we add up the weights of all the atoms contained in the feature substructure:

$w_{{\text{bit}}_q}=SU{M}_q(w_j^k)(3)$

where w_bitq denotes the weight of the q_th dimensional bit of the FCFPs vector, and the function SUM_q(⋅) denotes the sum of all the atomic weights contained in the feature substructure represented by the q_th dimensional bit of the FCFPs.

Then, the weighted Tanimoto similarity (Ioffe, 2010) between the reference drug and the comparison drug can be calculated as follows:

$S_{\text{d}}({\text{d}}_i,{\text{d}}_j)=\frac{{\sum }_{q=1}^{1024}\text{min}({\mathbf{\text{f}}}_{{\text{d}}_i}^q,w_{{\text{bit}}_q}{\mathbf{\text{f}}}_{{\text{d}}_j}^q)}{{\sum }_{q=1}^{1024}\text{max}({\mathbf{\text{f}}}_{{\text{d}}_i}^q,w_{{\text{bit}}_q}{\mathbf{\text{f}}}_{{\text{d}}_j}^q)}(4)$

where ${\mathbf{\text{f}}}_{{\text{d}}_i}^q$ and ${\mathbf{\text{f}}}_{{\text{d}}_j}^q$ denote the q_th dimension of the FCFPs vectors for the reference drug and the comparison drug.

Based on drug similarities, we can build a drug similarity network Net_d, where nodes are drugs. There are edges between the drugs if these drugs associate with the same microbe; the edges are weighted by drug similarities.

Microbe Similarity Network

To calculate microbe similarities, we use BLAST (Altschul et al., 1990) to make pairwise alignments of microbial genomes. Specifically, the main function of BLAST is to discover local similarity regions between sequences and then use the local sequence alignment algorithm (Smith and Waterman, 1981) to calculate the similarity. For example, ${\text{G}}_{\text{A}}={\text{g}}_{\text{A}}^1{\text{g}}_{\text{A}}^2\mathrm{\dots }{\text{g}}_{\text{A}}^n\mathrm{and}{\text{G}}_{\text{B}}={\text{g}}_{\text{B}}^1{\text{g}}_{\text{B}}^2\mathrm{\dots }{\text{g}}_{\text{B}}^m$ are the genome sequences of microbe A and microbe B, where n and m are the lengths of sequences G_A and G_B, respectively. BLAST creates the scoring matrix H_(n+1)×(m+1) and makes the first row and column elements zero. The formula for the element H_ij(H_ij ∈ H_(n+1)×(m+1),i = 1,2,…,n;j = 1,2,…,m) in this scoring matrix is:

${\mathbf{\text{H}}}_{ij}=\text{max}\{\begin{array}{c}\hfill {\mathbf{\text{H}}}_{i-1,j-1}+\text{Score}\hfill \\ \hfill {\mathbf{\text{H}}}_{i-k,j}-2\hfill \\ \hfill {\mathbf{\text{H}}}_{i,j-k}-2\hfill \\ \hfill 0\hfill \end{array}(\text{g}{}_{\text{A}}{}^i=\text{g}{}_{\text{B}}{}^j,\text{Score}=1;\text{g}{}_{\text{A}}{}^i\ne \text{g}{}_{\text{B}}{}^j,\text{Score}=-1)(5)$

the highest value in the matrix H_{(n + 1)×(m + 1)} is chosen as sw(G_A,G_B). The similarity between microbes A and B is adopted by the same definition as Yamanishi et al. (2008), as follows:

$S_{\text{b}}(\mathrm{A},\mathrm{B})=\frac{sw({\text{G}}_{\text{A}},{\text{G}}_{\text{B}})}{\sqrt{sw({\text{G}}_{\text{A}},{\text{G}}_{\text{A}})\times sw({\text{G}}_{\text{B}},{\text{G}}_{\text{B}})}}(6)$

Based on microbe similarities, we can build a microbe similarity network Net_b, where nodes are microbes. There are edges between the microbes if these microbes associate with the same drug; the edges are weighted by microbe similarities.

Nearest-Neighbor Aggregator for Drug–Microbe Pair Embeddings

In this section, inspired by the idea of KNN [K-Nearest-Neighbor (Cover and Hart, 1967)], we learn the substructures of the bipartite graph network to obtain the embedding representations of drug–microbe pairs.

First, we construct the drug–microbe bipartite graph network, G=(D,B,E), where D={d₁,d₂,…,d_m} represents m drugs, B={b₁,b₂,…,b_n} represents n microbes, and each edge (e_ij) in edge set E connects two nodes that belong to two different sets of vertexes (i.e., i in D, j in B). We regard the DMAs as bidirectional links. That is, e_dx→bp denotes the edge pointing from the drug d_x to the microbe b_p, and e_bp→dx denotes the edge pointing from the microbe b_p to the drug d_x. Correspondingly, the nearest-neighbor aggregator contains two blocks (Figure 2), the microbe-specific drug neighbor aggregator (MsDNA), and the drug-specific microbe neighbor aggregator (DsMNA). Due to their architectures being similar, we only illustrate the MsDNA block in this section.

FIGURE 2

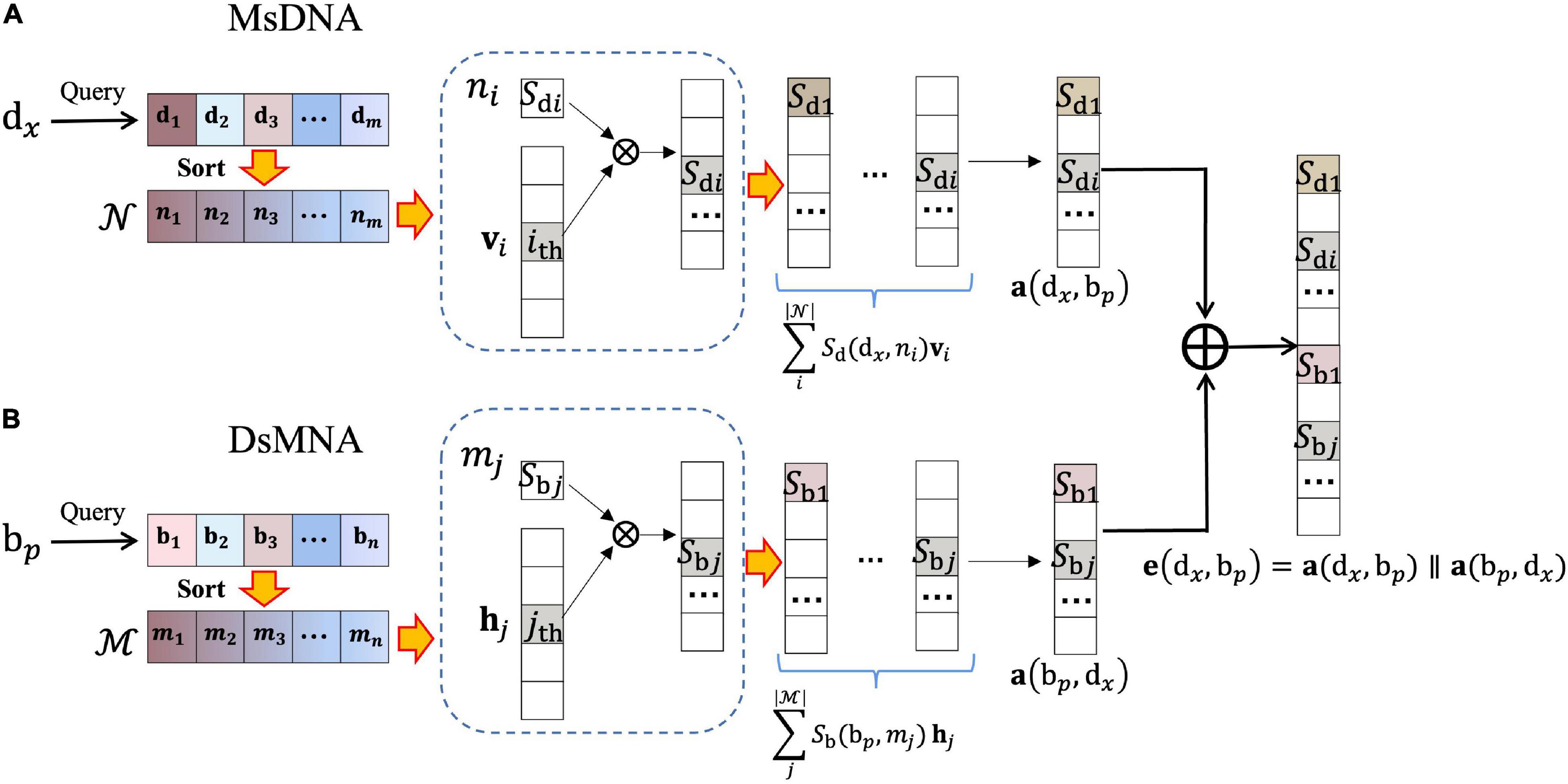
Figure 2. Nearest-Neighbor Aggregator block. (A) Microbe-specific drug neighbor aggregator (MsDNA); the embedding representation of the unidirectional edge, which is from the drug d_x to the microbe b_p. (B) Drug-specific microbe neighbor aggregator (DsMNA); the embedding representation of the unidirectional edge, which is from the microbe b_p to the drug d_x, where 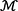^x⊆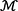 is a set of instantiated keywords, 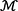^x denotes the neighbors of microbe b_p in the Net_b. S_b(b_p,m_j) denotes the similarity of b_p and m_j. h_j is the corresponding one-hot encoding vector of m_j.

Microbe-specific drug neighbor aggregator (Figure 2A) contains a virtual key dictionary; 𝒩={n₁,n₂,…,n_m} indicates all the drugs. In the dictionary, we imitate the idea of KNN to learn the substructures of the bipartite graph network, where virtual keys are sorted by their semantic nearest neighbors. In simple terms, n₁ denotes d_x itself, its nearest neighbor is the second key, and the farthest neighbor is the last key. The embedding representation of the edge, which is from drug d_x to microbe b_p, is formulated as follows:

$\mathbf{\text{a}}({\text{d}}_x,{\text{b}}_p)=\sum _i^{\left|𝒩\right|}{S}_{\text{d}}({\text{d}}_x,n_i){\mathbf{\text{v}}}_i(if{n}_i\notin {𝒩}^p,S_{\text{d}}({\text{d}}_x,n_i)=0)(7)$

where 𝒩^p⊆𝒩 is a set of instantiated keywords, and 𝒩^p denotes the neighbors of d_x in the Net_d. S_d(d_x,n_i) denotes the similarity of d_x and n_i, and v_i is the corresponding one-hot encoding vector of n_i (i.e., the one-hot encoding has a non-zero value only in the i_th element, and all other position elements are zero).

Similarly, DsMNA (Figure 2B) makes the single directional embedding representation from b_ptod_x as a(b_p,d_x). Then, the representation of drug–microbe pair could be encoded as

$\mathbf{\text{e}}({\text{d}}_x,{\text{b}}_p)=\left[\mathbf{\text{a}}({\text{d}}_x,{\text{b}}_p)\parallel \mathbf{\text{a}}({\text{b}}_p,{\text{d}}_x)\right](8)$

where e(d_x,b_p) is generated via the concatenation of bidirectional embedding, and ∥ is the concatenation operation. All the embedding representations of drug–microbe pairs could stack as a matrix E_k×g, where k is the number of all the drug–microbe pairs and g is the dimension of each embedding. The nearest-neighbor aggregator effectively learns the bipartite graph substructures, and E_k×g will be input into a feature attention block to select crucial features for achieving a better DMA prediction.

Feature Attention Block

To improve the performance of the prediction, we build the feature attention block (Figure 3) for updating the embedding of drug–microbe pairs.

FIGURE 3

Figure 3. Feature attention block. Input the representation matrix E_k×g into a set of DNNs, then we obtain an attention matrix M_k×gof drug–microbe embedding features. After the element-wise product operation of M_k×g and E_k×g, the final feature matrix ${\widetilde{\mathbf{\text{F}}}}_{k\times g}$ of the drug–microbe pairs is obtained.

Recall the equation of output feature representation in GAT (Velickovic et al., 2018):

$\overrightarrow{h_i^{\prime }}=\mathrm{\sigma }(\sum _{j\in {𝒦}_i}{\mathrm{\alpha }}_{ij}\mathbf{\text{W}}\overrightarrow{h_j})(9)$

where σ is a nonlinear activation function, 𝒦ⁱ is the first-order neighbors of node i (including i), α_ij is the coefficients computed by the attention mechanism, and W is a weight matrix. To make equation (9) easier to understand. We compute the coefficients as:

$\sum _{j\in {𝒦}_i}{\mathrm{\alpha }}_{ij}=\widetilde{\mathbf{\text{A}}}\odot \mathbf{\text{M}}(10)$

where $\widetilde{\mathbf{\text{A}}}=\mathbf{\text{A}}+\mathbf{\text{I}}$ is the adjacency matrix of the undirected graph G with added self-connections (Kipf and Welling, 2017), ⊙ is the element-wise product operation, and M is the attention matrix. Then, the layer-wise propagation rules in GAT can be formulated as:

${\mathbf{\text{H}}}^{(l+1)}=\mathrm{\sigma }(\left(\widetilde{\mathbf{\text{A}}}\odot \mathbf{\text{M}}\right){\mathbf{\text{H}}}^{(l)}{\mathbf{\text{W}}}^{(l)})(11)$

where σ is a nonlinear activation function, and W^(l) is the weight matrix of the l_th neural network layer.

Inspired by the conception of the layer-wise propagation rules in GAT, we calculate the augmented representation matrix ${\widetilde{\mathbf{\text{F}}}}_{k\times g}$ by

${\widetilde{\mathbf{\text{F}}}}_{k\times g}={\mathbf{\text{E}}}_{k\times g}\odot {\mathbf{\text{M}}}_{k\times g}(12)$

where E_k×g is the representation matrix of the drug–microbe pairs obtained from the nearest-neighbor aggregator, M_k×g is an attention matrix of E_k×g, and ⊙ is the element-wise product operation. We take the representation matrix E_k×g as a feature matrix F (F={f₁,f₂,…,f_g}), which is composed of g column vectors (f_i(i = 1,2,…,g)). The feature attention block mainly uses M_k×g to indicate the importance of features in the E_k×g. Each feature dimension f_i can be labeled as “selected” or “discarded” in a hard way, or be associated with a probability to be selected in a soft way; we employ DNNs to model the mapping by

${\mathbf{\text{m}}}_i=\text{DNNs}[{\mathbf{\text{f}}}_i](13)$

the DNN contains an input layer for each element of the feature dimension f_i and an output layer with sigmoid as its activation function.

In total, we build k×g DNNs to obtain M_k×g. The final feature matrix ${\widetilde{\mathbf{\text{F}}}}_{k\times g}$ of the drug–microbe pairs is obtained after the element-wise product operation of M_k×g and E_k×g. ${\widetilde{\mathbf{\text{F}}}}_{k\times g}$ is further fed into a predictor to achieve better predictive performance.

Predictor

To implement the link prediction in the drug–microbe bipartite graph network, an ordinary DNN is utilized as the binary predictor that contains an input layer for the embedding representation of drug–microbe pairs, a hidden layer with ReLU as its activation function, and the two-neuron output layer with Sigmoid as its activation function. The output layer generates a probability that indicates the association likelihood of the drug and the microbe. The probability is formulated as:

$P=\mathrm{\phi }(ℱ\left(\text{ReLU}[ℱ\left(\widetilde{\mathbf{\text{F}}}\right)]\right))(14)$

where φ is the sigmoid activation function, and ℱ(⋅) is the fully-connected layer.

The entire network of NNAN with the nearest-neighbor aggregator, feature attention weights, and DNN weights can be jointly optimized through the binary cross-entropy loss as follows:

$loss=\mathbf{\text{Y}}\text{log}(𝒟(\widetilde{\mathbf{\text{F}}}))+(1-\mathbf{\text{Y}})\text{log}(1-𝒟(\widetilde{\mathbf{\text{F}}}))+\mathrm{\lambda }ℛ(\mathrm{\theta })(15)$

where Y is the truth labels of drug–microbe pairs, 𝒟(⋅) is the DNN, θ denotes the weight parameters in the entire network, ℛ(⋅) is an L₂-norm, and λ is coefficient of the regularization item.

Experiments and Results

Data

In our experiments, two databases are collected from MDAD (Sun et al., 2018) and Zimmermann et al. (2019a), respectively. The former work MDAD (Sun et al., 2018) investigated 5,505 clinically or experimentally DMAs between 1,388 drugs and 180 microbes. After removing redundant information, these association entries are grouped into Database 1, which contains 999 drugs, 133 microbes, and 1,708 DMAs.

The latter work (Zimmermann et al., 2019a) originally studied how 76 kinds of human gut bacteria metabolize 271 oral drugs, and found that 176 out of 217 drugs are significantly consumed by at least one bacteria strain. These associations are grouped into Database 2, which includes 176 drugs, 76 bacteria, and 4,194 associations (These two databases are shown in Table 1).

TABLE 1

Table 1. The statistics of two databases.

Comparison

Since there are few existing approaches for predicting DMAs, we compare NNAN with three state-of-the-art methods, which were raised for bipartite link prediction.

• LAGCN (Yu et al., 2021b): A layer attention graph convolutional network for the drug–disease association prediction.

• NIMCGCN (Li et al., 2020): A neural inductive matrix completion with graph convolutional networks for miRNA–disease association prediction.

• GCNMDA (Long et al., 2020a): Predicting human microbe–drug associations via graph convolutional network with conditional random field.

To evaluate the performance of these methods, we regard the known DMA pairs as positive samples and unlabeled DMA pairs as negative samples (Peng et al., 2020; Li et al., 2022). We set up a 5-fold cross-validation scenario in which we randomly divide positive samples and negative samples into five groups, respectively. One group of positive samples and one group of negative samples are treated as test samples in turn for each round. The remaining groups are used for training purposes. Our model is trained by Gradient Descent Optimizer (Cauchy, 2009), with batch size 3,000 for 2,000 epochs, the initial learning rate is set to 0.9, and the regularization rate is set to 2e-4. We use AUROC (area under the receiver operating characteristic curve) and AUPRC (area under the precision-recall curve) as metrics to measure the DMA prediction performance. Moreover, we investigate the running time in terms of per epoch.

The comparison (Table 2) shows that NNAN obtains the best AUROC value (0.911) and the best AUPRC value (0.502) in Database 1. NNAN attains the next-highest AUROC value (0.902) and the best AUPRC value (0.840) in Database 2. To further present the performance of NNAN, we calculate the running time for one epoch of the baselines and NNAN, respectively. As presented, with the same computing equipment, NNAN takes the third-shortest running time in Database 1 and the shortest running time in Database 2. In general, we can see that NNAN are comparable in terms of AUROC, AUPRC, and computation time. It demonstrates that NNAN is superior to other methods on the databases we collected.

TABLE 2

Table 2. The performance comparison of DMA prediction.

Interpretability of Nearest Neighbor Attention Network

How does the NNAN interpret the hypothesis that “If a drug can associate with a microbe, the other drugs that associate with the microbe are usually the first l nearest neighbors to the drug.”

The model has two significant advantages to enhance interpretability. First, each column vector m_i of M_k×g indicates the global importance of each feature dimension f_i. Moreover, the element-wise product between E_k×g and M_k×g generates the importance map of embedding features.

We first use the MsDNA in the nearest-neighbor aggregator block to show how the representation of drug–microbe pairs can provide intuitive hints, on which embedding features lead to the association. For the queried drug d_x to the microbe b_p of associated, non-zero cells in the embedding representation of a(d_x,b_p) stand for its attention values derived from the drugs commonly linking b_p. Since the keys are sorted in descending order from the drug itself (n₁) to the farthest neighbor (n_m), the positions of non-zero cells are crucial to the final association.

Take Database 1 as an example. By calculating two average embedding vectors for approved DMAs and unlabeled drug–microbe pairs, we obtained a distribution along with the drug key dictionary from n₁ to n₆₆(Figure 4A). As illustrated, the significantly high values of embedding features occurring among the first l nearest neighbors reveal that a drug (d_x) associated with a specific microbe (b_p) can always find its top-l nearest neighbors among other drugs that associate with the same microbe. This observation demonstrates that a drug is possibly associated with the microbe if it has more non-zero value cells on the positions of the first l feature dimensions. This phenomenon could be caused by the fact that over 80% of approved drugs are of “follow-on” or “me-too” drugs. Due to high cost and high risk, the design of novel drugs, except for pioneer drugs, always starts from the structures of one or several existing drugs and then slightly modify them until meeting pharmacological needs (DiMasi and Faden, 2011). Analogously, the results of the DsMNA block along the microbe neighbor aggregator keys reveal that a microbe associated with a specific drug usually finds its near neighbors associated with the same drug.

FIGURE 4

Figure 4. Mensurable clues of embedding features to the association outcome. (A) The distribution of embedding features along with the sorted drug neighbor keys. (B) The distribution of feature importance along with sorted node neighbor keys. (C) The predictive performance with top-l features concerning l in terms of AUROC. (D) The predictive performance in terms of AUPRC.

Moreover, we illustrate how the feature attention matrix M_k×g can provide data-driven hints on which embedding features lead to the association. Since a high-value cell in M_k×g stands for a crucial feature dimension contributing to determine the association between a queried drug and a microbe, the importance m(i,:) of each feature f_i can be measured by the average of value entries in the i_th column of M_k×g (Figure 4B). The importance distribution along with the sorted drug neighbor keys illustrates that highly important features are usually located among the first l nearest neighbors. In addition, the predictive performance with top-l features concerning l is investigated (Figures 4C,D). The number of top features is tuned in the list {1, 6, 11, 16,…, 66}. As l is increasing to 16, the performance increases sharply in the top-l features. When l keeps increasing, the performance increases slowly, then even decreases at the greater value of l. Again, this illustration demonstrates that the selection of crucial features is significantly better than the set of all features.

In summary, both embedding feature matrix E_k×g, which is generated by the nearest-neighbor aggregator, and its feature attention matrix M_k×g provide mensurable clues to the association outcome.

To complement the verification of the interpretability of NNAN, we selected one microbe (i.e., Staphylococcus aureus, which is a common causative agent of food poisoning) and one drug (i.e., Hexyl gallate, which has strong antimalarial activity against Plasmodium falciparum) from Database 1, and there was an association between them (de Lima Pimenta et al., 2013). We calculated the similarities between drugs using Hexyl gallate as the reference molecule and sorted the drugs in order of their similarity to Hexyl gallate. Then, we picked the top 10 drugs and checked whether these drugs were associated with S. aureus in Database 1. Finally, we found out that 8 out of the top 10 ranked drugs for Hexyl gallate are associated with S. aureus (Table 3).

TABLE 3

Table 3. The associations among Staphylococcus aureus and ten drugs.

From Table 3, it is clear that a drug tends to associate with a microbe if it finds its top-l near neighbors associate with the same microbe. Moreover, the higher the ranks of its top-l near neighbors are, the more possible it is to associate with the microbe. This conclusion would be helpful to screen drug-like molecules.

Case Study of Novel Prediction

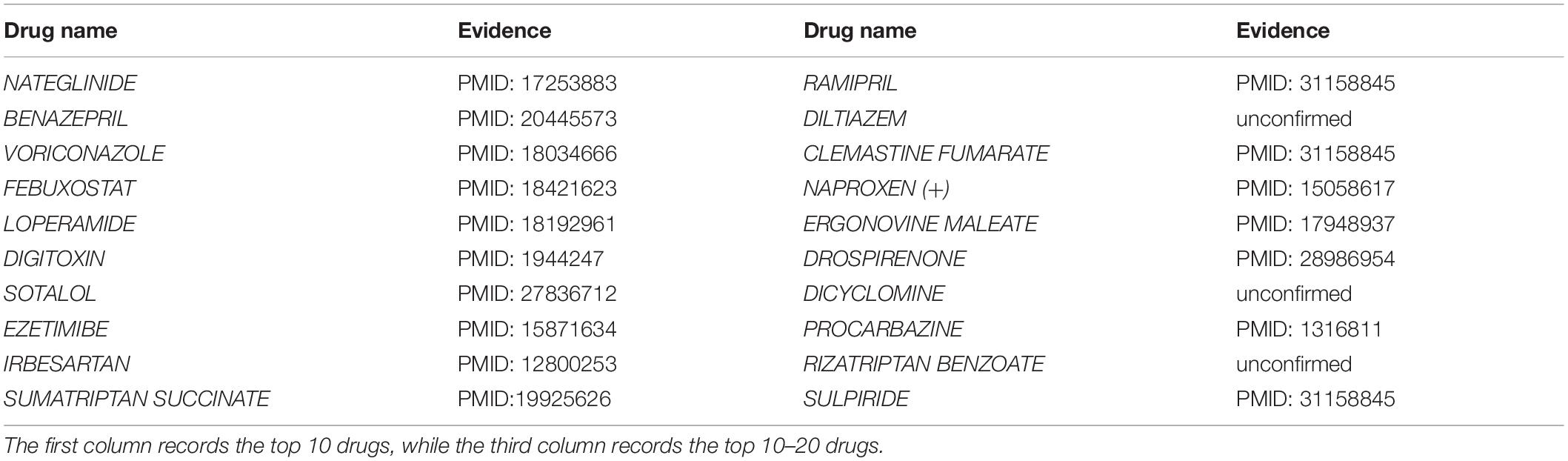
To further confirm the effectiveness of NNAN, we apply our model on one microbe (i.e., Bacteroides fragilis) in Database 2 as a case study. Bacteroides are the major human colonic commensal microbes (Kuwahara et al., 2004). Although B. fragilis is rare in comparison to other Bacteroides species, it is the most prevalent clinical isolation of the genus (Salyers, 1984). Thus, we select B. fragilis for the case study experiment.

Nearest neighbor attention network predicts potential associations between drugs and B. fragilis by scoring drug–microbe pairs (probability). The higher the score, the more likely the association between the drugs and B. fragilis exists. In the case study, we verified whether NNAN could find out potential linkages between B. fragilis and drugs. According to the ranking of potential DMAs, we validated the top 10, 20, and 50 predicted candidate drugs by a literature search. Eventually, the validation indicates that 10, 17, and 38 out of the top 10, 20, and 50 predicted drugs associated with B. fragilis were found by previously published literature. For example, 85% out of the top 20 predicted candidate drugs for B. fragilis are validated (Table 4); more details can be found in the Supplementary Material. These results of prediction demonstrate the ability of NNAN for predicting potential DMAs in practice.

TABLE 4

Table 4. Top 20 predicted drugs associated with Bacteroides fragilis.

Conclusion

This work has introduced NNAN, a deep learning-based bipartite graph network model to predict potential associations between drugs and microbes. NNAN calculates drug similarities using the weights of feature substructures. It provides an embedding representation based on the near neighbor aggregation for drug–microbe pairs, to enhance the explanation of DMAs. In addition, the model provides a crucial feature selection attention matrix for achieving more accurate predictions. These three components of NNAN jointly reveal that a drug associated with a specific microbe can always find its top-l near neighbors among other drugs that associate with the same microbe. Moreover, they uncover that the higher the ranks of its top-l near neighbors are, the more possible it is to associate with the microbe. Under both a cross-validation setting and a realistic potential linkage discovery setting, the empirical comparison of the proposed framework with three state-of-the-art baselines demonstrates that NNAN has significant competitive performance in predicting DMA. In addition, the framework of our model can also be evaluated in more similar biological issues (e.g., miRNA–disease, drug–target, and compound–protein associations prediction). Furthermore, there is still room to improve the model. We can set new experimental scenarios, which identify the DMAs for new drugs or new microbes, and can also integrate more biological databases to enrich the information of DMAs to improve the predictive ability.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

J-YS and HY designed and supervised the study. BZ engaged in study design, drafted the manuscript, performed experiments, and analyzed data. YX coded and implemented the model, performed experiments. PZ assisted with performing experiments. S-MY assisted with supervising the study. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by Shaanxi Provincial Key R&D Program, China (No. 2020KW-063, PI: J-YS) and National Natural Science Foundation of China (No. 61872297, PI: J-YS).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmicb.2022.846915/full#supplementary-material

References

Aagaard, K., Petrosino, J., Keitel, W., Watson, M., Katancik, J., Garcia, N., et al. (2013). The human microbiome project strategy for comprehensive sampling of the human microbiome and why it matters. FASEB J. 27, 1012–1022. doi: 10.1096/fj.12-220806

PubMed Abstract | CrossRef Full Text | Google Scholar

Altschul, S. F., Gish, W., Miller, W., Myers, E. W., and Lipman, D. J. (1990). Basic local alignment search tool. J. Mol. Biol. 215, 403–410.

Google Scholar

Bang, S., Ho Jhee, J., and Shin, H. (2021). Polypharmacy side effect prediction with enhanced interpretability based on graph feature attention network. Bioinformatics. 37, 2955–2962 doi: 10.1093/bioinformatics/btab174

PubMed Abstract | CrossRef Full Text | Google Scholar

Cauchy, A.-L. (2009). ANALYSE MATHMATIQUE. MÈthodc gÈnÈrale pour la rÈsolution des SystËmes d’Èquations SimultanÈes. Cambridge: Cambridge University Press.

Google Scholar

Cover, T. M., and Hart, P. E. (1967). Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 13, 21–27.

Google Scholar

de Lima Pimenta, A., Chiaradia-Delatorre, L. D., Mascarello, A., de Oliveira, K. A., Leal, P. C., Yunes, R. A., et al. (2013). Synthetic organic compounds with potential for bacterial biofilm inhibition, a path for the identification of compounds interfering with quorum sensing. Int. J. Antimicrob. Agents 42, 519–523. doi: 10.1016/j.ijantimicag.2013.07.006

PubMed Abstract | CrossRef Full Text | Google Scholar

DiMasi, J. A., and Faden, L. B. (2011). Competitiveness in follow-on drug R&D: a race or imitation? Nat. Rev. Drug Discov. 10, 23–27. doi: 10.1038/nrd3296

PubMed Abstract | CrossRef Full Text | Google Scholar

Haiser, H. J., Gootenberg, D. B., Chatman, K., Sirasani, G., Balskus, E. P., and Turnbaugh, P. J. (2013). Predicting and manipulating cardiac drug inactivation by the human gut bacterium Eggerthella lenta. Science 341, 295–298. doi: 10.1126/science.1235872

PubMed Abstract | CrossRef Full Text | Google Scholar

He, B. S., Peng, L. H., and Li, Z. (2018). Human microbe-disease association prediction with graph regularized non-negative matrix factorization. Front. Microbiol. 9:2560. doi: 10.3389/fmicb.2018.02560

PubMed Abstract | CrossRef Full Text | Google Scholar

Ioffe, S. (2010). “Improved consistent sampling, weighted minhash and L1 sketching,” in Proceedings of the 2010 IEEE International Conference on Data Mining, Sydney, 246–255.

Google Scholar

Jaacks, L. M., Vandevijvere, S., Pan, A., McGowan, C. J., Wallace, C., Imamura, F., et al. (2019). The obesity transition: stages of the global epidemic. Lancet Diabetes Endocrinol. 7, 231–240. doi: 10.1016/S2213-8587(19)30026-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Kashyap, P. C., Chia, N., Nelson, H., Segal, E., and Elinav, E. (2017). Microbiome at the Frontier of personalized medicine. Mayo Clin. Proc. 92, 1855–1864. doi: 10.1016/j.mayocp.2017.10.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Katz, L. (1953). A new status index derived from sociometric analysis. Psychometrika 18, 39–43. doi: 10.1007/bf02289026

CrossRef Full Text | Google Scholar

Khalili, H., Godwin, A., Choi, J. W., Lever, R., and Brocchini, S. (2012). Comparative binding of disulfide-bridged PEG-Fabs. Bioconjug. Chem. 23, 2262–2277. doi: 10.1021/bc300372r

PubMed Abstract | CrossRef Full Text | Google Scholar

Kipf, T. N., and Welling, M. (2017). Semi-supervised classification with graph convolutional networks. arXiv [Preprint] doi: 10.48550/arXiv.1609.02907

CrossRef Full Text | Google Scholar

Kuwahara, T., Yamashita, A., Hirakawa, H., Nakayama, H., Toh, H., Okada, N., et al. (2004). Genomic analysis of Bacteroides fragilis reveals extensive DNA inversions regulating cell surface adaptation. Proc. Natl. Acad. Sci. U S A. 101, 14919–14924. doi: 10.1073/pnas.0404172101

PubMed Abstract | CrossRef Full Text | Google Scholar

Landrum. (2010). RDKit: Open-Source Cheminformatics. Release 2014.03.1.

Google Scholar

Li, F., Dong, S., Leier, A., Han, M., Xu, J., et al. (2022). Positive-unlabeled learning in bioinformatics and computational biology: a brief review. Brief. Bioinform. 23:bbab461. doi: 10.1093/bib/bbab461

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Zhang, S., Liu, T., Ning, C., Zhang, Z., and Zhou, W. (2020). Neural inductive matrix completion with graph convolutional networks for miRNA-disease association prediction. Bioinformatics 36, 2538–2546. doi: 10.1093/bioinformatics/btz965

PubMed Abstract | CrossRef Full Text | Google Scholar

Lihong, P., Wang, C., Tian, X., Zhou, L., and Li, K. (2021). Finding lncRNA-protein interactions based on deep learning with dual-net neural architecture. IEEE/ACM Trans. Comput. Biol. Bioinform. 14:1. doi: 10.1109/TCBB.2021.3116232

PubMed Abstract | CrossRef Full Text | Google Scholar

Long, Y., and Luo, J. (2020). Association mining to identify microbe drug interactions based on heterogeneous network embedding representation. IEEE J. Biomed. Health Informatics 25, 266–275. doi: 10.1109/JBHI.2020.2998906

PubMed Abstract | CrossRef Full Text | Google Scholar

Long, Y., Wu, M., Kwoh, C. K., Luo, J., and Li, X. (2020a). Predicting human microbe-drug associations via graph convolutional network with conditional random field. Bioinformatics 36, 4918–4927. doi: 10.1093/bioinformatics/btaa598

PubMed Abstract | CrossRef Full Text | Google Scholar

Long, Y., Wu, M., Liu, Y., Kwoh, C. K., Luo, J., and Li, X. (2020b). Ensembling graph attention networks for human microbe-drug association prediction. Bioinformatics 36(Suppl_2), i779–i786. doi: 10.1093/bioinformatics/btaa891

PubMed Abstract | CrossRef Full Text | Google Scholar

Lynch, S. V., and Pedersen, O. (2016). The human intestinal microbiome in health and disease. N. Engl. J. Med. 375, 2369–2379.

Google Scholar

Peng, L., Shen, L., Liao, L., Liu, G., and Zhou, L. (2020). RNMFMDA: a microbe-disease association identification method based on reliable negative sample selection and logistic matrix factorization with neighborhood regularization. Front. Microbiol. 11:592430. doi: 10.3389/fmicb.2020.592430

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, L. H., Yin, J., Zhou, L., Liu, M. X., and Zhao, Y. (2018). Human microbe-disease association prediction based on adaptive boosting. Front. Microbiol. 9:2440. doi: 10.3389/fmicb.2018.02440

PubMed Abstract | CrossRef Full Text | Google Scholar

Riniker, S., and Landrum, G. A. (2013). Similarity maps – a visualization strategy for molecular fingerprints and machine-learning methods. J. Cheminform. 5:43. doi: 10.1186/1758-2946-5-43

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogers, D., and Hahn, M. (2010). Extended-connectivity fingerprints. J. Chem. Inf. Model. 50, 742–754. doi: 10.1021/ci100050t

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogers, D. J., and Tanimoto, T. T. A. (1960). Computer program for classifying plants. Science 132, 1115–1118. doi: 10.1126/science.132.3434.1115

PubMed Abstract | CrossRef Full Text | Google Scholar

Salyers, A. A. (1984). Bacteroides of the human lower intestinal tract. Annu. Rev. Microbiol. 38, 293–313. doi: 10.1146/annurev.mi.38.100184.001453

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwabe, R. F., and Jobin, C. (2013). The microbiome and cancer. Nat. Rev. Cancer. 13, 800–812.

Google Scholar

Smith, T. F., and Waterman, M. S. (1981). Identification of common molecular subsequences. J. Mol. Biol. 147, 195–197. doi: 10.1016/0022-2836(81)90087-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Sousa, T., Yadav, V., Zann, V., Borde, A., Abrahamsson, B., and Basit, A. W. (2014). On the colonic bacterial metabolism of azo-bonded prodrugsof 5-aminosalicylic acid. J. Pharm. Sci. 103, 3171–3175. doi: 10.1002/jps.24103

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, Y. Z., Zhang, D. H., Cai, S. B., Ming, Z., Li, J. Q., and Chen, X. M. D. A. D. (2018). A special resource for microbe-drug associations. Front. Cell. Infect. Microbiol. 8:424. doi: 10.3389/fcimb.2018.00424

PubMed Abstract | CrossRef Full Text | Google Scholar

Turnbaugh, P. J., Ley, R. E., Hamady, M., Fraser-Liggett, C. M., Knight, R., and Gordon, J. I. (2007). The human microbiome project. Nature 449, 804–810.

Google Scholar

Velickovic, P., Cucurull, G., Casanova, A., Romero, A., Liò, P., and Bengio, Y. (2018). Graph attention networks. arXiv [Preprint]. doi: 10.48550/arXiv.1710.10903

CrossRef Full Text | Google Scholar

Yamanishi, Y., Araki, M., Gutteridge, A., Honda, W., and Kanehisa, M. (2008). Prediction of drug-target interaction networks from the integration of chemical and genomic spaces. Bioinformatics 24, i232–i240.

Google Scholar

Younossi, Z. M., Koenig, A. B., Abdelatif, D., Fazel, Y., Henry, L., and Wymer, M. (2016). Global epidemiology of nonalcoholic fatty liver disease-meta-analytic assessment of prevalence, incidence, and outcomes. Hepatology 64, 73–84. doi: 10.1002/hep.28431

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, H., Dong, W., and Shi, J. Y. (2021a). RANEDDI: Relation-aware network embedding for prediction of drug-drug interactions. Inf. Sci. 582, 167–180.

Google Scholar

Yu, Z., Huang, F., Zhao, X., Xiao, W., and Zhang, W. (2021b). Predicting drug-disease associations through layer attention graph convolutional network. Brief. Bioinform. 22:bbaa243. doi: 10.1093/bib/bbaa243

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L., Yang, P., Feng, H., Zhao, Q., and Liu, H. (2021). Using network distance analysis to predict lncRNA-miRNA Interactions. Interdiscip. Sci. 13, 535–545. doi: 10.1007/s12539-021-00458-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Guan, J., and Zhou, S. (2021). FraGAT: a fragment-oriented multi-scale graph attention model for molecular property prediction. Bioinformatics 37, 2981–2987. doi: 10.1093/bioinformatics/btab195

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, Y., Ley, S. H., and Hu, F. B. (2018). Global aetiology and epidemiology of type 2 diabetes mellitus and its complications. Nat. Rev. Endocrinol. 14, 88–98. doi: 10.1038/nrendo.2017.151

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, L., Wang, Z., Tian, X., and Peng, L. (2021). LPI-deepGBDT: a multiple-layer deep framework based on gradient boosting decision trees for lncRNA-protein interaction identification. BMC Bioinform. 22:479. doi: 10.1186/s12859-021-04399-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, L., Duan, G., Yan, C., and Wang, J. (2019). “Prediction of microbe-drug associations based on KATZ measure,” in Proceedings of the 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), San Diego, CA.

Google Scholar

Zimmermann, M., Zimmermann-Kogadeeva, M., Wegmann, R., and Goodman, A. L. (2019b). Separating host and microbiome contributions to drug pharmacokinetics and toxicity. Science 363:eaat9931. doi: 10.1126/science.aat9931

PubMed Abstract | CrossRef Full Text | Google Scholar

Zimmermann, M., Zimmermann-Kogadeeva, M., Wegmann, R., and Goodman, A. L. (2019a). Mapping human microbiome drug metabolism by gut bacteria and their genes. Nature 570, 462–467. doi: 10.1038/s41586-019-1291-3

PubMed Abstract | CrossRef Full Text | Google Scholar