The influence of extracellular superoxide on iron redox chemistry and bioavailability to aquatic microorganisms

Superoxide, the one-electron reduced form of dioxygen, is produced in the extracellular milieu of aquatic microbes through a range of abiotic chemical processes and also by microbes themselves. Due to its ability to promote both oxidative and reductive reactions, superoxide may have a profound impact on the redox state of iron, potentially influencing iron solubility, complex speciation, and bioavailability. The interplay between iron, superoxide, and oxygen may also produce a cascade of other highly reactive transients in oxygenated natural waters. For microbes, the overall effect of reactions between superoxide and iron may be deleterious or beneficial, depending on the organism and its chemical environment. Here I critically discuss recent advances in understanding: (i) sources of extracellular superoxide in natural waters, with a particular emphasis on microbial generation; (ii) the chemistry of reactions between superoxide and iron; and (iii) the influence of these processes on iron bioavailability and microbial iron nutrition.

Introduction

Superoxide $\left({\text{O}}_2^{-}\right)$, an anion resulting from the transfer of one-electron to a molecule of oxygen, was first identified by Edward Neuman, a postdoctoral researcher working with Linus Pauling, in 1934 (Neuman, 1934) as part of Pauling’s ongoing interest in the nature of the chemical bond (Pauling, 1979). In aqueous solutions, superoxide exists in equilibrium with its conjugate acid, the hydroperoxyl (or perhydroxyl) radical $\text{(HO}{\text{O}}^{\bullet }\text{)}$ (Bielski et al., 1985). The anion dominates the equilibrium in solutions whose pH is above the pK_a = 4.8 (Bielski et al., 1985). This is the case in the majority of natural surface waters, and at pH ∼8.1, which is typical of marine waters and many carbonate-buffered freshwaters, superoxide is ∼2000-fold more abundant than hydroperoxyl. To distinguish between the superoxide anion and “total” superoxide (i.e., both ${\text{O}}_2^{-}$ and $\text{HO}{\text{O}}^{\bullet }$), I will represent “total” superoxide as ${\text{O}}_2^{-*}.$

${\text{O}}_2^{-*}$ has two chemical properties that produce a special relationship with Fe in natural aquatic environments. First, it may act as both a reductant (via its oxidation to O₂) and oxidant (via its reduction to H₂O₂), with the redox potentials of the ${\text{O}}_2/{\text{O}}_2^{-*}$ and ${\text{O}}_2^{-*}/{\text{H}}_{\text{2}}{\text{O}}_{\text{2}}$ couples in natural waters around neutral pH poised in such a way that ${\text{O}}_2^{-*}$ is thermodynamically able to react with a vast range of Fe complexes (Pierre et al., 2002). The second property arises from its unusual electronic structure. Despite possessing an odd number of valence shell electrons, the ${\text{O}}_2^{-}$ anion is resonance stabilized by virtue of its symmetry and exhibits very little free radical character (Pauling, 1931; Neuman, 1934; Sawyer, 1991); hence I follow the convention here of omitting the free radical symbol and representing the superoxide anion as ${\text{O}}_2^{-}.$ Thus in natural waters around pH 8 where the relatively unreactive ${\text{O}}_2^{-}$ dominates over $\text{HO}{\text{O}}^{\bullet },$ and in the absence of other suitably reactive partners, ${\text{O}}_2^{-*}$ has a half-life of tens of seconds to hours and has been measured to accumulate to typical concentrations in the range of 10–1000 pM (Rose et al., 2008b, 2010; Hansard et al., 2010; Shaked et al., 2010). These lifetimes are sufficiently long to ensure that ${\text{O}}_2^{-*}$ can diffuse well away from the site of its production, enabling it to influence local redox chemistry on a spatial scale that is biologically significant, while typical concentrations are sufficiently high to ensure that it can react at environmentally relevant rates. It is this critical balance between longevity and reactivity that renders ${\text{O}}_2^{-*}$ one of a select few extracellular reducing agents in natural waters that are able to exert a biologically significant influence on local redox chemistry. The combination of the overlapping redox potentials of the ${\text{O}}_2/{\text{O}}_2^{-*}$ couple with the redox potentials of wide range of couples of Fe(II)/Fe(III) species, and the ability of ${\text{O}}_2^{-*}$ to persist at sufficiently high concentrations, ensures that the fates of ${\text{O}}_2^{-*}$ and Fe are often closely tied in environmental systems, and also in many intracellular biological systems, to the extent that they have been called “partners in crime” (Liochev and Fridovich, 1999).

The existence of ${\text{O}}_2^{-*}$ has thus been known for nearly 90 years, initially being studied largely as a chemical curiosity due to its unusual electronic structure. In the 1960s, its importance in the aqueous intracellular environment was established with the discovery of superoxide dismutase (SOD), an enzyme whose role is to destroy ${\text{O}}_2^{-*}.$ The biological importance of ${\text{O}}_2^{-*}$ has been further reinforced by the discovery that SOD appears essential in aerobic organisms (McCord et al., 1971), and is found in nearly all aerobic forms of life (Wolfe-Simon et al., 2005) as well as many anaerobes (Gregory et al., 1978). Production of ${\text{O}}_2^{-*}$ in the intracellular environment, its reactions with Fe, and effects on biological processes, have consequently been extensively studied over the past 50 years (see, for example, Sawyer and Gibian, 1979; Sawyer and Valentine, 1981; Fridovich, 1986; Afanas’ev, 1989; Winterbourn, 1995). However it is only since the 1980s that the potential role of ${\text{O}}_2^{-*}$ in the aqueous extracellular environment has been examined in detail. Baxter and Carey (1983) established that ${\text{O}}_2^{-*}$ was formed during photolysis of humic substances in natural waters, while further pioneering work by Zika (Petasne and Zika, 1987; Micinski et al., 1993) and Zafiriou (1990) established that ${\text{O}}_2^{-*}$ occurs in marine waters, where it may participate in reactions with a range of biologically important compounds. There has been renewed interest in the role of ${\text{O}}_2^{-*}$ as a redox agent in natural waters in the last decade primarily because the development of new highly sensitive, rapid, and convenient analytical techniques (e.g., chemiluminescence of MCLA and its derivatives, with detection limits on the order of a few picomolar; Nakano et al., 1986; Nakano, 1998; Teranishi, 2007), has allowed determination of ${\text{O}}_2^{-*}$ concentrations (Rose et al., 2008a) and production rates (Godrant et al., 2009; Milne et al., 2009) at environmentally relevant values. The role of ${\text{O}}_2^{-*}$ was first accounted for in models of Fe speciation and bioavailability in natural waters by Miller et al. (1995), with increasing recognition of its potential importance reflected by inclusion of reactions between ${\text{O}}_2^{-*}$ and Fe in several more recent models (Weber et al., 2005, 2007; Fan, 2008).

The primary purpose of this paper is to provide a detailed overview of the ways in which ${\text{O}}_2^{-*}$ in the external milieu of microorganisms can modulate the chemical speciation of Fe, and thereby influence its biological availability. While drawing on some of the pioneering work on aqueous ${\text{O}}_2^{-*}$ chemistry in the intracellular environment (including its reactions with Fe), the scope of the paper will be limited primarily to the extracellular environment in natural waters. In addition, while the paper is intended to consider the influence of extracellular superoxide on iron redox chemistry and bioavailability to aquatic microorganisms in all natural waters, it is relatively biased toward marine systems, because it is in these systems that most recent advances on the subject have occurred. While many other aspects of ${\text{O}}_2^{-*}$ chemistry in natural waters are still being unraveled, including its role in cycles of other elements, this paper will consider only the role of ${\text{O}}_2^{-*}$ in modulating Fe chemistry. In particular, the following issues will be addressed with an attempt to identify major knowledge gaps and critical research questions where possible:

1. How is ${\text{O}}_2^{-*}$ produced in the extracellular milieu in natural waters?

2. By what mechanisms, and to what degree, can ${\text{O}}_2^{-*}$ modulate Fe chemistry in the extracellular environment?

3. How can ${\text{O}}_2^{-*}$ influence Fe bioavailability to microorganisms in aquatic environments, through direct and indirect means?

Sources of Extracellular Superoxide in Natural Waters

Overview

Theoretically, ${\text{O}}_2^{-*}$ can be produced via either the one-electron reduction of O₂ or the one-electron oxidation of H₂O₂. In practice, reduction of O₂ appears to be the dominant pathway for ${\text{O}}_2^{-*}$ production in natural waters, though oxidation of H₂O₂ has been shown to occur under some conditions (Moffett and Zafiriou, 1990). Like ${\text{O}}_2^{-},$ the dioxygen molecule also possesses an unusual electronic structure, with its lowest energetic state (ground state) possessing two unpaired electrons with parallel spins, i.e., its ground state is a triplet state biradical (Sawyer, 1991). Quantum mechanical restrictions (the Pauli exclusion principle) dictate that, under typical environmental conditions, triplet state dioxygen can react only extremely slowly with molecules possessing singlet state electronic configurations (e.g., most organic compounds), but much more readily with free radicals (e.g., organic radicals and transition metal ions), such that the reduction of dioxygen must proceed primarily via single electron transfer steps (Fridovich, 1998). This implies that reduction of dioxygen should always result in ${\text{O}}_2^{-*}$ production.

Attempting to identify sources of ${\text{O}}_2^{-*}$ in oxygenated waters is complicated, because the redox cycling of a range of relatively labile redox couples are intimately coupled in oxygenated natural waters; thus, trying to establish which redox reaction governs the system behavior is like the “chicken and egg” question of which came first. A common property of these labile redox-active compounds (LRACs) is that they are sufficiently labile to accept and donate their cargo of electrons, but also sufficiently long-lived to enable transport on biologically relevant spatial scales. Three major processes result in the occurrence of reduced LRACs in oxygenated surface waters: abiotic photochemistry, biological activity, and transport of reduced LRACs into (at least partially) oxygenated surface waters from other environments (e.g., at sediment-water interfaces, discharge of anoxic groundwaters, rainwater deposition, etc.). In the case of biological processes, the “ultimate” source of electrons is usually (but not always) water; in the case of abiotic photochemistry it is usually organic compounds, which are themselves often (although not always) derived from biological activity. Biological reduction in oxygenated waters is also predominantly powered ultimately via solar energy (either through photosynthesis, or respiration of reduced substrates that have been previously been produced by photosynthesis). In oxygenated waters, ${\text{O}}_2^{-*}$ can then be produced by reduction of O₂ directly through one of these processes, or through reduction of another LRAC that then reacts with O₂ to yield ${\text{O}}_2^{-*}.$ Thus the vast majority of ${\text{O}}_2^{-*}$ production in natural waters is driven ultimately by solar radiation, but the path by which this solar energy ultimately induces reduction of O₂ to ${\text{O}}_2^{-*}$ varies (Figure 1).

FIGURE 1

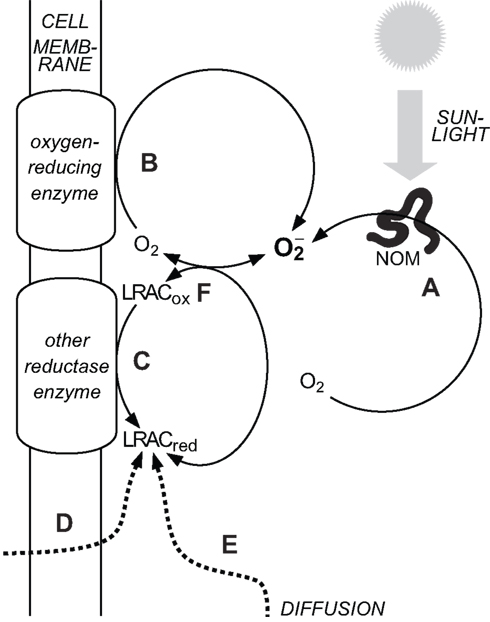
Figure 1. Major sources of ${\text{O}}_{\text{2}}^{-*}$ in natural waters. (A) Abiotic, photochemical oxidation of natural organic matter (NOM) with concomitant reduction of O₂. (B) Biological reduction of O₂ in the extracellular milieu via cell surface enzymes. (C) Biological reduction of oxidized labile redox-active compounds (LRAC_ox) in the extracellular milieu to form reduced labile redox-active compounds (LRAC_red) that subsequently reduce O₂ to ${\text{O}}_2^{-*}.$(D) Biological release of LRAC_red into the extracellular milieu that subsequently reduce O₂ to ${\text{O}}_2^{-*}.$ (E) Diffusion of LRAC_red produced under suboxic conditions into more oxygenated waters. (F) The ${\text{O}}_2/{\text{O}}_2^{-*}$ couple readily exchanges electrons with a range of other labile redox-active compounds in the extracellular milieu. Decay pathways for ${\text{O}}_2^{-*}$ are not shown.

The main pathways for reduction of O₂ to ${\text{O}}_2^{-*}$ can thus be broadly grouped into abiotic thermal (“dark”) processes, abiotic photochemical processes, and biologically mediated processes. Until recently, abiotic photochemistry in surface waters was thought to be the major pathway for ${\text{O}}_2^{-*}$ production in the extracellular environment (Cooper et al., 1989). A growing body of work has shown that aquatic microorganisms can also produce ${\text{O}}_2^{-*}$ extracellularly, and that the flux via this pathway may be at least as great as that via abiotic photochemistry (Hansard et al., 2010; Rose et al., 2010). However abiotic photochemistry is still likely to result in a non-negligible contribution to total extracellular superoxide production (ESP) in most sunlit waters, and in some cases may be the dominant source. The contribution of abiotic thermal production (through oxygenation of reduced LRACs) to overall rates of ESP in natural waters is unknown, although the observation that filtration to remove cells (and other particulates) does not always completely inhibit ESP (e.g., Rose et al., 2010) suggests that it may be substantial in some environments. These pathways are now considered in more detail.

Abiotic Thermal (“Dark”) Production

${\text{O}}_2^{-*}$ can theoretically be produced by oxygenation of a range of reduced LRACs that may occur in natural waters. The oxygenation of reduced metals [e.g., Fe(II), Mn(II), V(II), Cr(II), Cu(I), and Co(II)] has been proposed to generally occur via the Haber–Weiss mechanism (Haber and Weiss, 1934), resulting in the production of ${\text{O}}_2^{-}$ after the first step:

${\text{M}}^{n+}+{\text{O}}_2\to {\text{M}}^{\left(n+1\right)+}+{\text{O}}_2^{-}$(1)

Where Mⁿ⁺ represents the reduced form of the metal and M⁽ⁿ⁺¹⁾⁺ its oxidized form.

However it is not certain that these electron transfer steps always result in release of the free intermediate, as ${\text{O}}_2^{-}$ and peroxide anions $\left({\text{O}}_{\text{2}}^{\text{2}-}\right)$ both possess coordinative properties and may potentially remain bound in the inner coordination sphere of the oxidized metal center. Using computational chemistry methods, Rosso and Morgan (2002) concluded that V²⁺, Co²⁺, and Fe²⁺ were likely to react with O₂ via an outer-sphere mechanism, such that ${\text{O}}_2^{-}$ would be formed outside the inner coordination sphere (and presumably be able to diffuse into the bulk medium as the free anion), while Mn²⁺, Cr²⁺, and hydrolyzed Fe(II) species were suggested to react with O₂ via an inner-sphere process, such that ${\text{O}}_2^{-}$ would initially be coordinated to the metal center (Rosso and Morgan, 2002). Fe(II) complexed by EDTA and similar ligands also appears to react with O₂ via an inner-sphere process (Zang and van Eldik, 1990; Seibig and van Eldik, 1997).

Whether ${\text{O}}_2^{-*}$ formed in this way could subsequently participate in other reactions likely depends on how rapidly it can escape from the inner coordination sphere after electron transfer is complete. It is unclear how Fe(II) in natural waters might behave, but complexation of Fe(II) by natural organic matter (NOM) appears to substantially modify its oxygenation kinetics (e.g., Rose and Waite, 2003a and references therein), suggesting that further investigation of this issue is needed, ideally through both experimental and computational means. Hereafter, it will be assumed that reduction of O₂ ultimately results in production of unbound ${\text{O}}_2^{-*},$ even if it is initially formed in the inner coordination sphere of a metal complex. However, this uncertainty in our understanding of ${\text{O}}_2^{-*}$ behavior needs to be resolved in order to fully evaluate the relationship between ${\text{O}}_2^{-*}$ and Fe bioavailabilty in natural waters.

Other reduced LRACs in natural waters include reduced sulfur species (RSS) such as thiols and sulfides, and some reduced organic moieties. While the contribution of such species to ESP has not yet been evaluated, RSS may be found at measurable concentrations in oxic waters (Bowles et al., 2003; Luther and Rickard, 2005; Rickard and Luther, 2006) and at least some RSS yield ${\text{O}}_2^{-*}$ as a result of oxygenation (Rao et al., 1990). Certain redox-active moieties within NOM also react readily with oxygen (Ratasuk and Nanny, 2007; Aeschbacher et al., 2010), potentially yielding ${\text{O}}_2^{-*}$ (discussed further in the following section). The oxygenation chemistry (particularly thermodynamics) of a range of major LRACs present in natural waters has recently been described in considerable detail by Luther (2010), while the thermodynamics of the $\text{Fe}/{\text{O}}_2/{\text{O}}_2^{-*}$ system is discussed in detail by Pierre et al. (Pierre and Fontecave, 1999; Pierre et al., 2002).

Photochemical Production

Measured rates of photochemical ${\text{O}}_2^{-*}$ production in natural marine waters have typically been in the range of ∼0.3–500 nM h⁻¹ (Petasne and Zika, 1987; Micinski et al., 1993; Shaked et al., 2010). Rates of ${\text{O}}_2^{-*}$ production in natural freshwaters have not been reported in the literature, although laboratory experiments using simulated freshwater systems yielded similar rates (Garg et al., 2011a). The mechanism of abiotic photochemical ${\text{O}}_2^{-*}$ production from NOM has usually been represented by a reaction in which NOM is photoexcited to a triplet state, which subsequently transfers an electron to O₂ to yield ${\text{O}}_2^{-*}$ and an oxidized organic moiety (Cooper et al., 1988, 1989):

$\text{NOM}+hv+{\text{O}}_2\to \text{NO}{\text{M}}^{+}+{\text{O}}_2^{-*}$(2)

The pathway(s) by which this overall reaction occurs are still not certain, although the details are slowly being unraveled. While it was thought that photoexcited NOM may eject free aquated electrons, this now appears unlikely (Thomas-Smith and Blough, 2001). Instead, the photoexcited organic moiety can undergo a range of possible energetic and redox transitions, particularly in humic and fulvic substances that possess a wide range of functional groups and redox potentials. The mechanism of organic radical formation in photoexcited NOM was first studied in detail by Blough (1988) but, despite considerable advances over the last 20 years, the precise details of ${\text{O}}_2^{-*}$ formation still remain elusive. The mechanisms were thought to be similar to those involved in ${\text{O}}_2^{-*}$ production from photoexcited quinones, which have been studied extensively (e.g., Garg et al., 2007b and references therein), however the situation in humic and fulvic-type NOM is complicated considerably by the existence of multiple chromophores (Del Vecchio and Blough, 2002, 2004; Boyle et al., 2009) and redox-active moieties (Aeschbacher et al., 2010), many of which may be linked under exposure to light through charge-transfer complexes (Del Vecchio and Blough, 2004). More recently, Garg et al. (2011b) proposed a mechanism in which quinone-like moieties within NOM are reduced by some other electron donor within the NOM structure under solar radiation, with the reduced organic moiety then reacting with dissolved oxygen (in either the triplet or singlet state) to yield ${\text{O}}_2^{-*}$:

$\begin{array}{llll}& \text{NOM}+hv\underset{}{\overset{\text{organic}\text{electron}\text{donor}}{\to }}\text{NO}{\text{M}}^{-}& & \text{(3)}\\ & \text{NO}{\text{M}}^{-}+{\text{O}}_2\to \text{NO}\text{M}+{\text{O}}_2^{-*}& & \text{(4)}\end{array}$

The overall process is complicated considerably by formation of a range of other radical sinks for ${\text{O}}_2^{-*},$ but the net result is that NOM is oxidized by O₂ to yield ${\text{O}}_2^{-*}$ through the involvement of several moieties within the NOM, some of which may act as photocatalysts.

Consistent with the concept of labile transfer of electrons between the range of LRACs present in oxygenated waters, a second indirect mechanism of photochemical superoxide formation involves formation of reduced metals via ligand-to-metal charge-transfer reactions, with subsequent oxygenation of the reduced metal. The role of such reactions involving iron–organic complexes in marine systems has been recently reviewed by Barbeau (2006), and similar reactions can also occur with complexes of copper (Jones et al., 1985).

Biological Production

Biological production of ${\text{O}}_2^{-*}$ in the extracellular milieu has been reported from culture studies involving a wide range of environmentally occurring aquatic microorganisms, including eukaryotic microalgae from the class Raphidophyceae (Oda et al., 1997; Marshall et al., 2002, 2005; Yamasaki et al., 2004; Garg et al., 2007a); dinoflagellates and prymnesiophytes (Yamasaki et al., 2004; Marshall et al., 2005); marine diatoms from the genus Thalassiosira (Kustka et al., 2005); marine cyanobacteria from the genera Synechococcus (Rose et al., 2008b), Lyngbya (Rose et al., 2005) and Trichodesmium (Godrant et al., 2009); a marine alphaproteobacterium from the genus Roseobacter (Learman et al., 2011); the freshwater cyanobacterium Microcystis aeruginosa (Fujii et al., 2011); the unicellular protozoan coral symbiont Symbiodinium (Saragosti et al., 2010); fungi and yeasts including Aspergillus nidulans (Lara-Ortíz et al., 2003) and Saccharomyces cerevisiae (Shatwell et al., 1996), as reviewed by Aguirre et al. (2005); and the heterotrophic bacteria Paracoccus denitrificans (Henry and Vignais, 1980) and Escherichia coli (Korshunov and Imlay, 2006). Rates of ESP vary enormously between these different organisms, with the maximum reported rates being from the marine Raphidophycean Chattonella marina of up to ∼5 pmol cell⁻¹ h⁻¹ (Oda et al., 1997; Garg et al., 2007a). Additionally, recent field studies have provided evidence from several marine environments suggesting that a significant proportion of ESP occurs via biologically mediated processes, with measured rates of biological ESP up to 1 nM h⁻¹ in the Great Barrier Reef lagoon (Rose et al., 2010) and up to 20 nM h⁻¹ in the Gulf of Alaska (Hansard et al., 2010). These studies have predominantly involved either field studies in marine environments, or culture studies of organisms that typically inhabit marine environments, with notable exceptions being the studies involving M. aeruginosa, P. denitrificans (which is typically rather ubiquitous in soils), A. nidulans, S. cerevisiae, and E. coli. While there is still insufficient evidence to make definitive generalizations, the occurrence of these processes across such a wide range of microorganisms in the marine environment, coupled with evidence for ESP by a range of terrestrial multicellular organisms such as lichens (Beckett et al., 2003) and plants (Bolwell, 1999), suggests that microbial ESP probably occurs to at least some extent in the vast majority of surface waters.

Biological production of ${\text{O}}_2^{-*}$ in the intracellular environment has been studied for several decades and many of the processes involved are well understood. In eukaryotic organisms, intracellular ${\text{O}}_2^{-*}$ production is believed to be highly compartmentalized, with the majority occurring via reduction of O₂ inside the mitochondria and through the action of NADPH oxidase (NOX) enzymes, which are typically located inside vesicles (Auchère and Rusnak, 2002). In photosynthetic eukaryotes, ${\text{O}}_2^{-*}$ is also produced in significant amounts in the chloroplasts (Lesser, 2006). In prokaryotic organisms, which lack intracellular compartments separated by cellular membranes, the majority of intracellular ${\text{O}}_2^{-*}$ production is thought to occur during O₂ reduction by the respiratory electron transport chain (Auchère and Rusnak, 2002), which is also used for electron transport during photosynthesis in photosynthetic prokaryotes such as cyanobacteria (Lesser, 2006). It is extremely unlikely that such intracellular processes can be the direct source of ESP because the polar ${\text{O}}_2^{-}$ anion is unable to readily diffuse through the lipid bilayer that isolates the cytoplasm from the external milieu (Korshunov and Imlay, 2002). $\text{HO}{\text{O}}^{\bullet }$ can diffuse at a rate approaching that of water (permeability of P = 9 × 10⁻⁴ cm s⁻¹ = 3.2 × 10⁻² m h⁻¹; Korshunov and Imlay, 2002), but as $\text{HO}{\text{O}}^{\bullet }$ is only a small proportion of ${\text{O}}_2^{-*}$ around neutral pH, this flux is limited. The flux of ${\text{O}}_2^{-*}$ out of the cell is given by:

$\text{Flux}={\alpha }_{\text{HO}{\text{O}}^{\bullet }}PA\Delta \left[{\text{O}}_2^{-*}\right]$(5)

Where ${\alpha }_{\text{HO}{\text{O}}^{\bullet }}$ is the fraction of ${\text{O}}_2^{-*}$ that is in the $\text{HO}{\text{O}}^{\bullet }$ form, P is the permeability of $\text{HO}{\text{O}}^{\bullet }$, A is the cell surface area, and $\Delta \left[{\text{O}}_2^{-*}\right]$ is the difference between the intracellular and extracellular ${\text{O}}_2^{-*}$ concentrations. In a typical “healthy” cell, the steady-state intracellular ${\text{O}}_2^{-*}$ concentration is around 100 pM (Imlay and Fridovich, 1991). Considering an exemplary spherical cell with a diameter of 20 μm, and assuming that the steady-state extracellular ${\text{O}}_2^{-*}$ concentration ≪100 pM, the calculated flux is 8 zmol cell h⁻¹. Even if we assume that the cell is suffering from severe oxidative stress, resulting in an intracellular ${\text{O}}_2^{-*}$ concentration of 10 nM, the flux is still only 800 zmol cell h⁻¹. This is several orders of magnitude less than measured rates of ESP from the range of aquatic microorganisms surveyed to date. Additionally, ${\text{O}}_2^{-*}$ concentrations in the external milieu may be similar to, if not greater than, intracellular ${\text{O}}_2^{-*}$ concentrations, such that diffusion of ${\text{O}}_2^{-*}$ across the lipid bilayer, even if it could occur at substantial rates, would in fact occur into the cell under these conditions by virtue of the concentration gradient.

Another possible source of ESP is release of intracellular ${\text{O}}_2^{-*}$ during cell lysis. Assuming that the rate of cell lysis = rate of cell division to maintain a steady-state population, with spherical cells 20 μm in diameter under severe oxidative stress such that the intracellular ${\text{O}}_2^{-*}$ concentration was again 10 nM, then even in a rapidly growing population with a division rate of 1 h⁻¹ the rate of ESP by this pathway would be only 4 zmol cell h⁻¹. Of course more rapid lysis could temporarily result in a more rapid release of intracellular ${\text{O}}_2^{-*}$ by this pathway, but such rates could not be sustained to yield the steady-state concentrations of ${\text{O}}_2^{-*}$ that have been measured in natural waters to date. Thus the majority of ${\text{O}}_2^{-*}$ found in the extracellular milieu of aquatic microorganisms must, in general, be produced extracellularly.

While mechanisms of biological ESP have been reasonably well studied in human cells, mechanisms of biological ESP in aquatic microorganisms are generally not well understood. Enzymes from the NOX and dual oxidase (DUOX) families located at the cytoplasmic membrane are known to be responsible for ESP in the majority of human cells, notably including phagocytes responsible for the “respiratory burst” immunological defense phenomenon (Vignais, 2002; Lambeth, 2004). Cell surface located NOX enzymes have also been shown to be responsible for ESP in C. marina (Kim et al., 2000), the fungus A. nidulans (Lara-Ortíz et al., 2003) and numerous other fungi and yeasts (Aguirre et al., 2005), certain plant cells (Torres et al., 1998; Sagi and Fluhr, 2001), and the coral Stylophora pistillata and its symbiont Symbiodinium sp. (Saragosti et al., 2010). Addition of diphenyleneiodonium chloride (DPI), which is a specific inhibitor of NOX enzymes, has also been shown to dramatically inhibit ESP in cultures of the diatoms Thalassiosira weissflogii and T. pseudonana (Kustka et al., 2005). BLAST searches of sequenced genomes reveal the presence of genes encoding for polypeptide sequences similar to those found in NOX proteins in these two diatoms (Kustka et al., 2005) and in a wide range of other eukaryotic aquatic microorganisms, however this does not necessarily indicate the occurrence of ESP mediated by NOX enzymes in these organisms, since NOX enzymes are also found intracellularly as discussed previously. BLAST searches of the genomes of prokaryotic aquatic microorganisms reveal that such genes are not always present, suggesting that ESP by prokaryotes may occur via one or more other mechanisms.

Finally, it is worth reiterating that it is often difficult to establish which species is reduced first during ESP; in the case of biological ESP, it is not always clear whether O₂ is reduced to ${\text{O}}_2^{-*}$ directly by enzymes, or whether ${\text{O}}_2^{-*}$ is produced through oxygenation of some other reduced LRAC formed directly by enzymatic reduction. In the case of E. coli, ${\text{O}}_2^{-*}$ production in the organism’s periplasm has been inferred to occur through the oxidation of soluble, reduced quinones, with electrons originating from transfer across the cytoplasmic membrane via the respiratory electron transport chain (Korshunov and Imlay, 2006). The cell surface ferric reductase system of the yeast S. cerevisiae possesses similarities to the NOX system at the genetic level (Shatwell et al., 1996), and is capable of reducing a range of LRACs (Kosman, 2003) including O₂ to yield ${\text{O}}_2^{-*}$ (Lesuisse et al., 1996). The biogeochemical significance (if any) of which LRAC is reduced first is not yet certain, however it is clear that caution should be used when assigning a particular mechanism for cell surface reductase activity on the basis of genetic homology or biochemical studies conducted under a limited set of chemical conditions.

Chemistry of Reactions between Superoxide and Iron

Overview

In aqueous solutions, ${\text{O}}_2^{-*}$ can react in three major ways (Sawyer and Gibian, 1979; Sawyer and Valentine, 1981; Sawyer, 1991):

1. As a reductant. The ${\text{O}}_2^{-}$ anion is a mild reducing agent capable of directly donating electrons via an outer-sphere process to suitable electron acceptors (e.g., transition metals and their complexes).

2. As an oxidant. $\text{HO}{\text{O}}^{\bullet }$ is capable of oxidizing suitable electron donors via direct electron transfer, but this is highly unfavorable for the ${\text{O}}_2^{-}$ anion due to the extreme instability of the ${\text{O}}_2^{2-}$ anion in aqueous solution at most pH values. However, ${\text{O}}_2^{-}$ is capable of indirectly inducing oxidation by either hydrogen atom or proton extraction from suitable substrates, with subsequent reactions resulting in their net oxidation.

3. As a Lewis base (electron pair donor). The ${\text{O}}_2^{-}$ anion may be coordinated in the inner sphere of various metal ions in aqueous solution, and can also participate in radical–radical coupling with a range of organic radical cations.

The role of ${\text{O}}_2^{-*}$ as a Lewis base is restricted in natural aquatic environments because the maximum concentration of ${\text{O}}_2^{-*}$ that is attainable is typically too low (due to its consumption via other reactions) in comparison to other species to have any significant effect. In practice, therefore, ${\text{O}}_2^{-*}$ behaves primarily as a reductant or oxidant in natural waters. Early laboratory studies of reactions between aqueous Fe and ${\text{O}}_2^{-*}$ typically used pulse radiolysis to generate ${\text{O}}_2^{-*}$ and UV–visible spectrophotometry to observe the subsequent reactions (Jayson et al., 1969, 1973; Buettner et al., 1983; Bull et al., 1983; Rush and Bielski, 1985). While useful in understanding the chemistry of Fe and ${\text{O}}_2^{-*},$ results from these studies must be applied to environmental systems with caution because the use of high concentrations of both Fe and ${\text{O}}_2^{-*}$ could favor reactions that are not important at lower, environmentally relevant concentrations. This is particularly true for oxidation of Fe(II) by ${\text{O}}_2^{-*},$ where the initial step appears to typically involve coordination of ${\text{O}}_2^{-}$ in the inner sphere of Fe(II). Furthermore, natural systems involve a host of other competing reactions due to the range of other species present.

The potential effect of ${\text{O}}_2^{-*}$ on Fe in environmental systems was first specifically studied by Voelker and Sedlak (1995). They concluded that ${\text{O}}_2^{-*}$ functioned primarily as a reductant of Fe(III) over the pH range 5–8 (where ${\text{O}}_2^{-}$ dominates over $\text{HO}{\text{O}}^{\bullet }$), and that substantial amounts of Fe(II) could be expected to be produced in certain environmental systems as a result of this process. More recent studies have typically used lower concentrations of Fe and ${\text{O}}_2^{-*}$ that are more representative of what is typically found in natural systems, largely due to the possibilities afforded by the development of new techniques such as the MCLA chemiluminescence method, and have considered a range of different conditions that are more relevant to natural waters. Fe species can be broadly classified in such systems into three main groups:

1. Mononuclear inorganic complexes, which include hydrolysis species and a range of relatively weak complexes with small, commonly occurring inorganic ligands such as chloride, sulfate, bromide, fluoride, carbonate, and phosphate. These complexes interconvert rapidly compared to the other reactions we will consider, and may thus be assumed to be at equilibrium at all times.

2. Mononuclear organic complexes, which occur with a wide range of naturally occurring organic ligands such as humic and fulvic-type materials, polysaccharides, siderophores, and other biologically produced compounds.

3. Polynuclear complexes, which include amorphous oxyhydroxide solids, various iron minerals, and aggregates containing varying proportions of iron, organic material, and potentially other species.

Within each of these classes, individual Fe atoms may be present in either the Fe(II) or Fe(III) redox state, and the transformations between these redox states may be mediated by ${\text{O}}_2^{-*}$ (Figure 2).

FIGURE 2

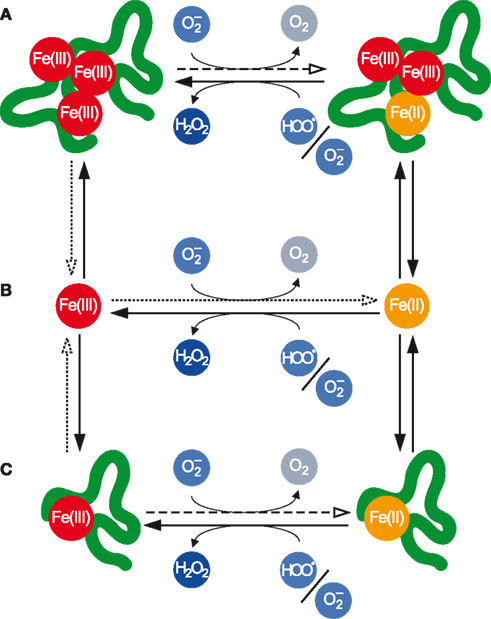
Figure 2. Transformations between various pools of Fe as mediated by ${\text{O}}_2^{-*}$ . (A) Polynuclear complexes, which contain multiple Fe atoms and may also contain other inorganic and organic ligands. (B) Mononuclear inorganic complexes. (C) Mononuclear organic complexes. Fe(III) in all pools may be reduced by the ${\text{O}}_2^{-}$ anion to Fe(II), while Fe(II) in all pools may be oxidized to Fe(III) primarily by $\text{HO}{\text{O}}^{\bullet },$ but also indirectly by ${\text{O}}_2^{-}.$ The dotted arrows denote the dissociative reduction (DR) pathway, while the dashed arrows denote the non-dissociative reduction (NDR) pathway for Fe(III) reduction by ${\text{O}}_2^{-*}.$

Thermodynamics

Due to pK_a of ${\text{O}}_2^{-}/\text{HO}{\text{O}}^{\bullet }$ being in the environmentally relevant range, and $\text{HO}{\text{O}}^{\bullet }$ being considerably more oxidizing than ${\text{O}}_2^{-},$ the standard redox potential of the ${\text{O}}_2/{\text{O}}_2^{-*}$ couple can vary considerably from +120 mV at pH ≪ 4.8 to −160 mV at pH ≫ 4.8 (Sawyer, 1991). In the majority of natural surface waters, which are in the neutral to slightly alkaline pH range, the standard redox potential of the ${\text{O}}_2/{\text{O}}_2^{-*}$ couple is thus −160 mV. Therefore, under standard conditions at around neutral pH, ${\text{O}}_2^{-*}$ is a mild reducing agent. In contrast, the standard redox potentials of various Fe(II)/Fe(III) couples vary from <−1000 to >+1000 mV depending on pH and complex speciation (Pierre and Fontecave, 1999; Pierre et al., 2002). Despite the overlap between the standard redox potentials of the ${\text{O}}_2/{\text{O}}_2^{-*}$ couple and those of many Fe(II)/Fe(III) species redox couples, an important caveat when considering the feasibility of redox reactions is that these redox potentials apply to standard conditions, i.e., [O₂] = $\left[{\text{O}}_2^{-*}\right]$ = [Fe(II)] species = [Fe(III)] species. As discussed in detail by Pierre et al. (2002), such conditions are irrelevant in most natural systems. Under conditions typical for a neutral air-saturated surface water (pH 7 and [O₂] = 250 μM), the actual redox potential of the ${\text{O}}_2/{\text{O}}_2^{-*}$ couple is +335 mV when $\left[{\text{O}}_2^{-*}\right]$ = 1 pM and +158 mV when $\left[{\text{O}}_2^{-*}\right]$ = 1 nM. An equally important consideration for the thermodynamic reducibility of a particular form of Fe by ${\text{O}}_2^{-*}$ is the concentration of relevant Fe(II) and Fe(III) species. The reduction of an organic Fe complex [denoted as Fe(II)L in the reduced state and Fe(III)L in the oxidized state] is thermodynamically feasible if:

$\begin{array}{l}\log \left(\left[\text{Fe}\left(\text{II}\right)\text{L}\right]/\left[\text{Fe}\left(\text{III}\right)\text{L}\right]\right)<\left(E_{{\text{Fe}}^{3+}\to {\text{Fe}}^{2+}}^0-E_{{\text{O}}_2\to {\text{O}}_2^{-*}}\right)/59\\ +\log \left(\left(K_{\text{Fe}\left(\text{II}\right)\text{L}}{\text{α}}_{{\text{Fe}}^{3+}}\right)/\left(K_{\text{Fe}\left(\text{III}\right)\text{L}}{\text{α}}_{{\text{Fe}}^{2+}}\right)\right)\end{array}$(6)

where the stability constants are mixed constants expressed as:

$\begin{array}{llll}{K}_{\text{Fe}\left(\text{II}\right)\text{L}}& =\frac{\left[\text{Fe}\left(\text{II}\right)\text{L}\right]}{\left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]\left[{\text{L}}^{\prime }\right]}& & \text{(7)}\\ K_{\text{Fe}\left(\text{III}\right)\text{L}}& =\frac{\left[\text{Fe}\left(\text{III}\right)\text{L}\right]}{\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]\left[{\text{L}}^{\prime }\right]}& & \text{(8)}\end{array}$

and where, under particular medium conditions, Fe(II)′ represents the sum of all monomeric inorganic Fe(II) species, Fe(III)′ represents the sum of all monomeric inorganic Fe(III) species, L′ represents the sum of all ligand species, ${\alpha }_{\text{F}{\text{e}}^{2+}}$ represents the ratio of [Fe²⁺]/[Fe(II)′], ${\alpha }_{\text{F}{\text{e}}^{3+}}$ represents the ratio of [Fe³⁺]/[Fe(III)′], and redox potentials are in millivolt (see Thermodynamics for the full derivation in Appendix).

Calculated values for some typical complexes around pH 8, where ${\alpha }_{\text{F}{\text{e}}^{2+}}=0.5$ and ${\alpha }_{\text{F}{\text{e}}^{3+}}=10^{-10}$ (Millero et al., 1995), are shown in Table 1. It is thermodynamically feasible to reduce a substantial proportion of Fe(III)L to Fe(II)L for some relatively strong Fe(III) complexes, such as that formed with EDTA in freshwater, provided that the ligand also forms a relatively strong Fe(II) complex. This contrasts with the case of DFB, which forms a much stronger complex with Fe(III) than with Fe(II), where reduction of Fe(III)L to Fe(II)L is thermodynamically feasible only at exceedingly low Fe(II)L:Fe(III)L ratios.

TABLE 1

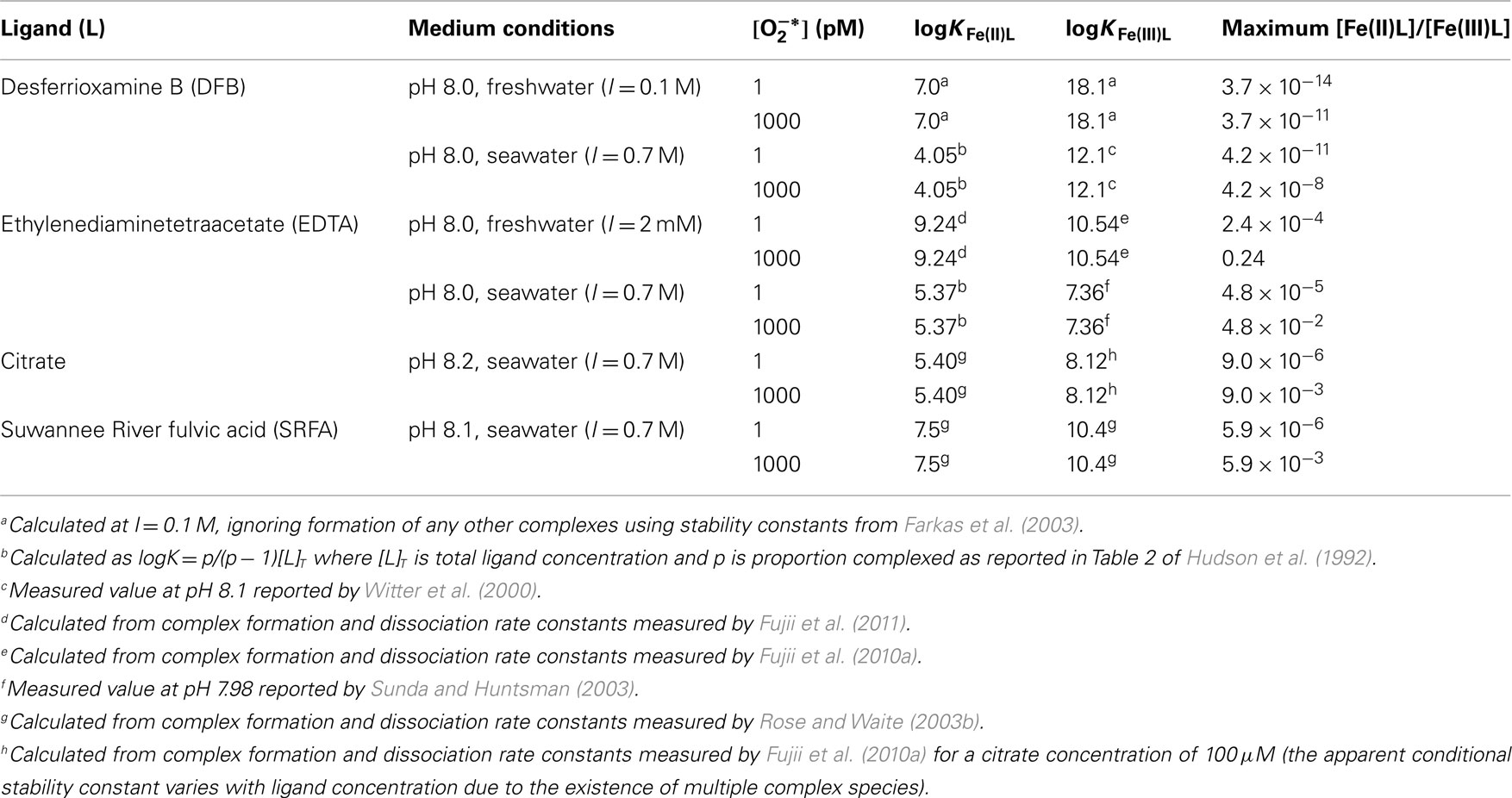
Table 1. Calculated ratios of [Fe(II)L]/[Fe(III)L] below which reduction of Fe(III)L to Fe(II)L by ${\text{O}}_2^{-*}$ is thermodynamically feasible for various Fe complexes in natural waters around pH 8.

However reduction of Fe(III) by ${\text{O}}_2^{-*}$ may be still environmentally important even when the thermodynamically permissible concentration of Fe(II)L is much less than that of Fe(III)L, because many microorganisms acquire iron from the dissolved inorganic pool rather than directly from organically complexes species. A more useful thermodynamic test, then, is whether ${\text{O}}_2^{-*}$ can increase the proportion of dissolved inorganic Fe, given that it is these forms of Fe that are usually the immediate substrate for uptake by aquatic microorganisms (Morel et al., 2008). According to the Nernst equation, reduction of Fe³⁺ to Fe²⁺ is thermodynamically feasible when:

$\begin{array}{l}\log \left(\left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]/\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]\right)<\log \left({\text{α}}_{{\text{Fe}}^{3+}}/{\text{α}}_{{\text{Fe}}^{2+}}\right)\\ +\left(E_{{\text{Fe}}^{3+}\to {\text{Fe}}^{2+}}^0-E_{{\text{O}}_2\to {\text{O}}_2^{-*}}\right)/59\end{array}$(9)

Thus at pH 8.1, it is thermodynamically feasible to attain ratios of [Fe(II)′]/[Fe(III)′] of up to ∼0.005 with 1 pM ${\text{O}}_2^{-*}$ and up to ∼5 with 1 nM ${\text{O}}_2^{-*}.$ Consequently, regardless of organic complex speciation, nanomolar concentrations of ${\text{O}}_2^{-*}$ can theoretically result in more Fe(II)′ than Fe(III)′ in an equilibrium or pseudo-equilibrium scenario.

While these types of calculations are useful for assessing the thermodynamic driving force and consequent feasibility of ${\text{O}}_2^{-*}$ as a reductant for Fe, they are really only useful to provide a general context for such reactions. It is often overlooked that environmental systems are not always at equilibrium (and in some environments, are never at equilibrium), and as a consequence, the usefulness of thermodynamics in such systems is limited. In particular, processes that can perturb the system can increase the thermodynamic feasibility, such as removal of Fe(II) by biological uptake (Pierre and Fontecave, 1999). In this case, a lower Fe(II) concentration can be maintained, increasing the driving force for reduction (Eq. 9). Because such systems are at steady-state rather than a true equilibrium, thermodynamics cannot be used to predict what the final system will look like, but if the composition [e.g., concentrations of ${\text{O}}_2^{-*},$ O₂, Fe(II), and Fe(III)] of the steady-state system is known, it can be used to understand the energetics of the system. However being able to predict what this steady-state system will look like is usually a major objective in environmental systems, and this can only be achieved by a more rigorous kinetic analysis.

Kinetics and Mechanisms

Within the three classes shown in Figure 2, there is potentially a multitude of individual Fe species. Speciation of the dissolved inorganic pool depends on pH and major ion composition of the aquatic system; in the case of the other two pools, speciation depends on these two factors and also the presence of various organic ligands (see Kinetics and Mechanisms for kinetic equations in Appendix).

Rush and Bielski (1985) studied the reactivity of Fe(II)′ and Fe(III)′ with ${\text{O}}_2^{-*}$ as a function of pH in the acidic to neutral range in detail. They determined that conditional rate constants for Fe(II) oxidation varied with pH over the range 1–7 primarily due to faster reactivity of Fe(II) with ${\text{O}}_2^{-}$ (rate constant = 1.0 × 10⁷ M⁻¹ s⁻¹) than $\text{HO}{\text{O}}^{\bullet }$ (rate constant = 1.2 × 10⁶ M⁻¹ s⁻¹), with no apparent influence of Fe(II) speciation on oxidation kinetics in this pH range. Similarly, over the pH range 0–7, Fe(III) was reduced rapidly by ${\text{O}}_2^{-}$ (rate constant = 1.5 × 10⁸ M⁻¹ s⁻¹) but negligibly slowly by $\text{HO}{\text{O}}^{\bullet }$ (rate constant <10³ M⁻¹ s⁻¹), again with no apparent influence of Fe(III) speciation. Similar values under acidic conditions have since been confirmed in more recent studies (Khaikin et al., 1996; Mansano-Weiss et al., 2002). Conditional rate constants for overall Fe(II) oxidation by ${\text{O}}_2^{-*}$ of k_ox,inorg = 1.0 × 10⁷ M⁻¹ s⁻¹ and Fe(III) reduction by ${\text{O}}_2^{-*}$ of k_red,inorg = 1.5 × 10⁸ M⁻¹ s⁻¹ are thus frequently used in kinetic studies of environmental systems at circum neutral pH, implicitly assuming that the values derived by Rush and Bielski can be extrapolated to systems with higher pH, lower Fe and ${\text{O}}_2^{-*}$ concentrations, and considerably more variable ionic composition (the original study considered only effects of Fe hydrolysis and sulfate complexation). Extrapolation of these values appears consistent with results in these studies, suggesting that this is valid, however with the advent of new, more sensitive techniques for ${\text{O}}_2^{-*}$ determination, these fundamental reactions warrant further attention.

In systems where organic complexation and/or polynuclear complex formation occur, a single conditional rate constant for Fe(III) reduction and another for Fe(II) oxidation by ${\text{O}}_2^{-*}$ cannot be derived; it is necessary to separately account for the reactions of ${\text{O}}_2^{-*}$ with mononuclear inorganic Fe and at least one organic and/or polynuclear Fe complex. Studies in model systems containing a single, well characterized synthetic ligand have confirmed that reduction of Fe(III) by ${\text{O}}_2^{-*}$ around neutral pH can occur via direct reduction of the complex (denoted “non-dissociative reduction,” or NDR), or via dissociation of the complex with subsequent reduction of the liberated Fe(III)′ (denoted “dissociative reduction,” or DR; Garg et al., 2007c,d; Fujii et al., 2008), as shown in Figure 2. The relative importance of these two pathways for Fe(III) reduction depends on the relative rates of complex dissociation, complex formation, Fe(III)′ reduction by ${\text{O}}_2^{-*},$ and Fe(III)L reduction by ${\text{O}}_2^{-*}.$ Under steady-state conditions where most Fe(III) is present in complexed form, the net rate of Fe(III) reduction by NDR is simply:

$k_{\text{red},\text{Fe}\left(\text{III}\right)\text{L}}\left[\text{Fe}\left(\text{III}\right)\text{L}\right]\left[{\text{O}}_2^{-*}\right]\approx k_{\text{red},\text{Fe}\left(\text{III}\right)\text{L}}{\left[\text{Fe}\left(\text{III}\right)\right]}_{\text{T}}\left[{\text{O}}_2^{-*}\right]$(10)

where k_red,Fe(III)L represents the rate constant for reduction of a particular Fe(III)L complex and the subscript T denotes the total concentration of all Fe(III) species. Thus, the apparent rate constant for NDR is simply k_NDR = k_red,Fe(III)L. Also, at steady-state:

$\begin{array}{llll}& \frac{\text{d}}{\text{d}t}\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]=k_{\text{d,Fe}\left(\text{III}\right)\text{L}}\left[\text{Fe}\left(\text{III}\right)\text{L}\right]-k_{f\text{,Fe(III)L}}\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]\left[\text{L}\right]& & \\ & -k_{\text{red},\text{inorg}}\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]\left[{\text{O}}_2^{-*}\right]=0& & \text{(11)}\\ & \Rightarrow \left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]=\frac{k_{\text{d},\text{Fe}\left(\text{III}\right)\text{L}}\left[\text{Fe}\left(\text{III}\right)\text{L}\right]}{k_{\text{f,Fe}\left(\text{III}\right)\text{L}}\left[\text{L}\right]+k_{\text{red,inorg}}\left[{\text{O}}_2^{-*}\right]}& & \text{(12)}\end{array}$

where k_d,Fe(III)L and k_f,Fe(III)L represent rate constants for the dissociation and formation, respectively, of a particular Fe(III)L complex. Hence the apparent rate constant for net Fe(III) reduction by DR is obtained from the equation:

$\begin{array}{llll}& k_{\text{red,inorg}}\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]\left[{\text{O}}_2^{-*}\right]=\frac{k_{\text{red,inorg}}{k}_{\text{d,Fe}\left(\text{III}\right)\text{L}}}{k_{\text{f,Fe}\left(\text{III}\right)\text{L}}\left[\text{L}\right]+k_{\text{red,inorg}}\left[{\text{O}}_2^{-*}\right]}& & \\ & \times \left[\text{Fe}\left(\text{III}\right)\text{L}\right]\left[{\text{O}}_2^{-*}\right]& & \text{(13)}\\ & \Rightarrow k_{\text{DR}}=\frac{k_{\text{red,inorg}}{k}_{\text{d,Fe}\left(\text{III}\right)\text{L}}}{k_{\text{f,Fe}\left(\text{III}\right)\text{L}}\left[\text{L}\right]+k_{\text{red,inorg}}\left[{\text{O}}_2^{-*}\right]}& & \text{(14)}\end{array}$

Thus the relative importance of the two processes is given by:

$k_{\text{NDR}}/k_{\text{DR}}=\frac{k_{\text{red,Fe}\left(\text{III}\right)\text{L}}\left(k_{\text{f,Fe}\left(\text{III}\right)\text{L}}\left[\text{L}\right]+k_{\text{red,inorg}}\left[{\text{O}}_2^{-*}\right]\right)}{k_{\text{red,inorg}}{k}_{\text{d,Fe}\left(\text{III}\right)\text{L}}}$(15)

All parameters in this equation will be influenced to varying extents by medium conditions (e.g., pH and ionic strength). Additionally, for a given ligand, the system pH, major ion composition, ligand concentration, and ${\text{O}}_2^{-*}$ concentration will have specific effects on particular parameters. The relative importance of NDR compared to DR will be increased by:

1. Decreasing concentrations of H⁺ (i.e., higher pH) or cations such as Ca²⁺ and Mg²⁺; the presence of these species will lower “free” ligand concentration, [L], by occupying sites within ligands that might otherwise complex Fe, thus decreasing the numerator of Eq. 15.

2. Increasing ligand concentrations; this will increase the numerator of Eq. 15.

3. Increasing ${\text{O}}_2^{-*}$ concentrations; this will increase the numerator of Eq. 15.

The affinity of the ligand for Fe(III) also has a major effect on the relative importance of DR and NDR, but this effect is complicated because two factors act in opposite ways. First, increasing the Fe(III) binding strength of the ligand will tend to increase k_f,Fe(III)L (increasing the numerator of Eq. 15) and/or decrease k_d,Fe(III)L (decreasing the denominator of Eq. 15); this leads to a relative increase in the importance of NDR relative to DR. However weaker Fe(III) complexes typically react faster with ${\text{O}}_2^{-*}$ than stronger complexes, as observed empirically for a range of synthetic Fe-binding ligands (Rose and Waite, 2005), such that increasing Fe(III) binding strength of the ligand will tend to decrease k_red,Fe(III)L. Rate constants for reduction of organic complexes of Fe(III) by ${\text{O}}_2^{-*}$ at pH 8 were found to be several orders of magnitude smaller than those for reduction of Fe(III)′, ranging from ∼10⁴ M⁻¹ s⁻¹ for reduction of the strong complex Fe(III)–DFB to ∼2 × 10⁶ M⁻¹ s⁻¹ for reduction of the relatively weak complex Fe(III)-salicylate (Rose and Waite, 2005). This trend is consistent with Marcus Theory for outer-sphere electron transfer processes (see Marcus and Sutin (1985) for a detailed review), which is the process by which reduction of transition metal complexes by ${\text{O}}_2^{-*}$ is thought to occur (Weinstock, 2008). In fact Marcus Theory relates the rate constant to the ratio of stability constants for the Fe(II) and Fe(III) complexes, not just the stability of the Fe(III) complex alone (Marcus and Sutin, 1985); however as ligands that form stronger complexes with Fe(III) often form weaker complexes with Fe(II), there is generally a consistent trend for slower reduction of stronger Fe(III) complexes by ${\text{O}}_2^{-*}.$

Polynuclear complexes are also able to be reduced by ${\text{O}}_2^{-*},$ as demonstrated in laboratory studies with amorphous ferric oxyhydroxide (AFO; Fujii et al., 2006) and in field studies with Saharan dust in seawater (Heller and Croot, 2011). A similar competition between DR and NDR would be expected to occur for polynuclear complexes. Fujii et al. (2006) found that in both very freshly formed AFO (which has a relatively small conditional stability constant) and aged AFO (which has a much larger conditional stability constant), Fe(II) production during reduction of AFO by ${\text{O}}_2^{-*}$ occurred almost entirely via DR. These experiments were performed in seawater at pH 8.2 using total Fe concentrations of 50–500 nM, which is a reasonable range in coastal marine systems, but using higher steady-state ${\text{O}}_2^{-*}$ concentrations than would be expected in most environments (∼20 nM cf. 0.1–1 nM measured in marine waters). These higher ${\text{O}}_2^{-*}$ concentrations would tend to increase the importance of NDR, which implies that at the lower ${\text{O}}_2^{-*}$ concentrations measured in natural waters to date, the process will almost certainly occur via DR. Given that aged AFO has a relatively large conditional stability constant, NDR might be expected to play a more substantial role, however polynuclear complexes (unlike mononuclear complexes) may permit extremely rapid intramolecular electron transfer from relatively labile Fe atoms (e.g., at the AFO surface) to less labile Fe atoms within the polymeric structure (Katz et al., 2010), inhibiting the release of Fe(II) potentially formed through this pathway. Whether this or some other phenomenon is responsible for the dominance of DR during reduction of aged AFO remains untested, however, and will require further experimental studies to resolve.

At lower pH values (3 and 5), $\text{HO}{\text{O}}^{\bullet }$ is a major oxidant of Fe(II) (Voelker et al., 1997). Around pH 8, where ${\text{O}}_2^{-}$ dominates over $\text{HO}{\text{O}}^{\bullet },$ Fujii et al. (2010b) determined rate constants for oxidation of complexes between Fe(II) and humic-type organic ligands by ${\text{O}}_2^{-*}$ in the range 6.9–23 × 10⁵ M⁻¹ s⁻¹, which were ∼4–5 orders of magnitude greater than corresponding rate constants for oxidation of the complexes by O₂. Given a typical dissolved O₂ concentration of ∼250 μM for natural waters in equilibrium with atmospheric O₂, this implies that ${\text{O}}_2^{-*}$ would be a negligibly minor oxidant of these Fe(II) complexes at the picomolar ${\text{O}}_2^{-*}$ concentrations that have been measured in natural waters. In contrast, Heller and Croot (2010) suggested that ${\text{O}}_2^{-*}$ may react with naturally occurring organic Fe(II) complexes found in the Southern Ocean with rate constants of up to ∼5 × 10⁷ M⁻¹ s⁻¹, which is around an order of magnitude greater than those for the humic-type complexes (Fujii et al., 2010b). This would suggest that ${\text{O}}_2^{-*}$ might contribute significantly to Fe(II) oxidation at the higher range of environmentally relevant ${\text{O}}_2^{-*}$ concentrations; however this can not be evaluated directly without also knowing the kinetics of reaction between the Fe(II) complexes and O₂, which were not determined in the Southern Ocean study. To date, oxidation of polynuclear Fe(II) by ${\text{O}}_2^{-*}$ has not been studied directly, although such a reaction would seem less environmentally relevant than reduction of polynulcear Fe(III) by ${\text{O}}_2^{-*},$ given the weaker tendency of Fe(II) to form polynuclear species. However, it is clear that more studies of the oxidation of organically complexed and polynuclear Fe(II) by ${\text{O}}_2^{-*}$ are required to better constrain the potential importance of ${\text{O}}_2^{-*}$ as an oxidant of Fe(II) in natural waters.

Indirect Effects of Reactions between Superoxide and Iron

While being primarily concerned with the effect of ${\text{O}}_2^{-*}$ on Fe speciation, it is also worth briefly considering the ability of reactions between ${\text{O}}_2^{-*}$ and Fe to generate other reactive intermediates, which may be biologically important. Perhaps the major such process is the Haber–Weiss cycle, in which ${\text{O}}_2^{-*}$ and Fe promote the formation of hydroxyl radicals $\left(\text{H}{\text{O}}^{\bullet }\right)$. It was initially thought that ${\text{O}}_2^{-*}$ could reduce H₂O₂ to yield $\text{H}{\text{O}}^{\bullet }:$

${\text{O}}_2^{-*}+{\text{H}}_2{\text{O}}_2\to {\text{O}}_2+\text{H}{\text{O}}^{\bullet }+\text{H}{\text{O}}^{-}$(16)

It has since been shown that this reaction does not occur directly, but represents the net result of a series of reactions involving ${\text{O}}_2^{-*}$ and Fe (Winterbourn, 1995; Koppenol, 2001):

$\begin{array}{llll}& {\text{O}}_2^{-*}+\text{Fe}\left(\text{III}\right)\to {\text{O}}_{\text{2}}+\text{Fe}\left(\text{II}\right)& & \text{(17)}\\ & {\text{O}}_2^{-*}+\text{Fe}\left(\text{II}\right)\underset{}{\overset{2{\text{H}}^{\text{ + }}}{\to }}{\text{H}}_2{\text{O}}_{\text{2}}+\text{Fe}\left(\text{III}\right)& & \text{(18)}\\ & {\text{H}}_2{\text{O}}_2+\text{Fe}\left(\text{II}\right)\to \text{H}{\text{O}}^{\bullet }+\text{H}{\text{O}}^{-}+\text{Fe}\left(\text{III}\right)& & \text{(19)}\end{array}$

The reaction in Eq. 19(the Fenton reaction) may produce Fe(IV) (ferryl iron) rather than $\text{O}{\text{H}}^{\bullet }$ under some conditions (Remucal and Sedlak, 2011):

${\text{H}}_2{\text{O}}_2+\text{Fe}\left(\text{II}\right)\to {\text{H}}_2\text{O}+\text{Fe}\left(\text{IV}\right){\text{O}}_2^{2+}$(20)

The biological importance of these processes lies in the ability of $\text{H}{\text{O}}^{\bullet }$ and/or Fe(IV) to oxidize a wide range of biologically important molecules, and constitutes one of the main pathways to oxidative stress. This only occurs when ${\text{O}}_2^{-*}$ is reduced by Fe(II) to form H₂O₂ [i.e., when ${\text{O}}_2^{-*}$ acts as an oxidant of Fe(II)] which, as discussed in the previous section, appears to be negligible at ${\text{O}}_2^{-*}$ concentrations that have so far been measured in natural waters. A second potential consequence of this series of reactions is the possibility that O₂ formed in the reaction shown in Eq. 17is in the excited singlet state rather than the triplet ground state. Singlet state dioxygen (¹O₂) is a powerful, but rather selective, oxidant of a range of biologically important molecules (Briviba et al., 1997). Formation of ¹O₂ from oxidation of ${\text{O}}_2^{-*}$ is only possible with a sufficiently powerful oxidant (Koppenol, 1976), which may or may not be satisfied by different Fe(II) species (Nanni et al., 1981).

Influence of Extracellular Superoxide on Iron Bioavailability and Microbial Iron Nutrition

Superoxide: A Force for Good or Evil?

${\text{O}}_2^{-*}$ is frequently associated with the concept of oxidative stress in cells, and has consequently developed a reputation as an enemy of healthy biological functioning. The detrimental effect of intracellular ${\text{O}}_2^{-*}$ can largely be attributed to two main types of processes (Fridovich, 1986, 1998; Cadenas, 1989; Auchère and Rusnak, 2002; Lesser, 2006):

1. interference with critical redox processes by adversely influencing the redox state of enzymes (particularly including enzymes containing iron) and other smaller molecules with specific biochemical functions; and

2. initiation of radical chain reactions, including as a precursor to much more reactive species such as $\text{H}{\text{O}}^{\bullet },$ Fe(IV), and ¹O₂ via the processes described previously.

Adverse effects caused by extracellular ${\text{O}}_2^{-*}$ in a typical aquatic environment near neutral pH could presumably result from similar processes that cause adverse effects inside the cell. The potential for processes in the extracellular environment to adversely affect cells is limited by the inability of ${\text{O}}_2^{-*}$ and many of its more reactive derivatives to cross cell membranes, which inhibits or prevents these species from reacting with the vast majority of enzymes and other biological molecules used for normal cellular function. Additionally, concentrations of Fe (and other promoters of free radical production) are usually much lower in the extracellular environment than the intracellular environment, which decreases formation rates of potentially damaging reactive derivatives by slowing reaction kinetics. The presence of other potential sinks can also help scavenge these reactive derivatives and thus confer additional protection to the cell.

However, in some cases, extracellular ${\text{O}}_2^{-*}$ is capable of inflicting cellular damage and may even be deliberately used in this fashion either to defend against invasions by other cells [e.g., the “oxidative burst” produced by human phagocyte cells (Vignais, 2002)] or as an agent of cellular warfare, as has been suggested some raphidophyceans such as C. marina (Oda et al., 1992). A frequently observed factor in these situations is the production of large amounts of ${\text{O}}_2^{-*}$ at relatively rapid rates. This can be rationalized on the basis that in order to produce H₂O₂ and subsequently $\text{H}{\text{O}}^{\bullet }$ and/or Fe(IV) at substantial rates, ${\text{O}}_2^{-*}$ must be reduced at substantial rates, as ${\text{O}}_2^{-*}$ production rates need to be fast enough to sustain relatively rapid formation of both H₂O₂ (through reduction of ${\text{O}}_2^{-*}$) and Fe(II) (or other reduced species) to oxidize H₂O₂ to $\text{H}{\text{O}}^{\bullet }$ [or to yield Fe(IV)]. In contrast, relatively low ${\text{O}}_2^{-*}$ production rates will result in relatively low H₂O₂ production rates and also relatively low concentrations of Fe(II) (or other reduced species), such that H₂O₂ is more likely to decay via pathways that do not result in $\text{H}{\text{O}}^{\bullet }$ or Fe(IV) formation. Thus, at the picomolar concentrations typically encountered in natural waters, ${\text{O}}_2^{-*}$ is unlikely to be particularly detrimental for aquatic microorganisms. This notion is further supported by evidence that a wide range of cells use ${\text{O}}_2^{-*}$ as a signaling molecule at low concentrations (Buetler et al., 2004), although given the limited number of studies on the roles and/or effects of extracellular ${\text{O}}_2^{-*}$ on living organisms, it is difficult to make definitive conclusions regarding this issue at present.

Nonetheless, picomolar concentrations of ${\text{O}}_2^{-*}$ have the potential to maintain mild reducing capacity in the extracellular environment. As discussed previously, under these conditions ${\text{O}}_2^{-*}$ is both thermodynamically and kinetically capable of reducing a wide range of Fe(III) species to Fe(II), thereby potentially increasing Fe bioavailability.

Can Extracellular Superoxide Production Increase Fe Bioavailability?

The analysis in Section “Kinetics and Mechanisms” separately considered rates of Fe(III) reduction and rates of Fe(II) oxidation by ${\text{O}}_2^{-*}$ for a range of different forms of Fe. While this provides useful insight into the mechanisms by which ${\text{O}}_2^{-*}$ can influence Fe speciation, and the relative importance of these various pathways under various conditions, the most important factor from the perspective of Fe bioavailability is the net result of these processes. Most organisms in natural waters are thought to use the mononuclear inorganic complexes, collectively represented as Fe(II)′ and Fe(III)′, as the substrate that is directly internalized by the cell (Morel et al., 2008). Thus while Fe from the other pools may be bioavailable in the sense that Fe contained within them may ultimately find its way into the cell, this can only occur after conversion to Fe(II)′ or Fe(III)′. The ability of ${\text{O}}_2^{-*}$ to influence Fe bioavailability therefore depends largely on whether its production increases the concentration of Fe(II)′ and/or Fe(III)′ at or near the sites of cellular uptake of these species.

A spatially homogeneous steady-state system in which Fe exists predominantly as a single type of organic complex, O₂ is assumed to be the only oxidant of Fe(II), and ${\text{O}}_2^{-*}$ is assumed to be the only reductant of Fe(III), is shown schematically in Figure 3. While such a system is highly simplified, it provides a useful basis to understand when ${\text{O}}_2^{-*}$ might increase Fe bioavailability. The number of variables can be further simplified by assuming a 1:1 Fe:L ratio for Fe(II)L and Fe(III)L, that the complex formation rate constants are independent of ligand type (consistent with control of complex formation by water loss kinetics, i.e., the complexes form via a perfect Eigen–Wilkins mechanism (Eigen and Wilkins, 1965) in which the electrostatic charge on L does not vary between different ligand types), and that the oxidation of Fe(II)L by O₂ and reduction of Fe(III)L by ${\text{O}}_2^{-*}$ are outer-sphere electron transfer processes that obey Marcus Theory perfectly. With these simplifications, analytical solutions for the steady-state concentrations of the Fe species can be derived as a function of the eight kinetic parameters shown in Figure 3. Four of these kinetic parameters (k_f,Fe(III)L, k_f,Fe(II)L, $k_{{\text{O}}_2,\text{inorg}}$, and k_red,inorg) are constants for specified [L], [O₂], and $\left[{\text{O}}_2^{-*}\right]$, while the remaining four kinetic parameters can all be expressed as functions of K_Fe(III)L and K_Fe(II)L (see Details of Spatially Homogeneous Steady-State Model For Fe′ Concentrations as a Function of Superoxide Concentrations for the full derivation in Appendix).

FIGURE 3

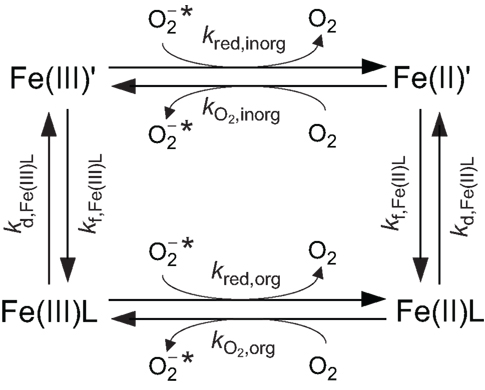
Figure 3. Simplified steady-state model for Fe chemistry in a spatially homogeneous system containing ${\text{O}}_{\text{2}}^{-*}$ and a single ligand (L) that forms a 1:1 complex with Fe, showing relevant rate constants.

Consider an illustrative typical coastal marine water in equilibrium with the atmosphere at pH 8.1, temperature 25°C, ionic strength of 0.7 M, constant ionic composition, [Fe]_T = 100 nM, and [L] = 1 μM. Steady-state [Fe(III)′], [Fe(II)′], and [Fe′]_T were calculated in Microsoft Excel from the relationships in Eqs A28 and A29 (see Appendix) at steady-state $\left[{\text{O}}_2^{-*}\right]$ of 0, 10, 100 pM, and 1 nM, considering a range of stability constants for Fe(III)L and Fe(II)L that are representative of what might be encountered in coastal marine waters (Figure 4). Provided Fe(II) forms relatively weak complexes, 1 nM ${\text{O}}_2^{-*}$ increases steady-state [Fe′]_T by nearly an order of magnitude compared to the absence of ${\text{O}}_2^{-*}$ across the whole range of K_Fe(III)L considered; the effect is smaller at 100 pM ${\text{O}}_2^{-*}$ and negligible at 10 pM ${\text{O}}_2^{-*}$ under the particular conditions in this example. In all cases, the increase in steady-state [Fe′]_T is due to production of Fe(II)′; steady-state [Fe(III)′] is mostly affected to a negligibly small extent by ${\text{O}}_2^{-*}.$ When Fe(II) forms relatively strong complexes while Fe(III) forms relatively weak complexes, the steady-state [Fe′]_T actually decreases due to the influence of ${\text{O}}_2^{-*};$ this is intuitively reasonable, as in this case the reduction of Fe(III) to Fe(II) would result in transformation to a less labile form (predominantly as the Fe(II)L complex). This effect is more pronounced at higher $\left[{\text{O}}_2^{-*}\right]$, as would be expected from such a mechanism. There is little evidence for naturally occurring ligands that form strong complexes with Fe(II) but weak complexes with Fe(III), however, suggesting that this latter scenario is unlikely to be important in most natural waters.

FIGURE 4

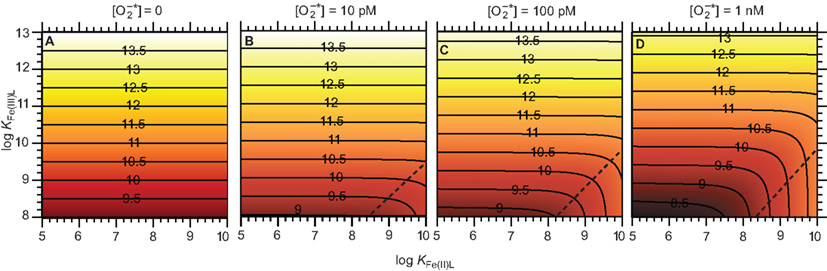
Figure 4. Effect of ${\text{O}}_{\text{2}}^{-*}$ on Fe bioavailability in a system containing a single Fe complexing ligand. (A) Steady-state $\left[{\text{O}}_2^{-*}\right]=0$(B) Steady-state $\left[{\text{O}}_2^{-*}\right]=100\text{\hspace{0.17em}pM}$ (C) Steady-state $\left[{\text{O}}_2^{-*}\right]=100\text{\hspace{0.17em}pM}$ (D) Steady-state $\left[{\text{O}}_2^{-*}\right]=1\text{\hspace{0.17em}nM}$. Panels show the resulting pFe′ [= −log[Fe′] _T = −log([Fe(II)′] + [Fe(III)′]) at steady-state. The contours shown in each panel represent constant pFe′ values, as indicated by the numbers marked on the contour lines. The region to the bottom right of the dashed lines in each panel approximately indicates conditions where the strength of the Fe(II) complex relative to that of the Fe(III) complex is sufficiently high that the presence of ${\text{O}}_2^{-*}$ decreases Fe bioavailability.

Under the conditions of the example above, it is clear that steady-state concentrations of ${\text{O}}_2^{-*}$ that are typical of those measured in natural waters have the potential to significantly increase Fe bioavailability. The same approach can be readily applied to natural waters with differing Fe concentrations, because the steady-state concentrations of Fe(II)′ and Fe(III)′ are simply proportional to [Fe]_T when all other parameters remain constant (Eqs A28 and A29 in Appendix). However, there are several other factors that must also be considered when attempting to apply this approach to other conditions:

1. Different values of [L] will influence k*_f,Fe(III)L = k_f,Fe(III)L[L] and k*_f,Fe(II)L = k_f,Fe(II)L[L], which will influence steady-state [Fe(II)′] and [Fe(III)′] in a non-linear manner.

2. Parameter values will vary independently with medium conditions (e.g., pH, ionic strength and ionic composition), which will also influence steady-state [Fe(II)′] and [Fe(III)′] in a non-linear manner.

3. Real ligands do not all form 1:1 complexes with Fe, nor do they all possess equal electrostatic charges. For this and other reasons, real complexes do not conform precisely to the Eigen–Wilkins mechanism, which means that values of k_f,Fe(III)L and k_f,Fe(II)L will not be independent of ligand type, and values of k_d,Fe(III)L and k_d,Fe(II)L will differ even between ligands with identical values of K_Fe(III)L and K_Fe(II)L. Similarly, real complexes do not conform precisely to Marcus Theory, such that values of $k_{{\text{O}}_2,\text{org}}$ and k_red,org will also differ between ligands with identical values of K_Fe(III)L and K_Fe(II)L.

4. In natural waters, a range of Fe complexes are likely to coexist.

5. In natural waters, oxidants other than O₂ and reductants other than ${\text{O}}_2^{-*}$ may influence Fe speciation. In particular, the possible role of ${\text{O}}_2^{-*}$ as an oxidant of Fe(II) has been ignored here.

This simplified model also neglects biological uptake of Fe(II)′ and/or Fe(III)′ as an additional sink of these species. While this is unlikely to be important at low cell densities, under bloom conditions or in laboratory cultures it may become important. Additionally, the assumption of spatial homogeneity neglects any role of transport processes. In reality, it is highly likely that spatial gradients for several of the species involved (e.g., ${\text{O}}_2^{-*},$ Fe(II)′, and Fe(III)′) will exist under some conditions at least.

In summary, while this analysis demonstrates that ${\text{O}}_2^{-*}$ can potentially increase Fe bioavailability under some conditions, whether this will actually occur depends strongly on the specific chemical conditions.

Do Organisms Exploit Superoxide Chemistry to Facilitate Fe Acquisition?

Since ${\text{O}}_2^{-*}$ can persist in circumneutral natural waters at picomolar concentrations due to biological and other processes, and can increase bioavailable Fe(II)′ and Fe(III)′ concentrations under some such conditions, the potential exists for organisms to exploit this chemistry to facilitate Fe acquisition. A simple test for the involvement of ${\text{O}}_2^{-*}$ in Fe uptake is whether addition of SOD to the external milieu decreases Fe uptake by an organism, on the basis that SOD will scavenge ${\text{O}}_2^{-*}$ and thereby prevent its reaction with Fe. This assay has been used to demonstrate the involvement of ${\text{O}}_2^{-*}$ in Fe uptake under particular conditions by several aquatic microorganisms in culture studies, including C. marina (Garg et al., 2007a), L. majuscula (Rose et al., 2005), and M. aeruginosa (Fujii et al., 2010a). The assay has also been used to demonstrate that ${\text{O}}_2^{-*}$ was apparently not involved in Fe uptake in experiments with cultures of the diatoms T. weissflogii and T. pseudonana (Kustka et al., 2005), and the green alga Chlorella kessleri (Middlemiss et al., 2001).

While the SOD addition assay would seem robust, care must be taken when interpreting and extrapolating results for three main reasons. First, in organisms possessing compartments external to the cytoplasmic membrane (e.g., the periplasm of Gram negative bacteria) or producing extracellular microenvironments (e.g., the glycocalyx of C. marina), SOD may not be able to access the site(s) of extracellular ${\text{O}}_2^{-*}$ production or Fe reduction due to the large size of the molecule (molecular mass ∼32 kDa). Thus if, for example, ${\text{O}}_2^{-*}$ production and subsequent Fe reduction and uptake were occurring in the periplasm of a Gram negative organism, the SOD addition assay would not result in inhibition of Fe uptake. Second, SOD concentrations employed in these assays are often much greater than those theoretically needed to ensure ${\text{O}}_2^{-*}$ concentrations are negligibly small in homogeneous solution. The need to use such large SOD concentrations may be partly related to failure to account for compartmentalization or other spatial heterogeneity, but may potentially be due to as yet unknown non-specific interference with or inhibition of Fe uptake. Finally, as seen above, ${\text{O}}_2^{-*}$ is only able to substantially increase Fe bioavailability under certain conditions. Therefore it is risky to generalize the potential role of ${\text{O}}_2^{-*}$ in Fe uptake based on culture studies under only a few conditions. This has been well demonstrated in studies on C. marina (Garg et al., 2007a) and M. aeruginosa (Fujii et al., 2010a) in which ${\text{O}}_2^{-*}$was found to aid Fe uptake under some conditions, but not others. To date there have been no reports of field experiments to test the role of ${\text{O}}_2^{-*}$ in Fe uptake under more environmentally relevant conditions than those used in culture studies, but such experiments would seem essential to truly test the potential role of ${\text{O}}_2^{-*}$ in Fe uptake by aquatic microorganisms in their natural habitats.

Understanding the potential role of ${\text{O}}_2^{-*}$ in Fe uptake is further complicated by the issue of which comes first: Fe reduction with subsequent ${\text{O}}_2^{-*}$ generation by oxygenation of the resulting Fe(II), or ${\text{O}}_2^{-*}$ generation with subsequent reduction of Fe. Reductive Fe uptake is now recognized to be a major strategy for Fe acquisition by a wide range of aquatic microorganisms (e.g., Maldonado and Price, 2001; Davey et al., 2003), facilitated by a general class of enzymes known as ferrireductases (Schröder et al., 2003; Kranzler et al., 2011). While extracellular ferrireductases vary in structure and location, in some cases at least they are capable of reducing O₂ to ${\text{O}}_2^{-*}$ in addition to reducing Fe(III) to Fe(II) (Lesuisse et al., 1996). Middlemiss et al. (2001) demonstrated in experiments with C. kessleri that while both Fe(II) and ${\text{O}}_2^{-*}$ were generated by the organism, SOD addition had no effect on Fe uptake rates, implying that Fe reduction by cell surface reductases was the first step in the process. It was thus suggested that rates of Fe reduction at the cell surface far exceeded rates of Fe uptake, and that the fate of Fe(II) in the bulk solution had no discernible influence on the kinetics of Fe uptake by the organism. Kustka et al. (2005) also found that addition of exogenous SOD had no effect on Fe uptake rates by T. weissflogii and T. pseudonana, despite a measurable increase in Fe(II) production in the bulk solution due to the presence of ${\text{O}}_2^{-*}$. It was thus suggested that under these experimental conditions, ${\text{O}}_2^{-*}$ simply converted existing Fe(III)′ into Fe(II)′ without changing the total Fe′ concentration, which is ultimately the substrate for uptake. In these cases, it would appear that ${\text{O}}_2^{-*}$ was neither required nor helpful for reductive Fe uptake, despite being produced in the process.

Regardless of whether the initial process is Fe reduction or ${\text{O}}_2^{-*}$ production, its occurrence at or near the cell surface will likely lead to gradients in Fe(II) and ${\text{O}}_2^{-*}$ concentrations away from the cell. If Fe(II) is released from a ferrireductase enzyme into solution prior to uptake, and the timescale of diffusive processes is faster than that of reactive processes, then the spatial distributions of Fe(II) and ${\text{O}}_2^{-*}$ at steady-state should be similar in both cases. However if the diffusive timescale is slower than the reactive timescale, then we would expect significantly higher Fe(II) concentrations near the cell surface in the former case, leading to faster Fe uptake kinetics and implying that reactions between Fe and ${\text{O}}_2^{-*}$ should have only a limited effect on Fe uptake kinetics. In the former case, it may also be possible that Fe(II) is passed directly from the ferrireductase enzyme to an uptake site, in which case we might expect very little (if any) Fe(II) to diffuse into the bulk solution. At present, the only model for reductive Fe uptake that considers spatial heterogeneity at the cellular scale is the Fe(II)s model of Shaked et al. (2005), which considers two pools of Fe: a pool near the cell surface, and another in the bulk solution. More detailed reacto-diffusive modeling would appear needed to quantitatively understand differences in behavior of the ferrireductase system versus a system in which Fe reduction is driven initially by ${\text{O}}_2^{-*}$ generation at the cell surface.

Under What Conditions Can Extracellular Superoxide Production Aid Iron Acquisition?

From the analysis and discussion in the previous sections, an attempt can be made to answer the general question of when will ${\text{O}}_2^{-*}$ assist in Fe uptake? Generally, ${\text{O}}_2^{-*}$ is unlikely to aid Fe uptake when:

1. [Fe′]_T is already high relative to cellular needs. Under these conditions, Fe uptake systems are likely to be near saturation, such that further increasing [Fe′]_T will not substantially increase Fe uptake rates.

2. Organic ligands form strong complexes with Fe(II) relative to those formed with Fe(III). Under these conditions, reduction of Fe(III) to Fe(II) will decrease [Fe′]_T and therefore hinder Fe acquisition.

3. The rate at which ${\text{O}}_2^{-*}$ is reduced to H₂O₂ is relatively fast. Under these conditions, a high rate of ${\text{O}}_2^{-*}$ production (by whatever means) is required to sustain a steady-state concentration of ${\text{O}}_2^{-*}$ that is sufficient to increase [Fe′]_T. Furthermore, relatively rapid production of H₂O₂ may promote formation of biologically harmful species such as $\text{H}{\text{O}}^{\bullet }.$

4. A large proportion of ${\text{O}}_2^{-*}$ is consumed through reactions with species that outcompete Fe(III) for ${\text{O}}_2^{-*}$ and remove electrons from the reactive pool by formation of relatively stable reduced species, e.g., other trace metals and organic radicals. In this case, the efficiency of electron transfer from ${\text{O}}_2^{-*}$ to Fe may again be relatively low and the process expensive for cells.

Thus, extracellular ${\text{O}}_2^{-*}$ is likely to aid Fe uptake when Fe′ concentrations in the absence of ${\text{O}}_2^{-*}$ would be low in terms of biological requirements; reduction of any Fe(III) complexes results in formation of relatively weak Fe(II) complexes; and rates of reduction of ${\text{O}}_2^{-*}$ to H₂O₂ are relatively low. However while these conditions would appear beneficial for cells in terms of promoting Fe bioavailability, this does not mean that cells would necessarily deliberately use ESP to assist in Fe acquisition; establishing the use of ESP in such a way would at least require evidence of regulation at the genetic level, which has not been convincingly demonstrated to date.

What types of environments would meet these criteria? Many marine waters are likely to do so, given that Fe′ is often present at low concentrations due to limited Fe supply and strong organic complexation of Fe(III) (e.g., Rue and Bruland, 1995). It is not certain that the corresponding Fe(II) complexes would always be relatively weak in comparison, but limited measurements of the strength of natural complexes in coastal waters suggests this is likely in some cases at least. Additionally, rates of ${\text{O}}_2^{-*}$ reduction to H₂O₂ would appear relatively low in relatively “clean” marine waters based on reported rates of H₂O₂ production (Palenik and Morel, 1988; Herut et al., 1998) and ${\text{O}}_2^{-*}$ decay (Hansard et al., 2010; Rose et al., 2010; Shaked et al., 2010). Many carbonate-buffered freshwaters might also satisfy these criteria, but there is insufficient information in the literature to draw definitive conclusions. Extracellular ${\text{O}}_2^{-*}$ might also be able to increase Fe bioavailability in some oxygenated sedimentary and soil environments with neutral to alkaline pH where [Fe(III)′] would be expected to be very low. In contrast, extracellular ${\text{O}}_2^{-*}$ is unlikely to increase Fe bioavailability in acidic environments (where Fe solubility would be higher and rates of ${\text{O}}_2^{-*}$ reduction to H₂O₂ relatively rapid) or waters rich in trace metal and/or organic species that could scavenge ${\text{O}}_2^{-*}$ much more effectively than Fe (e.g., highly polluted natural waters or some engineered aquatic systems). Finally, these criteria may not always be met in laboratory cultures. In particular, the widely used ligand EDTA forms rather strong complexes with Fe(II) in comparison to complexes with Fe(III) at pH 8 (Table 1), which will limit the ability of extracellular ${\text{O}}_2^{-*}$ to increase [Fe′]_T under some conditions. ${\text{O}}_2^{-*}$ has previously been observed to have little or no effect on Fe bioavailability in cultures where Fe is complexed by EDTA (Kustka et al., 2005; Garg et al., 2007a), which may be at least partly attributable to this effect, although factors including spatial heterogeneity may also be involved. Therefore, while useful for understanding particular processes, care must be taken in extrapolating such results to natural aquatic systems where ligands with similar properties are unlikely to dominate.

Concluding Remarks

${\text{O}}_2^{-*}$ is produced in the extracellular environment predominantly through univalent reduction of oxygen. This occurs mostly through (i) the oxygenation of relatively labile reduced compounds such as Fe(II) and Cu(I); (ii) abiotic photochemical oxidation of organic compounds; and (iii) biological production by a wide range of eukaryotic and prokaryotic organisms. Biological ESP appears primarily due to the activity of cell surface reductase enzymes that export electrons from the cell either directly to O₂, or to other labile electron acceptors that subsequently react with O₂ to yield ${\text{O}}_2^{-*}$. These processes can together maintain an environmentally significant concentration of ${\text{O}}_2^{-*}$in the extracellular milieu. The chemistry of Fe and ${\text{O}}_2^{-*}$ is intimately coupled in many oxygenated waters. ${\text{O}}_2^{-*}$ is thermodynamically and mechanistically capable of reducing a wide range of forms of Fe(III) under typical environmental conditions, including inorganic Fe(III)′, organically complexed Fe(III), and even solid (polynuclear) forms of Fe(III). Conversely, the oxidation of Fe(II) by O₂ is thought to produce ${\text{O}}_2^{-*}$ (although this has not yet been conclusively demonstrated). While ${\text{O}}_2^{-*}$ can also oxidize Fe(II), at sub-nanomolar ${\text{O}}_2^{-*}$ concentrations in neutral to alkaline solutions, this is likely to be a relatively unimportant reaction because O₂ will oxidize Fe(II) at much faster rates.

The net effect of ${\text{O}}_2^{-*}$ on Fe bioavailability depends not so much on the thermodynamic ability of ${\text{O}}_2^{-*}$ to reduce various forms of Fe(III), but on the net effect of ${\text{O}}_2^{-*}$ on steady-state concentrations of Fe(II)′ and Fe(III)′, which are the species actually internalized by most cells. In a spatially homogeneous steady-state system, ${\text{O}}_2^{-*}$ at concentrations >10 pM can increase [Fe′]_T (=[Fe(II)′] + [Fe(III)′]), provided that the dominant form(s) of Fe(II) (e.g., organic Fe(II) complexes) are relatively labile compared to the dominant form(s) of Fe(III). In a spatially homogeneous system, it is unimportant whether cell surface ferrireductases reduce Fe(III) to Fe(II) that then reacts with O₂ to yield ${\text{O}}_2^{-*},$ or whether cell surface oxygen reductases reduce O₂ to ${\text{O}}_2^{-*}$ that then reacts with Fe(III) to yield Fe(II), unless ferrireductases pass Fe(II) directly to the uptake site without release of free Fe(II). In such a system, direct reduction of O₂ by cells maybe more effective in increasing Fe bioavailability, since rates of O₂ reduction by an oxygen reductase may be faster than rates of Fe(III) reduction by a ferrireductase simply because the concentration of O₂ is much greater than that of Fe(III) in most oxygenated environments. However in a spatially heterogeneous system, a ferrireductase mechanism would likely be more efficient due to biological compartmentalization and diffusion resulting in higher concentrations of Fe(II)′ near the site of cellular uptake compared to in the bulk solution. Understanding the chemistry of Fe and ${\text{O}}_2^{-*}$ at a detailed mechanistic level, and a more rigorous understanding of the role of physical transport processes, is needed to fully assess the potential role of ${\text{O}}_2^{-*}$ in increasing Fe bioavailability in a range of aquatic environments. On the basis of the information presently available, however, it seems that extracellular ${\text{O}}_2^{-*}$ has the potential to significantly increase Fe bioavailability under some conditions at least and may therefore be an important part of the complicated process of Fe acquisition by aquatic organisms.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I wish to acknowledge the contributions over the past decade of my close colleague Prof. T. David Waite and his research group at the University of New South Wales to the work that underpinned the development of many of the ideas discussed in this paper. I also gratefully acknowledge funding from the Australian Research Council through projects DP0987188 and DP0987351 that partly supported the writing of this paper.

References

Aeschbacher, M., Sander, M., and Schwarzenbach, R. P. (2010). Novel electrochemical approach to assess the redox properties of humic substances. Environ. Sci. Technol. 44, 87–93.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Afanas’ev, I. B. (1989). Superoxide Ion Chemistry and Biological Implications. Boca Raton, FL: CRC Press.

Aguirre, J., Rios-Momberg, M., Hewitt, D., and Hansberg, W. (2005). Reactive oxygen species and development in microbial eukaryotes. Trends Microbiol. 13, 111–118.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Auchère, F., and Rusnak, F. (2002). What is the ultimate fate of superoxide anion in vivo? J. Biol. Inorg. Chem. 7, 664–667.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Barbeau, K. A. (2006). Photochemistry of organic iron(III) complexing ligands in oceanic systems. Photochem. Photobiol. 82, 1505–1516.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Baxter, R. M., and Carey, J. H. (1983). Evidence for photochemical generation of superoxide ion in humic waters. Nature 306, 575–576.

CrossRef Full Text

Beckett, R. P., Minibayeva, F. V., Vylegzhanina, N. N., and Tolpysheva, T. (2003). High rates of extracellular superoxide production by lichens in the suborder Peltigerineae correlate with indices of high metabolic activity. Plant Cell Environ. 26, 1827–1837.

CrossRef Full Text

Bielski, B. H. J., Cabelli, D. E., Arudi, R. L., and Ross, A. B. (1985). Reactivity of HO₂/O₂^- radicals in aqueous solution. J. Phys. Chem. Ref. Data 14, 1041–1100.

CrossRef Full Text

Blough, N. V. (1988). Electron paramagnetic resonance measurements of photochemical radical production in humic substances. 1. Effects of oxygen and charge on radical scavenging by nitroxides. Environ. Sci. Technol. 22, 77–82.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bolwell, G. P. (1999). Role of active oxygen species and NO in plant defence responses. Curr. Opin. Plant Biol. 2, 287–294.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bowles, K. C., Ernste, M. J., and Kramer, J. R. (2003). Trace sulfide determination in oxic freshwaters. Anal. Chim. Acta 477, 113–124.

CrossRef Full Text

Boyle, E. S., Guerriero, N., Thiallet, A., Vecchio, R. D., and Blough, N. V. (2009). Optical properties of humic substances and CDOM: relation to structure. Environ. Sci. Technol. 43, 2262–2268.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Briviba, K., Klotz, L. O., and Sies, H. (1997). Toxic and signaling effects of photochemically or chemically generated singlet oxygen in biological systems. Biol. Chem. 378, 1259–1265.

Pubmed Abstract | Pubmed Full Text

Buetler, T. M., Krauskopf, A., and Ruegg, U. T. (2004). Role of superoxide as a signaling molecule. Physiology 19, 120–123.

CrossRef Full Text

Buettner, G. R., Doherty, T. P., and Patterson, L. K. (1983). The kinetics of the reaction of superoxide radical with Fe(III) complexes of EDTA, DETAPAC and HEDTA. FEBS Lett. 158, 143–146.

CrossRef Full Text

Bull, C., Mcclune, G. J., and Fee, J. A. (1983). The mechanism of iron EDTA catalyzed superoxide dismutation. J. Am. Chem. Soc. 105, 5290–5300.

CrossRef Full Text

Cadenas, E. (1989). Biochemistry of oxygen toxicity. Annu. Rev. Biochem. 58, 79–110.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cooper, W. J., Zika, R. G., Petasne, R. G., and Fischer, A. M. (1989). “Sunlight-induced photochemistry of humic substances in natural waters: major reactive species,” in Aquatic Humic Substances: Influence on Fate and Treatment of Pollutants, eds I. H. Suffet, and P. MacCarthy (Washington: American Chemical Society), 333–362.

Cooper, W. J., Zika, R. G., Petasne, R. G., and Plane, J. M. C. (1988). Photochemical formation of hydrogen peroxide in natural waters exposed to sunlight. Environ. Sci. Technol. 22, 1156–1160.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Davey, M. S., Suggett, D. J., Geider, R. J., and Taylor, A. R. (2003). Phytoplankton plasma membrane redox activity: effect of iron limitation and interaction with photosynthesis. J. Phycol. 39, 1132–1144.

CrossRef Full Text

Del Vecchio, R., and Blough, N. V. (2002). Photobleaching of chromophoric dissolved organic matter in natural waters: kinetics and modeling. Mar. Chem. 78, 231–253.

CrossRef Full Text

Del Vecchio, R., and Blough, N. V. (2004). On the origin of the optical properties of humic substances. Environ. Sci. Technol. 38, 3885–3891.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eigen, M., and Wilkins, R. G. (1965). “Kinetics and mechanisms of formation of metal complexes,” in Mechanisms of Inorganic Reactions, eds R. K. Marmann, R. T. Fraser, and J. Bouman (Washington: American Chemical Society), 55–80.

Fan, S.-M. (2008). Photochemical and biochemical controls on reactive oxygen and iron speciation in the pelagic surface ocean. Mar. Chem. 109, 152–164.

CrossRef Full Text

Farkas, E., Enyedy, É. A., and Fábián, I. (2003). New insight into the oxidation of Fe(II) by desferrioxamine B (DFB): spectrophotometric and capillary electrophoresis (CE) study. Inorg. Chem. Commun. 6, 131–134.

CrossRef Full Text

Fridovich, I. (1986). Biological effects of the superoxide radical. Arch. Biochem. Biophys. 247, 1–11.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fridovich, I. (1998). Oxygen toxicity: a radical explanation. J. Exp. Biol. 201, 1203–1209.

Pubmed Abstract | Pubmed Full Text

Fujii, M., Dang, T. C., Rose, A. L., Omura, T., and Waite, T. D. (2011). Effect of light on iron uptake by the freshwater cyanobacterium Microcystis aeruginosa. Environ. Sci. Technol. 45, 1391–1398.

CrossRef Full Text

Fujii, M., Ito, H., Rose, A. L., Waite, T. D., and Omura, T. (2008). Superoxide-mediated Fe(II) formation from organically complexed Fe(III) in coastal waters. Geochim. Cosmochim. Acta 72, 6079–6089.

CrossRef Full Text

Fujii, M., Rose, A. L., Omura, T., and Waite, T. D. (2010a). Effect of Fe(II) and Fe(III) transformation kinetics on iron acquisition by a toxic strain of Microcystis aeruginosa. Environ. Sci. Technol. 44, 1980–1986.

CrossRef Full Text

Fujii, M., Rose, A. L., Waite, T. D., and Omura, T. (2010b). Oxygen and superoxide-mediated redox kinetics of iron complexed by humic substances in coastal seawater. Environ. Sci. Technol. 44, 9337–9342.

CrossRef Full Text

Fujii, M., Rose, A. L., Waite, T. D., and Omura, T. (2006). Superoxide-mediated dissolution of amorphous ferric oxyhydroxide in seawater. Environ. Sci. Technol. 40, 880–887.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Garg, S., Rose, A. L., Godrant, A., and Waite, T. D. (2007a). Iron uptake by the ichthyotoxic Chattonella marina (Raphidophyceae): impact of superoxide generation. J. Phycol. 43, 978–991.

CrossRef Full Text

Garg, S., Rose, A. L., and Waite, T. D. (2007b). Production of reactive oxygen species on photolysis of dilute aqueous quinone solutions. Photochem. Photobiol. 83, 904–913.

CrossRef Full Text

Garg, S., Rose, A. L., and Waite, T. D. (2007c). Superoxide mediated reduction of organically complexed iron(III): comparison of non-dissociative and dissociative reduction pathways. Environ. Sci. Technol. 41, 3205–3212.

CrossRef Full Text

Garg, S., Rose, A. L., and Waite, T. D. (2007d). Superoxide-mediated reduction of organically complexed iron(III): impact of pH and competing cations (Ca²⁺). Geochim. Cosmochim. Acta 71, 5620–5634.

CrossRef Full Text

Garg, S., Rose, A. L., and Waite, T. D. (2011a). Photochemical production of superoxide and hydrogen peroxide from natural organic matter. Geochim. Cosmochim. Acta 75, 4310–4320.

CrossRef Full Text

Garg, S., Rose, A. L., and Waite, T. D. (2011b). “Pathways contributing to the formation and decay of ferrous iron in sunlit natural waters,” in Aquatic Redox Chemistry, eds P. G. Tratnyek, T. J. Grundl, and S. B. Haderlein (Washington: American Chemical Society), 153–176.

Godrant, A., Rose, A. L., Sarthou, G., and Waite, T. D. (2009). A new method for the determination of extracellular production of superoxide from phytoplankton cells using MCLA and red-CLA as chemiluminescent probes. Limnol. Oceanogr. Methods 7, 682–692.

CrossRef Full Text

Gregory, E. M., Moore, W. E., and Holdeman, L. V. (1978). Superoxide dismutase in anaerobes: survey. Appl. Environ. Microbiol. 35, 988–991.

Pubmed Abstract | Pubmed Full Text

Haber, F., and Weiss, J. (1934). The catalytic decomposition of hydrogen peroxide by iron salts. Proc. R. Soc. Lond. A Math. Phys. Sci. 147, 332–351.

CrossRef Full Text

Hansard, S. P., Vermilyea, A. W., and Voelker, B. M. (2010). Measurements of superoxide radical concentration and decay kinetics in the Gulf of Alaska. Deep Sea Res. Part I Oceanogr. Res. Pap. 57, 1111–1119.

CrossRef Full Text

Heller, M. I., and Croot, P. L. (2010). Superoxide decay kinetics in the Southern Ocean. Environ. Sci. Technol. 44, 191–196.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Heller, M. I., and Croot, P. L. (2011). Superoxide decay as a probe for speciation changes during dust dissolution in Tropical Atlantic surface waters near Cape Verde. Mar. Chem. 126, 37–55.

CrossRef Full Text

Henry, M.-F., and Vignais, P. M. (1980). Production of superoxide anions in Paracoccus denitrificans. Arch. Biochem. Biophys. 203, 365–371.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Herut, B., Shoham-Frider, E., Kress, N., Fiedler, U., and Angel, D. L. (1998). Hydrogen peroxide production rates in clean and polluted coastal marine waters of the Mediterranean, Red and Baltic Seas. Mar. Pollut. Bull. 36, 994–1003.

CrossRef Full Text

Hudson, R. J. M., Covault, D. T., and Morel, F. M. M. (1992). Investigations of iron coordination and redox reactions in seawater using ⁵⁹Fe radiometry and ion-pair solvent extraction of amphiphilic iron complexes. Mar. Chem. 38, 209–235.

CrossRef Full Text

Imlay, J. A., and Fridovich, I. (1991). Assay of metabolic superoxide production in Escherichia coli. J. Biol. Chem. 266, 6957–6965.

Pubmed Abstract | Pubmed Full Text

Jayson, G. G., Keene, J. P., Stirling, D. A., and Swallow, A. J. (1969). Pulse-radiolysis study of some unstable complexes of iron. Trans. Faraday Soc. 65, 2453–2464.

CrossRef Full Text

Jayson, G. G., Parsons, B. J., and Swallow, A. J. (1973). Oxidation of ferrous ions by perhydroxyl radicals. J. Chem. Soc. Faraday Trans. 1 69, 236–242.

Jones, G. J., Waite, T. D., and Smith, J. D. (1985). Light-dependent reduction of copper(II) and its effect on cell-mediated thiol-dependent superoxide production. Biochem. Biophys. Res. Commun. 128, 1031–1036.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Katz, J. E., Gilbert, B., Zhang, X., Attenkofer, K., Falcone, R. W., and Waychunas, G. A. (2010). Observation of transient iron(II) formation in dye-sensitized iron oxide nanoparticles by time-resolved X-ray spectroscopy. J. Phys. Chem. Lett. 1, 1372–1376.

CrossRef Full Text

Khaikin, G. I., Alfassi, Z. B., Huie, R. E., and Neta, P. (1996). Oxidation of ferrous and ferrocyanide ions by peroxyl radicals. J. Phys. Chem. 100, 7072–7077.

CrossRef Full Text

Kim, D., Nakamura, A., Okamoto, T., Komatsu, N., Oda, T., Iida, T., Ishimatsu, A., and Muramatsu, T. (2000). Mechanism of superoxide anion generation in the toxic red tide phytoplankton Chattonella marina: possible involvement of NAD(P)H oxidase. Biochim. Biophys. Acta 1524, 220–227.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Koppenol, W. H. (1976). Reactions involving singlet oxygen and the superoxide anion. Nature 262, 420–421.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Koppenol, W. H. (2001). The Haber-Weiss cycle – 70 years later. Redox Rep. 6, 229–234.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Korshunov, S., and Imlay, J. A. (2006). Detection and quantification of superoxide formed within the periplasm of Escherichia coli. J. Bacteriol. 188, 6326–6334.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Korshunov, S. S., and Imlay, J. A. (2002). A potential role for periplasmic superoxide dismutase in blocking the penetration of external superoxide into the cytosol of Gram-negative bacteria. Mol. Microbiol. 43, 95–106.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kosman, D. J. (2003). Molecular mechanisms of iron uptake in fungi. Mol. Microbiol. 47, 1185–1197.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kranzler, C., Lis, H., Shaked, Y., and Keren, N. (2011). The role of reduction in iron uptake processes in a unicellular, planktonic cyanobacterium. Environ. Microbiol. 13, 2990–2999.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kustka, A., Shaked, Y., Milligan, A., King, D. W., and Morel, F. M. M. (2005). Extracellular production of superoxide by marine diatoms: contrasting effects on iron redox chemistry and bioavailability. Limnol. Oceanogr. 50, 1172–1180.

CrossRef Full Text

Lambeth, J. D. (2004). NOX enzymes and the biology of reactive oxygen. Nat. Rev. Immunol. 4, 181–189.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lara-Ortíz, T., Riveros-Rosas, H., and Aguirre, J. (2003). Reactive oxygen species generated by microbial NADPH oxidase NoxA regulate sexual development in Aspergillus nidulans. Mol. Microbiol. 50, 1241–1255.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Learman, D. R., Voelker, B. M., Vazquez-Rodriguez, A. I., and Hansel, C. M. (2011). Formation of manganese oxides by bacterially generated superoxide. Nat. Geosci. 4, 95–98.

CrossRef Full Text

Lesser, M. P. (2006). Oxidative stress in marine environments: biochemistry and physiological ecology. Annu. Rev. Physiol. 68, 253–278.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lesuisse, E., Casteras-Simon, M., and Labbe, P. (1996). Evidence for the Saccharomyces cerevisiae ferrireductase system being a multicomponent electron transport chain. J. Biol. Chem. 271, 13578–13583.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Liochev, S. I., and Fridovich, I. (1999). Superoxide and iron: partners in crime. IUBMB Life 48, 157–161.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Luther, G. W. III, and Rickard, D. T. (2005). Metal sulfide cluster complexes and their biogeochemical importance in the environment. J. Nanopart. Res. 7, 389–407.

CrossRef Full Text

Luther, G. W. III. (2010). The role of one- and two-electron transfer reactions in forming thermodynamically unstable intermediates as barriers in multi-electron redox reactions. Aquat. Geochem. 16, 395–420.

CrossRef Full Text

Maldonado, M. T., and Price, N. M. (2001). Reduction and transport of organically bound iron by Thalassiosira oceanica (Bacillariophyceae). J. Phycol. 37, 298–310.

CrossRef Full Text

Mansano-Weiss, C., Cohen, H., and Meyerstein, D. (2002). Reactions of peroxyl radicals with Fe(H₂O)₆²⁺. J. Inorg. Biochem. 91, 199–204.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Marcus, R. A., and Sutin, N. (1985). Electron transfers in chemistry and biology. Biochim. Biophys. Acta 811, 265–322.

Marshall, J.-A., De Salas, M., Oda, T., and Hallegraeff, G. (2005). Superoxide production by marine microalgae. I. Survey of 37 species from 6 classes. Mar. Biol. 147, 533–540.

CrossRef Full Text

Marshall, J.-A., Hovenden, M., Oda, T., and Hallegraeff, G. M. (2002). Photosynthesis does influence superoxide production in the ichthyotoxic alga Chattonella marina (Raphidophyceae). J. Plankton Res. 24, 1231–1236.

CrossRef Full Text

McCord, J. M., Keele, B. B., and Fridovich, I. (1971). An enzyme-based theory of obligate anaerobiosis: the physiological function of superoxide dismutase. Proc. Natl. Acad. Sci. U.S.A. 68, 1024–1027.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Micinski, E., Ball, L. A., and Zafiriou, O. C. (1993). Photochemical oxygen activation: superoxide radical detection and production rates in the eastern Caribbean. J. Geophys. Res. 98, 2299–2306.

CrossRef Full Text

Middlemiss, J. K., Anderson, A. M., Stratilo, C. W., and Weger, H. G. (2001). Oxygen consumption associated with ferric reductase activity and iron uptake by iron-limited cells of Chlorella kessleri (Cholophyceae). J. Phycol. 37, 393–399.

CrossRef Full Text

Miller, W. L., King, D. W., Lin, J., and Kester, D. R. (1995). Photochemical redox cycling of iron in coastal seawater. Mar. Chem. 50, 63–77.

CrossRef Full Text

Millero, F. J., Yao, W., and Aicher, J. (1995). The speciation of Fe(II) and Fe(III) in natural waters. Mar. Chem. 50, 21–39.

CrossRef Full Text

Milne, A., Davey, M. S., Worsfold, P. J., Achterberg, E. P., and Taylor, A. R. (2009). Real-time detection of reactive oxygen species generation by marine phytoplankton using flow injection-chemiluminescence. Limnol. Oceanogr. Methods 7, 706–715.

CrossRef Full Text

Moffett, J. W., and Zafiriou, O. C. (1990). An investigation of hydrogen peroxide chemistry in surface waters of Vineyard Sound with H₂¹⁸O₂ and ¹⁸O₂. Limnol. Oceanogr. 35, 1221–1229.

CrossRef Full Text

Morel, F. M. M., Kustka, A. B., and Shaked, Y. (2008). The role of unchelated Fe in the iron nutrition of phytoplankton. Limnol. Oceanogr. 53, 400–404.

CrossRef Full Text

Nakano, M. (1998). Detection of active oxygen species in biological systems. Cell. Mol. Neurobiol. 18, 565–579.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nakano, M., Sugioka, K., Ushijima, Y., and Goto, T. (1986). Chemiluminescence probe with Cypridina luciferin analog, 2-methyl-6-phenyl-3,7-dihydroimidazo[1,2-a]pyrazin-3-one, for estimating the ability of human granulocytes to generate O₂^-. Anal. Biochem. 159, 363–369.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nanni, E. J., Birge, R. R., Hubbard, L. M., Morrison, M. M., and Sawyer, D. T. (1981). Oxidation and dismutation of superoxide ion solutions to molecular oxygen. Singlet vs. triplet state. Inorg. Chem. 20, 737–741.

CrossRef Full Text

Neuman, E. W. (1934). Potassium superoxide and the three-electron bond. J. Chem. Phys. 2, 31–33.

CrossRef Full Text

Oda, T., Akaike, T., Sato, K., Ishimatsu, A., Takeshita, S., Muramatsu, T., and Maeda, H. (1992). Hydroxyl radical generation by red tide algae. Arch. Biochem. Biophys. 294, 38–43.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Oda, T., Nakamura, A., Shikayama, M., Kawano, I., Ishimatsu, A., and Muramatsu, T. (1997). Generation of reactive oxygen species by raphidophycean phytoplankton. Biosci. Biotechnol. Biochem. 61, 1658–1662.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Palenik, B., and Morel, F. M. M. (1988). Dark production of H₂O₂ in the Sargasso Sea. Limnol. Oceanogr. 33, 1606–1611.

CrossRef Full Text

Pauling, L. (1931). The nature of the chemical bond. II. The one-electron bond and the three-electron bond. J. Am. Chem. Soc. 53, 3225–3237.

CrossRef Full Text

Pauling, L. (1979). The discovery of the superoxide radical. Trends Biochem. Sci. 4, N270–N271.

CrossRef Full Text

Petasne, R. G., and Zika, R. G. (1987). Fate of superoxide in coastal sea water. Nature 325, 516–518.

CrossRef Full Text

Pierre, J. L., and Fontecave, M. (1999). Iron and activated oxygen species in biology: the basic chemistry. Biometals 12, 195–199.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pierre, J. L., Fontecave, M., and Crichton, R. R. (2002). Chemistry for an essential biological process: the reduction of ferric iron. Biometals 15, 341–346.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rao, D. N. R., Fischer, V., and Mason, R. P. (1990). Glutathione and ascorbate reduction of the acetaminophen radical formed by peroxidase. Detection of the glutathione disulfide radical anion and the ascorbyl radical. J. Biol. Chem. 265, 844–847.

Pubmed Abstract | Pubmed Full Text

Ratasuk, N., and Nanny, M. A. (2007). Characterization and quantification of reversible redox sites in humic substances. Environ. Sci. Technol. 41, 7844–7850.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Remucal, C. K., and Sedlak, D. L. (2011). “The role of iron coordination in the production of reactive oxidants from ferrous iron oxidation by oxygen and hydrogen peroxide,” in Aquatic Redox Chemistry, eds P. G. Tratnyek, T. J. Grundl, and S. B. Haderlein (Washington: American Chemical Society), 177–197.

Rickard, D., and Luther, G. W. III. (2006). Metal sulfide complexes and clusters. Rev. Mineral. Geochem. 61, 421–504.

CrossRef Full Text

Rose, A. L., Godrant, A., Furnas, M., and Waite, T. D. (2010). Dynamics of nonphotochemical superoxide production in the Great Barrier Reef lagoon. Limnol. Oceanogr. 55, 1521–1536.

CrossRef Full Text

Rose, A. L., Moffett, J. W., and Waite, T. D. (2008a). Determination of superoxide in seawater using 2-methyl-6-(4-methoxyphenyl)-3,7-dihydroimidazo[1,2-a]pyrazin-3(7H)-one chemiluminescence. Anal. Chem. 80, 1215–1227.

CrossRef Full Text

Rose, A. L., Webb, E. A., Waite, T. D., and Moffett, J. W. (2008b). Measurement and implications of nonphotochemically generated superoxide in the equatorial Pacific Ocean. Environ. Sci. Technol. 42, 2387–2393.

CrossRef Full Text

Rose, A. L., Salmon, T. P., Lukondeh, T., Neilan, B. A., and Waite, T. D. (2005). Use of superoxide as an electron shuttle for iron acquisition by the marine cyanobacterium Lyngbya majuscula. Environ. Sci. Technol. 39, 3708–3715.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rose, A. L., and Waite, T. D. (2003a). Effect of dissolved natural organic matter on the kinetics of ferrous iron oxygenation in seawater. Environ. Sci. Technol. 37, 4877–4886.

CrossRef Full Text

Rose, A. L., and Waite, T. D. (2003b). Kinetics of iron complexation by dissolved natural organic matter in coastal waters. Mar. Chem. 84, 85–103.

CrossRef Full Text

Rose, A. L., and Waite, T. D. (2005). Reduction of organically complexed ferric iron by superoxide in a simulated natural water. Environ. Sci. Technol. 39, 2645–2650.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rosso, K. M., and Morgan, J. J. (2002). Outer-sphere electron transfer kinetics of metal ion oxidation by molecular oxygen. Geochim. Cosmochim. Acta 66, 4223–4233.

CrossRef Full Text

Rue, E. L., and Bruland, K. W. (1995). Complexation of iron(III) by natural organic ligands in the Central North Pacific as determined by a new competitive ligand equilibration/adsorptive cathodic stripping voltammetric method. Mar. Chem. 50, 117–138.

CrossRef Full Text

Rush, J. D., and Bielski, B. H. J. (1985). Pulse radiolytic studies of the reactions of HO₂/O₂^- with Fe(II)/Fe(III) ions. The reactivity of HO₂/O₂^- with ferric ions and its implication on the occurrence of the Haber-Weiss reaction. J. Phys. Chem. 89, 5062–5066.

CrossRef Full Text

Sagi, M., and Fluhr, R. (2001). Superoxide production by plant homologues of the gp91^phox NADPH oxidase. Modulation of activity by calcium and by tobacco mosaic virus infection. Plant Physiol. 126, 1281–1290.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Saragosti, E., Tchernov, D., Katsir, A., and Shaked, Y. (2010). Extracellular production and degradation of superoxide in the coral Stylophora pistillata and cultured Symbiodinium. PLoS ONE 5, e12508. doi:10.1371/journal.pone.0012508

CrossRef Full Text

Sawyer, D. T. (1991). Oxygen Chemistry. New York: Oxford University Press.

Sawyer, D. T., and Gibian, M. J. (1979). The chemistry of superoxide ion. Tetrahedron 35, 1471–1481.

CrossRef Full Text

Sawyer, D. T., and Valentine, J. S. (1981). How super is superoxide? Acc. Chem. Res. 14, 393–400.

CrossRef Full Text

Schröder, I., Johnson, E., and De Vries, S. (2003). Microbial ferric iron reductases. FEMS Microbiol. Rev. 27, 427–447.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Seibig, S., and van Eldik, R. (1997). Kinetics of [Fe^II(edta)] oxidation by molecular oxygen revisited. New evidence for a multistep mechanism. Inorg. Chem. 36, 4115–4120.

CrossRef Full Text

Shaked, Y., Harris, R., and Klein-Kedem, N. (2010). Hydrogen peroxide photocycling in the Gulf of Aqaba, Red Sea. Environ. Sci. Technol. 44, 3238–3244.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shaked, Y., Kustka, A. B., and Morel, F. M. M. (2005). A general kinetic model for iron acquisition by eukaryotic phytoplankton. Limnol. Oceanogr. 50, 872–882.

CrossRef Full Text

Shatwell, K. P., Dancis, A., Cross, A. R., Klausner, R. D., and Segal, A. W. (1996). The FRE1 ferric reductase of Saccharomyces cerevisiae is a cytochrome b similar to that of NADPH oxidase. J. Biol. Chem. 271, 14240–14244.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sunda, W., and Huntsman, S. (2003). Effect of pH, light, and temperature on Fe-EDTA chelation and Fe hydrolysis in seawater. Mar. Chem. 84, 35–47.

CrossRef Full Text

Teranishi, K. (2007). Development of imidazopyrazinone red-chemiluminescent probes for detecting superoxide anions via a chemiluminescence resonance energy transfer method. Luminescence 22, 147–156.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thomas-Smith, T. E., and Blough, N. V. (2001). Photoproduction of hydrated electron from constituents of natural waters. Environ. Sci. Technol. 35, 2721–2726.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Torres, M. A., Onouchi, H., Hamada, S., Machida, C., Hammond-Kosack, K. E., and Jones, J. D. G. (1998). Six Arabidopsis thaliana homologues of the human respiratory burst oxidase (gp91^phox). Plant J. 14, 365–370.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vignais, P. V. (2002). The superoxide-generating NADPH oxidase: structural aspects and activation mechanism. Cell. Mol. Life Sci. 59, 1428–1459.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Voelker, B. M., Morel, F. M. M., and Sulzberger, B. (1997). Iron redox cycling in surface waters: effects of humic substances and light. Environ. Sci. Technol. 31, 1004–1011.

CrossRef Full Text

Voelker, B. M., and Sedlak, D. L. (1995). Iron reduction by photoproduced superoxide in seawater. Mar. Chem. 50, 93–102.

CrossRef Full Text

Weber, L., Völker, C., Oschlies, A., and Burchard, H. (2007). Iron profiles and speciation of the upper water column at the Bermuda Atlantic Time-series Study site: a model based sensitivity study. Biogeosciences 4, 689–706.

CrossRef Full Text

Weber, L., Völker, C., Schartau, M., and Wolf-Gladrow, D. A. (2005). Modeling the speciation and biogeochemistry of iron at the Bermuda Atlantic Time-series Study site. Global Biogeochem. Cycles 19, GB1019.

CrossRef Full Text

Weinstock, I. A. (2008). Outer-sphere oxidation of the superoxide radical anion. Inorg. Chem. 47, 404–406.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Winterbourn, C. C. (1995). Toxicity of iron and hydrogen peroxide: the Fenton reaction. Toxicol. Lett. 82–83, 969–974.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Witter, A. E., Hutchins, D. A., Butler, A., and Luther, G. W. (2000). Determination of conditional stability constants and kinetic constants for strong model Fe-binding ligands in seawater. Mar. Chem. 69, 1–17.

CrossRef Full Text

Wolfe-Simon, F., Grzebyk, D., Schofield, O., and Falkowski, P. G. (2005). The role and evolution of superoxide dismutases in algae. J. Phycol. 41, 453–465.

CrossRef Full Text

Yamasaki, Y., Kim, D.-I., Matsuyama, Y., Oda, T., and Honjo, T. (2004). Production of superoxide anion and hydrogen peroxide by the red tide dinoflagellate Karenia mikimotoi. J. Biosci. Bioeng. 97, 212–215.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zafiriou, O. C. (1990). Chemistry of superoxide ion-radical (O₂^–) in seawater. I. pKa_sw* (HOO) and uncatalyzed dismutation kinetics studied by pulse radiolysis. Mar. Chem. 30, 31–43.

CrossRef Full Text

Zang, V., and van Eldik, R. (1990). Kinetics and mechanism of the autoxidation of iron(II) induced through chelation by ethylenediaminetetraacetate and related ligands. Inorg. Chem. 29, 1705–1711.

CrossRef Full Text

Appendix

Additional Details of Chemistry of Reactions between Superoxide and Iron

Thermodynamics

Application of the Nernst equation, using measured or estimated values for the concentrations of the various species, is required to determine the environmental redox potential at 25°C:

$E=E^0+59log\left(\left[\text{Ox}\right]/\left[\text{Red}\right]\right)$(A1)

where Ox represents the oxidized form of the species, Red the reduced form, and E and E⁰ are in millivolt.

Consequently, under conditions typical for a neutral air-saturated surface water (pH 7 and [O₂] = 250 μM), the actual redox potential of the ${\text{O}}_2/{\text{O}}_2^{-*}$ couple is +335 mV when $\left[{\text{O}}_{\text{2}}^{-*}\right]$ = 1 pM and +158 mV when $\left[{\text{O}}_{\text{2}}^{-*}\right]$ = 1 nM. While Pierre et al. (2002) emphasize the importance of using actual concentrations of O₂ and ${\text{O}}_2^{-*}$ to calculate relevant redox potentials, an equally important consideration for the thermodynamic reducibility of a particular form of Fe by ${\text{O}}_2^{-*}$ is the concentration of relevant Fe(II) and Fe(III) species. This is well demonstrated by considering the case of some organic Fe complexes, which we denote as Fe(II)L in the reduced state and Fe(III)L in the oxidized state. Since:

$E^0=59logK$(A2)

where K is the equilibrium constant for the equilibrium redox reaction:

$\text{Ox}+n{\text{e}}^{-}\iff \text{Red}$(A3)

we obtain the relationship:

$\begin{array}{llll}{E}_{\text{F}{\text{e}}^{3+}\text{L}\to \text{F}{\text{e}}^{2+}\text{L}}^0& =E_{\text{F}{\text{e}}^{3+}\to \text{F}{\text{e}}^{2+}}^0+59log\left(K_{\text{F}{\text{e}}^{2+}\text{L}}/K_{\text{F}{\text{e}}^{3+}\text{L}}\right)& & \\ & =E_{\text{F}{\text{e}}^{3+}\to \text{F}{\text{e}}^{2+}}^0+59log\left(\left(K_{\text{Fe}\left(\text{II}\right)\text{L}}{\alpha }_{\text{F}{\text{e}}^{3+}}\right)/\left(K_{\text{Fe}\left(\text{III}\right)\text{L}}{\alpha }_{\text{F}{\text{e}}^{2+}}\right)\right)& & \text{(A4)}\end{array}$

where the stability constants are mixed constants expressed as:

$\begin{array}{llll}{K}_{\text{F}{\text{e}}^{2+}\text{L}}& =\frac{\left[\text{Fe}\left(\text{II}\right)\text{L}\right]}{\left[\text{F}{\text{e}}^{2+}\right]\left[{\text{L}}^{\prime }\right]}& & \text{(A5)}\\ K_{\text{F}{\text{e}}^{3+}\text{L}}& =\frac{\left[\text{Fe}\left(\text{III}\right)\text{L}\right]}{\left[\text{F}{\text{e}}^{3+}\right]\left[{\text{L}}^{\prime }\right]}& & \text{(A6)}\\ K_{\text{Fe}\left(\text{II}\right)\text{L}}& =\frac{\left[\text{Fe}\left(\text{II}\right)\text{L}\right]}{\left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]\left[{\text{L}}^{\prime }\right]}& & \text{(A7)}\\ K_{\text{Fe}\left(\text{III}\right)\text{L}}& =\frac{\left[\text{Fe}\left(\text{III}\right)\text{L}\right]}{\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]\left[{\text{L}}^{\prime }\right]}& & \text{(A8)}\end{array}$

and where, under particular medium conditions, Fe(II)′ represents the sum of all monomeric inorganic Fe(II) species, Fe(III)′ represents the sum of all monomeric inorganic Fe(III) species, L′ represents the sum of all ligand species, ${\alpha }_{\text{F}{\text{e}}^{2+}}$ represents the ratio of [Fe²⁺]/[Fe(II)′], and ${\alpha }_{\text{F}{\text{e}}^{3+}}$ represents the ratio of [Fe³⁺]/[Fe(III)′].

It is then relatively straightforward to rewrite the Nernst equation in terms of the stability constants of the Fe(III) complex and Fe(II) complex:

$E_{\text{F}{\text{e}}^{3+}\text{L}\to \text{F}{\text{e}}^{2+}\text{L}}=E_{\text{F}{\text{e}}^{3+}\text{L}\to \text{F}{\text{e}}^{2+}\text{L}}^0+59log\left(\left[\text{Fe}\left(\text{II}\right)\text{L}\right]/\left[\text{Fe}\left(\text{III}\right)\text{L}\right]\right)=E_{\text{F}{\text{e}}^{3+}\to \text{F}{\text{e}}^{2+}}^0+59\text{log}\left(\left(K_{\text{Fe}\left(\text{II}\right)\text{L}}{\alpha }_{\text{F}{\text{e}}^{3+}}\right)/\left(K_{\text{Fe}\left(\text{III}\right)\text{L}}{\alpha }_{\text{F}{\text{e}}^{2+}}\right)\right)+59log\left(\left[\text{Fe}\left(\text{II}\right)\text{L}\right]/\left[\text{Fe}\left(\text{III}\right)\text{L}\right]\right)$(A9)

The criterion that must be satisfied for a thermodynamic driving force toward Fe(III)L reduction is:

$E_{\text{F}{\text{e}}^{3+}\text{L}\to \text{F}{\text{e}}^{2+}\text{L}}>E_{{\text{O}}_{\text{2}}\to {\text{O}}_2^{-*}}$(A10)

which, in combination with Eq. A9, yields the necessary condition:

$log\left(\left[\text{Fe}\left(\text{II}\right)\text{L}\right]/\left[\text{Fe}\left(\text{III}\right)\text{L}\right]\right)<\left(E_{\text{F}{\text{e}}^{3+}\to \text{F}{\text{e}}^{2+}}^0-E_{{\text{O}}_{\text{2}}\to {\text{O}}_2^{-*}}\right)/59+log\left(\left(K_{\text{Fe}\left(\text{II}\right)\text{L}}{\alpha }_{\text{F}{\text{e}}^{3+}}\right)/\left(K_{\text{Fe}\left(\text{III}\right)\text{L}}{\alpha }_{\text{F}{\text{e}}^{2+}}\right)\right)$(A11)

According to the Nernst equation, reduction of Fe³⁺ to Fe²⁺ is thermodynamically feasible when:

$\begin{array}{llll}& E_{\text{F}{\text{e}}^{3+}\to \text{F}{\text{e}}^{2+}}=E_{\text{F}{\text{e}}^{3+}\to \text{F}{\text{e}}^{2+}}^0+59log\left(\left[\text{F}{\text{e}}^{3+}\right]/\left[\text{F}{\text{e}}^{2+}\right]\right)>E_{{\text{O}}_{\text{2}}\to {\text{O}}_2^{-*}}& & \text{(A12)}\\ & \text{i}\text{.e}\text{.}log\left(\left[\text{F}{\text{e}}^{3+}\right]/\left[\text{F}{\text{e}}^{2+}\right]\right)>\left(E_{{\text{O}}_{\text{2}}\to {\text{O}}_2^{-*}}-E_{\text{F}{\text{e}}^{3+}\to \text{F}{\text{e}}^{2+}}^0\right)/59& & \text{(A13)}\\ & \Rightarrow log\left(\left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]/\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]\right)<log\left({\alpha }_{\text{F}{\text{e}}^{3+}}/{\alpha }_{\text{F}{\text{e}}^{2+}}\right)+\left(E_{\text{F}{\text{e}}^{3+}\to \text{F}{\text{e}}^{2+}}^0-E_{{\text{O}}_{\text{2}}\to {\text{O}}_2^{-*}}\right)/59& & \text{(A14)}\end{array}$

Kinetics and Mechanisms

The reduction of each Fe(III) species by ${\text{O}}_2^{-*}$ can be represented by the following two general reactions:

$\begin{array}{llll}& \text{Fe}{\left(\text{III}\right)}_i+{\text{O}}_2^{-}\to \text{Fe}{\left(\text{II}\right)}_i+{\text{O}}_2& & \text{(A15)}\\ & \text{Fe}{\left(\text{III}\right)}_i+\text{HO}{\text{O}}^{\bullet }\to \text{Fe}{\left(\text{II}\right)}_i+{\text{O}}_2+{\text{H}}^{+}& & \text{(A16)}\end{array}$

where Fe(III)_i represents an individual Fe(III) species. The corresponding rate law equation is given by:

$-\frac{\text{d}}{\text{d}t}\left[\text{Fe}{\left(\text{III}\right)}_i\right]=k_{\text{red},{\text{O}}_2^{-},i}\left[\text{Fe}{\left(\text{III}\right)}_i\right]\left[{\text{O}}_{\text{2}}^{-}\right]+k_{\text{red},\text{HO}{\text{O}}^{\bullet },i}\left[\text{Fe}{\left(\text{III}\right)}_i\right]\left[\text{HO}{\text{O}}^{\bullet }\right]$(A17)

Since ${\text{O}}_2^{-}$ and $\text{HO}{\text{O}}^{\bullet }$ equilibrate much faster than the timescale of this reaction, we can write $\left[{\text{O}}_2^{-}\right]={\text{α}}_{{\text{O}}_2^{-}}\left[{\text{O}}_2^{-*}\right]$ and $\left[\text{HO}{\text{O}}^{\bullet }\right]={\alpha }_{\text{HO}{\text{O}}^{\bullet }}\left[{\text{O}}_2^{-*}\right]$ where ${\alpha }_{{\text{O}}_2^{-}}$ and ${\alpha }_{\text{HO}{\text{O}}^{\bullet }}$ are constants under constant medium conditions (pH, ionic strength, etc.). Thus the rate law equation becomes:

$-\frac{\text{d}}{\text{d}t}\left[\text{Fe}{\left(\text{III}\right)}_i\right]=\left(k_{\text{red},{\text{O}}_2^{-},i}{\alpha }_{{\text{O}}_2^{-}}+k_{\text{red},\text{HO}{\text{O}}^{\bullet },i}{\alpha }_{\text{HO}{\text{O}}^{\bullet }}\right)\left[\text{Fe}{\left(\text{III}\right)}_i\right]\left[{\text{O}}_2^{-*}\right]=k_{\text{red,}i}\left[\text{Fe}{\left(\text{III}\right)}_i\right]\left[{\text{O}}_2^{-*}\right]$(A18)

where ${\text{O}}_2^{-*}$ exhibits constant speciation under given constant medium conditions, and k_red,i is a conditional rate constant for reduction of Fe(III)_i under those conditions. The overall rate law for reduction of all Fe(III) species is then given by:

$-\frac{\text{d}}{\text{d}t}{\left[\text{Fe}\left(\text{III}\right)\right]}_{\text{T}}=-\frac{\text{d}}{\text{d}t}\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]-\frac{\text{d}}{\text{d}t}{\left[\text{Fe}\left(\text{III}\right)\right]}_{\text{org}}-\frac{\text{d}}{\text{d}t}{\left[\text{Fe}\left(\text{III}\right)\right]}_{\text{poly}}=\sum _{\text{all}x}{k}_{\text{red},x}\left[\text{Fe}{\left(\text{III}\right)}_x\right]\left[{\text{O}}_2^{-*}\right]+\sum _{\text{all}y}{k}_{\text{red},y}\left[\text{Fe}{\left(\text{III}\right)}_y\right]\left[{\text{O}}_2^{-*}\right]+\sum _{\text{all}z}{k}_{\text{red},z}\left[\text{Fe}{\left(\text{III}\right)}_z\right]\left[{\text{O}}_2^{-*}\right]$(A19)

where [Fe(III)]_T denotes the total concentration of Fe(III) in all classes; [Fe(III)′] denotes the total concentration of all Fe(III) species in the mononuclear inorganic class, [Fe(III)]_org denotes the total concentration of all Fe(III) species in the mononuclear organic class, and [Fe(III)]_poly denotes the total concentration of all Fe(III) species in the polynuclear class; and Fe(III)_x, Fe(III)_y, and Fe(III)_z denote individual Fe(III) species in the mononuclear inorganic, mononuclear organic, and polynuclear classes, respectively.

A similar analysis yields the rate law for oxidation of all Fe(II) species by ${\text{O}}_2^{-*}$:

$-\frac{\text{d}}{\text{d}t}{\left[\text{Fe}\left(\text{II}\right)\right]}_{\text{T}}=-\frac{\text{d}}{\text{d}t}\left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]-\frac{\text{d}}{\text{d}t}{\left[\text{Fe}\left(\text{II}\right)\right]}_{\text{org}}-\frac{\text{d}}{\text{d}t}{\left[\text{Fe}\left(\text{II}\right)\right]}_{\text{poly}}=\sum _{\text{all}x}{k}_{\text{ox,}x}\left[\text{Fe}{\left(\text{II}\right)}_x\right]\left[{\text{O}}_2^{-*}\right]+\sum _{\text{all}y}{k}_{\text{ox,y}}\left[\text{Fe}{\left(\text{II}\right)}_y\right]\left[{\text{O}}_2^{-*}\right]+\sum _{\text{all}z}{k}_{\text{ox,}z}\left[\text{Fe}{\left(\text{II}\right)}_z\right]\left[{\text{O}}_2^{-*}\right]$(A20)

where [Fe(II)]_T denotes the total concentration of Fe(II) in all classes; [Fe(II)′] denotes the total concentration of all Fe(II) species in the mononuclear inorganic class, [Fe(II)]_org denotes the total concentration of all Fe(II) species in the mononuclear organic class, and [Fe(II)]_poly denotes the total concentration of all Fe(II) species in the polynuclear class; and Fe(II)_x, Fe(II)_y, and Fe(II)_z denote individual Fe(II) species in the mononuclear inorganic, mononuclear organic, and polynuclear classes, respectively.

Mononuclear inorganic Fe(III) species equilibrate much faster than the timescale of their reactions with ${\text{O}}_2^{-*}$. Thus we can further simplify Eq. A19using the relationship:

$\sum _{\text{all}x}{k}_{\text{red},x}\left[\text{Fe}{\left(\text{III}\right)}_x\right]\left[{\text{O}}_2^{-*}\right]=\sum _{\text{all}x}{k}_{\text{red},x}{\alpha }_{\text{Fe}{\left(\text{III}\right)}_x}\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]\left[{\text{O}}_2^{-*}\right]=k_{\text{red},\text{inorg}}\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]\left[{\text{O}}_2^{-*}\right]$(A21)

where ${\alpha }_{\text{Fe}{\left(\text{III}\right)}_x}$ represents the ratio of [Fe(III)_x]/[Fe(III)′] and k_red,inorg is a conditional rate constant for reduction of all mononuclear inorganic Fe(III) species under particular, constant medium conditions.

Hence overall:

$-\frac{\text{d}}{\text{d}t}{\left[\text{Fe}\left(\text{III}\right)\right]}_{\text{T}}=k_{\text{red},\text{inorg}}\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]\left[{\text{O}}_2^{-*}\right]+\sum _{\text{all}y}{k}_{\text{red},y}\left[\text{Fe}{\left(\text{III}\right)}_y\right]\left[{\text{O}}_2^{-*}\right]+\sum _{\text{all}z}{k}_{\text{red},z}\left[\text{Fe}{\left(\text{III}\right)}_z\right]\left[{\text{O}}_2^{-*}\right]$(A22)

Similarly for oxidation of Fe(II) by ${\text{O}}_2^{-*}:$

$-\frac{\text{d}}{\text{d}t}{\left[\text{Fe}\left(\text{II}\right)\right]}_{\text{T}}=k_{\text{ox,inorg}}\left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]\left[{\text{O}}_2^{-*}\right]+\sum _{\text{all}y}{k}_{\text{ox,}y}\left[\text{Fe}{\left(\text{II}\right)}_y\right]\left[{\text{O}}_2^{-*}\right]+\sum _{\text{all}z}{k}_{\text{ox,z}}\left[\text{Fe}{\left(\text{II}\right)}_z\right]\left[{\text{O}}_2^{-*}\right]$(A23)

Details of Spatially Homogeneous Steady-State Model for Fe′ Concentrations as a Function of Superoxide Concentrations

The steady-state concentrations of the Fe species for the system shown in Figure 3 are controlled by eight parameters: k_f,Fe(III)L, k_d,Fe(III)L, k_f,Fe(II)L, k_d,Fe(II)L, $k_{{\text{O}}_2,\text{inorg}}$, k_red,inorg, $k_{{\text{O}}_2,\text{org}}$, and k_red,org, and can be determined by solving the resulting rate law equations for each Fe species subject to the steady-state condition d/dt = 0. The four resulting equations are not independent, so we also need to invoke a mass balance equation for Fe, leading to the following system of independent equations that must be solved in order to calculate the steady-state concentrations of the Fe species in the system:

$\begin{array}{llll}& \frac{\text{d}}{\text{d}t}\left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]=k_{\text{red},\text{inorg}}\left[{\text{O}}_2^{-*}\right]\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]-k_{{\text{O}}_2,\text{inorg}}\left[{\text{O}}_2\right]\left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]+k_{\text{d},\text{Fe}\left(\text{II}\right)\text{L}}\left[\text{Fe}\left(\text{II}\right)\text{L}\right]-k_{\text{f},\text{Fe}\left(\text{II}\right)\text{L}}\left[\text{L}\right]\left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]& & \text{(A24)}\\ & \frac{\text{d}}{\text{d}t}\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]=k_{{\text{O}}_{\text{2}},\text{inorg}}\left[{\text{O}}_{\text{2}}\right]\left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]-k_{\text{red},\text{inorg}}\left[{\text{O}}_2^{-*}\right]\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]+k_{\text{d},\text{Fe}\left(\text{III}\right)\text{L}}\left[\text{Fe}\left(\text{III}\right)\text{L}\right]-k_{\text{f,Fe}\left(\text{III}\right)\text{L}}\left[\text{L}\right]\left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]& & \text{(A25)}\\ & \frac{\text{d}}{\text{d}t}\left[\text{Fe}\left(\text{II}\right)\text{L}\right]=k_{\text{red},\text{org}}\left[{\text{O}}_2^{-*}\right]\left[\text{Fe}\left(\text{III}\right)\text{L}\right]-k_{{\text{O}}_2,\text{org}}\left[{\text{O}}_{\text{2}}\right]\left[\text{Fe}\left(\text{II}\right)\text{L}\right]+k_{\text{f},\text{Fe}\left(\text{II}\right)\text{L}}\left[\text{L}\right]\left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]-k_{\text{d,Fe}\left(\text{II}\right)\text{L}}\left[\text{Fe}\left(\text{II}\right)\text{L}\right]& & \text{(A26)}\\ & \left[\text{Fe}{\left(\text{III}\right)}^{\prime }\right]+\left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]+\left[\text{Fe}\left(\text{III}\right)\text{L}\right]+\left[\text{Fe}\left(\text{II}\right)\text{L}\right]={\left[\text{Fe}\right]}_{\text{T}}& & \text{(A27)}\end{array}$

This can be simplified to a system of linear equations by treating the steady-state concentrations of the other species in the system (L, O₂, and ${\text{O}}_2^{-*}$) as constants. In oxygen-saturated waters at 25°C, [O₂] = 250 μM ≫ [Fe]_T in most cases. Assuming [L] is constant is also reasonable provided [L] ≫ [Fe]_T, which is frequently the case, but even if not we can specify a constant amount of free, excess ligand for the present purposes provided the majority of Fe remains organically complexed under the range of scenarios investigated (which will be seen to be the case, as shown in Figure 4). Finally, we will specify a constant steady-state $\left[{\text{O}}_2^{-*}\right]$ and consider the effect of this value on steady-state [Fe(III)′], [Fe(II)′], and [Fe′]_T = [Fe(III)′] + [Fe(II)′].

Under these conditions, it is straightforward to solve the system of linear Eqs A24–A27 using a symbolic mathematics software package (the MATLAB Symbolic Math Toolbox in this case) to yield rather complicated analytical solutions for steady-state [Fe(II)′] and [Fe(III)′]:

$\begin{array}{llll}& \left[\text{Fe}{\left(\text{II}\right)}^{\prime }\right]=\frac{k_{\text{d},\text{Fe}\left(\text{II}\right)\text{L}}{k}_{\text{d,Fe}\left(\text{III}\right)\text{L}}{k}_{\text{red,inorg}}^{*}+k_{\text{d,Fe}\left(\text{II}\right)\text{L}}{k}_{\text{f,Fe}\left(\text{III}\right)\text{L}}^{*}{k}_{\text{red,org}}^{*}+k_{\text{d},\text{Fe}\left(\text{III}\right)\text{L}}{k}_{\text{red,org}}^{*}{k}_{\text{red,inorg}}^{*}+k_{\text{d,Fe}\left(\text{II}\right)\text{L}}{k}_{\text{red,inorg}}^{*}{k}_{\text{red,org}}^{*}}{\left(\begin{array}{c}\hfill k_{\text{d},\text{Fe}\left(\text{II}\right)\text{L}}{k}_{\text{d,Fe}\left(\text{III}\right)\text{L}}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}+k_{\text{d,Fe}\left(\text{II}\right)\text{L}}{k}_{\text{f,Fe}\left(\text{III}\right)\text{L}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}+k_{\text{d},\text{Fe}\left(\text{III}\right)\text{L}}{k}_{\text{f,Fe}\left(\text{II}\right)\text{L}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,org}}^{*}+k_{\text{d},\text{Fe}\left(\text{II}\right)\text{L}}{k}_{\text{d},\text{Fe}\left(\text{III}\right)\text{L}}{k}_{\text{red,inorg}}^{*}+\hfill \\ \hfill k_{\text{f,Fe}\left(\text{II}\right)\text{L}}^{*}{k}_{\text{f,Fe}\left(\text{III}\right)\text{L}}^{*}{k}_{{\text{O}}_{\text{2}},\text{org}}^{*}+k_{\text{d,Fe}\left(\text{III}\right)\text{L}}{k}_{\text{f,Fe}\left(\text{II}\right)\text{L}}^{*}{k}_{\text{red,inorg}}^{*}+k_{\text{d},\text{Fe}\left(\text{II}\right)\text{L}}{k}_{\text{f,Fe}\left(\text{III}\right)\text{L}}^{*}{k}_{\text{red,org}}^{*}+k_{\text{f},\text{Fe}\left(\text{II}\right)\text{L}}^{*}{k}_{\text{f,Fe}\left(\text{III}\right)\text{L}}^{*}{k}_{\text{red,org}}^{*}+\hfill \\ \hfill k_{\text{d,Fe}\left(\text{III}\right)\text{L}}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}{k}_{{\text{O}}_{\text{2}},\text{org}}^{*}+k_{\text{f,Fe}\left(\text{III}\right)\text{L}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,org}}^{*}+k_{\text{d},\text{Fe}\left(\text{II}\right)\text{L}}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}{k}_{\text{red,org}}^{*}+k_{\text{d},\text{Fe}\left(\text{III}\right)\text{L}}{k}_{{\text{O}}_{\text{2}}\text{org}}^{*}{k}_{\text{red,inorg}}^{*}+\hfill \\ \hfill k_{\text{f,Fe}\left(\text{II}\right)\text{L}}^{*}{k}_{{\text{O}}_{\text{2}},\text{org}}^{*}{k}_{\text{red,inorg}}^{*}+k_{\text{f,Fe}\left(\text{III}\right)\text{L}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}{k}_{\text{red,org}}^{*}+k_{\text{d},\text{Fe}\left(\text{II}\right)\text{L}}{k}_{\text{red,inorg}}^{*}{k}_{\text{red,org}}^{*}+k_{\text{f,Fe}\left(\text{II}\right)\text{L}}^{*}{k}_{\text{red,inorg}}^{*}{k}_{\text{red,org}}^{*}\hfill \\ \hfill \hfill \end{array}\right)}{\left[\text{Fe}\right]}_{\text{T}}& & \text{(A28)}\\ & \left[\text{Fe}\left({\text{III}}^{\prime }\right)\right]=\frac{k_{\text{d,Fe(II)L}}{k}_{\text{d,Fe(III)L}}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}+k_{\text{d,Fe(III)L}}{k}_{\text{f,Fe(II)L}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,org}}^{*}+k_{\text{d,Fe(III)L}}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,org}}^{*}+k_{\text{d,Fe(II)L}}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}{k}_{\text{red,org}}^{*}}{\left(\begin{array}{c}{k}_{\text{d,Fe(II)L}}{k}_{\text{d,Fe(III)L}}{k}_{{\text{O}}_{\text{2}},\text{inorg}}^{*}+k_{\text{d,Fe(II)L}}{k}_{\text{f,Fe(III)L}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}+k_{\text{d,Fe(III)L}}{k}_{\text{f,Fe(II)L}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,org}}^{*}+k_{\text{d,Fe(II)L}}{k}_{\text{d,Fe(III)L}}{k}_{\text{red,inorg}}^{*}+\hfill \\ k_{\text{f,Fe(II)L}}^{*}{k}_{\text{f,Fe(III)L}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,org}}^{*}+k_{\text{d,Fe(III)L}}{k}_{\text{f,Fe(II)L}}^{*}{k}_{\text{red,inorg}}^{*}+k_{\text{d,Fe(II)L}}{k}_{\text{f,Fe(III)L}}^{*}{k}_{\text{red,org}}^{*}+k_{\text{f,Fe(II)L}}^{*}{k}_{\text{f,Fe(III)L}}^{*}{k}_{\text{red,org}}^{*}+\hfill \\ k_{\text{d,Fe(III)L}}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,org}}^{*}+k_{\text{f,Fe(III)L}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,org}}^{*}+k_{\text{d,Fe(II)L}}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}{k}_{\text{red,org}}^{*}+k_{\text{d,Fe(III)L}}{k}_{{\text{O}}_{\text{2}}\text{,org}}^{*}{k}_{\text{red,inorg}}^{*}+\hfill \\ k_{\text{f,Fe(II)L}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,org}}^{*}{k}_{\text{red,inorg}}^{*}+k_{\text{f,Fe(III)L}}^{*}{k}_{{\text{O}}_{\text{2}}\text{,inorg}}^{*}{k}_{\text{red,inorg}}^{*}+k_{\text{d,Fe(II)L}}{k}_{\text{red,inorg}}^{*}{k}_{\text{red,org}}^{*}+k_{\text{f,Fe(II)L}}^{*}{k}_{\text{red,inorg}}^{*}{k}_{\text{red,org}}^{*}\hfill \end{array}\right)}{\left[\text{Fe}\right]}_{\text{T}}& & \text{(A29)}\end{array}$

where $k_{\text{f},\text{Fe}\left(\text{III}\right)\text{L}}^{*}=k_{\text{f},\text{Fe}\left(\text{II}\right)\text{L}}\left[\text{L}\right]$, $k_{\text{f},\text{Fe}\left(\text{II}\right)\text{L}}^{*}=k_{\text{f},\text{Fe}\left(\text{II}\right)\text{L}}\left[\text{L}\right]$, $k_{{\text{O}}_2,\text{inorg}}^{*}=k_{{\text{O}}_2,\text{inorg}}\left[{\text{O}}_2\right]$, $k_{\text{red},\text{inorg}}^{*}=k_{\text{red},\text{inorg}}\left[{\text{O}}_2^{-\text{*}}\right]$, $k_{{\text{O}}_2,\text{org}}^{*}=k_{{\text{O}}_2,\text{org}}\left[{\text{O}}_2\right]$, and $k_{\text{red,org}}^{*}=k_{\text{red,org}}\left[{\text{O}}_2^{-*}\right]$.

The number of variables can be further simplified by assuming a 1:1 Fe:L ratio for Fe(II)L and Fe(III)L, that the complex formation rate constants are independent of ligand type (consistent with control of complex formation by water loss kinetics, i.e., the complexes form via a perfect Eigen–Wilkins mechanism (Eigen and Wilkins, 1965) in which the electrostatic charge on L does not vary between different ligand types), and that the oxidation of Fe(II)L by O₂ and reduction of Fe(III)L by ${\text{O}}_2^{-*}$ are outer-sphere electron transfer processes that obey Marcus Theory perfectly. With these simplifications, we will consider an illustrative typical coastal marine water in equilibrium with the atmosphere at pH 8.1, temperature 25°C, ionic strength of 0.7 M, and constant ionic composition, specifying the following parameter values:

k_f,Fe(III)L = 5 × 10⁶ M⁻¹ s⁻¹, a typical value from Rose and Waite (2003b)

k_f,Fe(II)L = 5 × 10⁴ M⁻¹ s⁻¹, a typical value from Rose and Waite (2003b)

k_d,Fe(III)L = k_f,Fe(III)L/K_Fe(III)L s⁻¹ where K_Fe(III)L (M⁻¹) is as defined previously

k_d,Fe(II)L = k_f,Fe(II)L/K_Fe(II)L s⁻¹ where K_Fe(II)L (M⁻¹) is as defined previously

$k_{{\text{O}}_2,\text{inorg}}=13\text{M}$ ⁻¹ s⁻¹ (Rose and Waite, 2002)

k_red,inorg = 1.5 × 10⁸ M⁻¹ s⁻¹ (Bielski et al., 1985).

The remaining two parameters $k_{{\text{O}}_2,\text{org}}$ and k_red,org are specified by the Marcus relationship:

$\begin{array}{llll}{k}_{{\text{O}}_2,\text{org}}=\frac{k_{\text{diff}}}{1+\frac{k_{\text{diff}}}{K_{\text{d}}Z}exp\left(\frac{\lambda }{4RT}{\left(1+\frac{\Delta G_{\text{ox,org}}^0}{\lambda }\right)}^2\right)}& & & \text{(A30)}\\ k_{\text{red},\text{org}}=\frac{k_{\text{diff}}}{1+\frac{k_{\text{diff}}}{K_{\text{d}}Z}exp\left(\frac{\lambda }{4RT}{\left(1+\frac{\Delta G_{\text{red,org}}^0}{\lambda }\right)}^2\right)}& & & \text{(A31)}\end{array}$

where $\Delta G_{\text{ox,org}}^0$ and $\Delta G_{\text{red,org}}^0$ (kJ mol⁻¹) are expressed in terms of the conditional stability constants K_Fe(III)L and K_Fe(II)L, as described in Rose and Waite (2003a):

$\Delta G_{\text{red,org}}^0=-\Delta G_{\text{ox,org}}^0=10^{-6}F\left(E_{{\text{O}}_2\to {\text{O}}_2^{-*}}^0-E_{\text{F}{\text{e}}^{3+}\to \text{F}{\text{e}}^{2+}}^0-59log\left(K_{\text{Fe}\left(\text{II}\right)\text{L}}\right)/\left(K_{\text{Fe}\left(\text{III}\right)\text{L}}\right)\right)$(A32)

and $E_{{\text{O}}_2\to {\text{O}}_2^{-*}}^0=-160\text{mV}$ (Sawyer, 1991), $E_{\text{F}{\text{e}}^{3+}\to \text{F}{\text{e}}^{2+}}^0=+770\text{mV}$ (Morel and Hering, 1993), F = 9.649 × 10⁴ C mol⁻¹ (Morel and Hering, 1993), and we assume values of k_diff = 10¹⁰ M⁻¹ s⁻¹, k_diff/(K_dZ) = 0.1, and λ = 135 kJ mol⁻¹ as per Rose and Waite (2003a).

Consequently the parameters k_f,Fe(III)L, k_f,Fe(II)L, $k_{{\text{O}}_2,\text{inorg}}$, and k_red,inorg are constants (for a specified [L], [O₂], and $\left[{\text{O}}_2^{-*}\right]$), while the parameters k_d,Fe(III)L, k_d,Fe(II)L, $k_{{\text{O}}_2,\text{org}}$, and k_red,org are functions of K_Fe(III)L and K_Fe(II)L.

References

Morel, F. M. M., and Hering, J. G. (1993). Principles and Applications of Aquatic Chemistry. New York: Wiley.

Rose, A. L., and Waite, T. D. (2002). Kinetic model for Fe(II) oxidation in seawater in the absence and presence of natural organic matter. Environ. Sci. Technol. 36, 433–444.