A hydraulic control system integrating adaptive and PWM algorithms for hydro-mechanical continuously variable transmission

Introduction: With the development of technology, the hydraulic control system for hydro-mechanical continuously variable transmission has also made rapid progress. However, the traditional control system for hydro-mechanical continuously variable transmission has drawbacks such as efficiency loss and slow response speed. The study fused the adaptive and pulse width modulation algorithms to solve these problems effectively, and they were applied to the hydraulic mechanical continuously variable drive control system.

Method: First, the study analyzed the continuously variable transmission control of hydraulic machinery and designed the control scheme on the basis of the analysis. Then, a new scheme fusing adaptive and pulse-width modulation algorithms was proposed on the basis of the control scheme. Finally, simulation experiments and practical tests were carried out to verify the performance of the control scheme.

Results: The results showed that the time to reach the maximum pressure was 2.15 s when the volume of the pilot valve cavity was 5 × 10⁹/L. When the oil flow rate was 70 L/min, the corresponding maximum and minimum values of the main oil circuit pressure were 1.63 MPa and 0.37 MPa, respectively. The time to reach the maximum value of the pressure was 2.05 s, respectively. These values were in line with the design requirements and were better than the comparison values.

Discussion: These results confirm that the system has important theoretical and practical significance, which has a positive promoting effect on the development of the hydraulic machinery industry. This article aims to provide a new approach for research and application in related fields.

1 Introduction

Hydro-mechanical continuously variable transmission (HMCVT) technology is an innovative technology that combines hydraulic transmission with mechanical transmission. HMCVT has the advantages of high transmission efficiency, low noise, and high energy utilization, which is widely applied in the engineering (Fan and Kuang, 2021; Maczyszyn, 2019). However, the traditional hydraulic control system for HMCVT has some problems, such as high requirements for transmission efficiency and low control accuracy (Hu et al., 2020; Mazali et al., 2019). A control system for continuously variable transmission combining adaptive and pulse width modulation (PWM) algorithms was proposed to overcome these issues. Adaptive control algorithm can adjust control parameters in real-time and intelligently adjust the transmission process based on the actual operating status of system to optimize transmission efficiency. PWM is a method of controlling the output power by changing the pulse width of signal, which can achieve precise control (Zhang et al., 2022a; Yasien and Wala’a, 2019). The study first analyzed the control of HMCVT and designed relevant solutions. Then a system control scheme combining the adaptive and PWM algorithms was proposed. Finally, simulation experiments and practical tests were conducted, and the experimental results were analyzed and summarized. The research solves the limitations of traditional control methods and realizes the efficient and precise control of the continuously variable transmission system of hydraulic machinery through the innovation of algorithmic level and optimization of control strategy. The article aims to provide a new control method for the further development of HMCVT technology.

The first part of this study introduces the current research of the HMCVT control system and the adaptive and PWM algorithms in the application of the continuously variable transmission. Next, the study constructs the HMCVT control system based on the adaptive and PWM algorithms. Then the performance of the control system is verified by using the continuously variable transmission of the automobile wet clutch transmission as an experimental object. The final part summarizes the experimental results, and the advantages and disadvantages of using the method are analyzed.

2 Related works

HMCVT is a method of adjusting the transmission ratio by controlling the flow and pressure in the hydraulic system, which can make the mechanical transmission process more stable and efficient. Traditional mechanical transmission usually adopts a discrete transmission method, with a fixed transmission ratio that cannot be adjusted according to changes in working conditions. HMCVT can adjust the transmission ratio in real-time according to actual needs, thereby improving the performance and efficiency of mechanical systems. Numerous experts and scholars have conducted research on the HMCVT system. Morabito and Versaci (2001) designed a fuzzy neural method to address the shortcomings of non-intrusive turbine measurements in hydraulic mechanical drive systems. Fuzzy reasoning and the concepts of fuzzy curves and surfaces were utilized to estimate the location of the hole center from a reduced set of features. Hoodorozhkov et al. designed an automatic multi-flow gearbox to improve the dynamic characteristics of the vehicle using a mechanical continuously variable transmission. The transmission was proposed as a five-flow mechanical transmission and the kinematics of the eccentric conversion elements were described in detail. The results showed that the proposed mechanical automatic transmission had a higher total efficiency than a typical mechanical transmission, while there was no power flow interruption due to ratio changes during vehicle acceleration (Hoodorozhkov and Kozlenok, 2021). Zhang et al. (2022b) proposed a power return hydraulic transmission system to develop advanced power performance and reduce energy consumption. The system utilized the mathematical model of the power-train to obtain resonance characteristics. These results confirmed that the power-train resonance frequency of the system was excluded from the operating range of the engine (Zhang et al., 2022b).

Kharytonchyk and Kusyak proposed an adaptive control based on PWM signal frequency to make the dry friction clutch engaging quality ensured. These results confirmed that the algorithm achieved the adaptive control (Kharytonchyk et al., 2021). Ouyang et al. put forward a mathematical model for the electronic hydraulic actuator of heavy-duty automatic transmissions to predict the response performance of wet clutches to reduce fuel consumption and shift quality of heavy-duty automatic transmission vehicles. In this study, PWM was used to control the solenoid valve, pressurization valve, and pilot valve, simplifying the control formula of the clutch model. These results confirmed that the model had certain reference value for performance analysis and optimization of clutch actuators (Ouyang et al., 2019).

In summary, HMCVT can be achieved through hydraulic drive. The HMCVT control system adjusts the working parameters to achieve continuous adjustment of the transmission ratio, thereby meeting the precise transmission requirements under different working conditions. Traditional hydraulic mechanical transmission control systems have drawbacks such as efficiency loss, slow response speed, and high system complexity. Therefore, research is conducted on the fusion of the adaptive and PWM algorithms in a control system for HMCVT based on the summary of existing technologies. The article aims to provide better technical support for developing a hydraulic control system for HMCVT.

3 Design and analysis of hydraulic control system integrating adaptive and PWM algorithms for HMCVT

A hydraulic control system is a technology that can achieve HMCVT. This system achieves continuously variable speed change and power distribution by adjusting the working parameters of the hydraulic system, thereby achieving precise control of the mechanical transmission system.

3.1 Control analysis and scheme design of HMCVT

HMCVT is a method by using a hydraulic system to achieve continuously variable transmission. In the hydraulic control system for HMCVT, the speed ratio of the transmission device is controlled by changing the working pressure and flow rate of the hydraulic system, thereby achieving continuously variable transmission. There is a certain difference in power transmission between the mechanical part and the former, and the power transmission of the mechanical part varies in a step wise manner (Chen et al., 2019; Chen et al., 2021). In HMCVT, there are positive and negative phase conditions. Positive phase condition refers to the condition where the overall speed of the transmission system increases according to the output of the continuously variable transmission when the forward converging planetary array is running, which can be expressed by Formula 1 (Yan et al., 2022).

$n_j=\frac{1}{\left(1+K_1\right)}\left(n_t+K_1\cdot n_q\right)(1)$

In Formula 1, $K_1$ represents the correction factor value. $n_t$ represents the speed of the solar wheel. $n_q$ represents the gear speed. Negative phase condition refers to the situation where the overall speed of the transmission system increases as the output of the continuously variable transmission decreases when the planetary gear is operated in reverse, which can be represented by Formula 2.

$n_b=\left(1+k_2\right)\cdot n_j-k_2\cdot n_q(2)$

In Formula 2, $k_2$ represents the correction factor value. $n_j$ represents the speed of the planetary carrier. An important component of HMCVT system is the continuously variable transmission unit by combining Formulas 1, 2 with the characteristic analysis of HMCVT. In the study, hydraulic transmission units are used as a continuously variable transmission unit for a hydraulic control system for hydraulic mechanical transmission. The diversion and confluence devices are divided into two categories: ordinary planetary gear combination fixed gear group in the hydraulic mechanical transmission system. If the input speed and torque are determined in a fixed gear transmission, they can be allocated to other speeds and torques through the classification device in the fixed gear (Yao et al., 2021; Aikhuele, 2022). The speed and torque are output again after converging through this series of transmissions, and this process can be expressed by Formula 3.

$\left\{\begin{array}{l}{n}_1=n_2=i{n}_3\\ M_1-M_2-M_3/i\\ M_1{n}_1-M_2{n}_2-M_3{n}_3=0\end{array}\right.(3)$

In Formula 3, $n_1$ represents the input speed. $n_2$ and $n_3$ represent the allocated speed, respectively. $i$ represents the ratio of input to output. $M_1$ represents the input torque value. $M_2$ and $M_3$ represent the torque after distribution, respectively. According to analysis, when the overall structure of gear mechanism remains unchanged, the ratio of input speed to output speed remains unchanged. When one value is fixed, the other value is also fixed and does not change. Therefore, the use of fixed gear pairs to achieve power convergence or splitting is referred to as “convergence type” or “splitting type.” The fixed gear pair used in practical applications is called a “differential torque mechanism.” The analysis of hydraulic power diversion ratio and efficiency requires defining the ratio of hydraulic circuit’s output power to all output powers as the ratio of a certain hydraulic diversion circuit’s output power. The output power ratio can be calculated using Formula 4 (Huang et al., 2021).

$P=\frac{{\mathrm{{\rm P}}}_h}{-{\mathrm{{\rm P}}}_2}=\frac{{\mathrm{{\rm P}}}_3}{{\mathrm{{\rm P}}}_2}=\frac{M_3{n}_3}{M_2{n}_2}(4)$

In Formula 4, ${\mathrm{{\rm P}}}_h$ represents the output power of the hydraulic circuit. ${\mathrm{{\rm P}}}_2$ and represent the allocated structural input power, respectively. According to the mutual operation relationship between planetary arrays and the operation formula of differential gear trains, the conversion relationship formula for the transmission ratio of the transmission gear train can be derived, which can be represented by Formula 5.

$i_{21}=\frac{1}{\left(1+A\right)\left(1-{\mathrm{{\rm P}}}_h\right)}(5)$

In Formula 5, $A$ represents the characteristic coefficient of planetary array coupling. Through analysis, relevant selection plans can be clarified and reasonable combinations can be found. In the scheme of HMCVT system, the research ultimately chooses a variable flow pump constant flow motor as the main body of the continuously variable transmission unit. A proportional speed output mode is selected for transmission, and a combination of positive and negative converging planetary arrays is determined to form the main body of the converging device in this system. Thus, this can achieve efficient and stable operation of the mechanical hydraulic composite HMCVT system and ensure the stability and reliability of the system during operation. Figure 1 is a diagram of the HMCVT scheme.

Figure 1

Figure 1. Hydro-mechanical continuously variable drive program diagram.

In Figure 1, the HMCVT system is a transmission meshing mechanism consisting of a number of pairs of fixed-shaft gears assembled on top of the autonomous shift meshing casing a, casing b, the movement shafts 1 and 2, and the output shaft 3 at the bottom. Meanwhile, the system is designed with four working gears, i.e., four forward working transmission segments I, II, II, and IV and one reverse working segment R. The system is designed with four working gears.

3.2 Design and modeling of a control system for HMCVT integrating the adaptive and PWM algorithms

A control system for HMCVT is a device that utilizes hydraulic flow and pressure to achieve HMCVT. A control system that integrates the adaptive and PWM algorithms can achieve precise control of HMCVT. When designing a hydraulic control system, it is necessary to address issues such as torque fluctuations in HMCVT to improve the quality of shifting. For this reason, the hydraulic control system needs to meet some requirements, such as being able to achieve buffering pressure increase and decrease, control the minimum pressure to zero, have overload protection function, and have no interference between various hydraulic control branches (Yuan et al., 2022; Zeng et al., 2020). A hydraulic control system scheme is designed based on the above requirements in Figure 2. Due to the same structure of CH and CL hydraulic control branches, CH hydraulic control branch is chosen as the research object to study its working process in the buffered boosting state, sliding and bonding state, and buffered depressurization state.

Figure 2

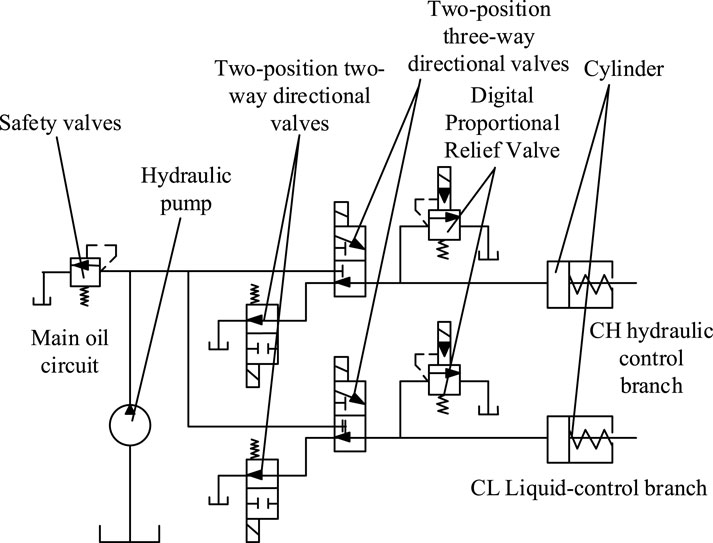
Figure 2. Hydraulic machinery continuously variable drive hydraulic control system schematic diagram.

It is necessary to consider the main oil circuit safety valve to protect the hydraulic system from overload damage when designing a hydraulic control system for HMCVT. The overflow pressure should be greater than the maximum control pressure of the digital proportional overflow valve to ensure that the safety valve does not affect the system pressure. The diameter of the inlet and outlet can be calculated through parameters such as nominal pressure, nominal flow rate, main valve opening pressure, and unloading pressure. The calculation of the diameter can be expressed by Formula 6 (Han et al., 2021).

$d_s\ge 1.134\sqrt{\frac{Q_g}{6000V_g}}(6)$

In Formula 6, $Q_g$ represents the nominal flow rate. $V_g$ represents the oil flow rate at the inlet and outlet ports. The diameter of the main valve seat hole can be represented by Formula 7.

$D_{1s}=d_s-e(7)$

In Formula 7, $e$ represents the valve seat installation value. After determining the main valve seat aperture, the next step is to calculate the size of the main valve core. The diameter of the main valve core can affect the opening and closing characteristics of the main oil circuit safety valve. The ratio of the area of the upper and lower sides of the main valve core directly determines the performance of the opening and closing characteristics. Based on experience, the ratio of the upper and lower areas of this core is generally taken as 0.95–0.98. When designing the main valve, a ratio of 0.96 is selected. The diameter of the main valve core is calculated using Formula 8 (Li et al., 2022).

$D_{2s}=D_{1s}\sqrt{\frac{A_{1s}}{A_{2s}}}(8)$

In Formula 8, $\frac{A_{1s}}{A_{2s}}$ represents the area ratio of main valve core’s upper and lower sides. The length of the valve sleeve that matches the main valve core can be calculated using Formula 9 (Gao et al., 2022).

$L_s=f\cdot D_{2s}(9)$

In Formula 9, $f$ represents the diameter of valve sleeve, with a value range of [0.6–1.5]. Because the diameter of the valve port of the main oil circuit safety valve seat is at a right angle, the angle of the half-cone angle is taken as 15°, which can provide better sealing performance. HMCVT is modeled after establishing a hydraulic control system. In the modeling, this study takes the hydraulic control branch in the hydraulic section as an example to illustrate, which has the same structure as the hydraulic mechanical control branch in the section hydraulic. The research establishes a digital proportional relief valve model and conducts experimental verification. Therefore, it is only necessary to reseal the digital proportional relief valve model in hydraulic control systems. The input of the model is the hydraulic control branch oil pressure $P_{CH}$. The output is the overflow flow $Q_{RV}$, including the flow through the high-speed on-off valve, safety valve, and main valve. The two-position three-way directional valve and two-position two-way valve are responsible for controlling the hydraulic flow direction and flow rate in the control system for HMCVT, respectively. These two are important components for achieving hydraulic system control. The main function of the two-position three-way electromagnetic directional valve is to switch the oil circuit, which achieves switching between the main oil and hydraulic control branch circuits by generating a fixed pressure difference (Du et al., 2019; Thenathayalan and Park, 2019). Therefore, when modeling, only the function of switching oil circuits needs to be considered. The input quantity is the output flow $Q_p$ of the oil source, and the output quantity is the flow $Q_{23}$ through this two-position three-way directional valve. The switch signal $Swich23-CH$ is used to control the status of the two-position three-way directional valve. When the signal is 1, the valve switches to the upper position and connects the oil source and the hydraulic control branch. The flow calculation can be expressed by Formula 10 (Pang et al., 2021).

$\left\{\begin{array}{l}{Q}_{23}=Q_{p}Swich23-CH=1\\ Q_{23}=0Swich23-CH=0\end{array}\right.(10)$

In Formula 10, $Q_p$ represents the oil input flow rate. The input of this two-position two-way valve model is the hydraulic control branch pressure, and the output is the flow rate passing through two-position two-way valve. When valve port is fully open, the flow rate through two-position two-way valve can be calculated by Formula 11.

$Q_{22}=C_b\pi D_b{\delta }_{b\max }\sqrt{\frac{2}{\rho }{P}_{CH}}(11)$

In Formula 11, $C_b$ represents the flow coefficient value at the valve port of a two-dimensional two-way valve. $D_b$ represents the diameter of the two-dimensional two-way valve method. $\delta$ represents the flow coefficient value. $\rho$ represents the oil density. $P_{CH}$ represents oil pressure. In this study, this two-position two-way valve will automatically open when the pressure is less than 0.4 MPa. At this point, the relationship between the flow rate passing through the two-position two-way valve and the control signal can be expressed by Formula 12.

$Q_{22}=\left\{\begin{array}{l}\frac{P_{CH}}{d_{bi}}Swich22-CH=1\\ 0Swich22-CH=0\end{array}\right.(12)$

In Formula 12, $d_{bi}$ represents the diameter of inlet and outlet ports.

According to Figure 3, the hydraulic mechanical continuously variable drive control system that fuses the adaptive and PWM algorithms is simplified to some extent to adapt it to practical use. The first is a linear simplification of the nonlinear characteristics. Because many components in a hydraulic system, such as pumps, valves, and motors, exhibit nonlinear characteristics. These nonlinear relationships are often approximated as linear to simplify the mathematical model. Then the dynamic response is simplified. In a real system, the dynamic response may be affected by a variety of factors, such as the viscosity of the hydraulic fluid, the damping, and the inertia of the system. These complex factors may be ignored or approximated to simplify the model. Finally, parameter simplification, a large number of parameters may need to be considered when building the mathematical model, such as the density of the hydraulic fluid, viscosity, leakage coefficients, and so on. It is assumed that these situations do not occur during the experiment to simplify the model. The mathematical model can be applied more effectively to analyze and optimize the performance of the HMCVT control system through these simplification measures.

Figure 3

Figure 3. Model of the hydraulic control system based on the PWM algorithm.

4 Application analysis of control system for HMCVT

This study took HMCVT of a wet clutch transmission as the experimental object to verify the performance and application effectiveness of the constructed system.

4.1 Application performance analysis based on control systems

A digital proportional relief valve model was studied to verify the performance of this control system. Digital proportional relief valve is a proportional control component used in hydraulic systems to achieve continuously variable transmission control of hydraulic machinery by controlling the flow rate of the hydraulic system. Specifically, the digital proportional relief valve controls the movement speed of the hydraulic motor or cylinder by adjusting the flow rate in the hydraulic system, thereby achieving transmission control of hydraulic machinery. The performance of the digital proportional relief valve was optimized to improve the control accuracy, response speed, and stability of the continuously variable transmission control system of hydraulic machinery by reasonably selecting and designing the volume of the pilot valve cavity. Figure 4 shows the effect of different pilot valve chamber volumes on the characteristics of digital proportional relief valves. The pilot valve chamber volume selected for this study was 5 × 10⁹/L.

Figure 4

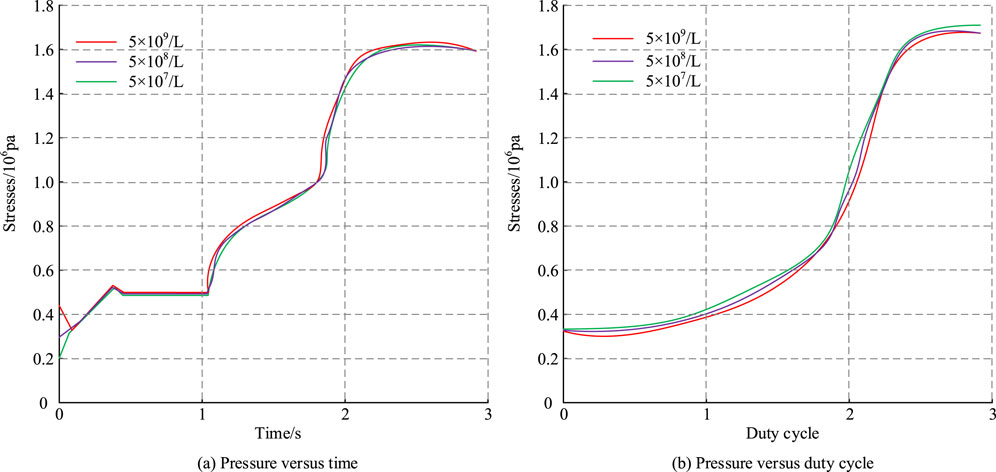
Figure 4. Comparison results of digital proportional relief valve characteristics with different pilot valve cavity volumes. (A) Pressure versus time (B) Pressure versus duty cycle.

According to Figure 4A, as the volume of the pilot valve chamber increased, the pressure response rate slowed down, and the pressure fluctuation also decreased. The time for main oil circuit to reach maximum pressure corresponding to 5 × 10⁷, 5 × 10⁸, and 5 × 10⁹/L volumes was 2.15, 2.35, and 2.51 s, respectively. According to Figure 4B, as the volume of pilot valve chamber changed, there was not much difference in the pressure curves under three volumes. This indicated that the volume change of pilot valve chamber did not affect the duty cycle of continuous pressure changes, which verified that the volume of pilot valve chamber selected in this study met the design requirements. The high-speed development valve is an important component, used to control this hydraulic system’s flow and pressure. The overall flow of this hydraulic system can be controlled by adjusting the valve port diameter of the high-speed development valve. Precise flow adjustment was achieved by combining it with the digital proportional relief valve control.

4.2 Practical application effect analysis of control systems

Research was conducted on applying the control system to HMCVT of automotive wet clutch transmissions to further verify the application effect of the control system. In the control system for HMCVT, the boost buffering characteristics were adopted. This effectively reduced hydraulic pulsation and impact in the system, thereby enhancing the stability and reliability of the transmission system and improving the work efficiency and service life of the mechanical transmission system. Figure 5 shows the results of the hydraulic control system’s boosting and buffering characteristics.

Figure 5

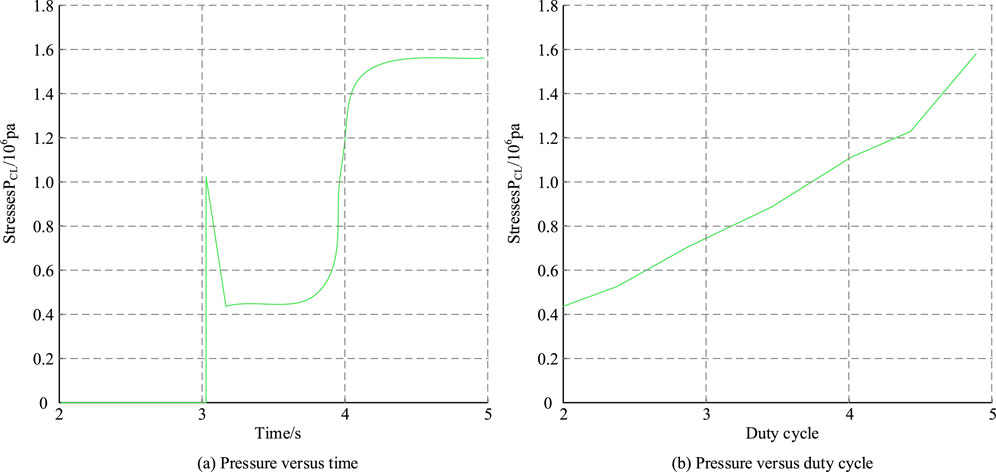
Figure 5. Hydraulic control system boost buffer characterization results. (A) Pressure versus time (B) Pressure versus duty cycle.

According to Figure 5A, within 0–3 s, the CL hydraulic control branch was connected to the fuel tank, and the oil circuit’s pressure was 0. After 3 s, the directional valve changed direction. At this point, the oil circuit was connected, and the oil pressure began to rise, reaching the maximum pressure value at 4.09 s. According to Figure 5B, when buffering between pressure and duty cycle, the range of duty cycle varied between 20% and 81% when the pressure continuously changed. When the duty cycle was less than 20%, the corresponding pressure value was 0.4 MPa, and the maximum value was 1.61 MPa. This indicated that the buffering characteristics in the control system designed in the study met the requirements of practical applications. The stability and smoothness of the system were improved by optimizing the boost buffer characteristics, the pressure shock and transmission instability were reduced, and the work quality and efficiency were improved. The static characteristics describe the relationship between the input and output of a system in a stable state. In the control system for HMCVT, the static characteristics reflect the impact of the control input signal on the system output. Static characteristics are mainly used to evaluate the performance of a hydraulic system in non-operating or stable operating conditions. The results of the static characteristics are important for understanding system performance, optimizing system design, and predicting system behavior. This study was validated by combining the dynamic characteristics of pressure reduction and buffering to further verify the control effect of the system on the displacement of each hydraulic control branch and clutch piston. Figure 6 shows the corresponding control effect.

Figure 6

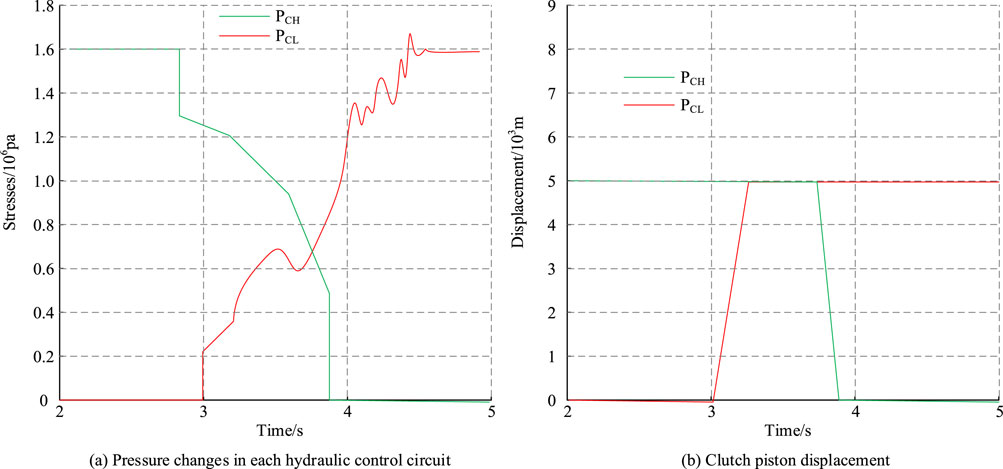
Figure 6. Results of the hydraulic control system on the displacements of each branch and clutch piston in the buck cushioning dynamic. (A) Pressure changes in each hydraulic control circuit (B) Clutch piston displacement.

According to Figures 6A, B, the end time of CH clutch sliding was 3.9 s, and the directional time of the corresponding 2-way directional valve was also 3.9 s. At this time, the duty cycle of PWM control signal decreased. After 3.9 s, the duty cycle reached 100%. The time for both clutches to slip and wear simultaneously was adjusted by adjusting the release time of CH clutch. This indicated that the constructed hydraulic control system adjusted the pressure buffering according to the actual pressure situation. This helped to reduce pressure shocks, improve transmission smoothness, increase system reliability and safety, providing guidance for further system optimization. The efficiency loss of the clutch under different states is further compared, and the results are shown in Table 1.

Table 1

Table 1. Comparison of efficiency losses in different states of the CH clutch.

Table 1 shows the comparison of efficiency loss values under different CH clutch states. The results show that when CH clutch is in a combined state, all its parameter values are 0. At the same time, compared with other parameters, it can be seen that the speed difference, strip torque, power loss and efficiency loss of CH clutch are proportional to each other, that is, when the speed is at the minimum of 40 rad/s, the corresponding remaining parameters are also the smallest, in which the strip torque is 15 N-m, the power loss is 1,200 W, and the efficiency loss is 10%. At the same time, when the maximum speed is 80 rad/s, the corresponding other parameter values are also maximum, where the strip torque is 40 N-m, the power loss is 3,200 W, and the efficiency loss is 20%. The results show that the disengaging state of the clutch has a significant impact on the efficiency of the system, while the engaged state of the clutch has a negligible impact on the efficiency. According to the research results of F Concli, we compare the loss shares under different allocation (Concli and Gorla, 2013). The relevant results are shown in Table 2.

Table 2

Table 2. Comparison of loss shares for different configurations.

Table 2 is a comparison of the loss share of five different configurations, the results show that the different configurations of the load-related losses, load-independent losses, other losses and total losses are somewhat different, by comparing the relevant configuration of the CVT can be found in the form of a combination of the load-related losses of the highest value of 30%, and at the same time, three kinds of CVT configurations of the load-independent losses are close to the value of the value of the CVT configurations, the maximum value of 18% of other losses and total losses are located in the maximum value level. The torque converter with lock-up clutch has the highest value of load-independent losses, with a value of 18%, while the other losses and total losses of this configuration are at the maximum level, with the other losses and total losses being 12% and 50%, respectively, so this configuration is suitable for driving conditions that require high efficiency, and the combination of the CVT and the hydrodynamic coupler has low load-independent losses, which makes it suitable for occasions with frequent start-ups.

5 Discussion

In the research results, with the increase of the pilot valve chamber volume, the pressure response rate as well as the pressure fluctuation are gradually reduced, and at this time, the time to reach the maximum pressure of the main oil circuit corresponding to the three volumes of 5 × 107/m3, 5 × 108/m3, and 5 × 109/m3 are 2.15 s, 2.35 s, and 2.51 s, respectively; meanwhile, the pressure of the oil circuit in the time of 0–3 s is 0, and 3 s after the reversing valve changes direction, the oil pressure starts to rise, and reaches the maximum value of pressure at 4.09 s. Secondly, in the process of buffering between the pressure and the duty cycle, the range of the duty cycle varies between 20% and 81% when the pressure changes continuously, and when the duty cycle is less than 20%, the pressure corresponds to the value of 0.4 MPa, and the maximum value of 1.61 MPa. Also there are some differences in the values of efficiency losses for different CH clutch states and in the share of losses for different configurations. At this stage, Y ZHAO et al. have designed a simple design for improving the tractor’s fuel economy, a simple single planetary gear was designed to consolidate the power and analyzed the energy as well as fuel consumption, the results show that the parasitic power is obtained when the variable pump displacement is negative and at the same time the maximum power of this hydro-mechanical transmission can reach to 87% as well as 89%, which is simpler in structure as compared to the hydro-mechanical transmission with Simpson’s planetary gears and consumes less energy as well as less fuel, the transmission is similar to the transmission is similar to the hydraulic transmission scheme described in the study (Zhao et al., 2023). Wang et al. (2024) designed a new type of variable structure dual-motor hydrostatic transmission system to improve the control performance and energy efficiency of the hydrostatic transmission system of the wheel loader, and also proposed a fuzzy sliding-mode control based multi-control strategy, which verified the stability of the transmission system by establishing a simulation model of the transmission system, and it was more effective than the traditional control strategy, and was able to actively adapt to disturbances, and was more efficient than traditional control strategy, and was able to actively adapt to disturbances, and was able to actively adapt to disturbances. And it can actively adapt to disturbances, and its transmission efficiency is improved by 30% compared with the traditional torque converter loader transmission system, which is important for reducing energy consumption, which is more similar to the research results (Wang et al., 2024). In summary, the research proposed stepless transmission system for hydraulic machinery has high accuracy and shows good performance in the control of hydraulic machinery.

6 Conclusion

The traditional control system for HMCVT has problems such as efficiency loss, slow response speed, and high system complexity. In this regard, a control system for HMCVT was designed by integrating the adaptive and PWM algorithms in the experiment. These results confirmed that there was a significant decrease in pressure when the CH hydraulic control branch was buffered. When the pressure of CL hydraulic control branch and the pressure of CH hydraulic control branch were at 0.58 MPa, there was a time crossing situation, with a time of 3.35 s. The end time of CH clutch sliding wear was 3.9 s, and the corresponding reversing time of two-way directional valve was also 3.9 s. At this time, the duty cycle of PWM control signal decreased. After 3.9 s, the duty cycle reached 100%. In summary, the research results of a control system for HMCVT that integrated the adaptive and PWM algorithms provided new solutions for the development of the hydraulic machinery industry. The design and implementation of this system fully utilized the advantages of adaptive control and PWM, improved the control accuracy and performance of hydraulic mechanical transmission, and had important theoretical and practical significance. However, there are still shortcomings in this research. Strategies related to pressure buffering control are designed, and the characteristics of the strategies are only open-loop control strategies. More algorithms can be combined to study closed-loop control strategies in the next step to achieve better system control effects. The paper can continue to deepen the research on the adaptive and PWM algorithms to explore more advanced and efficient control strategies. Meanwhile, this paper can focus on the reliability and safety of the system and develop a more stable and reliable HMCVT system to meet the needs of various complex application scenarios.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JC: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Supervision, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aikhuele, D. (2022). Development of a statistical reliability-based model for the estimation and optimization of a spur gear system. J. Comput. Cognitive Eng. 2 (2), 168–174. doi:10.47852/bonviewjcce2202153

CrossRef Full Text | Google Scholar

Chen, D. F., Cheng, A. B., Chiu, S. P. C., and Ting, J. C. (2021). Electromagnetic torque control for six-phase induction motor expelled continuously variable transmission clumped system using sage dynamic control system. Int. J. Appl. Electromagn. Mech. 65 (3), 579–608. doi:10.3233/jae-201512

CrossRef Full Text | Google Scholar

Chen, W., Lin, Y., Li, W., Liu, H., Tu, L., and Meng, H. (2019). Study on speed and torque control of a novel hydromechanical hybrid transmission system in wind turbine. IET Renew. Power Gener. 13 (9), 1554–1564. doi:10.1049/iet-rpg.2018.6105

CrossRef Full Text | Google Scholar

Concli, F., and Gorla, C. (2013). Influence of lubricant temperature, lubricant level and rotational speed on the churning power loss in an industrial planetary speed reducer: computational and experimental study. Int. J. Comput. Methods Exp. Meas. 1 (4), 353–366. doi:10.2495/cmem-v1-n4-353-366

CrossRef Full Text | Google Scholar

Du, J., Yai, D., Xue, Y., Liu, T., and Quan, W. (2019). Analysis of dual-rotor pm machine incorporating intelligent speed control suitable for CVT used in HEVs. IEICE Trans. Electron. 102 (1), 83–90. doi:10.1587/transele.e102.c.83

CrossRef Full Text | Google Scholar

Fan, P., and Kuang, Y. C. (2021). A novel line type optimization and theoretical equilibrium method analysis for common hypocycloid screw motor. Industrial Lubr. Tribol. 73 (6), 911–921. doi:10.1108/ILT-12-2020-0446

CrossRef Full Text | Google Scholar

Gao, J., Lou, D., Zhang, T., Fang, L., and Zhang, Y. (2022). Multivariable predictive functional control of a compound power-split hybrid electric vehicle. J. Automob. Eng. 236 (8), 1775–1794. doi:10.1177/09544070211046690

CrossRef Full Text | Google Scholar

Han, L., Ren, L., and Zhao, W. (2021). Safety threshold of the oil film stiffness of a CVT pulley–sheet friction pair based on mixed lubrication theory. Tribol. Trans. 64 (4), 633–643. doi:10.1080/10402004.2021.1893419

CrossRef Full Text | Google Scholar

Hoodorozhkov, S. I., and Kozlenok, A. V. (2021). Dynamics of a vehicle equipped with mechanical self-regulating stepless transmission. Int. Rev. Mech. Eng. 15 (1), 13–22. doi:10.15866/ireme.v15i1.19912

CrossRef Full Text | Google Scholar

Hu, X., Jing, C., and Li, P. Y. (2020). Modeling and experimental testing of the hondamatic inline hydromechanical transmission (iHMT). J. Dyn. Syst. Meas. Control 142 (5), 22–37. doi:10.1115/1.4046101

CrossRef Full Text | Google Scholar

Huang, M., Shi, C., Zhu, Y., Zhang, J., and Zhang, F. (2021). Design of gerotor pump and influence on oil supply system for hybrid transmission. Energies 14 (18), 5649–5713. doi:10.3390/en14185649

CrossRef Full Text | Google Scholar

Kharytonchyk, S. V., Kusyak, V. A., and Le, N. V. (2021). Control of pneumatic actuator for automated mechanical transmission dry friction clutch base on the pulse width modulation signal. Наука и техника 6 (1), 26–32. doi:10.21122/2227-1031-2021-20-1-26-32

CrossRef Full Text | Google Scholar

Li, J., Zhai, Z., Song, Z., Fu, S., Zhu, Z., and Mao, E. (2022). Optimization of the transmission characteristics of an HMCVT for a high-powered tractor based on an improved NSGA-II algorithm. J. Automob. Eng. 236 (13), 2831–2849. doi:10.1177/09544070211067961

CrossRef Full Text | Google Scholar

Maczyszyn, A. (2019). Energy loss coefficients i in a displacement pump and hydraulic motor used in hydrostatic drives. Pol. Marit. Res. 26 (3), 47–55. doi:10.2478/pomr-2019-0045

CrossRef Full Text | Google Scholar

Mazali, I. I., Husain, N. A., Tawi, K. B., Husain, N. A., and Asus, Z. (2019). Review of latest technological advancement in electro-mechanical continuously variable transmission. Int. J. Veh. Des. 81 (3-4), 166–190. doi:10.1504/ijvd.2019.10033893

CrossRef Full Text | Google Scholar

Morabito, E. C., and Versaci, M. (2001). A fuzzy neural approach to localizing holes in conducting plates. IEEE Trans. Magnetics 37 (5), 3534–3537. doi:10.1109/20.952655

CrossRef Full Text | Google Scholar

Ouyang, T., Li, S., Huang, G., Zhou, F., and Chen, N. (2019). Mathematical modeling and performance prediction of a clutch actuator for heavy-duty automatic transmission vehicles. Mech. Mach. Theory 136, 190–205. doi:10.1016/j.mechmachtheory.2019.03.003

CrossRef Full Text | Google Scholar

Pang, D., Zeng, G., Li, X., Guo, L., Zhao, F., and Sun, Z. C. (2021). Transient temperature field of planetary gear system in electro-mechanical transmission under different working conditions. Acta Armamentarii 42 (10), 2268–2277. doi:10.3969/j.issn.1000-1093.2021.10.023

CrossRef Full Text | Google Scholar

Thenathayalan, D., and Park, J. H. (2019). Individually regulated multiple-output WPT system with a single PWM and single transformer. IEEE J. Emerg. Sel. Top. Power Electron. 8 (4), 3542–3557. doi:10.1109/jestpe.2019.2925190

CrossRef Full Text | Google Scholar

Wang, X., Wang, Z., L Xie, L., Wang, S., and Ma, W. (2024). Research on the new hydrostatic transmission system of wheel loaders based on fuzzy sliding mode control. Energies 17 (3), 565–579. doi:10.3390/en17030565

CrossRef Full Text | Google Scholar

Yan, Z., Yin, D., Chen, L., and Shen, W. (2022). Research on the torsional vibration performance of a CVT powertrain with a dual-mass flywheel damper system. J. Automob. Eng. 236 (6), 1144–1154. doi:10.1177/09544070211036679

CrossRef Full Text | Google Scholar

Yao, J., Duan, C., Lee, C., and Zhou, Y. (2021). Study of wedge-actuated continuously variable transmission. SAE Int. J. Passeng. Cars-Mechanical Syst. 14 (6), 151–167. doi:10.4271/06-14-02-0010

CrossRef Full Text | Google Scholar

Yasien, F. R., and Wala’a, H. N. (2019). Speed controller of three phase induction motor using sliding mode controller. J. Eng. 25 (7), 118–133. doi:10.31026/j.eng.2019.07.07

CrossRef Full Text | Google Scholar

Yuan, C., Plummer, A., and Pan, M. (2022). Switching characteristics of a high-speed rotary valve for switched inertance hydraulic converters. Proc. Institution Mech. Eng. Part I J. Syst. Control Eng. 236 (7), 1421–1441. doi:10.1177/09596518221082445

CrossRef Full Text | Google Scholar

Zeng, X., Li, X., and Dong, B. (2020). Coordination control strategy for mode switching of a parallel hybrid electric system based on continuously variable transmission. SAE Int. J. Commer. Veh. 13 (2), 145–156. doi:10.4271/02-13-02-0010

CrossRef Full Text | Google Scholar

Zhang, Z., Ji, W., Yang, B., Hou, J., and Li, X. (2022a). Dynamic analysis and vibration reduction of mechanical-hydraulic coupled tunnel boring machine (TBM) main drive system. J. Mech. Eng. Sci. 236 (1), 115–125. doi:10.1177/09544062211029330

CrossRef Full Text | Google Scholar

Zhang, Z., Wang, H., Ge, S., and Li, M. (2022b). Torsional vibration analysis of a powertrain with a power reflux hydraulic transmission system. J. Vibroengineering 24 (3), 405–415. doi:10.21595/jve.2022.22237

CrossRef Full Text | Google Scholar

Zhao, Y., Chen, X., Song, Y., Wang, G., and Zhai, Z. (2023). Energy and fuel consumption of a new concept of hydro-mechanical tractor transmission. Sustainability 15 (14), 10809–10819. doi:10.3390/su151410809

CrossRef Full Text | Google Scholar