Propagation of elastic waves in adhesive contacts: experiment and numerical model

The entry and propagation of pores inside an adhesive interface between an elastomer and a rigid sphere were studied experimentally and simulated numerically. It was shown that mutually interacting events involving attachment–detachment of different segments of the elastomer to the indenter resulted in non-trivial patterns of spatially distributed contacts between them, which were additionally influenced by air penetration of the pores.

1 Introduction

One of the actively developing areas in contact mechanics is associated with the study of adhesive contacts (Brörmann et al., 2013; Sahli et al., 2018; Liu et al., 2024; Siniscalco et al., 2024). There is increasing interest regarding the study of adhesion because adhesion phenomena are easily observable in daily life. However, complex processes occur within adhesive contacts related to restructuring of the contact boundaries when the contacting surfaces shift mutually. These could be a combination of propagation of elastic waves in the contact zone, hysteresis phenomena, etc. Adhesion also has high significance in various applications, including robotics (Weston-Dawkes et al., 2021; Singh and Gupta, 2022), medicine (Ge and Chen, 2020; Zemljič-Jokhadar et al., 2021), biology (Gorb et al., 2019; van den Boogaart et al., 2022; Phiri et al., 2023), and other areas (Chernov et al., 2014; da Silva et al., 2018; Lyashenko and Liashenko, 2020).

This work is devoted to the experimental study of an intriguing phenomenon like the propagation of elastic waves that are generated in the adhesive contact zone when a solid indenter slides along the surface of a soft elastomer. Analogous waves were first observed in a classical work (Schallamach, 1971) and were therefore named as Schallamach waves. It has been shown that adhesion leads to complex processes caused by restructuring of the contact during tangential movements (Schallamach, 1971; Brörmann et al., 2013). The specificity of the present work is the consideration of quasistatic contacts since the indenter moves along the surface of the elastomer at a very low speed. Despite this, the passage of elastic waves is observed within the contact. The present work also proposes a dynamic model that allows description of the occurrences of the observed waves and their propagation using relatively simple and clearly observed dynamics with two-dimensional representations. Our experiment reveals a highly interesting feature: changes in the friction mode and characteristics of elastic wave propagation resulting from contamination of the friction surfaces and decrease in adhesion. Since the contact characteristics rely heavily on adhesive strength that varies over time, building a general theory or model of tangential adhesive contact presents a fundamentally difficult challenge. This implies that a different theory should be developed or adapted for each experimental system.

2 Experimental results

Using the experimental setup detailed in Lyashenko et al. (2024), we conducted an experiment in which a steel sphere of radius $R=40\text{\hspace{0.5em}mm}$ was pressed into a TANAC CRG N3005 elastomer sheet of thickness $h=5\text{\hspace{0.5em}mm}$ to a depth $d_{\max }=0.7\text{\hspace{0.5em}mm}$. After reaching $d_{\max }$, the indenter was moved in the tangential direction by a distance $x_{\max }=15\text{\hspace{0.5em}mm}$. Further, the indenter was pulled out in the vertical direction while the contact disappeared. The speed of the indenter was $v=3\mu \mathrm{m}/\mathrm{s}$, which allows the contact to be considered as quasistatic (Lyashenko and Popov, 2021).

An important feature of this experiment is the possibility of direct observation of the contact area as an optically transparent elastomer is used. This enables real-time observation of the dynamic processes inside the continuously restructuring contact zone. Figure 1 shows the experimental time dependences of the normal $F_N$ and tangential $F_x$ forces, contact area $A$, and average tangential stress

$〈\tau 〉=\frac{F_x}{A}.(1)$

Figure 1

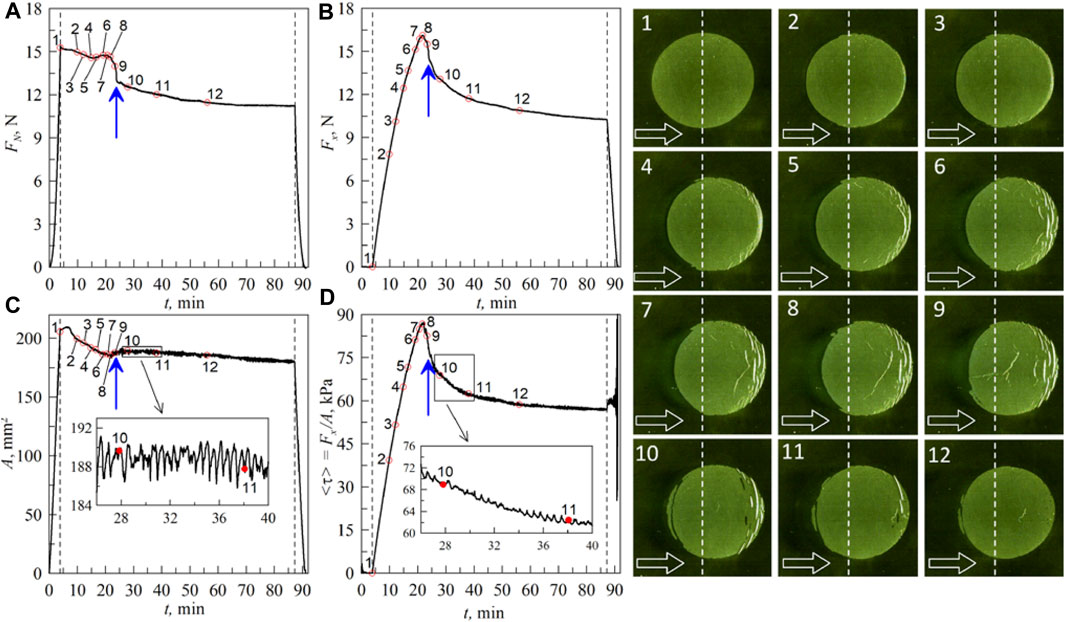
Figure 1. Experimental dependences of the (A) normal $F_N$ and (B) tangential $F_x$ forces, (C) contact area $A$, and (D) average value of shear stress $〈\tau 〉=F_x/A$ over time $t$. The right-side panel of the figure shows photographs of the contact area corresponding to points 1–12, which are indicated on all the experimental dependences.

The value $〈\tau 〉$ in Eq. (1) increases slightly with increase in the external load $F_N$ (Lyashenko et al., 2024). However, the maximum tangential stress ${\tau }_0$ at which sliding begins is a material parameter. To determine ${\tau }_0$, the two-term friction law (Berardo et al., 2019) can be used in the following form:

$F_x={\tau }_{0}A+\mu F_N(2)$

where μ is the friction coefficient. However, our experiments demonstrated that the adhesive properties decrease during sliding, consequently decreasing ${\tau }_0$ as well. Thus, we do not utilize Eq. (2) but rely on the friction force $F_x=〈\tau 〉A$, which is derived from Eq. (1). The dependences in Figure 1 demonstrate 12 characteristic points, whose contact configurations are as shown. Note that the two-term friction law of Eq. (2) is often used in tribology. As additional examples, the classical Derjaguin’s law (Derjaguin, 1934) and friction law for the boundary regime (Lyashenko et al., 2011) can be cited.

The point 1 in Figure 1 corresponds to the final moment of normal indentation. Up to this point, the contact area can be approximated as $A\approx \pi Rd$ (Hertz, 1881), where $d$ is the indentation depth and $a\approx {\left(Rd\right)}^{1/2}$ is the contact radius. Thus, the contact area at the indentation increases linearly, and the tangential force $F_x$ and stresses $〈\tau 〉$ are equal to zero. As seen from the photographs on the right side in Figure 1, during tangential movement, folds are formed initially on the surface of the elastomer owing to deformation at the leading edge of the contact; in our experimental pictures, these folds are seen as bright white stripes. Similar behaviors were observed in a recent experimental work (Yan et al., 2023), where it was shown via vertical cross sections that folds are realized. The number of folds increases with time, following which their partial sliding along the surface of the elastomer is realized. The process of fold sliding shows various dynamic phenomena: collapse of the folds into several folds or their unification and recombination.

The frictional force in the contact is $F_x=〈\tau 〉A$, where the contact area $A$ at a fixed indentation depth changes slightly. On the one hand, the frictional force increases with increases in the tangential stresses in the areas where the indenter has not yet reached the slip zone. These areas are instantly closer to the trailing edge of contact. On the other hand, $F_x$ decreases due to elastomer slipping at the leading edge of the contact. Owing to the actions of these two competing factors, the frictional force reaches a maximum at point 8, although the first instance of complete sliding over the entire surface of the indenter occurs later in the vicinity of point 9. This moment is marked in all the dependences by vertical arrows. We note that the contact may become non-simply connected during the friction process (photo 10 in Figure 1). Owing to air entrapment at the leading front, pores are formed in the contact zone (photos 10 and 11 in Figure 1), which then propagate along with the elastic deformation waves. Straightening and disappearance of the deformation folds are also often observed, because of which air pores may be formed in particular places. All mentioned processes are clearly visible in Supplementary Video S1. There are many studies that demonstrate the propagation of elastic waves in various adhesive systems (Brörmann et al., 2013; Viswanathan et al., 2015; Zhibo et al., 2021). However, in our work, we illustrate transitions between different adhesive regimes within a single experiment. Additionally, in the supplementary video, we present the evolution of the contact area alongside normal and tangential contact forces, contact areas, and shear stresses. These provide a better understanding of the processes occurring during wave propagation.

The observed folds propagation represents Schallamach waves (Schallamach, 1971; Viswanathan and Chandrasekar, 2022) in adhesive contacts. An interesting feature of the case considered here is that over time, the propagation of folds in the contact stops completely (photo 12 in Figure 1). Surprisingly, this occurs in the same experimental run and indicates a transition to a different friction regime.

It is noted that before the experiment, the indenter surface was briefly treated with a FeCl₃ solution, which greatly increased the adhesive strength of the contact against pull-off, meaning that the contact also becomes stronger to shearing. The properties of the indenter surface prepared in this manner degrade quickly upon contact with the elastomer and especially upon sliding. During sliding, the average stress $〈\tau 〉$ (Figure 1D) decreases. And after some time, the shear stress is not sufficient to deform the elastomer enough for fold formation.

Another important feature is the specific character of elastic wave propagation. In our case, these waves are visualized as the propagation of folds from the leading to trailing edges of the contact. However, the waves propagate intermittently. After the next slip of the fold, further propagation stops since it is fixed in another place of the indenter where the position is stable. This is because the stresses must reach a maximum value ${\tau }_0$ for a local slip to occur (Carpick and Salmeron, 1997; Degrandi-Contraires et al., 2012; Yashima et al., 2015; Sahli et al., 2018; Mergel et al., 2021), but the stresses decrease quickly and become less than τ₀ during a slip, which is necessary for continued slip. For further propagation of the fold, it is necessary that the stresses again reach τ₀, for which the indenter must again move to a critical value that requires time.

This is clearly visible in Supplementary Video S1, even though the video speed is 24 times faster than that of the original experiment. Note that even if the indenter moves with an extremely low speed, local slips occur with speeds that are many times higher. Therefore, to numerically simulate the process of fold propagation, it is necessary to construct a dynamic model with viscoelasticity and elastomer relaxation (Carbone et al., 2022; Papangelo and Ciavarella, 2023; Khudoynazarov, 2024). The processes under consideration are quite complex, so we limited our initial efforts to a simplified 1 + 1-dimensional model that allows us to trace the main features of fold propagation in the presence or absence of air in the folds.

3 Numerical model

The model essentially exploits the same numerical technique as in Lyashenko et al. (2023), where the elastic foundation was constructed from a set of interacting movable automata powered by a combination of short-range repulsion and long-range attraction. This allows the automata to naturally form a medium that maintains an elastically fixed distance between the neighbors. In the present work, we considered the contact between a rigid sphere and a planar elastic substrate. This is a standard tribological configuration characterized by adhesion, pressure, tangential shift, and other standard parameters (Stojanovic and Ivanović, 2014).

Formally one can treat the array of movable automata as a system of $N$ interacting “particles,” each of which is characterized by the vector radius ${\mathbf{r}}_i$, momentum ${\mathbf{p}}_i$, and interaction potential $U\left(\left|{\mathbf{r}}_i-{\mathbf{r}}_j\right|\right)$ corresponding to the Hamiltonian (Landau and Lifshitz, 1976):

$H\left({\mathbf{r}}_i,{\mathbf{p}}_i\right)=\frac{1}{2}{\displaystyle \sum _{i=1}^N}\frac{{\mathbf{p}}_i^2}{m_i}+\frac{1}{2}{\displaystyle \sum _{i,j=1}^N}U\left(\left|{\mathbf{r}}_i-{\mathbf{r}}_j\right|\right).$

In the majority of practically interesting cases, it is convenient to represent the interaction by a pair of potentials:

$U\left(\left|{\mathbf{r}}_i-{\mathbf{r}}_j\right|\right)=C\exp \left\{-{\left(\frac{{\mathbf{r}}_i-{\mathbf{r}}_j}{c}\right)}^2\right\}-D\exp \left\{-{\left(\frac{{\mathbf{r}}_i-{\mathbf{r}}_j}{d}\right)}^2\right\}$

where $C$ and $D$ define the magnitude, while $c$ and $d$ are the radii of attraction and repulsion, respectively. The natural equilibrium condition normally demands that $C\gg D$ and $c<d$. One of the surfaces in the experiment moves along the horizontal direction $x$. Here, the “upper” surface is a rigid movable sphere of radius $R_{sphere}$. Along the vertical axis, the system is limited by a substrate plate at $z=0$, which supports the system against normal load $P$ via the reflecting boundary $U_{down}=C_0\exp \left\{-z/c_0\right\}$.

To simulate the elastic system, we define the initial positions of the automata on an ordered grid, where node of the grid is connected to its neighbors by an elastic force, tending to conserve the initial distances between the nodes in the original structure. This interaction is caused by the potential

$U_{elastic}\left(\left|{\mathbf{r}}_i-{\mathbf{r}}_j\right|\right)=K_{ij}\left[1-{\left(\frac{{\mathbf{r}}_i-{\mathbf{r}}_j}{a}\right)}^2\right]\times \exp \left\{-{\left(\frac{{\mathbf{r}}_i-{\mathbf{r}}_j}{R_0}\right)}^2\right\}$

which leads to linear elastic forces at small deviations and automatically ensures that the nodes are connected to each other at the equilibrium distance $a$. Here, $R_0$ is the characteristic distance; at $R_0\gg a$, there are effective longitudinal and lateral stiffnesses of the material that return it to the original form when the external force is removed. As in our previous work (Lyashenko et al., 2023), we added an interaction between the sphere and segments of the elastic substrate. It is convenient to simulate these using sufficiently sharp but continuous potentials. For definiteness, we used strong exponential repulsion $U_{repuls}=U_0^{rep}\exp \left[-\left(r-R_{sphere}\right)/R_{repuls}\right]$ and short-range attraction $U_{adh}=U_0^{adh}\exp \left[-\left(r-R_{sphere}\right)/R_{adh}\right]$ in a narrow spherical belt around the surface. Here, $U_0^{rep}>0$ and $U_0^{adh}<0$, while both characteristic distances are much smaller than the radius of the sphere: $R_{repuls}\ll R_{sphere}$, $R_{adh}\ll R_{sphere}$.

The equations of motion can be written in standard form (Landau and Lifshitz, 1976) as $m_i\mathit{\partial }{\mathbf{v}}_i/\mathit{\partial }t=-\mathit{\partial }H\left({\mathbf{x}}_i,{\mathbf{p}}_i\right)/\mathit{\partial }{\mathbf{p}}_i={\mathbf{f}}_i^{\mathbf{r}}$, where ${\mathbf{v}}_i$ is the velocity of the ith particle. The interacting automata exchange momentum ${\mathbf{p}}_i$, owing to which a dissipation channel should exist to equilibrate the relative velocities of the particles. This interaction works at the relatively short mutual distance $c_v$ close to the equilibrium distance and needs to be introduced. Accordingly, we add an additive dissipation force ${\mathbf{f}}_i^v\propto {\displaystyle \sum _{j=1}^N}\left({\mathbf{v}}_i-{\mathbf{v}}_j\right)\exp \left\{-{\left[\left({\mathbf{r}}_i-{\mathbf{r}}_j\right)/c_v\right]}^2\right\}$ acting on each particle from the surroundings, with a corresponding dissipation constant $\eta$. The equations of motion formally assume the following form:

$m_i\frac{\mathit{\partial }{\mathbf{v}}_i}{\mathit{\partial }t}={\mathbf{f}}_i^{\mathbf{r}}-\eta {\mathbf{f}}_i^{\mathbf{v}}.(3)$

An analogous numerical approach and similar equations were recently used in Filippov et al. (2024a, 2024b). However, to simulate the effect of adhesion realistically, it has to be completed using a condition that specifies the circumstances where a segment of the substrate follows the sphere and is practically glued to it by adhesion. Thus, a given segment of the substrate is attached to the spherical surface when the distance between them is small enough $\left|R\left(x,y,z\right)-R_{sphere}\right|\le \delta R_{crit}$ and detached when the deviation from the surface exceeds a threshold $k\left(\left|\overrightarrow{r}-{\overrightarrow{r}}_0\right|\right)>f_{crit}$ defined by a critical force $f_{crit}$ at a given elastic constant $k$. The corresponding numerical procedure involves solving a set of dynamic equations for the particular segment if these threshold conditions are not satisfied or shifts the elastic segment together with the contacting sphere surface.

To proceed with this model, we applied an external load $F_z$ under which the sphere slowly moved to the surface while acquiring an equilibrium indentation. The vertical motion of its center $Z_c$ can be treated as overdamped and described by $\mathit{\partial }{Z}_c/\mathit{\partial }t=\gamma \left(-F_z+{\sum }_j{f}_{sphere}^z\left(r_j\right)\right)$, where ${\sum }_j{f}_{sphere}^z\left(r_j\right)$ is the sum of the vertical components of the forces from the elastic substrate. When a desirable indentation depth with $\mathit{\partial }{Z}_c/\mathit{\partial }t=0$ is established at a given load $F_z$, we fix the indenter and start pulling. In the simulations, we move the elastic foundation at a constant velocity $V_x=\text{const}$ in the horizontal direction. Owing to the stress and adhesion, the foundation bends and folds. In some places, the elastic material is closer to the indenter than in other places in front of the motion and apparently “jumps” into adhesive contact. As the motion continues, new folds are formed. The material containing indentations can also get close enough to the sphere and form new regions of adhesive contact. However, some empty pores remain between the contact regions; in these places, the elastic segments are still far enough from the hard sphere and are not glued adhesively to its surface. A general sketch of the configuration with such pores is shown in Figure 2A, where the sphere is shown in gray color. The configuration of the elastic surface is shown by the blue curve. The direction of horizontal motion of the substrate with velocity $V_x=\text{const}$ is depicted by the black arrow. The segments of the pore in Figure 2A are marked as connected colored (pink) points. This numerical experiment was purely that of a theoretical system with empty pores (say, in “vacuum”).

Figure 2

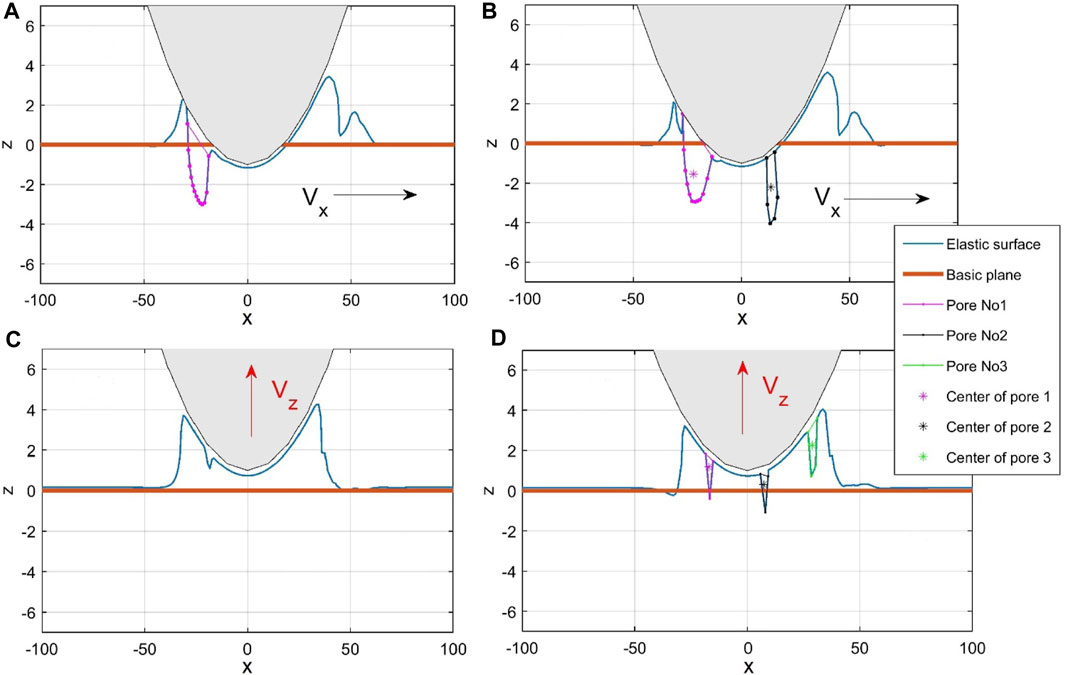
Figure 2. General sketch of the problem (A) without and (B) with air. (C) and (D) depict the same curves as in (A) and (B) at the final stage when the ball is gradually lifted from the substrate.

It is useful to apply this model to clarify the role of air in the real experiments, where air always exists (Koudine et al., 1997; Rand and Crosby, 2006). Air enters the pores and remains within them if the pores close after being formed. The trapped air produces a pressure that varies depending on the pore-size variations; this pressure grows inversely with the pore’s volume, such that the pressure decreases and slows the rate of expansion when it expands. When the pore shrinks, the air pressure increases and prevents collapse; hence, it is expected that the presence of air should stabilize the pores.

To incorporate air into the model, we added it as follows. In $\left\{x,z\right\}$ space, the boundary of each pore is a set of discrete segments between two limiting sequential points, where the distance $\delta r_s=\left|\mathbf{r}-{\mathbf{R}}_s\right|$ between the indenter and elastic foundation becomes zero. One can mark continuous groups of these segments (for example, by pink color as in Figure 2A), find their geometric center(s), and calculate the pore volume(s) in the 2d-plane $\left\{x,z\right\}$. Using this information, we can define the air pressure $P_{air}$. When the pore expands, the air inside behaves as an ideal gas, and its absolute pressure decreases inversely with the volume $V$. Thus, we have $P_{air}=P_{air}^{*}{V}^{*}/V$, where $P_{air}^{*}$ and $V^{*}$ are the pressure and volume at pore formation, respectively, at least in the limit when the volume is sufficiently large $V\gg V^{*}$. Conversely, when the pore shrinks to an extremely small volume, the compressed air behaves as a non-ideal gas; however, its pressure cannot grow infinitely and tends to a maximum possible value, at which point the air will obligatory leak out of the pore. Thus, in the model frame, we regularize the relation $P_{air}=P_{air}^{*}{V}^{*}/V$ to the following form: $P_{air}\approx P_{air}^{*}{V}^{*}/\left(V+V_{\min }\right)$. This restricts the pressure to an allowed maximum value of $P_{air}\to P_{air}^{*}{V}^{*}/V_{\min }$ when pore’s volume is much smaller than the original volume $V\ll V^{*}$. The internal pressure ${\mathbf{P}}_{air}$ is a vector force acting on the elastic segments surrounding each pore in the radial direction $\left(\mathbf{r}-{\mathbf{r}}_c\right)$ from the center ${\mathbf{r}}_c$ to the periphery. Now, we can formally redefine the equation of motion in the presence of air as follows (cf. Eq. (3)):

$m_i\frac{\mathit{\partial }{\mathbf{v}}_i}{\mathit{\partial }t}={\mathbf{f}}_i^{\mathbf{r}}-\eta {\mathbf{f}}_i^{\mathbf{v}}+{\mathbf{P}}_{iair}.$

Below, we present all the results as comparisons between the cases with and without air while maintaining all the other conditions constant. As a rule, ${\mathbf{P}}_{iair}$ leads to stabilization of the pores and supports coexistence of many pores simultaneously. To demonstrate this, Figure 2B and Figure 2D show the presence of air in different pores through different colors.

Slow vertical lifting of the indenter at the final stage of the routine is shown by the red arrow $V_z\ll V_x$ in Figure 2C and Figure 2D. Both of these are recorded at the same moment in time, close to complete detachment of the sphere. In the case with air, the pores still remain under the sphere almost to the end of the process.

The dynamic processes for the cases with and without air are demonstrated in Supplementary Video S2. Moreover, to enable direct visualization of the process in the form close to that in Figure 2, Supplementary Video S2 simultaneously shows data accumulation for the history of the processes, which are used to further depict them in static form as time–space maps in Figure 3.

Figure 3

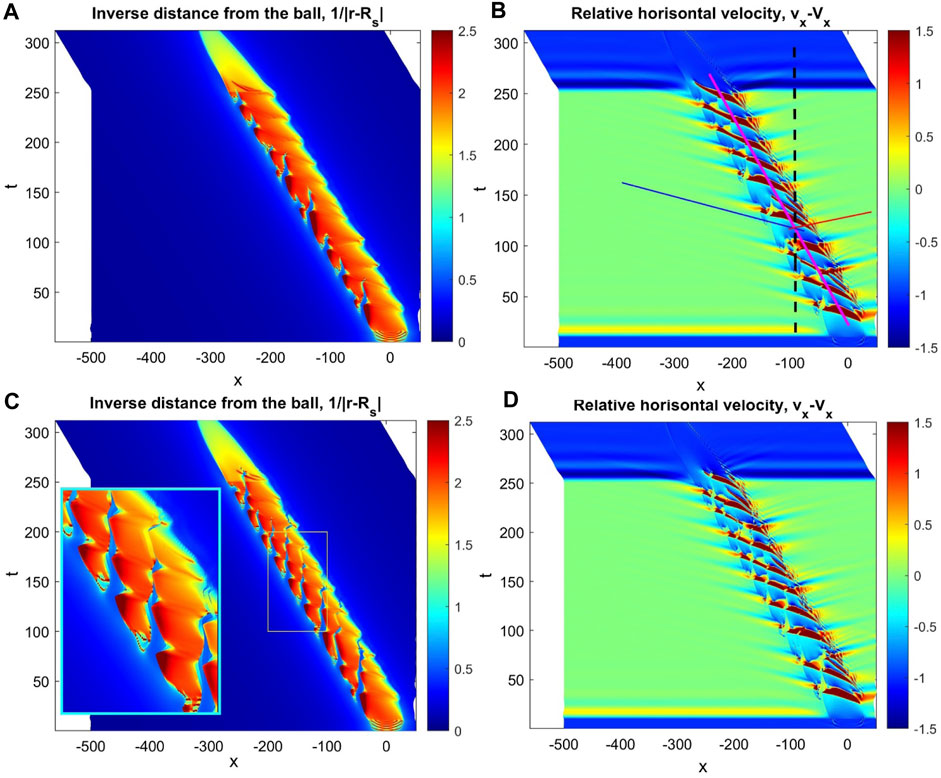
Figure 3. Time–space maps reproducing the recorded histories of inverse distance $1/\left|\mathbf{r}-{\mathbf{R}}_s\right|$ and relative horizontal velocity $\left(v_x-V_x\right)$ of the elastic foundation $v_x$ and sphere $V_x$ without and with air, as shown in subplots (A), (B) and (C), (D), respectively. The propagation of the pores is accompanied by elastic waves, which are faster than the motion of the sphere. Different slopes of the blue valleys in the velocity maps that are associated with the sphere and two families of collective excitations propagating in both directions are marked in the (B) in bold magenta as well as thin blue and red lines. Smaller inclinations of these lines correspond to faster propagation of the waves. The magnified inset in (C) illustrates the propagation of the chain of pores marked by the rectangle in the system.

In particular, these maps reproduce the histories recorded for the inverse distance $1/\left|\mathbf{r}-{\mathbf{R}}_s\right|$ and relative horizontal velocity $\left(v_x-V_x\right)$ of the elastic foundation $v_x$ and sphere $V_x$ without and with air; they are shown in the subplots (A), (B) and (C), (D) of Figure 3, respectively. From Supplementary Video S2, the static pictures show the entrance and movement of the pores under the sphere, which are visualized as deep blue valleys in Figure 3A. The pattern of the moving pores is accompanied by peculiarities of the relative velocity $\left(v_x-V_x\right)$ because the entrance of the pores causes movable elastic waves, which propagate faster than the sphere velocity. These are depicted with different slopes of the blue valleys in the velocity map, which are associated with the sphere and two families of collective excitations propagating in both directions; the corresponding motions are shown in Figure 3B by bold magenta as well as thin blue and red lines. Smaller inclination of the line with the vertical axis corresponds to faster propagation of the waves. The model allows us to estimate this velocity as 10 times higher than the speed of the indenter.

We also note the fine structures of the time-dependent distance between the sphere and elastic surface as well as mutual velocities in Figure 3C and Figure 3D, respectively. These complex structures of the depicted values are caused by the simultaneous presence of numerous pores. To elucidate the propagation of the chain of pores inside the system, we show a magnified fragment in Figure 3C marked by the rectangle. Integral information regarding the time-dependent volumes of the pores with and without air is shown in Figure 4A and Figure 4B, respectively. The different colors in the plots correspond exactly to the sequence of different pores shown in the instants in Figure 2. The numerical simulation supports the original idea that the pores exist (and coexist) longer upon being stabilized by the air pressure and that their individual curves overlap in time thereof (in other words, some of the pores exist simultaneously).

Figure 4

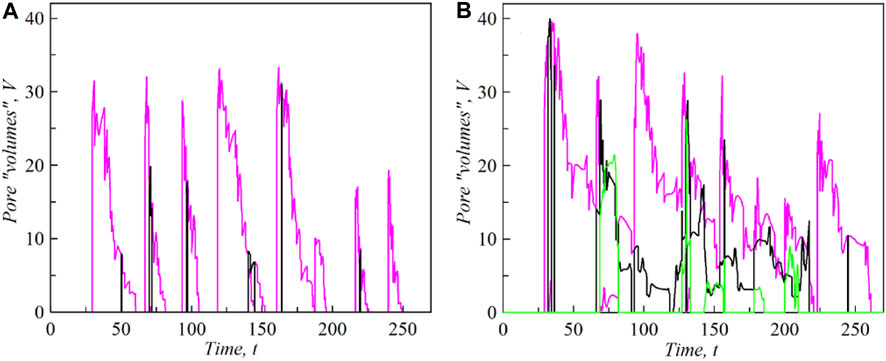
Figure 4. Time dependencies of the volumes of the pores $V$ in the systems (A) without and (B) with air inside the pores. Different colors correspond to the different pores.

Moreover, if the vertical velocity is not too high, some of the pores survive through the support of the air inside when the sphere starts to move out of the surface. They exist for a while inside the adhesive “bridge,” which connects the elastic foundation to the gradually receding sphere. To demonstrate this, we specially removed the sphere slowly at the rate of $V_z\ll V_x$ and recorded the pores without and with air in Supplementary Video S2 and in the static pictures shown in Figure 2C and Figure 2D for comparison. In the experiment, pore formation ceases over time owing to the reduction in the adhesive properties (see Figure 1). We did not incorporate this feature into the model; however, the decrease in adhesive strength can be easily accounted for, so it is sufficient to consider the temporal reduction in the critical force $f_{crit}$ at which sliding occurs (see the explanation after Eq. (3)).

4 Conclusion

This work presents an experiment on elastic wave propagation in adhesive contacts. Initially, the adhesive strength was increased via surface chemical treatment of the indenter. However, contamination reduced the adhesive strength over time, altering the friction mode visibly. Wrinkles formed during the initial sliding but ceased over time due to the diminished influence of adhesion. This highlights the absence of a universal adhesive friction mode, necessitating unique theoretical models for specific cases. The present study proposes a model detailing wrinkle formation and propagation under shear stress. We provide valuable insights to researchers on adhesive friction by showing the lack of a universal behavior in adhesive contacts despite existing studies aimed at establishing such behaviors.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, and any further inquiries may be directed to the corresponding author.

Author contributions

IL: Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft. AF: Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft. VP: Conceptualization, Funding acquisition, Project administration, Supervision, Writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. The authors acknowledge financial support from the Deutsche Forschungsgemeinschaft (DFG PO 810/55-3).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declare that they were an editorial board member of Frontiers at the time of submission. This had no impact on the peer review process and final decision.

The reviewer QL declared a shared affiliation with the author(s) to the handling editor at the time of review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2024.1400366/full#supplementary-material

SUPPLEMENTARY VIDEO S1 | Video of the experiment (see description in the text of the article).

SUPPLEMENTARY VIDEO S2 | Video of the simulation results (see description in the text of the article).

References

Berardo, A., Costagliola, G., Ghio, S., Boscardin, M., Bosia, F., and Pugno, N. M. (2019). An experimental-numerical study of the adhesive static and dynamic friction of micro-patterned soft polymer surfaces. Mater. Des. 181, 107930. doi:10.1016/j.matdes.2019.107930

CrossRef Full Text | Google Scholar

Brörmann, K., Barel, I., Urbakh, M., and Bennewitz, R. (2013). Friction on a microstructured elastomer surface. Tribol. Lett. 50, 3–15. doi:10.1007/s11249-012-0044-3

CrossRef Full Text | Google Scholar

Carbone, G., Mandriota, C., and Menga, N. (2022). Theory of viscoelastic adhesion and friction. Extreme Mech. Lett. 56, 101877. doi:10.1016/j.eml.2022.101877

CrossRef Full Text | Google Scholar

Carpick, R. W., and Salmeron, M. (1997). Scratching the surface: fundamental investigations of tribology with atomic force microscopy. Chem. Rev. 97 (4), 1163–1194. doi:10.1021/cr960068q

PubMed Abstract | CrossRef Full Text | Google Scholar

Chernov, S. V., Makukha, Z. M., Protsenko, I. Y., Nepijko, S. A., Elmers, H. J., and Schönhense, G. (2014). Test object for emission electron microscope. Appl. Phys. A 114 (4), 1383–1385. doi:10.1007/s00339-013-8010-y

CrossRef Full Text | Google Scholar

da Silva, L. F. M., Öchsner, A., and Adams, R. D. (2018). Handbook of adhesion technology (Cham: Springer). doi:10.1007/978-3-319-55411-2

CrossRef Full Text | Google Scholar

Degrandi-Contraires, E., Poulard, C., Restagno, F., and Léger, L. (2012). Sliding friction at soft micropatterned elastomer interfaces. Faraday Discuss. 156, 255–265. doi:10.1039/C2FD00121G

PubMed Abstract | CrossRef Full Text | Google Scholar

Derjaguin, B. (1934). Molekulartheorie der äußeren Reibung. Z. Phys. 88, 661–675. doi:10.1007/BF01333114

CrossRef Full Text | Google Scholar

Filippov, A. E., Nadein, K., Gorb, S. N., and Kovalev, A. (2024a). Bio-bearings: numerical model of the solid lubricant in the leg joints of insects. Tribol. Lett. 72 (1), 11. doi:10.1007/s11249-023-01815-3

CrossRef Full Text | Google Scholar

Filippov, A. E., Nadein, K., Gorb, S. N., and Kovalev, A. (2024b). Large-scale numerical simulation of the solid lubricant behavior in the leg joints of insects. Adv. Theory Simul. 7, 2301236. doi:10.1002/adts.202301236

CrossRef Full Text | Google Scholar

Ge, L., and Chen, S. (2020). Recent advances in tissue adhesives for clinical medicine. Polymers 12, 939. doi:10.3390/polym12040939

PubMed Abstract | CrossRef Full Text | Google Scholar

Gorb, S. N., Koch, K., and Heepe, L. (2019). Biological and biomimetic surfaces: adhesion, friction and wetting phenomena. Beilstein J. Nanotechnol. 10, 481–482. doi:10.3762/bjnano.10.48

PubMed Abstract | CrossRef Full Text | Google Scholar

Hertz, H. (1881). Ueber die Berührung fester elastischer Körper. für reine Angew. Math. 92, 156–171. doi:10.1515/9783112342404-004

CrossRef Full Text | Google Scholar

Khudoynazarov, K. (2024). Longitudinal-radial vibrations of a viscoelastic cylindrical three-layer structure. Facta Univ. Ser. Mech. Eng. doi:10.22190/FUME231219010K

CrossRef Full Text | Google Scholar

Koudine, A. A., Lambert, M., and Barquins, M. (1997). Some new experimental results on the Schallamach waves propagation by space-time analysis. Int. J. Adhes. Adhes. 17, 359–363. doi:10.1016/S0143-7496(97)00036-5

CrossRef Full Text | Google Scholar

Landau, L. D., and Lifshitz, E. M. (1976). Mechanics. 1. Butterworth-Heinemann.

Google Scholar

Liu, Y., Wang, H., Li, J., Li, P., and Li, S. (2024). Gecko-inspired controllable adhesive: structure, fabrication, and application. Biomimetics 9, 149. doi:10.3390/biomimetics9030149

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyashenko, I. A., Filippov, A. E., and Popov, V. L. (2023). Friction in adhesive contacts: experiment and simulation. Machines 11, 583. doi:10.3390/machines11060583

CrossRef Full Text | Google Scholar

Lyashenko, I. A., Khomenko, A. V., and Metlov, L. S. (2011). Nonlinear thermodynamic model of boundary friction. J. Frict. Wear 32, 113–123. doi:10.3103/S1068366611020061

CrossRef Full Text | Google Scholar

Lyashenko, I. A., and Liashenko, Z. M. (2020). Influence of tangential displacement on the adhesion force between gradient materials. Ukr. J. Phys. 65 (3), 205–216. doi:10.15407/ujpe65.3.205

CrossRef Full Text | Google Scholar

Lyashenko, I. A., Pham, T. H., and Popov, V. L. (2024). Effect of indentation depth on friction coefficient in adhesive contacts: experiment and simulation. Biomimetics 9, 52. doi:10.3390/biomimetics9010052

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyashenko, I. A., and Popov, V. L. (2021). Hysteresis in an adhesive contact upon a change in the indenter direction of motion: an experiment and phenomenological model. Tech. Phys. 66, 611–629. doi:10.1134/S1063784221040113

CrossRef Full Text | Google Scholar

Mergel, J. C., Scheibert, J., and Sauer, R. A. (2021). Contact with coupled adhesion and friction: computational framework, applications, and new insights. J. Mech. Phys. Solids. 146, 104194. doi:10.1016/j.jmps.2020.104194

CrossRef Full Text | Google Scholar

Papangelo, A., and Ciavarella, M. (2023). Detachment of a rigid flat punch from a viscoelastic material. Tribol. Lett. 71, 48. doi:10.1007/s11249-023-01720-9

CrossRef Full Text | Google Scholar

Phiri, R., Rangappa, S. M., Siengchin, S., and Marinkovic, D. (2023). Agro-waste natural fiber sample preparation techniques for bio-composites development: methodological insights. Facta Univ. Ser. Mech. Eng. 21 (4), 631–656. doi:10.22190/FUME230905046P

CrossRef Full Text | Google Scholar

Rand, C. J., and Crosby, A. J. (2006). Insight into the periodicity of Schallamach waves in soft material friction. Appl. Phys. Lett. 89 (26), 261907. doi:10.1063/1.2408640

CrossRef Full Text | Google Scholar

Sahli, R., Pallares, G., Ducottet, C., Ben Ali, I. E., Al Akhrass, S., Guibert, M., et al. (2018). Evolution of real contact area under shear and the value of static friction of soft materials. Proc. Natl. Acad. Sci. U. S. A. 115 (3), 471–476. doi:10.1073/pnas.1706434115

PubMed Abstract | CrossRef Full Text | Google Scholar

Schallamach, A. (1971). How does rubber slide? Wear 17, 301–312. doi:10.1016/0043-1648(71)90033-0

CrossRef Full Text | Google Scholar

Singh, K., and Gupta, S. (2022). Controlled actuation, adhesion, and stiffness in soft robots: a review. J. Intell. Robot. Syst. 106, 59. doi:10.1007/s10846-022-01754-6

CrossRef Full Text | Google Scholar

Siniscalco, D., Pessoni, L., Boussonnière, A., Castanet, A.-S., Billon, L., Vignaud, G., et al. (2024). Design of an azopolymer for photo-switchable adhesive applications. Coatings 14, 275. doi:10.3390/coatings14030275

CrossRef Full Text | Google Scholar

Stojanovic, B., and Ivanović, L. (2014). Tribomechanical systems in design. J. Balk. Tribol. 20 (1), 25–34.

Google Scholar

van den Boogaart, L. M., Langowski, J. K. A., and Amador, G. J. (2022). Studying stickiness: methods, trade-offs, and perspectives in measuring reversible biological adhesion and friction. Biomimetics 7, 134. doi:10.3390/biomimetics7030134

PubMed Abstract | CrossRef Full Text | Google Scholar

Viswanathan, K., and Chandrasekar, S. (2022). Fifty years of Schallamach waves: from rubber friction to nanoscale fracture. Phil. Trans. R. Soc. A 380, 20210339. doi:10.1098/rsta.2021.0339

PubMed Abstract | CrossRef Full Text | Google Scholar

Viswanathan, K., Mahato, A., and Chandrasekar, S. (2015). Nucleation and propagation of solitary Schallamach waves. Phys. Rev. E 91 (1), 012408. doi:10.1103/PhysRevE.91.012408

PubMed Abstract | CrossRef Full Text | Google Scholar

Weston-Dawkes, W. P., Adibnazari, I., Hu, Y.-W., Everman, M., Gravish, N., and Tolley, M. T. (2021). Gas-lubricated vibration-based adhesion for robotics. Adv. Intel. Syst. 3 (7), 2100001. doi:10.1002/aisy.202100001

CrossRef Full Text | Google Scholar

Yan, C., Chen, H. Y., Lai, P. Y., and Tong, P. (2023). Statistical laws of stick-slip friction at mesoscale. Nat. Commun. 14, 6221. doi:10.1038/s41467-023-41850-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Yashima, S., Romero, V., Wandersman, E., Frétigny, C., Chaudhury, M. K., Chateauminois, A., et al. (2015). Normal contact and friction of rubber with model randomly rough surfaces. Soft Matter 11, 871–881. doi:10.1039/c4sm02346c

PubMed Abstract | CrossRef Full Text | Google Scholar

Zemljič-Jokhadar, Š., Kokot, G., Pavlin, M., and Derganc, J. (2021). Adhesion and stiffness of detached breast cancer cells in vitro: Co-treatment with metformin and 2-Deoxy-d-glucose induces changes related to increased metastatic potential. Biology 10, 873. doi:10.3390/biology10090873

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhibo, C., Zhaoqian, S., Dandan, H., Genzong, L., Jian, W., Benlong, S., et al. (2021). From small wrinkles to Schallamach waves during rubber friction: in situ experiment and 3D simulation. Polym. Test. 96, 107084. doi:10.1016/j.polymertesting.2021.107084

CrossRef Full Text | Google Scholar