- 1Department of Electrical and Computer Engineering, Lehigh University, Bethlehem, PA, United States
- 2Department of Computer Science and Engineering, Lehigh University, Bethlehem, PA, United States
- 3Artificial Intelligence Thrust, Hong Kong University of Science and Technology (Guangzhou), Guangzhou, China
Graph neural networks (GNNs) have gained significant attention in diverse domains, ranging from urban planning to pandemic management. Ensuring both accuracy and robustness in GNNs remains a challenge due to insufficient quality data that contains sufficient features. With sufficient training data where all spatiotemporal patterns are well-represented, existing GNN models can make reasonably accurate predictions. However, existing methods fail when the training data are drawn from different circumstances (e.g., traffic patterns on regular days) than test data (e.g., traffic patterns after a natural disaster). Such challenges are usually classified under domain generalization. In this work, we show that one way to address this challenge in the context of spatiotemporal prediction is by incorporating domain differential equations into graph convolutional networks (GCNs). We theoretically derive conditions where GCNs incorporating such domain differential equations are robust to mismatched training and testing data compared to baseline domain agnostic models. To support our theory, we propose two domain-differential-equation-informed networks: Reaction-Diffusion Graph Convolutional Network (RDGCN), which incorporates differential equations for traffic speed evolution, and the Susceptible-Infectious-Recovered Graph Convolutional Network (SIRGCN), which incorporates a disease propagation model. Both RDGCN and SIRGCN are based on reliable and interpretable domain differential equations that allow the models to generalize to unseen patterns. We experimentally show that RDGCN and SIRGCN are more robust with mismatched testing data than state-of-the-art deep learning methods.
1 Introduction
Spatiotemporal prediction is a key task in many scientific and engineering domains, ranging from structural health monitoring (Morid et al., 2023), evolution of microstructures (Montes de Oca Zapiain et al., 2021), traffic management (Bui et al., 2022), weather forecasting (Longa et al., 2023), and disease control (Jayatilaka et al., 2020). With explosive growth in data collection technologies and sufficient training data, deep learning approaches (Yu et al., 2018; Wu et al., 2020) have come to dominate the field of data-driven prediction of complex systems. Among best-performing models, graph neural networks (GNNs) dominate due to their ability to incorporate spatiotemporal information (Han et al., 2021; Shang et al., 2021; Ji et al., 2022) so that dependent information at different locations and times can be captured and exploited to make more accurate predictions. However, as these models grow more complex, thus requiring substantial training data, their performance when test conditions are different from training conditions has been shown to be weak. The collection of data from all representative conditions is almost impossible in many domains, and so there is a need to develop methods for data-driven prediction that can handle this generalization.
Such challenges are usually classified under “domain generalization” (Figure 1), where a model is trained on a source domain but evaluated on a target domain with different characteristics (mismatches). Consider traffic speed prediction as a motivating example. It is well known that prediction algorithms perform poorly when traffic patterns are unexpectedly disrupted, for instance, due to extreme weather, natural disasters, or even special events. In our evaluation section, we will demonstrate this phenomenon more concretely, where state-of-the-art deep learning methods do not generalize well when dataset patterns are split between training (weekday) and test patterns (weekend). The challenge mentioned above can be formulated as learning with mismatched training data (Varshney, 2020), a problem that is often encountered in practice.
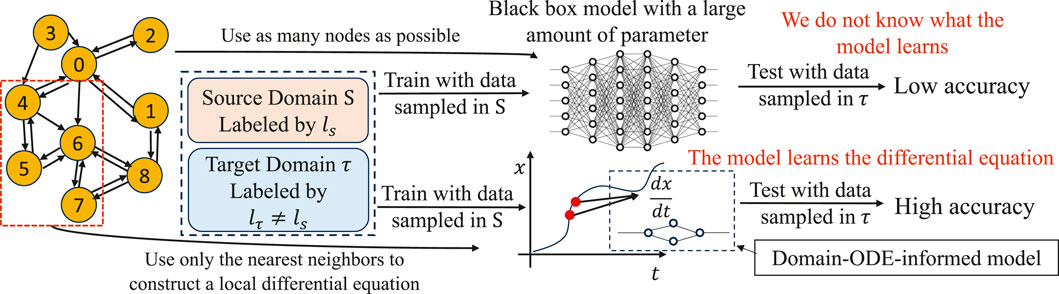
Figure 1. Training and test sets consist of a source domain S characterized by a labeling function ls, and a target domain τ distinguished by a different labeling function lτ ≠ ls. Data collection in the source domain is convenient, whereas acquiring data in the target domain is challenging and often only feasible at test time. Without integrating a domain ODE, a model, despite having numerous parameters, may experience diminished accuracy when tested with such mismatched patterns. Conversely, employing an architecture that integrates a domain ODE enables the model to capture local patterns and attain high accuracy even with previously unseen patterns, while requiring fewer parameters.
This leads to the main hypothesis of our paper: when scientific equations or physical models are available to capture the local spatiotemporal dynamics of vertices in a network, such that these dynamics remain consistent between training and test conditions, then machine learning models that incorporate these scientific equations can lower the generalization discrepancy of the learned model. In particular, we consider systems where local dynamics are available in the form of ordinary differential equations, which we use to construct a novel graph-convolution network structure for spatiotemporal prediction. We will use a known probably approximately correct (PAC) learning approach to quantify generalization discrepancy between predictions under different source and target labeling functions, proving mathematically that under certain learnability and symmetry assumptions on the labeling functions, incorporating the local dynamics can lower the discrepancy. We operationalize our approach by constructing two different dynamics-informed GCNs for application in traffic-speed prediction and influenza-like-illness (ILI) prediction using domain ordinary differential equations (ODEs). Our novel domain-ODE-informed neural networks called “Reaction-Diffusion Graph Convolutional Network” (RDGCN), and “Susceptible-Infectious-Recovered Graph Convolutional Network” (SIRGCN) augment GCNs with domain ODEs studied in transportation research (Bellocchi and Geroliminis, 2020) and disease epidemics (Stolerman et al., 2015). Through experimental evaluation on real datasets, we demonstrate that our novel-dynamics-informed GCNs are more robust in situations with data mismatches than baseline models in traffic speed prediction and influenza-like illness prediction. Furthermore, the prior knowledge encoded by the dynamics-informed architecture reduces the number of model parameters, thus requiring less training data. The model computations are better grounded in domain knowledge and are thus more accessible and interpretable for domain experts.
We highlight our contributions as follows:
• We study the challenge of graph-time-series prediction with mismatched data where the patterns in the training set are not representative of those in the test set.
• We theoretically prove the robustness of domain-ODE-informed GCNs to a particular form of domain generalization when the labeling function differs between the source and target domains. Specifically, we show that the generalization discrepancy is lower for the domain-ODE-informed learning model under certain conditions than a domain-independent learning model.
• We develop two novel domain-ODE-informed neural networks called “Reaction-Diffusion Graph Convolutional Network” (RDGCN), and “Susceptible-Infectious-Recovered Graph Convolutional Network”(SIRGCN) that augment GCNs with domain ODEs studied in transportation research (Bellocchi and Geroliminis, 2020) and disease epidemics (Stolerman et al., 2015).
• By conducting experimental assessments on authentic datasets, we illustrate that our innovative dynamics-informed GCNs exhibit greater robustness in scenarios featuring data mismatches than baseline models in both traffic speed prediction and influenza-like illness prediction.
• By integrating domain difference equations, the dynamics-informed GCNs can substantially decrease the quantity of model parameters, resulting in reduced training data requirements and accelerated training and inference processes.
The structure of this paper unfolds as follows. In Section 2, we provide a comprehensive background on graph neural networks (GNNs) for time-series prediction, elucidating the challenges encountered in achieving domain generalization within GNNs. Section 3 formalizes the problem by defining the generalization discrepancy between the source and target domains. Building upon this, Section 4 details our proposed methodology, introducing a novel approach that integrates domain differential equations into GCNs. Here, we outline the architecture of dynamics-informed graph convolutional networks (DGCNs), specifically tailored for spatiotemporal prediction tasks. The theoretical underpinnings of our approach are rigorously examined in Section 5, where we explore the generalization properties of DGCNs. Additionally, theoretical bounds on the discrepancy between source and target domains are derived. Section 6 showcases the practical application of DGCNs on real-world datasets, focusing on two case studies: RDGCN for predicting traffic speed evolution and SIRGCN for modeling disease propagation. Through these applications, we evaluate the effectiveness of DGCNs in mitigating the generalization gap. To further bolster our claims, Section 7 and 8 detail the experimental setup, results obtained, and an ablation study. These sections offer additional insights into the performance of RDGCN and SIRGCN, further validating our proposed methodology. In Section 9, we assess the model complexity of RDGCN and SIRGCN. Finally, in Section 10, we draw conclusions by summarizing the key findings and implications of our research. Additionally, we propose potential avenues for future research aimed at enhancing the generalization capabilities of DGCNs in the realm of time-series predictions.
2 Related work
2.1 Graph neural networks on time series predictions
GNNs have been widely utilized to enable great progress in dealing with graph-structured data (Kipf and Welling, 2017; Yu et al., 2018; Li et al., 2018; Cui et al., 2020) build spatiotemporal blocks to encode spatiotemporal features (Wu et al., 2020; Shang et al., 2021; Han et al., 2021; Veličković et al., 2018; Guo et al., 2019) and generate dependency graphs which only focus on “data-based” dependency where features at a vertex can be influenced by a vertex but not in its physical vicinity. None of these approaches exploit domain ODEs for better generalization and robustness.
2.2 Domain generalization
Domain generalization has gained increasing attention recently (Wang et al., 2022; Zhou et al., 2022; Robey et al., 2021; Zhou et al., 2021), and robustness to domain data with mismatched patterns is important in designing trustworthy models (Varshney, 2020). The goal is that a model learns to generalize to unseen domains. Many studies (Robey et al., 2021) assume that there is an underlying transformation between the source and target domain and use an extra model to learn the transformations (Xian et al., 2022); therefore, the training data must be sampled under at least two individual distributions. However, our approach addresses this challenge by incorporating a domain-specific ODE instead of using extra training processes that learn from the data from two individual domains or employing additional assumptions on transformations, thus working for arbitrary domain scenarios.
2.3 Domain dynamics, differential equations and neural ODEs
Time series are modeled using differential equations in many areas, such as chemistry (Scholz and Scholz, 2015) and transportation (van Wageningen-Kessels et al., 2015; Loder et al., 2019; Kessels and Kessels, 2019). These approaches focus on equations that reflect the most essential relationships. To incorporate differential equations into machine learning, many deep learning models based on neural ODEs (Chen et al., 2018; Jia and Benson, 2019; Asikis et al., 2022) have been proposed. Advancements extend to graph ODE networks (Ji et al., 2022; Choi et al., 2022; Jin et al., 2022) which use black-box differential equations to simulate continuous traffic-pattern evolution. However, the potential of domain knowledge to fortify algorithmic robustness against domain generalization has yet to be explored.
2.4 Integrating domain knowledge into deep learning
Incorporating domain knowledge in deep learning has been garnering growing interest (Van Der Voort et al., 1996; Chen et al., 2011; Kumar and Vanajakshi, 2015; Thodi et al., 2022). For example, Physics-Informed Neural Network (PINN) approaches (Raissi et al., 2019; Karniadakis et al., 2021) incorporate physics equations to augment deep learning. PINN has been extended to incorporate a macroscopic traffic model (Huang and Agarwal, 2020) to enhance learning in traffic state prediction. However, the integration of traffic models with the graphical structure of the transportation network has not been explored, particularly in the context of mismatched data.
2.5 Limited and mismatched data
Meta-learning (Finn et al., 2017) is often used to augment machine learning with limited data, through additional training processes. Mismatches between the training and test sets are frequently present in practical applications. Robustness to mismatched data is important in designing trustworthy models (Varshney, 2020). The optimization of supervised learning when the instance/label pairs have been permuted in a manner is proposed in Xian et al. (2022). Our approach, which incorporates domain ODEs, provides robustness under arbitrarily mismatch and limited data scenarios.
2.6 Model explainability
Intrinsically transparent ML models (Lakkaraju et al., 2016; Lou et al., 2012) based on simple rules or linear models are useful, in that their computation processes can be revealed to domain experts to increase model confidence. In contrast, we incorporate non-linear physical laws into graphical models to promote intrinsic explainability. In graph-based ML, understanding how neighbors lead to prediction on a mode is essential. Prior methods, such as Ying et al. (2019), use a surrogate model to approximate a graphical model and thus do not reveal the computational process of prediction models.
3 Problem definition
3.1 Notations
Given an unweighted graph
where ls is the labeling function in the source domain and
3.2 Problem definition
We aim to solve the problem of single domain generalization (Qiao et al., 2020; Wang et al., 2021; Fan et al., 2021). Given the past feature observations denoted as
where
Our objective is to develop a class of learning architectures to train a hypothesis that has low generalization discrepancy as measured above. Our approach, as delineated in the next section, will focus on the use of graph convolutional network architectures that incorporate the local spatiotemporal dynamics available in the form of ODEs.
4 Methodology
Let xi(t) denote a feature at vertex i at time t and
where
Constructing dynamics-informed GCNs involves three steps:
• Define the domain-specific graph. The unweighted graph
• Construct the feature-encoding function using the dynamic equation. We then generalize the local domain Eq. 2 to a graph-level representation:
where
• Define the network prediction function. To mitigate the effects of such pattern mismatches in Eq. 3, we propose the GCN incorporating domain ODEs, which is a family of GCNs that incorporate the domain equations fi to learn only the immediate dynamics to be robust to the domain generalization. We use a feature extraction function, O, to encode inputs by selecting the relevant input by utilizing a domain graph:
where ⊗ is the Kronecker product and
5 Proof of robustness to domain generalization
We will discuss the application-specific GCNs in the subsequent section. In this section, we will prove that when the underlying local spatiotemporal dynamics (as defined by the fi function in Eq. 1) connect the features at consecutive time points, the approach that incorporates the dynamics is more robust to the domain generalization problem defined by the discrepancy equation in Eq. 2. Similar to the approach in Redko et al. (2020), we assume that the training set is sampled from the source domain and the test data are sampled from the target domain. In this study, we formulate the mismatch problem as a difference between labeling functions in the source and target domains where the immediate time and nearest neighbor dynamics (function F) are unchanging across domains. In contrast, the impact of long-term and distant neighbor patterns (function G) varies between source and target domains. We observe that although both Gs (resp. Gτ) and F utilize X(t) as part of their input, they consistently select features from distinct vertices. There is thus no overlap between inputs of Gs (resp. Gτ) and F.
Under such a mismatch scenario, we prove the methods that use data to learn the complete labeling function in the source domain using long-term patterns and data from vertices outside the neighborhood. We use
Assumption 1. (Learnability) There exists
Assumption 2. (Symmetry) Let
Assumption 1 ensures the learnability of the hypotheses. Assumption 2 ensures that the statistical impact of the long-term pattern is unbiased and symmetric3. The above assumptions lead to the following Lemmas about optimal hypotheses learned by domain-agnostic methods, such as the baselines, and those learned by dynamics-informed methods, such as ours.
Lemma 1.
Proof. Follows Assumption 1 when
Lemma 2. If (1) h2 is trained with data sampled from
Proof. We prove this by contradiction. If
When sufficient training data are provided, Lemma 1 guarantees that baseline models can accurately capture the ground truth labeling function, including the local spatio-temporal dynamics, long-term patterns, and those from vertices beyond the neighborhood in the training dataset. Additionally, Lemma 2 ensures that domain-ODE-informed models can accurately learn the ground truth differential equation representing the local spatiotemporal dynamics.
To theoretically establish the enhanced robustness of our approach, we assume the PAC learnability of
and
We will now demonstrate that
where h′ is any other hypothesis. The following theorem proves our result.
Theorem 1. If (1) the training data are sampled from the source domain where Assumption 2 is true, (2) the loss function L(h, l) obeys the triangular inequality, then the discrepancy should satisfy
Proof. By the definition of discrepancy in Eq. 1, we know
where (a) follows from Jensen’s equality (|⋅| is convex) and (b) follows from the triangle inequality (which implies |L (x, y)|≥|L (x, z) − L (y, z)|, for any
where (c) follows from the definition of the supremum (the least element that is greater than or equal to each element in the set). Thus, from Eq. 12 and Eq. 13 together
For
Hence, we have shown that
Theorem 1 illustrate that models trained using lengthy time sequences and distant vertices are not reliable when there are mismatches between the labeling functions in the source and target domains. Loss functions that include mean absolute error (MAE) satisfy the triangle inequality assumption. We note that the triangle inequality assumption precludes using mean squared error (MSE) as a loss function. Subsequent to Theorem 2, we prove a discrepancy result that specifically holds true for MSE as a loss function. In the following, we discuss the discrepancy when using MSE loss based on the assumption that the pattern-specific dependence gi in the labeling function exhibits 0 or negative correlation between source and target domains. Under this assumption, we will show that the MSE-based discrepancy is lower for the dynamics-informed learned hypothesis compared to the class of hypotheses that learn the complete labeling function in the source domain.
Assumption 3. (Non-positive Covariance) Let
Assumption 3 ensures a significant distinction between the source and target domains. Specifically, a zero covariance implies that long-term patterns and distant-vertex patterns in the source and target domains are unrelated4 while negative covariance indicates that patterns causing positive changes in the source domain may induce negative changes in the target domain5. Based on this assumption, the following theorem proves our result when using MSE loss.
Theorem 2. If (1) the training data are sampled from the source domain where Assumptions 2 and 3 are true, (2) the loss function L(h, l) is mean squared error (MSE), (3) the error bound of h1 and h2 in Eq. 5 and Eq. 6 satisfies ϵ1 ≥ϵ2, then the discrepancy should satisfy
Proof. The main idea of the proof is to demonstrate that under Assumption 3, there exists a hypothesis in the class
Theorem 2 demonstrates that models trained with MSE loss using lengthy time sequences and distant vertices are unreliable in the presence of mismatches between the labeling functions in the source and target domains. Specifically for MSE loss, if the training loss of domain-ODE-informed GCNs matches or exceeds that of a deep neural network model, the latter becomes unreliable for predictions in the target domain. We notice a special case when hypotheses h2 could perfectly learn a labeling function using the data—if
Corollary 1. If (1) the training data are sampled from the source domain where Assumptions 2 and 3 are true, (2) the loss function L(h, l) is MSE, (3)
Proof. The proof follows by setting
6 Application of domain-ODE informed GCNs
Without incorporating domain ODEs, most GNNs need longer data streams to make accurate predictions. For instance, black-box predictors in the traffic domain require 12 time points to predict traffic speeds, whereas the domain informed GCN we develop requires only one as it explicitly incorporates the immediate dynamics instead of learning arbitrary functions (see Eq. 7). In the following part of this section, we will use the reaction–diffusion equation and SIR-network differential equation as examples to develop practical dynamics-informed GCNs.
6.1 Reaction diffusion GCN for traffic speed prediction
The authors in Bellocchi and Geroliminis (2020) proposed the reaction–diffusion approach to reproduce traffic measurements such as speed and congestion using few observations. The domain differential equations included a Diffusion term that tracks the influence in the direction of a road segment, while the Reaction term captures the influence opposite the road direction. Since each sensor is placed on one side of a road segment and measures the speed along that specific direction,
where ρ(i,j) and σ(i,j) are the diffusion and reaction parameters, respectively;
In the following, we incorporate this reaction–diffusion (RD) equation using the steps outlined in the methodology section to build a novel GCN model for the dynamics-informed prediction of traffic speed. The architecture of RDGCN is shown in Figure 2.
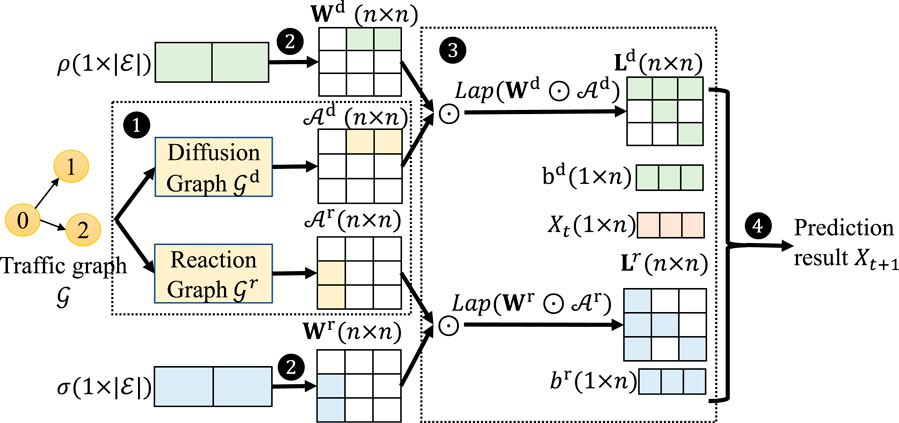
Figure 2. Reaction-Diffusion Graph Convolutional Network architecture for graph with
Step 1: Define reaction and diffusion parameters. We define a diffusion graph
Step 2: Construct an RD feature encoding function. Let Ld (resp. Lr) be the corresponding Laplacian of the combination of diffusion (resp. reaction) weight tensor Wd (resp. Wr) and diffusion (resp. reaction) adjacency matrices
where ⊙ denotes the Hadamard product, Degree (∗) is to calculate the degree matrix of an input adjacency matrix, and
Step 3: Using Eq. 4, we can define a prediction:
where Ld and Lr are the reaction and diffusion functions constructed earlier, corresponding to the function F = (LdXt + bd) + tanh (LrXt + br) predicting the traffic speed using the reaction parameters ρ and the diffusion parameters σ (see ❹ in Figure 2).
6.2 Susceptible–infected–recovered (SIR)-GCN for infectious disease prediction
The SIR model is a typical model describing the temporal dynamics of an infectious disease by dividing the population into three categories: susceptible to the disease, infectious, and recovered with immunity. The SIR model is widely used in the study of diseases such as influenza and COVID (Cooper et al., 2020). Our approach is based on the SIR-Network Model proposed to model the spread of dengue fever (Stolerman et al., 2015), which we describe as follows. Let Si(t), Ii(t), and Ri(t) denote the number of susceptible, infectious, and recovered at vertex
The spread of infection between vertices is modeled using sparse travel matrices Φ ∈ [0,1]n×n as
where βi is the infection rate at vertex i, representing the probability that a susceptible population is infected at vertex i, γ is the recovery rate, representing the probability that an infected population is recovered, and
Step 1: Derive the susceptible and recovered numbers and define the travel matrices. We first define parameter β ∈ [0,1]n (n is the number of vertices) representing the infection rate, and parameter γ ∈ [0, 1] representing the recovered rate. Since the total population at vertex i is assumed to be a constant, the network level recovered and susceptible number is
where dτ is the time interval for each sample, which we set to 1, N is the total number of the population of each state/prefecture, and t0 is the starting time of the current epidemic (see ❶ in Figure 3). Next, the travel graph
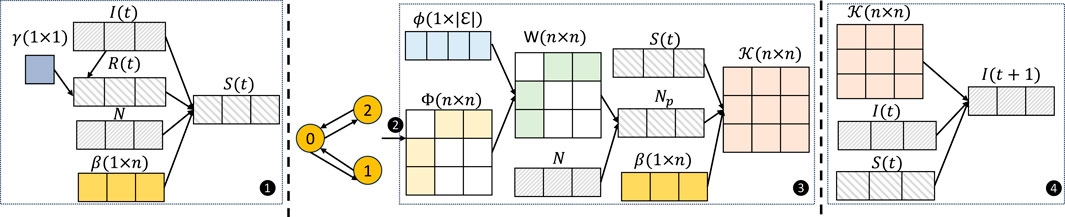
Figure 3. Susceptible-infected-recovered-GCN architecture for graph with
Step 2: Construct the SIR function. Define
where I(t) is the feature (X(t) mentioned earlier) representing the number of infectious people. Then, the transformation matrix
The dynamics-informed feature encoding function O is utilized to approximate the counts of susceptible and recovered populations and to estimate the infectious people likely to travel, approximated by the transportation data (see ❸ in Figure 3).
Step 3: Using Eq. 4 and 8, 9, the prediction is defined as:
(see ❹ in Figure 3).
7 Evaluation
In this section, we compare the performance of these domain-ODE-informed GCNs with baselines when tested with mismatched data and demonstrate that our approach is more robust to such mismatched scenarios.
7.1 Experiment settings
7.1.1 Datasets
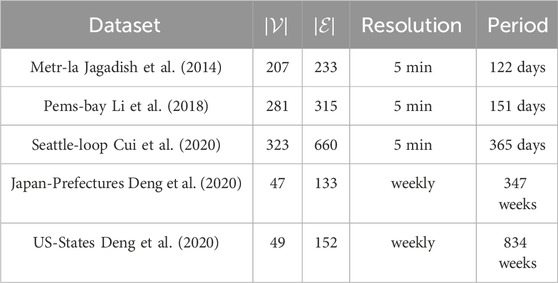
Our experiments are conducted on three real-world datasets (Metra-la, Pems-bay, and Seattle-loop) for traffic prediction and on two real-world datasets (in Japan and US) for disease prediction. The details are shown in Table 1.
7.1.2 Evaluation metric
The loss function we use is the mean absolute error and the root mean squared error:
7.1.3 Baselines
For traffic prediction tasks, we compare RDGCN with STGCN (Yu et al., 2018), MTGNN (Wu et al., 2020), GTS (Shang et al., 2021), STGNCDE (Choi et al., 2022), and MTGODE (Jin et al., 2022). They are influential and the best-performing deep learning models for predicting traffic speed using historical speed alone. We also use Model-Agnostic Meta-Learning (MAML) (Finn et al., 2017) to help baseline models, and our approach adapts quickly to tasks using good initial weights generated by MAML. For disease prediction, we compare SIRGCN with two state-of-the-art models for infection prediction: ColaGNN (Deng et al., 2020) and EpiGNN (Xie et al., 2023).
7.1.4 Evaluation
We assume that all zeros in the datasets are missing values, and we remove the predicted speed when the ground truth is 0, or when the last speed recorded is 0.
7.1.5 Hyperparameter settings
RDGCN and SIRGCN are optimized via Adam. The batch size is set as 64. The learning rate is set as 0.001, and the early stopping strategy is used with a patience of 30 epochs. These settings are the same as those used in baseline models to set up a fair comparison. In traffic speed prediction, the training and validation sets are split by a ratio of 3:1 from the weekday subset, and the test data are sampled from the weekend subset with different patterns. As for baselines, we use identical hyperparameters as released in their works. In ILI prediction, the training and validation set are split by a ratio of 5:2 from the winter–summer subset, and the test data are sampled from the spring–fall subset with different patterns. The susceptible population at the beginning of each ILI period is 10% of the total population in each prefecture or state. As for baselines, we also use identical hyperparameters as released in their works. We approximate the total number of populations by the average of the annual sum of infectious cases multiplied by 10. In contrast to black-box baseline models, our model is domain-ODE-informed, and the architecture is determined by the physical network and the domain differential equations.
7.1.6 MAML settings
Our experiment involved the following steps. 1) We randomly selected sequences of 12 consecutive weekdays (the same as in the limited and mismatched data experiment), and sampled 4-h data as the training set. We evaluated the model with hourly data on weekends. 2) We divided the training set into two equal parts: the support set and the query set. 3) We used the support set to compute adapted parameters. 4) We used the adapted parameters to update the MAML parameters on the query set. 5) We repeated this process 200 times to obtain initial parameters for the baseline model. 6) We trained baselines using the obtained initial parameters. The learning rate for the inner loop was 0.00005, and for the outer loop was 0.0005, and MAML was trained for 200 epochs.
7.2 Results and analysis
7.2.1 Mismatched data experiments for RDGCN
We first explore the performance of the models when they are trained using mismatched data from certain conditions and tested using alternate, mismatched conditions. Specifically, the models were trained for 4-h data on weekdays (e.g., 8:00–12:00 on weekdays) and selected and evaluated with hourly data on weekends (e.g., 13:00–14:00 on weekends). In limited data and mismatched conditions (Figure 4A), the training set consists of data from five different sequences of 12 consecutive weekdays selected randomly from the available data. This experiment aims to replicate scenarios where data collection is challenging, and traffic patterns undergo rapid changes. In mismatched conditions without data limitations (Figure 4B), the training set consists of data from all available weekdays. This captures instances where data collection is comparatively less arduous, although the traffic pattern retains the potential to shift swiftly. The results are shown in Figure 4, where each curve denotes the average test prediction MAE and RMSE of models. In Figure 4A, we compare the performance of our approach with that of the STGCN, MTGNN, GTS, MTGODE, STGNCDE, and RDGCN in the mismatched data, when the training process is augmented with MAML. Figure 4B plots the prediction MAE and RMSE of baseline models and RDGCN over time, given all available weekday data. Corresponding numerical results is shown in Table 2.
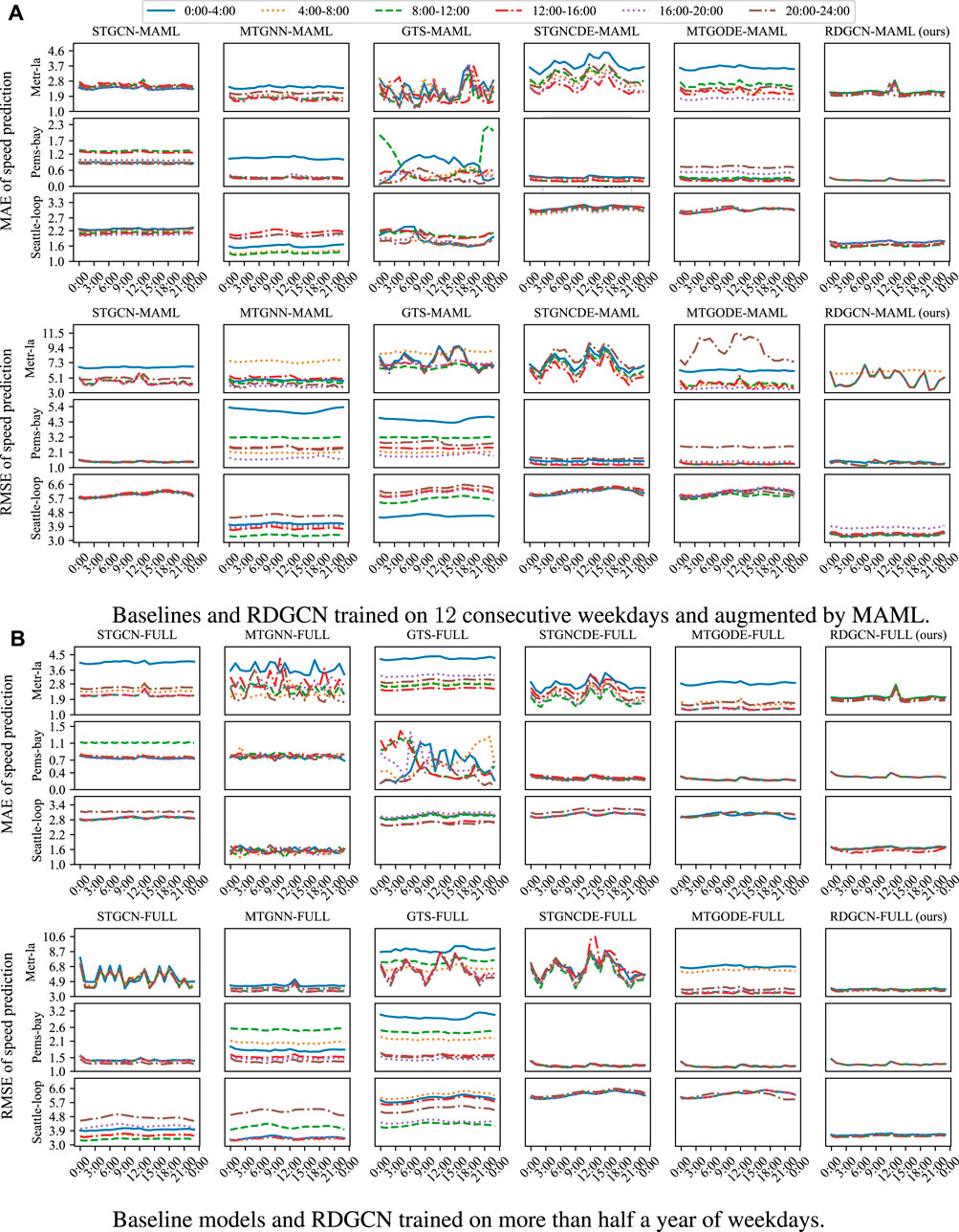
Figure 4. (A) The results of RDGCN are very close regardless of the period of the training set. (B) Even though all the models are trained using all available weekdays, the results of RDGCN are still closer, regardless of the period, than baseline models.
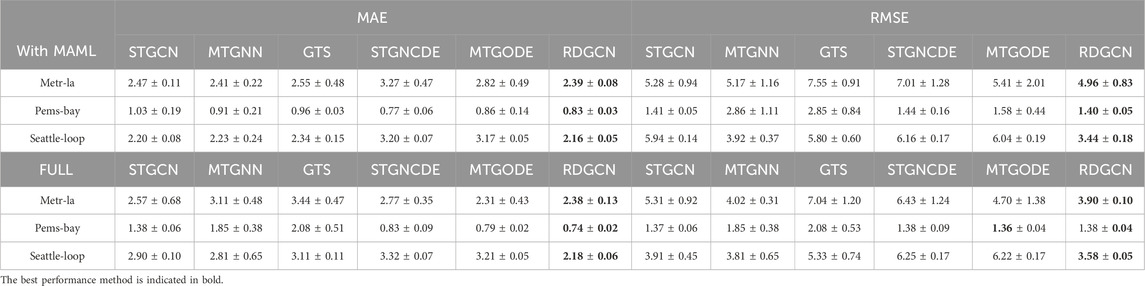
Table 2. Numerical result of Figure 4: the mean and STD of prediction MAE, RMSE of RDGCN, and baselines on three real-world datasets.
In Figure 4, all RDGCN models have nearly identical performance regardless of which time window of data is used for training. The MAE of all the RDGCN models is uniformly low (i.e., small y-axis values), and there is very low variance in performance across RDGCN models trained with different time windows (i.e., the curves of average MAE is close to the curves of maximum MAE). However, the performance of baseline models is significantly different depending on the training set, and some can have a relatively high MAE (e.g., the curve of STGCN on the Pems-bay dataset has much higher MAE values than that for RDGCN over time). From Figure 4B, we can see that even when the model is trained using all available weekday data, RDGCN outperforms the baseline models where the variance is across time, and across models is very low. While more data bring some gain to baseline models, its impact on RDGCN is fairly limited, indicating that RDGCN performs well in different testing domains without needing additional training data. In Table 2, RDGCN has lower MAE and lower RMSE loss with less variance, which further supports the observation in Figure 4. We admit that MTGODE also works well in Pems-bay when full data are used for training, but the superiority is not significant.
These test results support our hypothesis that incorporating traffic dynamics into the learning model makes it more robust to this kind of domain generalization (data from mismatched training and testing conditions). We speculate that this is a consequence of our model capturing the relative changes in speed through the dynamical equations, whereas existing baseline models are black-box models that derive complex functions of the absolute speed values across time. In effect, when there is a mismatch, the underlying nature of traffic dynamics is less likely to be impacted, whereas the complex patterns of absolute speed values might vary significantly across domains. This is particularly true when dealing with limited data that do not contain all possible patterns. At the same time, RDGCN is designed to make predictions based on neighboring vertices, so even if the speed patterns of a distant sensor and a close sensor are similar (e.g., both are free flow), the model uses close sensors to make predictions. We note that the prediction of RDGCN is not uniformly better than that of baselines (e.g., the prediction of MTGNN trained by Seattle weekday data from 8:00 to 12:00 is better than the prediction of RDGCN), and one possible reason is that speed pattern mismatches between weekdays and weekends are not always significant (e.g., when the training weekday is a holiday). Furthermore, the predictions of MTGNN and MTGODE exhibit a slight superiority over RDGCN in the Metr-la dataset in certain windows. Our conjecture is that the mix-hop layers enable these models to assign higher significance to learn short-term patterns, which likely does not change much between the training and test data. We acknowledge that RDGCN is not always better than baselines under RMSE, as when STGCN is trained with weekday data from 16:00–20:00 in Metr-la. One possible reason is that the mismatches between the training and test data are not significant during the corresponding time period. The prediction results of RDGCN in terms of RMSE may not always be stable. For instance, when considering the models for the 4:00–8:00 time period in Metr-la, we observe distinct prediction outcomes. This variation could be due to the difference between the pattern of the morning rush hour during selected weekdays and the pattern during weekends. When the training set includes all available weekday data, the predictions of RDGCN demonstrate stability. Although real-world data under situations such as disasters are hard to obtain, our approach of splitting the dataset emulates test scenarios that are sufficiently different from the training dataset to demonstrate the robustness of our approach.
7.2.2 Mismatched data experiments for SIRGCN
We explored the performance of SIRGCN under mismatched situations. Since infection spread and travel patterns vary from season to season, we trained our model and the baseline models with ILI data recorded in summer and winter and tested the predictions on data in spring and fall. The result is shown in Table 3, where each element denotes the MAE and RMSE under different seasons.
The results demonstrate that SIRGCN performs consistently better under the mismatched data scenario with low MAE and RMSE than the baseline models. Although SIRGCN does not significantly outperform the deep-learning-based ColaGNN model, we note that SIRGCN makes predictions using only the latest observation at one time point augmented by approximating the total susceptible and recovered populations, as specified by the domain equations, whereas the baselines which consider the disease propagation as a black-box model require more than 7 years data to train and 20 weeks-worth of data to make their predictions.
The two datasets are used for testing, but the theory can also apply to other applications, such as air quality forecasting and molecular simulation, where there are underlying graphical models and the ODE domain is well developed. Overall, these evaluations validate the main hypothesis of this paper wherein integrating domain differential equations into GCN allows for better robustness.
8 Ablation study
8.1 Analysis of RDGCN in traffic speed prediction
8.1.1 Are reaction and diffusion processes essential?
In this section, we investigate the prediction models that incorporate the reaction and the diffusion equations independently under limited and mismatched data to understand whether both the reaction and diffusion processes are essential. We use the same training set (i.e., 12 consecutive working days selected randomly) and test set (i.e., hourly weekend data) as Section 7.2. The curves of MAE versus time using the model incorporating the reaction equation, the diffusion equation, and the reaction-diffusion equation are shown in Figure 5A, and the corresponding curves of RMSE versus time are shown in Figure 5B.
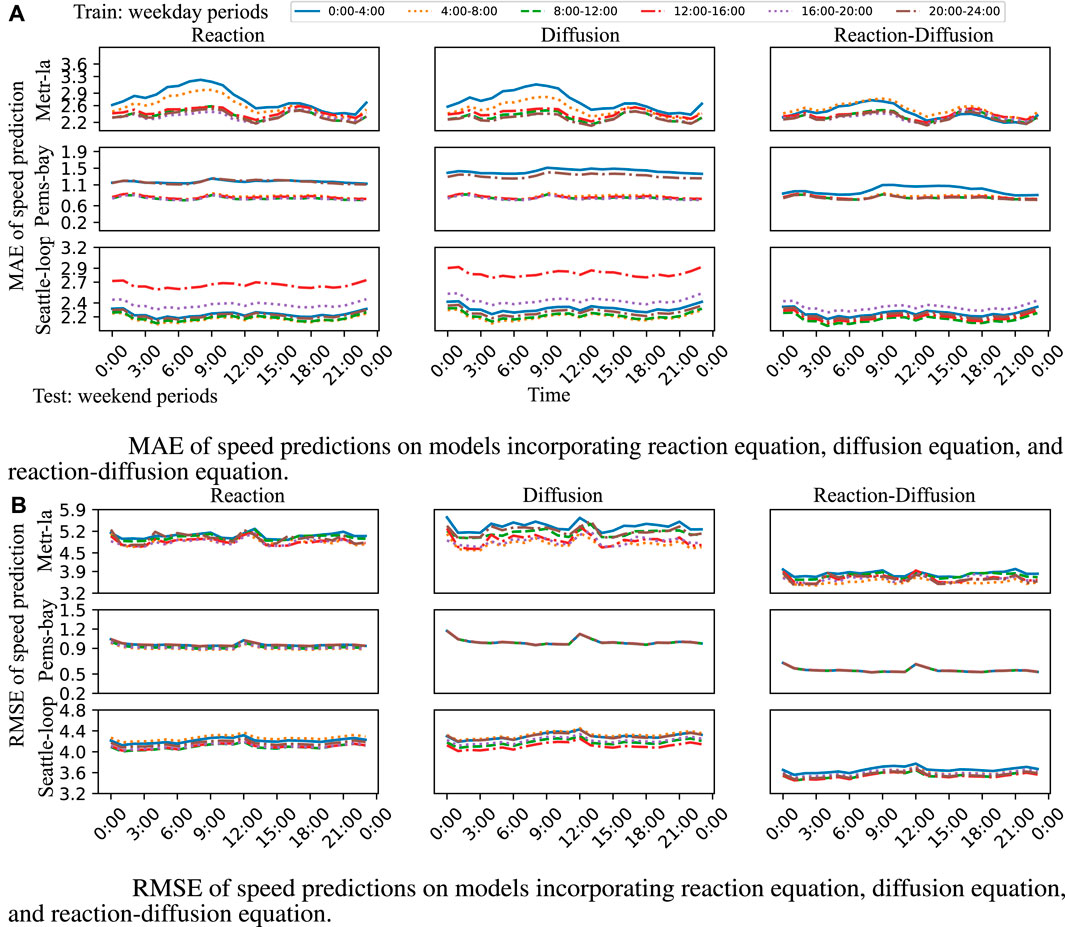
Figure 5. The predictions of the reaction–diffusion model, employing both MAE and RMSE loss, exhibit lower prediction error, whereas the predictions of only the reaction models or only the diffusion models demonstrate weaker performance in at least one time period. (A) MAE of speed predictions on models incorporating reaction equation, diffusion equation, and reaction-diffusion equation. (B) RMSE of speed predictions on models incorporating reaction equation, diffusion equation, and reaction-diffusion equation.
Figure 5 indicates that the predictions of all models with the reaction–diffusion equation provide low MAE/RMSE with low variance (i.e., the difference between curves with the highest and lowest MAE/RMSE is small) over time. However, the predictions of the reaction models only and the diffusion models only have weaker performance in at least one time period. We speculate that using only the reaction equation or the diffusion equation is not sufficient to completely capture the dynamics of the traffic speed change. Furthermore, the prediction of the model incorporating the reaction–diffusion equation is not uniformly better than the prediction of the model incorporating only the reaction or diffusion equation. One possible reason is that the reaction or diffusion processes do not always exist in a specific period (e.g., if two neighboring road segments are in free-flow during the test period, the traffic speeds at the two segments do not affect each other. Thus, there is neither diffusion nor reaction between these two road segments). These observations further strengthen that both the reaction and diffusion processes are necessary for a reliable prediction.
8.1.2 Impact of data volume
We further investigate the influence of training data volume on the performance of baseline models and RDGCN under a mismatched setting. We focus on assessing the adequacy of training data for both morning (8:00–12:00) and evening rush hour (16:00–20:00) scenarios using the Metr-la dataset. These periods exhibit considerable patterns and exhibit relatively minor mismatches between the training and test datasets. To this end, we randomly select contiguous weekdays ranging from 20% to the entire dataset for training the models. The MAE of speed prediction across varying quantities of training data is shown in Figure 6.
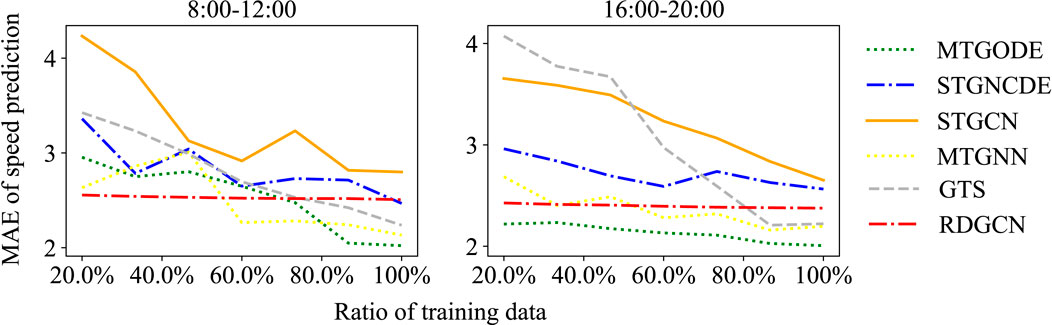
Figure 6. Feeding more training data does not lead to a significant change in the MAE of RDGCN’s prediction.
Figure 6 showcases the performance characteristics of the RDGCN and baseline models over the specified time intervals. Remarkably, the performance of RDGCN remains consistent irrespective of the training dataset size. Conversely, the predictive capabilities of STGNCDE and MTGODE are notably contingent upon the amount of training data employed. The observed trend underscores increased training data volume and directly correlates with enhanced prediction accuracy. In the morning rush hour, MTGODE achieves optimal performance with approximately 75% of training data (equivalent to 60 weekdays), while STGNCDE demonstrates comparable performance when trained on the entire weekday dataset. We note that the superiority of RDGCN over baseline models is not universally consistent, as elucidated earlier. Notably, integrating domain differential equations drastically reduces the size of the hypothesis class, thereby filtering out erroneous hypotheses often prevalent in conventional black-box graph learning models. Consequently, domain-differential-equation-informed GCNs exhibit remarkable robustness on relatively smaller training datasets.
8.2 Analysis of SIRGCN in ILI prediction
8.2.1 Do the infection rates vary among different vertices?
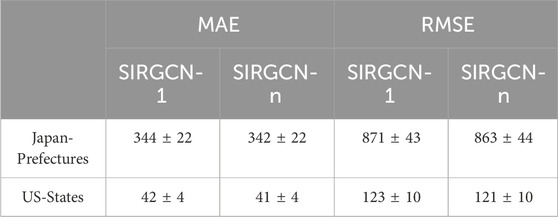
In this section, we delve into the question of whether we require an individual infection rate for each vertex in ILI prediction. We specifically examine two approaches: one where we assign a unique infection rate, denoted βi, to each vertex i, resulting in a SIRGCN with n infection rates (SIRGCN-n), and another approach where we assign a single infection rate, denoted β, to all vertices (SIRGCN-1). We report the MAE and RMSE of the prediction under mismatched data (trained using winter–summer data and test using spring–fall data) in Table 4.
Table 4 shows that employing multiple infection rates leads to more accurate predictions, particularly in the case of the US-state dataset. By assigning individual infection rates to each vertex, we achieve a reduction of 2.4% in MAE (and 1.6% in RMSE). However, the advantage of utilizing multiple infection rates is less pronounced
8.2.2 Predictions in different seasons
Learning patterns across different trends become challenging when baseline models are not trained using the same trend. For example, during winter the infectious number shows an increasing trend, whereas during spring it exhibits a decreasing trend. Figure 7 shows the predicted number of infectious cases alongside the ground truth data, revealing that SIRGCN’s prediction aligns better with the ground truth. Conversely, EpiGNN’s prediction performs poorly during the decline phase and when the number of infections approaches 0.
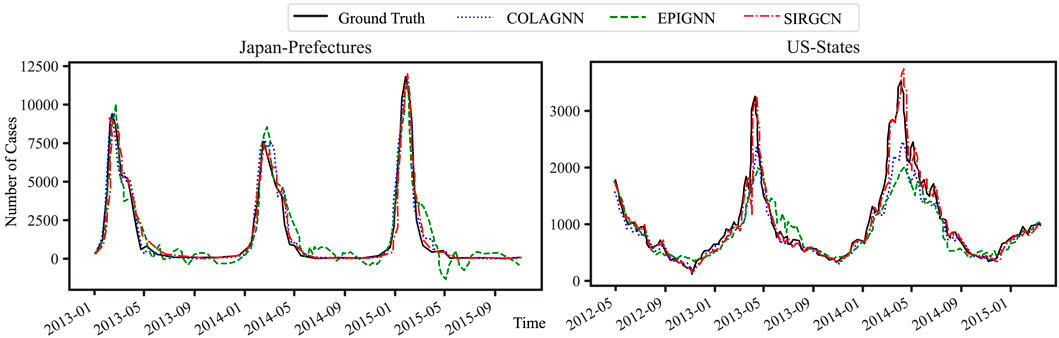
Figure 7. SIRGCN can make accurate predictions in the decreasing phase, while EpiGNN makes bad predictions in the corresponding phase.
In the case of US-state ILI prediction in May 2014, both COLAGNN and EPIGNN fail to make accurate predictions around the peak, while SIRGCN demonstrates its effectiveness during the corresponding period with the help of the SIR-network model.
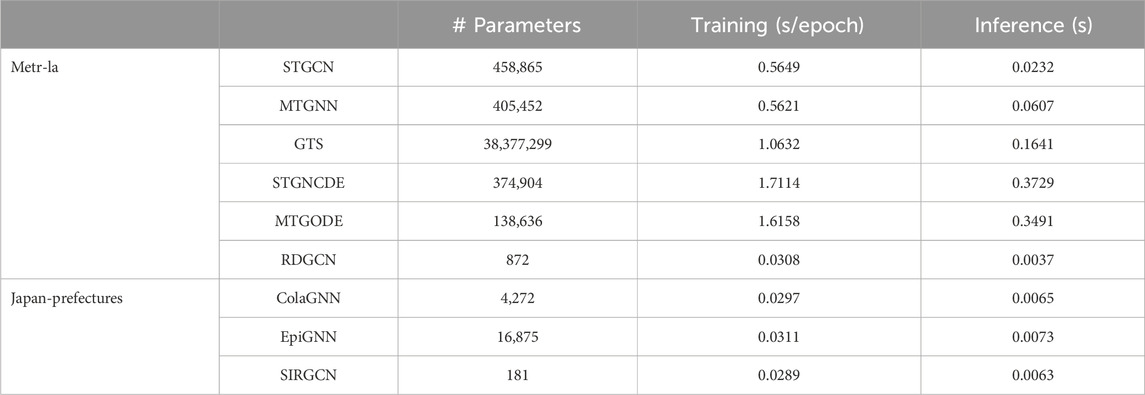
9 Model efficiency in computation time
The training and inference times (on two NVIDIA-2080ti graphic cards) of STGCN, MTGNN, GTS, STGNCDE, STGODE, and RDGCN on the Metr-la dataset are demonstrated in Table 5. It is observed that RDGCN takes less time in both training and inference than the other models. This efficiency can be attributed to RDGCN’s significantly fewer parameters in contrast to the baseline models. While the spatial convolutional layers exhibit similar complexities across all baseline models, the baseline models use richer temporal layers containing tens of thousands of parameters. In a traffic network where the number of edges is only slightly greater than the number of vertices, the parameter count of RDGCN
The training and inference time of ColaGNN, EpiGNN, and SIRGCN are shown in Table 5. SIRGCN has significantly fewer parameters than the baseline models. We acknowledge that the computational time of SIRGCN is similar to that of the baseline models, as the baselines are not as deep or dense as traffic prediction models and do not require a large amount of data for training.
10 Conclusion
In this paper, we investigate the challenging problem of graph time-series prediction when training and test data are drawn from different or mismatched scenarios. To address this challenge, we propose a methodological approach to integrate domain differential equations in graph convolutional networks to capture the common data behavior across data distributions. We theoretically justify the robustness of this approach under certain conditions on the underlying domain and data. By operationalizing our approach, we propose two novel dynamics-informed GCNs: RDGCN and SIRGCN. These architectures fuse traffic speed reaction-diffusion equations and susceptible-infected-recovered infectious disease spread equations, respectively. Through rigorous numerical evaluation, we demonstrate the robustness of our models in mismatched data scenarios. Both models can significantly reduce the number of parameters while maintaining prediction accuracy and robustness, thus requiring less training data and shorter training time. The findings showcased in this study underscore the transformative potential of domain-ODE-informed models as a burgeoning category within the domain of graph neural networks. This framework can pave the way for future exploration addressing the challenges of domain generalization in other contexts.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
YS: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing–original draft, and writing–review and editing. CC: investigation, visualization, and writing–review and editing. YX: investigation, visualization, and writing–review and editing. SX: conceptualization, funding acquisition, investigation, supervision, and writing–review and editing. RB: conceptualization, funding acquisition, investigation, supervision, and writing–review and editing. PV: conceptualization, funding acquisition, investigation, project administration, resources, supervision, and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was partly funded through a Lehigh internal Accelerator Grant, Grants CCF-1617889 and IIS-1909879 from the National Science Foundation and the U.S. Office of Naval Research under Grant N00014-22-1-2626. SX was partly supported by the Education Bureau of Guangzhou Municipality and the Guangzhou-HKUST (GZ) Joint Funding Program (Grant 583 No. 2023A03J0008).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2024.1397131/full#supplementary-material
Footnotes
1E.g., congestion is caused by the increasing traffic demand.
2E.g., temporary change of travel demand.
3In the Supplementary Appendix, we show that the datasets used satisfy these assumptions.
4E.g., consider the evolution of traffic speed: during morning rush hour, training data reflect significant traffic demand influencing speed, whereas test data from midnight reflect negligible traffic demand, and thus no speed change.
5E.g., during the morning rush hour, a two-hop neighbor facilitates positive speed changes for the target. However, as the evening rush hour ensues, the same two-hop neighbor can result in negative speed changes due to shifts in population flow, with cars redirecting to different vertices at night.
References
Asikis, T., Böttcher, L., and Antulov-Fantulin, N. (2022). Neural ordinary differential equation control of dynamics on graphs. Phys. Rev. Res. 4, 013221. doi:10.1103/physrevresearch.4.013221
Bellocchi, L., and Geroliminis, N. (2020). Unraveling reaction-diffusion-like dynamics in urban congestion propagation: insights from a large-scale road network. Sci. Rep. 10, 4876. doi:10.1038/s41598-020-61486-1
Bui, K.-H. N., Cho, J., and Yi, H. (2022). Spatial-temporal graph neural network for traffic forecasting: an overview and open research issues. Appl. Intell. 52, 2763–2774. doi:10.1007/s10489-021-02587-w
Chen, C., Hu, J., Meng, Q., and Zhang, Y. (2011). “Short-time traffic flow prediction with arima-garch model,” in 2011 IEEE Intelligent Vehicles Symposium (IV) (IEEE), Baden-Baden, Germany, June, 2011, 607–612.
Chen, R. T., Rubanova, Y., Bettencourt, J., and Duvenaud, D. K. (2018). Neural ordinary differential equations. Adv. neural Inf. Process. Syst. 31.
Choi, J., Choi, H., Hwang, J., and Park, N. (2022). Graph neural controlled differential equations for traffic forecasting. Proc. AAAI Conf. Artif. Intell. 36, 6367–6374. doi:10.1609/aaai.v36i6.20587
Cooper, I., Mondal, A., and Antonopoulos, C. G. (2020). A sir model assumption for the spread of covid-19 in different communities. Chaos, Solit. Fractals 139, 110057. doi:10.1016/j.chaos.2020.110057
Cui, Z., Ke, R., Pu, Z., Ma, X., and Wang, Y. (2020). Learning traffic as a graph: a gated graph wavelet recurrent neural network for network-scale traffic prediction. Transp. Res. Part C Emerg. Technol. 115, 102620. doi:10.1016/j.trc.2020.102620
Deng, S., Wang, S., Rangwala, H., Wang, L., and Ning, Y. (2020). “Cola-gnn: cross-location attention based graph neural networks for long-term ili prediction,” in CIKM, Virtual Event, October 2020.
Fan, X., Wang, Q., Ke, J., Yang, F., Gong, B., and Zhou, M. (2021). “Adversarially adaptive normalization for single domain generalization,” in CVPR, Nashville, TN, USA, June, 2021.
Finn, C., Abbeel, P., and Levine, S. (2017). “Model-agnostic meta-learning for fast adaptation of deep networks,” in ICML, Sydney, Australia, August, 2017.
Guo, S., Lin, Y., Feng, N., Song, C., and Wan, H. (2019). Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. AAAI 33, 922–929. doi:10.1609/aaai.v33i01.3301922
Han, L., Du, B., Sun, L., Fu, Y., Lv, Y., and Xiong, H. (2021). “Dynamic and multi-faceted spatio-temporal deep learning for traffic speed forecasting,” in SIGKDD, Virtual Event Singapore, August, 2021.
Huang, J., and Agarwal, S. (2020). “Physics informed deep learning for traffic state estimation,” in 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, September, 2020, 1–6.
Jagadish, H. V., Gehrke, J., Labrinidis, A., Papakonstantinou, Y., Patel, J. M., Ramakrishnan, R., et al. (2014). Big data and its technical challenges. Commun. ACM 57, 86–94. doi:10.1145/2611567
Jayatilaka, G., Hassan, J., Marikkar, U., Perera, R., Sritharan, S., Weligampola, H., et al. (2020). Use of artificial intelligence on spatio-temporal data to generate insights during covid-19 pandemic: a review. Available at: https://www.medrxiv.org/content/10.1101/2020.11.22.20232959v5.
Ji, J., Wang, J., Jiang, Z., Jiang, J., and Zhang, H. (2022). Stden: towards physics-guided neural networks for traffic flow prediction. Proc. AAAI Conf. Artif. Intell. 36, 4048–4056. doi:10.1609/aaai.v36i4.20322
Jia, J., and Benson, A. R. (2019). Neural jump stochastic differential equations. Adv. Neural Inf. Process. Syst. 32.
Jin, M., Zheng, Y., Li, Y.-F., Chen, S., Yang, B., and Pan, S. (2022). Multivariate time series forecasting with dynamic graph neural odes. IEEE Trans. Knowl. Data Eng. 35, 9168–9180. doi:10.1109/tkde.2022.3221989
Karniadakis, G. E., Kevrekidis, I. G., Lu, L., Perdikaris, P., Wang, S., and Yang, L. (2021). Physics-informed machine learning. Nat. Rev. Phys. 3, 422–440. doi:10.1038/s42254-021-00314-5
Kipf, T. N., and Welling, M. (2017). Semi-supervised classification with graph convolutional networks. ICLR.
Kumar, S. V., and Vanajakshi, L. (2015). Short-term traffic flow prediction using seasonal arima model with limited input data. Eur. Transp. Res. Rev. 7, 21–29. doi:10.1007/s12544-015-0170-8
Kuznetsov, V., and Mohri, M. (2016). “Time series prediction and online learning,” in COLT, New-York City, USA, June, 2016.
Lakkaraju, H., Bach, S. H., and Leskovec, J. (2016). “Interpretable decision sets: a Joint framework for description and prediction,” in SIGKDD, San Francisco, USA, August, 2016, 1675–1684.
Li, Y., Yu, R., Shahabi, C., and Liu, Y. (2018). “Diffusion convolutional recurrent neural network: data-driven traffic forecasting,” in ICLR, Vancouver Convention Center, Vancouver CANADA, May, 2018.
Loder, A., Ambühl, L., Menendez, M., and Axhausen, K. W. (2019). Understanding traffic capacity of urban networks. Sci. Rep. 9, 16283–16310. doi:10.1038/s41598-019-51539-5
Longa, A., Lachi, V., Santin, G., Bianchini, M., Lepri, B., Lio, P., et al. (2023). Graph neural networks for temporal graphs: state of the art, open challenges, and opportunities. Available at: https://arxiv.org/abs/2302.01018.
Lou, Y., Caruana, R., and Gehrke, J. (2012). “Intelligible models for classification and regression,” in SIGKDD, Beijing, China, August, 2012.
Maier, A. K., Syben, C., Stimpel, B., Würfl, T., Hoffmann, M., Schebesch, F., et al. (2019). Learning with known operators reduces maximum error bounds. Nat. Mach. Intell. 1, 373–380. doi:10.1038/s42256-019-0077-5
Montes de Oca Zapiain, D., Stewart, J. A., and Dingreville, R. (2021). Accelerating phase-field-based microstructure evolution predictions via surrogate models trained by machine learning methods. npj Comput. Mater. 7 (3), 3. doi:10.1038/s41524-020-00471-8
Morid, M. A., Sheng, O. R. L., and Dunbar, J. (2023). Time series prediction using deep learning methods in healthcare. ACM Trans. Manag. Inf. Syst. 14, 1–29. doi:10.1145/3531326
Qiao, F., Zhao, L., and Peng, X. (2020). “Learning to learn single domain generalization,” in CVPR, Seattle, WA, United States, June, 2020.
Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2019). Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707. doi:10.1016/j.jcp.2018.10.045
Redko, I., Morvant, E., Habrard, A., Sebban, M., and Bennani, Y. (2020). A survey on domain adaptation theory: learning bounds and theoretical guarantees. Available at: https://arxiv.org/abs/2004.11829.
Robey, A., Pappas, G. J., and Hassani, H. (2021). “Model-based domain generalization,” in Advances in Neural Information Processing Systems 34, 20210–20229.
Scholz, G., and Scholz, F. (2015). First-order differential equations in chemistry. ChemTexts 1, 1–12. doi:10.1007/s40828-014-0001-x
Shang, C., Chen, J., and Bi, J. (2021). “Discrete graph structure learning for forecasting multiple time series,” in ICLR, Virtual Only Conference, May, 2021.
Stolerman, L. M., Coombs, D., and Boatto, S. (2015). Sir-network model and its application to dengue fever. SIAM J. Appl. Math. 75, 2581–2609. doi:10.1137/140996148
Thodi, B. T., Khan, Z. S., Jabari, S. E., and Menéndez, M. (2022). Incorporating kinematic wave theory into a deep learning method for high-resolution traffic speed estimation. IEEE Trans. Intelligent Transp. Syst. 23, 17849–17862. doi:10.1109/tits.2022.3157439
Van Der Voort, M., Dougherty, M., and Watson, S. (1996). Combining kohonen maps with arima time series models to forecast traffic flow. Transp. Res. Part C Emerg. Technol. 4, 307–318. doi:10.1016/s0968-090x(97)82903-8
van Wageningen-Kessels, F., Van Lint, H., Vuik, K., and Hoogendoorn, S. (2015). Genealogy of traffic flow models. EURO J. Transp. Logist. 4, 445–473. doi:10.1007/s13676-014-0045-5
Varshney, K. R. (2020). “On mismatched detection and safe, trustworthy machine learning,” in CISS, Princeton, NJ, USA, March, 2020.
Veličković, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., and Bengio, Y. (2018). “Graph attention networks,” in ICLR, Vancouver Convention Center, Vancouver CANADA, April, 2018.
Wang, J., Lan, C., Liu, C., Ouyang, Y., Qin, T., Lu, W., et al. (2022). Generalizing to unseen domains: a survey on domain generalization. TKDE 35, 1. doi:10.1109/tkde.2022.3178128
Wang, Z., Luo, Y., Qiu, R., Huang, Z., and Baktashmotlagh, M. (2021). “Learning to diversify for single domain generalization,” in ICCV, Montreal, Canada, October, 2021.
Wu, Z., Pan, S., Long, G., Jiang, J., Chang, X., and Zhang, C. (2020). “Connecting the dots: multivariate time series forecasting with graph neural networks,” in SIGKDD, Virtual Conference, August, 2020.
Xhonneux, L.-P., Qu, M., and Tang, J. (2020). “Continuous graph neural networks,” in ICML, Virtual Conference, July, 2020.
Xian, X., Hong, M., and Ding, J. (2022). “Mismatched supervised learning,” in ICASSP, Singapore, May, 2022.
Xie, F., Zhang, Z., Li, L., Zhou, B., and Tan, Y. (2023). “Epignn: exploring spatial transmission with graph neural network for regional epidemic forecasting,” in ECML PKDD, Torino, September, 2023, 469–485.
Ying, R., Bourgeois, D., You, J., Zitnik, M., and Leskovec, J. (2019). Gnn explainer: a tool for post-hoc explanation of graph neural networks. Available at: https://arxiv.org/abs/1903.03894.
Yu, B., Yin, H., and Zhu, Z. (2018). “Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting,” in IJCAI, Stockholmsmässan, July, 2018.
Zhou, K., Liu, Z., Qiao, Y., Xiang, T., and Loy, C. C. (2021). Domain generalization in vision: a survey. Available at: https://arxiv.org/abs/2103.02503.
Keywords: ODE-based computation model, graph convolutional networks, out-of-distribution generalization, spatiotemporal prediction, reaction-diffusion equation, time series
Citation: Sun Y, Chen C, Xu Y, Xie S, Blum RS and Venkitasubramaniam P (2024) On the generalization discrepancy of spatiotemporal dynamics-informed graph convolutional networks. Front. Mech. Eng 10:1397131. doi: 10.3389/fmech.2024.1397131
Received: 06 March 2024; Accepted: 16 May 2024;
Published: 12 July 2024.
Edited by:
Ke Li, Schlumberger, United StatesReviewed by:
Xiaolong He, Ansys, United StatesGuannan Zhang, Oak Ridge National Laboratory (DOE), United States
Copyright © 2024 Sun, Chen, Xu, Xie, Blum and Venkitasubramaniam. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Parv Venkitasubramaniam, cGF2MzA5QGxlaGlnaC5lZHU=
 Yue Sun
Yue Sun Chao Chen
Chao Chen Yuesheng Xu
Yuesheng Xu Sihong Xie
Sihong Xie Rick S. Blum
Rick S. Blum Parv Venkitasubramaniam
Parv Venkitasubramaniam