The effects of Surfactin on sprayed droplets in flat fan, full cone, and low energy precision application bubbler nozzles: droplet formation and spray breakup

Introduction: Agriculture is the largest user of water globally (i.e., 70% of freshwater use) and within the United States (i.e., 42% of freshwater use); irrigation ensures crops receive adequate water, thereby increasing crop yields. Surfactants have been used in various agricultural spray products to increase spray stability and alter droplet sizes.

Methods: The effects of the addition of surfactant (0.1 wt% Surfactin; surface tension of 29.2 mN/m) to distilled water (72.79 mN/m) on spray dynamics and droplet formation were investigated in four flat fan (206.8–413.7 kPa), one full cone (137.9–413.7 kPa), and three LEPA bubbler (41.4–103.4 kPa) nozzles via imaging.

Results and discussion: The flat fan and cone nozzles experienced second wind-induced breakup (i.e., unstable wavelengths drive breakup) of the liquid sheets exiting the nozzle; the addition of surfactant resulted in an increased breakup length and a decreased droplet size. The fan nozzles volumetric median droplet diameter decreased with the addition of surfactant (e.g., decreased by 26.3–65.6 μm in one nozzle). The full cone nozzle volumetric median droplet diameter decreased initially with the addition of surfactant (27.8, 14.3, and 13.4 μm at 137.9, 206.8, and 310.3 kPa respectively), but increased at 413.7 kPa (24.3 μm). Sprays from the bubbler nozzles were measured and observed to experience Rayleigh (i.e., the droplets form via capillary pinching at the end of the jet) and first wind-induced breakup (i.e., air impacts breakup along with capillary pinching). The effect of Surfactin on droplet size was minimal for the 41.4 kPa bubbler nozzle. The addition of surfactant increased the diameter of the jet or ligament formed from the bubbler plate, thereby increasing the breakup length and the droplet size at 68.9 and 103.4 kPa (droplet size increased by 750.6 and 4,462.7 μm, respectively).

1 Introduction

Agriculture is the largest user of water globally (i.e., 70% of freshwater use) and within the United States (42% of freshwater use) (Lehr et al., 2005; KDA, 2019; USGS, 2019; FAO, 2020; UNICEF, 2021; USDA, 2022). Irrigation ensures crops receive adequate water, thereby increasing crop yields; while irrigated cropland makes up 20% of all cropland globally, it produces 40% of the global crop production (Lehr et al., 2005; FAO, 2020). Different designs of agricultural nozzles are used for various spray applications. Flat fan sprays apply uniform coverage, while cone nozzles tend to have smaller droplet sizes than fan nozzles (Makhnenko et al., 2021) and, therefore, have less variance in droplet size (Kooij et al., 2018). Sprinkler irrigation systems (e.g., center pivots) are used for irrigation on 55% of irrigated cropland in the United States (Chen et al., 2022) and are considered a water-saving irrigation technology (Lehr et al., 2005; Li et al., 2015; Jiang et al., 2019; Chen et al., 2022; Wang et al., 2022). Low energy precision application (LEPA) bubbler nozzles for sprinkler irrigation have a more precise application of water, allowing for overall less water use than spray nozzles. Additionally, they operate lower to the ground than other sprinkler nozzles, reducing the potential for spray drift (i.e., the sprayed liquid does not make it to the intended plants or soil) (Trout and Kincaid, 2007; Peters et al., 2016; Adeyemi et al., 2017; Fontela, 2018; Oker et al., 2021). One of the main considerations for the irrigation design of sprinklers over LEPA is the reduction of field runoff in relation to the soil type, irrigation (well) capacity, field topography, and field management (Rogers et al., 2008). Droplet dynamics are impacted by fluid properties (e.g., surface tension, density, and viscosity), environmental factors (e.g., humidity, temperature), and external forces (gravity, pressure, flow, electric fields) (Leach et al., 2006; Ristenpart et al., 2006; Boreyko and Chen, 2009; Chen and Li, 2010; Nath and Boreyko, 2016; Chen et al., 2017; Nath et al., 2017; Huber et al., 2019; Noori et al., 2020; 2021; Shams Taleghani and Sheikholeslam Noori, 2022; Kingsley and Chiarot, 2023). For nozzle applications, the nozzle design and geometry will also impact breakup length, spray angle, and droplet size (Fraser et al., 1962; Shavit and Chigier, 1995; Butler Ellis et al., 2001; Silva, 2006; Qin et al., 2010; Davanlou et al., 2015; Payri et al., 2015; Asgarian et al., 2020; Sijs and Bonn, 2020; Sijs et al., 2021; Jalili et al., 2023).

Four atomization regimes exist for jets (Figure 1), which dictates breakup: Rayleigh (i.e., droplets are larger than the spray orifice; the droplets form via capillary pinching at the end of the jet); first wind-induced (i.e., air impacts breakup resulting in droplets of similar size to the spray orifice); second wind-induced (i.e., unstable wavelengths drive breakup into droplets smaller than the spray orifice); and atomization (i.e., droplets are immediately stripped off the jet or sheet when exiting the orifice at high velocities, resulting in droplets up to two orders of magnitude smaller than the orifice) (Reitz and Lin, 1998; Post and Hewitt, 2018; Bertola and Brenn, 2020). Rayleigh breakup is driven by surface tension forces and first wind-induced breakup occurs due to both surface tension forces and aerodynamic forces; these breakup regimes are observed in the bubbler nozzle. Second wind-induced breakup—the dominant mechanism of breakup in fan and cone spray nozzles—occurs due to aerodynamic waves, which form in spray sheets and jets, resulting in the disintegration or breakup of the sheet or jet into ligaments (Fraser et al., 1962; Ford and Furmidge, 1967; Butler Ellis et al., 2001; Dexter, 2001; Lee et al., 2012; Saha et al., 2012; Kooij et al., 2018; Post and Hewitt, 2018; Asgarian et al., 2020; Sijs et al., 2021). For pure liquids (e.g., ethanol), decreasing the surface tension will decrease the breakup length of a spray (Shavit and Chigier, 1995; Butler Ellis et al., 2001; Davanlou et al., 2015).

FIGURE 1

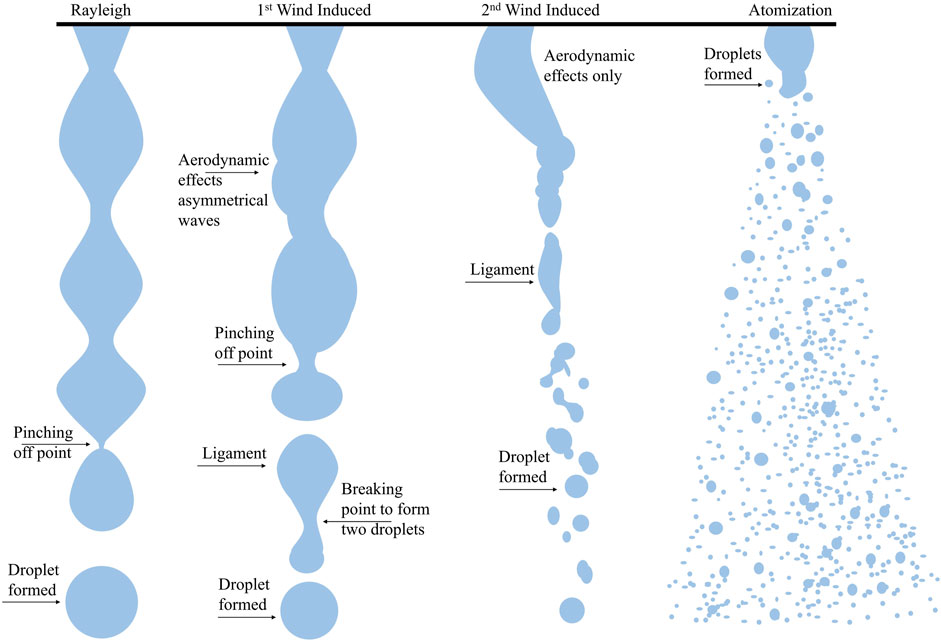
FIGURE 1. The four methods of breakup into droplets. Rayleigh breakup is dominated by surface tension forces where droplets are pinched off the end of the jet, the droplets are the same diameter or larger than the jet diameter. First wind-induced breakup is still driven by surface tension force but with the addition of aerodynamic forces, the droplets formed are similar in size to the jet diameter. Second wind-induced breakup is dominated by aerodynamic forces on the jet and results in droplets smaller than the jet diameter or nozzle orifice. Atomization occurs at the nozzle exit and results in droplets much smaller than the nozzle orifice.

The droplet size is impacted by spray dynamics and is related to the breakup length. For example, increasing the operating pressure (Solomon et al., 1985; Butler Ellis and Tuck, 1999; Negeed et al., 2011; Davanlou et al., 2015; Wang et al., 2015; Broniarz-Press et al., 2016; Kooij et al., 2018; Nadeem et al., 2019; Li et al., 2021; Makhnenko et al., 2021; Chen et al., 2022) or increasing the breakup length (Qin et al., 2010; Wang et al., 2015; Kooij et al., 2018; Nadeem et al., 2019; Asgarian et al., 2020; Sijs et al., 2021) will decrease the droplet size. The droplet size also decreases in pure liquids with a decreased surface tension (Butler Ellis and Tuck, 1999; Butler Ellis et al., 2001; Dexter, 2001; Davanlou et al., 2015; Sijs and Bonn, 2020; Makhnenko et al., 2021). When propan-1-ol ($\sigma =50.5\pm 0.5$ mN/m at breakup), a pure liquid, was added to water in a flat fan nozzle the droplet size was reduced 9 µm (Butler Ellis et al., 2001).

Surfactants are used in various agricultural spray products to increase spray stability and alter droplet sizes to improve the performance of the agricultural spray (Makhnenko et al., 2021; Sijs et al., 2021). Surfactant solutions alter spray dynamics similarly to pure liquids; however, decreasing the surface tension via surfactant has an inconsistent effect on breakup length and droplet size (Shavit and Chigier, 1995; Butler Ellis et al., 1997; Butler Ellis and Tuck, 1999; Butler Ellis et al., 2001; Sijs and Bonn, 2020; Sijs et al., 2021); some breakup lengths and droplet sizes from literature are given in Supplementary Table S1. Various increases in breakup length have been observed from approximately 1–20 mm depending on the surfactant, concentration, nozzle, and pressure (Butler Ellis and Tuck, 1999; Butler Ellis et al., 2001; Sijs and Bonn, 2020; Sijs et al., 2021). Breakup lengths were additionally observed to decrease by similar amounts with the addition of surfactant (Butler Ellis and Tuck, 1999). This inconsistency is due to a time-dependent, dynamic surface tension; it begins near the surface tension of the bulk liquid (e.g., water) and decreases as the spray moves further from the nozzle and the surface age increases (Defay et al., 1971; Ferri and Stebe, 2000; Rosen and Kunjappu, 2012a; b; Shavit and Chigier, 1995; Sijs and Bonn, 2020; Sijs et al., 2021). Literature also shows surfactant within the soil alters the evaporation dynamics, potentially decreasing water loss (Dekker et al., 2005; Fernández-Gálvez and Mingorance, 2010; Lehrsch et al., 2011; Raddadi et al., 2018; Lowe et al., 2019; Gutierrez et al., 2022).

Prior literature investigating fan and cone nozzles indicates the effects of surfactant on spray dynamics depend on the nozzle geometry and the type of surfactant; however, there is limited research investigating surfactants in nozzles such as the bubbler nozzle. The research objectives of this paper are to investigate how the addition of Surfactin to distilled water affects the spray dynamics (the breakup length, the spray angle, and droplet size) under various nozzles (flat fan nozzle, full cone nozzles, bubbler nozzle) and operating pressures. The surfactant, Surfactin, was investigated based on its biological origin and prior research (Gutierrez et al., 2022).

2 Materials and methods

2.1 Experimental apparatus

An experimental apparatus was designed to evaluate the effects of a surfactant, Surfactin (SurfPro Surfactin, CAS # 302933-83-1, C₅₃H₉₃N₇O₁₃), on spray dynamics of different sprayer nozzles and LEPA bubbler irrigation nozzles (Figure 2A, nozzles details given in Figure 2B, and images of the nozzles used in Figures 2C–F). The sprayer nozzles were selected for similarity to nozzles used in previous literature. The LEPA bubbler nozzle was selected for its water-saving capacity; other sprinkler nozzles were not investigated due to imaging field-of-view limitations. Surfactin was added to distilled water at a 0.1 wt% concentration (Section 2.2). The distilled water and surfactant solution were stored in two separate tanks; the distilled water was in a 113.6 L tank and the surfactant solution was in an 18.9 L tank. The fluid (i.e., distilled water or 0.1 wt% Surfactin solution) was pulled from a water tank via a pump, a bypass loop followed. A pressure relief valve was added to ensure operating pressure did not exceed the upper limit of the nozzles. A Coriolis flow meter (Emerson model F025S319CCAAEZZZR/2700I12BBAEZZZ) measured the mass flow rate, a thermocouple (TMQ316SS-062G-3) recorded, in LabVIEW, the temperature of the spray before entering the nozzle, and an absolute pressure transducer (Omega PX309-200A5V) recorded, in LabVIEW, the pressure of the spray entering the nozzle. The spray was collected and returned to the tank using a pump. The ambient pressure (Omega PX409-100G5V) was recorded in LabVIEW to obtain the gage operating pressure of the nozzle. The ambient temperature and relative humidity (Omega OM-24 Data Logger) of the room were also monitored. Uncertainties for pressure, temperature, relative humidity, and the mass flow rate are given in Table 1.

FIGURE 2

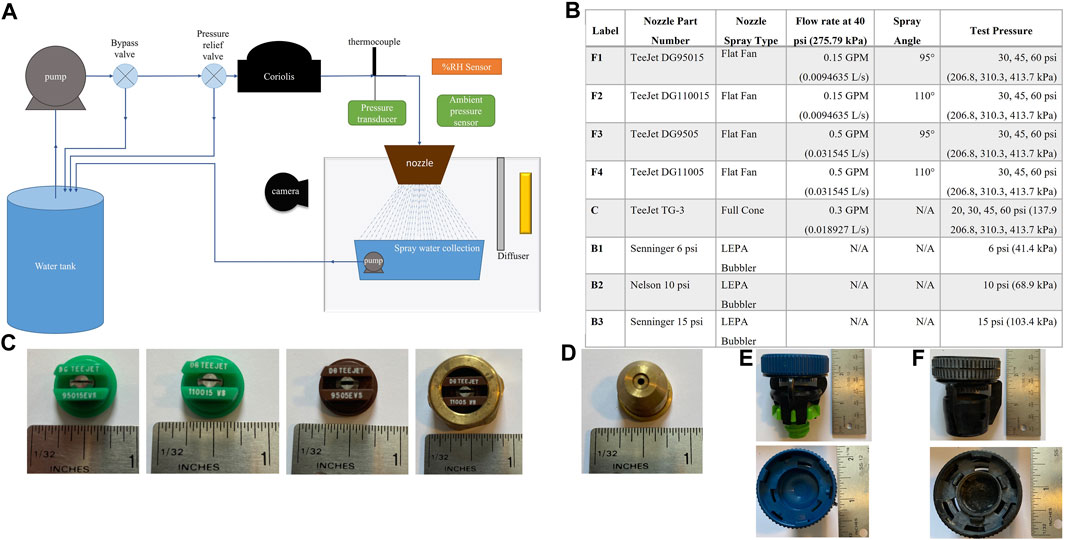
FIGURE 2. (A) Diagram of the spray apparatus. Fluid (distilled water or surfactant solution) is pumped to the nozzle (fan, cone, bubbler) and sprayed into open air. The sprayed fluid is collected and sent back to the original tank. The spray is backlit and images of the spray are captured using a high-speed camera. The pressure, temperature, and mass flow rate of the fluid are monitored, and the temperature and relative humidity of the room are monitored. (B) Table of the investigated nozzles and their properties. (C) Images of the TeeJet flat fan nozzles used, ruler for approximate scale. From left to right, nozzles F1 (DG95015), F2 (DG110015), F3 (DG9505), F4 (DG11005). (D) Image of the TeeJet full cone nozzle used (TeeJet TG-3), ruler for approximate scale. (E) Image of the Senninger nozzle used (B1 and B3), ruler for approximate scale. (F) Image of the Nelson nozzle used (B2), ruler for approximate scale.

TABLE 1

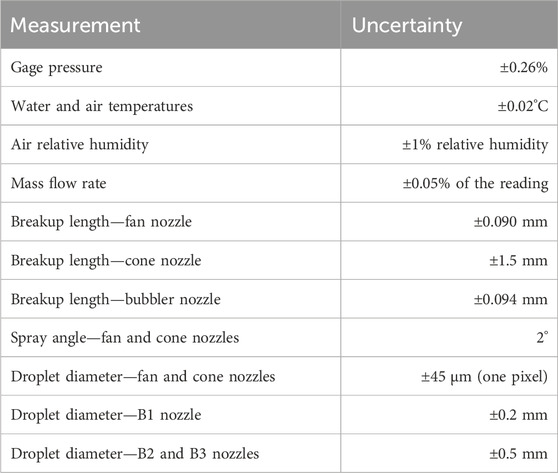
TABLE 1. Uncertainties for measurements. The uncertainty for the breakup length for the fan and bubbler nozzles is two pixels, while for the cone nozzle, it is larger due to visual uncertainties. The uncertainty for the droplet diameter in the fan and cone nozzles is one pixel. The uncertainty for the droplet diameter in the bubbler nozzle increases with pressure due to imaging complications capturing the larger droplets as the velocity increases.

The fluid was sprayed into ambient air where a Fastec IL5 camera captured images of the spray in FasMotion. An LED high-speed photo flash (Vela One) was used to backlight the image, and the light was diffused using ground glass (Edmund Optics 250 mm SQ 120 grit) against the light and white fabric between the light and the spray. The flash was set to a pulse length of 5 µs, and a burst strobe count of 4 with an interval of 250 µs. The flash was connected to the camera via a trigger (Miops Camera Trigger, UPC 791154017609). Twenty images of each nozzle at each operating pressure were taken.

2.2 Surfactin mixture

Surfactant was mixed into distilled water at various concentrations. Surface tension data of the solutions were acquired by Augustine Scientific. Surface tension measurements were recorded at 20°C by the Wilhelmy plate method, ASTM1331 (Supplementary Table S2). For the surfactant solution, 0.1 wt% was selected due to the surface tension value of 29.2 mN/m. An initial 15 L of solution was mixed; 7.5 g of Surfactin was slowly added to 1 L of distilled water while being mixed by a magnetic mixer at 800 RPM. Once completely mixed, it was added to the 18.9 L tank. A second liter was mixed with the same method, with 7.5 g of Surfactin. 13 L of pure distilled water was then added to the 5-gallon tank.

2.3 Image processing

The images were processed in ImageJ using the following technique: despeckle (a median filter) was used, the contrast was enhanced (0.3% saturated pixels), find edges was used, and the image was converted to black and white using the “make binary” function. The ImageJ binary function “close” was used to close semi-circles and unfilled-in droplets. Droplet areas were then obtained using the ImageJ “Analyze Particles” function; an upper boundary (5,500,000 μm²) was used to exclude the intact sheet and spray ligaments, and the results were saved as a .csv file. The unitless circularity of each droplet was determined by ImageJ (Eq. 1) and reported in the images .csv file,

$circularity=4\pi \frac{{\left[Area\right]}_i}{{\left[Perimeter\right]}_i^2}.(1)$

A value of 1 indicates a perfect circle and approaching 0 is an elongated shape. Due to the number of droplets, Python was used to process the data. The circularity of the droplets was sorted into bins, sized 0.1, from 0 to 1 based on the nozzle type and pressure.

Using the droplet areas in the .csv files, individual droplet diameters were determined,

$d_i=\sqrt{\frac{4A_i}{\pi }}(2)$

where d is the droplet diameter, A is the droplet area, and $i$ is the droplet index (Malot and Blaisot, 2000; Zhu et al., 2011). The volumetric median diameter ($D_{V50}$) is the diameter of the droplets based on the median droplet volume observed in an image. The $D_{V50}$ was determined using the individual droplet diameters ($d_i$). First, the volume of each individual droplet ($V_i$) was determined (Zhu et al., 2011),

$V_i=(\pi *d_i^3)/6(3)$

and the median volume was found ($V_{median}$) and used to determine the volumetric median diameter,

$D_{V50}={\left(\frac{6V_{median}}{\pi }\right)}^{1/3}.(4)$

The breakup length was determined using ImageJ’s straight line tool; a line was drawn to measure the distance from the center of the nozzle to the point where there were no connections (e.g., ligaments) to the spray sheet. The spray angle was measured using the ImageJ angle tool; the angle of each edge of the spray sheet and the top of the nozzle was marked, measured, and used to determine the spray angle (Figure 3).

FIGURE 3

FIGURE 3. Image of flat fan (F1) spray at 206.8 kPa (30 psi) using ImageJ to measure the breakup length and the two angles of the spray sheet edges with the nozzle. The breakup length is 24.328 µm, ${\theta }_1=136°$ and ${\theta }_2=131°$ resulting in a spray angle of $87°$.

3 Results and discussion

3.1 Surfactant’s effects in fan and cone nozzles

Spray breakup from the fan (Figure 4) and cone (Figure 5) nozzles were consistent with the breakup mechanisms for second wind-induced breakup. Breakup happened downstream of the nozzle and created droplets smaller than the nozzle orifice diameter and the waves resulting in breakup were visible (Squire, 1953; Dombrowski and Johns, 1963; Reitz and Lin, 1998; Gordillo and Pérez-Saborid, 2005; Wang and Fang, 2015; Asgarian et al., 2020). Additionally, increasing the spray pressure resulted in a decrease in breakup length in the fan (for nozzle F1, increasing the pressure from 206.8 to 413.7 kPa resulted in an 11% decrease in breakup length for distilled water) and cone nozzles (increasing the pressure from 137.9 to 413.7 kPa resulted in a 15% decrease in breakup length for distilled water) for both the distilled spray and the surfactant solution spray (Supplementary Table S3); the breakup length for second wind induced breakup is inversely proportional to the spray velocity (Etzold et al., 2018).

FIGURE 4

FIGURE 4. Spray images from the F1 nozzle (A) distilled water at 206.8 kPa (30 psi) with a D_V50 = 194.8 µm and L_b = 25.5 mm, (B) surfactant solution at 206.8 kPa (30 psi) with a D_V50=133.8 µm and L_b = 26.0 mm, (C) distilled water at 310.3 kPa (45 psi) with a D_V50=179.2 µm and L_b = 24.0 mm, (D) surfactant solution at 310.3 kPa (45 psi) with a D_V50 = 133.8 µm and L_b = 26.1 mm, (E) distilled water at 413 kPa (60 psi) with a D_V50 = 137.8 µm and L_b = 21.9 mm, (F) surfactant solution at 413.7 kPa (60 psi) with a D_V50 = 123.9 µm and L_b = 23.7 mm.

FIGURE 5

FIGURE 5. Spray images from the cone nozzle (C), (A) distilled water at 137.9 kPa (20 psi) with a D_V50 = 142.2 µm and L_b = 18.3 mm, (B) surfactant solution at 137.9 kPa (20 psi) with a D_V50 = 119.2 µm and L_b = 19.3 mm, (C) distilled water at 206.8 kPa (30 psi) with a D_V50 = 131.6 µm and L_b = 15.4 mm, (D) surfactant solution at 206.8 kPa (30 psi) with a D_V50 = 119.2 µm and L_b = 19.4 mm, (E) distilled water at 310.3 kPa (45 psi) with a D_V50 = 131.9 µm and a L_b = 15.6 mm, (F) surfactant solution at 310.3 kPa (45 psi) with a D_V50 = 130.5 µm and L_b = 18.6 mm, (G) distilled water at 413.7 kPa (60 psi) with a D_V50 = 119.1 µm and L_b = 15.5 mm, (H) surfactant solution at 413.7 kPa (60 psi) with a D_V50 of 130.5 µm and a breakup length of 18.0 mm.

3.1.1 Surfactant’s effect on breakup length and spray angle in fan and cone nozzles

The addition of surfactant resulted in an increase in the breakup length, as shown in Figure 6A and Supplementary Table S3. The fan nozzle (F1, F2, F3, and F4) breakup length increased by 5%–48%. The breakup length at 310.3 kPa (45 psi) may be the most affected by the surfactant due to being considered a transition in droplet size categories by the manufacturer [i.e., at 310.3 kPa (45 psi), the F1 and F2 nozzles transitioned from medium to fine droplets and the F3 and F4 nozzles transitioned from coarse to medium droplets]. The breakup length of the cone nozzle (C) increases 6%–28%, due to the Surfactin. Contrary to pure liquids (Shavit and Chigier, 1995; Butler Ellis et al., 2001; Davanlou et al., 2015), the decreased surface tension of the surfactant solution did not decrease the breakup length of the spray from the fan nozzle; it instead increased it in conjunction with previous research showing that some surfactants increase the breakup length [e.g., increased between 1 and 20 mm and decreased 10 mm (Butler Ellis and Tuck, 1999), increased 1.7 mm (Sijs et al., 2021), and increased 0–3 mm (Shavit and Chigier, 1995)].

FIGURE 6

FIGURE 6. Graphs of the (A) Average breakup length for the fan and cone nozzles with distilled water spray and surfactant solution spray at different pressures. For each nozzle, the breakup length is longer for the surfactant solution than the distilled water and (B) average spray angle for the fan and cone nozzles with distilled water spray and surfactant solution spray at different pressures.

Theoretical modeling of the breakup length results in a proportional dependence of the breakup length on the surface tension of the fluid as well as the wavelength of the spray (Levich and Krylov, 1969; Etzold et al., 2018),

$L_b=\frac{2.5\ln \left(\frac{a}{c}\right)\sigma }{U_{jet}^2}\sqrt{\frac{{\rho }_l}{{\rho }_{air}^3}}(5)$

where $\mathit{ln}\left(\frac{a}{c}\right)$ is the initial disturbance factor, $\sigma$ is the surface tension, ${\rho }_l$ and ${\rho }_{air}$ are the density of the liquid and air, respectively, and $U_{jet}$ is the velocity of the jet. While the equilibrium surface tension of the fluid is decreased due to the surfactant, the spray experiences a dynamic surface tension and slowing of the sheet acceleration, thereby increasing the spray sheets stability and potentially increasing the breakup length (Levich and Krylov, 1969; Butler Ellis et al., 2001; Battal et al., 2003; Weiss, 2004; Makhnenko et al., 2021; Sijs et al., 2021).

The increased breakup length will minimally decrease the distance between the point where droplets are formed and the soil. The optimum spray height for nozzles F1 and F3 is 127 mm and for F3 and F4 is 508 mm (TeeJet, 2014). The fan nozzles breakup length only increased by 0.3%–9% of the optimum spray height, thereby minimally impacting the potential for drift.

Increasing the pressure in the fan and cone nozzles resulted in a slight increase in the spray angle of the fan nozzles and a slight decrease in the cone nozzle spray angle. The addition of surfactant to the spray decreased the spray angle (Figure 6B). In the fan nozzle, the spray angle decreased by 1°–5°; in the cone nozzle, the spray angle decreased by 1°–8°. The averages for the distilled water spray and the surfactant solution spray fall within the standard deviations for each other.

3.1.2 Surfactant’s effects on droplet size in fan and cone nozzles

The droplet size in the fan and cone nozzles decreased as the operating pressure of the nozzle increased (Supplementary Table S4 and Figure 7), consistent with the literature (Solomon et al., 1985; Butler Ellis and Tuck, 1999; Negeed et al., 2011; Davanlou et al., 2015; Wang et al., 2015; Broniarz-Press et al., 2016; Kooij et al., 2018; Nadeem et al., 2019; Li et al., 2021; Makhnenko et al., 2021; Chen et al., 2022). The addition of Surfactin to the distilled water decreased the volumetric median droplet diameter (D_V50) of each fan nozzle by 4%–33% (Supplementary Table S4 and Figure 7). For each fan nozzle, the surfactant solution’s largest D_V50 (i.e., lowest operating pressure) had a smaller D_V50 than the smallest distilled water D_V50 (i.e., the highest operating pressure); in the F1 nozzle, the smallest D_V50 from the distilled spray was 157.9 μm at 413.7 kPa (60 psi) while the largest D_V50 for the surfactant spray was smaller at 134.6 μm at 206.8 kPa (30 psi). The F1 nozzle was affected the most, as it was designed for both the smallest flow rate as well as the smallest spray angle. This design potentially allows for more surfactant to reach the spray interface before droplets break off the spray sheet, thereby allowing more surfactant to exist in the droplets and making breakup into smaller droplets easier. In addition to the surfactant decreasing the D_V50 of the fan nozzles, it decreased the range of $D_{V50}$ values across instances (Figure 8).

FIGURE 7

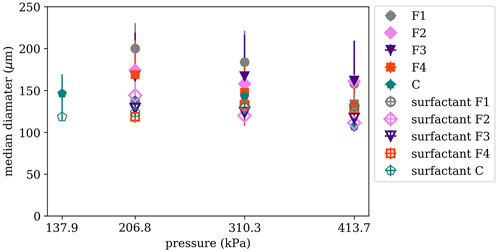
FIGURE 7. Graph of the median droplet size for different nozzles and spray conditions (pressures and spray solution) based on twenty images. The droplet median diameter is smaller for the surfactant solution than the distilled water for every nozzle, excluding nozzle C. The median droplet diameter for nozzle C at 413.7 kPa increases for the surfactant solution.

FIGURE 8

FIGURE 8. Box and whisker plots of the median droplet diameters for the flat fan nozzles over 20 images (A) distilled water F1 nozzle, (B) surfactant solution F1 nozzle, (C) distilled water F2 nozzle, (D) surfactant solution F2 nozzle, (E) distilled water F3 nozzle, (F) surfactant solution F3 nozzle, (G) distilled water F4 nozzle, (H) surfactant solution F4 nozzle.

The surfactant solution decreased the volumetric median droplet diameter, D_V50, in the C nozzle (Figure 7 and Supplementary Table S4) by 27.8 µm (19%), 14.3 µm (10%), and 13.4 µm (9%) at 137.9, 206.8, and 310.3 kPa, respectively; the volumetric median droplet diameter D_V50 increased by 131.1 µm (23%) at 413.7 kPa. The full cone nozzle had more droplets forming than the fan nozzle due to the more 3-D cone shape compared to the flat fan, thereby allowing more droplet interactions and coalescence, and droplet interactions with the spray sheet creating breakup in areas not observed (Saha et al., 2012; Davanlou et al., 2015). The decrease in droplet size is expected with an increase in breakup length; as the spray sheet moves from the nozzle it becomes thinner, thereby decreasing the size of the droplets (Dombrowski and Johns, 1963; Qin et al., 2010; Wang et al., 2015; Kooij et al., 2018; Nadeem et al., 2019; Asgarian et al., 2020; Agbaglah, 2021; Li et al., 2021; Makhnenko et al., 2021; Sijs et al., 2021).

The measured droplet diameters for the distilled water were within those estimated using Fraser et al.’s (1962) model (Eq. 6) (Figure 9),

$d=3.78{\left(\frac{\lambda h}{2\pi }\right)}^{\frac{1}{2}}(6)$

where $\lambda$ is the wavelength and was measured experimentally using ImageJ and h is the sheet thickness, given by $h=\frac{A_{nozzle}}{L_b\theta }$ (Dexter, 2001), where $A_{nozzle}$ is the area of the nozzle and $\theta$ is the spray angle in radians. The F1 and F2 nozzle wavelengths were observed between 1.2–3 mm for distilled water and 1.3–4.4 mm for the surfactant solution. The F3 and F4 nozzle wavelengths were observed between 1.5–4.4 mm for distilled water and 2.0–6.0 mm for the surfactant solution. For the surfactant solution, the model over-predicts the droplet size. For example, none of the surfactant droplets for the F1 and F2 nozzles which experienced a wavelength of 4 mm interacts with the $\lambda =4mm$ line (Figure 9). This is likely due to the dynamic surface tension the surfactant solution experiences.

FIGURE 9

FIGURE 9. Droplet modeling using Fraser’s droplet diameter model (Eq. 6) compared to the measured distilled water and surfactant solution droplet sizes for (A) nozzles F1 and F2 and (B) nozzles (F3 and F4).

The droplets formed in the fan and cone nozzles tended to be very circular (Figures 10A, B). Circularity was measured by ImageJ from 0 to 1, with 0 being the most elongated and least circular shape and 1 being a perfect circle (Eq. 1). The distribution of circularity for the surfactant solution was comparable to the distilled water’s circularity distribution; over half of the droplets for both the surfactant solution and the distilled water had a circularity between 0.8 and 1 and a small percentage of droplets were between 0 and 0.1. The rest of the circularity bins for the surfactant solution had similar frequencies to the distilled water, as well. While the smaller droplets had circularities anywhere from 0 to 1, the larger droplets tended to be fewer in number and elongated, i.e., closer to 0 (Figures 10C, D).

FIGURE 10

FIGURE 10. Graphs of droplet circularity. Histograms of the droplet circularity in the fan and cone nozzles at 45 psi for (A) distilled water spray and (B) surfactant solution. A majority of the droplets are circular for both the distilled water and surfactant solution (0.8–1.0). The circularity of droplets in F1 compared to the droplet diameter for (C) distilled sprayed droplets and (D) surfactant solution sprayed droplets.

3.2 Surfactant’s effects in bubbler nozzles

In contrast to the fan and cone nozzles, the breakup length increased in the bubbler nozzle (Figure 11) with an increase in the spray pressure, in both the distilled spray and the surfactant solution spray (Supplementary Table S5), indicating a different breakup regime. Small disturbances were observed in many of the jet ligaments of the bubbler nozzle before droplets were pinched off the end and formed. Jet ligaments experiencing aerodynamic effects before droplets were formed were also observed (Figure 12).

FIGURE 11

FIGURE 11. Spray from bubbler nozzles (A) 41.4 kPa bubbler nozzle (B1) distilled water spray with nozzle tip in view, (B) 68.9 kPa bubbler nozzle (B2) distilled water spray with top of image 2.0 mm from the tip of the nozzle, (C) 103.4 kPa bubbler nozzle distilled water spray with top of image 25.0 mm from tip of the nozzle, (D) 41.4 kPa bubbler nozzle (B1) surfactant solution spray with nozzle tip in view, (E) 68.9 kPa bubbler nozzle (B2) surfactant solution spray with top of image 46.0 mm from the tip of the nozzle, (F) 103.4 kPa bubbler nozzle (B3) surfactant solution spray 199.2 mm from the tip of the nozzle.

FIGURE 12

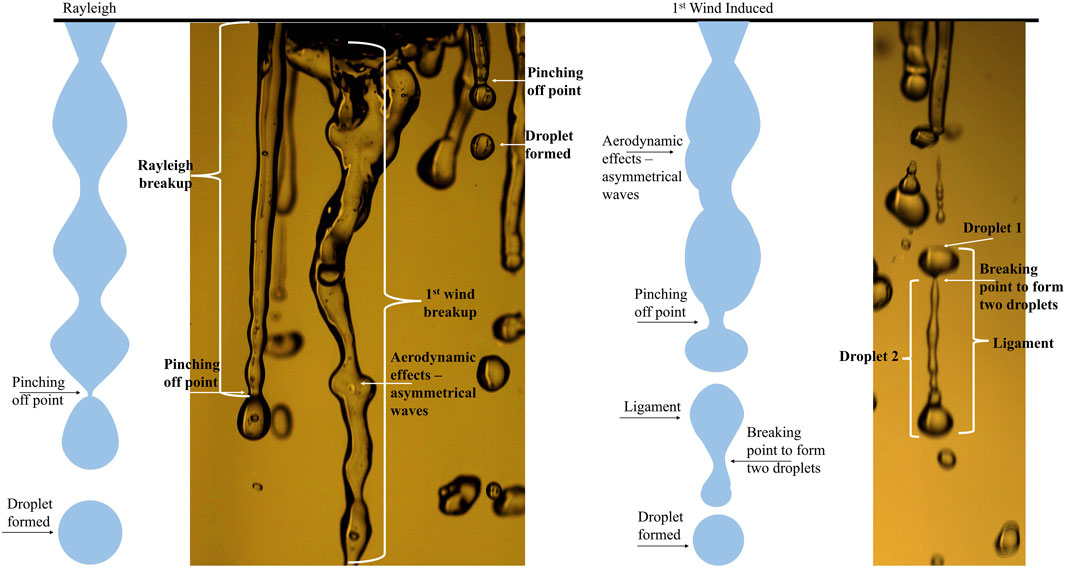
FIGURE 12. Comparison of Figure 1 Rayleigh and first wind breakup mechanisms to experimental images. In Rayleigh breakup, symmetric waves are observed and a pinching-off point for droplet formation from the jet is seen. In first wind breakup, asymmetrical waves are observed, ligaments can break off of the main jet before forming into droplets, and a pinching off point from the jet is observed.

The bubbler nozzle experienced Rayleigh and first wind breakup. The droplet diameters were larger than or equal to the jet diameter they broke off from (e.g., for 10 psi distilled water, $d_{jet}=2.75mm<d_{droplet}=5.34mm$) in line with the expectation of droplets from Rayleigh and first wind jet break up (Reitz and Lin, 1998; Dumouchel, 2008; Delteil et al., 2011; Wang and Fang, 2015). In the Rayleigh breakup regime, the breakup length increases linearly with the increasing velocity of the jet spray (Figure 13) (Reitz and Lin, 1998; Kalaaji et al., 2003; Wang and Fang, 2015). The model for Rayleigh breakup length (Eq. 7) depends on the We and Oh numbers which both depend inversely proportional to the surface tension of the fluid $(We\sim \frac{1}{\sigma },Oh\sim \frac{1}{\sqrt{\sigma }})$ (Grant and Middleman, 1966; Reitz and Lin, 1998; Kalaaji et al., 2003; Gordillo and Pérez-Saborid, 2005; Wang and Fang, 2015);

$L_b=19.5d_{jet}W{e}^{0.5}{\left(1+3Oh\right)}^{0.85}(7)$

therefore, the Rayleigh breakup length model depends inversely on the surface tension. The decrease in surface tension increased the breakup length (Figure 13). As the velocity increases, the effects of the surface tension grow; therefore the difference between the breakup lengths for the distilled water versus the surfactant solution is expected to be larger (Grant and Middleman, 1966; Wang and Fang, 2015). Additionally, with larger jet diameters, the breakup length also increases.

FIGURE 13

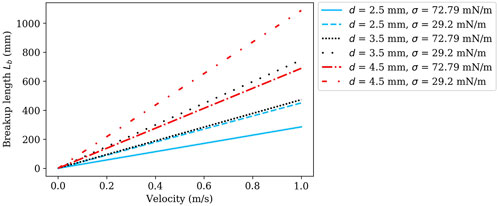
FIGURE 13. Predicted breakup length based on velocity at various jet diameters (2.5, 3.5, and 4.5 mm) for distilled water (σ = 72.79 mN/m) and surfactant solution (σ = 29.2 mN/m), using Eq. 7.

3.2.1 Effects of surfactant on breakup length in bubbler nozzles

The addition of surfactant increased the breakup length in the bubbler nozzles; the effects were more prominent at the higher pressures (i.e., higher velocities) (Figure 14A), as expected from the trends in Figure 13. The average breakup length for B1 increased by 5.1 mm (15%), for B2 it increased by 30.4 mm (65%), and for B3 by 187.7 mm (341%). In addition to the effect on the breakup length, the surfactant impacted the ligament diameter of the bubbler nozzle (Figure 14B and Supplementary Table S5). These ligaments formed from the liquid flowing over the bubbler plate and were used as an equivalent to jet diameter for the Rayleigh breakup length. The B1 nozzle experienced a negligible decrease in the average ligament diameter of 0.15 mm. The B2 nozzle experienced a slight increase in the average ligament diameter of 0.66 mm. The B3 nozzle experienced an increase in the average ligament diameter of 1.48 mm. The increased ligament size created a larger barrier to breakup (i.e., the necessary wave amplitude to prompt breakup is larger), thereby increasing the breakup length, similar to how increasing the nozzle orifice diameter increases the breakup length. The amplitude of disturbances must be larger to result in breakup. The surfactant solution resulted in ligaments forming together into fewer, larger ligaments, compared to the distilled water.

FIGURE 14

FIGURE 14. Graphs of the bubbler nozzles breakup lengths, ligament diameters, and droplet size. (A) bubbler nozzle average breakup length (B) average ligament diameter for 41.4, 68.9, and 103.4 kPa (6, 10, and 15 psi) (C) The breakup length compared to the ligament diameter for the bubbler nozzle with the Rayleigh characterization breakup length $L_b\cong 1.89*d_{jet}$ (Reitz and Lin, 1998; Kalaaji et al., 2003; Gordillo and Pérez-Saborid, 2005) and the first wind predicted breakup length magnitude (D) Graph of average initial droplet diameter formed from bubbler nozzle ligament (E) The droplet diameter compared to the breakup length for the bubbler nozzle with a best fit line (F) The droplet diameter compared to the bubbler ligament’s diameter. Droplet sizes similar to or greater than the ligament’s diameter is a characteristic of Rayleigh breakup ($d_{lig}=d_{init.drop}$).

While the ligament of jet diameter plays a role in the increased breakup length, the surfactant’s reduction of surface tension is also important. As observed in Figure 14C, for B2 and B3 the breakup length for similarly sized ligaments tends to be larger for the surfactant solution compared to the distilled water; this is more visible for the B3 nozzle. For the B1 nozzle, this is not as readily seen; the breakup length is similar for the distilled water and surfactant solution. This is in line with the Rayleigh breakup length model (Eq. 7) which predicts larger breakup lengths for smaller surface tensions and a greater effect with higher velocities.

LEPA bubbler nozzles operate 203.2–457.2 mm from the ground (Senninger, 2023). Compared to the operation height the B1 increased breakup length was minimal; the sheet length increased by 1.1% of the larger operation height (457.2 mm) and 2.5% of the smaller operation height (203.2 mm). The amount of drift will likely not be affected by this breakup length increase. In the B2 nozzle, the breakup length increased by 6.6% of the largest height and 15% of the smaller height; drift could be decreased by the increased sheet length. In the B3 nozzle, the breakup length increased by 44% of the larger height and 98% of the smaller height; therefore, making the conditions less favorable for drift to occur.

3.2.2 Surfactant’s effects on droplet size in bubbler nozzles

In contrast to the fan and cone nozzles, the addition of surfactant to distilled water in the bubbler nozzle increased the droplet size for the B2 and B3 and decreased the droplet size minimally in B1 (Supplementary Table S6 and Figure 14D). The B1 nozzle droplet diameter decrease of 0.40 mm (8%) was in line with the small decrease in ligament size. Additionally, with the increased ligament diameter of B2 and B3, the initial droplet diameter also increased; 0.75 mm (14%) and 4.18 mm (69%), respectively. Since the ligament diameter and the breakup length are directly related, there is also a correlation between the breakup length and the droplet size; as the breakup length increases, the droplet size increases (Figure 14E).

The initial droplet diameters were either around the same size as the ligament diameter or were larger, again, indicating Rayleigh breakup and first wind breakup (Figure 14F). The droplet diameter is dependent on the initial jets or ligaments formed coming off the bubbler plate. The droplet diameters for the distilled water had a standard deviation of 1.2, 0.9, and 1.6 mm for B1, B2, and B3, respectively; for the surfactant solution spray, the droplet diameters had a standard deviation of 1.6, 1.5, and 2.3 mm for B1, B2, and B3, respectively. The increase in deviation for the B3 nozzle was due to the increase in breakup length. Larger droplets increase the likelihood of droplets reaching the soil. The impact of the increased droplet diameter on infiltration and water distribution within the soil is important to investigate in future works.

4 Conclusion

Understanding the effects of Surfactin on droplet dynamics is integral in investigating methods to reduce irrigation water without altering crop yields. Surfactants may retain moisture in the soil when water is scarce (Dekker et al., 2005; Fernández-Gálvez and Mingorance, 2010; Lehrsch et al., 2011; Raddadi et al., 2018; Lowe et al., 2019; Gutierrez et al., 2022). Spraying a surfactant solution can introduce Surfactin to the soil; however, the spray dynamics will be altered. Conclusions for the spray droplet dynamics comparing 0.1 wt% Surfactin to distilled water are:

• The surfactant solution (0.1 wt% Surfactin, surface tension of 29.2 mN/m) resulted in an increased breakup length in the fan, cone, and bubbler nozzles, contrary to prior literature decreasing the surface tension with pure liquids. The breakup length for the fan nozzles, depending on the pressure, increased 5%–48%, the cone nozzle increased 6%–28%, and the bubbler nozzle increased 15%–341%. While increasing the breakup length has the potential to decrease drift, the increase of the breakup length is small compared to the placement of the nozzle from the ground.

• In line with the increase in breakup length, the surfactant solution decreased the volumetric median droplet diameter in the fan nozzle 4%–33%. Decreased droplet size can increase the risk of drift.

• The median diameter of the droplets for the fan nozzle was compared to the model developed by Fraser et al. (1962). The distilled water droplets matched with varying wavelengths and the surfactant solution’s droplets were overpredicted due to the use of the equilibrium surface tension; dynamic surface tension could be investigated and used.

• The surfactant solution decreased the volumetric median droplet diameter in the cone nozzle for 137.9, 206.8, and 310.3 kPa (20, 30, and 45 psi), but increased it for 413.7 kPa (60 psi) pressure. This is likely due to the more three-dimensional effects of this nozzle compared to the more two-dimensional fan nozzle.

• The surfactant solution increased the ligament sizes of the bubbler nozzles thereby increasing the size of the droplets by 14% at 68.9 kPa (10 psi) and 69% at 103.4 kPa (15%), in line with Rayleigh breakup.

• The increased breakup lengths of the B2 and B3 bubbler nozzles can decrease the potential for drift.

• Potential future research includes investigating the effect of surfactant in the spray on infiltration into the soil.

Data availability statement

The data is available in Mendeley https://data.mendeley.com/datasets/r6ddtmwxw9/1.

Author contributions

ES-C: Conceptualization, Formal Analysis, Investigation, Writing–original draft. JA: Conceptualization, Funding acquisition, Resources, Writing–review and editing. AB: Formal Analysis, Writing–review and editing. MD: Conceptualization, Formal Analysis, Funding acquisition, Supervision, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Science Foundation Grants #1651451 and #1828571.

Acknowledgments

The authors would like to thank Adan Cernas for his assistance in building the experimental apparatus.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2024.1354664/full#supplementary-material

References

Adeyemi, O., Grove, I., Peets, S., and Norton, T. (2017). Advanced monitoring and management systems for improving sustainability in precision irrigation. Sustainability 9, 353–351.029. doi:10.3390/su9030353

CrossRef Full Text | Google Scholar

Agbaglah, G. (2021). Breakup of thin liquid sheets through hole–hole and hole–rim merging. J. Fluid Mech. 911, A23–A23.15. doi:10.1017/jfm.2020.1016

CrossRef Full Text | Google Scholar

Asgarian, A., Heinrich, M., Schwarze, R., Bussmann, M., and Chattopadhyay, K. (2020). Experiments and modeling of the breakup mechanisms of an attenuating liquid sheet. Int. J. Multiph. Flow 130, 103347. doi:10.1016/j.ijmultiphaseflow.2020.103347

CrossRef Full Text | Google Scholar

Battal, T., Bain, C. D., Weiß, M., and Darton, R. C. (2003). Surfactant adsorption and Marangoni flow in liquid jets: I. Experiments. J. colloid interface Sci. 263, 250–260. doi:10.1016/s0021-9797(03)00253-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertola, V., and Brenn, G. (2020). Transport phenomena across interfaces of complex fluids: drops and sprays, transport phenomena in complex fluids. Berlin, Germany: Springer, 293–360.

CrossRef Full Text | Google Scholar

Boreyko, J. B., and Chen, C.-H. (2009). Self-propelled dropwise condensate on superhydrophobic surfaces. Phys. Rev. Lett. 103, 184501. doi:10.1103/physrevlett.103.184501

PubMed Abstract | CrossRef Full Text | Google Scholar

Broniarz-Press, L., Włodarczak, S., Matuszak, M., Ochowiak, M., Idziak, R., Szulc, T., et al. (2016). The effect of orifice shape and the injection pressure on enhancement of the atomization process for pressure-swirl atomizers. Crop Prot. 82, 65–74. doi:10.1016/j.cropro.2016.01.005

CrossRef Full Text | Google Scholar

Butler Ellis, M., and Tuck, C. (1999). How adjuvants influence spray formation with different hydraulic nozzles. Crop Prot. 18, 101–109. doi:10.1016/s0261-2194(98)00097-0

CrossRef Full Text | Google Scholar

Butler Ellis, M., Tuck, C., and Miller, P. (1997). The effect of some adjuvants on sprays produced by agricultural flat fan nozzles. Crop Prot. 16, 41–50. doi:10.1016/s0261-2194(96)00065-8

CrossRef Full Text | Google Scholar

Butler Ellis, M., Tuck, C., and Miller, P. (2001). How surface tension of surfactant solutions influences the characteristics of sprays produced by hydraulic nozzles used for pesticide application. Colloids Surfaces A Physicochem. Eng. Aspects 180, 267–276. doi:10.1016/s0927-7757(00)00776-7

CrossRef Full Text | Google Scholar

Chen, L., and Li, Z. (2010). Bouncing droplets on nonsuperhydrophobic surfaces. Phys. Rev. E 82, 016308. doi:10.1103/physreve.82.016308

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, R., Li, H., Wang, J., Guo, X., and Song, Z. (2022). Comparisons of spray characteristics between non-circular and circular nozzles with rotating sprinklers. Appl. Eng. Agric. 38, 61–75. doi:10.13031/aea.14688

CrossRef Full Text | Google Scholar

Chen, X., Doughramaji, N., Betz, A. R., and Derby, M. M. (2017). Droplet ejection and sliding on a flapping film. AIP Adv. 7. doi:10.1063/1.4979008

CrossRef Full Text | Google Scholar

Davanlou, A., Lee, J. D., Basu, S., and Kumar, R. (2015). Effect of viscosity and surface tension on breakup and coalescence of bicomponent sprays. Chem. Eng. Sci. 131, 243–255. doi:10.1016/j.ces.2015.03.057

CrossRef Full Text | Google Scholar

Defay, R., Pétré, G., and Matijević, E. (1971). Dynamic surface tension. Surf. Colloid Sci., 27–81.

Google Scholar

Dekker, L. W., Oostindie, K., Kostka, S. J., and Ritsema, C. J. (2005). Effects of surfactant treatments on the wettability of a water repellent grass-covered dune sand. Soil Res. 43, 383–395. doi:10.1071/sr04090

CrossRef Full Text | Google Scholar

Delteil, J., Vincent, S., Erriguible, A., and Subra-Paternault, P. (2011). Numerical investigations in Rayleigh breakup of round liquid jets with VOF methods. Comput. Fluids 50, 10–23. doi:10.1016/j.compfluid.2011.05.010

CrossRef Full Text | Google Scholar

Dexter, R. W. (2001). The effect of fluid properties on the spray quality from a flat fan nozzle. West Conshohocken, PA: ASTM SPECIAL TECHNICAL PUBLICATION, 27–43.

Google Scholar

Dombrowski, N., and Johns, W. (1963). The aerodynamic instability and disintegration of viscous liquid sheets. Chem. Eng. Sci. 18, 470–214. doi:10.1016/0009-2509(63)80037-8

CrossRef Full Text | Google Scholar

Dumouchel, C. (2008). On the experimental investigation on primary atomization of liquid streams. Exp. fluids 45, 371–422. doi:10.1007/s00348-008-0526-0

CrossRef Full Text | Google Scholar

Etzold, M., Deswal, A., Chen, L., and Durst, F. (2018). Break-up length of liquid jets produced by short nozzles. Int. J. Multiph. Flow 99, 397–407. doi:10.1016/j.ijmultiphaseflow.2017.11.006

CrossRef Full Text | Google Scholar

FAO (2020). Overcoming water challenges in agriculture, 1–210.

Google Scholar

Fernández-Gálvez, J., and Mingorance, M. (2010). Vapour and liquid hydrophobic characteristics induced by presence of surfactants in an agricultural soil. Geoderma 154, 321–327. doi:10.1016/j.geoderma.2009.11.002

CrossRef Full Text | Google Scholar

Ferri, J. K., and Stebe, K. J. (2000). Which surfactants reduce surface tension faster? A scaling argument for diffusion-controlled adsorption. Adv. Colloid Interface Sci. 85, 61–97. doi:10.1016/s0001-8686(99)00027-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Fontela, J. (2018). Lower pressure for higher efficiency. New Delhi: Irrigation Today. Irrigation Association, 25–26.

Google Scholar

Ford, R., and Furmidge, C. (1967). The formation of drops from viscous Newtonian liquids sprayed through fan-jet nozzles. Br. J. Appl. Phys. 18, 335–388-1. doi:10.1088/0508-3443/18/3/312

CrossRef Full Text | Google Scholar

Fraser, R., Eisenklam, P., Dombrowski, N., and Hasson, D. (1962). Drop formation from rapidly moving liquid sheets. AIChE J. 8, 672–680. doi:10.1002/aic.690080522

CrossRef Full Text | Google Scholar

Gordillo, J., and Pérez-Saborid, M. (2005). Aerodynamic effects in the break-up of liquid jets: on the first wind-induced break-up regime. J. Fluid Mech. 541, 1–20. doi:10.1017/s0022112005006026

CrossRef Full Text | Google Scholar

Grant, R. P., and Middleman, S. (1966). Newtonian jet stability. AIChE J. 12, 669–678. doi:10.1002/aic.690120411

CrossRef Full Text | Google Scholar

Gutierrez, M. M., Cameron-Harp, M. V., Chakraborty, P. P., Stallbaumer-Cyr, E. M., Morrow, J. A., Hansen, R. R., et al. (2022). Investigating a microbial approach to water conservation: effects of Bacillus subtilis and Surfactin on evaporation dynamics in loam and sandy loam soils. Front. Sustain. Food Syst. 6, 1–16. doi:10.3389/fsufs.2022.959591

CrossRef Full Text | Google Scholar

Huber, R. A., Campbell, M., Doughramaji, N., and Derby, M. M. (2019). Vibration-enhanced droplet motion modes: simulations of rocking, ratcheting, ratcheting with breakup, and ejection. J. Fluids Eng. 141. doi:10.1115/1.4042037

CrossRef Full Text | Google Scholar

Jalili, B., Jalili, P., Ommi, F., and Domiri Ganji, D. (2023). Experimental study on the nozzle-shape effect on liquid jet characteristics in gaseous crossflow. Front. Mech. Eng. 9. doi:10.3389/fmech.2023.1207894

CrossRef Full Text | Google Scholar

Jiang, Y., Li, H., Chen, C., Hua, L., and Zhang, D. (2019). Hydraulic performance and jet breakup characteristics of the impact sprinkler with circular and non-circular nozzles. Appl. Eng. Agric. 35, 911–924. doi:10.13031/aea.13268

CrossRef Full Text | Google Scholar

Kalaaji, A., Lopez, B., Attane, P., and Soucemarianadin, A. (2003). Breakup length of forced liquid jets. Phys. Fluids 15, 2469–2479. doi:10.1063/1.1593023

CrossRef Full Text | Google Scholar

KDA (2019). Water use data collection and use [fact sheet]. Kansas, USA: Kansas Department of Agriculture Division of Water Services, 1–2.

Google Scholar

Kingsley, B. J., and Chiarot, P. R. (2023). Polyimide films manufactured using partially wet electrospray deposition. ACS Appl. Polym. Mater. 5, 1797–1809. doi:10.1021/acsapm.2c01891

CrossRef Full Text | Google Scholar

Kooij, S., Sijs, R., Denn, M. M., Villermaux, E., and Bonn, D. (2018). What determines the drop size in sprays? Phys. Rev. X 8, 031019–31113. doi:10.1103/physrevx.8.031019

CrossRef Full Text | Google Scholar

Leach, R., Stevens, F., Langford, S., and Dickinson, J. (2006). Dropwise condensation: experiments and simulations of nucleation and growth of water drops in a cooling system. Langmuir 22, 8864–8872. doi:10.1021/la061901+

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J., Saha, A., Basu, S., and Kumar, R. (2012). “Effects of injection pressure on spray atomization characteristics with measurement technique cross-validation,” in Proceedings of the 12th Triennial International Conference on Liquid Atomization and Spray Systems, Heidelberg, Germany, September 2012, 2–6.

Google Scholar

Lehr, J., Keeley, J., and Lehr, J. (2005). 3.8.43 sprinkler irrigation, water encyclopedia, volumes 1-5. John Wiley and Sons, 581–582.

Google Scholar

Lehrsch, G., Sojka, R., Reed, J., Henderson, R., and Kostka, S. (2011). Surfactant and irrigation effects on wettable soils: runoff, erosion, and water retention responses. Hydrol. Process. 25, 766–777. doi:10.1002/hyp.7866

CrossRef Full Text | Google Scholar

Levich, V., and Krylov, V. (1969). Surface-tension-driven phenomena. Annu. Rev. fluid Mech. 1, 293–316. doi:10.1146/annurev.fl.01.010169.001453

CrossRef Full Text | Google Scholar

Li, S., Chen, C., Wang, Y., Kang, F., and Li, W. (2021). Study on the atomization characteristics of flat fan nozzles for pesticide application at low pressures. Agriculture 11, 309. doi:10.3390/agriculture11040309

CrossRef Full Text | Google Scholar

Li, Y., Bai, G., and Yan, H. (2015). Development and validation of a modified model to simulate the sprinkler water distribution. Comput. Electron. Agric. 111, 38–47. doi:10.1016/j.compag.2014.12.003

CrossRef Full Text | Google Scholar

Lowe, M.-A., Mathes, F., Loke, M. H., McGrath, G., Murphy, D. V., and Leopold, M. (2019). Bacillus subtilis and surfactant amendments for the breakdown of soil water repellency in a sandy soil. Geoderma 344, 108–118. doi:10.1016/j.geoderma.2019.02.038

CrossRef Full Text | Google Scholar

Makhnenko, I., Alonzi, E. R., Fredericks, S. A., Colby, C. M., and Dutcher, C. S. (2021). A review of liquid sheet breakup: perspectives from agricultural sprays. J. Aerosol Sci. 157, 105805. doi:10.1016/j.jaerosci.2021.105805

CrossRef Full Text | Google Scholar

Malot, H., and Blaisot, J. B. (2000). Droplet size distribution and sphericity measurements of low-density sprays through image analysis. Part. Part. Syst. Charact. Meas. Descr. Part. Prop. Behav. Powders Other Disperse Syst. 17, 146–158. doi:10.1002/1521-4117(200012)17:4<146::aid-ppsc146>3.0.co;2-4

CrossRef Full Text | Google Scholar

Nadeem, M., Nguyen-Quang, T., Diallo, C., Venkatadri, U., and Havard, P. (2019). Contribution to spraying nozzle study: a comparative investigation of imaging and simulation approaches. Pak. J. Agric. Sci. 56, 215–224. doi:10.21162/PAKJAS/19.7750

CrossRef Full Text | Google Scholar

Nath, S., Ahmadi, S. F., and Boreyko, J. B. (2017). A review of condensation frosting. Nanoscale Microscale Thermophys. Eng. 21, 81–101. doi:10.1080/15567265.2016.1256007

CrossRef Full Text | Google Scholar

Nath, S., and Boreyko, J. B. (2016). On localized vapor pressure gradients governing condensation and frost phenomena. Langmuir 32, 8350–8365. doi:10.1021/acs.langmuir.6b01488

PubMed Abstract | CrossRef Full Text | Google Scholar

Negeed, E.-S. R., Hidaka, S., Kohno, M., and Takata, Y. (2011). Experimental and analytical investigation of liquid sheet breakup characteristics. Int. J. Heat Fluid Flow 32, 95–106. doi:10.1016/j.ijheatfluidflow.2010.08.005

CrossRef Full Text | Google Scholar

Noori, M. S., Taleghani, A. S., and Rahni, M. T. (2020). Phenomenological investigation of drop manipulation using surface acoustic waves. Microgravity Sci. Technol. 32, 1147–1158. doi:10.1007/s12217-020-09839-3

CrossRef Full Text | Google Scholar

Noori, M. S., Taleghani, A. S., and Rahni, M. T. (2021). Surface acoustic waves as control actuator for drop removal from solid surface. Fluid Dyn. Res. 53, 045503. doi:10.1088/1873-7005/ac12af

CrossRef Full Text | Google Scholar

Oker, T. E., Sheshukov, A. Y., Aguilar, J., Rogers, D. H., and Kisekka, I. (2021). Evaluating soil water redistribution under mobile drip irrigation, low-elevation spray application, and low-energy precision application using HYDRUS. J. Irrigation Drainage Eng. 147. doi:10.1061/(asce)ir.1943-4774.0001553

CrossRef Full Text | Google Scholar

Payri, R., Salvador, F. J., Gimeno, J., and Viera, J. P. (2015). Experimental analysis on the influence of nozzle geometry over the dispersion of liquid n-dodecane sprays. Front. Mech. Eng. 1, 165787. doi:10.3389/fmech.2015.00013

CrossRef Full Text | Google Scholar

Peters, R. T., Neibling, H., Stroh, R., Molaei, B., and Mehanna, H. (2016). “Low energy precision application (LEPA) and low elevation spray application (LESA) trials in the Pacific Northwest,” in Proceedings of 2016 California Alfalfa and Forage Symposium, 1–21.

Google Scholar

Post, S. L., and Hewitt, A. J. (2018). Flat-fan spray atomization model. Trans. ASABE 61, 1249–1256. doi:10.13031/trans.12572

CrossRef Full Text | Google Scholar

Qin, K., Tank, H., Wilson, S., Downer, B., and Liu, L. (2010). Controlling droplet-size distribution using oil emulsions in agricultural sprays. Atomization Sprays 20, 227–239. doi:10.1615/atomizspr.v20.i3.40

CrossRef Full Text | Google Scholar

Raddadi, N., Giacomucci, L., Marasco, R., Daffonchio, D., Cherif, A., and Fava, F. (2018). Bacterial polyextremotolerant bioemulsifiers from arid soils improve water retention capacity and humidity uptake in sandy soil. Microb. Cell Factories 17, 83–12. doi:10.1186/s12934-018-0934-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Reitz, R., and Lin, S. (1998). Drop and spray formation from a liquid jet. Annu. Rev. Fluid Mech. 30, 85–105. doi:10.1146/annurev.fluid.30.1.85

CrossRef Full Text | Google Scholar

Ristenpart, W., McCalla, P., Roy, R., and Stone, H. A. (2006). Coalescence of spreading droplets on a wettable substrate. Phys. Rev. Lett. 97, 064501. doi:10.1103/physrevlett.97.064501

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogers, D. H., Alam, M., and Shaw, L. K. (2008). Considerations for nozzle package selection for center pivots. Agricultural experiment station and cooperative extension service. (Kansas: KSRE)

Google Scholar

Rosen, M. J., and Kunjappu, J. T. (2012a). Characteristics features of surfactant, Surfactants and interfacial phenomena. Hoboken, New Jersey: John Wiley and Sons, 1–33.

Google Scholar

Rosen, M. J., and Kunjappu, J. T. (2012b). Reduction of surface and interfactial tension by surfactants, Surfactants and interfacial phenomena. Hoboken, New Jersey: John Wiley and Sons, 208–242.

Google Scholar

Saha, A., Lee, J. D., Basu, S., and Kumar, R. (2012). Breakup and coalescence characteristics of a hollow cone swirling spray. Phys. fluids 24, 124103. doi:10.1063/1.4773065

CrossRef Full Text | Google Scholar

Senninger (2023). Lepa - low energy precision application | pivot irrigation product.

Google Scholar

Shams Taleghani, A., and Sheikholeslam Noori, M. (2022). Numerical investigation of coalescence phenomena, affected by surface acoustic waves. Eur. Phys. J. Plus 137, 975. doi:10.1140/epjp/s13360-022-03175-8

CrossRef Full Text | Google Scholar

Shavit, U., and Chigier, N. (1995). The role of dynamic surface tension in air assist atomization. Phys. Fluids 7, 24–33. doi:10.1063/1.868725

CrossRef Full Text | Google Scholar

Sijs, R., and Bonn, D. (2020). The effect of adjuvants on spray droplet size from hydraulic nozzles. Pest Manag. Sci. 76, 3487–3494. doi:10.1002/ps.5742

PubMed Abstract | CrossRef Full Text | Google Scholar

Sijs, R., Kooij, S., and Bonn, D. (2021). How surfactants influence the drop size in sprays from flat fan and hollow cone nozzles. Phys. Fluids 33, 1–11. doi:10.1063/5.0066775

CrossRef Full Text | Google Scholar

Silva, L. L. (2006). The effect of spray head sprinklers with different deflector plates on irrigation uniformity, runoff and sediment yield in a Mediterranean soil. Agric. water Manag. 85, 243–252. doi:10.1016/j.agwat.2006.05.006

CrossRef Full Text | Google Scholar

Solomon, K. H., Kincaid, D. C., and Bezdek, J. C. (1985). Drop size distributions for irrigation spray nozzles. Trans. ASAE 28, 1966–1974. doi:10.13031/2013.32550

CrossRef Full Text | Google Scholar

Squire, H. (1953). Investigation of the instability of a moving liquid film. Br. J. Appl. Phys. 4, 167–169. doi:10.1088/0508-3443/4/6/302

CrossRef Full Text | Google Scholar

TeeJet, (2014). TeeJet technologies catalog 51A. Glendale Heights, Illinois: Teejet.

Google Scholar

Trout, T. J., and Kincaid, D. C. (2007). “On-farm system design and operation and land management,” in Irrigaton of agricultural crops. Editors R. J. Lascano, and R. E. Sojika (Madison, WI: American Society of Agronomy Inc.), 133–179.

Google Scholar

UNICEF (2021). Water security for all.

Google Scholar

USDA (2022). Land values 2022 summary august 2022. United States: United States Department of Agriculture, 1–22.

Google Scholar

USGS (2019). Irrigation water use.

Google Scholar

Wang, F., and Fang, T. (2015). Liquid jet breakup for non-circular orifices under low pressures. Int. J. Multiph. Flow 72, 248–262. doi:10.1016/j.ijmultiphaseflow.2015.02.015

CrossRef Full Text | Google Scholar

Wang, J., Song, Z., Chen, R., Yang, T., and Tian, Z. (2022). Experimental study on droplet characteristics of rotating sprinklers with circular nozzles and diffuser. Agriculture 12, 987–987.021. doi:10.3390/agriculture12070987

CrossRef Full Text | Google Scholar

Wang, S., Dorr, G., Khashehchi, M., and He, X. (2015). Performance of selected agricultural spray nozzles using particle image velocimetry. J. Agric. Sci. Technol. 17, 601–613. doi:10.1016/j.ijmultiphaseflow.2015.02.015

CrossRef Full Text | Google Scholar

Weiss, M. (2004). Surfactant adsorption and Marangoni flow in liquid jets. Oxford, UK: University of Oxford.

Google Scholar

Zhu, H., Salyani, M., and Fox, R. D. (2011). A portable scanning system for evaluation of spray deposit distribution. Comput. Electron. Agric. 76, 38–43. doi:10.1016/j.compag.2011.01.003

CrossRef Full Text | Google Scholar

Nomenclature