Efficient design of sandwich panels with cellular truss cores and large phononic band gaps using surrogate modeling and global optimization

Recent advancements in additive manufacturing technologies and topology optimization techniques have catalyzed a transformative shift in the design of architected materials, enabling increasingly complex and customized configurations. This study delves into the realm of engineered cellular materials, spotlighting their capacity to modulate the propagation of mechanical waves through the strategic creation of phononic band gaps. Focusing on the design of sandwich panels with cellular truss cores, we aim to harness these band gaps to achieve pronounced wave suppression within specific frequency ranges. Our methodology combines surrogate modeling with a comprehensive global optimization strategy, employing three machine learning algorithms—k-Nearest Neighbors (kNN), Random Forest Regression (RFR), and Artificial Neural Networks (ANN)—to construct predictive models from parameterized finite element (FE) analyses. These models, once trained, are integrated with Particle Swarm Optimization (PSO) to refine the panel designs. This approach not only facilitates the discovery of optimal truss core configurations for targeted phononic band gaps but also showcases a marked increase in computational efficiency over traditional optimization methods, particularly in the context of designing for diverse target frequencies.

1 Introduction

In nature, we can find many materials that possess exceptional properties resulting from millions of years of evolutionary processes. A remarkable example of this is the intricate porous structure found in the core of bones, which far surpasses the structural efficiency of most artificial materials created by humans. The concept of incorporating design principles found in natural materials into man-made materials can be achieved through architected designs. While embedding architecture into materials is not new, recent advancements in additive manufacturing technologies have revolutionized the creation of cellular materials with increasingly complex and tailored designs. These technologies allow for precise control over the internal structure and properties of the materials, offering unprecedented possibilities for material engineers (Guo et al., 2021; Kladovasilakis et al., 2022; Yang et al., 2023b).

Furthermore, the field of topological optimization has made significant steps in modifying the architecture of materials to achieve specific objectives such as high strength, stiffness, and lightweight. By leveraging computational algorithms and mathematical optimization techniques, researchers can explore and manipulate the arrangement of material within a given volume. This approach allows for the creation of materials with optimized structural properties, resulting in enhanced performance and efficiency. Numerous studies have extensively demonstrated the efficacy of these architected materials and topological optimization approaches (Schaedler and Carter, 2016b; Yang et al., 2024).

Engineered cellular materials possess interesting static properties and can also be utilized to control the propagation of mechanical waves. One such example is the creation of phononic band gaps. Phononic materials can suppress the propagation of mechanical waves within a specific frequency range, and this property has been extensively studied in recent years (Hussein, Leamy, and Ruzzene, 2014). Researchers have designed phononic materials with tailored band gap properties using novel design strategies and advanced manufacturing techniques. These materials have potential applications in a wide range of fields, such as energy absorption, sound insulation, and vibration damping. Various researchers have investigated the band gap behavior of two-dimensional periodic cellular materials (Jensen, 2003; Ruzzene and Scarpa, 2005; Liebold-Ribeiro and Körner, 2014; Warmuth and Körner, 2015), observing significant band gaps in the case of chiral quadratic and hexagonal lattice configurations. In addition, it can be concluded that lattices with high coordination numbers enable the generation of band gaps, with the struts acting as mechanical resonators (Wang et al., 2015). These investigations show that if the geometrical or material properties of the struts are altered, it is possible to manipulate the corresponding band gap. Therefore, a natural extension is the application of topology optimization techniques in the design of lattice materials with phononic band gaps.

Various topology optimization strategies have been used in phononic materials to maximize the band gap between two adjacent bands in the phononic band diagram, where the common design variables correspond to the material properties or geometrical characteristics of the struts used to create the lattice. Some of the optimization tools used include genetic algorithms (GA) (Gazonas et al., 2006; Bilal and Hussein, 2011; Liu et al., 2014), particle swarm optimization (PSO) (Guo and Zhang, 2022; Tikani, Ziaei-Rad, and Moosavi, 2023), bidirectional evolutionary structural optimization (BESO) (Fan et al., 2016), and gradient-based optimization algorithms (Yi et al., 2019; Quinteros et al., 2021a; Cool et al., 2024). Other investigations have implemented multi-objective optimization strategies for phononic materials, considering mass or stiffness restrictions (Dong et al., 2014), the topology of perforated plates (Hedayatrasa et al., 2016b), or phononic plates with tunable band gaps under equiaxial stretch (Hedayatrasa et al., 2016a).

The optimization problem for the band gap can be highly demanding due to the large number of objective function evaluations required, which involves solving multiple eigenvalue problems. The computational effort also grows rapidly as the model dimension, or the number of design variables increases. To overcome this challenge, researchers have explored surrogate optimization techniques that rely on machine learning and deep learning algorithms (Muhammad and Lim, 2022; Kudela et al., 2023). Surrogate models are approximations of input-output relationships built from sampled data obtained by high-fidelity numerical simulations. These models allow for quicker identification of local or global optima, and since they can make predictions much faster than the high-fidelity simulations, the computational cost associated with the optimization based on surrogate models is generally negligible. Bacigalupo et al. (2020) applied machine learning techniques for band gap optimization of a periodic tetrachiral metamaterial. They implemented a surrogate optimization strategy based on a combination of Radial Basis Functions networks and quasi-Monte Carlo sequences. The performance was compared to a traditional approach based on the evaluation of the objective function using the high-fidelity model, demonstrating that a similar solution is obtained in a much shorter time with surrogate optimization. Dong et al. (2020) introduced a surrogate modeling approach to design an elastic metamaterial structure formed of unit cells. They employed a multi-layer feedforward artificial neural network (ANN) to predict the band diagram, with hyperparameters fine-tuned using genetic algorithms (GA). Based on the trained and optimized ANN model, the authors utilized the Nelder-Mead (NM) algorithm to find the optimal design that maximizes the band gap. Li et al. (2020) proposed a novel data-driven approach that integrates image-based finite element analysis and deep learning techniques for designing 2D phononic crystals (PnCs). In this case, an autoencoder is trained to extract topological features from test images. Finite element analysis is then employed to evaluate the band gaps of the samples. A multi-layer perceptron is also trained to uncover the inherent relationship between the band gaps and topological properties. With the trained models, Li et al. (2020) constructed phononic crystals that exhibit anticipated band gaps, thereby demonstrating the effectiveness of their approach. Gurbuz et al. (2021) developed a novel design technique for two-dimensional PnCs by employing conditional generative adversarial networks (GANs). To improve the performance of the proposed conditional GAN, they introduced a multi-input channel design that considers the underlying relationship between cell shapes and their associated transmission loss. This approach allows the GAN to suggest cell geometries tailored to achieve the desired metamaterial transmission behavior. Kudela et al. (2023) presents an innovative methodology for the topology optimization of phononic crystals by replacing traditional, computationally intensive solvers with a deep learning (DL) model for fast prediction of dispersion diagrams. The study showcases the effectiveness of combining surrogate DL models with genetic algorithms for optimizing phononic crystal geometries, aiming at efficiently designing materials with tailored band gaps.

On the other hand, cellular materials are highly desirable for use as cores in sandwich panels (Schaedler and Carter, 2016a). Sandwich panels consist of thin face sheets or skins and a lightweight, thicker core sandwiched between the skins to achieve superior bending stiffness. Sandwich panels with lattice-based cellular cores are particularly attractive in applications requiring multifunctional materials, such as lightweight and high-strength structural materials. While various investigations have been carried out to find the optimal cell that maximizes the stiffness-to-weight ratio in these types of panels (Liu and Lu, 2004; Liu et al., 2006), little attention has been paid to designing sandwich panels with vibration attenuation (band gap) properties. Recently, researchers have begun to explore the use of cellular cores with band gap properties. Guo et al. (2021)conduct a comprehensive investigation into the dynamics of a 3D-printed sandwich beam with an hourglass lattice truss core. It presents a theoretical model validated through finite element analysis and experimental tests. The study introduces a novel vibration suppression technique using a non-linear energy sink (NES), demonstrating its effectiveness through parametric studies. Sun et al. (2021) studied the vibroacoustic properties of sandwich beams with a square truss core, achieving significant vibration reduction in specific frequency ranges. Quinteros et al. (2021a) optimized the phononic band gap of a periodic sandwich structure with a square core topology, demonstrating the feasibility of designing sandwich panels with cellular cores that exhibit large phononic band gaps. Gazzola et al. (2022) present a study on designing and modeling a novel single-phase sandwich panel for acoustic insulation applications, utilizing architected cellular materials with a focus on achieving significant phononic band gaps. The research introduces an innovative approach by incorporating a periodic structure with a specially designed unit cell, enhancing the panel’s sound transmission loss (STL) capabilities, especially in resonance-dominated frequency ranges. Cool et al. (2024) developed a topology optimization framework focused on the vibroacoustic design of sandwich structure cores. The primary objective is to minimize sound transmission through these structures while maintaining volume and structural stiffness constraints.

The aim of this investigation is to develop a computationally efficient framework based on surrogate models for designing sandwich panels with cellular truss cores capable of exhibiting large phononic band gaps. The study investigates different truss core configurations and employs surrogate modeling combined with a global optimization strategy to facilitate the optimization process. Thus, as far as our knowledge, this is the first effort toward maximizing band gaps based on surrogate models for sandwich panels with cellular truss cores.

In our investigation, we selected k-Nearest Neighbors (kNN), Random Forest Regression (RFR), and Artificial Neural Networks (ANN) as surrogate models to span a range of complexities and learning paradigms, allowing us to assess their adaptability to our specific problem domain. kNN, with its simplicity and minimal assumption about data structure, offers an intuitive baseline for comparison. RFR introduces more complexity through ensemble learning, providing robustness against overfitting and the ability to capture nonlinear relationships. ANN, representing the most complex model, has the capacity for high-dimensional function approximation, making it potent for capturing intricate patterns within the data. This selection enables a comprehensive evaluation of surrogate modeling techniques, from straightforward to highly complex, to identify the most effective approach for designing sandwich panels with cellular truss cores exhibiting large phononic band gaps. Our choice aligns with recent advancements in machine learning applications for engineering problems (Yang et al., 2023a; Yang et al., 2023b).

These surrogate models were trained using data generated from a parameterized finite element (FE) model developed explicitly for the panels under investigation. The input parameters utilized in the machine learning models were directly associated with the topology and geometry of the truss cores, while the output parameters consisted of the central frequency and width of the band gaps. The optimization is performed in an iterative procedure, where the process starts optimizing band gaps using a trained surrogate model. Then, the configuration identified as optimal is included in the database to repeat the process. This iterative strategy gradually increases the accuracy of the surrogate model close to the optimal design. The optimization algorithm adopted in this bi-level framework corresponds to a PSO (Han and Zhang, 2012). PSO’s inherent ability to converge swiftly toward optimal solutions while maintaining diversity in the search space aligns well with the characteristics of our problem domain. This allowed us to effectively search for optimal truss core configurations, resulting in sandwich panels with band gaps around desired design frequencies.

In selecting PSO as our optimization algorithm, we recognize its well-documented strengths and limitations. According to Nayak et al. (2023), PSO is distinguished as the most successful optimization algorithm among available nature-inspired algorithms due to its high efficiency and adaptability across various dynamic environments. This makes it particularly suitable for our iterative optimization framework, designed to optimize phononic band gaps. PSO’s simplicity, combined with its effectiveness in navigating complex search spaces, underscores its selection for this complex task. Despite PSO’s sensitivity to parameter settings, its proven track record across diverse applications from networking to power generation justifies our choice (Gad, 2022). The rest of the paper is organized as follows. Section 2 presents the sandwich panel of interest and briefly describes the band gap identification using band diagrams. Section 3 presents the details of the bi-level optimization framework proposed, while Section 4 contains the results obtained after implementing the proposed framework on the sandwich panels studied. Finally, Section 5 contains the most relevant conclusions drawn from this study.

2 Sandwich panels and phononic band gaps

2.1 Band gaps in periodic structures

Phononic band gaps arise from the periodic arrangement of structures within a material, affecting elastic wave propagation. In the context of elastic waves, the Floquet-Bloch wave theory can describe the behavior of a material with a periodic structure by representing the elastic waves as a superposition of Bloch waves. In a structural finite element model, periodic boundary conditions can be imposed using the Floquet-Bloch wave theory by assuming that the displacement of the material at one end of the unit cell is equal to the displacement of the material at the other end. This assumption can be written mathematically as (Quinteros et al., 2021b):

$\mathbf{u}\left(\mathbf{X}+\mathbf{r}\right)=\mathbf{u}\left(\mathbf{X}\right)e^{j\mathbf{k}\bullet \mathbf{r}}(1)$

Here, $\mathbf{X}$ denotes the coordinate of a particular material point, $\mathbf{r}$ is the periodicity length of the cell, $\mathbf{k}$ is the wave vector, and $j$ represents the imaginary unit. Once periodic boundary conditions have been imposed, the finite element model can be used to calculate the vibrational modes of the unit cell:

$\left(\mathbf{K}\left(\mathbf{k}\right)-{\omega }_i^2\mathbf{M}\left(\mathbf{k}\right)\right){\mathit{u}}_i=\mathbf{0}(2)$

where ${\omega }_i$ is the frequency associated with the vibration mode ${\mathit{u}}_i$, $\mathbf{K}$ is the stiffness matrix of the unit cell, and $\mathbf{M}$ is the mass matrix of the unit cell. It should be noted that the stiffness and mass matrices after applying the periodic boundary condition are functions of the wave vector $\mathbf{k}$.

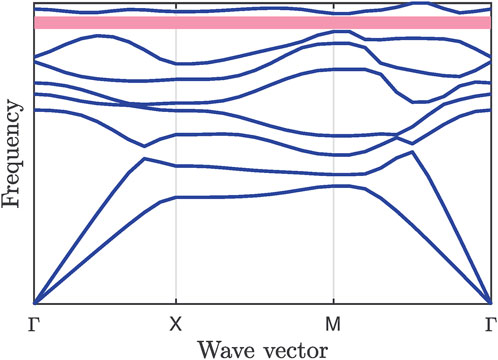
The band diagram of the periodic structure can be constructed by solving Eq. 2 for wave vectors within the perimeter of the irreducible Brillouin zone (Maldovan, 2013). Figure 1 presents an example of a band diagram where it is possible to observe the relationship between the frequency and the wave vector for each vibration mode. In a band diagram, a band gap is represented by a range of frequencies where frequencies ${\omega }_i$ are not associated with any wave vector. This means that the material does not allow the propagation of elastic waves in this frequency range, effectively acting as a frequency stopband. In a band diagram, the band gap appears as a gap between two consecutive bands, as it is shown in the pink region in Figure 1. For this work, the bands that define the band gaps are named the upper and lower bands.

Figure 1

Figure 1. Example of a band diagram exhibiting a band gap.

The size and location of the band gap in the diagram depend on the material’s properties and the unit cell’s geometry. In general, wider band gaps correspond to stronger phononic isolation properties of the material, making it more effective at controlling the propagation of elastic waves.

2.2 Sandwich panels studied

The proposed study examines sandwich panels featuring lattice-based cellular cores, as depicted in Figure 2. These topologies are inspired by existing designs documented in the literature (Schaedler and Carter, 2016a). The first core topology consists of zig-zag trusses intersecting at the center of the cell. On the other hand, the second and third topologies comprise an arrangement of 3 × 3 basis units. In the second panel, the basis unit takes on a pyramidal shape, while in the third panel, the basis unit consists of upright and inverted pyramids connected by their apexes.

Figure 2

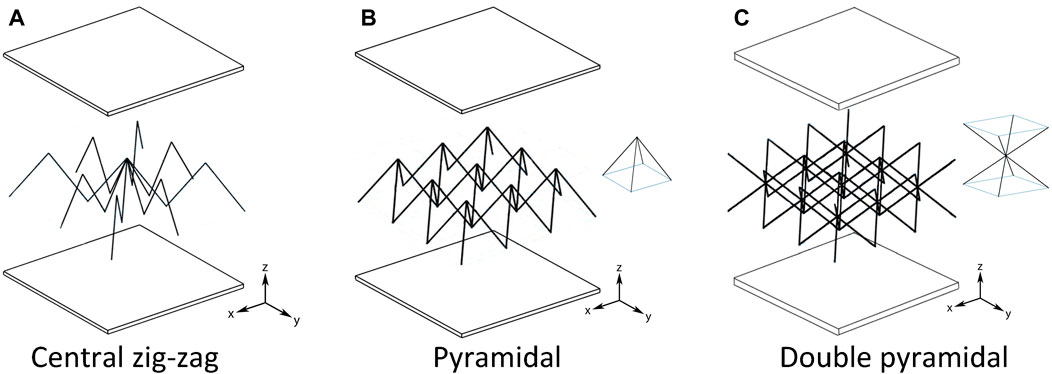
Figure 2. Unit cells of the sandwich panels under consideration. (A) Central zig-zag. (B) Pyramidal. (C) Double Pyramidal.

All configurations are subjected to a periodic boundary condition by implementing the Floquet-Bloch wave theory. The periodicity is enforced along all four sides of the unit cell when observing it from a top-down perspective. These core configurations were specifically chosen to achieve symmetry with respect to the x-axis, y-axis, and 45-degree axis, as demonstrated in Figure 3. This figure depicts a top-down and isometric view of the core topologies, highlighting the Irreducible Brillouin Zone (IBZ) in gray. In this visualization, members with the same color share the same properties. Also, each color is labeled with a unique number, allowing the differentiation between members. In this sense, each panel contains six different members.

Figure 3

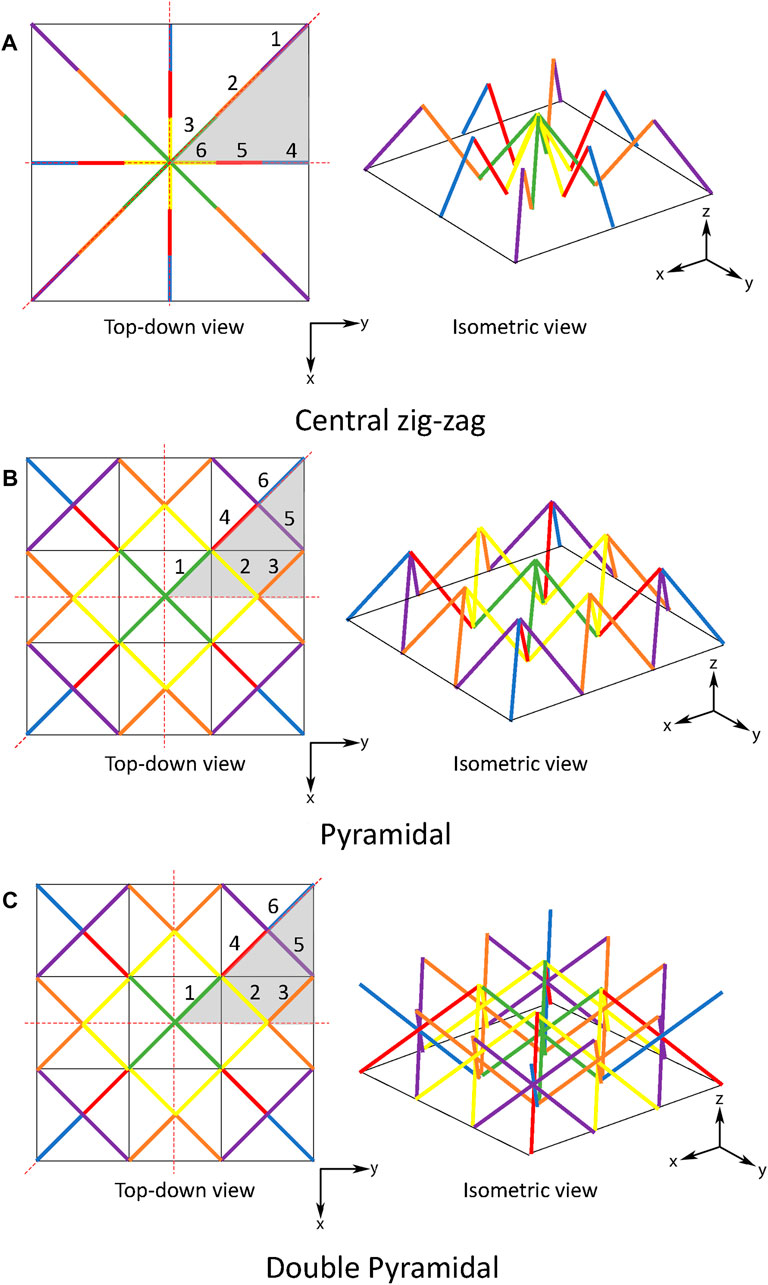
Figure 3. Top-down and isometric view of the core topologies, illustrating the Irreducible Brillouin Zone (IBZ) (in light gray). The same colors indicate members with equal properties. (A) Central zig-zag. (B) Pyramidal. (C) Double Pyramidal.

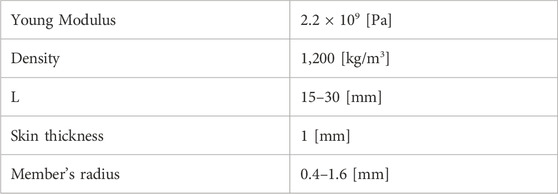
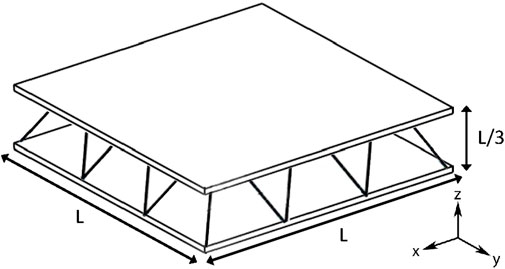
Given the possibility of manufacturing the panels through 3D printing, we have utilized a standard resin commonly employed in SLA printing as the material for both the panel’s core and skins. The three sandwich panel configurations have the same nominal geometrical and material properties for the unit cells. These are summarized in Table 1 and illustrated in Figure 4. The optimization process involves adjusting the cell length (L) and the radius of the truss members within a range of values. As a result, seven design variables need to be optimized for each sandwich panel.

Table 1

Table 1. Unit cell nominal properties.

Figure 4

Figure 4. Unit cell dimensions.

3 Proposed framework for designing phononic sandwich panels

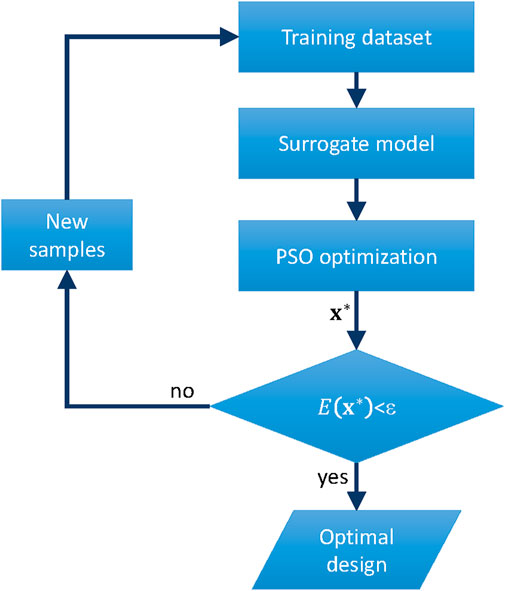
The proposed framework is based on four main steps. It begins with the development of parameterized FE models, enabling the establishment of periodic boundary conditions and generating band diagrams to extract the central frequency and width of the primary band gap. Subsequently, in step two, datasets are built tailored to each core topology, encompassing various combinations of FE model parameters. These datasets serve as the foundation for training and testing machine learning models. In the third step, random or grid search strategies are adopted to select optimal architectures for the machine learning models. In the last step, the optimization is performed by adopting the surrogate model to evaluate the objective function. The details of this implementation are presented below.

3.1 Geometrical parametrization (step 1)

Each panel (unit cell) is modeled by adopting a finite element strategy developed in MATLAB’s Structural Dynamics Toolbox (SDT) (Lieven, 2013). Then, the periodic boundary conditions are imposed, and the band diagrams are generated. The central frequency and width of the main band gap are then extracted from the band diagram, as shown in Figure 5.

Figure 5

Figure 5. Scheme of a parameterized FE model.

Now, let ${∆\omega }_n$, ${\mathrm{\omega }}_n$, and ${\mathrm{\omega }}_{n+1}$ denote the frequency gap between bands $n$ and $n+1$, the vector containing the frequencies of band $n$, and the vector containing the frequencies of band $n+1$, respectively. Then, ${∆\omega }_n$ is determined by the difference between the minimum value in ${\mathrm{\omega }}_{n+1}$ and the maximum value in ${\mathrm{\omega }}_n$:

${∆\omega }_n=\min {\mathbf{\omega }}_{n+1}-\max {\mathbf{\omega }}_n(3)$

It is important to note that ${∆\omega }_n$ can be negative, indicating the absence of a gap between the bands. Adopting this definition, the main band gap width is obtained by:

${∆\omega }_{n^{*}}=\max \left({∆\omega }_1,{∆\omega }_2,\dots ,{∆\omega }_N\right)(4)$

Here, $n^{*}$ represents the index of the maximum gap. It is worth mentioning that a band gap exists as long as ${∆\omega }_{n^{*}}$ is positive. For any other case, the structure does not present band gaps.

The central frequency is defined as:

${\omega }_{n^{*}}=\frac{\min {\mathbf{\omega }}_{n^{*}+1}+\max {\mathbf{\omega }}_{n^{*}}}{2}(5)$

Ultimately, the parametrization facilitates the identification of ${∆\omega }_{n^{*}}$ and ${\omega }_{n^{*}}$ as an implicit function of the geometrical attributes of the sandwich panel.

3.2 Datasets generation (step 2)

Two datasets are created here to train and test the machine learning models. These datasets are constructed for each core topology using various combinations of FE model parameters, which correspond to the length of the cell and the radius of the six struts defined previously in Figure 3. From now on, this geometrical model parameters are denoted as $\mathbf{x}$. The Latin Hypercube sampling technique is employed to generate a set of model parameters using the range presented in Table 1. Each sample of model parameters is used to identify the band gap width and its central value. In this study, ten thousand samples are generated for each core topology.

The dataset is normalized using a max-min normalization, a crucial step in machine learning. Data normalization standardizes the scale and distribution of features, ensuring fairness, preventing biases, equalizing feature importance, and enhancing the convergence and stability of models (Cabello-Solorzano et al., 2023). After normalization, the input and output pairs fall within the range of zero to one. Finally, the dataset for each topology is divided into training and validation datasets.

3.3 Training machine learning models (step 3)

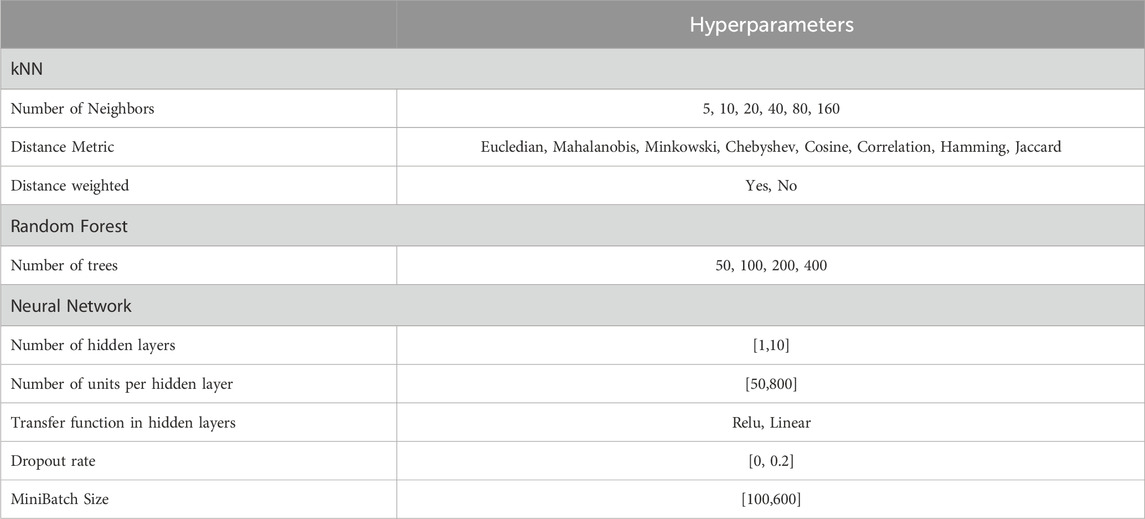
Here, machine learning models’ architectures are selected using a random search or grid search strategy, in which the training database is used to train the models, and the validation dataset is employed to evaluate their performance. This process aids in selecting the most suitable network architecture and ensures that the models have been adequately trained and validated before being used as a surrogate model. In particular, three machine learning algorithms are used: kNN, RFR, and ANN (refer to the Supplementary Appendix for an in-depth discussion on these algorithms).

The hyperparameters of the kNN and RFR algorithms were selected using a grid search technique, which involved defining a grid of predefined values for each hyperparameter and evaluating the model’s performance for each combination. On the other hand, ANNs often have a high number of hyperparameters, which makes exhaustively evaluating all possible combinations infeasible using a grid search. To overcome this challenge, a random search approach was employed instead. The random search allows for more efficient exploration of the hyperparameter space, making it practical to evaluate a diverse set of hyperparameter combinations without considering every possible combination. Ultimately, the trained machine learning model approximates ${∆\omega }_{n^{*}}$ and ${\omega }_{n^{*}}$ for a new given model parameter $\mathbf{x}$. The approximations for ${∆\omega }_{n^{*}}$ and ${\omega }_{n^{*}}$ after max-min normalization are denoted as ${∆\stackrel{\sim }{\omega }}_S\left(\mathbf{x}\right)$ and ${\stackrel{\sim }{\omega }}_S\left(\mathbf{x}\right)$, respectively.

3.4 Optimization based on surrogate models (step 4)

The last step of the process involves surrogate optimization, where the goal is to identify a configuration with a band gap centered around a target frequency while maximizing its width. To accomplish this, PSO is employed along with the following formulation that guides the optimization process:

${\mathbf{x}}^{*}=\underset{\mathbf{x}}{\min }\alpha \left|{\stackrel{\sim }{\omega }}_S\left(\mathbf{x}\right)-{\stackrel{\sim }{\omega }}_{target}\right|-\left(1-\alpha \right){∆\stackrel{\sim }{\omega }}_S\left(\mathbf{x}\right)(6)$

Here, ${\stackrel{\sim }{\omega }}_{target}$ denotes the target central frequency, also normalized using the same max-min normalization as the training database. The constant $\alpha$ is utilized to control the relative importance of each term in the objective function. It is important to note that the central frequency and the band gap width are expected to fall within the range of values between zero and one, as they have been normalized. Please refer to the Supplementary Appendix for a detailed explanation of the PSO optimization method.

The solution given by the surrogate PSO optimization is only an approximation to the true optimum and, therefore, can be improved. This improvement is achieved by refining the surrogate model with new sample points. The process involves evaluating the optimal design variables ${\mathbf{x}}^{*}$ with the surrogate and the high-fidelity (FE) models. The optimization process can be terminated if the difference between them is below a certain threshold. Otherwise, new sample points are added to the training dataset, and the surrogate model is rebuilt. This process is repeated until the differences between models meet the stopping threshold (ε), as shown in Figure 6. This process is known as a bi-level surrogate optimization framework (Han and Zhang, 2012). The error function used to compare the solution with both the surrogate and the high-fidelity models is the following:

$E\left({\mathbf{x}}^{*}\right)=‖{\stackrel{\sim }{\omega }}_S\left({\mathbf{x}}^{*}\right)-{\stackrel{\sim }{\omega }}_T\left({\mathbf{x}}^{*}\right)‖+‖∆{\stackrel{\sim }{\omega }}_S\left({\mathbf{x}}^{*}\right)-∆{\stackrel{\sim }{\omega }}_T\left({\mathbf{x}}^{*}\right)‖(7)$

where ${\stackrel{\sim }{\omega }}_T\left(\mathbf{x}\right)$ and ${∆\stackrel{\sim }{\omega }}_T\left(\mathbf{x}\right)$ correspond to the central frequency and width obtained from the high-fidelity model and have undergone max-min normalization, respectively.

Figure 6

Figure 6. Flowchart of the surrogate-based optimization with a bi-level framework.

4 Performance of the proposed framework

4.1 Finite element models and databases

In the high-fidelity model (FE), the skins are modeled using four-node shell elements, each having five degrees of freedom per node. Similarly, the struts are modeled using beam elements, with two nodes per element and six degrees of freedom per node. Both skins and struts are defined by the material and geometrical properties outlined in Table 1, ensuring consistency in model parameters. The interface between struts and skins is assumed to be a rigid connection, simplifying the interaction for the sake of analysis without sacrificing significant accuracy in the overall model’s response, The size of the elements is determined through a mesh refinement process to control accuracy. The skins are discretized using a 12 × 12 arrangement of shell elements, while each strut is modeled using two beam elements; this mesh is represented in Figure 7.

Figure 7

Figure 7. Representation of the mesh for the different topologies studied. (A) Central zig-zag. (B) Pyramidal. (C) Double Pyramidal.

In these FE models, periodic boundary conditions are applied at the edges of the skins. This approach effectively simulates the behavior of an infinite lattice by considering the repetitive nature of the unit cells. Once these boundary conditions are imposed, the eigenvalue problem for each wavevector in the Irreducible Brillouin Zone (IBZ) is tackled using the Lanczos algorithm. Band diagrams are computed following the methodology described in section 2.1. This analysis allows for the determination of the band gap width and central frequency using Eqs 4, 5, respectively.

Figure 8 presents the distribution of band gaps obtained for the ten thousand samples of each topology, displaying the normalized band gap width against the central frequency. In this case, the normalized band gap width is calculated by dividing the band gap width by the central frequency.

Figure 8

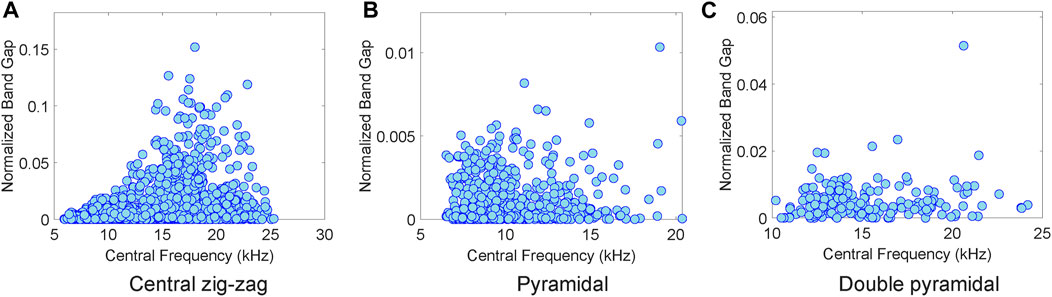
Figure 8. Distribution of band gaps in the numerical database. The central zig-zag topology displays the largest band gaps, succeeded by the double pyramidal configuration. In contrast, the pyramidal topology demonstrates comparatively narrower band gaps. (A) Central zig-zag. (B) Pyramidal. (C) Double Pyramidal.

Notably, out of the ten thousand model parameter combinations, only a few exhibit band gaps. For the central zig-zag topology, approximately 20.6% of the cases in the numerical database demonstrate band gaps. This proportion decreases to 6.6% for the pyramidal topology and reduces further to 1.9% for the double pyramidal core. Furthermore, the results depicted in Figure 8 indicate that the central zig-zag topology yields the most significant band gaps, followed by the double pyramidal topology, while the pyramidal topology exhibits relatively smaller band gaps.

4.2 Surrogate models

The numerical database was divided into training and validation databases, consisting of nine thousand and one thousand cases, respectively. All combinations of parameters were considered, even those without band gaps. This decision was made to ensure a smooth transition during the optimization process, gradually moving from cases with no band gap towards ones that approach the presence of a band gap.

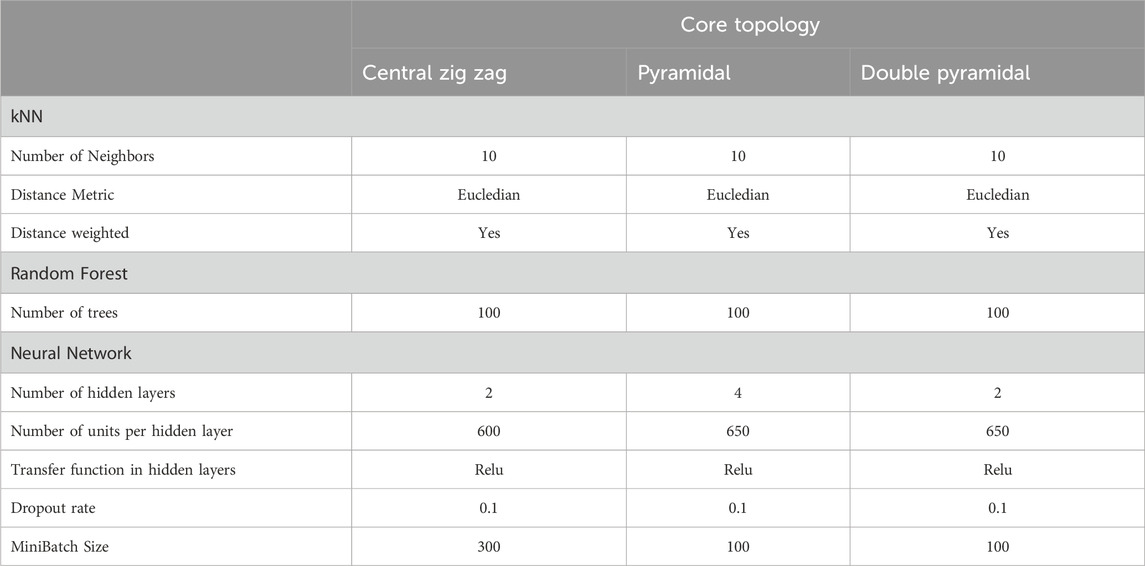
Table 2 lists the hyperparameter values evaluated for fine-tuning the three machine learning models employed. Meanwhile, Table 3 summarizes the optimal hyperparameters chosen through grid search for the kNN and Random Forest models and via random search for the ANN models. Interestingly, there is a notable consistency in the optimal hyperparameters across these models.

Table 2

Table 2. Hyperparameter values evaluated for fine-tuning.

Table 3

Table 3. Selected model’s hyperparameters.

Despite the structural differences, the datasets for the three core topologies share similar underlying characteristics and behaviors, which play a crucial role in the notable consistency of optimal hyperparameters across different modeled structures. This commonality suggests that the fundamental principles governing their behavior are similar, leading to a uniform response from each machine learning algorithm to the datasets. Consequently, this results in a consistent selection of optimal hyperparameters within each algorithm across the structures. To mitigate concerns of bias in hyperparameter selection, the grid search was carefully designed to comprehensively explore the hyperparameter space (as shown in Table 2), ensuring an effective and unbiased optimization process.

Figure 9 depicts the Root Mean Square Error (RMSE) associated with the model’s prediction for the band gap width and central frequency. The performance of the random forest method is notably inferior compared to the other methods when predicting the central frequency, while its performance is comparable when predicting the width of the band gap. The kNN model performs best for the central zig-zag topology, exhibiting the lowest RMSE. On the other hand, for the pyramidal and double pyramidal topologies, the NN model demonstrates superior predictive capability, resulting in lower RMSE values.

Figure 9

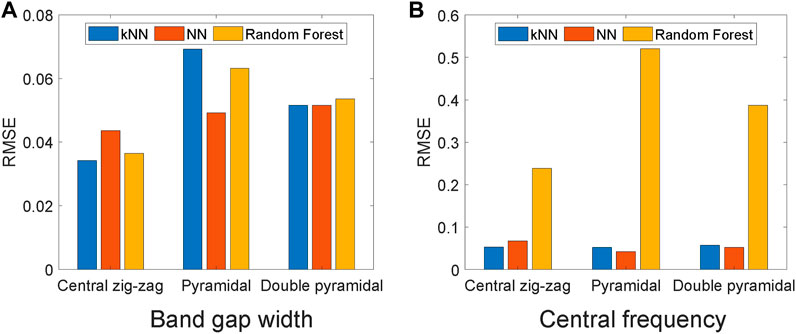
Figure 9. Comparison of Root Mean Square Error (RMSE) across models. The kNN and NN models exhibit lower prediction errors with comparable results. (A) Band gap width. (B) Central frequency.

As an illustrative example, Figure 10 showcases the prediction results of the surrogate model for the pyramidal core topology. While a clear correlation exists between the actual and predicted values, the coefficient of determination (R²) suggests potential enhancement. This observation supports the need for implementing a bi-level subrogate optimization strategy. By adopting this approach, the surrogate model can be enhanced with additional sample points in the proximity as the optimization process progresses towards the optimum solution. This iterative improvement of the surrogate model allows for a more accurate representation of the underlying system, ultimately leading to improved optimization results.

Figure 10

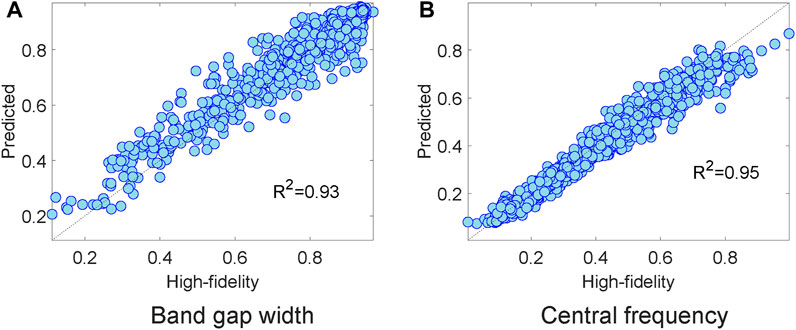
Figure 10. The band gap width and central frequency, normalized using the max-min method, are presented for the pyramidal core topology. A clear correlation between the actual and predicted values is evident. However, the coefficient of determination (R2) indicates potential for improvement. (A) Band gap width. (B) Central frequency.

4.3 Surrogate optimization

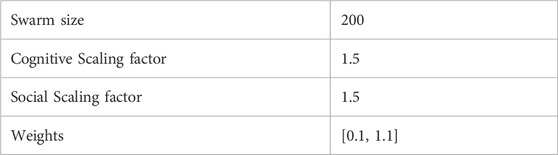
The optimization is performed using PSO, the specific configuration of the algorithm can be found in Table 4. These settings were determined through grid search considering different combinations of parameters. The maximum stall generation parameter is employed to establish a stopping criterion. In this context, the PSO optimization halts if there is no noticeable enhancement in the best solution after 20 generations. This safeguard ensures that the optimization process concludes if no significant progress is observed within the specified number of iterations. In Eq. (12), the parameter α was assigned a value of 0.7. This value was determined through a pareto frontier testing to achieve a balance between the width of the band gap and its central frequency. The aim was to ensure a large band gap width, with the central frequency deviating no more than 5% from the desired target.

Table 4

Table 4. PSO settings.

Figure 11 presents the Pareto frontier for a zig-zag core system, targeting an operational frequency of 15 kHz. It illustrates the optimal trade-offs between the first and second objective terms under varying α values. The red vertical line highlights a 5% deviation from the target frequency, delineating the limit for acceptable solution variation. This analysis is crucial for selecting solutions that adeptly minimize the second objective term—essentially maximizing the band gap width—while maintaining the mean band gap frequency close to the desired target. In this scenario, achieving this balance is accomplished with an α value of 0.7. The optimization was conducted to target three specific frequencies: 1.2, 1.5, and 1.8 kHz, all of which lie within the band gaps observed in the training databases. Since the kNN and ANN models displayed similar outcomes for the three structures examined, it was decided to compare their efficiency during the optimization. Figure 12 illustrates the band gaps achieved post-optimization using ANN surrogate optimization (ANN SO) and kNN surrogate optimization (kNN SO), juxtaposed against the band gaps from the training database. This comparison assesses whether the optimization yields superior results than the cases in the database.

Figure 11

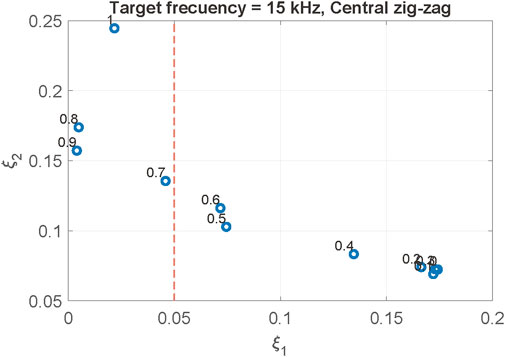
Figure 11. Pareto frontier analysis for multiobjective optimization per Eq. 6, showcasing optimal trade-offs between ξ₁ (first objective term) and ξ₂ (second objective term) for varying values of the constant α. The red vertical line indicates a 5% deviation from the target frequency.

Figure 12

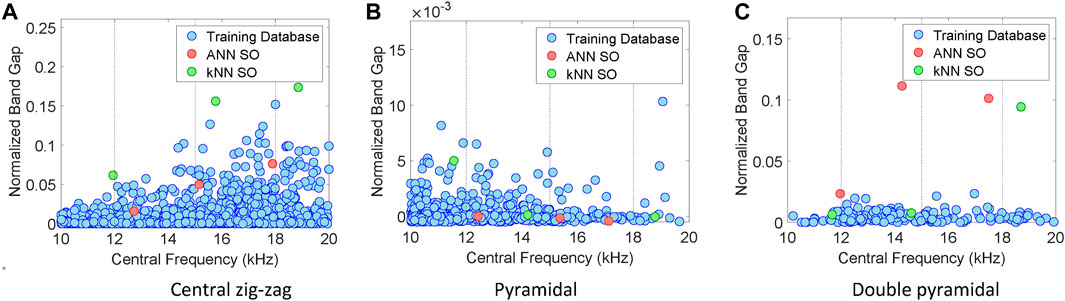
Figure 12. Comparison of band gaps derived from ANN surrogate optimization (ANN SO) and kNN surrogate optimization (kNN SO) with those in the training database. While the central zig-zag and double pyramidal topologies exhibit significant post-optimization improvements in band gap widths, the pyramidal topology remains largely unchanged. (A) Central zig-zag. (B) Pyramidal. (C) Double Pyramidal.

Upon examining the results in Figure 12, when we compare the band gap widths obtained after optimization to those in the database, we see some clear improvements for the central zig-zag and double pyramidal topologies. For band gaps close to the target average frequency (within a 5% difference), the designs from kNN SO with a zig-zag pattern are 1.3, 1.2, and 1.1 times wider than the training database. Meanwhile, designs from ANN SO with a double pyramid shape have band gaps that are 1.2, 5.2, and 8.3 times the database’s sizes. Conversely, the pyramidal structure did not fare well, with its optimal results not surpassing the database’s. The band gaps in the pyramidal model are narrow, closely mirroring the surrogate model’s error magnitude, which inherently challenges the optimization.

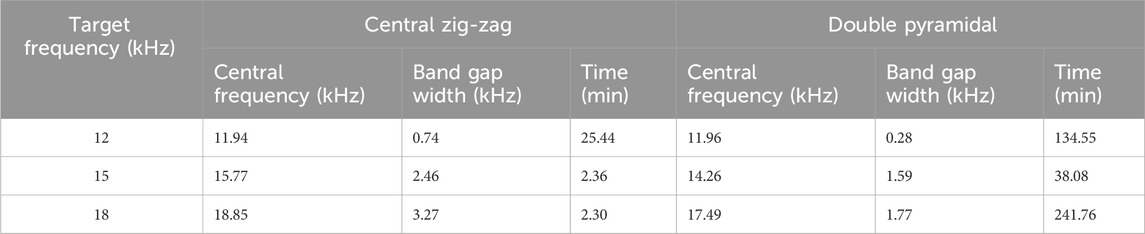
Given that the pyramidal structure did not yield significant band gaps in the training database and during optimization, the detailed analysis will concentrate on the remaining two cases. Convergence curves for the bi-level surrogate optimization strategy across the central zig-zag and double pyramidal structures for all target frequencies are depicted in Figure 13. A distinct disparity in convergence speed is evident between the two models. The central zig-zag model converges rapidly, ranging between 1 and 17 iterations, whereas the double pyramidal model requires up to 110 iterations for its convergence error to gradually meet the stopping criteria. This variation in convergence rate appears to be influenced by the choice of the machine learning model, either kNN or NN. This is reflected in the optimization times presented in Table 5, where it is evidenced that wider band gaps are obtained in the case of the central zig-zag in shorter times.

Figure 13

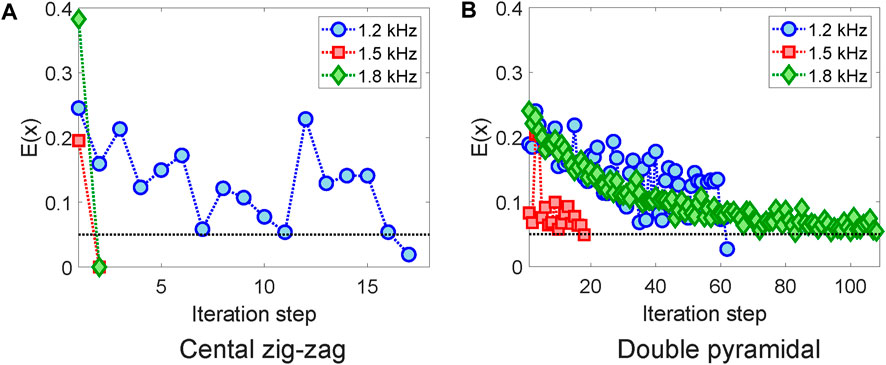
Figure 13. Convergence curves of the bi-level surrogate optimization strategy. A notable difference in convergence speed can be observed between the two topologies, potentially attributed to the selection of the machine learning model, whether kNN or NN. (A) Central zig-zag. (B) Pyramidal.

Table 5

Table 5. Surrogate optimization results.

Optimizing directly with a finite element model demands extensive computational resources, specifically about 12,000 evaluations per target frequency, underlining the method’s high computational demand. This process, requiring approximately 18,000 min, is as time-consuming as creating the surrogate model’s training database. However, the real advantage of the surrogate model lies in its efficiency post-initial setup. It allows for quick adaptation to new frequencies or objectives without redoing all evaluations. This makes it exceptionally efficient for producing various designs rapidly. In addition, the bi-level surrogate optimization further enhances precision by aligning the surrogate model’s outcomes with the high-fidelity model’s results, ensuring accurate design optimization across different frequencies.

Figure 14 displays the band diagrams corresponding to initial case where all struts have an equal radius of 1.6 mm and the cell length is set to 30, in comparison to the optimal solutions derived after optimization, clearly highlighting the distinct band gaps that manifest precisely at the predefined frequencies. This visualization underscores the efficacy of the optimization process in achieving the targeted vibration characteristics. Finally, Table 6 outlines the parameters of the structural model post-optimization for the central zig-zag topology. In every instance, elements at the cell’s center possess the maximum radius.

Figure 14

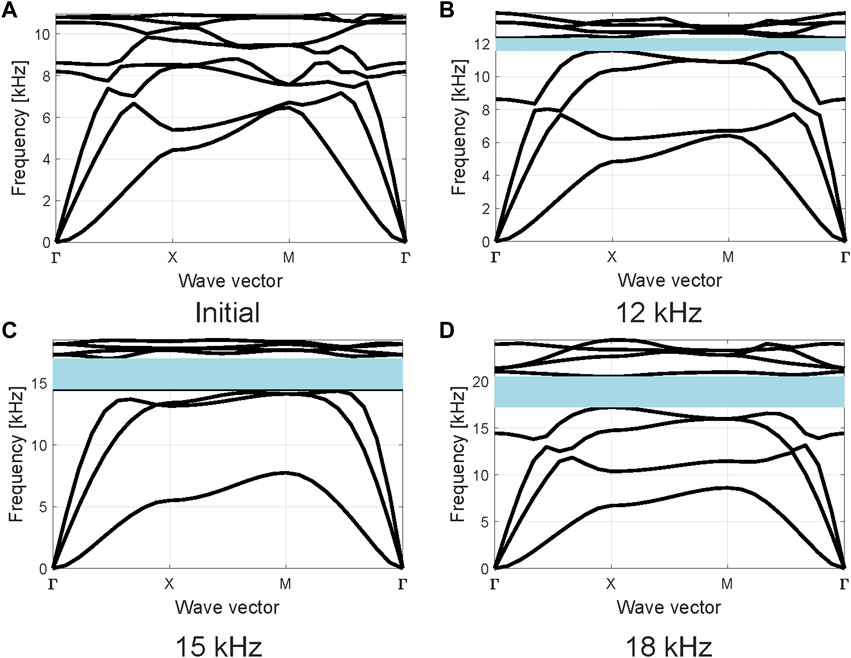
Figure 14. Band diagram comparisons for initial and optimized configurations in central zig-zag topology, (A) Initial configuration, (B) 12 kHz, (C) 15 kHz and (D) 18 kHz. The diagrams highlight the presence of distinct band gaps at specific target frequencies across three different optimization scenarios.

Table 6

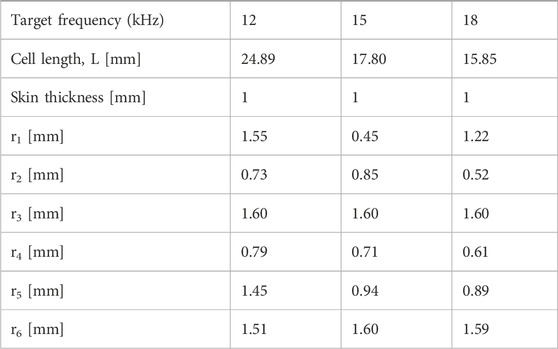
Table 6. Structural model’s parameters obtained after optimization for the central zig-zag topology.

5 Conclusion

This study introduces an effective strategy for designing sandwich panels with cellular truss cores that show large phononic band gaps. The objective was to implement different truss core designs to have band gaps at specific frequencies and as wide as possible. A combination of a surrogate model and a global optimization technique was employed to enhance and expedite the design process.

Finite element models of the sandwich panels were developed, focusing on three primary core designs: central zig-zag, pyramidal, and double pyramidal. Among the numerous combinations tested for each design, only a select few achieved the desired band gaps. Notably, the central zig-zag configuration proved superior, succeeding in approximately one-fifth of the trials and providing wider band gaps.

Surrogate models were constructed utilizing three machine learning algorithms: k-Nearest Neighbors (kNN), Random Forest Regression (RFR), and Artificial Neural Networks (ANNs). While the Random Forest showed proficiency in predicting the band gap width, its performance in forecasting the central frequency of the band gap was less consistent. Among the core designs, kNN excelled for the central zig-zag topology, whereas ANN was more suited for the pyramidal topology.

The surrogate models were combined with Particle Swarm Optimization (PSO) to enhance the designs. Notably, the central zig-zag and double pyramidal configurations saw marked improvements, with the band gap widths expanding between 1.1 and 8.3 times compared to those in the training database. In contrast, refining the pyramidal design proved challenging due to its limited band gaps. Post-optimization, the band diagrams revealed that the band gaps closely matched the chosen frequencies, showing less than a 5% deviation from the target central frequency. This underscores the efficacy of the proposed design approach.

It is worth noting that if only the finite element models were used, the optimization process could take considerable time - even weeks based on computational capabilities. Setting up a surrogate model takes about the same time at first. However, once it is set up, the surrogate model works faster and better, especially when we need different designs quickly. So, the optimization based on surrogate models is a convenient choice for projects where we need to try out many designs.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

VM: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. IP: Data curation, Formal Analysis, Investigation, Methodology, Validation, Writing–original draft, Writing–review and editing. RF: Formal Analysis, Methodology, Supervision, Writing–review and editing. RR: Formal Analysis, Methodology, Supervision, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The authors acknowledge the financial support provided by the Chilean National Fund for Scientific and Technological Development (FONDECYT) under grant No. 1210442.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2024.1329345/full#supplementary-material

References

Bacigalupo, A., Gnecco, G., Lepidi, M., and Gambarotta, L. (2020). Machine-learning techniques for the optimal design of acoustic metamaterials. J. Optim. Theory Appl. 187 (3), 630–653. doi:10.1007/s10957-019-01614-8

CrossRef Full Text | Google Scholar

Bailey, T. (1978). A note on distance-weighted k-nearest neighbor rules. Trans. Syst. Man, Cybern. 8, 311–313. doi:10.1109/TSMC.1978.4309958

CrossRef Full Text | Google Scholar

Bilal, O. R., and Hussein, M. I. (2011). Ultrawide phononic band gap for combined in-plane and out-of-Plane waves. Phys. Rev. E 84 (6), 065701. doi:10.1103/physreve.84.065701

PubMed Abstract | CrossRef Full Text | Google Scholar

Cabello-Solorzano, K., Araujo, I. O. D., Peña, M., Correia, L., and Tallón-Ballesteros, A. J. (2023). “The impact of data normalization on the accuracy of machine learning algorithms: a comparative analysis,” in 18th International Conference on Soft Computing Models in Industrial and Environmental Applications (SOCO 2023). doi:10.1007/978-3-031-42536-3_33

CrossRef Full Text | Google Scholar

Cool, V., Sigmund, O., Aage, N., Naets, F., and Deckers, E. (2024). Vibroacoustic topology optimization for sound transmission minimization through sandwich structures. J. Sound Vib. 568, 117959. doi:10.1016/j.jsv.2023.117959

CrossRef Full Text | Google Scholar

Dong, H. W., Su, X. X., and Wang, Y. S. (2014). Multi-objective optimization of two-dimensional porous phononic crystals. J. Phys. D Appl. Phys. 47, 155301. doi:10.1088/0022-3727/47/15/155301

CrossRef Full Text | Google Scholar

Dong, J., Qin, Q.-H., and Yi, X. (2020). Nelder–Mead optimization of elastic metamaterials via machine-learning-aided surrogate modeling. Int. J. Appl. Mech. 12 (01), 2050011. doi:10.1142/S1758825120500118

CrossRef Full Text | Google Scholar

Eberhart, R., and Kennedy, J. (1995). “A new optimizer using particle swarm theory,” in MHS’95. Proceedings of the sixth international symposium on micro machine and human science (Nagoya, Japan: IEEE), 39–43. doi:10.1109/MHS.1995.494215

CrossRef Full Text | Google Scholar

Fan, Li, Yang, X. H., Meng, F., and Zhou, S. (2016). Evolutionary topological design for phononic band gap crystals. Struct. Multidiscip. Optim. 54 (3), 595–617. doi:10.1007/s00158-016-1424-3

CrossRef Full Text | Google Scholar

Gad, A. G. (2022). Particle swarm optimization algorithm and its applications: a systematic review. Archives Comput. Methods Eng. 29 (5), 2531–2561. doi:10.1007/s11831-021-09694-4

CrossRef Full Text | Google Scholar

Gazonas, G. A., Weile, D. S., Wildman, R., and Mohan, A. (2006). Genetic algorithm optimization of phononic bandgap structures. Int. J. Solids Struct. 43 (18–19), 5851–5866. doi:10.1016/j.ijsolstr.2005.12.002

CrossRef Full Text | Google Scholar

Gazzola, C., Caverni, S., and Corigliano, A. (2022). Design and modeling of a periodic single-phase sandwich panel for acoustic insulation applications. Front. Mater. 9, 1005615. doi:10.3389/fmats.2022.1005615

CrossRef Full Text | Google Scholar

Guo, J. C., and Zhang, Z. (2022). Mass inertia moment-based design of band gap characteristics in zigzag beam-supported stepped phononic crystals. Appl. Phys. A 128 (2), 126. doi:10.1007/s00339-022-05267-9

CrossRef Full Text | Google Scholar

Guo, Z., Hu, G., Jiang, J., Yu, L., Li, X., and Liang, J. (2021). Theoretical and experimental study of the vibration dynamics of a 3D-printed sandwich beam with an hourglass lattice truss core. Front. Mech. Eng. 7, 651998. doi:10.3389/fmech.2021.651998

CrossRef Full Text | Google Scholar

Gurbuz, C., Kronowetter, F., Dietz, C., Eser, M., Schmid, J., and Marburg, S. (2021). Generative adversarial networks for the design of acoustic metamaterials. J. Acoust. Soc. Am. 149 (2), 1162–1174. doi:10.1121/10.0003501

PubMed Abstract | CrossRef Full Text | Google Scholar

Hagan, M. T., Demuth, H. B., Beale, M. H., and Jesús, O.De (2014). Neural network design. 2nd Edition.

Google Scholar

Han, Z.-H., and Zhang, K.-S. (2012). “Surrogate-based optimization,” in Real-world applications of genetic algorithms. Editor O. Roeva (Editorial InTechOpen London, UK: Books on Demand), 343–362.

CrossRef Full Text | Google Scholar

Hedayatrasa, S., Abhary, K., Uddin, M., and Ng, C.-T. (2016b). Optimum design of phononic crystal perforated plate structures for widest bandgap of fundamental guided wave modes and maximized in-plane stiffness. J. Mech. Phys. Solids 89, 31–58. doi:10.1016/j.jmps.2016.01.010

CrossRef Full Text | Google Scholar

Hedayatrasa, S., Abhary, K., Uddin, M. S., and Guest, J. K. (2016a). Optimal design of tunable phononic bandgap plates under equibiaxial stretch. Smart Mater. Struct. 25 (5), 055025. doi:10.1088/0964-1726/25/5/055025

CrossRef Full Text | Google Scholar

Hussein, M. I., Leamy, M. J., and Ruzzene, M. (2014). Dynamics of phononic materials and structures: historical origins, recent progress, and future outlook. Appl. Mech. Rev. 66 (4), 040802. doi:10.1115/1.4026911

CrossRef Full Text | Google Scholar

Jensen, J. S. (2003). Phononic band gaps and vibrations in one- and two-dimensional mass–spring structures. J. Sound Vib. 266 (5), 1053–1078. doi:10.1016/S0022-460X(02)01629-2

CrossRef Full Text | Google Scholar

Kladovasilakis, N., Tsongas, K., Karalekas, D., and Tzetzis, D. (2022). Architected materials for additive manufacturing: a comprehensive review. Materials 15 (17), 5919. doi:10.3390/ma15175919

PubMed Abstract | CrossRef Full Text | Google Scholar

Kramer, O. (2013). “K-nearest Neighbors,” in Dimensionality Reduction with unsupervised nearest Neighbors. Intelligent systems reference library 51 (New York: Springer).

CrossRef Full Text | Google Scholar

Kudela, P., Ijjeh, A., Radzienski, M., Miniaci, M., Pugno, N., and Ostachowicz, W. (2023). Deep learning aided topology optimization of phononic crystals. Mech. Syst. Signal Process. 200, 110636. doi:10.1016/j.ymssp.2023.110636

CrossRef Full Text | Google Scholar

Li, X., Ning, S., Liu, Z., Yan, Z., Luo, C., and Zhuang, Z. (2020). Designing phononic crystal with anticipated band gap through a deep learning based data-driven method. Comput. Methods Appl. Mech. Eng. 361, 112737. doi:10.1016/j.cma.2019.112737

CrossRef Full Text | Google Scholar

Liebold-Ribeiro, Y., and Körner, C. (2014). Phononic band gaps in periodic cellular materials: phononic band gaps in periodic cellular materials. Adv. Eng. Mater. 16 (3), 328–334. doi:10.1002/adem.201300064

CrossRef Full Text | Google Scholar

Lieven, N. A. J. (2013). Structural dynamics Toolbox primer. Bristol, UK: SDTools.

Google Scholar

Liu, J.-S., and Lu, T. J. (2004). Multi-objective and multi-loading optimization of ultralightweight truss materials. Int. J. Solids Struct. 41 (3–4), 619–635. doi:10.1016/j.ijsolstr.2003.10.003

CrossRef Full Text | Google Scholar

Liu, T., Deng, Z. C., and Lu, T. J. (2006). Design optimization of truss-cored sandwiches with homogenization. Int. J. Solids Struct. 43 (25–26), 7891–7918. doi:10.1016/j.ijsolstr.2006.04.010

CrossRef Full Text | Google Scholar

Liu, Z., Wu, B., and He, C. (2014). Band-gap optimization of two-dimensional phononic crystals based on genetic algorithm and FPWE. Waves Random Complex Media 24 (3), 286–305. doi:10.1080/17455030.2014.901582

CrossRef Full Text | Google Scholar

Maldovan, M. (2013). Sound and heat revolutions in phononics. Nature 503 (7475), 209–217. doi:10.1038/nature12608

PubMed Abstract | CrossRef Full Text | Google Scholar

Muhammad, J. K., and Lim, C. W. (2022). Machine learning and deep learning in phononic crystals and metamaterials – a review. Mater. Today Commun. 33, 104606. doi:10.1016/j.mtcomm.2022.104606

CrossRef Full Text | Google Scholar

Nayak, J., Swapnarekha, H., Naik, B., Dhiman, G., and Vimal, S. (2023). 25 Years of particle swarm optimization: flourishing voyage of two decades. Archives Comput. Methods Eng. 30 (3), 1663–1725. doi:10.1007/s11831-022-09849-x

CrossRef Full Text | Google Scholar

Poli, R., Kennedy, J., and Blackwell, T. (2007). Particle swarm optimization: an overview. Swarm Intell. 1 (1), 33–57. doi:10.1007/s11721-007-0002-0

CrossRef Full Text | Google Scholar

Prasath, V. B. S., Arafat Abu Alfeilat, H., Hassanat, A. B. A., Lasassmeh, O., Tarawneh, A. S., Alhasanat, M. B., et al. (2019). Effects of distance measure choice on K-nearest neighbor classifier performance: a review. Big Data 7 (4), 221–248. doi:10.1089/big.2018.0175

PubMed Abstract | CrossRef Full Text | Google Scholar

Quinteros, L., Meruane, V., and Cardoso, E. L. (2021a). Phononic band gap optimization in truss-like cellular structures using smooth P-norm approximations. Struct. Multidiscip. Optim. 64 (1), 113–124. doi:10.1007/s00158-021-02862-x

CrossRef Full Text | Google Scholar

Quinteros, L., Meruane, V., Cardoso, E. L., and Ruiz, R. O. (2021b). Phononic bandgap optimization in sandwich panels using cellular truss cores. Materials 14 (18), 5236. doi:10.3390/ma14185236

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruzzene, M., and Scarpa, F. (2005). Directional and band-gap behavior of periodic auxetic lattices. Phys. Status Solidi (b) 242 (3), 665–680. doi:10.1002/pssb.200460385

CrossRef Full Text | Google Scholar

Schaedler, T. A., and Carter, W. B. (2016a). Architected cellular materials. Annu. Rev. Mater. Res. 46, 187–210. doi:10.1146/annurev-matsci-070115-031624

CrossRef Full Text | Google Scholar

Schaedler, T. A., and Carter, W. B. (2016b). Architected cellular materials. Annu. Rev. Mater. Res. 46 (1), 187–210. doi:10.1146/annurev-matsci-070115-031624

CrossRef Full Text | Google Scholar

Sun, L., Li, J., and Xiao, Y. (2021). Broad and low frequency bandgap in truss core sandwich beam. Mech. Solids 56 (3), 421–429. doi:10.3103/S0025654421030122

CrossRef Full Text | Google Scholar

Tikani, V., Ziaei-Rad, S., and Moosavi, H. (2023). Bandgap and wave attenuation optimization of tetra-chiral metamaterial using PSO algorithm. J. Vib. Control, 10775463231177489. doi:10.1177/10775463231177489

CrossRef Full Text | Google Scholar

Wang, P., Casadei, F., Kang, S. H., and Bertoldi, K. (2015). Locally resonant band gaps in periodic beam lattices by tuning connectivity. Phys. Rev. B 91 (2), 020103. doi:10.1103/PhysRevB.91.020103

CrossRef Full Text | Google Scholar

Warmuth, F., and Körner, C. (2015). Phononic band gaps in 2D quadratic and 3D cubic cellular structures. Materials 8 (12), 8327–8337. doi:10.3390/ma8125463

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, C., Li, Z., Xu, P., Huang, H., Huo, Y., and Wei, Y. (2024). Prediction method of impact deformation mode based on multimodal fusion with point cloud sequences: applied to thin-walled structures. Adv. Eng. Inf. 59, 102238. doi:10.1016/j.aei.2023.102238

CrossRef Full Text | Google Scholar

Yang, C., Meng, K., Yang, L., Guo, W., Xu, P., and Zhou, S. (2023a). Transfer learning-based crashworthiness prediction for the composite structure of a subway vehicle. Int. J. Mech. Sci. 248, 108244. doi:10.1016/j.ijmecsci.2023.108244

CrossRef Full Text | Google Scholar

Yang, C., Yang, L., Guo, W., and Xu, P. (2023b). Deep learning based structural damage identification for the strain field of a subway bolster. Alexandria Eng. J. 81, 264–283. doi:10.1016/j.aej.2023.09.031

CrossRef Full Text | Google Scholar

Yi, G., Shin, Y. C., Yoon, H., Jo, S., and Youn, B. D. (2019). Topology optimization for phononic band gap maximization considering a target driving frequency. JMST Adv. 1 (1–2), 153–159. doi:10.1007/s42791-019-00019-y

CrossRef Full Text | Google Scholar