- 1Beijing Power Machinery Institute, Beijing, China
- 2HIWING Technology Academy of CASIC, Beijing, China
- 3Research Institute of Aero-Engine, Beihang University, Beijing, China
- 4National Key Laboratory of Science and Technology on Aero-Engine and Aero-Thermodynamics, Beihang University, Beijing, China
A pre-cooled combined engine based on a closed helium (He) cycle offers high specific thrust and high specific impulse. Therefore, evaluation of the performance of such an engine is crucial for engine applications and key technology research. This study employs an analytical approach to investigate the effects of key parameters on the performance of a pre-cooled core engine, assuming a perfect gas model. The findings revealed that the specific thrust and specific impulse of the pre-cooled core engine are related to the pressurized coefficient of the airflow passage and equivalence ratio (ER). An increase in the pressurized coefficient leads to an increase in both specific thrust and specific impulse. However, within a certain range, although the specific thrust is positively correlated with the ER, the specific impulse is greatly reduced. With specific component parameters and a fixed thermodynamic cycle, a minimum ER exists, which satisfies the cycle-matching requirement. Moreover, the value of the minimum ER is related to the closed-cycle efficiency. For a pre-cooled core engine with a simple closed He cycle, the minimum ER is approximately 2.5–3.5.
1 Introduction
In recent years, the concept of reusable hypersonic vehicles in near space has attracted considerable research attention (Crawford, 2016; Yixiang, 2016). The key technology for such vehicles is a combined engine operable across a wide range of Mach numbers (Wen-hui, 2018; Xuhui, 2020). Inlet flow pre-cooling is an important way to broaden the operating Mach number range of an engine. Several countries have conducted a considerable amount of preliminary research on pre-cooled cycle engines. Among them, the “Synergetic Air-Breathing Rocket Engine” (SABRE) series and Scimitar engine concepts proposed by the British company Reaction Engines have received worldwide attention owing to their superior performance (Varvill and Bond, 2003; Jivraj, 2004). As shown in Figure 1, the SABRE4 and Scimitar schemes evolved from the early SABRE3 scheme by adding bypass and reheating components to improve the cruise-specific impulse of the engine and solve a frost problem in the pre-cooler (Jivraj, 2004; Hempsell, 2010).
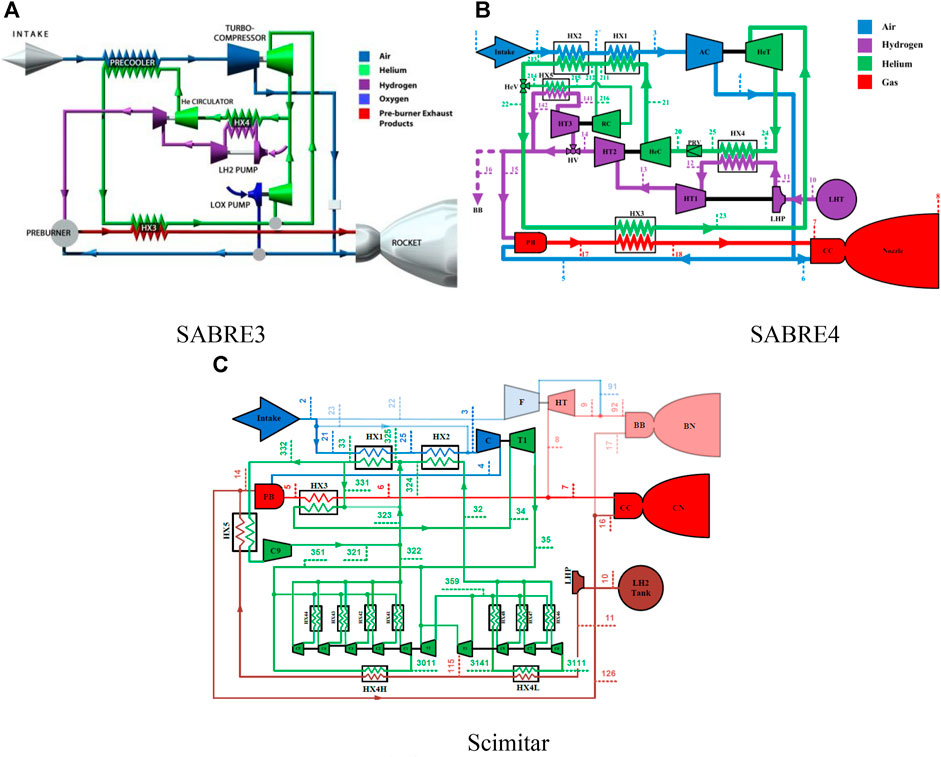
FIGURE 1. “Synergetic Air-Breathing Rocket Engine” (SABRE) and Scimitar engine cycles. HX1∼2, Precooler; AC/C, Air Compressor; HeT/T1, Helium Turbine; HX3, Gas/Helium Heat Exchanger; HX4/HX4H/HX4L/HX5, Hydrogen/Helium Heat Exchanger; HX41∼48, Helium Cycle Regenerator; HeV, Confluence Valve; HeC/C1∼9, Helium Compressor; RC, Recycle Compressor; PRV, Pressure Recovery Valve; LHT, Liquid Hydrogen Tank; LHP, Liquid Hydrogen Pump; HT1∼3, Hydrogen Turbine; HV, Hydrogen Valve; BB, Bypass Burner; PB, Pre-burner; CC, Core Combustor; CN, Core Nozzle; BN, Bypass Nozzle; F, Bypass fan; HT, Gas Turbine.
With continuous breakthroughs in key technologies and positive evaluation results from the United States Air Force Research Laboratory (Zhicheng, 2015), the SABRE engine has attracted significant research and development funding and attention (Zy, 2015; E.S. Agency, 2011). Numerous research studies have been conducted on pre-cooling combined engines inspired by the progress of the SABRE engine (Zhengping, 2015; Zhang et al., 2017; Yuan, 2020; Zheng-ping, 2021). Fernández-Villacé and Paniagua (2013) indicated that a pre-cooled engine based on a closed cycle improves efficiency by recovering thermal energy from the freestream and aeroshell. However, the classic efficiency figures based on first-principle analyses were inaccurate performance indicators for the resulting combined cycle. Accordingly, the author defined an availability effectiveness parameter and then analyzed the Scimitar cycle, ultimately providing the availability loss distribution of the cycle at typical flight speeds. Zhang et al. (2017) conducted a classical availability analysis on the SABRE cycle and found that unburned hydrogen (H2) was the largest source of availability loss in the system. The equivalence ratio (ER) is the main influence on the cycle; it can be regulated by adjusting the parameters of the helium (He) cycle. Xuanfei (2020) argued that all pre-cooled engines could be simplified to a fundamentally similar cycle. The author proposed a unified cycle model and conducted a theoretical analysis. Then, the influences of the design parameters on the theoretical pressure ratio and engine performance were studied using numerical methods.
In general, existing research has mainly focused on the evolution and optimization of a pre-cooled engine’s thermodynamic cycle, such as the integration of a parallel heat return system. However, relatively few studies exist concerning the relationship between the performance of a pre-cooled engine and the parameters of its key components for a given thermodynamic cycle. Pre-cooled engines with closed cycles entail numerous components and intricate interrelationships among the coupled parameters. Such research would greatly aid in implementing an effective engine design. Accordingly, based on a simplified pre-cooled core engine model, this study analyzes the relationship between the key thermodynamic parameters and the specific thrust and specific impulse performance of the engine. Then, the relationships between the thermal efficiency of the closed He cycle and the parameters of the closed-cycle components are discussed.
2 Analysis of the pre-cooled core engine model
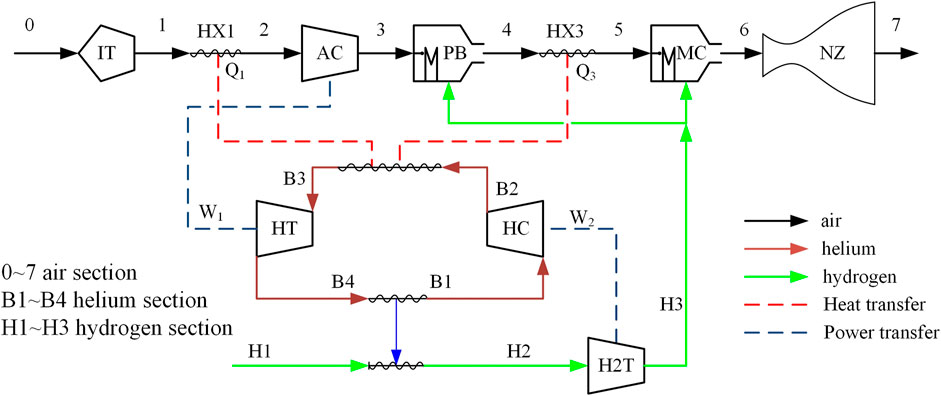
The SABRE3 scheme (as shown in Figure 2) includes air-breathing and rocket modes. The air-breathing mode includes a bypass combustor and the core engine (Varvill and Bond, 2008). This study focuses on analyzing the performance of the core engine in the air-breathing mode of SABRE3. The pre-cooled core engine model can be simplified, as discussed in detail in the following paragraphs.
The main parameters for evaluating the performance of the core engine are the specific thrust and specific impulse.
2.1 Specific thrust
For simplicity, it is assumed that the airflow at the outlet of the nozzle is fully expanded at the design point. The specific thrust can be expressed as follows:
Here,
Evidently, the specific thrust is related to three variables: the flight speed
The product of the total pressure recovery coefficients of each component from sections 0–7 is defined as
The total pressure of the airflow in Section 7 is given as
Here,
In the aforementioned expression,
Meanwhile, assuming
The fuel ER is defined as the ratio of the actual fuel-to-air mass ratio to the stoichiometric fuel-to-air mass ratio as follows:
The mass flow rate ratio between H2 and air is 1:34.5 when stoichiometric combustion occurs. Therefore,
Simplifying the aforementioned formulas and substituting them into the expression for specific thrust yields
The specific thrust of the engine is related to eight parameters (denoted by the superscript * for the total parameters and the superscript
In the aforementioned expression,
For H2 combustion in air with different ERs, the reaction equations are as follows:
Based on the relationships between the components and averaged parameters of the mixture, the average molecular weight of the combustion gas mixture under different ERs can be obtained as
The gas constant and adiabatic index of the gas mixture can be expressed as
In Eq. 16,
The value of
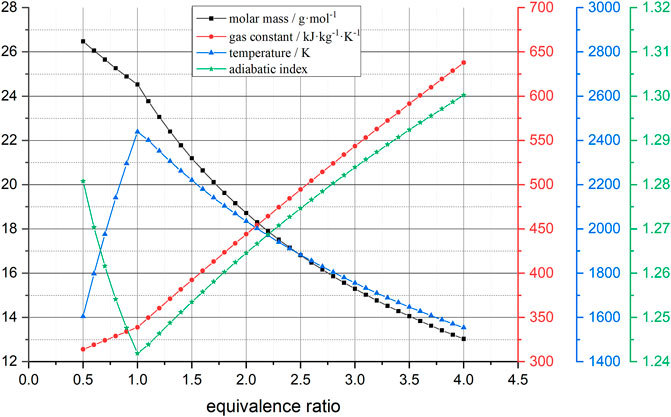
FIGURE 3. Relationships of gas parameters to equivalence ratio. When the quantity ratio is 1, the combustion temperature is the maximum.
The actual combustion temperature is lower than the theoretical combustion temperature owing to factors such as incomplete combustion and heat dissipation to the environment. Thus, the actual specific thrust is smaller than that obtained from the theoretical analysis. The effects of incomplete combustion and external heat dissipation are ignored to simplify the analysis. Therefore, the specific thrust can be expressed as follows:
At the design point,
A pressurized coefficient
Figure 4 shows the relationships between the specific thrust and pressurized coefficient, as well as between the specific thrust and ER. Compared to traditional turbojet and ramjet engines, the pre-cooled core engine, which uses an He turbine (HT) to drive the air compressor, does not expand the air through a gas turbine. This results in a significant increase in the total pressure at the nozzle exit, the specific thrust that is more than twice that of traditional air-breathing engines under similar cycle parameters.
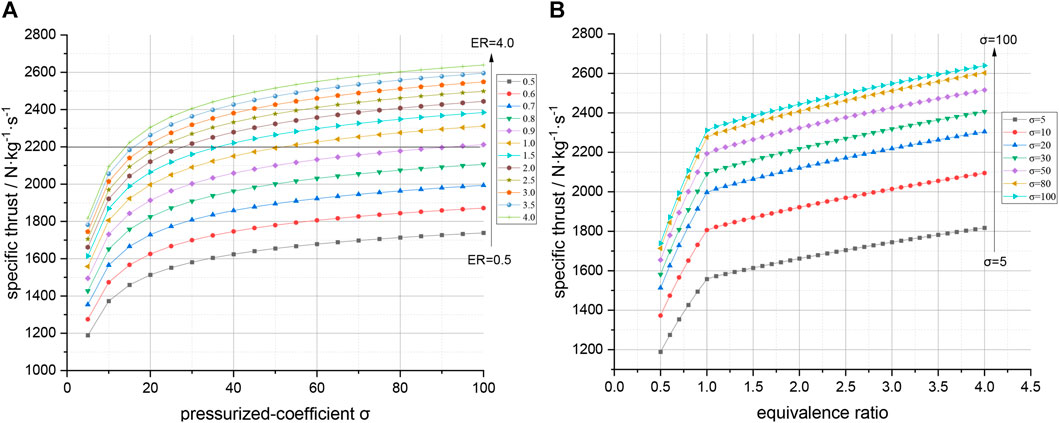
FIGURE 4. Relationships between specific thrust, pressurized coefficient, and equivalence ratio. (A) The specific thrust increases with an increase in the pressurized coefficient. (B) A positive correlation exists between the specific thrust and equivalence ratio within a certain range.
Figure 4A shows that the relationship between the pressurized coefficient and specific thrust is logarithmic. The specific thrust increases with an increase in the pressurized coefficient. At present, the engine with the highest total pressure ratio in the world is GE9X, with a total pressure ratio of 61. Considering the total pressure loss of each component of the airflow path, the pressurized coefficient is approximately 45. However, the pressurized coefficient needs to be considered in combination with the engine indicators and the difficulty of the component design.
Figure 4B shows that the trend of the specific thrust with the equivalent ratio has a significant difference at approximately ER = 1, but both show a positive linear correlation. When ER < 1, the combustion temperature of the main combustion chamber increases with the equivalent ratio. The gas flow rate in Section 7 increases gradually owing to the increase in the fuel flow rate, resulting in an increase in the specific thrust. When ER > 1, the excess H2 absorbs the heat generated by combustion, resulting in a decrease in the theoretical combustion temperature. However, the excess H2 acts as a working fluid in Section 7, increasing the mass flow rate of the nozzle. Therefore, the specific thrust increases with the equivalent ratio, but the slope is smaller than with ER < 1. Nevertheless, an excessively high equivalent ratio may lead to problems such as unstable combustion and flameouts. Therefore, it can be considered that a positive correlation exists between the specific thrust and ER within a certain range.
2.2 Specific impulse
The specific impulse of an engine is defined as the thrust produced per unit mass flow rate of the fuel burned and can be expressed as follows:
The constant “g” represents the acceleration of gravity and is taken as 9.8 m/s2. The equation shows that the specific impulse of the engine is only related to the pressurized coefficient and ER (i.e., it is independent of other factors):
Figures 5A, B show the relationships of the specific impulse with the ER and pressurized coefficient, respectively. It can be seen that the specific impulse of the core engine increases with the increase in the pressurized coefficient but is negatively correlated with the ER. Similar to the situation of the specific thrust, the relationship between the specific impulse and pressurized coefficient is approximately logarithmic.
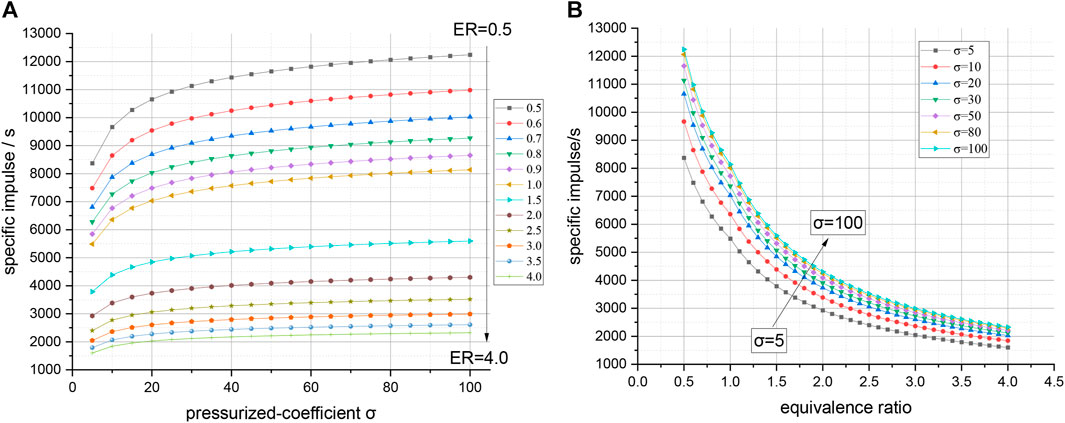
FIGURE 5. Relationships between specific impulse, pressurized coefficient, and equivalence ratio. The specific impulse of the core engine increases with an increase in pressurized coefficient but decreases with an increasing equivalent ratio.
3 Research on the influence of closed-cycle efficiency
The previous analysis shows that the engine’s specific thrust and specific impulse are only related to the pressurized coefficient and ER. However, unlike the pressurized coefficient, the ER of the engine is not an independent design parameter. Under certain component performance and thermodynamic cycle conditions, a minimum ER exists. When the ER is lower than this minimum value, the engine cannot be matched. The most significant manifestation of this phenomenon is that the effectiveness of the low-temperature heat exchanger (HX4 in Figure 2) exceeds 1.
Webber et al. (2006) stated that at a thermal capacity ratio of 1 between the pre-cooler and the low-temperature heat exchanger, the entropy increase in the system is minimal and the cycle thermal efficiency is the highest. At this time, the required liquid H2 flow rate for cooling is approximately 2.5 times that required for stoichiometric combustion.
In actual engineering design, the maximum temperature of He can reach 1,200 K if the heat capacity ratio is kept at 1, which is higher than the current material tolerance limit of 950 K. Therefore, the general design equivalent ratio is higher than 2.5. Taking the thermodynamic cycle shown in Figure 2 as an example, the required liquid H2 flow for cooling is approximately 2.5–3.5 times the equivalent combustion liquid H2 flow. Thus, the overall ER is approximately 2.5–3.5.
In the thermodynamic cycle of Figure 2, the closed He cycle system plays a role in the heat-to-power conversion. QH denotes the heat absorbed from the airflow path through the pre-cooler and high-temperature heat exchanger, and WT denotes the power generated to drive the air compressor. QC is the heat transferred to the liquid H2 through the low-temperature heat exchanger. A simplified model of the closed He cycle is shown in Figure 6.
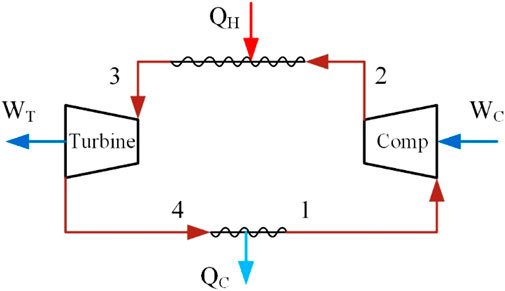
FIGURE 6. Closed-cycle diagram. Turbine, Helium Turbine; Comp, Helium Compressor; 1∼4, Cycle Section Number.
The thermal efficiency is the ratio of the net output power of the cycle to the heat absorbed by the cycle and is calculated as follows:
Evidently, improvement in the thermal efficiency of the closed cycle would reduce the amount of heat that needs to be cooled by the liquid H2, resulting in a lower overall ER. In practical matching, an increase in the closed-cycle thermal efficiency from 20% to 30% reduces the overall ER from 3.8 to 2.6, resulting in a 42% increase in the engine’s total specific impulse.
Assuming that He is an ideal gas with a constant adiabatic index and specific heat at constant pressure, the ratio between the maximum temperature and minimum temperature of the cycle can be defined as the cycle temperature ratio:
Thus, the aforementioned calculations can be transformed as
The calculations according to the balance of pressure in the closed cycle are
Here,
Figures 7, 8, 9, 10 show the relationships between the cycle efficiency and component parameters.
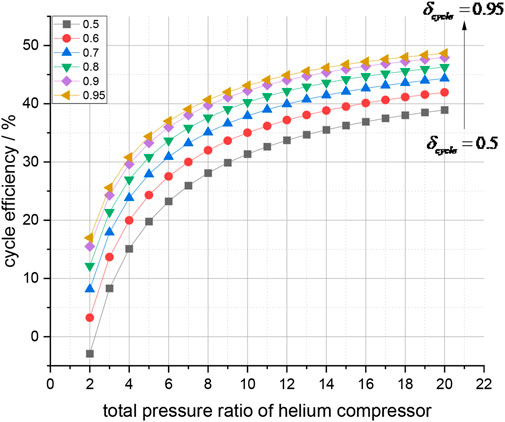
FIGURE 7. Thermal efficiency and compressor pressure ratio. The cycle thermal efficiency increases with an increase in the compressor pressure ratio
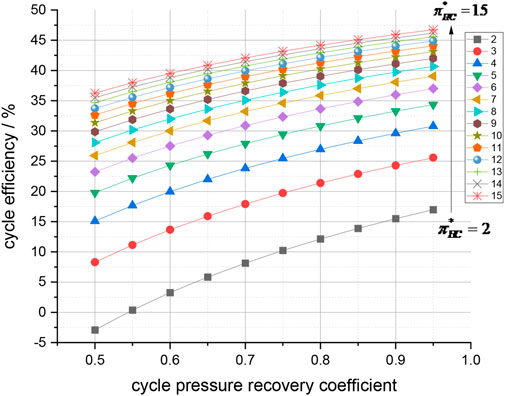
FIGURE 8. Thermal efficiency and cycle pressure recovery coefficient. The cycle pressure loss coefficient and cycle thermal efficiency demonstrate an approximately linear relationship
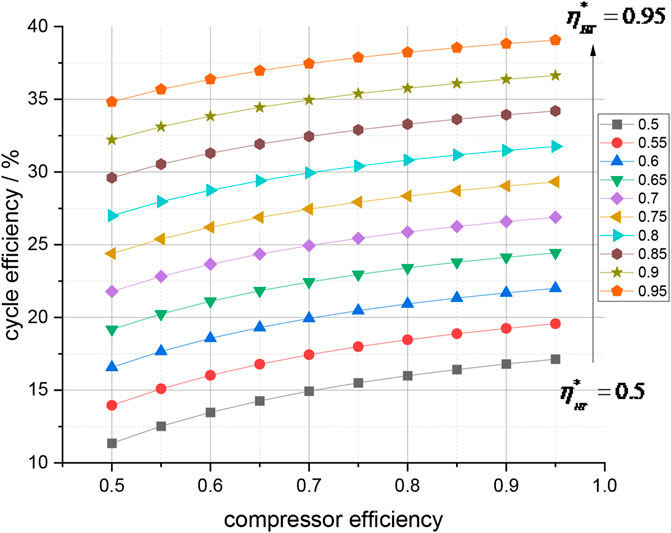
FIGURE 9. Cycle efficiency and turbomachinery efficiency. The cycle efficiency shows an approximately linear relationship with the compressor efficiency
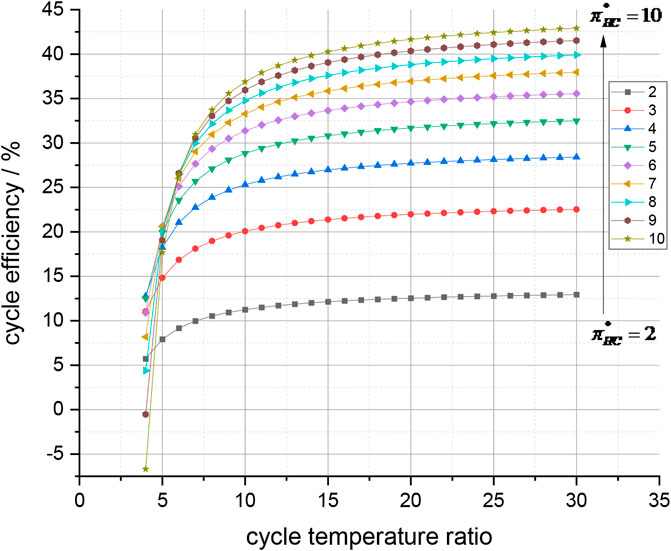
FIGURE 10. Cycle efficiency and cycle temperature ratio. The temperature ratio has a greater impact on high-pressure ratio cycles
Figures 7, 8 indicate that under certain component efficiency and cycle temperature ratios, the cycle thermal efficiency increases with an increase in the compressor pressure ratio. The cycle pressure loss coefficient and cycle thermal efficiency demonstrate an approximately linear relationship. For low-pressure ratio cycles (e.g.,
In Figure 9, the cycle efficiency shows an approximately linear relationship with the compressor and turbine efficiency. When the efficiency of turbomachinery increases by 10%, the cycle efficiency increases by approximately 0.5%–2%. The relationship between the cycle temperature ratio and cycle thermal efficiency in Figure 10 shows that the temperature ratio has a greater impact on high-pressure ratio cycles. When the temperature ratio increases from 10 to 20, the efficiency of the low-pressure ratio (e.g.,
4 Method validation
We performed engine performance calculations with the system parameters of Fernández Villacé (2013) at Ma5. The comparison of thrust and specific impulse is shown in Table 1. The thrust coefficients of nozzles are considered in the literature, but no specific design parameters are given. Therefore, a thrust coefficient of 0.9–1.0 was selected for calculation in this section. The results show an error of 3.27–12.43% for specific thrust and 4.08–13.63% for specific impulse.

TABLE 1. Thrust and specific impulse at Ma5 in the literature (Fernández Villacé, 2013), with the thrust coefficient from 0.9 to 1.0.
Next, we performed a validation calculation for the ground point of the engine shown in the literature (Cao-Bin et al., 2021) with a thrust factor of 0.9. The results of the calculation are shown in Table 2. The results show that the errors of the thrust and specific impulse are 3.06% and 3.93, respectively.
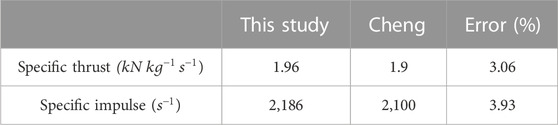
TABLE 2. Thrust and specific impulse at the ground point, with an error of about 3% from the results in the literature (Cao-Bin et al., 2021).
5 Conclusion
This study established a performance analysis model for a pre-cooled engine core with a simple closed He cycle. Based on the perfect gas assumption, research was conducted on the relationships between the specific thrust, specific impulse, and engine parameters. The conclusions are as follows:
(1) A new performance analysis method based on analytical methods was proposed for providing overall performance analyses of pre-cooled core engines with closed He cycles, providing a new means for quickly and intuitively establishing the relationships between the overall performances of pre-cooled core engines and their component parameters.
(2) The specific thrust and specific impulse performance of the pre-cooled core engine are related to the pressurized coefficient and ER. The specific thrust is positively correlated with the pressurized coefficient and ER. The specific impulse increases with an increase in the pressurized coefficient and decreases with an increase in the ER. Considering the engine performance and the difficulty of compressor design, the pressurization factor should be selected from 20 to 40.
(3) The liquid H2 flow rate used for cooling is approximately 2.5–3.5 times that of the equivalent combustion flow rate; in other words, the ER is approximately 2.5–3.5, with the lowest ER related to the thermal efficiency of the closed He cycle. Improvement in the efficiency of the closed cycle is an effective approach to reducing the ER.
(4) The thermal efficiency of closed He cycles is related to five parameters: the He compressor pressure ratio, cycle total pressure recovery coefficient, cycle temperature ratio, compressor efficiency, and turbine efficiency. At present, turbomachinery efficiency is already at a relatively high level, and it is difficult to greatly improve it. The cycle efficiency can be improved by increasing the cycle temperature ratio and the total pressure ratio of the He compressor. If the temperature ratio increases from 10 to 20, the efficiency of the low-pressure ratio (e.g.,
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.
Author contributions
MT-L: conceptualization, methodology, investigation, formal analysis, and writing—original draft; JX-F: software, methodology, investigation, data curation, and writing—original draft; LG-D: visualization and investigation; LZ-D: visualization, and writing—review and editing; GH: analysis and/or interpretation of data; HX-G: analysis and/or interpretation of data; DP-C: revising the manuscript critically for important intellectual content. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Cao-Bin, C., R-Heng, Z., and Tong-Ling, M., (2021). Characterization of a pre-cooled engine with closed Brayton cycle. Propuls. Technol. 42 (08), 1749–1760. doi:10.13675/j.cnki.tjjs.190868
Crawford, I. A. (2016). The long-term scientific benefits of a space economy. Space Policy 37, 58–61. doi:10.1016/j.spacepol.2016.07.003
Fernández-Villacé, V., and Paniagua, G. (2013). On the exergetic effectiveness of combined-cycle engines for high speed propulsion. Energy 51, 382–394. doi:10.1016/j.energy.2012.11.051
Hempsell, M. (2010). Progress on the sklon and SABRE development programme. United Kingdom: Reaction Engines Limited.
Jivraj, F. (2004). “The scimitar precooled Mach 5 engine,” in 2nd European Conference for Aerospace Sciences (EUCASS), Florida, United States, 11-14 July 2004.
Varvill, R., and Bond, A. (2003). A comparison of propulsion concepts for SSTO reusable launchers. JBIS 56.
Fernández Villacé, V. (2013). “Simulation, design and analysis of air-breathing combined-cycle engines for high speed propulsion,”. Doctoral. doi:10.20868/UPM.thesis.23340
Webber, H., Bond, A., and Hempsell, M. (2006). “Sensitivity of pre-cooled air-breathing engine performance to heat exchanger design parameters[C]//,” in 57th International Astronautical Congress, Valencia, Spain, October 2006.
Wen-hui, L., (2018). Technical challenge and potential solution for aerospace combined cycle engine. J. Propuls. Technol. 39. doi:10.13675/j.cnki.tjjs.2018.10.002
Xuanfei, Y. (2020). Research on thermodynamic cycle and control law of precooled airbreathing propulsion system. Harbin, China: School of Energy Science and Engineering,Harbin Institute of Technology.
Xuhui, Z. (2020). Future application of combined cycle propulsion technology. Sci. Technol. Rev. 38. doi:10.3981/j.issn.1000-7857.2020.12.002
Yixiang, L. (2016). Research on the development history of US hypersonic aircrafts. Harbin, China: School of Astronautics,Harbin Institute of Technology.
Yuan, G., (2020). Maximum state control schedule research on deeply precooled combined cycle engine in airbreathing mode. Propuls. Technol. 41. doi:10.3981/j.issn.1000-7857.2020.12.002
Zhang, J., Wang, Z., and Li, Q. (2017). Thermodynamic efficiency analysis and cycle optimization of deeply precooled combined cycle engine in the air-breathing mode. Acta Astronaut. 138, 394–406. doi:10.1016/j.actaastro.2017.06.011
Zheng-ping, Z., (2021). Research progress on hypersonic precooled airbreathing engine technology. Aeroengine 47. doi:10.13477/j.cnki.aeroengine.2021.04.002
Zhengping, Z., (2015). Precooling technology study of hypersoic aeroengine. Acta Aeronaytica Astronaut. Sinica 36. doi:10.7527/S1000-6893.2015.0144
Nomenclature
Keywords: pre-cooled core engine, closed helium cycle, overall performance, specific thrust, specific impulse
Citation: Tong-Ling M, Xue-Feng J, Guo-Dong L, Zhen-De L, Han G, Xue-Gang H and Peng-Cheng D (2023) Effects of key parameters on performance of a pre-cooled core engine based on the closed helium cycle. Front. Mech. Eng 9:1208468. doi: 10.3389/fmech.2023.1208468
Received: 19 April 2023; Accepted: 16 June 2023;
Published: 04 July 2023.
Edited by:
Qiu Wang, Chinese Academy of Sciences (CAS), ChinaReviewed by:
Hyoung Jin Lee, Inha University, Republic of KoreaAlexander Wiedermann, MAN Energy Solutions SE, Germany
Copyright © 2023 Tong-Ling, Xue-Feng, Guo-Dong, Zhen-De, Han, Xue-Gang and Peng-Cheng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jiang Xue-Feng, OTcxMTAwNjQyQHFxLmNvbQ==
 Ma Tong-Ling1
Ma Tong-Ling1 Jiang Xue-Feng
Jiang Xue-Feng