Hydraulic accumulators in energy efficient circuits

Hydraulic accumulators have long been used in hydraulic circuits. Applications vary from keeping the pressure within a circuit branch to saving load energy. Among these applications, storing and releasing energy has gained attention in recent years due to the need for efficient circuits. In this sense, accumulators are the hydraulic counterparts of batteries and capacitors in electrical circuits. From hydraulic hybrid vehicles to complex agricultural machinery, accumulators have been successfully implemented, and significant energetic gains have been reported. This article reviews typical applications where accumulators can be used to this end and discusses the challenges that still have to be overcome in each situation.

1 Introduction

Hydraulic accumulators are the fluid equivalent of electrical capacitors (Yudell and Van de Ven, 2017; Leon-Quiroga et al., 2020). As such, they have been used to store energy. Their applications include hybrid vehicles (Costa and Sepehri, 2015; U.S. Environmental Protection Agency, 2020; Pourmovahed et al., 1992; Deppen et al., 2012; Deppen et al., 2015; Beachley et al., 1983; Ho and Ahn, 2010; Chapp, 2004; Chen et al., 2022; Sprengel and Ivantysynova, 2013), wind and wave energy extraction (Dutta et al., 2014; Fan et al., 2016a; Fan et al., 2016b; Fan et al., 2016c; Irizar and Andreasen, 2017; Fan and Mu, 2020), excavators and machinery alike (Heybroek et al., 2012; Lin and Wang, 2012; Shen et al., 2013; Hippalgaonkar and Ivantysynova, 2016a; Hippalgaonkar and Ivantysynova, 2016b; Ren et al., 2018; Yu and Ahn, 2020; Bertolin and Vacca, 2021). Accumulators have also been used as low-pressure tanks in closed hydraulic circuits (Çalışkan et al., 2015; Costa and Sepehri, 2019), shock absorbers (Porumamilla et al., 2008), and as part of switched hydraulic circuits, where hydraulic power at the actuator is controlled by fast-switching hydraulic valves instead of spool valves (to reduce throttling losses) (Brown et al., 1988; De Negri et al., 2014; Kogler and Scheidl, 2016; Yudell and Van de Ven, 2017).

With respect to their constructive type, accumulators are categorized into gas-loaded, weight-loaded, and spring-loaded types (Costa and Sepehri, 2015). Gas-loaded (hydropneumatic) accumulators are the most commonly used in hydraulic circuits, being evidenced in all references quoted so far, and are the focus of this article. However, it is important to say something about weight- and spring-loaded accumulators before we continue.

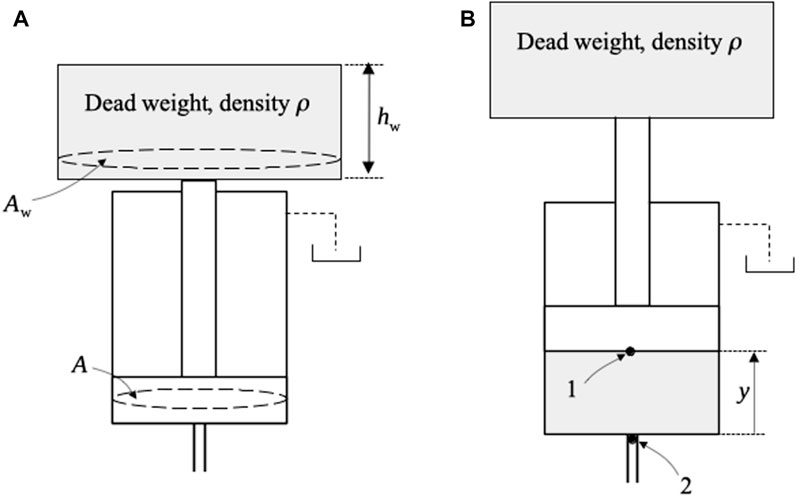
Weight-loaded accumulators provide a (nearly) constant pressure during discharge since they store potential gravitational energy within a vertically moving mass, as illustrated in Figure 1.

FIGURE 1

FIGURE 1. Weight-loaded accumulator: (A) uncharged and (B) charged.

Particularly, the output static pressure at point 2 (Figure 1B) depends on the elevation height, $y$, of the dead weight. However, the difference between pressures at points 1 and 2 should be negligible, given the magnitude of the pressure at point 1. Thus, we might say that weight-loaded accumulators, except for the fact that they must be heavy and always placed in an upright position, should be an ideal choice. Unfortunately, this type of accumulator is not practical for the majority of hydraulic applications. For instance, with reference to Figure 1A, we consider an accumulator with a cylindrical dead weight $A_{\mathrm{w}}{h}_{\mathrm{w}}$, where $A_{\mathrm{w}}=nA$ ($n$ is an arbitrary number). The weight vertical dimension, $h_{\mathrm{w}}$, necessary to create an output pressure, $p$, is easily obtained as $h_{\mathrm{w}}=p/\left(\rho ng\right)$, where $g$ is the gravitational acceleration. Therefore, a $10\mathrm{M}\mathrm{P}\mathrm{a}$ pressure output in an accumulator with an iron dead weight ($\rho =7874\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$) and whose cross-sectional area is three times the cylinder area ($n=3$) would require $h_{\mathrm{w}}=43.2\mathrm{m}$, which is obviously not acceptable.

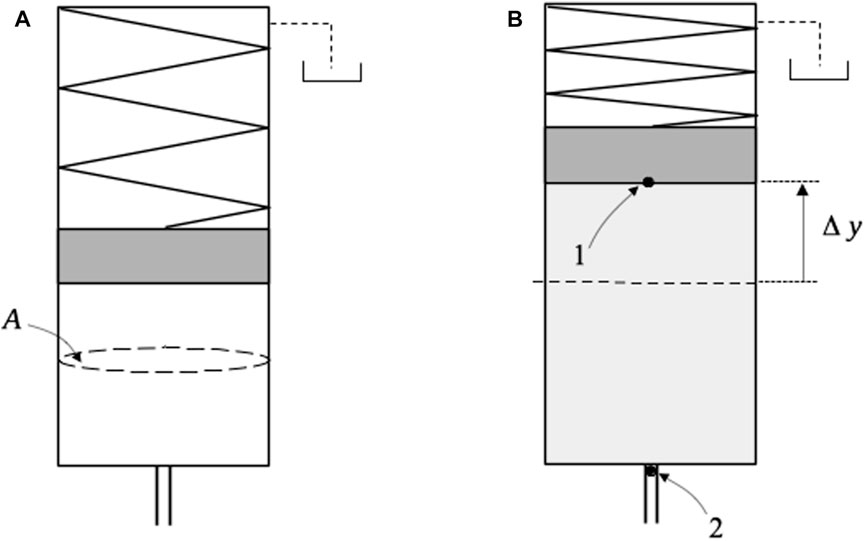
Figure 2A shows the schematic representation of a spring-loaded accumulator. As hydraulic oil enters, the spring is compressed and the piston moves upward at distance $∆y$ (Figure 2B). As a result, a force $F\left(∆y\right)$ is produced (not shown in the figure), creating a pressure $p=F/A$ within the oil chamber. Linearity between $F$ and $∆y$ is not an inherent characteristic, but it is usually the case for common springs. When the fluid within the accumulator is static, pressures at points 1 and 2 are practically equalized. Note that there is no need for placement in a vertical position, and given that the output pressure does not remain constant during discharge, this type of accumulator is somewhat similar to the gas-loaded accumulator to be introduced next. However, the high requirements placed on the spring stiffness and more complex mechanical construction have limited this type of accumulator to applications with small pressures and low storage capacities (Chen et al., 2022).

FIGURE 2

FIGURE 2. Spring-loaded accumulator: (A) uncharged and (B) charged.

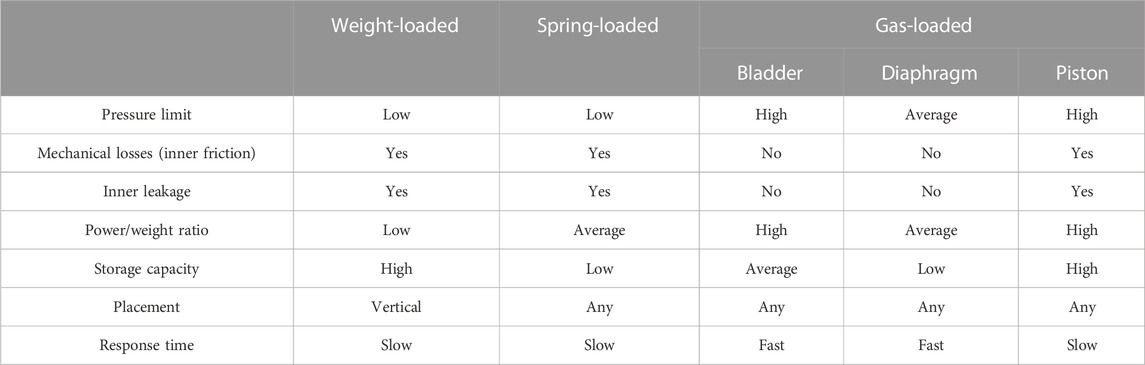
The most common type of hydraulic accumulator is the gas-loaded accumulator. Typically, gas-loaded accumulators have a gas chamber separated from the oil by a bladder or diaphragm, with the great advantage of not having moving elements and, consequently, leaks. Piston-type gas accumulators also exist (Pfeffer et al., 2016), but there is an inherent leakage risk as well as the added inertia of the moving separator (piston). Figure 3 illustrates the three types of gas-loaded accumulators.

FIGURE 3

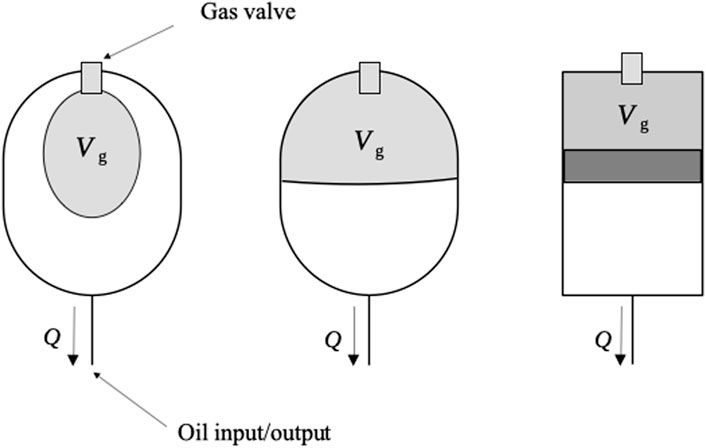
FIGURE 3. Gas-loaded accumulator types: (from left to right) bladder, diaphragm, and piston accumulators.

By far, gas-loaded accumulators are the most used in hydraulic circuits. A comparison between the accumulator types is given in Table 1.

TABLE 1

TABLE 1. Brief relative comparison between weight-, spring-, and gas-loaded accumulators.

In Section 2, we present a brief mathematical analysis of gas-loaded accumulators.

2 Mathematical modeling of gas-loaded accumulators

Considering that the accumulators illustrated in Figure 3 are isothermally loaded, the simplest relationship between the input pressure and the gas chamber volume can be obtained from the perfect gas law.

$p=\frac{mRT}{V_{\mathrm{g}}}(1)$

where $p$ is the (absolute) pressure inside the accumulator, $m$ is the mass of the contained gas, $R$ is the gas constant, and $V_{\mathrm{g}}$ is the volume of the gas chamber. Here, we assume that the situation is static or at least very close to it in the sense that the fluid dynamics effects caused by oil entering/leaving the accumulator are disregarded (a fairly reasonable assumption in hydraulic circuits).

In Eq. 1, we have considered that the accumulator gas is ideal and that the heat transfer between the accumulator and the environment guarantees an isothermal process. In many situations, the resulting simplified model (1) is adequate to simulate an actual scenario (Dutta et al., 2014; Fan et al., 2016a; Pfeffer et al., 2016). However, a more general approach consists in treating the charging/discharging process as lying somewhere between isothermal and adiabatic and using the polytropic relation $p{V}^n=k_0$, where $n$ is the polytropic index and $k_0$ is a constant (Kogler and Scheidl, 2016; Zhao et al., 2019; Liu et al., 2020). Some have chosen to model the accumulator using a much more elaborate equation of the state for the gas (Pourmovahed et al., 1992). For the purpose of introduction, in this section, Eq. 1 is sufficient and will be used as a basis for the discussion that follows.

The input/output oil flow, $Q$, is determined from Eq. 1 as

$Q=\frac{d{V}_{\mathrm{g}}}{dt}=-C_{\mathrm{A}}\frac{dp}{dt}(2)$

where $C_{\mathrm{A}}$ is the capacitance (as in electrical circuits) and is dependent on the absolute pressure, $p$.

$C_{\mathrm{A}}=\frac{mRT}{p^2}(3)$

Equations 2, 3 can be solved for some particular situations. For instance, consider the case where the accumulator is discharged into a tank at pressure $p_0$ through an orifice, as shown in Figure 4. In such a case, the orifice equation $Q=C\sqrt{p-p_0}$, where $C$ is the orifice coefficient, can be combined with Eqs 2, 3, resulting in

$\frac{dp}{dt}=-a_0{p}^2\sqrt{p-p_0}(4)$

where $a_0$ is a constant given by

$a_0=\frac{C}{mRT}(5)$

FIGURE 4

FIGURE 4. Accumulator discharging to tank through a fixed orifice.

Equation 4 can be integrated by making $p=p_{\mathrm{i}\mathrm{n}}$ (initial pressure load) at $t=0$. Note that the integration variables, $p$ and $t$, have been replaced with the dummy variables, $p^{*}$ and $t^{*}$, since they also appear as the upper limits of the integrals. The resulting expression can be simplified if we approximate $\sqrt{p^{*}-p_0}\cong \sqrt{p^{*}}$, which is quite reasonable in hydraulic circuits, where the gauge pressure $\left(p^{*}-p_0\right)$, is not much different from the absolute pressure, $p^{*}$:

$a_0{\int }_0^{t}d{t}^{*}=a_{0}t=-{{\displaystyle \int }}_{p_{\mathrm{i}\mathrm{n}}}^p\left[\frac{d{p}^{*}}{{\left(p^{*}\right)}^2\sqrt{p^{*}-p_0}}\right]\cong -{{\displaystyle \int }}_{p_{\mathrm{i}\mathrm{n}}}^p\left[\frac{d{p}^{*}}{{\left(p^{*}\right)}^{\frac{5}{2}}}\right]=\frac{2}{3}\left[p_{\mathrm{i}\mathrm{n}}^{\left(-\frac{3}{2}\right)}-p^{\left(-\frac{3}{2}\right)}\right](6)$

From Eq. 6, we obtain the pressure within the gas chamber as a function of time

$p={\left[p_{\mathrm{i}\mathrm{n}}^{\left(-\frac{3}{2}\right)}-\frac{3a_{0}t}{2}\right]}^{\left(-\frac{2}{3}\right)}(7)$

Equation 7 has a practical implication. If a gas-loaded accumulator is used to drive an actuator, both flow and force change in time. The only possible way of keeping a constant pressure, $p$, for example, is by changing $a_0$, given by Eq. 5, into a function of time in such a way that the second term within the brackets in Eq. 7 becomes constant.

As a general rule, pressure control in gas-loaded accumulators is carried out through a variable orifice, where $C$ in Eq. 5 continuously changes, which implies energy dissipation. Proportional valves can be used to this end, as illustrated in Figure 5. By sensing pressures $p$ and $p_{\mathrm{L}}$, the proportional pressure reducing valve, V, can be adjusted to keep the load pressure, $p_{\mathrm{L}}$, at a pre-determined value.

FIGURE 5

FIGURE 5. Pressure control using a piloted pressure-reducing valve.

A novel way of providing a constant pressure output was proposed by Van de Ven (2013). The idea was to modify the accumulator such that the gas would act on a variable piston area, $A\left(x\right)$, as illustrated in Figure 6.

FIGURE 6

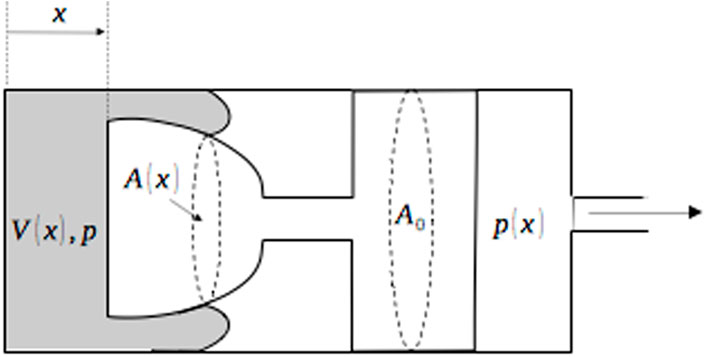
FIGURE 6. Constant pressure gas-loaded accumulator (Van de Ven, 2013).

For the simplest scenario, when the perfect gas law is applied to an isothermal process and dynamic forces are disregarded, $p\left(x\right)A_0=pA\left(x\right)$. Therefore, the pressure $p\left(x\right)$ at the accumulator output, shown in Figure 6, is given by

$p\left(x\right)=\frac{A\left(x\right)mRT}{V\left(x\right)A_0}(8)$

The solution proposed by Van de Ven (2013) adds a moving mass to the accumulator, and although dynamic forces are not considered in Eq. 8, they might play an important role in transient behavior.

Another approach to the variable-pressure problem consists in changing the compressed gas volume, $V_{\mathrm{g}}$, in Eqs 1, 2 (Liu et al., 2020). Figure 7 illustrates the concept. With the solenoid of valve $V_1$ activated, the compressed gas chamber volume is $V_{\mathrm{g}}=V_{\mathrm{g}1}+V_{\mathrm{g}2}$. On the other hand, the auxiliary gas accumulator, R, has its volume, $V_{\mathrm{g}2}$, controlled by the proportional valve $V_2$. Note that if $V_1$ is not activated, no additional gas volume is added to the accumulator A. Here, we note the need for a good controller to set the gas regulator, R, according to the circuit demands.

FIGURE 7

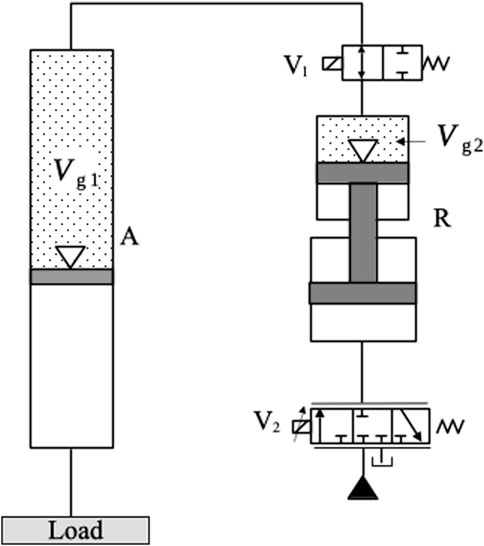
FIGURE 7. Variable gas volume accumulator (Liu et al., 2020).

Other concepts have been suggested that allow for controlling the output pressure. For instance, Zhao et al. (2019) introduces a piston-type gas accumulator where the variable pressure at the accumulator output is counterbalanced by a mechanical device attached to the piston. The resulting design (not shown here) is relatively complex and involves a cam mechanism together with roller bearings.

In the following sections, we describe typical uses of gas-loaded accumulators in hydraulic circuits as energy storage components.

3 Energy storage and reuse from multiple actuators

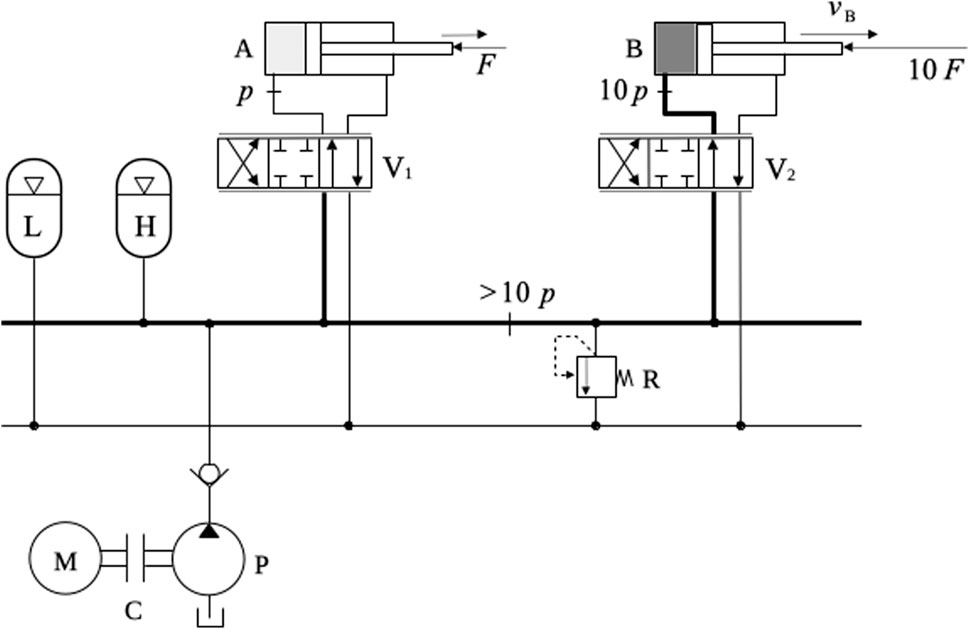
In many situations, accumulators can be used to store energy during motoring quadrants, i.e., when energy flows from the load into the hydraulic circuit. In one case scenario, accumulators can store energy from several hydraulic actuators and/or motors through a common pressure rail (CPR) system. To illustrate the CPR concept, the circuit shown in Figure 8 is considered. In the figure, we observe a high-pressure accumulator, H, and a low-pressure accumulator, L. The pressure differential between accumulators H and L provides the driving force for cylinders A and B, which move against resistive loads, $F$ and $10F$. Assuming that the cylinders are identical, the required pressures at the cap sides are $p$ and $10p$, respectively. Accumulator H must then supply a pressure somewhat higher than $10p$ to compensate for the losses at valve V₂. On the other hand, in order to produce the ten times–lower pressure required at cylinder A, high throttling losses are produced at valve V₁, lowering the energetic efficiency of the whole circuit (Costa and Sepehri, 2019). This drawback has been addressed, and solutions have been proposed below. Nevertheless, a positive characteristic of CPRs is the capability of harvesting load energy. For instance, consider that the direction of $v_{\mathrm{B}}$ is reversed, while the external load, $10F$, remains unaltered. In such cases, cylinder B is driven by the external force, $10F$, and energy coming from the load can be stored within the accumulator H.

FIGURE 8

FIGURE 8. Common pressure rail (CPR).

CPRs can be considerably improved through the substitution of directional valves with hydraulic transformers, where throttling losses are not an issue (Shen et al., 2013). In fact, the design evolution of hydraulic transformers has recently drawn the attention of heavy machine manufacturers to the use of CPRs as a means of increasing the energetic performance (Heybroek et al., 2012).

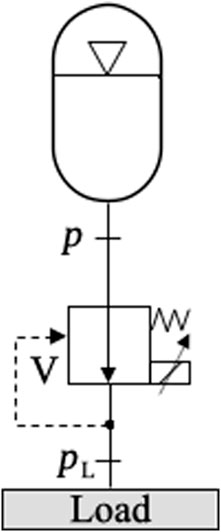
It is possible to use accumulators to store load energy even when one single actuator is present, as shown in Figure 9.

FIGURE 9

FIGURE 9. Hydraulic circuit with one actuator (CPR-style design).

In Figure 9, the low-pressure accumulator has been replaced by the tank. The cylinder lifts a load of mass $m$ through the activation of solenoid y. The accumulator stores potential energy coming from the load when y is deactivated. For comparison, the circuit design preserves the CPR style, as shown in Figure 8.

Valve-controlled actuators are accompanied by losses at the cylinder control valve. This is the case even when there is no flow reduction, as in Figure 9, where no velocity control is required for the cylinder. More energy efficient circuits eliminate cylinder control valves altogether, where stored energy is not dissipated into heat. Circuits such as these are denominated pump-controlled actuators [or “hydrostatic actuators” (Costa and Sepehri, 2015)] and are a direct evolution from “hydrostatic transmissions,” where a hydraulic motor is directly connected to the pump. We deal with hydrostatic transmissions and actuators in Section 4.

4 Energy storage and reuse in hydrostatic transmissions and actuators

There are two ways how we can use an accumulator to store energy from the load in a hydrostatic transmission or actuator. The first way is by connecting the high- and low-pressure accumulators directly to the main hydraulic circuit. The second way is by creating a secondary circuit with its own pump/motor where the accumulators are placed. Figure 10 shows two application examples.

FIGURE 10

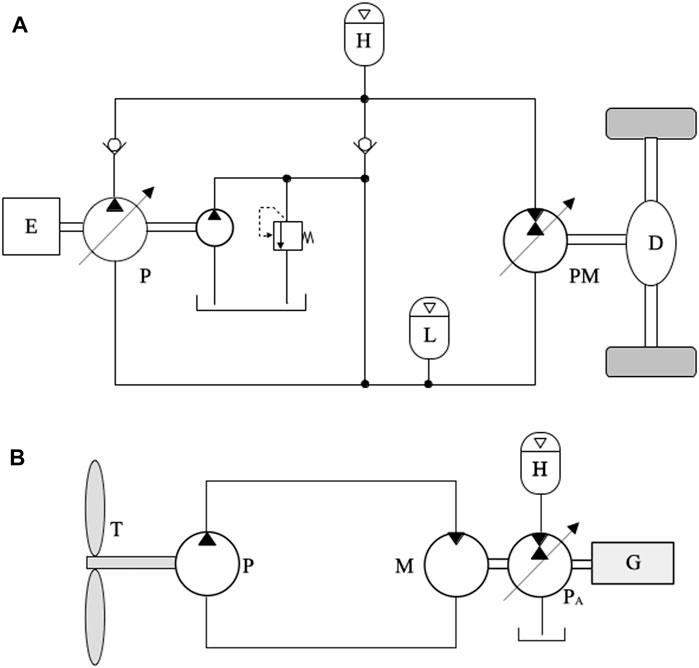
FIGURE 10. (A) Inline accumulators in a hybrid automobile transmission [reproduced from Costa and Sepehri (2015)] and (B) secondary accumulator circuit in a wind generator [reproduced from Dutta et al. (2014)].

Figure 10A shows the circuit for a hydraulic hybrid automobile (Costa and Sepehri, 2015). The engine, E, supplies energy to the wheels through pump, P, connected to the pump/motor, PM, which drives the differential, D. This is a fairly simple circuit, and many improvements have been made through the years (U.S. Environmental Protection Agency, 2020; Deppen et al., 2012; Ho and Ahn, 2010; Sprengel and Ivantysynova, 2013). The accumulator H is charged whenever energy flows from D to PM or when the automobile is idle, while the engine is still running. In both cases, energy that would otherwise be wasted is stored in H.

One clear disadvantage of placing the accumulator in parallel to the main hydraulic circuit is that the effective bulk modulus of the system is drastically reduced. In the particular case of an automobile, the effect is a “spongy” feeling to the driver due to the much lower response time (Sprengel and Ivantysynova, 2013). An inline accumulator precludes the need of additional mechanical devices, such as the one shown in Figure 10B, where a secondary circuit connected to another pump/motor is employed. Secondary circuits of this kind were first proposed by Wendel (2002) and are explained in detail by Costa and Sepehri (2015), where they are given the name “energy storage circuit.” In Figure 10B, a fixed-displacement pump, P, is driven by the wind turbine, T. The variable displacement motor, M, is connected to an auxiliary pump/motor, P_A, which is responsible for transferring fluid between the high-pressure accumulator, H, and the tank (low-pressure accumulator). The stored energy can be used to help the motor drive the shaft of the electricity generator, G. In the particular case of the circuit shown in Figure 10B, the idea is to store energy whenever the wind speed is higher than a rated value and subsequently reuse the stored energy when the wind speed falls below it (Dutta et al., 2014). The use of a variable displacement motor, M, provides the high transmission ratio, which is necessary because of the high angular speed required by the generator (Costa and Sepehri, 2015).

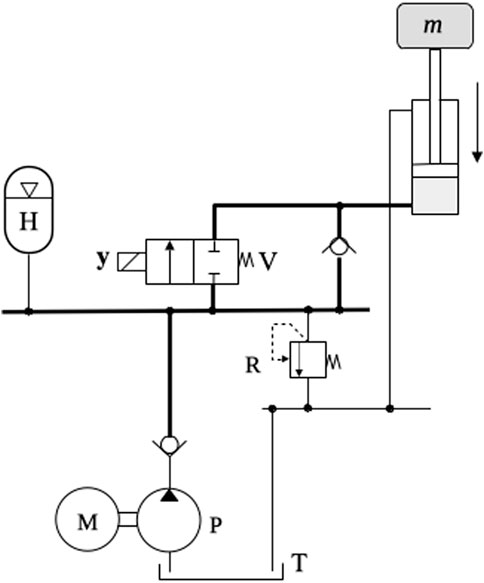
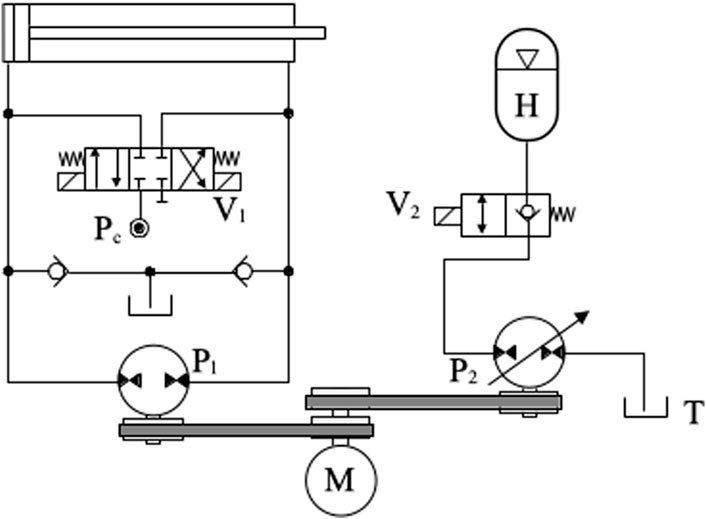
Hydrostatic actuators can also benefit from accumulators to store energy from the load. Figure 11 shows an electrohydrostatic actuator where an energy storage circuit is connected to the main pump. The circuit shown in Figure 11 is based on a design proposed by Costa and Sepehri (2015). Other circuit designs can be found in Hippalgaonkar and Ivantysynova (2016a) and Hippalgaonkar and Ivantysynova (2016b).

FIGURE 11

FIGURE 11. Energy storage circuit connected to a single-rod electrohydrostatic actuator.

With reference to Figure 11, valve V₁, connected to a low-pressure source, P_c, is used to compensate for the uneven flows coming into and out of the differential cylinder [see Costa and Sepehri (2019) for details on the way in which valve V₁ operates]. Since the pump and cylinder are directly connected, it is possible to transfer energy from the load to the main pump, P₁. When this happens, we say that the circuit operates in the motoring mode, and P₁ acts as a hydraulic motor. A belt and pulley transmission is used to connect P₁ to the secondary pump P₂, which loads the accumulator H when it pumps oil from the tank T. The variable displacement of the pump/motor, P₂, can be shifted between a positive and negative value so that it guarantees that the flow between the tank and the accumulator is correctly directed. The energy stored in H can be later reused to assist the main pump, P₁, by activating valve V₂, thus reducing the overall energy consumption.

5 Accumulators in digital hydraulics

One interesting manner of providing a variable flow into the actuator without the use of throttling valves is through the use of a fast-switching electrovalve, V, as shown in Figure 12A. The idea is to modulate the electrical pulse width, $\lambda T$ ($0<\lambda <1$), of solenoid y (Figure 12B), in such a way that the periodic flow at port 2, $Q_{24}$, may decrease/increase over a time, $T$, which is defined as the “duty cycle” (De Negri et al., 2014). This pulse-width modulation (PWM) technique can thus be used to control the cylinder velocity. Throttling will still exist, since there is a valve in between the pressure source and actuator, but it will be minimal when compared to a conventional valve control (as shown in Figure 8). The problem with the circuit shown in Figure 12A is that $Q_{24}$ is a pulsating flow, as illustrated in Figure 12C, which is obviously not practical in hydraulic circuits. The flow, $Q_{24}\left(t\right)$, in Figure 12C, corresponds to a hypothetical circuit where no pressure losses, fluid density, or inner volumes are factored in.

FIGURE 12

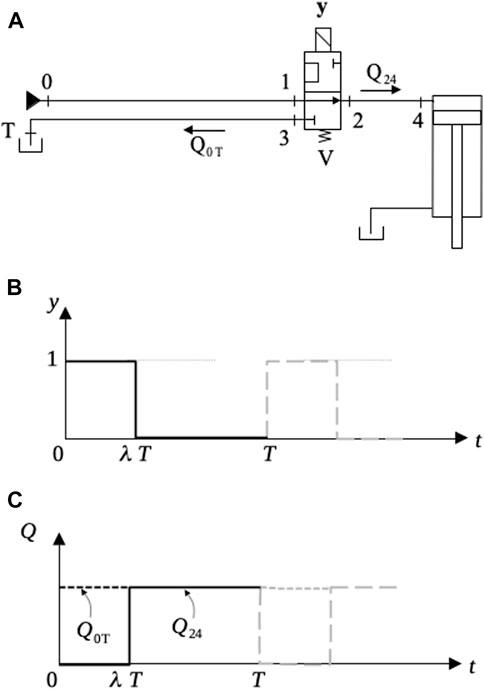
FIGURE 12. Pulse modulation flow control. (A) Hydraulic circuit, (B) Valve control signal, (C) Circuit flows.

Now consider the design shown in Figure 13 where an accumulator, H, is added to the circuit. In the figure, we have represented line 0-1 as in Brown et al. (1988) to emphasize the fact that it is a real conduit with an inner diameter, $d$, and length, $L$. In Figure 13, the accumulator plays the role of an energy absorber/releaser, acting in parallel with the natural inertia of the fluid inside the hydraulic line. Following Kogler and Scheidl (2016), we denominated the pipeline 0-1 “inertance tube.”

FIGURE 13

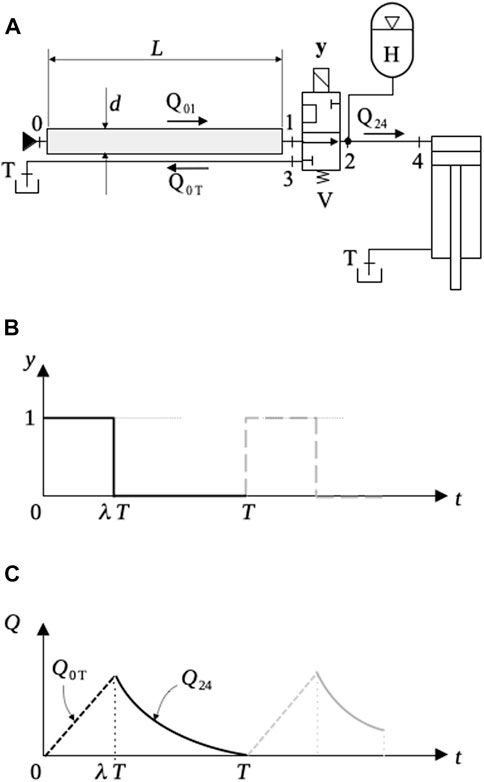
FIGURE 13. Ideal switched inertance circuit. (A) Hydraulic circuit, (B) Valve control signal, (C) Circuit flows.

Disregarding viscous losses in the circuit shown in Figure 12, the Second Law of Newton can be applied between points 0 and 1. Considering the hydraulic fluid with density $\rho$, we have

$∆p\left(\frac{\pi D^2}{4}\right)=\rho L\left(\frac{\pi D^2}{4}\right)\frac{d{v}_{\mathrm{f}}}{dt}(9)$

where $∆p=\left(p_0-p_{\mathrm{T}}\right)$ when $\left(0<t<\lambda T\right)$ and $∆p=\left(p_0-p_4\right)$ when $\left(\lambda T<t<T\right)$. $v_{\mathrm{f}}$ is the average speed within the inertance tube. Since there are no pressure losses, we have assumed that $p_1=p_3=p_{\mathrm{T}}$ (when y is activated) and $p_2=p_4$ (when y is deactivated).

Equation 9 can be simplified and written as a function of the flow, $Q_{01}=\left(4v_{\mathrm{f}}\right)/\left(\pi L{d}^2\right)$, which is as follows:

$\frac{d{Q}_{01}}{dt}=\frac{∆p}{L_{\mathrm{f}}}(10)$

where $L_{\mathrm{f}}$ plays the same role as the inductance in electrical circuits and is given by

$L_{\mathrm{f}}=\frac{4\rho L}{\pi d^2}(11)$

Integrating Eq. 10 for $\left(0<t<\lambda T\right)$ and $\left(\lambda T<t<T\right)$ yields, respectively, we get

$\left\{\begin{array}{l}\begin{array}{ccc}{Q}_{01}\left(t\right)=Q_{01}\left(0\right)+\left(\frac{p_0-p_T}{L_{\mathrm{f}}}\right)t& \mathrm{f}\mathrm{o}\mathrm{r}& 0<t<\lambda T\end{array},\\ \begin{array}{ccc}{Q}_{01}\left(t\right)=Q_{01}\left(\lambda \Delta t\right)+\left(\frac{p_0-p_4}{L_{\mathrm{f}}}\right)\left(t-\lambda \Delta t\right)& \mathrm{f}\mathrm{o}\mathrm{r}& \lambda T<t<T\end{array}\end{array}\right.(12)$

In Figure 12C, we see the behavior of $Q_{0\mathrm{T}}\left(t\right)=Q_{01}\left(t\right)$, when y is activated at ($0<t<\lambda T$), assuming that $Q_{01}\left(0\right)=0$. Instead of the abrupt change from 0 to a constant value, $Q_{0\mathrm{T}}$, that we observe in Figure 12C, the flow grows linearly, according to the first equation in Eq. 12. Likewise, when y is deactivated, the pressure $p_4$ starts growing. Subsequently, $Q_{24}\left(t\right)=Q_{01}\left(t\right)$ decreases linearly according to the second equation in Eq. 12. The presence of the accumulator, H, changes the behavior of $Q_{24}\left(t\right)$ into an exponential curve, as shown in Figure 11. In fact, the accumulator guarantees that $Q_{24}\left(t\right)$ never falls abruptly to zero, even in circuits where $L_{\mathrm{f}}$ is low. By choosing different values of $T$ and $\lambda$, it is possible to ensure that the flow, $Q_{24}$, remains greater than zero.

Switched inertance circuits are challenging in many ways. The switching frequency, for instance, is an issue in conventional spool valves. Rotary valves have been suggested as a substitute; however, dynamic problems such as the appearance of cavitation voids in the fluid have been observed (Brown et al., 1988). Nevertheless, this is a promising field in which hydraulic accumulators play an important part.

6 Conclusion

In this review article, we presented some major fields where hydraulic accumulators can be used to increase energy efficiency and performance. The challenges concerning pressure and flow output have also been addressed, where we see that attempts have been made to produce a constant-pressure response. Still, no solution has become commercial, but as in many other aspects of technology, this may be a simple matter of time. It must also be said here that hydraulic accumulators have other aspects that not explored in this article, such as energy loss during charge and discharge due to non-isothermal behavior. These are themselves complex and would not be fairly covered in a single article, so a choice had to be made even in this article to pick up some significant aspects out of a fairly large choice of approaches. We thus know that it is not possible, by any means, to cover all aspects concerning hydraulic accumulators, especially if we note that new circuits and new designs are constantly being developed. The idea, however, has been to introduce the state-of-the-art and expose the challenges and achievements obtained so far in some significant fields of application.

Author contributions

GC contributed to conception, design, and writing of the manuscript. NS contributed by reviewing and improving the content of the submitted version. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Beachley, N. H., Anscomb, C., and Burrows, C. R. (1983). Minimization of energy storage requirements for internal combustion engine hybrid vehicles. J. Dyn. Sys., Meas. Control 105 (2), 113–119. doi:10.1115/1.3149641

CrossRef Full Text | Google Scholar

Bertolin, M., and Vacca, A. (2021). An energy efficient power-split hybrid transmission system to drive hydraulic implements in construction machines. ASME. J. Dyn. Sys., Meas. Control. 143 (10), 101005. doi:10.1115/1.4051035

CrossRef Full Text | Google Scholar

Brown, F. T., Tentarelli, S. C., and Ramachandran, S. (1988). A hydraulic rotary switched-inertance servo-transformer. ASME. J. Dyn. Sys., Meas. Control. 110 (2), 144–150. doi:10.1115/1.3152664

CrossRef Full Text | Google Scholar

Çalışkan, H., Balkan, T., and Platin, B. E. (2015). A complete analysis and a novel solution for instability in pump controlled asymmetric actuators. ASME. J. Dyn. Sys., Meas. Control. 137 (9), 091008. doi:10.1115/1.4030544

CrossRef Full Text | Google Scholar

Chapp, R. (2004). Combined optimisation of design and power management of the hydraulic hybrid propulsion system for the 6 × 6 medium truck. Int. J. Veh. Des. Heavy Veh. Des. 3 (4), 372–402. doi:10.1504/IJHVS.2004.005458

CrossRef Full Text | Google Scholar

Chen, Y., Zhang, T., Zhang, H., Zhang, Z., Jia, Q., Chen, H., et al. (2022). Study on the effect of hydraulic energy storage on the performance of electro-mechanical-hydraulic power-coupled electric vehicles. Electronics 11, 3344. doi:10.3390/electronics11203344

CrossRef Full Text | Google Scholar

Costa, G. K., and Sepehri, N. (2019). Four-quadrant analysis and system design for single-rod hydrostatic actuators. ASME. J. Dyn. Sys., Meas. Control. 141 (2), 021011. doi:10.1115/1.4041382

CrossRef Full Text | Google Scholar

Costa, G. K., and Sepehri, N. (2015). Hydrostatic transmissions and actuators—operation, modelling and applications. Chichester - UK: Wiley.

Google Scholar

De Negri, V. J., Wang, P., Plummer, A., and Johnston, D. N. (2014). Behavioural prediction of hydraulic step-up switching converters. Int. J. Fluid Power 15 (1), 1–9. doi:10.1080/14399776.2014.882057

CrossRef Full Text | Google Scholar

Deppen, T. O., Alleyne, A. G., Meyer, J. J., and Stelson, K. A. (2015). Comparative study of energy management strategies for hydraulic hybrids. ASME. J. Dyn. Sys., Meas. Control. 137 (4), 041002. doi:10.1115/1.4028525

CrossRef Full Text | Google Scholar

Deppen, T. O., Alleyne, A. G., Stelson, K. A., and Meyer, J. J. (2012). Optimal energy use in a light weight hydraulic hybrid passenger vehicle. ASME. J. Dyn. Sys., Meas. Control. 134 (4), 041009. doi:10.1115/1.4006082

CrossRef Full Text | Google Scholar

Dutta, R., Wang, F., Bohlmann, B. F., and Stelson, K. A. (2014). Analysis of short-term energy storage for midsize hydrostatic wind turbine. ASME. J. Dyn. Sys., Meas. Control. 136 (1), 011007. doi:10.1115/1.4025249

CrossRef Full Text | Google Scholar

Fan, Y., and Mu, A. (2020). Adaptive fuzzy Proportion Integration Differentiation control in hydraulic offshore wind turbine for optimal power extraction based on the estimated wind speed. Energy Sci. Eng. 8, 1604–1619. doi:10.1002/ese3.618

CrossRef Full Text | Google Scholar

Fan, Y., Mu, A., and Ma, T. (2016c). Design and control of a point absorber wave energy converter with an open loop hydraulic transmission. Energy Convers. Manag. 121, 13–21. doi:10.1016/j.enconman.2016.04.107

CrossRef Full Text | Google Scholar

Fan, Y., Mu, A., and Ma, T. (2016a). Modeling and control of a hybrid wind-tidal turbine with hydraulic accumulator. Energy 112, 188–199. ISSN 0360-5442. doi:10.1016/j.energy.2016.06.072

CrossRef Full Text | Google Scholar

Fan, Y., Mu, A., and Ma, T. (2016b). Study on the application of energy storage system in offshore wind turbine with hydraulic transmission. Energy Convers. Manag. 110, 338–346. doi:10.1016/j.enconman.2015.12.033

CrossRef Full Text | Google Scholar

Heybroek, K., Vael, G., and Palmberg, J. (2012). “Towards resistance-free hydraulics in construction machinery,” in Proceedings of the 8th International Fluid Power Conference, Dresden, Germany, March 26-28, 2012, 123–138.

Google Scholar

Hippalgaonkar, R., and Ivantysynova, M. (2016a). Optimal power management of hydraulic hybrid mobile machines—Part I: Theoretical studies, modeling and simulation. ASME. J. Dyn. Sys., Meas. Control. 138 (5), 051002. doi:10.1115/1.4032742

CrossRef Full Text | Google Scholar

Hippalgaonkar, R., and Ivantysynova, M. (2016b). Optimal power management of hydraulic hybrid mobile machines—Part II: Machine implementation and measurements. ASME. J. Dyn. Sys., Meas. Control. 138 (5), 051003. doi:10.1115/1.4032743

CrossRef Full Text | Google Scholar

Ho, T. H., and Ahn, K. K. (2010). Modeling and simulation of hydrostatic transmission system with energy regeneration using hydraulic accumulator. J. Mech. Sci. Technol. 24, 1163–1175. doi:10.1007/s12206-010-0313-8

CrossRef Full Text | Google Scholar

Irizar, V., and Andreasen, C. S. (2017). Hydraulic pitch control system for wind turbines: Advanced modeling and verification of an hydraulic accumulator. Simul. Model. Pract. Theory 79, 1–22. ISSN 1569-190X. doi:10.1016/j.simpat.2017.09.002

CrossRef Full Text | Google Scholar

Kogler, H., and Scheidl, R. (2016). Energy efficient linear drive Axis using a hydraulic switching converter. ASME. J. Dyn. Sys., Meas. Control. 138 (9), 091010. doi:10.1115/1.4033412

CrossRef Full Text | Google Scholar

Leon-Quiroga, J., Newell, B., Krishnamurthy, M., Gonzalez-Mancera, A., and Garcia-Bravo, J. (2020). Energy efficiency comparison of hydraulic accumulators and ultracapacitors. Energies 13, 1632. doi:10.3390/en13071632

CrossRef Full Text | Google Scholar

Lin, T., and Wang, Q. (2012). Hydraulic accumulator-motor-generator energy regeneration system for a hybrid hydraulic excavator. Chin. J. Mech. Eng. 25, 1121–1129. doi:10.3901/cjme.2012.06.1121

CrossRef Full Text | Google Scholar

Liu, Y., Xu, Z., Hua, L., and Zhao, X. (2020). Analysis of energy characteristic and working performance of novel controllable hydraulic accumulator with simulation and experimental methods. Energy Convers. Manag. 221, 113196. ISSN 0196-8904. doi:10.1016/j.enconman.2020.113196

CrossRef Full Text | Google Scholar

Pfeffer, A., Glück, T., Kemmetmüller, W., and Kugi, A. (2016). Mathematical modelling of a hydraulic accumulator for hydraulic hybrid drives. Math. Comput. Model. Dyn. Syst. 22 (5), 397–411. doi:10.1080/13873954.2016.1174716

CrossRef Full Text | Google Scholar

Porumamilla, H., Kelkar, A. G., and Vogel, J. M. (2008). Modeling and verification of an innovative active pneumatic vibration isolation system. ASME. J. Dyn. Sys., Meas. Control. 130 (3), 031001. doi:10.1115/1.2807049

CrossRef Full Text | Google Scholar

Pourmovahed, A., Beachley, N. H., and Fronczak, F. J. (1992). Modeling of a hydraulic energy regeneration system: Part I—analytical treatment. ASME. J. Dyn. Sys., Meas. Control. 114 (1), 155–159. doi:10.1115/1.2896497

CrossRef Full Text | Google Scholar

Ren, H., Lin, T., Zhou, S., Huang, W., and Miao, C. (2018). Novel automatic idle speed control system with hydraulic accumulator and control strategy for construction machinery. Appl. Sci. 8, 496. doi:10.3390/app8040496

CrossRef Full Text | Google Scholar

Shen, W., Jiang, J., Su, X. 2, and Karimi, H. R. (2013). Energy-saving analysis of hydraulic hybrid excavator based on common pressure Rail. Sci. World J. 2013, 1–12. doi:10.1155/2013/560694

CrossRef Full Text | Google Scholar

Sprengel, M., and Ivantysynova, M. (2013). “Investigation and energetic analysis of a novel hydraulic hybrid architecture for on-road vehicles,” in The 13th Scandinavian International Conference on Fluid Power, SICFP2013, Linkoping, Sweden, June 3-5; 2013.

CrossRef Full Text | Google Scholar

U.S. Environmental Protection Agency (2020). How series hydraulic hybrid vehicles work. Web Page, Available at: https://archive.epa.gov/otaq/technology/web/html/how-it-works.html (Accessed January 10, 2023).

Google Scholar

Van de Ven, J. D. (2013). Constant pressure hydraulic energy storage through a variable area piston hydraulic accumulator. Appl. Energy 105, 262–270. ISSN 0306-2619. doi:10.1016/j.apenergy.2012.12.059

CrossRef Full Text | Google Scholar

Wendel, G. R. (2002). “Hydraulic system configurations for improved efficiency,” in Proceedings of the 49th National Conference on Fluid Power – NCFP, USA, 567–573.

CrossRef Full Text | Google Scholar

Yu, Y. X., and Ahn, K. K. (2020). Energy regeneration and reuse of excavator swing system with hydraulic accumulator. Int. J. Precis. Eng. Manuf.-Green Tech. 7, 859–873. doi:10.1007/s40684-019-00157-7

CrossRef Full Text | Google Scholar

Yudell, A. C., and Van de Ven, J. D. (2017). Soft switching in switched inertance hydraulic circuits. ASME. J. Dyn. Sys., Meas. Control. 139 (12), 121007. doi:10.1115/1.4036887

CrossRef Full Text | Google Scholar

Zhao, D., Ge, W., Mo, X., Liu, B., and Dong, D. (2019). Design of A New hydraulic accumulator for transient large flow compensation. Energies 12 (16), 3104. doi:10.3390/en12163104

CrossRef Full Text | Google Scholar