Numerical realization of a semi-active virtual acoustic black hole effect

Noise mitigation by means of the acoustic black hole (ABH) effect is a well-known engineering solution. However, the conventional method of applying ABH effect which requires modification of the structure geometry has various limitations which encourage the research of virtual ABH concept. In this study, the effect of ABH was applied through introducing virtual stiffness by a shunt circuit. According to the force-voltage electric analogy, stiffness has an inverse relationship with capacitance. So that the ABH effect can be virtually realized by following a power law profile using an array of independent capacitive shunts. The concept is studied through finite element simulation developing a macro code in ANSYS Parametric Design Language (APDL). To evaluate the influence of capacitance profile on the acoustic radiated power, parametric studies are conducted. Based on the results of the parametric studies, the capacitance profile is tuned for minimum radiated power. It is revealed that the virtual acoustic black hole (ABH) effect can offer 10.29%, 6.37%, and 7.47% reduction in the radiated power from the first to the last targeted mode, respectively. The virtual ABH effect introduced in this study can be used for semi-active structural noise isolation without any weight or manufacturing penalty.

1 Introduction

The increasing requirement for noise management in industries has led to a substantial research being conducted on noise cancellation methods (Simons and Waters, 2004; Wang, 2010; Towers et al., 2021). Sound emission can be generally classified to structure-borne and air-borne noise. Structure-born noise occurs when a mechanism vibrates due to direct mechanical contact with the vibration source. Air-borne noise is produced by a source which radiates directly to the air (Berendt et al., 1967). Usually, the structure-borne noise requires significant attention since it is a low-frequency tonal noise which cannot be controlled by conventional barrier or insulation methods (Ngai and Ng, 2003; Fathiah Waziralilah et al., 2018). Passive techniques are often adopted to dampen the structure-borne noise despite a significant weight penalty often associated.

The effectiveness of electronic damping as a low-cost and lightweight passive technique is examined for its vibroacoustic attenuation effect by many authors (Park and Inman, 2003; Zhao et al., 2016; Suryakant et al., 2022). A case study revealed 7 dB reduction in sound transmission achieved by a shunt circuit for a clamped plate excited by a sound source in the frequency range of 10–1,000 Hz (Ahmadian and Jeric, 2001). Another study revealed at least a 57% reduction in radiated noise for a clamped plate excited by a shaker in the frequency range of 0–245 Hz (Ahmadian et al., 2001).

Another efficient solution for noise cancellation is the acoustic black hole (ABH) effect, a passive, lightweight, and economic technique. According to the ABH effect theory, the vibration wave can be focalized and diminished to zero due to an exponential reduction in the host structure thickness (Li and Ding, 2018; Hook et al., 2019; Mousavi et al., 2022). The thickness exponential function and position of ABH are determinative factors for the amount of energy trapped (Rothe et al., 2016; Liang et al., 2022). There exist several restrictions in the introduction of the ABH effect to the geometry. The dependency of ABH profile position on its efficiency limits its isolation effect to a few modes of resonance (Zhang et al., 2019; Gao et al., 2022). Another shortcoming of the ABH effect is its inadequacy at low frequencies (Denis et al., 2014; Li et al., 2021; Liang et al., 2021). In one study, the effective frequency range of ABH is broadened by integrating shunt damping and transferring the energy from low to high frequencies (Zhang et al., 2022). An inevitable condition for ABH geometries is that the host structure must be large enough to allow carving out the power law profile which is a limitation in vehicle and aero applications (Ji et al., 2018; Park et al., 2019). This constraint is overcome partially by using ABH-inspired active electronic dampening in conjunction with the force-current electric analogy by Maugan et al. (2019).

The use of semi-active systems, also known as adaptive systems, for noise isolation has received attention in the last decade (Bein et al., 2008; Zhu et al., 2017; Wrona et al., 2021a). With the help of semi-active systems, certain resonant peaks can be attenuated while also adverse impacts of vibration absorbers on non-target modes may be prevented. Using the shunt technique in an adaptive manner, one may absorb noise and vibration at various modes by proper adjustment of the shunt circuit impedances (Soong and Spencer, 2000; Corr and Clark, 2001; Niederberger et al., 2003; Bein et al., 2008). Optimizing tuning variable which determines the control states is a common task for semi-active shunt approach (Gonzalez-Buelga et al., 2014). The control states can consist of ON and OFF modes (Wrona et al., 2021b), or it can take several states as reported by Li and Zhu (2021) using a rheostat to introduce numerous resistance levels.

Limitations associated with physical ABH execution such as low-frequency inefficiency (Denis et al., 2014; Li et al., 2021; Liang et al., 2021), space occupation (Ji et al., 2018; Park et al., 2019), and tunability to narrow frequency ranges (Zhang et al., 2019; Gao et al., 2022) motivates the research to apply the ABH effect virtually through a semi-active strategy.

In the present study, a beam structure is covered by an array of piezoelectric elements shunted by capacitors to impose the power law stiffness profile virtually. To attenuate the three resonant peaks of the beam which contribute in the radiated noise, the shunt circuit is tuned in terms of power law function. The present approach can be applied to ultra-thin structures where physically applying the ABH effect is impossible. To the best of our knowledge, this is the first study to introduce the concept of virtual ABH effect integrated with force-voltage analogy as a semi-active noise mitigation approach.

2 Materials and methods

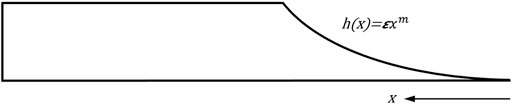
To explain the ABH effect, consider a wedge whose variable thickness follows a power law profile as $h\left(x\right)=\epsilon x^m$ (ε and m > 0 ), shown by Figure 1. If $k\left(x\right)$ is the local wave number of a flexural wave, the total wave transit time through the wedge can be derived by Eq. 1.

$\tau ={\int }_0^{x}k\left(x\right)dx(1)$

FIGURE 1

FIGURE 1. Ideal wedge shape with power law profile.

Considering k_p as the wave number of quasi-longitudinal waves, the local wave number can be expressed by Eq. 2 for a wedge with a power-law profile.

$k\left(x\right)={12}^{\frac{1}{4}}{k}_p{\left(\epsilon x^m\right)}^{-1/2}(2)$

By substitution of Eq. 2 into Eq. 1, it can be seen that the integral diverges for $m\ge 2$. It means that if the wedge is designed ideally, the wave never reaches the edge. This perfect absorption is known as ABH effect which is imposed by geometry (Krylov and Tilman, 2004).

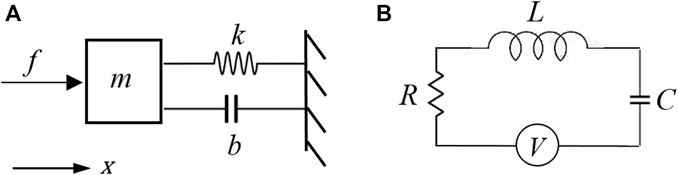
In the present study it is of interest to introduce the ABH effect imposed not by geometry but by applying the electric analogy. In this regard, consider a dynamic system consisting of a mass (m), a spring (k), and a damper (b) subjected to the excitation f as given by Figure 2A. Moreover, take a basic electric circuit with resistance (R), inductance (I), capacitance (C), subjected to a voltage V as given by Figure 2B.

FIGURE 2

FIGURE 2. (A) Basic dynamic system, (B) analogeous electrical circuit.

The force-voltage analogy can be established as

$F\approx V(3)$

Eq. 3 can be derived as

$m\left(\frac{d^{2}x}{d{t}^2}\right)+b\left(\frac{dx}{dt}\right)+kx\approx \left(L\left(\frac{di}{dt}\right)+Ri+\frac{1}{C}\int idt\right)(4)$

Hence, Eq. 4 implies that capacitance is relevant to the reverse of stiffness (Darleux et al., 2022).

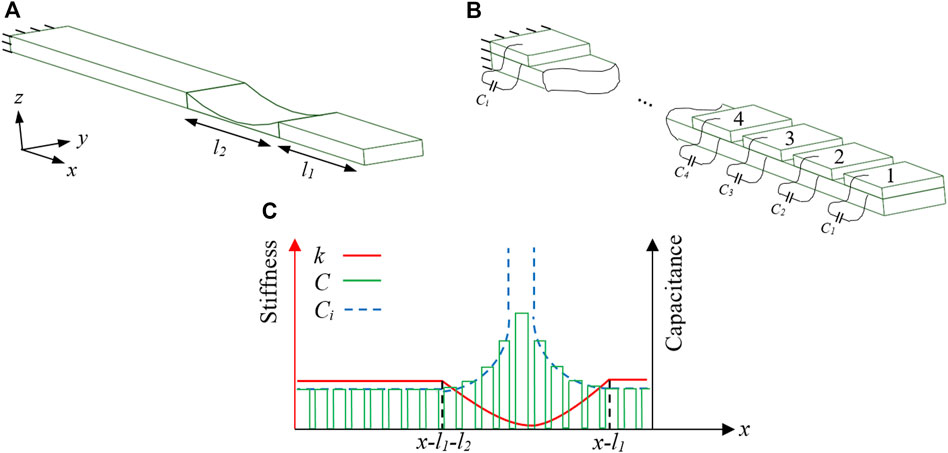
In this regard, the ABH effect imposed by geometry (see Figure 3A) is virtually defined by considering i number of piezoelectric elements with equal distances attached on a beam surface (see Figure 3B). Each piezoelectric element is shunted independently by a capacitor. The ideal ABH stiffness, ideal capacitance, and real capacitance for the beam structure are well noted by k, C_i, and C, respectively (see Figure 3C). Here, two points should be emphasized for a better understanding of the problem. First, the lower limit of real and ideal capacitance is always non-zero which means an artificial thickness is added along the beam. Second, the maximum value of capacitance is infinite for an ideal ABH (C_i) shown by Figure 3C. However, the present modeling cannot simulate an ideal ABH for two reasons: (a) the beam initial thickness cannot be set to zero, and (b) there is a geometry constraint that corresponds to the distance between piezoelectric patches. So that the maximum capacitance is not infinite but as big as super capacitors.

FIGURE 3

FIGURE 3. (A) physical ABH, (B) virtual ABH, (C) stiffness, and capacitance variations.

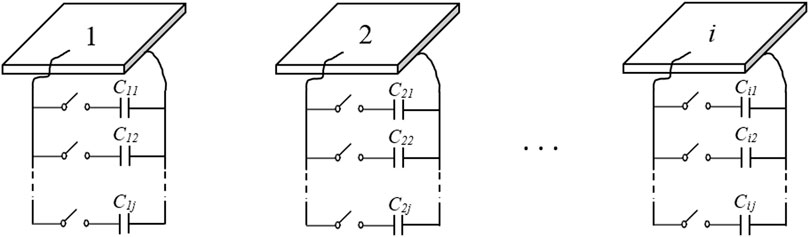
By tuning the capacitive shunt technique, maximum capacitance should be defined at the beam antinode and effective noise isolation is expected, consequently. Since the antinode position is variable from mode to mode, a semi-active scheme can be adopted to change the power law profile, and attenuate several modes. So that the capacitance values can be switched among various states as depicted by Figure 4. To absorb the j^th mode of resonance, a series of i number of capacitors can be considered as {C_1j, C_2j, ..., C_ij}, tunable to the corresponding mode according to power law as indicated by Eq. 5.

$C_{ij}=C_{\mathit{max}}{a_i}^{-n}(5)$

Where C_max is the maximum value of capacitance which can be taken by one or more than one capacitors depending on the target mode to be tuned. Moreover, a_i represents the element of an arithmetic progression, the first term of which is 1 and the difference between terms is r as expressed by Eq. 6.

$a_i=1+\left(i-1\right)r(6)$

FIGURE 4

FIGURE 4. Capacitive shunts apply semi-active scheme applied to shunted piezoelectric elements.

The effectiveness of the proposed semi-active scheme can be evaluated by solving the harmonic analysis of the cantilever beam. The vibrating beam excites the surrounding air and emits noise. The sound power corresponding to the radiated noise can be represented as the integral of the acoustic intensity along the normal direction on a given surface Γ as

$P={\iint }_{\mathit{\Gamma }}\stackrel{\rightharpoonup }{I}.\stackrel{\rightharpoonup }{n}d\mathit{\Gamma }(7)$

where I is the acoustic intensity, $\stackrel{\rightharpoonup }{n}$ is the normal vector, and $\mathrm{\Gamma }$ is the structure-air interface. The power carried by the acoustic wave per unit area in the normal surface direction is known as the acoustic intensity given by (Hambric and Taylor, 1994)

$\stackrel{\rightharpoonup }{I}=\frac{1}{2}RE\left(p.\stackrel{\rightharpoonup }{v}\right)(8)$

where p and v refer to the radiated acoustic pressure, and particle velocity vector of air, respectively. By establishing continuity of velocity at the solid/air interface, the structural velocity will be equaled to air particle velocity as

$v_{s,n}=v_{air}=\frac{p}{{\rho }_{air}{c}_{air}}(9)$

where v_s,n, v_air, ρ_air (1.2041 kg/m3), c_air, and p correspond to the structure normal velocity, air particle velocity, air density, sound speed in air, and acoustic pressure, respectively. The equivalent sound power released from the vibrating structure can be represented as a function of the structure’s vibration velocity by substitution of Eq. 9 into Eq. 8. As employed in this study, the equivalent radiated power (ERP) and its level (ERPL) can be obtained as (Kim et al., 2019)

$ERP=\frac{1}{2}{\rho }_{air}{c}_{air}{\int }_{\mathit{\Gamma }}{\left|v_{s,n}\right|}^{2}d\mathit{\Gamma }(10)$

$ERPL=10\log \left(\frac{ERP}{W_{ref}}\right)\left[dB\right]\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}{W}_{ref}={10}^{-12}\left[\mathrm{W}\right](11)$

The present study proposes a finite element solution using APDL¹ to solve the harmonic problem. By finite element discretization of the integral in Eq. 10, the power radiated all over the 3D beam faces can be calculated.

To minimize the radiated power, the power law profile of capacitance is required to be optimally tuned. By substitution of Eq. 6 into Eq. 5, the capacitance profile can be expressed as

$C_{ij}=C_{\mathit{max}}{\left(1+\left(i-1\right)r\right)}^{-n}(12)$

So that optimization of parameters r and n can offer minimum radiated noise. The area under frequency reponse curve which has been used as a performance measure in some studies (Joshi et al., 2010; Sarigul et al., 2018), is considered as the optimization objective function. The optimization algorithm is provided by Eq. 13.

$\left\{\begin{array}{c}\mathit{Min}U\\ U={\int }_{f_{\mathit{min}}}^{f_{\mathit{max}}}ERPdf,\hspace{1em}{U}_{\mathit{min}}=U\left(C_{opt}\right)\\ f_{\mathit{min}}+f_{\mathit{max}}=2f_{resonance}\end{array}\right.(13)$

Where C_opt can be obtained based on optimum values of r and n. Thus, for semi-active noise isolation, the optimization must be conducted for frequency intervals centered by the resonance frequency. Then, the semi-active treatment function for a frequency range including N number of eigenfrequencies can be expressed as follows.

$C_{semi-active}={\displaystyle \sum }_{i=1}^N\left(C_{{opt}_i}{H}^{*}+C_{SHC}\left(1-H^{*}\right)\right)(14)$

Where H^* is a distribution function defined by Heaviside functions as given by Eq. 15.

$H^{*}=Heaviside\left(f-f_{\mathit{min}}\right)+Heaviside\left(f-f_{\mathit{max}}\right)(15)$

The semi-active function (Eq. 14) allows to select the frequency intervals for isolation based on the optimal capacitance profile, and deselect the frequency intervals where the isolator is not effective by short-circuiting the piezo-patches. Accordingly, the short circuit capacitance equals to zero (C_SHC). Therefore, the semi-active treatment function can be expressed as

$C_{semi-active}={\displaystyle \sum }_{i=1}^N{C}_{{opt}_i}{H}^{*}(16)$

3 Results

At first, a validation study is carried out to check the accuracy of present numerical modeling. Next, the numerical model for realization of ABH effect is introduced and considered for parametric studies. Based on optimization of parametric studies results, a semi-active noise treatment is applied.

3.1 Validation of numerical modeling

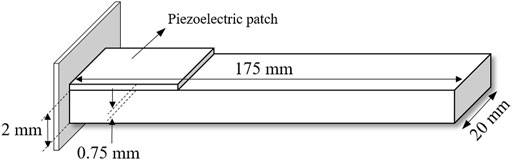
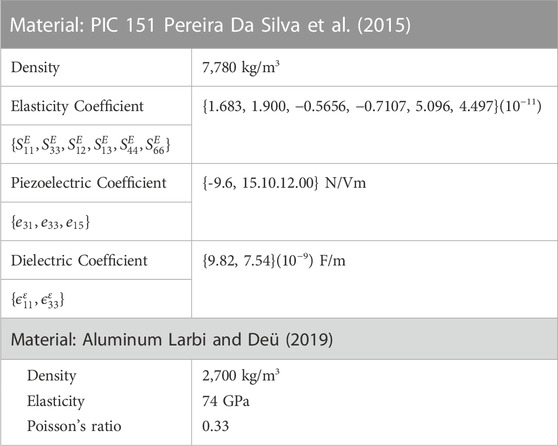
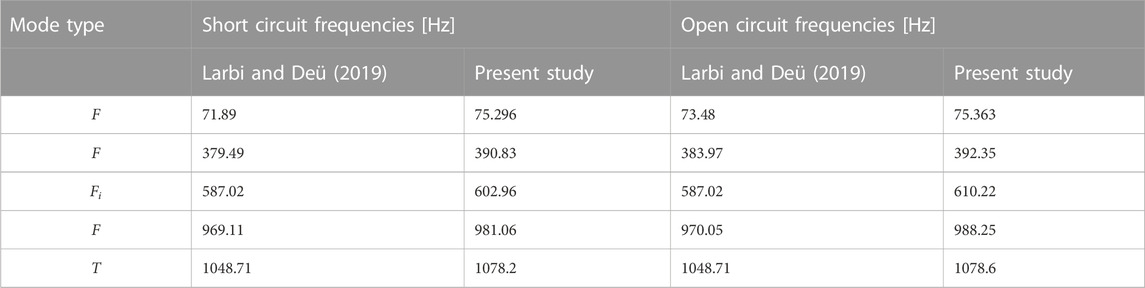
The present numerical model has been validated by comparison with numerical findings reported by Larbi and Deü (Larbi and Deü, 2019). Using solid elements for the host structure and Circu94 elements for the piezoelectric patch, calculations have been made for the eigenanalysis of a cantilever steel beam with a piezoelectric PIC 151 ceramic patch (see Figure 5) which properties are given by Table 1. Both open- and short-circuit conditions are considered to obtain the results for the eigenanalysis. The discrepancy of results reported by Table 2 attributes to different finite element modeling techniques as well as different elements type and number.

FIGURE 5

FIGURE 5. Cantilever beam with piezoelectric element attachment: dimensions.

TABLE 1

TABLE 1. Material properties for the cantilever beam and piezoelectric ceramic patch.

TABLE 2

TABLE 2. Verification of numerical simulation for a cantilever with open/short shunt circuit.

3.2 Numerical realization of virtual ABH effect

For the numerical realization of virtual ABH effect, a steel cantilever beam with L_b = 11.19 cm length, W_b = 5 mm width, and T_b = 1 mm thickness is assumed. The beam is covered by 20 piezoelectric elements with L_p = 5 mm edge length, and T_p = 0.3T_b thickness positioned at equal distances to each other. The beam is excited by harmonic out-of-plane displacement applied at the free end. A structural damping coefficient of 0.01 is adopted (Devasia et al., 1993).

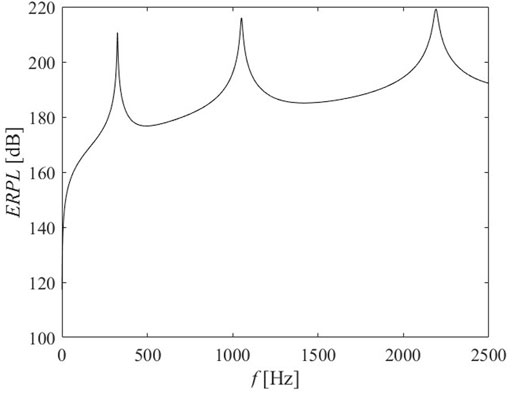
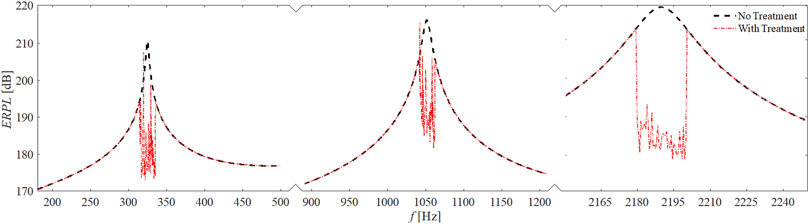
The ERPL response for the beam structure with shorted shunt circuit is presented by Figure 6. As a result, the three eigenmodes dominant in the ERPL response are targeted for attenuation.

FIGURE 6

FIGURE 6. ERPL response of the beam when the shunt circuit is shorted.

3.2.1 Parametric study

Parametric studies are carried out to figure out the influence of power law formulation constants (n and r) described by Eq. 12, on the structure response. In this regard, particular capacitance profiles assigned for the first three modes of resonance which contribute to the overall radiated noise are given by Figure 7. The capacitance profiles are minimum and maximum at nodes and antinodes of vibration displacement mode shape, respectively. Between each node and antinode, the capacitance varies according to power law formulation.

FIGURE 7

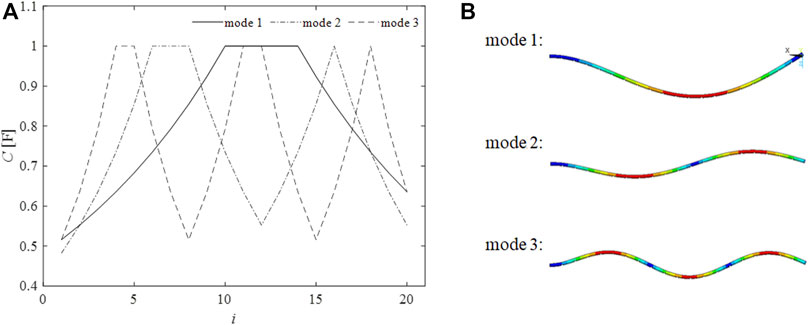
FIGURE 7. (A) Capacitance profiles (r = 0.02, n = 4) adopted for different resonance modes, (B) eigenmode shapes.

The results of parametric studies are reported by Figures 8–13. It is well revealed that the capacitance profile constants (n and r) are the tuning parameters responsible for the radiated power response. Compared to the short-circuit case, the application of virtual ABH effect results a heavily fluctuant response due to trapping the elastic wave.

FIGURE 8

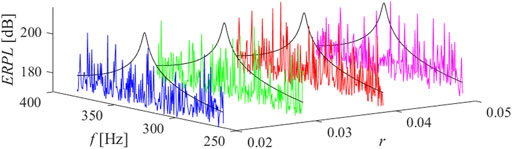
FIGURE 8. ERPL around the first mode of resonance, n = 4, ̶ short circuit, ̶ r = 0.02, ̶ r = 0.03, ̶ r = 0.04, ̶ r = 0.05.

FIGURE 9

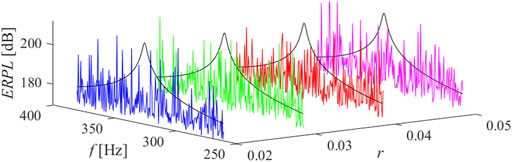
FIGURE 9. ERPL around the first mode of resonance, n = 5, ̶ short circuit, ̶ r = 0.02, ̶ r = 0.03, ̶ r = 0.04, ̶ r = 0.05.

FIGURE 10

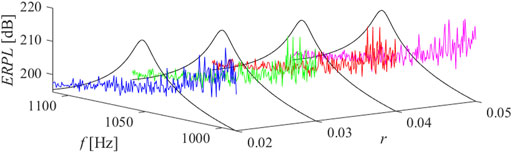
FIGURE 10. ERPL around the second mode of resonance, n = 4, ̶ short circuit, ̶ r = 0.02, ̶ r = 0.03, ̶ r = 0.04, ̶ r = 0.05.

FIGURE 11

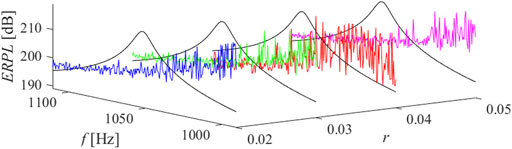
FIGURE 11. ERPL around the second mode of resonance, n = 5, ̶ short circuit, ̶ r = 0.02, ̶ r = 0.03, ̶ r = 0.04, ̶ r = 0.05.

FIGURE 12

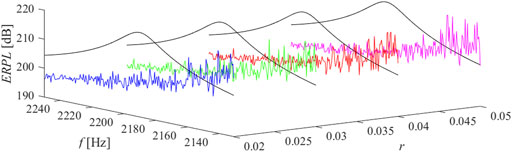
FIGURE 12. ERPL around the third mode of resonance, n = 4, ̶ short circuit, ̶ r = 0.02, ̶ r = 0.03, ̶ r = 0.04, ̶ r = 0.05.

FIGURE 13

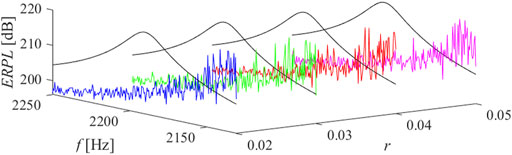
FIGURE 13. ERPL around the third mode of resonance, n = 5, ̶ short circuit, ̶ r = 0.02, ̶ r = 0.03, ̶ r = 0.04, ̶ r = 0.05.

3.2.2 Semi-active noise isolation

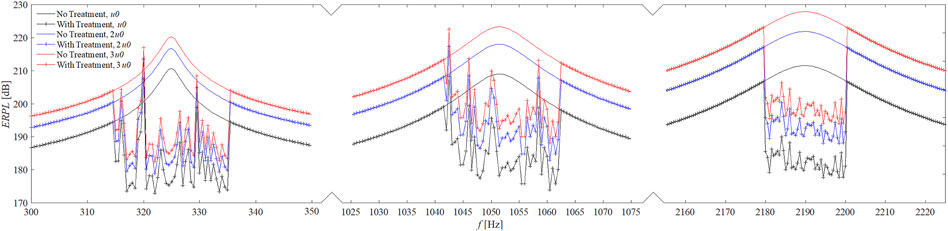
The results of parametric studies reported by Figures 8–13 are considered for optimization. So that the optimal values of r and n are chosen for each mode of resonance. The vibrating beam is treated semi-actively considering optimal parameters of (r, n) taken as (0.02, 5), (0.04, 5), and (0.05, 4), respectively for the first, the second and the third targeted modes of resonance. The treatment is applied at the vicinity of resonance with a radius of 10 Hz. The semi-active treatment function is expressed as follows.

$\begin{array}{l}{C}_{semi-active}=C_{\left(r=0.02,n=5\right)}*\left(H^{*}\left(f-315\right)+H^{*}\left(f-335\right)\right)\\ +\dots C_{\left(r=0.04,n=5\right)}*\left(H^{*}\left(f-1042\right)+H^{*}\left(f-1062\right)\right)\\ +\dots C_{\left(r=0.05,n=4\right)}*\left(H^{*}\left(f-2180\right)+H^{*}\left(f-2200\right)\right)\end{array}(17)$

The results of this semi-active treatment is represented by Figure 14. The radiated power is attenuated by the rates of 10.29%, 6.37%, and 7.47% from the first to the last targeted modes, respectively.

FIGURE 14

FIGURE 14. ERPL frequency response with and without semi-active treatment.

In order to assess the influence of loading, harmonic excitations with $u_0$, and ${2u}_0$ amplitudes are imposed. The results reported by Figure 15 indicate the system is linear for all studied resonances with and without treatment.

FIGURE 15

FIGURE 15. ERPL frequency response with different excitation amplitudes.

4 Conclusion

A numerical model is developed to realize the ABH effect virtually with the help of capacitive shunt circuits. The main objective is to attenuate structure-born noise for several resonance modes by proposing a semi-active approach. Theoretically, virtually imposing the ABH effect is feasible through the electrical analogy which equalizes stiffness with capacitance.

A noteworthy advantage of virtual ABH effect is the potential for semi-active use which is obviously impossible with the ABH effect imposed by geometry. In addition, the geometrical restrictions related to the physical manifestation of the ABH effect do not apply to the virtual method.

For two main reasons the virtual ABH effect deviates from the ideal ABH effect: 1. Since the energy conversion rate in piezoelectric material is not 100%, the ABH effect can never be idealized. 2. The capacitance profile is discrete along the beam due to the distance between piezoelectric elements which is unavoidable.

The results of present numerical modeling for the first eigenmodes which contribute in overall radiated noise revealed at least 6.37% improvement for noise radiation. The attenuation is well achieved by breaking down each peak to many more peaks which results an effective absorption effect. Although the present approach targets the first three eigenmodes, expanding the effective frequency range requires an increasing of the number of piezo-patches to tune the shunt impedance with respect to the eigenmode shapes.

Finally, due to the weight and space limitation in vehicle and aero applications, the structures are too thin to be carved out for an ABH geometric profile. Thus, the virtual ABH effect can be considered as a solution not only to overcome the mentioned restriction, but also to apply a multi-mode structural noise isolation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SS conceived and formulated the problem, developed the macro-code, analyzed the results, and wrote the paper. GP, FF, and SD supervised the research work as academic supervisors and reviewed the manuscript. PK supervised the research as an industry supervisor.

Funding

This project has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 860243.

Acknowledgments

The author would like to acknowledge all the Institutions and Partners involved within the LIVE-I project.

Conflict of interest

Author PK was employed by the company Adaptronica sp z o o, R&D Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹ANSYS Parametric Design Language.

References

Ahmadian, M., and Jeric, K. M. (2001). Effect of shunted piezoelectric materials on increasing sound transmission loss. Smart Struct. Mater. 4331, 273–280. doi:10.1117/12.432710

CrossRef Full Text | Google Scholar

Ahmadian, M., Jeric, K. M., and Inman, D. J. (2001). An experimental evaluation of smart damping materials for reducing structural noise and vibrations. J. Vib. Acoust. Trans. ASME 123, 533–547. doi:10.1115/1.1389459

CrossRef Full Text | Google Scholar

Bein, T., Bös, J., Herold, S., Mayer, D., Melz, T., and Thomaier, M. (2008). Smart interfaces and semi-active vibration absorber for noise reduction in vehicle structures. Aerosp. Sci. Technol. 12, 62–73. doi:10.1016/j.ast.2007.10.008

CrossRef Full Text | Google Scholar

Berendt, R. D., Winzer, G. E., and Burroughs, C. B. (1967). A Guide to Airborne, Impact, and Structure Borne Noise-control in Multifamily Dwellings: Prepared for the Federal Housing Administration. Washington, DC: US Department of Housing and Urban Development.

Google Scholar

Corr, L. R., and Clark, W. W. (2001). Energy dissipation analysis of piezoceramic semi-active vibration control. J. Intell. Mater. Syst. Struct. 12, 729–736. doi:10.1177/104538901400438028

CrossRef Full Text | Google Scholar

Darleux, R., Lossouarn, B., Giorgio, I., dell’Isola, F., and Deü, J. F. (2022). Electrical analogs of curved beams and application to piezoelectric network damping. Math. Mech. Solids 27, 578–601. doi:10.1177/10812865211027622

CrossRef Full Text | Google Scholar

Denis, V., Pelat, A., Gautier, F., and Elie, B. (2014). Modal Overlap Factor of a beam with an acoustic black hole termination. J. Sound. Vib. 333, 2475–2488. doi:10.1016/j.jsv.2014.02.005

CrossRef Full Text | Google Scholar

Devasia, S., Meressi, T., Paden, B., and Bayo, E. (1993). Piezoelectric actuator design for vibration suppression: Placement and sizing. J. Guid. Control. Dyn. 16, 859–864. doi:10.2514/3.21093

CrossRef Full Text | Google Scholar

Fathiah Waziralilah, N., Abu, A., Quen, L. K., Unuh, M. H., and Hee, L. M. (2018). Suppression of structure-borne noise in a rectangular enclosure. IOP Conf. Ser. Mater. Sci. Eng. 409, 012019. doi:10.1088/1757-899X/409/1/012019

CrossRef Full Text | Google Scholar

Gao, W., Qin, Z., and Chu, F. (2022). Broadband vibration suppression of rainbow metamaterials with acoustic black hole. Int. J. Mech. Sci. 228, 107485. doi:10.1016/j.ijmecsci.2022.107485

CrossRef Full Text | Google Scholar

Gonzalez-Buelga, A., Clare, L. R., Cammarano, A., Neild, S. A., Burrow, S. G., and Inman, D. J. (2014). An optimised tuned mass damper/harvester device. Struct. Control Heal. Monit. 21, 1154–1169. doi:10.1002/stc.1639

CrossRef Full Text | Google Scholar

Hambric, S. A., and Taylor, P. D. (1994). Comparison of experimental and finite element structure-borne flexural power measurements for a straight beam. J. Sound. Vib. 170, 595–605. doi:10.1006/jsvi.1994.1089

CrossRef Full Text | Google Scholar

Hook, K., Cheer, J., and Daley, S. (2019). A parametric study of an acoustic black hole on a beam. J. Acoust. Soc. Am. 145, 3488–3498. doi:10.1121/1.5111750

PubMed Abstract | CrossRef Full Text | Google Scholar

Ji, H., Luo, J., Qiu, J., and Cheng, L. (2018). Investigations on flexural wave propagation and attenuation in a modified one-dimensional acoustic black hole using a laser excitation technique. Mech. Syst. Signal Process. 104, 19–35. doi:10.1016/j.ymssp.2017.10.036

CrossRef Full Text | Google Scholar

Joshi, P., Mulani, S. B., Gurav, S. P., and Kapania, R. K. (2010). Design optimization for minimum sound radiation from point-excited curvilinearly stiffened panel. J. Aircr. 47, 1100–1110. doi:10.2514/1.44778

CrossRef Full Text | Google Scholar

Kim, H. G., Nerse, C., and Wang, S. (2019). Topography optimization of an enclosure panel for low-frequency noise and vibration reduction using the equivalent radiated power approach. Mater. Des. 183, 108125. doi:10.1016/j.matdes.2019.108125

CrossRef Full Text | Google Scholar

Krylov, V. V., and Tilman, F. J. B. S. (2004). Acoustic ‘black holes’ for flexural waves as effective vibration dampers. J. Sound. Vib. 274, 605–619. doi:10.1016/j.jsv.2003.05.010

CrossRef Full Text | Google Scholar

Larbi, W., and Deü, J. F. (2019). Reduced order finite element formulations for vibration reduction using piezoelectric shunt damping. Appl. Acoust. 147, 111–120. doi:10.1016/j.apacoust.2018.04.016

CrossRef Full Text | Google Scholar

Li, H., Touzé, C., Pelat, A., and Gautier, F. (2021). Combining nonlinear vibration absorbers and the Acoustic Black Hole for passive broadband flexural vibration mitigation. Int. J. Non. Linear. Mech. 129, 103558. doi:10.1016/j.ijnonlinmec.2020.103558

CrossRef Full Text | Google Scholar

Li, J. Y., and Zhu, S. (2021). Advanced vibration isolation technique using versatile electromagnetic shunt damper with tunable behavior. Eng. Struct. 242, 112503. doi:10.1016/j.engstruct.2021.112503

CrossRef Full Text | Google Scholar

Li, X., and Ding, Q. (2018). Analysis on vibration energy concentration of the one-dimensional wedge-shaped acoustic black hole structure. J. Intell. Mater. Syst. Struct. 29, 2137–2148. doi:10.1177/1045389X18758184

CrossRef Full Text | Google Scholar

Liang, H., Liu, X., Yuan, J., Bao, Y., Shan, Y., and He, T. (2022). Influence of acoustic black hole array embedded in a plate on its energy propagation and sound radiation. Appl. Sci. 12, 1325–1423. doi:10.3390/app12031325

CrossRef Full Text | Google Scholar

Liang, X., Chu, J., Tan, J., Nie, S., Liu, B., Zheng, X., et al. (2021). Spontaneous catastrophe behaviour in acoustic black holes at low frequencies. Appl. Acoust. 180, 108109. doi:10.1016/j.apacoust.2021.108109

CrossRef Full Text | Google Scholar

Maugan, F., Chesne, S., Monteil, M., Collet, M., and Yi, K. (2019). Enhancement of energy harvesting using acoustical-black-hole-inspired wave traps. Smart Mater. Struct. 28, 075015. doi:10.1088/1361-665X/ab1f11

CrossRef Full Text | Google Scholar

Mousavi, A., Berggren, M., and Wadbro, E. (2022). How the waveguide acoustic black hole works: A study of possible damping mechanisms. J. Acoust. Soc. Am. 4279, 4279–4290. doi:10.1121/10.0011788

PubMed Abstract | CrossRef Full Text | Google Scholar

Ngai, K. W., and Ng, C. F. (2003). Structure-borne noise and vibration of concrete box structure and rail viaduct. J. Sound. Vib. 255, 281–297. doi:10.1006/jsvi.2001.4155

CrossRef Full Text | Google Scholar

Niederberger, D., Morari, M., and Pietrzko, S. (2003). Adaptive resonant shunted piezoelectric devices for vibration suppression. Smart Struct. Mater. 5056, 213–224. doi:10.1117/12.483388

CrossRef Full Text | Google Scholar

Park, C. H., and Inman, D. J. (2003). Enhanced piezoelectric shunt design. Shock Vib. 10, 127–133. doi:10.1155/2003/863252

CrossRef Full Text | Google Scholar

Park, S., Kim, M., and Jeon, W. (2019). Experimental validation of vibration damping using an Archimedean spiral acoustic black hole. J. Sound. Vib. 459, 114838. doi:10.1016/j.jsv.2019.07.004

CrossRef Full Text | Google Scholar

Pereira Da Silva, L., Larbi, W., and Deü, J. F. (2015). Topology optimization of shunted piezoelectric elements for structural vibration reduction. J. Intell. Mater. Syst. Struct. 26, 1219–1235. doi:10.1177/1045389X14538533

CrossRef Full Text | Google Scholar

Rothe, S., Ghaffari Mejlej, V., Langer, S. C., and Vietor, T. (2016). Optimal adaptation of acoustic black holes by evolutionary optimization algorithms. Pamm 16, 625–626. doi:10.1002/pamm.201610301

CrossRef Full Text | Google Scholar

Sarigul, A. S., Arpaz, O., and Secgin, A. (2018). “An analysis on the coupled vibro-acoustic response characteristics of cavity-type structures,” in Conference proceedings of the society for experimental mechanics series (Cham: Springer), 476–482. doi:10.15406/paij.2018.02.00127

CrossRef Full Text | Google Scholar

Simons, M. W., and Waters, J. R. (2004). Sound control in buildings - A guide to Part E of the building regulations. London, United Kingdom: Blackwell Publishing.

Google Scholar

Soong, T. T., and Spencer, B. F. (2000). Active, semi-active and hybrid control of structures. Bull. New Zeal. Soc. Earthq. Eng. 33, 387–402. doi:10.5459/bnzsee.33.3.387-402

CrossRef Full Text | Google Scholar

Suryakant, C. N., Singh, A., Ramdas, R., Dighe, K., and Ramamoorthy, S. (2022). Enhanced absorption in structural acoustic silencers using piezo-shunting. J. Acoust. Soc. Am. 152, 1112–1122. doi:10.1121/10.0013573

PubMed Abstract | CrossRef Full Text | Google Scholar

Towers, D., Anderson, D., Thompson, D., and Degrande, G. (2021). Noise and vibration mitigation for rail transportation systems. Cham: Springer.

Google Scholar

Wang, X. (2010). Vehicle noise and vibration refinement. Cambridge, UK: Woodhead Publishing Limited.

Google Scholar

Wrona, S., Pawelczyk, M., and Cheng, L. (2021a). A novel semi-active actuator with tunable mass moment of inertia for noise control applications. J. Sound. Vib. 509, 116244. doi:10.1016/j.jsv.2021.116244

CrossRef Full Text | Google Scholar

Wrona, S., Pawelczyk, M., and Cheng, L. (2021b). Semi-active links in double-panel noise barriers. Mech. Syst. Signal Process. 154, 107542. doi:10.1016/j.ymssp.2020.107542

CrossRef Full Text | Google Scholar

Zhang, L., Kerschen, G., and Cheng, L. (2022). Nonlinear features and energy transfer in an Acoustic Black Hole beam through intentional electromechanical coupling. Mech. Syst. Signal Process. 177, 109244. doi:10.1016/j.ymssp.2022.109244

CrossRef Full Text | Google Scholar

Zhang, Y., Chen, K., Zhou, S., and Wei, Z. (2019). An ultralight phononic beam with a broad low-frequency band gap using the complex lattice of acoustic black holes. Appl. Phys. Express 12, 077002–077005. doi:10.7567/1882-0786/ab2a6d

CrossRef Full Text | Google Scholar

Zhao, G., Alujevia, N., Depraetere, B., Pinte, G., and Sas, P. (2016). Adaptive-passive control of structure-borne noise of rotating machinery using a pair of shunted inertial actuators. J. Intell. Mater. Syst. Struct. 27, 1584–1599. doi:10.1177/1045389X15600080

CrossRef Full Text | Google Scholar

Zhu, Y. W., Zhu, F. W., Zhang, Y. S., and Wei, Q. G. (2017). The research on semi-active muffler device of controlling the exhaust pipe’s low-frequency noise. Appl. Acoust. 116, 9–13. doi:10.1016/j.apacoust.2016.09.011

CrossRef Full Text | Google Scholar

Nomenclature

a_i arithmetic progression element

b damping coefficient

C capacitance

c_air sound speed in air

C_i the capacitance corresponding to the i^th capacitor

C_max maximum capacitance

C_opt Optimal capacitance profile

C_semi-active Semi-active treatment function

F force

H^* A distribution function

I sound intensity

k stiffness

k_p wave number of quasi-longitudinal waves

L inductance

l₁ and l₂ the portions of length on a typical beam

m mass

n the power corresponding to power law

p sound pressure

P sound power

r the common difference between terms in an arithmetic progression

t time

u displacement

v velocity

v_s,n the velocity normal to a surface element

v_air air velocity

V voltage

W_ref reference power

Γ area

ρ_air air density

τ wave transit time through a wedge

Subscriptions

ERP equivalent radiated power

ERPL equivalent radiated power level