Design of artificial vascular devices: Hemodynamic evaluation of shear-induced thrombogenicity

Blood-circulating devices such as oxygenators have offered life-saving opportunities for advanced cardiovascular and pulmonary failures. However, such systems are limited in the mimicking of the native vascular environment (architecture, mechanical forces, operating flow rates and scaffold compositions). Complications involving thrombosis considerably reduce their implementation time and require intensive anticoagulant treatment. Variations in the hemodynamic forces and fluid-mediated interactions between the different blood components determine the risk of thrombosis and are generally not taken sufficiently into consideration in the design of new blood-circulating devices. In this Review article, we examine the tools and investigations around hemodynamics employed in the development of artificial vascular devices, and especially with advanced microfluidics techniques. Firstly, the architecture of the human vascular system will be discussed, with regards to achieving physiological functions while maintaining antithrombotic conditions for the blood. The aim is to highlight that blood circulation in native vessels is a finely controlled balance between architecture, rheology and mechanical forces, altogether providing valuable biomimetics concepts. Later, we summarize the current numerical and experimental methodologies to assess the risk of thrombogenicity of flow patterns in blood circulating devices. We show that the leveraging of both local hemodynamic analysis and nature-inspired architectures can greatly contribute to the development of predictive models of device thrombogenicity. When integrated in the early phase of the design, such evaluation would pave the way for optimised blood circulating systems with effective thromboresistance performances, long-term implantation prospects and a reduced burden for patients.

1 Introduction

Cardiovascular and respiratory diseases are major causes of death worldwide. The demand for grafts and transplantations has never been stronger despite the few donors available. The global transplantation market size is projected to grow by two-fold before 2028 (Market Research Report on Transplantation, Fortune Business Insights, 2021). As a consequence, over the last few years, the medical devices industry has redirected towards the development of extracorporeal blood circuits. These transportation systems aim to replace deteriorated or missing vital functions such as oxygenation or cardiac support. Although mostly used for rapid assistance, artificial circulation systems are intended to temporarily replace the organ function. However, these devices suffer from highly thrombogenic potential, with thrombosis being the leading cause of failure (Jaffer et al., 2015; Hastings et al., 2016; Labarrere et al., 2020). While several strategies to limit blood damage have centred around biocompatible materials and better coatings, another less studied approach focuses on flow path and fluid mechanics (Kuchinka et al., 2021) which will be of interest in this review.

There is a major need to decipher the role of flow field and associated forces on the cellular dynamics in thrombogenic events (Nesbitt et al., 2009; Maxwell et al., 2016; Receveur et al., 2020). Interestingly, physiological vascular system naturally achieves blood circulation with a remarkable efficacy. It indeed demonstrates a high control over biomechanical parameters such as velocity, viscosity or shear forces in a balance manner. When this equilibrium gets affected, thrombosis which is a severe vessel disruption defined by the formation of occlusive clots, can threaten the circulation of the blood. Far from the vascular microcirculation, blood-circulating devices frequently experience occlusive thrombi after an extended period of use. The paths taken by the blood indeed display non-physiologic flows and architectures, which translate into strong mechanical forces. In particular, shear stress alters the interactions between the red blood cells (RBCs), platelets and the channel walls (Fisher and Rossmann, 2009; Kim and Ku, 2022), as well as the cellular diversity which can influence the blood’s intricate rheological properties. Blood-circulating devices such as catheters, membrane oxygenator devices, or cannulas have a fairly wide scope of application to fulfil biological functions including transportation, oxygenation, filtration or flow control, but leaving blood damage underevaluated or unconsidered.

Blood flow fields arising from medical devices design play a role in hypercoagulation and thrombogenicity (Abruzzo et al., 2022; Kuczaj et al., 2022). The underlying mechanisms need to be fully understood to identify parameters influencing these detrimental events. Drawing a comprehensive and spatiotemporal picture of the phenomenon must consider the complexity of blood as a heterogenous suspension, but also the mechanical environment of the blood flow. Blood is formed of solid corpuscles - RBCs, white blood cells, and platelets—in a liquid plasma. Plasma can be described as an aqueous solution of organic molecules, proteins, and salts. How all these components interact together in a dynamic flow is not yet fully understood. Platelets have a pivotal role in thrombosis. These anuclear and discoid blood cells measuring approximately 2–3 µm in diameter act primarily as regulators of hemostasis. In conjunction with endothelial cells (EC) which cover a pro-thrombotic sub-endothelium, platelets actively participate in the initiation of the coagulation cascade. Made from biomaterials, blood-circulating devices walls are rapidly covered with adsorbed proteins, providing sites for interactions. Platelets can engage in a similar shear-dependant bonding in these environments (Van Rooij et al., 2021), triggering a suite of responses including activation of the coagulation cascade, platelet activation and aggregation (Labarrere et al., 2020).

Evaluation of blood damage has greatly evolved since the first experiments performed on blood. From simplified models to complex mechanistic approaches, a large set of metrics to quantify hemolysis and thrombogenic risks are available (Tables 2, 3). Together with increasing insights into complex fluid dynamics and computational tools, blood flow fields characterisation provides novel approaches in shear-induced thrombogenicity evaluation.

2 Biomechanics and architecture: Imitating nature’s hemodynamic and patterns

Artificial blood circulating devices such as ECMO systems minimise the importance of blood preservation aspects naturally achieved by the human vasculature. These devices are often invasive procedures for a patient. as they require a large volume of blood simply to prime the system, in addition to anticoagulant therapy. The blood is continuously removed from the body, pumped through a foreign structure increasing the risk of thrombosis, although fulfilling vital functions (reoxygenation, filtration or transport). Flow field and rheology dictate the hemodynamic properties of any blood path and its thrombogenic nature by extension. Deciphering these intricate mechanisms can provide some answers regarding what enables a safe perfusion, what parameters can threaten flow integrity in in vivo and in vitro (Corti et al., 2022; Valipour, 2022), but most importantly how thrombosis is likely to be formed and how to prevent it. As the main challenge lies in the development of long-lasting vascular devices with a reduced use of anticoagulant, the implementation of biomimetic concepts in medical device design to reduce blood damage, thrombosis and hypercoagulation is one valuable direction. In this section, we will go through biomimetic aspects and discuss the different physiological parameters of fluid flow, with a specific focus on blood-circulation systems.

2.1 Architecture, flow and design principles of the microvascular network

The vascular system is a vast network distributing oxygen and nutrients towards the organs while collecting deoxygenated blood, waste, and carbon dioxide. These essential functions are achieved by diverse structures from the largest arteries close to the heart, to the arterioles and capillaries (whose dimensions allow for an effective diffusion of gas and nutrients). The blood is then brought back to the heart and lungs via venules and veins. Blood distribution is carried out thanks to an impressive ability to downscale the flow path dimensions, guaranteeing a blood perfusion down to the smallest scales of our body with a minimal loss of pressure (Nitzsche et al., 2022). Several studies have characterised and modelled the structure vascular networks evidencing key organisational features to achieve physiological purposes (Wechsatol et al., 2002; Smith et al., 2019; Cury et al., 2021).

2.1.1 Efficient blood delivery

The successive branching and splitting of the largest vessels into smallest enable efficient blood delivery. In the early development stage, the process of vasculogenesis creates a first primitive network, which is completed during vessel sprouting. In hemodynamic analysis, an analogy with electric circuits can be used. The microcirculation is arranged in a set of in-series and in-parallel vessels, where each vascular segment gives rise to a new generation of microvessels (Figure 1). In this analogy, the blood flow rate and pressure drop are equivalent to an electric current and voltage respectively. Dissipative effects due to blood viscosity stand for a hydraulic resistance (Hu et al., 2012). Intuitively, both design and parallelised architecture of the vascular network guarantee a progressive decrease of the total hydraulic resistance throughout the network and greatly enhance the blood flow, as highlighted by Poiseuille’s law (Liu and Jing, 2021; Pozdin et al., 2021). In addition, blood slows down as the total cross-sectional area increases. Vascular damages such as thrombosis or atherosclerosis affect the flow resistance of individual segments operating a partial or complete blockage (acute thrombosis). When examining the contribution of individual vessels regarding the total hydraulic resistance of the network, one can clearly see how much the site of occlusion affects the viability of the whole system. Circulation models were implemented recently to emulate physiological disruptions including thrombotic events over the entire scales ranges of the vascular network. Through the construction of a tree-shaped network, the study led by Rojas et al., provided novel approaches in liver blood circulation, and shed light on the importance of architecture on blood flow distribution and thus hemodynamics. (Torres Rojas et al., 2021). In such architecture, occlusions in the early generations will dramatically impact the hemodynamic properties of all the dependants vessels due to a reduced blood supply (Rojas et al., 2015), whereas localized events in the smallest capillaries have very little effect on the overall resistance of the system.

FIGURE 1

FIGURE 1. Biological allometries related to vascular branching. In largest vessels such as arteries, the pulsative flow is dominant, area-preserving principle allow to minimise wave reflections phenomena. The branching ratio exponent can vary but remains around ½ whether the bifurcations is symmetric or asymmetric. For smallest vessels such as capillaries, the viscous forces are crucial, and the network follow an area-increasing behaviour. Murray’s law is recovered in such conditions.

2.1.2 Allometric scaling for energy minimisation

Allometric scaling refers to phenomenological relationships that govern the structure and features of an organism according to its body mass. A broad theory of biological allometries have been applied to the human vascular network, which similar to plants, has evolved towards an optimal arrangement of vessels (Hughes, 2015; Razavi et al., 2018; Chaui-Berlinck and Bicudo, 2021). Metabolic allometric scaling, which drives the amount of energy and materials taken from a system, is perhaps the most fundamental assumption (Saghian et al., 2022). Thus, the overall network architecture obeys design principles to minimise energy loss and maximise space-filling to ensure effective distribution of oxygen and nutrients to physiological entities. Two contributions to energy loss can be distinguished and are presented in Figure 2: dissipation and wave reflection. While dissipation accounts for the majority of energy lost in small capillaries where the surface-to-volume ratio is the highest, wave reflection has a greater influence in pulsative flow conditions, such as in arteries (Savage et al., 2008).

FIGURE 2

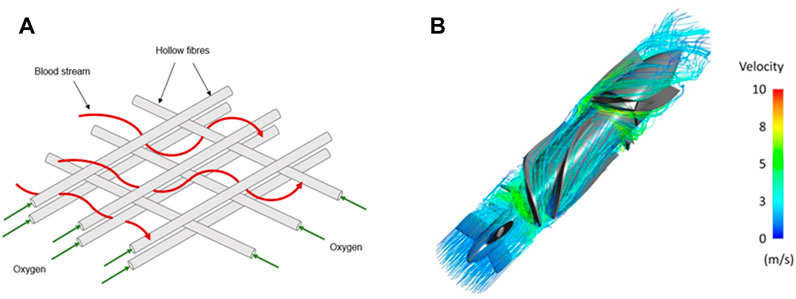
FIGURE 2. Blood streamlines in classical blood-circulating devices. Blood stream navigating through a compact net of hollow fibres transporting oxygen in classical EMCOs (A) or blood pump (B). In both cases, blood undergoes major flow disturbances that include expansions and constrictions. Panel B is modified from Romanova et al., 2022.

First introduced by Hess-Murray in 1926, the principle of minimum work within a vascular system was derived. It accounts for the metabolic costs involved in the maintenance of the blood in the vessel and the dissipation by friction generated by the bifurcations. The theory of dissipation minimisation takes the form of a power law connecting the radii of a parent and n daughter vessels at a branching point with a ratio $n^{-1/3}$ (Figure 2). It also implies a shear constant (for symmetrical bifurcation) and area-increasing behaviour that is dominant in the smallest vessels (Murray, 1926). In mammals, this feature reduces blood flow in the capillaries to levels allowing adequate oxygenation and metabolite transport. A general model for biological allometries was later developed by West, Brown and Enquist (WBE) and attributes a well-known allometric scaling exponent of $3/4$ relating metabolic rate to body mass (West et al., 1997). Interestingly, general branching features in biological networks across plants and animals display analogous features under WBE framework, including area-preservation, despite different physiological aims (Brummer et al., 2021). Detailed upon space-filling principle, WBE model gives a description of pulsative networks such as aorta and arteries resulting in branching nodes with a ratio $n^{-1/2}$ when minimising wave reflection (West et al., 1997). While symmetrical bifurcation was a core assumption of WBE theory, asymmetric branching also shows a convergence to the same metabolic scaling exponent (Brummer et al., 2017).

It is clear that the transition between area-preserving to area-increasing remains an issue in the global description of biological networks. Nevertheless, it is established that blood is much slower to enable oxygenation in the capillaries than in the aorta suggesting area-increasing branching is necessary somewhere in the network. In addition, the mere fact that vascular networks exhibit a non-uniform shear distribution and increased as the vessels reach the capillary size (arteries: 10s^-1, capillaries: 2,000 s^-1 (Doriot et al., 2000; Reneman and Hoeks, 2008; Sakariassen et al., 2015)) confirm the difficulties to predict where the transition would occur regarding the flow regime. Additionally, the observations carried out by Zamir and colleagues pointed out that the cube exponent in the power law proposed by Murray was incompatible with the whole vascular system and was likely varying along the tree (Zamir et al., 1992). Such deviations from the cubic exponent were observed in arterial bifurcations where the velocity is higher than in the rest of the vascular tree. At these junctions, the optimal exponent showed to be closer to two, climbing to three in the arterioles and capillaries, confirming that the predictions of Hess-Murray’s law are closer to reality for the smallest scales of our body (Roy and Woldenberg, 1982; Reneman and Hoeks, 2008; Sciubba, 2016). This range of variation could even be extended in case of vascular damage and severe thrombotic events.

2.2 Fluid shear stress in blood vessels

When blood circulates in a vessel, the vascular endothelium and circulating cells experience strong hemodynamic forces modulated by the vessel morphology and the mechanical environment. Among them, shear stress is a frictional force per unit of surface applied to each fluid particle whenever a fluid is set in motion. A moving fluid experiences drag forces on solid boundaries identified as wall shear stress (WSS), and will not have any velocity relative to the surface in contact (no-slip condition). It is well established that fluid shear stress plays a critical role in vascular physiology (Roux et al., 2020). The mechanical constraints are perceived and interpreted by endothelial and circulating cells determining their behaviour, fate, and phenotype through mechano-sensing pathways (Chistiakov et al., 2017; Mehta et al., 2021; Support et al., 2021; Swain and Liddle, 2021; Haroon et al., 2022). In addition, the diversity of vessel architecture and network exposes the blood to various flow patterns and, as a result, imposes mechanical constraints. Interestingly, vessel bifurcations, branching nodes and curvatures are very sensitive regions of the vascular network, where blood flow is likely to be disturbed. It includes low and oscillatory shear stress (LOSS), which are often related to major phenotypic alterations (Edgar et al., 2021; Strecker et al., 2021; Kumar et al., 2022). The shear magnitude is also altered in smallest vessels, resulting from the natural scale reduction or from partially obstructed and stenotic vessels (Ebrahimi and Bagchi, 2022). The latter can cause a sudden increase in local shear stress enhancing thrombotic risks: concentration of coagulation agonists by reduction of blood velocity, deficiency of vascular integrity and alteration of blood constituent phenotype (Davies, 2009).

2.3 Rheology in vascular networks

Blood rheology refers to the mechanical behaviour of blood when flowing. The fluid properties vary depending on the constraints applied and dimensions, altering its velocity profile, viscosity and force repartition along the stream. In cannula or centrifugal pumps, blood perfusion systems have macroscopic dimensions and operate at fairly high flow rates. The bulk viscosity of blood is the viscosity witnessed when flowing in vessels much larger than the suspended particles. In this case, and in flows operating at shear rates above 100 s^-1, blood can be considered as a continuum and a Newtonian assumption is generally legitimate (Mandal, 2005). Alternatively, in microfluidic-based biomimetic platforms, the blood circulating network displays smaller dimensions where flow is dominated by the effects of viscosity. In such cases, non-Newtonian behaviour is considered since viscous interactions outweigh inertial forces. Many in vitro systems using high shear rates are employed to model stenosed vessels, and where non-Newtonian could be emphasised (Receveur et al., 2020; Van Rooij et al., 2021; Zhao et al., 2021). It is thus clear that optimisation of microscale blood-circulating devices requires the consideration of such rheological features.

Particle size brings an intrinsic complexity: non-Newtonian properties of the blood become even more important and determinant when the fluidic circuit has dimensions approximately around 10 microns, which corresponds to the average diameter of a RBC (Pries et al., 1989). In contrast with RBCs, individual platelets have little influence on blood rheology due to their small size and relatively low concentration (1%–2% of the blood volume). Several models have been employed to characterise blood rheology (Lecarpentier et al., 2016; Liu et al., 2021; Pialot et al., 2021). It is generally accepted that blood acts as a shear-thinning fluid, a decrease of its apparent viscosity is observed as the shear rate magnitude increases (Fisher and Rossmann, 2009) (Figure 1).

Hematocrit also participates in the hemodynamic interactions inside blood capillaries (Boal, 2001; Spann et al., 2016; Bouchnita et al., 2021). Known to fluctuate from one patient to another, hematocrit can reach 45% and can significantly modify the rheological properties of blood, including its viscosity and cellular interactions (Nader et al., 2019; Trejo-soto and Hernández-machado, 2022). In fact, the impact of hematocrit is particularly clear from a micro-rheological point of view: when analysing the in vivo distribution of RBCs, it was observed that the vascular network, and more specifically the subsequent and smallest generations, experience a heterogeneous distribution of hematocrit as a consequence of successive microvascular bifurcations and uneven velocity distributions (Chien et al., 1985; Fenton et al., 1985; Pries et al., 1989). RBCs naturally deform and align with flow streamlines to reduce the frictional forces between cells and the walls. Subsequently, the structuring of the plasma/RBCs two-phase flow concentrates the position of RBCs in the centre of the vessels to generate a strong haematocrit gradient (Závodszky et al., 2019). The migration of RBCs in the smallest structures, known as Fåhraeus–Lindqvist, highlights that this local reduction of hematocrit generates a decline in blood apparent viscosity as the vessel size decreases (Lindqvist and Fahraeus, 1930; Farina et al., 2021). Therefore, the endothelium is in contact mostly with plasma-rich layers, which minimise the shear forces and flow resistance. In the microcirculation (vessels less than 10 µm), the viscosity experiences a sharp increase as it reaches the diameter of RBCs, associated with the dissipation of the lubricative plasma layer (Lighthill, 1968; Guibert et al., 2010) (Figure 1).

Current medical devices have diverse blood flow paths, and operate scale reduction and constriction to facilitate their operations. Classical ECMO circuits commonly show a set of very packed fibres where blood flow is repeatedly constricted and expanded from the inlet to the outlet to enhance the oxygenation rate (Fukuda et al., 2020; Conway et al., 2021). Similarly, centrifugal pumps integrate sharp impellers and blades in order to rapidly accelerate the blood (Figure 3) (Fox et al., 2022). It is therefore clear that the blood rheological properties and interactions with the walls of the system are likely to be altered throughout the circulation and be responsible for the device disruption.

FIGURE 3

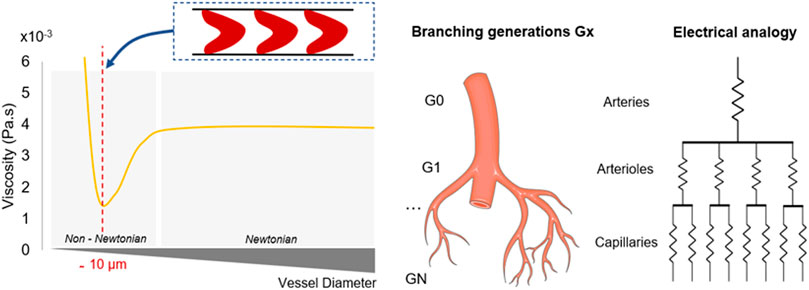
FIGURE 3. Physical parameters associated with vessel radius reduction. Figures on the left detail the rheological properties of the blood regarding the shrinkage of the vessels throughout the network. Shear forces and non-Newtonian influence increase as the vessel radius decreases. Viscosity reaches a minimum when the vessel diameter equals the RBCs dimension, before experiencing a sharp increase. On the right, the electrical analogy describes the successive splitting which enables to parallelise the flow. Microchannels are getting smaller, more numerous and resistive. Murray’s law dictates the dimensions of each generation depending on the previous generations characteristics, while maintaining constant shear forces.

2.4 Biomimetism in blood-circulating devices

Biomimetic principles are increasingly considered to guide design of vascular networks. They are applied differently depending on the size of the perfusion system, from microcapillary to macrovessel size systems.

2.4.1 Microcapillary-size devices (diameter <1 mm)

For blood-circulating devices - and more specifically capillaries systems - microfluidics brings novel possibilities in the development of miniaturised, branched architectures. Benefits include micrometric control over geometries including scale reduction, surface of exchanges and mechanical forces. Artificial oxygenators greatly benefit from these principles and display flow distributions arrays in accordance to Murray’s law (Lachaux et al., 2021; Santos et al., 2021; Vedula et al., 2022). These circuits shown in Figures 4A, B achieve a progressive scale reduction from the largest channels to microcapillaries where chemical transport of gas and nutrients will occur faster and more efficiently, contained within a compact manifold. Such geometries enable the maintenance of physiologically relevant shear stress magnitudes and flow rates. A similar approach was applied to the design of a tissue-engineered liver scaffold, integrating a venous scaling throughout the generations of the network (Hoganson et al., 2010; Torres Rojas et al., 2021). Furthermore, novel biomimetic scaffolds based on triply periodic minimal surface (TPMS) theory were developed for fluid-circulation devices. Using a permeability-based design approach, membranes display modules with improved flow distribution overcoming non-uniform and stagnant patterns found in hollow fibres membranes of oxygenators (Hesselmann et al., 2022). TPMS-scaffolds morphology has a markedly high surface area to volume ratio and highly controlled porosity similar to native cellular conditions (Vijayavenkataraman et al., 2018). Two modules are shown in Figure 4C illustrating the permeability-driven optimisation used for a membrane oxygenator design.

FIGURE 4

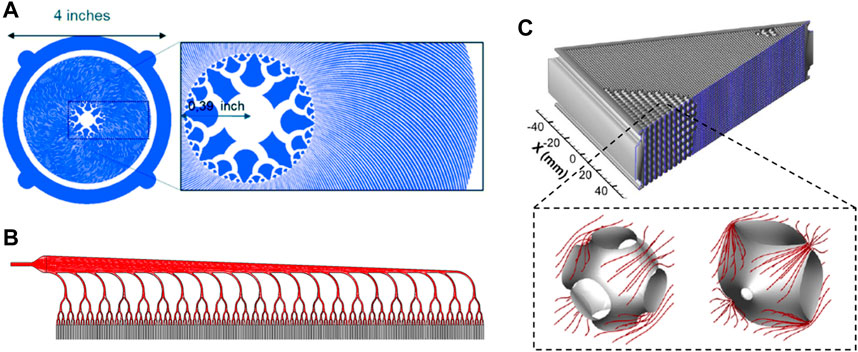
FIGURE 4. Biomimetic approaches in oxygenators design. (A, B) present two different blood distribution methods in microfluidic oxygenators allowing for a progressive scale reduction of the microchannels. (C) details a TPMS-based membrane oxygenators whose modules have been optimised upon their permeability ensuring improved flow distribution. Panel A is modified from Lachaux et al., 2021. Panel B is modified from Vedula et al., 2022. Panel C is modified from Hesselmann et al., 2022.

2.4.2 Macrovessel-size devices (diameter >1 mm)

Biomimetics can also be applied to bigger implanted devices in contact with blood flow. Currently, a majority of blood devices display macrometric circulation networks where physiological flow is pulsative. The introduction of axial and centrifugal pumps to clinical practice have generated major thrombotic complications (Hastings et al., 2016) Devices with diminished pulsatility create non-physiological continuous flow and likely introduce increased pressure gradients in the circulation (Cheng et al., 2014; Major et al., 2020). Wave membranes blood pump are novel approaches for pulsatile flow integration in which blood is moved by wave propagation systems. Both frequency and amplitude of the waves can be monitored to mimic physiological flow (Martinolli et al., 2022). Bileaflet valves are typically subjected to high flow rates and relative changes in volume throughout the cardiac cycle. Technical designs of the valves are inspired by profiles of a native valve, which is optimised to resist and adapt to natural variations in vessel diameter, blood volume and oscillations (Hofferberth et al., 2020).

Biomimetic features contribute to a safe and durable system. However, the intrinsic architecture of human vasculature naturally disturbs the blood flow which undergoes diverse mechanical constraints (Chistiakov et al., 2017). The development of artificial vasculature would allow high control over hydrodynamic parameters to prevent unsolicited and damaging reactions in the blood.

3 Mechanisms of shear-induced thrombosis

Blood-contacting and circulating devices such as catheters, extracorporeal membrane oxygenator EMCOs, or stents are challenged by the formation of thrombus especially during long term implantation. The formation of acute thrombi is one of the most frequent sources of failure (Jaffer et al., 2015; Murphy et al., 2015). Artificial surfaces from biomedical devices poorly recapitulate the physiological environment in terms of architecture, biochemistry and forces. As Virchow’s triad details, the alteration of the endothelium, including internal shear stresses, together with blood flow disturbances (stasis and turbulence) and hypercoagulability, are the three pillars contributing to thrombogenicity (Kumar et al., 2010).

When blood interacts with a foreign material, a rapid absorption of plasma protein occurs. This is believed to be the precursor of thrombosis, as it involved an aggregation of platelets and fibrin on the surface, trapping RBCs (Hoefer et al., 2020). In laminar conditions, velocity and concentration gradients, together with collisions, spontaneously transport the platelets towards the walls, enhancing these interactions. In addition, thrombosis models and recent findings from in vivo experiments using circulating systems have identified multiple activation and aggregation mechanisms operating at distinct shear range (Jackson et al., 2009; Casa et al., 2015). Platelets have a diverse assortment of protein receptors on their membrane including integrin ${\alpha }_{IIb}{\beta }_3$ and GPIb-V-IX, which are selectively involved upon shear magnitude or hemodynamic perturbations. It is therefore clear that hemodynamic conditions and biomechanical constraints drive cell-cell and cell-material interactions and highly influence thrombosis formation (Roka-Moiia et al., 2021). Unravelling platelet behaviour and the mechanisms of clot formation in dynamic and sheared conditions is one of the biggest challenges when developing artificial blood circulatory devices suitable for long-term treatments. In the following section, we will review the current models of shear-dependant cellular dynamics and interactions leading to occlusive thrombus.

3.1 Transport: Platelet margination

Clot formation lies on the ability of blood cells, in particular platelets, to reach vessel walls and interact with the proteins immobilized onto it. The effects of local fluid mechanical environment on platelet-ligands interactions are of utmost importance. Extensive studies have reviewed platelets behaviour in both vascular and in-vitro environments and have highlighted an enriched near-wall layer within the first microns of the vessels, where RBCs are completely depleted (Zhao et al., 2012; Sugihara-seki and Takinouchi, 2021). Platelet distribution profile across the flow was also analysed with mathematical models. (Spann et al., 2016; Závodszky et al., 2019), confirming a cross-flow migration of platelets in circulating channels. This phenomenon is known as platelet margination and is believed to result from interconnected mechanisms which will be reviewed in this section.

3.1.1 Cell-cell hemodynamics interactions

Platelet margination is monitored by their interaction with RBCs in circulating blood and local fluid dynamics. RBCs density in the blood, their deformability and stiffness participate and are necessary for the margination to occur. Platelets circulating alone or with extremely low hematocrit are less likely accumulate on the vessel walls, indicating that RBCs volume affect platelet trajectories, with a stronger impact under dynamic and stressed conditions (Turitto and Weiss, 1980). Zhao et al. confirmed the contribution of hematocrit to platelet margination, observing a significant difference in platelet probability distribution when hematocrit was doubled from 10% to 20% (Zhao et al., 2012). Platelets have a stiffer membrane compared to RBCs which have an easier faculty to deform. The gradient of stiffness within the cell population enhanced the rate of collisions between deformable red blood cells and stiffer particles (Czaja et al., 2020). This segregation of stiffer particles has been simulated by Zhao et al., in arteriole-like ducts showing that platelet-like spherical beads were pushed due to volume exclusion (Munn and Dupin, 2008; Zhao et al., 2012).

3.1.2 Shear-induced diffusion

When blood flows through a vessel, the laminar regime reveals a gradient of velocity directed normal to the wall. In response to the non-slip condition (zero speed on the walls), a non-zero mean lateral velocity leads the blood particles to progressively diffuse from the centre of the vessels to the edge. Several corresponding studies demonstrated a remarkable contribution of shear-induced RBC-platelet collisions on the lateral motion of individual platelets (Kotsalos et al., 2022; Li et al., 2023). The analysis of RBC dynamics under flow conditions also suggested that high levels of shear resulted in a 1000-fold increase in platelet diffusivity to the walls (Taylor, 1953; Leighton and Acrivos, 1987; Casa et al., 2015). As Crowl and Fogelson pointed out, margination occurs rapidly in sheared conditions, within a few microseconds at physiological capillaries shear rates (1,100 s^-1) (Crowl and Fogelson, 2010; 2011). Nevertheless, shear stress was found to have a less dramatic impact on platelet lateral margination than hematocrit, even though it clearly enhances the process (Zhao et al., 2007).

Altogether, platelet behaviour and activity is altered in blood circulating devices, with adhesion rates driven by interactions with RBCs, a critical factor for acute thrombus development (Spann et al., 2016). These findings provide useful insight on the influence of hemodynamic environment eon platelet-protein membrane binding and thus adhesion, which are predominant processes initiating thrombus development.

3.2 Platelet adhesion and activation upon shear hemodynamics

Physiological blood circulation exhibits a wide range of shear rates (from 10 to 200 s^-1 in veins, 500–800 s^-1 in larges arteries and almost 2,000 s^-1 in the capillaries (Gogia and Neelamegham, 2015)). Platelet adhesion and aggregation occur over this range of magnitude, and even to greater extent at higher and pathological shear rates. There is an interesting paradigm in the role of platelets in the bloodstream: their circulation close to the walls is necessary for haemostasis through a strong adhesion to damaged vessel. However, their adhesion also actively contributes to pathological thrombotic occlusion, particularly at elevated shear rates.

The involvement of the different receptors and ligands acting as thrombogenic factors, and how they regulate clot formation under sheared conditions has become a research area of focus (Jackson et al., 2009; Casa et al., 2015; Rana et al., 2019) (Table 1). The first step in thrombus formation is the immobilisation of plasma proteins on the surface. As previously mentioned, in the case of artificial circulatory networks, polymer provide an attractive surface for rapid protein adsorption (Wilson et al., 2005; Horbett, 2019). Adversely, physiological thrombogenic surfaces can arise from endothelial damages exposing subendothelial collagen to the blood circulation (Andrews et al., 2003). Fibrinogen and von Willebrand factor (VWF) are the two main proteins adsorbed and immobilized on inner surfaces (Grunkemeier et al., 2000; Kwak et al., 2005). VWF is a long multimeric glycoprotein adopting a coiled and compact conformation under low shear forces. When unfolded, the protein contains a central domain called A1 that has a high affinity for platelet receptors (Ju et al., 2016; Denorme et al., 2019).

TABLE 1

TABLE 1. Morphology and adhesive interactions associated to shear rate levels.

3.2.1 Low-intermediate shear rate (< 1,000 s^-1)

Under low shear rate perfusion in normal physiology (such as venous flow), platelets interact with adsorbed fibrinogen and collagen via their glycoprotein VI (GPVI) receptors. The integrin ${\alpha }_{IIb}{\beta }_3$ (also known as GPIIb/IIIa) located on platelet membranes enhances the arrest of free platelets onto immobilised fibrinogen (Savage et al., 1998; Maxwell et al., 2016; Xu et al., 2021) (Figure 5). The strong integrin ${\alpha }_{IIb}{\beta }_3$—fibrinogen interaction guarantees a firm and immediate adhesion of the platelet on contact with the surface (Savage et al., 1996). The work conducted by Ruggeri et al., in 1996 reveals the contribution of integrins in platelet deposition and adhesion across this range of shear rates. Blood perfused in a parallel plate flow chamber coated with immobilised fibrinogen revealed maximal platelet deposition at lower shear rates, with almost no binding at shear rates reaching 1,500 s^-1. This interaction is selectively engaged under low shear conditions: as the binding rate with integrin ${\alpha }_{IIb}{\beta }_3$ is considered to be relatively slow, bonds may form if the drag forces do not overcome integrins bond strength (Savage et al., 1996). It is important to mention that shear rate only impacts initial platelet adhesion and the binding of integrins to fibrinogen remained stable at higher levels (Savage et al., 1996). On the biochemical aspect, adhered platelets also tend to activate and demonstrate an upregulation of ${\alpha }_{IIb}{\beta }_3$ affinity on their membrane enhancing platelet-platelet interactions through soluble fibrinogen. Therefore, the secretion and release of thrombogenic agonists through alpha-granules (ADP, Thromboxane TXA2, Ultra-large von Willebrand factor (ULVWF)) by activated platelets monitors a shift in their phenotype, which progressively exhibits filopodia-like structures (Maxwell et al., 2016).

FIGURE 5

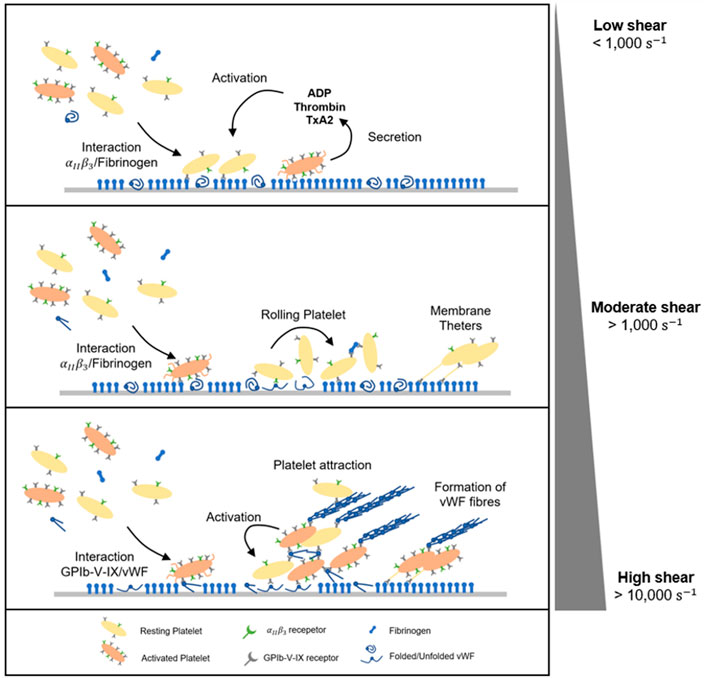
FIGURE 5. Dynamic of platelet adhesion and aggregation under flow. At low shear rate (<1,000 s^-1), platelets adhesion and aggregation are predominantly driven by integrins ${\alpha }_{IIb}{\beta }_3$ receptors with fibrinogen as ligand. At moderate shear rate (<10,000 s^-1), VWF fibres adopt both folded and unfolded conformations capturing platelets via their receptor GPIb-V-IX. Due to the fast dissociation rate, platelet translocate and roll over the surface and engage a very stable binding with fibrinogen as well. At higher and pathological shear rates (<10,000 s^-1), platelets interact exclusively with immobilized VWF which form large and unstable aggregates and long fibres capturing both activated and inactivated platelets.

3.2.2 Moderate shear rate (1,000–10,000 s^-1)

Investigations on blood circulation in microfluidics at moderate shear rates (exceeding 1,000 s^-1) have shown a two-stage platelet adhesion mechanism. First, as an additional interaction mediating platelet adhesion, glycoproteins GpIb-V-IX (more specifically GPIbα) bridge to immobilized von Willebrand Factor to arrest platelets on the surface (Savage et al., 1996; Reininger et al., 2006). Under moderate shear, VWF molecules unfold to reveal the A1 domain which bonds to platelet receptor GPIb (Siedlecki et al., 1996). A1- GPIb adhesive binding is fast but reversible. The interaction induces a mechanism of platelet translocation whereby flowing platelets can quickly bond/debond, exhibiting a rolling motion on the wall surface (Lackner et al., 2020; Pujos et al., 2022). In the second stage, the rolling motion of platelets prolongs their contact with adsorbed fibrinogen, providing sufficient time for the strong ${\alpha }_{IIb}{\beta }_3$—fibrinogen bonds to be established (Figure 5). The surface translocation then generates several morphological switches (Andrews et al., 2003). As the platelet engage into smooth rolling interactions, intermediate shear rates (1,000–10,000 s^-1) introduce membrane tethers. These are smooth cylinders of lipid bilayer derived from the platelet membrane, which function as contact points between integrins GPIIb/IIIa and amino acids in VWF C1 domain. These membrane extensions have the ability to stretch in order to resist the hemodynamic drag forces imposed by the flow and extend the adhesion time of the platelets, further stabilising the emerging aggregate (Dopheide et al., 2002; Reininger et al., 2006; Mountford et al., 2015; Abidin et al., 2022).

3.2.3 Pathological shear rate (> 10,000 s^-1)

It is important to emphasise that aggregate formation does not necessarily require platelet activation (Ruggeri et al., 2006). On the contrary, circulating platelets are able to initiate binding and aggregation without first being activated, which is the case in the presence of pathological shear stress or disturbed flows. VWF binding to the platelet membrane GpIb-V-IX complex triggers activation of platelet GPIIb/IIIa receptors as wells as an accumulation of intracellular calcium. Activated platelets secrete soluble prothrombotic agonists inside the aggregate. These soluble factors include ADP, thromboxane (TxA2) or thrombin and are actively released in the blood plasma, stabilising the plug and promoting the recruitment of flowing platelets (Ruggeri et al., 2006). In addition, high shear rates lead to platelet membrane inversion including the externalisation of phosphatidylserine (PS), a phospholipid normally located in the cytoplasm of resting platelets (Sweedo et al., 2021). This redistribution on activated platelets leads to a 40-fold increase in phosphatidyl serine expression after platelet activation (Thiagarajan and Tait, 1990; Dachary-Prigent et al., 1993; Sun et al., 1993). PS translocation propagates the further platelet activation cascade within the aggregates (Ryan et al., 2020) Finally, pathological conditions including vessel lumen reduction and/or obstruction may cause shear rate rise at extremely high levels above 10,000 s^-1. Under these conditions, platelet thrombus formation is dominated by VWF-dependant interactions, mainly via GPIb-V-IX. Aggregates emerge from soluble VWF multimers, which are in their complete unfolded and fibrous conformation (Figure 5) (Zhussupbekov et al., 2022). The fibres easily bind to already adhered and tethered platelets on immobilized VWF forming a net on the surface. At the same time, the A1 domain mediates the capture of flowing platelets, further activated within the large and unstable aggregate (Colace and Diamond, 2014; Fu et al., 2017; Liu et al., 2022). VWF biomechanical processes have been characterised in silico and bring useful insight in shear-induced platelet activation under flow (Pushin et al., 2020; Kim and Ku, 2022; Belyaev and Kushchenko, 2023).

3.2.4 Disturbed and elongated shear rate: Microgradients

It is generally accepted that high shear stresses are vectors of platelet aggregation leading to occlusive thrombosis. The different mechanisms of platelet adhesion and aggregation are rather simplified models and descriptions. Blood circulation is not only a laminar flow and will experience local hemodynamic environments, with regions of velocity changes. These can be attributed to the inherent non-Newtonian properties of blood, but also shear rate gradients in cases of vessel constriction where fluid quickly accelerates and decelerates, or turbulences occurring at branching nodes (Chistiakov et al., 2017).

Although the effects of hemodynamic forces on VWF monomeric fibres is demonstrated, there is still no consensus on a critical shear rate needed to initiate platelet aggregation. It is understood that immobilized VWF is likely to remain in its unfolded conformation at shear rates around 3,000 s^-1 whereas an elongation of soluble VWF needs higher shear up to 5,000 s^-1 (Siedlecki et al., 1996; Kuwahara et al., 2002; Schneider et al., 2007). However, recent observations have questioned the existence of such a threshold, showing in particular that VWF could be involved at lower shear magnitudes of, around 1,500 s^-1 (Receveur et al., 2020) and in the context of shear rate gradients (Hoefer et al., 2020; Van Rooij et al., 2021). In a shear gradient context, it was observed that VWF unfolding increased at two-fold lower flow rates when compared to constant shear flows (Zhang, 2009; Sing and Alexander-katz, 2010). Corresponding studies revealed that rapid alterations of the flow through shear microgradients promoted discoid platelet aggregation in the post-stenotic region, or micro-vessel curvatures (Nesbitt et al., 2009; Rooij et al., 2020; Spieker et al., 2021). It suggests that the rapid decrease in shear rate restructures the filamentous membrane tethers and allows integrins ${\alpha }_{IIb}{\beta }_3$ to considerably stabilise the aggregate. Platelet aggregation has been characterized in microfluidic devices by Receveur et al., suggesting that fibrinogen was responsible only for platelet adhesion in a simple constant shear flow, whereas together with the action of VWF became thrombogenic in an accelerated flow. Thrombosis driven by shear microgradients is bi-phasic: initially slow as platelet are recruited by immobilized VWF and fibrinogen, followed by a dramatic growth of VWF fibres (Receveur et al., 2020).

4 Evaluation of blood damage and device thrombogenicity

Thrombosis relies on several stakeholders, which interact in different manners depending on the mechanical environment. Design optimisation of blood-circulating devices can use our understanding of shear-induced thrombosis to improve the evaluation of the thrombogenic performances and reduce the heavy reliance on anticoagulant medication. In the sections below, we detail the latest investigations used to assess shear-induced blood damage and thrombogenicity and identify the hemodynamic factors that can be integrated in future design optimisation approaches.

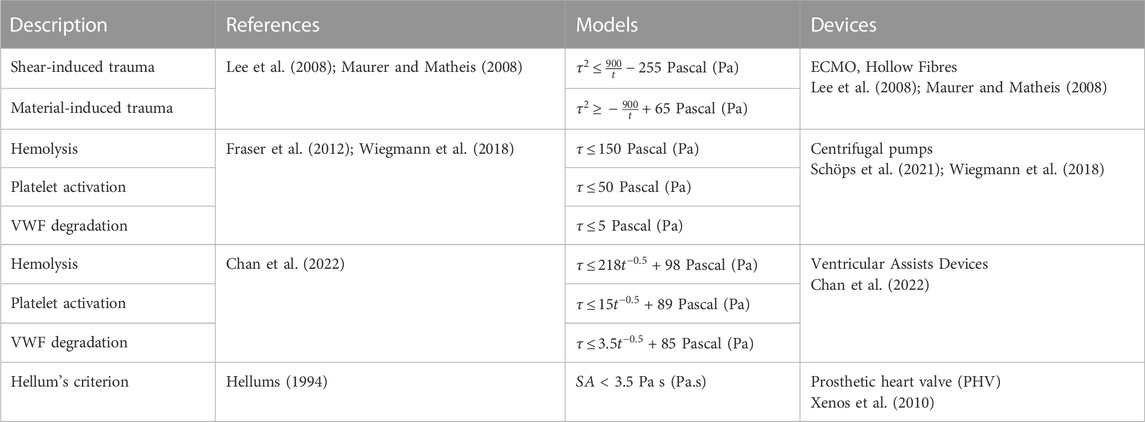
4.1 Setting critical thresholds: Role of shear and time

Three main factors are used to quantify blood damage and thrombogenicity: hemolysis, platelet activation, and VWF condition. Firstly, hemolysis is described as a permanent injury of RBCs leading to the release of haemoglobin in the plasma and is widely considered as a risk factor for thrombosis and its quantification (Capecchi et al., 2021). Platelet and VWF damages are two additional indicators. Based on the phenomenological approach to thrombosis under dynamic conditions covered in the previous section, studies have established critical limits for these three metrics. The threshold value for hemolysis was estimated around 150 Pa (Alemu and Bluestein, 2007), while those for platelet and VWF interactions are significantly lower at 19 Pa and 5 Pa with adherent surfaces, with thrombogenic proteins (VWF and fibrinogen) respectively. Surface and volumetric segmentation of the flow field is commonly used as alternative method to quantify the blood mechanical loading and better visualise critical design features (Buck et al., 2018; Wiegmann et al., 2018; He et al., 2021). A statistical distribution of shear levels and velocities quantifies the proportion of the surface or volume experiencing forces above the prescribed threshold, with regards to the total volume. In this respect, a study led by Wiegmann and colleagues explored slight design changes of a centrifugal pump and demonstrated that both stagnation zones and number of particles exposed to high shear can be reduced, by altering clearance gaps and the number of impeller blades (Wiegmann et al., 2018). In the latest prototypes of bioprosthetic total artificial heart (A-ATH), blood volume fraction enduring pathological shear stress was employed to analyse the influence of the cardiac output on designs hemocompatibility (Poitier et al., 2022).

Currently, blood circulating device manufacturers orient their design process to achieve specific operating flow rates (4–7 L/min for ECMO-based devices, 1–6 L/min for cannulas (Makdisi and Wang, 2015)) with minimal hemolysis. The hemolytic index (HI) shown in Table 2 quantifies the plasma-free hemoglobin relative to the total hemoglobin, regarding the exposure of blood to shear stress for a given duration. This equation gives a first appreciation of the hemolytic performances of a device according to the contact time between the blood and the surfaces (Romanova et al., 2022). Although being extensively used as a gold-standard to minimize flow-induced thrombogenicity (Taskin et al., 2012; Zhang et al., 2020), this metric does not account for the contribution of other thrombogenic components (platelets and VWF) in sheared environments. In fact, RBCs are relatively resilient to shear due to their rigid membrane, and have a negligible influence since they flow in the low shear central region because of Fåhraeus–Lindqvist effect (Lindqvist and Fahraeus, 1930). Moreover, shear-induced hemolysis was observed at levels of shear rate more than ten-fold higher than the ones noted for platelets and VWF interactions (Klaus et al., 2002; Chan et al., 2022). These observations call into question the use of the hemolysis as unique indicator of thrombogenicity.

TABLE 2

TABLE 2. Existing models based on a thresholding approach for blood damage.

Blood exposure time to surfaces is yet a key parameter in thrombosis as it outlines how both platelets and VWF can respond to wider range of mechanical stimuli. Indeed, constant thresholds are unable to fully recapitulate the mechanisms of platelet activation and aggregation: a prolonged exposure of blood to low shear rates likely promotes equal platelet damage as high shear rates for short exposure times (Soares et al., 2013). Interestingly, extremely low shear cannot balance extended contact with a material, and are referred to stagnation zones. These regions display velocity fields within which interactions between blood cells and immobilized proteins are emphasised and there is an increased concentration of agonists. Table 2 details existing models extrapolated from experimental data that explore RBC, platelets and VWF behaviour according to shear and time. They also show that VWF intervenes primarily in the process of thrombosis (Chan et al., 2022). These models where originally defined via a large matrix of experimental data (in shear and time), provided by various studies completed under diverse conditions (rheometer, microfluidics, hollow fibres). Although a clear trend appears for the thresholds of platelet and VWF damage, caution should be taken when applying them in experimental models outside their field of definition.

4.2 Computational fluid dynamics: Numerical modelling of local thrombotic risks

Current methods to assess medical device thrombogenicity do not provide sufficient insight in the local hemodynamics. Mechanical heart valves show highly damaging regions near the leaflets where platelets experience strong forces out to the physiological range (Roudaut et al., 2007; Dangas et al., 2016; Wang et al., 2021). Similarly, ECMO circuits introduce local increase of shear near the oxygenating fibres, as well as around the connectors (Sun et al., 2020; Conway et al., 2021). Currently, actual mechanical blood damage lies on estimations since there is no proper model accounting for all phenomena and complexity that define blood circulation. Multiple shear magnitudes define a single trajectory, and the scalar wall shear stress (WSS) as standard value cannot recapitulate the whole shear history. As a consequence, there is a need for appropriate assessment of thrombotic risks accounting for the local mechanical description of the whole blood flow, including time-varying shear stresses (shear microgradients) and the cumulative effect of unsteady shear levels.

Recently, computational fluid dynamics (CFD) has gained interest as tool for early-stage medical devices development. It can be employed to track the journey of platelets throughout the fluidic network or the displacement of critical regions (artificial valves and ventricles) under constraints, and to provide a reliable appreciation of the local mechanical state (Figure 6). Numerical simulations easily generate a large number of platelet trajectories and provide a “mechanical footprint” of the flow while highlighting regions with a higher risk of damage (Hatoum et al., 2021; Yang et al., 2022). Computing statistical distributions such as the probability density of the shear and exposure time from relevant trajectories offers a clear quantification of mechanical constraints, their intensity and frequency. These parameters can then be employed to compare and optimise designs. Schöps et al. have used this method to quantify the number of threshold exceedances over CFD-derived streamlines, with respect to the residence time (Schöps et al., 2021). Combined with CFD simulations, statistical analysis of streamlines-derived metrics presented in Table 3 offers an interesting approach to assess hemodynamic features of complex blood flows.

FIGURE 6

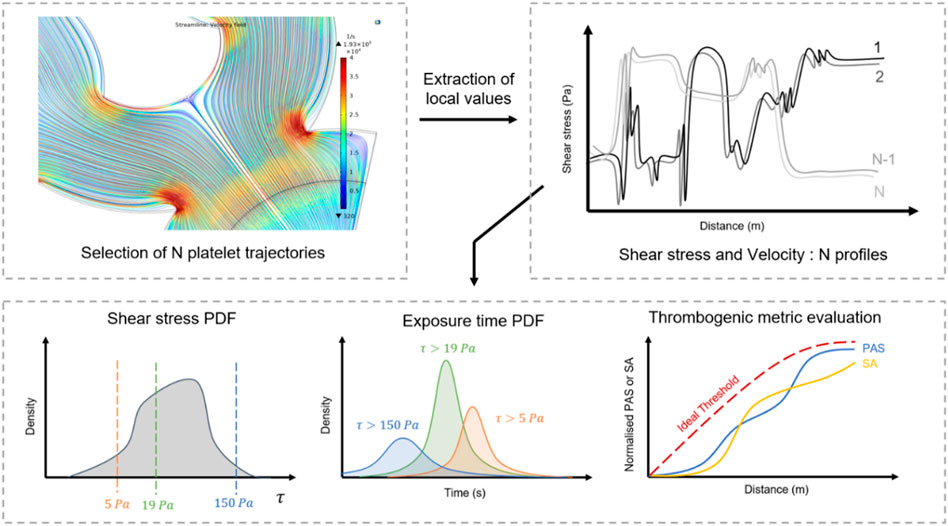
FIGURE 6. Optimisation flow chart from CFD analysis of device thrombogenicity. Computational fluid dynamics provide local mechanical history of a large population of flowing platelets. The statistical analysis of their mechanical experience: shear stress, time of exposure, thrombogenic metrics enable to draw a global picture of the risks of clotting related to the design.

TABLE 3

TABLE 3. Existing models based on a cumulative approach for blood damages.

4.2.1 Platelet Activation State

In the light of the major contribution of platelets in thrombosis, Nobili et al. applied a cumulative damage theory, originally developed for RBC (Yeleswarapu et al., 1995; Grigioni et al., 2005), to quantify platelet activation state (PAS) in dynamic conditions (Table 3). This model relies on a prior activation history term and the instantaneous constant mechanical loading (Nobili et al., 2008). Following the same logic, a new description for the regions of shear gradients was introduced to depict a more accurate description of the mechanical profile along the trajectory (Soares et al., 2013). Furthermore, the PAS formula relates to actual biological markers for platelet degradation. In stressed environment, platelet activation leads to the conversion of prothrombin into thrombin, which acts as a strong agonist generating further activations via a feedback loop. Similarly, modified prothrombin produces acetylated thrombin which does not contribute to any activation and can easily be quantified, assimilated as a direct marker of shear-induced platelet activation (Jesty and Bluestein, 1999). This method combines computational fluid dynamics and biological assessment of platelet activation and provides a direct quantification of a streamline thrombogenicity considering diverse mechanical loading histories (Xenos et al., 2010). The latter study provided some insights into the platelets resilience to shear stress, and their behaviour post-exposure. Interestingly, coupled with experimental results, the model revealed that platelets become activated by very short but strong pulse of shear without recovering their initial and quiescent state under low shear conditions. In addition, an initial pre-exposure to high shear facilitates their activation even at physiological shear. These findings highlight the importance of including previous stress histories in the analysis of platelet sensitivity to activation (Soares et al., 2013).

4.2.2 Stress accumulation

Stress accumulation (SA) is an additional metric which sums the instantaneous product of shear stress and exposure time between successive nodes of platelet streamline. This parameter indicates the level of activation of a trajectory and should remain lower than 35 dyne s/cm² for save blood transport, according to Hellums criterion (Hellums et al., 1987). Stress accumulation is often integrated in the optimisation procedure as a comparative indicator (Chiu et al., 2019). Girdhar and colleagues led a robust comparison of Left Ventricular Assist devices (LVADs), using the stress accumulation to select the features guaranteeing optimal thrombogenic performances. The optimized version of the VAD was selected after several iterative design modifications on the impeller and showed a markedly reduced stress accumulation among platelet trajectories. More importantly, it caused an order of magnitude lower platelet activation rate when compared with the original design (Girdhar et al., 2012). Similarly, Buck et al. investigated the thrombogenicity of two blood path architectures as part of an implantable artificial kidney (Buck et al., 2018).

4.2.3 Thrombotic risks

Associated with computational fluid dynamics, various numerical models are proposed to predict localised thrombus risks in blood-circulating device designs (Menichini and Yun, 2016; Wu et al., 2020; Bouchnita et al., 2021; Li et al., 2022). The majority of these models integrate a combination of mechanical and biochemical contributions: first the computing velocity, pressure and shear stress fields with Navier-Stokes equations. Utilising the knowledge of the mechanical and physiological environment, a large number of models compute species transport in the system with an Eulerian approach by solving convection-diffusion-reaction equations (Stiehm et al., 2019; Wu et al., 2020). Several components concentrations including the ones of resting or activated platelets, chemical agonists such as adenosine diphosphate (ADP) or thrombin, are processed through a systems of partial differential equations (PDEs) (Sorensen et al., 1999; Leiderman and Fogelson, 2011). Some models have also proposed a direct dependence of these concentrations either with mechanical or chemical cues, through both source terms or diffusivity (Wootton et al., 2001; Menichini and Yun, 2016). Using such models, Blum and colleagues demonstrated that activated platelets concentration in HeartMate II pumps correlated with thrombus events frequency (Figure 7), suggesting that such computational markers have potential as surrogates for thrombus modelling (Blum et al., 2022; Qiao et al., 2022).

FIGURE 7

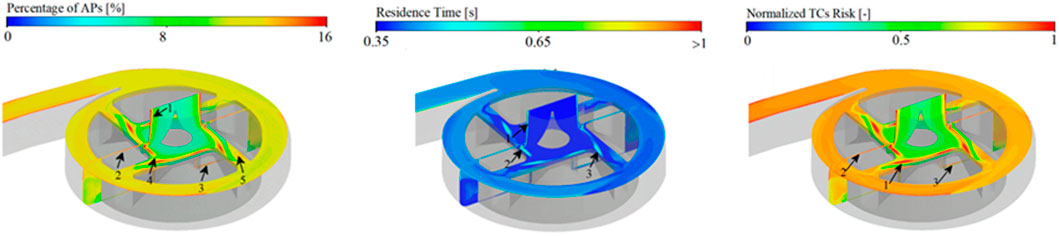
FIGURE 7. Thrombotic risks modelling. Quantification of thrombotic clots risk (right panel) upon activated platelet concentration (left panel), residence time (centre panel). Panel is modified from Li et al., 2022.

Regions with high thrombotic risk are also characterised by their longer residence times. Residence time can be modelled as a passive tracer entering the blood-circulating device and transported with the flow (Figure 7). Along with high activated platelets concentrations, the latter is computed using Eulerian description to evaluate thrombotic clots (Menichini and Yun, 2016; Li et al., 2022). Moreover, Lagrangian methods also provide a valuable description of residence time for individual platelets along their trajectory, but they require extensive computational costs compared with Eulerian methods.

5 Discussion

Thrombotic failures of medical devices with blood circulation show that anticoagulant treatments are no longer sufficient to guarantee a viable implantation (Cossette et al., 2010; Dhakal et al., 2016). They are designed as last-resort temporary solutions to recapitulate deteriorated vital function in clinically vulnerable patients. However, the damages inflicted on the flowing blood while flowing is difficult to apprehend and inevitably reduces the implantation time. Thrombosis is one of the major complications associated with the failure of blood flow devices (Jaffer et al., 2015; Murphy et al., 2015).

Although made from biocompatible materials, current blood-circulating devices do not sufficiently reflect the physiological environment of a blood vessel. Human vascular network, just like the circulatory systems of leaves, is characterised by a complex and hierarchical architecture, to optimise flow distribution and scale-down the vessels. It displays a diverse mechanical environment centred around shear forces, and an architecture alleviating physiological needs while preserving the blood. In that regard, design of medical devices is moving towards new biomimetics considerations in an attempt to improve the anti-thrombotic properties.

Different biomaterials are used to manufacture blood-circulating devices used in clinical practice. The exposure of patient blood to foreign materials whose walls are covered with adsorbed proteins, providing sites for thrombotic interactions. Many studies have brought significant contributions to the biomaterials-driven thrombosis fields, with regard to innovative coatings for instance, material composition or surface modification (Han et al., 2022; Jamiolkowski et al., 2022). . In addition to shear-induced interactions mentioned in this review, material induced trauma resulting from biomaterial interactions relies on even more complex couplings that should be considered for thrombogenicity evaluation.

While interests have long been focused on the efficacy and functionality of the device (transport, oxygenation, filtration), current challenges have arisen in the reduction of blood damages in order to extend the device lifetime and reduce anticoagulant use. The hemodynamic evaluation of artificial vascular devices is heading in that direction: detect and reduce any harmful patterns such as high shear stresses, gradients and stagnant regions. However, the existing parameters in the literature do not make it possible to establish device thrombogenicity. This work presents the state-of-the art of the methodologies that provide the foundations of tools to assess thrombogenic performances. Investigating the hemodynamics of blood circulating devices via computational fluid dynamics simulations have broadened the knowledge of blood’s behaviour in complex flow fields and geometries. In particular, streamline analysis can mimic real-time blood cells trajectories and capture the local mechanical information and interactions of a bulk flow with a greater than preceding analytical models. CFD modelling denotes a pertinent and economical approach to elucidate the effects of design alterations on the long-term performances of a device. Integrating such practice in the medical device industry pipeline as part of an early optimisation phase would save time both in prototyping and manufacturing.

In addition, the microscale modelling through CFD allows the integration of complex non-Newtonian properties of blood that should be considered when the circulating channels have comparable dimensions as the circulating cells. Precisely, artificial vascular systems mostly operate with continuous perfusion at fairly high flow rates (reaching up to 7L/min). Designing micrometric-scaled blood circulating systems capable to treat large volumes as efficiently as our vascular system is certainly a formidable biomimetic challenge for the years to come.

Author contributions

TF conceived and wrote the manuscript AD, GN, SC, WA contributed in the writing and reviewing the manuscript CP, ER, CMP reveiwed the manuscript All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This research being submitted has received funding from the European Union’s Horizon 2020 research and innovation programme under Marie Skłodowska-Curie grant agreement No. 860034.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abidin, N. A. Z., Poon, E. K. W., Szydzik, C., Timofeeva, M., Akbaridoust, F., Brazilek, R. J., et al. (2022). An extensional strain sensing mechanosome drives adhesion - independent platelet activation at supraphysiological hemodynamic gradients. BMC Biol. 20, 73. doi:10.1186/s12915-022-01274-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Abruzzo, A., Gorantla, V., and Thomas, S. E. (2022). Venous thromboembolic events in the setting of extracorporeal membrane oxygenation support in adults: A systematic review. Thrombosis Res. 212, 58–71. doi:10.1016/j.thromres.2022.02.015

CrossRef Full Text | Google Scholar

Alemu, Y., Girdhar, G., Xenos, M., Sheriff, J., Jesty, J., Einav, S., et al. (2010). Design optimization of a mechanical heart valve for reducing valve thrombogenicity—a case study with ATS valve. ASAIO J. 56, 389–396. doi:10.1097/MAT.0b013e3181e65bf9

PubMed Abstract | CrossRef Full Text | Google Scholar

Alemu, Y., and Bluestein, D. (2007). Flow-induced platelet activation and damage accumulation in a mechanical heart valve: Numerical studies. Numer. Studies’ 31 (9), 677–688. doi:10.1111/j.1525-1594.2007.00446.x

CrossRef Full Text | Google Scholar

Andrews, R. K., Gardiner, E., Shen, Y., Whisstock, J., and Berndt, M. (2003). Glycoprotein ib-IX-V. Int. J. Biochem. Cell Biol. 35 (8), 1170–1174. doi:10.1016/S1357-2725(02)00280-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Belyaev, A. V., and Kushchenko, Y. K. (2023). Biomechanical activation of blood platelets via adhesion to von Willebrand factor studied with mesoscopic simulations. Biomechanics Model. Mechanobiol., 1–24. doi:10.1007/s10237-022-01681-3

CrossRef Full Text | Google Scholar

Blackshear, P. L., Dorman, F. D., and Steinback, J. H. (1965). Some mechanical effects that infuence hemolysis. Trans. Am. Soc. Artif. Intern Organs 11, 112–117. doi:10.1097/00002480-196504000-00022

PubMed Abstract | CrossRef Full Text | Google Scholar

Bluestein, D., Niu, L., Schoephoerster, R. T., and Dewanjee, M. K. (1997). Fluid mechanics of arterial stenosis: Relationship to the development of mural thrombus. Ann. Biomed. Eng. 25 (9), 344–356. doi:10.1007/bf02648048

PubMed Abstract | CrossRef Full Text | Google Scholar

Blum, C., GroB-Hardt, S., Steinseifer, U., and Neidlin, M. (2022). An accelerated thrombosis model for computational fluid dynamics simulations in rotary blood pumps. Cardiovasc. Eng. Technol. 13 (4), 638–649. doi:10.1007/s13239-021-00606-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Boal, D. (2001). Mechanics of the cell. Cambridge University Press. doi:10.1017/CBO9780511810954

CrossRef Full Text | Google Scholar

Bouchnita, A., Belyaev, A. V., and Volpert, V. (2021). Multiphase continuum modeling of thrombosis in aneurysms and recirculation zones. Phys. Fluids 33 (9), 093314. doi:10.1063/5.0057393

CrossRef Full Text | Google Scholar

Brummer, A. B., Lymperopoulos, P., Shen, J., Tekin, E., Bentley, L. P., Buzzard, V., et al. (2021). Branching principles of animal and plant networks identified by combining extensive data, machine learning and modelling. J. R. Soc. Interface 18 (174), 20200624. doi:10.1098/rsif.2020.0624

PubMed Abstract | CrossRef Full Text | Google Scholar

Brummer, A. B., Savage, V. M., and Enquist, B. J. (2017). A general model for metabolic scaling in self-similar asymmetric networks. PLOS Comput. Biol. 13, 10053944–e1005425. doi:10.1371/journal.pcbi.1005394

CrossRef Full Text | Google Scholar

Buck, A. K. W., Goebel, S. G., Goodin, M. S., Wright, N. J., Groszek, J. J., Moyer, J., et al. (2018). Original article submission: Platelet stress accumulation analysis to predict thrombogenicity of an artificial kidney. J. Biomechanics 69, 26–33. doi:10.1016/j.jbiomech.2018.01.014

CrossRef Full Text | Google Scholar

Capecchi, M., Ciavarella, A., Artoni, A., Abbattista, M., and Martinelli, I. (2021). Thrombotic complications in patients with immune-mediated hemolysis. J. Clin. Med. 10 (1764), 1764. doi:10.3390/jcm10081764

PubMed Abstract | CrossRef Full Text | Google Scholar

Casa, L. D. C., Deaton, D. H., and Ku, D. N. (2015). Role of high shear rate in thrombosis. J. Vasc. Surg. 61 (4), 1068–1080. doi:10.1016/j.jvs.2014.12.050

PubMed Abstract | CrossRef Full Text | Google Scholar

Chan, C. H. H., Simmonds, M. J., Fraser, K. H., Igarashi, K., Ki, K. K., Murashige, T., et al. (2022). Discrete responses of erythrocytes, platelets, and von Willebrand factor to shear. J. Biomechanics 130, 110898. doi:10.1016/j.jbiomech.2021.110898

CrossRef Full Text | Google Scholar

Chaui-Berlinck, J. G., and Bicudo, J. E. P. W. (2021). The scaling of blood pressure and volume. MDPI foundations, 145–154.

CrossRef Full Text | Google Scholar

Cheng, A., Williamitis, C. A., and Slaughter, M. S. (2014). Comparison of continuous-flow and pulsatile-flow left ventricular assist devices: Is there an advantage to pulsatility. Ann. Cardiothorac. Surg. 3 (6), 573–581. doi:10.3978/j.issn.2225-319X.2014.08.24

PubMed Abstract | CrossRef Full Text | Google Scholar

Chien, S., Tvetenstrand, C. D., Epstein, M. A., and Schmid-Schonbein, G. W. (1985). Model studies on distributions of blood cells at microvascular bifurcations. Am. J. Physiology - Heart Circulatory Physiology 17 (4), H568–H576. doi:10.1152/ajpheart.1985.248.4.h568

CrossRef Full Text | Google Scholar

Chistiakov, D. A., Orekhov, A. N., and Bobryshev, Y. V. (2017). Effects of shear stress on endothelial cells: Go with the flow. Acta Physiol. 219 (2), 382–408. doi:10.1111/apha.12725

CrossRef Full Text | Google Scholar

Chiu, W. C., Tran, P. L., Khalpey, Z., Lee, E., Woo, Y. R., Slepian, M. J., et al. (2019). Device thrombogenicity emulation: An in silico predictor of in vitro and in vivo ventricular assist device thrombogenicity. Sci. Rep. 9, 2946. doi:10.1038/s41598-019-39897-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Colace, T., and Diamond, S. (2014). Direct observation of von Willebrand factor elongation and fiber formation on collagen during acute whole blood exposure to pathological flow. Arteriosclerosis, Thrombosis, Vasc. Biol. 33 (1), 105–113. doi:10.1161/atvbaha.112.300522

CrossRef Full Text | Google Scholar

Consolo, F., Sheriff, J., Gorla, S., Magri, N., Bluestein, D., Pappalardo, F., et al. (2017). High frequency components of hemodynamic shear stress profiles are a major determinant of shear-mediated platelet activation in therapeutic blood recirculating devices. Sci. Rep. 7 (1), 4994–5014. doi:10.1038/s41598-017-05130-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Conway, R. G., Zhang, J., Jeudy, J., Evans, C., Li, T., Wu, Z. J., et al. (2021). Computed tomography angiography as an adjunct to computational fluid dynamics for prediction of oxygenator thrombus formation. Perfus. (United Kingdom) 36 (3), 285–292. doi:10.1177/0267659120944105

CrossRef Full Text | Google Scholar

Corti, M., Zingaro, A., Dede’, L., and Quarteroni, A. M. (2022). Impact of atrial fibrillation on left atrium haemodynamics: A computational fluid dynamics study. Comput. Biol. Med. 150, 106143–106152. doi:10.1016/j.compbiomed.2022.106143

PubMed Abstract | CrossRef Full Text | Google Scholar

Cossette, B., Pelletier, M. E., Carrier, N., Turgeon, M., Leclair, C., Charron, P., et al. (2010). Evaluation of bleeding risk in patients exposed to therapeutic unfractionated or low-molecular-weight heparin: A cohort study in the context of a quality improvement initiative. Ann. Pharmacother. 44, 994–1002. doi:10.1345/aph.1M615

PubMed Abstract | CrossRef Full Text | Google Scholar

Crowl, L., and Fogelson, A. L. (2011). Analysis of mechanisms for platelet near-wall excess under arterial blood flow conditions. J. Fluid Mech. 676, 348–375. doi:10.1017/jfm.2011.54

CrossRef Full Text | Google Scholar

Crowl, L., and Fogelson, A. L. (2010). Computational model of whole blood exhibiting lateral platelet motion induced by red blood cells. Numer. Methods Biomed. Eng. 26, 471–487. doi:10.1002/cnm.1274

CrossRef Full Text | Google Scholar

Cury, L. F. M., Talou, G. D. M., and Blanco, P. J. (2021). Parallel generation of extensive vascular networks with application to an archetypal human kidney model. R. Soc. Open Sci. 8, 210973. doi:10.1098/rsos.210973

PubMed Abstract | CrossRef Full Text | Google Scholar

Czaja, B., Gutierrez, M., Zavodszky, G., de Kanter, D., Hoekstra, A., and Eniola-Adefeso, O. (2020). The influence of red blood cell deformability on hematocrit profiles and platelet margination. PLOS Comput. Biol. 16, e1007716–e1007718. doi:10.1371/journal.pcbi.1007716

PubMed Abstract | CrossRef Full Text | Google Scholar

Dachary-Prigent, J., Freyssinet, J., Pasquet, J., Carron, J., and Nurden, A. (1993). Annexin V as a probe of aminophospholipid exposure and platelet membrane vesiculation: A flow cytometry study showing a role for free sulfhydryl groups. Blood 81 (10), 2554–2565. doi:10.1182/blood.v81.10.2554.2554

PubMed Abstract | CrossRef Full Text | Google Scholar

Dangas, G. D., Weitz, J. I., Giustino, G., Makkar, R., and Mehran, R. (2016). Prosthetic heart valve thrombosis. J. Am. Coll. Cardiol. 68 (24), 2670–2689. doi:10.1016/j.jacc.2016.09.958

PubMed Abstract | CrossRef Full Text | Google Scholar

Davies, P. F. (2009). Hemodynamic shear stress and the endothelium in cardiovascular pathophysiology. Nat. Clin. Pract. Cardiovasc. Med. 6 (1), 16–26. doi:10.1038/ncpcardio1397

PubMed Abstract | CrossRef Full Text | Google Scholar

Denorme, F., Vanhoorelbeke, K., and Meyer, S. F. D. (2019). von Willebrand factor and platelet glycoprotein ib: A thromboinflammatory Axis in stroke. Front. Immunol. 10, 2884–2888. doi:10.3389/fimmu.2019.02884

PubMed Abstract | CrossRef Full Text | Google Scholar

Dhakal, P., Rayamajhi, S., Verma, V., Gundabolu, K., and Bhatt, V. R. (2016). Reversal of anticoagulation and management of bleeding in patients on anticoagulants. Clin. Appl. Thrombosis/Hemostasis 23, 410–415. doi:10.1177/1076029616675970

CrossRef Full Text | Google Scholar

Dopheide, S. M., Maxwell, M. J., and Jackson, S. P. (2002). Shear-dependent tether formation during platelet translocation on von Willebrand factor. Blood 99 (1), 159–167. doi:10.1182/blood.V99.1.159

PubMed Abstract | CrossRef Full Text | Google Scholar

Doriot, P. A., Dorsaz, P. A., Dorsaz, L., De Benedetti, E., Chatelain, P., and Delafontaine, P. (2000). In-vivo measurements of wall shear stress in human coronary arteries. Coron. Artery Dis. 11 (6), 495–502. doi:10.1097/00019501-200009000-00008

PubMed Abstract | CrossRef Full Text | Google Scholar

Ebrahimi, S., and Bagchi, P. (2022). A computational study of red blood cell deformability effect on hemodynamic alteration in capillary vessel networks. Sci. Rep. 12, 4304. doi:10.1038/s41598-022-08357-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Edgar, L. T., Franco, C. A., Gerhardt, H., and Bernabeu, M. O. (2021). On the preservation of vessel bifurcations during flow-mediated angiogenic remodelling. PLOS Comput. Biol. 17 (679368), e1007715–e1007722. doi:10.1371/journal.pcbi.1007715

PubMed Abstract | CrossRef Full Text | Google Scholar

Farina, A., Rosso, F., and Fasano, A. (2021). A continuum mechanics model for the Fåhræus-Lindqvist effect. J. Biol. Phys. 47 (3), 253–270. doi:10.1007/s10867-021-09575-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Fenton, B. M., Carr, R. T., and Cokelet, G. R. (1985). Nonuniform red cell distribution in 20 to 100 μm bifurcations. Microvasc. Res. 29 (1), 103–126. doi:10.1016/0026-2862(85)90010-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Fisher, C., and Rossmann, J. S. (2009). Effect of non-Newtonian behavior on hemodynamics of cerebral aneurysms. J. Biomechanical Eng. 131 (9), 091004–091009. doi:10.1115/1.3148470

CrossRef Full Text | Google Scholar

Fiusco, F., Broman, L. M., and Wittberg, L. P. (2022). Blood pumps for extracorporeal membrane oxygenation: Platelet activation during different operating conditions. ASAIO J. 68, 79–86. doi:10.1097/MAT.0000000000001493

PubMed Abstract | CrossRef Full Text | Google Scholar

Fox, C. S., Palazzolo, T., Hirschhorn, M., Stevens, R. M., Rossano, J., Day, S. W., et al. (2022). Development of the centrifugal blood pump for a hybrid continuous flow pediatric total artificial heart: Model, make, measure. Front. Cardiovasc. Med. 9, 886874–886913. doi:10.3389/fcvm.2022.886874

PubMed Abstract | CrossRef Full Text | Google Scholar

Fraser, K. H., Zhang, T., Taskin, M. E., Griffith, B. P., and Wu, Z. J. (2012). A quantitative comparison of mechanical blood damage parameters in rotary ventricular assist devices: Shear stress, exposure time and hemolysis index. J. Biomechanical Eng. 134 (8), 081002–081011. doi:10.1115/1.4007092

CrossRef Full Text | Google Scholar

Fu, H., Jiang, Y., Yang, D., Scheiflinger, F., Wong, W. P., and Springer, T. A. (2017). Flow-induced elongation of von Willebrand factor precedes tension-dependent activation. Nat. Commun. 8 (324), 324. doi:10.1038/s41467-017-00230-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Fuchs, G., Berg, N., Broman, L. M., and Prahl Wittberg, L. (2018). Flow-induced platelet activation in components of the extracorporeal membrane oxygenation circuit. Sci. Rep. 8 (1), 13985–13989. doi:10.1038/s41598-018-32247-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Fukuda, M., Tokumine, A., Noda, K., and Sakai, K. (2020). Newly developed pediatric membrane oxygenator that suppresses excessive pressure drop in cardiopulmonary bypass and extracorporeal membrane oxygenation (Ecmo). Membranes 10 (11), 362–426. doi:10.3390/membranes10110362

PubMed Abstract | CrossRef Full Text | Google Scholar

Girdhar, G., Xenos, M., Alemu, Y., Chiu, W. C., Lynch, B. E., Jesty, J., et al. (2012). Device thrombogenicity emulation: A novel method for optimizing mechanical circulatory support device thromboresistance. PLoS ONE 7 (3), 324633–e32510. doi:10.1371/journal.pone.0032463

CrossRef Full Text | Google Scholar

Gogia, S., and Neelamegham, S. (2015). Role of fluid shear stress in regulating VWF structure, function and related blood disorders. Biorheology 52 (5–6), 319–335. doi:10.3233/BIR-15061

PubMed Abstract | CrossRef Full Text | Google Scholar

Grigioni, M., Morbiducci, U., D’Avenio, G., Benedetto, G. D., and Gaudio, C. D. (2005). A novel formulation for blood trauma prediction by a modified power-law mathematical model. Biomechanics Model. Mechanobiol. 4 (4), 249–260. doi:10.1007/s10237-005-0005-y

CrossRef Full Text | Google Scholar

Grunkemeier, J. M., Tsai, W., McFarland, C., and Horbett, T. (2000). The effect of adsorbed fibrinogen, fibronectin, von Willebrand factor and vitronectin on the procoagulant state of adherent platelets. Biomaterials 21 (22), 2243–2252. doi:10.1016/S0142-9612(00)00150-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Guibert, R., Fonta, C., and Plouraboué, F. (2010). A new approach to model confined suspensions flows in complex networks: Application to blood flow. Transp. Porous Media 83 (1), 171–194. doi:10.1007/s11242-009-9492-0

CrossRef Full Text | Google Scholar

Han, Q., Shea, S. M., Arleo, T., Qian, J. Y., and Ku, D. N. (2022). Thrombogenicity of biomaterials depends on hemodynamic shear rate. Artif. Organs 46, 606–617. doi:10.1111/aor.14093

PubMed Abstract | CrossRef Full Text | Google Scholar

Haroon, M., Bloks, N. G., Deldicque, L., Koppo, K., Seddiqi, H., Bakker, A. D., et al. (2022). Fluid shear stress-induced mechanotransduction in myoblasts: Does it depend on the glycocalyx. Exp. Cell Res. 417 (1), 113204. doi:10.1016/j.yexcr.2022.113204

PubMed Abstract | CrossRef Full Text | Google Scholar

Hastings, S. M., Deshpande, S. R., Wagoner, S., Maher, K., and Ku, D. N. (2016). Thrombosis in centrifugal pumps: Location and composition in clinical and in vitro circuits. Int. J. Artif. Organs 39 (4), 200–204. doi:10.5301/ijao.5000498

PubMed Abstract | CrossRef Full Text | Google Scholar

Hatoum, H., Singh-Gryzbon, S., Esmailie, F., Ruile, P., Neumann, F. J., Blanke, P., et al. (2021). Predictive model for thrombus formation after transcatheter valve replacement. Cardiovasc. Eng. Technol. 12 (6), 576–588. doi:10.1007/s13239-021-00596-x

PubMed Abstract | CrossRef Full Text | Google Scholar

He, G., Zhang, J., Shah, A., Berk, Z. B., Han, L., Dong, H., et al. (2021). Flow characteristics and hemolytic performance of the new Breethe centrifugal blood pump in comparison with the CentriMag and Rotaflow pumps. Int. J. Artif. Organs 44 (11), 829–837. doi:10.1177/03913988211041635

PubMed Abstract | CrossRef Full Text | Google Scholar

Hellums, J. D. (1994). 1993 Whitaker lecture: Biorheology in thrombosis research. Ann. Biomed. Eng. 22, 445–455. doi:10.1007/bf02367081

PubMed Abstract | CrossRef Full Text | Google Scholar

Hellums, J. D., Peterson, D. M., Stathopoulos, N. A., Moake, J. L., and Giorgio, T. D. (1987). Studies on the mechanisms of shear-induced platelet activation. Cereb. Ischemia Hemorheol., 80–89. doi:10.1007/978-3-642-71787-1_8

CrossRef Full Text | Google Scholar

Hesselmann, F., Halwes, M., Bongartz, P., Wessling, M., Cornelissen, C., Schmitz-Rode, T., et al. (2022). Tpms - based membrane lung with locally - modified permeabilities for optimal flow distribution. Sci. Rep. 12, 7160–7213. doi:10.1038/s41598-022-11175-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoefer, T., Rana, A., Niego, B., Jagdale, S., Albers, H. J., Gardiner, E. E., et al. (2020). Targeting shear gradient activated von Willebrand factor by the novel single-chain antibody A1 reduces occlusive thrombus formation <i&gt;in vitro&lt;/i&gt;. Haematologica 106, 2874–2884. doi:10.3324/haematol.2020.250761

CrossRef Full Text | Google Scholar

Hofferberth, S. C., Saeed, M. Y., Tomholt, L., Fernandes, M. C., Payne, C. J., Price, K., et al. (2020). A geometrically adaptable heart valve replacement. Sci. Transl. Med. 4006 (12), eaay4006–13. doi:10.1126/scitranslmed.aay4006

CrossRef Full Text | Google Scholar

Hoganson, D. M., Pryor, H. I., Spool, I. D., Burns, O. H., Gilmore, J. R., and Vacanti, J. P. (2010). Principles of biomimetic vascular network design applied to a tissue-engineered liver scaffold. Tissue Eng. - Part A 16 (5), 1469–1477. doi:10.1089/ten.tea.2009.0118

PubMed Abstract | CrossRef Full Text | Google Scholar

Horbett, T. A. (2019). Fibrinogen adsorption to biomaterials. J. Biomed. Mat. Res. A 106 (10), 2777–2788. doi:10.1002/jbm.a.36460

CrossRef Full Text | Google Scholar

Hu, D., Cai, D., and Rangan, A. V. (2012). Blood vessel adaptation with fluctuations in capillary flow distribution. PLoS ONE 7 (9), e45444. doi:10.1371/journal.pone.0045444

PubMed Abstract | CrossRef Full Text | Google Scholar

Hughes, A. D. (2015). Optimality, cost minimization and the design of arterial networks. Artery Res. 10, 1–10. doi:10.1016/j.artres.2015.01.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Jackson, S. P., Nesbitt, W. S., and Westein, E. (2009). Dynamics of platelet thrombus formation. J. Thrombosis Haemostasis 7, 17–20. doi:10.1111/j.1538-7836.2009.03401.x

CrossRef Full Text | Google Scholar

Jaffer, I. H., Fredenburgh, J., Hirsh, J., and Weitz, J. (2015). Medical device-induced thrombosis: What causes it and how can we prevent it? J. Thrombosis Haemostasis 13 (S1), S72–S81. doi:10.1111/jth.12961

CrossRef Full Text | Google Scholar

Jamiolkowski, M. A., Patel, M., Golding, M. D., Malinauskas, R. A., and Lu, Q. (2022). Comparison of animal and human blood for in vitro dynamic thrombogenicity testing of biomaterials. Artif. Organs 46, 2400–2411. doi:10.1111/aor.14366

PubMed Abstract | CrossRef Full Text | Google Scholar

Jesty, J., and Bluestein, D. (1999). Acetylated prothrombin as a substrate in the measurement of the procoagulant activity of platelets: Elimination of the feedback activation of platelets by thrombin. Anal. Biochem. 272 (1), 64–70. doi:10.1006/abio.1999.4148

PubMed Abstract | CrossRef Full Text | Google Scholar

Ju, L., Chen, Y., Zhou, F., Lu, H., Cruz, M. A., and Zhu, C. (2016). Von Willebrand factor-A1 domain binds platelet glycoprotein Ibα in multiple states with distinctive force-dependent dissociation kinetics. Thrombosis Res. 136 (3), 606–612. doi:10.1016/j.thromres.2015.06.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, D. A., and Ku, D. N. (2022). Structure of shear-induced platelet aggregated clot formed in an in vitro arterial thrombosis model. Blood Adv. 6 (9), 2872–2883. doi:10.1182/bloodadvances.2021006248

PubMed Abstract | CrossRef Full Text | Google Scholar

Klaus, S., Korfer, S., Mottaghy, K., Reul, H., and Glasmacher, B. (2002). In vitro blood damage by high shear flow: Human versus porcine blood. Int. J. Artif. Organs 25 (4), 306–312. doi:10.1177/039139880202500409

PubMed Abstract | CrossRef Full Text | Google Scholar

Kotsalos, C., Raynaud, F., Latt, J., Dutta, R., Dubois, F., Zouaoui Boudjeltia, K., et al. (2022). Shear induced diffusion of platelets revisited. Front. Physiology 13, 985905–985909. doi:10.3389/fphys.2022.985905

CrossRef Full Text | Google Scholar

Kuchinka, J., Willems, C., Telyshev, D. V., and Groth, T. (2021). Control of blood coagulation by hemocompatible material surfaces—a review. Bioengineering 8 (12), 215–226. doi:10.3390/bioengineering8120215

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuczaj, A., Hudzik, B., Kaczmarski, J., and Przybylowski, P. (2022). Hemostasis disturbances in continuous-flow left ventricular assist device (CF-lvad) patients — rationale and study design. J. Clin. Med. 11 (3712), 3712. doi:10.3390/jcm11133712

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, D. R., Hanlin, E., Glurich, I., Mazza, J. J., and Yale, S. H. (2010). Virchow’s contribution to the understanding of thrombosis and cellular biology. Clin. Med. Res. 8 (3–4), 168–172. doi:10.3121/cmr.2009.866

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, N., Abdul, R. P. S. M., Khan, K. S. H., and Kyriacou, P. A. (2022). Influence of blood pressure and rheology on oscillatory shear index and wall shear stress in the carotid artery. J. Braz. Soc. Mech. Sci. Eng. 44 (11), 510–516. doi:10.1007/s40430-022-03792-5

CrossRef Full Text | Google Scholar

Kuwahara, M., Sugimoto, M., Tsuji, S., Matsui, H., Mizuno, T., Miyata, S., et al. (2002). Platelet shape changes and adhesion under high shear flow. Arteriosclerosis, Thrombosis, Vasc. Biol. 22 (2), 329–334. doi:10.1161/hq0202.104122

CrossRef Full Text | Google Scholar

Kwak, D., Wu, Y., and Horbett, T. A. (2005). ‘Fibrinogen and von Willebrand ’ s factor adsorption are both required for platelet adhesion from sheared suspensions to polyethylene preadsorbed with blood plasma’. Wiley Period. 74A, 69–83. doi:10.1002/jbm.a.30365

CrossRef Full Text | Google Scholar

Labarrere, C. A., Dabiri, A. E., and Kassab, G. S. (2020). Thrombogenic and inflammatory reactions to biomaterials in medical devices. Front. Bioeng. Biotechnol. 8, 123–218. doi:10.3389/fbioe.2020.00123

PubMed Abstract | CrossRef Full Text | Google Scholar

Lachaux, J., Hwang, G., Arouche, N., Naserian, S., Harouri, A., Lotito, V., et al. (2021). A compact integrated microfluidic oxygenator with high gas exchange efficiency and compatibility for long-lasting endothelialization. Lab a Chip 21, 4791–4804. doi:10.1039/d1lc00356a

PubMed Abstract | CrossRef Full Text | Google Scholar

Lackner, J. M., Imbir, G., Trembecka-Wojciga, K., Plutecka, H., Jasek-Gajda, E., et al. (2020). Rolling or two-stage aggregation of platelets on the surface of thin ceramic coatings under in vitro simulated blood flow conditions. ACS Biomaterials Sci. Eng. 6, 898–911. doi:10.1021/acsbiomaterials.9b01074

CrossRef Full Text | Google Scholar

Lecarpentier, E., Bhatt, M., Bertin, G. I., Deloison, B., Salomon, L. J., Deloron, P., et al. (2016). Computational fluid dynamic simulations of maternal circulation: Wall shear stress in the human placenta and its biological implications. PLoS ONE 11 (1), 01472622–e147318. doi:10.1371/journal.pone.0147262

CrossRef Full Text | Google Scholar

Lee, J. K., Kung, H. H., and Mockros, L. F. (2008). Microchannel technologies for artificial lungs: (1) theory. ASAIO J. 54 (4), 372–382. doi:10.1097/MAT.0b013e31817ed9e1

PubMed Abstract | CrossRef Full Text | Google Scholar

Leiderman, K., and Fogelson, A. L. (2011). Grow with the flow: A spatial – temporal model of platelet deposition and blood coagulation under flow. Math. Med. Biol. 28, 47–84. doi:10.1093/imammb/dqq005

PubMed Abstract | CrossRef Full Text | Google Scholar

Leighton, D., and Acrivos, A. (1987). The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439. doi:10.1017/S0022112087002155

CrossRef Full Text | Google Scholar

Li, L., Wang, S., Han, K., Qi, X., Ma, S., et al. (2023). Quantifying shear-induced margination and adhesion of platelets in microvascular blood flow. J. Mol. Biol. 435, 167824–167910. doi:10.1016/j.jmb.2022.167824

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Wang, H., Xi, Y., Sun, A., Deng, X., Chen, Z., et al. (2022). A new mathematical numerical model to evaluate the risk of thrombosis in three clinical ventricular assist devices. MDPI Bioeng. 9 (9), 235. doi:10.3390/bioengineering9060235

CrossRef Full Text | Google Scholar

Lighthill, M. J. (1968). Pressure-forcing of tightly fitting pellets along fluid-filled elastic tubes. J. Fluid Mech. 34 (1), 113–143. doi:10.1017/S0022112068001795

CrossRef Full Text | Google Scholar

Lindqvist, R., and Fahraeus, T. (1930). The viscosity of the blood in narrow capillary tubes. Am. J. Physiology 96, 562–568. doi:10.1152/ajplegacy.1931.96.3.562

CrossRef Full Text | Google Scholar

Liu, F., and Jing, D. (2021). Optimization of a fractal treelike microchannel network with uniform roughness for laminar flow. Chem. Eng. Technol. 44 (10), 1814–1819. doi:10.1002/ceat.202100196

CrossRef Full Text | Google Scholar

Liu, H., Lan, L., Abrigo, J., Ip, H. L., Soo, Y., Zheng, D., et al. (2021). Comparison of Newtonian and non-Newtonian fluid models in blood flow simulation in patients with intracranial arterial stenosis. Front. Physiology 12, 718540–718611. doi:10.3389/fphys.2021.718540

CrossRef Full Text | Google Scholar

Liu, Z. L., Bresette, C., Aidun, C. K., and Ku, D. N. (2022). SIPA in 10 milliseconds: VWF tentacles agglomerate and capture platelets under high shear. Blood Adv. 6 (8), 2453–2465. doi:10.1182/bloodadvances.2021005692

PubMed Abstract | CrossRef Full Text | Google Scholar

Major, R., Gawlikowski, M., Sanak, M., Lackner, J. M., and Kapis, A. (2020). Design, manufacturing technology and in-vitro evaluation of original, polyurethane, petal valves for application in pulsating ventricular assist devices. Polymers 12 (2986), 2986–3016. doi:10.3390/polym12122986

PubMed Abstract | CrossRef Full Text | Google Scholar

Makdisi, G., and Wang, I. (2015). Extra corporeal membrane oxygenation (ECMO) review of a lifesaving technology. J. Thorac. Dis. 7 (20), 166–176. doi:10.3978/j.issn.2072-1439.2015.07.17

CrossRef Full Text | Google Scholar

Mandal, P. K. (2005). An unsteady analysis of non-Newtonian blood flow through tapered arteries with a stenosis. Int. J. Non-Linear Mech. 40 (1), 151–164. doi:10.1016/j.ijnonlinmec.2004.07.007

CrossRef Full Text | Google Scholar

Marom, G., Chiu, W. C., Slepian, M. J., and Bluestein, D. (2014). Numerical model of total artificial heart hemodynamics and the effect of its size on stress accumulation. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2014, 5651–5654. doi:10.1109/EMBC.2014.6944909

PubMed Abstract | CrossRef Full Text | Google Scholar

Martinolli, M., Cornat, F., and Vergara, C. (2022). Computational fluid – structure interaction study of a new wave membrane blood pump. Cardiovasc. Eng. Technol. 13 (3), 373–392. doi:10.1007/s13239-021-00584-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Maurer, A. N., and Matheis, G. (2008). The artificial lung. Adv. Tissue Eng., 887–901. doi:10.1142/9781848161832_0040

CrossRef Full Text | Google Scholar

Maxwell, M. J., Westein, E., Nesbitt, W. S., Giuliano, S., Dopheide, S. M., and Jackson, S. P. (2016)., 109. The, 566–576. doi:10.1182/blood-2006-07-028282Identification of a 2-stage platelet aggregation process mediating shear-dependent thrombus formationBlood2

CrossRef Full Text | Google Scholar

Mehta, V., Pang, K. L., Givens, C. S., Chen, Z., Huang, J., Sweet, D. T., et al. (2021). Mechanical forces regulate endothelial-to-mesenchymal transition and atherosclerosis via an Alk5-Shc mechanotransduction pathway. Sci. Adv. 7, eabg5060–13. doi:10.1126/sciadv.abg5060

PubMed Abstract | CrossRef Full Text | Google Scholar

Menichini, C., and Yun, X. (2016). Mathematical modeling of thrombus formation in idealized models of aortic dissection: Initial findings and potential applications. J. Math. Biol. 73 (5), 1205–1226. doi:10.1007/s00285-016-0986-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Mountford, J. K., Petitjean, C., Putra, H. W. K., McCafferty, J. A., Setiabakti, N. M., Lee, H., et al. (2015). The class II PI 3-kinase, PI3KC2α, links platelet internal membrane structure to shear-dependent adhesive function. Nat. Commun. 6, 6535. doi:10.1038/ncomms7535

PubMed Abstract | CrossRef Full Text | Google Scholar

Munn, L. L., and Dupin, M. M. (2008). Blood cell interactions and segregation in flow. Ann. Biomed. Eng. 36 (4), 534–544. doi:10.1007/s10439-007-9429-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Murphy, D. A., Hockings, L. E., Andrews, R. K., Aubron, C., Gardiner, E. E., Pellegrino, V. A., et al. (2015). Extracorporeal membrane oxygenation — hemostatic complications. Transfus. Med. Rev. 29 (2), 90–101. doi:10.1016/j.tmrv.2014.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Murray, C. D. (1926). The physiological principle of minimun work applied to the angle of branching of arteries. J. General Physiology 9 (4), 835–841. doi:10.1085/jgp.9.6.835

CrossRef Full Text | Google Scholar

Nader, E., Skinner, S., Romana, M., Fort, R., Lemonne, N., Guillot, N., et al. (2019). Blood rheology: Key parameters, impact on blood flow, role in sickle cell disease and effects of exercise. Front. Physiology 10, 1329–1414. doi:10.3389/fphys.2019.01329

CrossRef Full Text | Google Scholar

Nesbitt, W. S., Westein, E., Tovar-Lopez, F. J., Tolouei, E., Mitchell, A., Fu, J., et al. (2009). A shear gradient-dependent platelet aggregation mechanism drives thrombus formation. Nat. Med. 15 (6), 665–673. doi:10.1038/nm.1955

PubMed Abstract | CrossRef Full Text | Google Scholar

Nitzsche, B., Rong, W. W., Goede, A., Hoffmann, B., Scarpa, F., Kuebler, W. M., et al. (2022). Coalescent angiogenesis — Evidence for a novel concept of vascular network maturation. Angiogenesis 25 (1), 35–45. doi:10.1007/s10456-021-09824-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Nobili, M., Sheriff, J., Morbiducci, U., Redaelli, A., and Bluestein, D. (2008). Platelet activation due to hemodynamic shear stresses: Damage accumulation model and comparison to in vitro measurements. ASAIO J. 54, 64–72. doi:10.1097/MAT.0b013e31815d6898

PubMed Abstract | CrossRef Full Text | Google Scholar

Pialot, B., Gachelin, J., Provost, J., and Couture, O. (2021). Exploitation of blood non - Newtonian properties for ultrasonic measurement of hematocrit. Sci. Rep. 11, 10208–10210. doi:10.1038/s41598-021-89704-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Poitier, B., Chocron, R., Peronino, C., Philippe, A., Pya, Y., Rivet, N., et al. (2022). Bioprosthetic total artificial heart in autoregulated mode is biologically hemocompatible: Insights for multimers of von Willebrand factor. Arteriosclerosis, Thrombosis, Vasc. Biol. 42 (4), 470–480. doi:10.1161/ATVBAHA.121.316833

CrossRef Full Text | Google Scholar

Pozdin, V. A., Erb, D., Downey, M., Rivera, K. R., and Daniele, M. (2021). Monitoring of random microvessel network formation by in-line sensing of flow rates: A numerical and in vitro investigation. Sensors Actuators 331, 112970. doi:10.1016/j.sna.2021.112970

CrossRef Full Text | Google Scholar

Pries, A. R., Ley, K., Claassen, M., and Gaehtgens, P. (1989). Red cell distribution at microvascular bifurcations. Microvasc. Res. 101, 81–101. doi:10.1016/0026-2862(89)90018-6

CrossRef Full Text | Google Scholar

Pujos, J., Reyssat, M., and Goff, A. L. (2022). Experimental and numerical study of platelets rolling on a von Willebrand factor-coated surface. Med. Eng. Phys. 55, 25–33. doi:10.1016/j.medengphy.2018.03.005

CrossRef Full Text | Google Scholar

Pushin, D. M., Salikhova, T. Y., Zlobina, K. E., and Guria, G. T. (2020). Platelet activation via dynamic conformational changes of von Willebrand factor under shear. PLOS One 15, e0234501–e0234517. doi:10.1371/journal.pone.0234501

PubMed Abstract | CrossRef Full Text | Google Scholar

Qiao, Y., Luo, K., and Fan, J. (2022). Computational prediction of thrombosis in food and drug administration ’ s benchmark nozzle. Front. Physiology 13, 867613–867710. doi:10.3389/fphys.2022.867613

CrossRef Full Text | Google Scholar

Rana, A., Westein, E., Niego, B., and Hagemeyer, C. E. (2019). Shear-Dependent platelet aggregation: Mechanisms and therapeutic opportunities. Front. Cardiovasc. Med. 6, 141–221. doi:10.3389/fcvm.2019.00141

PubMed Abstract | CrossRef Full Text | Google Scholar

Razavi, M. S., Shirani, E., and Kassab, G. S. (2018). Scaling laws of flow rate, vessel blood volume, lengths, and transit times with number of capillaries. Front. Physiology 9, 581. doi:10.3389/fphys.2018.00581

CrossRef Full Text | Google Scholar

Receveur, N., Nechipurenko, D., Knapp, Y., Yakusheva, A., Maurer, E., Denis, C. V., et al. (2020). Shear rate gradients promote a bi-phasic thrombus formation on weak adhesive proteins, such as fibrinogen in a VWF-dependent manner. Haematologica 105 (10), 2471–2483. doi:10.3324/haematol.2019.235754

PubMed Abstract | CrossRef Full Text | Google Scholar

Reininger, A. J., et al. (2006). Mechanism of platelet adhesion to von Willebrand factor and microparticle formation under high shear stress. Blood 107 (9), 3537–3545. doi:10.1182/blood-2005-02-0618

PubMed Abstract | CrossRef Full Text | Google Scholar

Reneman, R. S., and Hoeks, A. P. G. (2008). Wall shear stress as measured in vivo: Consequences for the design of the arterial system. Med. Biol. Eng. Comput. 46 (5), 499–507. doi:10.1007/s11517-008-0330-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Rojas, A. M. T., Meza Romero, A., Pagonabarraga, I., Travasso, R. D. M., and Corvera Poire, E. (2015). Obstructions in vascular networks: Relation between network morphology and blood supply. PLoS ONE 10, e0128111. doi:10.1371/journal.pone.0128111

PubMed Abstract | CrossRef Full Text | Google Scholar

Roka-Moiia, Y., Ammann, K. R., Miller-Gutierrez, S., Sweedo, A., Palomares, D., Italiano, J., et al. (2021). Shear-mediated platelet activation in the free flow II: Evolving mechanobiological mechanisms reveal an identifiable signature of activation and a bi-directional platelet dyscrasia with thrombotic and bleeding features. J. Biomechanics 123, 110415. doi:10.1016/j.jbiomech.2021.110415

CrossRef Full Text | Google Scholar

Romanova, A. N., Pugovkin, A. A., Denisov, M. V., Ephimov, I. A., Gusev, D. V., Walter, M., et al. (2022). Hemolytic performance in two generations of the sputnik left ventricular assist device: A combined numerical and experimental study. J. Funct. Biomaterials 13 (1), 7. doi:10.3390/jfb13010007

CrossRef Full Text | Google Scholar

Rooij, B. J. M. V., Zavodszky, G., Hoekstra, A. G., and Ku, D. N. (2020). Biorheology of occlusive thrombi formation under high shear: In vitro growth and shrinkage. Sci. Rep. 1, 1860418604–1860418611. doi:10.1038/s41598-020-74518-7

CrossRef Full Text | Google Scholar

Roudaut, R., Serri, K., and Lafitte, S. (2007). Thrombosis of prosthetic heart valves: Diagnosis and therapeutic considerations. Heart 93, 137–142. doi:10.1136/hrt.2005.071183

PubMed Abstract | CrossRef Full Text | Google Scholar

Roux, E., Bougaran, P., Dufourcq, P., and Couffinhal, T. (2020). Fluid shear stress sensing by the endothelial layer. Front. Physiology 11, 861–917. doi:10.3389/fphys.2020.00861

CrossRef Full Text | Google Scholar

Roy, A., and Woldenberg, M. (1982). A generalization of the optimal models of arterial branching. Bull. Math. Biol. 44 (3), 349–360. doi:10.1016/s0092-8240(82)80016-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruggeri, Z. M., Orje, J. N., Habermann, R., Federici, A. B., and Reininger, A. J. (2006). Activation-independent platelet adhesion and aggregation under elevated shear stress. Blood 108 (6), 1903–1910. doi:10.1182/blood-2006-04-011551

PubMed Abstract | CrossRef Full Text | Google Scholar

Ryan, Y. R., Walk, R., Palomares, D. E., Ammann, K. R., Dimasi, A., Italiano, J. E., et al. (2020). Platelet activation via shear stress exposure induces a differing pattern of biomarkers of activation versus biochemical agonists. Thrombosis Haemostasis 120 (120), 776–792. doi:10.1055/s-0040-1709524

PubMed Abstract | CrossRef Full Text | Google Scholar

Saghian, R., Cahill, L. S., Rahman, A., Serghides, L., McDonald, C. R., Debebe, S. K., et al. (2022). Allometric scaling relationships in mouse placenta. J. R. Soc. Interface 19, 20220579. doi:10.1098/rsif.2022.0579

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakariassen, K. S., Orning, L., and Turitto, V. T. (2015). The impact of blood shear rate on arterial thrombus formation. Future Sci. OA 1 (4), FSO30. doi:10.4155/fso.15.28

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, J., Vedula, E. M., Lai, W., Isenberg, B. C., Lewis, D. J., Lang, D., et al. (2021). Toward development of a higher flow rate hemocompatible biomimetic microfluidic blood oxygenator. Micromachines 12 (8), 888. doi:10.3390/mi12080888

PubMed Abstract | CrossRef Full Text | Google Scholar

Savage, B., Almus-jacobs, F., and Ruggeri, Z. M. (1998). Specific synergy of multiple substrate – receptor interactions in platelet thrombus formation under flow. Cell 94, 657–666. doi:10.1016/s0092-8674(00)81607-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Savage, B., Saldı, E., and Ruggeri, Z. M. (1996). Initiation of platelet adhesion by arrest onto fibrinogen or translocation on von Willebrand factor. Cell 84, 289–297. doi:10.1016/s0092-8674(00)80983-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Savage, V. M., Deeds, E. J., and Fontana, W. (2008). Sizing up allometric scaling theory. PLoS ONE 4 (9), e1000171. doi:10.1371/journal.pcbi.1000171

CrossRef Full Text | Google Scholar

Schneider, S. W., Nuschele, S., Wixforth, A., Gorzelanny, C., Alexander-Katz, A., Netz, R. R., et al. (2007). Shear-induced unfolding triggers adhesion of von Willebrand factor fibers. Proc. Natl. Acad. Sci. U. S. A. 104 (19), 7899–7903. doi:10.1073/pnas.0608422104

PubMed Abstract | CrossRef Full Text | Google Scholar

Schöps, M., GroB-Hardt, S. H., Schmitz-Rode, T., Steinseifer, U., Brodie, D., Clauser, J. C., et al. (2021). Hemolysis at low blood flow rates: In-vitro and in-silico evaluation of a centrifugal blood pump. J. Transl. Med. 19 (1), 2–10. doi:10.1186/s12967-020-02599-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Sciubba, E. (2016). A critical reassessment of the hess – Murray law. MDPI Entropy 18 (18), 283. doi:10.3390/e18080283

CrossRef Full Text | Google Scholar

Siedlecki, C. A., Lestini, B., Kottke-Marchant, K., Eppell, S., Wilson, D., and Marchant, R. (1996). Shear-dependent changes in the three-dimensional structure of human von Willebrand factor. Blood 88 (8), 2939–2950. doi:10.1182/blood.v88.8.2939.bloodjournal8882939

PubMed Abstract | CrossRef Full Text | Google Scholar

Sing, C. E., and Alexander-katz, A. (2010). Elongational flow induces the unfolding of von Willebrand factor at physiological flow rates. Biophysical J. 98 (9), L35–L37. doi:10.1016/j.bpj.2010.01.032

CrossRef Full Text | Google Scholar

Smith, A. F., Doyeux, V., Berg, M., Peyrounette, M., Haft-Javaherian, M., Larue, A. E., et al. (2019). Brain capillary networks across species: A few simple organizational requirements are sufficient to reproduce both structure and function. Front. Physiology 10, 233–322. doi:10.3389/fphys.2019.00233

CrossRef Full Text | Google Scholar

Soares, J. S., Sheriff, J., and Bluestein, D. (2013). A novel mathematical model of activation and sensitization of platelets subjected to dynamic stress histories. Biomechanics Model. Mechanobiol. 12 (6), 1127–1141. doi:10.1007/s10237-013-0469-0

CrossRef Full Text | Google Scholar

Sorensen, E. N., Burgreen, G. W., Wagner, W. R., and Antaki, J. F. (1999). Computational simulation of platelet deposition and activation: I. Model development and properties. Ann. Biomed. Eng. 27, 436–448. doi:10.1114/1.200

PubMed Abstract | CrossRef Full Text | Google Scholar

Spann, A. P., Campbell, J. E., Fitzgibbon, S. R., Rodriguez, A., Cap, A. P., Blackbourne, L. H., et al. (2016). The effect of hematocrit on platelet adhesion: Experiments and simulations. Biophysical J. 111 (3), 577–588. doi:10.1016/j.bpj.2016.06.024

CrossRef Full Text | Google Scholar

Spieker, C. J., Zavodszky, G., Mouriaux, C., van der Kolk, M., Gachet, C., Mangin, P. H., et al. (2021). The effects of micro-vessel curvature induced elongational flows on platelet adhesion. Ann. Biomed. Eng. 49 (12), 3609–3620. doi:10.1007/s10439-021-02870-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Stiehm, M., Borowski, F., Kaule, S., Ott, R., Pfensig, S., Siewert, S., et al. (2019). Computational flow analysis of the washout of an aortic valve by means of Eulerian transport equation. Curr. Dir. Biomed. Eng. 5 (1), 123–126. doi:10.1515/cdbme-2019-0032

CrossRef Full Text | Google Scholar

Strecker, C., Krafft, A. J., Kaufhold, L., Hullebrandt, M., Treppner, M., Ludwig, U., et al. (2021). Carotid geometry and wall shear stress independently predict increased wall thickness — a longitudinal 3D mri study in high-risk patients. Front. Cardiovasc. Med. 8, 723860–723911. doi:10.3389/fcvm.2021.723860

PubMed Abstract | CrossRef Full Text | Google Scholar

Sugihara-seki, M., and Takinouchi, N. (2021). Margination of platelet-sized particles in the red blood cell suspension flow through square microchannels. MDPI Micromachines 12 (12), 1175. doi:10.3390/mi12101175

CrossRef Full Text | Google Scholar

Sun, J., Bird, P., and Salem, H. H. (1993). Interaction of annexin V and platelets: Effects on platelet function and protein S binding. Thrombosis Res. 69 (3), 289–296. doi:10.1016/0049-3848(93)90026-K

CrossRef Full Text | Google Scholar

Sun, W., Wang, S., Chen, Z., Zhang, J., Li, T., Arias, K., et al. (2020). Impact of high mechanical shear stress and oxygenator membrane surface on blood damage relevant to thrombosis and bleeding in a pediatric ECMO circuit. WILEY Artif. Organs 44 (44), 717–726. doi:10.1111/aor.13646

CrossRef Full Text | Google Scholar

Support, A. C., Perkins, I. L., Kanamarlapudi, V., Moriarty, C., and Ali, S. (2021). Hemodilution increases the susceptibility of red blood cells to mechanical shear stress during in vitro hemolysis testing. ASAIO 67, 632–641. doi:10.1097/MAT.0000000000001280

CrossRef Full Text | Google Scholar

Swain, S. M., and Liddle, R. A. (2021). Piezo1 acts upstream of TRPV4 to induce pathological changes in endothelial cells due to shear stress. J. Biol. Chem. 296, 100171. doi:10.1074/jbc.RA120.015059

PubMed Abstract | CrossRef Full Text | Google Scholar

Sweedo, A., Wise, L. M., Roka-Moiia, Y., Arce, F. T., Saavedra, S. S., Sheriff, J., et al. (2021). Shear-mediated platelet activation is accompanied by unique alterations in platelet release of lipids. Cell. Mol. Bioeng. 14 (6), 597–612. doi:10.1007/s12195-021-00692-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Taskin, M. E., Fraser, K. H., Zhang, T., Wu, C., Griffith, B. P., and Wu, Z. J. (2012). Evaluation of Eulerian and Lagrangian models for hemolysis estimation. ASAIO J. 58 (4), 363–372. doi:10.1097/MAT.0b013e318254833b

PubMed Abstract | CrossRef Full Text | Google Scholar

Taylor, G. (1953). Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 219 (1137), 186–203. doi:10.1098/rspa.1953.0139

CrossRef Full Text | Google Scholar

Thiagarajan, P., and Tait, J. F. (1990). Binding of annexin V/placental anticoagulant protein I to platelets: Evidence for phosphatidylserine exposure in the procoagulant response of activated platelets. J. Biol. Chem. 265 (29), 17420–17423. doi:10.1016/s0021-9258(18)38177-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Torres Rojas, A. M., Lorente, S., Hautefeuille, M., and Sanchez-Cedillo, A. (2021). Hierarchical modeling of the liver vascular system. Front. Physiology 12, 733165–733212. doi:10.3389/fphys.2021.733165

CrossRef Full Text | Google Scholar

Trejo-soto, C., and Hernández-machado, A. (2022). Normalization of blood viscosity according to the hematocrit and the shear rate. Micromachines 13, 357–420. doi:10.3390/mi13030357

PubMed Abstract | CrossRef Full Text | Google Scholar

Turitto, V. T., and Weiss, H. J. (1980). Red blood cells: Their dual role in thrombus formation. Science 207 (4430), 541–543. doi:10.1126/science.7352265

PubMed Abstract | CrossRef Full Text | Google Scholar

Valipour, P. (2022). Effects of coiling embolism on blood hemodynamic of the MCA aneurysm: A numerical study. Sci. Rep. 12 (1), 22029. doi:10.1038/s41598-022-26208-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Rooij, B. J. M., et al. (2021). Haemodynamic flow conditions at the initiation of high-shear platelet aggregation: A combined in vitro and cellular in silico study: High shear thrombosis: In vitro and silico. Interface Focus 11 (1), 1–11. doi:10.1098/rsfs.2019.0126rsfs20190126

CrossRef Full Text | Google Scholar

Vedula, E. M., Isenberg, B. C., Santos, J., Lai, W., Lewis, D. J., Sutherland, D., et al. (2022). Multilayer scaling of a biomimetic microfluidic oxygenator. ASAIO J. Publ. Ah 68, 1312–1319. doi:10.1097/mat.0000000000001647

CrossRef Full Text | Google Scholar

Vijayavenkataraman, S., Zhang, L., Zhang, S., Hsi Fuh, J. Y., and Lu, W. F. (2018). Triply periodic minimal surfaces sheet scaffolds for tissue engineering applications: An optimization approach toward biomimetic scaffold design. ACS Appl. Bio Mat. 1, 259–269. doi:10.1021/acsabm.8b00052

CrossRef Full Text | Google Scholar

Wang, S., Griffith, B. P., and Wu, Z. J. (2021). Device-induced hemostatic disorders in mechanically assisted circulation. Clin. Appl. Thrombosis/Hemostasis 27, 107602962098237. doi:10.1177/1076029620982374

CrossRef Full Text | Google Scholar

Wechsatol, W., Lorente, S., and Bejan, A. (2002). Optimal tree-shaped networks for fluid flow in a disc-shaped body. Int. J. Heat Mass Transf. 45 (25), 4911–4924. doi:10.1016/S0017-9310(02)00211-9

CrossRef Full Text | Google Scholar

West, G. B., Brown, J. H., and Enquist, B. J. (1997). A general model for the origin of allometric scaling laws in biology. Science 122, 122–126. doi:10.1126/science.276.5309.122

CrossRef Full Text | Google Scholar

Wiegmann, L., Boes, S., de Zelicourt, D., Thamsen, B., Schmid Daners, M., Meboldt, M., et al. (2018). Blood pump design variations and their influence on hydraulic performance and indicators of hemocompatibility. Ann. Biomed. Eng. 46 (3), 417–428. doi:10.1007/s10439-017-1951-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, C. J., Clegg, R. E., Leavesley, D. I., and Pearcy, M. J. (2005). Mediation of biomaterial–cell interactions by adsorbed proteins: A review. Tissue Eng. 11, 1–18. doi:10.1089/ten.2005.11.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Wootton, D. M., Markou, C. P., Hanson, S. R., and Ku, D. N. (2001). A mechanistic model of acute platelet accumulation in thrombogenic stenoses. Ann. Biomed. Eng. 29, 321–329. doi:10.1114/1.1359449

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, W., Zhussupbekov, M., Aubry, N., Antaki, J. F., and Massoudi, M. (2020). Simulation of thrombosis in a stenotic microchannel: The effects of vWF-enhanced shear activation of platelets. Int. J. Eng. Sci. 147, 103206. doi:10.1016/j.ijengsci.2019.103206

PubMed Abstract | CrossRef Full Text | Google Scholar

Xenos, M., Girdhar, G., Alemu, Y., Jesty, J., Slepian, M., Einav, S., et al. (2010). Device thrombogenicity emulator (dte) − design optimization methodology for cardiovascular devices: A study in two bileaflet mhv designs. J. Biomechanics 43 (12), 2400–2409. doi:10.1016/j.jbiomech.2010.04.020

CrossRef Full Text | Google Scholar

Xu, Z., Liang, Y., Delaney, M. K., Zhang, Y., Kim, K., Li, J., et al. (2021). Shear and integrin outside-in signaling activate NADPH-oxidase 2 to promote platelet activation. Arteriosclerosis, Thrombosis, Vasc. Biol. 41, 1638–1653. doi:10.1161/ATVBAHA.120.315773

CrossRef Full Text | Google Scholar

Yang, W., Peng, S., Xiao, W., Hu, Y., Wu, H., and Li, M. (2022). CFD-based flow channel optimization and performance prediction for a conical axial maglev blood pump. Sensors 22 (4), 1642. doi:10.3390/s22041642

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeleswarapu, K. K., Antaki, J. F., Kameneva, M. V., and Rajagopal, K. R. (1995). A mathematical model for shear-induced hemolysis. Artif. Organs 19 (7), 576–582. doi:10.1111/j.1525-1594.1995.tb02384.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Zamir, M., Sinclair, P., and Wonnacott, T. H. (1992). Relation between diameter and flow in major branches of the arch of the aorta. J. Biomechanics 25 (11), 1303–1310. doi:10.1016/0021-9290(92)90285-9

CrossRef Full Text | Google Scholar

Závodszky, G., Van Rooij, B., Czaja, B., Azizi, V., de Kanter, D., and Hoekstra, A. G. (2019). Red blood cell and platelet diffusivity and margination in the presence of cross-stream gradients in blood flows. Phys. Fluids 31 (3), 031903. doi:10.1063/1.5085881

CrossRef Full Text | Google Scholar

Zhang, J., Chen, Z., Griffith, B. P., and Wu, Z. J. (2020). Computational characterization of flow and blood damage potential of the new maglev CH-VAD pump versus the HVAD and HeartMate II pumps. Int. J. Artif. Organs 43 (10), 653–662. doi:10.1177/0391398820903734

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Halvorsen, K., Zhang, C. Z., Wong, W. P., and Springer, T. A. (2009). Mechanoenzymatic cleavage of the ultralarge vascular protein von Willebrand factor. Science 324, 1330–1334. doi:10.1126/science.1170905

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, H., Shaqfeh, E. S. G., and Narsimhan, V. (2012). Shear-induced particle migration and margination in a cellular suspension. Phys. Fluids 24 (1), 011902. doi:10.1063/1.3677935

CrossRef Full Text | Google Scholar

Zhao, R., Kameneva, M. V., and Antaki, J. F. (2007). Investigation of platelet margination phenomena at elevated shear stress. Biorheology 44 (3), 161–177.

PubMed Abstract | Google Scholar

Zhao, Y. C., Vatankhah, P., Goh, T., Michelis, R., Kyanian, K., Zhang, Y., et al. (2021). Hemodynamic analysis for stenosis microfluidic model of thrombosis with refined computational fluid dynamics simulation. Sci. Rep. 11 (1), 6875–6910. doi:10.1038/s41598-021-86310-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhussupbekov, M., Mendez Rojano, R., Wu, W. T., and Antaki, J. F. (2022). von Willebrand Factor unfolding mediates platelet deposition in a model of high-shear thrombosis. Biophysical J. 121 (21), 4033–4047. doi:10.1016/j.bpj.2022.09.040

CrossRef Full Text | Google Scholar