Accelerated dispersion curve calculations for periodic vibro-acoustic structures

Over the years, metamaterials have shown their potential in a wide range of different disciplines, e.g. optics, electromagnetics, dynamics etc. Metamaterials are, often periodic, engineered structures made of conventional materials but which exhibit properties not encountered in nature. In the field of noise and vibration, metamaterials have received increasing interest since they can obtain frequency ranges of high noise and vibration attenuation, called stop bands. Their performance is often investigated by means of dispersion curves, which are calculated based on a single unit cell and assuming a structure of infinite periodic extent. Nowadays, the attenuation of acoustic and structural waves is commonly tackled as two separate problems, whereby either acoustic or structural dispersion curves are used. Recently, vibro-acoustic unit cell designs have come to the fore which can exhibit appealing characteristics, such as simultaneous structural and acoustic stop bands. To consider the vibro-acoustic coupling in these unit cell designs during the performance predictions, vibro-acoustic dispersion curve calculations are thus required. However, these computations are typically cumbersome to perform due to the associated high computational cost and therefore, often, uncoupled dispersion curves are used during the performance assessment. Although several unit cell model order reduction approaches have recently been proposed to accelerate the dispersion curve computations, such as the Bloch mode synthesis (BMS) and Generalized Bloch mode synthesis (GBMS), they are not readily applicable to vibro-acoustic unit cells. To accelerate vibro-acoustic dispersion curve calculations, this work extends the BMS and GBMS techniques towards 2D and 3D periodic vibro-acoustic systems. To balance accuracy versus speed, the extended BMS reduction basis is constructed using a split set of vibro-acoustic coupled modes, while the extended GBMS reduction basis uses the uncoupled modes. Several verification cases demonstrate that strongly accelerated vibro-acoustic dispersion curve computations are achieved whereby the vibro-acoustic coupling inside the unit cell is accurately accounted for.

1 Introduction

In the past decades, wave control by means of metamaterial structures is extensively researched in different disciplines, e.g. electromagnetics, dynamics etc. (Hussein et al. (2014)). Metamaterials are, often periodic, engineered structures made of conventional materials which exhibit properties not encountered in nature. In the field of elastic and acoustic wave control, metamaterials have shown potential for attenuating noise and vibrations in specific frequency ranges, called stop bands. Two types of metamaterials are commonly distinguished: 1) phononic crystals which rely on Bragg scattering (Hussein et al. (2014)) and 2) locally resonant metamaterials which are based on Fano-type interference (Liu et al. (2000)). The performance of metamaterials is often investigated by means of dispersion curves (Bloch (1929)). These use as an input the smallest non-repetitive part of the structure, denoted as the unit cell (UC), while assuming infinite periodicity by applying the Bloch-Floquet theorem. The UC is commonly modeled using the finite element (FE) technique due to its suitability to discretize complex designs and its availability in commercial software packages. The dispersion curves give a relation between the frequency and propagation constant and contain information on the wave propagation in the infinite periodic structure. Several approaches exist to determine the dispersion curves, 1) the direct approach imposes real frequencies and solves the dispersion eigenvalue problem for the corresponding propagation constants, while 2) the inverse technique imposes the propagation constants and solves for the frequencies (Hussein et al. (2014)).

Nowadays, metamaterials are mostly designed to attenuate either acoustic or structural waves, resulting in purely acoustic or structural phononic crystals and locally resonant metamaterials e.g. Claeys et al. (2013); Yamamoto (2018) etc. Note that structural metamaterials can be used in vibro-acoustic context while no vibro-acoustic stop band is present, e.g. Claeys et al. (2016). Since either structural or acoustic bandgaps are achieved, their performance is typically investigated with purely structural or acoustic dispersion curves, respectively. Recently, an increasing trend is observed towards intricate vibro-acoustic UC designs, consisting of a solid and an air phase, which aim to obtain extraordinary performance characteristics such as: 1) simultaneous structural and acoustic bandgaps, e.g. Bilal et al. (2018); Li et al. (2022) or 2) structural and acoustic resonances are combined to achieve multiple peaks in the sound transmission loss performance, e.g. Roca and Hussein (2021). To include the effects of the vibro-acoustic coupling during the design and performance assessment of these novel structures, vibro-acoustic dispersion curves are required. Although vibro-acoustic dispersion curves contain valuable information, uncoupled dispersion curves are often computed in the literature to circumvent the high computational cost associated with the coupled dispersion curve calculations. Purely structural or acoustic dispersion curve calculations are already cumbersome to compute due to the presence of (often) many degrees-of-freedom (DOFs) in the complex UC designs and the high number of required propagation constant evaluations. This computational cost increases for vibro-acoustic dispersion curves due to the nature of the (coupled) vibro-acoustic system and the increase of the DOFs in the vibro-acoustic system description, e.g. (u,p)-formulation.

The high dispersion curve calculation cost can be reduced by using model order reduction (MOR) techniques: a UC model with less DOFs is constructed while preserving the important dynamic information of the reference model. Several UC MOR techniques exist, ranging from wave-based methods (cf. Hussein (2009)) to component mode synthesis techniques such as the Bloch mode synthesis (BMS) and generalized BMS (GBMS) (cf. Krattiger and Hussein (2014; 2018)) and hybrid methods (cf. Boukadia et al. (2018); Droz et al. (2016)). This work builds upon the (G)BMS techniques, since they have the advantage that the reduction of the UC happens without a dependency on the wave propagation constants. The BMS method reduces the interior DOFs with a truncated set of normal modes, while the GBMS also reduces the boundary DOFs with a set of boundary modes. It are Craig-Bampton techniques which were first derived by Krattiger and Hussein (2014, 2018) for the acceleration of the direct dispersion curve computation of 2D periodic media. Recently, the (G)BMS methods were extended towards 1) inverse dispersion curve computation by Palermo and Marzani (2016), 2) 3D periodic structures by Cool et al. (2021a,b) and 3) damped UC designs by Aladwani et al. (2022). All techniques have, until now, only been applied to purely structural or acoustic UC designs. The Craig-Bampton method has been extended in a substructuring context for the analysis of vibro-acoustic finite systems. Wolf (1977) suggested the use of uncoupled structural and acoustic modes for the construction of the reduction basis, while Ma and Hagiwara (1991) and Stammberger and Voss (2008) proposed the use of both the coupled left and right eigenvectors. Recently, Maess and Gaul (2006); Herrmann et al. (2010) have shown the applicability of the Craig-Bampton method while reducing the interior and boundary DOFs for the frequency response calculation of fluid-filled piping systems. The extension and applicability of the Craig-Bampton method in a UC reduction context for the acceleration of vibro-acoustic dispersion curves is, however, yet to be investigated.

In this work, the BMS and GBMS techniques are extended towards 2D and 3D periodic vibro-acoustic UCs to enable accelerated vibro-acoustic dispersion curve computations. The efficiency and accuracy of the extended methodologies are investigated using 2D and 3D vibro-acoustic UC models, consisting of a solid and an air phase, which contain a large number of DOFs and differ not only in the periodicity dimensionality but also in the vibro-acoustic coupling strength.

This paper is structured as follows. Section 2 gives an overview of the applied vibro-acoustic FE UC model and dispersion curve calculation. Next, the extended BMS and GBMS model reduction technique are proposed. Section 3 elaborates on two numerical verification cases focusing on the achieved acceleration and accuracy of the methods. Conclusions are given in Section 4.

2 Methodology

This section gives an overview of the applied vibro-acoustic FE modeling, the dispersion curve calculation and the BMS and GBMS MOR techniques for vibro-acoustic UCs. For sake of brevity, the methodologies are elaborated for 2D periodic structures. Using the work of Cool et al. (2021a), these can be readily extended towards 3D periodic structures.

2.1 Vibro-acoustic UC model

Several techniques exist in the literature to discretize a vibro-acoustic system. In this work, the (u, p)-formulation is used in which the structural DOFs are the displacements u and the acoustic DOFs are the pressures p (Fahy and Gardonio, 2007). The equations of motion of an undamped vibro-acoustic FE UC with N DOFs are given in matrix format by:

$\left(-{\omega }^2\underset{\mathbf{M}}{\underbrace{\left[\begin{array}{cc}\hfill {\mathbf{M}}_s\hfill & \hfill \mathbf{0}\hfill \\ \hfill {\rho }_a{\mathbf{C}}^T\hfill & \hfill {\mathbf{M}}_a\hfill \end{array}\right]}}+\underset{\mathbf{K}}{\underbrace{\left[\begin{array}{cc}\hfill {\mathbf{K}}_s\hfill & \hfill -\mathbf{C}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{K}}_a\hfill \end{array}\right]}}\right)\underset{\mathbf{q}}{\underbrace{\left[\begin{array}{c}\hfill \mathbf{u}\hfill \\ \hfill \mathbf{p}\hfill \end{array}\right]}}=\underset{\mathbf{f}}{\underbrace{\left[\begin{array}{c}\hfill {\mathbf{f}}_s\hfill \\ \hfill {\mathbf{f}}_a\hfill \end{array}\right]}},(1)$

in which ω is the radial frequency, $\mathbf{q},\mathbf{f}\in {\mathbb{R}}^{N\times 1}$ are the generalized nodal DOFs (displacement u and pressure p) and force vectors, and $\mathbf{M},\mathbf{K}\in {\mathbb{R}}^{N\times N}$ are the mass and stiffness matrices. The subscript s and a represent, respectively, the structural and acoustic parts, C is the coupling matrix and ρ_a is the density of the acoustic medium. The FE model matrices are extracted from commercial FE software, i.e. Siemens Simcenter 3D is used in this work.

2.2 Dispersion curve calculation

Starting from the FE UC model, dispersion curves can be computed which describe the wave propagation in the corresponding infinite periodic structure. The curves are obtained by applying the Bloch-Floquet theorem by Bloch (1929) to the UC model. The theorem states that the generalized DOFs and forces on the UC boundaries are scaled with ${\lambda }_x=e^{j{\mu }_x}$ and ${\lambda }_y=e^{j{\mu }_y}$ when moving along the periodicity lattice vectors from one UC to the next UC, with μ = (μ_x, μ_y) the propagation vector. By partitioning the UC according to the interior and boundary DOFs (Figure 1) and when no external excitation is present, the Bloch-Floquet periodic boundary conditions and force equilibrium are formulated using the periodicity matrix Λ:

$\mathbf{q}={\left[{\mathbf{q}}_I^T{\mathbf{q}}_L^T{\mathbf{q}}_R^T{\mathbf{q}}_B^T{\mathbf{q}}_T^T{\mathbf{q}}_{BL}^T{\mathbf{q}}_{BR}^T{\mathbf{q}}_{TL}^T{\mathbf{q}}_{TR}^T\right]}^T,\mathbf{q}=\mathbf{\Lambda }\tilde{\mathbf{q}},{\mathbf{\Lambda }}^H\mathbf{f}=\mathbf{0}(2)$

in which H represents the Hermitian transpose, $\tilde{\mathbf{q}}$ represents the periodic DOF vector and

$\mathbf{\Lambda }=\left[\begin{array}{cccc}\hfill \mathbf{I}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{\Lambda }}_x\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{\Lambda }}_y\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{\Lambda }}_{x,y}\hfill \end{array}\right],{\mathbf{\Lambda }}_i=\left[\begin{array}{c}\hfill \mathbf{I}\hfill \\ \hfill {\lambda }_i\mathbf{I}\hfill \end{array}\right],{\mathbf{\Lambda }}_{i,j}=\left[\begin{array}{c}\hfill \mathbf{I}\hfill \\ \hfill {\lambda }_i\mathbf{I}\hfill \\ \hfill {\lambda }_j\mathbf{I}\hfill \\ \hfill {\lambda }_i{\lambda }_j\mathbf{I}\hfill \end{array}\right],\tilde{\mathbf{q}}=\left[\begin{array}{c}\hfill {\mathbf{q}}_I\hfill \\ \hfill {\mathbf{q}}_L\hfill \\ \hfill {\mathbf{q}}_B\hfill \\ \hfill {\mathbf{q}}_{BL}\hfill \end{array}\right].(3)$

FIGURE 1

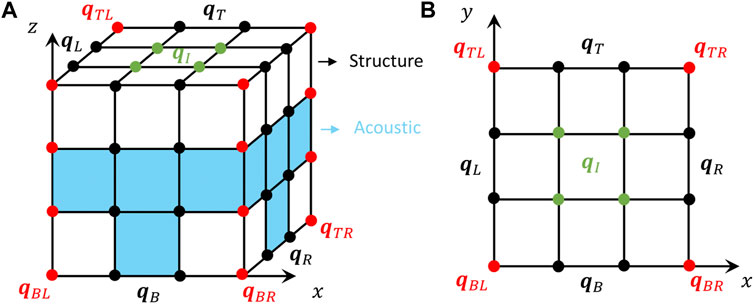
FIGURE 1. Schematic visualization of the node groups for a 2D periodic vibro-acoustic UC: (A) three-dimensional view, (B) top view.

Note that for a 3D periodic UC design, the node partitioning needs to be adapted, see the work of Cool et al. (2021a). Combining Eqs 1, 2 leads to the dispersion eigenvalue problem which governs the wave propagation characteristics of the 2D infinite periodic structure:

$\left(\tilde{\mathbf{K}}-{\omega }^2\tilde{\mathbf{M}}\right)\tilde{\mathbf{q}}=\mathbf{0},\tilde{\mathbf{K}}={\mathbf{\Lambda }}^H\mathbf{K}\mathbf{\Lambda },\tilde{\mathbf{M}}={\mathbf{\Lambda }}^H\mathbf{M}\mathbf{\Lambda }.(4)$

Different approaches exist to solve this eigenvalue problem, since it is both a function of ω and μ (Hussein et al. (2014)). In this work, the ω(μ)-approach is applied: first a set of real μ is imposed and next Eq. 4 is solved towards ω. This leads to free wave propagation solutions, which are typically used to identify band gaps. The set of real μ-combinations are only selected along the Irreducible Brillouin Contour (IBC) of the UC (Kittel (2010)). In this work, Eq. 4 is solved in Matlab using the built-in function eigs.

2.3 Model order reduction

The computational cost associated with the dispersion curve calculation quickly increases with the number of UC DOFs and the number of imposed μ-combinations since Eq. 4 needs to be solved for each μ-pair. MOR techniques are employed to accelerate these computations. In this work, the BMS technique by Krattiger and Hussein (2014) and GBMS technique by Krattiger and Hussein (2018) are extended towards the use for vibro-acoustic UCs. The techniques are component mode synthesis methods in which the UC is divided into the interior and boundary part. Both methods are projection-based MOR techniques in which a projection basis $\mathbf{B}\in {\mathbb{C}}^{N\times N_B}$ is constructed using modal information to reduce the mass and stiffness matrices from dimension N to N_B (with N_B ≪ N):

$\mathcal{M}={\mathbf{B}}^T\mathbf{M}\mathbf{B},\mathcal{K}={\mathbf{B}}^T\mathbf{K}\mathbf{B}.(5)$

After reducing the UC model matrices, the Bloch-Floquet BCs will be enforced to solve the dispersion eigenvalue problem. Following sections describe the construction of the reduction basis B for both methodologies.

2.3.1 Bloch mode synthesis

The BMS method only reduces the interior (both structural and acoustic) DOFs of the UC. Therefore, the coupled vibro-acoustic full order model (FOM) system of Eq. 1 is first divided into the interior (I) and boundary (A) part of the entire UC:

$\left(\left[\begin{array}{cc}\hfill {\mathbf{K}}_{II}\hfill & \hfill {\mathbf{K}}_{IA}\hfill \\ \hfill {\mathbf{K}}_{AI}\hfill & \hfill {\mathbf{K}}_{AA}\hfill \end{array}\right]-{\omega }^2\left[\begin{array}{cc}\hfill {\mathbf{M}}_{II}\hfill & \hfill {\mathbf{M}}_{IA}\hfill \\ \hfill {\mathbf{M}}_{AI}\hfill & \hfill {\mathbf{M}}_{AA}\hfill \end{array}\right]\right)\left[\begin{array}{c}\hfill {\mathbf{q}}_I\hfill \\ \hfill {\mathbf{q}}_A\hfill \end{array}\right]=\mathbf{0},(6)$

in which q_I represents the N_I interior DOFs and q_A the N_A boundary DOFs. Next, the projection matrix B is constructed by reducing the interior part with a Craig-Bampton approach: the interior DOFs are approximated by a linear combination of a set of fixed interface normal modes ${\mathbf{\Phi }}_I^t$ and a set of static constraint modes ${\mathbf{\Psi }}_{IA}^t$:

$\left[\begin{array}{c}\hfill {\mathbf{q}}_I\hfill \\ \hfill {\mathbf{q}}_A\hfill \end{array}\right]=\mathbf{B}\left[\begin{array}{c}\hfill {\mathit{\eta }}_I\hfill \\ \hfill {\mathbf{q}}_A\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill {\mathbf{\Phi }}_I^t\hfill & \hfill {\mathbf{\Psi }}_{IA}^t\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{I}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\mathit{\eta }}_I\hfill \\ \hfill {\mathbf{q}}_A\hfill \end{array}\right],(7)$

in which η_I is the reduced set of interior modal DOFs. In the literature, Craig-Bampton techniques exist using fixed or free interface normal modes, e.g. Voormeeren et al. (2010). In this work, the fixed interface normal modes are used because only structure-structure and acoustic-acoustic interactions occur on the boundary between adjacent UCs. Note that both the structural and acoustic boundary DOFs are kept as physical DOFs, allowing straightforward application of the Bloch-Floquet BCs to the reduced DOF set.

${\mathbf{\Phi }}_I^t$ is constructed starting from the coupled vibro-acoustic fixed interface normal modes corresponding to the n_I smallest eigenfrequencies:

$\left({\mathbf{K}}_{II}-{\omega }_i^2{\mathbf{M}}_{II}\right){\mathit{\varphi }}_I^i=\mathbf{0},i=1\dots n_I.(8)$

However, these coupled eigenmodes do not form an efficient reduction basis since the system matrices are unsymmetric leading to the right eigenvectors not being mutually orthogonal (Creixell-Mediante et al. (2018)). Therefore, the fixed interface normal modes are divided into the structural and acoustic parts:

${\mathit{\varphi }}_I^i=\left[\begin{array}{c}\hfill {\mathit{\varphi }}_{s,I}^i\hfill \\ \hfill {\mathit{\varphi }}_{a,I}^i\hfill \end{array}\right],{\mathbf{\Phi }}_{s,I}=\left[\begin{array}{cccc}\hfill {\mathit{\varphi }}_{s,I}^1\hfill & \hfill {\mathit{\varphi }}_{s,I}^2\hfill & \hfill \dots \hfill & \hfill {\mathit{\varphi }}_{s,I}^{n_I}\hfill \end{array}\right],{\mathbf{\Phi }}_{a,I}=\left[\begin{array}{cccc}\hfill {\mathit{\varphi }}_{a,I}^1\hfill & \hfill {\mathit{\varphi }}_{a,I}^2\hfill & \hfill \dots \hfill & \hfill {\mathit{\varphi }}_{a,I}^{n_I}\hfill \end{array}\right].(9)$

Due to the splitting, the reduced system matrix can become singular. A normalization of the modes after the division, denoted by ${\widehat{\mathbf{\Phi }}}_{s,I}$ and ${\widehat{\mathbf{\Phi }}}_{a,I}$, solves these numerical problems. Finally, the applied ${\mathbf{\Phi }}_I^t$ reads:

${\mathbf{\Phi }}_I^t=\left[\begin{array}{cc}\hfill {\widehat{\mathbf{\Phi }}}_{s,I}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\widehat{\mathbf{\Phi }}}_{a,I}\hfill \end{array}\right].(10)$

The N_I interior DOFs are now reduced to 2n_I DOFs. For purely structural or acoustic problems, the number of n_I is commonly determined using a frequency-based truncation criterion: the modes up to two times the maximum frequency of interest are typically included (Krattiger and Hussein (2014)). However, for vibro-acoustic problems this does not guarantee a good accuracy. In Boily and Charron (1999), a truncation rule which applies the information of the coupling terms is proposed to identify which modes are most important to include. In this work, instead, the commonly applied truncation criterion is applied with a higher frequency tolerance (four times the maximum frequency of interest).

The static constraint modes ${\mathbf{\Psi }}_{IA}^t$ represent the influence of the boundary motion on the interior part. One option is to compute this using the vibro-acoustic system matrices:

${\mathbf{\Psi }}_{IA}^t=-{\mathbf{K}}_{II}^{-1}{\mathbf{K}}_{IA}.(11)$

Another option is to compute the static constraint modes for the structural and acoustic parts separately, without taking into account any coupling (Herrmann et al. (2010)):

${\mathbf{\Psi }}_{s,IA}=-{\mathbf{K}}_{s,II}^{-1}{\mathbf{K}}_{s,IA},{\mathbf{\Psi }}_{a,IA}=-{\mathbf{K}}_{a,II}^{-1}{\mathbf{K}}_{a,IA},{\mathbf{\Psi }}_{IA}^t=\left[\begin{array}{cc}\hfill {\mathbf{\Psi }}_{s,IA}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{\Psi }}_{a,IA}\hfill \end{array}\right].(12)$

The difference between both approaches is that the former considers an extra dependency of the boundary pressure DOFs on the interior displacement DOFs arising from the coupling matrix C. Although using the coupled system matrices takes more information into account, it is opted to use the separated approach in this work because 1) the computation cost to compute the static constraint modes with the coupled system matrices quickly increases with number of DOFs and 2) the separated approach has the advantage that the structure of the original model is preserved upon projection.

2.3.2 Generalized Bloch mode synthesis

Since the BMS technique only reduces the interior DOFs, an extra reduction can take place by reducing the boundary DOFs, using the GBMS method, first proposed by Krattiger and Hussein (2018). Starting from the BMS, an extra boundary transformation matrix L is constructed to also approximate the boundary DOFs using a reduced set of modal boundary DOFs: q_A = Lη_A. The reduction basis B becomes:

$\left[\begin{array}{c}\hfill {\mathbf{q}}_I\hfill \\ \hfill {\mathbf{q}}_A\hfill \end{array}\right]=\mathbf{B}\left[\begin{array}{c}\hfill {\mathit{\eta }}_I\hfill \\ \hfill {\mathit{\eta }}_A\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill {\mathbf{\Phi }}_I^t\hfill & \hfill {\mathbf{\Psi }}_{IA}^t\mathbf{L}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{L}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\mathit{\eta }}_I\hfill \\ \hfill {\mathit{\eta }}_A\hfill \end{array}\right].(13)$

The transformation matrix L is constructed as follows. After the BMS reduction of the system according to Eq. 5, the BMS reduced system is first partitioned according to η_I and q_A:

$\left(\left[\begin{array}{cc}\hfill {\mathcal{K}}_{II}\hfill & \hfill {\mathcal{K}}_{IA}\hfill \\ \hfill {\mathcal{K}}_{AI}\hfill & \hfill {\mathcal{K}}_{AA}\hfill \end{array}\right]-{\omega }^2\left[\begin{array}{cc}\hfill {\mathcal{M}}_{II}\hfill & \hfill {\mathcal{M}}_{IA}\hfill \\ \hfill {\mathcal{M}}_{AI}\hfill & \hfill {\mathcal{M}}_{AA}\hfill \end{array}\right]\right)\left[\begin{array}{c}\hfill {\mathit{\eta }}_I\hfill \\ \hfill {\mathbf{q}}_A\hfill \end{array}\right]=\mathbf{0}.(14)$

Next, the boundary motion is approximated by a truncated set of normal modes. Since the boundary only consists of one layer of DOFs, the coupling between the structural and acoustic parts is not taken into account in this work. Moreover, as for the BMS technique, using the coupled modes was found to lead to slow convergence. Separate structural and acoustic boundary modes are, therefore, computed instead according to:

$\left({\mathcal{K}}_{s,AA}-{\omega }_j^2{\mathcal{M}}_{s,AA}\right){\mathit{\varphi }}_{s,A}^j=\mathbf{0},{\mathbf{\Phi }}_{s,A}=\left[\begin{array}{cccc}\hfill {\mathit{\varphi }}_{s,A}^1\hfill & \hfill {\mathit{\varphi }}_{s,A}^2\hfill & \hfill \dots \hfill & \hfill {\mathit{\varphi }}_{s,A}^{n_{s,A}}\hfill \end{array}\right],n_{s,A}\ll N_{s,A}(15)$

and

$\left({\mathcal{K}}_{a,AA}-{\omega }_j^2{\mathcal{M}}_{a,AA}\right){\mathit{\varphi }}_{a,A}^j=\mathbf{0},{\mathbf{\Phi }}_{a,A}=\left[\begin{array}{cccc}\hfill {\mathit{\varphi }}_{a,A}^1\hfill & \hfill {\mathit{\varphi }}_{a,A}^2\hfill & \hfill \dots \hfill & \hfill {\mathit{\varphi }}_{a,A}^{n_{a,A}}\hfill \end{array}\right],n_{a,A}\ll N_{a,A}.(16)$

In contrast to the selection of n_I, no frequency criterion can be used to select n_s,A and n_a,A (Herrmann et al. (2010)). Since the GBMS reduction is applied before the Bloch-Floquet BCs, the reduced modal boundary DOFs need to contain the same compatibility conditions as the FOM. The compatibility conditions are imposed to the system for the structural and acoustic parts separately. They are ensured by first partitioning the mode sets Φ_s,A and Φ_a,A according to the different boundary parts, cf. Eq. 2. Next, the sets which need to be compatible are combined. These combined sets are orthogonalized with a singular value decomposition into new bases Φ_p, with p representing the DOFs which are combined e.g. Φ_s,LR is the basis for the structural boundary DOFs of the left and right face of the UC. All new bases are combined to construct the transformation matrix L:

$\mathbf{L}=\left[\begin{array}{cccccc}\hfill {\mathbf{I}}_2\otimes {\mathbf{\Phi }}_{s,LR}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{I}}_2\otimes {\mathbf{\Phi }}_{a,LR}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{I}}_2\otimes {\mathbf{\Phi }}_{s,BT}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{I}}_2\otimes {\mathbf{\Phi }}_{a,BT}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{I}}_4\otimes {\mathbf{\Phi }}_{s,E}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{I}}_4\otimes {\mathbf{\Phi }}_{a,E}\hfill \end{array}\right],(17)$

with I_i the identity matrix of dimension i and E all edge DOFs (BL, BR, TR, TL), cf. Figure 1.

3 Numerical verification

This section discusses a 2D and 3D verification case to investigate the efficiency and accuracy of the proposed BMS and GBMS method for the calculation of vibro-acoustic dispersion curves. Both cases contain a solid and an air phase, while they differ in the dimension of periodicity and the strength of the vibro-acoustic coupling. All calculations are performed on a laptop with 32 GB RAM and a 2.6 GHz Intel Core i7-9540 processor using Matlab R2019b. A relative frequency error of the reduced order model (ROM) with respect to the FOM is used to quantify the accuracy of the computed dispersion curves:

${ϵ}_{\mathit{rel}}=\left|\frac{{\omega }_{\mathit{ROM}}-{\omega }_{\mathit{FOM}}}{{\omega }_{\mathit{FOM}}}\right|.(18)$

3.1 2D periodic case

The first case is based on the vibro-acoustic 2D periodic UC of Roca and Hussein (2021), visualized in Figure 2A. It consist of a hollow plate with a hollow pillar on top. It is opted to choose a UC with the pillar in the middle because it is favorable for the efficiency of the BMS and GBMS technique to choose the UC with the lowest number of boundary DOFs to start with, as shown in Cool et al. (2021b). The in-plane UC dimensions are 25 × 25 mm, the other geometrical dimensions can be found in Roca and Hussein (2021), only the plate wall thickness is decreased to 0.25 mm to increase the vibro-acoustic coupling effect. The structural material is polymeric ABS (Young’s modulus E = 1,627 MPa, density ρ = 1,050 kg/m³, Poisson’s ratio ν = 0.35), while the voids are filled with air (ρ_a = 1.225 kg/m³, c_a = 340 m/s). The UC is discretized using commercial FE software with 84424 structural and 46644 acoustic linear tetrahedral elements. This leads to a FOM with 97680 DOFs from which 86448 structural and 11232 acoustic. The frequency range of interest goes from 0 Hz till 4,500 Hz, leading to the calculation of the first 16 dispersion curves. The dispersion curves are calculated along the IBC (Figure 2B) with a propagation constant resolution of 0.02π. The dispersion curve calculation of the FOM, which contains 95010 DOFs after applying the Bloch-Floquet BCs, takes 5,648 s. The vibro-acoustic dispersion curves, together with the purely structural and acoustic curves, are shown in Figure 2C. The difference between the coupled and uncoupled dispersion curves indicates a strong vibro-acoustic coupling.

FIGURE 2

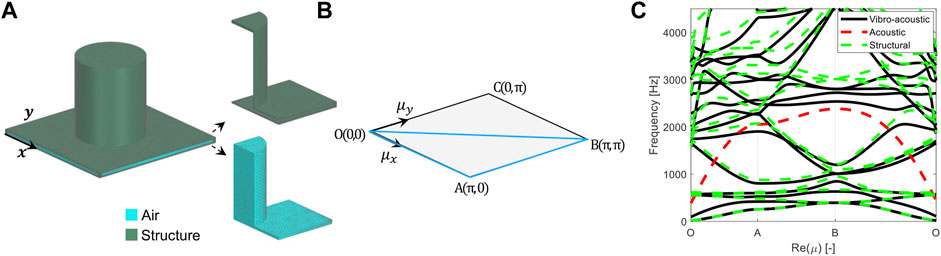
FIGURE 2. (A) FE model of the vibro-acoustic 2D periodic UC with a detail of one fourth of the acoustic and structural part, (B) IBC in reciprocal wave space, (C) Coupled vibro-acoustic and uncoupled structural and acoustic FOM dispersion curves.

To accelerate the dispersion curve calculation, the BMS technique is applied with n_I = 50 modes according to four times the maximum frequency of interest criterion. This results in a ROM of 5,416 DOFs or 2,746 DOFs after applying the Bloch-Floquet BCs. The total time to obtain the dispersion curves with the BMS technique is 369 s, of which 45.7% is due to the construction of the ROM (Figure 3A). The dispersion curve calculation is therefore accelerated with a factor 15.3 with respect to the FOM. Figure 3B shows the resulting dispersion curves and the corresponding relative error, cf. Eq. 18. An accurate dispersion curve prediction is obtained with an error of 6 ⋅ 10^–3 or smaller. Note that the relative error increases with increasing frequency due to the validity of the modal reduction basis.

FIGURE 3

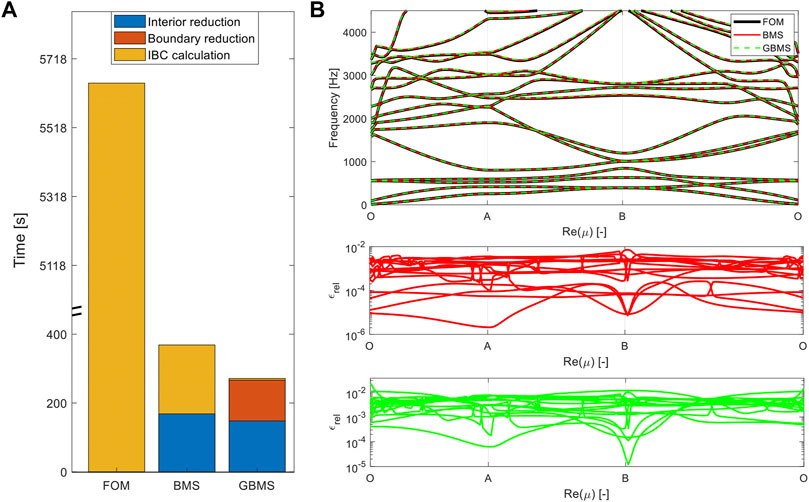
FIGURE 3. Results of the vibro-acoustic 2D periodic case. (A) Comparison of the different calculation times for the construction of the ROM and the dispersion curve calculation. (B) Dispersion curves of FOM and ROMs with corresponding relative error.

To further accelerate the dispersion curve calculation, the boundary DOFs are also reduced with the GBMS technique. n_s,A = 100 and n_a,A = 30 are chosen for the structural and acoustic parts, respectively. This results in a reduced system with 704 DOFs, or 390 DOFs after applying the Bloch-Floquet BCs. With this reduction, the total calculation time reduces further to 271 s, from which merely 4.9 s are required for the IBC calculation (Figure 3A). This represents an acceleration with a factor 20.8 with respect to the FOM. Remark that not the full BMS construction time is required to set-up the GBMS reduction basis, which explains the reduced time for the interior reduction with the GBMS method. Figure 3B shows the resulting dispersion curves and the corresponding relative error. The relative error using the GBMS technique is slightly larger than with the BMS technique due to the additional approximation of the boundary DOFs, but still an accurate prediction is obtained with a relative error smaller than 1 ⋅ 10^–2. An overview of the results in terms of the DOFs, total required time and obtained relative error is given in Table 1.

TABLE 1

TABLE 1. Overview of the results: DOFs after applying the Bloch-Floquet BCs, the total required time and the relative error when applying the BMS and GBMS technique to the vibro-acoustic 2D periodic case.

3.2 3D periodic case

The second case is based on the vibro-acoustic 3D periodic UC of Li et al. (2022) (Figure 4A). It combines a mass-in-mass local resonance system with Helmholtz resonators to obtain a simultaneous bandgap for structural and acoustic waves. The UC dimension is 50 × 50 × 50 mm. The geometry is simplified with respect to Li et al. (2022), while the geometric parameters are tuned to obtain an overlapping structural and acoustic bandgap. The structure consists of resin (E = 2,600 MPa, ρ = 1,300 kg/m³, ν = 0.4), while air has the same properties as before. Only the non-closed air compartments, resulting in the acoustic bandgap, are considered to the example Li et al. (2022). The UC is discretized with 80592 structural and 51712 acoustic linear tetrahedral elements resulting in 82093 DOFs, with 69060 structural and 13033 acoustic ones. The frequency range of interest goes from 0 Hz till 5,000 Hz. 23 dispersion curves are computed along the IBC (Figure 4B) with a propagation constant resolution of 0.02π. Applying the Bloch-Floquet BCs to the FOM results in a system with 76750 DOFs. The dispersion curve calculation using this FOM takes 19650 s. The vibro-acoustic dispersion curves, together with the purely structural and acoustic curves, are shown in Figure 4C. An acoustic bandgap is detected between 1,201 Hz and 1,338 Hz, while a structural bandgap is present between 1,166 Hz and 2,433 Hz. The separately computed dispersion curves overlap with the coupled ones, indicating that only a weak vibro-acoustic coupling is present.

FIGURE 4

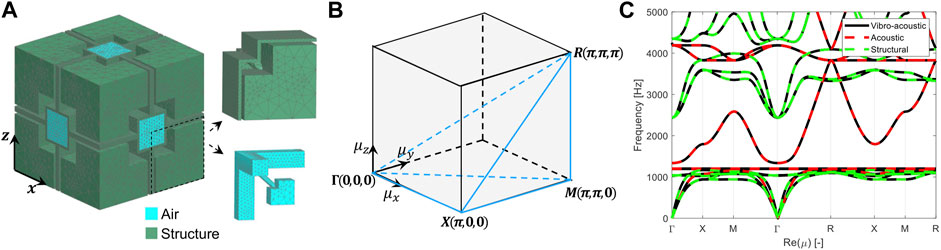
FIGURE 4. (A) FE model of the vibro-acoustic 3D periodic UC with a detail of one eighth of the acoustic and structural part, (B) IBC in reciprocal wave space, (C) Coupled vibro-acoustic and uncoupled structural and acoustic FOM dispersion curves.

To accelerate the dispersion curve calculation, the interior DOFs are reduced with n_I = 95. With this technique, the FOM reduces to a system with 10696 DOFs, or 5,353 DOFs after applying the Bloch-Floquet BCs. The total time to construct the ROM and compute the dispersion curves along the IBC, takes 3,028 s, from which 387.7 s are needed for the construction of the ROM (Figure 5A). This represents an acceleration with a factor 6.5 with respect to the FOM calculation. Figure 5B shows the resulting dispersion curves and the corresponding relative error. Good accuracy is obtained with an error smaller than 4 ⋅ 10^–3 with respect to the FOM dispersion curves.

FIGURE 5

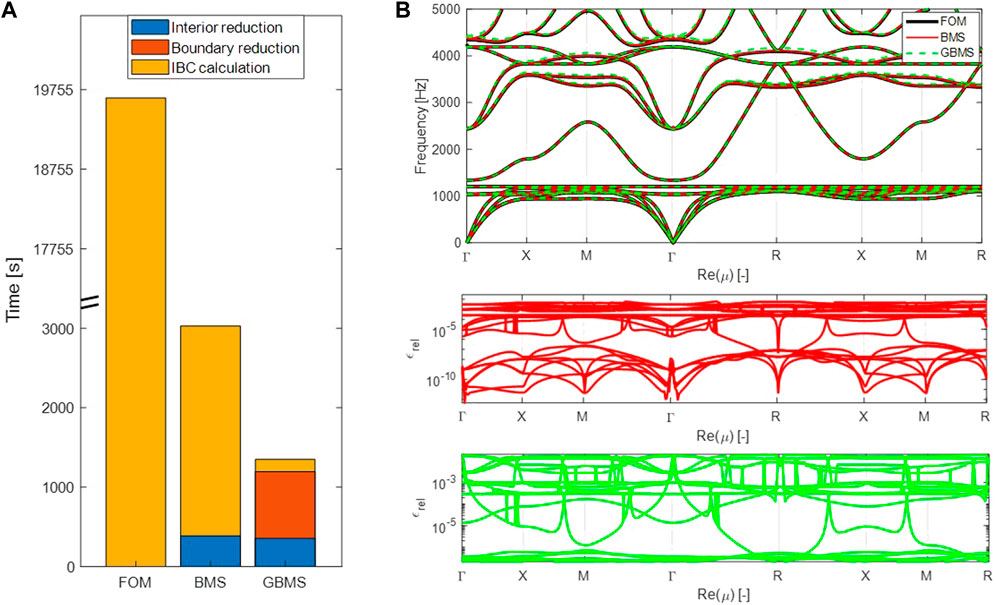
FIGURE 5. Results of the vibro-acoustic 3D periodic case. (A) Comparison of the different calculation times for the construction of the ROM and the dispersion curve calculation. (B) Dispersion curves of FOM and ROMs with corresponding relative error.

To further reduce the computation time, the boundary DOFs are reduced by applying the GBMS with n_s,A = 300 and n_a,A = 45. The resulting ROM consist of 2,638 DOFs, or 1,324 DOFs after applying the Bloch-Floquet BCs. The total computation time to set up the ROM and compute the dispersion curves is 1,348 s, with 153 s required for the dispersion curve calculation itself (Figure 5A). This is an acceleration with a factor 14.6 with respect to the FOM calculation. Figure 5B shows the dispersion curves and corresponding relative errors. It is concluded that the dispersion curves can be obtained in a considerably reduced time while maintaining a good accuracy with relative error smaller than 2 ⋅ 10^–2. An overview of the results in terms of the DOFs, total required time and obtained relative error is given in Table 2.

TABLE 2

TABLE 2. Overview of the results: DOFs after applying the Bloch-Floquet BCs, the total required time and the relative error when applying the BMS and GBMS technique to the vibro-acoustic 3D periodic case.

4 Conclusion

In this work, the BMS and GBMS reduction techniques are extended towards 2D and 3D periodic vibro-acoustic UCs to achieve efficient vibro-acoustic dispersion curve computations. The BMS reduction basis is constructed using a partitioned set of vibro-acoustic coupled modes, while the construction of the GBMS does not take into account the vibro-acoustic coupling. With two numerical case studies, it is shown that the extended BMS and GBMS methods enable strongly accelerated vibro-acoustic dispersion curves computations while preserving a good accuracy. Due to the accelerated dispersion curve predictions, the presented methodology is particularly interesting in cases where numerous dispersion curve calculations are required, e.g. optimization of bandgap designs, assessment of design variants etc.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

VC developed the software, performed the numerical simulations and prepared the first draft of the manuscript. All authors contributed to the study conceptualization, design, methodology, formal analysis, writing of the manuscripts and the manuscripts revision. All authors have read and approved the submitted version.

Funding

The research of VC (fellowship no. 11G4421N) and LV (fellowship no. 1271621N) is funded by a grant from the Research Foundation—Flanders (FWO).

Acknowledgments

Internal Funds KU Leuven are gratefully acknowledged for their support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aladwani, A., Nouh, M., and Hussein, M. (2022). State-space Bloch mode synthesis for fast band-structure calculations of non-classically damped phononic materials. Comput. Methods Appl. Mech. Eng. 396, 115018. doi:10.1016/j.cma.2022.115018

CrossRef Full Text | Google Scholar

Bilal, O., Ballagi, D., and Daraio, C. (2018). Architected lattices for simultaneous broadband attenuation of airborne sound and mechanical vibrations in all directions. Phys. Rev. Appl. 10, 054060. doi:10.1103/physrevapplied.10.054060

CrossRef Full Text | Google Scholar

Bloch, F. (1929). Über die quantenmechanik der elektronen in kristallgittern. Z. Phys. 52, 555–600. doi:10.1007/bf01339455

CrossRef Full Text | Google Scholar

Boily, S., and Charron, F. (1999). The vibroacoustic response of a cylindrical shell structure with viscoelastic and poroelastic materials. Appl. Acoust. 58, 131–152. doi:10.1016/s0003-682x(98)00070-x

CrossRef Full Text | Google Scholar

Boukadia, R., Droz, C., Ichchou, M., and Desmet, W. (2018). A Bloch wave reduction scheme for ultrafast band diagram and dynamic response computation in periodic structures. Finite Elem. Analysis Des. 148, 1–12. doi:10.1016/j.finel.2018.05.007

CrossRef Full Text | Google Scholar

Claeys, C., Deckers, E., Pluymers, B., and Desmet, W. (2016). A lightweight vibro-acoustic metamaterial demonstrator: Numerical and experimental investigation. Mech. Syst. Signal Process. 70, 853–880. doi:10.1016/j.ymssp.2015.08.029

CrossRef Full Text | Google Scholar

Claeys, C., Vergote, K., Sas, P., and Desmet, W. (2013). On the potential of tuned resonators to obtain low-frequency vibrational stop bands in periodic panels. J. Sound. Vib. 332, 1418–1436. doi:10.1016/j.jsv.2012.09.047

CrossRef Full Text | Google Scholar

Cool, V., Van Belle, L., Claeys, C., Deckers, E., and Desmet, W. (2021a). “(Generalized) Bloch mode synthesis for the fast dispersion curve calculation of 3D periodic metamaterials,” in INTER-NOISE and NOISE-CON congress and conference proceedings (Washington, DC: Institute of Noise Control Engineering), 263, 2102–2113.

CrossRef Full Text | Google Scholar

Cool, V., Van Belle, L., Claeys, C., Deckers, E., and Desmet, W. (2021b). Impact of the unit cell choice on the efficiency of dispersion curve calculations using GBMS. J. Vibr. Acoust.. doi:10.1115/1.4051817

CrossRef Full Text | Google Scholar

Creixell-Mediante, E., Jensen, J., Naets, F., Brunskog, J., and Larsen, M. (2018). Adaptive parametric model order reduction technique for optimization of vibro-acoustic models: Application to hearing aid design. J. Sound. Vib. 424, 208–223. doi:10.1016/j.jsv.2018.03.013

CrossRef Full Text | Google Scholar

Droz, C., Zhou, C., Ichchou, M., and Lainé, J.-P. (2016). A hybrid wave-mode formulation for the vibro-acoustic analysis of 2D periodic structures. J. Sound. Vib. 363, 285–302. doi:10.1016/j.jsv.2015.11.003

CrossRef Full Text | Google Scholar

Fahy, F., and Gardonio, P. (2007). Sound and structural vibration: Radiation, transmission and response. 2nd edition. London, UK: Elsevier.

Google Scholar

Herrmann, J., Maess, M., and Gaul, L. (2010). Substructuring including interface reduction for the efficient vibro-acoustic simulation of fluid-filled piping systems. Mech. Syst. Signal Process. 24, 153–163. doi:10.1016/j.ymssp.2009.05.003

CrossRef Full Text | Google Scholar

Hussein, M., Leamy, M. J., and Ruzzene, M. (2014). Dynamics of phononic materials and structures: Historical origins, recent progress, and future outlook. Appl. Mech. Rev. 66, 040802. doi:10.1115/1.4026911

CrossRef Full Text | Google Scholar

Hussein, M. (2009). Reduced Bloch mode expansion for periodic media band structure calculations. Proc. R. Soc. A 465, 2825–2848. doi:10.1098/rspa.2008.0471

CrossRef Full Text | Google Scholar

Kittel, C. (2010). Introduction to solid state physics. New York: Wiley.

Google Scholar

Krattiger, D., and Hussein, M. (2014). Bloch mode synthesis: Ultrafast methodology for elastic band-structure calculations. Phys. Rev. E 90, 063306. doi:10.1103/physreve.90.063306

PubMed Abstract | CrossRef Full Text | Google Scholar

Krattiger, D., and Hussein, M. (2018). Generalized Bloch mode synthesis for accelerated calculation of elastic band structures. J. Comput. Phys. 357, 183–205. doi:10.1016/j.jcp.2017.12.016

CrossRef Full Text | Google Scholar

Li, G., Chen, Y., Chen, W., Liu, J., and He, H. (2022). Local resonance–Helmholtz lattices with simultaneous solid-borne elastic waves and air-borne sound waves attenuation performance. Appl. Acoust. 186, 108450. doi:10.1016/j.apacoust.2021.108450

CrossRef Full Text | Google Scholar

Liu, Z., Zhang, X., Zhu, Y. Y., Yang, Z., and Chan, C. T. (2000). Locally resonant sonic materials. Science 289, 1734–1736. doi:10.1126/science.289.5485.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, Z.-D., and Hagiwara, I. (1991). Improved mode-superposition technique for modal frequency response analysis of coupled acoustic-structural systems. AIAA J. 29, 1720–1726. doi:10.2514/3.10795

CrossRef Full Text | Google Scholar

Maess, M., and Gaul, L. (2006). Substructuring and model reduction of pipe components interacting with acoustic fluids. Mech. Syst. Signal Process. 20, 45–64. doi:10.1016/j.ymssp.2005.02.008

CrossRef Full Text | Google Scholar

Palermo, A., and Marzani, A. (2016). Extended bloch mode synthesis: Ultrafast method for the computation of complex band structures in phononic media. Int. J. Solids Struct. 100, 29–40. doi:10.1016/j.ijsolstr.2016.06.033

CrossRef Full Text | Google Scholar

Roca, D., and Hussein, M. (2021). Broadband and intense sound transmission loss by a coupled-resonance acoustic metamaterial. Phys. Rev. Appl. 16, 054018. doi:10.1103/physrevapplied.16.054018

CrossRef Full Text | Google Scholar

Stammberger, M., and Voss, H. (2008). “Automated multi-level substructuring for a fluid-solid vibration problem,” in Num. Math. And adv. Appl. (Berlin, Germany: Springer), 563–570.

Google Scholar

Voormeeren, S., Van der Valk, P., and Rixen, D. (2010). A general mixed boundary model reduction method for component mode synthesis. IOP Conf. Ser. Mater. Sci. Eng 10, 012116. doi:10.1088/1757-899X/10/1/012116

CrossRef Full Text | Google Scholar

Wolf, J. A. (1977). Modal synthesis for combined structural-acoustic systems. AIAA J. 15, 743–745. doi:10.2514/3.60685

CrossRef Full Text | Google Scholar

Yamamoto, T. (2018). Acoustic metamaterial plate embedded with helmholtz resonators for extraordinary sound transmission loss. J. Appl. Phys. 123, 215110. doi:10.1063/1.5025570

CrossRef Full Text | Google Scholar