- 1Department of Mechanical Engineering, University of California at Berkeley, Berkeley, CA, United States
- 2Department of Materials Design and Innovation, University at Buffalo, Buffalo, NY, United States
Bulk layered materials, such as graphite and molybdenum disulfide, have long been used as solid lubricants in various industrial applications. The weak interlayer van der Waals interactions in these materials generate a low shear slip-plane, which reduces the interfacial friction. The cumulative trends toward device miniaturization have increased the need for basic knowledge of the nanoscale friction of contact-mode devices containing layered materials. Further, the decomposition and degradation of bulk layered solids subjected to shear forces are detrimental to their lubricating characteristics. Layered-structure materials, such as graphene, hexagonal boron nitride, and MXenes consisting of single or few atomic layers, behave as a new class of lubricious substances when deposited at a sliding interface. The exceptional mechanical strength, thermal conductivity, electronic properties, large theoretical specific area, and chemical inertness of these materials make them ideal antifriction materials for continuous sliding interfaces, especially when operated at elevated temperatures. These properties hold great promise for widespread applications both in dry environments, such as solid film lubrication for micro/nano-electromechanical systems, nanocomposite materials, space lubrication, and optical devices, as well as in wet environments, such as desalination membranes, lubricant additives, and nanofluidic transporters. However, accurate and reliable prediction of the frictional behavior of layered-structure materials is challenging due to the complex physicochemical transformations encountered under tribostress. The presence of a liquid in the vicinity of a surface in wet-environment applications further complicates the lubrication behavior of layered-structure materials. Furthermore, insight into the origins of interfacial friction and adhesion due to localized contact interactions can be accomplished by atomic-level experimental techniques and computational methods, such as atomic force microscope (AFM) in combination with molecular dynamics (MD) and density functional theory (DFT). The AFM setup mimics asperity-asperity contact at the atomic level and can measure the friction force of layered-structure materials, whereas MD and DFT can provide insight into the chemomechanical transformations commencing at hidden interfaces, which cannot be detected by experimental methods. The objective of this review article is threefold. First, the relationship between friction and potential energy surface is examined for different layered-structure material systems, and the parameters that mainly affect the energy corrugation are interpreted in the context of reported results. Second, the atomic-scale friction mechanisms of layered-structure materials in dry or vacuum environments are discussed in light of experimental and theoretical findings, focusing on the most crucial frictional energy dissipation mechanisms. Third, the complex mechanisms affecting the nanosccale friction of layered-structure materials incorporated in liquid media are introduced for ionic, polar, and non-polar solutions.
1 Introduction
Growing energy demands have dramatically increased the consumption of non-renewable energy sources. According to recent reports, the transportation sector accounts for 24.3% of the overall energy consumption (Pandemic drives down U.S. energy use in 2020, 2021) in the United States. Engine efficiency and performance are adversely impacted by frictional losses encountered at moving mechanical components of vehicles, representing about 25–40% of a vehicle’s fuel energy (Holmberg and Erdemir, 2017). More importantly, 32.2% of the overall energy sources used in various industry and transportation sectors are petroleum-based, significantly contributing to CO2 emissions (Woydt, 2021). Unequivocally, developing fuel-efficient automobiles by mitigating friction losses is critical to reducing fuel dependency worldwide and lowering the impact of climate change (World Energy Outlook, 2011). Lubrication is one of the most effective approaches to reducing friction between sliding surfaces.
Materials with layered structures, such as graphite, molybdenum disulfide (MoS2), and boron nitride (BN), have long been used as solid lubricants in various technologies, including micro/nano-electromechanical systems (Lemme et al., 2020, 2022; Zhu et al., 2020), electronic devices (Bhushan, 2001; Clauss, 2012), and biomedical implants for joint replacement (Spear et al., 2015) (Figure 1A). In layered materials, the atoms of each layer are strongly bonded via covalent bonds, demonstrating high mechanical strength. However, these materials exhibit low shear strength because the interlayers are weakly bonded by van der Waals forces. The friction behavior of layered-structure materials is highly dependent on the environment in which these solid lubricants function. For instance, macroscale measurements have illustrated that bulk MoS2 exhibits extremely low friction in vacuum or dry environments but not at high humidity levels (Pritchard and Midgley, 1969; Khare and Burris, 2013), whereas graphite demonstrates enhanced lubrication behavior in humid environments (Farshchi-Tabrizia et al., 2008; Rietsch et al., 2013). The advent of two-dimensional (2D) crystalline materials, i.e., materials consisting of a single or few layers of atoms in a honeycomb structure, has motivated the design of next-generation lubricants for both dry (Rapoport et al., 1997; Kim et al., 2011; Berman et al., 2014, 2018; Xiao and Liu, 2017) and wet (Zu and Han, 2009; Song and Li, 2011) atmospheres. When 2D materials are used as solid lubricants or additives in base oils, they reduce the coefficient of friction by at least an order of magnitude and the wear rate by as much as four orders of magnitude compared to the bare contact (Kim et al., 2011; An et al., 2014; Berman et al., 2014; Gupta et al., 2016). 2D layers demonstrate unique mechanical properties (Lee et al., 2008; Bertolazzi et al., 2011) (e.g., the in-plane elastic modulus of graphene is 1 TPa (Lee et al., 2008) and that of MoS2 is ∼270 GPa (Liu et al., 2014)), thermal characteristics (e.g., 3,000–5000 W/m.K thermal conductivity for graphene (Balandin et al., 2008)), electronic properties (e.g., zero bandgap for graphene) (Zhan et al., 2012)), and chemical behavior (Berman et al., 2014). Therefore, they are desirable lubricant additives for components operating in extreme conditions (Ermakov et al., 2015). The intrinsic chemistry and functionality of 2D materials can be tuned to enhance their compatibility with various oils and solvents, thereby enabling their usage as lubricant additives, desalination membranes (Heiranian et al., 2015), and nanofluidic transporters (Secchi et al., 2016), as well as their chemical exfoliation of 2D layers (Parvez et al., 2015) (Figure 1B). Further, advances in scalable exfoliation methods and surface functionalization approaches have rendered 2D materials ideal for lubricant formulations (Tao et al., 2017; Xiao and Liu, 2017).
FIGURE 1. Examples of industrial applications of layered-structure materials in (A) dry and (B) wet environments.
Atomic-scale tribology is concerned with the physicochemical processes that determine the friction behavior of sliding surfaces displaying atomic/nanoscale roughness. Nanoscopic asperities at sliding surfaces can generate extremely high contact stresses, consequently augmenting surface damage that leads to the loss of material. The atomic force microscope (AFM) is the most widely used setup for nanotribological studies because it allows for accurate measurement of interatomic forces at nano/pico-Newton resolution. Additionally, the AFM probe provides a contact geometry that closely resembles nanoscopic asperity contacts, thereby aiding the study of atomic-scale surface force interactions and associated deformation and wear processes commencing during normal loading and reciprocal sliding. Molecular dynamics (MD) complement experimental measurements by providing a detailed atomistic description of the 2D surface, the AFM probe, and the surrounding environment, thus facilitating a mechanistic interpretation of the energy dissipation pathways in hidden contacts. MD simulations are usually performed for a system of interacting atoms to compute the interatomic forces (atomic stresses) and potential energy of the system under different loading and temperature conditions (Szlufarska et al., 2008). Therefore, atomistic investigations that use combinatorial experimental and molecular simulations can elucidate fundamental energy dissipation phenomena at various surfaces (Smolyanitsky et al., 2012).
The quality of the surface and hence the interfacial interactions between layered materials or against the asperities of the opposed sliding surface can be controlled by tuning the chemical, physical, electronic, and mechanical behavior of the surface. Despite numerous investigations concerned with the impact of these properties on the nanoscale friction of 2D layers in dry conditions, a limited number of investigations have been performed to study the role of liquid molecules in the friction behavior of these materials in wet environments. In a liquid medium, there are several phenomena responsible for the friction behavior of the surface in the nanoscale. For instance, in humid environments, the formation of a capillary between an AFM probe and the surface resulting from Laplace pressure increases the interfacial adhesion by generating a larger contact area, consecutively increasing the friction force (Greiner et al., 2012). Further, the specific arrangement of the liquid molecules in the vicinity of layered-structure materials increases the liquid density in those regions, affecting the net interactions with the surface and, in turn, the friction force (Diao et al., 2019; Baboukani et al., 2021).
In this article, atomic-scale friction models that elucidate the origin of interatomic interactions and friction forces are introduced first, followed by a discussion of classical friction models of 2D materials and an assessment of the ability of 2D materials to achieve superlubricity. Further, a comprehensive summary of the atomic-scale friction mechanisms of 2D materials in vacuum, air, and dry gas is provided, with special emphasis given to the load dependence of the friction force at the nanoscale and the anomalous friction behavior of 2D materials, particularly deviations from Amontons’ friction law in various environments. Furthermore, some unique friction behavior of 2D materials, such as friction force strengthening and load-dependent friction hysteresis observed under different environmental conditions, are interpreted in the context of experimental and simulation results. Finally, the friction behavior of layered-structure materials in liquid media and the effect of liquid molecular layering at contact interfaces are discussed in light of recent findings.
2 Atomic-scale friction
2.1 Friction models
Several models have been introduced to describe the fundamental origins of friction when two bodies slide against each other. The Prandtl-Tomlinson (PT) and Frenkel-Kontorova (FK) models use the one-dimensional (1D) motion of surface atoms (Popov and Gray, 2012; Schwarz and Hölscher, 2016) and elucidate the origins of friction in terms of the energy required for a hopping event when an atom moves along a corrugated potential defined by atomic periodicity. The PT model can be used to simulate friction force microscopy (FFM) testing, by modeling a tiny mass (representing the AFM tip) dragged by a spring (with a spring constant k representing the simultaneous contributions of the normal and lateral stiffness of the AFM microcantilever) over a 1D periodic potential at a constant scanning velocity vs (Figure 2A). The total PT potential U comprises two components accounting for the AFM tip-substrate interactions and the elastic strain energy stored in the AFM microcantilever and is given by (Vanossi et al., 2013)
where U0 is the potential amplitude, a is the lattice constant of the crystalline surface, and x is the coordinate of the point mass. The energy barrier ΔE is defined as the difference between the first minimum and the maximum of the PT potential, i.e., 2U0.
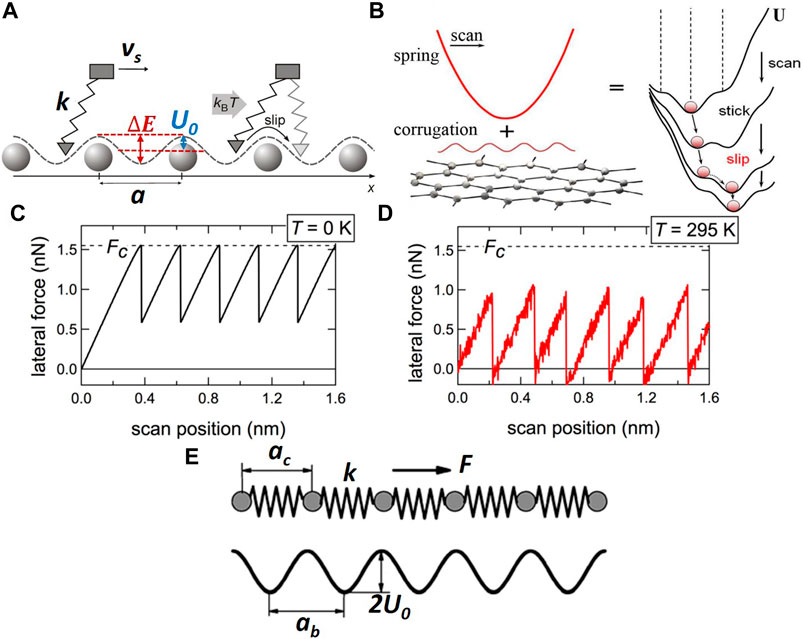
FIGURE 2. Atomic-scale friction models. (A) Schematic of the Prandtl-Tomlinson (PT) model (Schwarz and Hölscher, 2016) representing a point mass that resembles an AFM tip attached to a body by a spring having a spring constant k, which is dragged over a surface (the circles represent surface atoms) that possesses a periodic potential with a periodicity ab. (B) Schematic showing the energy profile for a soft spring (low stiffness). According to the PT model, the total potential energy (i.e., the sum of the spring-substrate interaction potential (sinusoidal) and the spring potential) yields a stick-slip behavior (Vanossi et al., 2013). (C) Stick-slip patterns for a point-like mass (e.g., the AFM tip) at T = 0 K. Slip occurs when the lateral force reaches a critical value Fc. (D) Stick-slip patterns at T = 295 K. Slip occurs at a lower force than the critical lateral force Fc (Schwarz and Hölscher, 2016). (E) Schematic of the Frenkel-Kontorova (FK) model (Hu et al., 2013) where atoms connected with springs of length ac having a spring constant k interact with a harmonic surface potential of periodicity ab and an energy corrugation equal to 2U0.
For springs with relatively low stiffness, the point mass resolves a saw tooth-like motion characteristic of stick-slip behavior (Figure 2B). When a critical value of U(x) (or critical lateral force Fc at T = 0 K (Figure 2C) is reached, the point mass jumps from one potential minimum to an adjacent minimum, and the inflection point (
where β is a parameter determined by the shape of the potential and
Nanocontacts established between the apex of an AFM probe and a surface usually contain hundreds of atoms interacting with each other. However, the PT model does not account for the coupling of the interatomic interactions (Alhama et al., 2011; Schwarz and Hölscher, 2016). In the FK model, N interacting atoms are connected by harmonic springs (atomic chain) and subjected to the external 1D periodic potential (Figure 2E) to describe kink-related plasticity in crystals. The total potential in the FK model is the sum of three terms associated with the kinetic energy of the atomic chain, the harmonic interaction of the nearest atom neighbors in the atomic chain, which has an elastic constant k and an equilibrium distance ac, and the interaction of the atomic chain with the periodic potential U0 that has a periodicity ab. Thus, the FK Hamiltonian potential is given by (Vanossi et al., 2013)
where pi, m, and xi are the momentum, mass, and location of the ith atom, respectively. According to the FK model, the theoretical yield strength of a crystal is obtained when an atomic plane is displaced by a lattice distance. In this process, the kinks in the structure play a critical role because the activation energy for kink motion is much smaller than the amplitude of the substrate potential U0; consequently, it is easier for these kinks to move than the atoms. Atomic systems with higher kink concentrations experience a more significant motion because the kink motion is directly correlated to the mass transport along the atomic chain. The tribological processes simulated by this model depend on the kink excitation that defines the mobility of the atomic chain.
The FK model also provides insight into the dependence of friction on the commensurability of the atomic chain with respect to the substrate. Commensurability illuminates how atomic-scale friction is affected by the length-scale correlation between the interacting atomic chain and the underlying substrate with periodicity ac and ab, respectively. For full commensurability (ground state) between an atomic chain with N atoms and an underlying substrate with
2.2 Superlubricity
A unique phenomenon is encountered when the crystal lattices of two sliding bodies are incommensurate, resulting in extremely low coefficient of friction
where SCC is the total overlap area of the top and bottom circles (atoms) corresponding to the two adjacent layers (Figure 3C). The good agreement between experimental and theoretical (PT model) results of a graphene bilayer indicate that the friction force correlates to the corrugation of RI at different misfit angles (Figure 3D). This correlation illuminates a direct relationship between superlubricity and the geometrical configuration of the stacked layers, i.e., the degree of lattice commensurability of bilayer graphene (Hod, 2012). In a comparative study of the friction properties of bilayer graphene and MoS2/MoSe2 van der Waals heterostructures that present a relative misfit angle between the layers, superlubricity was extended to a wide range of misfit angles that generated a lower coefficient of friction for the MoS2/MoSe2 heterostructure than the graphene bilayer (Figures 3E, F) (Ru et al., 2020). Large wavelength Moiré superlattices can be obtained by annealing van der Waals bilayer heterostructures at elevated temperatures. It has been reported that the rotation of the top graphene layer stacked on hexagonal boron nitride (h-BN) due to thermal annealing leads to the manipulation of the misfit angle, resulting in practically zero static friction force (Wang et al., 2016). The superlubricity of the graphene/h-BN heterostructure stems from the dynamic behavior of the graphene/h-BN interface (Zhang S. et al., 2022). The hexagonal Moiré pattern for this heterostructure is observed at low loads (Figure 3G). Increasing the applied load leads to stretching of the Moiré structure along the fast scanning direction, resulting in a higher friction force. With the instigation of AFM tip sliding, the top layer of graphene is stretched gradually to adapt to the h-BN lattice structure. The graphene top layer is destabilized when sufficient deformation is accumulated and abruptly snaps back at the period coinciding with the Moiré pattern, resulting in stick-slip friction behavior. The alignment of 2D layers on the support substrate (e.g., germanium (Ge)) yields ultralow friction. This behavior of the graphene layer can be observed even after fluorination and oxidation due to the formation of Moiré superlattices between these 2D layers and the Ge substrate. (The surface modification of graphene usually increases friction, as explained in the following sections.) Figure 3H illustrates a regular atomic-scale stick-slip pattern, and the low frictional energy dissipation (area of the friction trace loop) indicates the formation of a superlattice structure for the fluorinated graphene/Ge(111) and graphene/Ge(111) heterostructures (Zheng et al., 2016). Similarly, high superlubricity has also been reported for several other van der Waals heterostructures, such as fluorinated graphene (FG)/MoS2 (Wang et al., 2014), graphene/h-BN (Leven et al., 2013; Mandelli et al., 2017), graphene/MoS2 (Wang et al., 2017), borophene/graphene (Xu et al., 2022), and 2D-tellurene/graphene (Ru et al., 2021). The intrinsic lattice mismatch between the adjacent layers and the formation of Moiré superlattices incommensurate during the 2D layer stacking eliminates the local energy barriers (potential energy corrugations), hence lowering the coefficient of friction (Wang et al., 2014). However, in the case of homostructure 2D layers, it is difficult to maintain the incommensurate configurations between the stacking layers because of the inherent orientation commensurability of the lattices (Kabengele and Johnson, 2021). Nevertheless, it has been suggested that the commensurability of the graphene/graphene homostructure can be changed by applying a strain to the graphene layer (Dong et al., 2020). In light of the foregoing studies, it may be inferred that the superlubricity of 2D bilayers strongly depends on both the contact size and the relative misfit angle between the adjacent layers (Bai et al., 2022).
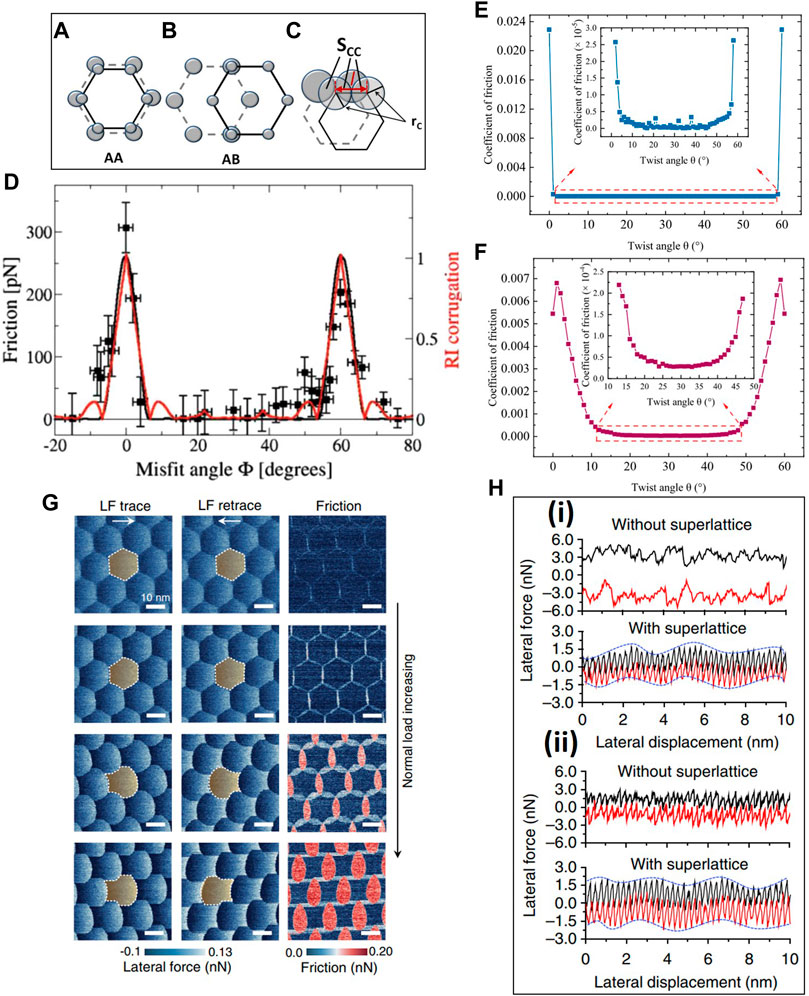
FIGURE 3. Superlubricity of layered-structure materials. Stacking modes of graphene bilayers at the (A) highest (AA) and (B) lowest (AB) potential energy surface barrier, and (C) definition of the registry index (RI), representing the projected overlap area between the atoms (circles) of the two layers (particularly for bilayer graphene). (D) Friction force and RI versus misfit angle (defined as the angle between the top and the bottom layers in the corresponding stacking, i.e., ϕ = 0
3 Load-dependent friction and robustness of Amonton’s law
According to the classical theory of friction proposed by Amontons (Gao et al., 2004; Schwarz and Hölscher, 2016), the friction force Ff at the macroscale shows a linear dependence on the applied load L through the coefficient of friction μ (Ff = μ L) and independence on the apparent contact area and relative sliding velocity. However, measurements of the electrical conductivity of metal-metal interfaces have shown a proportionality between load and real area of contact, which is defined as the sum of the microscopic asperity contacts (Bowden and Tabor, 2001). However, friction force acting at the asperities at the inception of interfacial sliding is also proportional to the real area of contact Ar, leading to a constant Ff/L ratio (i.e., coefficient of friction), which is in agreement with Amontons’ first law of friction. However, an elastic analysis of a non-adhering sphere of radius R sliding over a flat surface (Wenning et al., 2001) shows that Ar
The friction law represented by Eq. 5 has been proven to hold for a wide range of macroscopic and microscopic sliding contacts. In fact, MD simulations have shown that Eq. 5 can be extended to the nanoscale, where the load is not proportional to Ar, and the load is given by L = Le + La, where Le is the elastic restoring force of the deformed asperities and La is a surface adhesive force originating from van der Waals, dipole-dipole, Columbic, capillary, hydrogen bonding, etc. surface forces. Moreover, considering that Ff =
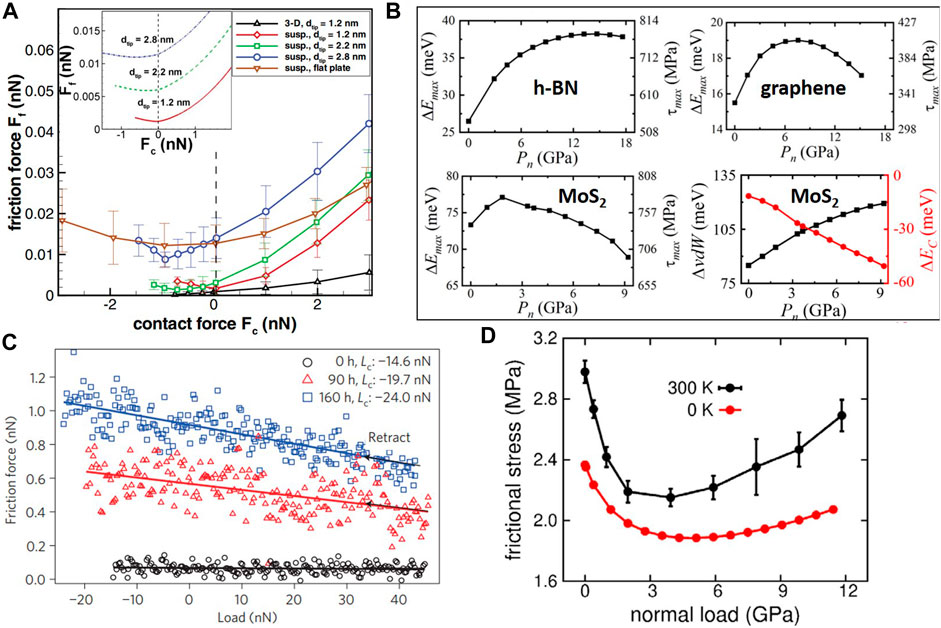
FIGURE 4. Deviation of atomic-scale friction of layered-structure materials from Amontons’ friction law. (A) MD results of the friction force Ff versus contact force (load) Fc for suspended single-layer graphene sliding against single-wall carbon nanotube AFM tips of diameter d (the inset shows results for spherical fullerene tips of diameter d) (Smolyanitsky and Killgore, 2012). (B) Maximum energy barrier ΔEmax (left axis) versus contact pressure Pn for MoS2, h-BN, and graphene homostructure bilayers (Li et al., 2020). The right bottom figure illustrates the van der Waals (black squares, left axis) and Coulomb (red circles, right axis) energies as a function of contact pressure for MoS2. (C) Friction force versus load (unloading regime) for graphite at different times of exposure to an oxygen atmosphere (Lc is the adhesive (attractive) force between the AFM tip and the graphene layer for 0, 90, and 160 h of exposure to oxygen) (Deng et al., 2012). (D) Friction stress (i.e., the ratio of the friction force to the contact area) versus load for a graphene monolayer stacked onto a four-layer thick h-BN substrate (Moiré superstructure) at 0 and 300 K (Mandelli et al., 2019).
First-principle calculations have also revealed a non-monotonic variation of the friction force with the load of 2D bilayer structures, such as MoS2, h-BN, and graphene (Li et al., 2020). Figure 4B shows the effect of contact pressure Pn on the maximum energy barrier
The breakdown of Amontons’ law has also been observed in nanoscale FFM experiments with multilayer bulk graphite during the retraction of the probe (unloading) (Mandelli et al., 2019). Specifically, the friction force of freshly cleaved graphite surfaces (measured before and after the exposure to oxygen for 60 and 90 h) increased as the load decreased during the retraction of the AFM tip (Figure 4C) (Deng et al., 2012). In addition, the aging time affected both the friction force and the coefficient of friction (slopes of fitted lines in Figure 4C). The increase of the pull-off force with the exposure time to oxygen was attributed to the increased surface hydrophilicity, which was induced by oxygen chemisorption. MD simulations demonstrated localized delamination of the topmost graphene layer by the sliding AFM probe, which was related to the ratio of the probe-surface adhesion to the exfoliation energy of graphite. Localized separation of the graphite lamellae by the probe was predicted when the former ratio was greater than one (Deng et al., 2012). It was presumed that interlayer bond stretching, lateral displacement of the deformed region, and the increase of the driving force to push the deformed region as the probe was unloaded were responsible for the observed friction behavior (Deng et al., 2012). An increase of the friction force with decreasing contact pressure has also been observed with layered graphene/h-BN Moiré superstructures at low contact pressures. Figure 4D shows the non-monotonic frictional behavior of this 2D heterostructure bilayer at two different temperatures (Mandelli et al., 2019). It was supposed that the out-of-plane atomic motion played a critical role in the resulting friction behavior.
4 Friction mechanisms of layered-structure materials
The profoundly different friction behavior of 2D materials compared to their 3D bulk counterparts is attributed to their unique structure and electronic state that vary significantly from those of their 3D bulk structures. Associated fundamental concepts of nanoscale friction of 2D layers are discussed in this section.
4.1 Potential energy surface
At the fundamental level, the mobility of 2D layers against each other is governed by the potential energy surface (PES) corrugation. Since friction is an interfacial process, the PES is controlled by the energy associated with the interactions between the opposing surfaces. Thus, the PES landscape between an AFM tip and a 2D layer (Vazirisereshk et al., 2020a) or between two 2D layers controls the friction behavior. The PES corrugation (the 2D Prandtl-Tomlinson energy projected on the xy-plane) represents the interlayer interaction energies measured as a function of the relative translational displacement of the 2D layers (Reguzzoni et al., 2012; Lebedev et al., 2016). The interplay between electrostatic, van der Waals, and Pauli contributions to the 2D layer sliding interface is controlled by the relative position of the atoms in two adjacent 2D layers (or the atoms in the 2D layer and the AFM tip), which changes during sliding (Levita et al., 2014). Generally, it has been shown that the PES profiles of 2D bilayer systems display two minima separated by a maximum point, while sliding along the y-direction marked with the red dots in Figure 5B (Ye et al., 2015; Vazirisereshk et al., 2019), as shown in Figure 5A for four different 2D homostructure bilayers (Levita et al., 2015). The absolute minimum of the PES corrugation (Min1) corresponds to the AB stacking (Figure 3B) for graphene (chalcogen atom on top of molybdenum atom for 2D transition metal dichalcogenides (TMDs)). In contrast, the absolute maximum represents the AA stacking (Figure 3A) of graphene (chalcogen atom on top of chalcogen atom). The saddle point and secondary minimum (Min2) are obtained upon displacing the top layer by 1/6 and 1/3 along the unit cell diagonal, respectively, illustrated with solid red lines. Compared to the graphene bilayer, an increase in the corrugation energy is observed for the TMD bilayers. Higher van der Waals interactions due to the larger chalcogen and transition metal atoms compared to the carbon atoms and the Pauli repulsion between the chalcogen atoms are responsible for the higher corrugation potential observed with the TMD bilayers than the graphene bilayer. The increase of the PES corrugation of the TMD bilayers correlates with the increase in electronegativity of the chalcogen atoms (from S to Te). The energy profiles in the xy-plane (Figure 5B) of the foregoing 2D homostructure bilayers are shown in Figures 5C–F. The white lines show the minimum energy paths obtained by connecting the minima of the corrugated potential (Levita et al., 2015).
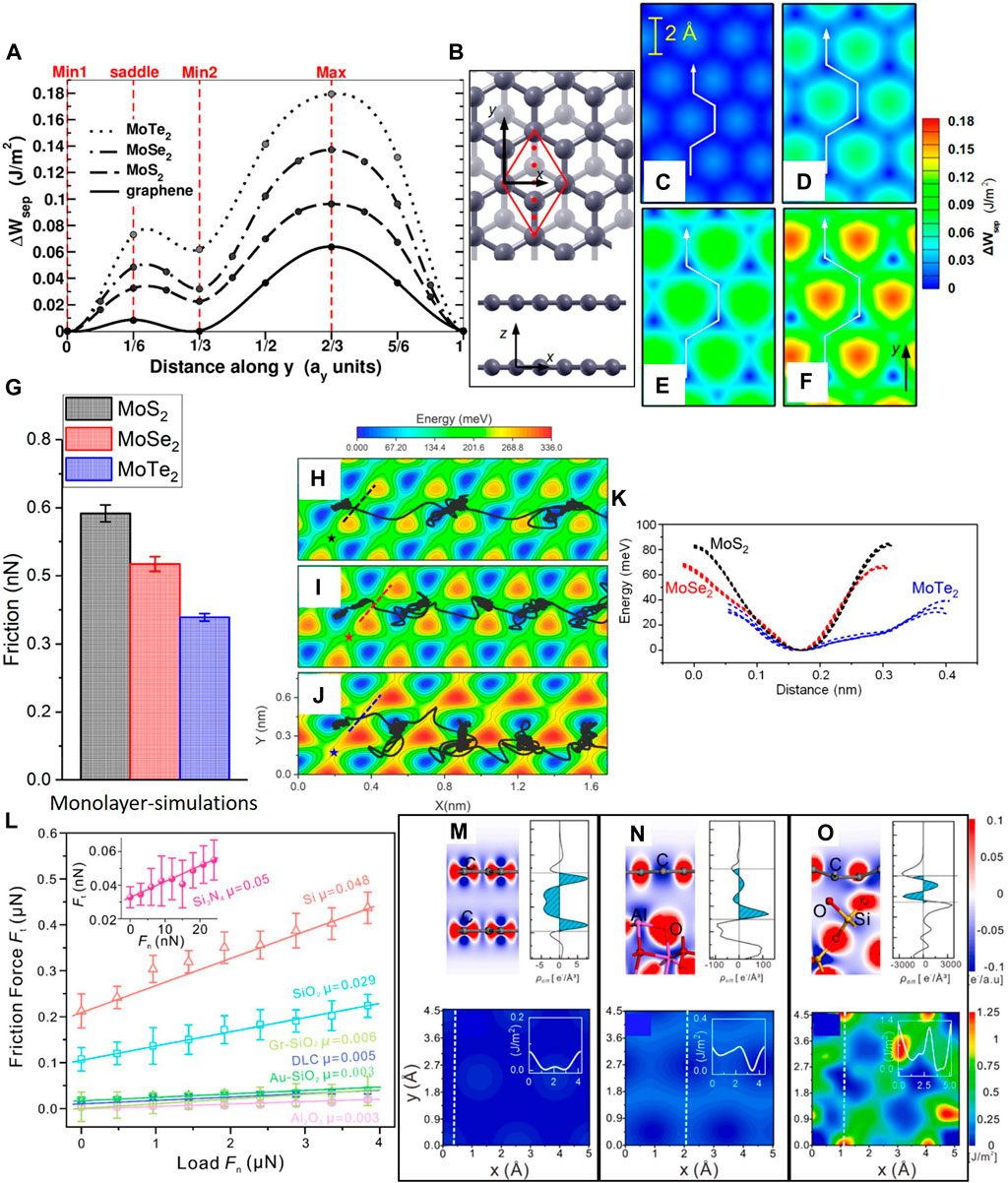
FIGURE 5. The effect of potential energy surface (PES) corrugation on the friction behavior of layered-structure materials. (A) Separation work ΔWsep (PES) profiles of MoTe2, MoSe2, MoS2, and graphene homostructure bilayers versus sliding distance in the y-direction (denoted by red dots in (B) and given as a fraction of the lattice distance ay in the y-direction). (B) Plane view (top) and side view (bottom) of a graphene bilayer structure (the dark and light gray atoms in the plane view correspond to the top and bottom graphene layers). PES maps of (C) graphene, (D) MoS2, (E) MoSe2, and (F) MoTe2 homostructure bilayers for sliding of the top layer over the bottom layer in the y-direction. All of the results shown in (A)–(F) were obtained from DFT calculations (Levita et al., 2015). (G) Friction force due to a SiO2 tip sliding against a MoS2, MoSe2, and MoTe2 monolayer. PES corrugation maps of a SiO2 tip sliding against (H) MoS2, (I) MoSe2, and (J) MoTe2 monolayers (the black lines show the sliding trajectories of the center of mass of the tip). (K) PES profiles were measured at four different saddle points for the MoS2, MoSe2, and MoTe2 monolayers. Results shown in (G)–(K) were derived from MD simulations (Vazirisereshk et al., 2020b). (L) Load-dependent friction forces for different AFM tips sliding on graphite. Charge density differences (
Although the MoS2 monolayer displays the lowest PES corrugation (Figure 5H), it still exhibits higher friction than the MoSe2 and MoTe2 monolayers (Figure 5G), contrary to expectation. The trajectory of the AFM tip’s center of mass on the PES corrugation demonstrates that the tip does not move along the sliding direction (Figures 5H–J); instead, it jumps between minimum energy points by crossing close to the saddle points in the PES corrugation. The curvature of the energy at the saddle point correlates to the lattice constant. Among the three 2D layers, the MoTe2 has the largest lattice constant, resulting in a smoother upward curvature at the saddle point in the direction perpendicular to the minimum energy path compared to other monolayers (Figure 5K). Hence, the AFM tip experiences a higher lateral force as it passes across the narrower saddle point for MoS2 than MoSe2 and MoTe2 (Vazirisereshk et al., 2020b). These measurements show the contribution of the maximum energy barrier (peak-to-valley energy) and the shape of the potential corrugation on the friction force of 2D layers. It is possible to manipulate the PES landscape between the AFM tip and the 2D layers by tuning the scanning direction of the AFM tip over these layers (Vazirisereshk et al., 2020a).
The interfacial charge density and its variation during sliding of van der Waals interacting layers, such as graphene/graphite layers or an AFM tip sliding against 2D layers, determine the overall adhesion force and the corrugation of the PES (Wolloch et al., 2018). Nanoscale load-dependent friction forces were measured experimentally on graphite using different AFM tips (Figure 5L). Charge density differences (
4.2 Thickness-dependent friction behavior
Thickness-dependent friction has remained a subject of debate for many years. The friction behavior of 2D materials, such as graphene, h-BN, MoS2, WS2, and NbSe2, has been investigated as a function of the number of layers. For a wide range of conditions, i.e., humidity, applied load, and substrate material, a monotonic decrease in friction has been reported with increasing number of 2D layers (Li et al., 2010; Xu et al., 2011; Cho et al., 2013; Fang et al., 2017). Figures 6A, B illustrate a layer dependence of the friction force of few-layer graphene and bulk graphite and their corresponding atomic-scale stick-slip patterns during sliding, respectively. Friction loops show a gradual increase in lateral force at the inception of sliding, resulting in a tilted friction loop (slopes are shown with dotted lines). This phenomenon (known as friction strengthening) is more pronounced for single-layer graphene and weakens with increasing number of layers. The thickness dependence and strengthening of friction depend on the bending stiffness and the in-plane rigidity of the 2D layers (Figure 6C). During sliding, the contact adhesion forces and the inherent flexibility of the elastic sheets define the pucker of the 2D sheet in front of the AFM tip. This deformation enhances the contact area between the tip and the 2D layer (Figure 6D), consequently increasing the friction force. Puckering is less prominent in the case of thicker layers (n > 5) due to the higher bending stiffness of the multilayer sheets (D = n3D0, where D is the out-of-plane bending stiffness, n is the number of layers, and D0 is the bending stiffness of a single-layer 2D material (Li et al., 2010)), resulting in friction forces lower than the single-layer friction force. The increase of the contact area due to puckering enhances the lateral force required for advancing slip, causing a tilting of the lateral signals over a short sliding distance (Lee et al., 2010).
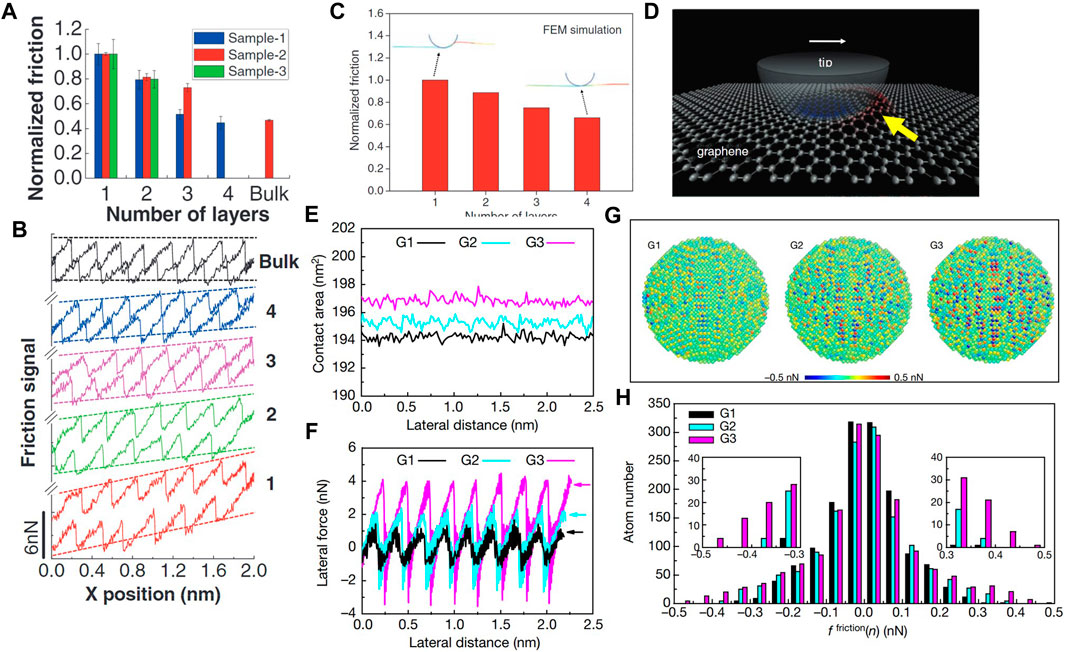
FIGURE 6. The effect of contact quantity and quality on friction of layered-structure materials (Lee et al., 2010; Li et al., 2016). (A) Friction force of few-layer graphene and bulk graphite (normalized by the friction force of single-layer graphene) measured with a silicon AFM tip in a dry atmosphere. (B) Friction loops revealing stick-slip behavior of few-layer graphene (numbers 1
To investigate the effect of the contact area on the friction of 2D materials, suspended single-layer graphene with varying degrees of wrinkles induced by different compressive strains was tested with the AFM (Li et al., 2016). Despite the slight increase in real contact area (Figure 6E), a profound effect of compressive strain on friction was encountered (Figure 6F). However, the per-atom friction force distributions (Figure 6G) and corresponding histograms (Figure 6H) reveal a higher compressive strain in front of the tip, which produced a greater number of pinning sites that intensified the interfacial interaction. Therefore, it may be inferred that not only the real area of contact (i.e., the number of atoms within the range of interatomic forces) but also the quality of the contact control the strength of the pinning sites, playing significant roles in the layer-dependent friction behavior of few-layer graphene (Li et al., 2016).
MXenes (metal carbides, nitrides, and carbonitrides) is an emerging family of layered-structure materials. The dependence of the friction force on the number of layers of MXenes has been investigated more recently. It has been found that single-layer Ti3C2Tx (Tx is the functional group of a compound or a combination of compounds, e.g.,
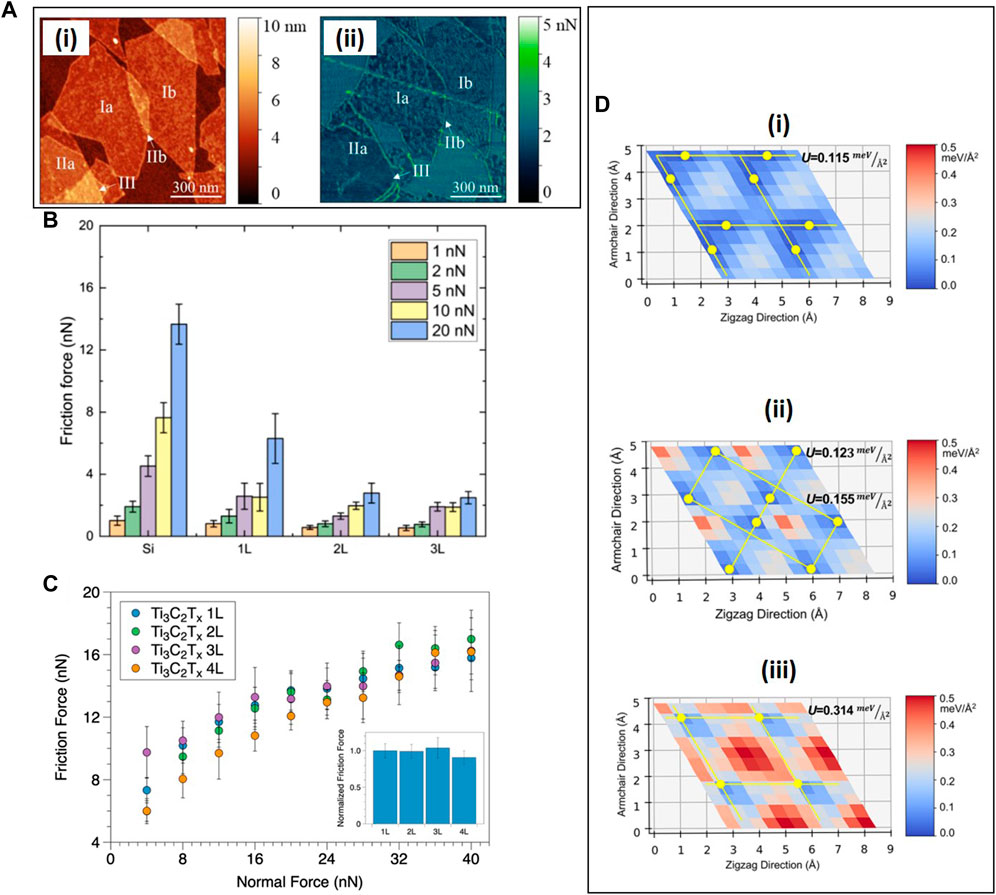
FIGURE 7. Thickness-dependent friction of 2D MXene layers. (A) AFM topographic (i) and friction map (ii) images of few-layer Ti3C2Tx deposited on SiO2/Si substrates (Kozak et al., 2022). (B) Thickness-dependent friction forces of few-layer Ti3C2Tx MXenes for different loads (Pendyala et al., 2022). (C) Load-dependent friction force of few-layer Ti3C2Tx (1
4.3 Electronic and phononic effects
The kinetic energy generated during sliding is dissipated either electronically and/or phononically through the damping of the surface atom vibrations (Park et al., 2006; Qi et al., 2008). A likely energy dissipation process affecting thickness-dependent friction may be electron-phonon coupling. The lattice vibrations in 2D layers induced by the sliding process are damped by electronic excitations due to electron-phonon coupling. Because this effect is milder in the case of two-layer graphene than single-layer graphene, undamped lattice vibrations may develop during the slip of two-layer graphene. Thus, analogous to overcoming the energy barrier by thermal vibrations, a relatively small lateral (friction) force is needed to initiate slip of a multilayer 2D material with undamped lattice vibrations (Filleter et al., 2009). A dependence of the friction force on phonon transport has also been observed at the nanoscale (Torres et al., 2006; Wang et al., 2007; Prasad and Bhattacharya, 2017). In a study aimed to elucidate the contribution of excited acoustic modes on the friction of a graphene layer in the commensurate-incommensurate transition, it was found that the friction force due to a graphene tip sliding against a rigid graphene layer can be controlled by prestraining the graphene layer (Dong et al., 2020). Prestraining (either tensile or compressive) caused the excitation of fewer acoustic modes, resulting in less friction energy dissipation (Dong et al., 2020). An atomic-scale friction study of semiconductor surfaces revealed significant differences in friction due to atom charge accumulation (Park et al., 2006). Moreover, the fluctuations of the interfacial charge density in 2D van der Waals heterostructures (graphene/TMDs) induced by the sliding process affect the PES corrugations and friction of these layers (Wang et al., 2017). The former studies indicate that because atomic vibrations, electronic excitations, and charge accumulations to the atoms of layered-structure materials are coupled, they influence the PES corrugation and, consequently, the friction behavior.
4.4 Chemical effects
Chemical modification of 2D layers by functionalization (Figure 8A) is a versatile method for altering the surface chemistry and obtaining desired properties at the contact interface. Specifically, functionalization is an effective method for tuning the mechanical (Ko et al., 2013), electrical (Byun et al., 2011; Lee et al., 2013), and chemical (Mao et al., 2013; Bagherzadeh and Farahbakhsh, 2015) properties of 2D layers and, consequently, modulate the nanotribological characteristics. For instance, graphene fluorination increases significantly the out-of-plane bending stiffness, which is strongly affected by out-of-plane vibrations (the so-called flexural phonons). This effect enhances the friction force for fluorinated graphene compared to pristine graphene. The friction energy at the atomic scale is initially dissipated by damping of the softest phonons (Kwon et al., 2012). DFT calculations have shown that stiffening of the graphene layers can be achieved not only by fluorination but also by other chemical functionalizations, such as oxidation and hydrogenation (Ko et al., 2013). Figure 8B shows the total energy versus the out-of-plane deformation for different chemically modified graphene layers. A higher energy is needed to deform the functionalized graphene layers than the pristine graphene. The reduced out-of-plane deformation of chemically modified graphene layers may be attributed to the isotropic directional sp3 bonds of these layers (Ko et al., 2013). Moreover, FFM and MD results have shown a much higher friction force between a silicon AFM tip and fluorinated graphene than pristine graphene (Li et al., 2014). Figure 8C shows the corrugation amplitude of the PES for a silicon tip and fluorinated graphene as a function of fluorination degree (F/C ratio) and applied load. An increase in the interaction energy with fluorine atom content is evident at all loads. It has been contended that fluorination enhances the corrugation potential because of the concentration of negative charges at the fluorine atoms. Electrostatic interactions due to the polarized bonds between the fluorine and the carbon atoms dominate the van der Waals forces, consequently affecting the PES (Li et al., 2014).
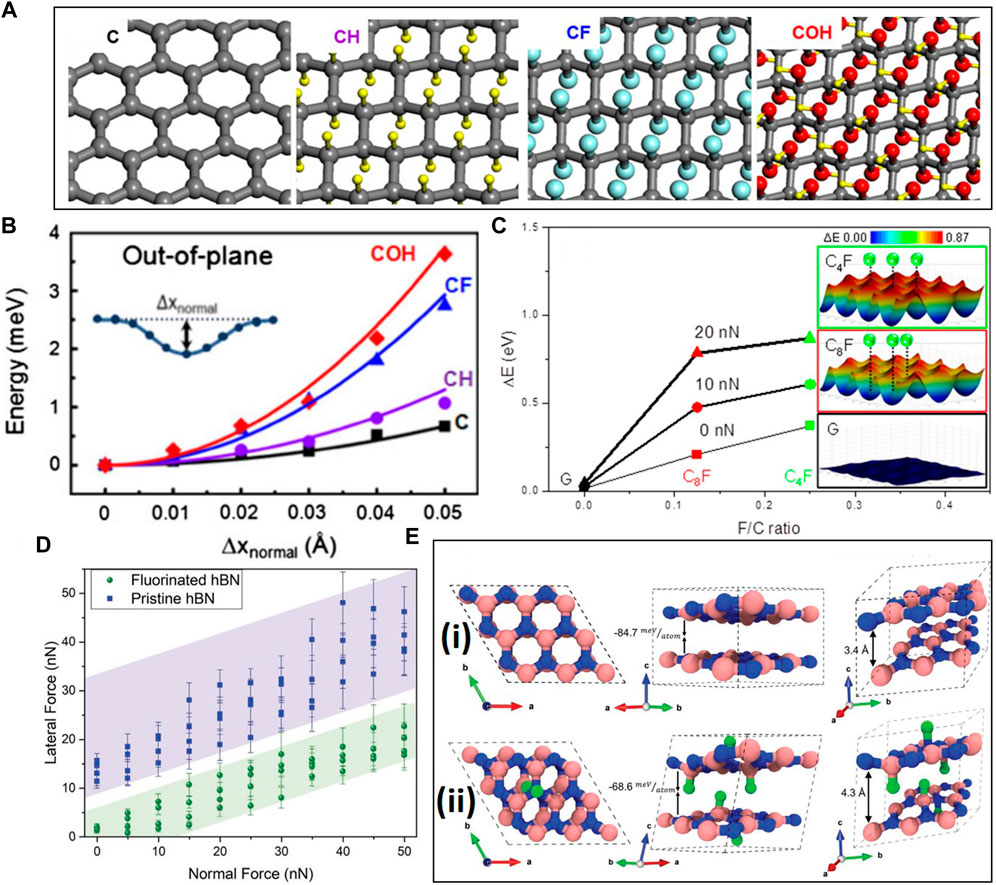
FIGURE 8. The effect of chemical modification on the friction of layered-structure materials. (A) Atomic structure of functionalized graphene layers (C: graphene, CH: hydrogenated graphene, CF: fluorinated graphene, and COH: hydroxidized graphene). (B) Friction energy versus out-of-plane deformation Δxnormal for different functionalized graphene layers (Ko et al., 2013). (C) PES amplitude ΔE versus atomic fluorine content and applied load for a silicon AFM tip interacting with a graphene layer obtained from MD simulations. The insets illustrate the energy corrugation of graphene with various atomic fluorine contents (Li et al., 2014). (D) Friction force of pristine and fluorinated h-BN versus normal force (load). The blue and green shadows represent error ranges. (E) Optimized geometry of (i) h-BN and (ii) fluorinated h-BN obtained from DFT calculations. The pink, blue, and green atoms are B, N, and F, respectively (Meiyazhagan et al., 2021).
Functional groups can also influence adhesive characteristics and surface roughness. For example, the higher friction of hydrogenated graphene compared to pristine graphene has been attributed to the higher surface roughness of the former material (Dong et al., 2013). Functionalized graphene layers are more susceptible to airborne adsorbates than pristine graphene, which can also contribute to the higher friction of functionalized graphene surfaces (Fessler et al., 2014). Conversely, h-BN fluorination reduces the friction force compared to pristine h-BN in the load range of 0
It is noted that the foregoing dissipation mechanisms in layered-structure materials influence each other. Figure 9A shows a detailed map of these mechanisms that includes the main constituents and illustrates the interdependences between the constituents. In view of the simultaneous contributions of the dissipation mechanisms to the friction behavior of layered-structure materials, a physics-based machine learning (ML) model was used to predict the friction response of 2D bilayers (Sattari Baboukani et al., 2020). This was accomplished by generating a database of the mechanical, electrical, chemical, and thermal properties of 2D layers belonging to the graphene and TMD families to train the ML model. The maximum PES of these 2D homostructure bilayers was determined from the pairwise correlations of the properties of the 2D layers (Figure 9B) that affect the friction behavior. The transfer learning approach was used to predict the maximum PES corrugation of ten 2D bilayer systems (Figure 9C). The good agreement between the MD and DFT estimated (green triangles) and ML predicted (blue squares) energy barriers of hydrogenated graphene (h-Gr) and WS2 bilayers illustrates the accuracy of this approach. According to the former methodology, the 2D bilayers from the graphene family are characterized by lower energy barriers, and the polarity and size of the chalcogen atoms in the TMD family control the energy barrier height of the 2D bilayers from this group.
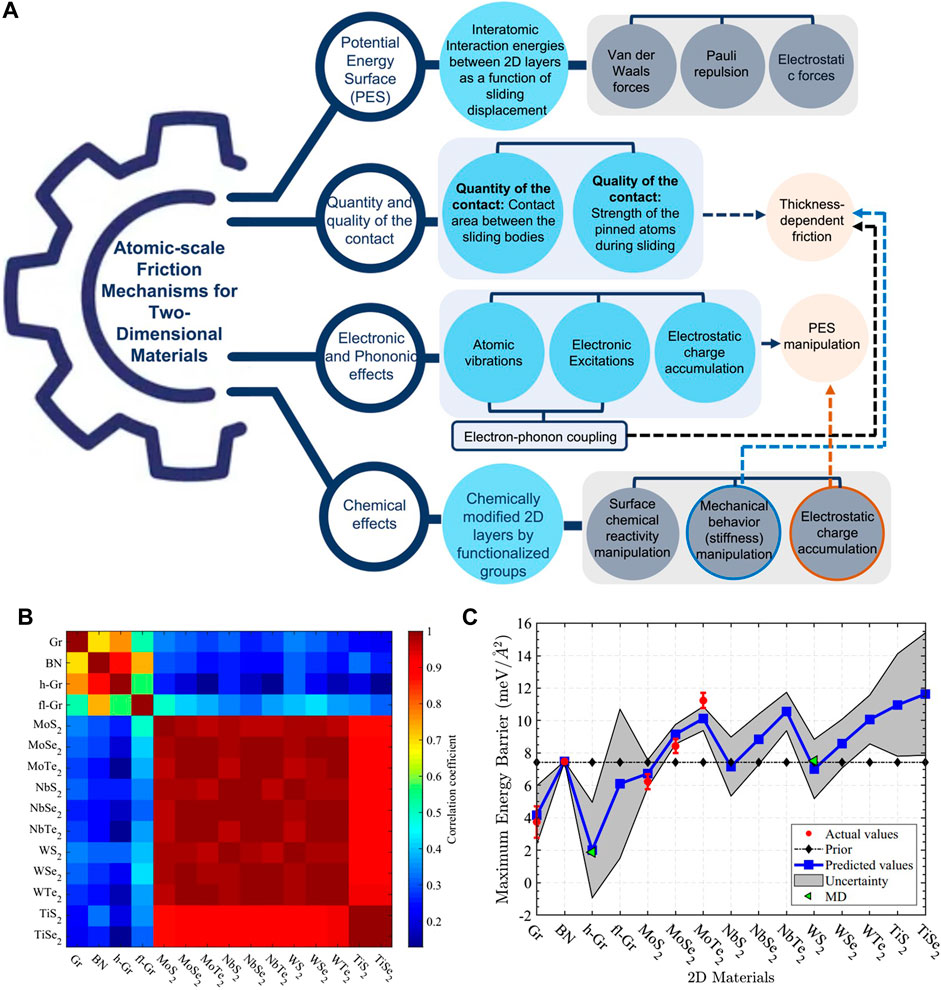
FIGURE 9. (A) Atomic-scale friction mechanisms of layered-structure materials and their interdependence. A machine learning (ML) method was used to predict the friction of 2D homostructure bilayers (Sattari Baboukani et al., 2020): (B) pairwise correlation of the geometrical, mechanical, electronic, and thermal properties of fifteen 2D bilayers that directly affect friction (the red scale shows higher pairwise correlation) and (C) maximum (peak-to-valley) energy barrier (PES) of different 2D homostructure bilayers computed from the maximum PES, quoted from the literature for graphene (Gr), BN, MoS2, MoSe2, and MoTe2 2D homostructure bilayers, and the correlation between 2D layer properties and maximum PES. To validate the ML model, the maximum PES of hydrogenated graphene (h-Gr) and WS2 homostructure bilayers estimated from MD simulations (green triangles) are compared with predicted values.
5 Friction anisotropy
Friction strengthening is a type of friction anisotropy associated with the gradual increase of the friction force from the onset of sliding until reaching a steady state, resulting in tilting of the friction force loop. This atomic-scale friction strengthening in layered-structure materials depends on several factors, including the number of 2D layers (Almeida et al., 2016; Zeng et al., 2018b; Peng et al., 2020), the relative velocity and sliding direction of the scanning AFM tip (Almeida et al., 2016), the applied load (Peng et al., 2020), the adhesive interactions between the substrate and the layered-structure material (Cho et al., 2013), and the chemical structure of the 2D layers (functional groups) (Zeng et al., 2018b). The role of these parameters in friction strengthening discussed in this subsection is based on the earlier demonstrated effect of the 2D layer thickness on friction, where layer-dependent friction strengthening was shown to depend on the degree of puckering and the quality of the contact between the AFM tip and the 2D layers (Lee et al., 2010; Li et al., 2016). An investigation of the effect of sliding velocity on friction strengthening in the case of a silicon AFM tip sliding on few-layer graphene illuminated time-dependent interactions at the tip/graphene contact interface (Zeng et al., 2018a). Specifically, weaker friction strengthening (smaller slope of the dashed lines shown in Figure 10A) was encountered at higher sliding velocities, which was attributed to inadequate time for the graphene layer to undergo configurational changes, even though the interaction forces between the tip and the graphene layer were weaker at higher velocities than lower velocities. A similar dependence of friction strengthening on sliding velocity has been reported for single-layer graphene (Peng et al., 2020); however, the enhancement of friction strengthening with decreasing sliding velocity was observed only at light loads because the puckering and contact stress distribution produced insignificant changes in friction strengthening at high loads. More pronounced friction strengthening was observed when a silicon tip was slid against a graphene monolayer in an armchair direction instead of a zigzag mode (Figure 10B) (Almeida et al., 2016). This friction anisotropy, which is characteristic of few-layer graphene but not bulk graphite, is indicative of the anisotropic nature of the flexural deformation amplitudes of single-layer graphene instigated by the tip movement.
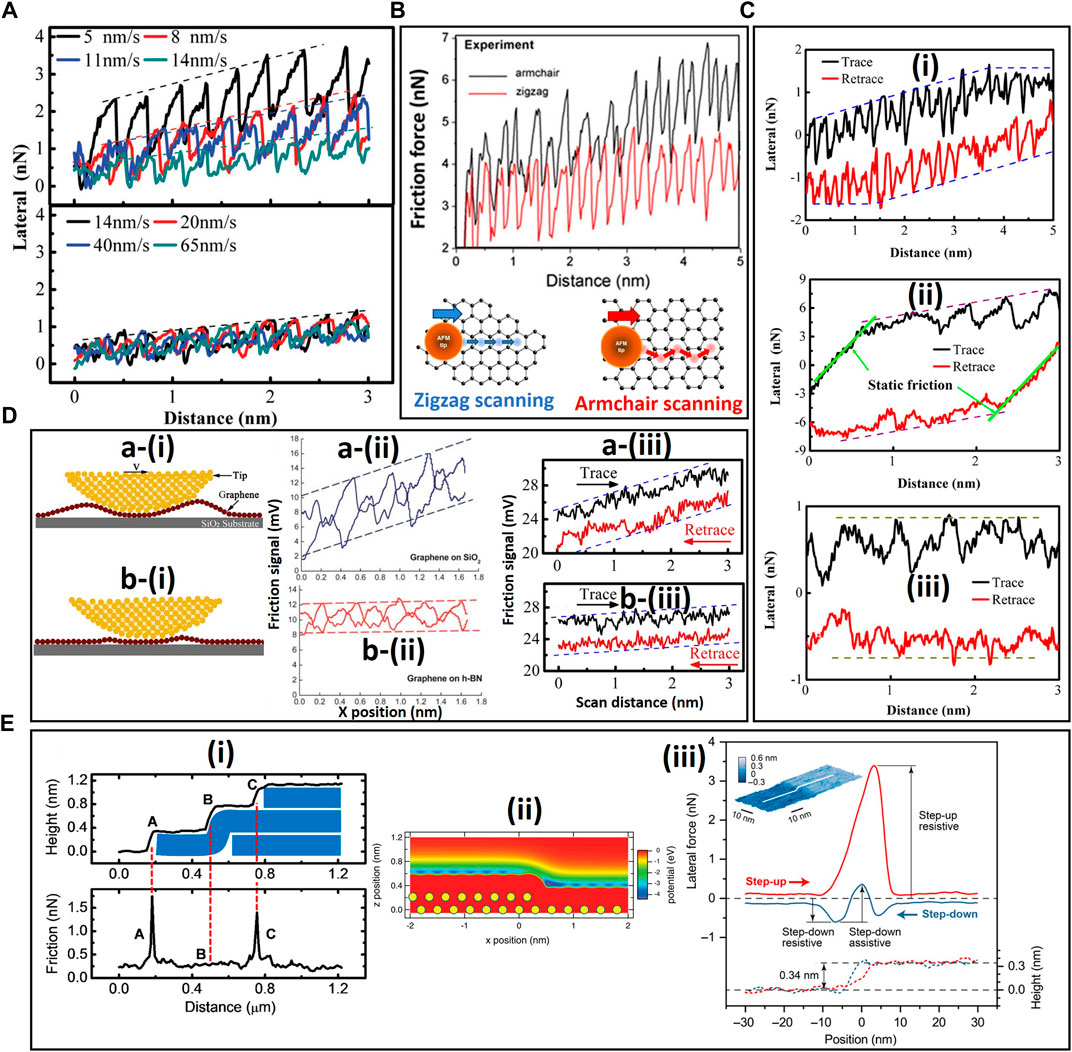
FIGURE 10. Friction anisotropy in layered-structure materials. (A) Effect of sliding velocity on friction force strengthening for a silicon AFM tip sliding on a 0.5-nm-thick graphene layer (Zeng et al., 2018a). (B) Effect of sliding direction on friction force strengthening for a silicon AFM tip sliding on a graphene monolayer in armchair and zigzag path configurations. The schematics represent the spatial distribution of local PES minima for the sliding AFM tip following zigzag and armchair paths (the blue and red circles represent stick points and the arrows indicate slip jumps) (Almeida et al., 2016). (C) Effect of chemical modification on friction force strengthening for a silicon AFM tip sliding against (i) graphene, (ii) graphene oxide, and (iii) fluorinated graphene layers (Zeng et al., 2018b). (D) Substrate effect on friction strengthening in 2D layer materials (Cho et al., 2013; Zeng et al., 2017). Schematics show an AFM tip sliding over a graphene layer, which is (a–i) weakly and (b–i) strongly bonded to a substrate. Friction force strengthening in the case of a silicon AFM tip dragged over a graphene layer supported by (a–ii) a low adhesive strength SiO2 substrate and (b–ii) a high adhesive strength h-BN. Friction force signals due to a silicon AFM tip sliding over a 0.8-nm-thick graphene layer deposited on a SiO2 substrate (a–iii) before and (b–iii) after 3 min of plasma treatment. (E) Friction at the step edges of layered-structure materials: (i) Step height profile (top) and friction force (bottom) along the edges of a HOPG surface with a single-atom (0.34 nm) step height (Lee et al., 2015). (ii) PES at a graphene step measured with a silicon AFM tip (Hölscher et al., 2008). (iii) Lateral force and step-height profile at a graphene edge measured with a silica AFM tip (Chen Z. et al., 2019).
Friction strengthening in the first few nanometers of sliding has also been reported for functionalized graphene layers, such as graphene oxide (GO) and fluorinated graphene (FG) (Figure 10C) (Zeng et al., 2018b). In fact, higher static friction and more prominent friction strengthening occurred with GO [Figure 10C(ii)] than graphene [Figure 10C(i)]. The lack of friction strengthening in the case of FG [Figure 10C(iii)] is attributed to the instantaneous saturation of the interfacial interactions between the silicon tip and the FG layer. In the ambient environment, the adhesion force measured on the GO surface is dominated by capillary and van der Waals forces. Sliding-induced puckering at the GO surface increased the interfacial contact area, consequently intensifying the capillary and van der Waals forces. In addition, the accumulation of oxygen-containing functional groups at the hydrophilic GO surface strengthened the hydrogen bond interactions between the silicon tip and the GO surface. Alternatively, in the case of the highly hydrophobic FG layer, the effects of the capillary force and hydrogen bond interactions on the adhesion force were insignificant. Hence, friction strengthening did not occur with the FG layer due to the limited puckering (Zeng et al., 2018b). A dependence of friction strengthening on the properties of the substrate of layered-structure materials has also been observed in a recent study (Peng et al., 2020).
Atomic-scale stick-slip behavior has been observed for a silicon tip sliding against single-layer graphene deposited on SiO2 [Figure 10D(a-ii)] and h-BN [Figure 10D(b-ii)] substrates; however, friction strengthening was significantly more pronounced for the graphene/SiO2 contact interface. The foregoing finding was attributed to the suppression of puckering due to the strong adhesion of the graphene layer to the h-BN substrate, as illustrated schematically in Figure 10D(a-i) (weak interfacial adhesion) and Figure 10D(b-i) (strong interfacial adhesion). The adhesive strength between the 2D layer material and the substrate can be enhanced by various surface modification methods, such as plasma surface treatment. Additionally, changes in the atomic configuration of graphene, endowed by a low adhesive strength to the substrate, may promote atomic pinning and a higher commensurate state, thereby enhancing friction strengthening. This is shown by a comparison of the friction responses of graphene deposited on an untreated SiO2 substrate (low interfacial adhesion) [Figure 10D(a-iii)] and a plasma-treated SiO2 substrate (high interfacial adhesion) [Figure 10D(b-iii)] (Zeng et al., 2017). Similar friction strengthening was observed for a silicon AFM tip sliding against a highly oxidized graphene layer deposited on a copper substrate. The high oxidation level reduced the interfacial adhesive strength leading to puckering and wrinkling in front of the AFM tip, which were conducive to friction strengthening (Zhao et al., 2019). The foregoing study also showed that wear of the graphene layers commenced in the wrinkled areas. The adhesive strength between a 2D layer and a substrate can also be affected by substrate roughness. Rough substrates are characterized by a lower interfacial adhesive strength, leading to the formation of wrinkles and folds and the enhancement of puckering in front of the tip, consequently promoting friction strengthening (Peng et al., 2020). Therefore, the adhesive strength between a 2D layer and the substrate greatly contributes to the friction strengthening and the wear resistance of these layers (Zhao et al., 2019; Liu et al., 2022).
Another type of friction anisotropy of layered-structure materials is the higher friction force encountered at step edges of 2D layers exposed to the environment, as shown in Figure 10E(i) for graphene (Lee et al., 2015). Since these edges are more susceptible to environmental adsorbates, they may be terminated by hydroxyl (
6 Load-dependent friction hysteresis
Friction hysteresis is defined as the increase of the friction force with the load (loading) and the development of a higher or lower friction force upon the subsequent decrease of the load (unloading) than that measured during the loading. This frequently observed behavior of layered-structure materials depends on the contact conditions (Feiler et al., 2007; Dedinaite et al., 2010; Egberts et al., 2014; Ye et al., 2016; Gong et al., 2018). For example, the deposition of a graphene monolayer on polycrystalline copper by chemical vapor deposition (CVD) has been reported to lower the friction force under ambient conditions by a factor in the range of ∼1.5
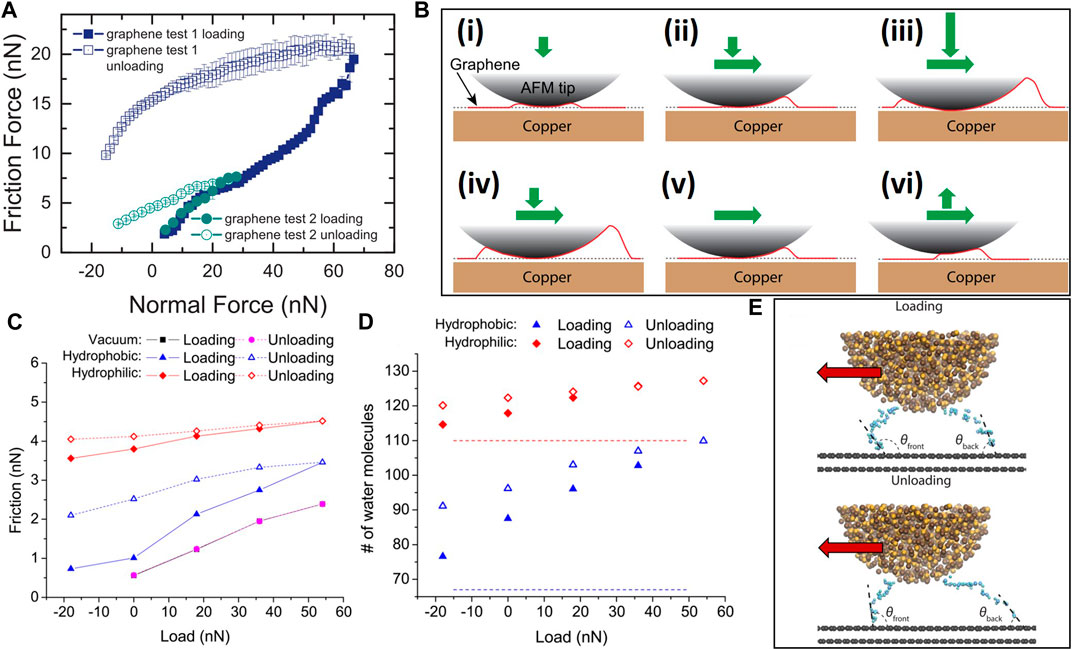
FIGURE 11. Friction force hysteresis of graphene. (A) The friction force hysteresis produced by a silicon AFM tip dragged onto CVD-grown graphene (Egberts et al., 2014). (B) Schematic of the deformed configuration of a graphene sheet (red line) supported by a copper substrate interacting with a silicon AFM tip at the instances of (i) initial contact, (ii) inception of sliding, (iii) load increase, (iv) load decrease after reaching a maximum, (v) zero load, and (vi) adhesive force development during unloading (Egberts et al., 2014). MD simulations showing (C) the load-dependence of the friction force generated by an amorphous SiO2 tip sliding on hydrophobic (contact angle = 112°) and hydrophilic (contact angle = 40°) graphene monolayers in vacuum and humid air, (D) the water-graphene contact area estimated by the number of water molecules in contact with the hydrophobic and hydrophilic graphene monolayers during loading and unloading (the blue and red dashed lines indicate the water contact area for hydrophobic and hydrophilic graphene, respectively, in the absence of the tip), and (E) snapshots of the water configuration between a graphene substrate and a SiO2 tip moving in the direction of the red arrow at the inception of loading (top) and after unloading (bottom) (Ye et al., 2016).
A load-dependent friction force hysteresis of single-layer graphene may also originate from changes in the contact area caused by environmental adsorbents. The adsorption of airborne contaminants on graphene may intensify the adhesive force between the AFM tip and the graphene surface, thus reducing the recovery of out-of-plane deformation of graphene during unloading. Removing environmental adsorbents from the surface of graphene by annealing is an effective method of lowering adhesion that may even lead to a negative load-dependent friction force hysteresis, i.e., lower friction forces during unloading than loading. The absence of a friction force hysteresis in experiments performed with bulk graphite confirms that the out-of-plane deformation (puckering) and the sliding history are responsible for this behavior. Because the adsorption of water molecules on a graphene surface is unavoidable in the ambient, the friction behavior of the graphene layers can be fairly erratic. MD simulations of a SiO2 tip sliding on a graphene monolayer show the development of a friction force hysteresis in atmospheric conditions, which is especially pronounced with hydrophobic graphene, but not in vacuum (Figure 11C) (Ye et al., 2016). Moreover, the contact area (estimated by the number of water molecules present in the contact) was also found to exhibit a load-dependent hysteresis (Figure 11D). Hydrophilic contact interfaces are characterized by higher friction because of the larger water-graphene contact area than hydrophobic contact interfaces. During loading, the water molecules trapped at the contact interface are pushed downwards, spreading on the graphene surface, increasing the contact area, and decreasing the contact angle (Figure 11E, top). During unloading, however, the AFM tip pulls the water up and lowers the contact area (Figure 11E, bottom), leading to the evolution of a friction force hysteresis. The difference between the water contact angles at the front and the back of the tip is more significant for hydrophobic graphene, resulting in more pronounced load-dependent friction force hysteresis (Ye et al., 2016). AFM studies of few-layer graphene have also confirmed that the relative humidity plays a significant role in the overall friction behavior and the evolution of the friction force hysteresis (Egberts et al., 2014). In a high-humidity environment, surface oxidation and/or adsorption of oxygen-containing species increase the surface energy of graphene, also enhancing the friction force hysteresis (Gong et al., 2018; Hasz et al., 2018).
7 Friction behavior of layered-structure materials in liquid media
The friction behavior of layered-structure materials in contact with liquids is a subject of significant interest due to the wide range of applications, e.g., lubricant additives (Liu et al., 2019), desalination membranes (Heiranian et al., 2015), nanofluidic transporters (Secchi et al., 2016), and chemical exfoliation of 2D layers (Huo et al., 2015) (Figure 1B). Despite numerous studies dealing with the nanotribological behavior of layered-structure materials in dry environments, there have been fewer studies in liquid media. In view of the rapidly increasing applications of 2D layers in liquid media, basic knowledge of their friction characteristics in wet environments is of paramount importance.
The friction behavior of layered-structure materials is profoundly different in liquid media than in vacuum and dry environments. Atomic-scale adhesion forces of 2D layers immersed in liquid media are lower than those in air, and are mainly dominated by van der Waals and electrostatic forces rather than capillary forces in humid atmospheres (Robinson et al., 2013). Furthermore, the structure and arrangement of liquid molecules confined at a flooded contact interface differ significantly from those of the bulk liquid counterparts, affecting the motion of these molecules, the slip length, and, in turn, the interfacial friction behavior (Tocci et al., 2014). Specifically, liquid molecules confined to the proximity of the atomically flat surface of 2D layers tend to arrange in layered structures. The increased density of solvent molecules at the contact interface affects the interaction energies, shear-activation lengths, and the energy barrier for slip instigation. Additionally, the interfacial interactions between the liquid molecules and layered-structure materials modulate the PES corrugation and, in turn, the friction behavior. The friction behavior of layered-structure materials fully immersed in ionic liquids, water, and non-polar liquids is examined next.
7.1 Ionic liquids
Layered-structure materials have been proven to be promising candidates in various leading technologies where these materials are in direct contact with ionic liquids, such as electrodes in the electrochemical energy storage (Augustyn and Gogotsi, 2017; Kato et al., 2018), electro/photocatalysis (Zhang X. et al., 2022), and batteries (Sahu and Zwolak, 2019). The arrangement of ionic liquids near the surface can modify the electrical and friction behavior. For example, AFM tribological studies of CVD-grown graphene immersed in 1-ethyl-3-methylimidazolium tris trifluorophosphate (EMIM FAP)—an ionic liquid—have shown prominent interfacial liquid layering (Figure 12A) compared to sucrose 60 wt% in aqueous solution (Figure 12B). Significantly larger slip lengths were observed with graphene immersed in EMIM FAP (Figure 12C) (Greenwood et al., 2021). The slip length depends on the energy barrier that the molecules must overcome to slide and can be associated with the energy landscape of the graphene/liquid interface. Therefore, a more ordered ionic liquid structure is characterized by a lower energy barrier (Figures 12D,E), suggesting that molecular layering of ionic liquids is related to the greater slip lengths at the interface (Greenwood et al., 2021). It has also been found that the layered structure of ionic fluid films in the vicinity of a graphene surface results in multiple adhesion force minima that are less than the adhesive forces between the solid surfaces. The tribological behavior of graphene can be tuned by changing the concentration of the ionic fluid film (Diao et al., 2019). Strongly hydrated cations retain more water in the confined fluid film, increasing the shear-activation length and, in turn, augmenting slip on the graphene surface. The presence of ionic species in water can also affect the thermal activation energy for instigating slip at the interface. The ordered cation/anion layering of ionic liquids on other smooth surfaces, such as silica, has been correlated to low friction (Lertola et al., 2018).
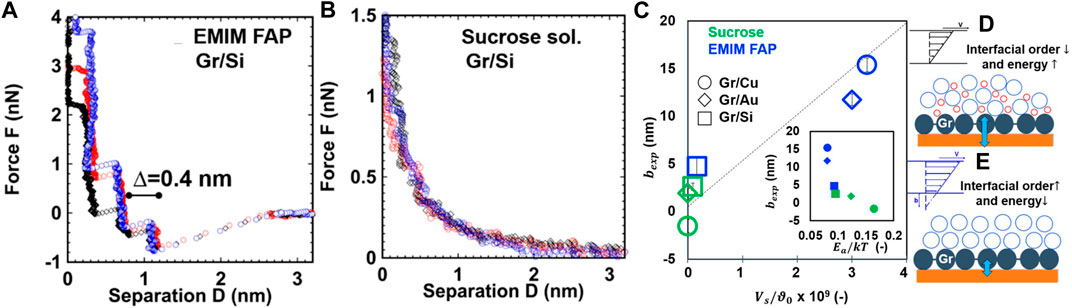
FIGURE 12. Friction behavior of layered-structure materials in ionic liquids (Greenwood et al., 2021). Solvation layers were detected in three different normal force-separation responses obtained with a sharp silicon AFM tip and graphene deposited on a silicon substrate that was fully immersed in (A) 1-ethyl-3-methylimidazolium tris trifluorophosphate (EMIM FAP) ionic liquid and (B) sucrose solution (Δ represents the thickness of the solvation layers). (C) Hydrodynamic force measurements of the slip length bexp versus slip velocity Vs (normalized by a liquid constant
7.2 Water
The small thickness and large surface area of layered-structure materials make them ideal for water purification (Carmalin Sophia et al., 2016; Dervin et al., 2016), applications in water-based lubricant additives (Xie et al., 2018), and photocatalysis (Singh et al., 2015). The friction of graphene is influenced by the flow of water molecules, which is affected by their arrangement in the vicinity of the surface (Neek-Amal et al., 2016). Ordering of water molecules has been observed adjacent to 2D layers (Lee et al., 2019; Go et al., 2021). MD simulations have provided insight into the contribution of ordered water layers (hydration layers) to the origin of stick-slip behavior of few-layer graphene (Vilhena et al., 2016). A similar friction force response was found for a diamond tip sliding on a graphene slab in vacuum or immersed in water (Figure 13A). The diamond tip coming in contact with the graphene immersed in water (Figure 13B) penetrates through the hydration layers and then slides over the indented graphene surface (Figure 13D). Two dominant peaks were realized in the normal force-distance response (Figure 13E), representing the breakthrough of the AFM tip from the hydration layers at the surface, before direct contact of the AFM tip with the graphene surface (Figure 13C). Interestingly, besides these two dominant peaks, the normal force-distance responses of graphene in water and vacuum are quite similar. However, another study of the load-dependent friction of single-layer graphene immersed in water showed an abrupt increase of the friction force for loads above ∼60 nN (Figure 13F), which was attributed to squeeze-out of the hydration layers on the graphene surface (Diao et al., 2019).
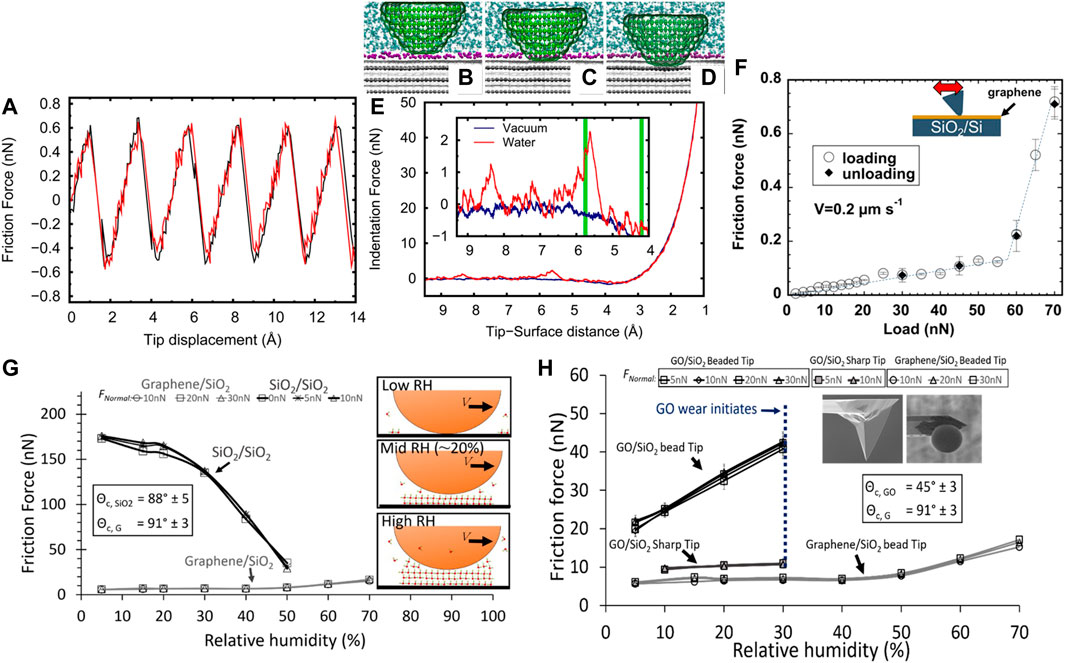
FIGURE 13. The dependence of friction on water molecule layering in the surface vicinity of layered-structure materials. (A) MD simulations of the variation of the friction force during sliding of a diamond tip on graphene in vacuum (black curve) and in water (red curve) revealing stick-slip behavior (Vilhena et al., 2016). MD simulated atomic configurations of the diamond tip (green atoms) interacting with a graphene layer (dark gray atoms) (the van der Waals surface of the graphene layers is shown in light gray) immersed in water (oxygen molecules in water are shown in cyan color) at three characteristic stages: (B) initial contact of the tip with the first hydration layer (purple color atoms), (C) penetration of the tip through the first hydration layer, and (D) sliding of the tip over the penetrated graphene layer (Vilhena et al., 2016). (E) Indentation force versus distance between the bottom tip atom and the top layer of graphene (the inset highlights two force peaks associated with breaking of the hydration layers) (Vilhena et al., 2016). (F) Friction force versus load for a silicon AFM tip sliding against a single-layer graphene on a SiO2/Si substrate immersed in water (Diao et al., 2019). (G) Friction force versus relative humidity for a SiO2 AFM tip sliding on graphene and SiO2 layers supported by a SiO2 substrate (the schematics of the sliding tip at different humidity levels illustrate a transition from solid/solid to solid/liquid contact) (Arif et al., 2018). (H) Friction force versus relative humidity for a graphene oxide (GO)-decorated SiO2 sharp tip and a graphene-decorated larger radius (bead) SiO2 tip sliding against a graphene layer (Arif et al., 2018).
Although molecular layering was found to reduce the friction of 2D layers, a similar trend was not observed with other conditions (Robinson et al., 2013; Arif et al., 2018). In a study of the friction behavior of few-layer graphene immersed in water or a non-polar solvent, the ordering of the non-polar molecules on the graphene surface resulted in a solid-like layer, which yielded a higher shear force compared to graphene in water, demonstrating that a liquid-like behavior aids the sliding process (Robinson et al., 2013). Another investigation focused on the effects of relative humidity (RH) and water intercalation on the nanotribological behavior of graphene, graphene oxide (GO), and bare silica (SiO2) (Arif et al., 2018). A significant decrease in the friction force was observed with SiO2 when the RH was increased above ∼20–30%, whereas the friction force for graphene showed a trend to increase slightly above ∼40–50% RH (Figure 13G). The water molecules bound to the SiO2 surface form an ice-like solid structure. At high RH, the adsorption of more water molecules leads to a more lubricous water-like layer on top of the existing ice-like layer, decreasing the friction force (Arif et al., 2018) (Figure 13G). Despite a similar state transition of the water molecules on the graphene surface, the friction force increased with the RH, and neither ice-like nor water-like structures were as lubricous as the pristine graphene layer (Arif et al., 2018). Furthermore, graphene is characterized by limited intercalation of water molecules between its basal plane and the SiO2 substrate when exposed to water due to its non-reactive edges. However, the higher water intercalation observed with GO and SiO2 leads to the formation of clusters that induce swelling of the GO layer. The reduced out-of-plane stiffness of GO makes it more susceptible to puckering and delamination. The higher surface roughness and PES corrugation of the GO also contribute to the development of a higher friction force. In addition, the size of the water meniscus at the sliding tip played a key role in the friction response. Specifically, a much higher friction force was measured with a large radius (bead) tip that promoted the formation of a larger capillary meniscus than a sharp tip (Figure 13H) (Arif et al., 2018).
The arrangement of liquid molecules at the interface also affects the PES landscape, consecutively altering the friction characteristics of layered-structure materials. Water density profiles in the vicinity of single-layer graphene and h-BN obtained from MD simulations show a higher density of water molecules adjacent to both layer surfaces (Figure 14A) (Tocci et al., 2014). The overlap between the two water density profiles indicates a similar water structure at the graphene and h-BN surfaces (Figures 14B, C); however, the friction coefficient of the h-BN layer is three times higher than that of graphene. This discrepancy is attributed to differences in the free energy (an approximation of the PES corrugation) profiles. In particular, higher corrugations were observed with the h-BN layer (Figure 14E) than the graphene layer (Figure 14D) in water (Tocci et al., 2014). In another investigation on the effect of water between graphene sheets or inside carbon nanotubes (CNTs) with a varying radius of curvature (Falk et al., 2010), the friction coefficient of graphene sheets demonstrated a dependence on the confinement of the water film. Water transportation through the CNTs assisted by curvature-induced commensurability achieved superlubricity for a CNT radius of ∼0.4 nm over the entire range of sliding velocity (Figure 14F). The extremely low friction of CNTs with the smallest radius of curvature was linked to smoothening of the PES corrugation, resulting from water-carbon interactions in the water-CNT incommensurate stacking (Figures 14G, H) (Falk et al., 2010).
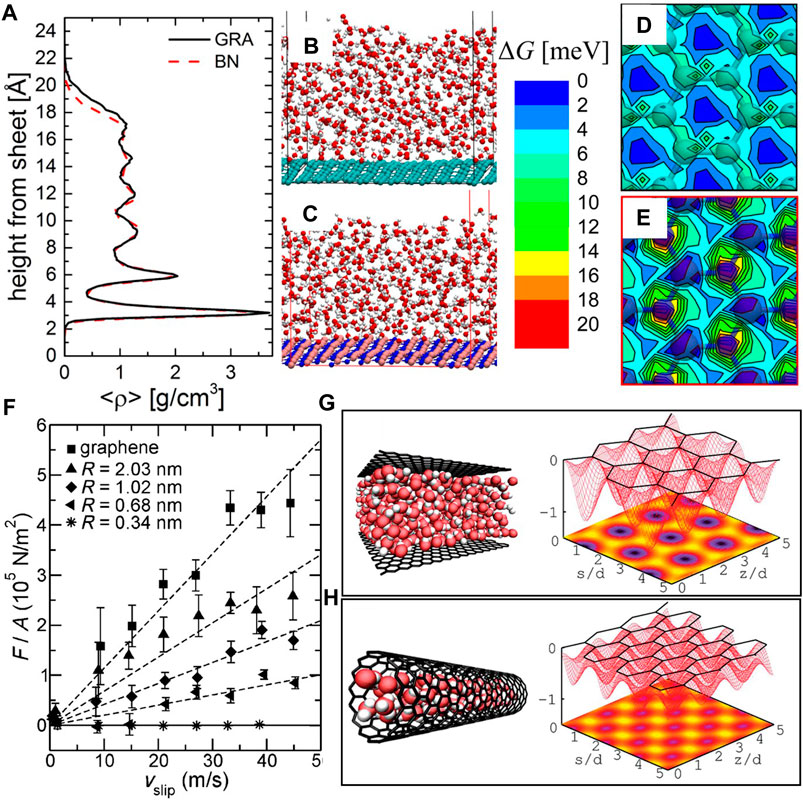
FIGURE 14. Friction of layered-structure materials immersed in water and modification of the PES in the presence of water. (A) Average density ⟨ρ⟩ profile of a water film on single layers of graphene and h-BN and molecular configuration of the water film on (B) graphene and (C) h-BN (O and H atoms are shown in red and white colors, respectively) (Tocci et al., 2014). Free energy ΔG distribution of water film at the contact surface of (D) graphene and (E) h-BN (Tocci et al., 2014). (F) Friction force F (normalized by the contact area A) versus slip velocity Vslip for a graphene slab and CNTs of different radius of curvature R sliding against a graphene slab fully immersed in water. MD results of the PES corrugation experienced by water molecules (G) adjacent to the graphene slab and (H) inside a CNT (Falk et al., 2010).
7.3 Non-polar liquids
An effective approach for minimizing the friction force in mechanical components and, hence, mitigating energy consumption, is using layered-structure materials as additives in oil-based lubricants (Liu L. et al., 2018; Guo et al., 2021). Force spectroscopy has been used to investigate the molecular layering of different base oils used in machine lubrication on graphite, mica, and polished steel surfaces. The formation of organized molecular layers (solvation layers) depends on the specific interactions between the oil molecules and the confining surfaces. For instance, although molecular layering of n-hexadecane (linear C16H32 structure) was observed on graphite, mica, and steel surfaces, the thickness of the hexadecane layer adjacent to the graphite surface was 15% less than that of the alkane layers on the mica and steel surfaces (Krass et al., 2018), indicating a packed structure of the alkane layer on the graphite surface. The stronger interaction of the hexadecane molecules with graphite compared to mica and steel enhanced layer ordering in the vicinity of the graphite surface. Molecular layering has also been discovered with oil molecules exhibiting more complex structures (exemplified by the number of atoms and molecular configuration), such as poly-(1-decane) tetramers and undecamers on graphite (Krass et al., 2018).
An AFM investigation of the nanotribological behavior of graphene deposited on a smooth steel surface and immersed in a non-polar liquid (n-hexadecane) showed that the structure of the molecular layers, controlled by the interaction of the surface with the liquid molecules, differed on graphene and steel surfaces, as evidenced by surface topography maps (Figures 15A, B) (Krämer et al., 2019). Higher force steps in the normal force versus tip-sample distance were obtained with graphene than steel (Figure 15C), indicating a higher ordering of the hexadecane molecules on the graphene surface. Consequently, squeezing out the hexadecane layers on the graphene layer required a higher normal force compared to the steel substrate. While irregular stick-slip occurred on the steel surface (Figure 15B, bottom), the graphene surface exhibited regularity in the stick-slip behavior with a peak-to-peak distance equal to ∼2.1 nm (Figure 15A, bottom), consistent with the molecular length of hexadecane. The greater layering of hexadecane on the graphene surface yielded a threefold decrease in friction force compared to steel (Krämer et al., 2019).
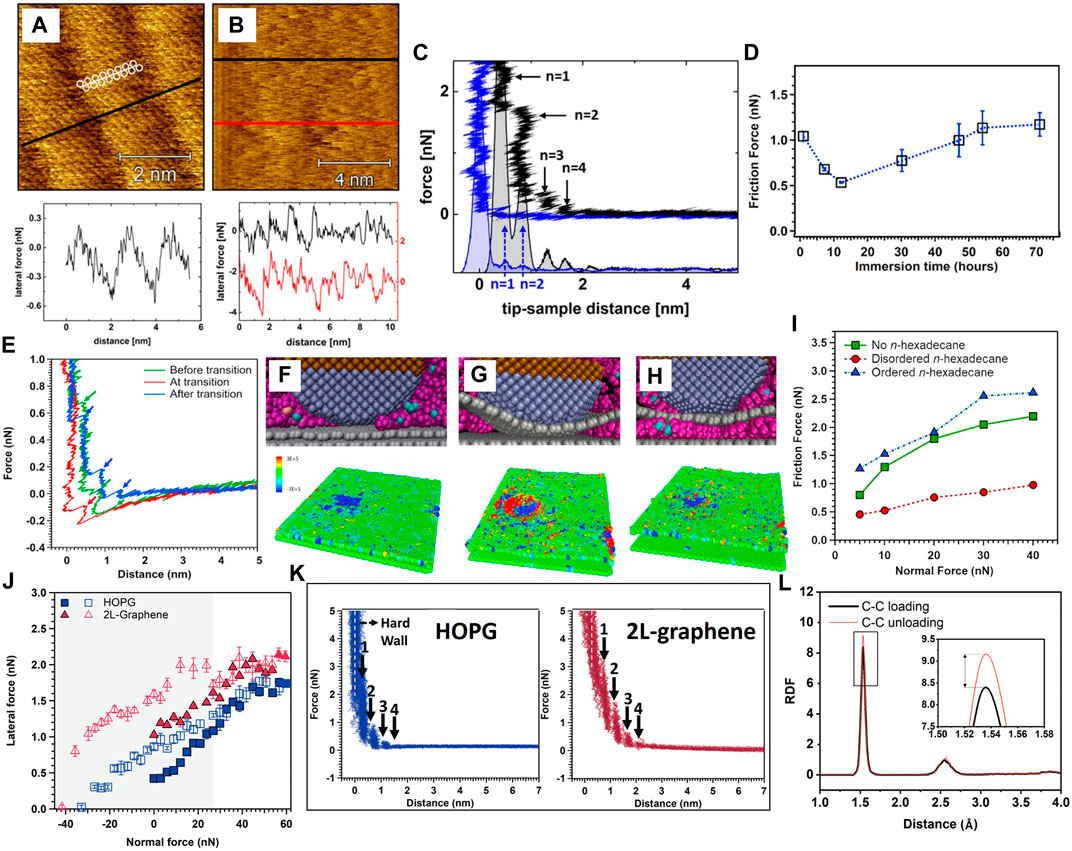
FIGURE 15. Friction of 2D graphene layers in a non-polar solvent (n-hexadecane). High-resolution lateral (friction) force maps revealing stick-slip behavior during sliding of a silicon AFM tip on (A) graphene (regular stick-slip behavior; the schematic represents a hexadecane molecule) and (B) steel (irregular stick-slip behavior) (Krämer et al., 2019). (C) Normal force versus separation distance between a silicon AFM tip and graphene (black) and stainless steel (blue) surfaces (Krämer et al., 2019). (D) Normal force versus separation distance between a silicon AFM tip and a graphene monolayer deposited on a silica substrate obtained before, at the instant of, and after the transition from descending to ascending friction force (Baboukani et al., 2021). (E–H) MD simulation results of (top) atomic configurations of a silicon tip in the proximity of graphene immersed in n-hexadecane obtained before (left), at the instant of (middle), and after (right) the transition from descending to ascending friction force (the tip silicon atoms, the hexadecane molecules, and the graphene atoms are shown in purple, pink, and gray color, respectively), and (bottom) atomic stress distributions on the graphene layer due to sliding of the silicon tip from left to right (red colored atoms indicate a compressive stress) (Baboukani et al., 2021). (I) Friction force versus normal force for a silicon tip sliding on a graphene monolayer in the absence and presence of ordered and disordered n-hexadecane obtained from MD simulations (Baboukani et al., 2021). (J) Load-dependent friction force hysteresis of HOPG and two-layer (2L) graphene immersed in n-hexadecane for loads less than ∼30 nN. (K) Overlay of ∼50 force-displacement curves for graphitic surfaces immersed in n-hexadecane. (L) The radial distribution function (RDF) of the C–C pairs in n-hexadecane during the loading and unloading phases (Baboukani et al., 2022).
Hexadecane molecular layering on silica-supported graphene monolayers has been reported to change upon equilibration (Baboukani et al., 2021). Specifically, gradual diffusion and intercalation of the hexadecane molecules between the graphene monolayer and the silica substrate was observed, and a transition from descending to ascending friction force occurred at a critical immersion time (Figure 15D). A larger number of force steps in the normal force-distance response were encountered before and after the aforementioned transition (Figure 15E) than during the transition period. It was presumed that the rearrangement of the hexadecane molecules at the graphene-silica confinement was responsible for the changes in the molecular layering of the hexadecane at the graphene surface. MD simulations revealed three possible configurations of the hexadecane molecules intercalated between the graphene monolayer and the silica substrate, i.e., no molecules (Figure 15F, top), disordered molecules (Figure 15G, top), and ordered molecules (Figure 15H, top) before, at the instant of, and after the transition of the friction force, respectively. MD results showed the lowest friction force for the disordered configuration of hexadecane confined between the graphene monolayer and the silica substrate (Figure 15I). Despite the larger contact area developed between the AFM tip and the graphene layer in the case of disordered hexadecane (Figure 15G, top) compared to no hexadecane (Figure 15F, top) and ordered hexadecane (Figure 15H, top), a significantly larger number of carbon atoms of the graphene monolayer were subjected to a compressive stress, as shown in the per-atom stress distribution at the bottom of Figures 15F–H, especially behind the AFM tip, aiding the shearing process for this configuration. Therefore, the nanotribological performance of 2D layers can be modulated by tuning the solvation structures of the liquid molecules in the surface vicinity. Moreover, AFM nanotribological measurements on the graphitic surfaces, including few-layer graphene and HOPG immersed in n-hexadecane, revealed the evolution of a friction force hysteresis for a load of ∼30 nN, with higher friction forces measured during unloading than loading (Figure 15J). Up to four organized layers of n-hexadecane formed on the graphitic surfaces (Figure 15K). MD simulations suggested that the measured friction force hysteresis was due to the no recovery of the n-hexadecane molecules at the contact interface during unloading. The radial distribution function (RDF) of the C–C pair in the hexadecane molecules in front of an AFM tip sliding on two-layer graphene (Figure 15L) show a larger RDF peak during unloading compared to loading, implying that the higher density of n-hexadecane molecules in the vicinity of the contact enhanced the friction force. The ordered layers of n-hexadecane were squeezed out of the contact interface upon the inception of sliding, leading to the development of a molecular pile-up in front of the AFM tip that induced friction strengthening. However, for loads higher than 30 nN, all ordered layers of n-hexadecane were squeezed out as soon as the AFM tip contacted the graphitic layers. Thus, similar friction forces were measured during loading and unloading at high loads (Baboukani et al., 2022).
8 Concluding remarks
The origin of atomic-scale friction was interpreted in the context of two fundamental models, the Prandtl-Tomlinson (PT) model and the Frenkel-Kontorova (FK) model, which illuminate the nature of stick-slip friction behavior at the nanoscale. The FK model has been used to study the unique friction characteristics of 2D layers, where the vanishingly small friction forces between the layers result in superlubricity. According to the PT and FK friction models, the potential energy surface (PES) corrugations of layered-structure materials sliding either against each other or an AFM tip controls the friction behavior. The main contributors to the PES corrugations are van der Waals forces, electrostatic interactions, and Pauli repulsion. The out-of-plane deformation (puckering) of layered-structure materials increases the contact area (quantity of contact) and the number of 2D layer atoms contributing to the friction force by pinning at the contact interface (quality of contact). The friction behavior of layered-structure materials can be controlled by tuning the electronic structure and/or chemical modification.
Some of the unusual nanotribological characteristics of layered-structure materials encountered under various conditions, such as the deviation of the friction behavior from the classical Amontons’ friction law, friction strengthening, and friction force hysteresis, were interpreted in light of experimental and simulation results. Due to the escalating number of applications of layered-structure materials used in liquid media, particular attention was given to the friction behavior in the presence of ionic, polar, and non-polar liquids. It was established that the arrangement of the liquid molecules in the vicinity of layered-structure materials strongly influences the friction force. It was also shown that the configuration and alignment of the liquid molecules at the surfaces of layered-structure materials are controlled by the interactions between the layers and the liquid molecules.
Despite significant advances in the fundamental understanding of the nanotribological properties of layered-structure materials derived from previous investigations, specifically the origins of atomic-scale friction in various dry and wet environments, further studies must be carried out to fully explore the applicability range of these novel materials. In particular, it is imperative that future investigations of the friction behavior of traditional layered-structure materials, such as those belonging to the graphene and TMD families, focus on the chemical nature of these 2D materials, e.g., functionalized graphene, the recently developed structures from the MXene families (Gao et al., 2017), and borophene (Meng et al., 2017), on the friction characteristics of these novel materials.
It is well-known that superlubricity is a unique tribological behavior of layered-structure materials, which can be achieved by stacking 2D layers of different kinds. Although various 2D heterostructures have been designed to achieve practically frictionless contacts, designing double/multilayered-structure complex heterostructures to tune friction to the application requirements is another challenging direction. Moreover, the insight into how liquid molecules alter PES corrugations of layered-structure materials during sliding suggests that cancellation of atomic forces may be attainable. For this reason, it is valuable to examine the possibility of accomplishing superlubricity by immersing layered-structure materials in different solvents and manipulating the PES corrugation. Another important research direction is to explore how the unique structure of the solvent molecules in the vicinity of layered-structure materials can be further utilized to modulate friction at the nanoscale. The discrepancies in previous investigations aimed to explain the effect of liquid molecular layering on the friction behavior of layered-structure materials suggest that further studies must be devoted to further elucidate the fundamental issues related to the surface chemistry of 2D layers and its effect on the alignment of solvent molecules in the vicinities of the confining surfaces, which directly influence the friction behavior and other transport properties.
The importance of understanding the frictional response of layered-structure materials in different environments is critical to modifying the surface characteristics of these materials to meet specific application requirements under different ambient conditions and various length scales. Consequently, more in-depth studies must be carried out to elucidate the friction mechanisms of emerging layered-structure materials to be used in various environments.
Author contributions
BSB collected most of the pertinent literature, created the figures, and wrote the first draft of the paper. PCN provided comments and remarks to the final manuscript. KK defined the scope of the entire work, supervised the work of BSB, examined the accumulated results, and edited the final manuscript. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alhama, F., Marín, F., and Moreno, J. A. (2011). An efficient and reliable model to simulate microscopic mechanical friction in the Frenkel–Kontorova–Tomlinson model. Comput. Phys. Commun. 182, 2314–2325. doi:10.1016/j.cpc.2011.06.006
Almeida, C. M., Prioli, R., Fragneaud, B., Cançado, L. G., Paupitz, R., Galvão, D. S., et al. (2016). Giant and tunable anisotropy of nanoscale friction in graphene. Sci. Rep. 6, 31569. doi:10.1038/srep31569
An, V., Irtegov, Y., and de Izarra, C. (2014). Study of tribological properties of nanolamellar WS2 and MoS2 as additives to lubricants. J. Nanomater. 2014, 865839. doi:10.1155/2014/865839
Arif, T., Colas, G., and Filleter, T. (2018). Effect of humidity and water intercalation on the tribological behavior of graphene and graphene oxide. ACS Appl. Mat. Interfaces 10, 22537–22544. doi:10.1021/acsami.8b03776
Augustyn, V., and Gogotsi, Y. (2017). 2D materials with nanoconfined fluids for electrochemical energy storage. Joule 1, 443–452. doi:10.1016/j.joule.2017.09.008
Baboukani, B. S., Pitkar, A., Ye, Z., and Nalam, P. C. (2022). Load-dependent friction hysteresis for graphitic surfaces in n-hexadecane. Adv. Mat. Interfaces 52, 2201249. doi:10.1002/admi.202201249
Baboukani, B. S., Watuthanthrige, N. D. A., Ye, Z., and Nalam, P. C. (2021). Effect of structural transitions of n-hexadecane in nanoscale confinement on atomic friction. Carbon 183, 428–437. doi:10.1016/j.carbon.2021.07.035
Bagherzadeh, M., and Farahbakhsh, A. (2015). “Surface functionalization of graphene,” in Graphene materials: Fundamentals and emerging applications. Editors A. Tiwari, and M. Syväjärvi (Beverly, MA: Scrivener Publishing), 25–65.
Bai, H., Bao, H., Li, Y., Xu, H., Li, S., and Ma, F. (2022). Moiré pattern based universal rules governing interfacial superlubricity: A case of graphene. Carbon 191, 28–35. doi:10.1016/j.carbon.2022.01.047
Balandin, A. A., Ghosh, S., Bao, W., Calizo, I., Teweldebrhan, D., Miao, F., et al. (2008). Superior thermal conductivity of single-layer graphene. Nano Lett. 8, 902–907. doi:10.1021/nl0731872
Berman, D., Erdemir, A., and Sumant, A. V. (2018). Approaches for achieving superlubricity in two-dimensional materials. ACS Nano 12, 2122–2137. doi:10.1021/acsnano.7b09046
Berman, D., Erdemir, A., and Sumant, A. V. (2014). Graphene: A new emerging lubricant. Mat. Today 17, 31–42. doi:10.1016/j.mattod.2013.12.003
Bertolazzi, S., Brivio, J., and Kis, A. (2011). Stretching and breaking of ultrathin MoS2. ACS Nano 5, 9703–9709. doi:10.1021/nn203879f
Bhushan, B. (2001). Modern tribology handbook. Vol. I. Principles of tribology. Boca Raton, FL: CRC Press.
Bowden, F. P., and Tabor, D. (2001). The friction and lubrication of solids. Canbridge, UK: Clarendon Press.
Byun, I.-S., Yoon, D., Choi, J. S., Hwang, I., Lee, D. H., Lee, M. J., et al. (2011). Nanoscale lithography on monolayer graphene using hydrogenation and oxidation. ACS Nano 5, 6417–6424. doi:10.1021/nn201601m
Carmalin Sophia, A., Lima, E. C., Allaudeen, N., and Rajan, S. (2016). Application of graphene based materials for adsorption of pharmaceutical traces from water and wastewater - A review. Desalination Water Treat. 57, 27573–27586. doi:10.1080/19443994.2016.1172989
Chen, J., and Gao, W. (2017). Unconventional behavior of friction at the nanoscale beyond Amontons’ law. ChemPhysChem 18, 2033–2039. doi:10.1002/cphc.201700378
Chen, L., Chen, Z., Tang, X., Yan, W., Zhou, Z., Qian, L., et al. (2019). Friction at single-layer graphene step edges due to chemical and topographic interactions. Carbon 154, 67–73. doi:10.1016/j.carbon.2019.07.081
Chen, Z., Khajeh, A., Martini, A., and Kim, S. H. (2019). Chemical and physical origins of friction on surfaces with atomic steps. Sci. Adv. 5, eaaw0513. doi:10.1126/sciadv.aaw0513
Cho, D.-H., Wang, L., Kim, J.-S., Lee, G.-H., Kim, E. S., Lee, S., et al. (2013). Effect of surface morphology on friction of graphene on various substrates. Nanoscale 5, 3063–3069. doi:10.1039/c3nr34181j
Clauss, F. J. (2012). Solid lubricants and self-lubricating solids. 1st edition. New York, NY: Academic Press.
Dedinaite, A., Thormann, E., Olanya, G., Claesson, P. M., Nyström, B., Kjøniksen, A.-L., et al. (2010). Friction in aqueous media tuned by temperature-responsive polymer layers. Soft Matter 6, 2489–2498. doi:10.1039/c003320k
Deng, Z., Klimov, N. N., Solares, S. D., Li, T., Xu, H., and Cannara, R. J. (2013). Nanoscale interfacial friction and adhesion on supported versus suspended monolayer and multilayer graphene. Langmuir 29, 235–243. doi:10.1021/la304079a
Deng, Z., Smolyanitsky, A., Li, Q., Feng, X.-Q., and Cannara, R. J. (2012). Adhesion-dependent negative friction coefficient on chemically modified graphite at the nanoscale. Nat. Mat. 11, 1032–1037. doi:10.1038/nmat3452
Derjaguin, B. (1934). Molekulartheorie der äußeren Reibung. Z. Phys. 88, 661–675. doi:10.1007/bf01333114
Derjaguin, B. V., Muller, V. M., and Toporov, Y. P. (1975). Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 53, 314–326. doi:10.1016/0021-9797(75)90018-1
Dervin, S., Dionysiou, D. D., and Pillai, S. C. (2016). 2D nanostructures for water purification: Graphene and beyond. Nanoscale 8, 15115–15131. doi:10.1039/c6nr04508a
Diao, Y., Greenwood, G., Wang, M. C., Nam, S., and Espinosa-Marzal, R. M. (2019). Slippery and sticky graphene in water. ACS Nano 13, 2072–2082. doi:10.1021/acsnano.8b08666
Dienwiebel, M., Verhoeven, G. S., Pradeep, N., Frenken, J. W. M., Heimberg, J. A., and Zandbergen, H. W. (2004). Superlubricity of graphite. Phys. Rev. Lett. 92, 126101. doi:10.1103/physrevlett.92.126101
Dong, Y., Tao, Y., Feng, R., Zhang, Y., Duan, Z., and Cao, H. (2020). Phonon dissipation in friction with commensurate–incommensurate transition between graphene membranes. Nanotechnology 31, 285711. doi:10.1088/1361-6528/ab86ec
Dong, Y., Vadakkepatt, A., and Martini, A. (2011). Analytical models for atomic friction. Tribol. Lett. 44, 367–386. doi:10.1007/s11249-011-9850-2
Dong, Y., Wu, X., and Martini, A. (2013). Atomic roughness enhanced friction on hydrogenated graphene. Nanotechnology 24, 375701. doi:10.1088/0957-4484/24/37/375701
Egberts, P., Han, G. H., Liu, X. Z., Johnson, A. T. C., and Carpick, R. W. (2014). Frictional behavior of atomically thin sheets: Hexagonal-shaped graphene islands grown on copper by chemical vapor deposition. ACS Nano 8, 5010–5021. doi:10.1021/nn501085g
English, L. Q., Sato, M., and Sievers, A. J. (2001). Nanoscale intrinsic localized modes in an antiferromagnetic lattice. J. Appl. Phys. 89, 6707–6709. doi:10.1063/1.1362639
Ermakov, V. A., Alaferdov, A. V., Vaz, A. R., Perim, E., Autreto, P. A. S., Paupitz, R., et al. (2015). Burning graphene layer-by-layer. Sci. Rep. 5, 11546. doi:10.1038/srep11546
Falk, K., Sedlmeier, F., Joly, L., Netz, R. R., and Bocquet, L. (2010). Molecular origin of fast water transport in carbon nanotube membranes: Superlubricity versus curvature dependent friction. Nano Lett. 10, 4067–4073. doi:10.1021/nl1021046
Fang, L., Liu, D.-M., Guo, Y., Liao, Z.-M., Luo, J.-B., and Wen, S.-Z. (2017). Thickness dependent friction on few-layer MoS2, WS2, and WSe2. Nanotechnology 28, 245703. doi:10.1088/1361-6528/aa712b
Farshchi-Tabrizia, M., Kappl, M., and Butt, H.-J. (2008). Influence of humidity on adhesion: An atomic force microscope study. J. Adhes. Sci. Technol. 22, 181–203. doi:10.1163/156856108x306948
Feiler, A. A., Stiernstedt, J., Theander, K., Jenkins, P., and Rutland, M. W. (2007). Effect of capillary condensation on friction force and adhesion. Langmuir 23, 517–522. doi:10.1021/la060456f
Fessler, G., Eren, B., Gysin, U., Glatzel, T., and Meyer, E. (2014). Friction force microscopy studies on SiO2 supported pristine and hydrogenated graphene. Appl. Phys. Lett. 104, 041910. doi:10.1063/1.4863832
Filleter, T., McChesney, J. L., Bostwick, A., Rotenberg, E., Emtsev, K. V., Seyller, Th., et al. (2009). Friction and dissipation in epitaxial graphene films. Phys. Rev. Lett. 102, 086102. doi:10.1103/physrevlett.102.086102
Gao, G., O’Mullane, A. P., and Du, A. (2017). 2D MXenes: A new family of promising catalysts for the hydrogen evolution reaction. ACS Catal. 7, 494–500. doi:10.1021/acscatal.6b02754
Gao, J., Luedtke, W. D., Gourdon, D., Ruths, M., Israelachvili, J. N., and Landman, U. (2004). Frictional forces and Amontons’ law: From the molecular to the macroscopic scale. J. Phys. Chem. B 108, 3410–3425. doi:10.1021/jp036362l
Go, T. W., Lee, D., Choi, W., and Park, J. Y. (2021). Atomic scale friction properties of confined water layers. J. Vac. Sci. Technol. A 39, 060803. doi:10.1116/6.0001384
Gong, P., Ye, Z., Yuan, L., and Egberts, P. (2018). Evaluation of wetting transparency and surface energy of pristine and aged graphene through nanoscale friction. Carbon 132, 749–759. doi:10.1016/j.carbon.2018.02.093
Greenwood, G., Kim, J. M., Zheng, Q., Nahid, S. M., Nam, S., and Espinosa-Marzal, R. M. (2021). Effects of layering and supporting substrate on liquid slip at the single-layer graphene interface. ACS Nano 15, 10095–10106. doi:10.1021/acsnano.1c01884
Greiner, C., Felts, J. R., Dai, Z., King, W. P., and Carpick, R. W. (2012). Controlling nanoscale friction through the competition between capillary adsorption and thermally activated sliding. ACS Nano 6, 4305–4313. doi:10.1021/nn300869w
Guo, Y., Zhou, X., Lee, K., Yoon, H. C., Xu, Q., and Wang, D. (2021). Recent development in friction of 2D materials: From mechanisms to applications. Nanotechnology 32, 312002. doi:10.1088/1361-6528/abfa52
Gupta, B., Kumar, N., Panda, K., Dash, S., and Tyagi, A. K. (2016). Energy efficient reduced graphene oxide additives: Mechanism of effective lubrication and antiwear properties. Sci. Rep. 6, 18372. doi:10.1038/srep18372
Hasz, K. R., Vazirisereshk, M. R., Martini, A., and Carpick, R. W. (2021). Bifurcation of nanoscale thermolubric friction behavior for sliding on MoS2. Phys. Rev. Mat. 5, 083607. doi:10.1103/physrevmaterials.5.083607
Hasz, K., Ye, Z., Martini, A., and Carpick, R. W. (2018). Experiments and simulations of the humidity dependence of friction between nanoasperities and graphite: The role of interfacial contact quality. Phys. Rev. Mat. 2, 126001. doi:10.1103/physrevmaterials.2.126001
Heiranian, M., Farimani, A. B., and Aluru, N. R. (2015). Water desalination with a single-layer MoS2 nanopore. Nat. Commun. 6, 8616. doi:10.1038/ncomms9616
Hod, O. (2012). Interlayer commensurability and superlubricity in rigid layered materials. Phys. Rev. B 86, 075444. doi:10.1103/physrevb.86.075444
Hod, O. (2010). Quantifying the stacking registry matching in layered materials. Isr. J. Chem. 50, 506–514. doi:10.1002/ijch.201000052
Holmberg, K., and Erdemir, A. (2017). Influence of tribology on global energy consumption, costs and emissions. Friction 5, 263–284. doi:10.1007/s40544-017-0183-5
Hölscher, H., Ebeling, D., and Schwarz, U. D. (2008). Friction at atomic-scale surface steps: Experiment and theory. Phys. Rev. Lett. 101, 246105. doi:10.1103/physrevlett.101.246105
Hu, Y., Ma, T., and Wang, H. (2013). Energy dissipation in atomic-scale friction. Friction 1, 24–40. doi:10.1007/s40544-013-0002-6
Huo, C., Yan, Z., Song, X., and Zeng, H. (2015). 2D materials via liquid exfoliation: A review on fabrication and applications. Sci. Bull. (Beijing) 60, 1994–2008. doi:10.1007/s11434-015-0936-3
Johnson, K. L., Kendall, K., and Roberts, A. D. (1971). Surface energy and the contact of elastic solids. Proc. Roy. Soc. Lond. A 324, 301–313.
Kabengele, T., and Johnson, E. R. (2021). Theoretical modeling of structural superlubricity in rotated bilayer graphene, hexagonal boron nitride, molybdenum disulfide, and blue phosphorene. Nanoscale 13, 14399–14407. doi:10.1039/d1nr03001a
Kato, K., Sayed, F. N., Babu, G., and Ajayan, P. M. (2018). All 2D materials as electrodes for high power hybrid energy storage applications. 2D Mat. 5, 025016. doi:10.1088/2053-1583/aaad29
Khare, H. S., and Burris, D. L. (2013). The effects of environmental water and oxygen on the temperature-dependent friction of sputtered molybdenum disulfide. Tribol. Lett. 52, 485–493. doi:10.1007/s11249-013-0233-8
Kim, K.-S., Lee, H.-J., Lee, C., Lee, S.-K., Jang, H., Ahn, J.-H., et al. (2011). Chemical vapor deposition-grown graphene: The thinnest solid lubricant. ACS Nano 5, 5107–5114. doi:10.1021/nn2011865
Ko, J.-H., Kwon, S., Byun, I.-S., Choi, J. S., Park, B. H., Kim, Y.-H., et al. (2013). Nanotribological properties of fluorinated, hydrogenated, and oxidized graphenes. Tribol. Lett. 50, 137–144. doi:10.1007/s11249-012-0099-1
Kozak, A., Hofbauerová, M., Halahovets, Y., Pribusová-Slušná, L., Precner, M., MiČuŠík, M., et al. (2022). Nanofriction properties of mono- and double-layer Ti3C2Tx MXenes. ACS Appl. Mat. Interfaces 14, 36815–36824. doi:10.1021/acsami.2c08963
Krämer, G., Kim, C., Kim, K.-S., and Bennewitz, R. (2019). Single layer graphene induces load-bearing molecular layering at the hexadecane-steel interface. Nanotechnology 30, 46LT01. doi:10.1088/1361-6528/ab3cab
Krass, M.-D., Krämer, G., Dellwo, U., and Bennewitz, R. (2018). Molecular layering in nanometer-confined lubricants. Tribol. Lett. 66, 87. doi:10.1007/s11249-018-1041-y
Kwon, S., Ko, J.-H., Jeon, K.-J., Kim, Y.-H., and Park, J. Y. (2012). Enhanced nanoscale friction on fluorinated graphene. Nano Lett. 12, 6043–6048. doi:10.1021/nl204019k
Lebedev, A. V., Lebedeva, I. V., Knizhnik, A. A., and Popov, A. M. (2016). Interlayer interaction and related properties of bilayer hexagonal boron nitride: Ab initio study. RSC Adv. 6, 6423–6435. doi:10.1039/c5ra20882c
Lee, C., Li, Q., Kalb, W., Liu, X.-Z., Berger, H., Carpick, R. W., et al. (2010). Frictional characteristics of atomically thin sheets. Science 328, 76–80. doi:10.1126/science.1184167
Lee, C., Wei, X., Kysar, J. W., and Hone, J. (2008). Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 321, 385–388. doi:10.1126/science.1157996
Lee, H., Jeong, H., Suh, J., Doh, W. H., Baik, J., Shin, H.-J., et al. (2019). Nanoscale friction on confined water layers intercalated between MoS2 flakes and silica. J. Phys. Chem. C 123, 8827–8835. doi:10.1021/acs.jpcc.8b11426
Lee, H., Lee, H.-B.-R., Kwon, S., Salmeron, M., and Park, J. Y. (2015). Internal and external atomic steps in graphite exhibit dramatically different physical and chemical properties. ACS Nano 9, 3814–3819. doi:10.1021/nn506755p
Lee, W.-K., Haydell, M., Robinson, J. T., Laracuente, A. R., Cimpoiasu, E., King, W. P., et al. (2013). Nanoscale reduction of graphene fluoride via thermochemical nanolithography. ACS Nano 7, 6219–6224. doi:10.1021/nn4021746
Lemme, M. C., Akinwande, D., Huyghebaert, C., and Stampfer, C. (2022). 2D materials for future heterogeneous electronics. Nat. Commun. 13, 1392. doi:10.1038/s41467-022-29001-4
Lemme, M. C., Wagner, S., Lee, K., Fan, X., Verbiest, G. J., Wittmann, S., et al. (2020). Nanoelectromechanical sensors based on suspended 2D materials. Research 2020, 8748602. doi:10.34133/2020/8748602
Lertola, A. C., Wang, B., and Li, L. (2018). Understanding the friction of nanometer-thick fluorinated ionic liquids. Ind. Eng. Chem. Res. 57, 11681–11685. doi:10.1021/acs.iecr.8b03044
Leven, I., Krepel, D., Shemesh, O., and Hod, O. (2013). Robust superlubricity in graphene/h-BN heterojunctions. J. Phys. Chem. Lett. 4, 115–120. doi:10.1021/jz301758c
Levita, G., Cavaleiro, A., Molinari, E., Polcar, T., and Righi, M. C. (2014). Sliding properties of MoS2 layers: Load and interlayer orientation effects. J. Phys. Chem. C 118, 13809–13816. doi:10.1021/jp4098099
Levita, G., Molinari, E., Polcar, T., and Righi, M. C. (2015). First-principles comparative study on the interlayer adhesion and shear strength of transition-metal dichalcogenides and graphene. Phys. Rev. B 92, 085434. doi:10.1103/physrevb.92.085434
Li, H., Shi, W., Guo, Y., and Guo, W. (2020). Nonmonotonic interfacial friction with normal force in two-dimensional crystals. Phys. Rev. B 102, 085427. doi:10.1103/physrevb.102.085427
Li, H., Wang, J., Gao, S., Chen, Q., Peng, L., Liu, K., et al. (2017). Superlubricity between MoS2 monolayers. Adv. Mat. 29, 1701474. doi:10.1002/adma.201701474
Li, Q., Lee, C., Carpick, R. W., and Hone, J. (2010). Substrate effect on thickness-dependent friction on graphene. Phys. Stat. Sol. 247, 2909–2914. doi:10.1002/pssb.201000555
Li, Q., Liu, X.-Z., Kim, S.-P., Shenoy, V. B., Sheehan, P. E., Robinson, J. T., et al. (2014). Fluorination of graphene enhances friction due to increased corrugation. Nano Lett. 14, 5212–5217. doi:10.1021/nl502147t
Li, S., Li, Q., Carpick, R. W., Gumbsch, P., Liu, X. Z., Ding, X., et al. (2016). The evolving quality of frictional contact with graphene. Nature 539, 541–545. doi:10.1038/nature20135
Liu, K., Yan, Q., Chen, M., Fan, W., Sun, Y., Suh, J., et al. (2014). Elastic properties of chemical-vapor-deposited monolayer MoS2, WS2, and their bilayer heterostructures. Nano Lett. 14, 5097–5103. doi:10.1021/nl501793a
Liu, L., Zhou, M., Jin, L., Li, L., Mo, Y., Su, G., et al. (2019). Recent advances in friction and lubrication of graphene and other 2D materials: Mechanisms and applications. Friction 7, 199–216. doi:10.1007/s40544-019-0268-4
Liu, L., Zhou, M., Li, X., Jin, L., Su, G., Mo, Y., et al. (2018). Research progress in application of 2D materials in liquid-phase lubrication system. Materials 11, 1314. doi:10.3390/ma11081314
Liu, Y., Jiang, Y., Sun, J., Wang, Y., Qian, L., Kim, S. H., et al. (2022). Inverse relationship between thickness and wear of fluorinated graphene: “Thinner is better”. Nano Lett. 22, 6018–6025. doi:10.1021/acs.nanolett.2c01043
Liu, Y., Song, A., Xu, Z., Zong, R., Zhang, J., Yang, W., et al. (2018). Interlayer friction and superlubricity in single-crystalline contact enabled by two-dimensional flake-wrapped atomic force microscope tips. ACS Nano 12, 7638–7646. doi:10.1021/acsnano.7b09083
Mandelli, D., Leven, I., Hod, O., and Urbakh, M. (2017). Sliding friction of graphene/hexagonal–boron nitride heterojunctions: A route to robust superlubricity. Sci. Rep. 7, 10851. doi:10.1038/s41598-017-10522-8
Mandelli, D., Ouyang, W., Hod, O., and Urbakh, M. (2019). Negative friction coefficients in superlubric graphite–hexagonal boron nitride heterojunctions. Phys. Rev. Lett. 122, 076102. doi:10.1103/physrevlett.122.076102
Mao, H. Y., Lu, Y. H., Lin, J. D., Zhong, S., Wee, A. T. S., and Chen, W. (2013). Manipulating the electronic and chemical properties of graphene via molecular functionalization. Prog. Surf. Sci. 88, 132–159. doi:10.1016/j.progsurf.2013.02.001
Meiyazhagan, A., Serles, P., Salpekar, D., Oliveira, E. F., Alemany, L. B., Fu, R., et al. (2021). Gas-phase fluorination of hexagonal boron nitride. Adv. Mat. 33, 2106084. doi:10.1002/adma.202106084
Meng, F., Chen, X., Sun, S., and He, J. (2017). Electronic and magnetic properties of pristine and hydrogenated borophene nanoribbons. Physica E. 91, 106–112. doi:10.1016/j.physe.2017.04.014
Neek-Amal, M., Peeters, F. M., Grigorieva, I. V., and Geim, A. K. (2016). Commensurability effects in viscosity of nanoconfined water. ACS Nano 10, 3685–3692. doi:10.1021/acsnano.6b00187
Ouyang, W., de Wijn, A. S., and Urbakh, M. (2018). Atomic-scale sliding friction on a contaminated surface. Nanoscale 10, 6375–6381. doi:10.1039/c7nr09530a
Ouyang, W., Hod, O., and Urbakh, M. (2021). Registry-dependent peeling of layered material interfaces: The case of graphene nanoribbons on hexagonal boron nitride. ACS Appl. Mat. Interfaces 13, 43533–43539. doi:10.1021/acsami.1c09529
Pandemic drives down U.S. energy use in 2020 (2021). Available at: https://www.llnl.gov/news/pandemic-drives-down-us-energy-use-2020 (Accessed November 29, 2021).
Park, J. Y., Ogletree, D. F., Thiel, P. A., and Salmeron, M. (2006). Electronic control of friction in silicon pn junctions. Science 313, 186. doi:10.1126/science.1125017
Parvez, K., Yang, S., Feng, X., and Müllen, K. (2015). Exfoliation of graphene via wet chemical routes. Synth. Met. 210, 123–132. doi:10.1016/j.synthmet.2015.07.014
Pendyala, P., Lee, J., Kim, S. J., and Yoon, E.-S. (2022). Layer-dependent frictional properties of Ti3C2Tx MXene nanosheets. Appl. Surf. Sci. 603, 154402. doi:10.1016/j.apsusc.2022.154402
Peng, Y., Zeng, X., Yu, K., and Lang, H. (2020). Deformation induced atomic-scale frictional characteristics of atomically thin two-dimensional materials. Carbon 163, 186–196. doi:10.1016/j.carbon.2020.03.024
Popov, V. L., and Gray, J. A. T. (2012). Prandtl-Tomlinson model: History and applications in friction, plasticity, and nanotechnologies. J. Appl. Math. Mech. (Z. Angew. Math. Mech. (ZAMM)) 92, 683–708. doi:10.1002/zamm.201200097
Prasad, M. V. D., and Bhattacharya, B. (2017). Phononic origins of friction in carbon nanotube oscillators. Nano Lett. 17, 2131–2137. doi:10.1021/acs.nanolett.6b04310
Pritchard, C., and Midgley, J. W. (1969). The effect of humidity on the friction and life of unbonded molybdenum disulphide films. Wear 13, 39–50. doi:10.1016/0043-1648(69)90430-x
Qi, Y., Park, J. Y., Hendriksen, B. L. M., Ogletree, D. F., and Salmeron, M. (2008). Electronic contribution to friction on GaAs: An atomic force microscope study. Phys. Rev. B 77, 184105. doi:10.1103/physrevb.77.184105
Rapoport, L., Bilik, Y., Feldman, Y., Homyonfer, M., Cohen, S. R., and Tenne, R. (1997). Hollow nanoparticles of WS2 as potential solid-state lubricants. Nature 387, 791–793. doi:10.1038/42910
Reguzzoni, M., Fasolino, A., Molinari, E., and Righi, M. C. (2012). Potential energy surface for graphene on graphene: Ab initio derivation, analytical description, and microscopic interpretation. Phys. Rev. B 86, 245434. doi:10.1103/physrevb.86.245434
Rietsch, J.-C., Brender, P., Dentzer, J., Gadiou, R., Vidal, L., and Vix-Guterl, C. (2013). Evidence of water chemisorption during graphite friction under moist conditions. Carbon 55, 90–97. doi:10.1016/j.carbon.2012.12.013
Robinson, B. J., Kay, N. D., and Kolosov, O. V. (2013). Nanoscale interfacial interactions of graphene with polar and nonpolar liquids. Langmuir 29, 7735–7742. doi:10.1021/la400955c
Ru, G., Qi, W., Tang, K., Wei, Y., and Xue, T. (2020). Interlayer friction and superlubricity in bilayer graphene and MoS2/MoSe2 van der Waals heterostructures. Tribol. Int. 151, 106483. doi:10.1016/j.triboint.2020.106483
Ru, G., Qi, W., Wei, Y., Tang, K., and Xue, T. (2021). Superlubricity in bilayer isomeric tellurene and graphene/tellurene van der Waals heterostructures. Tribol. Int. 159, 106974. doi:10.1016/j.triboint.2021.106974
Sahu, S., and Zwolak, M. (2019). Colloquium: Ionic phenomena in nanoscale pores through 2D materials. Rev. Mod. Phys. 91, 021004. doi:10.1103/revmodphys.91.021004
Sattari Baboukani, B., Ye, Z., Reyes, K. G., and Nalam, P. C. (2020). Prediction of nanoscale friction for two-dimensional materials using a machine learning approach. Tribol. Lett. 68, 57. doi:10.1007/s11249-020-01294-w
Schwarz, U. D., and Hölscher, H. (2016). Exploring and explaining friction with the Prandtl–Tomlinson model. ACS Nano 10, 38–41. doi:10.1021/acsnano.5b08251
Secchi, E., Marbach, S., Niguès, A., Stein, D., Siria, A., and Bocquet, L. (2016). Massive radius-dependent flow slippage in carbon nanotubes. Nature 537, 210–213. doi:10.1038/nature19315
Serles, P., Hamidinejad, M., Demingos, P. G., Ma, L., Barri, N., Taylor, H., et al. (2022). Friction of Ti3C2Tx MXenes. Nano Lett. 22, 3356–3363. doi:10.1021/acs.nanolett.2c00614
Serpini, E., Rota, A., Valeri, S., Ukraintsev, E., Rezek, B., Polcar, T., et al. (2019). Nanoscale frictional properties of ordered and disordered MoS2. Tribol. Int. 136, 67–74. doi:10.1016/j.triboint.2019.03.004
Shi, P., Lu, Y., Sun, J., Tang, C., Wang, Y., Jiang, L., et al. (2022). Towards a deeper understanding of superlubricity on graphite governed by interfacial adhesion. Carbon 199, 479–485. doi:10.1016/j.carbon.2022.08.035
Singh, A. K., Mathew, K., Zhuang, H. L., and Hennig, R. G. (2015). Computational screening of 2D materials for photocatalysis. J. Phys. Chem. Lett. 6, 1087–1098. doi:10.1021/jz502646d
Smolyanitsky, A., and Killgore, J. P. (2012). Anomalous friction in suspended graphene. Phys. Rev. B 86, 125432. doi:10.1103/physrevb.86.125432
Smolyanitsky, A., Killgore, J. P., and Tewary, V. K. (2012). Effect of elastic deformation on frictional properties of few-layer graphene. Phys. Rev. B 85, 035412. doi:10.1103/physrevb.85.035412
Song, H.-J., and Li, N. (2011). Frictional behavior of oxide graphene nanosheets as water-base lubricant additive. Appl. Phys. A 105, 827–832. doi:10.1007/s00339-011-6636-1
Spear, J. C., Ewers, B. W., and Batteas, J. D. (2015). 2D-nanomaterials for controlling friction and wear at interfaces. Nano Today 10, 301–314. doi:10.1016/j.nantod.2015.04.003
Szlufarska, I., Chandross, M., and Carpick, R. W. (2008). Recent advances in single-asperity nanotribology. J. Phys. D: Appl. Phys. 41, 123001. doi:10.1088/0022-3727/41/12/123001
Tao, H., Zhang, Y., Gao, Y., Sun, Z., Yan, C., and Texter, J. (2017). Scalable exfoliation and dispersion of two-dimensional materials – An update. Phys. Chem. Chem. Phys. 19, 921–960. doi:10.1039/c6cp06813h
Tocci, G., Joly, L., and Michaelides, A. (2014). Friction of water on graphene and hexagonal boron nitride from ab initio methods: Very different slippage despite very similar interface structures. Nano Lett. 14, 6872–6877. doi:10.1021/nl502837d
Torres, E. S., Gonçalves, S., Scherer, C., and Kiwi, M. (2006). Nanoscale sliding friction versus commensuration ratio: Molecular dynamics simulations. Phys. Rev. B 73, 035434. doi:10.1103/physrevb.73.035434
Vanossi, A., Manini, N., Urbakh, M., Zapperi, S., and Tosatti, E. (2013). Colloquium: Modeling friction: From nanoscale to mesoscale. Rev. Mod. Phys. 85, 529–552. doi:10.1103/revmodphys.85.529
Vazirisereshk, M. R., Hasz, K., Carpick, R. W., and Martini, A. (2020a). Friction anisotropy of MoS2: Effect of tip–sample contact quality. J. Phys. Chem. Lett. 11, 6900–6906. doi:10.1021/acs.jpclett.0c01617
Vazirisereshk, M. R., Hasz, K., Zhao, M.-Q., Johnson, A. T. C., Carpick, R. W., and Martini, A. (2020b). Nanoscale friction behavior of transition-metal dichalcogenides: Role of the chalcogenide. ACS Nano 14, 16013–16021. doi:10.1021/acsnano.0c07558
Vazirisereshk, M. R., Ye, H., Ye, Z., Otero-de-la-Roza, A., Zhao, M.-Q., Gao, Z., et al. (2019). Origin of nanoscale friction contrast between supported graphene, MoS2, and a graphene/MoS2 heterostructure. Nano Lett. 19, 5496–5505. doi:10.1021/acs.nanolett.9b02035
Vilhena, J. G., Pimentel, C., Pedraz, P., Luo, F., Serena, P. A., Pina, C. M., et al. (2016). Atomic-scale sliding friction on graphene in water. ACS Nano 10, 4288–4293. doi:10.1021/acsnano.5b07825
Wang, D., Chen, G., Li, C., Cheng, M., Yang, W., Wu, S., et al. (2016). Thermally induced graphene rotation on hexagonal boron nitride. Phys. Rev. Lett. 116, 126101. doi:10.1103/physrevlett.116.126101
Wang, H., Hu, Y.-Z., and Zhang, T. (2007). Simulations on atomic-scale friction between self-assembled monolayers: Phononic energy dissipation. Tribol. Int. 40, 680–686. doi:10.1016/j.triboint.2005.11.003
Wang, L.-F., Ma, T.-B., Hu, Y.-Z., Zheng, Q., Wang, H., and Luo, J. (2014). Superlubricity of two-dimensional fluorographene/MoS2 heterostructure: A first-principles study. Nanotechnology 25, 385701. doi:10.1088/0957-4484/25/38/385701
Wang, L., Zhou, X., Ma, T., Liu, D., Gao, L., Li, X., et al. (2017). Superlubricity of a graphene/MoS2 heterostructure: A combined experimental and DFT study. Nanoscale 9, 10846–10853. doi:10.1039/c7nr01451a
Wang, Z.-J., Ma, T.-B., Hu, Y.-Z., Xu, L., and Wang, H. (2015). Energy dissipation of atomic-scale friction based on one-dimensional Prandtl-Tomlinson model. Friction 3, 170–182. doi:10.1007/s40544-015-0086-2
Weber, B., Suhina, T., Junge, T., Pastewka, L., Brouwer, A. M., and Bonn, D. (2018). Molecular probes reveal deviations from Amontons’ law in multi-asperity frictional contacts. Nat. Commun. 9, 888. doi:10.1038/s41467-018-02981-y
Weiss, M., and Elmer, F.-J. (1996). Dry friction in the Frenkel-Kontorova-Tomlinson model: Static properties. Phys. Rev. B 53, 7539–7549. doi:10.1103/physrevb.53.7539
Wolloch, M., Levita, G., Restuccia, P., and Righi, M. C. (2018). Interfacial charge density and its connection to adhesion and frictional forces. Phys. Rev. Lett. 121, 026804. doi:10.1103/physrevlett.121.026804
Woydt, M. (2021). The importance of tribology for reducing CO2 emissions and for sustainability. Wear 474–475, 203768. doi:10.1016/j.wear.2021.203768
Xiao, H., and Liu, S. (2017). 2D nanomaterials as lubricant additive: A review. Mat. Des. 135, 319–332. doi:10.1016/j.matdes.2017.09.029
Xie, H., Jiang, B., Dai, J., Peng, C., Li, C., Li, Q., et al. (2018). Tribological behaviors of graphene and graphene oxide as water-based lubricant additives for magnesium alloy/steel contacts. Materials 11, 206. doi:10.3390/ma11020206
Xu, L., Ma, T.-B., Hu, Y.-Z., and Wang, H. (2011). Vanishing stick–slip friction in few-layer graphenes: The thickness effect. Nanotechnology 22, 285708. doi:10.1088/0957-4484/22/28/285708
Xu, Y., Zhu, X., Cheng, Z., Lu, Z., He, W., and Zhang, G. (2022). A novel ultra-low friction heterostructure: Aluminum substrate-honeycomb borophene/graphene heterojunction. Comput. Mat. Sci. 205, 111236. doi:10.1016/j.commatsci.2022.111236
Ye, Z., Egberts, P., Han, G. H., Johnson, A. T. C., Carpick, R. W., and Martini, A. (2016). Load-dependent friction hysteresis on graphene. ACS Nano 10, 5161–5168. doi:10.1021/acsnano.6b00639
Ye, Z., Otero-de-la-Roza, A., Johnson, E. R., and Martini, A. (2015). Oscillatory motion in layered materials: Graphene, boron nitride, and molybdenum disulfide. Nanotechnology 26, 165701. doi:10.1088/0957-4484/26/16/165701
Zekonyte, J., and Polcar, T. (2015). Friction force microscopy analysis of self-adaptive W–S–C coatings: Nanoscale friction and wear. ACS Appl. Mat. Interfaces 7, 21056–21064. doi:10.1021/acsami.5b05546
Zeng, X., Peng, Y., and Lang, H. (2017). A novel approach to decrease friction of graphene. Carbon 118, 233–240. doi:10.1016/j.carbon.2017.03.042
Zeng, X., Peng, Y., Liu, L., Lang, H., and Cao, X. (2018a). Dependence of the friction strengthening of graphene on velocity. Nanoscale 10, 1855–1864. doi:10.1039/c7nr07517k
Zeng, X., Peng, Y., Yu, M., Lang, H., Cao, X., and Zou, K. (2018b). Dynamic sliding enhancement on the friction and adhesion of graphene, graphene oxide, and fluorinated graphene. ACS Appl. Mat. Interfaces 10, 8214–8224. doi:10.1021/acsami.7b19518
Zhan, D., Yan, J., Lai, L., Ni, Z., Liu, L., and Shen, Z. (2012). Engineering the electronic structure of graphene. Adv. Mat. 24, 4055–4069. doi:10.1002/adma.201200011
Zhang, S., Yao, Q., Chen, L., Jiang, C., Ma, T., Wang, H., et al. (2022). Dual-scale stick-slip friction on graphene/h-BN Moire’ superlattice structure. Phys. Rev. Lett. 128, 226101. doi:10.1103/physrevlett.128.226101
Zhang, X., Chen, A., Chen, L., and Zhou, Z. (2022). 2D materials bridging experiments and computations for electro/photocatalysis. Adv. Energy Mat. 12, 2003841. doi:10.1002/aenm.202003841
Zhao, S., Zhang, Z., Wu, Z., Liu, K., Zheng, Q., and Ma, M. (2019). The impacts of adhesion on the wear property of graphene. Adv. Mat. Interfaces 6, 1900721. doi:10.1002/admi.201900721
Zheng, X., Gao, L., Yao, Q., Li, Q., Zhang, M., Xie, X., et al. (2016). Robust ultra-low-friction state of graphene via moiré superlattice confinement. Nat. Commun. 7, 13204. doi:10.1038/ncomms13204
Zhu, J., Liu, X., Shi, Q., He, T., Sun, Z., Guo, X., et al. (2020). Development trends and perspectives of future sensors and MEMS/NEMS. Micromachines 11, 7. doi:10.3390/mi11010007
Keywords: friction, graphene, layered-structure materials, lubricant additives, MXenes, potential energy surface, van der Waals interactions
Citation: Sattari Baboukani B, Nalam PC and Komvopoulos K (2022) Nanoscale friction characteristics of layered-structure materials in dry and wet environments. Front. Mech. Eng 8:965877. doi: 10.3389/fmech.2022.965877
Received: 10 June 2022; Accepted: 18 October 2022;
Published: 05 December 2022.
Edited by:
Philipp G. Grützmacher, Vienna University of Technology, AustriaReviewed by:
Mehmet Z. Baykara, University of California, Merced, United StatesLinmao Qian, Southwest Jiaotong University, China
Copyright © 2022 Sattari Baboukani, Nalam and Komvopoulos. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Prathima C. Nalam, cHJhdGhpbWFAYnVmZmFsby5lZHU=; Kyriakos Komvopoulos, a3lyaWFrb3NAbWUuYmVya2VsZXkuZWR1
 Behnoosh Sattari Baboukani
Behnoosh Sattari Baboukani Prathima C. Nalam2*
Prathima C. Nalam2* Kyriakos Komvopoulos
Kyriakos Komvopoulos