Insight in thermomechanical constitutive modeling of shape memory polymers

Shape memory polymers (SMPs) are a new member of the smart materials family. SMPs have found wide applications or potential applications in almost all manmade structures and devices. In order to better design smart structures and devices using SMPs, thermomechanical constitutive modeling is essential. In this insight paper, we will focus on presenting several multi-length-scale and multi-physics modeling frameworks, including the thermodynamics consistent model, elasto-viscoplastic model, statistical mechanics model, and phase evaluation law model. The SMPs modeled will include amorphous one-way shape memory polymers, semicrystalline one-way shape memory polymers, semicrystalline two-way shape memory polymers, and functional and mechanical damage effects on SMPs. Finally, we will give some in-depth perspectives on future development in this area of study.

Introduction

Shape memory polymers (SMPs) can store a prescribed shape for a long time and recover them by specific external trigger, for example, heat. SMPs have the potential to be deployed in various engineering structures and devices, including, but are not limited to, automotive (Lendlein and Kelch, 2002; Hu et al., 2012; Meng and Li, 2013; Zhao et al., 2015), aerospace (Leng et al., 2008; Liu et al., 2014), marine time (Ma et al., 2021), oil and gas (Taleghani et al., 2017; Santos et al., 2018; Mansour et al., 2019; Santos et al., 2021; Tabatabaei et al., 2021), geothermal (Elhag et al., 2021; Magzoub et al., 2021; Mohamed et al., 2022), civil engineering (Li and Xu, 2011a; Li et al., 2013b; Li et al., 2015; Ouyang and Li, 2009), and biomedical industries (Lendlein and Langer, 2002; Small et al., 2010). The same as any engineering materials, constitutive laws are essential to design and manufacture SMPs into engineering structures and devices because constitutive laws are a key component in forming the governing differential equations. For SMPs, the constitutive laws, or stress–strain relationships, are more complex than classical engineering materials because they depend on external loading and loading rate, time and temperature, damage status, and programming history. Particularly, programming is a special step to make SMPs exhibit the shape memory effect (SME). Using thermally triggered SMPs as an example, a typical hot programming may consist of the following steps: 1) heating the SMP to above its transition temperature (the glass-transition temperature for amorphous SMPs or the melting temperature for semicrystalline SMPs), resting isothermally for a while (for instance 30 min) to make sure a uniform temperature within the SMP specimen; 2) loading the specimen by the desired type of loads to the designed pre-strain; 3) cooling down to below the transition temperature while holding the load or displacement constant; and 4) unloading at the end of cooling (Lendlein and Kelch, 2002). The programmed SMP specimens can be then heated up again to above the transition temperature to cause free shape recovery (if no constraint is applied) or fully constrained stress recovery (if zero recovery strain is allowed) or partially constrained stress recovery (if some strain is allowed to recover). While hot programming is popular for thermally triggered SMPs, it needs the heating and cooling steps and is energy-consuming. Therefore, cold programming, that is, programming isothermally at the glassy state, has also been proposed (Li and Xu, 2011b; Li and Shojaei, 2012; Li, 2014; Li and Wang, 2016; Xiao and Tian, 2019). The requirement is that the load applied during cold programming must cause yielding and plastic deformation of the SMPs. Usually, the longer the time of loading the specimen, the more the structural relaxation and the better the shape fixity ratio.

In recent years, many efforts have been made to model the constitutive behavior of SMPs. Several representative approaches include the rheological model (Tobushi et al., 1997; Bhattacharyya, and Tobushi, 2000), elasto-viscoplastic model (Nguyen et al., 2008a; Chen and Nguyen, 2011; Balogun and Mo, 2016; Li et al., 2017a; Li and Liu, 2018), phase evolution law model (Liu et al., 2006; Li et al., 2017b), molecular dynamics model (Diani and Gall, 2007; Wick, et al., 2021), statistical mechanics model (Shojaei and Li, 2014b), and multibranch model (Gu et al., 2014; Yu et al., 2014). In 2013, Nguyen (2013) summarized the constitutive models for SMPs. A recent comprehensive review article was published by Yarali et al. (2020). Most recently, Yan and Li published a tutorial paper on modeling SMPs (Yan and Li, 2022).

Since 2010, our lab at Louisiana State University has developed several constitutive models for various SMPs. The focus of this insight paper is to use the models developed in our lab in tandem with models developed by other labs to shed some lights into the various ways of modeling SMPs. The paper will be arranged in the following sections. In Thermomechanical constitutive modeling of amorphous SMPs, we will present modeling on amorphous SMPs, including the elasto-viscoplastic model, phase evolution law model, and four-chain model. In Thermomechanical constitutive modeling of semicrystalline SMPs, our focus will be on modeling semicrystalline SMPs, including one-way shape memory polymers and two-way shape memory polymers. In Modeling of SMPs including mechanical and functional damage effects, we will focus on modeling amorphous SMPs with mechanical and functional damage effects within the continuum damage mechanics framework. In Challenges and future perspectives, we will present our perspectives on future development in this research direction. In Conclusion, we will conclude this paper.

Thermomechanical constitutive modeling of amorphous SMPs

Elasto-viscoplastic model

To address the time dependence and complicated deformation response of SMPs that are largely overlooked in the early-stage one-dimensional small-strain models, the thermo-viscoelastic-plastic-based structure–function approach has since been intensively pursued in many of the subsequent computational efforts. Such studies, in lieu of representing the shape memory behaviors as a class of special but purely elastic problems, mathematically elucidated the experimentally observed hysteresis from a structural and stress relaxation perspective, which, in particular, propelled the model predictability into the three-dimensional large strain domain as well as intimately intertwined the shape memory phenomena and the glass-transition physics.

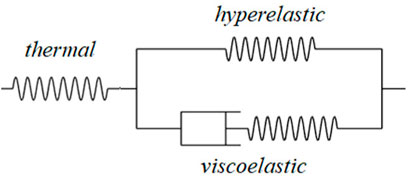
The initial attempt pioneered by Diani et al. (2006) in fact represented a conceptual extension of the standard linear solid model rheology. Later macroscopic intermediate models by Xu and Li (2010), Baghani et al. (2012), Baghani et al. (2014), and Li et al. (2014) provided further enhancement by resolving the rate-dependent shape memory responses through various forms of multi-phase viscoelastic mixture analogy. A schematic example of such rheological representation proposed in Xu and Li (2010) is illustrated in Figure 1 below.

FIGURE 1

FIGURE 1. Linear rheological representation of multi-phase viscoelastic mixture analogy.

Leveraging combinations of hyperelasticity and viscoplasticity into the constitutive formulation to capture both the molecular chain orientation at elevated temperatures and the sluggish mechanical response below T_g, Qi et al. (2008) presented an integrated experimental and computational study in the finite deformation region which was then implemented into finite element analysis. Despite still employing a similar phenomenological first-order three-phase transition method to describe the amorphous SMP through terms of phase fractions, the model introduced a concept that the deformation of the newly formed glassy phase (F_T) should originate from a redistribution of the total deformation (F) as elaborated in Eqs 1, 2 below for any incremental change during a monotonic thermal loading from step n to n+1, which effectively eliminates the need of purely nonphysical descriptions such as histories of “stored strain” (Qi et al., 2008).

$\mathrm{\Delta }{\mathit{F}}_T^{n+1}=\{\begin{array}{cc}{\mathit{F}}^{n+1}{\left({\mathit{F}}^n\right)}^{-1}& \mathrm{\Delta }T\ne 0\\ \mathit{I}& \mathrm{\Delta }T=0\end{array}(1)$

$F_T^{n+1}=\mathrm{\Delta }{F}_T^{n+1}{F}_T^n(2)$

The representation of the underlying material morphology evolution that had frequently relied on the phase transition analogy was eventually favored for a structural and stress relaxation-based interpretation at the core of the physical glass-transition process as inspired by Nguyen and co-workers (Nguyen et al., 2008a; Nguyen et al., 2008b). The shape memory phenomena of the amorphous SMP were argued to be primarily driven by the drastic change of molecular chain mobility and the local rearrangement capability of macromolecular chain segments to restore the structural equilibrium. The structural relaxation occurs instantaneously at high temperatures above T_g but responds slowly below it and thus effectively locks the structure in a nonequilibrium configuration and a temporary shape macroscopically as well during cooling. Heating brings back the mobility which then allows for the shape recovery. A combined structural relaxation model of Tool’s fictive temperature T_f (Tool, 1946) and Adam-Gibbs’s description of the temperature-dependent retardation time τ_R (Adam and Gibbs, 1965) was then adopted, along with a modified Eyring model of viscous flow, into a thermoviscoelastic framework of which the one-dimensional linear rheology is illustrated below in Figure 2, where a volumetric thermal response spring is followed by a mechanical response component consisting of a hyperelastic spring that represents the mobile rubbery state in parallel with a Maxwell element corresponding to the viscoelastic stress relaxation.

FIGURE 2

FIGURE 2. One-dimensional rheological representation of the thermoviscoelastic model.

The expression of the isobaric thermal deformation Ω_T responding to a temperature change from T₀ to T thus included a time-dependent nonequilibrium part δ^neq that was in turn evaluated following an evolution equation proposed by Tool (Tool, 1946) as follows (Qi et al., 2008):

${\Omega }_T=1+ {\alpha }_r\left(T-T_0\right)+\left(-\left({\alpha }_r-{\alpha }_g\right)\left(T-T_f\right)\right)=1+{\alpha }_r\left(T-T_0\right)+{\delta }^{neq}(3)$

$\frac{d{\delta }^{neq}}{dt}=-\frac{1}{{\tau }_R}{\delta }^{neq}- \left(-\left({\alpha }_r-{\alpha }_g\right)\frac{dT}{dt}\right)(4)$

where α_r and α_g are the rubbery and glassy volumetric thermal expansion coefficients, respectively; T_f is Tool’s fictive temperature, and δ^neq measures the departure from the equilibrium.

Since such an integrated structural and stress relaxation approach has proven to be quite effective in interpreting and reproducing the amorphous SMP morphological evolution, researchers continue to make strides in this direction to improve the model sophistication for better representation of the complicated thermo-elasto-visco-plastic behaviors. For example, in view of the potential to capture both thermal and mechanical behaviors in a single thermodynamically consistent manner, Gu et al. (2017) adopted a more definite physics-based internal state variable description in the vicinity of the glass transition following the previous work by Lion and Peters (2010). Concerning that the assumption of the same temperature and structural dependence being shared between structural relaxation time and stress relaxation times may not be well inclusive, Zeng et al. (2018) introduced uncoupled structural and stress relaxation mechanisms which are linked only through an internal state variable that reflects the degree of volume departure from equilibrium. On the other hand, Westbrook et al. (2011) incorporated extra nonequilibrium rubbery Maxwell branches in a similar scheme of the generalized viscoelastic model or Prony series to capture the multitude of relaxation modes, while Xiao et al. (2013) further extended the formulation of the relaxation times for structure, stress, and viscous flow into multiple discrete relaxation processes and indicated that the recovery response can be potentially well engineered through designed shape fixity thermomechanical profiles that are not solely limited to deformation upon heating.

Li and Xu (2011b) proposed a continuum finite-strain-based thermo-viscoelastic-viscoplastic model through an integrated experimental and theoretical effort with a focus on characterizing the shape fixity and recovery of amorphous SMPs programmed by cold compression, in which it was contended and demonstrated that it is the creation of a nonequilibrium configuration rather than a necessity of a temperature event that eventually underpins the acquiring of the shape memory capacity. In light of the fact that the postulation of a single exponential structural relaxation process would potentially lead to missing “memory effects” of the thermal deformation in response to successive temperature changes as described by Kovacs et al. (1979), a continuous structural relaxation spectrum as shown below was employed, where Tool’s fictive temperature is defined and a response function following Moynihan et al. (1976) was adopted. Here, 0<β ≤ 1 describes the nonexponential attribute of the relaxation process and τ_s measures the characteristic retardation time of the volume creep in the formulation of the dimensionless material time difference Δς (Li and Xu, 2011b)

$T_f\left(t\right)=T\left(t\right)-{\displaystyle \underset{t_0}{\overset{t}{\int }}exp \left[-{\left(\mathrm{\Delta }\varsigma \right)}^{\beta }\right]dT\left(t\right)}(5)$

$\mathrm{\Delta }\varsigma =\varsigma \left(t\right)-\varsigma \left(t^{\prime }\right)={\displaystyle \underset{t^{\prime }}{\overset{t}{\int }}\frac{dt}{{\tau }_s}}(6)$

From a similar perspective, later advancement by Dai et al. (2020) further considered the rejuvenation-induced strain softening in the constitutive relations along with the incorporation of the relaxation mechanism into the strain hardening representation to account for the effects from the dissipative orientation process.

Most recently, aiming for a reconciliation between the need for modeling the physical significance and the complexities arising from the material parameter calibration, Su and Peng (2018) derived the constitutive equations through energy decomposition in accordance with the second law of thermodynamics and instituted a temperature-dependent weight function in formulating the material parameters through the shape memory cycle. Subsequent refinement pursued by Wang et al. (2021) then advocated that the parameter identification could be further simplified by adopting a modified Adam-Gibbs model and Arrhenius-type time–temperature superposition shift factor along with a physics-based viscosity expression.

Phase evolution law-based model

Of all the approaches on constitutive modeling of SMPs, the phase evolution law-based model has attracted much attention (Liu et al., 2006). The reason for this is that by treating the programming and shape recovery process as a phenomenon of phase change or more accurately evolution from an active phase to a frozen phase in hot programming and evolution from a frozen phase to an active phase during shape recovery, the shape memory effect is fully controlled by the phase evolution law. Although this concept seems to have a clearer physical interpretation in semicrystalline shape memory polymers, because the shape memory effect can be understood as crystallization–melt transition (Long et al., 2009; Westbrook et al., 2010; Scalet et al., 2015), this approach has been more popular in modeling amorphous thermoset shape memory polymers (TSMPs). In 2006, Liu et al. (2006) proposed the phase evolution law model for constitutive modeling of TSMPs, which has been further refined by other researchers (Baghaniet al., 2012; Chen and Lagoudas, 2008a; Chen and Lagoudas, 2008b; Gilormini and Diani, 2012; Guo et al., 2016; Kafka, 2008; Kazakeviciute-Makovska et al., 2012; Kim et al., 2010; Li and Liu, 2018; Long et al., 2009; Pieczyska et al., 2015; Qi et al., 2008; Reese et al., 2010; Scalet et al., 2015; Volk et al., 2011; Wang et al., 2009; Xu and Li, 2010; Yan and Li, 2019). It is noted that this approach can only be applied to hot programming of TSMPs; for cold programming, which is a process of programming TSMPs isothermally in the glassy state until yielding (Xu and Li, 2011; Li and Shojaei, 2012; Li et al., 2013a; Li, 2014; Li and Wang, 2016; Li and Xu, 2011b), the phase evolution law approach cannot be used because there is no substantial phase transition during the cold programming process.

In a broader sense, the phase evolution law-based approach has a deeper root in constitutive modeling of materials, with the original model for shape memory alloys (SMAs). The pseudoelastic thermomechanical response, shape memory effect, and stress-induced phase transformation phenomena for SMAs were described by Dachkovski and Böhm, 2004; Müller and Bruhns, 2006; Auricchio et al., 2007; Popov and Lagoudas, 2007; Thamburaja and Ekambaram, 2007; Hassan et al., 2008; Moumni et al., 2008; Reese and Christ, 2008; Wang et al., 2008; Levitas and Ozsoy, 2009a; Levitas and Ozsoy, 2009b; Thamburaja and Nikabdullah, 2009. Unlike SMAs, which have a clear phase change from martensite to austenite during shape recovery, TSMPs may not see such a clear phase change, although there is some evidence that thermoset polymers are generally heterogeneous in the nanoscale, with highly crosslinked regions or domains dispersed in a lightly crosslinked matrix (Magonov and Reneker, 1997; Morsch et al., 2015). In other words, it seems that TSMPs may be treated as a two-phase composite for the convenience of mathematical modeling. With the treatment as a two-phase composite, several composite materials theories can be utilized to determine its effective elastic properties (Hill, 1965; Mori and Tanaka, 1973; Hori and Nemat-Nasser, 1993; Ju and Chen, 1994; Hu and Weng, 2000; Li and Wang, 2005; Peng et al., 2009; Westbrook et al., 2010).

In the first paper published by Liu et al. (2006), the authors proposed a phenomenological concept, that is, TSMPs are made of two phases: active phase and frozen phase. During hot programming, the TSMPs are almost 100% active phase in the rubbery state, and with cooling, the active phase is gradually transferred to the frozen phase, and at the glassy state, the majority of the TSMPs is in the frozen phase. The pre-strain is fixed in the frozen phase due to the loss of mobility of the polymer chains. During shape recovery, the molecules gradually gain mobility with heating, and the frozen phase is gradually transferred to the active phase. As a result of the phase transition, the stored pre-strain is released, and the shape is recovered. Later, the concept proposed by Liu et al. (2006) was further developed. For example, Chen and Lagoudas (2008a; 2008b) established a three-dimensional framework, which was used by Volk et al. (2011) to determine the shape memory effect of shape memory polyurethane (SMPU). A three-phase phenomenological model [one hard segment phase and two (active and frozen) soft segment phases] was developed by Kim et al. (2010) to predict the deformation behavior of SMPUs. Wang et al. (2009) considered the heating rate and hysteresis. In 2008, Qi et al. (2008) developed a three-dimensional finite deformation model for the thermomechanical behavior of TSMPs, which was based on the evolution of the deformation energy from an entropy-based state to an enthalpy-based state. In the framework of both macromechanics and micromechanics, Reese et al. (2010) developed a new model. In the small strain regime, Baghani et al. (2012) presented a three-dimensional phenomenological model under time-dependent multiaxial thermomechanical loadings. Gilormini and Diani (2012) combined the model of Liu et al. (2006) with the homogenization approach, which got rid of the uniform stress assumption and may be more appropriate. Recently, researchers have been seeking more physical bases for the concept of the phase evolution law. For example, Guo et al. (2016) proposed a physics-based constitutive model for TSMPs. Yang and Li (2016) developed a new physics-based phase evolution law by treating the TSMP as a two-phase composite with frozen domains dispersed in the active phase matrix. They proposed that the shape fixity and shape recovery were governed by the free energy change during the programming and recovery process, see Figures 3A,B. Most recently, Yan and Li (2019) proposed another physical process of the phase evolution. For the case of hot programming, a TSMP is almost 100% in the active phase in the rubbery state. However, some frozen phase nuclei may form and disappear dynamically. As the temperature drops, the high-energy active phase may move to the frozen phase nuclei, dump the kinetic energy, and adhere to the surface of the frozen nuclei. As a result, the frozen phase grows and the active phase reduces with further temperature dropping, until the majority of the TSMP becomes frozen in the glassy state, see the schematic in Figure 3C. Based on this understanding, the basic building block or unit cell of the two-phase model is a frozen phase coated by an active layer, see Figure 3D. As against the previous isostress or isostrain assumption, this new unit cell does not have isostress or isostrain in the active and frozen phases. Some typical phase evolution laws proposed by other groups are summarized in Table 1.

FIGURE 3

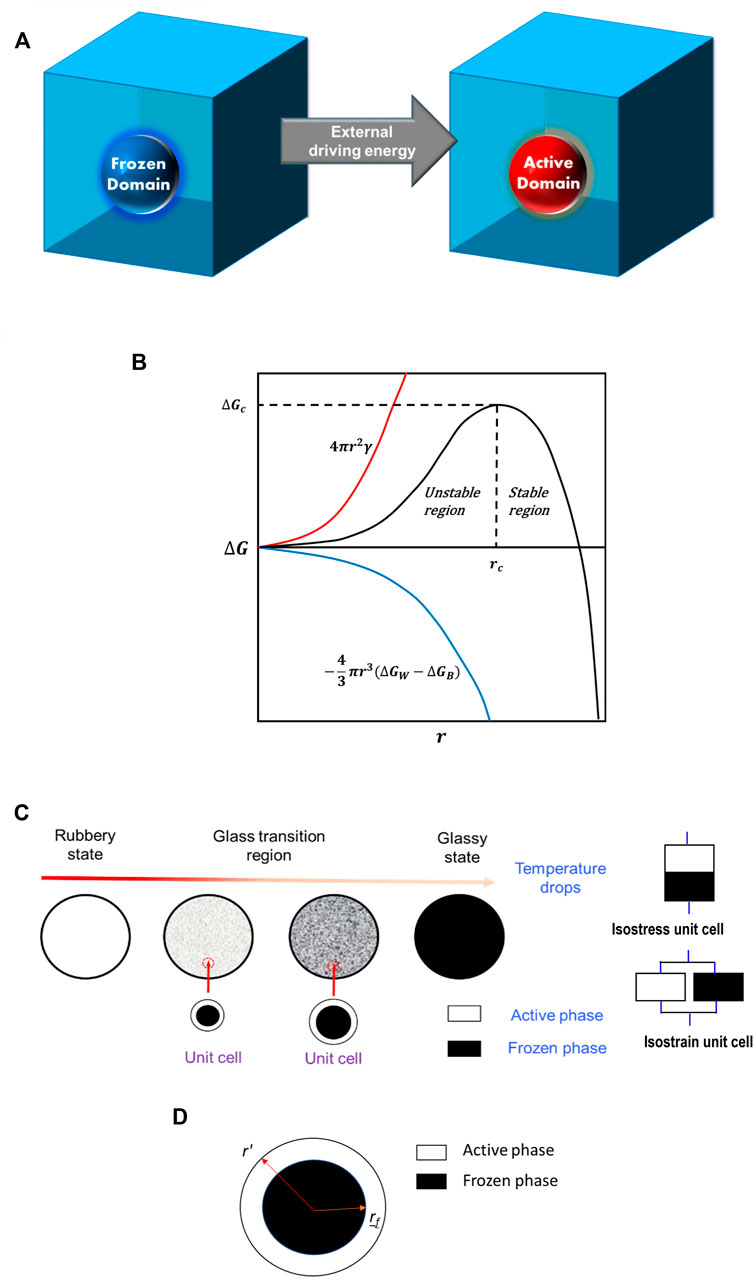
FIGURE 3. (A) Schematic illustration of how a frozen domain (blue sphere) in the frozen phase matrix (blue cube) evolves into an active domain (red sphere). (B) Free-energy change caused by the appearance of the active domain as a function of domain radius $r$. $\mathrm{\Delta }{G}_c$ is the energy change when the domain size reaches the critical value $r_c$. The domains with $r>r_c$ will be stabilized in the active phase (and may grow infinitely upon perturbation), while the domains with $r<r_c$ will revert to the frozen phase upon fluctuations. (Reproduced with permission from International Journal of Plasticity, 80:168-186, (2016). Copyright 2016 Elsevier.) (C) Schematic of transition from the active phase to frozen phase as the temperature drops (left) and isostress and isostrain unit cells (right), which are currently used in the literature. (D) Proposed two-phase unit cell, which is neither isostress nor isostrain (Reproduced with permission from Smart Materials and Structures, 28: 095030 (2019). Copyright 2019 IOP.)

TABLE 1

TABLE 1. Frozen phase volume fraction functions proposed in existing literature studies.

Figures 4A–C show the performance of the new model by Yang and Li (2016). It is seen that this model can reasonably reproduce the test results by Liu et al. (2006). On the other hand, Yan and Li used their model in finite element analysis of a dogbone specimen under uniaxial loading. Figure 4D shows the comparison between the finite element modeling results and experimental results. Again, it is seen that the model can reasonably capture the experimental results.

FIGURE 4

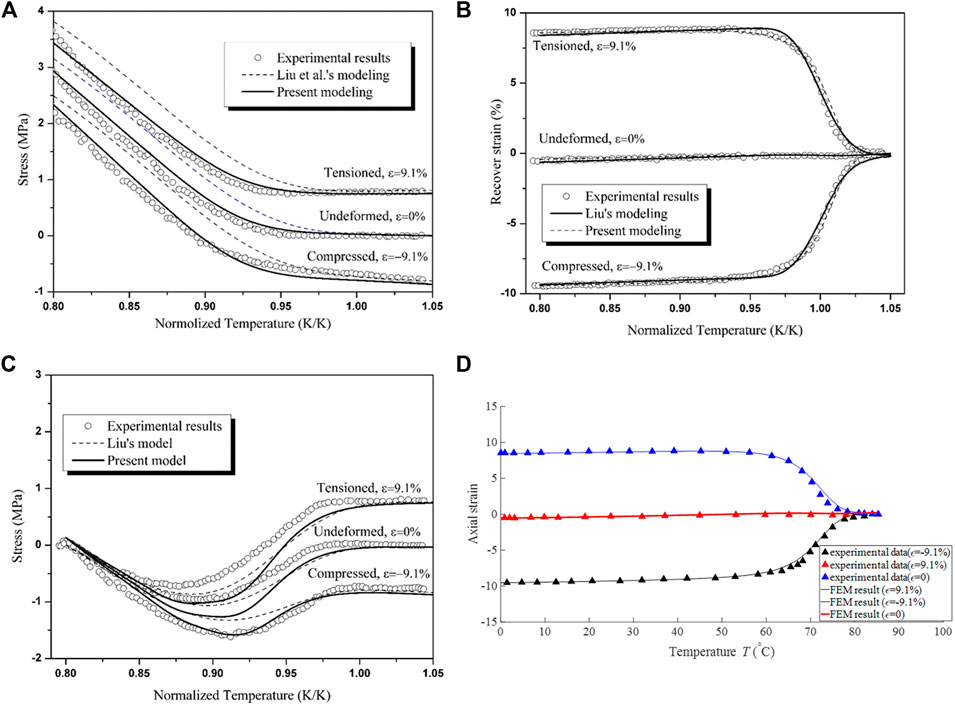
FIGURE 4. Modeling results for (A) stress responses of SMPs during cooling under different pre-strain conditions; (B) free strain recovery tests of SMPs programmed by different pre-strains [Reproduced with permission from International Journal of Plasticity, 80:168-186, (2016). Copyright 2016 Elsevier]. (C) constraint stress recovery tests of SMPs programmed by different pre-strains; (D) comparison between experimental results and finite element analysis results of a dogbone specimen under uniaxial loading [Reproduced with permission from Smart Materials and Structures, 28: 095030, (2019). Copyright 2019 IOP].

Four-chain model

In solid mechanics modeling, a macroscopically homogeneous body can be characterized by a representative volume element (RVE). In doing so, both the material points in the heterogeneous body or isotropic body can be effectively modeled and the connection between macroscopic deformation and microscopic deformation can be bridged. In the past, most studies on SMPs utilized the Arruda-Boyce eight-chain diagonal model (Aruda and Boyce, 1993). This model has found its wide applications in a variety of SMP modeling (Qi et al., 2008; Li and Xu, 2011b; Ge et al., 2014; Xiao and Tian, 2019). However, by observing the unit cell in the SMP network, Yan and Li, (2020a) argued that the conventional Arruda-Boyce eight-chain diagonal model is not suitable for describing the microscopic RVE or unit cell for a recently discovered SMP made of EPON-IPD (Fan and Li, 2018). Therefore, they introduced a tetrahedron unit cell to replace the commonly used Arruda-Boyce RVE model, see Figure 5. Furthermore, in order to reasonably describe the dramatic stress recovery for EPON-IPD, they borrowed an idea from an early developed fiber-forming polymer model (Lyons, 1958), that is, a novel modulus transition mechanism. That is, with increasing deformation, the energy source gradually transits from bond rotation in the low-energy state to bond stretch in the high-energy state. The Cauchy stress is divided into three parts, that is, rubbery stress ${\mathit{\sigma }}_r$, the switchable hyperelastic stress ${\mathit{\sigma }}_g^r$, and viscoplastic stress ${\mathit{\sigma }}_g^p$, which reads (Yan and Li, 2020a)

$\mathit{\sigma }={\text{f}}_r{\mathit{\sigma }}_r+{\text{f}}_g\left({\mathit{\sigma }}_g^p+{\mathit{\sigma }}_g^r\right)(7)$

where f_g and f_r are the volume fractions of the glassy phase and rubbery phase, respectively. The three stress components can be written as

${\mathit{\sigma }}_r=2\left[M_r\left(\mathit{I}-\frac{1}{3}{I}_1{\mathit{F}}^{-1}{\mathit{F}}^{-T}\right)\right]\mathit{F}{\mathit{F}}^T-\frac{1}{J}\left({\mathit{\sigma }}_r\frac{\partial \mathit{E}}{\partial \mathit{F}}+\mathit{E}\frac{\partial {\mathit{\sigma }}_r}{\partial \mathit{F}}\right){\mathit{F}}^T-\left(\frac{\partial {\stackrel{⌢}{p}}_r}{\partial \mathit{F}}\right){\mathit{F}}^T-3{\kappa }_r{\alpha }_r\left(\theta -{\theta }_0\right)\mathit{I}(8)$

${\mathit{\sigma }}_g^r=H\left(E_{eq}-E_c\right)\left(2\left[M_g\left(\mathit{I}-\frac{1}{3}{I}_1{\mathit{F}}_g^{r^{-1}}{\mathit{F}}_g^{r^{-T}}\right)\right]{\mathit{F}}_g^r{\mathit{F}}_g^{r^T}-\left({\mathit{\sigma }}_g\frac{\partial {\mathit{E}}_g^r}{\partial {\mathit{F}}_g^r}+\mathit{E}\frac{\partial {\mathit{\sigma }}_g^r}{\partial {\mathit{F}}_g^r}\right){\mathit{F}}_g^{r^T}-\left(\frac{\partial {\stackrel{⌢}{p}}_g}{\partial {\mathit{F}}_g^r}\right){\mathit{F}}_g^{r^T}-3{\kappa }_g{\alpha }_g\left(\theta -{\theta }_0\right)\mathit{I}\right)(9)$

${\mathit{\sigma }}_g^p=\frac{1}{J^e}\left[{\mathit{C}}^e:{\mathit{E}}^e-3{\alpha }_g{\kappa }_g\left(\theta -{\theta }_0\right)\mathit{I}\right](10)$

in which J^e, C^e, and κ_g are the Jacobin for the elastic part, the isotropic elasticity tensor, and the bulk modulus for the glassy phase, respectively. M_r and M_g are two functions with respect to microscopic deformation quantities. E is the Biot strain tensor. θ and θ₀ are the current temperature and initial temperature, respectively. The subscripts “r” and “g” represent the rubbery state and glassy state, respectively. Meanwhile, Yan and Li (2020a) believe that this energy transition corresponds to a change from entropy-driven deformation to enthalpy-driven deformation. The model was validated in three scenarios, that is, uniaxial deformation in the glassy state, the step-relaxation loading in the robbery state, and the recovery stress under different programming strains, and all of them can well capture the experiment trends.

FIGURE 5

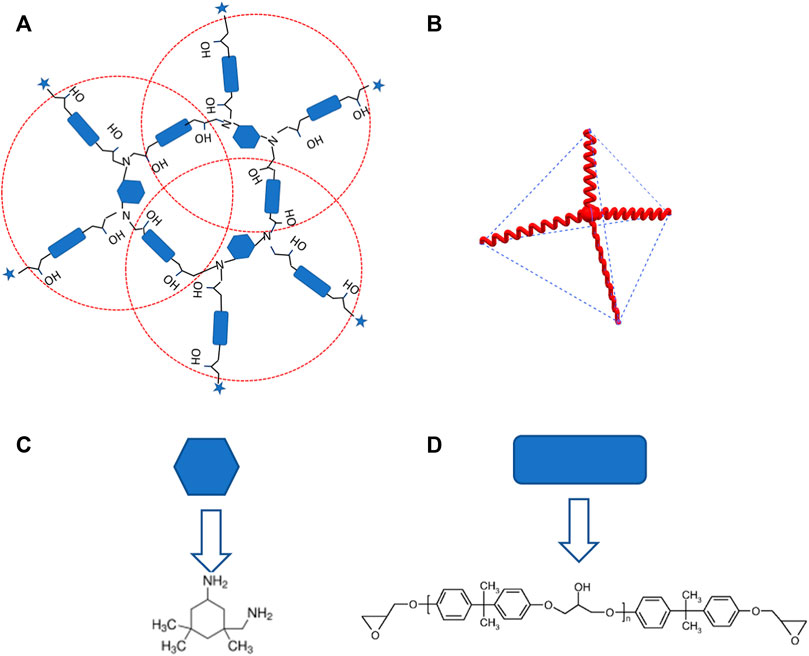
FIGURE 5. (A) Planar schematic for the molecular configuration of the EPON-IPD network; (B) unit cell in the EPON-IPD network; (C) monomer of isophorone diamine (IPD); (D) partial structure of the epoxy resin (EPON 826); ⋆represents the extended structure. For each dotted red circle in (A), it consists of one IPD at the center, connected by four epoxy arms, which are the EPON epoxy monomers. In three dimensions, this planar schematic is represented by the tetrahedron unit cell in (B). From (A), it is seen that every epoxy monomer arm is shared by two-unit cells, growing into the three-dimensional space network. [Reproduced with permission from Journal of Applied mechanics, 87(6): 061007, (2020a). Copyright 2020 American Society of Mechanical Engineers].

Thermomechanical constitutive modeling of semicrystalline SMPs

Modeling of semicrystalline one-way shape memory polymers

Amorphous and crystalline polymers are both constituted from randomly disordered molecular chains. During the polymerization process, if the randomness of molecular chains is preserved, a specific structure could be developed during the crystallization process in which the disordered polymeric network is oriented in predefined directions. Polymer crystallization may include 1) temperature gradient-induced crystallization, in which the crystalline lamellae are oriented with respect to the largest temperature gradients (Shojaei et al., 2013), 2) stress-induced crystallization in which external thermomechanical loadings are utilized to align the molecular chains (Shojaei et al., 2013; Lu et al., 2018), and 3) chemical processes. Due to the statistical nature of the crystallization processes, the resulting microstructure contains 10 wt% up to 80 wt% crystalline segments, while the remaining molecular chains retain their amorphous structure. The composite structure made of amorphous and crystalline phases is called the semicrystalline polymer, and their properties are dominated by both crystalline and amorphous segments (Seefried et al., 1975; Brunette et al., 1982; Tobushi et al., 1997; Shojaei et al., 2013).

Phase separation and stress-induced crystallization processes may alter the microstructure of the semicrystalline SMPs in which crystalline and amorphous phase separation may occur. The phase separation, induced during severe thermomechanical loading, may alter the amorphous, crystalline, and morphological textures of the semicrystalline polymers. Since the thermomechanical properties of crystalline and amorphous polymers have been well studied in the literature, one could utilize the established properties to predict the performance of semicrystalline polymers using the multiscale analysis methodology. These methods, which have been used for reinforced composites, can effectively correlate the micro-constituent properties to the macroscale mechanical behavior. Li and Shojaei (2012) developed a physically consistent micromechanics framework to correlate the macroscopic mechanical responses to the microscale constitutive behaviors. The developed constitutive models are further expanded to capture SMP polymer performance in self-healing structures.

One of the major challenges in structural damage healing is the need for an external stimulus to bring the fractured surfaces in contact, that is, sealing the crack, before the actual healing can occur (Li and Uppu, 2010). Li and Shojaei (2012) developed a novel self-healing scheme that utilizes SMP fibers to stitch the crack faces. In this process, the crack surfaces are forced in contact through constrained shape recovery of tension-programmed SMP fibers which are embedded in the body (Zhang et al., 2016a; Zhang and Li, 2016; Zhang et al., 2016b). For example, an SMP fiber-reinforced grid skeleton, as shown in Figure 6, could act like stitch a cut in the human skin by suture. The scheme illustrated in Figure 6 is a practical bio-mimetic solution, and it is feasible to manufacture using existing SMP fibers (Li et al., 2012; Li and Zhang, 2013; Shojaei and Li, 2013).

FIGURE 6

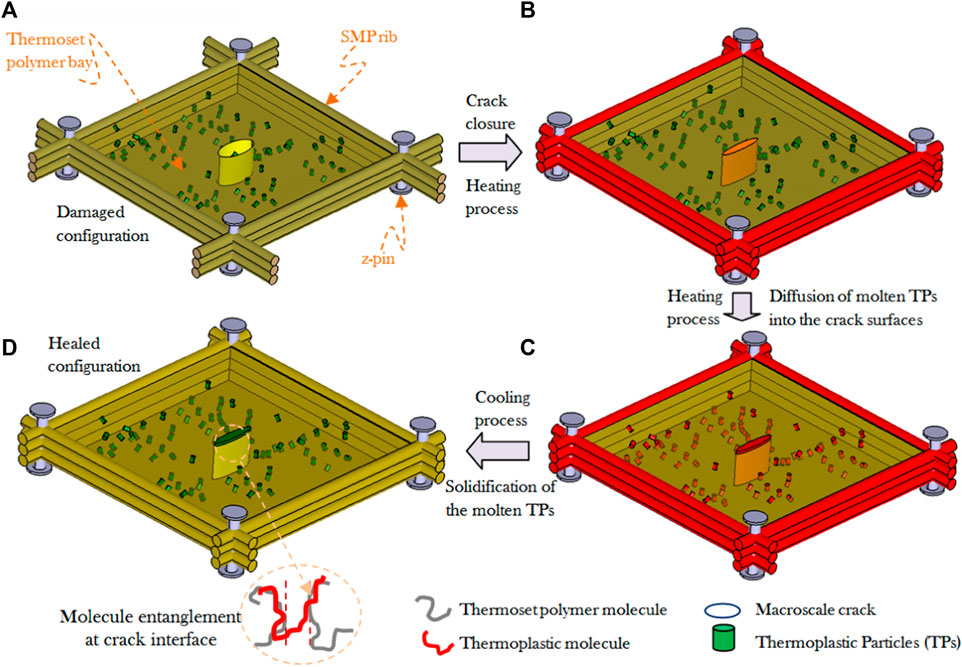
FIGURE 6. Bio-inspired healing composite structure consists of the SMP fiber grid. (A) Unit cell of the SMP grid (ribs and z-pins) with a macroscopic crack (T < T_g), (B) crack closure process (T > T_g), (C) thermoplastic particle melting process (T > T_m), and (D) cooling down process (T < T_g). For more details, refer to Li and Shojaei, 2012 [Reproduced with permission from Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science 468, 2319-2346, (2012). Copyright 2012 Royal Society].

Because manufacturing of the systems shown in Figure 6 is costly and time-consuming, a modeling tool is required to study the performance of different configurations. Li and Shojaei (2012) and Shojaei and Li (2013) developed a multiscale viscoplastic model to predict the thermomechanical behaviors of the SMP fibers. Particularly, they considered the cyclic hardening and stress recovery responses in their model. The physics-based models consider the stress-induced crystallization as well as the evolution of the morphological texture. Thermomechanical cycling test data of the SMP fibers are utilized to evaluate the performance of the proposed constitutive laws. In the case of viscoplastic laws, each individual microconstituent is modeled to establish microstress and microstrain states within each of these phases. Averaging techniques is then incorporated, within the micromechanics framework, to correlate the microstates to macroscale constitutive behavior. The main goal in this multiscale modeling approach is to incorporate experimentally characterizable material inputs versus numerical curve fitting parameters when compared to the phenomenological models.

In the case of amorphous microconstituents, the well-established Boyce model is used for modeling the inelastic deformation. For details of the constitutive modeling and material parameters, the interested reader may refer to Boyce et al., 1989; Li and Shojaei, 2012; Nemat-Nasser and Hori, 1993; Shojaei and Li, 2013; Shojaei et al., 2014a. The plastic multiplier for the amorphous microconstituent is defined as follows:

$\left|{\dot{\gamma }}^p\right|={\dot{\gamma }}_0^a\exp \left[-A\frac{s+ap}{\theta }\left(1-{\left(\frac{\left|\tau \right|}{s+ap}\right)}^{5/6}\right)\right](11)$

where the plastic strain is driven by both the pressure and shear stress. The material parameters and the evolution laws are defined in Boyce et al., 1989.

In the case of the crystalline phase, three different inelastic deformation mechanisms were considered by Shojaei and Li, 2013: (a) crystallographic slip, (b) twining, and (c) martensite transformations. The inelastic crystalline stretch rate tensor, ${\dot{D}}_{ij}^{cp}$, is defined by (Lee et al., 1993; Shojaei and Li, 2013)

${\dot{D}}_{ij}^{cp}={\displaystyle \sum _{\alpha =1}^K{\dot{\gamma }}^{\left(\alpha \right)}{R}_{ij}^{\left(\alpha \right)}}(12)$

where $R_{ij}^{\left(\alpha \right)}$ is the symmetric part of the Schmid tensor and $\alpha$ denotes the crystalline slip plane in which the shear rate, ${\dot{\gamma }}^{\left(\alpha \right)}$, is defined. Please refer to Lee et al., 1993; Shojaei and Li, 2013 for the details.

To link microconstituents’ thermomechanical response to macroscale constitutive behavior, a multiscale micromechanics modeling framework was developed by Li and Shojaei (2012) and Shojaei and Li (2013). Viscoelastic-viscoplastic behavior in amorphous and crystalline phases and the morphological texture updates are incorporated in this framework (Li and Shojaei, 2012). In the case of the amorphous microstate, the texture is updated using the stress-induced crystallization process. In the case of the crystalline microstate, the texture is updated via evolution of the crystallographic axes under applied stresses (Li and Shojaei, 2012; Shojaei and Li, 2013).

Shojaei and Li (2013) generalized the two-phase transformation field analysis (TFA); micromechanics was originally developed by Dvorak et al. (Dvorak, 1990; Dvorak 1992; Dvorak and Benveniste 1992). The modification allowed to utilize TFA for capturing large deformations in semicrystalline polymers. Interested readers may refer to Shojaei and Li, 2013 for the details. In the modified TFA framework, a representative volume element (RVE), as shown in Figure 7, is utilized to develop the micromechanics correlations. The crystalline microconstituents in the semicrystalline polymer are modeled as inclusions embedded in the amorphous phase, see Figure 7 (Shojaei and Li, 2013). The fibrous and penny shape inclusions are respectively depicted in Figures 7A,B, where the interfacial unit vector configurations are shown in Figure 7C.

FIGURE 7

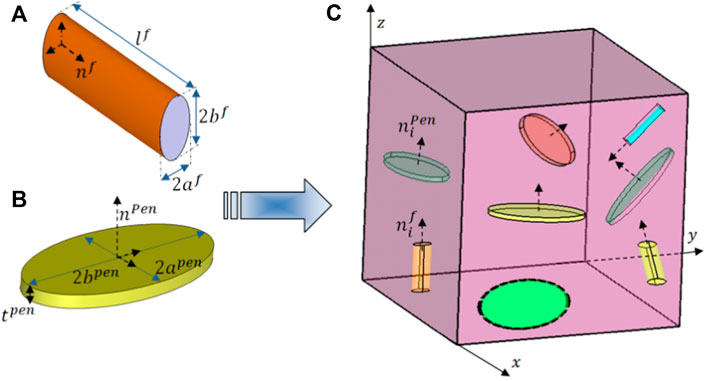
FIGURE 7. Schematic representations of (A) fibrous inclusion, (B) Penny-shape inclusion, and (C) assembled RVE in a micro length scale (Shojaei and Li, 2013) [Reproduced with permission from International Journal of Plasticity, 42: 31-49., (2013). Copyright 2013 Elsevier].

The stress/strain concentration tensors and micromechanics averaging techniques are then incorporated to link the microscale and macroscale thermomechanical behaviors in semicrystalline SMPs. The details of micromechanics formulation can be found in Shojaei and Li, 2013, in which macroscopic RVEs are divided into subvolumes.

The test data from Szymczyk et al. (2011) are shown in Figures 8A,B together with the simulation results. As discussed by Shojaei and Li (2013), the experimental test results are utilized to model the soft segment (Figure 8A) and to calculate the material parameters for the amorphous subphase. The crystalline subphase constitutive model is calibrated using hard segment test data (Figure 8B). The calibrated model is then utilized to model a 20 wt% soft segment copolymer, as shown in Figure 8C (Shojaei and Li, 2013).

FIGURE 8

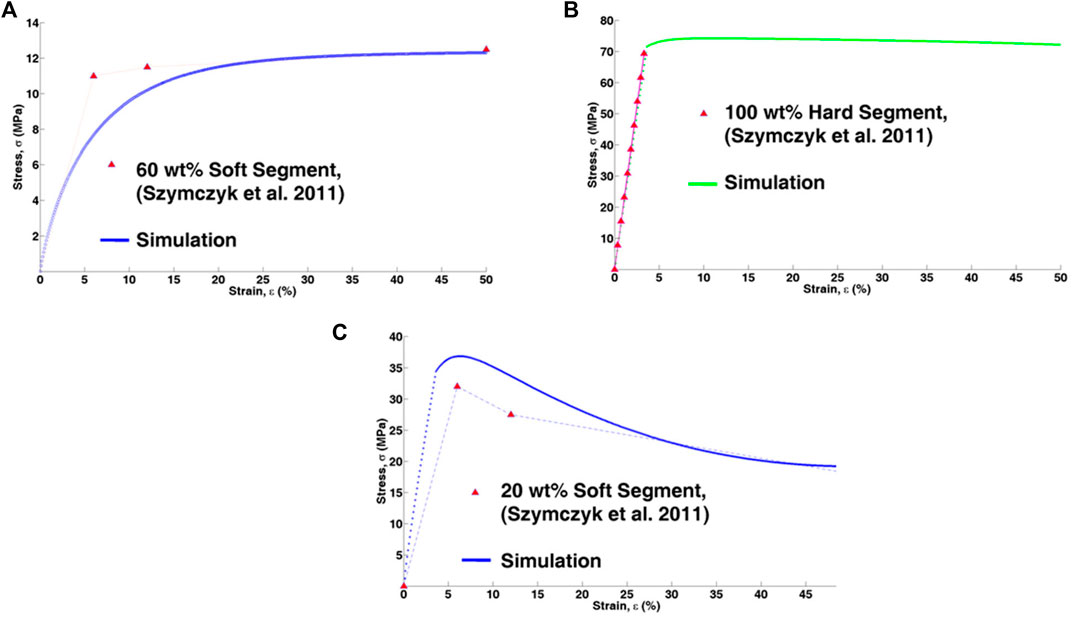
FIGURE 8. (A) Amorphous computation module calibration, (B) crystalline computation module calibration, (C) performance of the model in capturing 20 wt% soft segment tensile test experiment (Szymczyk et al., 2011; Shojaei and Li 2013). [Reproduced with permission from International Journal of Plasticity, 42: 31-49., (2013). Copyright 2013 Elsevier].

Figure 9 shows the simulation and test data for an amorphous SMP under compression loading (Shojaei and Li, 2013).

FIGURE 9

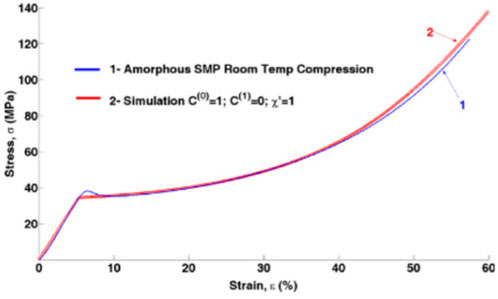
FIGURE 9. Compression test of an amorphous SMP matrix versus simulation data (Shojaei and Li, 2013). [Reproduced with permission from International Journal of Plasticity, 42: 31-49., (2013). Copyright 2013 Elsevier].

Modeling of semicrystalline two-way shape memory polymers

The two-way shape memory effect (2W-SME) was first reported for liquid crystalline elastomers by (Thomesen et al., 2002). To date, it has been found in a number of polymers (Chung et al., 2008; Lee et al., 2008; Qin and Mather, 2009; Hong et al., 2010; Xie, 2010; Li et al., 2011; Raquez et al., 2011; Brömmel et al., 2012; Meng et al., 2013; Zhou et al., 2014; Lu and Li, 2016; Pandini et al., 2016; Lu et al., 2017; Lu et al., 2018; Sarrafan et al., 2022). Among them, the semicrystalline two-way shape memory polymer (2W-SMP) was discovered by Chung et al. (Chung et al., 2008) and will be the focus of this section.

The modeling works for the shape memory polymer (SMP) dated from Tobushi et al.’s model in 1997 (Tobushi et al., 1997), and later on, plenty of constitutive models were developed (Liu et al., 2006; Qi et al., 2008; Xu and Li, 2011; Shojaei and Li, 2014b; Yang and Li, 2016; Yan and Li, 2019; Yan et al., 2020b). However, these works mainly focus on amorphous one-way shape memory polymers (1W-SMPs), and only a few theoretical studies were conducted on semi-crystalline 2W-SMPs (Westbrook et al., 2010; Dolynchuk et al., 2014; Scalet et al., 2018; Yan et al., 2020b; Zeng et al., 2021). Basically, the detailed model frameworks accord with the modeling approach proposed by Yan and Li (2022). To be specific, these models were constructed by depending on Newton’s law of motion and three basic physical laws (i.e., thermodynamics laws, conservation of mass, and conservation of momentum) and some auxiliary equations (see Figure 10). In fact, 2W-SME still inherits the most classical physical characteristics of 1W-SME, such as temperature-dependent moduli, phase transition, heating rate sensitivity, and so on. However, as shown in Figure 11, 2W-SME bears two unique characteristics that 1W-SME lacks. First, 2W-SME can only be realized by applying pre-tension programing. Second, the phase transition for 2W-SME possesses a first-order phase transformation (between the amorphous phase to crystalline phase), while 1W-SME possesses a second-order phase transformation that completely occurs in the amorphous phase (between the glassy state to rubbery state). Because of the pre-tension, crystallites are mainly generated along the loading direction and the tensile stress is stored in the material. In the next work step, further crystallization will mainly occur along the direction of pre-tension; hence, the 2W-SMP cannot be viewed as an isotropic material anymore. This crystallization further induces an abnormal cooling-induced elongation (CIE) and a heating-induced contraction (HIC), which are the keys for the simulation.

FIGURE 10

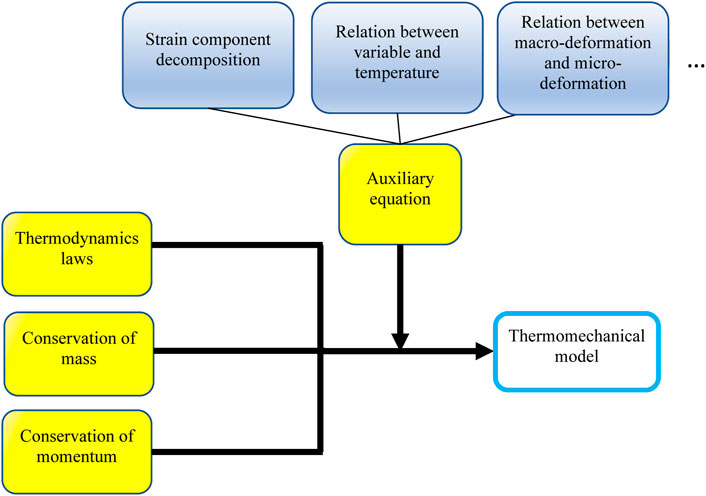
FIGURE 10. Flowchart of the general thermomechanical model for SMPs [Reproduced with permission from Journal of Applied Physics, 131: 111101, (2022). Copyright 2022 American Institute of Physics].

FIGURE 11

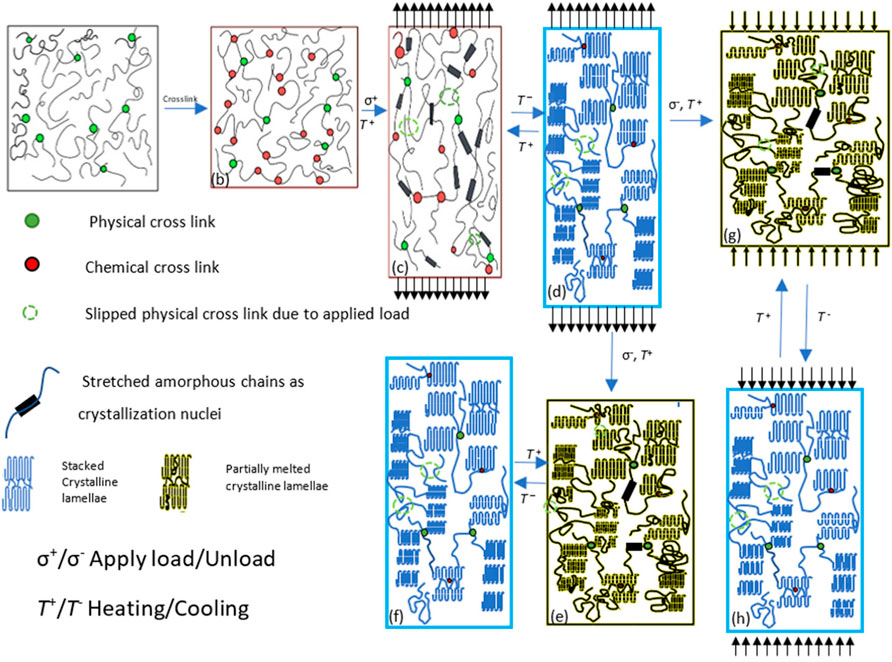
FIGURE 11. Schematic of how the chemically crosslinked two-way shape memory polymer works at a molecular level [redrawn from Figure 1 in ref (Yan et al., 2020b); T: temperature; σ: stress] [Reproduced with permission from Int. J. Mech. Sci., 177 (2020). Copyright 2020 from Elsevier].

In the proposed models, every model possesses some unique characteristics. For example, Dolychunk et al.’s model (Dolynchuk et al., 2014) is built based on the microscopic level, which is different from other phenomenological models. This model considers the conformation change and establishes the relation between the affine microscopic deformation of the crystalline chain and amorphous chain and the macroscopic deformation. The other models are phenomenological models and were established based on the framework of continuum mechanics. Among them, Westbrook et al.’s model (Westbrook et al., 2010) is a pioneer work, wherein they established an implementable one-dimensional model and simply assumed that both the amorphous phase and crystalline phase are linear elastic materials. Also, a simple phase evolution law was proposed, which is connected to the stresses in two phases to illustrate the CIE and HIC. Later, Scalet et al. also (Scalet et al., 2018) presented a simple isostress one-dimensional rheological model and comprehensively investigated the multiple applicabilities. In this model, they presented a new exponential function for the phase evolution law. It is shown that this model can well describe the 2W-SMP with a high crosslinked density and the 2W-SME under higher pre-tension. In 2020, Yan et al. (2020b) proposed a three-dimensional model based on Barot et al.’s model (Rao and Rajagopal, 2002; Barot et al., 2008). This model comprehensively studied three types of 2W-SMEs, that is, quasi 2W-SME, true 2W-SME, and advanced 2W-SME. Additionally, in order to model the stretch under multiple thermomechanical loading, they first introduced Mullins effects into 2W-SME modeling and enabled it well to simulate the gradually softened effects for some advanced 2W-SMEs. A most recent three-dimensional model was developed by Zeng et al. (2021), wherein they introduced a new switch to quantify the strain generated by CIH and HIC. In a nutshell, from the standpoint of view for engineering applications, the present models are able to well capture the variety of 2W-SME responses under different experimental loadings; hence, they are well behaved. However, from the aspect of physics, these models are not perfect and still bear three disadvantages. First, most of them simulated crystallinity by assuming that crystallinity only relates to temperature, which actually does not capture the underlying physics. As indicated above, crystallites are produced along the loading direction, which means that the crystallization and stress are interactively coupled, and this is not reflected by the models. Second, although a few three-dimensional models were developed, they resorted to one-dimensional experiments for validation, which could be less convincible. Third, there are still too many parameters in the models. To be specific, these parameters mainly come from two aspects, that is, establishment of the free-energy function and construction of the phase-transition function. In the future, it is expected that the three disadvantages can be resolved with a further understanding of physics. Additionally, it should be mentioned that recent machine learning models (Yan et al., 2021a; Yan et al., 2021b) indicate that the behaviors for SMP (such as recovery stress, moduli, etc.) can be completely determined once we know the chemical structures of the SMP monomers. It provides another thought for researchers to develop constitutive models or at least determine key parameters for 2W-SMPs.

Modeling of SMPs including mechanical and functional damage effects

Similar to all other mechanical engineering materials, SMPs also experience various types of damages during production, transportation, installation, and service. An additional damage mechanism in SMP composites happens when they undergo programming and shape recovery processes. Shojaei and Li (2014b) proposed a unified modeling scheme within the continuum damage mechanics (CDM) framework to capture these two different categories of damages in SMPs: 1) physical damage or mechanical damage (MD), which are associated with the duty and life cycle of the SMP composites, and 2) nonmechanical damage or functional damage (FD), which is associated with their thermomechanical (TM) programming and shape recovery cycles. In other words, MD damage captures structural damages that may result in a weaker composite structure, and FD damage give rise to the loss of SMP shape recovery functionality (Shojaei and Li, 2014). It is experimentally demonstrated that SMPs under cyclic TM programming and recovery may gradually lose their functionality, such as reduction in their shape recovery ratio and stress recovery ratio (Shojaei and Li, 2014). The FD damage contributes to degradation of the functionality in SMPs, but this FD damage may not necessarily deteriorate the structural properties such as elastic properties.

Shojaei and Li (2014) proposed a modeling framework and addressed the need for a physically consistent CDM theoretical framework for capturing MD and FD damages in SMPs. The statistical mechanics provides a powerful simulation tool for modeling the deformation mechanisms in SMPs. Due to the nature of deformation mechanisms in polymeric materials, developing physically consistent statistical models that can capture polymer chain deformation mechanisms could be very valuable. A successful statistical model could capture various data sources including manufacturing data, loading history, and TM history. Also, statistical approaches could be used to drive confidence level information about the predicted results that is currently not available for non-statistical-based constitutive models. To capture thermomechanical behavior of SMP polymers, Shojaei and Li (2014) proposed a physically consistent model within the statistical mechanics framework that is formulated within the finite deformation kinematics framework. The developed constitutive models were utilized to study the behavior of SMPs during both the programming and in-service duty cycles. Then, the MD and FD damage mechanisms are coupled with the statistical constitutive behavior to provide a full modeling scheme for SMP composites. The main advantages of the proposed physics-based statistical constitutive laws, as compared to the existing ones, include 1) reducing the effort needed for curve fitting to determine model parameters and 2) modeling flexibility in simulating the nonlinear response of amorphous, semicrystalline, and crystalline SMPs. The proposed constitutive laws consider several deformation mechanisms, including temperature-dependent material properties, glass-transition loss events, shape recovery transient events, stress relaxation, and damage effects. Interested readers may refer to Shojaei and Li, 2014 for the details of the constitutive laws.

As discussed in Shojaei and Li, 2014, the finite deformation kinematics is utilized, in which the deformation gradient, $F_{ij}$, is utilized to link the Lagrangian $x_i\left(X_i,t\right)$ and Eulerian $X_i\left(x_i,t\right)$ material coordinates,

$F_{ij}=\partial x_i/\partial X_j(13)$

The multiplicative decomposition of the total deformation gradient, $F_{ij}$, into the elastic $F_{ij}^e$, plastic $F_{ij}^p$, and damage $F_{ij}^d$ gradients is then used to facilitate the numerical solution of coupled plasticity damage via return mapping algorithms (Shojaei and Li, 2014)

$F_{ij}=F_{ik}^e{F}_{kl}^p{F}_{lj}^d(14)$

Shojaei and Li (2014) utilized two sets of constitutive models, namely, “Background” and “Shape memory affected” properties, to model the thermomechanical behavior of SMPs. A nonprogrammed SMP is modeled similar to conventional polymers. The background constitutive laws capture the properties of a nonprogrammed SMP. In the case of a programmed SMP, shape memory affected constitutive laws are utilized to capture the thermomechanical behavior. It is noted that both the “Background” and “Shape memory affected” properties are coupled, which are interrelated via constitutive relations.

Shape recovery and glass-transition events

Shojaei and Li (2014) utilized statistical mechanics to model shape recovery and glass-transition events. Gaussian distribution and its cumulative norm can effectively capture the recovery transition, that is, $T_r$ for a programmed SMP, and the glass transition, that is, $T_g$, as discussed in (Shojaei and Li, 2014). Gaussian distributions are assumed for the shape recovery and the glass-transition events. The normal distribution is defined through ‘$dnor{m}_r$’ and ‘$dnor{m}_g$’ terms, respectively, and their respective cumulative values, that is, ‘$pnor{m}_r$’ and ‘$dnor{m}_g$’, are defined as follows (Shojaei and Li, 2014):

$\begin{array}{l}dnor{m}_{\#}\left(T,T_{\#},{\sigma }_{\#}\right)=\frac{1}{\sigma \sqrt{2\pi }}\times exp\left(-\left(\frac{{\left(T-T_{\#}\right)}^2}{2{\sigma }_{\#}}\right)\right) \\ pnor{m}_{\#}\left(T,T_{\#},{\sigma }_{\#}\right)={\displaystyle \underset{T_1}{\overset{T_2}{\int }}dnor{m}_{\#}\left(T,T_{\#},{\sigma }_{\#}\right)dT}\end{array}(15)$

where the subscript “#” will accordingly be replaced with “g” or “r” to indicate the “glass transition” or the “recovery transition” processes, respectively. The dynamic mechanical analysis (DMA) test data can be used to obtain the material parameters in Eq. 15, see (Shojaei and Li, 2014).

Background storage elastic moduli

Statistical terms for the elastic tensile modulus E, decomposed into elastic storage modulus, that is, E′, and loss modulus, that is, E”, were proposed in Shojaei and Li, 2014. The elastic tensile, E′, and bulk, B’, storage moduli are constitutively prescribed as follows (Shojaei and Li, 2014):

$\begin{array}{l}{E}^{\prime }=E_0^{\prime } \times \frac{\left(1-pnor{m}_g\right)}{\left(1-pnor{m}_g^{\mathit{max}}\right)} \\ B^{\prime }=B_0^{\prime } \times \frac{\left(1-pnor{m}_g\right)}{\left(1-pnor{m}_g^{\mathit{max}}\right)} \end{array}(16)$

where $E_0^{\prime }$, and $B_0^{\prime }$ are reference elastic and bulk moduli, respectively. Also, $pnor{m}_g^{\mathit{max}}$ is the max value of $pnor{m}_g$. Interested readers may refer to Shojaei and Li, 2014 for a full description of the mathematical model.

Shojaei and Li (2014) studied the SMP shape memory modeling and functional damage (FD) phenomena within the context of statistical mechanics. In a thermomechanical cycle, three main factors dominate the shape recovery in SMPs, which include 1) pre-strain, 2) stress relaxation effect during programming, that is, loading time, and 3) the rate of heating (Shojaei and Li, 2014). A thermomechanical cycle of SMPs includes several mechanisms, which are experimentally observed, including the following: 1) higher recovery strain can be achieved with higher holding times at elevated temperatures, 2) the effect of heating rate during shape recovery can increase the transition temperature but not the recovery strain, and 3) the FD leads to reduction or total loss of shape memory functionality, which is larger with higher programming strain and high thermomechanical cycles.

Shojaei and Li (2014) proposed that the damage mechanics of SMPs should be classified into two distinct classes (Figure 12): 1) mechanical damage (MD): damage induced during operational conditions and under their service loads, and 2) FD: induced during thermomechanical cycles. The MD definition helps to identify lifetime- and reliability-related issues, while FD can be used to characterize SMP programming and shape recovery performance.

FIGURE 12

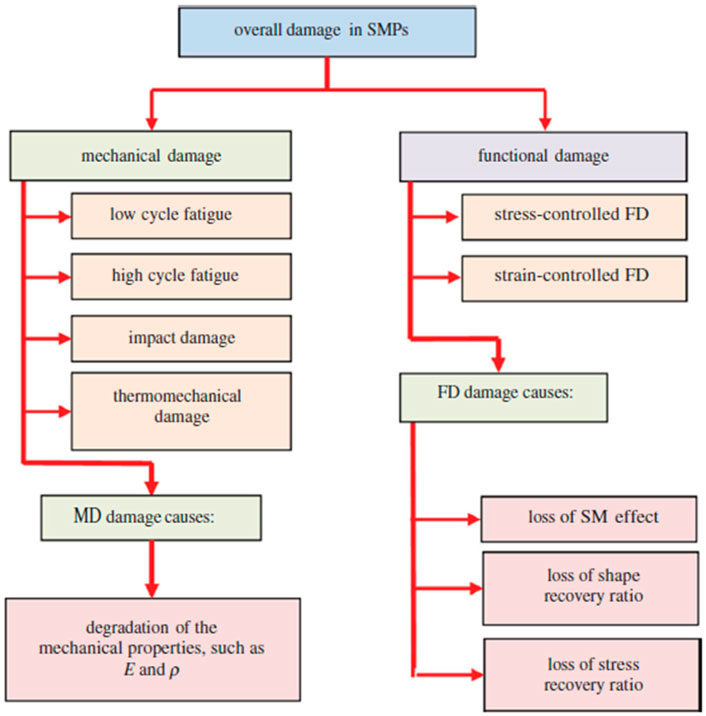
FIGURE 12. Flowchart for the damage categories in an SMP system (Shojaei and Li, 2014). [Reproduced with permission from Proceedings of the Royal Society A, 470: 20140199., (2014). Copyright 2014 Royal Society].

Constitutive models for MD and FD of SMPs were developed based upon continuum damage mechanics (CDM), please refer to (Shojaei and Li, 2014) for details. Figures 13–19 highlight the performance of the developed statistical model in capturing different aspects of SMP thermomechanical behavior under service loads as well as during the programming cycles. Figure 13 illustrates the performance of the proposed framework in capturing glass-transition events. Figures 14A,B show respectively the model performance in capturing strain rate-dependent and temperature-dependent yield behavior of SMPs. The elasto-viscoplastic behavior of SMPs is studied in Figures 15A,B, in which the strain rate effect and temperature effects have been modeled. Figure 16 shows the effect of programming strain levels on the final shape recovery process. In Figure 17, the heating rate effect on the shape recovery process is demonstrated. The effect of the holding (relaxation) time on the recovered strain level is studied in Figure 18. Experimental data as well as simulation results for the FD of SMPs are depicted in Figure 19.

FIGURE 13

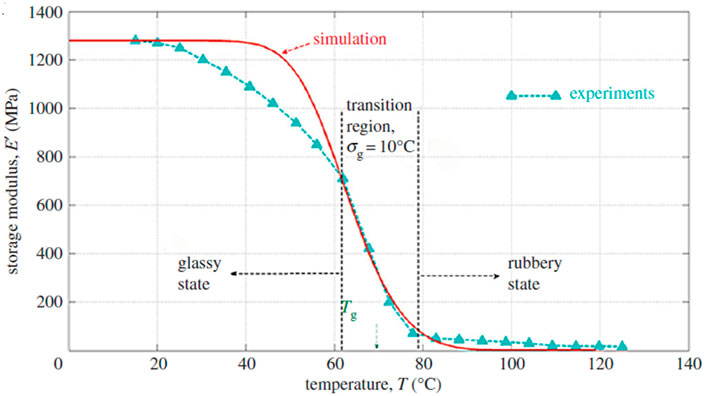
FIGURE 13. Experimental and simulation results for the storage tensile modulus, E, with storage modulus $E_0^{\prime }$= 1,290 MPa (Shojaei and Li, 2014). [Reproduced with permission from Proceedings of the Royal Society A, 470: 20140199., (2014). Copyright 2014 Royal Society].

FIGURE 14

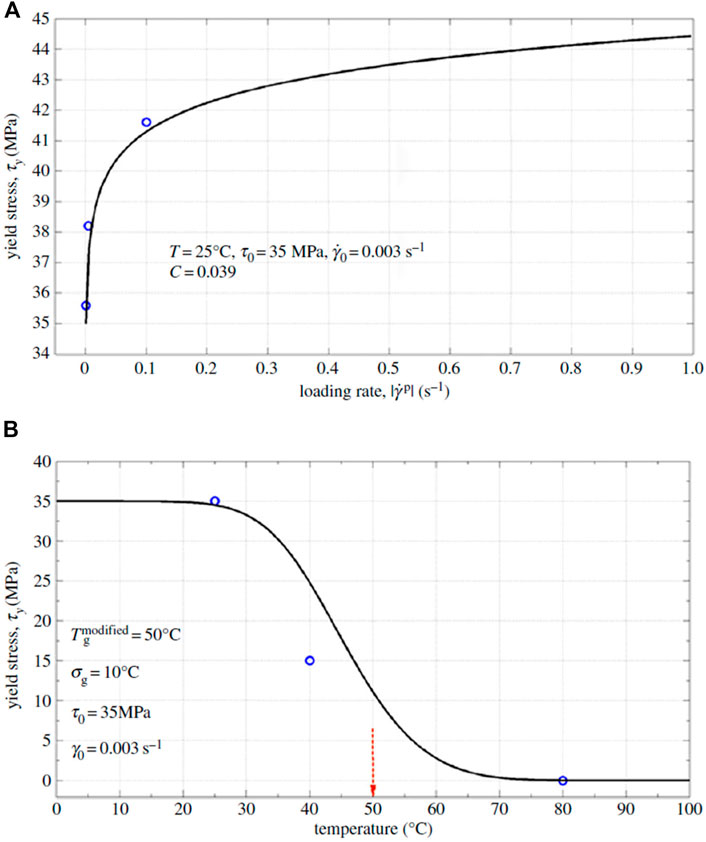
FIGURE 14. Comparison of experimental and simulation results for (A) strain rate-dependent and (B) temperature-dependent yield stresses. Circles denote experimental results, and the solid line denotes simulation results (Shojaei and Li, 2014). [Reproduced with permission from Proceedings of the Royal Society A, 470: 20140199., (2014). Copyright 2014 Royal Society].

FIGURE 15

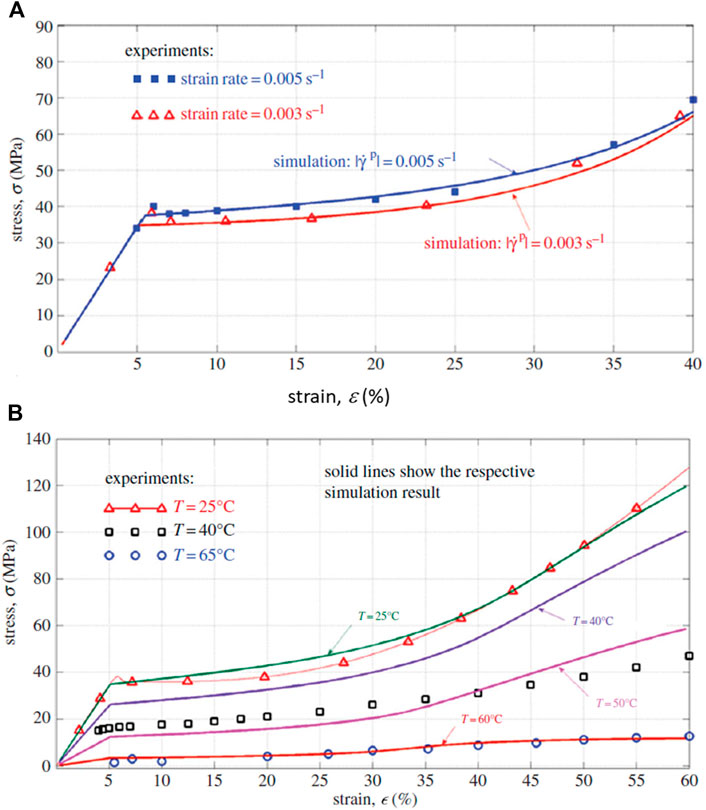
FIGURE 15. Comparison of experimental and simulation results for the viscoplastic stress–strain responses to (A) rate and (B) temperature (Shojaei and Li, 2014). [Reproduced with permission from Proceedings of the Royal Society A, 470: 20140199., (2014). Copyright 2014 Royal Society].

FIGURE 16

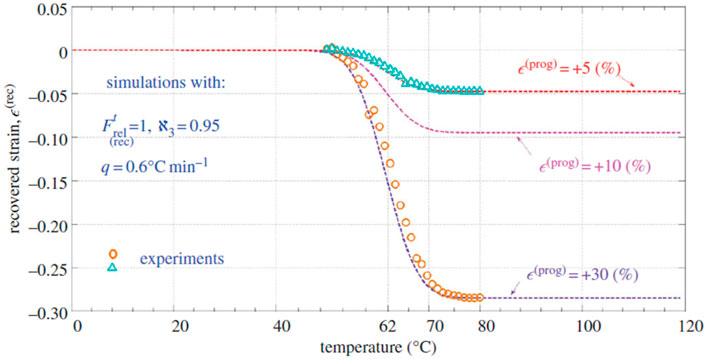
FIGURE 16. Comparison of experimental and simulation results for the effect of pre-strain levels on the final shape recovery process (Shojaei and Li, 2014). [Reproduced with permission from Proceedings of the Royal Society A, 470: 20140199., (2014). Copyright 2014 Royal Society].

FIGURE 17

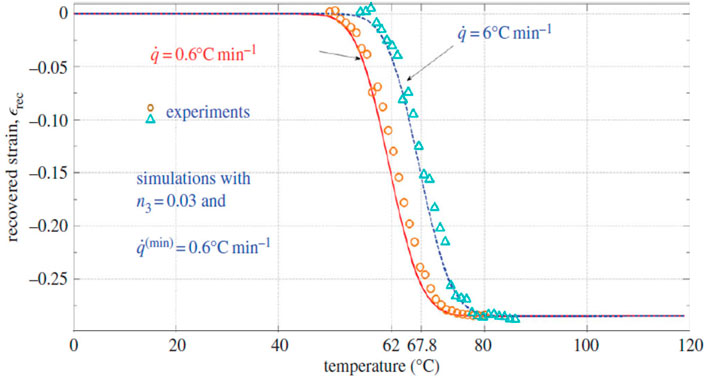
FIGURE 17. Dependence of the shape recovery process on the heating rate (Shojaei and Li, 2014). [Reproduced with permission from Proceedings of the Royal Society A, 470: 20140199., (2014). Copyright 2014 Royal Society].

FIGURE 18

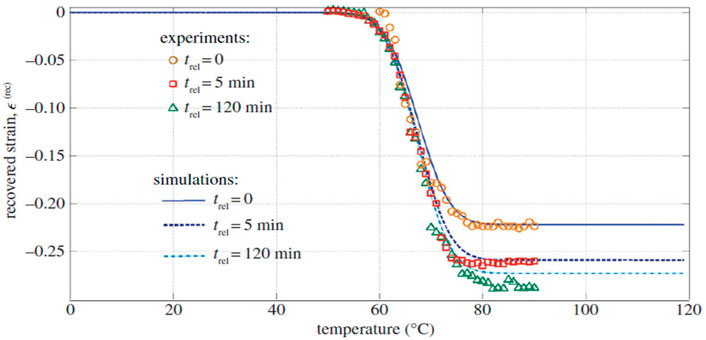
FIGURE 18. Dependence of recovered strain [(prog) = +0.3] on the holding or relaxation time t_rel (Shojaei and Li, 2014). [Reproduced with permission from Proceedings of the Royal Society A, 470: 20140199., (2014). Copyright 2014 Royal Society].

FIGURE 19

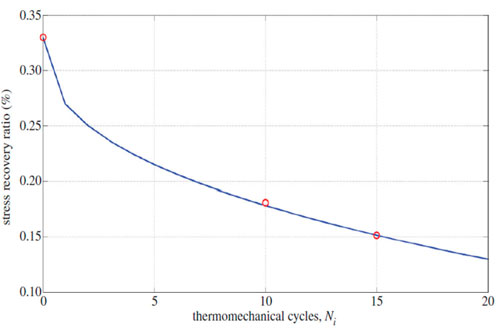
FIGURE 19. Effect of FD on the stress recovery ratio for a one-dimensional constrained stress recovery. Circles denote experimental results for confined shape recovery, and the solid line denotes simulation results (Shojaei and Li, 2014). [Reproduced with permission from Proceedings of the Royal Society A, 470: 20140199., (2014). Copyright 2014 Royal Society].

Challenges and future perspectives

Since the first SMP was discovered in 1985, considerable advancements have been made in designing, synthesizing, and manufacturing SMP-based devices and structures. Discovery of new SMPs is accelerated by the understanding of the mechanisms controlling the shape memory effect. Our understanding of the mechanisms controlling the shape memory effect for various types of SMPs has been progressing quickly, which in turn helps designing new SMPs. For example, our initial understanding of the driving force for the shape memory effect of thermoset SMPs is primarily through entropy change, that is, entropy reduction during programming and entropy increase during shape recovery (Behl and Lendlein, 2007; Meng and Li, 2013), which leads to many thermoset SMPs with very low recovery stress in the rubbery state. Our new understanding indicates that energy input during programming can also be stored through enthalpy increases by bond length change and bond angle change, which is stable at the glassy state due to steric hindrance (Fan and Li, 2018; Yan and Li, 2020a; Wick et al., 2021). Upon heating, the stored energy will be released, leading to shape and/or stress recovery. Based on this understanding, polymers with high recovery stress in the rubbery state have been designed, synthesized, and characterized (Fan and Li, 2018; Li et al., 2018; Feng and Li, 2021b). It is envisioned that with the ever-increasing discovery of new SMPs, constitutive modeling will continuously be an essential player in the design and manufacturing of new SMP-based structures and devices. For example, Yan and Li (2020a) developed a four-chain model to describe the constitutive behavior of enthalpy-driven SMPs, which was also validated by molecular dynamics simulation (Wick et al., 2021).

A recent development in amorphous SMPs is the combination of the shape memory effect and other functionalities, such as self-healing and recycling capabilities within the framework of vitrimers (Montarnal, et al., 2011; Lu et al., 2012; Gandini, 2013; Denissen et al., 2015; Obadia, et al., 2015; Chao et al., 2016; de Luzuriaga, et al., 2016; Lu et al., 2016; Zhang et al., 2016; Lu et al., 2017; Nishimura, et al., 2017; Rottger, et al., 2017; Li et al., 2018; Feng et al., 2019; Yuan et al., 2019; Feng et al., 2020a; Feng and Li, 2020b; Konlan et al., 2020; Suslu et al., 2020; Feng and Li, 2021a; Feng and Li, 2021b; Feng and Li, 2021c; Feng and Li, 2022; Konlan et al., 2022), which seamlessly utilized the shape memory effect to close the wide-opened crack first and heal the closed crack by the adaptable covalent network (CAN), per the close-then-heal (CTH) strategy initiated in Li’s lab (John and Li, 2010; Li and John, 2008; Li and Nettles, 2010; Li and Uppu, 2010; Nji and Li, 2010a; Nji and Li, 2010b; Nji and Li, 2012). The combination of the shape memory effect with flame retardancy is another new development (Feng et al., 2019; Feng et al., 2020a; Feng et al., 2020b; Feng and Li, 2021a; Feng and Li, 2021b; Feng and Li, 2022; Zhang et al., 2022). SMPs for four-dimensional printing are also a new development (Ge et al., 2016; Tibbits, 2014; Kuang et al., 2018; Li et al., 2018; Li et al., 2019; Feng et al., 2021a). Clearly, these new types of multifunctional SMPs involve multi-length scale and multi-time scale as well as multi-physics, including coupling between CANs and the shape memory effect and phase change and compositional change during fire hazard. Efforts are thus needed to provide new constitutive models to describe these new types of multifunctional SMPs.

However, one grand challenge facing this community is that the existing constitutive modeling frameworks either lack generality or consist of too many curve fitting parameters or are impractical for engineering design or lack an understanding of molecular length scale mechanisms. For example, elasto-viscoplastic models and phase evolution law models consist of a large number of parameters, and some of them must be determined by curve fitting, which make the models work only for a limited number of SMPs and cannot be generalized for other SMPs. Some models such as rheological models are simple to use but clearly lack molecular scale insights. Some models such as molecular dynamics simulation are limited to a short time scale and very small strain and are also very time-consuming for computation, which is not proper for engineering design. Therefore, there is a clear need for more in-depth understanding of the mechanisms controlling the shape memory effect. The more the use of physical parameters such as gas constant, Boltzmann constant, and Avogadro number, the simpler and more general the model and the more applicable the model in practice.

One possible solution is through machine learning. With enough training data, machine learning algorithms can learn the hidden features, for example, the correlation between the molecular structures and material properties. Because of this, machine learning has been widely used in discovering new materials, including metals and alloys (Wen et al., 2019), ceramics (Yuan et al., 2018), drugs (Guyon et al., 2002), and polymers (Wu et al., 2019). Yan et al. (2021a, 2021b) also used machine learning and discovered new thermoset SMPs, which have been validated either by molecular dynamics simulation or by experimental testing (Wick et al., 2021). Shafe et al. (2022) studied the effect of atomistic fingerprints on thermomechanical properties of epoxy-diamine thermoset shape memory polymers, which facilitates machine learning discovery of TSMPs. Recently, we also established both forward and inverse machine learning frameworks and discovered quite a few columns, lattice unit cells, and thin-walled structures with much improved structural capacities, including structures three-dimensional-printed by SMPs (Challapalli and Li, 2020; Challapalli et al., 2021a; Challapalli et al., 2021b; Challapalli and Li, 2021). Following the same line, it is expected that machine learning may also be used to establish the constitutive laws for SMPs. Actually, machine learning has been used to establish constitutive laws for rocks (Wang and Sun, 2018), liquids (Tartakovsky et al., 2020), and other solids (Masi et al., 2021). In the field of computational mechanics, the majority of applications of machine learning were related to supervised learning, which trains feed-forward neural networks to replace rate- and path-dependent constitutive laws for solid mechanics problems (Ghaboussi et al., 1991; Furukawa and Yagawa, 1998). A different approach has recently been proposed (Kirchdoerfer and Ortiz, 2016), where the supervised learning process was implemented without using the artificial neural network. Instead, a new constrained optimization approach that minimized the discrepancy between measured and predicted responses was proposed. In this approach, the universally accepted knowledge, such as the conservation of mass, conservation of energy, conservation of momentum, thermodynamics laws, and so on, was used as a constraint of the minimization problems. Consequently, by finding the saddle point of a constrained optimization problem, local data sets that were closest to the satisfaction of constraints were located and used to provide incremental updates of elasticity problems. This method has been extended to plasticity problems in Ibanez et al., 2018 by reintroducing the yield surface and enforcing perfect plasticity. It is expected that machine learning, informed by physics and bounded by physical laws such as conservation laws and thermodynamics laws, will be one of the useful tools in developing constitutive models for SMPs.

Conclusion

In this work, multiple modeling frameworks, developed in Li’s research lab within the past few years, have been reviewed and elucidated. The frameworks discussed include thermodynamics, phase evolution laws, unit cells, statistical mechanics, and continuum damage mechanics. When possible, physical insights were discussed. A large number of relevant references from other research labs were cited. Perspectives on future development were discussed in the context of challenges facing the existing model frameworks, fast growth in new multifunctional SMPs, and the potential use of the emerging machine learning technology in establishing thermomechanical constitutive models for SMPs. We hope that this insight paper will provide some fundamental knowledge on the common constitutive modeling frameworks of SMPs and shed some lights on future development in this amazing research direction.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the US National Science Foundation under grant number OIA-1946231 and the Louisiana Board of Regents for the Louisiana Materials Design Alliance (LAMDA) and the US National Science Foundation under grant number HRD-1736136.

Conflict of interest

WX was employed by the company Vitro Architectural Glass.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

Adam, G., and Gibbs, J. (1965). On the temperature dependence of cooperative relaxation properties in glass‐forming liquids. J. Chem. Phys. 43 (1), 139–146. doi:10.1063/1.1696442

CrossRef Full Text | Google Scholar

Aruda, E. M., and Boyce, M. C. (1993). A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 41, 389–412. doi:10.1016/0022-5096(93)90013-6

CrossRef Full Text | Google Scholar

Auricchio, F., Reali, A., and Stefanelli, U. (2007). A three-dimensional model describing stress-induced solid phase transformation with permanent inelasticity. Int. J. Plasticity 23, 207–226. doi:10.1016/j.ijplas.2006.02.012

CrossRef Full Text | Google Scholar

Baghani, M., Arghavani, J., and Naghdabadi, R. (2014). A finite deformation constitutive model for shape memory polymers based on Hencky strain. Mech. Mater. 73, 1–10. doi:10.1016/j.mechmat.2013.11.011

CrossRef Full Text | Google Scholar

Baghani, M., Naghdabadi, R., Arghavani, J., and Sohrabpour, S. (2012). A thermodynamically-consistent 3D constitutive model for shape memory polymers. Int. J. Plasticity 35, 13–30. doi:10.1016/j.ijplas.2012.01.007

CrossRef Full Text | Google Scholar

Balogun, O. A., and Mo, C. (2016). Three-dimensional thermomechanical viscoelastic model for shape memory polymers with binding factor. J. Intelligent Material Syst. Struct. 27, 1908–1916. doi:10.1177/1045389x15610905

CrossRef Full Text | Google Scholar

Barot, G., Rao, I. J., and Rajagopal, K. R. (2008). A thermodynamic framework for the modeling of crystallizable shape memory polymers. Int. J. Eng. Sci. 46, 325–351. doi:10.1016/j.ijengsci.2007.11.008

CrossRef Full Text | Google Scholar

Behl, M., and Lendlein, A. (2007). Shape‐memory polymers. Mater. Today 10 (4), 20–28. doi:10.1016/s1369-7021(07)70047-0

CrossRef Full Text | Google Scholar

Bhattacharyya, A., and Tobushi, H. (2000). Analysis of the isothermal mechanical response of a shape memory polymer rheological model. Polym. Eng. Sci. 40, 2498–2510. doi:10.1002/pen.11381

CrossRef Full Text | Google Scholar

Boyce, M. C., Parks, D. M., and Argon, A. S. (1989). Plastic flow in oriented glassy polymers. Int. J. Plasticity 5, 593–615. doi:10.1016/0749-6419(89)90003-x

CrossRef Full Text | Google Scholar

Brömmel, F., Kramer, D., and Finkelmann, H. (2012). in Liquid crystal elastomers: Materials and applications. Editor W. H. de Jeu (Berlin, Germany: Springer).

Google Scholar

Brunette, C. M., Hsu, S. L., and MacKnight, W. J. (1982). Hydrogen-bonding properties of hard-segment model compounds in polyurethane block copolymers. Macromolecules 15, 71–77. doi:10.1021/ma00229a014

CrossRef Full Text | Google Scholar

Challapalli, A., Konlan, J., Patel, D., and Li, G. (2021a). Discovery of cellular unit cells with high natural frequency and energy absorption capabilities by an inverse machine learning framework. Front. Mech. Eng. 7, 779098. doi:10.3389/fmech.2021.779098

CrossRef Full Text | Google Scholar

Challapalli, A., and Li, G. (2020). 3D printable biomimetic rod with superior buckling resistance designed by machine learning. Sci. Rep. 10, 20716. doi:10.1038/s41598-020-77935-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Challapalli, A., and Li, G. (2021). Machine learning assisted design of new lattice core for sandwich structures with superior load carrying capacity. Sci. Rep. 11, 18552. doi:10.1038/s41598-021-98015-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Challapalli, A., Patel, D., and Li, G. (2021b). Inverse machine learning framework for optimizing lightweight metamaterials. Mat. Des. 208, 109937. doi:10.1016/j.matdes.2021.109937

CrossRef Full Text | Google Scholar

Chao, A., Negulescu, J., and Zhang, D. H. (2016). Dynamic covalent polymer networks based on degenerative imine bond exchange: Tuning the malleability and self-healing properties by solvent. Macromolecules 49, 6277–6284. doi:10.1021/acs.macromol.6b01443

CrossRef Full Text | Google Scholar

Chen, X., and Nguyen, T. D. (2011). Influence of thermoviscoelastic properties and loading conditions on the recovery performance of shape memory polymers. Mech. Mater. 43, 127–138. doi:10.1016/j.mechmat.2011.01.001

CrossRef Full Text | Google Scholar

Chen, Y.-C., and Lagoudas, D. C. (2008a). A constitutive theory for shape memory polymers. Part I: Large deformations. J. Mech. Phys. Solids 56, 1752–1765. doi:10.1016/j.jmps.2007.12.005

CrossRef Full Text | Google Scholar

Chen, Y.-C., and Lagoudas, D. C. (2008b). A constitutive theory for shape memory polymers. Part II: A linearized model for small deformations. J. Mech. Phys. Solids 56, 1766–1778. doi:10.1016/j.jmps.2007.12.004

CrossRef Full Text | Google Scholar

Chung, T., Romo-Uribe, A., and Mather, P. T. (2008). Two-way reversible shape memory in a semicrystalline network. Macromolecules 41, 184–192. doi:10.1021/ma071517z

CrossRef Full Text | Google Scholar

Dachkovski, S., and Böhm, M. (2004). Finite thermoplasticity with phase changes based on isomorphisms. Int. J. Plasticity 20, 323–334. doi:10.1016/s0749-6419(03)00082-2

CrossRef Full Text | Google Scholar

Dai, L., Tian, C., and Xiao, R. (2020). Modeling the thermo-mechanical behavior and constrained recovery performance of cold-programmed amorphous shape-memory polymers. Int. J. Plasticity 127, 102654. doi:10.1016/j.ijplas.2019.102654

CrossRef Full Text | Google Scholar

de Luzuriaga, A. R., Martin, R., Markaide, N., Rekondo, A., Cabanero, G., Rodriguez, J., et al. (2016). Epoxy resin with exchangeable disulfide crosslinks to obtain reprocessable, repairable and recyclable fiber-reinforced thermoset composites. Mat. Horiz. 3, 241–247. doi:10.1039/c6mh00029k

CrossRef Full Text | Google Scholar

Denissen, W., Rivero, G., Nicolay, R., Leibler, L., Winne, J. M., Du Prez, F. E., et al. (2015). Vinylogous urethane vitrimers. Adv. Funct. Mat. 25, 2451–2457. doi:10.1002/adfm.201404553

CrossRef Full Text | Google Scholar

Diani, J., and Gall, K. (2007). Molecular dynamics simulations of the shape-memory behaviour of polyisoprene. Smart Mat. Struct. 16, 1575–1583. doi:10.1088/0964-1726/16/5/011

CrossRef Full Text | Google Scholar

Diani, J., Liu, Y., and Gall, K. (2006). Finite strain 3D thermoviscoelastic constitutive model for shape memory polymers. Polym. Eng. Sci. 46 (4), 486–492. doi:10.1002/pen.20497

CrossRef Full Text | Google Scholar

Dolynchuk, O., Kolesov, I., and Radusch, H. J. (2014). Thermodynamic description and modeling of two-way shape-memory effect in crosslinked semicrystalline polymers. Polym. Adv. Technol. 25, 1307–1314. doi:10.1002/pat.3335

CrossRef Full Text | Google Scholar

Dvorak, G. J., and Benveniste, Y. (1992). On transformation strains and uniform fields in multiphase elastic media. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 437, 291–310.

Google Scholar

Dvorak, G. J. (1990). On uniform fields in heterogeneous media. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 431, 89–110.

Google Scholar

Dvorak, G. J. (1992). Transformation field analysis of inelastic composite materials. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 437, 311–327.

Google Scholar

Elhag, M., Salehi, S., Li, G., Fan, J., and Teodoriu, C. (2021). Loss circulation prevention in geothermal drilling by shape memory polymer. Geothermics 89, 101943. doi:10.1016/j.geothermics.2020.101943

CrossRef Full Text | Google Scholar

Fan, J., and Li, G. (2018). High enthalpy storage thermoset network with giant stress and energy output in rubbery state. Nat. Commun. 9 (1), 642. doi:10.1038/s41467-018-03094-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, X., Fan, J., Li, A., and Li, G. (2020a). Biobased tannic acid crosslinked epoxy thermosets with hierarchical molecular structure and tunable properties: Damping, shape memory and recyclability. ACS Sustain. Chem. Eng. 8 (2), 874–883. doi:10.1021/acssuschemeng.9b05198

CrossRef Full Text | Google Scholar

Feng, X., Fan, J., Li, A., and Li, G. (2019). Multi-reusable thermoset with anomalous flame triggered shape memory effect. ACS Appl. Mat. Interfaces 11 (17), 16075–16086. doi:10.1021/acsami.9b03092

CrossRef Full Text | Google Scholar

Feng, X., and Li, G. (2021b). Catalyst-free β-hydroxy phosphate ester exchange for robust fire-proof vitrimers. Chem. Eng. J. 417, 129132. doi:10.1016/j.cej.2021.129132

CrossRef Full Text | Google Scholar

Feng, X., and Li, G. (2021a). High-temperature shape memory photopolymer with intrinsic flame retardancy and record-high recovery stress. Appl. Mater. Today 23, 101056. doi:10.1016/j.apmt.2021.101056

CrossRef Full Text | Google Scholar

Feng, X., and Li, G. (2021c). Room-temperature self-healable and mechanically robust thermoset polymers for healing delamination and recycling carbon fibers. ACS Appl. Mat. Interfaces 13 (44), 53099–53110. doi:10.1021/acsami.1c16105

CrossRef Full Text | Google Scholar

Feng, X., and Li, G. (2022). UV curable, flame retardant, and pressure-sensitive adhesives with two-way shape memory effect. Polymer 249, 124835. doi:10.1016/j.polymer.2022.124835

CrossRef Full Text | Google Scholar

Feng, X., and Li, G. (2020b). Versatile phosphate diester based flame retardant vitrimers via catalyst-free mixed transesterification. ACS Appl. Mat. Interfaces 12 (51), 57486–57496. doi:10.1021/acsami.0c18852

CrossRef Full Text | Google Scholar

Furukawa, T., and Yagawa, G. (1998). Implicit constitutive modelling for viscoplasticity using neural networks. Int. J. Numer. Methods Eng. 43, 195–219. doi:10.1002/(sici)1097-0207(19980930)43:2<195::aid-nme418>3.0.co;2-6

CrossRef Full Text | Google Scholar

Gandini, A. (2013). The furan/maleimide diels-alder reaction: A versatile click-unclick tool in macromolecular synthesis. Prog. Polym. Sci. 38, 1–29. doi:10.1016/j.progpolymsci.2012.04.002

CrossRef Full Text | Google Scholar

Ge, Q., Luo, X., Iversen, C. B., Nejad, H. B., Mather, P. T., Dunn, M. L., et al. (2014). A finite deformation thermomechanical constitutive model for triple shape polymeric composites based on dual thermal transitions. Int. J. Solids Struct. 51, 2777–2790. doi:10.1016/j.ijsolstr.2014.03.029

CrossRef Full Text | Google Scholar

Ge, Q., Sakhaei, A., Lee, H., Dunn, C., Fang, X., Dunn, M., et al. (2016). Multimaterial 4D printing with tailorable shape memory polymers. Sci. Rep. 6, 31110. doi:10.1038/srep31110

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghaboussi, J., Garrett, J. H., and Wu, X. (1991). Knowledge-based modeling of material behavior with neural networks. J. Eng. Mech. 117, 132–153. doi:10.1061/(asce)0733-9399(1991)117:1(132)

CrossRef Full Text | Google Scholar

Gilormini, P., and Diani, J. (2012). On modeling shape memory polymers as thermoelastic two-phase composite materials. Comptes Rendus Mécanique 340, 338–348. doi:10.1016/j.crme.2012.02.016

CrossRef Full Text | Google Scholar

Gu, J., Leng, J., and Sun, H. (2017). A constitutive model for amorphous shape memory polymers based on thermodynamics with internal state variables. Mech. Mater. 111, 1–14. doi:10.1016/j.mechmat.2017.04.008

CrossRef Full Text | Google Scholar

Gu, J., Sun, H., and Fang, C. (2014). A multi-branch finite deformation constitutive model for a shape memory polymer based syntactic foam. Smart Mat. Struct. 24, 025011. doi:10.1088/0964-1726/24/2/025011

CrossRef Full Text | Google Scholar

Guo, X., Liu, L., Zhou, B., Liu, Y., and Leng, J. (2016). Constitutive model for shape memory polymer based on the viscoelasticity and phase transition theories. J. Intelligent Material Syst. Struct. 27 (3), 314–323. doi:10.1177/1045389x15571380

CrossRef Full Text | Google Scholar

Guyon, I., Weston, J., Barnhill, S., and Vapnik, V. (2002). Gene selection for cancer classification using support vector machines. Mach. Learn. 46 (1-3), 389–422. doi:10.1023/a:1012487302797

CrossRef Full Text | Google Scholar

Hassan, T., Taleb, L., and Krishna, S. (2008). Influence of non-proportional loading on ratcheting responses and simulations by two recent cyclic plasticity models. Int. J. Plasticity 24, 1863–1889. doi:10.1016/j.ijplas.2008.04.008

CrossRef Full Text | Google Scholar

Hill, R. (1965). A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 13, 213–222. doi:10.1016/0022-5096(65)90010-4

CrossRef Full Text | Google Scholar

Hong, S. J., Yu, W. R., and Youk, J. H. (2010). Two-way shape memory behavior of shape memory polyurethanes with a bias load. Smart Mat. Struct. 19 (3), 035022. doi:10.1088/0964-1726/19/3/035022

CrossRef Full Text | Google Scholar

Hori, M., and Nemat-Nasser, S. (1993). Double-inclusion model and overall moduli of multi-phase composites. Mech. Mater. 14, 189–206. doi:10.1016/0167-6636(93)90066-z

CrossRef Full Text | Google Scholar

Hu, G., and Weng, G. (2000). Some reflections on the Mori-Tanaka and Ponte Casta-eda-Willis methods with randomly oriented ellipsoidal inclusions. Acta Mech. 140, 31–40. doi:10.1007/bf01175978

CrossRef Full Text | Google Scholar

Hu, J., Zhu, Y., Huang, H., and Lu, J. (2012). Recent advances in shape–memory polymers: Structure, mechanism, functionality, modeling and applications. Prog. Polym. Sci. 37, 1720–1763. doi:10.1016/j.progpolymsci.2012.06.001

CrossRef Full Text | Google Scholar

Ibanez, R., Abisset-Chavanne, E., Aguado, J. V., Gonzalez, D., Cueto, E., Chinesta, F., et al. (2018). A manifold learning approach to data-driven computational elasticity and inelasticity. Arch. Comput. Methods Eng. 25, 47–57. doi:10.1007/s11831-016-9197-9

CrossRef Full Text | Google Scholar

John, M., and Li, G. (2010). Self-healing of sandwich structures with a grid stiffened shape memory polymer syntactic foam core. Smart Mat. Struct. 19 (7), 075013. doi:10.1088/0964-1726/19/7/075013

CrossRef Full Text | Google Scholar

Ju, J., and Chen, T. (1994). Effective elastic moduli of two-phase composites containing randomly dispersed spherical inhomogeneities. Acta Mech. 103, 123–144. doi:10.1007/bf01180222

CrossRef Full Text | Google Scholar

Kafka, V. (2008). Shape memory polymers: A mesoscale model of the internal mechanism leading to the SM phenomena. Int. J. Plasticity 24, 1533–1548. doi:10.1016/j.ijplas.2007.11.001

CrossRef Full Text | Google Scholar

Kazakeviciute-Makovska, R., Steeb, H., and Aydin, A. Ö. (2012). On the evolution law for the frozen fraction in linear theories of shape memory polymers. Arch. Appl. Mech. 82, 1103–1115. doi:10.1007/s00419-012-0615-7

CrossRef Full Text | Google Scholar

Kim, J. H., Kang, T. J., and Yu, W.-R. (2010). Thermo-mechanical constitutive modeling of shape memory polyurethanes using a phenomenological approach. Int. J. Plasticity 26, 204–218. doi:10.1016/j.ijplas.2009.06.006

CrossRef Full Text | Google Scholar

Kirchdoerfer, T., and Ortiz, M. (2016). Data-driven computational mechanics. Comput. Methods Appl. Mech. Eng. 304, 81–101. doi:10.1016/j.cma.2016.02.001

CrossRef Full Text | Google Scholar

Konlan, J., Mensah, P., Ibekwe, S., Crosby, K., and Li, G. (2020). Vitrimer based composite laminates with shape memory alloy Z-pins for repeated healing of impact induced delamination. Compos. Part B Eng. 200, 108324. doi:10.1016/j.compositesb.2020.108324

CrossRef Full Text | Google Scholar

Konlan, J., Mensah, P., Ibekwe, S., and Li, G. (2022). A laminated vitrimer composite with strain sensing, delamination self-healing, deicing, and room-temperature shape restoration properties. J. Compos. Mater. 56, 2267–2278. doi:10.1177/00219983221098225

CrossRef Full Text | Google Scholar

Kovacs, A., Aklonis, J., Hutchinson, J., and Rimos, A. (1979). Isobaric volume and enthalpy recovery of glasses: II. A transparent multiparameter theory. J. Polym. Sci. Polym. Phys. Ed. 17 (7), 1097–1162. doi:10.1002/pol.1979.180170701

CrossRef Full Text | Google Scholar

Kuang, X., Chen, K., Dunn, C., Wu, J., Li, V., Qi, J. J., et al. (2018). 3D printing of highly stretchable, shape-memory, and self-healing elastomer toward novel 4D printing. ACS Appl. Mat. Interfaces 10, 7381–7388. doi:10.1021/acsami.7b18265

CrossRef Full Text | Google Scholar

Lee, B. J., Parks, D. M., and Ahzi, S. (1993). Micromechanical modeling of large plastic deformation and texture evolution in semi-crystalline polymers. J. Mech. Phys. Solids 41, 1651–1687. doi:10.1016/0022-5096(93)90018-b

CrossRef Full Text | Google Scholar

Lee, K. M., Knight, P. T., Chung, T., and Mather, P. T. (2008). Polycaprolactone - POSS chemical/physical double networks. Macromolecules 41, 4730–4738. doi:10.1021/ma800586b

CrossRef Full Text | Google Scholar

Lendlein, A., and Kelch, S. (2002). Shape memory polymers. Angew. Chem. Int. Ed. 41 (12), 2034. doi:10.1002/1521-3773(20020617)41:12<2034::aid-anie2034>3.0.co;2-m

CrossRef Full Text | Google Scholar

Lendlein, A., and Langer, R. (2002). Biodegradable, elastic shape-memory polymers for potential biomedical applications. Science 296, 1673–1676. doi:10.1126/science.1066102

PubMed Abstract | CrossRef Full Text | Google Scholar

Leng, J., Lv, H., Liu, Y., and Du, S. (2008). Synergic effect of carbon black and short carbon fiber on shape memory polymer actuation by electricity. J. Appl. Phys. 104, 104917. doi:10.1063/1.3026724

CrossRef Full Text | Google Scholar

Levitas, V. I., and Ozsoy, I. B. (2009a). Micromechanical modeling of stress-induced phase transformations. Part 1. Thermodynamics and kinetics of coupled interface propagation and reorientation. Int. J. Plasticity 25, 239–280. doi:10.1016/j.ijplas.2008.02.004

CrossRef Full Text | Google Scholar

Levitas, V. I., and Ozsoy, I. B. (2009b). Micromechanical modeling of stress-induced phase transformations. Part 2. Computational algorithms and examples. Int. J. Plasticity 25, 546–583. doi:10.1016/j.ijplas.2008.02.005

CrossRef Full Text | Google Scholar

Li, A., Challapalli, A., and Li, G. (2019). 4D printing of recyclable lightweight Architectures using high recovery stress shape memory polymer. Sci. Rep. 9, 7621. doi:10.1038/s41598-019-44110-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, A., Fan, J., and Li, G. (2018). Recyclable thermoset shape memory polymers with high stress and energy output via facile UV-curing. J. Mat. Chem. A Mat. 6, 11479–11487. doi:10.1039/c8ta02644k

CrossRef Full Text | Google Scholar

Li, G., Ajisafe, O., and Meng, H. (2013a). Effect of strain hardening of shape memory polymer fibers on healing efficiency of thermosetting polymer composites. Polymer 54, 920–928. doi:10.1016/j.polymer.2012.12.046

CrossRef Full Text | Google Scholar

Li, G., Ji, G., and Meng, H. (2015). Shape memory polymer-based sealant for a compression sealed joint. J. Mat. Civ. Eng. 27 (6), 04014196. doi:10.1061/(asce)mt.1943-5533.0001150

CrossRef Full Text | Google Scholar

Li, G., and John, M. (2008). A self-healing smart syntactic foam under multiple impacts. Compos. Sci. Technol. 68 (15-16), 3337–3343. doi:10.1016/j.compscitech.2008.09.009

CrossRef Full Text | Google Scholar

Li, G., King, A., Xu, T., and Huang, X. (2013b). Behavior of thermoset shape memory polymer based syntactic foam sealant trained by hybrid two-stage programming. J. Mat. Civ. Eng. 25 (3), 393–402. doi:10.1061/(asce)mt.1943-5533.0000572

CrossRef Full Text | Google Scholar

Li, G., Meng, H., and Hu, J. (2012). Healable thermoset polymer composite embedded with stimuli-responsive fibres. J. R. Soc. Interface 9 (77), 3279–3287. doi:10.1098/rsif.2012.0409

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, G., and Nettles, D. (2010). Thermomechanical characterization of a shape memory polymer based self-repairing syntactic foam. Polymer 51, 755–762. doi:10.1016/j.polymer.2009.12.002

CrossRef Full Text | Google Scholar

Li, G. (2014). Self-healing composites: Shape memory polymer based structures. West Sussex, UK: John Wiley & Sons.

Google Scholar

Li, G., and Shojaei, A. (2012). A viscoplastic theory of shape memory polymer fibres with application to self-healing materials. Proc. R. Soc. A 468, 2319–2346. doi:10.1098/rspa.2011.0628

CrossRef Full Text | Google Scholar

Li, G., and Uppu, N. (2010). Shape memory polymer based self-healing syntactic foam: 3-D confined thermomechanical characterization. Compos. Sci. Technol. 70 (9), 1419–1427. doi:10.1016/j.compscitech.2010.04.026

CrossRef Full Text | Google Scholar

Li, G., and Wang, A. (2016). Cold, warm, and hot programming of shape memory polymers. J. Polym. Sci. Part B Polym. Phys. 54, 1319–1339. doi:10.1002/polb.24041

CrossRef Full Text | Google Scholar

Li, G., and Xu, T. (2011a). Thermomechanical characterization of shape memory polymer–based self-healing syntactic foam sealant for expansion joints. J. Transp. Eng. 137 (11), 805–814. doi:10.1061/(asce)te.1943-5436.0000279

CrossRef Full Text | Google Scholar

Li, G., and Xu, W. (2011b). Thermomechanical behavior of thermoset shape memory polymer programmed by cold-compression: Testing and constitutive modeling. J. Mech. Phys. Solids 59, 1231–1250. doi:10.1016/j.jmps.2011.03.001

CrossRef Full Text | Google Scholar

Li, G., and Zhang, P. (2013). A self-healing particulate composite reinforced with strain hardened short shape memory polymer fibers. Polymer 54 (18), 5075–5086. doi:10.1016/j.polymer.2013.07.010

CrossRef Full Text | Google Scholar

Li, J., Rodgers, W. R., and Xie, T. (2011). Semi-crystalline two-way shape memory elastomer. Polymer 52, 5320–5325. doi:10.1016/j.polymer.2011.09.030

CrossRef Full Text | Google Scholar

Li, L., and Wang, T. (2005). A unified approach to predict overall properties of composite materials. Mater. Charact. 54, 49–62. doi:10.1016/j.matchar.2004.10.005

CrossRef Full Text | Google Scholar

Li, Y., He, Y., and Liu, Z. (2017a). A viscoelastic constitutive model for shape memory polymers based on multiplicative decompositions of the deformation gradient. Int. J. Plasticity 91, 300–317. doi:10.1016/j.ijplas.2017.04.004

CrossRef Full Text | Google Scholar

Li, Y., Hu, J., and Liu, Z. (2017b). A constitutive model of shape memory polymers based on glass transition and the concept of frozen strain release rate. Int. J. Solids Struct. 124, 252–263. doi:10.1016/j.ijsolstr.2017.06.039

CrossRef Full Text | Google Scholar

Li, Y., and Liu, Z. (2018). A novel constitutive model of shape memory polymers combining phase transition and viscoelasticity. Polymer 143, 298–308. doi:10.1016/j.polymer.2018.04.026

CrossRef Full Text | Google Scholar

Lion, A., and Peters, J. (2010). Coupling effects in dynamic calorimetry: Frequency-dependent relations for specific heat and thermomechanical responses - a one-dimensional approach based on thermodynamics with internal state variables. Thermochim. Acta 500, 76–87. doi:10.1016/j.tca.2009.12.014

CrossRef Full Text | Google Scholar

Liu, Y., Gall, K., Dunn, M. L., Greenberg, A. R., and Diani, J. (2006). Thermomechanics of shape memory polymers: Uniaxial experiments and constitutive modeling. Int. J. Plasticity 22, 279–313. doi:10.1016/j.ijplas.2005.03.004

CrossRef Full Text | Google Scholar

Liu, Y. J., Du, H. Y., Liu, L. W., and Leng, J. S. (2014). Shape memory polymers and their composites in aerospace applications: A review. Smart Mat. Struct. 23 (2), 023001. doi:10.1088/0964-1726/23/2/023001

CrossRef Full Text | Google Scholar

Long, K. N., Scott, T. F., Qi, H. J., Bowman, C. N., and Dunn, M. L. (2009). Photomechanics of light-activated polymers. J. Mech. Phys. Solids 57, 1103–1121. doi:10.1016/j.jmps.2009.03.003

CrossRef Full Text | Google Scholar

Lu, L., Cao, J., and Li, G. (2018). Giant reversible elongation upon cooling and contraction upon heating for a crosslinked cis poly(1, 4-butadiene) system at temperatures below zero Celsius. Sci. Rep. 8, 14233. doi:10.1038/s41598-018-32436-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, L., Fan, J., and Li, G. (2016). Intrinsic healable and recyclable thermoset epoxy based on shape memory effect and transesterification reaction. Polymer 105, 10–18. doi:10.1016/j.polymer.2016.10.013

CrossRef Full Text | Google Scholar

Lu, L., and Li, G. (2016). One-way multishape-memory effect and tunable two-way shape memory effect of ionomer poly(ethylene-co-methacrylic acid). ACS Appl. Mat. Interfaces 8, 14812–14823. doi:10.1021/acsami.6b04105

CrossRef Full Text | Google Scholar

Lu, L., Pan, J., and Li, G. (2017). Recyclable high performance epoxy based on transesterification reaction. J. Mat. Chem. A 5, 21505–21513. doi:10.1039/c7ta06397k

CrossRef Full Text | Google Scholar

Lu, Y. X., Tournilhac, F., Leibler, L., and Guan, Z. B. (2012). Making insoluble polymer networks malleable via olefin metathesis. J. Am. Chem. Soc. 134, 8424–8427. doi:10.1021/ja303356z

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyons, W. J. (1958). Theoretical values of the dynamic stretch moduli of fiber-forming polymers. J. Appl. Phys. 29, 1429–1433. doi:10.1063/1.1722962

CrossRef Full Text | Google Scholar

Ma, L. W., Wang, J. K., Zhang, D. W., Huang, Y., Huang, L. Y., Wang, P. J., et al. (2021). Dual-action self-healing protective coatings with photothermal responsive corrosion inhibitor nanocontainers. Chem. Eng. J. 404, 127118. doi:10.1016/j.cej.2020.127118

CrossRef Full Text | Google Scholar

Magonov, S. N., and Reneker, D. H. (1997). Characterization of polymer surfaces with atomic force microscopy. Annu. Rev. Mat. Sci. 27, 175–222. doi:10.1146/annurev.matsci.27.1.175

CrossRef Full Text | Google Scholar

Magzoub, M., Anyaezu, T., Salehi, S., Li, G., Fan, J., Teodoriu, C., et al. (2021). Evaluating sealability of blended smart polymer and fiber additive for geothermal drilling with the effect of fracture opening size. J. Petroleum Sci. Eng. 206, 108998. doi:10.1016/j.petrol.2021.108998

CrossRef Full Text | Google Scholar

Mansour, A., Taleghani, A. D., Salehi, S., Li, G., and Ezeakacha, C. (2019). Smart lost circulation materials for productive zones. J. Pet. Explor. Prod. Technol. 9 (1), 281–296. doi:10.1007/s13202-018-0458-z

CrossRef Full Text | Google Scholar

Masi, F., Stefanou, I., Vannucci, P., and Maffi-Berthier, V. (2021). Thermodynamics-based artificial neural networks for constitutive modeling. J. Mech. Phys. Solids 147, 104277. doi:10.1016/j.jmps.2020.104277

CrossRef Full Text | Google Scholar

Meng, H., and Li, G. (2013). A review of stimuli-responsive shape memory polymer composites. Polymer 54 (9), 2199–2221. doi:10.1016/j.polymer.2013.02.023

CrossRef Full Text | Google Scholar

Meng, H., Mohamadian, H., Stubblefield, M., Jerro, D., Ibekwe, S., Pang, S. S., et al. (2013). Various shape memory effects of stimuli-responsive shape memory polymers. Smart Mat. Struct. 22 (9), 093001. doi:10.1088/0964-1726/22/9/093001

CrossRef Full Text | Google Scholar

Mohamed, A., Salehi, S., Ahmed, A., and Li, G. (2022). Experimental study on rheological and settling properties of shape memory polymer for fracture sealing in geothermal formations. J. Petroleum Sci. Eng. 208 (3), 109535. doi:10.1016/j.petrol.2021.109535

CrossRef Full Text | Google Scholar

Montarnal, D., Capelot, M., Tournilhac, F., and Leibler, L. (2011). Silica-like malleable materials from permanent organic networks. Science 334, 965–968. doi:10.1126/science.1212648

PubMed Abstract | CrossRef Full Text | Google Scholar

Mori, T., and Tanaka, K. (1973). Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 21, 571–574. doi:10.1016/0001-6160(73)90064-3

CrossRef Full Text | Google Scholar

Morsch, S., Liu, Y., Lyon, S., and Gibbon, S. (2015). Insights into epoxy network nanostructural heterogeneity using AFM-IR. ACS Appl. Mat. Interfaces 8, 959–966. doi:10.1021/acsami.5b10767

CrossRef Full Text | Google Scholar

Moumni, Z., Zaki, W., and Nguyen, Q. S. (2008). Theoretical and numerical modeling of solid–solid phase change: Application to the description of the thermomechanical behavior of shape memory alloys. Int. J. Plasticity 24, 614–645. doi:10.1016/j.ijplas.2007.07.007

CrossRef Full Text | Google Scholar

Moynihan, C., Easteal, A., Debolt, M., and Tucker, J. (1976). Dependence of the fictive temperature of glass on cooling rate. J. Am. Ceram. Soc. 59, 12–16. doi:10.1111/j.1151-2916.1976.tb09376.x

CrossRef Full Text | Google Scholar

Müller, C., and Bruhns, O. (2006). A thermodynamic finite-strain model for pseudoelastic shape memory alloys. Int. J. Plasticity 22, 1658–1682. doi:10.1016/j.ijplas.2006.02.010

CrossRef Full Text | Google Scholar

Nemat-Nasser, S., and Hori, M. (1993). Micromechanics: Overall properties of heterogeneous materials. Amsterdam: Elsevier.

Google Scholar

Nguyen, T. D. (2013). Modeling shape-memory behavior of polymers. Polym. Rev. 53, 130–152. doi:10.1080/15583724.2012.751922

CrossRef Full Text | Google Scholar

Nguyen, T. D., Qi, H. J., Castro, F., and Long, K. (2008a). A thermoviscoelastic model for amorphous shape memory polymers: Incorporating structural and stress relaxation. J. Mech. Phys. Solids 56, 2792–2814. doi:10.1016/j.jmps.2008.04.007

CrossRef Full Text | Google Scholar

Nguyen, T. D., Yakacki, C., Brahmbhatt, P., and Chambers, M. (2008b). Modeling the relaxation mechanisms of amorphous shape memory polymers. Adv. Mat. 22, 3411–3423. doi:10.1002/adma.200904119

CrossRef Full Text | Google Scholar

Nishimura, Y., Chung, J., Muradyan, H., and Guan, Z. B. (2017). Silyl ether as a robust and thermally stable dynamic covalent motif for malleable polymer design. J. Am. Chem. Soc. 139, 14881–14884. doi:10.1021/jacs.7b08826

PubMed Abstract | CrossRef Full Text | Google Scholar

Nji, J., and Li, G. (2010b). A biomimic shape memory polymer based self-healing particulate composite. Polymer 51 (25), 6021–6029. doi:10.1016/j.polymer.2010.10.021

CrossRef Full Text | Google Scholar

Nji, J., and Li, G. (2010a). A self-healing 3D woven fabric reinforced shape memory polymer composite for impact mitigation. Smart Mat. Struct. 19 (3), 035007. doi:10.1088/0964-1726/19/3/035007

CrossRef Full Text | Google Scholar

Nji, J., and Li, G. (2012). Damage healing ability of A shape memory polymer based particulate composite with small thermoplastic contents. Smart Mat. Struct. 21 (2), 025011. doi:10.1088/0964-1726/21/2/025011

CrossRef Full Text | Google Scholar

Obadia, M. M., Mudraboyina, B. P., Serghei, A., Montarnal, D., and Drockenmuller, E. (2015). Reprocessing and recycling of highly cross-linked ion-conducting networks through transalkylation exchanges of C-N bonds. J. Am. Chem. Soc. 137, 6078–6083. doi:10.1021/jacs.5b02653

PubMed Abstract | CrossRef Full Text | Google Scholar

Ouyang, Z., and Li, G. (2009). Cohesive zone model based analytical solutions for adhesively bonded pipe joints under torsional loading. Int. J. Solids Struct. 46 (5), 1205–1217. doi:10.1016/j.ijsolstr.2008.10.021

CrossRef Full Text | Google Scholar

Pandini, S., Dioni, D., Paderni, K., Messori, M., Toselli, M., Bontempi, E., et al. (2016). The two-way shape memory behaviour of crosslinked poly(ϵ-caprolactone) systems with largely varied network density. J. Intell. Mat. Syst. Struct. 27, 1388–1403. doi:10.1177/1045389x15591384

CrossRef Full Text | Google Scholar

Peng, X., Hu, N., Zheng, H., and Fukunaga, H. (2009). Evaluation of mechanical properties of particulate composites with a combined self-consistent and Mori–Tanaka approach. Mech. Mater. 41, 1288–1297. doi:10.1016/j.mechmat.2009.07.006

CrossRef Full Text | Google Scholar

Pieczyska, E., Maj, M., Kowalczyk-Gajewska, K., Staszczak, M., Gradys, A., Majewski, M., et al. (2015). Thermomechanical properties of polyurethane shape memory polymer–experiment and modelling. Smart Mat. Struct. 24, 045043. doi:10.1088/0964-1726/24/4/045043

CrossRef Full Text | Google Scholar

Popov, P., and Lagoudas, D. C. (2007). A 3-D constitutive model for shape memory alloys incorporating pseudoelasticity and detwinning of self-accommodated martensite. Int. J. Plasticity 23, 1679–1720. doi:10.1016/j.ijplas.2007.03.011

CrossRef Full Text | Google Scholar

Qi, H. J., Nguyen, T. D., Castro, F., Yakacki, C. M., and Shandas, R. (2008). Finite deformation thermo-mechanical behavior of thermally induced shape memory polymers. J. Mech. Phys. Solids 56, 1730–1751. doi:10.1016/j.jmps.2007.12.002

CrossRef Full Text | Google Scholar

Qin, H., and Mather, P. T. (2009). Combined one-way and two-way shape memory in a glass-forming nematic network. Macromolecules 42, 273–280. doi:10.1021/ma8022926

CrossRef Full Text | Google Scholar

Rao, I. J., and Rajagopal, K. R. (2002). A thermodynamic framework for the study of crystallization in polymers. Z. Angew. Math. Phys. 53, 365–406. doi:10.1007/s00033-002-8161-8

CrossRef Full Text | Google Scholar

Raquez, J. M., Vanderstappen, S., Meyer, F., Verge, P., Alexandre, M., Thomassin, J. M., et al. (2011). Design of cross-linked semicrystalline poly(ε-caprolactone)-based networks with one-way and two-way shape-memory properties through Diels-Alder reactions. Chem. Eur. J. 17, 10135–10143. doi:10.1002/chem.201100496

CrossRef Full Text | Google Scholar

Reese, S., Böl, M., and Christ, D. (2010). Finite element-based multi-phase modelling of shape memory polymer stents. Comput. Methods Appl. Mech. Eng. 199, 1276–1286. doi:10.1016/j.cma.2009.08.014

CrossRef Full Text | Google Scholar

Reese, S., and Christ, D. (2008). Finite deformation pseudo-elasticity of shape memory alloys–constitutive modelling and finite element implementation. Int. J. Plasticity 24, 455–482. doi:10.1016/j.ijplas.2007.05.005

CrossRef Full Text | Google Scholar

Rottger, M., Domenech, T., van der Weegen, R., Nicolay, A. B. R., and Leibler, L. (2017). High-performance vitrimers from commodity thermoplastics through dioxaborolane metathesis. Science 356, 62–65. doi:10.1126/science.aah5281

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, L., Taleghani, A. D., and Li, G. (2018). Expandable proppants to moderate production drop in hydraulically fractured wells. J. Nat. Gas Sci. Eng. 55, 182–190. doi:10.1016/j.jngse.2018.04.026

CrossRef Full Text | Google Scholar

Santos, L., Taleghani, A. D., and Li, G. (2021). Nanosilica-treated shape memory polymer fibers to strengthen wellbore cement. J. Petroleum Sci. Eng. 196, 107646. doi:10.1016/j.petrol.2020.107646

CrossRef Full Text | Google Scholar

Sarrafan, S., Feng, X., and Li, G. (2022). A soft syntactic foam actuator with high recovery stress, actuation strain, and energy output. Mater. Today Commun. 31, 103303. doi:10.1016/j.mtcomm.2022.103303

CrossRef Full Text | Google Scholar

Scalet, G., Auricchio, F., Bonetti, E., Castellani, L., Ferri, D., Pachera, M., et al. (2015). An experimental, theoretical and numerical investigation of shape memory polymers. Int. J. Plasticity 67, 127–147. doi:10.1016/j.ijplas.2014.10.006

CrossRef Full Text | Google Scholar

Scalet, G., Pandini, S., Messori, M., Toselli, M., and Auricchio, F. (2018). A one-dimensional phenomenological model for the two-way shape-memory effect in semi-crystalline networks. Polymer 158, 130–148. doi:10.1016/j.polymer.2018.10.027

CrossRef Full Text | Google Scholar

Seefried, C. G., Koleske, J. V., and Critchfield, F. E. (1975). Thermoplastic urethane elastomers. Ii. Effects of variations in hard-segment concentration. J. Appl. Polym. Sci. 19, 2503–2513. doi:10.1002/app.1975.070190913

CrossRef Full Text | Google Scholar

Shafe, A., Wick, C. D., Peters, A. J., Liu, X., and Li, G. (2022). Effect of atomistic fingerprints on thermomechanical properties of epoxy-diamine thermoset shape memory polymers. Polymer 242, 124577. doi:10.1016/j.polymer.2022.124577

CrossRef Full Text | Google Scholar

Shojaei, A., and Li, G. (2014b). Thermomechanical constitutive modelling of shape memory polymer including continuum functional and mechanical damage effects. Proc. R. Soc. A 470, 20140199. doi:10.1098/rspa.2014.0199

CrossRef Full Text | Google Scholar

Shojaei, A., and Li, G. (2013). Viscoplasticity analysis of semicrystalline polymers: A multiscale approach within micromechanics framework. Int. J. Plasticity 42, 31–49. doi:10.1016/j.ijplas.2012.09.014

CrossRef Full Text | Google Scholar

Shojaei, A., Li, G., Fish, J., and Tan, P. J. (2014a). Multi-scale constitutive modeling of ceramic matrix composites by continuum damage mechanics. Int. J. Solids Struct. 51 (23–24), 4068–4081. doi:10.1016/j.ijsolstr.2014.07.026

CrossRef Full Text | Google Scholar

Shojaei, A., Li, G., and Voyiadjis, G. Z. (2013). Cyclic viscoplastic-viscodamage analysis of shape memory polymers fibers with application to self-healing smart materials. J. Appl. Mech. 80 (1), 011014. doi:10.1115/1.4007140

CrossRef Full Text | Google Scholar

Small, W., Singhal, P., Wilson, T. S., and Maitland, D. J. (2010). Biomedical applications of thermally activated shape memory polymers. J. Mat. Chem. 20 (17), 3356. doi:10.1039/b923717h

CrossRef Full Text | Google Scholar

Su, X., and Peng, X. (2018). A 3D finite strain viscoelastic constitutive model for thermally induced shape memory polymers based on energy decomposition. Int. J. Plasticity 110, 166–182. doi:10.1016/j.ijplas.2018.07.002

CrossRef Full Text | Google Scholar

Suslu, H., Fan, J., Ibekwe, S., Jerro, D., Mensah, P., Li, G., et al. (2020). Shape memory alloy reinforced vitrimer composite for healing wide-opened cracks. Smart Mat. Struct. 29, 065008. doi:10.1088/1361-665x/ab85a7

CrossRef Full Text | Google Scholar

Szymczyk, A., Nastalczyk, J., Sablong, R. J., and Roslaniec, Z. (2011). The influence of soft segment length on structure and properties of poly(trimethylene terephthalate)-block-poly(tetramethylene oxide) segmented random copolymers. Polym. Adv. Technol. 22, 72–83. doi:10.1002/pat.1858

CrossRef Full Text | Google Scholar

Tabatabaei, M., Taleghani, A. D., Li, G., and Zhang, T. (2021). Combination of shape-memory capability and self-assembly to plug wide remote fractures. MRS Commun. 11, 770–776. doi:10.1557/s43579-021-00130-z

CrossRef Full Text | Google Scholar

Taleghani, A. D., Li, G., and Moayeri, M. (2017). Smart expandable cement additive to achieve better wellbore integrity. J. Energy Resour. Technol. 139 (6), 062903. doi:10.1115/1.4036963

CrossRef Full Text | Google Scholar

Tartakovsky, A. M., Marrero, C. O., Perdikaris, P., Tartakovsky, G. D., and Barajas-Solano, D. (2020). Physics-informed deep neural networks for learning parameters and constitutive relationships in subsurface flow problems. Water Resour. Res. 56 (5), e2019WR026731. doi:10.1029/2019wr026731

CrossRef Full Text | Google Scholar

Thamburaja, P., and Ekambaram, R. (2007). Coupled thermo-mechanical modelling of bulk-metallic glasses: Theory, finite-element simulations and experimental verification. J. Mech. Phys. Solids 55, 1236–1273. doi:10.1016/j.jmps.2006.11.008

CrossRef Full Text | Google Scholar

Thamburaja, P., and Nikabdullah, N. (2009). A macroscopic constitutive model for shape-memory alloys: Theory and finite-element simulations. Comput. Methods Appl. Mech. Eng. 198, 1074–1086. doi:10.1016/j.cma.2008.11.016

CrossRef Full Text | Google Scholar

Tibbits, S. (2014). 4D printing: Multi‐material shape change. Archit. Des. 84, 116–121. doi:10.1002/ad.1710

CrossRef Full Text | Google Scholar

Tobushi, H., Hashimoto, T., Hayashi, S., and Yamada, E. (1997). Thermomechanical constitutive modeling in shape memory polymer of polyurethane series. J. Intelligent Material Syst. Struct. 8, 711–718. doi:10.1177/1045389x9700800808

CrossRef Full Text | Google Scholar

Tool, A. (1946). Relation between inelastic deformability and thermal expansion of glass in its annealing range. J. Am. Ceram. Soc. 29 (9), 240–253. doi:10.1111/j.1151-2916.1946.tb11592.x

CrossRef Full Text | Google Scholar

Volk, B. L., Lagoudas, D. C., and Maitland, D. J. (2011). Characterizing and modeling the free recovery and constrained recovery behavior of a polyurethane shape memory polymer. Smart Mat. Struct. 20, 094004. doi:10.1088/0964-1726/20/9/094004

CrossRef Full Text | Google Scholar

Wang, K., and Sun, W. C. (2018). A multiscale multi-permeability poroplasticity model linked by recursive homogenizations and deep learning. Comput. Methods Appl. Mech. Eng. 334, 337–380. doi:10.1016/j.cma.2018.01.036

CrossRef Full Text | Google Scholar

Wang, X., Xu, B., and Yue, Z. (2008). Micromechanical modelling of the effect of plastic deformation on the mechanical behaviour in pseudoelastic shape memory alloys. Int. J. Plasticity 24, 1307–1332. doi:10.1016/j.ijplas.2007.09.006

CrossRef Full Text | Google Scholar

Wang, Y., Wang, J., and Peng, X. (2021). Refinement of a 3D finite strain viscoelastic constitutive model for thermally induced shape memory polymers. Polym. Test. 96, 107139. doi:10.1016/j.polymertesting.2021.107139

CrossRef Full Text | Google Scholar

Wang, Z., Li, D., Xiong, Z., and Chang, R. (2009). Modeling thermomechanical behaviors of shape memory polymer. J. Appl. Polym. Sci. 113, 651–656. doi:10.1002/app.29656

CrossRef Full Text | Google Scholar

Wen, C., Zhang, Y., Wang, C. X., Xue, D. Z., Bai, Y., Antonov, S., et al. (2019). Machine learning assisted design of high entropy alloys with desired property. Acta Mater. 170, 109–117. doi:10.1016/j.actamat.2019.03.010

CrossRef Full Text | Google Scholar

Westbrook, K., Kao, P., Castro, F., Ding, Y., and Qi, H. (2011). A 3D finite deformation constitutive model for amorphous shape memory polymers: A multi-branch modeling approach for nonequilibrium relaxation processes. Mech. Mater. 43 (12), 853–869. doi:10.1016/j.mechmat.2011.09.004

CrossRef Full Text | Google Scholar

Westbrook, K. K., Parakh, V., Chung, T., Mather, P. T., Wan, L. C., Dunn, M. L., et al. (2010). Constitutive modeling of shape memory effects in semicrystalline polymers with stretch induced crystallization. J. Eng. Mater. Technol. 132, 041010. doi:10.1115/1.4001964

CrossRef Full Text | Google Scholar

Wick, C., Peters, A., and Li, G. (2021). Quantifying the contributions of energy storage in a thermoset shape memory polymer with high stress recovery: A molecular dynamics study. Polymer 213, 123319. doi:10.1016/j.polymer.2020.123319

CrossRef Full Text | Google Scholar

Wu, S., Kondo, Y., Kakimoto, M. A., Yang, B., Yamada, H., Kuwajima, I., et al. (2019). Machine-learning-assisted discovery of polymers with high thermal conductivity using a molecular design algorithm. npj Comput. Mat. 5, 66. doi:10.1038/s41524-019-0203-2

CrossRef Full Text | Google Scholar

Xiao, R., Choi, J., Lakhera, N., Yakacki, C., Frick, C., Nguyen, T., et al. (2013). Modeling the glass transition of amorphous networks for shape-memory behavior. J. Mech. Phys. Solids 61 (7), 1612–1635. doi:10.1016/j.jmps.2013.02.005

CrossRef Full Text | Google Scholar

Xiao, R., and Tian, C. (2019). A constitutive model for strain hardening behavior of predeformed amorphous polymers: Incorporating dissipative dynamics of molecular orientation. J. Mech. Phys. Solids 125, 472–487. doi:10.1016/j.jmps.2019.01.008

CrossRef Full Text | Google Scholar

Xie, T. (2010). Tunable polymer multi-shape memory effect. Nature 464, 267–270. doi:10.1038/nature08863

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, W., and Li, G. (2010). Constitutive modeling of shape memory polymer based self-healing syntactic foam. Int. J. Solids Struct. 47, 1306–1316. doi:10.1016/j.ijsolstr.2010.01.015

CrossRef Full Text | Google Scholar

Xu, W., and Li, G. (2011). Thermoviscoplastic modeling and testing of shape memory polymer based self-healing syntactic foam programmed at glassy temperature. J. Appl. Mech. 78, 061017. doi:10.1115/1.4004554

CrossRef Full Text | Google Scholar

Yan, C., Feng, X., and Li, G. (2021a). From drug molecules to thermoset shape memory polymers: A machine learning approach. ACS Appl. Mat. Interfaces 13 (50), 60508–60521. doi:10.1021/acsami.1c20947

CrossRef Full Text | Google Scholar

Yan, C., Feng, X., Wick, C., Peters, A., and Li, G. (2021b). Machine learning assisted discovery of new thermoset shape memory polymers based on a small training dataset. Polymer 214, 123351. doi:10.1016/j.polymer.2020.123351

CrossRef Full Text | Google Scholar

Yan, C., and Li, G. (2020a). A mechanism-based four-chain constitutive model for enthalpy-driven thermoset shape memory polymers with finite deformation. J. Appl. Mech. 87, 061007. doi:10.1115/1.4046583

CrossRef Full Text | Google Scholar

Yan, C., and Li, G. (2019). Design oriented constitutive modeling of amorphous shape memory polymers and its application to multiple length scale lattice structures. Smart Mat. Struct. 28, 095030. doi:10.1088/1361-665x/ab230c

CrossRef Full Text | Google Scholar

Yan, C., and Li, G. (2022). Tutorial: Thermomechanical constitutive modeling of shape memory polymers. J. Appl. Phys. 131, 111101. doi:10.1063/5.0080897

CrossRef Full Text | Google Scholar

Yan, C., Yang, Q., and Li, G. (2020b). A phenomenological constitutive model for semicrystalline two-way shape memory polymers. Int. J. Mech. Sci. 177, 105552. doi:10.1016/j.ijmecsci.2020.105552

CrossRef Full Text | Google Scholar

Yang, Q., and Li, G. (2016). Temperature and rate dependent thermomechanical modeling of shape memory polymers with physics based phase evolution law. Int. J. Plasticity 80, 168–186. doi:10.1016/j.ijplas.2015.09.005

CrossRef Full Text | Google Scholar

Yarali, E., Taheri, A., and Baghani, M. (2020). A comprehensive review on thermomechanical constitutive models for shape memory polymers. J. Intelligent Material Syst. Struct. 31 (10), 1243–1283. doi:10.1177/1045389x20916795

CrossRef Full Text | Google Scholar

Yu, K., Ge, Q., and Qi, H. J. (2014). Reduced time as a unified parameter determining fixity and free recovery of shape memory polymers. Nat. Commun. 5, 3066. doi:10.1038/ncomms4066

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, J. S., Xiong, W., Zhou, X. H., Zhang, Y., Shi, D., Li, Z. C., et al. (2019). 4-Hydroxyproline-Derived sustainable polythioesters: Controlled ring-opening polymerization, complete recyclability, and facile functionalization. J. Am. Chem. Soc. 141, 4928–4935. doi:10.1021/jacs.9b00031

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, R. H., Liu, Z., Balachandran, P. V., Xue, D. Q., Zhou, Y. M., Ding, X. D., et al. (2018). Accelerated discovery of large electrostrains in BaTiO3-based piezoelectrics using active learning. Adv. Mat. 30 (7), 1702884. doi:10.1002/adma.201702884

CrossRef Full Text | Google Scholar

Zeng, H., Leng, J., Gu, J., and Sun, H. (2018). A thermoviscoelastic model incorporated with uncoupled structural and stress relaxation mechanisms for amorphous shape memory polymers. Mech. Mater. 124, 18–25. doi:10.1016/j.mechmat.2018.05.010

CrossRef Full Text | Google Scholar

Zeng, H., Sun, H., and Gu, J. (2021). Modeling the one-way and two-way shape memory effects of semi-crystalline polymers. Smart Mat. Struct. 30, 095020. doi:10.1088/1361-665x/ac179e

CrossRef Full Text | Google Scholar

Zhang, B. R., Digby, Z. A., Flum, J. A., Chakma, P., Saul, J. M., Sparks, J. L., et al. (2016). Dynamic thiol-michael chemistry for thermoresponsive rehealable and malleable networks. Macromolecules 49, 6871–6878. doi:10.1021/acs.macromol.6b01061

CrossRef Full Text | Google Scholar

Zhang, P., Ayaugbokor, U., Ibekwe, S., Jerro, D., Pang, S. S., Mensah, P., et al. (2016a). Healing of polymeric artificial muscle reinforced ionomer composite by resistive heating. J. Appl. Polym. Sci. 133 (28), 43660. doi:10.1002/app.43660

CrossRef Full Text | Google Scholar

Zhang, P., and Li, G. (2016). Fishing line artificial muscle reinforced composite for impact mitigation and on-demand damage healing. J. Compos. Mater. 50 (30), 4235–4249. doi:10.1177/0021998316636454

CrossRef Full Text | Google Scholar

Zhang, P., Ogunmekan, B., Ibekwe, S., Jerro, D., Pang, S. S., Li, G., et al. (2016b). Healing of shape memory polyurethane fiber reinforced syntactic foam subjected to tensile stress. J. Intelligent Material Syst. Struct. 27 (13), 1792–1801. doi:10.1177/1045389x15610912

CrossRef Full Text | Google Scholar

Zhang, X., Eichenb, Y., Miao, Z., Zhang, S., Cai, Q., Liu, W., et al. (2022). Novel Phosphazene-Based flame retardant polyimine vitrimers with Monomer-Recovery and high performances. Chem. Eng. J. 440, 135806. doi:10.1016/j.cej.2022.135806

CrossRef Full Text | Google Scholar

Zhao, Q., Qi, H. J., and Xie, T. (2015). Recent progress in shape memory polymer: New behavior, enabling materials, and mechanistic understanding. Prog. Polym. Sci. 49–50, 79–120. doi:10.1016/j.progpolymsci.2015.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, J., Turner, S. A., Brosnan, S. M., Li, Q., Carrillo, J. M. Y., Nykypanchuk, D., et al. (2014). Shapeshifting: Reversible shape memory in semicrystalline elastomers. Macromolecules 47, 1768–1776. doi:10.1021/ma4023185

CrossRef Full Text | Google Scholar