Design and Applications of Integrated Transducers in Commercial CMOS Technology

Monolithic integration of Microelectromechanical Systems (MEMS) directly within CMOS technology offers enhanced functionality for integrated circuits (IC) and the potential improvement of system-level performance for MEMS devices in close proximity to biasing and sense circuits. While the bulk of CMOS-MEMS solutions involve post-processing of CMOS chips to define freely-suspended MEMS structures, there are key applications and conditions under which a solid, unreleased acoustic structure composed of the CMOS stack is preferred. Unreleased CMOS-MEMS devices benefit from lower barrier-to-entry with no post-processing of the CMOS chip, simplified packaging, robustness under acceleration and shock, stress gradient insensitivity, and opportunities for frequency scaling. This paper provides a review of advances in unreleased CMOS-MEMS devices over the past decade, with focus on dispersion engineering of guided waves in CMOS, acoustic confinement, CMOS-MEMS transducers, and large signal modeling. We discuss performance limits with standard capacitive transduction, with emphasis on performance boost with emerging CMOS materials including ferroelectrics under development for memory.

2 Introduction

Traditional MEMS transducer-based Surface and Bulk Acoustic Wave (SAW and BAW) technology has revolutionized the telecommunications sector over the past two decades, at present enabling the integration of more than a 100 high-performance filters into a handheld device (Ruby, 2015; Hagelauer et al., 2018). Likewise, CMOS-integrated MEMS transducers promise an enabling technology in multiple domains, including clock generation and routing (Srivastava et al., 2021a), chip security (Willers et al., 2016), oscillatory computing (Mahboob and Yamaguchi, 2008; Mahboob et al., 2011; Nikonov et al., 2015; Jackson et al., 2018; Romera et al., 2018; Corti et al., 2021), and adaptive filters for next-generation radio communication (He et al., 2020) because of their inherent size, weight, and power (SWaP) advantages together with the ease of impedance matching and reduced electrical parasitics.

While MEMS transducers are most commonly integrated with CMOS at the PCB or package level, monolithic integration into standard CMOS processes has been a longtime research effort (Fedder et al., 2008). The primary drawback of MEMS-first and MEMS-last approaches is the increased implementation cost due to added process complexity. This paper reviews an alternate approach to integration of unreleased CMOS-MEMS devices in commercial processes without the need for post-CMOS fabrication steps to freely suspend mechanical structures. Additional advantages of unreleased implementations include reduced acceleration sensitivity and lowered susceptibility to reliability concerns arising out of chip dicing and packaging operations (Ivira et al., 2006). This has been demonstrated for unreleased devices such as Solidly Mounted Resonators (SMRs) (Birdsall et al., 2002) and SAW resonators (Tiersten et al., 1986) which exhibit acceleration sensitivities in the 1–2 ppb/g range as compared to released Film Bulk Acoustic Resonator (FBAR) devices which can have sensitivities up to 80 ppb/g (Ruby et al., 2012). Thus far, unreleased CMOS-MEMS devices have included resonant body transistors (RBTs) in the front end of line (FEOL) of IBM12RF 32 nm SOI (Marathe et al., 2014) and GlobalFoundries 14LPP processes (Anderson et al., 2021; Rawat et al., 2022), as well as back end of line (BEOL) resonators in Texas Instruments’ HPE035 130 nm FeRAM process (He et al., 2019; He et al., 2020). Table 1 briefly compares the implementation details and performance parameters of these different CMOS-MEMS designs, which are depicted with traditional MEMS integration approaches in Figure 1. This set of devices exemplify the range of frequencies and performance which can be designed for across different technology nodes.

TABLE 1

TABLE 1. Comparison of CMOS-MEMS designs implemented in different process technologies.

FIGURE 1

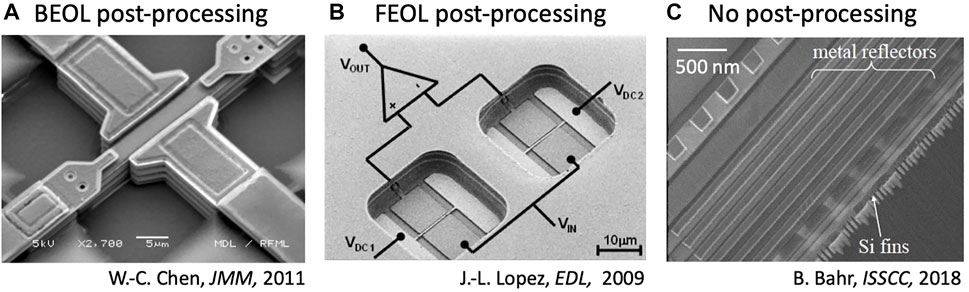
FIGURE 1. Scanning Electron Micrographs as representative examples of post-processing approaches for CMOS-MEMS devices. (A) Sacrificial etching of Back End of Line (BEOL) layers in CMOS to generate suspended MEMS structures in metal and dielectric layers (Chen et al., 2011). (B) Post-processing of both BEOL and FEOL layers to create suspended MEMS devices using high-quality FEOL materials such as the polysilicon gate layer (Lopez et al., 2009). In both (A,B), CMOS-MEMS transducers are air-gap capacitors for both drive and sense. (C) Solid-state CMOS-MEMS resonators with no post-processing to the standard CMOS chip (Bahr et al., 2018). Devices are not released, with acoustic waveguides designed from BEOL and FEOL layers to sustain acoustic modes. Periodic structures along the wafer define frequency, dispersion characteristics, and lateral confinement of the acoustic vibrations in the chip. Transduction leverages the transistor gate dielectric for driving acoustic modes, and transistor drain current for sensing vibrations. Figures © IEEE, reprinted with permission.

These devices utilize internal dielectric transduction (Weinstein and Bhave, 2007; Weinstein and Bhave, 2009) arising out of FEOL gate-oxide capacitance (Marathe et al., 2012) or piezoelectric transduction based on BEOL (He et al., 2019) ferroelectric materials for actuation of the resonance cavity. Sensing of the resonant mode in the same manner as actuation, can also be done capacitively or piezoelectrically. However, the high capacitive feedthrough in the former makes it prohibitively difficult to incorporate. In such cases, a novel resonant sensing scheme enabled by CMOS integration can be utilized, which involves modulation in the electrical characteristics of a sense transistor embedded within the resonant cavity. In this active sensing technique, the periodic stress/strain induces changes to the electronic bandstructure of the channel material resulting in the superposition of a time varying current over the bias current which can then be read out. Carefully engineered modal stress/strain field localization in the transistor channel region and related intricacies for active sensing will be extensively discussed. In devices based on BEOL-integrated ferroelectrics, piezoelectric drive as well as sense transduction are employed due to higher transduction efficiency of the piezoelectric transduction.

A challenging aspect of integrated CMOS-MEMS devices beyond drive and sense transduction, is the design of a low-loss acoustic resonance cavity which is of paramount importance as far as the overall device Q-factor (key performance parameter) is concerned. First generation RBT devices (Marathe et al., 2012) utilized Acoustic Bragg Reflectors (ABRs) in the longitudinal resonance direction to attain mode localization but the absence of confinement in the BEOL and substrate region resulted in low Q values. A more efficient technique of designing and utilizing a BEOL phononic crystal with a bandgap centered around the mode of interest was employed in the second generation of CMOS-MEMS RBTs (Bahr et al., 2015) which resulted in a 10× Q improvement over the previous generation of devices. The challenge of this approach is that such a structure may be limited by design rule constraints, requiring co-optimization of confinement and resonator design (Bahr et al., 2015; Bahr et al., 2016a). In the latest generation of CMOS-MEMS RBTs (Bahr et al., 2018; Anderson et al., 2021), a phononic waveguiding based approach is used as opposed to separate design of cavity and confinement structures. Acoustic dispersion engineering based design leads to confinement in the BEOL region through PnCs/plate reflectors, in the substrate region through the phenomenon of index guiding and in the lateral periodicity direction through lattice constant mismatch resulting in up to 56× increase in the Q-factor. The same phononic waveguiding approach was also used to design BEOL ferroelectric capacitor based CMOS-MEMS resonators. A comprehensive comparison of different performance metrics of these device across different technologies and operating conditions will also be provided in the paper.

The complexity of commercial processes with their multitude of materials, layers, and geometries means that it is often prohibitive to simulate an entire resonator structure in 3D. Owing to this reason and the differential phononic waveguide based design, it becomes necessary to design such devices primarily based on a unit cell of the structure with periodic boundary conditions. The discrepancies arising out of these simulation conditions are addressed here with reference to measured device characteristics. The avenues available to the designer in subsequent design iterations to mitigate performance impacts due to variations caused by manufacturing, differing material properties, metal fill and other sources is also discussed. Current devices with internal dielectric transduction tend to use significantly higher number of drive unit cells than sense, with the sense units at the center of the structure where the periodic boundary assumptions are most valid. At the lateral ends of the cavity, both gradual (adiabatic) and abrupt terminations have been studied, with gradual terminations shown to moderately boost Q (Joannopoulos et al., 2008; Anderson et al., 2021). The choice of termination for the cavity may have a large impact in the location and magnitude of spurious modes, again requiring careful consideration by the designer.

To enable system-level design for different applications of these integrated CMOS-MEMS devices, accurate modeling is a necessity. Initial models employed the modified Butterworth-van-Dyke (MBVD) model to represent the drive transducers and the resonant cavity and controlled current sources for active transistor sensing (Bahr, 2016a). Since these models are small-signal in nature, they are not suitable for use in oscillator applications where large signal swings are encountered. Subsequent device compact models (Bahr et al., 2016b; Bahr et al., 2016c) captured the relevant physics appropriately but were based on theoretical formulations which are not applicable to the complex structures and mode shapes exhibited in the most advanced CMOS-MEMS RBTs. An experimentally-backed, all-encompassing compact model has been developed (Rawat et al., 2022) for this class of CMOS-MEMS devices which can be used for all system-level design scenarios. Detailed modeling aspects of integrated CMOS-MEMS devices are also presented in this paper.

While these CMOS-integrated transducers have been demonstrated in several technology nodes, none have yet taken advantage of recent advances in CMOS-compatible ferroelectric materials. The integration of doped HfO₂ films into commercial processes brings with it the promise of more efficient piezoelectric actuation (Trentzsch et al., 2016; Hakim et al., 2021), potentially reducing the power and size requirements for CMOS-integrated resonators even further. Other such potential opportunities for performance enhancement as well as new applications are also discussed.

3 Grated CMOS Phononic Waveguide Resonator Design

In the optical domain, devices based on photonic sub-wavelength gratings (SWG) exhibit lower propagation loss than their strip waveguide counterparts, alongside demonstration of tuning of macroscopic optical properties such as refractive index in various material platforms (Rosenblatt et al., 1997; Wang et al., 2016; Kazanskiy et al., 2020; Donzella et al., 2015; Wang et al., 2014; Bock et al., 2010; Cheben et al., 2010). These devices are comprised of lithographically-defined periodic slow-wave structures using two distinct materials with a lattice constant smaller than the wavelength of light. The periodic medium has a higher effective refractive index and is bounded by the lower refractive index substrate below and cladding materials on either side as shown in Figure 2A. Owing to this refractive index profile along the z-direction, an optical mode is capable of being completely confined within the grating structure, an extensively investigated phenomenon known as index guiding. Optical couplers, wavelength multiplexers and filters have been demonstrated using this design principle. The acoustic/phononic analogue of index guiding can be seen in certain Sezawa and Love wave based SAW devices such as those in (Takai et al., 2017; Nakagawa et al., 2019), comprised of metal electrode gratings on a piezoelectric layer atop a higher acoustic velocity layer. The SAW mode is vertically confined in the piezoelectric layer with low bulk radiative losses due to index guiding resulting in significant improvement in propagation loss relative to unguided SAW modes in bulk piezoelectric substrates.

FIGURE 2

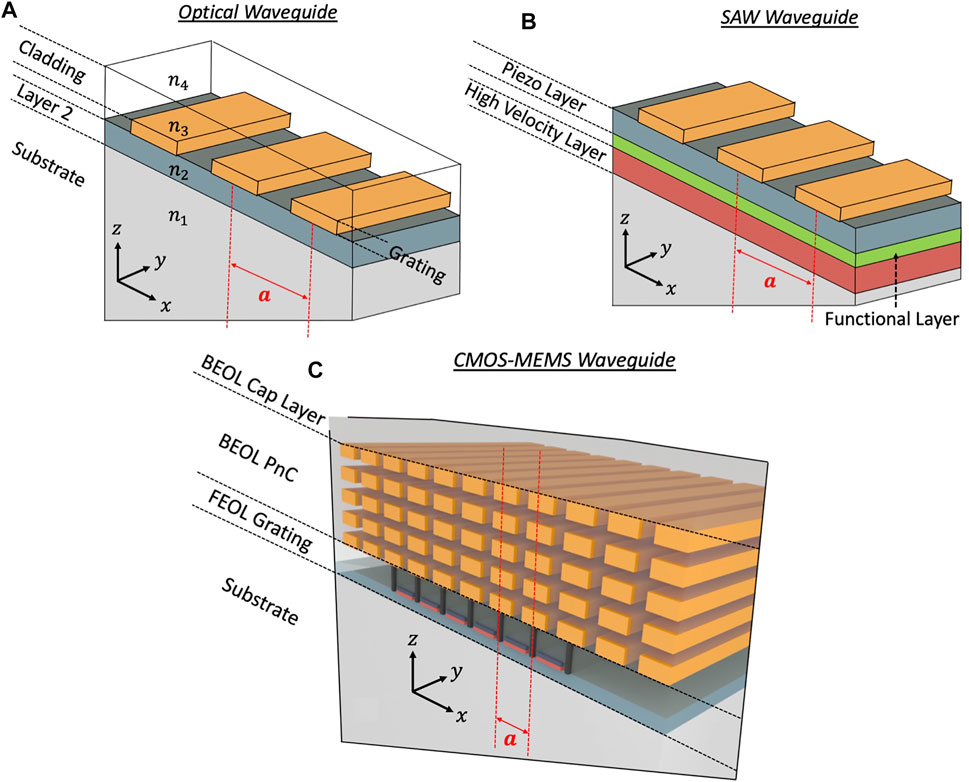
FIGURE 2. (A) Photonic SWG waveguide with lattice constant a and the effective refractive index of the grating structure comprising of n₃ and n₄ higher than the indices n₁, n₂ and n₃ of the surrounding media. (B) IHP SAW grating waveguide structure having a lattice constant a depicting the piezoelectric amd patterned metal layers atop functional and high-velocity layers. (C) CMOS phononic waveguide grating structure with patterned BEOL PnC and lattice constant a.

Toward the goal of acoustic wave propagation and confinement in CMOS, the same fundamental index guiding principles can be used to obtain phononic waveguiding in conventional CMOS platforms by utilizing periodic FEOL/BEOL materials within the constraints of the Design Rules (DRs) set by the technology under consideration. Depending on availability of electromechanical transduction mechanisms in the FEOL and/or BEOL regions, the aforementioned grating can be created using transistor layers and source-drain-gate contacts or using BEOL transducer materials respectively. The resulting grated waveguide is a slow wave structure capable of supporting modes with acoustic velocities lower than the substrate and other surrounding regions. Figure 2C shows the schematic for a FEOL phononic waveguide implemented in a planar CMOS process with the distinct regions necessary for efficient waveguiding. In modern CMOS process nodes the BEOL dielectrics are typically low-k dielectrics which have higher viscoelastic loss as compared to the high intrinsic Q-factor silicon substrate. Therefore, it is important to confine the mode as close to the substrate and as far away from the BEOL dielectrics as possible to achieve a high overall Q-factor. While the FEOL grating by itself, bounded by the substrate and the BEOL material stack, may be capable of sustaining a waveguide mode, this would be a sub-optimal implementation because of significant field penetration into the lossy BEOL materials. For further confinement in the z-direction, a BEOL Phononic Crystal (PnC) structure comprised of the available metal levels is utilized as shown in Figure 2C. In this section, each of these design aspects associated with CMOS grated waveguide resonators is discussed in further detail.

3.1 BEOL PnC Design

Phononic crystals are the acoustic analogues of photonic crystals (Kushwaha et al., 1993; Sigalas and Economou, 1993) composed of periodic arrangement of materials having different acoustic velocities. PnCs exhibit effective material properties that are not otherwise achievable using conventional materials (Khelif and Adibi, 2015). One emergent macroscopic property from the periodic nature of PnCs is the existence of acoustic band-gaps (BGs), which are frequency ranges within which acoustic waves are forbidden to propagate. Acoustic wave manipulation in SAW and slab propagation scenarios such as in (Olsson and El-Kady, 2008) has been previously demonstrated to create a gamut of devices ranging from PnC waveguides and resonators to add-drop filters. PnCs having band-gaps centered on resonance frequencies have been employed to enhance the Q-factor of MEMS resonators by either being used as tethers for the released structure (Wang and Weinstein, 2011; Lin et al., 2014; Wang et al., 2015; Gokhale and Gorman, 2017; Rawat et al., 2017) or in the surrounding region to prevent acoustic energy leakage (Siddiqi and Lee, 2018).

PnCs for acoustic wave or modal confinement at RF and mm-Wave frequencies in CMOS can be realized using patterned BEOL metals embedded in dielectric materials (Bahr et al., 2014; Bahr et al., 2015; Anderson et al., 2021), used for electrical routing on chip. The primary goal of the BEOL PnC design is to maximize the phononic band-gap by optimizing the lateral metal width/spacing and via inclusion/exclusion limited by the waveguide lattice constant and the design rule checks (DRCs). The optimized PnC is then used to confine the mode in the FEOL grating and transduction layer by preventing acoustic propagation vertically up through the CMOS stack. Acoustic impedance contrast between the BEOL metal and dielectric materials specific to the process is one of the primary factors that determines the band-gap width.

A higher impedance contrast is expected to lead to a higher band-gap width, hence CMOS processes such as planar IBM12RF and FinFET GF 14LPP with copper (Cu) metal and low-k dielectrics are capable of producing band-gap widths ranging from 1.07 to 3.8 GHz. On the other hand, low impedance contrast processes such as the IBM 130 nm and XFab 180 nm processes that make use of copper (Cu) or Tungsten (W) metals embedded in the Silicon-di-Oxide (SiO₂) dielectric result in significantly lower band-gaps ranging from 0.3 to 0.72 GHz (Bahr, 2016b). PnCs implemented in older process technologies that make use of Aluminum as the BEOL metal do not provide a usable bandgap. This is owing to the low impedance contrast between Aluminum and the BEOL dielectric material (primarily SiO₂ in these processes).

Figure 3A illustrates the implementation of a 2D PnC unit cell in the IBM12RF process BEOL for vertical acoustic confinement with the corresponding band structure. The band structure depicting the dispersion characteristics of the PnC are obtained using FEM Eigenfrequency simulations with Floquet Periodic Boundary Conditions (PBCs) by spanning the wave-vector $\vec{k}$ along the edges of the Irreducible Brillouin Zone (IBZ) as shown Figures 3A,B. A complete band-gap of 3.03 GHz is obtained for the 2D PnC under consideration. Figure 3B illustrates the phononic bandstructure of a BEOL reflector plate having the same Cu thickness and unit cell dimensions as the PnC unit cell in Figure 3A. Comparing the dispersion characteristics of the two types of cells, it can be seen that the reflector plate exhibits only a partial BG of 3.49 GHz along the X-M direction and not a complete BG like the PnC. This implies that the reflector plate, while capable of providing confinement for acoustic waves perfectly along the X-M direction, is not capable of blocking oblique leakage in the Γ-M direction like in the PnC. The reflector plate provides inferior overall confinement. However, in cases where DRC prohibits PnC dimensions corresponding to required BG characteristics, it is a valid option for device design. As an example in the case of a 32 GHz Resonant Fin Transistor design, PnC dimensions small enough for creating a BG around these frequencies are not allowed, thus multi-metal layer plate reflectors are employed (Bahr et al., 2018).

FIGURE 3

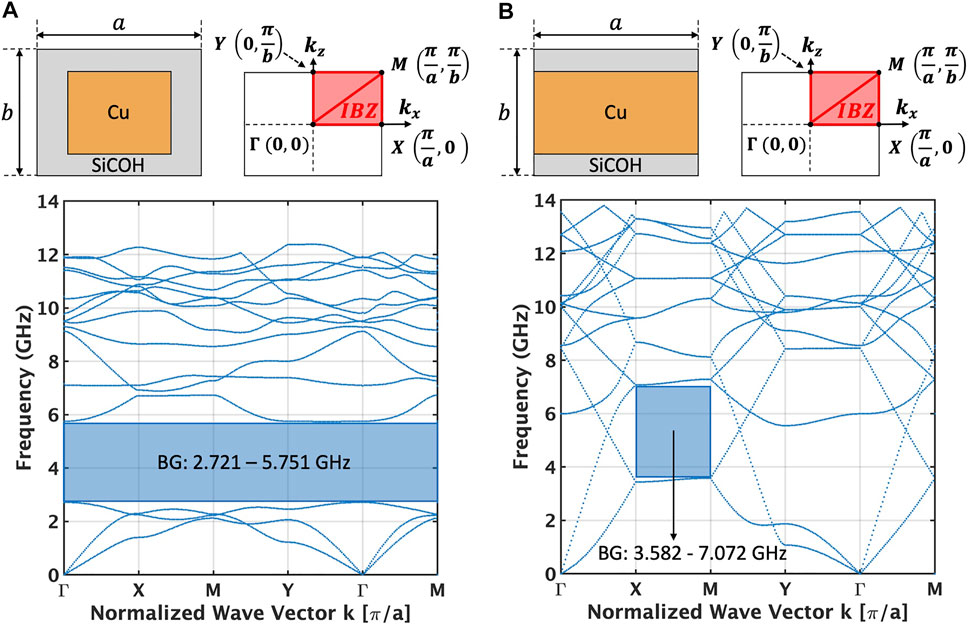
FIGURE 3. (A) Acoustic bandstructure for a BEOL PnC unit cell implemented in the IBM12RF SOI process exhibiting a complete band-gap. (B) Acoustic bandstructure for a BEOL reflector plate unit cell implemented in the IBM12RF SOI process exhibiting a partial band-gap along the X-M direction only.

3.2 Waveguide Dispersion Engineering

As has been established, phononic waveguiding is achieved in CMOS FEOL layers through index guiding and vertical PnC confinement. When appropriately designed, the guided mode is confined in the FEOL region with maximum stress concentration around the channel region of transistors, where electromechanical transducers are located. Waveguide acoustic dispersion is critical in optimizing device performance. The same 2D FEM Eigenfrequency simulation procedure used in the case of the PnC dispersion characteristics is also used for waveguides. Since the waveguide structure is periodic along the propagation x-direction only, single 2D and 3D array elements as shown in Figure 4A for IBM 32SOI RBT and (b) for GF14LPP RBT, respectively, are used to calculate the dispersion characteristics by varying the x-component of the wave-vector $\vec{k}$ ie. k_x along the edge of the IBZ.

FIGURE 4

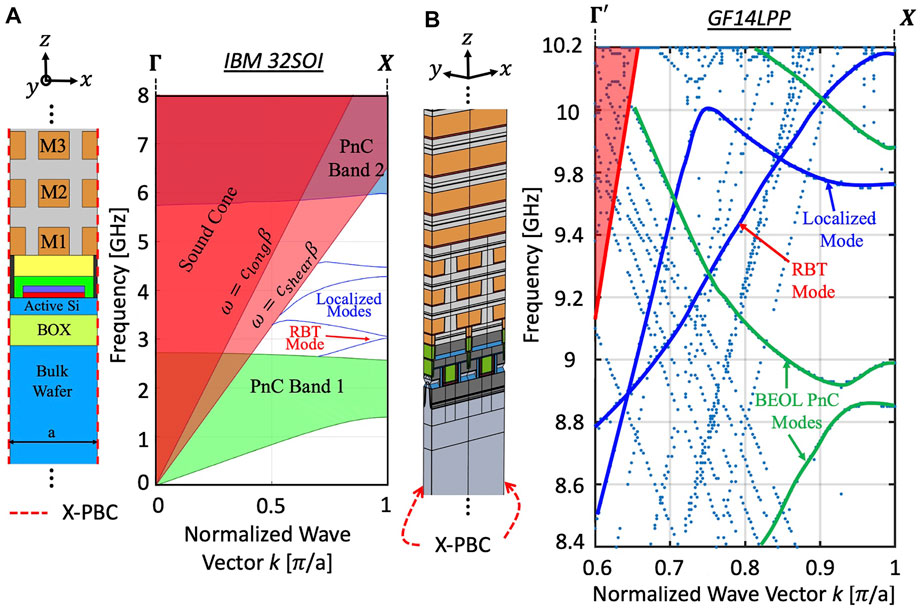
FIGURE 4. (A) A single waveguide 2D unit cell with x-direction periodic boundary conditions corresponding to the IBM12RF process together with its bandstructure showing various modes that exist and the sound cones. This figure is a reprint of Figure 3 in (Bahr and Weinstein, 2016) reprinted with the permission of the Transducer Research Foundation (B) A 3D waveguide unit cell for the fin-Resonant Body Transistor (fRBT) device implemented in the GF14LPP process and the corresponding bandstructure with different modes.

From the obtained dispersion characteristics as shown in Figure 4, it can be seen that a multitude of modes, which are valid Eigenstate solutions for the structure, are obtained. Of these, localized waveguide modes lying below the longitudnal and shear wave sound cones of the substrate are of interest since these modes propagate in the FEOL region where they can be actuated and sensed effectively. BEOL PnC modes propagate only in the PnC region and are not capable of being interacted with electromechanically. For minimizing the acoustic leakage into the bulk substrate, the effective $|\vec{k}|$ distance between the point X in the IBZ and the edge of the soundcone at the same frequency is to be maximized. This ensures the lowest coupling of the targeted RBT mode to the bulk propagation states improving the mode index guiding and thereby raising the overall Q-factor.

The device designer has multiple avenues for augmenting the targeted mode by tuning the waveguide structural parameters within the confines of the DRCs to get the desired Q as well as effective electromechanical transduction. As can be inferred from the unit cells in Figure 4, a change in the transistor gate length changes the dispersion characteristics which can be used to set the resonance frequency to the desired value as well as to design appropriate waveguide terminations (discussed later). To enhance stress concentration in the gate/channel region of the transistor, it is sometimes useful to add a gate contact along with the first level metal routing to the unit cell. For a given lattice constant, the width and spacing of the BEOL metal PnCs can be also be adjusted to maximize channel stress. Similarly, in the case of BEOL phononic waveguides comprising of FeCAP transducers (He et al., 2019; He et al., 2020), the lower limit of the spacing between the individual transducers as set by the DRCs governs the attainable lowest frequency. The available degrees of freedom for tuning the waveguide dispersion are the transducer length, addition/removal of vias and the BEOL PnC metal width, spacing and arrangement.

3.3 Lateral Acoustic Confinement

While index guiding and BEOL PnCs allow for vertical confinement in the z-direction, in order to create a resonator, terminations in the horizontal x- and y-directions are also required. The terminations on either side of the waveguide along the direction of propagation (x-direction) act as reflectors, trapping energy within the waveguide cavity where electromechanical transduction can occur. The efficiency with which the terminations reflect acoustic energy back into the cavity determines the overall Q-factor of the device considering radiative losses. The primary goal in designing appropriate terminations for the waveguide cavity is to provide adequate reflectivity while minimizing scattering at the cavity-termination boundary.

Initial waveguided RBT designs such as those demonstrated in (Bahr et al., 2015) relied on reflections due to abrupt cavity terminations on either side together with a Tungsten contact bulk tie. While the acoustic impedance mismatch between the cavity and the termination regions does provide reflection, it also introduces significant amount of bulk scattering which is one of the factors limiting the overall measured Q-factor of the device to 260. A more efficient method for lateral confinement is to use the termination waveguides which have the same structure as the cavity waveguide but a different lattice constant as shown in Figure 5A. As can be seen in the complex dispersion relations in Figure 5B, the targeted RBT mode in the cavity region is not capable of coupling to any of the guided modes in the termination waveguide at the same frequency f_res because of the significant distance between them in the k − space. A large wavenumber detuning Δ is required for coupling between guided modes in the cavity and termination waveguides leading to confinement. While there may be low k − space overlap between the targeted mode and the BEOL PnC modes in the termination at the same frequency, the spatial separation and polarization difference between them prevents any coupling from taking place. The termination lattice constant is optimized for the maximum Q-factor associated with radiative losses. 2D and unit-cell based 3D finite element models are indispensable for overall device design but do not take into account finite cavity aperture along the y-direction. Dispersion engineering similar to that in laterally confined SAW devices (Inoue et al., 2007; Solal et al., 2010; Inoue et al., 2013) ensures that there is minimal lateral acoustic leakage out of the cavity and into the surrounding regions.

FIGURE 5

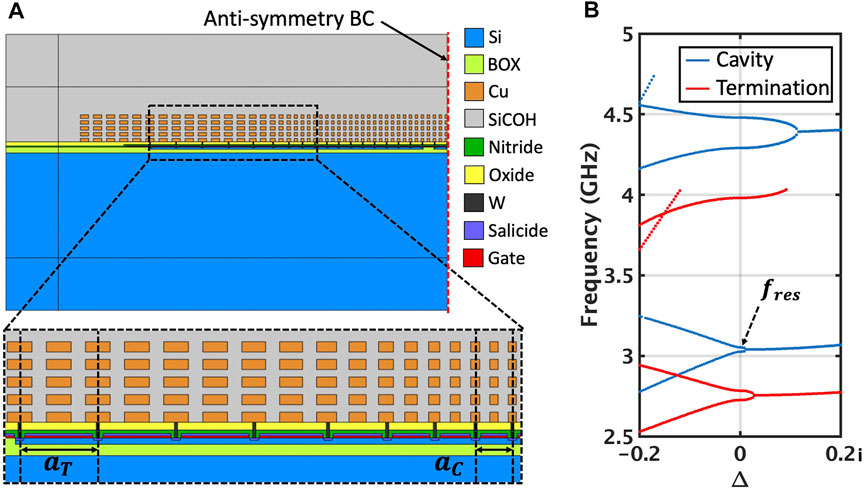
FIGURE 5. (A) Schematic showing half of the IBM12RF RBT 2D-FEM model with an Anti-symmetric Boundary Condition (BC). The adiabatic transition from the cavity lattice constant a_C to the termination lattice constant a_T can also be seen. (B) Complex bandstructure for the waveguide and termination regions with the x-axis representing wavenumber detuning from the point X in the IBZ. The cavity waveguide mode has a resonance at f_res.

To further improve lateral confinement, smooth adiabatic transition from the cavity lattice constant to the termination lattice constant can be employed. According to the Adiabatic Theorem (Johnson et al., 2002; Bahr, 2016b), a sufficiently slow transition from the cavity to terminations can practically eliminate any scattering at their interface. This technique has previously been adopted for photonic waveguides (Johnson et al., 2003; Üstün and Kurt, 2011; Oskooi et al., 2012) to couple light into slow light structures and for creating adiabatic bends. Other equivalent phononic demonstrations of adiabatic transitions can be seen in (Dehghannasiri et al., 2016; Shao et al., 2019).

3.4 Effective Modal Transduction

The transducers, whether in FEOL or BEOL, form a part of the cavity waveguide. Hence, effective electromechanical transduction is closely linked to the mode design, drive/sense configuration, constraints set by the DRCs and the transducer type. From a general drive transducer perspective, to maximize energy transfer to the device, the physical overlap between the transducer drive force and the modal displacement displacement field should be maximized. This can be quantified using the following equations (Rawat et al., 2022) for the equivalent displacement of a mode together with the resulting effective stiffness k_eq:

$W_e=|F_e|u_{i,eq}=\frac{1}{A_{\mathit{act}}}{\iint }_{A_{\mathit{act}}}\overrightarrow{F_e}.\overrightarrow{u_i}dA(1)$

$k_{eq}=\frac{2E_{\mathit{stored}}}{|u_{i,eq}^2|}(2)$

where $\overrightarrow{F_e}$ is the applied electrostatic force, u_i,eq is the equivalent modal displacement, $\overrightarrow{u_i}$ is the vector displacement field of the actuation surface having an area A_act, and E_stored is the stored energy. In a sub-optimal design, the drive force and the displacement field maxima are misaligned causing a reduction in the effective displacement, increase in the effective stiffness, and hence a reduction in the motional capacitance of the mechanical series equivalent circuit. The transduction efficiency $(k_{\mathit{eff}}^2)$ which is given by the ratio of the motional capacitance to the static transducer capacitance, reduces. This implies that in a sub-optimal design, the majority of the incident electrical signal is reflected back with a small fraction of the overall energy making it to the device. This is also applicable for the sense transducer. This transducer design principle highlights an important trade-off in the overall device performance wherein the mode design for requirements for high-Q and high-$k_{\mathit{eff}}^2$ may be at odds. It may so happen that the designed mode maximises the overlap integral in Eq. 1 but in doing so the mode is concentrated in low-Q materials such as metals and intermetal dielectrics, which lowers the overall Q-factor. In the case of transistor sensing as implemented in the IBM12RF and GF14LPP devices, the primary goal is to design the mode such that the stress in the transistor channel can be maximized. Additionally, in order to ensure that the $k_{\mathit{eff}}^2$ is maximized, modes have to be designed such that the ratio of the transducer volume to the overall modal volume is as high as possible.

At the frequency corresponding to the mode of interest, it can be observed from the typical bandstructure of a waveguide unit cell (Figure 4A), that it is possible to excite not only the targeted mode but also modes that are either close to or within the sound cone. If the coupling between the drive force and the modes in the sound cone is significant, it would result in low Q due to radiative losses through modes that can propagate freely in the substrate. The designed waveguide modes typically operate at point X in the IBZ which means that the acoustic fields in adjacent unit cells in the cavity are 180^o out of phase as shown in Figure 6A. To minimize coupling to the sound cone and to maximize coupling to the targeted mode, fully differential drive and sense transduction is preferred in the cavity, corresponding to a single large spatial frequency component at point X in the k − space IBZ. A complete mathematical treatment for the same can be found in (Bahr, 2016b). Fully differential drive and sense is also useful from an applications perspective since it eliminates any common-mode noise. It may not always be possible to achieve fully differential drive and sense, in the case of the Resonant Fin Transistor (RFT) devices it is not possible to differentially contact each transistor fin owing to DRC restrictions. In such cases a compromise is reached by driving three adjacent fins and skipping four fins in between as shown in Figure 6B. This configuration is also capable of driving the differential mode albeit with a lower coupling since one of the three fins in the transducer finger has an opposite acoustic field polarity to the other two resulting in overlap cancellation.

FIGURE 6

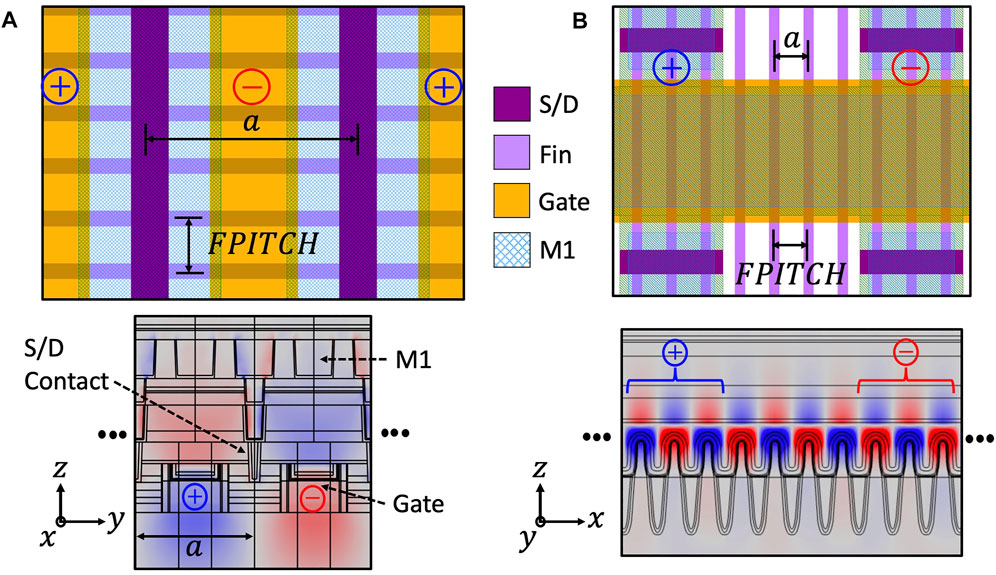
FIGURE 6. (A) Layout and y-stress plot for a pair of unit cells in an 11.8 GHz Fin Resonant Body Transistor (fRBT) device in GF14LPP. (B) Layout and y-Stress plot for a 32 GHz Resonant Fin Transistor (RFT) device in GF14LPP depicting the 3-skip-4 drive transducer configuration.

4 Electromechanical Conversion

For electromechanical drive and sensing, there are many CMOS-integrable transduction mechanisms (Huber et al., 1997; Yang and Xu, 2017) that may be used including the shape memory effect (Hunter et al., 1991), phase transition materials (Shi et al., 2019; Huang et al., 2021), and electrothermal (Gilgunn et al., 2008; Koh et al., 2011; Zope et al., 2020). Shape memory alloys and phase change actuators promise large work densities for demanding microrobotics applications, but have not yet been integrated in any commercial CMOS technology. These technologies are also limited to relatively low duty cycles (kHz to low MHz) that make them unsuitable for high frequency transduction.

Electrothermal actuators are notable in that they are easily realizable in commercial MEMS processes (Abbasalipour et al., 2018) and offer moderate work densities (Zope et al., 2020). Furthermore, they are predicted to scale well into the GHz regime (Rahafrooz and Pourkamali, 2011; Ramezany and Pourkamali, 2018) as thermal time constants decrease with decreasing size. Most commonly used, however, is direct energy-conserving electromechanical conversion using capacitive and piezoelectric transducers.

4.1 Capacitive Transduction

Air gap capacitive transduction has been successfully utilized in commercial devices for many years (Partridge and Tabatabaei, 2009). Such devices are typically integrated either at the wafer packaging level or through custom post-processing (Fedder et al., 2008; Lopez et al., 2009; Chen et al., 2011; Lapisa et al., 2011). Since the electromechanical coupling coefficient in air gap transducers increases as gap size shrinks, significant effort has gone into innovative processing techiques for achieving high aspect ratio structures (Ayazi, 2002; Ozgurluk et al., 2020). As target frequencies scale into the mmWave spectrum and required physical dimensions approach 10s of nm, a more practical solution is to utilize the dielectric layers available in the standard CMOS stack for internal dielectric transduction, where the driving dielectric is incorporated into the resonant structure (Weinstein and Bhave, 2009). Such an approach avoids the processing challenges of a high aspect ratio air gap release step, eliminates concerns over stiction that arise as air transducer gap sizes shrink, and provides a motional impedance that shrinks with increasing frequency and with decreasing dielectric thickness. At high enough frequencies (700 MHz–8 GHz in silicon, crystallographic orientation dependent), the acoustic wavelength scales below the phonon mean free path length of the material (the Landau-Rumer regime), leading to f×Q products that scale with increasing frequency (Braginsky et al., 1986; Tabrizian et al., 2009). Beyond the standard dielectrics available in CMOS, it is also possible to utilize a reverse biased diode’s depletion capacitance in place of a standard dielectric film (Hwang and Bhave, 2011). This approach combines the scaling benefits of internal dielectric transduction with the potential to utilize a high-Q single crystal silicon resonator structure and was further integrated with JFET sensing in (Hwang et al., 2011). The main challenge of depletion-layer actuation comes from designing a resonant structure of interest around the available junctions in each technology. In SOI processes this approach can be combined with a release step to remove underlying oxide, obviating the need for a waveguided mode to prevent energy leakage to the underlying layers. Select capacitive resonators operating at low voltage in very high frequency (VHF) and above are highlighted in Table 2.

TABLE 2

TABLE 2. Overview of several approaches to scaling capacitive transduction via shrinking air gap thickness and utilization of depletion capacitance actuation.

4.2 Piezoelectric and Ferroelectric Transduction

Compared to capacitively-transduced resonators, piezoelectric transducers are highly desired for their high electromechanical coupling coefficient which enable large fractional bandwidths required for 5G and beyond (Yang et al., 2020). Research efforts in this area include Al_xSc_1−xN (Fichtner et al., 2019), LiNbO₃ (Hackett et al., 2021), PbZr_xTi_1−xO₃ [PZT] (He et al., 2020), HfZrO₂ [HZO] (Hakim et al., 2021) and doped HfO₂ thin films (Schroeder et al., 2014; Anderson et al., 2018). BAW resonators based on AlN (Ruby et al., 2001a) and LiNbO₃ SAW devices in standalone packaged chips have been available for several years. Work on the commercial integration of LiNbO₃ with silicon is ongoing (Lee et al., 2003) and Al_xSc_1−xN has been demonstrated co-packaged with CMOS (Shih et al., 2019; Liu et al., 2020). PZT, on the other hand, is commercially available in the CMOS BEOL in the Texas Instruments 130 nm FeRAM process. PZT and low leakage Al_xSc_1−xN films have typical thicknesses of 100+ nm (Fichtner et al., 2020), with recent Al_xSc_1−xN films demonstrated with some leakage down to 25 nm (Rassay et al., 2021). While chemical solution deposited HfO₂ and HZO films have been demonstrated as thick as 1 μm (Schenk et al., 2020), other deposition techniques generally range from 50 nm (Quan et al., 2020; Tharpe et al., 2021a) down to sub-10 nm thicknesses (Wei et al., 2018), opening the door for piezoelectric integration into the FEOL transistor gate oxides (Trentzsch et al., 2016).

In addition to their piezoelectric properties, all of these films with the exception of AlN also exhibit ferroelectricity - the formation of a bistable polarization state in response to applied electric field. Perovskite-based ferroelectric RAM (FeRAM) has been a commercial product for many years and is prized for long retention times and radiation hardness (Arimoto and Ishiwara, 2004; Gerardin and Paccagnella, 2010), but has been limited in application scope due to large (100+ nm) ferroelectric film thicknesses required to achieve a usable memory window. With the advent of highly scaled ferroelectric films in the last 11 years, ferroelectric polarization-based memory is now a leading contender for next-generation CMOS memory (Trentzsch et al., 2016). The polarization of these ferroelectric films can be represented via the Landau-Khalatnikov model as a double-well free energy landscape with respect to dielectric polarization charge. As external electric field is applied to the ferroelectric, the energy landscape tilts until one well vanishes (at the coercive field, E_c) and the state of the ferroelectric domain switches, as shown in Figure 7A. When field is removed, the ferroelectric film will settle into a non-zero remnant polarization, P_r (Rabe et al., 2007).

FIGURE 7

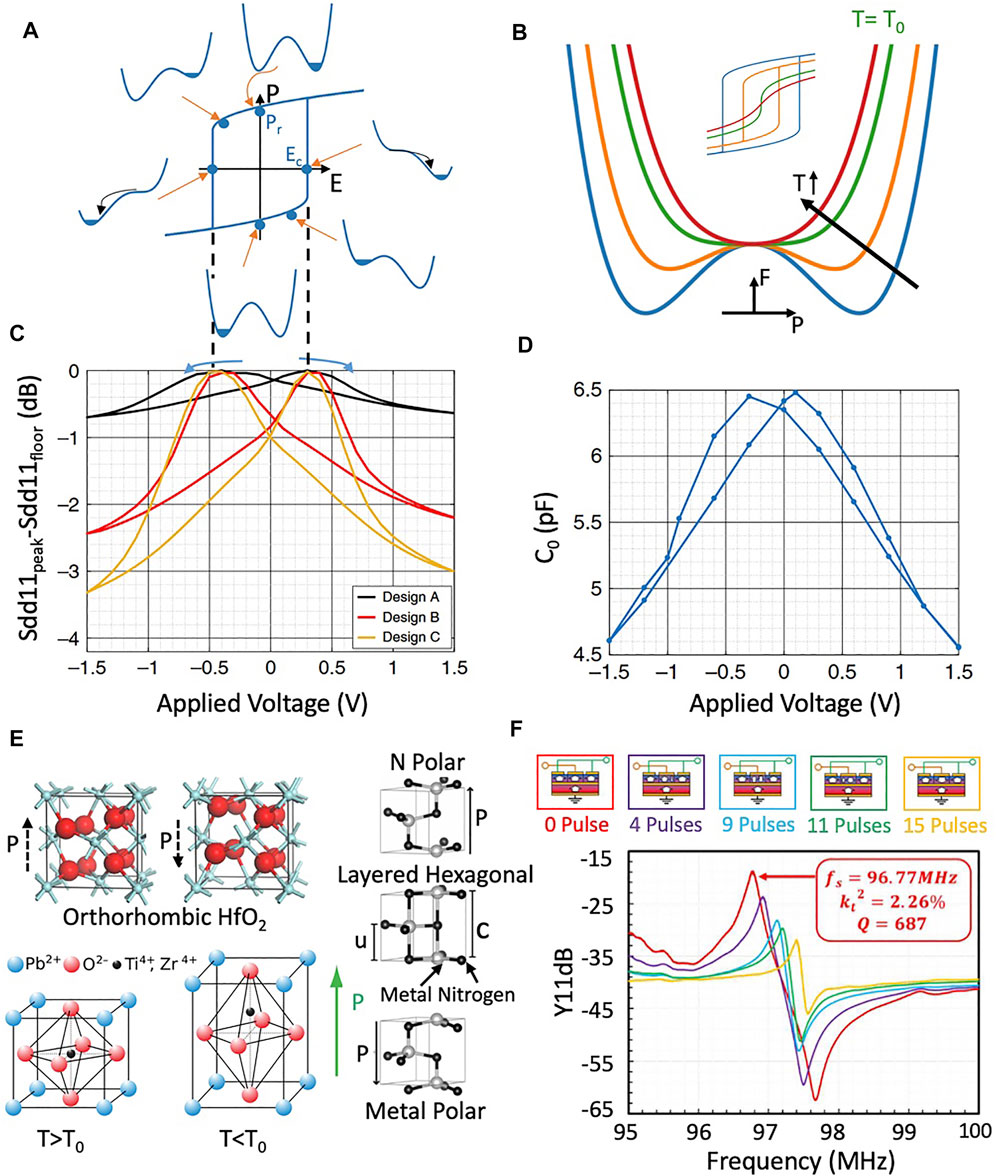
FIGURE 7. (A) Ferroelectric films exhibit two stable energy states at nonzero polarization, modeled via Landau theory (Rabe et al., 2007). When applied field tilts the energy landscape of the ferroelectric domain such that the occupied well disappears, the domain switches into the other polarization state. (B) As temperature increases, the depth of the wells in the free energy profile decrease (decreasing coercive field) until they disappear altogether at the Curie temperature (shown in green). Above this temperature (red curve), hysteresis disappears and the stable energy minimum occurs at zero polarization, as shown by the inset. The differential curvature of this profile, proportional to the inverse of capacitance, approaches zero at the Curie temperature, leading to a large increase in effective dielectric constant near zero field. (C) The programmability of ferroelectric hysteresis for tunable transduction has been experimentally demonstrated in CMOS (He et al., 2019) with parallel resonance in Sdd11 trending to zero at the coercive voltage as shown in (A) Designs A-C all share a unit cell design, but highlight some of the techniques that can be used to reduce scattering and boost quality factor in unreleased resonators. Designs B and C employing lateral terminating blocks as discussed in Section 3.3 to extend the cavity periodicity beyond the transduced region, while C furthermore replaces square array vias in the out of plane direction with a single rectangular via, reducing scattering. (D) These devices also demonstrated a change in electrical capacitance as a function of bias due to the non-quadratic energy landscape associated with ferroelectrics. (E) Unit cells, clockwise from top left, of ferroelectric materials PZT, AlScN, and HfO₂ show bi-stable non-centrosymmetric behaviour indicative of ferroelectric materials (Rabe et al., 2007; Pinin, 2010; Boescke et al., 2011; Fichtner et al., 2019). (F) Coercive field is not a set value but is a function of pulse width and voltage level, with probabilistic switching of domain. This has been exploited in (Dabas et al., 2022) to explore partial switching of AlScN at lower voltages for applications in temperature compensation. HfO₂ structure in (E) reproduced from Boescke et al., 2011 with permission of AIP Publishing. Parts (C–E) excepting PZT unit cell copyright IEEE, reprinted from (He et al., 2019; Fichtner et al., 2020, and Dabas et al., 2022) with permission.

Much like flash memory, where trapped charge on a floating gate leads to a threshold voltage shift in the associated transistor, ferroelectric remnant polarization can also be used to induce a threshold voltage shift when integrated as a gate dielectric in transistors. Unlike flash, however, polarization charge comes from the state of the crystal lattice, leading to potentially enhanced endurance (Trentzsch et al., 2016). One concern in metal-ferroelectric-semiconductor devices is the presence of a depolarization field across the ferroelectric when bias is removed, reducing retention time. This is due to required charge neutrality between the ferroelectric film and any dielectric buffer layer that may exist at the ferroelectric-semiconductor interface, and should be minimized by maximizing the ratio of the buffer layer to ferroelectric film capacitance (Arimoto and Ishiwara, 2004). Ferroelectric switching voltage for these memory devices (and for programmable ferroelectric transducers) is set by the coercive voltage - given by the product of coercive field and ferroelectric film thickness. In metal-ferroelectric-insulator-semiconductor (MFIS) structures, the write voltage required may be much higher due to voltage drop across the buffer layer, as well as asymmetric due to non-zero flat band voltage and semiconductor surface potential. This is described by

$V_{\mathit{applied}}=V_{\mathit{ferro}}+V_{\mathit{dielec}}+{\mathrm{\Psi }}_s+V_{fb},(3)$

where V_applied is the total voltage applied to the stack, V_ferro is the voltage in the ferroelectric layer that contributes to switching and transduction, V_dielec is the voltage drop across a dielectric buffer layer, Ψ_s is the semiconductor surface potential, and V_fb is the flat band voltage of the MFIS stack (Anderson et al., 2018). For example, a 10 nm ferroelectric HfO₂ thin film with a 1 nm interfacial SiO₂ may result in over 1/3 of the applied voltage dropping across the dielectric due to the large difference in permittivity between the two films. Of an applied voltage then, only a fraction may go to switching the ferroelectric film, lowering attainable P_r vs. an equivalent metal-ferroelectric-metal stack in the same V_DD. This must be taken into account along with E_c if designing an FEOL MFIS transducer to determine the maximum thickness of ferroelectric material usable for a given process supply voltage.

In polycrystalline thin films, there exist several domains with independent states and a distribution of coercive fields, leading to the potential for intermediate states of remnant polarization. With domains all aligned in the same direction, these films behave similarly to standard piezoelectric films. If partially switched, however, the piezoelectric response of opposing domains will be out of phase and will cancel each other out, leading to a lower effective coupling coefficient (He et al., 2020). This phenomenon can be leveraged for programmable transduction in applications such as voltage controlled oscillators as well as adaptive filters. As these devices are scaled down in area the total number of domains decrease and analog-like ferroelectric switching gives way to discrete jumps in polarization charge as individual domains switch, which may limit tuning in some analog applications (Mulaosmanovic et al., 2017).

The coercive field required to switch thin film ferroelectric domains is not constant with frequency, but rather increases as pulse width decreases, with switching commonly limited by domain propagation in thicker films (Fichtner et al., 2020) and domain nucleation limited switching demonstrated in 10 nm Si:HfO₂ films (Mulaosmanovic et al., 2017). This property, while limiting the speed at which radios utilizing ferroelectrics can be reconfigured, can also be exploited to provide fine tuning of resonators, with sensitivity of domains to a specific programming voltage determined by programming pulse width (Dabas et al., 2022).

The ferroelectric properties of these films are also temperature sensitive. As seen in Figure 7B, the energy barrier between states decreases with increasing temperature until a critical point (the Curie temperature) at which the stable polarization states no longer exist (Rabe et al., 2007). These and other typical properties of leading ferroelectric films are given in Table 3, with the polarizable unit cells of PZT, Al_xSc_1−xN, and HfO₂ depicted in Figures 7C–E. While the Curie temperature is well above standard operating temperatures for CMOS devices, the changes in ferroelectric properties may be important for precision frequency or timing applications.

TABLE 3

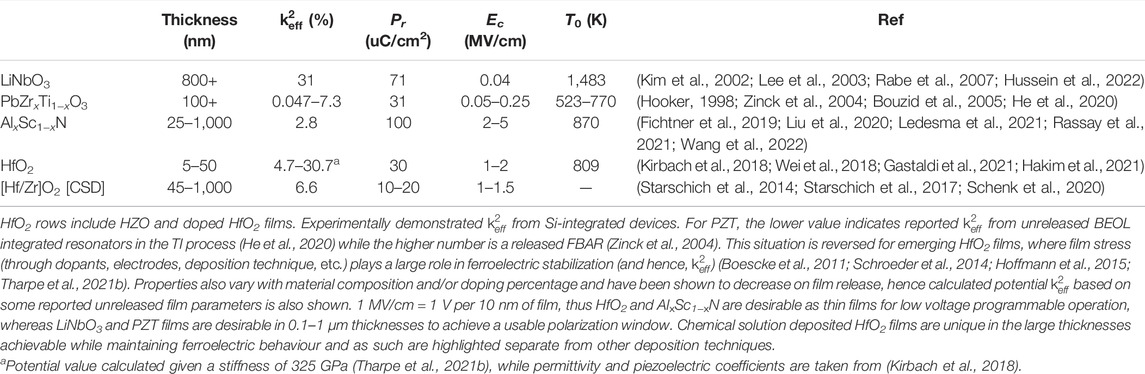
TABLE 3. Potential value calculated given a stiffness of 320 GPa (Tharpe et al., 2021b), while permittivity and piezoelectric coefficients are taken from (Kirbach et al., 2018).

In hafnium oxide films, ferroelectricity emerges from the stabilization of a non-centrosymmetric orthorhombic phase (Boescke et al., 2011) through a combination of dopant species (Schroeder et al., 2014; Anderson et al., 2018), dopant distribution (Lomenzo et al., 2014), and electrode composition (Hoffmann et al., 2015) altering grain formation (Lederer et al., 2020) and providing stabilizing stress in the film, with even pure HfO₂ films showing ferroelectric behavior under 10 nm thicknesses (Polakowski and Müller, 2015). The impact of metalization before or after anneal of the ferroelectric properties of resulting HfO₂ ferroelectrics has been demonstrated (Mueller et al., 2012), as has the relaxation of stress due to HZO film release, decreasing orthorhombic phase and hence ferroelectricity (Tharpe et al., 2021b) - a property of particular concern for released MEMS applications. An additional complicating factor is the change in ferroelectric and piezoelectric properties with cycling (Mart et al., 2020; Kirbach et al., 2021) as individual grains rotate to align with applied field (Lederer et al., 2019). Experimentally reported d_33,f values for HfO₂ ferroelectric films have reached 20 pm/V (Kirbach et al., 2018; Schenk et al., 2020), with even higher values predicted for doped ZrO₂ films (Falkowski and Kersch, 2020). Being measured from a thin film structure, this value is expected to differ from bulk by a geometry dependent factor (Guo et al., 2013).

The coercive field of Al_xSc_1−xN films drops as Sc doping percentage increases, making the ferroelectric properties easier to utilize (Fichtner et al., 2020). This comes at the cost of decreasing P_r, however, so optimal material composition may change based on design requirements (Liu et al., 2020; Park et al., 2020). Additionally, the field at which domains switch in Al_xSc_1−xN films is on the order of a few MV/cm (Fichtner et al., 2020), requiring high voltages to switch at today’s grown thicknesses. HfO₂ and PZT ferroelectrics, on the other hand, can be easily switched with voltages available in standard CMOS technologies.

4.3 Active Semiconductor Sensing

At mmWave frequencies, on-chip parasitics must be considered as part of integrated circuit design. Particularly in unreleased resonators, feedthrough capacitance can lead to poor stop-band rejection (Anderson et al., 2021) which must be overcome. One method to do so in FEOL-integrated resonators is to utilize available semiconductor devices to provide amplification in the mechanical to electrical conversion through bandstructure interactions. Semiconductor electron devices such as field effect transistors, junctionless nanowire transistors, and PN diodes are sensitive to strain and therefore able to detect acoustic vibrations (Weinstein and Bhave, 2010a; Hwang and Bhave, 2011; Bartsch et al., 2014). These active sense mechanisms offer opportunities to isolate and amplify the mechanical signal relative to electrical feed-through, providing enhanced sensitivity most critical in the GHz regime of operation. In addition, sense transistor biasing can also allow for real-time performance or power consumption tuning. When not in use, the sense circuitry can be turned off altogether, whereas when in operation it can be operated at a maximum gate bias and the drain bias selected either in the linear regime for maximum efficiency or in the saturation regime for maximum performance (Anderson et al., 2021).

While atomistic simulation tools such as VASP (VASP, 2022), Quantum ATK (QuantumATK, 2022), and Victory Atomistic (Victory Atomistic, 2022) can be used to calculate strained semiconductor band structure, a combination of empirical equations can also be used to account for the bandgap and mobility modulation in active sensors such as FETs, BJTs, and PN diodes. To a first order, the bandgap can be modeled to be linearly dependent on strain (Bardeen and Shockley, 1950). This modulation of the bandgap will result in a change in intrinsic carrier concentration and, hence, a change in the onset of strong inversion and a shift in the threshold voltage of a transistor (Anderson et al., 2021).

Mobility modulation due to the carrier transfer effect and changes in effective mass can be captured with transverse and longitudinal piezoresistive coefficients (π) as

$\mu \left(\sigma \right)=\frac{{\mu }_0}{1+{\pi }_L{\sigma }_L+{\pi }_T{\sigma }_T}(4)$

and can be used in either active (Marathe et al., 2014; Anderson et al., 2018) or passive (Rahafrooz and Pourkamali, 2011; Abbasalipour et al., 2018; Ramezany and Pourkamali, 2018; Zope et al., 2020) sensing schemes. These coefficients change depending on crystallographic orientation and have been studied extensively in silicon (Kanda, 1991). While it is prudent to use average or effective stress/strain values for hand calculations with these equations, these effects can also be modeled as position-dependent and solved via TCAD if a detailed mode shape is known from finite element analysis (Li et al., 2012).

In FET transducers, these changes in semiconductor band structure are measured by a change in drain current. By observing the long channel square law model (Tsividis and McAndrew, 2010) it can be shown to the first order that the change in drain current due to dielectric transduction, the piezoresistive effect, and bandgap modulation can be written as

$\mathrm{\Delta }{I}_D=I_{D0}\ast \left(A_{\mu }+A_{C_{ox}}+A_{\mu }{A}_{C_{ox}}\right)-\mathrm{\Delta }{V}_T\ast f\left\{\mu ,C_{ox},V_{DS}\right\}(5)$

for the linear regime and

$\mathrm{\Delta }{I}_D=I_{D0}\ast \left(A_{\mu }+A_{C_{ox}}+A_{\mu }{A}_{C_{ox}}\right)-\mathrm{\Delta }{V}_T\ast f\left\{\mu ,C_{ox},V_{GS},V_{DS}\right\}(6)$

in saturation, where A_μ, $A_{C_{ox}}$ are constants for a given stress and f represents a function multiplying ΔV_T (Anderson et al., 2021). As the contribution from dielectric transduction is relatively small compared to the piezoresistive modulation, it can be understood from these expressions that the transduced change in transistor drain current will have a piezoresistive component directly proportional to DC bias current, as well as a term that is a function of both the piezoresistive effect and bandgap/threshold voltage modulation. The impact of each of these components on transduction can be seen in Figures 8A,B. When implementing active semiconductor sensing in a new material or technology, care should be taken to verify that bandgap and effective mass modulation will not cancel each other or performance will be degraded.

FIGURE 8

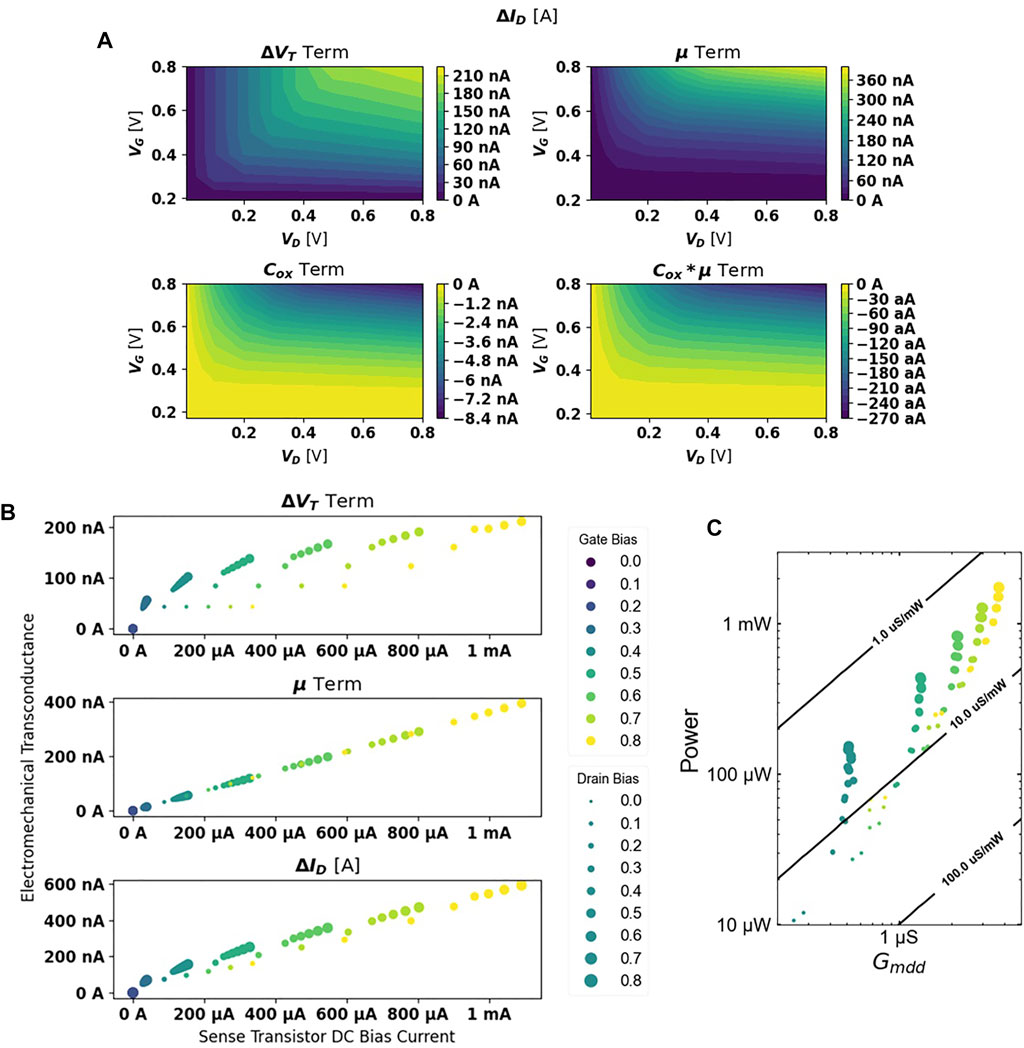
FIGURE 8. (A) Predicted contributions from bandgap and piezoresistive modulation show an ≈ 800× improvement in sense transduction over standard dielectric transduction. (B) Piezoresistive contribution scales linearly with drain current, while the bandgap modulation term is maximized by setting V_D as high as possible for a given V_G. (C) DC power required for a given G_mdd. Iso-efficiency contours show degrading power efficiency for larger required G_mdd. For a given required transconductance, designers can maximize power efficiency by biasing at high gate voltage and low drain bias. Adapted from (Anderson et al., 2021; Anderson et al., 2022).

In short channel devices, there are a number of effects that alter drain current including velocity saturation, vertical field degradation, drain induced barrier lowering, channel length modulation, gate-induced drain leakage, and quantum mechanical effects, among others (Colinge, 2008). Many of these effects are important since they reduce drain bias current and/or carrier mobility, lowering the transduced signal. Velocity saturation is notable in the fact that both optical emission and phonon emission - the two main mobility loss mechanisms as lateral field increases - are related to effective mass (Sze and Ng, 2006). Therefore, saturation velocity V_sat is itself modulated with strain, with the relation modeled in (Lochtefeld and Antoniadis, 2001) as:

$\frac{\mathrm{\Delta }{v}_{\mathit{sat}}}{v_{\mathit{sat0}}}=\alpha \frac{\mathrm{\Delta }\mu }{{\mu }_0}.(7)$

with an experimentally measured α around 0.5.

The largest challenge with unreleased CMOS-integrated active resonators demonstrated to date stems from relatively low mechanical transconductance (μS). 14 nm fRBT devices, highlighted in Figure 8C, require significant sense transistor current draw to achieve maximum g_mdd. This metric can be improved further through more efficient transduction using FEOL ferroelectric films as well as refinements to acoustic confinement in the cavity to enhance Q.

While the square law model is overly-simplified for today’s commercial devices, a similar approach can be taken to implement these effects in more complex surface potential multigate models such as those utilized for finFETs (Colinge, 2008).

5 Compact Modeling

Prior to deploying monolithically-integrated CMOS-MEMS resonators in applications such as oscillators and filters, system-level simulations are required for design and performance tuning. Various tools such as Finite Element Analysis (FEA) for capturing the electromechanical behaviour, Electromagnetic/circuit extraction and TCAD for semiconductor physics are required to analyze and design the device itself but cannot be used collectively with modern circuit simulation methodologies. Therefore, low computational effort based accurate compact models that capture the device behavior, are validated against measured data and are capable of being used in all circuit simulation scenarios are required for monolithic CMOS-MEMS devices.

Typically, a modified Butterworth-van-Dyke (MBVD) model for capacitive and piezoelectric MEMS devices (Ruby et al., 2001b; Zuo et al., 2008; Lu et al., 2019) is obtained through extraction from RF measurement data. A typical two-port MBVD model primarily consists of a motional branch corresponding to the effective mass, stiffness and damping of the relevant resonance mode, transducer capacitance and a capacitive feedthrough branch in parallel with the motional branch. In the case of BEOL released CMOS-MEMS devices such as the one in (Chen et al., 2011), the conventional MBVD model is sufficient for system design. Other variants of such devices, as that in (Zope et al., 2020) employ thermal piezoresistive transduction which require changes to the MBVD model to reflect the appropriate transduction mechanisms. Models based on extracted data are capable of accurately capturing the device performance but need to be updated when design parameters are changed. Physics based compact models on the other hand are capable of predicting changes in device characteristics with a change in design. As discussed briefly in the previous section, monolithic capacitively-driven CMOS-MEMS devices have a very low $k_{\mathit{eff}}^2$. The motional current is completely buried under feedthrough in the intrinsic MOSCAP transducers making direct parameter extraction immensely challenging. Moreover, in systems and scenarios exhibiting large signal excursions, the small signal model is not expected to be accurate owing to the highly non-linear nature of the transduction mechanisms. Large-signal compact models have previously been developed for both released (Bahr et al., 2016b) and unreleased (Bahr et al., 2016c) RBT devices. Although these models are large signal in nature, they rely on the analytic formulations of the resonator mode shape and do not accurately capture the device parasitics. Integrated CMOS-MEMS devices almost always exhibit complex mode shapes which are not possible to describe analytically. Electrical feedthrough between the device terminals owing to parasitics significantly influence the device performance making accurate extraction and parasitics model integration with the device model of significant importance. Since the device characteristics also vary with temperature, models are also required to be thermally-aware.

In the comprehensive large signal fRBT compact model (Figure 9C) described in (Rawat et al., 2022), an Eigenfrequency based extraction methodology is used together with accurate layout parasitic extraction and modifications of the BSIM-CMG finFET model (Duarte et al., 2015). This enables a general modeling methodology for CMOS RBTs exhibiting complex mode shapes and physical interactions between electrical, mechanical and thermal domains. In the employed modal extraction methodology, an equivalence is established between the multi-degree-of-freedom (DoF) targeted resonant mode and a single DoF mass-spring-damper system using a 3D FEM Eigenfrequency simulation model. Modified BSIM-CMG models compatible with the GF14LPP process PDK are used for both the actuating MOSCAPs as well as the sense transistors to incorporate electromechanical conversion. The modified sense transistor model takes into account changes in transistor characteristics such as mobility, threshold voltage and saturation velocity due to stress in the resonant cavity. The full model for the device is fully integrated within the GF14LPP PDK enabling ease of system design and simulation. This measurement validated compact model for the fRBT device has also been shown to be applicable in simulation scenarios such as Periodic Steady State (PSS), Periodic AC (PAC) etc. In the case of BEOL-integrated FeCAP resonators, a version of the MBVD model as depicted in Figure 9A (He et al., 2019) is employed. In these devices, it is possible to bias the alternating transducers with distinct polarizations. Hence the electromechanical transformation ratios T₁ and T₂ for the two ports of the device can be distinct. Moreover, the bottom plate of the ferroelectric capacitors are all connected to a grounded poly-gate layer whose resistance R_g is incorporated into the model alongside other parasitic series interconnect resistances R₁ and R₂. The parameter extraction is carried out by fitting the model response to the measured S₂₁ of the device. In the case where the FeCAP resonators are to be operated differentially, a conventional MBVD model fitted to measured one-port differential S_dd11 can be employed (He et al., 2020) as shown in Figure 9B.

FIGURE 9

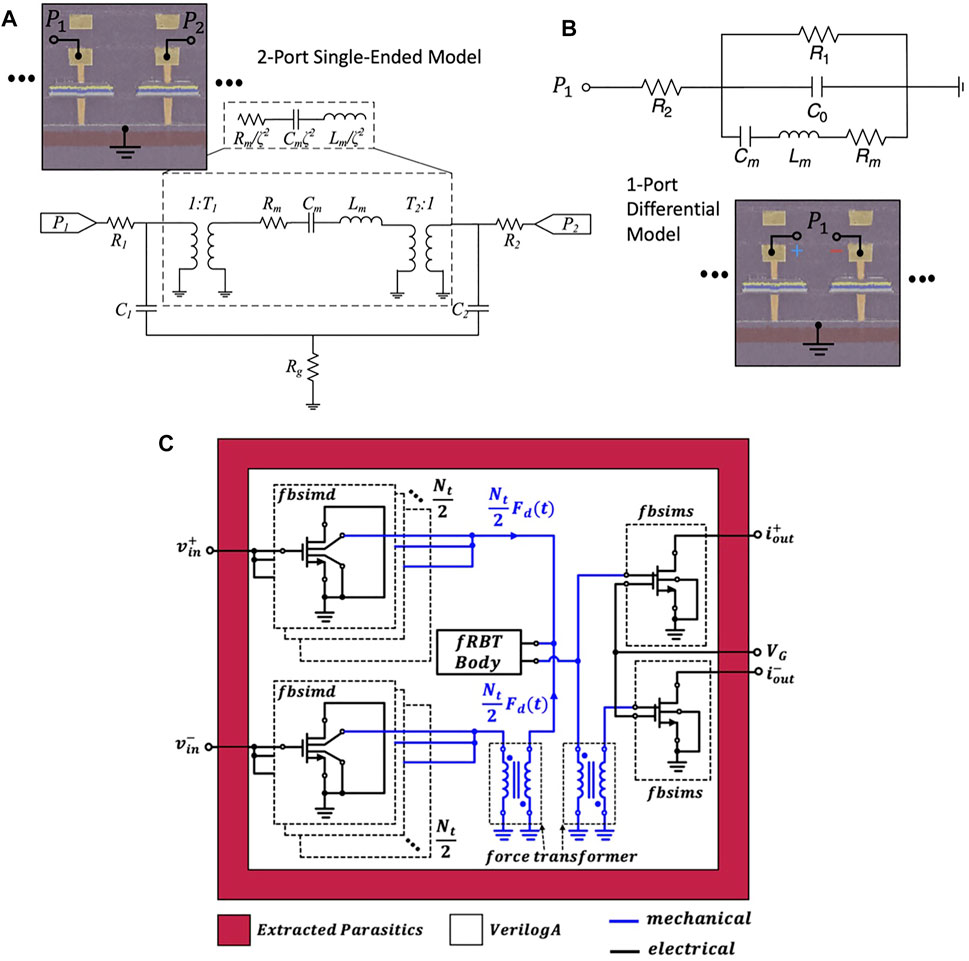
FIGURE 9. (A) Two-port MBVD model for the FeCAP resonator consisting of the motional branch components (R_m, L_m and C_m), transduction capacitances (C₁ and C₂), parasitic resistances (R₁ and R₂) and electromechanical transduction factors (T₁ and T₂). (B) One-port differential model for the FeCAP resonator. (C) Compact model schematic for the GF14LPP fRBT device comprising of the modified BSIM-CMG transistor modes (fbsims and fbsimd), the extracted motional parameters (fRBT Body) and additional force transformers to ensure correct differential operation of the device.

6 System Design and Applications

The foremost applications of monolithic CMOS-MEMS resonant devices are in RF oscillator and filter designs across different frequency bands of operation. The primary consideration in the design of filters is achieving a large bandwidth of operation while having a low insertion loss in the passband. CMOS-MEMS resonant devices that exhibit a low $k_{\mathit{eff}}^2$ (capacitively transduced) are unsuitable for this particular application. Devices having CMOS-integrated ferroelectric materials would be the ideal candidates for filter design because of the significantly higher $k_{\mathit{eff}}^2$ values (Table 3). Filter design may be undertaken completely in the acoustic domain (Johnson, 1997; Bannon et al., 2000; Weinstein et al., 2007) or by electrically coupling multiple devices (similar to the designs in (Ruby et al., 2001a; Ruby et al., 2004; Piazza et al., 2007)). Since waveguiding in both the FEOL and BEOL regions of the CMOS stack has been successfully demonstrated, different coupled phononic cavity topologies may be used as depicted in (Olsson and El-Kady, 2008) to create add/drop filters. Because of the tunable nature of ferroelectric transduction, as demonstrated in (He et al., 2019; He et al., 2020), the resulting filters can be re-configurable in nature which is not feasible in conventional FBAR and SAW based designs. A possible limitation of filters created using ferroelectrically transduced CMOS-MEMS devices is the nonlinear nature of ferroelectric transduction under the application of large signal swings which limits the power handling of these devices, thereby limiting the achievable Input Third Order Intercept Point (IIP3).

Availability of integrated ferroelectric transducers also enables the development of acoustic transducers/sensors for a wide variety of applications. High-overtone bulk acoustic resonance (HBAR) modes have been observed in measurement beyond the waveguided resonance frequency of the CMOS-MEMS FeCAP resonator (He et al., 2018; He et al., 2019; He et al., 2020). Existence of these modes is indicative of possible uses in applications such as fingerprint sensing (Tang et al., 2016; Jiang et al., 2017), chip-scale acoustic communication (Hoople et al., 2014; Kuo et al., 2014) etc. Moreover, appropriate design of the FeCAP waveguide and reflectors can generate high-frequency ultrasonic transducers for high resolution ultrasonic imaging (Bahr et al., 2019).

Conventional design topologies for integrated RF-MEMS oscillators using CMOS-MEMS resonators are not applicable owing to the small impedance of the intrinsic transduction capacitance C₀ in the devices at RF and mm-Wave operating frequencies. In order to obtain as large an output signal as possible from the device, its geometry is designed so as to maximize the capacitance C₀. The large C₀ in-turn places limitations on the design of oscillation-sustaining circuitry and must therefore be compensated. It has been shown that for a 30 GHz RFT device having a Q-factor of 10,000 and motional resistance of 332 Ω, fundamental limits of oscillator phase noise (−132 dBc/Hz) can be achieved (Srivastava et al., 2021b) by using inductive compensation of the static capacitance C₀. The inductor in this complementary cross-coupled oscillator topology is designed to resonate out the RFT static capacitance at the targeted resonance frequency. Similarly, active transistor sensing with an electromechanical transconductance g_m,mech of 1 μS in the same 30 GHz RFT device can be utilized in a series feedback oscillator topology (Srivastava et al., 2021a). Alongside capacitive drive, inductive current-to-voltage conversion at the device output together with a tuned amplifier stage can be used to realize low phase noise oscillations. The resonant network of the tuned amplifier absorbs the large intrinsic device C₀ at the input. Using this oscillator topology, a figure-of-metrit (FoM) of 228 dBc/Hz has been shown as being achievable with a phase noise of −140 dBc/Hz at 1 MHz offset from the oscillation frequency of 30 GHz. It is hence possible to achieve significantly better performance integrated oscillators as compared to purely LC based oscillators.

The devices and methods outlined here are the tip of the iceberg in terms of possibilities for seamless CMOS-MEMS integration. Exploitation of mechanical vibrations inside CMOS is currently limited by several factors, including incomplete characterization of individual thin film material properties within the CMOS stack, speed of design iteration and limited footprint for design optimization, computational costs of full 3D multiphysics simulation, and conservative design rules limiting lithographically-defined geometric optimization.

Particularly as CMOS foundries begin to launch ferroelectric materials within the transistor gate stack for memory and negative capacitance devices, there are exciting opportunities for CMOS-MEMS designers to work cooperatively with the foundry for short-loop, fast iteration, large-scale optimization across the full Design of Experiment. Joint efforts such as these promise new functionality to emerging technology platforms designed from the ground up. The designs and concepts discussed here can be translated to these modified platforms, opening doors for radio systems including tunable oscillators and switchable filter banks, novel nonlinear acoustic signal processing, oscillatory computation, and integrated sensor systems for IoT.

Author Contributions

UR contributed to sections on phononic waveguide design, compact modeling, system design and applications as well as introduction. JA contributed to the electromechanical conversion and introduction sections. This review was guided by DW.

Funding

This work was funded by the DARPA Young Faculty Award (Grant No. N66001-10-1-4046) aimed at studying active electromechanical transduction in standard CMOS with no post-processing, by the NSF CAREER Award (Grant No. 1150493) focused on active transducers in multiple IC material platforms, by the DARPA UPSIDE program (Grant No. 12405-301701-DS) focused on non-Boolean signal processing leveraging emerging devices including the Resonant Body Transistor, and by the DARPA MIDAS program (Grant No. FA8650-18-1-7904) targeting large-scale tiled MIMO programmable antenna arrays.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbasalipour, A., Kumar, V., Ramezany, A., and Pourkamali, S. (2018). “Thermal Piezoresistive Resonant Mass Balance Implemented in a Standard CMOS Process,” in 2018 IEEE International Frequency Control Symposium (IFCS), 1–4. doi:10.1109/fcs.2018.8597576

CrossRef Full Text | Google Scholar

Anderson, J. D., Merkel, J., MacMahon, D., and Kurinec, S. K. (2018). Evaluation of Si:HfO2 Ferroelectric Properties in MFM and MFIS Structures. IEEE J. Electron Devices Soc. 6, 525–534. doi:10.1109/jeds.2018.2826978

CrossRef Full Text | Google Scholar

Anderson, J., He, Y., Bahr, B., and Weinstein, D. (2022). Dataset for “X-Band Fin Resonant Body Transistors in 14nm CMOS Technology”. Available at: https://zenodo.org/record/5899507.

Google Scholar

Anderson, J., He, Y., Bahr, B., and Weinstein, D. (2021). X-band Fin Resonant Body Transistors in 14nm CMOS Technology. arXiv:2107.00608 [physics.app-ph]. Available at: https://arxiv.org/abs/2107.00608.

Google Scholar

Arimoto, Y., and Ishiwara, H. (2004). Current Status of Ferroelectric Random-Access Memory. MRS Bull. 29 (11), 823–828. doi:10.1557/mrs2004.235

CrossRef Full Text | Google Scholar

Ayazi, F. (2002). The HARPSS Process for Fabrication of Precision MEMS Inertial Sensors. Mechatronics 12 (9), 1185–1199. doi:10.1016/S0957-4158(02)00023-5

CrossRef Full Text | Google Scholar

Bahr, B., Cook, B., and Summerfelt, S. (2019). “High Frequency Cmos Ultrasonic Transducer,” uS Patent Application No. 16/590,354.

Google Scholar

Bahr, B., Daniel, L., and Weinstein, D. (2016). “Optimization of Unreleased CMOS-MEMS RBTs,” in 2016 IEEE International Frequency Control Symposium (IFCS), 1–4. doi:10.1109/fcs.2016.7563592

CrossRef Full Text | Google Scholar

Bahr, B., He, Y., Krivokapic, Z., Banna, S., and Weinstein, D. (2018). “32GHz Resonant-Fin Transistors in 14nm FinFET Technology,” in 2018 IEEE International Solid - State Circuits Conference - (ISSCC), 348–350. doi:10.1109/isscc.2018.8310327

CrossRef Full Text | Google Scholar

Bahr, B., Marathe, R., and Weinstein, D. (2014). “Phononic Crystals for Acoustic Confinement in Cmos-Mems Resonators,” in 2014 IEEE International Frequency Control Symposium (FCS), 1–4. doi:10.1109/fcs.2014.6859980

CrossRef Full Text | Google Scholar

Bahr, B., Marathe, R., and Weinstein, D. (2015). Theory and Design of Phononic Crystals for Unreleased CMOS-MEMS Resonant Body Transistors. J. Microelectromech. Syst. 24 (5), 1520–1533. doi:10.1109/jmems.2015.2418789

CrossRef Full Text | Google Scholar

Bahr, B. (2016). Monolithically Integrated MEMS Resonators and Oscillators in Standard IC Technology. PhD Thesis (Boston: Massachusetts Institute of Technology).

Bahr, B. W. A. (2016). Monolithically Integrated MEMS Resonators and Oscillators in Standard IC Technology. Thesis (Cambridge, MA, USA: Massachusetts Institute of Technology). Available at: http://dspace.mit.edu/handle/1721.1/105569.

Bahr, B., Weinstein, D., and Daniel, L. (2016). Released Resonant Body Transistor (RBT) Model. Available at: https://nanohub.org/publications/17/supportingdocs?v=1.

Google Scholar

Bahr, B., and Weinstein, D. (2016). “VERTICAL ACOUSTIC CONFINEMENT FOR HIGH-Q FULLY-DIFFERENTIAL CMOS-RBTS,” in 2016 Solid-State, Actuators, and Microsystems Workshop Technical Digest (Hilton Head, South Carolina, USA: Transducer Research Foundation), 88–91. Available at: https://transducer-research-foundation.org/technical_digests/HiltonHead_2016/hh2016_0088.pdf.

CrossRef Full Text | Google Scholar

Bahr, B. W., Weinstein, D., and Daniel, L. (2016). Unreleased 1D CMOS Resonant Body Transistor with MIT Virtual Source (URBT-MVS) Model. Available at: https://nanohub.org/publications/132/1.

Google Scholar

Bannon, F. D., Clark, J. R., and Nguyen, C. T.-C. (2000). High-q Hf Microelectromechanical Filters. IEEE J. Solid-State Circuits 35 (4), 512–526. doi:10.1109/4.839911

CrossRef Full Text | Google Scholar

Bardeen, J., and Shockley, W. (1950). Deformation Potentials and Mobilities in Non-polar Crystals. Phys. Rev. 80 (1), 72–80. doi:10.1103/physrev.80.72

CrossRef Full Text | Google Scholar

Bartsch, S. T., Arp, M., and Ionescu, A. M. (2014). Junctionless Silicon Nanowire Resonator. IEEE J. Electron Devices Soc. 2 (2), 8–15. doi:10.1109/jeds.2013.2295246

CrossRef Full Text | Google Scholar

Birdsall, S. A., Dever, P. B., Donovan, J. B., Driscoll, M. M., Lakin, K. M., and Pham, T. H. (2002). Measurement of Static and Vibration-Induced Phase Noise in Uhf Thin-Film Resonator (Tfr) Filters. IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 49 (5), 643–648. doi:10.1109/tuffc.2002.1002463

CrossRef Full Text | Google Scholar

Bock, P. J., Cheben, P., Schmid, J. H., Lapointe, J., Delâge, A., Janz, S., et al. (2010). Subwavelength Grating Periodic Structures in Silicon-On-Insulator: a New Type of Microphotonic Waveguide. Opt. Express 18 (19), 20251251–20251262. doi:10.1364/OE.18.020251

CrossRef Full Text | Google Scholar

Boescke, T. S., Muller, J., Brauhaus, D., Schroder, U., and Bottger, U. (2011). Ferroelectricity in Hafnium Oxide Thin Films. Appl. Phys. Lett. 99 (10), 102903. doi:10.1063/1.3634052

CrossRef Full Text | Google Scholar

Bouzid, A., Bourim, E. M., Gabbay, M., and Fantozzi, G. (2005). PZT Phase Diagram Determination by Measurement of Elastic Moduli. J. Eur. Ceram. Soc. 25 (13), 3213–3221. doi:10.1016/j.jeurceramsoc.2004.07.018

CrossRef Full Text | Google Scholar

Braginsky, V. B., Mitrofanov, V. P., and Panov, V. I. (1986). Systems with Small Dissipation. Chicago, IL: University of Chicago Press. Available at: https://press.uchicago.edu/ucp/books/book/chicago/S/bo5973099.html.

Google Scholar

Cheben, P., Bock, P. J., Schmid, J. H., Lapointe, J., Janz, S., Xu, D.-X., et al. (2010). Refractive Index Engineering with Subwavelength Gratings for Efficient Microphotonic Couplers and Planar Waveguide Multiplexers. Opt. Lett. 35 (15), 2526–2528. doi:10.1364/ol.35.002526

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, W.-C., Fang, W., and Li, S.-S. (2011). A Generalized CMOS-MEMS Platform for Micromechanical Resonators Monolithically Integrated with Circuits. J. Micromech. Microeng. 21 (6), 065012. doi:10.1088/0960-1317/21/6/065012

CrossRef Full Text | Google Scholar

Cheng, T. J., and Bhave, S. A. (2010). “High-Q, Low Impedance Polysilicon Resonators with 10 Nm Air Gaps,” in 2010 IEEE 23rd International Conference on Micro Electro Mechanical Systems (MEMS), 695–698. doi:10.1109/memsys.2010.5442311

CrossRef Full Text | Google Scholar

Colinge, J.-P. (2008). FinFETs and Other Multi-Gate Transistors. 1st ed. New York, NY: Springer-Verlag. doi:10.1007/978-0-387-71752-4

CrossRef Full Text | Google Scholar

Corti, E., Cornejo Jimenez, J. A., Niang, K. M., Robertson, J., Moselund, K. E., Gotsmann, B., et al. (2021). Coupled VO2 Oscillators Circuit as Analog First Layer Filter in Convolutional Neural Networks. Front. Neurosci. 2021, 628254. doi:10.3389/fnins.2021.628254

PubMed Abstract | CrossRef Full Text | Google Scholar

Dabas, S., Mo, D., Rassay, S., and Tabrizian, R. (2022). “Intrinsically Tunable Laminated Ferroelectric Scandium Aluminum Nitride Extensional Resonator Based on Local Polarization Switching,” in 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS), 1050–1053. doi:10.1109/mems51670.2022.9699790

CrossRef Full Text | Google Scholar

Dehghannasiri, R., Pourabolghasem, R., Eftekhar, A. A., and Adibi, A. (2016). Integrated Phononic Crystal Resonators Based on Adiabatically-Terminated Phononic Crystal Waveguides. AIP Adv. 6 (12), 121603. doi:10.1063/1.4968614

CrossRef Full Text | Google Scholar

Donzella, V., Sherwali, A., Flueckiger, J., Grist, S. M., Fard, S. T., and Chrostowski, L. (2015). Design and Fabrication of Soi Micro-ring Resonators Based on Sub-wavelength Grating Waveguides. Opt. Express 23 (4), 4791–4803. doi:10.1364/oe.23.004791

PubMed Abstract | CrossRef Full Text | Google Scholar

Duarte, J. P., Khandelwal, S., Medury, A., Hu, C., Kushwaha, P., Agarwal, H., et al. (2015). “Standard FinFET Compact Model for Advanced Circuit Design,” in ESSCIRC Conference 2015 - 41st European Solid-State Circuits Conference (ESSCIRC), 196–201.

Google Scholar

Falkowski, M., and Kersch, A. (2020). Optimizing the Piezoelectric Strain in ZrO2- and HfO2-Based Incipient Ferroelectrics for Thin-Film Applications: An Ab Initio Dopant Screening Study. ACS Appl. Mat. Interfaces 12 (29), 32915–32924. doi:10.1021/acsami.0c08310

PubMed Abstract | CrossRef Full Text | Google Scholar

Fedder, G. K., Howe, R. T., Tsu-Jae King Liu, T. K., and Quevy, E. P. (2008). Technologies for Cofabricating MEMS and Electronics. Proc. IEEE 96 (2), 306–322. doi:10.1109/jproc.2007.911064

CrossRef Full Text | Google Scholar

Fichtner, S., Lofink, F., Wagner, B., Schönweger, G., Kreutzer, T.-N., Petraru, A., et al. (2020). “Ferroelectricity in AlScN: Switching, Imprint and Sub-150 Nm Films,” in 2020 Joint Conference of the IEEE International Frequency Control Symposium and International Symposium on Applications of Ferroelectrics (IFCS-ISAF), 1–4. doi:10.1109/ifcs-isaf41089.2020.9234883

CrossRef Full Text | Google Scholar

Fichtner, S., Wolff, N., Lofink, F., Kienle, L., and Wagner, B. (2019). AlScN: A III-V Semiconductor Based Ferroelectric. J. Appl. Phys. 125 (11), 114103. doi:10.1063/1.5084945

CrossRef Full Text | Google Scholar

Gastaldi, C., Cavalieri, M., Saeidi, A., O’Connor, E., Kamaei, S., Rosca, T., et al. (2021). Intrinsic Switching in Si-Doped HfO2: A Study of Curie–Weiss Law and its Implications for Negative Capacitance Field-Effect Transistor. Appl. Phys. Lett. 118 (19), 192904. doi:10.1063/5.0052129

CrossRef Full Text | Google Scholar

Gerardin, S., and Paccagnella, A. (2010). Present and Future Non-volatile Memories for Space. IEEE Trans. Nucl. Sci. 57 (6), 3016–3039. doi:10.1109/tns.2010.2084101

CrossRef Full Text | Google Scholar

Gilgunn, P. J., Jingwei Liu, J., Sarkar, N., and Fedder, G. K. (2008). CMOS-MEMS Lateral Electrothermal Actuators. J. Microelectromech. Syst. 17 (1), 103–114. doi:10.1109/jmems.2007.911373

CrossRef Full Text | Google Scholar

Gokhale, V. J., and Gorman, J. J. (2017). Approaching the Intrinsic Quality Factor Limit for Micromechanical Bulk Acoustic Resonators Using Phononic Crystal Tethers. Appl. Phys. Lett. 111 (1), 013501. doi:10.1063/1.4990960

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, Q., Cao, G. Z., and Shen, I. Y. (2013). Measurements of Piezoelectric Coefficient D33 of Lead Zirconate Titanate Thin Films Using a Mini Force Hammer. J. Vib. Acoust. 135 (1), 6881. doi:10.1115/1.4006881

CrossRef Full Text | Google Scholar

Hackett, L., Miller, M., Brimigion, F., Dominguez, D., Peake, G., Tauke-Pedretti, A., et al. (2021). Towards Single-Chip Radiofrequency Signal Processing via Acoustoelectric Electron-Phonon Interactions. Nat. Commun. 12 (1), 2769. doi:10.1038/s41467-021-22935-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Hagelauer, A., Fattinger, G., Ruppel, C. C. W., Ueda, M., Hashimoto, K.-y., and Tag, A. (2018). Microwave Acoustic Wave Devices: Recent Advances on Architectures, Modeling, Materials, and Packaging. IEEE Trans. Microw. Theory Techn. 66 (10), 4548–4562. doi:10.1109/tmtt.2018.2854160

CrossRef Full Text | Google Scholar

Hakim, F., Tharpe, T., and Tabrizian, R. (2021). Ferroelectric-on-Si Super-high-frequency Fin Bulk Acoustic Resonators with Hf0.5Zr0.5O2 Nanolaminated Transducers. IEEE Microw. Wirel. Compon. Lett. 31 (6), 701–704. doi:10.1109/lmwc.2021.3067509

CrossRef Full Text | Google Scholar

He, Y., Bahr, B., Si, M., Ye, P., and Weinstein, D. (2020). A Tunable Ferroelectric Based Unreleased RF Resonator. Microsystems Nanoeng. 6 (1), 8. doi:10.1038/s41378-019-0110-1

CrossRef Full Text | Google Scholar

He, Y., Bahr, B., Si, M., Ye, P., and Weinstein, D. (2019). “Switchable Mechanical Resonance Induced by Hysteretic Piezoelectricity in Ferroelectric Capacitors,” in 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems Eurosensors XXXIII (TRANSDUCERS EUROSENSORS XXXIII), 717–720. doi:10.1109/transducers.2019.8808623

CrossRef Full Text | Google Scholar

He, Y., Bahr, B., and Weinstein, D. (2018). “A ferroelectric capacitor (FECAP) based unreleased resonator,” in 2018 Solid-State, Actuators, and Microsystems Workshop Technical Digest (Hilton Head, South Carolina, USA: Transducer Research Foundation), 71–74. Available at: https://transducer-research-foundation.org/technical_digests/HiltonHead_2018/hh2018_0071.pdf.

CrossRef Full Text | Google Scholar

Hoffmann, M., Schroeder, U., Schenk, T., Shimizu, T., Funakubo, H., Sakata, O., et al. (2015). Stabilizing the Ferroelectric Phase in Doped Hafnium Oxide. J. Appl. Phys. 118 (7), 072006. doi:10.1063/1.4927805

CrossRef Full Text | Google Scholar

Hooker, M. W. (1998). Properties of PZT-Based Piezoelectric Ceramics between -150 and 250 C,” Lockheed Martin Engineering and Sciences Co. Tech. Rep. Nas. 1 (26), 208708. Available at: https://ntrs.nasa.gov/citations/19980236888.

Google Scholar

Hoople, J., Kuo, J., Ardanuç, S., and Lal, A. (2014). “Chip-scale Reconfigurable Phased-Array Sonic Communication,” in 2014 IEEE International Ultrasonics Symposium, 479–482.

CrossRef Full Text | Google Scholar

Huang, C., Anderson, J., Peana, S., Chen, X., Ramanathan, S., and Weinstein, D. (2021). Perovskite Nickelate Actuators. J. Microelectromechanical Syst. 30, 488–493. doi:10.1109/jmems.2021.3067189

CrossRef Full Text | Google Scholar

Huber, J. E., Fleck, N. A., and Ashby, M. F. (1997). The Selection of Mechanical Actuators Based on Performance Indices. Proc. Math. Phys. Eng. Sci. 453 (1965), 2185–2205. doi:10.1098/rspa.1997.0117

CrossRef Full Text | Google Scholar

Hunter, I. W., Hollerbach, J. M., and Ballantyne, J. (1991). A Comparative Analysis of Actuator Technologies for Robotics. Robot. Rev. 2, 299–342.

Google Scholar

Hussein, H. M. E., Colombo, L., and Cassella, C. (2022). “A LiNbO3-Based Subharmonic Tag for Passive and Far-Field Identification,” in 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS), 1022–1025.

Google Scholar

Hwang, E., and Bhave, S. A. (2011). Transduction of High-Frequency Micromechanical Resonators Using Depletion Forces in P-N Diodes. IEEE Trans. Electron Devices 58 (8), 2770–2776. doi:10.1109/ted.2011.2158103

CrossRef Full Text | Google Scholar

Hwang, E., Driscoll, A., and Bhave, S. A. (2011). “Platform for JFET-Based Sensing of RF MEMS Resonators in CMOS Technology,” in 2011 International Electron Devices Meeting, 20.4.1–20.4.4. doi:10.1109/iedm.2011.6131591

CrossRef Full Text | Google Scholar

Inoue, S., Nakamura, K., Nakazawa, H., Tsutsumi, J., Ueda, M., and Satoh, Y. (2013). “Analysis of Rayleigh Wave Radiations from Leaky Saw Resonators,” in 2013 IEEE International Ultrasonics Symposium (IUS) (Prague, Czech Republic: IEEE), 1953–1956. doi:10.1109/ultsym.2013.0498

CrossRef Full Text | Google Scholar

Inoue, S., Tsutsumi, J., Matsuda, T., Ueda, M., Ikata, O., and Satoh, Y. (2007). Analysis and Suppression of Side Radiation in Leaky Saw Resonators. IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 54 (8), 1692–1699. doi:10.1109/tuffc.2007.441

PubMed Abstract | CrossRef Full Text | Google Scholar

Ivira, B., Fillit, R. Y., Benech, P., Ndagijimana, F., Parat, G., and Ancey, P. (2006). “Baw Resonators Reliability in the Ghz Range,” in IECON 2006 - 32nd Annual Conference on IEEE Industrial Electronics, 3133–3138. doi:10.1109/iecon.2006.347778

CrossRef Full Text | Google Scholar

Jackson, T., Pagliarini, S., and Pileggi, L. (2018). “An Oscillatory Neural Network with Programmable Resistive Synapses in 28 Nm CMOS,” in 2018 IEEE International Conference on Rebooting Computing (ICRC), 1–7. doi:10.1109/icrc.2018.8638600

CrossRef Full Text | Google Scholar

Jiang, X., Tang, H.-Y., Lu, Y., Ng, E. J., Tsai, J. M., Boser, B. E., et al. (2017). Ultrasonic Fingerprint Sensor with Transmit Beamforming Based on a Pmut Array Bonded to Cmos Circuitry. IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 64 (9), 1401–1408. doi:10.1109/tuffc.2017.2703606

PubMed Abstract | CrossRef Full Text | Google Scholar

Joannopoulos, J. D., Johnson, S., Winn, J., and Meade, R. (2008). Photonic Crystals : Molding the Flow of Light. 2nd ed. Princeton, NJ, USA: Princeton University Press.

Google Scholar

Johnson, R. A. (1997). “Introduction to Electromechanical Filters,” in CRC Handbook of ELECTRICAL FILTERS (Boca Raton, Florida, USA: CRC Press), 11.

Google Scholar

Johnson, S. G., Bienstman, P., Skorobogatiy, M. A., Ibanescu, M., Lidorikis, E., and Joannopoulos, J. D. (2002). Adiabatic Theorem and Continuous Coupled-Mode Theory for Efficient Taper Transitions in Photonic Crystals. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 66, 066608. doi:10.1103/PhysRevE.66.066608

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, S., Povinelli, M., Bienstman, P., Skorobogatiy, M., Soljacic, M., Ibanescu, M., et al. (2003). “Coupling, Scattering, and Perturbation Theory: Semi-analytical Analyses of Photonic-Crystal Waveguides,” in Proceedings of 2003 5th International Conference on Transparent Optical Networks, 103–109.

Google Scholar

Kanda, Y. (1991). Piezoresistance Effect of Silicon. Sensors Actuators A Phys. 28 (2), 83–91. doi:10.1016/0924-4247(91)85017-I

CrossRef Full Text | Google Scholar

Kazanskiy, N. L., Khonina, S. N., and Butt, M. A. (2020). Subwavelength Grating Double Slot Waveguide Racetrack Ring Resonator for Refractive Index Sensing Application. Sensors 20 (12), 3416. doi:10.3390/s20123416

PubMed Abstract | CrossRef Full Text | Google Scholar

Khelif, A., and Adibi, A. (2015). Phononic Crystals. Berlin, Germany: Springer.

Google Scholar

Kim, S., Gopalan, V., and Gruverman, A. (2002). Coercive Fields in Ferroelectrics: A Case Study in Lithium Niobate and Lithium Tantalate. Appl. Phys. Lett. 80 (15), 2740–2742. doi:10.1063/1.1470247

CrossRef Full Text | Google Scholar

Kirbach, S., Kühnel, K., and Weinreich, W. (2018). “Piezoelectric Hafnium Oxide Thin Films for Energy-Harvesting Applications,” in 2018 IEEE 18th International Conference on Nanotechnology (IEEE-NANO), 1–4. doi:10.1109/nano.2018.8626275

CrossRef Full Text | Google Scholar

Kirbach, S., Lederer, M., Eßlinger, S., Mart, C., Czernohorsky, M., Weinreich, W., et al. (2021). Doping Concentration Dependent Piezoelectric Behavior of Si:HfO2 Thin-Films. Appl. Phys. Lett. 118 (1), 012904. doi:10.1063/5.0026990

CrossRef Full Text | Google Scholar

Koh, K. H., Lee, C., Lu, J.-H., and Chen, C.-C. (2011). “Development of CMOS MEMS Thermal Bimorph Actuator for Driving Microlens,” in 16th International Conference on Optical MEMS and Nanophotonics, 153–154. doi:10.1109/omems.2011.6031057

CrossRef Full Text | Google Scholar

Kuo, J., Hoople, J., Ardanuç, S., and Lal, A. (2014). “Towards Ultrasonic Through-Silicon Vias (Utsv),” in 2014 IEEE International Ultrasonics Symposium, 483–486.

CrossRef Full Text | Google Scholar

Kushwaha, M. S., Halevi, P., Dobrzynski, L., and Djafari-Rouhani, B. (1993). Acoustic Band Structure of Periodic Elastic Composites. Phys. Rev. Lett. 71, 2022–2025. doi:10.1103/physrevlett.71.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

Lapisa, M., Stemme, G., and Niklaus, F. (2011). Wafer-Level Heterogeneous Integration for MOEMS, MEMS, and NEMS. IEEE J. Sel. Top. Quantum Electron. 17 (3), 629–644. doi:10.1109/jstqe.2010.2093570

CrossRef Full Text | Google Scholar

Lederer, M., Kämpfe, T., Olivo, R., Lehninger, D., Mart, C., Kirbach, S., et al. (2019). Local Crystallographic Phase Detection and Texture Mapping in Ferroelectric Zr Doped HfO2 Films by Transmission-EBSD. Appl. Phys. Lett. 115 (22), 222902. doi:10.1063/1.5129318

CrossRef Full Text | Google Scholar

Lederer, M., Kämpfe, T., Vogel, N., Utess, D., Volkmann, B., Ali, T., et al. (2020). Structural and Electrical Comparison of Si and Zr Doped Hafnium Oxide Thin Films and Integrated FeFETs Utilizing Transmission Kikuchi Diffraction. Nanomaterials 10 (2), 384. doi:10.3390/nano10020384

PubMed Abstract | CrossRef Full Text | Google Scholar

Ledesma, E., Zamora, I., Uranga, A., and Barniol, N. (2021). “9.5 % Scandium Doped ALN PMUT Compatible with Pre-processed CMOS Substrates,” in 2021 IEEE 34th International Conference on Micro Electro Mechanical Systems (MEMS), 887–890.

Google Scholar

Lee, T.-C., Lee, J.-T., Robert, M. A., Wang, S., and Rabson, T. A. (2003). Surface Acoustic Wave Applications of Lithium Niobate Thin Films. Appl. Phys. Lett. 82 (2), 191–193. doi:10.1063/1.1534413

CrossRef Full Text | Google Scholar

Li, X., Ye, Z., Tan, Y., and Wang, Y. (2012). A Two-Dimensional Analysis Method on STI-Aware Layout-dependent Stress Effect. IEEE Trans. Electron Devices 59 (11), 2964–2972. doi:10.1109/ted.2012.2214389

CrossRef Full Text | Google Scholar

Lin, C.-M., Hsu, J.-C., Senesky, D. G., and Pisano, A. P. (2014). “Anchor Loss Reduction in Aln Lamb Wave Resonators Using Phononic Crystal Strip Tethers,” in 2014 IEEE International Frequency Control Symposium (FCS), 1–5. doi:10.1109/fcs.2014.6859944

CrossRef Full Text | Google Scholar

Liu, Y., Kuo, J., Davaji, B., Gund, V., Lal, A., Sharma, J., et al. (2020). “Characterization of AlScN on CMOS,” in 2020 Joint Conference of the IEEE International Frequency Control Symposium and International Symposium on Applications of Ferroelectrics (IFCS-ISAF), 1–5. doi:10.1109/ifcs-isaf41089.2020.9234939

CrossRef Full Text | Google Scholar

Lochtefeld, A., and Antoniadis, D. A. (2001). Investigating the Relationship between Electron Mobility and Velocity in Deeply Scaled NMOS via Mechanical Stress. IEEE Electron Device Lett. 22 (12), 591–593. doi:10.1109/55.974587

CrossRef Full Text | Google Scholar

Lomenzo, P. D., Takmeel, Q., Zhou, C., Liu, Y., Fancher, C. M., Jones, J. L., et al. (2014). The Effects of Layering in Ferroelectric Si-Doped HfO2 Thin Films. Appl. Phys. Lett. 105 (7), 072906. doi:10.1063/1.4893738

CrossRef Full Text | Google Scholar

Lopez, J. L., Verd, J., Uranga, A., Giner, J., Murillo, G., Torres, F., et al. (2009). A CMOS-MEMS RF-Tunable Bandpass Filter Based on Two High- $Q$ 22-MHz Polysilicon Clamped-Clamped Beam Resonators. IEEE Electron Device Lett. 30 (7), 718–720. doi:10.1109/led.2009.2022509

CrossRef Full Text | Google Scholar

Lu, R., Li, M.-H., Yang, Y., Manzaneque, T., and Gong, S. (2019). Accurate Extraction of Large Electromechanical Coupling in Piezoelectric Mems Resonators. J. Microelectromech. Syst. 28 (2), 209–218. doi:10.1109/jmems.2019.2892708

CrossRef Full Text | Google Scholar

Mahboob, I., Flurin, E., Nishiguchi, K., Fujiwara, A., and Yamaguchi, H. (2011). Interconnect-free Parallel Logic Circuits in a Single Mechanical Resonator. Nat. Commun. 2 (1), 198. doi:10.1038/ncomms1201

PubMed Abstract | CrossRef Full Text | Google Scholar

Mahboob, I., and Yamaguchi, H. (2008). Bit Storage and Bit Flip Operations in an Electromechanical Oscillator. Nat. Nanotech 3 (5), 275–279. doi:10.1038/nnano.2008.84

PubMed Abstract | CrossRef Full Text | Google Scholar

Marathe, R., Bahr, B., Wang, W., Mahmood, Z., Daniel, L., and Weinstein, D. (2014). Resonant Body Transistors in IBM's 32 Nm SOI CMOS Technology. J. Microelectromech. Syst. 23 (3), 636–650. doi:10.1109/jmems.2013.2283720

CrossRef Full Text | Google Scholar

Marathe, R., Wang, W., and Weinstein, D. (2012). “Si-based Unreleased Hybrid MEMS-CMOS Resonators in 32nm Technology,” in 2012 IEEE 25th International Conference on Micro Electro Mechanical Systems (MEMS), 729–732. doi:10.1109/memsys.2012.6170289

CrossRef Full Text | Google Scholar

Mart, C., Kämpfe, T., Hoffmann, R., Eßlinger, S., Kirbach, S., Kühnel, K., et al. (2020). Piezoelectric Response of Polycrystalline Silicon‐Doped Hafnium Oxide Thin Films Determined by Rapid Temperature Cycles. Adv. Electron. Mat. 6 (3), 1901015. doi:10.1002/aelm.201901015

CrossRef Full Text | Google Scholar

Mueller, S., Mueller, J., Singh, A., Riedel, S., Sundqvist, J., Schroeder, U., et al. (2012). Incipient Ferroelectricity in Al-Doped HfO2 Thin Films. Adv. Funct. Mat. 22 (11), 2412–2417. doi:10.1002/adfm.201103119

CrossRef Full Text | Google Scholar

Mulaosmanovic, H., Ocker, J., Müller, S., Schroeder, U., Müller, J., Polakowski, P., et al. (2017). Switching Kinetics in Nanoscale Hafnium Oxide Based Ferroelectric Field-Effect Transistors. ACS Appl. Mat. Interfaces 9 (4), 3792–3798. doi:10.1021/acsami.6b13866

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakagawa, R., Iwamoto, H., and Takai, T. (2019). “Low Velocity i.h.P. Saw Using Al/pt Electrodes for Miniaturization,” in 2019 IEEE International Ultrasonics Symposium (IUS), 2083–2086. doi:10.1109/ultsym.2019.8925860

CrossRef Full Text | Google Scholar

Nikonov, D. E., Csaba, G., Porod, W., Shibata, T., Voils, D., Hammerstrom, D., et al. (2015). Coupled-Oscillator Associative Memory Array Operation for Pattern Recognition. IEEE J. Explor. Solid-State Comput. Devices Circuits 1, 85–93. doi:10.1109/jxcdc.2015.2504049

CrossRef Full Text | Google Scholar

Olsson, R. H., and El-Kady, I. (2008). Microfabricated Phononic Crystal Devices and Applications. Meas. Sci. Technol. 20 (1), 012002. doi:10.1088/0957-0233/20/1/012002

CrossRef Full Text | Google Scholar

Oskooi, A., Mutapcic, A., Noda, S., Joannopoulos, J. D., Boyd, S. P., and Johnson, S. G. (2012). Robust Optimization of Adiabatic Tapers for Coupling to Slow-Light Photonic-Crystal Waveguides. Opt. Express 20 (19), 21558. doi:10.1364/OE.20.021558

PubMed Abstract | CrossRef Full Text | Google Scholar

Ozgurluk, A., Peleaux, K., and Nguyen, C. T.-C. (2020). “Single-Digit-Nanometer Capacitive-Gap Transduced Micromechanical Disk Resonators,” in 2020 IEEE 33rd International Conference on Micro Electro Mechanical Systems (MEMS), 222–225. doi:10.1109/mems46641.2020.9056204

CrossRef Full Text | Google Scholar

Park, M., Hao, Z., Dargis, R., Clark, A., and Ansari, A. (2020). Epitaxial Aluminum Scandium Nitride Super High Frequency Acoustic Resonators. J. Microelectromech. Syst. 29 (4), 490–498. doi:10.1109/jmems.2020.3001233

CrossRef Full Text | Google Scholar

Partridge, A., and Tabatabaei, S. (2009). “Silicon MEMS Oscillators for High Speed Digital Systems,” in 2009 IEEE Hot Chips 21 Symposium (HCS), 1–25. doi:10.1109/hotchips.2009.7478376

CrossRef Full Text | Google Scholar

Piazza, G., Stephanou, P. J., and Pisano, A. P. (2007). Single-chip Multiple-Frequency Aln Mems Filters Based on Contour-Mode Piezoelectric Resonators. J. Microelectromech. Syst. 16 (2), 319–328. doi:10.1109/jmems.2006.889503

CrossRef Full Text | Google Scholar

Pinin (2010). Perovskite Structure of PZT. Available at: https://en.wikipedia.org/w/index.php?title=Lead_zirconate_titanate&oldid=1057656462.

Google Scholar

Polakowski, P., and Müller, J. (2015). Ferroelectricity in Undoped Hafnium Oxide. Appl. Phys. Lett. 106 (23), 232905. doi:10.1063/1.4922272

CrossRef Full Text | Google Scholar

Pourkamali, S., Ho, G. K., and Ayazi, F. (2007). Low-Impedance VHF and UHF Capacitive Silicon Bulk Acoustic-Wave Resonators—Part II: Measurement and Characterization. IEEE Trans. Electron Devices 54 (8), 2024–2030. doi:10.1109/TED.2007.901405

CrossRef Full Text | Google Scholar

Quan, Z., Wang, M., Zhang, X., Liu, H., Zhang, W., and Xu, X. (2020). Excellent Ferroelectricity of 50 Nm-Thick Doped HfO2 Thin Films Induced by Annealing with a Rapid-Heating-Temperature Process. AIP Adv. 10 (8), 085024. doi:10.1063/5.0013511

CrossRef Full Text | Google Scholar

QuantumATK (2022). QuantumATK. Available at: https://www.synopsys.com/silicon/quantumatk.html.

Google Scholar

Rabe K. M., Ahn C. H, and Triscone J.-M. (Editors) (2007). Physics of Ferroelectrics: A Modern Perspective, Ser. Topics in Applied Physics (Berlin ; New York: Springer), Vol. 105.

Google Scholar

Rahafrooz, A., and Pourkamali, S. (2011). High-Frequency Thermally Actuated Electromechanical Resonators with Piezoresistive Readout. IEEE Trans. Electron Devices 58 (4), 1205–1214. doi:10.1109/ted.2011.2105491

CrossRef Full Text | Google Scholar

Ramezany, A., and Pourkamali, S. (2018). Ultrahigh Frequency Nanomechanical Piezoresistive Amplifiers for Direct Channel-Selective Receiver Front-Ends. Nano Lett. 18 (4), 2551–2556. doi:10.1021/acs.nanolett.8b00242

PubMed Abstract | CrossRef Full Text | Google Scholar

Rassay, S., Hakim, F., Li, C., Forgey, C., Choudhary, N., and Tabrizian, R. (2021). A Segmented-Target Sputtering Process for Growth of Sub-50 Nm Ferroelectric Scandium–Aluminum–Nitride Films with Composition and Stress Tuning. Phys. Status Solidi (RRL) – Rapid Res. Lett. 15 (5), 2100087. doi:10.1002/pssr.202100087

CrossRef Full Text | Google Scholar

Rawat, U., Bahr, B., and Weinstein, D. (2022). Analysis and Modeling of an 11.8 Ghz Fin Resonant Body Transistor in a 14nm Finfet Cmos Process. IEEE Trans. Ultrasonics, Ferroelectr. Freq. Control 69, 1399–1412. doi:10.1109/tuffc.2022.3147973

CrossRef Full Text | Google Scholar

Rawat, U., Nair, D. R., and DasGupta, A. (2017). Piezoelectric-on-silicon Array Resonators with Asymmetric Phononic Crystal Tethering. J. Microelectromech. Syst. 26 (4), 773–781. doi:10.1109/jmems.2017.2665473

CrossRef Full Text | Google Scholar

Romera, M., Talatchian, P., Tsunegi, S., Abreu Araujo, F., Cros, V., Bortolotti, P., et al. (2018). Vowel Recognition with Four Coupled Spin-Torque Nano-Oscillators. Nature 563 (7730), 230–234. doi:10.1038/s41586-018-0632-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenblatt, D., Sharon, A., and Friesem, A. A. (1997). Resonant Grating Waveguide Structures. IEEE J. Quantum Electron. 33 (11), 2038–2059. doi:10.1109/3.641320

CrossRef Full Text | Google Scholar

Ruby, R. (2015). A Snapshot in Time: The Future in Filters for Cell Phones. IEEE Microw. 16 (7), 46–59. doi:10.1109/mmm.2015.2429513

CrossRef Full Text | Google Scholar

Ruby, R., Bradley, P., Clark, D., Feld, D., Jamneala, T., and Wang, K. (2004). “Acoustic Fbar for Filters, Duplexers and Front End Modules,” in 2004 IEEE MTT-S International Microwave Symposium Digest (IEEE Cat. No.04CH37535), 931–934.

Google Scholar

Ruby, R., Bradley, P., Larson, J., Oshmyansky, Y., and Figueredo, D. (2001). “Ultra-miniature High-Q Filters and Duplexers Using FBAR Technology,” in 2001 IEEE International Solid-State Circuits Conference. Digest of Technical Papers. ISSCC (Cat. No.01CH37177), 120–121.

Google Scholar

Ruby, R., Bradley, P., Oshmyansky, Y., Chien, A., and Larson, J. (2001). “Thin Film Bulk Wave Acoustic Resonators (Fbar) for Wireless Applications,” in 2001 IEEE Ultrasonics Symposium. Proceedings. An International Symposium (Cat. No.01CH37263), 813–821.

Google Scholar

Ruby, R., Small, M., Bi, F., Lee, D., Callaghan, L., Parker, R., et al. (2012). Positioning Fbar Technology in the Frequency and Timing Domain. IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 59 (3), 334–345. doi:10.1109/tuffc.2012.2202

PubMed Abstract | CrossRef Full Text | Google Scholar

Schenk, T., Godard, N., Mahjoub, A., Girod, S., Matavz, A., Bobnar, V., et al. (2020). Toward Thick Piezoelectric HfO 2 ‐Based Films. Phys. Status Solidi RRL 14 (3), 1900626. doi:10.1002/pssr.201900626

CrossRef Full Text | Google Scholar

Schroeder, U., Yurchuk, E., Müller, J., Martin, D., Schenk, T., Polakowski, P., et al. (2014). Impact of Different Dopants on the Switching Properties of Ferroelectric Hafniumoxide. Jpn. J. Appl. Phys. 53 (8S1), 08LE02. doi:10.7567/jjap.53.08le02

CrossRef Full Text | Google Scholar

Shao, L., Maity, S., Zheng, L., Wu, L., Shams-Ansari, A., Sohn, Y.-I., et al. (2019). Phononic Band Structure Engineering for High-Q Gigahertz Surface Acoustic Wave Resonators on Lithium Niobate. Phys. Rev. Appl. 12 (1), 014022. doi:10.1103/physrevapplied.12.014022

CrossRef Full Text | Google Scholar

Shi, R., Cai, X., Wang, W., Wang, J., Kong, D., Cai, N., et al. (2019). Single‐Crystalline Vanadium Dioxide Actuators. Adv. Funct. Mat. 29 (20), 1900527. doi:10.1002/adfm.201900527

CrossRef Full Text | Google Scholar

Shih, V., Cheng, S., Lin, Y.-R., Lin, A., Liao, Y.-J., Lin, C.-H., et al. (2019). “Highly Reliable Piezoelectric Process Technology in Volume Foundry for Emerging Mems Applications,” in 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems Eurosensors XXXIII (TRANSDUCERS EUROSENSORS XXXIII), 190–193. doi:10.1109/transducers.2019.8808685

CrossRef Full Text | Google Scholar

Siddiqi, M. W. U., and Lee, J. E.-Y. (2018). Wide Acoustic Bandgap Solid Disk-Shaped Phononic Crystal Anchoring Boundaries for Enhancing Quality Factor in Aln-On-Si Mems Resonators. Micromachines 9 (8), 413. doi:10.3390/mi9080413

PubMed Abstract | CrossRef Full Text | Google Scholar

Sigalas, M., and Economou, E. N. (1993). Band Structure of Elastic Waves in Two Dimensional Systems. Solid State Commun. 86 (3), 141–143. doi:10.1016/0038-1098(93)90888-t

CrossRef Full Text | Google Scholar

Solal, M., Gratier, J., Aigner, R., Gamble, K., Abbott, B., Kook, T., et al. (2010). “Transverse Modes Suppression and Loss Reduction for Buried Electrodes Saw Devices,” in 2010 IEEE International Ultrasonics Symposium, 624–628.

CrossRef Full Text | Google Scholar

Srivastava, A., Chatterjee, B., Rawat, U., He, Y., Weinstein, D., and Sen, S. (2021). A mmWave Oscillator Design Utilizing High-Q Active-Mode On-Chip MEMS Resonators for Improved Fundamental Limits of Phase Noise. arXiv:2107.01953 [eess]. Available at: http://arxiv.org/abs/2107.01953.

Google Scholar

Srivastava, A., Chatterjee, B., Rawat, U., He, Y., Weinstein, D., and Sen, S. (2021). Analysis and Design Considerations for Achieving the Fundamental Limits of Phase Noise in Mmwave Oscillators with On-Chip Mems Resonator. IEEE Trans. Circuits Syst. II 68 (4), 1108–1112. doi:10.1109/tcsii.2020.3030074

CrossRef Full Text | Google Scholar

Starschich, S., Griesche, D., Schneller, T., Waser, R., and Bottger, U. (2014). Chemical Solution Deposition of Ferroelectric Yttrium-Doped Hafnium Oxide Films on Platinum Electrodes. Appl. Phys. Lett. 104 (20), 4. doi:10.1063/1.4879283

CrossRef Full Text | Google Scholar

Starschich, S., Schenk, T., Schroeder, U., and Boettger, U. (2017). Ferroelectric and Piezoelectric Properties of Hf1-xZrxO2 and Pure ZrO2 Films. Appl. Phys. Lett. 110 (18), 182905. doi:10.1063/1.4983031

CrossRef Full Text | Google Scholar

Sze, S. M., and Ng, K. K. (2006). Physics of Semiconductor Devices. 3rd ed. Hoboken, N.J: Wiley-Interscience.

Google Scholar

Tabrizian, R., Rais-Zadeh, M., and Ayazi, F. (2009). “Effect of Phonon Interactions on Limiting the f.Q Product of Micromechanical Resonators,” in TRANSDUCERS 2009 - 2009 International Solid-State Sensors, Actuators and Microsystems Conference, 2131–2134. doi:10.1109/sensor.2009.5285627

CrossRef Full Text | Google Scholar

Takai, T., Iwamoto, H., Takamine, Y., Fuyutsume, T., Nakao, T., Hiramoto, M., et al. (2017). “I.h.p. Saw Technology and its Application to Microacoustic Components (Invited),” in 2017 IEEE International Ultrasonics Symposium (IUS), 1–8.

CrossRef Full Text | Google Scholar

Tang, H.-Y., Lu, Y., Jiang, X., Ng, E. J., Tsai, J. M., Horsley, D. A., et al. (2016). 3-d Ultrasonic Fingerprint Sensor-On-A-Chip. IEEE J. Solid-State Circuits 51 (11), 2522–2533. doi:10.1109/jssc.2016.2604291

CrossRef Full Text | Google Scholar

Tharpe, T., Hakim, F., and Tabrizian, R. (2021). “In-Plane Bulk Acoustic Resonators Using 50nm-Thick Nano-Laminated Ferroelectric Hf0. 5Zr0. 5O2,” in 2021 21st International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers) (Orlando, FL, USA: IEEE), 313–316. doi:10.1109/transducers50396.2021.9495745

CrossRef Full Text | Google Scholar

Tharpe, T., Zheng, X.-Q., Feng, P. X.-L., and Tabrizian, R. (2021). Resolving Mechanical Properties and Morphology Evolution of Free‐Standing Ferroelectric Hf 0.5 Zr 0.5 O 2. Adv. Eng. Mater 23 (12), 2101221. doi:10.1002/adem.202101221

CrossRef Full Text | Google Scholar

Tiersten, H. F., Stevens, D. S., and Weglein, R. D. (1986). Acceleration Sensitivity of Surface Acoustic Wave Resonators. Appl. Phys. Lett. 48 (2), 97–99. doi:10.1063/1.96947

CrossRef Full Text | Google Scholar

Trentzsch, M., Flachowsky, S., Richter, R., Paul, J., Reimer, B., Utess, D., et al. (2016). “A 28nm HKMG Super Low Power Embedded NVM Technology Based on Ferroelectric FETs.”in 2016 IEEE International Electron Devices Meeting (IEDM).” (San Francisco, CA, USA: IEEE), 11.5.1–11.5.4. doi:10.1109/iedm.2016.7838397

CrossRef Full Text | Google Scholar

Tsividis, Y., and McAndrew, C. (2010). Operation and Modeling of the MOS Transistor. 3rd ed. New York: Oxford University Press.

Google Scholar

Üstün, K., and Kurt, H. (2011). “Efficient and Compact Coupling to Slow Light Structures,” in 16th International Conference on Optical MEMS and Nanophotonics, 105–106.

Google Scholar

VASP (2022). VASP - Vienna Ab Initio Simulation Package. Available at: https://www.vasp.at/.

Google Scholar

Victory Atomistic (2022). Victory Atomistic. Available at: https://silvaco.com/tcad/atomistic-simulation/.

Google Scholar

Wang, J., Glesk, I., and Chen, L. R. (2014). Subwavelength Grating Filtering Devices. Opt. Express 22 (13), 15335–15345. doi:10.1364/OE.22.015335

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Park, M., and Ansari, A. (2022). High-Temperature Acoustic and Electric Characterization of Ferroelectric Al $_0.7$ Sc $_0.3$ N Films. J. Microelectromechanical Syst. 31, 234–240. doi:10.1109/JMEMS.2022.3147492

CrossRef Full Text | Google Scholar

Wang, S., Popa, L. C., and Weinstein, D. (2015). “Tapered Phononic Crystal Sawresonator in gan,” in 2015 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), 1028–1031.

CrossRef Full Text | Google Scholar

Wang, W., and Weinstein, D. (2011). “Acoustic Bragg Reflectors for Q-Enhancement of Unreleased Mems Resonators,” in 2011 Joint Conference of the IEEE International Frequency Control and the European Frequency and Time Forum (FCS) Proceedings, 1–6. doi:10.1109/fcs.2011.5977903

CrossRef Full Text | Google Scholar

Wang, Z., Xu, X., Fan, D., Wang, Y., and Chen, R. T. (2016). High Quality Factor Subwavelength Grating Waveguide Micro-ring Resonator Based on Trapezoidal Silicon Pillars. Opt. Lett. 41 (14), 3375–3378. doi:10.1364/ol.41.003375

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, Y., Nukala, P., Salverda, M., Matzen, S., Zhao, H. J., Momand, J., et al. (2018). A Rhombohedral Ferroelectric Phase in Epitaxially Strained Hf0.5Zr0.5O2 Thin Films. Nat. Mater 17 (12), 1095–1100. doi:10.1038/s41563-018-0196-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Weinstein, D., and Bhave, S. (2010). “Acoustic Resonance in an Independent-Gate FinFET,” in 2010 Solid-State, Actuators, and Microsystems Workshop Technical Digest (Hilton Head, South Carolina, USA: Transducer Research Foundation), 459–462. Available at: https://transducer-research-foundation.org/technical_digests/HiltonHead_2010/hh2010_0459.pdf.

CrossRef Full Text | Google Scholar

Weinstein, D., and Bhave, S. A. (2009). Internal Dielectric Transduction in Bulk-Mode Resonators. J. Microelectromech. Syst. 18 (6), 1401–1408. doi:10.1109/jmems.2009.2032480

CrossRef Full Text | Google Scholar

Weinstein, D., and Bhave, S. A. (2007). “Internal Dielectric Transduction of a 4.5 GHz Silicon Bar Resonator,” in 2007 IEEE International Electron Devices Meeting, 415–418.

CrossRef Full Text | Google Scholar

Weinstein, D., Bhave, S. A., Tada, M., Mitarai, S., Morita, S., and Ikeda, K. (2007). “Mechanical Coupling of 2d Resonator Arrays for Mems Filter Applications,” in 2007 IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum, 1362–1365. doi:10.1109/freq.2007.4319299

CrossRef Full Text | Google Scholar

Weinstein, D., and Bhave, S. A. (2010). The Resonant Body Transistor. Nano Lett. 10 (4), 1234–1237. doi:10.1021/nl9037517

PubMed Abstract | CrossRef Full Text | Google Scholar

Willers, O., Huth, C., Guajardo, J., and Seidel, H. (2016). “MEMS Gyroscopes as Physical Unclonable Functions,” in Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, ser. CCS ’16 (New York, NY, USA: Association for Computing Machinery), 591–602. doi:10.1145/2976749.2978295

CrossRef Full Text | Google Scholar

Yang, S., and Xu, Q. (2017). A Review on Actuation and Sensing Techniques for MEMS-Based Microgrippers. J. Micro-Bio Robotics 13 (1), 1–14. doi:10.1007/s12213-017-0098-2

CrossRef Full Text | Google Scholar

Yang, Y., Lu, R., and Gong, S. (2020). High $Q$ Antisymmetric Mode Lithium Niobate MEMS Resonators with Spurious Mitigation. J. Microelectromech. Syst. 29 (2), 135–143. doi:10.1109/jmems.2020.2967784

CrossRef Full Text | Google Scholar

Zinck, C., Defay, E., Volatier, A., Caruyer, G., Tanor, D., and Figuiere, L. (2004). “Design, Integration and Characterization of PZT Tunable FBAR,” in 14th IEEE International Symposium on Applications of Ferroelectrics, 2004. ISAF-04. 2004, 29–32.

Google Scholar

Zope, A. A., Chang, J.-H., Liu, T.-Y., and Li, S.-S. (2020). A CMOS-MEMS Thermal-Piezoresistive Oscillator for Mass Sensing Applications. IEEE Trans. Electron Devices 67 (3), 1183–1191. doi:10.1109/TED.2020.2969967

CrossRef Full Text | Google Scholar

Zuo, C., Sinha, N., Van der Spiegel, J., and Piazza, G. (2008). “Multi-frequency Pierce Oscillators Based on Piezoelectric Aln Contour-Mode Mems Resonators,” in 2008 IEEE International Frequency Control Symposium, 402–407. doi:10.1109/freq.2008.4623028

CrossRef Full Text | Google Scholar