CMOS-MEMS Oscillator Architecture and Phase Noise: A Mini-Review

Over the past two decades, the advancement in microelectromechanical systems (MEMS) has been making headway in the development of miniaturized mechanical structures with integrated electronics. By adopting the existing layer in the complementary metal–oxide–semiconductor (CMOS) fabrication platform, the so-called “CMOS-MEMS” technology offers an intrinsic circuit-MEMS integration scheme, paving the way to realize monolithic micromechanical oscillators for frequency control and sensing applications. To enhance the functionality of the oscillator, it is cardinal to understand the secrets behind the resonator and circuit design techniques to generate high spectral purity signals. As the oscillator characteristics heavily depend on the resonator’s motional parameters, the circuit configuration is determined in accordance with the post-CMOS processing technology and the mode shape of the resonator. In this mini-review, we attempt to summarize and appraise studies related to the design and optimization of CMOS-MEMS oscillators and to give directions for future researchers in terms of phase noise.

Introduction

Electronic oscillators are the most fundamental building block in almost any electronic system for a variety of applications such as frequency control (Achenbach et al., 2000) and environmental sensing (Bianchi et al., 2000; Walls and Gagnepain, 2002). In addition to traditional quartz resonator-based reference oscillators (Vittoz et al., 1988) and quartz crystal microbalance (QCM) sensors (Ferrari et al., 2006), miniaturized oscillators using microelectromechanical systems (MEMS) technology have been intensively studied in both academia and industry over the past two decades (Lavasani et al., 2011; Chance et al., 2014; Zaliasl et al., 2015; Naing et al., 2020; Kalia et al., 2021; Chang et al., 2022) to be used in demanding applications with size constraints. Among the existing MEMS oscillator fabrication approaches, the CMOS-MEMS technology is one of the most promising approaches to achieving the monolithic integration of mechanical resonators and electronic circuits (Xie et al., 2002; Dai et al., 2005; Chen et al., 2011; Li C.-S. et al., 2012; Chen et al., 2019; Valle et al., 2021). In this approach, MEMS mechanical structures can be formed from the back-end of line (BEOL) metal/dielectric (Verd et al., 2006; Li et al., 2012c; Li et al., 2015b; Liu et al., 2018) or the front-end of line (FEOL) polysilicon layers (Verd et al., 2005; Lopez et al., 2009) by removing predefined sacrificial layers, thereby eliminating the thermal budget constraints that are often encountered in other custom IC-MEMS integration processes (Fedder et al., 2008). Although the constituent materials of the CMOS-MEMS resonators are limited to the composite metals, dielectrics, and polysilicon, it still features great mechanical properties such as high-quality factor (Q) (Chen et al., 2012; Li et al., 2015a) and low-temperature coefficient of frequency (TCF) (Liu and Li, 2019), providing potential for being used in practical oscillator applications.

To make up an oscillator, the CMOS-MEMS resonator is connected in a positive feedback loop with a CMOS amplifier on the same chip (Verd et al., 2008). Such a monolithic integration scheme helps reduce the parasitic capacitance between the MEMS resonator and the amplifier, hence extending the available bandwidth of the amplifier and reducing the input-referred noise. According to the feedback oscillator theories, the Barkhausen stability criterion should be met: 1) the loop gain at the oscillation frequency equals unity, and 2) the phase delay in the oscillation loop should be equal to a multiple of 2π (Rhea, 2010). Despite the simplicity of the concept, implementing a high-performance CMOS-MEMS oscillator is not an easy task. There are several parameters to evaluate the overall performance of an oscillator, including the oscillation frequency, temperature stability, power dissipation, and phase noise. Since phase noise represents random fluctuations in the phase of the output signal (Rubiola, 2008), it should be kept as low as possible to enhance oscillator stability, which is critical for precision applications such as timing references and high-resolution sensors. However, the most challenging issue to achieve low-noise CMOS-MEMS oscillator is the high motional resistance (R_m) of the on-chip MEMS resonator. Although several energy transduction mechanisms including electrostatic (Li et al., 2015c), thermal-piezoresistive (Zope and Li, 2021), and capacitive-piezoresistive (Li C.-S. et al., 2013) have been explored in CMOS-MEMS technology, the electrostatic transduction is the most widely adopted scheme in resonator due to its simplicity. Since the typical transduction gap size from 400 to 1,000 nm is limited by lithographic limitations in 0.35 and 0.18 μm CMOS platforms (Li C.-S. et al., 2012; Chen et al., 2019), typical CMOS-MEMS resonator impedance lies in the MΩ range in previous reports even under high bias voltages (Liu et al., 2013). As will be shown in the next section, such a high impedance not only raises the design complexity and difficulty of the sustaining circuit but also contributes a significant portion to the phase noise. In addition to R_m, recent studies also confirm that the inherent nonlinearity in CMOS-MEMS resonators also plays a key role in the phase noise spectrum (Li et al., 2018). In order to make a breakthrough in the performance of existing CMOS-MEMS oscillators, it is crucial to understand the characteristics of the prior arts.

Phase Noise Model for Complementary Metal–Oxide–Semiconductor-Microelectromechanical Systems Oscillators

To capture the important parameters that contributed phase noise in both MEMS resonator and CMOS circuit, an equivalent circuit model is depicted in Figure 1A. The circuit is divided into two stages where the first stage is a transimpedance amplifier (TIA) to convert the motional current $i_m$ from the resonator to the corresponding voltage $v_{TIA}$ and the second stage is a gain-boosting amplifier to provide an additional gain $A$ to satisfy the Barkhausen criterion. Note that the transimpedance gain should be in ohms rather than V/V. At the oscillation frequency $f_o$, the overall gain $R_A=R_{TIA}\cdot A$ should be greater than the equivalent resonator impedance $Z_m$ and the overall feedback phase is ${\phi }_{TIA}+{\phi }_A+{\phi }_{MEMS}=2n\pi$. Considering a practical resonator with a certain nonlinear effect, $Z_m$ is greater than $R_m$ in a general case (Pardo et al., 2012). Based on this circuit, the phase noise of the oscillator can be expressed as

$\mathrm{ℒ}\left(f_m\right)=10\log \left\{\frac{\left(4kT{Z}_m+\frac{\overline{i_n^2}}{\mathrm{\Delta }f}{Z}_m^2\right)}{2\overline{V_{OUT}^2}}\left(1+{\left(\frac{f_o}{2Q_{\text{eff}}{f}_m}\right)}^2\right)+{\left|\frac{\partial f_n}{\partial V_{OUT}}\right|}^2\frac{S_{An}\left(f_m\right)}{f_m^2}\right\}(1)$

where $k$ is the Boltzmann constant, $T$ is the temperature in Kelvin, $f_m$ is the offset frequency from carrier, $\overline{i_n^2}/\Delta f$ is the input-referred current noise density of the TIA stage, $Q_{\text{eff}}$ is the equivalent quality factor of a nonlinear resonator, ${\left|\partial f/\partial V_{OUT}\right|}^2$ is a coefficient to describe the A-f effect of an nonlinear MEMS resonator (Li et al., 2018), and $S_{An}\left(f_m\right)$ is the amplitude noise spectrum of the oscillator. According to Eq. 1, the first component of phase noise is obviously from the Leeson effect and the second component is from the nonlinear amplitude-to-phase modulation (AM-PM) effect (Ward and Duwel, 2011).

FIGURE 1

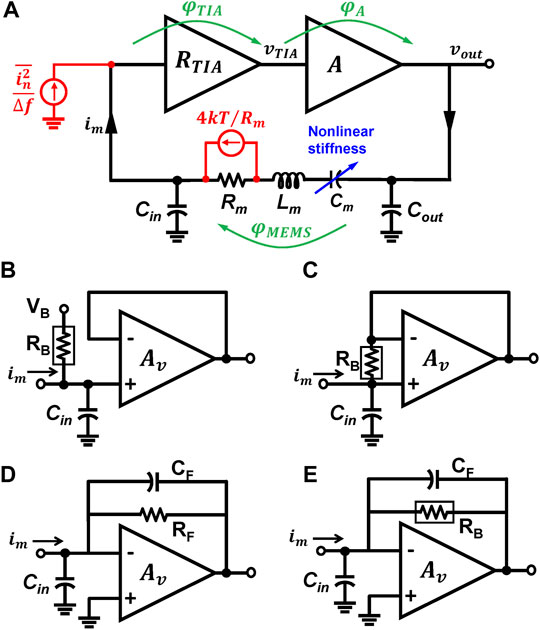
FIGURE 1. Circuit architecture of a general CMOS-MEMS oscillator: (A) overall oscillator circuit with noise sources; (B) voltage buffer as input stage; (C) voltage buffer with feedback biasing technique as input stage; (D) resistive feedback transimpedance amplifier (R-TIA) as input stage; (E) charge integrator (CI) as input stage.

From Eq. 1, it can be seen that the overall phase noise is dominated by the amplified circuit noise, $\left(\overline{i_n^2}/\Delta f\right)\cdot Z_m^2$. Since the typical values of $Z_m$ lies in MΩ range for CMOS-MEMS resonators, the input-referred current noise of the TIA stage should be designed as low as possible to minimize this term. The resonator current noise $4kT{Z}_m$ is not significant for CMOS-MEMS devices. Therefore, some amplifier architecture, such as regulated-cascode TIA (Nabki et al., 2009), is not suitable for CMOS-MEMS oscillator design due to its high input-referred current noise. In addition to the impedance issue, when the resonator is driven at a large vibrating magnitude, the phase noise-folding caused by the AM-PM conversion can be described as an additive term, which dominates the close-to-carrier phase noise (Lee et al., 2011). To solve this issue, several design techniques such as high-stiffness driving (Su et al., 2015) and phase-feedback (Li et al., 2014) schemes were explored and implemented in CMOS-MEMS.

Complementary Metal-Oxide-Semiconductor-Microelectromechanical Systems Oscillator Architecture

Voltage Buffer as Input Stage

To compensate for the R_m of the CMOS-MEMS resonator, a high-transimpedance gain is desired. The simplest architecture uses a single capacitor to perform current-to-voltage conversion based on the charge integration over a sensing capacitor, C_in, as shown in Figure 1B. To preciously control the value of C_in without affecting by the external parasitic capacitance, the resonator output is connected to a voltage buffer. An example is provided in (Li H.-C. et al., 2012) where the buffer is implemented by a two-stage source-follower circuit. Noted that the bias voltage of the input transistor is supplied through a high impedance pseudo resistor implemented with a subthreshold n-type MOSFET. In addition, as the pseudo resistor offers TΩ impedance, the input-referred current noise is low, which is favorable for low noise oscillator implementations. A subsequent voltage amplifier and phase compensation circuit are typically added after the voltage buffer to fulfill the oscillation condition. In addition to conventional all-pass filter-based phase compensation, a phase-locked loop (PLL) driving circuit is investigated in (Li H.-C. et al., 2012) to offer a wide-bandwidth frequency tracking. The implemented CMOS-MEMS PLL is used in mass sensor array systems (Wei and Lu, 2012), demonstrating a minimum mass resolution of only 23 pg by tracking the frequency shift over 12 MEMS resonant sensors.

Another voltage buffer-based sensing circuit was proposed by Verd et al., 2008 where the PMOS pseudo resistor is connected to the feedback loop, as shown in Figure 1C. Since the readout circuit is a unity-gain feedback buffer, the increase in C_in caused by the Miller effect and stray capacitance in the feedback path is negligible. The loop phase is compensated through the clever arrangement of the output impedance of the second stage amplifier and the parasitic capacitance at the driving port. In (Verd et al., 2008), a 6.32 MHz oscillator was demonstrated based on a very small CMOS-MEMS resonator (10 μm $\times$ 0.6 μm) with a huge R_m near 26 MΩ. In this example, we notice that the close-to-carrier phase noise appears 1/f² trend. This behavior implies that the resonator is still operated under linear conditions since the quality factor is low (∼100). On the other hand, the far-from-carrier phase noise of −94 dBc/Hz is limited by R_m, which can be explained by Eq. 1. When the oscillator is used in mass sensing applications, the combined mass resolution of 0.9 ag/Hz according to the frequency stability of 1.59 Hz for a typical averaging time of 1 s.

Resistive Transimpedance Amplifier as Input Stage

Series-resonant topology is often chosen in capacitive MEMS oscillators to minimize the degradation of the resonator’s quality factor caused by the loading effect. A resistive feedback transimpedance amplifier (R-TIA) can be a suitable candidate for the sustaining circuit due to its low input impedance offered by the shunt-shunt feedback configuration, as depicted in Figure 1D. A typical R-TIA is composed of an operational amplifier, a resistive element R_F, and an optional damping capacitor C_F. In contrast to the voltage buffer-first topology described in the previous section, which runs the oscillator outside the 3-dB bandwidth of the entire sustaining circuit, in the series-resonant topology, the circuit bandwidth remains above the oscillation frequency. To design a high-frequency CMOS-MEMS oscillator, the R-TIA must feature a very high gain-bandwidth product to fulfill the oscillation condition, which consequently burns large dc power (Nguyen and Howe, 1999). As a result, the series-resonant topology is only compatible with those MEMS resonators with moderate R_m (mostly sub-MΩ) to offer reasonable phase noise under low power operation.

Although the application of series-resonant topology in CMOS-MEMS oscillator is difficult due to the relatively large R_m, there are still some vital examples (Li M.-H. et al., 2013; Li et al., 2015d; Su et al., 2015). In Li et al. (2015d), a 1.2 MHz CMOS-MEMS oscillator is designed with a 4-stage amplifier as the sustaining circuit. The circuit is designed based on a single-ended common-source amplifier to minimize the noise and power consumption. An overall tunable gain of 126–160 dBΩ, a maximum bandwidth of 20 MHz, and low input-referred noise of 0.6 pA/rtHz are obtained and burns only 1.3 mW, which is suitable for most CMOS-MEMS oscillator implementation in the MHz range. In this example, the phase noise of the oscillator at 1-kHz offset from the carrier is −112 dBc/Hz and at a 1-MHz offset is −120 dBc/Hz, resulting in an oscillator figure of merit (FoM) of −172.4 dB. Such a performance is comparable to other 2-chip MEMS oscillators (Lin et al., 2003) and MEMS-on-CMOS oscillators (Huang et al., 2008), which represents a breakthrough in monolithic CMOS-MEMS oscillator technology. Moreover, the same sustaining circuit is incorporated in an ultra-low-power oven-controlled oscillator design (Liu et al., 2016), which shows a maximum frequency variation below 4 ppm across a 90°C temperature span with sub-mW ovenization power.

With the development of CMOS-MEMS technology, novel resonators with deep sub-micron transduction gaps have been developed in recent years to further reduce R_m and thus be more advantageous in oscillator implementation. An example is given in Bhosale et al. (2021) where a clamp-clamp beam resonator with a submicron gap of 400 nm is configured with an R-TIA to form a compact active pixel based on the TiN-C post-CMOS process. The phase noise achieves -99.7 dB at 1-kHz offset and is lower than −120 dBc/Hz at 1-MHz offset thanks to the low R_m of the resonator, yielding decent frequency stability of 420 ppb for parallel sensing applications.

Charge Integrator as Input Stage

Charge integrator (CI) is a popular topology for emerging applications owing to its ultra-low noise behavior (Crescentini et al., 2013). A typical continuous-time charge integrator is composed of a feedback capacitor and a biasing resistor R_B, as given in Figure 1E. Once R_B is implemented by a diode-based pseudo resistor, the circuit behavior is dominated by the capacitor. Unlike the voltage buffer topology discussed in the Voltage Buffer as Input Stage section, its integral gain is sensitive to the stray capacitance of the input node; the virtual short behavior at the input of the op-amp effectively eliminates the C_in at the input node to provide an accurate integral gain merely determined by C_F. In addition, as the R_B offers TΩ impedance, the input-referred current noise can be as low as sub-100 fA/rtHz (Crescentini et al., 2013), which is even better than the voltage-buffer topology.

As the charge integrator offers a phase shift of $\pi /2$, it needs additional phase compensation to satisfy the oscillation criteria (Riverola et al., 2017; Uranga et al., 2017). There are several ways to address the issue. The most common method is to build a Pierce-type oscillator circuit with the additional phase shift of the resonator and the input and output capacitors. In Verd et al. (2013), an 11-MHz Pierce CMOS-MEMS oscillator with a resonator feedthrough cancellation scheme is demonstrated with a dc-bias voltage of only 3 V. The circuit noise of 80 fA/rtHz is about 10X lower than an R-TIA shown in other works (Li et al., 2015d), which is the key to achieve low phase noise floor. The phase noise floor achieves −109 dBc/Hz is attributed to the large R_m > 5 MΩ and low output power of −17 dBm.

On the other hand, the integrator-differentiator TIA (ID-TIA) is also being explored in CMOS-MEMS oscillator applications (Li et al., 2016a; Li et al., 2016b). It is composed of two stages where the first stage is a CI, and the second stage is a differentiator. Since the differentiator provides an opposite phase shift to the CI, the overall phase shift through ID-TIA can be zero, thus offering a good condition for series-resonant oscillation. In Li et al. (2016a), and ultra-low-noise ID-TIA based 1.2 MHz 150 μW CMOS-MEMS oscillator demonstrates a good phase noise of −120 dBc/Hz at 1-kHz offset, which features a FOM of 190 dB with a resonator Q of 1900 and R_m of 2 MΩ. Such a FOM is superior to many MEMS oscillators designed in different technologies (Lin et al., 2003; Huang et al., 2008).

Phase Noise Optimization of Complementary Metal-Oxide-Semiconductor-Microelectromechanical Systems Oscillators

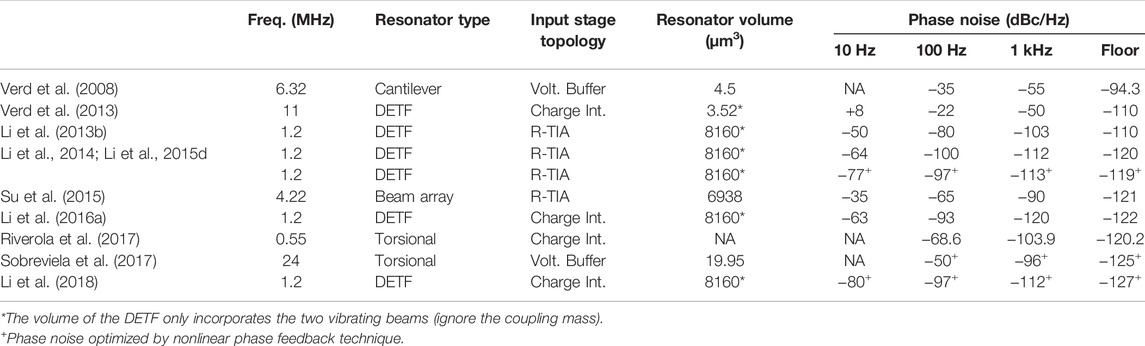
Through the articles that have been discussed in the Complementary Metal-Oxide-Semiconductor-Microelectromechanical Systems Oscillator Architecture section, we observe large discrepancies in phase noise between distinct CMOS-MEMS oscillators, which can be attributed to differences in the dc-bias voltage, resonator volume, vibrating mode shape, and transduction gap size. To understand the reason behind this, the state-of-the-art CMOS-MEMS oscillators are tabulated in Table 1 with their phase noise at different offsets. Apparently, the oscillators based on tiny resonators with small transduction gaps (Verd et al., 2008; Verd et al., 2013) feature worse close-to-carrier phase noise compared to the other samples. This is because the tiny resonator elements usually have strong mechanical and bias-dependent nonlinearities (Chen et al., 2022), so the phase noise caused by the AM-PM effect is more pronounced. To overcome this issue, despite the conventional approach which operates the oscillator at lower carrier power to guarantee a linear MEMS operation, it has recently been demonstrated that the close-to-carrier phase noise can be effectively suppressed by increasing the excitation power as operating the MEMS resonator in the nonlinear regime (Yurke et al., 1995; Kenig et al., 2012). For a typical nonlinear Duffing resonator, there are two bifurcation points that present a steep phase-frequency slope to potentially minimize the AM-PM conversion coefficient. It has been shown theoretically and experimentally in a nanoelectromechanical oscillator system (Villanueva et al., 2013), that the phase noise of the nonlinear oscillator is greatly improved by operating the feedback phase closed to the lower bifurcation point.

TABLE 1

TABLE 1. Phase noise comparison.

For CMOS-MEMS oscillators, nonlinear AM-PM noise cancellation is firstly explored by (Li et al., 2014) based on a double-ended tuning fork resonator. By operating the oscillator at the lower bifurcation point through a variable-gain R-TIA, it can be observed that the phase noise changes drastically (close to 30 dB at 10 Hz offset) when the applied bias voltage is perturbed by only 0.1 V. The nonlinear phase noise cancellation leads to a great performance improvement, which is only 7 dB above the theoretical limit predicted by Leeson’s model. In addition, this method is not restricted to a specific oscillator topology. The phase noise optimization is also achieved through an off-chip phase shifter circuit and supply voltage (V_DD) adjustment in other nonlinear CMOS-MEMS oscillator studies (Sobreviela et al., 2017; Uranga et al., 2017). In a recent study (Li et al., 2018), a 1.2 MHz 180 μW DETF oscillator combined with ultra-low-noise ID-TIA and nonlinear phase noise optimization technique achieves phase noise of -80 dB and -127 dB at 10-Hz and 1-MHz offsets, respectively, yielding a very competitive FOM of 189.3 dB.

Conclusion

CMOS-MEMS oscillator is an important technology to produce on-chip frequency references and oscillating sensors. In this review, we focused on the recent advances in CMOS-MEMS oscillators in terms of oscillator circuit topologies and phase noise performances. For high impedance resonators, it is reasonable to use voltage buffers and charge integrators as MEMS-circuit interfaces to take the advantage of their low input-referred noise. On the other hand, for low impedance resonators, resistive feedback TIA with moderate gain becomes a more suitable topology to avoid saturation and Q-loading effect. On the phase noise, it has been pointed out that the resonator impedance is the fundamental limit of the phase noise spectrum since the noise at the circuit input will be amplified by a factor of R_m to satisfy the oscillation criteria. Finally, the phase noise optimization based on phase feedback technique and nonlinear MEMS resonator operation is reviewed, which is a useful technique for oscillator stability improvements. So far, the CMOS-MEMS oscillators have been designed based on flexural mode resonators. The low stiffness characteristic becomes a fundamental limitation of frequency scaling. Thus, for future CMOS-MEMS oscillator designs, high-Q and high-frequency bulk-mode resonators (Chen et al., 2012) will be a potential solution to overcome current performance limitations.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

The author would like to thank the financial support from the Ministry of Science and Technology (MOST) of Taiwan under grant MOST 110-2636-E-007-012.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Achenbach, R., Feuerstack-Raible, M., Hiller, F., Keller, M., Meier, K., Rudolph, H., et al. (2000). A Digitally Temperature-Compensated crystal Oscillator. IEEE J. Solid-state Circuits 35 (10), 1502–1506. doi:10.1109/4.871329

CrossRef Full Text | Google Scholar

Bhosale, K., Chen, C.-Y., Li, M.-H., and Li, S.-S. (2021). “Standard CMOS Integrated Ultra-compact Micromechanical Oscillating Active Pixel Arrays,” in the 34th IEEE Int. Micro Electro Mechanical Systems Conf. (MEMS’21), 157–160. doi:10.1109/MEMS51782.2021.9375392

CrossRef Full Text | Google Scholar

Bianchi, N. A., Karam, J.-M. M., and Courtois, B. (2000). ALC crystal Oscillators Based Pressure and Temperature Measurement Integrated Circuit for High Temperature Oil Well Applications. IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 47 (5), 1241–1245. doi:10.1109/58.869071

PubMed Abstract | CrossRef Full Text | Google Scholar

Chance, G., Meyer, T., Stoeckl, S., Neurauter, B., Patane, G., Neubauer, B., et al. (2014). “Integrated MEMS Oscillator for Cellular Transceivers,” in 2014 IEEE International Frequency Control Symposium (FCS) (IEEE), 1–3. doi:10.1109/FCS.2014.6859910

CrossRef Full Text | Google Scholar

Chang, C.-Y., Pillai, G., and Li, S.-S. (2022). “Phase Noise Optimization of Piezoelectric Bulk Mode MEMS Oscillators Based on Phase Feedback in Secondary Loop,” in the 35th IEEE Int. Micro Electro Mechanical Systems Conf (Virtual: MEMS’22), 212–215. doi:10.1109/mems51670.2022.9699576

CrossRef Full Text | Google Scholar

Chen, C.-Y., Li, M.-H., Zope, A. A., and Li, S.-S. (2019). A CMOS-Integrated MEMS Platform for Frequency Stable Resonators-Part I: Fabrication, Implementation, and Characterization. J. Microelectromech. Syst. 28 (5), 744–754. doi:10.1109/JMEMS.2019.2936149

CrossRef Full Text | Google Scholar

Chen, H.-Y., Shih, P.-I., Li, M.-H., and Li, S.-S. (2022). “5V-Bias Cmos-Mems Capacitive Resonator with RM,” in 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (Virtual: MEMS’22), 1042–1045. doi:10.1109/MEMS51670.2022.9699766

CrossRef Full Text | Google Scholar

Chen, W.-C., Fang, W., and Li, S.-S. (2011). A Generalized CMOS-MEMS Platform for Micromechanical Resonators Monolithically Integrated with Circuits. J. Micromech. Microeng. 21 (6), 065012. doi:10.1088/0960-1317/21/6/065012

CrossRef Full Text | Google Scholar

Chen, W.-C., Fang, W., and Li, S.-S. (2012). “VHF CMOS-MEMS Oxide Resonators with Q > 10,000,” in Proceedings, 2012 IEEE Int. Frequency Control Symp (Baltimore, MD: IFCS’12), 1–4. doi:10.1109/FCS.2012.6243706

CrossRef Full Text | Google Scholar

Cheng-Syun Li, C.-S., Ming-Huang Li, M.-H., Cheng-Chi Chen, C.-C., Chi-Hang Chin, C.-H., and Sheng-Shian Li, S.-S. (2015a). A Low-Voltage CMOS-Microelectromechanical Systems Thermal-Piezoresistive Resonator with $Q > 10\,000$. IEEE Electron. Device Lett. 36 (2), 192–194. doi:10.1109/LED.2014.2382553

CrossRef Full Text | Google Scholar

Crescentini, M., Bennati, M., Carminati, M., and Tartagni, M. (2014). Noise Limits of CMOS Current Interfaces for Biosensors: A Review. IEEE Trans. Biomed. Circuits Syst. 8 (2), 278–292. doi:10.1109/TBCAS.2013.2262998

PubMed Abstract | CrossRef Full Text | Google Scholar

Dai, C.-L., Chiou, J.-H., and Lu, M. S.-C. (2005). A Maskless post-CMOS Bulk Micromachining Process and its Application. J. Micromech. Microeng. 15, 2366–2371. doi:10.1088/0960-1317/15/12/019

CrossRef Full Text | Google Scholar

Fedder, G. K., Howe, R. T., Tsu-Jae King Liu, T.-J. K., and Quevy, E. P. (2008). Technologies for Cofabricating MEMS and Electronics. Proc. IEEE 96 (2), 306–322. doi:10.1109/JPROC.2007.911064

CrossRef Full Text | Google Scholar

Ferrari, M., Ferrari, V., Marioli, D., Taroni, A., Suman, M., and Dalcanale, E. (2006). In-liquid Sensing of Chemical Compounds by QCM Sensors Coupled with High-Accuracy ACC Oscillator. IEEE Trans. Instrum. Meas. 55 (3), 828–834. doi:10.1109/TIM.2006.873792

CrossRef Full Text | Google Scholar

Huikai Xie, H., Erdmann, L., Xu Zhu, X., Gabriel, K. J., and Fedder, G. K. (2002). Post-CMOS Processing for High-Aspect-Ratio Integrated Silicon Microstructures. J. Microelectromech. Syst. 11 (2), 93–101. doi:10.1109/84.993443

CrossRef Full Text | Google Scholar

Kalia, S., Bahr, B., Dinc, T., Haroun, B., and Sankaran, S. (2021). “An Ultra-low Close-In Phase Noise Series-Resonance BAW Oscillator in a 130-nm BiCMOS Process,” in IEEE Asian Solid-State Circuits Conference (A-SSCC) (IEEE), 1–3. doi:10.1109/A-SSCC53895.2021.9634779

CrossRef Full Text | Google Scholar

Kenig, E., Cross, M. C., Villanueva, L. G., Karabalin, R. B., Matheny, M. H., Lifshitz, R., et al. (2012). Optimal Operating Points of Oscillators Using Nonlinear Resonators. Phys. Rev. E 86, 056207. doi:10.1103/PhysRevE.86.056207

PubMed Abstract | CrossRef Full Text | Google Scholar

Lavasani, H. M., Pan, W., Harrington, B., Abdolvand, R., and Ayazi, F. (2011). A 76 dB$\Omega $ 1.7 GHz 0.18 $\mu$m CMOS Tunable TIA Using Broadband Current Pre-amplifier for High Frequency Lateral MEMS Oscillators. IEEE J. Solid-state Circuits 46 (1), 224–235. doi:10.1109/JSSC.2010.2085890

CrossRef Full Text | Google Scholar

Lee, H. K., Ward, P. A., Duwel, A. E., Salvia, J. C., Qu, Y. Q., Melamud, R., et al. (2011). “Verification of the Phase-Noise Model for MEMS Oscillators Operating in the Nonlinear Regime,” in 2011 16th International Solid-State Sensors (Beijing: Actuators and Microsystems Conference), 510–513. doi:10.1109/TRANSDUCERS.2011.5969667

CrossRef Full Text | Google Scholar

Li, C.-S., Hou, L.-J., and Li, S.-S. (2012a). Advanced CMOS-MEMS Resonator Platform. IEEE Electron. Device Lett. 33 (2), 272–274. doi:10.1109/LED.2011.2175695

CrossRef Full Text | Google Scholar

Li, C.-S., Li, M.-H., Chin, C.-H., and Li, S.-S. (2013a). Differentially Piezoresistive Sensing for CMOS-MEMS Resonators. J. Microelectromech. Syst. 22 (6), 1361–1372. doi:10.1109/JMEMS.2013.2257689

CrossRef Full Text | Google Scholar

Li, H.-C., Tseng, S.-H., Huang, P.-C., and Lu, M. S.-C. (2012b). Study of CMOS Micromachined Self-Oscillating Loop Utilizing a Phase-Locked Loop-Driving Circuit. J. Micromech. Microeng. 22, 055024. doi:10.1088/0960-1317/22/5/055024

CrossRef Full Text | Google Scholar

Li, M.-H., Chen, C.-Y., Chen, W.-C., and Li, S.-S. (2015c). A Vertically Coupled MEMS Resonator Pair for Oscillator Applications. J. Microelectromech. Syst. 24 (3), 528–530. doi:10.1109/JMEMS.2015.2421555

CrossRef Full Text | Google Scholar

Li, M.-H., Chen, C.-Y., Chin, C.-H., Li, C.-S., and Li, S.-S. (2014). “Optimizing the Close-To-Carrier Phase Noise of Monolithic CMOS-MEMS Oscillators Using Bias-dependent Nonlinearity,” in IEEE Int. Electron Devices Mtg (San Francisco, CA: IEDM’14). 22.3.1-22.3.4. doi:10.1109/IEDM.2014.7047100

CrossRef Full Text | Google Scholar

Li, M.-H., Chen, C.-Y., Li, C.-S., Chin, C.-H., Chen, C.-C., and Li, S.-S. (2013b). “Foundry-CMOS Integrated Oscillator Circuits Based on Ultra-low Power Ovenized CMOS-MEMS Resonators,” in IEEE Int. Electron Devices Mtg (Washington, DC: IEDM’13), 18.4.1–18.4.4. doi:10.1109/IEDM.2013.6724654

CrossRef Full Text | Google Scholar

Li, M.-H., Chen, C.-Y., Li, C.-S., Chin, C.-H., and Li, S.-S. (2015d). A Monolithic CMOS-MEMS Oscillator Based on an Ultra-low-power Ovenized Micromechanical Resonator. J. Microelectromech. Syst. 24 (2), 360–372. doi:10.1109/JMEMS.2014.2331497

CrossRef Full Text | Google Scholar

Li, M.-H., Chen, C.-Y., Li, C.-S., Chin, C.-H., and Li, S.-S. (2015b). Design and Characterization of a Dual-Mode CMOS-MEMS Resonator for TCF Manipulation. J. Microelectromech. Syst. 24 (2), 446–457. doi:10.1109/JMEMS.2014.2332884

CrossRef Full Text | Google Scholar

Li, M.-H., Chen, C.-Y., and Li, S.-S. (2018). A Study on the Design Parameters for MEMS Oscillators Incorporating Nonlinearities. IEEE Trans. Circuits Syst. 65 (10), 3424–3434. doi:10.1109/TCSI.2018.2832982

CrossRef Full Text | Google Scholar

Li, M.-H., Chen, C.-Y., Liu, C.-Y., and Li, S.-S. (2016a). A Sub-150- BEOL-Embedded CMOS-MEMS Oscillator with a 138-dB Ultra-low-noise TIA. IEEE Electron. Device Lett. 37 (5), 648–651. doi:10.1109/LED.2016.2538772

CrossRef Full Text | Google Scholar

Li, M.-H., Tseng, K.-J., Liu, C.-Y., Chen, C.-Y., and Li, S.-S. (2016b). “An 8V 50μW 1.2MHz CMOS-MEMS Oscillator,” in IEEE Int. Freq. Contr. Symp. (New Orleans, LA: IFCS’16), 1–3. doi:10.1109/FCS.2016.7563591

CrossRef Full Text | Google Scholar

Liu, C.-Y., Li, M.-H., Ranjith, H. G., and Li, S.-S. (2016). “A 1 MHz 4 Ppm CMOS-MEMS Oscillator with Built-In Self-Test and Sub-mW Ovenization Power,” in IEEE Int. Electron Devices Mtg (San Francisco, CA: IEDM’16). 26.7.1-26.7.4. doi:10.1109/IEDM.2016.7838488

CrossRef Full Text | Google Scholar

Liu, J.-R., and Li, W.-C. (2019). Temperature-compensated CMOS-MEMS Resonators via Electrical Stiffness Frequency Pulling. J. Micromech. Microeng. 30 (1), 014002. doi:10.1088/1361-6439/ab50ef

CrossRef Full Text | Google Scholar

Liu, J.-R., Lu, S.-C., Tsai, C.-P., and Li, W.-C. (2018). A CMOS-MEMS Clamped-Clamped Beam Displacement Amplifier for Resonant Switch Applications. J. Micromech. Microeng. 28 (6), 065001. doi:10.1088/1361-6439/aab112

CrossRef Full Text | Google Scholar

Liu, Y.-C., Tsai, M.-H., Chen, W.-C., Li, M.-H., Li, S.-S., and Fang, W. (2013). Temperature-compensated CMOS-MEMS Oxide Resonators. J. Microelectromech. Syst. 22 (5), 1054–1065. doi:10.1109/JMEMS.2013.2263091

CrossRef Full Text | Google Scholar

Lopez, J. L., Verd, J., Uranga, A., Giner, J., Murillo, G., Torres, F., et al. (2009). A CMOS-MEMS RF-Tunable Bandpass Filter Based on Two High- $Q$ 22-MHz Polysilicon Clamped-Clamped Beam Resonators. IEEE Electron. Device Lett. 30 (7), 718–720. doi:10.1109/LED.2009.2022509

CrossRef Full Text | Google Scholar

Ming-Huang Li, M.-H., Wen-Chien Chen, W.-C., and Sheng-Shian Li, S.-S. (2012c). Mechanically Coupled CMOS-MEMS Free-free Beam Resonator Arrays with Enhanced Power Handling Capability. IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 59 (3), 346–357. doi:10.1109/TUFFC.2012.2203

PubMed Abstract | CrossRef Full Text | Google Scholar

Nabki, F., Allidina, K., Ahmad, F., Cicek, P.-V., and El-Gamal, M. N. (2009). A Highly Integrated 1.8 GHz Frequency Synthesizer Based on a MEMS Resonator. IEEE J. Solid-state Circuits 44 (8), 2154–2168. doi:10.1109/JSSC.2009.2022914

CrossRef Full Text | Google Scholar

Naing, T. L., Rocheleau, T. O., Alon, E., and Nguyen, C. T.-C. (2020). Low-Power MEMS-Based Pierce Oscillator Using a 61-MHz Capacitive-Gap Disk Resonator. IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 67 (7), 1377–1391. doi:10.1109/TUFFC.2020.2969530

PubMed Abstract | CrossRef Full Text | Google Scholar

Nguyen, C. T.-C., and Howe, R. T. (1999). An Integrated CMOS Micromechanical Resonator High-Q Oscillator. IEEE J. Solid-state Circuits 34 (4), 440–455. doi:10.1109/4.753677

CrossRef Full Text | Google Scholar

Pardo, M., Sorenson, L., and Ayazi, F. (2012). An Empirical Phase-Noise Model for MEMS Oscillators Operating in Nonlinear Regime. IEEE Trans. Circuits Syst. 59 (5), 979–988. doi:10.1109/TCSI.2012.2195129

CrossRef Full Text | Google Scholar

Rhea, R. W. (2010). Discrete Oscillator Design: Linear, Nonlinear, Transient, and Noise Domains. Norwood, MA: Artech House.

Google Scholar

Riverola, M., Sobreviela, G., Torres, F., Uranga, A., and Barniol, N. (2017). Single-resonator Dual-Frequency BEOL-Embedded CMOS-MEMS Oscillator with Low-Power and Ultra-compact TIA Core. IEEE Electron. Device Lett. 38 (2), 273–276. doi:10.1109/LED.2016.2644870

CrossRef Full Text | Google Scholar

Rubiola, E. (2008). Phase Noise and Frequency Stability in Oscillators. Cambridge University Press.

Google Scholar

Sobreviela, G., Riverola, M., Torres, F., Uranga, A., and Barniol, N. (2017). Optimization of the Close-To-Carrier Phase Noise in a CMOS-MEMS Oscillator Using a Phase Tunable Sustaining-Amplifier. IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 64 (5), 888–897. doi:10.1109/TUFFC.2017.2667881

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, H.-C., Li, M.-H., Chen, C.-Y., and Li, S.-S. (2015). A Single-Chip Oscillator Based on a Deep-Submicron gap CMOS-MEMS Resonator Array with a High-Stiffness Driving Scheme. 18th Int. Conf. Solid-state Sensors Actuators (Transducers’15), 133–136. doi:10.1109/TRANSDUCERS.2015.7180879

CrossRef Full Text | Google Scholar

Uranga, A., Sobreviela, G., Riverola, M., Torres, F., and Barniol, N. (2017). Phase-noise Reduction in a CMOS-MEMS Oscillator under Nonlinear MEMS Operation. IEEE Trans. Circuits Syst. 64 (12), 3047–3055. doi:10.1109/TCSI.2017.2758860

CrossRef Full Text | Google Scholar

Valle, J., Fernandez, D., Gibrat, O., and Madrenas, J. (2021). Manufacturing Issues of BEOL CMOS-MEMS Devices. IEEE Access 9, 83149–83162. doi:10.1109/ACCESS.2021.3086867

CrossRef Full Text | Google Scholar

Verd, J., Abadal, G., Teva, J., Gaudo, M. V., Uranga, A., Borrise, X., et al. (2005). Design, Fabrication, and Characterization of a Submicroelectromechanical Resonator with Monolithically Integrated CMOS Readout Circuit. J. Microelectromech. Syst. 14 (3), 508–519. doi:10.1109/JMEMS.2005.844845

CrossRef Full Text | Google Scholar

Verd, J., Uranga, A., Abadal, G., Teva, J. L., Torres, F., LÓpez, J., et al. (2008). Monolithic Cmos MEMS Oscillator Circuit for Sensing in the Attogram Range. IEEE Electron. Device Lett. 29 (2), 146–148. doi:10.1109/LED.2007.914085

CrossRef Full Text | Google Scholar

Verd, J., Uranga, A., Segura, J., and Barniol, N. (2013). “A 3V CMOS-MEMS Oscillator in 0.35μm CMOS Technology,” in 17th Int. Conf. on Solid-State Sensors & Actuators (Transducers’13), 806–809. doi:10.1109/Transducers.2013.6626889

CrossRef Full Text | Google Scholar

Verd, J., Uranga, A., Teva, J., Lopez, J. L., Torres, F., Esteve, J., et al. (2006). Integrated CMOS-MEMS with On-Chip Readout Electronics for High-Frequency Applications. IEEE Electron. Device Lett. 27 (6), 495–497. doi:10.1109/LED.2006.875147

CrossRef Full Text | Google Scholar

Villanueva, L. G., Kenig, E., Karabalin, R. B., Matheny, M. H., Lifshitz, R., Cross, M. C., et al. (2013). Surpassing Fundamental Limits of Oscillators Using Nonlinear Resonators. Phys. Rev. Lett. 110, 177208. doi:10.1103/PhysRevLett.110.177208

PubMed Abstract | CrossRef Full Text | Google Scholar

Vittoz, E. A., Degrauwe, M. G. R., and Bitz, S. (1988). High-performance crystal Oscillator Circuits: Theory and Application. IEEE J. Solid-state Circuits 23 (3), 774–783. doi:10.1109/4.318

CrossRef Full Text | Google Scholar

Walls, F. L., and Gagnepain, J.-J. (1992). Environmental Sensitivities of Quartz Oscillators. IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 39 (2), 241–249. doi:10.1109/58.139120

PubMed Abstract | CrossRef Full Text | Google Scholar

Ward, P., and Duwel, A. (2011). Oscillator Phase Noise: Systematic Construction of an Analytical Model Encompassing Nonlinearity. IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 58 (1), 195–205. doi:10.1109/TUFFC.2011.1786

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, G.-C., and Lu, M. S.-C. (2012). Design and Characterization of a CMOS MEMS Capacitive Resonant Sensor Array. J. Micromech. Microeng. 22, 125030. doi:10.1088/0960-1317/22/12/125030

CrossRef Full Text | Google Scholar

Wen-Lung Huang, W.-L., Zeying Ren, Z., Yu-Wei Lin, Y.-W., Hsien-Yeh Chen, H.-Y., Lahann, J., and Nguyen, C. T.-C. (2008). “Fully Monolithic CMOS Nickel Micromechanical Resonator Oscillator,” in IEEE 21st Int. Conf. Micr. Electro. Mech. Syst (Tucson, AZ: MEMS’08), 10–13. doi:10.1109/MEMSYS.2008.4443580

CrossRef Full Text | Google Scholar

Yu-Wei Lin, Y.-W., Seungbae Lee, S., Zeying Ren, Z., and Nguyen, C. T. C. (2003). “Series-resonant Micromechanical Resonator Oscillator,” in IEEE Int. Electron Devices Mtg (Washington, DC: IEDM’03), 961–964. doi:10.1109/IEDM.2003.1269438

CrossRef Full Text | Google Scholar

Yurke, B., Greywall, D. S., Pargellis, A. N., and Busch, P. A. (1995). Theory of Amplifier-Noise Evasion in an Oscillator Employing a Nonlinear Resonator. Phys. Rev. A. 51 (5), 4211–4229. doi:10.1103/PhysRevA.51.4211

PubMed Abstract | CrossRef Full Text | Google Scholar

Zaliasl, S., Salvia, J. C., Hill, G. C., Chen, L. W., Joo, K., Palwai, R., et al. (2015). A 3 Ppm 1.5 × 0.8 Mm 2 1.0 ΜA 32.768 kHz MEMS-Based Oscillator. IEEE J. Solid-state Circuits 50 (1), 291–302. doi:10.1109/JSSC.2014.2360377

CrossRef Full Text | Google Scholar

Zope, A. A., and Li, S.-S. (2021). Balanced Drive and Sense CMOS thermal Piezoresistive Resonators and Oscillators. IEEE Electron. Device Lett. 42 (2), 232–235. doi:10.1109/LED.2020.3044391

CrossRef Full Text | Google Scholar