Interlayer Friction in Graphene/MoS2, Graphene/NbSe2, Tellurene/MoS2 and Tellurene/NbSe2 van der Waals Heterostructures

Two-dimensional (2D) materials have a wide range of applications in the field of molecular-level solid lubrication due to their ultrahigh mechanical strength and extremely low friction properties at the nanoscale. In this work, we investigated the interlayer friction properties of four different heterostructures, namely, graphene/MoS₂, graphene/NbSe₂, α-tellurene/MoS₂ and α-tellurene/NbSe₂, using a molecular dynamics (MD) method. The effects of a series of influencing factors on the interlayer friction were investigated. The results show that for the four heterostructures, the influence laws of layer number, temperature, and normal load on interlayer friction show consistency. The twist angle can effectively regulate the interlayer friction of these 2D materials, but the superlubricity phenomenon cannot occur for α-Te/MoS₂ and α-Te/NbSe₂ systems. Furthermore, we address the origin of friction in detail, emphasizing the contribution of edge pinning and interface sliding resistance to the frictional force of the heterostructure. The friction decreases with increasing temperature and sliding speed due to the reduction in the interlayer adhesion force. The present findings provide a deep understanding of friction control and contribute much to the design of robust 2D superlubricity systems.

Introduction

Friction has a profound influence on people’s modern lives and industrial production. It is estimated that all kinds of friction consume 1/3 of the world’s disposable energy. In addition, the wear caused by friction is the main cause of mechanical damage, which is more serious at the nanoscale. As the size of devices decreases and the specific surface area increases, surface force and surface effect become the main factors affecting the performance and life of nanodevices. Therefore, it is of great significance to effectively reduce friction and wear.

Hirano and Shinjo theoretically predicted that the static friction force between two rigid surfaces in incommensurate contact may approach zero (Hirano and Shinjo, 1990; Shinjo and Hirano, 1993) and named this phenomenon superlubricity. However, there are no absolutely rigid substances or materials in nature. The discovery and rise of two-dimensional materials, represented by graphene (Novoselov et al., 2004), provides a new opportunity for the design and development of ideal solid lubricants. The graphene monolayer has only one atomic layer thickness (0.335 nm), which is the thinnest material known thus far. Graphene has strong in-plane stiffness because of its strong covalent bond. However, the relatively weak interlayer van der Waals (vdW) interactions make it easy to achieve interlayer slip. With these properties, two-dimensional materials prove to be ideal vehicles for achieving superlubricity. However, this superlubricity shows low friction only in the incommensurate state. In addition, another mechanism exists to generate low friction. According to the mechanism of thermal escape motion (Washizu et al., 2012; Maeda and Washizu, 2018), graphene in the stacking state of the commensurate level can also produce ultralow friction. While chasing the performance of graphene, a large number of 2D materials have been prepared, such as transition metal dichalcogenides (TMDCs), black phosphorus, and h-BN. In 2017, Zhu et al. predicted a new 2D monolayer material (Zhu et al., 2017), i.e., tellurene, by first-principles calculations. Different from two-dimensional layered materials, there is no layered structure in the bulk structure of 2D tellurene. Although these two-dimensional materials are only a few atomic layers thick, their anti-friction effect is comparable to that of bulk lubricated materials. The discovery of the excellent mechanical and tribological properties of two-dimensional materials further promotes the study of their friction behavior.

For two crystalline surfaces of bulk materials, the interfacial commensurate formed during contact has a significant effect on sliding friction. In 2004, a pioneering experimental demonstration of nanoscale superlubricity in graphite contacts was performed by Dienwiebel et al. (Dienwiebel et al., 2004), who discovered that the origin of ultralow friction in graphite lies in the incommensurability between rotating graphite layers. In addition, the superlubricity of MoS₂, which is also commonly used as a solid lubricant, has been extensively investigated by researchers. Tasuku et al. (Onodera et al., 2010) investigated the slip anisotropy of bilayer MoS₂ using a molecular dynamics approach, and the results showed that the lubrication of MoS₂ is largely dependent on its interlayer contact at the atomic scale. However, the implementation of superlubricity is mostly limited to the nanoscale, and any surface defects or surface roughness can destroy the superlubricity when scaled to larger scales. With tireless efforts, Zheng et al. observed self-retracting motion in a graphite island system (Zheng et al., 2008), which successfully extended superlubricity to the macroscopic scale. However, for the 2D homostructural systems, even in the incommensurate ultralow friction configuration, the interface contact state has a tendency to rotate toward the aligned proportional configuration during sliding and eventually lock in the high friction state (Filippov et al., 2008). In addition, the superlubricity properties of zero-dimensional carbon nanoscrolls (Berman et al., 2015) and one-dimensional carbon nanotubes (Zhang et al., 2013) have received extensive attention and have achieved superlubricity in macroscopic contacts.

To avoid the above problems, researchers have attempted to stack different 2D materials to form 2D van der Waals heterostructures. Due to the intrinsic lattice constant mismatch at the interface, incommensurability exists even in the aligned configuration, which helps to achieve robust structural superlubricity. Song et al. investigated the sliding process of graphene flakes on the h-BN surface and found that sufficiently large graphene flakes will produce a very stable superlubric state when sliding on the h-BN surface (Song et al., 2018). Unlike the superlubricity behavior between bilayer graphene, the graphene/h-BN heterostructure retains superlubricity even in the aligned configuration. Furthermore, researchers have made a number of significant advances in liquid superlubric systems. Luo et al. discovered other ultralow friction systems, such as Brasenia Schreiber (BS) mucilage (Li et al., 2012) and mixed aqueous solutions of glycerol and boric acid (Zhang et al., 2011), and experimentally investigated their superlubricity performance (Zheng and Liu, 2014; Xiao et al., 2019). Based on these studies, researchers have conducted many more detailed studies on factors affecting interlayer friction, such as rotation angle, sample thickness, shape and size, temperature, sliding direction, sliding speed, and normal load (Zwörner et al., 1998; Miura and Kamiya, 2002; Dienwiebel et al., 2004; Verhoeven et al., 2004; Filippov et al., 2008; Lee et al., 2009; Filleter and Bennewitz, 2010; Lee et al., 2010; Li et al., 2010; Ye et al., 2012; Dietzel et al., 2013; Leven et al., 2013; van Wijk et al., 2013; Levita et al., 2014; Li et al., 2016; Dietzel et al., 2017; Mandelli et al., 2017; Wang et al., 2019a; Gongyang et al., 2020; Qu et al., 2020; Ru et al., 2020; Vazirisereshk et al., 2020; Ru et al., 2021). Specifically, Ru et al. (Ru et al., 2020) compared the interlayer friction between the graphene/graphene system and the MoS₂/MoSe₂ system and explored the effect of temperature, slide direction, relative velocity, and normal force on the frictional force. Unfortunately, there is no unified explanation for how these factors affect friction.

In this work, we investigated the interlayer friction properties of four different two-dimensional heterostructures, i.e., graphene/MoS₂, graphene/NbSe₂, α-tellurene/MoS₂ and α-tellurene/NbSe₂, by molecular dynamics methods. Furthermore, the interlayer friction properties of the heterogeneous structures were investigated in detail for different stacking angles, contact areas, contact shapes, thicknesses, temperatures, sliding directions, sliding velocities and normal loads. The relationship between interlayer friction and influencing factors was thoroughly discussed.

Methodology

All simulations were performed using the large-scale atomic/molecular massively parallel simulator LAMMPS (Plimpton, 1995). It should be noted first that a total of four heterostructure systems were built in this work for comparative study of the interlayer superlubricity characteristics of 2D materials, specifically graphene/MoS₂, graphene/NbSe₂, α-Te/NbSe₂, and α-Te/MoS₂. In all systems, MoS₂ and NbSe₂ were used as the lower substrate materials, while graphene and α-Te were set as the upper sliders. The two-dimensional schematic models of the planes are shown in Figures 1A–D for MoS₂, NbSe₂, graphene, and α-Te, while their lattice parameters are 3.22 Å (Mehmood et al., 2021), 3.53 Å (Alemayehu et al., 2015), 2.46 Å (Yang et al., 2018), and 4.15 Å (Wang et al., 2018), respectively. As shown in Figure 1E, we introduce the simulation model by taking the graphene/NbSe₂ system as an example (see SupplementaryFigure S1 in the Supplementary Information S1 for the details of the α-Te/NbSe₂ system), and the other systems are similar. The model consists of a single-layer graphene sheet and a single-layer NbSe₂ as the substrate. Specifically, the bottommost Se atoms of NbSe₂ are fixed, which appear like the atoms in the experiment where they are strongly adsorbed on the substrate. In addition, we consider the frictional characteristics of the heterogeneous structures formed by different shapes of graphene sheets, such as triangular, rectangular and hexagonal sheets. Figure 2 shows the three heterostructures formed by three different shapes of graphene sheets twisted by 30° and stacked with the substrate.

FIGURE 1

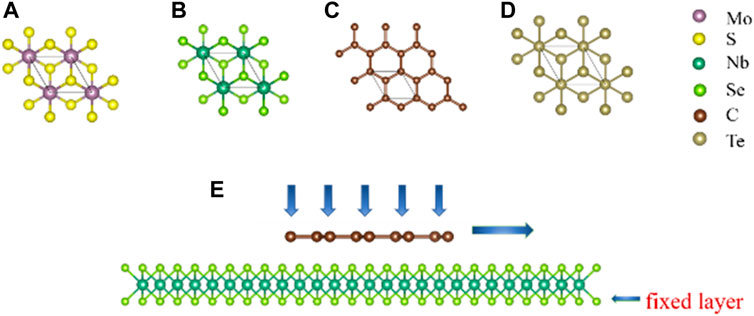
FIGURE 1. Schematic diagram of the model used for molecular dynamics simulations. (A–D) Crystal structure diagrams, where (A) MoS_2, (B) NbSe_2, (C) graphene and (D) α-Te are shown. (E) Side view of the simulation model. The sheet is connected to a spring that slides at a constant speed over different substrates (MoS₂ and NbSe₂).

FIGURE 2

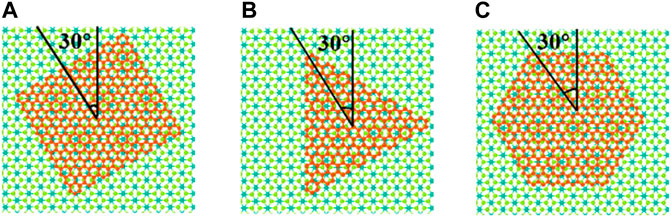
FIGURE 2. The atomic model diagram of the heterostructure composed of different shapes: (A) rectangle, (B) triangle and (C) hexagon stacked on the substrate.

The key to molecular dynamics simulations is to determine the interactions between near-neighbor atoms. In our simulations, the C-C atom interactions were described by the reactive empirical bond order (REBO) potential (Brenner et al., 2002). The Stillinger-Weber (SW) potential (Jiang and Zhou, 2017) was used to describe the covalent interactions within the Mo-S, Nb-Se, and Te-Te interlayers (Ru et al., 2021). The Lennard–Jones (LJ) potential function was used to describe the vdW interaction between 2D layers. Specifically, the parameters of the LJ potential for simulation are listed in Tables 1 and 2 (Rappe et al., 1992). For the description of the potential function of the interaction force between layers of 2D materials, it is reported that similar results can be obtained from the study of interlayer friction using the LJ potential and the Kolmogorov-Crespi (KC) potential (Wang et al., 2019b). In addition, the LJ potential can significantly speed up the simulation. Therefore, the vdW forces between 2D materials were described using the LJ potential in the present work. The cut-off length of the LJ potential was set to 10 Å.

TABLE 1

TABLE 1. LJ parameters for graphene/MoS₂ and graphene/NbSe₂ systems.

TABLE 2

TABLE 2. LJ parameters for the α-Te/MoS₂ and α-Te/NbSe₂ systems.

The present MD simulation mainly included two processes: relaxation and sliding. We relaxed each system for 50 ps under the NVT ensemble, which allowed us to obtain a more stable configuration. Afterwards, the sliding sheet on the substrate was connected to a harmonic spring with stiffness K = 10 eV Å⁻², which was pulled in the X direction with a constant velocity V = 1 Å/ps. The whole sliding process lasted for 400 ps. Throughout the simulation, a constant normal force F_n = 0.02 nN/atom was applied to the uppermost atom of the slider, and the rotation of the slider was limited during relaxation and sliding (see Supplementary Figure S1 for details). The periodic boundary conditions were used in the X and Y directions, while the free boundary condition was applied in the Z-direction. In all simulations, the time step was set to 1 fs. We chose the Nose–Hoover thermostat method to control the temperature unless the effect of temperature on the friction properties was considered; otherwise, the temperature was kept at T = 1 K.

According to the calculation method proposed by Liu et al. (Liu and Zhang, 2011), the friction force along the X-direction is computed as $\overline{Fx}=\frac{1}{n\lambda }{\displaystyle \underset{0}{\overset{n\lambda }{\int }}{f}_x\left(s\right)ds}$, where λ is the moving period, n is the number of periods, f is the instantaneous friction, and s is the time step of relative sliding. Similarly, we compute the normal force in the Z-direction using $\overline{Fz}=\frac{1}{n\lambda }{\displaystyle \underset{0}{\overset{n\lambda }{\int }}{f}_z\left(s\right)ds}$. The coefficient of friction is the ratio between the friction force at the interfaces and the normal load, which is $\mu =\overline{Fx}/\overline{Fz}$. In addition, unless otherwise specified, the term “friction” in this paper refers to the total frictional force of the interlayer sliding.

Results and Discussion

Effect of Torsion Angle on Friction

We investigated the effect of the interlayer twisting angle on the frictional performance of four new heterostructures. In Figure 3, the interlayer friction of the heterostructure is clearly shown to vary with the rotation angle at a constant normal force of 0.02 nN/atom and a temperature of 1 K. The number of atoms of the upper sheet is denoted as N. For the graphene/MoS₂ and graphene/NbSe₂ systems, the friction coefficient shows a periodic variation with the rotation angle. This is consistent with the previous results of Song et al. (Song et al., 2018). The curve takes 60° as the period and is determined by the periodic hexagonal lattice structure. When the rotation angle is 0° and 60°, the friction coefficient reaches the maximum, and the heterostructure is in the aligned contact state. The friction coefficient is at its lowest at a rotation angle of 30°. Furthermore, we considered the effect of temperature on the interlayer friction performance for various rotation angles, and the results are shown in Supplementary Figure S2. The increase in temperature leads to an increase in the thermal vibration of the atoms, which results in a decrease in the interlayer frictional resistance, and then the dependence of the friction coefficient on the rotation angle is weakened. As shown in Figures 3B–F, we compared the friction coefficients obtained by sliding sheets of different sizes on the substrate, and we can perceive that the smaller the size of the sheet is, the more difficult it is to achieve superlubricity (see Effect of Torsion Angle on Friction for a detailed discussion). The larger the size of the sheet is, the larger the range of angles to achieve superlubricity. Comparing these two different systems, the friction coefficient of graphene/NbSe₂ is lower than that of graphene/MoS₂ under the same conditions. This is due to the greater lattice mismatch of the graphene/NbSe₂ heterostructure. In comparison with the graphene/graphene homostructure system (Ru et al., 2020), it can be seen that the friction coefficient of the homogeneous structure system is higher than that of the heterostructure in the aligned contact state. In addition, the homostructure system is more sensitive to the rotation angle, while the friction coefficient of the heterostructure decreases slowly after the change in the rotation angle. This is consistent with previous studies (Dienwiebel et al., 2004; Filippov et al., 2008; Wang et al., 2019a; Ru et al., 2020).

FIGURE 3

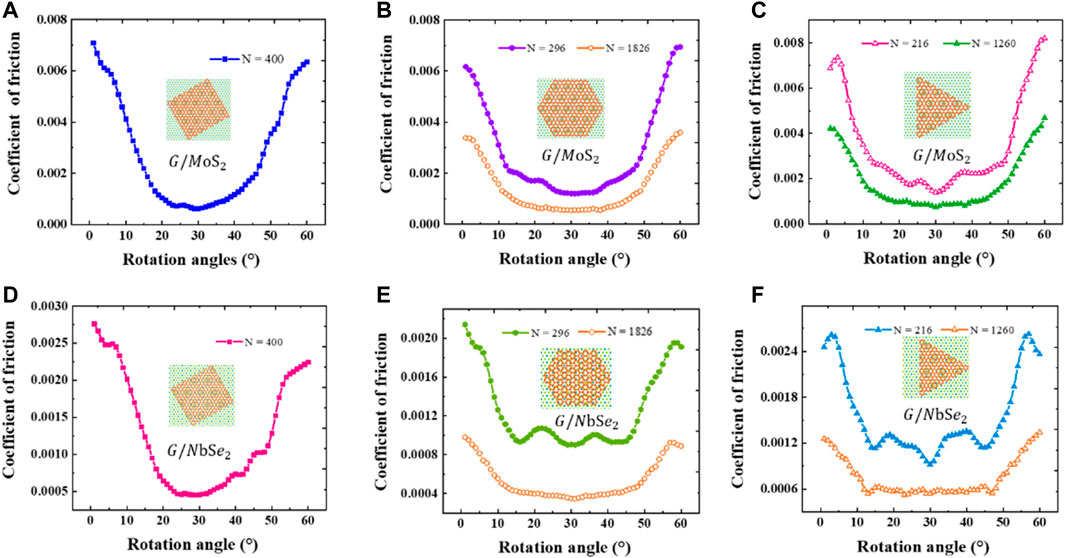
FIGURE 3. Variation in the interlayer friction coefficient with rotation angle for van der Waals heterostructures of different shapes. (A–C) graphene/MoS₂; (D–F) graphene/NbSe₂.

By combining the analysis with the potential energy surface (PES), we further explored the relationship between the rotation angle and the friction force. At the microscopic scale, potential energy fluctuations at the interface are the origin of kinetic friction (Guo et al., 2011). Therefore, we mapped the potential energy surface = profile of the heterostructure at different rotation angles, as shown in Figure 4. The interlayer interaction energy between the top graphene sheet and the substrate was calculated using the LJ potential as a function of the position coordinates of the center mass of the sheet (X- and Y-axes chosen along the armchair and zig-zag directions, respectively) and the relative twist angle θ. From Figure 4, we can clearly see that for graphene/MoS₂ and graphene/NbSe₂ heterostructures, the PES fluctuations at the rotation angle θ = 0° are much larger than those at other angles because the lattice of the graphene sheet and the substrate form an aligned contact. The corresponding PES fluctuations at other rotation angles are smoother. The smoother the PES fluctuations are, the less energy consumed in the sliding process, and the system structure is more likely to enable structural superlubricity.

FIGURE 4

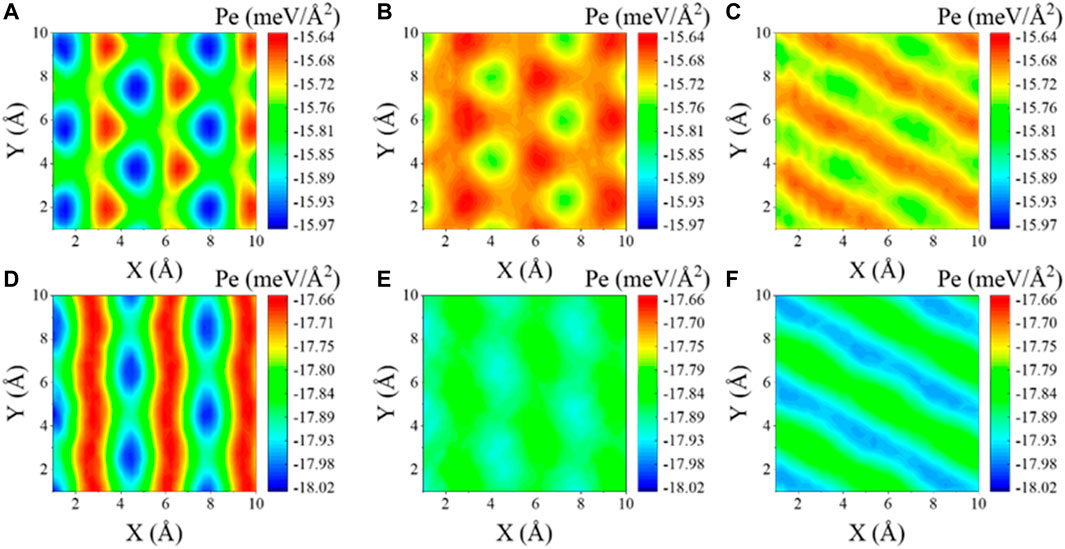
FIGURE 4. Effective interaction potential energy surface of the heterostructure. (A–C) Potential energy surface (PES) of graphene/MoS₂ heterostructure with different rotation angles, where (A) θ = 0°; (B) θ = 15°; (C) θ = 30°; (D–F) PES of graphene/NbSe₂ heterostructure with different rotation angles, where (D) θ = 0°; (E) θ = 15°; (F) θ = 30°.

In the same way, we investigated the interlayer sliding behavior of α-Te/MoS₂ and α-Te/NbSe₂ heterostructures under the same simulation conditions, as shown in Figure 5. From the calculation results in Figures 5A–C, it can be found that for the α-Te/MoS₂ heterostructure, the interlayer friction shows an obvious periodicity with the change in rotation angles. However, for the α-Te/NbSe₂ heterostructure, the periodicity of the interlayer friction is not significant when the slider size is small. After increasing the size, the periodicity gradually appears. Since the lattice periodicity is broken at the boundaries, this leads to a reduction in the binding of the boundary atoms. As a result, the boundary atoms are more active than the central atoms. A smaller slider size means more pronounced edge effects, which we discuss in detail in Effect of Torsion Angle on Friction. To further elucidate the reason for the variation in friction with angle for the α-Te/MoS₂ and α-Te/NbSe₂ systems, we plotted the sliding potential energy surface configurations of these two systems, as shown in Figure 6. We can clearly see that the degree of undulation of the potential energy surface corresponds to the magnitude of the friction coefficient. A small undulation of potential energy means that the system has a small energy loss during sliding, i.e., a small sliding resistance. For both heterostructures, α-Te/MoS₂ and α-Te/NbSe₂, the potential energy surface is flatter when the interlayer twist angle is 15° than when the twist angles are 0° and 30°. In Figure 5, these two heterostructures do have lower friction coefficients at a rotation angle of 15°, and both are consistent with the results from the potential energy surface calculation. Meanwhile, we found that for α-Te/MoS₂ and α-Te/NbSe₂ heterostructures, the rotation angle regulates the interlayer friction of the system, but superlubricity cannot occur (the coefficient of friction is greater than one thousandth of an order of magnitude). The α-Te/MoS₂ and α-Te/NbSe₂ heterostructures require more potential barriers to be overcome in the slip path than the graphene/MoS₂ and graphene/NbSe₂ heterostructures due to the dominance of the frictional mechanism of interfacial sliding resistance in tellurene heterostructures. However, for graphene heterojunctions, friction is dominated by boundary effects, as detailed in the analysis in Effect of Torsion Angle on Friction.

FIGURE 5

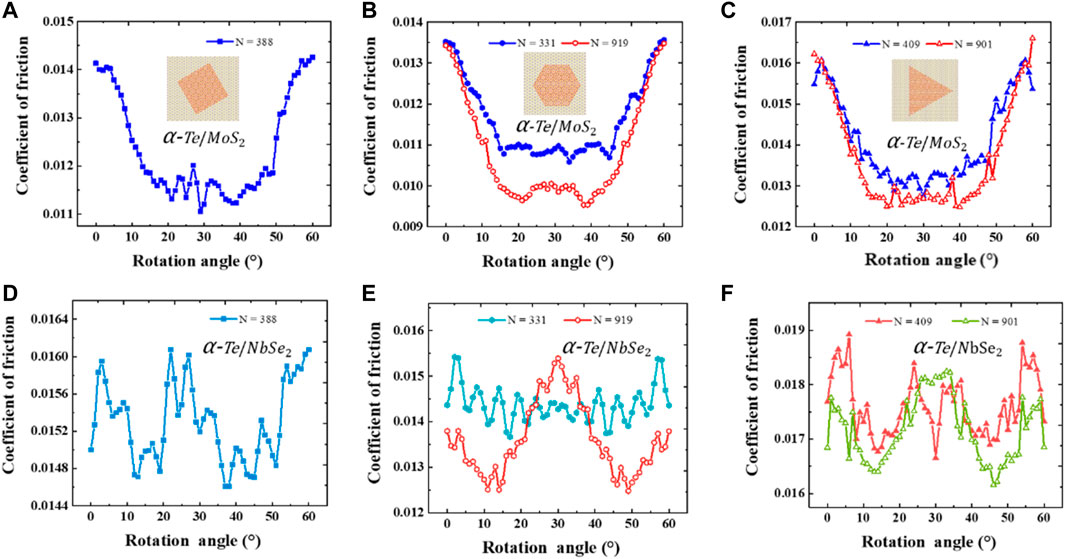
FIGURE 5. Variation in the interlayer friction coefficient with rotation angle for van der Waals heterostructures of different shapes. (A–C) α-Te/MoS₂; (D–F) α-Te/NbSe₂. The slider shapes in (D–F) are rectangular, triangular and hexagonal, respectively.

FIGURE 6

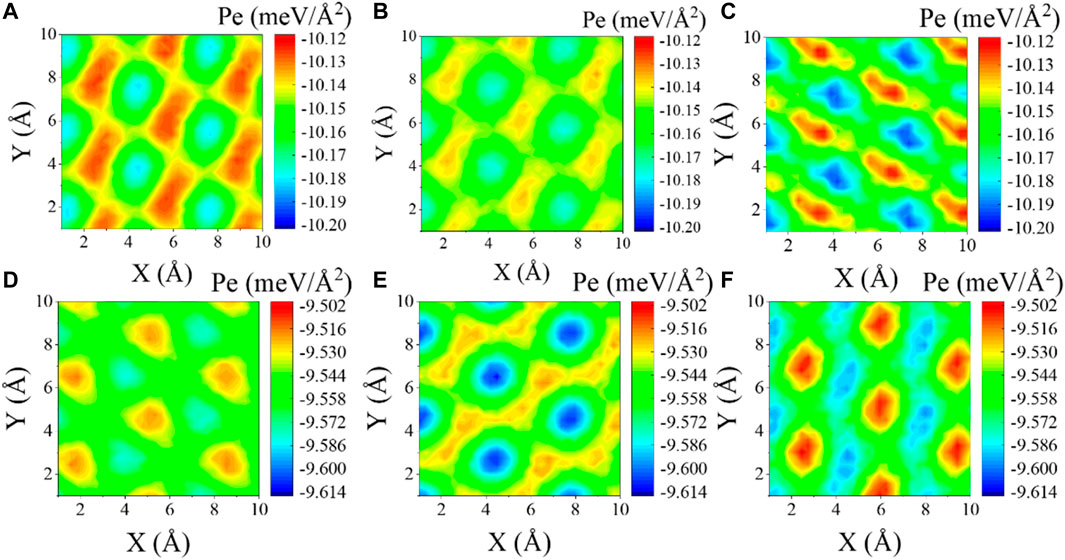
FIGURE 6. Effective interaction potential energy surface of the heterostructure. (A–C) PES of the α-Te/MoS₂ heterostructure with different rotation angles, where (A) θ = 0°; (B) θ = 15°; and (C) θ = 30°. (D–F) PES of the α-Te/NbSe₂ heterostructure with different rotation angles, where (D) θ = 0°; (E) θ = 15°; and (F) θ = 30°.

Effect of Contact Size on Friction

Friction is independent of the macroscopic contact area because the actual area of contact on the atomic scale is a fraction of the total surface area. However, at the atomic scale, it is crucial to understand the relationship between contact size and friction to control friction. Mandelli et al. found that for all contact sizes considered, the commensurate homogeneous interface exhibits highly dissipative viscous slip motion, leading to size-independent static and dynamic friction (Mandelli et al., 2017). In contrast, incommensurate interfaces have significant size effects. In this section, we investigate the relationship between contact size and friction for heterogeneous structures that are under aligned contact.

Herein, we discuss the variation of the frictional force with size for three different shapes of sliders using the parameter, i.e., the perimeter-to-area ratio (P/A), which has been used in reference (Belghachi and Khelifi, 2006). The higher the value of P/A is, the larger the proportion of atoms at the edge of the slider. As shown in Figure 7, for the four heterostructures, the friction of the heterostructures tends to decrease with increasing P/A, which is consistent with the conclusion of previous calculations (Wang et al., 2019c). In addition, Figure 7 shows that the friction decreases at a faster rate when P/A < 0.2, with an approximately linear decrease. However, when P/A>0.2, the rate of decline gradually slows down. As mentioned before, in our MD simulation, normal loading is achieved by loading 0.02 nN to each atom of the outermost layer of the slider. A larger slider implies a larger normal load. Due to the different structures of graphene and α-Te, the same contact area corresponds to different amounts of normal load. Therefore, we redrew the relationship curve between the friction coefficient and P/A, as shown in Supplementary Figure S3 (Supplementary Information S1). The coefficient of friction vs. specific perimeter (P/A) for the heterostructures by graphene and α-Te exhibited different variation trends. For the graphene/MoS₂ and graphene/NbSe₂ heterostructures, the friction coefficient increases linearly with increasing P/A, which means that the smaller the slider size is, the higher the frictional resistance. A smaller slider size also means a higher percentage of atoms at the edge. However, for the α-Te/MoS₂ and α-Te/NbSe₂ heterostructures, the friction coefficient decreases linearly with increasing P/A, implying that the larger the slider size is, the larger the frictional resistance. A larger slider size also means a larger contact area at the interface. This indicates that they have two completely different friction mechanisms.

FIGURE 7

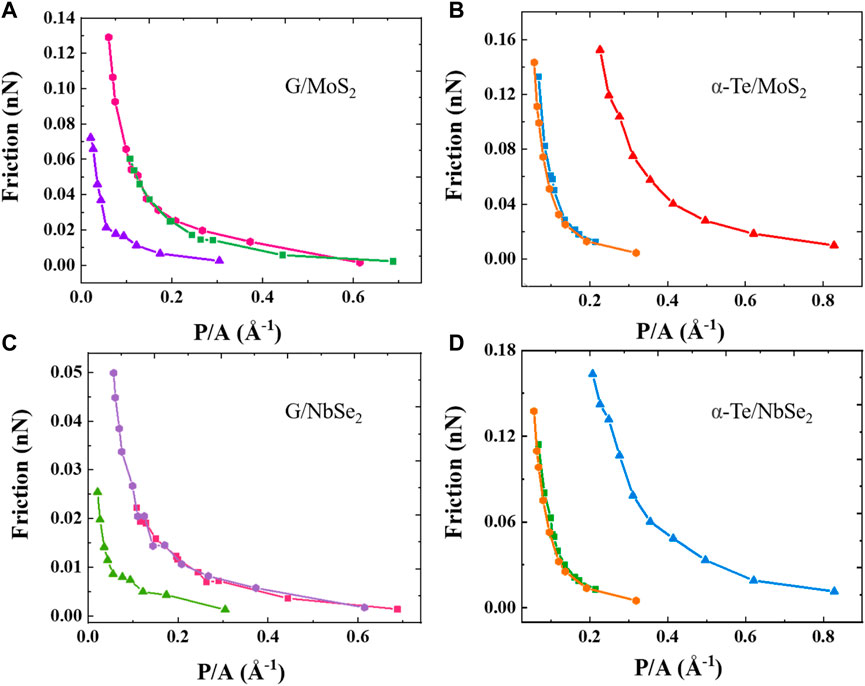
FIGURE 7. Friction force as a function of perimeter/area. (A) graphene/MoS₂; (B) α-Te/MoS₂; (C) graphene/NbSe₂; (D) α-Te/NbSe₂. The shape of the data points represents the shape of the slider in the MD simulation, which are rectangular, triangular, and hexagonal.

To further investigate the two different interlayer friction mechanisms, we plotted the variation in the friction force (average to each atom of the slider) with a specific perimeter (P/A). The ratio of edge atoms to internal atoms decreases as the slider size increases (as shown in Supplementary Figure S4, Supplementary Material S1), and the contribution of the edge atoms to the system friction decreases. In the graphene/MoS₂ and graphene/NbSe₂ heterostructures, as shown in Figures 8A,C, the single-atom friction shows a linear increase with increasing P/A of the graphene slider. This phenomenon is related to the fact that the friction mainly comes from the contact interface edge pinning. The same conclusion was shown by Qu et al. (Qu et al., 2020), where they separated the inner area of the slider contact interface from the edge area, calculated the friction force of both separately, and confirmed experimentally that the friction force mainly comes from the edge. In addition, edge atoms can exhibit large distortions due to their low confinement, which can lead to large friction (Guo et al., 2011; Mandelli et al., 2017).

FIGURE 8

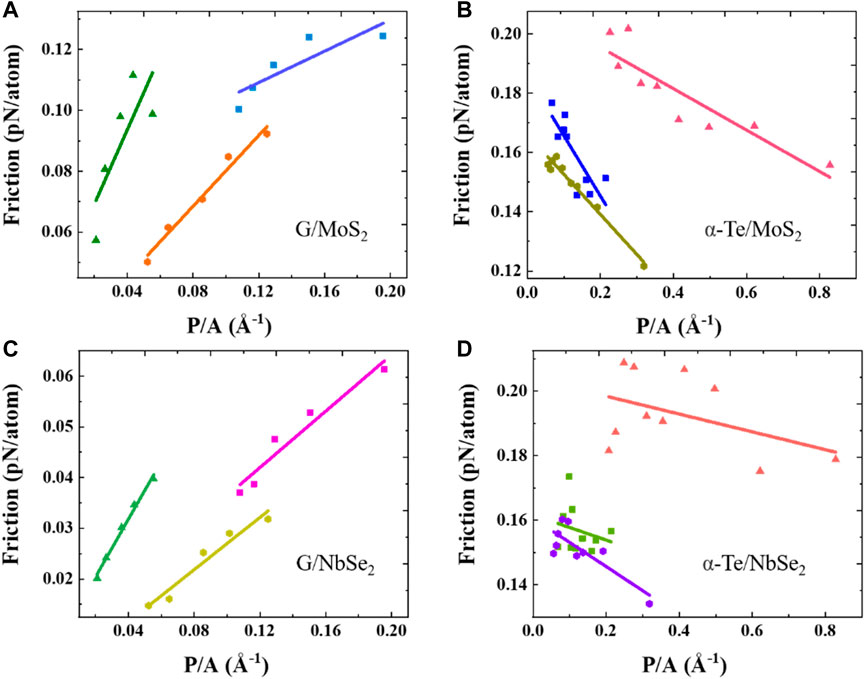
FIGURE 8. Variation in frictional force with size for different shaped sliders. (A) Graphene/MoS₂; (B) α-Te/MoS₂; (C) Graphene/NbSe₂; (D) α-Te/NbSe₂. The shape of the data points represents the shape of the slider in the MD simulation, which are rectangular, triangular and hexagonal. The solid line is obtained by least squares fitting based on the data points.

However, in the α-Te/MoS₂ and α-Te/NbSe₂ heterostructures, as shown in Figures 8B,D, the abnormal phenomenon was observed, i.e., a trend of decreasing friction (averaged to each atom) with increasing P/A. The increase in P/A means that the percentage of boundary atoms increases. The friction shows a decreasing trend, indicating that for this heterostructure, the interlayer friction is not dominated by edge pinning but due to the in-plane interface sliding resistance mainly contributing to the friction. Liao et al. defined the shear strength S and edge-pinning strength E of a finite size slider as follows (Liao et al., 2021):

$\begin{array}{c}S=\frac{F_r}{A}\end{array}(1)$

$\begin{array}{c}E=\frac{F_r}{P}\end{array}(2)$

where $F_r$ is the frictional force, A is the area of the domain, and P is the perimeter of the slider. When the friction is mainly influenced by the sliding resistance at the interface, the shear strength S is constant with respect to the slider area. When the friction force is mainly from edge pinning, E is constant with respect to the slider perimeter. As shown in Figure 9, we plotted the shear strength S versus domain area for the four systems. In addition, the inset shows the trend of the corresponding edge pinning strength E with the domain perimeter.

FIGURE 9

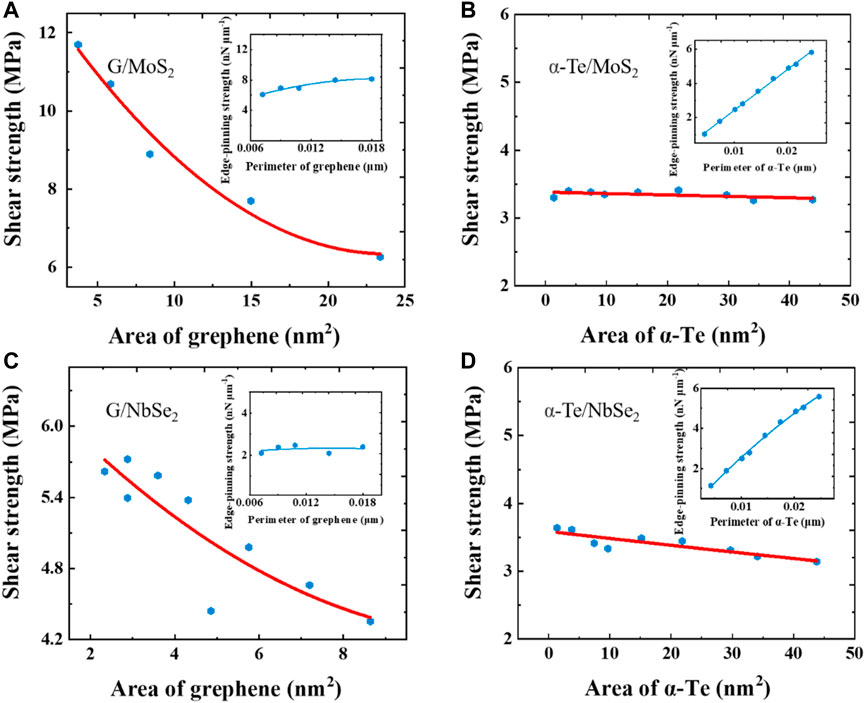
FIGURE 9. Shear strength and edge-pinning strength for different heterostructures. (A) Graphene/MoS₂; (B) α-Te/MoS₂; (C) Graphene/NbSe₂; (D) α-Te/NbSe₂. The inset shows the corresponding edge pinning strength trend with the domain perimeter. The solid lines in the figures are obtained by least squares fitting based on the data points.

In the graphene/MoS₂ and graphene/NbSe₂ heterostructures, as shown in Figures 9A,C, the edge pinning strength E is constant relative to the perimeter of the slider. We believe that the friction force mainly comes from the edge. In the α-Te/MoS₂ and α-Te/NbSe₂ heterostructures, as shown in Figures 9B,D, the shear strength S is constant relative to the area of the slider. We believe that in these two systems, the friction force is dominated by the sliding resistance in the interface.

According to the Prandtl-Tomlinson model (Tomlinson, 1929), when the upper moving atom falls into the potential well formed by the static atoms, if the upper atom moves, it is necessary to overcome the potential barrier of the potential well, resulting in increased resistance. However, if the upper atoms do not fall into the potential well, the resistance is very small when moving. This atomic-scale resistance is friction in the macro view, which is also the origin of friction. For the systems mentioned above, that is, a two-dimensional material slider sliding on the two-dimensional material plane, we can regard the two-dimensional material matrix as a potential field. From the atomic level, the contribution of each atom of the slider to the friction force depends on the extent to which the atom falls into the matrix potential well. The deeper it falls into the potential well, the greater its contribution to the friction force, and the shallower it falls into the potential well, the smaller the contribution to friction. From the slider, each atom on the contact surface of the same slider is the same, but the position of the atom is different. The range of atomic motion in the sliding process is different, which leads to the fact that if the range of atomic motion is large, the atom easily falls into the potential well of the matrix. The range of atomic motion can be expressed by the mean-square displacement (MSD) of the atom (Kubečka et al., 2016). By using the built-in commands in the Lammps software, we can easily calculate the mean square displacement of the system atoms with the corresponding defining equation shown below:

$\begin{array}{c}MSD=\langle \frac{1}{N}{\displaystyle \sum _{i=1}^N{\left[r_i\left(t_0+t\right)-r_i\left(t_0\right)\right]}^2}\rangle \end{array}(3)$

where N is the number of particles, t represents time, r (t₀ + t)-r (t₀) is the vector distance passed by a given particle in a period of time, and <...> is the mean of the system synthesis after equilibrium.

In other words, the contribution of the slider atom to the friction is related to the MSD of the atom. If the MSD of the atom is large, the contribution to the friction is large; otherwise, the contribution to the friction is small.

As shown in Figure 10, we distinguish the slider into two parts: the edge and the inner area. We further calculated the average MSD of the atoms in the two areas separately and averaged over the whole MD trajectory. The final calculation results are presented in Table 3.

FIGURE 10

FIGURE 10. Schematic diagram of the edge (green) and inner (yellow) areas of the slider.

TABLE 3

TABLE 3. Average root-mean-square displacement of atoms of rectangular sliders during sliding*.

For the graphene/MoS₂ heterostructure, the average atomic displacement in the edge area is significantly larger than the average displacement in the central area, which indicates that the edge atoms have a relatively larger range of motion, and thus, the edge atoms are more likely to be trapped in the energy minimum of the substrate, leading to the edge pinning effect. Thus, the edge atoms cause more friction than the central atoms, and for the total friction of the slider, the contribution of the edge atoms dominates.

For the α-Te/MoS₂ heterostructure, the displacements of the atoms in the boundary region remain larger than the displacements of the atoms in the inner region, which can be explained by the fact that edge effects are always available for a finite size slider. Differently from the graphene/MoS₂ system, the atoms in the internal region of the α-Te slider also have a large atomic shift, which indicates that the internal atoms are equally prone to fall into the potential wells formed by the substrate, and the frictional force increases with the increase of the interfacial contact area; therefore, for the α-Te/MoS₂ heterostructure, the interfacial sliding resistance is the main source of frictional force.

In general, the boundary pinning effect exists in all studied sliders. For graphene/MoS₂ and graphene/NbSe₂ heterostructure systems, this boundary pinning is the main source of friction. For α-Te/MoS₂ and α-Te/NbSe₂ heterostructures, the in-plane atomic pinning effect is more obvious; that is, boundary pinning is not the main source of friction, and in-plane interface friction plays a leading role.

Effect of the Number of Slider Layers on Friction

Monolayer graphene has been reported to have higher friction than multilayer graphene and graphite (Lee et al., 2009); however, the underlying mechanism remains to be discussed. Earlier studies attributed the increased friction of thinner two-dimensional samples to puckering and local pinning (Lee et al., 2010; Li et al., 2010; Ye et al., 2012; Li et al., 2016). In our simulations, graphene sheets with different layer thicknesses were chosen to slide on the substrate with the number of graphene layers (M) varying from 1 to 10. Meanwhile, we also considered three shapes: triangular, rectangular, and hexagonal sheets. For different shapes, the number of atoms per layer (N) is 1980, 1860 and 1,260. The initial spacing between adjacent layers of graphene is set to 0.34 nm. Figure 11 shows the relationship between the friction force and the number of layers of graphene with different shapes. In general, a smaller number of layers corresponds to a larger frictional force. The friction coefficient shows a decreasing trend as the number of graphene layers increases, and the decreasing trend slows down when the number of layers M > 4.

FIGURE 11

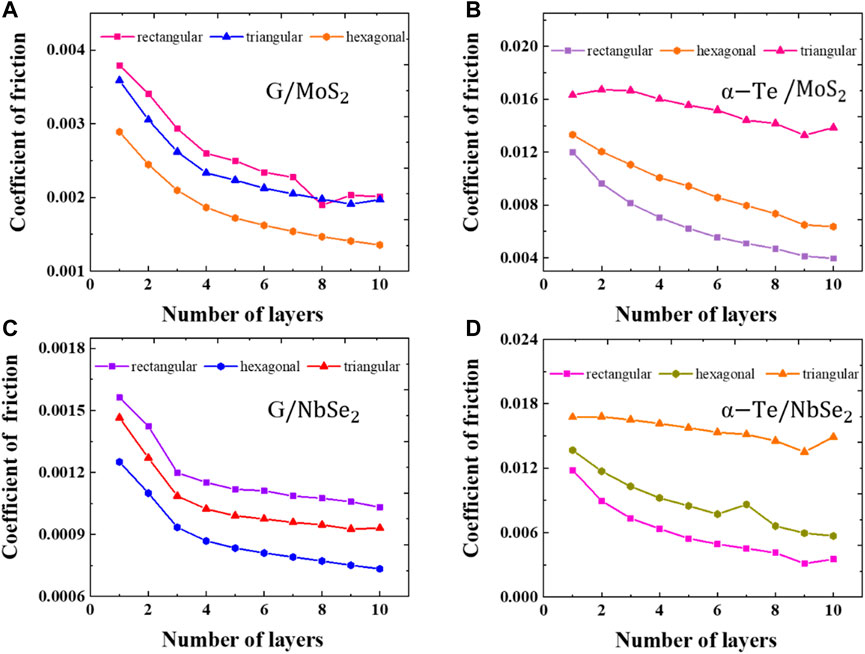
FIGURE 11. Effect of the number of graphene layers on interlayer friction. (A) graphene/MoS₂ heterostructure; (B) graphene/NbSe₂ heterostructure. (C) α-Te/MoS₂ heterostructure; (D) α-Te/NbSe₂ heterostructure. The shape of the data points represents the shape of the slider in the MD simulation, which are rectangular, triangular, and hexagonal.

According to the theory given in reference (Liao et al., 2021), the interlayer friction comes from two parts: one is caused by adhesion, and the other is caused by increasing load. When the load is constant, the magnitude of friction changes with the change in adhesion. When we simulate the relationship between the number of layers and friction, the load is also constant. According to the literature (Pourzand et al., 2013), the interlayer adhesion decreases with increasing layer thickness (number of layers). That is, as the number of layers of the slider increases, the adhesion between the slider and the substrate decreases, resulting in a decrease in friction, as shown in Figure 11.

Effect of Temperature on Friction

For a further comparative study of the effect of temperature on the interlayer friction of different systems, simulations were carried out for four heterostructures at temperatures of 1 K, 50 K, 100 K, 150 K, 200 K, 250 and 300 K. Throughout our simulations, the normal load and slip velocity were set to 0.02 nN/atom and 1 Å/ps, respectively. The sliding direction of the slider is set to slide along the X-direction. The simulation results are shown in Figure 12. We find that the variation trend of the friction force of the four systems with temperature is almost the same; in other words, the friction first decreases with increasing temperature and then remains essentially constant, which is consistent with previous reports (Zhao et al., 2007; Smolyanitsky, 2015; Gongyang et al., 2020).

FIGURE 12

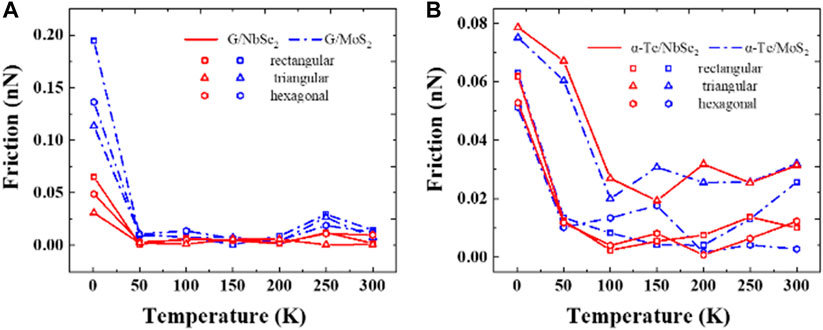
FIGURE 12. Effect of temperature on the interlayer friction. The shape of the data points represents the shape of the slider in the simulation, which are rectangular, triangular, and hexagonal. (A) graphene/MoS₂ and graphene/NbSe₂ heterostructures; (B) α-Te/MoS₂ and α-Te/NbSe₂ heterostructures.

The influence of temperature on the interlayer friction of the heterostructure can be explained as follows: as mentioned above, the interlayer friction of the two-dimensional van der Waals heterostructure can be regarded as being composed of two parts (Liao et al., 2021): one is from the adhesion between layers (interlayer interaction), and the other is the friction caused by loading (related to the structure of the two-dimensional material). To study the effect of temperature on friction, we have taken the same load in the simulation. In this way, we only need to study the relationship between interlayer adhesion and temperature. Deng et al. show theoretical studies that (Deng and Berry, 2016), with the increase of temperature, atomic thermal vibration intensifies, and nanoscale ripples will inevitably appear in two-dimensional materials, resulting in the reduction of effective contact area and the reduction of adhesion force. The conclusion that the interlayer adhesion force of two-dimensional materials decreases with increasing temperature has been confirmed by experiments (Polfus et al., 2021).

We calculated the coordinates of the upper S atoms of the base material MoS₂ in the Z-axis direction, which is intended to indicate the degree of fluctuation of the sliding contact interface. (see Supplementary Figure S5). It can be clearly seen that the contact interface between the slider and substrate fluctuates greatly, while it remains flat in other noncontact regions. In addition, as shown in Supplementary Figure S5B, the kinetic energy distribution of the contact interface is higher than that of other regions. This result shows that it is the nanoscale ripple in the contact interface that directly leads to the reduction of the real contact area. In other words, the interlayer friction of two-dimensional materials decreases with increasing temperature. It is worth mentioning that the interlayer friction changes rapidly with temperature and soon reaches a constant value, which is similar for the four systems, indicating that the nanoscale ripple no longer increases after reaching a certain temperature, the adhesion force reaches a constant value, and the interlayer friction also reaches a constant value.

Effect of Slide Direction on Friction

Interlayer friction anisotropy in two-dimensional materials has been studied for a long time, and there is evidence that interlayer friction anisotropy in two-dimensional materials is caused by different lattice orientations. Here, we compare the variation in interlayer friction in four heterostructures when the slider moves along different sliding directions. We selected the upper slider to slide along the 0°, 15°, 30°, 45°, 60°, 75° and 90° directions, where 0° exactly corresponds to the sliding direction along the X-direction. The normal load was set to a constant 0.02 nN/atom, and the sliding speed was set at 1 Å/ps.

To further explicitly describe the effect of slip direction on interlayer friction, the system temperature was set to 1 K for the simulation. As shown in Figure 13, we can find that the variation in the friction force with the slip direction is relatively small for the heterostructures; that is, the heterostructures have lower friction anisotropy than the homostructures, which is consistent with the conclusions in previous research works (Ru et al., 2020). Due to the natural lattice mismatch of the heterogeneous structure, even when the heterogeneous structure is in aligned contact, the upper slider can slide smoothly regardless of the sliding direction, thus exhibiting a small frictional anisotropy. The friction anisotropy still shows variability for different heterogeneous structural systems. As shown in Figure 13B, both α-Te/MoS₂ and α-Te/NbSe₂ heterostructures have greater anisotropy than the graphene/MoS₂ and graphene/NbSe₂ systems and exhibit a significant 60° periodicity. Compared with the latter, the potential energy surface of the former fluctuates greatly during the sliding process, showing more obvious anisotropy.

FIGURE 13

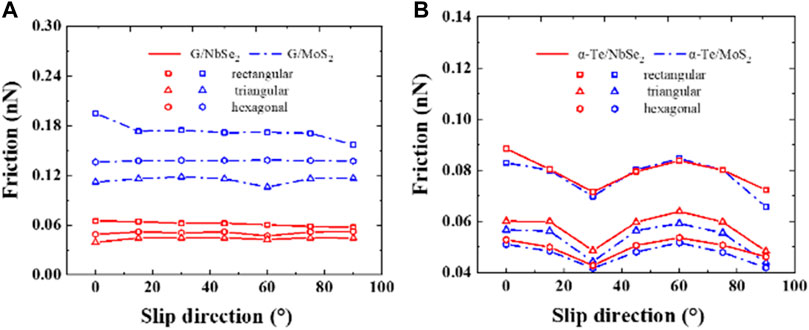
FIGURE 13. Effect of slide direction on interlayer friction. The shape of the data points represents the shape of the slider in the simulation, which are rectangular, triangular, and hexagonal. (A) graphene/MoS₂ and graphene/NbSe₂; (B) α-Te/MoS₂ and α-Te/NbSe₂.

Effect of Sliding Velocity on Friction

We further studied the velocity-dependent interlayer friction. The normal load was kept at 0.02 nN/atom, the sliding direction was fixed along the X-direction, and the system temperature was controlled at 1 K. The detailed results are shown in Figure 14.

FIGURE 14

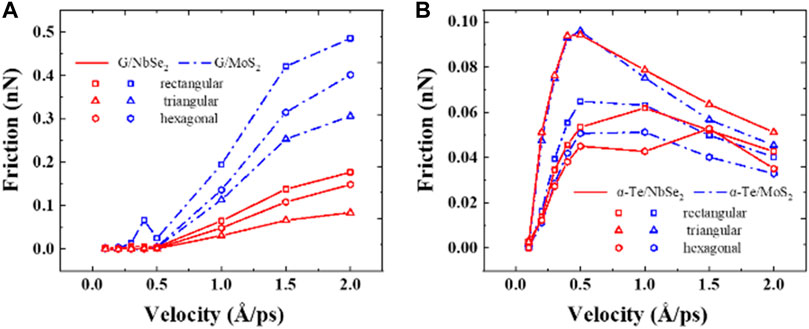
FIGURE 14. Effect of sliding velocity on interlayer friction. The shape of the data points represents the shape of the slider in the simulation, which are rectangular, triangular, and hexagonal. (A) graphene/MoS₂ and graphene/NbSe₂ heterostructures; (B) α-Te/MoS₂ and α-Te/NbSe₂ heterostructures.

As seen from Figure 14A, for the graphene/MoS₂ and graphene/NbSe₂ heterostructures, the friction force remains essentially constant at low sliding speeds, while it increases significantly with increasing speed. The simulation results are the same as those reported in the previous literature (Zwörner et al., 1998; Sheehan and Lieber, 2017). Additionally, Zwörner demonstrated experimentally that the linear increase in friction with sliding speed at large sliding speeds is due to the strong damping effect (Zwörner et al., 1998). However, we obtained completely different results in the α-Te/MoS₂ and α-Te/NbSe₂ heterostructures. As the sliding velocity increases from 0.1 to 0.5 Å/ps, the friction force increases approximately linearly. However, when the sliding speed exceeds 0.5 Å/ps, there is a decreasing tendency for the friction, as shown in Figure 14B. We find that for α-Te/MoS₂ and α-Te/NbSe₂ heterostructures, as the sliding speed increases, the temperature in the contact part will also increase, i.e., the local temperature increases significantly with increasing sliding velocity. The increase in system temperature comes from the increased atomic thermal vibration during high-speed sliding, as mentioned in Effect of temperature on friction, which leads to an increase in friction in the α-Te/MoS₂ and α-Te/NbSe₂ systems. It has been reported that surface-to-surface contact contributes to thermal activation. Thermal activation, in turn, is closely related to the sliding speed (Smolyanitsky, 2015). When the sliding velocity is relatively fast, thermal activation may occur, resulting in a smaller slip resistance, thus showing a decrease in friction, as shown in Figure 14B.

Effect of Normal Load on Friction

We studied the normal load versus interlayer friction for the four heterostructures, while the chosen normal loads were 0.02, 0.1, 0.2 and 0.5 nN/atom. The simulation results are shown in Figure 15.

FIGURE 15

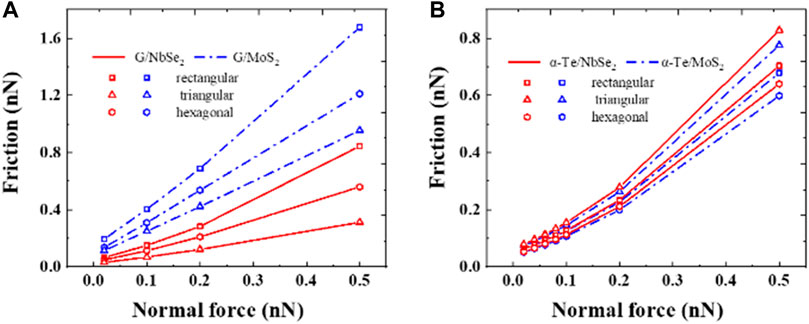
FIGURE 15. Effect of normal forces on interlayer friction. The shape of the data points represents the shape of the slider in the simulation, which are rectangular, triangular, and hexagonal. (A) graphene/MoS₂ and graphene/NbSe₂ heterostructures; (B) α-Te/MoS₂ and α-Te/NbSe₂ heterostructures.

It is found that the normal load is approximately linearly related to the friction in the heterostructures studied, agreeing with the results of previous studies (Miura and Kamiya, 2002; Lee et al., 2009; Filleter and Bennewitz, 2010; van Wijk et al., 2013; Levita et al., 2014; Baykara et al., 2018; Wang et al., 2019a). Large normal loads tend to cause deformation of the plane. In addition, for a single layer slider, an increase in normal load means a decrease in layer spacing. The effective contact area of the system interface increases, leading to the stick-slip phenomenon in the system. As a result, the interaction between atoms becomes stronger, leading to a linear increase in friction.

Conclusion

In this paper, we investigated in detail the interlayer friction of four different van der Waals heterostructures by molecular dynamics methods, while the effects from different factors (i.e., stacking angles, contact areas, contact shapes, thicknesses, temperatures, sliding directions, sliding velocities and normal loads) have been studied and discussed. Many important laws relating to interlayer friction have been found, and the main are the following:

(1) The twist angle can effectively regulate the interlayer friction of van der Waals heterostructures. When the heterostructures are in aligned contact, the fluctuation of PES during sliding is the largest, and the friction coefficient reaches the maximum. Moreover, we found that the superlubricity phenomenon cannot occur for α-Te/MoS₂ and α-Te/NbSe₂ systems.

(2) In the graphene/MoS2 and graphene/NbSe2 systems, the interlayer friction shows a linear increase with increasing slider specific perimeter P/A, while in the α-Te/MoS₂ and α-Te/NbSe₂ systems, it shows a significantly opposite trend. The reason for this discrepancy is that edge pinning and in-plane interfacial friction play dominant roles in different heterostructures.

(3) For the four heterostructures, the influence laws of the number of layers, temperature, and normal load on interlayer friction show consistency. However, the effect of velocity on the frictional force of the four heterostructures shows significant variability. The increase in temperature is from the increase in the atomic thermal vibration at the contact part during the high-speed sliding, leading to the anomalous variation in friction in the α-Te/MoS₂ and α-Te/NbSe₂ systems.

The present work reveals the evolution laws of friction under various influences and provides a reference for the design of a two-dimensional system with ultralow interlayer friction.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YW: Software, Methodology, Writing—Original draft preparation. GR: Software, Methodology, Writing—Review and Editing WQ: Conceptualization, Writing—Review and Editing, Supervision KT: Data curation TX|: Resources.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 52072308) and the Fundamental Research Funds for the Central Universities (Grant Nos.. 3102021MS0404 and 3102019JC001).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2022.879561/full#supplementary-material

References

Alemayehu, M. B., Falmbigl, M., Grosse, C., Ta, K., Fischer, S. F., and Johnson, D. C. (2015). Structural and Electrical Properties of a New ([SnSe]1.16)1(NbSe2)1 Polytype. J. Alloys Comp. 619, 861–868. doi:10.1016/j.jallcom.2014.09.084

CrossRef Full Text | Google Scholar

Baykara, M. Z., Vazirisereshk, M. R., and Martini, A. (2018). Emerging Superlubricity: A Review of the State of the Art and Perspectives on Future Research. Appl. Phys. Rev. 5, 041102. doi:10.1063/1.5051445

CrossRef Full Text | Google Scholar

Belghachi, A., and Khelifi, S. (2006). Modelling of the Perimeter Recombination Effect in GaAs-Based Micro-solar Cell. Solar Energ. Mater. solar Cell 90, 1–14. doi:10.1016/j.solmat.2005.01.009

CrossRef Full Text | Google Scholar

Berman, D., Deshmukh, S. A., Sankaranarayanan, S. K. R. S., Erdemir, A., and Sumant, A. V. (2015). Macroscale Superlubricity Enabled by Graphene Nanoscroll Formation. Science 348, 1118–1122. doi:10.1126/science.1262024

PubMed Abstract | CrossRef Full Text | Google Scholar

Brenner, D. W., Shenderova, O. A., Harrison, J. A., Stuart, S. J., Ni, B., and Sinnott, S. B. (2002). A Second-Generation Reactive Empirical Bond Order (REBO) Potential Energy Expression for Hydrocarbons. J. Phys. Condens. Matter 14, 783–802. doi:10.1088/0953-8984/14/4/312

CrossRef Full Text | Google Scholar

Deng, S., and Berry, V. (2016). Wrinkled, Rippled and Crumpled Graphene: an Overview of Formation Mechanism, Electronic Properties, and Applications. Mater. Today 19, 197–212. doi:10.1016/j.mattod.2015.10.002

CrossRef Full Text | Google Scholar

Dienwiebel, M., Verhoeven, G. S., Pradeep, N., Frenken, J. W. M., Heimberg, J. A., and Zandbergen, H. W. (2004). Superlubricity of Graphite. Phys. Rev. Lett. 92, 126101. doi:10.1103/physrevlett.92.126101

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietzel, D., Brndiar, J., Štich, I., and Schirmeisen, A. (2017). Limitations of Structural Superlubricity: Chemical Bonds versus Contact Size. ACS Nano 11, 7642–7647. doi:10.1021/acsnano.7b02240

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietzel, D., Feldmann, M., Schwarz, U. D., Fuchs, H., and Schirmeisen, A. (2013). Scaling Laws of Structural Lubricity. Phys. Rev. Lett. 111, 235502. doi:10.1103/physrevlett.111.235502

PubMed Abstract | CrossRef Full Text | Google Scholar

Filippov, A. E., Dienwiebel, M., Frenken, J. W., Klafter, J., and Urbakh, M. (2008). Torque and Twist against Superlubricity. Phys. Rev. Lett. 100, 046102. doi:10.1103/PhysRevLett.100.046102

PubMed Abstract | CrossRef Full Text | Google Scholar

Filleter, T., and Bennewitz, R. (2010). Structural and Frictional Properties of Graphene Films on SiC(0001) Studied by Atomic Force Microscopy. Phys. Rev. B 81, 155412. doi:10.1103/physrevb.81.155412

CrossRef Full Text | Google Scholar

Gongyang, Y., Ouyang, W., Qu, C., Urbakh, M., Quan, B., Ma, M., et al. (2020). Temperature and Velocity Dependent Friction of a Microscale Graphite-DLC Heterostructure. Friction 8, 462–470. doi:10.1007/s40544-019-0288-0

CrossRef Full Text | Google Scholar

Guo, Z., Chang, T., Guo, X., and Gao, H. (2011). Thermal-induced Edge Barriers and Forces in Interlayer Interaction of Concentric Carbon Nanotubes. Phys. Rev. Lett. 107, 105502. doi:10.1103/physrevlett.107.105502

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirano, M., and Shinjo, K. (1990). Atomistic Locking and Friction. Phys. Rev. B 41, 11837–11851. doi:10.1103/physrevb.41.11837

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, J., and Zhou, Y. (2017). Handbook of Stillinger-Weber Potential Parameters for Two-Dimensional Atomic Crystals. London, United Kingdom: IntechOpen. Available at: https://www.intechopen.com/books/6638

Google Scholar

Kubečka, J., Uhlík, F., and Košovan, P. (2016). Mean Squared Displacement from Fluorescence Correlation Spectroscopy. Soft Matter 12, 3760–3769. doi:10.1039/c6sm00296j

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C., Li, Q., Kalb, W., Liu, X.-Z., Berger, H., Carpick, R. W., et al. (2010). Frictional Characteristics of Atomically Thin Sheets. Science 328, 76–80. doi:10.1126/science.1184167

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, H., Lee, N., Seo, Y., Eom, J., and Lee, S. (2009). Comparison of Frictional Forces on Graphene and Graphite. Nanotechnology 20, 325701. doi:10.1088/0957-4484/20/32/325701

PubMed Abstract | CrossRef Full Text | Google Scholar

Leven, I., Krepel, D., Shemesh, O., and Hod, O. (2013). Robust Superlubricity in Graphene/h-BN Heterojunctions. J. Phys. Chem. Lett. 4, 115–120. doi:10.1021/jz301758c

PubMed Abstract | CrossRef Full Text | Google Scholar

Levita, G., Cavaleiro, A., Molinari, E., Polcar, T., and Righi, M. C. (2014). Sliding Properties of MoS2 Layers: Load and Interlayer Orientation Effects. J. Phys. Chem. C 118, 13809–13816. doi:10.1021/jp4098099

CrossRef Full Text | Google Scholar

Li, J., Liu, Y., Luo, J., Liu, P., and Zhang, C. (2012). Excellent Lubricating Behavior of Brasenia Schreberi Mucilage. Langmuir 28, 7797–7802. doi:10.1021/la300957v

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Q., Lee, C., Carpick, R. W., and Hone, J. (2010). Substrate Effect on Thickness-dependent Friction on Graphene. Phys. Stat. Sol. (B) 247, 2909–2914. doi:10.1002/pssb.201000555

CrossRef Full Text | Google Scholar

Li, S., Li, Q., Carpick, R. W., Gumbsch, P., Liu, X. Z., Ding, X., et al. (2016). The Evolving Quality of Frictional Contact with Graphene. Nature 539, 541–545. doi:10.1038/nature20135

PubMed Abstract | CrossRef Full Text | Google Scholar

Liao, M., Nicolini, P., Du, L., Yuan, J., Wang, S., Yu, H., et al. (2021). UItra-low friction and edge-pinning effect in large-lattice-mismatch van der Waals heterostructures. Nat. Mater. 21, 47–53. doi:10.1038/s41563-41021-01058-4156410.1038/s41563-021-01058-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, P., and Zhang, Y. W. (2011). A Theoretical Analysis of Frictional and Defect Characteristics of Graphene Probed by a Capped Single-Walled Carbon Nanotube. Carbon 49, 3687–3697. doi:10.1016/j.carbon.2011.05.004

CrossRef Full Text | Google Scholar

Maeda, T., and Washizu, H. (2018). Mechanism of Ultra-low Friction of Multilayer Graphene Studied by All Atom Molecular Dynamics. Microsyst Technol. 24, 757–764. doi:10.1007/s00542-017-3398-5

CrossRef Full Text | Google Scholar

Mandelli, D., Leven, I., Hod, O., and Urbakh, M. (2017). Sliding Friction of Graphene/hexagonal -boron Nitride Heterojunctions: a Route to Robust Superlubricity. Sci. Rep. 7, 10851. doi:10.1038/s41598-017-10522-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Mehmood, F., Pachter, R., Back, T. C., Boeckl, J. J., Busch, R. T., and Stevenson, P. R. (2021). Two-dimensional MoS2 2H, 1T, and 1T′ Crystalline Phases with Incorporated Adatoms: Theoretical Investigation of Electronic and Optical Properties. Appl. Opt. 60, G232–G242. doi:10.1364/ao.433239

PubMed Abstract | CrossRef Full Text | Google Scholar

Miura, K., and Kamiya, S. (2002). Observation of the Amontons-Coulomb Law on the Nanoscale: Frictional Forces between MoS 2 Flakes and MoS 2 Surfaces. Europhys. Lett. 58, 610–615. doi:10.1209/epl/i2002-00439-9

CrossRef Full Text | Google Scholar

Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., et al. (2004). Electric Field Effect in Atomically Thin Carbon Films. Science 306, 666–669. doi:10.1126/science.1102896

PubMed Abstract | CrossRef Full Text | Google Scholar

Onodera, T., Morita, Y., Nagumo, R., Miura, R., Suzuki, A., Tsuboi, H., et al. (2010). A Computational Chemistry Study on Friction of H-MoS2. Part II. Friction Anisotropy. J. Phys. Chem. B 114, 15832–15838. doi:10.1021/jp1064775

PubMed Abstract | CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Polfus, J. M., Muñiz, M. B., Ali, A., Barragan‐Yani, D. A., Vullum, P. E., Sunding, M. F., et al. (2021). Temperature‐Dependent Adhesion in van der Waals Heterostructures. Adv. Mater. Inter. 8, 2100838. doi:10.1002/admi.202100838

CrossRef Full Text | Google Scholar

Pourzand, H., Pai, P., and Tabib-Azar, M. (2013). “Thickness Dependent Adhesion Force and its Correlation to Surface Roughness in Multilayered Graphene,” in SENSORS, 2013 IEEE, Baltimore, MD, USA, 3-6 Nov. 2013 (IEEE), 1–4. doi:10.1109/icsens.2013.6688415

CrossRef Full Text | Google Scholar

Qu, C., Wang, K., Wang, J., Gongyang, Y., Carpick, R. W., Urbakh, M., et al. (2020). Origin of Friction in Superlubric Graphite Contacts. Phys. Rev. Lett. 125, 126102. doi:10.1103/physrevlett.125.126102

PubMed Abstract | CrossRef Full Text | Google Scholar

Rappe, A. K., Casewit, C. J., Colwell, K. S., Goddard, W. A., and Skiff, W. M. (1992). UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 114, 10024–10035. doi:10.1021/ja00051a040

CrossRef Full Text | Google Scholar

Ru, G., Qi, W., Tang, K., Wei, Y., and Xue, T. (2020). Interlayer friction and superlubricity in bilayer graphene and MoS2/MoSe2 van der Waals heterostructures. Tribology Int. 151, 106483. doi:10.1016/j.triboint.2020.106483

CrossRef Full Text | Google Scholar

Ru, G., Qi, W., Wei, Y., Tang, K., and Xue, T. (2021). Superlubricity in bilayer isomeric tellurene and graphene/tellurene van der Waals heterostructures. Tribology Int. 159, 106974. doi:10.1016/j.triboint.2021.106974

CrossRef Full Text | Google Scholar

Sheehan, P. E., and Lieber, C. M. (2017). Friction between van der Waals Solids during Lattice Directed Sliding. Nano Lett. 17, 4116–4121. doi:10.1021/acs.nanolett.7b00871

PubMed Abstract | CrossRef Full Text | Google Scholar

Shinjo, K., and Hirano, M. (1993). Dynamics of Friction: Superlubric State. Surf. Sci. 283, 473–478. doi:10.1016/0039-6028(93)91022-h

CrossRef Full Text | Google Scholar

Smolyanitsky, A. (2015). Effects of thermal Rippling on the Frictional Properties of Free-Standing Graphene. RSC Adv. 5, 29179–29184. doi:10.1039/c5ra01581b

CrossRef Full Text | Google Scholar

Song, Y., Mandelli, D., Hod, O., Urbakh, M., Ma, M., and Zheng, Q. (2018). Robust Microscale Superlubricity in Graphite/hexagonal boron Nitride Layered Heterojunctions. Nat. Mater 17, 894–899. doi:10.1038/s41563-018-0144-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Tomlinson, G. A. (1929). CVI.A Molecular Theory of Friction. Lond. Edinb. Dublin Phil|philos. Mag. J. Sci. 7, 905–939. doi:10.1080/14786440608564819

CrossRef Full Text | Google Scholar

van Wijk, M. M., Dienwiebel, M., Frenken, J. W. M., and Fasolino, A. (2013). Superlubric to Stick-Slip Sliding of Incommensurate Graphene Flakes on Graphite. Phys. Rev. B 88, 235423. doi:10.1103/physrevb.88.235423

CrossRef Full Text | Google Scholar

Vazirisereshk, M. R., Hasz, K., Carpick, R. W., and Martini, A. (2020). Friction Anisotropy of MoS2: Effect of Tip-Sample Contact Quality. J. Phys. Chem. Lett. 11, 6900–6906. doi:10.1021/acs.jpclett.0c01617

PubMed Abstract | CrossRef Full Text | Google Scholar

Verhoeven, G. S., Dienwiebel, M., and Frenken, J. W. M. (2004). Model Calculations of Superlubricity of Graphite. Phys. Rev. B 70, 165418. doi:10.1103/physrevb.70.165418

CrossRef Full Text | Google Scholar

Wang, J., Cao, W., Song, Y., Qu, C., Zheng, Q., and Ma, M. (2019). Generalized Scaling Law of Structural Superlubricity. Nano Lett. 19, 7735–7741. doi:10.1021/acs.nanolett.9b02656

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, K., Qu, C., Wang, J., Ouyang, W., Ma, M., and Zheng, Q. (2019). Strain Engineering Modulates Graphene Interlayer Friction by Moiré Pattern Evolution. ACS Appl. Mater. Inter. 11, 36169–36176. doi:10.1021/acsami.9b09259

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W., Shen, J., and He, Q. C. (2019). Microscale Superlubricity of Graphite under Various Twist Angles. Phys. Rev. B 99, 054103. doi:10.1103/physrevb.99.054103

CrossRef Full Text | Google Scholar

Wang, X. H., Wang, D. W., Yang, A. J., Koratkar, N., Chu, J. F., Lv, P. L., et al. (2018). Effects of Adatom and Gas Molecule Adsorption on the Physical Properties of Tellurene: a First Principles Investigation. Phys. Chem. Chem. Phys. 20, 4058–4066. doi:10.1039/c7cp07906k

PubMed Abstract | CrossRef Full Text | Google Scholar

Washizu, H., Kajita, S., Tohyama, M., Ohmori, T., Nishino, N., Teranishi, H., et al. (2012). Mechanism of Ultra Low Friction of Multilayer Graphene Studied by Coarse-Grained Molecular Simulation. Faraday Discuss. 156, 279–291. doi:10.1039/c2fd00119e

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, C., Li, J., Chen, L., Zhang, C., Zhou, N., Qing, T., et al. (2019). Water-based Superlubricity in Vacuum. Friction 7, 192–198. doi:10.1007/s40544-018-0212-z

CrossRef Full Text | Google Scholar

Yang, G., Li, L., Lee, W. B., and Ng, M. C. (2018). Structure of Graphene and its Disorders: a Review. Sci. Tech. Adv. Mater. 19, 613–648. doi:10.1080/14686996.2018.1494493

PubMed Abstract | CrossRef Full Text | Google Scholar

Ye, Z., Tang, C., Dong, Y., and Martini, A. (2012). Role of Wrinkle Height in Friction Variation with Number of Graphene Layers. J. Appl. Phys. 112, 116102. doi:10.1063/1.4768909

CrossRef Full Text | Google Scholar

Zhang, C.-H., Ma, Z.-Z., Luo, J.-B., Lu, X.-C., and Wen, S.-Z. (2011). Superlubricity of a Mixed Aqueous Solution. Chin. Phys. Lett. 28, 056201. doi:10.1088/0256-307x/28/5/056201

CrossRef Full Text | Google Scholar

Zhang, R., Ning, Z., Zhang, Y., Zheng, Q., Chen, Q., Xie, H., et al. (2013). Superlubricity in Centimetres-Long Double-Walled Carbon Nanotubes under Ambient Conditions. Nat. Nanotech 8, 912–916. doi:10.1038/nnano.2013.217

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, X., Hamilton, M., Sawyer, W. G., and Perry, S. S. (2007). Thermally Activated Friction. Tribol Lett. 27, 113–117. doi:10.1007/s11249-007-9220-2

CrossRef Full Text | Google Scholar

Zheng, Q., Jiang, B., Liu, S., Weng, Y., Lu, L., Xue, Q., et al. (2008). Self-retracting Motion of Graphite Microflakes. Phys. Rev. Lett. 100, 067205. doi:10.1103/PhysRevLett.100.067205

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, Q., and Liu, Z. (2014). Experimental Advances in Superlubricity. Friction 2, 182–192. doi:10.1007/s40544-014-0056-0

CrossRef Full Text | Google Scholar

Zhu, Z., Cai, X., Yi, S., Chen, J., Dai, Y., Niu, C., et al. (2017). Multivalency-Driven Formation of Te-Based Monolayer Materials: A Combined First-Principles and Experimental Study. Phys. Rev. Lett. 119, 106101. doi:10.1103/physrevlett.119.106101

PubMed Abstract | CrossRef Full Text | Google Scholar

Zwörner, O., Hölscher, H., Schwarz, U. D., and Wiesendanger, R. (1998). The Velocity Dependence of Frictional Forces in point-contact Friction. Appl. Phys. A 66, S263–S267.

Google Scholar