
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mech. Eng., 28 April 2022
Sec. Thermal and Mass Transport
Volume 8 - 2022 | https://doi.org/10.3389/fmech.2022.876655
 Zheng Chang1
Zheng Chang1 Jing Ma1
Jing Ma1 Kunpeng Yuan1
Kunpeng Yuan1 Jiongzhi Zheng2
Jiongzhi Zheng2 Bin Wei3
Bin Wei3 Mohammed Al-Fahdi4
Mohammed Al-Fahdi4 Yufei Gao1
Yufei Gao1 Xiaoliang Zhang1*
Xiaoliang Zhang1* Hezhu Shao5*
Hezhu Shao5* Ming Hu4*
Ming Hu4* Dawei Tang1*
Dawei Tang1*The Mg3Sb2−xBix family has emerged as the potential candidates for thermoelectric applications due to their ultra-low lattice thermal conductivity (
The term Zintl phase was firstly proposed by F. Laves (Kauzlarich et al., 2007; Kauzlarich et al., 2016), as a German scientist, indicating a collection of materials within the general class of intermetallics, and the compounds can be understood by a formal electron transfer from a positively-charged metal to a negatively-charged element. In particular, the rich chemistry and evolution of structural complexity of Zintl phase compounds become a series of promising thermoelectric (TE) materials because of their “phonon-glass electron-crystal (PGEC)” (Shuai et al., 2017; Rowe, 2018) structures. The ideal concept presents that a high-performance TE material should have an excellent electrical conductivity of crystals, but also have a higher phonon-scattering rate like glass, where the cation region act as “phonon-glass” and the anion region play as “electron crystal” to alter phonon thermal and electrical transport properties. More interestingly, the structural complexity of Zintl phase compounds is mainly manifested in the diversity of anionic frameworks composed of internal covalent bonds, and the anionic framework can be roughly divided into zero-dimensional (0D) cluster, one-dimensional (1D) chain, two-dimensional (2D) planar, and complex three-dimensional (3D) network structures in accordance with the spatial extension. The 0D cluster structures include Sr3AlSb3 (Zevalkink et al., 2013) and Yb14MnSb11 (Brown et al., 2006), and Yb14MnSb11 in the high temperature region can reach 1, in which the maximum Seebeck coefficient of Sr3AlSb3 is 500 μV K−1 in the medium temperature region. Herein, the figure of merit defined as
Recently, the Mg3Sb2−xBix compounds have become one of the most widely studied TE materials owing to their abundant and inexpensive constituent elements. Experimental measurements and theoretical calculations suggested that the
In this work, we performed the first-principles calculations combining with the BTE and the EPA approximation (as a more predictive approach than the deformation potential approximation method) (Samsonidze and Kozinsky, 2018) to systematically calculate and detailedly analyze the phonon thermal and TE transport properties of 2D Mg3Sb2−xBix within a wide range of temperature. It is found that, through our theoretical calculations, 2D Mg3Sb2−xBix (x = 0, 1, and 2) compounds possess an abnormal
The phonon thermal and electrical transport properties have been calculated by the plane-wave pseudopotential approach within the density functional theory (DFT) (Hohenberg and Kohn, 1964), which is employed in the Vienna Ab-initio Simulation Package (VASP) (Kresse and Furthmüller, 1996) software along with projector augmented-wave (PAW) potential (Bliichl, 1994). To ensure the good convergence of electrons and ions during structural optimizations, the plane-wave cutoff energy of the 2D Mg3Sb2−xBix compounds was set as 500 eV, and a Monkhorst-Pack k-point grid of 15 × 15 × 1 was used to ensure accurate calculation. A Hellmann-Feynman force convergence threshold of 10–4 eV A−1 was adopted, and the energy convergence threshold between the two steps was set to be 10–6 eV. To avoid the effect of the interaction between adjacent layers, 2D Mg3Sb2−xBix unit cells were added a 20 Å thickness of vacuum slab along the out-of-plane direction. We next calculated the electronic band structures using the Perdew, Burke, and Ernzerhof (PBE) functional (Perdew et al., 1996) and the hybrid Heyd–Scuseria–Ernzerhof (HSE06) functional (Paier et al., 2006), and different functionals are designed to obtain accurate band results for 2D Mg3Sb2−xBix materials. The
Herein, 2D Mg3Sb2−xBix (x = 0, 1, and 2) compounds belong to a typical hexagonal structure with the space group P3m1 (No. 156) which is made up of the cationic layer of Mg2+ and the anionic layer of [Mg2(Sb2−xBix)]2− as shown in Figure 1. It has been found that the bonds between ionic Mg2+ layers and covalent [Mg2(Sb2−xBix)]2− layers can be broken to produce a corresponding 2D materials (Gorai et al., 2016; Zhang et al., 2018). Figures 1A, B represents schematic illustration of 2D Mg3Sb2−xBix (x = 0, 1, and 2), and their calculated lattice constants within the PBE-level are 4.736 Å, 4.794 Å, and 4.843 Å, respectively, which are close to the lattice parameters for corresponding 3D Mg3Sb2 (4.573 Å) (Huang et al., 2019) and 3D Mg3Bi2 (4.666 Å) (Zhang and Iversen, 2019). Meanwhile, during the structural relaxation of 2D Mg3Sb2−xBix, we did not consider the too weak van der Waals effect, which has been reported and investigated in previous work (Zhang et al., 2018). Meanwhile, we also present the first Brillouin zone path (Γ-M-K-Γ) with high-symmetry points, named Γ (0, 0, 0), M (1/2, 0, 0), and K (1/3, 1/3, 0), as illustrated in Figure 1C. It is obviously seen that two cases of Mg atoms exist in the primitive cell of 2D Mg3Sb2−xBix, named by Mg1 and Mg2 (see the inset of the Figures 2B, D, F. Interestingly, between Mg and Sb atoms interactions caused by the corresponding electrical properties has been confirmed, which can occur in a Mg-Sb bonding interaction for the all Mg1 and Mg2 cases in N-type doping Mg3Sb2 (Sun et al., 2019). Therefore, it should be noted that the bonding characteristic in 2D Mg3Sb2−xBix compounds may directly determine their electronic and phononic structures and thus play a crucial role in the calculations of TE properties.
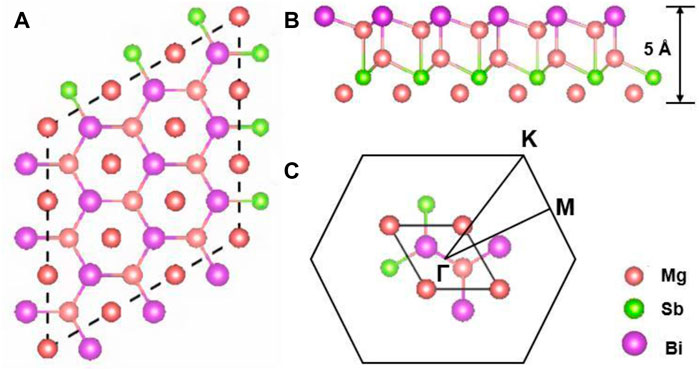
FIGURE 1. Schematic illustration of 2D Mg3Sb2−xBix in a 5 × 5 × 1 supercell: (A) top view and (B) side view; Mg, Sb ,and Bi are represented orange, green and purple, respectively. (C) The corresponding primitive cell and the first Brillouin zone path with high-symmetry points in 2D Mg3Sb2−xBix compounds.
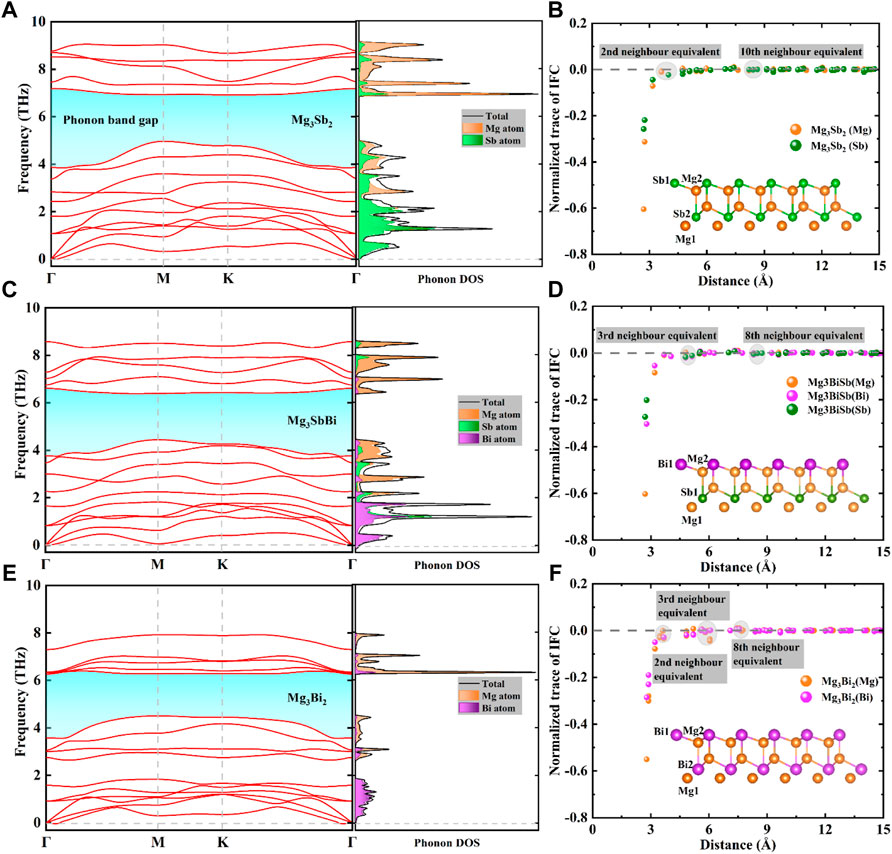
FIGURE 2. Calculated phonon dispersion curves and atom-projected density of states (DOS) for (A) 2D Mg3Sb2, (C) 2D Mg3SbBi and (E) 2D Mg3Bi2. The colored shapes highlight phonon band gaps in these compounds. Normalized trace of interatomic force constant (IFC) tensors as a function of atomic distances of (B) 2D Mg3Sb2, (D) 2D Mg3SbBi and (F) 2D Mg3Bi2, respectively.
The 2D Mg3Sb2−xBix family has five atoms in the primitive cell, and the corresponding phonon dispersion curves and phonon harmonicity results are depicted in Figure 2. We found that the above compounds have not imaginary vibrational frequency in the phonon dispersion curves, indicating the dynamic stability of the 2D Mg3Sb2−xBix compounds in this study (Chang et al., 2021). Meanwhile, it can be seen from Figure 2 that the mixing of acoustic phonons and low-frequency optical phonons exist a stronger phonon scattering processes, which indicates a lower
Figures 2B, D, F show the presence of long-ranged interaction among these compounds, and to further compare and analyze the IFCs between Mg atom and Sb/Bi atoms, traces of IFC tensors are normalized by the trace values of the self-interacting IFC tensor in the above compounds. For instance, second-nearest neighbours, separated by ∼4 Å (including Mg1-Sb1, Mg1-Sb2, and Mg1-Mg2, etc.,), have interactions that are comparable to those of tenth-nearest neighbours, spaced ∼9 Å apart, and much weaker than first-neighbours interactions in Figure 2B. Clearly, there are very similar phenomenon for normalized trace of IFC in 2D Mg3SbBi and Mg3Bi2 structures, excepting for the reduced distances at same nearest neighbours cases by the increased Bi content. Herein, we calculate the IFC tensor on the basis of first-principles calculations as follow (Lee et al., 2014; Li et al., 2020a; Li et al., 2020b):
where
Finally, the normalization is calculated by the trace value of self-interaction force constants:
In addition, to describe accurately the related IFCs in the calculation of
Based on the more accurate second- and third-order IFCs from the normalized trace of IFC data, we firstly calculate the
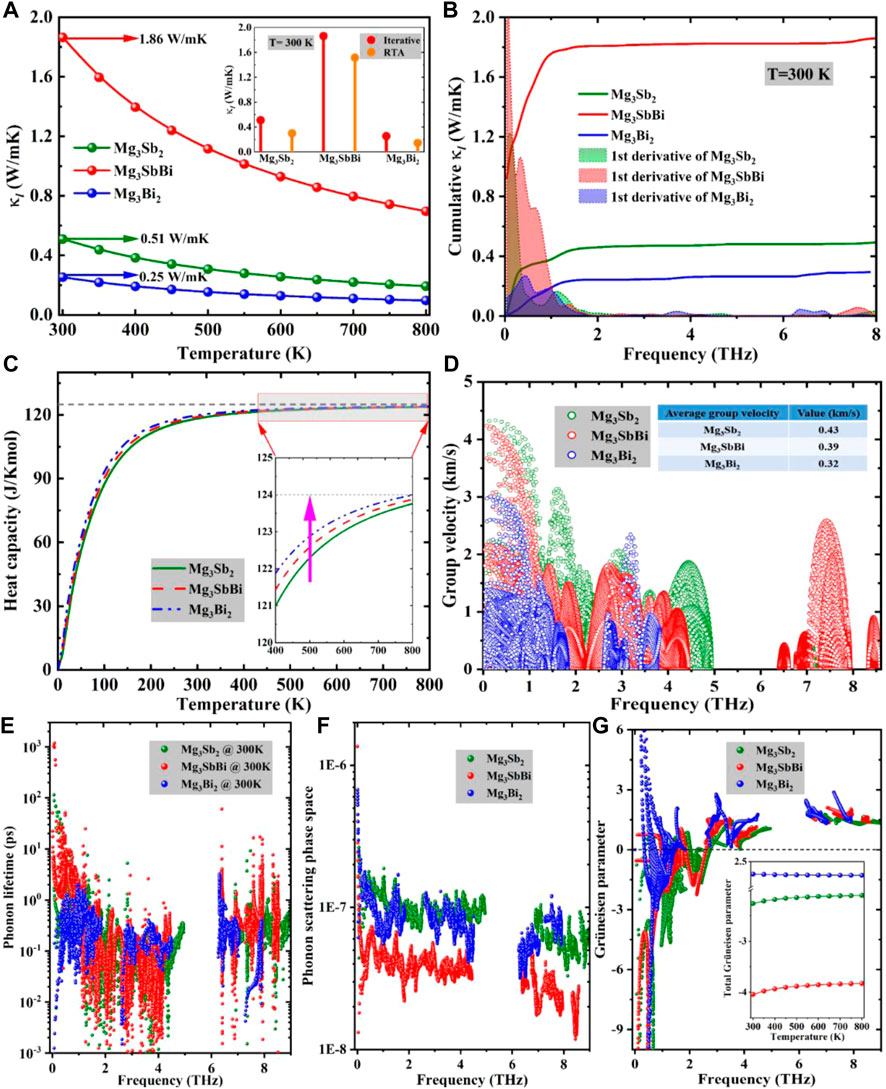
FIGURE 3. (A) Calculated
Obviously, with the increase of cumulative
Interestingly, none of the Cv and the vg can explain the relatively higher
where
It is well known that the superior TE performance in a material results from an intrinsic ultra-low
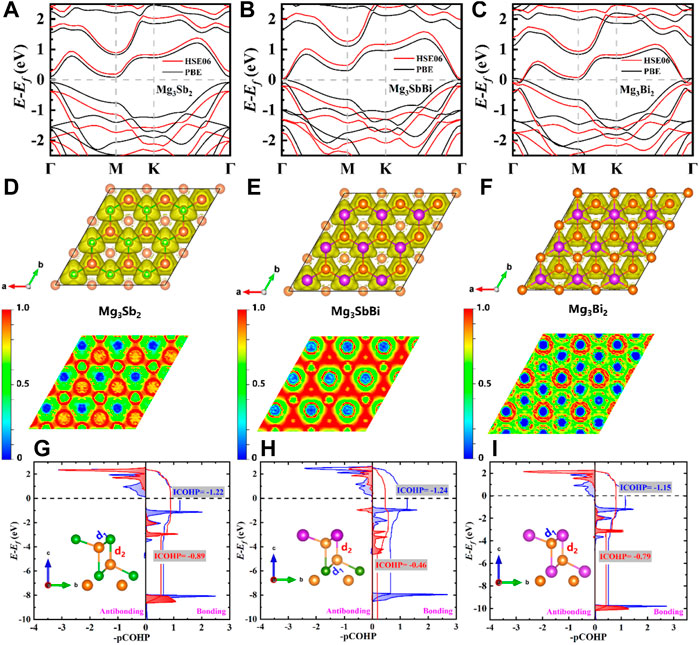
FIGURE 4. Calculated electronic band structures of (A) 2D Mg3Sb2, (B) 2D Mg3SbBi, and (C) 2D Mg3Bi2 by using HSE06 (solid red lines) and PBE function potentials (solid black lines), and the Fermi-level (Ef) is set to 0 eV. Top view (upper) and the corresponding slice projection along (001) plane (down) of 2D Mg3Sb2−xBix electron localization function (ELF) for (D) 2D Mg3Sb2, (E) 2D Mg3SbBi, and (F) 2D Mg3Bi2, respectively. Calculated the projected Crystal Orbital Hamilton Population (pCOHP) curves of 2D Mg3Sb2−xBix pairwise interactions (including d1 and d2) versus energy for (G) 2D Mg3Sb2, (H) 2D Mg3SbBi, and (I) 2D Mg3Bi2. Herein, the bond behind mechanism of both d1 and d2 was investigated and studied by the standalone computer program Local Orbital Basis Suite towards Electronic-Structure Reconstruction (LOBSTER) program (Maintz et al., 2016).
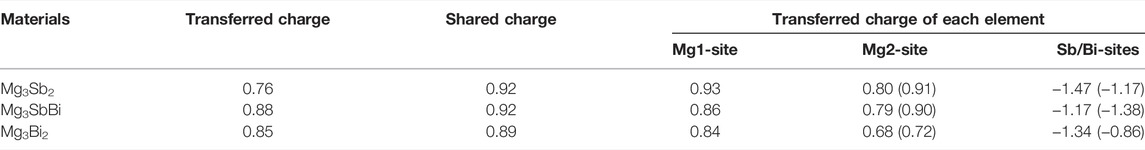
TABLE 1. Comparison of transferred and shared charges (
Usually, the several approaches, including the constant relaxation time approximation (Singh and Mazin, 1997; Madsen, 2006; Madsen and Singh, 2006; Yang et al., 2008), the deformation potential approximation (Sjakste et al., 2006; Murphy-Armando et al., 2010; Wang et al., 2011), and Wannier interpolation (Giustino et al., 2007; Bernardi et al., 2014; Qiu et al., 2015), can directly determine the electronic transport coefficients by solving the BTE theory. Herein, we used the EPA method to compute the corresponding parameters (
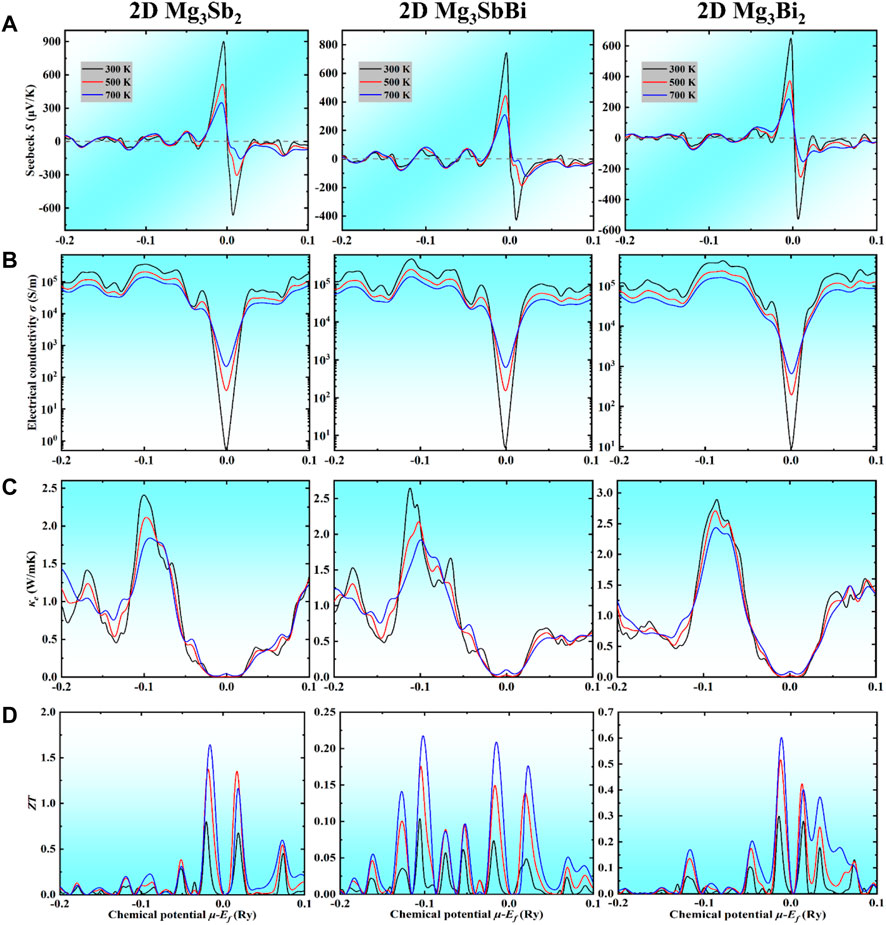
FIGURE 5. Calculated TE transport coefficients for the 2D Mg3Sb2−xBix family as a function of chemical potential (μ) shifted with respect to the Ef at 300 K, 500 K, and 700 K, respectively. (A) Seebeck coefficient, (B) electrical conductivity, (C) electronic thermal conductivity, and (D) the corresponding ZT. Herein, the negative and positive (μ−Ef) represent the corresponding P-type and N-type samples doped, respectively.
It is well known that the trends of
In summary, we have systematically investigated the TE transport properties of the family of Mg3Sb2−xBix (x = 0, 1, and 2) monolayers. Our results present that the three typical materials possess extremely lower lattice thermal conductivities, including 2D Mg3Sb2 (∼0.51 W/mK), 2D Mg3SbBi (∼1.86 W/mK), and 2D Mg3Bi2 (∼0.25 W/mK) at 300 K, respectively, while a heavier atomic mass in a compound usually possesses a lower
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
ZC, JM, KY, XZ, and DT designed research. ZC: Conceptualization, Software, Formal analysis, Writing—original draft and editing, Data curation. KY, MA-F, and MH: Formal analysis, Writing—review and editing. JZ, YG, and HS performed the part calculations. All authors analyzed data and discussed results.
This work was supported by the National Natural Science Foundation of China [Grant Nos 51720105007, 52076031, 11602149, 51806031, 52176166) and the Fundamental Research Funds for the Central Universities [DUT19RC(3)006], and the computing resources from the Supercomputer Center of Dalian University of Technology. Research reported in this publication was supported in part by the U.S. National Science Foundation (Award Number 1905775, 2030128).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2022.876655/full#supplementary-material
Bernardi, M., Vigil-Fowler, D., Lischner, J., Neaton, J. B., and Louie, S. G. (2014). Ab InitioStudy of Hot Carriers in the First Picosecond after Sunlight Absorption in Silicon. Phys. Rev. Lett. 112, 257402. doi:10.1103/physrevlett.112.257402
Biele, R., and D'agosta, R. (2022). Transport Coefficients of Layered TiS 3. Phys. Rev. Mater. 6, 014004. doi:10.1103/physrevmaterials.6.014004
Brown, S. R., Kauzlarich, S. M., Gascoin, F., and Snyder, G. J. (2006). Yb14MnSb11: New High Efficiency Thermoelectric Material for Power Generation. Chem. Mater. 18, 1873–1877. doi:10.1021/cm060261t
Chang, C., Wu, M., He, D., Pei, Y., Wu, C.-F., Wu, X., et al. (2018). 3D Charge and 2D Phonon Transports Leading to High Out-Of-Plane ZT in N-type SnSe Crystals. Science 360, 778–783. doi:10.1126/science.aaq1479
Chang, Z., Yuan, K., Sun, Z., Zhang, X., Gao, Y., Qin, G., et al. (2021). Ultralow Lattice thermal Conductivity and Dramatically Enhanced Thermoelectric Properties of Monolayer InSe Induced by an External Electric Field. Phys. Chem. Chem. Phys. 23, 13633–13646. doi:10.1039/d1cp01510a
Chen, X., Wu, H., Cui, J., Xiao, Y., Zhang, Y., He, J., et al. (2018). Extraordinary Thermoelectric Performance in N-type Manganese Doped Mg3Sb2 Zintl: High Band Degeneracy, Tuned Carrier Scattering Mechanism and Hierarchical Microstructure. Nano Energy 52, 246–255. doi:10.1016/j.nanoen.2018.07.059
Fitzgerel, R. K., and Verhoek, F. H. (1960). The Law of Dulong and Petit. . Chem. Educ. 37 (10), 545–549. doi:10.1021/ed037p545
Giustino, F., Cohen, M. L., and Louie, S. G. (2007). Electron-phonon Interaction Using Wannier Functions. Phys. Rev. B 76, 165108. doi:10.1103/physrevb.76.165108
Gorai, P., Toberer, E. S., and Stevanović, V. (2016). Computational Identification of Promising Thermoelectric Materials Among Known quasi-2D Binary Compounds. J. Mater. Chem. A. 4, 11110–11116. doi:10.1039/c6ta04121c
He, H., Stearrett, R., Nowak, E. R., and Bobev, S. (2010). Baga2Pn2 (Pn = P, as): New Semiconducting Phosphides and Arsenides with Layered Structures. Inorg. Chem. 49, 7935–7940. doi:10.1021/ic100940b
Hicks, L. D., and Dresselhaus, M. S. (1993). Effect of Quantum-Well Structures on the Thermoelectric Figure of merit. Phys. Rev. B 47, 12727–12731. doi:10.1103/physrevb.47.12727
Hohenberg, P., and Kohn, W. (1964). Inhomogeneous Electron Gas. Phys. Rev. 136, B864–B871. doi:10.1103/physrev.136.b864
Huang, S., Wang, Z., Xiong, R., Yu, H., and Shi, J. (2019). Significant Enhancement in Thermoelectric Performance of Mg3Sb2 from Bulk to Two-Dimensional Mono Layer. Nano Energy 62, 212–219. doi:10.1016/j.nanoen.2019.05.028
Imasato, K., Kang, S. D., Ohno, S., and Snyder, G. J. (2018). Band Engineering in Mg3Sb2 by Alloying with Mg3Bi2 for Enhanced Thermoelectric Performance. Mater. Horiz. 5, 59–64. doi:10.1039/c7mh00865a
Kauzlarich, S. M., Brown, S. R., and Jeffrey Snyder, G. (2007). Zintl Phases for Thermoelectric Devices. Dalton Trans., 2099–2107. doi:10.1039/b702266b
Kauzlarich, S. M., Zevalkink, A., Toberer, E., and Snyder, G. J. (2016). Zintl Phases: Recent Developments in Thermoelectrics and Future Outlook.
Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54, 11169–11186. doi:10.1103/physrevb.54.11169
Lee, S., Esfarjani, K., Luo, T., Zhou, J., Tian, Z., and Chen, G. (2014). Resonant Bonding Leads to Low Lattice thermal Conductivity. Nat. Commun. 5, 3525–3528. doi:10.1038/ncomms4525
Li, J., Liu, P.-F., Zhang, C., Shi, X., Jiang, S., Chen, W., et al. (2020a). Lattice Vibrational Modes and Phonon thermal Conductivity of Single-Layer GaGeTe. J. Materiomics 6, 723–728. doi:10.1016/j.jmat.2020.04.005
Li, J., Yang, J., Shi, B., Zhai, W., Zhang, C., Yan, Y., et al. (2020b). Ternary Multicomponent Ba/Mg/Si Compounds with Inherent Bonding Hierarchy and Rattling Ba Atoms toward Low Lattice thermal Conductivity. Phys. Chem. Chem. Phys. 22, 18556–18561. doi:10.1039/d0cp02792h
Li, W., Carrete, J., A. Katcho, N. N., and Mingo, N. (2014). ShengBTE: A Solver of the Boltzmann Transport Equation for Phonons. Comp. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015
Li, W., and Mingo, N. (2014). Lattice Dynamics and thermal Conductivity of Skutterudites CoSb 3 and IrSb 3 from First Principles: Why IrSb 3 Is a Better thermal Conductor Than CoSb 3. Phys. Rev. B 90, 094302. doi:10.1103/physrevb.90.094302
Lindsay, L., and Broido, D. A. (2008). Three-phonon Phase Space and Lattice thermal Conductivity in Semiconductors. J. Phys. Condens. Matter 20, 165209. doi:10.1088/0953-8984/20/16/165209
Liu, Z.-Y., Zhu, J.-L., Tong, X., Niu, S., and Zhao, W.-Y. (2020). A Review of CoSb 3-based Skutterudite Thermoelectric Materials. J. Adv. Ceramics, 1–27. doi:10.1007/s40145-020-0407-4
Madsen, G. K. H. (2006). Automated Search for New Thermoelectric Materials: the Case of LiZnSb. J. Am. Chem. Soc. 128, 12140–12146. doi:10.1021/ja062526a
Madsen, G. K. H., and Singh, D. J. (2006). BoltzTraP. A Code for Calculating Band-Structure Dependent Quantities. Comp. Phys. Commun. 175, 67–71. doi:10.1016/j.cpc.2006.03.007
Maintz, S., Deringer, V. L., Tchougréeff, A. L., and Dronskowski, R. (2016). LOBSTER: A Tool to Extract Chemical Bonding from Plane‐wave Based DFT. Wiley Online Library.
Manz, T. A., and Limas, N. G. (2016). Introducing DDEC6 Atomic Population Analysis: Part 1. Charge Partitioning Theory and Methodology. RSC Adv. 6, 47771–47801. doi:10.1039/c6ra04656h
Murphy-Armando, F., Fagas, G., and Greer, J. C. (2010). Deformation Potentials and Electron−Phonon Coupling in Silicon Nanowires. Nano Lett. 10, 869–873. doi:10.1021/nl9034384
Nam, H. N., Suzuki, K., Nguyen, T. Q., Masago, A., Shinya, H., Fukushima, T., et al. (2021). Low-temperature Acanthite-like Phase of Cu $ _ {2} $ S: A First-Principles Study on Electronic and Transport Properties. arXiv preprint arXiv:2110.09117.
Ohno, S., Imasato, K., Anand, S., Tamaki, H., Kang, S. D., Gorai, P., et al. (2018). Phase Boundary Mapping to Obtain N-type Mg3Sb2-Based Thermoelectrics. Joule 2, 141–154. doi:10.1016/j.joule.2017.11.005
Okubo, K., and Tamura, S.-I. (1983). Two-phonon Density of States and Anharmonic Decay of Large-Wave-Vector LA Phonons. Phys. Rev. B 28, 4847–4850. doi:10.1103/physrevb.28.4847
Paier, J., Marsman, M., Hummer, K., Kresse, G., Gerber, I. C., and Ángyán, J. G. (2006). Screened Hybrid Density Functionals Applied to Solids. J. Chem. Phys. 124, 154709. doi:10.1063/1.2187006
Peng, B., Zhang, H., Shao, H., Xu, Y., Zhang, X., and Zhu, H. (2016). Low Lattice thermal Conductivity of Stanene. Sci. Rep. 6 (1), 1–10. doi:10.1038/srep20225
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865
Poudel, B., Hao, Q., Ma, Y., Lan, Y., Minnich, A., Yu, B., et al. (2008). High-thermoelectric Performance of Nanostructured Bismuth Antimony telluride Bulk Alloys. Science 320, 634–638. doi:10.1126/science.1156446
Qiu, B., Tian, Z., Vallabhaneni, A., Liao, B., Mendoza, J. M., Restrepo, O. D., et al. (2015). First-principles Simulation of Electron Mean-Free-Path Spectra and Thermoelectric Properties in Silicon. Epl 109, 57006. doi:10.1209/0295-5075/109/57006
Samsonidze, G., and Kozinsky, B. (2018). Accelerated Screening of Thermoelectric Materials by First‐Principles Computations of Electron-Phonon Scattering. Adv. Energ. Mater. 8, 1800246. doi:10.1002/aenm.201800246
Shi, X., Wang, X., Li, W., and Pei, Y. (2018). Advances in Thermoelectric Mg3Sb2and its Derivatives. Small Methods 2, 1800022. doi:10.1002/smtd.201800022
Shi, X., Zhang, W., Chen, L. D., and Yang, J. (2005). Filling Fraction Limit for Intrinsic Voids in Crystals: Doping in Skutterudites. Phys. Rev. Lett. 95, 185503. doi:10.1103/physrevlett.95.185503
Shu, R., Zhou, Y., Wang, Q., Han, Z., Zhu, Y., Liu, Y., et al. (2019). Mg3+ δ Sb X Bi2− X Family: A Promising Substitute for the State-Of-The-Art N-type Thermoelectric Materials Near Room Temperature. Adv. Funct. Mater. 29, 1807235. doi:10.1002/adfm.201807235
Shuai, J., Mao, J., Song, S., Zhang, Q., Chen, G., and Ren, Z. (2017). Recent Progress and Future Challenges on Thermoelectric Zintl Materials. Mater. Today Phys. 1, 74–95. doi:10.1016/j.mtphys.2017.06.003
Silvi, B., and Savin, A. (1994). Classification of Chemical Bonds Based on Topological Analysis of Electron Localization Functions. Nature 371, 683–686. doi:10.1038/371683a0
Singh, D. J., and Mazin, I. I. (1997). Calculated Thermoelectric Properties of La-Filled Skutterudites. Phys. Rev. B 56, R1650–R1653. doi:10.1103/physrevb.56.r1650
Sjakste, J., Tyuterev, V., and Vast, N. (2006). Ab Initiostudy ofΓ−Xintervalley Scattering in GaAs under Pressure. Phys. Rev. B 74, 235216. doi:10.1103/physrevb.74.235216
Sun, X., Li, X., Yang, J., Xi, J., Nelson, R., Ertural, C., et al. (2019). Achieving Band Convergence by Tuning the Bonding Ionicity in N‐type Mg 3 Sb 2. J. Comput. Chem. 40, 1693–1700. doi:10.1002/jcc.25822
Wang, F. Q., Zhang, S., Yu, J., and Wang, Q. (2015). Thermoelectric Properties of Single-Layered SnSe Sheet. Nanoscale 7, 15962–15970. doi:10.1039/c5nr03813h
Wang, J., Xia, S.-Q., and Tao, X.-T. (2012). A5Sn2As6 (A = Sr, Eu). Synthesis, Crystal and Electronic Structure, and Thermoelectric Properties. Inorg. Chem. 51, 5771–5778. doi:10.1021/ic300308w
Wang, Z., Wang, S., Obukhov, S., Vast, N., Sjakste, J., Tyuterev, V., et al. (2011). Thermoelectric Transport Properties of Silicon: Toward Anab Initioapproach. Phys. Rev. B 83, 205208. doi:10.1103/physrevb.83.205208
Wood, M., Imasato, K., Anand, S., Yang, J., and Snyder, G. J. (2020). The Importance of the Mg-Mg Interaction in Mg3Sb2-Mg3Bi2 Shown through Cation Site Alloying. J. Mater. Chem. A. 8, 2033–2038. doi:10.1039/c9ta11328b
Wu, Y., Ma, C., Chen, Y., Mortazavi, B., Lu, Z., Zhang, X., et al. (2020). New Group V Graphyne: Two-Dimensional Direct Semiconductors with Remarkable Carrier Mobilities, Thermoelectric Performance, and thermal Stability. Mater. Today Phys. 12, 100164. doi:10.1016/j.mtphys.2019.100164
Xia, S.-Q., and Bobev, S. (2007). Cation−Anion Interactions as Structure Directing Factors: Structure and Bonding of Ca2CdSb2 and Yb2CdSb2. J. Am. Chem. Soc. 129, 4049–4057. doi:10.1021/ja069261k
Xin, J., Li, G., Auffermann, G., Borrmann, H., Schnelle, W., Gooth, J., et al. (2018). Growth and Transport Properties of Mg3X2 (X = Sb, Bi) Single Crystals. Mater. Today Phys. 7, 61–68. doi:10.1016/j.mtphys.2018.11.004
Yang, J., Li, H., Wu, T., Zhang, W., Chen, L., and Yang, J. (2008). Evaluation of Half-Heusler Compounds as Thermoelectric Materials Based on the Calculated Electrical Transport Properties. Adv. Funct. Mater. 18, 2880–2888. doi:10.1002/adfm.200701369
Yang, Z., Yuan, K., Meng, J., Zhang, X., Tang, D., and Hu, M. (2020). Why thermal Conductivity of CaO Is Lower Than that of CaS: a Study from the Perspective of Phonon Splitting of Optical Mode. Nanotechnology 32, 025709. doi:10.1088/1361-6528/abbb4c
Yue, S.-Y., Qin, G., Zhang, X., Sheng, X., Su, G., and Hu, M. (2017). Thermal Transport in Novel Carbon Allotropes with S P 2 or S P 3 Hybridization: An Ab Initio Study. Phys. Rev. B 95, 085207. doi:10.1103/physrevb.95.085207
Zeng, J., He, X., Liang, S.-J., Liu, E., Sun, Y., Pan, C., et al. (2018). Experimental Identification of Critical Condition for Drastically Enhancing Thermoelectric Power Factor of Two-Dimensional Layered Materials. Nano Lett. 18, 7538–7545. doi:10.1021/acs.nanolett.8b03026
Zevalkink, A., Pomrehn, G., Takagiwa, Y., Swallow, J., and Snyder, G. J. (2013). Thermoelectric Properties and Electronic Structure of the Zintl-phase Sr3AlSb3. ChemSusChem 6, 2316–2321. doi:10.1002/cssc.201300518
Zevalkink, A., Zeier, W. G., Pomrehn, G., Schechtel, E., Tremel, W., and Snyder, G. J. (2012). Thermoelectric Properties of Sr3GaSb3 - a Chain-Forming Zintl Compound. Energy Environ. Sci. 5, 9121–9128. doi:10.1039/c2ee22378c
Zhang, J., Song, L., Sist, M., Tolborg, K., and Iversen, B. B. (2018). Chemical Bonding Origin of the Unexpected Isotropic Physical Properties in Thermoelectric Mg3Sb2 and Related Materials. Nat. Commun. 9 (1), 1–10. doi:10.1038/s41467-018-06980-x
Zhang, J., and Iversen, B. B. (2019). Fermi Surface Complexity, Effective Mass, and Conduction Band Alignment in N-type Thermoelectric Mg3Sb2 - xBix from First Principles Calculations. J. Appl. Phys. 126, 085104. doi:10.1063/1.5107484
Zhang, J., Song, L., and Iversen, B. B. (2019). Insights into the Design of Thermoelectric Mg3Sb2 and its Analogs by Combining Theory and experiment. npj Comput. Mater. 5, 1–17. doi:10.1038/s41524-019-0215-y
Zhang, X., and Zhao, L.-D. (2015). Thermoelectric Materials: Energy Conversion between Heat and Electricity. J. Materiomics 1, 92–105. doi:10.1016/j.jmat.2015.01.001
Zhao, L.-D., Lo, S.-H., Zhang, Y., Sun, H., Tan, G., Uher, C., et al. (2014). Ultralow thermal Conductivity and High Thermoelectric Figure of merit in SnSe Crystals. Nature 508, 373–377. doi:10.1038/nature13184
Keywords: two-dimensional zintl phase compounds, phonon thermal transport, thermoelectric performance, electron-phonon averaged approximation, Boltzmann transport equation
Citation: Chang Z, Ma J, Yuan K, Zheng J, Wei B, Al-Fahdi M, Gao Y, Zhang X, Shao H, Hu M and Tang D (2022) Zintl Phase Compounds Mg3Sb2−xBix (x = 0, 1, and 2) Monolayers: Electronic, Phonon and Thermoelectric Properties From ab Initio Calculations. Front. Mech. Eng 8:876655. doi: 10.3389/fmech.2022.876655
Received: 15 February 2022; Accepted: 22 March 2022;
Published: 28 April 2022.
Edited by:
Yaguo Wang, University of Texas at Austin, United StatesReviewed by:
Shangchao Lin, Shanghai Jiao Tong University, ChinaCopyright © 2022 Chang, Ma, Yuan, Zheng, Wei, Al-Fahdi, Gao, Zhang, Shao, Hu and Tang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaoliang Zhang, emhhbmd4aWFvbGlhbmdAZGx1dC5lZHUuY24=; Hezhu Shao, aHpzaGFvQHd6dS5lZHUuY24=; Ming Hu, aHVAc2MuZWR1; Dawei Tang, ZHd0YW5nQGRsdXQuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.