- Nantes Université, Ecole Centrale Nantes, CNRS, GeM, UMR 6183, F‐44000 Nantes, France
Within the context of immiscible biphasic flow in porous media, when the nonwetting fluid invades the pore spaces which are a priori saturated with the wetting fluid, capillary forces dominate if the pore network is formed by fine-grained soils. Owing to the cohesion-less frictional behavior of such soils, a capillary force–driven fracturing phenomenon has been put forward by some researchers. Unlike the purely mechanistic tensile force–driven mode-I fracturing that typically has been attributed to the formation of desiccation cracks in soils, attempts to model this alternate capillarity-driven mechanism have not yet been realized at a continuum scale. However, the macro-scale counterpart of the capillary energy associated with the various pore-scale menisci is well-established as the interfacial energy characterized by the soil-water retention curve. An investigation of the possible contribution of this interfacial energy in supplying the dissipation related to fracture initiation is the essence of this work, inspired by the vast literature on gradient damage modeling.
1 Introduction
How can mode-I fractures initiate on the surface of saturated granular geomaterials which are under compressive effective stress states when subjected to forced drainage or drying boundary conditions? This question has been intriguing some researchers for the last decade especially in the light of the prevailing assessment that in homogeneous desiccating soils, macroscopic surface cracks can appear only in the presence of tensile stresses induced by zero displacement boundary conditions or by moisture gradients through the thickness of the sample capable of inducing nontrivial stress concentration, see for example Peron et al. (2009); Cordero et al. (2021). Indeed, following Shin and Santamarina (2010, 2011), a different mechanism can be invoked to explain opening-like fractures appearing at the drained/drying surface of uncemented granular materials, which is compatible with their fundamental behavior to exhibit a cohesive state only under compressive effective stresses. In this case, fracturing is hypothesized to be caused by the forced invasion of the pore network by either immiscible or miscible fluids. In the study by Shin and Santamarina (2010) water-saturated slurry of clay in a cylindrical chamber was subjected to pressure by a superposed immiscible nonwetting fluid (oil). This is a scenario which unambiguously generates compressive effective stresses within the confined sample with the ratio of horizontal to vertical effective stresses less than 1, which is typical of granular media. Drainage was initiated by opening a port below the sample. Following an initial settlement of the sediment, mode-I fracture initiation was observed at sub-millimeter defects on the invasion surface, and these fractures propagated vertically downward and laterally within a plane normal to the minor principal effective stress. This definitely cannot be explained through a tensile stress–driven mechanism. In Shin and Santamarina (2010, 2011), it has been hypothesized that such fracture initiation and the initiation of pattern-forming surface fractures typical to desiccating soils are due to capillary pressure overwhelming the maximum pressure that a granular material can resist before a new fluid–fluid interface is formed. In a more recent publication, Cordero et al. (2017), the effects of suction and compressibility of the overall granular material on desiccation fracture formation have been discussed. A similar configuration has also been investigated using the Discrete Element Method by Jain and Juanes (2009); in this case, however, a local condition for fracture opening has been identified, on the basis of classical fracture mechanics, requiring the gas pressure to exceed the minimum compressive stress.
Looking at the macroscopic modeling of such behavior of granular geomaterials, few contributions can be retrieved from the literature assuming brittle fracture to be allowed under tensile stresses and shear stresses. We refer among others to Peron et al. (2013) and to those approaches that even model the fracture nucleation/propagation, for instance, the phase-field approaches proposed by Choo and Sun (2018); Cajuhi et al. (2018) and references therein. However, these approaches are not adapted to model the triggering of opening-like fractures under purely compressive effective stresses on the surface of saturated granular materials when subjected to forced drainage or drying boundary conditions. This is the reason why a new phase-field model is proposed here, which assumes the micro-scale grain reorganization to not affect the macroscopic stiffness of the material but its retention properties, hence allowing for the characterization of a damage criterion comparing a given threshold with the released capillary energy rather than with the elastic one. On the other hand, it is to be noted that rock-like geomaterials are known (Zhou, 2005, 2006; Zhou et al., 2008; Spetz et al., 2021) to exhibit, under overall compressive loading, a dilatation of pre-existing defects leading to their further opening-mode propagation. However, the current work is neither intended to describe such materials/geometry nor such loading scenarios.
This work is organized as follows. The proposed approach is presented in Section 2. Section 3 is devoted to presenting the numerical algorithm implementing the aforementioned phase-field approach, while in Section 4, the desiccation problem is formulated and solved, discussing the stability of damage profiles and their capability to induce damage localization. Conclusions and perspectives are briefly drawn in Section 5.
2 Mathematical Model
2.1 A Damaged Porous Solid
The partially saturated porous medium is described here adopting the classical approach of continuum poromechanics as presented by Coussy (2004), to which we refer for a detailed presentation; the notation used hereafter is consistent with that of the aforementioned reference. According to this classical approach to partial saturation, a porous solid is understood as a so-called ‘wetted’ porous skeleton with a thin layer of fluid attached to the pore walls, and thus a contribution to the stored energy of the porous solid is attributed to the fluid–fluid and solid–fluid interfaces. This interfacial energy density is obtained as the cumulative work carried out by a macroscopic capillary pressure difference between the wetting and the nonwetting fluids in modifying the relative fluid volume fractions within the pores.
Now, the formation of a fracture due to grain/pore reorganization, as hypothesized by Shin and Santamarina (2010, 2011), results in a discontinuity of the porous material. This “absence” of porous material within a fracture would mean, locally, a complete loss of retention property toward the wetting fluid and thus a loss of the ability of the porous medium to store interfacial energy. In the current study, a scalar damage variable, α, is introduced in order to describe the effects of grain/pore reorganization within the porous solid, in the regime of compressive effective stresses, as briefly discussed in the Introduction. Damage is thus assumed to induce a reduction in the air-entry pressure and in general to degrade the retention properties of the porous medium, which is equivalent to a reduction of the cumulative interfacial energy stored.
Accordingly, the degraded retention relation between the saturation degree of the wetting fluid, Sw, and the degraded macroscopic capillary pressure, pc, reads,
where a(α) is a damage law whose functional form is elaborated at a later point. pw is the pore-pressure of the wetting fluid in a degraded porous solid, and
is assumed where, αvG and n are the model parameters, g is the acceleration due to gravity, and ρw is the mass density of liquid water. It is to be noted that residual saturation is assumed to be vanishing for simplicity but its incorporation is trivial.
Also, the assumptions leading to Richards’ equation (Hilfer and Steinle, 2014) are adopted, in particular the hypothesis of a passive non-wetting phase is assumed, leading to pc ≈ −pw in Eq. 1. While the above development serves as a reasonable first assumption for investigation, a complete modeling approach should also involve the degradation of the resistance to fluid flow within the damaged zone and eventually along localized fracture planes. With the abovementioned assumptions, the transient hydraulic problem governing the evolution of pore-pressure, pw, within the porous solid is written as,
where the intrinsic permeability ϰ is assumed to be independent of α and
Appropriate boundary conditions compliment the aforementioned partial differential equation (PDE) which could be either an imposed flux representing a natural boundary condition or an imposed pressure representing a Dirichlet boundary condition.
We consider an nd-dimensional domain,
1) The scalar internal variable, α ∈ [0, 1], is assigned the role of describing the extent of damage in the sense of loss of retention properties. α = 0 denotes an intact healthy skeleton whose retention properties are described by the standard retention curve, whereas α = 1 denotes a fully damaged skeleton whose retention properties are degraded and can only hold vanishing or residual amounts of wetting fluid.
2) For a given unit volume of porous solid in its reference configuration, the bulk energy density, W, accounting for the internal energy and the dissipation due to material degradation, is a state function characterized by
3) In a similar way as the construction of the standard gradient damage model (Marigo et al., 2016) for the solid continuum, the porous solid is assumed to be dissipative in a nonlocal sense due to the dependency of the bulk energy density on the gradient of damage. The particular expression of the bulk energy density is assumed to be
The different terms of the aforementioned expression are explained below.
a) The energy density of the porous solid, Ψs(ɛ, ϕ, Sw, α), encompasses the contributions due to the deformation of the porous skeleton, resulting in solid strains and changes in porosity and, also, the interfacial energy contribution due to formation/annihilation of interfaces. Adopting the concept of energy separation (Coussy, 2004) between the free energy of the porous skeleton and the interfacial energy we obtain,
Here, a specific choice is made that would result in the aforementioned postulate that damage means the degradation of only the retention properties and not the poroelastic properties. The latter would have been the choice for modeling tensile mode fracture as carried out, for instance, by Cajuhi et al. (2018). The choice made here allows to isolate the investigation of fracture formation just due to the ‘release’ of interfacial energy. Specifically, we assume a degradation of the form,
consistent with the definition of the degraded capillary pressure in Eq. 1. In Figure 1, the two functions pc(Sw, α) and U(Sw, α) are depicted with the assumed degradation behavior.
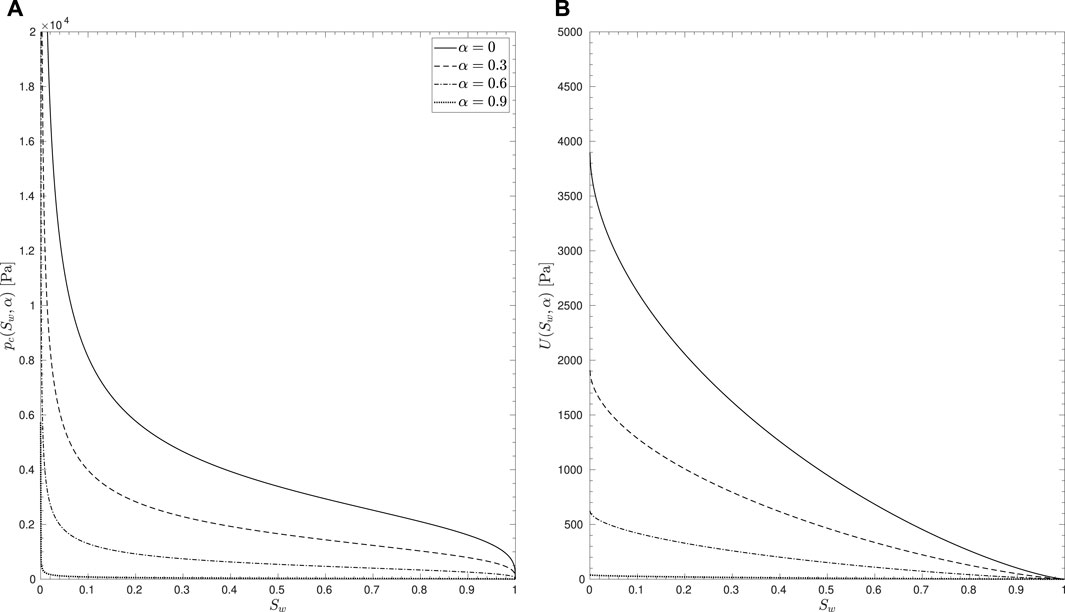
FIGURE 1. Proposed degradation of the retention properties with evolution of damage depicted for material properties taken from Table 1, (A) macroscopic capillary pressure, pc(Sw, α), in Eq. 1, (B) interfacial energy density, U(Sw, α), in Eq. 7.
While various choices of the functional form of a(α) are possible, we make a specific choice following the standard gradient damage modeling,
where kℓ is a small positive constant used solely for numerical purposes to govern the fully damaged state. Accordingly, when α grows from 0 to 1, the interfacial energy density degrades to a vanishing value. The consequence on the damage evolution due to the abovementioned choices is discussed further.
Now concerning the free energy density of the skeleton, a possible form that retrieves back the classical Biot’s linear constitutive relations as its state equations reads as,
where the notations are borrowed from Coussy (2004).
b) The second term in Eq. 5 is the local part of the dissipated energy,
growing from 0 when α = 0, to a positive constant w1 < + ∞ when α = 1. In accordance with the developments in the study by Pham et al. (2011a), since w′(α) > 0, there exists an elastic phase preceding damage initiation and the finiteness of w1 ensures that the energy dissipated during a homogeneous evolution of α from 0 to 1 is as well finite. However, w1 is not related to fracture toughness in the classical sense. Rather, it is to be viewed as related to a threshold beyond which the grains that form the skeleton start to ‘slip’ at their contacts, thus characterizing a dissipative phenomenon that accompanies the release of built-up interfacial energy and the creation of a new fluid–fluid interface.
c) The last term in Eq. 5 is the nonlocal dissipation, which is assumed to be a quadratic function of the gradient of α and is intended for regularization allowing localizations of finite thickness. ℓ appears with the physical dimension of a length that in the context of gradient damage modeling is intended to control the localization thickness.
d) The dual relations associated with the state variables in Eq. 5 are obtained as follows,
2.2 Evolution Problem
Now, we pose the evolution problem for the solution triplet (u, ϕ, α) of the poromechanical damage problem using a variational approach similar to the developments in the studies by Pham and Marigo (2010a, 2010b). The principles governing the evolution are elaborated for the current problem concerning the porous solid.
The variational approach is based on the definition of a suitable total energy of the body under consideration (i.e., the porous solid), that is associated with the triplet of admissible states
where L2(Ω) is the Lebesgue space of square-integrable functions equipped with an L2-norm and H1(Ω) is the Sobolev space of square-integrable functions whose weak gradients are also also square-integrable.
This definition of total energy at each time t is given as the integral over the whole domain of the bulk energy density minus the potential of external forces,
Since the focus here is on the porous solid, the external loading concerns not only bulk forces and tractions exerted on the solid skeleton, which in this case are assumed to vanish for the sake of simplicity, but also zeroth-order bulk actions tending to modify from inside the porosity of the solid. This time-dependent bulk action is obviously related to the presence of fluids in the porous network and is, therefore, coupled with the solution of the hydraulic problem, governed by Eq. 3. In a similar way as in the case of fully saturated porous materials, working this action of the change of Lagrangian porosity, it will coincide with the average pore-pressure,
Remark: We assume that all the fields are sufficiently smooth in time, allowing for the following developments. Also, we consider only the states of damage where α < 1 and the saturation degree Sw > 0. This is done so that in the following analysis, the total energy remains finite.
Now, we are in a position to setup the principles of the variational approach for the evolution in Ω of
1) Irreversibility of damage: t↦αt must be nondecreasing. Consequently, the admissible states accessible from αt belong to the space
2) Stability: The state (ut, ϕt, αt) must be directionally stable in the sense that for all
3) Energy balance: During the evolution t↦(ut, ϕt, αt), the following energy balance must hold,
where the classical definition of equivalent pore-pressure is adapted to the current context,
2.3 First-Order Stability and Necessary Conditions
Equilibrium equation and damage criterion can be obtained as first-order stability conditions starting from Eq. 17. In addition, since the solution now involves ϕt, an associated zeroth-order balance equation is expected to appear.
We start again by expanding the perturbed energy up to the second-order,
where for the sake of compactness of the notation, we denoted the directions
In Eq. 20, the partial derivatives of bulk energy density are functions of state (ut, ϕt, αt) given by Eq. 12.
Dividing Eq. 19 by h and passing to the limit h → 0 gives,
which is the so-called first-order stability condition and can be viewed as characterizing stationarity of the state (ut, ϕt, αt). In Eq. 23, testing with φ = ϕt and β = αt and noting that
where a stress tensor can obviously be identified as,
Similarly, testing with v = ut and β = αt in Eq. 23, one obtains the zeroth-order balance equation associated with small variations in ϕt,
Finally, using Eq. 24 and Eq. 26 in Eq. 23 gives the variational form of the non-local damage criterion
Using classical localization arguments of calculus of variations, one can obtain from Eq. 24 and Eq. 26 and Eq. 27 the following local forms, respectively, with corresponding boundary conditions,
where
Equation 29 is the local form of the zeroth-order balance law associated with variations in porosity. Rearranging it, one can identify the relation which in classical poromechanics is characterized as the constitutive relation for porosity,
Remark: The aforementioned formulation results in an equivalent equilibrium equation to be resolved in tandem with the zeroth-order balance law for variations in porosity. This can be seen by substituting Eq. 31 into the equilibrium equation, Eq. 28, giving,
In the abovementioned formula, the classical stress tensor for unsaturated poroelasticity can be identified as,
This equivalence between the formulations is exploited further for the purpose of numerical approximation.
Since we have assumed that the evolution is smooth in time, taking a time derivative of the Energy balance leads to,
Integrating by parts the gradient terms and further using the local form of the equilibrium equations Eq. 28 and the zeroth-order balance law, Eq. 29 gives,
Owing to the irreversibility of damage everywhere in Ω and the local inequalities Eq. 30, the two integrals on the right-hand side of the abovementioned equation are positive or equal to zero. So, both of them should vanish. Further using classical localization arguments, we obtain the so-called consistency conditions or the Karush–Kuhn–Tucker (KKT) conditions applicable everywhere in Ω and on the boundary ∂Ω respectively,
These conditions can be read in tandem with the Irreversibility of damage. The first condition states that everywhere in Ω, the damage increases only if the local form of the damage criterion Eq. 30 is an equality, and if it is a strict inequality, then damage does not increase. The second condition states that everywhere on the boundary ∂Ω, if damage increases then the spatial derivative normal to the boundary vanishes.
3 Numerical Approximation and Algorithm
Adopting a similar approach to that extensively used for the standard gradient damage modeling, see Bourdin et al. (2000); an alternate minimization algorithm is proposed to solve the nonconvex minimization problem of the regularized energy functional, considering that when minimized separately for u, ϕ, and α, the individual minimization problems are convex.
If one assumes an absence of damage modeling, numerical approximation of the poromechanical problem can be carried out using the finite element method and resolving in tandem the equilibrium equation, Eq. 24, and the zeroth-order balance law for variations in porosity, Eq. 29, in their variational forms subject to prescribed boundary conditions. As per the earlier remark, here, we exploit the equivalence between the aforementioned formulation and the classical equilibrium equation of unsaturated poroelasticity. Specifically, we resolve the latter for the poromechanical part of the problem. For the transient hydraulic problem, on the other hand, we resolve the mixed-head form of the governing equation for pore-water pressure, Eq. 3, with Eq. 4. In the presence of damage, which is the current context, the damage problem is resolved by the minimization of the total energy under the unilateral constraint of the irreversibility of damage.
Given the solution triplet (un−1, pn−1, αn−1) of the solid and fluid problems at time-step (n − 1), Algorithm 1 describes the alternating algorithm to obtain the solution at time-step n. Spatial discretization is carried out using linear Lagrange finite elements for approximating p, α, and quadratic elements for u. The time derivative within Eq. 3 for the hydraulic problem is discretized using the implicit Euler scheme of first-order. The coupled problem for solid displacement and fluid pressure,
where the unilateral constraint αn−1 ≤ α ≤ 1 is the time-discrete version of the irreversibility of damage. Numerically, we solve this minimization problem using a bound-constrained optimization solver routine available as part of the TAO library (Balay et al., 2021). The convergence criterion of the alternating algorithm, at each iteration i, is the comparison against a tolerance, the ℓ2-norm of the difference between the damage solutions of successive iterations,
4 Two-Dimensional Desiccation Problem
The abovementioned modeling approach is now applied to study the desiccation of soils. As already mentioned in the Introduction, this test case comes from the various desiccation experiments that can be found in the literature, Peron et al. (2009); Shin and Santamarina (2010, 2011); Stirling (2014) to name a few. Typical desiccation experiments are carried out by subjecting a certain mass of fully saturated soil to air-drying under controlled temperature and relative humidity. For numerical purposes, the flux on the drying face/s is estimated (Stirling, 2014) using the discharge rate that is calculated from experimental measurements of mass loss of water.
Furthermore, we consider a plane-strain assumption owing to the transverse dimension of the samples in all the experiments being larger than the vertical depth. This assumption does not drastically affect the aforementioned developments. Specifically, the in-plane stress components can still be obtained from the relation Eq. 33 with the definition of stiffness tensor in index notation,
λ and μ are, respectively, the first and second Lamé parameters that are related to Young’s modulus, E, and Poisson’s ratio, ν, of the empty porous skeleton. So, the boundary value problem formed by the coupled system of equations Eq. 3, Eq. 32, and the bound-constrained minimization with respect to α, Eq. 37, are resolved with appropriately defined boundary and initial conditions as laid out further in Section 4.1 and following the algorithm described in Algorithm 1. The material properties of the porous medium and the parameters of the model chosen for the purpose of the simulations are listed in Table 1, which are in the range typical of silica sands saturated with an air–water mixture.

TABLE 1. Material properties and model parameters used throughout the article unless mentioned otherwise.
During the experiments in the aforementioned literature, two stages were observed in the drying process. The first stage involves large irreversible deformations with the degree of saturation close to 1 and the second stage involves a noticeable decrease in the saturation degree and with smaller deformations. Fracture initiation usually was associated with the sample close to full saturation and the air–water interface coinciding with the apparent soil surface. In the current modeling context, damage initiation is associated with the threshold, w1, appearing within the local dissipation contribution, Eq. 11, to the bulk energy density and this, as mentioned earlier, is understood as not directly related to fracture toughness of the material but to the creation of a new fluid–fluid interface within the porous medium. Nevertheless, w1 is a parameter that depends on the material and boundary conditions. For instance, Holtzman et al. (2012) have shown experimentally that fracturing is the preferred mode of invasion of air into water-saturated granular media when the confining stress is lower. So, this threshold can only be characterized through experimental observation of fracture initiation, viewed as a localization of the damage variable within the model. For the purpose of the current investigation, various values of w1 are tested that either initiate damage or not, and in the former case, the possibility of localization is studied.
4.1 Problem Setup
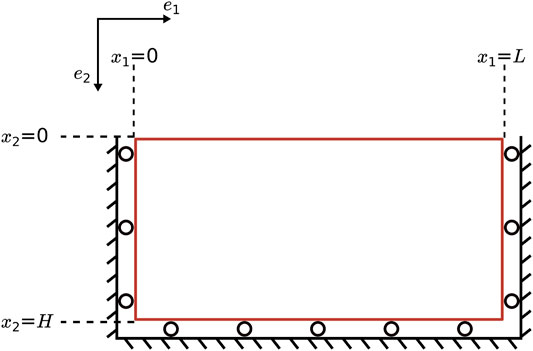
The reference initial configuration is a rectangular domain Ω = (0, L) × (0, H) as shown in the Figure 2 with the boundary ∂Ω = {(x1 = 0) ∪ (x1 = L) ∪ (x2 = 0) ∪ (x2 = H)}. At time t = 0, it is assumed that the porous solid is completely intact, stress-free, and fully saturated giving,
x ∈ Ω is the position vector given by x = x1e1 + x2e2. The horizontal and vertical displacements are set to vanish, respectively, on the lateral (x1 = 0, x1 = L) and the bottom (x2 = H) faces along with the shear stresses at those boundaries. The top face at x2 = 0 is a free surface. These set of mechanical boundary conditions ∀t ≥ 0 read,
Damage is not prescribed and is free to evolve at all the boundaries whenever the damage criterion is met. Accordingly, the natural boundary condition on damage reads,
For the hydraulic problem, the lateral and bottom faces are set to be impermeable. The loading is carried out by a constant imposed outward flux, − qfe2, on the top face, thus inducing a drying effect. While the drying flux measured using the discharge rates in Stirling (2014) is found to be a function of time, we choose to make a simplifying assumption of constant flux. These boundary conditions ∀t ≥ 0 read,
4.2 One-Dimensional Base Solutions
It can be seen from the problem setup that the geometry, material properties, and initial conditions are invariant along the x1-direction. The loading and boundary conditions on the top and bottom faces are as well-invariant along the x1-direction. The boundary conditions on the lateral faces demand vanishing gradients of the solution along the x1-direction. So, even though the problem does not render itself for obtaining an easy exact solution due to its nonlinearity, one can a priori anticipate the existence of a particular class of solutions that are homogeneous in the x1-direction and are dependent only on x2. Such solutions are termed here as base solutions. In fact, to obtain the base solutions, one just needs to solve the problem in one-dimension along the x2-direction with appropriate boundary conditions, instead of the full two-dimensional problem posed earlier. This is the purpose that is explained in this section. Rigorous mathematical proof of the existence and uniqueness of such base solutions for all times is out of the scope of the current work. Instead, we exhibit numerically these solutions for t > 0.
The domain of the one-dimensional problem is defined
In view of the damage criterion, Eq. 30, with the definition of average pore-pressure,
where Eq. 1 gives
Figures 3, 4 show the time evolution of the solution and functions of the solution, with H = 1.0m, qf = 10m.s−1, and w1 = 1000N.m−3. The material properties correspond to sand and the fluid combination to air–water. It can be seen that initially, damage does not evolve anywhere in the domain even though flux-induced desaturation initiates at x2 = 0 and progresses into the domain. During this stage of evolution, the strain remains compressive and the porosity reduces from the initial value as expected within the unsaturated zone. However, once the damage criterion becomes equality, damage initiates at x2 = 0. With damage growing from 0, the saturation degree degrades close to 0, indicating invasion of the air phase while the pore-water pressure only reduces slightly in magnitude. The paths followed by the solutions for different thresholds, w1, in the space (St, pt) are shown in Figure 5. It is clear that the path followed during the initial damage evolution is that of a ‘softening’ with respect to pore-water pressure. It is also interesting to observe that even though the drying flux at the boundary continues to drive the desaturation process, the damage stagnates at a maximum value at larger times, and this is replicated also within the domain, thus creating a zone of uniform damage. This is due to the simultaneous reduction in the magnitude of the first driving term in Eq. 43 with increasing damage so that after a certain value of damage, the criterion does not become an equality anymore, even though desaturation progresses.
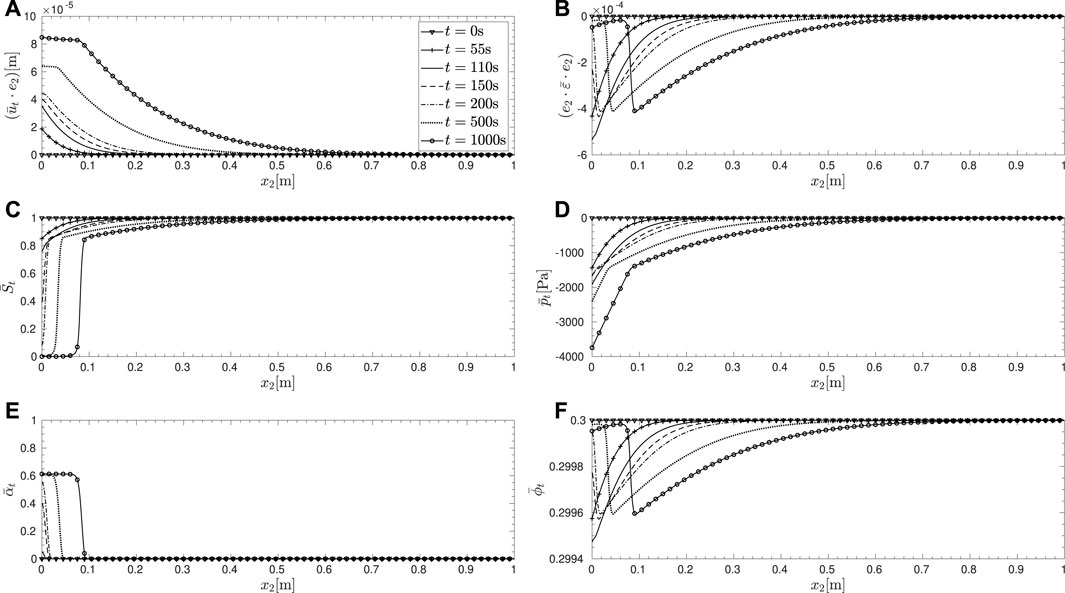
FIGURE 3. Evolution of the one-dimensional base solution and functions of the solution within the full computational domain,
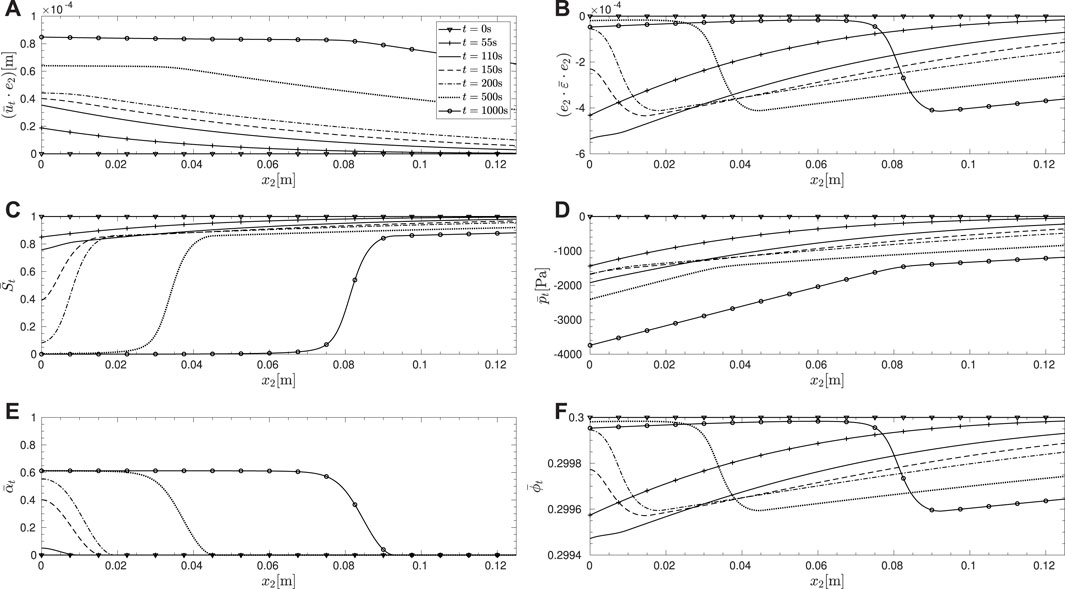
FIGURE 4. Evolution in Figure 3 shown within a restricted computational domain,
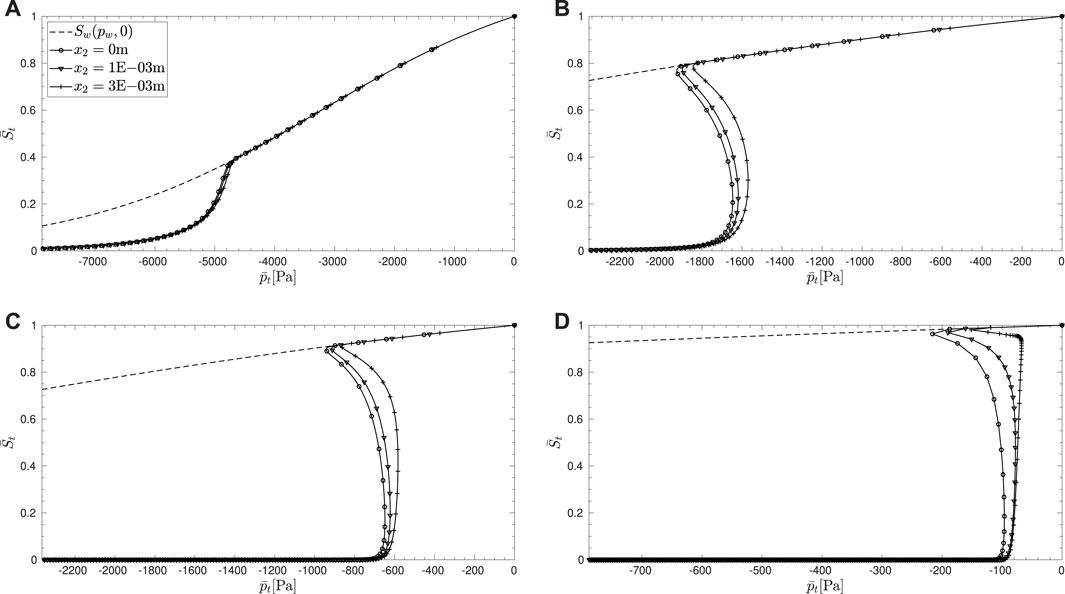
FIGURE 5. Path followed by the solution in the space (St, pt) at the boundary x2 = 0m and two locations within the domain close to this boundary for values of w1 (A) 2000 N.m−3 (B) 1000 N.m−3, (C) 500 N.m−3, and (D) 100 N.m−3. The dashed line represents the standard non-degraded retention curve.
Figure 6 shows the time evolution of damage for different thresholds, w1. In all cases, the damage initiates at x2 = 0 as anticipated and then propagates into the domain supported by a finite depth, dt, that increases with time. Lower thresholds are characterized by earlier initiation of damage and a damage value closer to 1 at the drying boundary.
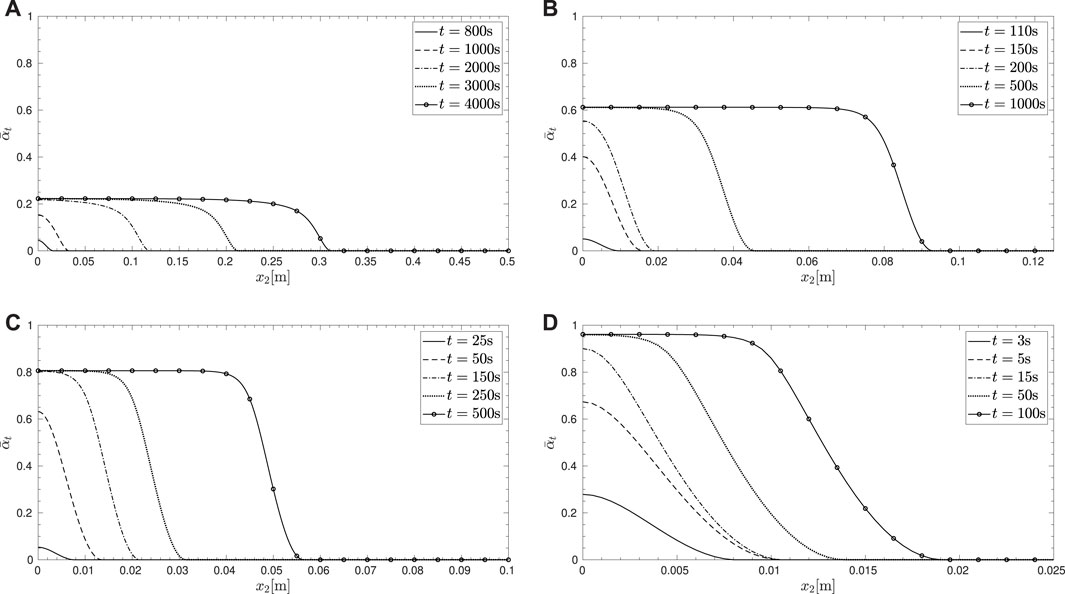
FIGURE 6. Evolution of damage for values of w1 (A) 2000 N.m−3, (B) 1000 N.m−3, (C) 500 N.m−3, and (D) 100 N.m−3.
4.3 Bifurcation From and Instability of the Fundamental Branch
The one-dimensional base solutions resolved in Section 4.2 are the x1-homogeneous solutions or the so-called fundamental states of the corresponding two-dimensional problem. These solutions are denoted by
4.3.1 Loss of Stability
By construction of the fundamental state,
By virtue of the equilibrium, Eq. 24, and zeroth-order balance, Eq. 26, the FDD in Eq. 44 reduces to,
with the directions
where
Undamaged States:
For t < td,
which is positive. Hence, full stability of the fundamental state is guaranteed for t < td.
Damaged States:
For t ≥ td, the damage criterion is an equality within the damaged strip
and only if the above inequality is not strict. It should be noted that in the abovementioned equation, the expression of SDD is given by Eq. 21 and not by the reduced Eq. 47 owing to the possibility of
The directions
Noting, for the moment, that SDD in the damaged states is evaluated at the fundamental state and analysis of the condition in Eq. 48 is deferred to a later moment in view of studying the possibility of bifurcations.
Synopsis: While the undamaged states are fully stable, the damaged states are conditionally stable and this condition amounts to verifying the positive definiteness of the quadratic form
4.3.2 Possibility of Bifurcations
As mentioned earlier, the notion of bifurcation from the fundamental branch is intertwined with the availability of admissible solution state/s other than the fundamental one. This amounts to studying the evolution problem at time t + η, with η > 0 small enough, knowing that the solution has followed the fundamental branch up until t, that is, knowing the solution at t is
Furthermore, a smooth growth of the damage zone is assumed within the time interval (t, t + η). More detail of such a hypothesis can be found in Sicsic et al. (2014). Now, if the solution continues to stay on the fundamental branch, then it implies that
Imposing (ut+η, ϕt+η, αt+η) to satisfy the three evolution principles in Section 2.2, we get:
1) Irreversibility of damage: Damage must be nondecreasing, that is,
2) Stability: Directional stability implies first-order stability which at (ut+η, ϕt+η, αt+η) reads,
As analyzed earlier for loss of stability of the fundamental state at time t, for directions
Whereas for directions such that
with1,
3) Energy Balance: The energy balance at time t + η reads,
A first expansion of
where ‖ ⋅‖ denotes the norm of
The following definitions are obtained by differentiating with respect to time the energy balance written at time t,
The term
The rate problem: Subtracting Eq. 60 from Eq. 54 gives the following inequality that the rate at any time t > 0,
To verify if any rate other than the x1-homogeneous rate,
Whereas by choosing
Adding Eq. 62 and Eq. 63, we get the inequality,
This condition holds true only if
Synopsis: The uniqueness of the x1-homogeneous rate solution of the rate problem and consequently the impossibility of bifurcation from the fundamental branch are ensured by the positive definiteness of the quadratic form
Remark: One can notice from the abovementioned results that both the loss of stability of the fundamental state and the possibility of bifurcation from it amounts to studying the positive definiteness of the same quadratic form,
4.4 Characterization of Bifurcations
Now we are in a position to study the possibility of bifurcations by assuming general forms of the directions in which the quadratic form is to be applied. To this end, let
While choosing the abovementioned decomposition, the boundary conditions that apply to the admissible perturbations to the fundamental state are a priori adapted to
Owing to the classical constitutive relation for porosity, Eq. 31, obtained by rearranging the zeroth-order balance law for variations in porosity, the abovementioned definition of ɛ(vk) and the boundary conditions of the hydraulic problem for pt, Eq. 42, one can justify the form assumed for
Exploiting the orthogonality among different Fourier modes allows to uncouple them and evaluate the functional
where functions denoted
where μk denotes the eigenvalues and
Accordingly, the criterion for bifurcation, Eq. 66, at each time t > 0 can be translated to,
with
4.4.1 Indicative Study of Bifurcations
While the true possibility of bifurcations could be understood by the criterion Eq. 71, we can investigate the behavior of the coefficients of the quadratic form
By virtue of Eq. 21, we can classify the various terms within the functional as follows:
with
We can conclude that the first term,
The term
In view of the above analysis, one can study the strength of
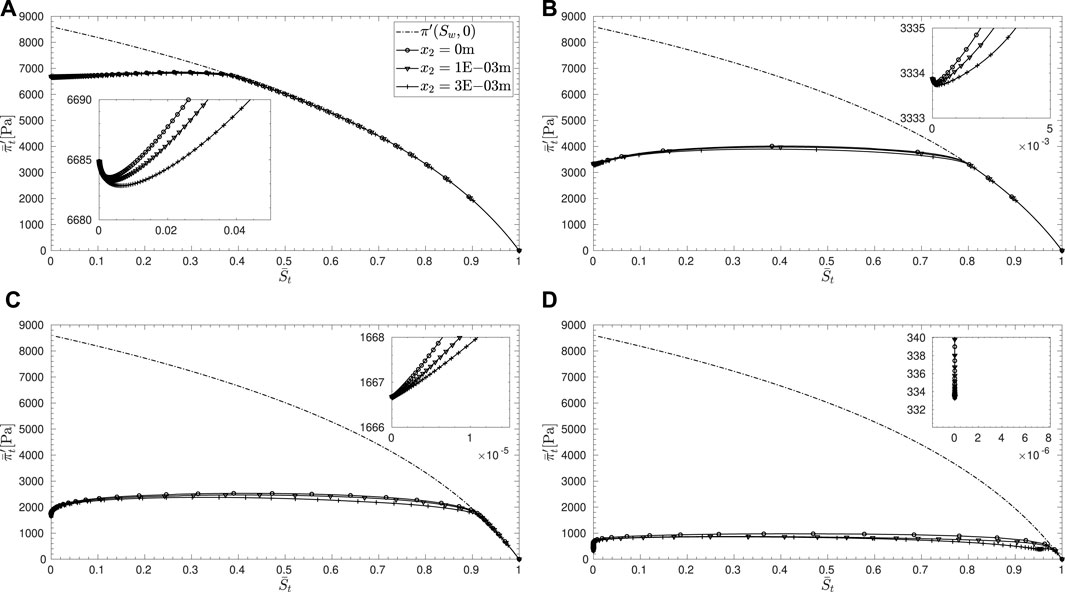
FIGURE 7. Evolution of the functions,
5 Conclusion
In this study, a novel approach to modeling of capillary force–driven fracturing phenomenon has been proposed, inspired by the experimental results mainly obtained by Shin and Santamarina (2010, 2011). For this purpose, the required ingredient, a damage mechanism, is postulated and described by a scalar damage variable, following a similar approach as the one proposed by Marigo et al. (2016) that describes fractures in brittle materials. However, the driving force behind the damage evolution is revisited to replicate the capillary forces that are in action at the pore-scale. The analysis starts with the postulation of a damaged porous solid and its associated energy density. Following this, the evolution problem for damage is derived starting from a total energy of the porous solid and in accordance with the variational approach based on the three principles of the irreversibility of damage, stability, and energy balance, assuming a minimization principle to hold true at each time. This lays the foundation for studying the possibility of fracture initiation in a two-dimensional desiccation problem. A loss of stability and bifurcation analysis is carried out starting from the resolution of one-dimensional solutions. An indicative study reveals that at the current state, the model does not exhibit a clear bifurcation and similarly loss of stability of the base solution, which should induce damage localization, notwithstanding the behavior of
While the solution of an eigenproblem could reveal more details, we claim that the lack of clear bifurcation is due to the simplified approach adopted in this study. Specifically, we did not account comprehensively for the degradation of the resistance to fluid flow within the damaged zone and eventually along localized fracture planes. This could, in principle, be achieved via a suitable coupling between the intrinsic permeability and the damage parameter, for instance, as proposed in Miehe et al. (2015). This will be part of our future investigations.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
SO: Conceptualization, Methodology, Formal analysis, Data curation, and Writing–Original Draft; GS: Conceptualization, Reviewing, and Supervision; PK: Conceptualization, Reviewing, and Supervision.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors would like to acknowledge the support of the Agence Nationale de la Recherche (ANR), project STOWENG (Project-ANR-18-CE05-0033), and that of Centre National de la Recherche Scientifique (CNRS), project changement climatique AAP-2020 APPI-SMILE.
Footnotes
1Note the restriction of
References
Alnaes, M. S., Blechta, J., Hake, J., Johansson, A., Kehlet, B., Logg, A., et al. (2015). The Fenics Project Version 1.5. Archive Numer. Softw. 3. doi:10.11588/ans.2015.100.20553
Balay, S., Abhyankar, S., Adams, M. F., Benson, S., Brown, J., Brune, P., et al. (2021). PETSc/TAO Users Manual. Tech. Rep. ANL-21/39. Lemont, IL: Argonne National Laboratory. Revision 3.16.
Benallal, A., and Marigo, J.-J. (2006). Bifurcation and Stability Issues in Gradient Theories with Softening. Model. Simul. Mat. Sci. Eng. 15, S283–S295. doi:10.1088/0965-0393/15/1/s22
Bourdin, B., Francfort, G. A., and Marigo, J.-J. (2000). Numerical Experiments in Revisited Brittle Fracture. J. Mech. Phys. Solids. 48, 797–826. doi:10.1016/S0022-5096(99)00028-9
Cajuhi, T., Sanavia, L., and De Lorenzis, L. (2018). Phase-field Modeling of Fracture in Variably Saturated Porous Media. Comput. Mech. 61, 299–318. doi:10.1007/s00466-017-1459-3
Choo, J., and Sun, W. (2018). Coupled Phase-Field and Plasticity Modeling of Geological Materials: From Brittle Fracture to Ductile Flow. Comput. Methods Appl. Mech. Eng. 330, 1–32. doi:10.1016/j.cma.2017.10.009
Cordero, J. A., Prat, P. C., and Ledesma, A. (2021). Experimental Analysis of Desiccation Cracks on a Clayey Silt from a Large-Scale Test in Natural Conditions. Eng. Geol. 292, 106256. doi:10.1016/j.enggeo.2021.106256
Cordero, J. A., Useche, G., Prat, P. C., Ledesma, A., and Santamarina, J. C. (2017). Soil Desiccation Cracks as a Suction-Contraction Process. Géotechnique Lett. 7, 279–285. doi:10.1680/jgele.17.00070
Hilfer, R., and Steinle, R. (2014). Saturation Overshoot and Hysteresis for Twophase Flow in Porous Media. Eur. Phys. J. Spec. Top. 223, 2323–2338. doi:10.1140/epjst/e2014-02267-x
Holtzman, R., Szulczewski, M. L., and Juanes, R. (2012). Capillary Fracturing in Granular Media. Phys. Rev. Lett. 108, 264504. doi:10.1103/PhysRevLett.108.264504
Jain, A. K., and Juanes, R. (2009). Preferential Mode of Gas Invasion in Sediments: Grain-Scale Mechanistic Model of Coupled Multiphase Fluid Flow and Sediment Mechanics. J. Geophys. Res. 114. doi:10.1029/2008JB006002
Marigo, J.-J., Maurini, C., and Pham, K. (2016). An Overview of the Modelling of Fracture by Gradient Damage Models. Meccanica 51, 3107–3128. doi:10.1007/s11012-016-0538-4
Miehe, C., Mauthe, S., and Teichtmeister, S. (2015). Minimization Principles for the Coupled Problem of Darcy-biot-type Fluid Transport in Porous Media Linked to Phase Field Modeling of Fracture. J. Mech. Phys. Solids. 82, 186–217. doi:10.1016/j.jmps.2015.04.006
Peron, H., Hueckel, T., Laloui, L., and Hu, L. B. (2009). Fundamentals of Desiccation Cracking of Fine-Grained Soils: Experimental Characterisation and Mechanisms Identification. Can. Geotech. J. 46, 1177–1201. doi:10.1139/T09-054
Peron, H., Laloui, L., Hu, L.-B., and Hueckel, T. (2013). Formation of Drying Crack Patterns in Soils: a Deterministic Approach. Acta Geotech. 8, 215–221. doi:10.1007/s11440-012-0184-5
Pham, K., Amor, H., Marigo, J.-J., and Maurini, C. (2011a). Gradient Damage Models and Their Use to Approximate Brittle Fracture. Int. J. Damage Mech. 20, 618–652. doi:10.1177/1056789510386852
Pham, K., and Marigo, J.-J. (2010b). Approche variationnelle de l'endommagement : II. Les modèles à gradient. Comptes Rendus Mécanique 338, 199–206. doi:10.1016/j.crme.2010.03.012
Pham, K., and Marigo, J.-J. (2010a). Approche variationnelle de l'endommagement : I. Les concepts fondamentaux. Comptes Rendus Mécanique 338, 191–198. doi:10.1016/j.crme.2010.03.009
Pham, K., Marigo, J.-J., and Maurini, C. (2011b). The Issues of the Uniqueness and the Stability of the Homogeneous Response in Uniaxial Tests with Gradient Damage Models. J. Mech. Phys. Solids. 59, 1163–1190. doi:10.1016/j.jmps.2011.03.010
Shin, H., and Santamarina, J. C. (2011). Desiccation Cracks in Saturated Fine-Grained Soils: Particle-Level Phenomena and Effective-Stress Analysis. Géotechnique 61, 961–972. doi:10.1680/geot.8.P.012
Shin, H., and Santamarina, J. C. (2010). Fluid-driven Fractures in Uncemented Sediments: Underlying Particle-Level Processes. Earth Planet. Sci. Lett. 299, 180–189. doi:10.1016/j.epsl.2010.08.033
Sicsic, P., Marigo, J.-J., and Maurini, C. (2014). Initiation of a Periodic Array of Cracks in the Thermal Shock Problem: A Gradient Damage Modeling. J. Mech. Phys. Solids. 63, 256–284. doi:10.1016/j.jmps.2013.09.003
Spetz, A., Denzer, R., Tudisco, E., and Dahlblom, O. (2021). A Modified Phase-Field Fracture Model for Simulation of Mixed Mode Brittle Fractures and Compressive Cracks in Porous Rock. Rock Mech. Rock Eng. 54, 5375–5388. doi:10.1007/s00603-021-02627-4
Stirling, R. A. (2014). Multiphase Modelling Of Desiccation Cracking In Compacted Soil. Ph.D. thesis. Newcastle: Newcastle University.
van Genuchten, M. T. (1980). A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 44, 892–898. doi:10.2136/sssaj1980.03615995004400050002x
Zhou, X.-P., Zhang, Y.-X., Ha, Q.-L., and Zhu, K.-S. (2008). Micromechanical Modelling of the Complete Stress-Strain Relationship for Crack Weakened Rock Subjected to Compressive Loading. Rock Mech. Rock Eng. 41, 747–769. doi:10.1007/s00603-007-0130-2
Zhou, X. P. (2005). Localization of Deformation and Stress-Strain Relation for Mesoscopic Heterogeneous Brittle Rock Materials under Unloading. Theor. Appl. Fract. Mech. 44, 27–43. doi:10.1016/j.tafmec.2005.05.003
Keywords: unsaturated porous media, capillarity, gradient damage modeling, localization, stability, drainage, desiccation cracks
Citation: Ommi SH, Sciarra G and Kotronis P (2022) Variational Approach to Damage Induced by Drainage in Partially Saturated Granular Geomaterials. Front. Mech. Eng 8:869568. doi: 10.3389/fmech.2022.869568
Received: 04 February 2022; Accepted: 06 May 2022;
Published: 21 October 2022.
Edited by:
Mohamed A. Eltaher, King Abdulaziz University, Saudi ArabiaReviewed by:
Giuseppe Zurlo, National University of Ireland Galway, IrelandXiaoping Zhou, Chongqing University, China
Copyright © 2022 Ommi, Sciarra and Kotronis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Siddhartha H. Ommi, c2lkZGhhcnRoYS1oYXJzaGEub21taUBlYy1uYW50ZXMuZnI=
 Siddhartha H. Ommi
Siddhartha H. Ommi Giulio Sciarra
Giulio Sciarra Panagiotis Kotronis
Panagiotis Kotronis