Fluid-Driven Instabilities in Granular Media: From Viscous Fingering and Dissolution Wormholes to Desiccation Cracks and Ice Lenses

Single and multi-phase fluids fill the pore space in sediments; phases may include gases (air, CH₄, CO₂, H₂, and NH₃), liquids (aqueous solutions or organic compounds), and even ice and hydrates. Fluids can experience instabilities within the pore space or trigger instabilities in the granular skeleton. Then, we divided fluid-driven instabilities in granular media into two categories. Fluid instabilities at constant fabric take place within the pore space without affecting the granular skeleton; these can result from hysteresis in contact angle and interfacial tension (aggravated in particle-laden flow), fluid compressibility, changes in pore geometry along the flow direction, and contrasting viscosity among immiscible fluids. More intricate fluid instabilities with fabric changes take place when fluids affect the granular skeleton, thus the evolving local effective stress field. We considered several cases: 1) open-mode discontinuities driven by drag forces, i.e., hydraulic fracture; 2) grain-displacive invasion of immiscible fluids, such as desiccation cracks, ice and hydrate lenses, gas and oil-driven openings, and capillary collapse; 3) hydro-chemo-mechanically coupled instabilities triggered by mineral dissolution during the injection of reactive fluids, from wormholes to shear band formation; and 4) instabilities associated with particle transport (backward piping erosion), thermal changes (thermo-hydraulic fractures), and changes in electrical interparticle interaction (osmotic-hydraulic fractures and contractive openings). In all cases, we seek to identify the pore and particle-scale positive feedback mechanisms that amplify initial perturbations and to identify the governing dimensionless ratios that define the stable and unstable domains. A [N/m] Contact line adhesion

1 Introduction

Contrary to the generalized use of equivalent continuum models, instabilities often emerge and determine the macroscale response of granular materials. They can result from mechanical actions (e.g., shear and compaction bands) or from coupled processes such as hydro-mechanically coupled hydraulic fractures or chemo-mechanically coupled contraction cracks. Multi-phase fluids add additional mechanisms that can result in pore-scale and macro-scale instabilities, from Haines jumps to segregated ice lenses and giant desiccation cracks.

Instabilities can determine deformation and pressure fields and control fluid transport and the “geo-plumbing” of the formation. Furthermore, instabilities affect the upscaling of laboratory results to the field and all engineering analyses and designs such as foundations, subsurface structures, resource recovery and geological storage.

At the macro-scale, instabilities imply a non-convex potential energy surface (Kochmann and Bertoldi, 2017). At the particle/pore-scale, instabilities involve positive feedback mechanisms that exacerbate the effects of initial perturbations.

Table 1 compiles observed/reported fluid-driven instabilities that take place at constant fabric or cause fabric changes. The following sections analyze the evolution of such fluid-driven instabilities in granular materials to identify underlying pore and particle scale processes. We conducted cast analyses within the framework of particle/pore scale dimensionless ratios to identify the governing parameters that define stable and unstable regimes.

TABLE 1

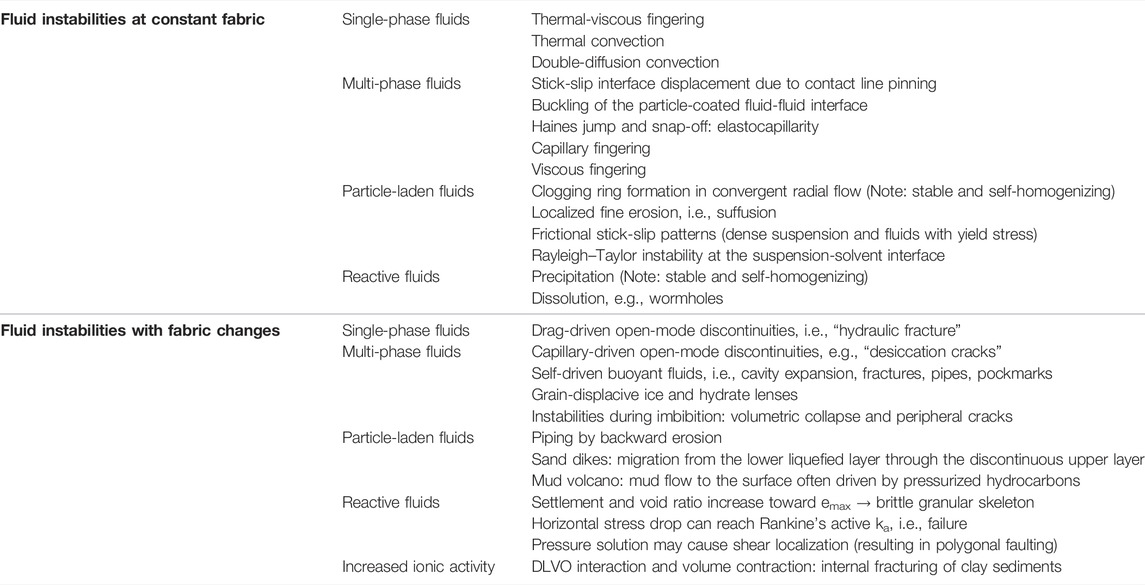
TABLE 1. Fluid-driven instabilities in granular materials. Examples are organized into instabilities 1) at constant fabric and 2) with fabric changes.

2 Fluid Instabilities at Constant Fabric

We first consider the various forms of instabilities that emerge during fluid invasion/flow through a rigid porous medium, i.e., without mechanical coupling. We explore single and multi-phase fluids, particle-laden fluids, and reactive fluids.

2.1 Multi-Phase Fluids

The pore space in sediments is often occupied by more than one fluid. Multi-phase fluids affect unsaturated soil behavior, oil and gas recovery, energy chemical geostorage, CO₂ geostorage, and the remediation of ground contaminated with light non-aqueous phase liquids (LNAPLs) or dense non-aqueous phase liquids (DNAPLs). The various phases may include gases (air, CH₄, CO₂, H₂, NH₃), liquids (aqueous solutions and organic compounds), and even ice and hydrates.

Fundamental Concepts

Interfacial tension. A molecule at the interface between two fluids experiences different intermolecular forces than the same molecule in the bulk fluid (Figure 1). This asymmetry manifests as a surface tension between the phases. Dissolved salts, surfactants, and suspended colloids affect the surface tension; the Gibbs adsorption isotherm relates the interfacial tension under thermodynamic equilibrium $\gamma$ to the surface excess concentration $\text{Γ}$ of the chemical species in the fluid relative to their bulk concentration $C_b$ (Gibbs, 1878). Dissolved CaCl₂ and NaCl have a negative adsorption $\Gamma <0$ and the interfacial tension increases with salt concentration (Al-Sahhaf et al., 2005; Bachu and Bennion, 2009); on the other hand, some components such as amphiphilic surfactant molecules tend to migrate towards the interface, i.e., positive adsorption $\Gamma >0$, and the interfacial tension decreases with concentration until surfactants in the bulk solution form micelles when $C_b$ exceeds the critical micelle concentration CMC (Mulligan et al., 2001).

FIGURE 1

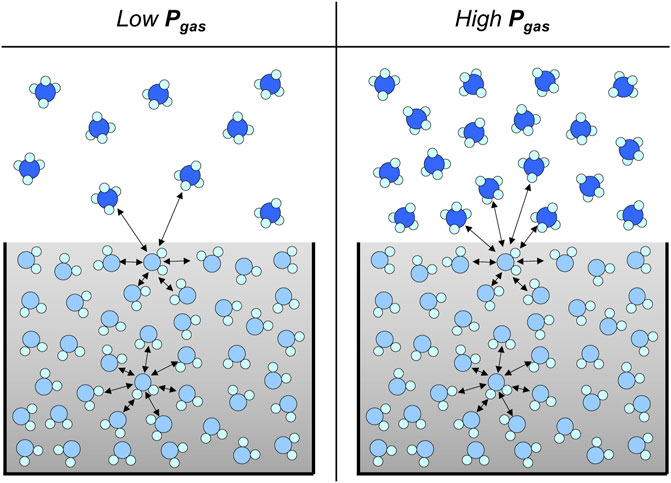
FIGURE 1. Interfacial tension. Intermolecular forces at the interface between a liquid and a gas to demonstrate that the interfacial tension decreases with increasing gas pressure.

Fluid interfaces contract and extend as they traverse the converging-diverging pore geometry in soils. Thus, we should consider the transient state of the interface instead of the equilibrium state in the analysis of multi-phase fluid flow (Jang et al., 2016; Liu et al., 2021). Time-dependent adsorption/desorption of surfactants or colloidal particles (e.g., nanoparticles, bacteria, and asphaltenes) controls interfacial tension during interface expansion and contraction. The Langmuir model provides the simplest description of adsorption and desorption kinetics (Langmuir, 1918; Chang and Franses, 1992; He et al., 2015). The adsorption energy increases with particle size; therefore, particles larger than >10 nm tend to experience irreversible adsorption into the interface in contrast to surfactants (Hua et al., 2016). Figure 2 shows the interfacial tension hysteresis loop of a surfactant solution and a nanofluid droplet in a decane bath (silica nanoparticles: d = 76 nm; surfactant: CTAB). Surfactant-coated interfaces exhibit higher hysteresis compared to particle-coated interfaces; in both cases, the interfacial tension increases during rapid droplet expansion.

FIGURE 2

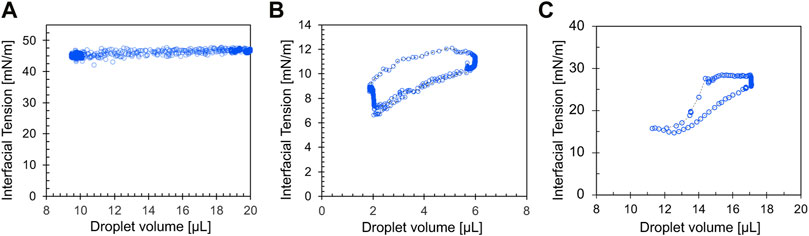
FIGURE 2. Interfacial tension hysteresis. (A) Water droplet in decane. (B) CTAB solution droplet in decane. (C) Nanofluid droplet in decane. (Benitez, 2022).

Contact angle. Young’s equation predicts the contact angle $\theta$ from force-equilibrium between the interfacial tensions that emerge at the fluid–liquid ${\text{γ}}_{LV}$, liquid–solid ${\gamma }_{LS}$, and fluid–solid ${\gamma }_{VS}$ interfaces (Figure 3A, Young, 1805):

$\cos \theta =\frac{{\gamma }_{VS}-{\gamma }_{LS}}{{\text{γ}}_{LV}}.$

FIGURE 3

FIGURE 3. Contact angle: the effect of contact line adhesion on contact angle hysteresis. (A) Young’s contact angle. (B) Advancing contact angle. (C) Receding contact angle.

In contrast to the single thermodynamic contact angle predicted by Young’s equation, interfaces can exhibit a range of contact angles between two asymptotic values: the advancing contact angle ${\theta }_A$ and the receding contact angle ${\theta }_R$. Contact angle hysteresis results from surface roughness, chemical inhomogeneities in the solid surface, and solutes in the liquid (de Gennes, 1985; Eral et al., 2013).

The three phases, L-V-S, meet at the contact line. The contact line adhesion A acts against the intended motion and it can be estimated from the advancing and receding contact angles (Figures 3B,C):

${\gamma }_{LV}\cos {\theta }_a+A={\gamma }_{VS}-{\gamma }_{LS},$

${\gamma }_{LV}\cos {\theta }_r-A={\gamma }_{VS}-{\gamma }_{LS}.$

The experimentally measured lateral adhesion force between a liquid droplet and a solid shows the maximum static adhesion followed by a reduced kinetic adhesion, which is remarkably analogous to solid-solid friction (Gao et al., 2018). Surfactants and particles adsorbed at the interface result in complex interface-substrate interaction which alters the contact line pinning.

Non-convex displacement-dependent capillary pressure. The varying pore geometry along the invasion path, transient contact angle behavior, and hysteretic interfacial tension result in non-convex capillary pressure vs. displacement signatures.

1) Varying pore-geometry along the invasion path. Consider the displacement of a wetting liquid by a non-wetting fluid across a pore constriction with a sinusoidal geometry as illustrated in Figure 4A (viscosity and gravity effects are negligible for small capillary and Bond numbers). The pressure difference between the wetting and the non-wetting fluids Δu(x) at position x is a function of the surface tension $\gamma$, the contact angle $\theta$ and the local pore wall angle α(x):

$\text{Δ}u\left(x\right)=u_w-u_n=-\frac{4\gamma \cos \left[\theta -\alpha \left(x\right)\right]}{d\left(x\right)},$

where $d\left(x\right)$ is the pore diameter at position x. The computed capillary pressure for a sinusoidal pore (of circular cross section) shows that the interface experiences a concave-to-convex transition and the capillary pressure reverses sign when the argument [θ-α(x)] crosses 90°.

2) Contact line pinning and sliding. Typically, the contact line remains pinned onto the pore wall until it reaches the asymptotic contact angle; thereafter, the contact line slides and the advancing contact angle remains constant (Figure 5A). For nanoparticle coated fluid interfaces, they may reach a peak contact angle followed by a pronounced post-peak relaxation to a lower contact angle during steady displacement (Figures 5B,C).

3) Buckling of nanoparticle coated interfaces. The particle surface coverage increases as the interface area decreases across a pore constriction; eventually, a particle shell forms and interfacial tension reverses to compression (Liu et al., 2021). At some point, the shell may buckle or crumple. The buckling resistance is determined by particle-particle and particle-interface interactions. And boundary conditions affect buckling patterns (Meyer et al., 2006; Liu et al., 2021).

FIGURE 4

FIGURE 4. Haines jumps. (A) Elastic and capillary interactions. Pore scale mechanisms: (B) soft fluid by entrapped gas bubble; (C) deformable soft matrix; (D) interacting menisci (modified from Sun and Santamarina, 2019b).

FIGURE 5

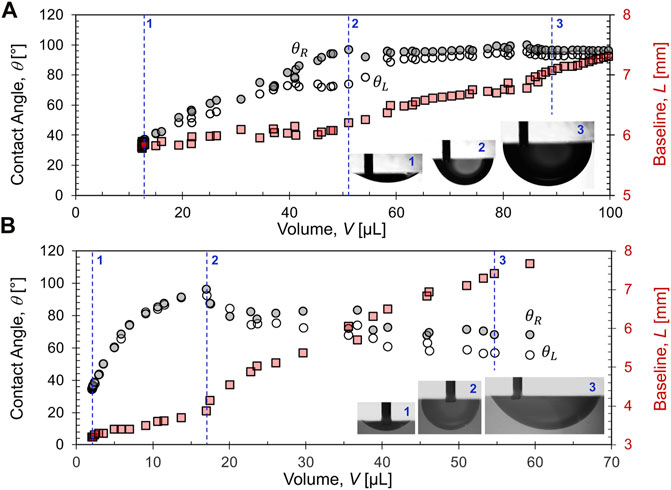
FIGURE 5. Contact line sliding and jumping. (A) Oil droplet in DI water. (B) Oil droplet in nanofluid (data from Sun et al., 2022).

Soft-system response → Instabilities (Haines jumps and snap-offs). The system deforms in response to changes in capillary pressure. Common causes for a soft system response include 1) the presence of entrapped gas, 2) interacting menisci, and 3) a deformable solid matrix (Figure 4—Note: a deformable solid matrix implies mechanical coupling with the mineral skeleton). Then, displacement-dependent capillarity couples with pressure-dependent volume change to cause “jump” instabilities similar to frictional stick-slip (Sun and Santamarina, 2019b). The sudden local jump of the fluid interface—often known as a Haines jump—causes a transient pressure change and fluid redistribution (Morrow and Szabo, 1970; Gauglitz and Radke, 1989; Berg et al., 2013).

The actual system volume response $V_{sys}$ combines the invaded pore volume $V_{\text{pore}}$ with the system’s volume change $V_{\text{el}}$ due to a pressure change:

$V_{\mathrm{sys}}=V_{\mathrm{pore}}-V_{\mathrm{el}}.$

A jump will occur during either advancing or receding when the resultant ΔP-vs-$V_{\text{sys}}$ curve is multivalued, for example, across the pore throat (Sun and Santamarina, 2019b). Then, the potential for instabilities will relate to the pressure required for a volumetric compression ∼ r³ given the system stiffness k (Pa/m³) and the capillarity pressure that can arise at the pore constriction of radius r; in dimensionless form:

${\mathrm{N}}_{\mathrm{ec}}\propto \frac{K r^4}{\gamma \cos \left(\theta \right)}.$

A system with an elastocapillary number N_ec<1 is prone to Haines instabilities.

Wetting fluids transported along corners and crevices or left behind during sudden jumps, i.e., “snap-off,” may accumulate at pore throats to form plugs that split the traversing non-wetting fluid (Figure 6). Snap-offs and plugs result in foam generation inside the porous medium (Lenormand et al., 1983; Peña et al., 2009).

FIGURE 6

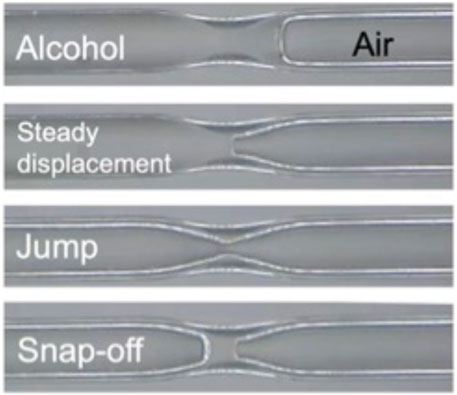
FIGURE 6. Changes in pore geometry along the advancing path: jumps and snap-offs (Jang et al., 2016).

Viscous and capillary fingers. Immiscible fluid displacement is controlled by capillary force F_C, viscous force F_D, and the buoyant force F_b. Critical dimensionless numbers are the capillary number, the viscous ratio and the Bond number (Chatzis and Morrow, 1984; Lenormand et al., 1988; Dawson and Roberts, 1997; Ferer et al., 2004; Santamarina and Jang, 2011; Zhao et al., 2016; see Zhao et al., 2019 for pore-scale modeling methods):

$\mathrm{Capillary number: Ca}=\frac{\mu v}{\gamma \cos \theta } ,$

$\mathrm{Viscous ratio: M}=\frac{{\mu }_{inv}}{{\mu }_{def}},$

$\mathrm{Bond number:Bo}=\frac{\text{Δ}\rho g{L}^2}{\gamma }.$

Patterns observed during immiscible fluid invasion (i.e., non-wetting) fall into domains defined by these dimensionless numbers: stable displacement takes place at large M and Ca; viscous fingering at small M and large Ca; and capillary fingering at large M and small Ca (Figure 7). The Rayleigh-Taylor instability, observed when a lighter fluid ascends through a heavier fluid, develops at large Bond numbers. Different invasion modes lead to distinct fluid pressure fields: the pressure drop occurs mainly in the more viscous phase, i.e., the invading phase in stable displacement or the defending phase in viscous fingering; on the other hand, the viscous pressure drop is negligible compared to the capillary pressure difference between the fluids in the capillary fingering regime (An et al., 2020).

FIGURE 7

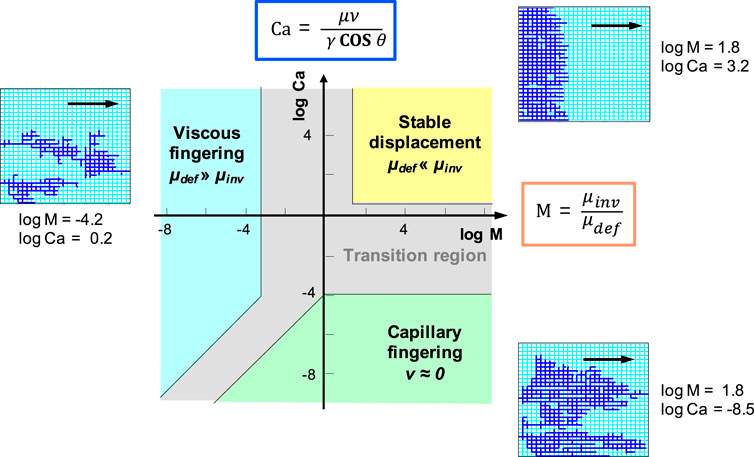
FIGURE 7. Mixed fluid instabilities at constant fabric. Regimes for viscous fingering, capillary fingering, and stable displacement in the space defined by the capillary number Ca and viscous ratio M (Schematic representation—after Lenormand et al., 1988. Pore network simulations are conducted by Sheng Dai.).

Viscous fingering can also occur in a single phase fluid due to thermal effects, such as during the injection of a hot liquid (low viscosity) into a porous medium saturated with the same liquid at low temperature (higher viscosity)Note: invasion regularizes as temperature homogenizes) (Helfrich, 1995; Islam and Azaiez, 2010). Thermal viscous fingering may be accompanied by convective currents triggered by the fluid’s thermal expansion and density changes.

2.2 Reactive Fluids

Inherent pore size variability results in preferential flow pathways across sediments; in fact, as few as 10% of pores may be responsible for more than 50% of the total flow rate (Jang et al., 2011). Note: Flow channeling is even more pronounced in fractures and fractured rock masses (National Academies of Sciences, Engineering, and Medicine, 2020; Cardona et al., 2021). These preferential flow paths will also deliver the majority of the reactants to cause either dissolution or precipitation within the soil mass.

Precipitation is a self-homogenizing process: it reduces transport along preferential flow paths and reactive fluids deviate to other pathways. On the other hand, dissolution tends to localize due to positive feedback; preferential flow channels enlarge and lead to increased flow focusing and “wormhole” formation (Menke et al., 2017; Derr et al., 2020). Wormholes affect dam stability (Romanov et al., 2003), CO₂ sequestration (Kim and Santamarina, 2015), groundwater transport in karst terrain (Dreybrodt, 1990), and acid stimulation of oil reservoirs (Fredd and Scott Fogler, 1998; Al-Arji et al., 2021). In the absence of advection, diffusive reactant transport promotes homogeneous dissolution.

The previous discussion suggests that dissolution topologies in rigid porous media such as in rocks depend on three concurrent processes: diffusion, advection, and chemical reaction. Two dimensionless ratios combine the three time scales for advection t_adv, diffusion t_diff, and reaction t_r for a channel length L_ch:

$\mathrm{Damköhler number Da}=\frac{t_{adv}}{t_r}\propto \frac{k{L}_{ch}}{v},$

$\mathrm{Péclet number Pe}=\frac{t_{diff}}{t_{adv}}\propto \frac{v{L}_{ch}}{D},$

where the process parameters are the kinetic rate of the reaction k [1/s], the average pore velocity v [m/s] and the diffusion coefficient D [m²/s]. The Pe-Da diagram in Figure 8 captures the space for the various dissolution topologies: compact dissolution, conical wormhole, dominant wormhole, ramified wormhole, and uniform dissolution regimes. Low advection velocities—long t_adv and small Pe—allow reactant consumption near the inlet and instabilities cannot develop; conversely, very high advection velocities—short t_adv, high Pe and small Da—carry reactants throughout the porous medium from inlet to outlet and favors a stable homogeneous dissolution. Wormholes develop with intermediate flow rates—large Da and Pe-—so that reactants act preferentially along flow channels. Finally, we note that extensive dissolution in granular materials will cause fabric changes, as discussed later in this manuscript.

FIGURE 8

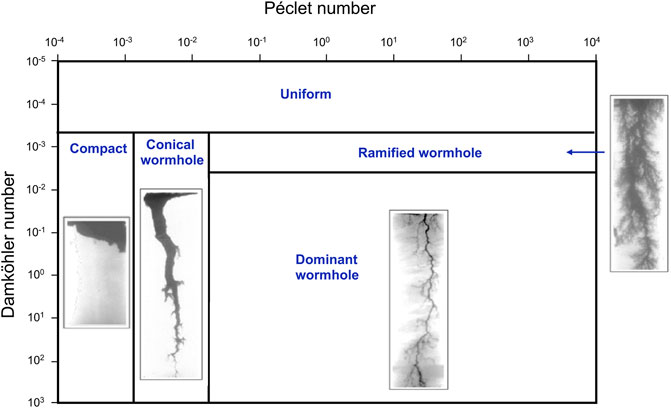
FIGURE 8. Dissolution regimes without fabric changes. Instabilities in the space defined by Péclet and Damköhler numbers (modified by Golfier et al., 2002; images from Fredd, 2000).

2.3 Particle-Laden Fluids

Particle-laden fluids are common in nature (e.g., ground water flow) and frequently used in engineered applications (tremie submerged construction, drilling muds, and well stimulation and proppants).

Particle inclusion changes the liquid density, rheology, and interfacial properties. Density triggers convective fingers in water columns, as seen during the release of mine waste slurries in large water bodies (Rayleigh-Taylor instability; Lange et al., 1998; Völtz et al., 2002).

The suspension viscosity increases with a higher mineral volume fraction and more frequent inter-particle interactions result in fluids with yield stress; then, instabilities readily emerge. For example, air injection into dense granular suspensions results in bubble migration with frictional stick-slip characteristics and viscous fingering (Sandnes et al., 2011).

A particle embedded in a moving fluid experiences buoyant weight F_B, drag F_D, inertia against motion changes F_I, and electrical interaction with pore walls F_wall (it combines van der Waals and electrostatic forces, including hydrophobic adhesion forces). These forces combine to produce self-stabilizing clogging rings in convergent radial flow (negative feedback during fluid extraction), and fingered erosion during outward fluid flow (positive feedback during fluid injection) (Valdes and Santamarina, 2006; Valdes and Carlos Santamarina., 2007; Liu et al., 2019). The dimensionless ratios between interacting forces define the various particle migration regimes in terms of the particle size d, obstacle size D, particle and fluid mass densities ${\rho }_p$ and ${\rho }_f$, fluid viscosity $\mu$, fluid velocity $v$, and gravity g:

$\mathrm{Contact}\mathrm{number}\mathrm{=}\frac{\mathrm{Wall}\mathrm{interaction}}{\mathrm{Drag}}{\mathrm{N}}_{\mathrm{ad}}=\frac{F_{wall}}{F_D}\propto \frac{F_{wall}}{\mu dv},$

$\mathrm{Archimedes}\mathrm{number}=\frac{\mathrm{Bouyant weight}}{\mathrm{Drag}}\mathrm{Ar}=\frac{F_B}{F_D}\propto \frac{g{d}^2\left({\rho }_p-{\rho }_f\right)}{\mu v},$

$\mathrm{Stokes}\mathrm{number}=\frac{\mathrm{Inertia}}{\mathrm{Drag}}\mathrm{Stk}=\frac{F_I}{F_D}\propto \frac{{\rho }_p{d}^{2}v}{\mu D}.$

Clogged pore constrictions alter flow in nearby open paths, affect retardation, and may promote neighboring clogging. Experimental observations show that the probability of neighboring clogging is much higher than the probability of independent clogging (Liot et al., 2018; Van Zwieten et al., 2018; Liu et al., 2019).

Under mixed-phase conditions, particle-laden fluids may experience preferential particle accumulation at the interface with other immiscible fluids, e.g., hydrophobic nanoparticles suspended in water. This situation may stabilize interfaces and hinder coalescence (e.g., Pickering emulsions) or prompt pore-scale interfacial instabilities such as interface buckling and the stick-slip response of the contact line, as reviewed earlier. Under radial flow conditions (fluid injection), particle bands develop away from the injection point due to gravity and inertia; additional injection can break the particle bands and form erosion fingers (Kim et al., 2017).

3 Fluid-Driven Instabilities With Fabric Changes

Pressure gradients, capillarity, mineral dissolution, and various forms of flow localization in rigid porous media may collude with the granular nature of soils and sediments to give rise to mechanically coupled instabilities that cause fabric changes. At the macroscale, mechanical coupling implies changes in effective stress. At the particle scale, these instabilities reflect the interplay between particle level forces. The following sections analyze fluid-driven instabilities with fabric changes and the underlying forces; given the wide range of possible interactions, the list is limited to frequently encountered field conditions.

3.1 Single-Phase Fluid—Miscible Invasion

The effective stress principle σ’ = σ-u anticipates a gradient in effective stress when there is a fluid pressure gradient dσ’/dx = −du/dx. At the particle level, the flowing fluid gradually transfers its pressure as viscous drag onto the particles; hence, pressure decreases and interparticle skeletal forces accumulate in the direction of fluid flow. Then, the ab initio formation of a fluid-driven open mode discontinuity involves the following sequence of events: fluid injection at a point causes radial fluid flow; drag forces push particles away from the injection point, i.e., cavity expansion; tangential extension and the particles’ relative displacement result in a surface imperfection that facilitates preferential fluid flow; arising tangential drag forces cause further interparticle separation (Figure 9C). The positive feedback built into this sequence of events leads to the development of open-mode discontinuities, including planar “hydraulic fractures” (Shin and Santamarina, 2010; 2011b; Carrillo and Bourg, 2021) as well as tubular pipes (Cartwright and Santamarina, 2015). Note: the term “open-mode discontinuity” is preferred instead of “fracture” in the context of granular materials, i.e., without cohesion; moreover, models that are based on classical fracture mechanics are inadequate for the analysis of open mode discontinuities in granular materials.

FIGURE 9

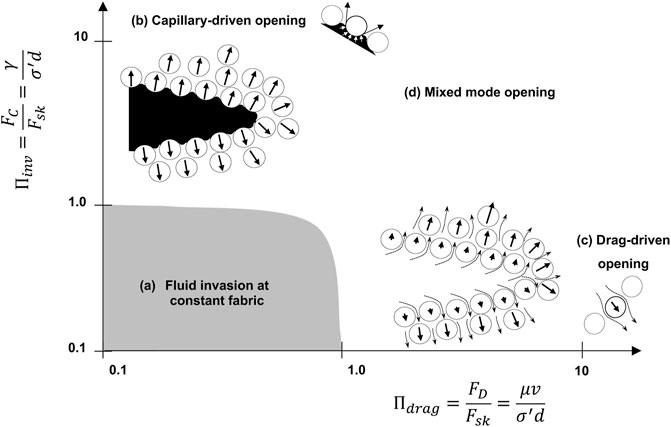
FIGURE 9. Grain-displacive open-mode discontinuities. (A) Fluid invasion without fabric changes. (B) Capillary-driven opening: surface tension and the difference in fluid pressures across the fluid interface are responsible for the resulting particle forces. (C) Drag-driven opening: drag forces push particles and accumulate away from the opening. (D) Mixed mode opening.

Particles experience two forces in single-phase fluid flow (without changes in pore fluid chemistry): the skeletal force $F_{Sk}$ and the drag force $F_D$. The associated dimensionless ratio is

${\mathrm{\Pi }}_{drag}=\frac{F_D}{F_{Sk}}\propto \frac{\mu v}{\sigma \prime d}.$

Therefore, high invasion velocity v, low effective stress σ’ and small grain size d favor the development of drag-driven open-mode discontinuities.

Earthquakes are natural triggers of fluid-driven localizations. When saturated loose sands liquefy during an earthquake, the liquefied layer typically forms at a depth 5 m < z < 20 m, i.e., sufficiently deep to be contractive but shallow enough so that the dynamic strain exceeds the elastic threshold strain (Ishihara, 1993; 1997). During liquefaction, the effective stress vanishes and the pore fluid pressure reaches the overburden stress (Ishihara, 1993; Lee and Santamarina, 2007). The excess pore pressure may gradually drain through the upper unliquefied layer or trigger a vertical open-mode discontinuity for rapid drainage; in fact, the aligned sand boils often observed on grassy fields reveal the underlying open discontinuity that links the liquefied layer to the surface (Chameau et al., 1991; Bardet and Kapuskar, 1993; Schneider and Mayne, 2000; Sukkarak et al., 2021).

3.2 Multi-Phase Fluids—Immiscible Invasion

Immiscible fluids experience capillarity in the pore space of granular materials, and the wetting fluid is at a lower pressure than the non-wetting fluid, Δu = u_n-u_w. The granular skeleton picks up the pressure difference in terms of a change in effective stress (hence, Bishop’s model). At the particle scale, the capillary force acting on a particle F_C = πd⋅γ can significantly alter the preexisting effective stress dependent particle forces F_sk = σ′d², where d is the particle diameter and γ the interfacial tension. The ratio between these two forces

${\mathrm{\Pi }}_{inv}=\frac{F_C}{F_{Sk}}\propto \frac{\gamma }{\sigma \prime d}$

defines two distinct invasion regimes (Figure 9 - Shin and Santamarina, 2011b; see also Holtzman et al., 2012; Carrillo and Bourg, 2021):

1) pore-invasive ${\text{Π}}_{inv}=\gamma /\left({\sigma }^{\prime }d\right)\ll 1$: the non-wetting phase travels from pore-to-pore across pore throats without disturbing the granular skeleton.

2) grain-displacive ${\text{Π}}_{inv}=\gamma /\left({\sigma }^{\prime }d\right)\gg 1$: the capillary pressure displaces sediment grains away from the invading phase.

In general, invasion is grain-displacive in fine-grained sediments at low effective stress. Still, other forms of mixed-fluid instabilities can take place in coarse-grained sediments, but these are mechanically decoupled from the granular skeleton (refer to “fluid-driven instabilities at constant fabric” described in the previous section).

The concepts of interfacial tension, contact angle, and capillary pressure explored earlier for immiscible fluids can be extended to analyze other systems, including water-ice (i.e., frozen ground engineering) and water-hydrates (i.e., hydrates bearing sediments). Often, the immiscible fluid invades the boundary and remains as a continuous phase. However, ice, hydrate, and gas bubbles, may nucleate inside the porous. Examples of gas nucleation include exsolution during depressurization (e.g., sampling marine sediments), water cavitation (e.g., rapid shear induced dilation under undrained conditions), or heat-induced phase transformation. Boundary invasion or internal nucleation may result in the same degree of saturation, yet there are salient differences in other macroscale physical properties such as the capillarity pressure vs. degree of saturation, relative permeabilities, bulk stiffness, consolidation, and shear strength (Sills et al., 1991; Rebata-Landa and Santamarina, 2012; Jang and Santamarina, 2014).

Desiccation cracks: non-wetting air invasion into a water-saturated sediment. Consider a clay bed sedimented from a slurry. The supernatant water evaporates until the air-water interface reaches the sediment surface. Further evaporation requires the interface to go down, but the air-water clings onto the water-wet mineral grains, dragging them down (internally, the water experiences suction and the effective stress increases). Eventually, the sediment will resist further compaction, and additional suction causes the air-water interface to invade the sediment, starting at the largest pores (often associated with surface defects). At the invaded defect, suction causes particle displacement normal to and away from the air-water interface. Thus particles displace away from each other at the tip, further air invasion takes place, and eventually forms a desiccation crack (Figures 10A,B; Shin and Santamarina, 2011b; 2011a; Cordero et al., 2017). Desiccation cracks may also nucleate and grow within the sediment, i.e., beneath the surface, when suction triggers gas exsolution or cavitation within the sediment (Figure 10C - Zhao and Santamarina, 2020).

FIGURE 10

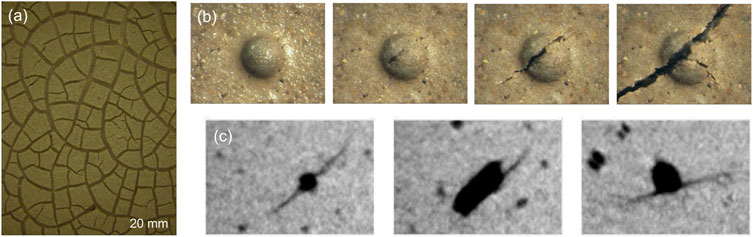
FIGURE 10. Grain-displacive non-wetting fluid invasion: desiccation cracks. (A) Surface desiccation cracks (Shin and Santamarina, 2011b). (B) Crack initiation at a surface defect during drying (Shin and Santamarina, 2011a). (C) Internal desiccation cracks observed using X-ray micro CT (Zhao and Santamarina, 2020).

Non-wetting buoyant fluid columns. Buoyant oil or gas with a density ρ_b may mobilize long column heights H; then, the capillary pressure at the top of the column is $\text{Δ}u=H·\left({\rho }_w-{\rho }_b\right)g$. In agreement with the aforementioned discussion, the buoyant column may migrate upwards by pore-invasion or it may cause grain-displacement and propagate an open-mode discontinuity. We captured high-resolution grain-displacive gas invasion patterns by injecting air into transparent sediments subjected to controlled effective stress (see Sun and Santamarina, 2019a for details). Gas ascends as bubbles at very low effective stress and high ${\text{Π}}_{inv}$ (Figure 11A). At intermediate effective stresses, the gas inclusion starts growing as a succession of cavity expansion events (Figures 11B, B); gradually, the cavity develops corners and edges; local fractures initiate at high curvature zones and eventually grow to form either one or two thin circular planar openings, or “fractures” (Figures 11B,C). Gases expand as the water pressure decreases during ascension and often form pockmarks when they reach the seafloor.

FIGURE 11

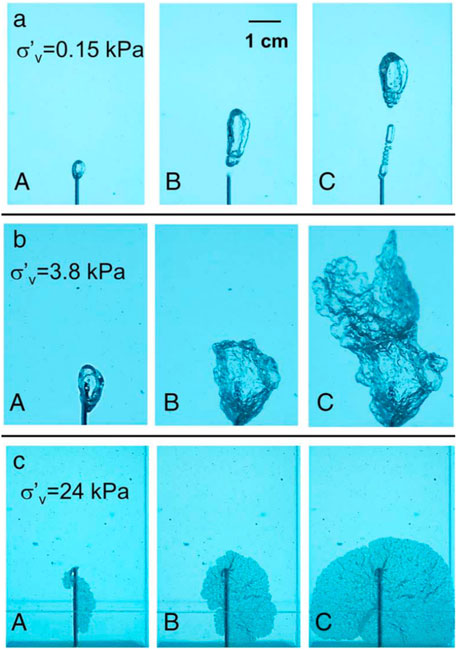
FIGURE 11. Grain-displacive gas migration in a transparent fine-grained granular medium at different vertical effective stress levels: (A) bubble at ${\sigma }^{\text{′}}=0.15\text{ kPa}$; (B) cavity expansion followed by planar opening at ${\sigma }^{\text{′}}=3.8\text{ kPa}$; and (C) open discontinuity at ${\sigma }^{\text{′}}=24\text{ kPa}$ (Sun and Santamarina, 2019a).

Non-wetting ice and hydrate growth in sediments - The local effective stress. Ice and hydrates require the proper pressure and temperature conditions for phase stability; in addition, hydrate formation is typically gas-limited. When appropriate, both ice and hydrate nucleate on mineral surfaces (heterogeneous nucleation) and grow into the pore space until they reach the surrounding pore walls. Further growth of the non-wetting ice or hydrate phases is either pore invasive ${\text{Π}}_{inv}=\gamma /\left({\sigma }^{\prime }d\right)\ll 1$ or grain displacive ${\text{Π}}_{inv}=\gamma /\left({\sigma }^{\prime }d\right)\gg 1$. Hydrate or ice lenses and veins result from grain displacive formation (Dai et al., 2012; Lei and Santamarina, 2018). Tomographic images in Figure 12 show various ice topologies in different sediments: 1) the sand specimen shows no ice lenses (pore-invasive ice growth); 2) the bentonite specimen is massively crisscrossed by ice lenses (grain-displacive); 3) the onion-like lens structure that develops in the high water content kaolinite specimen reflects the interplay among ice formation, stress changes, and the evolving sediment compaction with cryo-suction; thus, there are no ice lenses in the core.

FIGURE 12

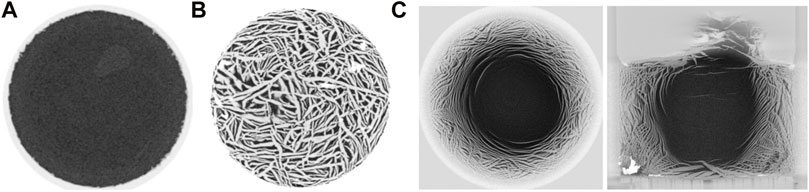
FIGURE 12. Frozen soil. (A) Pore invasive ice formation in sand (no lenses). Grain-displacive ice lenses in (B) bentonite paste and in (C) kaolinite paste (Viggiani et al., 2015).

The onion-like topology of ice lenses in Figure 12C suggests that the growth of grain-displacive instabilities reflects the evolving local effective stress. To test this hypothesis, we prepared cylindrical disk specimens using water saturated kaolinite paste; after consolidation to ${\sigma }_z^{\prime }=30\text{kPa}$ in cylindrical oedometers, the 10 cm diameter and 7 cm thick specimens were extruded from the k_o cell and a radial V-shaped slice was cut and removed from each specimen. Then, we imposed tension at the center of some specimens by pulling the groove walls apart (200 g weights), and compression by sitting other specimens on lateral supports (Yun, 2005). In all tension cases, an ice lens formed and propagated vertically from the groove tip following the tensile field (Figure 13A). In contrast, lenses did not form at the center when the grove tip was under compression (Figure 13B). These results and the onion-shaped topology of ice lenses in Figure 12 confirm that the growth of mechanically-coupled grain-displacive instabilities responds to and alters the local effective stress field (Note: this observation applies to all instabilities discussed in this section).

FIGURE 13

FIGURE 13. Grain-displacive ice lens formation is affected by and eventually affects the local effective stress (Note: this observation applies to all fluid-driven instabilities that affect fabric). (A) Ice lens nucleates and grows at the tip of the wedge when the tip is under tension. (B) Ice lenses grow at various locations at a distance from the tip when the tip is under compression. Sketches on the left show the experimental configurations (Yun, 2005).

Wetting fluid imbibition: capillary contraction. Spontaneous water imbibition into a dry or partially saturated hydrophilic soil tends to cause volume contraction as capillary forces pull particles towards the invading water front. Potential instabilities include peripheral open-mode discontinuities surrounding the area subjected to wetting, and pronounced volume collapse (e.g., collapsible loess—combines cementation dissolution and loss of suction at interparticle contacts—Barden, McGown and Collins, 1973; Houston et al., 1988; Rinaldi et al., 2001; Lourenco et al., 2012; Bruchon et al., 2013; Li et al., 2016). On the other hand, partially saturated, dense soils and soils with swelling minerals may swell when water content increases (Berney, 2004).

3.3 Reactive Fluid Flow

Reactive fluids traverse the granular medium, causing either mineral dissolution or precipitation. Precipitation is self-homogenizing because transmissivity decreases more rapidly along the more conductive pathways (i.e., negative feedback); overall, precipitation produces a marked increase in stiffness, dilative tendency, and strength (by either adding cohesion or increasing the friction angle —Jung et al., 2012).

On the other hand, post-depositional dissolution is significantly more complex. Initially, dissolution evolves as predicted in the dimensionless Pe-Da space for rigid porous media (Figure 8). Rather than wormhole formation (limited by arching instability), grain dissolution readily affects interparticle coordination and forces, triggers fabric rearrangement, and the void ratio evolves towards a stress-dependent terminal value closer to e_max. Consequently, both hydraulic and mechanical properties are affected; in particular, there is an increased contractive tendency (Cha and Santamarina, 2014). Furthermore, experimental and discrete element DEM simulation results show that 1) the horizontal stress ratio k_o decreases during dissolution and it can reach the active value k_a (i.e., internal shear failure), often followed by horizontal stress recovery; 2) the anisotropy in coordination reaches a maximum as the stress ratio approaches k_a, and 3) there is a marked difference in the internal fabric between the initial and post-dissolution conditions even if boundary stresses return to similar values (Shin and Santamarina, 2009; Cha and Santamarina, 2016, 2019a).

Minerals dissolve preferentially at grain contacts under high stress. Solutes diffuse towards the pore space and reprecipitate on unstressed grain surfaces nearby. (Note: this phenomenon is known as pressure solution Weyl, 1959; Rutter, 1983; Etheridge et al., 1984; Fowler and Yang, 1999; Croizé et al., 2010). Pressure-dependent mineral dissolution adds additional complexity: strong force chains in the granular skeleton collude with force-dependent dissolution to create the positive feedback dissolution that promotes the emergence of shear localization as the stress ratio (or force anisotropy) reaches failure conditions under zero lateral strain and constant vertical stress boundary conditions (Cha and Santamarina, 2019b). In the shear band, the porosity is higher and the coordination number is lower than in the surrounding soil mass, strong force chains form and grains experience faster dissolution (Figure 14). Shear discontinuities triggered by mineral dissolution may explain the non-tectonic origin of polygonal faults observed in marine sediments and lacustrine deposits (Cartwright and Dewhurst, 1998; Shin et al., 2008).

FIGURE 14

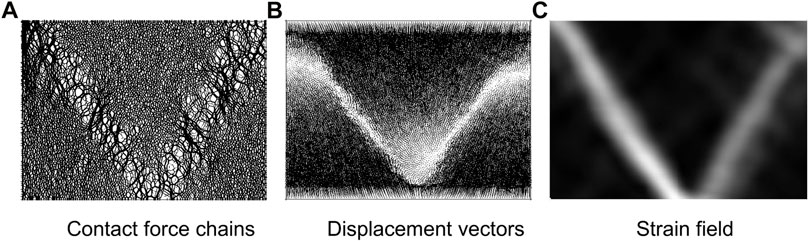
FIGURE 14. Shear bands during dissolution. Pressure solution creates the positive feedback mechanism that leads to shear band formation (modified from Cha and Santamarina, 2019b).

3.4 Particle-Laden Fluids

Flowing fluids can remove and drag grains away. Particle deposition takes place downstream as the flow velocity decreases and its carrying capacity diminishes. The geological record has extensive evidence of sediment erosion-and-deposition phenomena, including: cm-scale sand boils downstream of eroding dams; km-scale mud volcanoes (e.g., Lusi—Indonesia); pipes; and sand dikes observed in marine seismic sections (Hovland et al., 2002; Chand et al., 2012; Moss et al., 2012).

At low fine content, the overburden load is carried by the skeleton-forming coarse grains, and load-free fine particles can be detached and dragged away (Skempton and Brogan, 1994; Moffat et al., 2011). In this case, particle erosion is accompanied by an increase in hydraulic conductivity but without volume change (Suffusion—Fannin et al., 2015). Soils sensitive to suffusion fall under the GF(F), G(F), G(G), GS(S), S(F), or S(S) groups in the Revised Soil Classification System (See Castro et al., 2022). At the macroscale, the feedback mechanism in suffusion resembles dissolution channeling, yet mass removal takes place as grains rather than dissolved species.

On the other hand, energy-intensive erosion may gradually destabilize the load carrying skeleton, causing significant volumetric contraction and even skeletal collapse (suffosion). Regressive or backward erosion piping is a major concern in dam stability (a potential mechanism behind the Teton dam’s failure—Sherard, 1987). It requires long seepage pathways to minimize the gradient at the exit or filters against clay cores to prevent fine migration (Li and Jonathan Fannin, 2008; Chang and Zhang, 2013; Hendron, 2013; Robbins and Van Beek, 2015; Santamarina et al., 2019).

3.5 Instabilities Caused by Other Fluid-Skeleton Couplings

All forms of energy are coupled, including thermal, chemical, hydraulic, and mechanical THCM (Mitchell, 1991). Under the right boundary conditions, mechanically-coupled processes can eventually cause instabilities in granular media. Two examples follow:

1) Thermo-hydro-mechanical THM coupling: thermal water expansion can build up pore pressure and cause a hydraulic fracture if the rate of heating is higher than the rate of pore water pressure dissipation; both are diffusion processes, therefore the ratio ${\text{Π}}_{THM}=D_T/c_v$ between the thermal diffusion D_T and pressure diffusion c_v coefficients determines the domain for this localization. For saturated soils, the thermal diffusion coefficient varies between D_T = 4⋅10⁻⁷ m²/s for clays to D_T = 8⋅10⁻⁷ m²/s for sands, while the coefficient of consolidation can range between c_v ≤ 10^–8 m²/s for clays to c_v ≥ 10^–3 m²/s for sands (Márquez et al., 2016). Clearly, ${\text{Π}}_{THM}$ increases for high specific surface soils thus clay-controlled fabrics are prone to thermal fracking. Given its massive expansion, water-to-steam transformation is particularly detrimental (the expansion ratio is ∼1,600 at atmospheric pressure). Figure 15 shows two examples of thermal fracking: a mud ball exposed to microwave heating (Figure 15A) and a sedimentary layer subjected to lava flow (Figure 15B).

2) Chemo-hydro-mechanical CHM coupling: A diffusing salt front causes a pressure front that precedes it. The pressure front can produce a hydraulic fracture, followed by surface contraction cracks above it (recently observed by Mengwei Liu in our laboratory). These CHM-driven instabilities result from changes in electrical interparticle forces (van der Waals, double layer, osmotic) and may emerge in high specific surface fine-grained clayey sediments. By contrast, the dissolution-based instabilities described earlier apply to coarse-grained sediments such as silts and sands.

FIGURE 15

FIGURE 15. Thermo-hydro fractures. (A) Extensively fractured kaolinite paste after heating in microwave oven (scale = 1 mm). (B) Natural thermo-hydro fracture (scale = 25 m–Madain Saleh, Saudi Arabia).

4 Discussion

The previous sections identified a wide range of localizations and described the underlying positive feedback mechanisms conducive to instabilities. Table 2 summarizes the critical dimensionless ratios involved in these processes. In all cases, we focused on pore and particle scale phenomena to analyze the initiation and evolution of instabilities.

TABLE 2

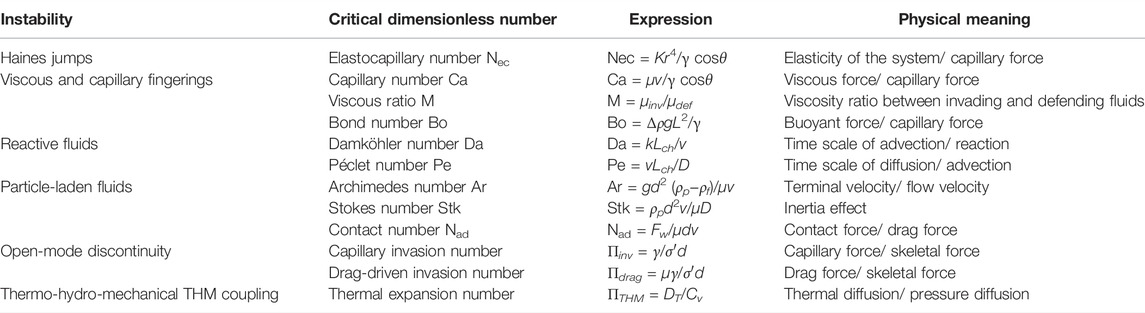
TABLE 2. Pore/particle scale dimensionless ratios that define the domains for fluid-driven instabilities. The selected ratios presented here resemble the analysis in the text.

Forces. The magnitude of interparticle forces is a function of grain-size; therefore, grain-size plays a central role in defining the space for various instabilities. Table 3 lists interparticle forces and corresponding equations for first-order estimates. We can see that grain weight F_W, buoyancy and inertia relate to volume f (d³), the force acting on a grain that is part of a load carrying skeleton F_sk scales with its area f (d²), while drag F_D, capillary F_C, and electrical interactions are proportional to size f(d). These equations define straight lines in log-log plots; therefore, the different forces intersect at specific particle sizes. For example, self-weight and the capillary force are equal at d ≈ 2 mm; self-weight prevails for larger particles while capillarity gains relevance for finer soils. Similarly, we can anticipate that electrical interactions gain relevance for high specific surface submicron particles and vanish in silts and sands.

TABLE 3

TABLE 3. Particle-level forces. They scale with d, d²⁺, and d³. The ratio between the skeletal force and all other forces confirms the importance of the particle buoyant weight in coarse-grained sediments and of capillary, drag, and electrical forces on phenomena that take place in fine-grained sediments (Mitchell, 1976; Santamarina, 2003).

Instability, nucleation, and growth. Scaling analyses and dimensionless ratios hide the intricate physical details at the pore/grain scales that eventually lead to macroscale instabilities. Localizations start at nucleation sites that are typically associated with the inherent variability in granular materials. For example, liquefaction and shear band formation are delayed in homogeneous sands compared to heterogeneous specimens at the same density (Frost et al., 2019). Similarly, desiccation cracks start at surface or subsurface imperfections, or “dimples” (see Figure 11), and dissolution wormholes evolve from the preferential conduction paths initially present in the porous network. In fact, numerical simulations that capture natural variability systematically render more “natural” results (e.g., a porosity random field with or without spatial correlation).

After nucleation, positive feedback mechanisms sustain further growth. For example, there are pronounced differences in the interparticle forces around an open-mode discontinuity triggered by viscous forces (hydraulic fracture) and by capillary forces (e.g., desiccation crack or ice lens). Yet, particle forces cause unloading and extension at the opening tip in both cases, which favors water invasion (in hydraulic fractures) and interface invasion (in desiccation cracks and ice lenses). Therefore, macroscale simulations require particularly sensitive relations between the permeability and void ratio (hydraulic fracture), or the entry pressure and void ratio (in desiccation cracks).

We can extend this discussion to all forms of fluid-driven granular instabilities; analysis and simulations must capture the governing conditions in terms of dimensionless ratios, recognize the local pore and grain-scale processes, identify the source of positive feedback, and select constitutive relations with high sensitivity to local changes.

Local vs. global instabilities. The evolution of local instabilities may cease and not evolve into large scale instabilities. For example, 1) the contact line displacement for a liquid advancing on a flat surface consists of numerous local stick-slip events, yet the macro-scale movement and front geometry may appear smooth (high frequency jumps are aliased in most observations); 2) pore-scale Haines jumps do not necessarily define macroscale invasion patterns; and 3) viscous fingers reach a characteristic length scale. On the other hand, dissolution wormholes can grow beyond the scale of the engineering problem under consideration. In some cases, the upscaling of local instabilities to global instabilities will depend on global properties such as spatial variability in grain size, pore size, mineralogy, and contact forces.

5 Conclusion

Fluid-driven instabilities are ubiquitous in soils and sediments. However, they are often overlooked in the interpretation of laboratory studies as well as in analytical solutions and numerical simulations. These instabilities can emerge across scales and are readily observed in millimeter-scale microfluidic chips to kilometer-scale features in the geological record.

Some fluid-driven instabilities take place within the pore space without affecting the granular skeleton. These instabilities are driven by differences in viscosity between the invading and the defending fluids, interfacial tension, and capillarity and cause characteristic invasion patterns. Pore-scale capillary instabilities result from a combination of hysteresis in contact angle and interfacial tension, elastic deformations, and the longitudinal pore geometry. Sudden jumps in fluid interfaces and associated snap-offs cause rapid redistribution of phases. Particle-laden fluids may also cause instabilities in rigid porous media.

More intricate instabilities take place when fluids affect the granular skeleton. In general, hydro-thermo-chemo-mechanically coupled processes affect the sediment structure and can cause instabilities under certain conditions.

Fluid-driven instabilities coupled with fabric changes can be generated by viscous forces in single-phase fluid injection (hydraulic fracture) or by capillary forces produced by an immiscible fluid (grain-displacive invasion: desiccation cracks, ice and hydrate lenses, gas and oil-driven openings, and capillary collapse). The marked differences between viscosity and capillarity-driven open-mode discontinuities require careful analysis prior to numerical modeling.

Mineral dissolution caused by the injection of reactive fluids evolves as a function of the interplay between various rates (advection, diffusion, and reaction), the spatial distribution of reactive minerals, and the granular skeleton response during dissolution. Instabilities include wormhole formation and the emergence of shear bands (even in sediments under zero lateral strain conditions).

Other fluid-driven instabilities in granular materials are associated with particle transport (piping erosion), thermal changes (thermo-hydraulic fractures), and changes in electrical interparticle interaction (osmotic-hydraulic fractures and contractive openings).

In all cases, instabilities involve some form of positive feedback mechanism; conversely, self-homogenizing processes tend to be stabilizing for fluid flow and granular stability. The types of instabilities and their evolving topologies can be systematically organized in the space defined by dimensionless ratios of time (or rate), length scales, and forces (or pressure and stress).

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

G. Abelskamp edited the manuscript. M. Benitez obtained the hysteretic interfacial tension and contact angle data. Support for this research was provided by the KAUST Endowment.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Arji, H., Al-Azman, A., Le-Hussain, F., and Regenauer-Lieb, K. (2021). Acid Stimulation in Carbonates: A Laboratory Test of a Wormhole Model Based on Damköhler and Péclet Numbers. J. Petroleum Sci. Eng. 203, 108593. doi:10.1016/J.PETROL.2021.108593

CrossRef Full Text | Google Scholar

Al-Sahhaf, T., Elkamel, A., Suttar Ahmed, A., and Khan, A. R. (2005). The Influence of Temperature, Pressure, Salinity, and Surfactant Concentration on the Interfacial Tension of the N-Octane-Water System. Chem. Eng. Commun. 192, 667–684. doi:10.1080/009864490510644

CrossRef Full Text | Google Scholar

An, S., Erfani, H., Godinez‐Brizuela, O. E., and Niasar, V. (2020). Transition From Viscous Fingering to Capillary Fingering: Application of GPU‐Based Fully Implicit Dynamic Pore Network Modeling. Water Resour. Res. 56 (12), e2020WR028149. doi:10.1029/2020WR028149

CrossRef Full Text | Google Scholar

Andújar Márquez, J., Martínez Bohórquez, M., and Gómez Melgar, S. (2016). Ground Thermal Diffusivity Calculation by Direct Soil Temperature Measurement. Application to Very Low Enthalpy Geothermal Energy Systems. Sensors 16, 306. doi:10.3390/s16030306

PubMed Abstract | CrossRef Full Text | Google Scholar

Bachu, S., and Bennion, D. B. (2009). Interfacial Tension between CO2, Freshwater, and Brine in the Range of Pressure from (2 to 27) MPa, Temperature from (20 to 125) °C, and Water Salinity from (0 to 334 000) mg·L−1. J. Chem. Eng. Data 54, 765–775. doi:10.1021/je800529x

CrossRef Full Text | Google Scholar

Barden, L., McGown, A., and Collins, K. (1973). The Collapse Mechanism in Partly Saturated Soil. Eng. Geol. 7, 49–60. doi:10.1016/0013-7952(73)90006-9

CrossRef Full Text | Google Scholar

Bardet, J. P., and Kapuskar, M. (1993). Liquefaction Sand Boils in San Francisco during 1989 Loma Prieta Earthquake. J. Geotech. Engrg. 119, 543–562. doi:10.1061/(asce)0733-9410(1993)119:3(543)

CrossRef Full Text | Google Scholar

Benitez, M. D. (2022). Compex Fluids for Geo-Energy Applications. PhD thesis.

Google Scholar

Berg, S., Ott, H., Klapp, S. A., Schwing, A., Neiteler, R., Brussee, N., et al. (2013). Real-time 3D Imaging of Haines Jumps in Porous Media Flow. Proc. Natl. Acad. Sci. U.S.A. 110, 3755–3759. doi:10.1073/pnas.1221373110

PubMed Abstract | CrossRef Full Text | Google Scholar

Berney, E. S. (2004). A Partially Saturated Constitutive Theory for Compacted Fills. Available at: https://apps.dtic.mil/sti/citations/ADA425462 (Accessed April 26, 2022).doi:10.21236/ada425462

CrossRef Full Text | Google Scholar

Bruchon, J.-F., Pereira, J.-M., Vandamme, M., Lenoir, N., Delage, P., and Bornert, M. (2013). Full 3D Investigation and Characterisation of Capillary Collapse of a Loose Unsaturated Sand Using X-Ray CT. Granul. Matter 15, 783–800. doi:10.1007/s10035-013-0452-6

CrossRef Full Text | Google Scholar

Cardona, A., Finkbeiner, T., and Santamarina, J. C. (2021). Natural Rock Fractures: From Aperture to Fluid Flow. Rock Mech. Rock Eng. 54, 5827–5844. doi:10.1007/s00603-021-02565-1

CrossRef Full Text | Google Scholar

Carrillo, F. J., and Bourg, I. C. (2021). Capillary and Viscous Fracturing during Drainage in Porous Media. Phys. Rev. E 103, 063106. doi:10.1103/PhysRevE.103.063106

PubMed Abstract | CrossRef Full Text | Google Scholar

Cartwright, J. A., and Dewhurst, D. N. (1998). Layer-bound Compaction Faults in Fine-Grained Sediments. Geol. Soc. Am. Bull. 110, 1242–1257. doi:10.1130/0016-7606(1998)110<1242:lbcfif>2.3.co;2

CrossRef Full Text | Google Scholar

Cartwright, J., and Santamarina, C. (2015). Seismic Characteristics of Fluid Escape Pipes in Sedimentary Basins: Implications for Pipe Genesis. Mar. Petroleum Geol. 65, 126–140. doi:10.1016/j.marpetgeo.2015.03.023

CrossRef Full Text | Google Scholar

Castro, G. M., Park, J., and Santamarina, J. C. (2022). Revised Soil Classification System RSCS: Implementation and Engineering Implications. Submitt. Publ.

Google Scholar

Cha, M., and Santamarina, J. C. (2014). Dissolution of Randomly Distributed Soluble Grains: Post-dissolution K0-Loading and Shear. Géotechnique 64, 828–836. doi:10.1680/geot.14.p.115

CrossRef Full Text | Google Scholar

Cha, M., and Santamarina, J. C. (2016). Hydro-chemo-mechanical Coupling in Sediments: Localized Mineral Dissolution. Geomechanics Energy Environ. 7, 1–9. doi:10.1016/j.gete.2016.06.001

CrossRef Full Text | Google Scholar

Cha, M., and Santamarina, J. C. (2019a). Localized Dissolution in Sediments under Stress. Granul. Matter 21, 79. doi:10.1007/s10035-019-0932-4

CrossRef Full Text | Google Scholar

Cha, M., and Santamarina, J. C. (2019b). Pressure-dependent Grain Dissolution Using Discrete Element Simulations. Granul. Matter 21, 101. doi:10.1007/s10035-019-0960-0

CrossRef Full Text | Google Scholar

Chameau, J. L., Clough, G. W., Reyna, F., and Frost, J. D. (1991). Liquefaction Response of San Francisco Bayshore Fills. Bull. Seismol. Soc. Am. 81, 1998–2018. doi:10.1785/BSSA0810051998

CrossRef Full Text | Google Scholar

Chand, S., Thorsnes, T., Rise, L., Brunstad, H., Stoddart, D., Bøe, R., et al. (2012). Multiple Episodes of Fluid Flow in the SW Barents Sea (Loppa High) Evidenced by Gas Flares, Pockmarks and Gas Hydrate Accumulation. Earth Planet. Sci. Lett. 331-332, 305–314. doi:10.1016/j.epsl.2012.03.021

CrossRef Full Text | Google Scholar

Chang, C. H., and Franses, E. I. (1992). Modified Langmuir-Hinselwood Kinetics for Dynamic Adsorption of Surfactants at the Air/water Interface. Colloids Surfaces 69, 189–201. doi:10.1016/0166-6622(92)80230-Y

CrossRef Full Text | Google Scholar

Chang, D. S., and Zhang, L. M. (2013). Extended Internal Stability Criteria for Soils under Seepage. Soils Found. 53, 569–583. doi:10.1016/j.sandf.2013.06.008

CrossRef Full Text | Google Scholar

Chatzis, I., and Morrow, N. R. (1984). Correlation of Capillary Number Relationships for Sandstone. Soc. Pet. Eng. J. 24, 555–562. doi:10.2118/10114-pa

CrossRef Full Text | Google Scholar

Cordero, J. A., Useche, G., Prat, P. C., Ledesma, A., and Santamarina, J. C. (2017). Soil Desiccation Cracks as a Suction-Contraction Process. Géotechnique Lett. 7, 279–285. doi:10.1680/jgele.17.00070

CrossRef Full Text | Google Scholar

Croizé, D., Renard, F., Bjørlykke, K., and Dysthe, D. K. (2010). Experimental Calcite Dissolution under Stress: Evolution of Grain Contact Microstructure during Pressure Solution Creep. J. Geophys. Res. 115 (B9). doi:10.1029/2010JB000869

CrossRef Full Text | Google Scholar

Dai, S., Santamarina, J. C., Waite, W. F., and Kneafsey, T. J. (2012). Hydrate Morphology: Physical Properties of Sands with Patchy Hydrate Saturation. J. Geophys. Res. 117, B11205. doi:10.1029/2012JB009667

CrossRef Full Text | Google Scholar

Dawson, H. E., and Roberts, P. V. (1997). Influence of Viscous, Gravitational, and Capillary Forces on DNAPL Saturation. Groundwater 35, 261–269. doi:10.1111/j.1745-6584.1997.tb00083.x

CrossRef Full Text | Google Scholar

de Gennes, P.-G. (1985). Wetting: Statics and Dynamics. Rev. Mod. Phys. 57, 827–863. doi:10.1103/revmodphys.57.827

CrossRef Full Text | Google Scholar

Derr, N. J., Fronk, D. C., Weber, C. A., Mahadevan, A., Rycroft, C. H., and Mahadevan, L. (2020). Flow-Driven Branching in a Frangible Porous Medium. Phys. Rev. Lett. 125, 158002. doi:10.1103/PhysRevLett.125.158002

PubMed Abstract | CrossRef Full Text | Google Scholar

Dreybrodt, W. (1990). The Role of Dissolution Kinetics in the Development of Karst Aquifers in Limestone: a Model Simulation of Karst Evolution. J. Geol. 98, 639–655. doi:10.1086/629431

CrossRef Full Text | Google Scholar

Eral, H. B., ’t Mannetje, D. J. C. M., and Oh, J. M. (2013). Contact Angle Hysteresis: A Review of Fundamentals and Applications. Colloid Polym. Sci. 291, 247–260. doi:10.1007/s00396-012-2796-6

CrossRef Full Text | Google Scholar

Etheridge, M. A., Wall, V. J., Cox, S. F., and Vernon, R. H. (1984). High Fluid Pressures During Regional Metamorphism and Deformation: Implications for Mass Transport and Deformation Mechanisms. J. Geophys. Res. 89, 4344–4358. doi:10.1029/jb089ib06p04344

CrossRef Full Text | Google Scholar

Fannin, R. J., Arulrajah, A., Slangen, P., Evans, R., Arulrajah, A., and Evans, R. (2015). Discussion: On the Distinct Phenomena of Suffusion and Suffosion. Geotech. Lett. 5, 129–130. doi:10.1680/jgele.15.0001710.1680/geolett.15.00017

CrossRef Full Text | Google Scholar

Ferer, M., Ji, C., Bromhal, G. S., Cook, J., Ahmadi, G., and Smith, D. H. (2004). Crossover from Capillary Fingering to Viscous Fingering for Immiscible Unstable Flow: Experiment and Modeling. Phys. Rev. E 70, 16303. doi:10.1103/PhysRevE.70.016303

PubMed Abstract | CrossRef Full Text | Google Scholar

Fowler, A. C., and Yang, X. (1999). Pressure Solution and Viscous Compaction in Sedimentary Basins. J. Geophys. Res. 104, 12989–12997. doi:10.1029/1998jb900029

CrossRef Full Text | Google Scholar

Fredd, C. N. (2000). Dynamic Model of Wormhole Formation Demonstrates Conditions for Effective Skin Reduction During Carbonate Matrix Acidizing. SPE Permian Basin Oil Gas. Recover. Conf. Proc. doi:10.2118/59537-ms

CrossRef Full Text | Google Scholar

Fredd, C. N., and Fogler, H. S. (1998). Influence of Transport and Reaction on Wormhole Formation in Porous Media. AIChE J. 44, 1933–1949. doi:10.1002/aic.690440902

CrossRef Full Text | Google Scholar

Frost, J. D., Roy, N., Chen, C.-C., Park, J.-Y., Jang, D.-J., Lu, Y., et al. (2019). Quantitative Analysis of Microstructure Properties and Their Influence on Macroscale Response. KSCE J. Civ. Eng. 23, 3777–3792. doi:10.1007/S12205-019-0713-Y

CrossRef Full Text | Google Scholar

Gao, N., Geyer, F., Pilat, D. W., Wooh, S., Vollmer, D., Butt, H.-J., et al. (2018). How Drops Start Sliding over Solid Surfaces. Nat. Phys. 14, 191–196. doi:10.1038/nphys4305

CrossRef Full Text | Google Scholar

Gauglitz, P. A., and Radke, C. J. (1989). Dynamics of Haines Jumps for Compressible Bubbles in Constricted Capillaries. AIChE J. 35, 230–240. doi:10.1002/aic.690350207

CrossRef Full Text | Google Scholar

Gibbs, J. W. (1878). On the Equilibrium of Heterogeneous Substances. Am. J. Sci. s3-16, 441–458. doi:10.2475/ajs.s3-16.96.441

CrossRef Full Text | Google Scholar

Golfier, F., Zarcone, C., Bazin, B., Lenormand, R., Lasseux, D., and Quintard, M. (2002). On the Ability of a Darcy-Scale Model to Capture Wormhole Formation during the Dissolution of a Porous Medium. J. Fluid Mech. 457, 213–254. doi:10.1017/S0022112002007735

CrossRef Full Text | Google Scholar

He, Y., Yazhgur, P., Salonen, A., and Langevin, D. (2015). Adsorption-desorption Kinetics of Surfactants at Liquid Surfaces. Adv. Colloid Interface Sci. 222, 377–384. doi:10.1016/j.cis.2014.09.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Helfrich, K. R. (1995). Thermo-viscous Fingering of Flow in a Thin Gap: A Model of Magma Flow in Dikes and Fissures. J. Fluid Mech. 305, 219–238. doi:10.1017/S0022112095004605

CrossRef Full Text | Google Scholar

Hendron, A. (2013). Improving Dam Safety with Lessons Learned from Case Histories of Dam Failures and Unacceptable Dam Performance. Karl Terzaghi Lect.

Google Scholar

Holtzman, R., Szulczewski, M. L., and Juanes, R. (2012). Capillary Fracturing in Granular Media. Phys. Rev. Lett. 108, 264504. doi:10.1103/PhysRevLett.108.264504

PubMed Abstract | CrossRef Full Text | Google Scholar

Houston, S. L., Houston, W. N., and Spadola, D. J. (1988). Prediction of Field Collapse of Soils Due to Wetting. J. Geotechnical Eng. 114114, 401–458. doi:10.1061/(asce)0733-9410(1988)114:1(40)

CrossRef Full Text | Google Scholar

Hovland, M., Gardner, J. V., and Judd, A. G. (2002). The Significance of Pockmarks to Understanding Fluid Flow Processes and Geohazards. Geofluids 2, 127–136. doi:10.1046/j.1468-8123.2002.00028.x

CrossRef Full Text | Google Scholar

Hua, X., Bevan, M. A., and Frechette, J. (2016). Reversible Partitioning of Nanoparticles at an Oil-Water Interface. Langmuir 32, 11341–11352. doi:10.1021/ACS.LANGMUIR.6B02255

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishihara, K. (1993). Liquefaction and Flow Failure during Earthquakes. Géotechnique 43, 351–451. doi:10.1680/geot.1993.43.3.351

CrossRef Full Text | Google Scholar

Ishihara, K. (1997). Soil Behaviour in Earthquake Geotechnics. Choice Rev. Online 34, 5113. doi:10.5860/choice.34-5113

CrossRef Full Text | Google Scholar

Islam, M. N., and Azaiez, J. (2010). Miscible Thermo-Viscous Fingering Instability in Porous Media. Part 1: Linear Stability Analysis. Transp. Porous Med. 84, 821–844. doi:10.1007/s11242-010-9555-2

CrossRef Full Text | Google Scholar

Jang, J., Narsilio, G. A., and Santamarina, J. C. (2011). Hydraulic Conductivity in Spatially Varying Media-A Pore-Scale Investigation. Geophys. J. Int. 184, 1167–1179. doi:10.1111/j.1365-246X.2010.04893.x

CrossRef Full Text | Google Scholar

Jang, J., and Santamarina, J. C. (2014). Evolution of Gas Saturation and Relative Permeability during Gas Production from Hydrate-Bearing Sediments: Gas Invasion vs. Gas Nucleation. J. Geophys. Res. Solid Earth 119, 116–126. doi:10.1002/2013JB010480

CrossRef Full Text | Google Scholar

Jang, J., Sun, Z., and Santamarina, J. C. (2016). Capillary Pressure across a Pore Throat in the Presence of Surfactants. Water Resour. Res. 52, 9586–9599. doi:10.1002/2015WR018499

CrossRef Full Text | Google Scholar

Jung, J.-W., Santamarina, J. C., and Soga, K. (2012). Stress-strain Response of Hydrate-Bearing Sands: Numerical Study Using Discrete Element Method Simulations. J. Geophys. Res. 117, 4202. doi:10.1029/2011JB009040

CrossRef Full Text | Google Scholar

Kim, J., Xu, F., and Lee, S. (2017). Formation and Destabilization of the Particle Band on the Fluid-Fluid Interface. Phys. Rev. Lett. 118, 074501. doi:10.1103/PhysRevLett.118.074501

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, S., and Santamarina, J. C. (2015). Reactive Fluid Flow in CO 2 Storage Reservoirs: A 2‐D Pore Network Model Study. Greenh. Gas. Sci. Technol. 5, 462–473. doi:10.1002/ghg.1487

CrossRef Full Text | Google Scholar

Kochmann, D. M., and Bertoldi, K. (2017). Exploiting Microstructural Instabilities in Solids and Structures: From Metamaterials to Structural Transitions. Appl. Mech. Rev. 69 (5). doi:10.1115/1.4037966

CrossRef Full Text | Google Scholar

Lange, A., Schröter, M., Scherer, M. A., Engel, A., and Rehberg, I. (1998). Fingering Instability in a Water-Sand Mixture. Eur. Phys. J. B 4, 475–484. doi:10.1007/s100510050405

CrossRef Full Text | Google Scholar

Langmuir, I. (1918). The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. J. Am. Chem. Soc. 40, 1361–1403. doi:10.1021/ja02242a004

CrossRef Full Text | Google Scholar

Lee, J.-S., and Santamarina, J. C. (2007). Seismic Monitoring Short-Duration Events: Liquefaction in 1gmodels. Can. Geotech. J. 44, 659–672. doi:10.1139/T07-020

CrossRef Full Text | Google Scholar

Lei, L., and Santamarina, J. C. (2018). Laboratory Strategies for Hydrate Formation in Fine‐Grained Sediments. J. Geophys. Res. Solid Earth 123, 2583–2596. doi:10.1002/2017JB014624

CrossRef Full Text | Google Scholar

Lenormand, R., Touboul, E., and Zarcone, C. (1988). Numerical Models and Experiments on Immiscible Displacements in Porous Media. J. Fluid Mech. 189, 165–187. doi:10.1017/s0022112088000953

CrossRef Full Text | Google Scholar

Lenormand, R., Zarcone, C., and Sarr, A. (1983). Mechanisms of the Displacement of One Fluid by Another in a Network of Capillary Ducts. J. Fluid Mech. 135, 337–353. doi:10.1017/S0022112083003110

CrossRef Full Text | Google Scholar

Li, M., and Fannin, R. J. (2008). Comparison of Two Criteria for Internal Stability of Granular Soil. Can. Geotech. J. 45, 1303–1309. GIF. doi:10.1139/T08-046/ASSET/IMAGES/T08-046IE17H

CrossRef Full Text | Google Scholar

Li, P., Vanapalli, S., and Li, T. (2016). Review of Collapse Triggering Mechanism of Collapsible Soils Due to Wetting. J. Rock Mech. Geotechnical Eng. 8, 256–274. doi:10.1016/j.jrmge.2015.12.002

CrossRef Full Text | Google Scholar

Liot, O., Singh, A., Bacchin, P., Duru, P., Morris, J. F., and Joseph, P. (2018). Pore Cross-Talk in Colloidal Filtration. Sci. Rep. 8, 12460. doi:10.1038/s41598-018-30389-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Q., Sun, Z., and Santamarina, J. C. (2021). Self-assembled Nanoparticle-Coated Interfaces: Capillary Pressure, Shell Formation and Buckling. J. Colloid Interface Sci. 581, 251–261. doi:10.1016/j.jcis.2020.07.110

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Q., Zhao, B., and Santamarina, J. C. (2019). Particle Migration and Clogging in Porous Media: A Convergent Flow Microfluidics Study. J. Geophys. Res. Solid Earth 124, 9495–9504. doi:10.1029/2019JB017813

CrossRef Full Text | Google Scholar

Menke, H. P., Bijeljic, B., and Blunt, M. J. (2017). Dynamic Reservoir-Condition Microtomography of Reactive Transport in Complex Carbonates: Effect of Initial Pore Structure and Initial Brine pH. Geochimica Cosmochimica Acta 204, 267–285. doi:10.1016/j.gca.2017.01.053

CrossRef Full Text | Google Scholar

Meyer, E. E., Rosenberg, K. J., and Israelachvili, J. (2006). Recent Progress in Understanding Hydrophobic Interactions. Proc. Natl. Acad. Sci. U.S.A. 103, 15739–15746. doi:10.1073/pnas.0606422103

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, J. K. (1991). Conduction Phenomena: From Theory to Geotechnical Practice. Géotechnique 41, 299–340. doi:10.1680/geot.1991.41.3.299

CrossRef Full Text | Google Scholar

Mitchell, J. K. (1976). Fundamental of Soil Behaviour. Hoboken, New Jersey, United States: John Wiley & Sons.

Google Scholar

Moffat, R., Fannin, R. J., and Garner, S. J. (2011). Spatial and Temporal Progression of Internal Erosion in Cohesionless Soil. Can. Geotech. J. 48, 399–412. doi:10.1139/t10-071

CrossRef Full Text | Google Scholar

Morrow, N. R., and Szabo, J. O. (1970). Physics and Thermodynamics of Capillary Action in Porous Media. Ind. Eng. Chem. 62, 32–56. doi:10.1021/ie50726a006

CrossRef Full Text | Google Scholar

Moss, J. L., Cartwright, J., and Moore, R. (2012). Evidence for Fluid Migration Following Pockmark Formation: Examples from the Nile Deep Sea Fan. Mar. Geol. 303-306, 1–13. doi:10.1016/j.margeo.2012.01.010

CrossRef Full Text | Google Scholar

Mulligan, C. N., Yong, R. N., and Gibbs, B. F. (2001). Surfactant-enhanced Remediation of Contaminated Soil: a Review. Eng. Geol. 60, 371–380. doi:10.1016/S0013-7952(00)00117-4

CrossRef Full Text | Google Scholar

National Academies of Sciences and Medicine, E (2020). Characterization, Modeling, Monitoring, and Remediation of Fractured Rock. Washington, D.C., United States: National Academies Press.

Google Scholar

Peña, T. J., Carvalho, M. S., and Alvarado, V. (2009). Snap-off of a Liquid Drop Immersed in Another Liquid Flowing through a Constricted Capillary. AIChE J. 55, 1993–1999. doi:10.1002/aic.11839

CrossRef Full Text | Google Scholar

Rebata-Landa, V., and Santamarina, J. C. (2012). Mechanical Effects of Biogenic Nitrogen Gas Bubbles in Soils. J. Geotech. Geoenviron. Eng. 138, 128–137. doi:10.1061/(asce)gt.1943-5606.0000571

CrossRef Full Text | Google Scholar

Robbins, B. A., and Van Beek, V. M. (2015). Backward Erosion Piping: A Historical Review and Discussion of Influential Factors. Assoc. State Dam Saf. Off. Dam Saf. 2, 919–938.

Google Scholar

Romanov, D., Gabrovšek, F., and Dreybrodt, W. (2003). Dam Sites in Soluble Rocks: A Model of Increasing Leakage by Dissolutional Widening of Fractures beneath a Dam. Eng. Geol. 70, 17–35. doi:10.1016/S0013-7952(03)00073-5

CrossRef Full Text | Google Scholar

Rutter, E. H. (1983). Pressure Solution in Nature, Theory and Experiment. J. Geol. Soc. 140, 725–740. doi:10.1144/gsjgs.140.5.0725

CrossRef Full Text | Google Scholar

Sandnes, B., Flekkøy, E. G., Knudsen, H. A., Måløy, K. J., and See, H. (2011). Patterns and Flow in Frictional Fluid Dynamics. Nat. Commun. 2, 288. doi:10.1038/ncomms1289

PubMed Abstract | CrossRef Full Text | Google Scholar

Santamarina, J. C., and Jang, J. (2011). Energy Geotechnology: Implications of Mixed Fluid Conditions. Available at: https://egel.kaust.edu.sa/Documents/Papers/Santamarina_2010a.pdf (Accessed September 29, 2019).

Google Scholar

Santamarina, J. C. (2003). Soil Behavior at the Microscale: Particle Forces. Geotechnical-Special-Publication, 25–56. doi:10.1061/40659(2003)2

CrossRef Full Text | Google Scholar

Santamarina, J. C., Torres-Cruz, L. A., and Bachus, R. C. (2019). Why Coal Ash and Tailings Dam Disasters Occur. Science. 364, 526–528. doi:10.1126/SCIENCE.AAX1927

PubMed Abstract | CrossRef Full Text | Google Scholar

Schneider, J. A., and Mayne, P. W. (2000). “Liquefaction Response of Soils in Mid-America Evaluated by Seismic Cone Tests,” in Innovations and Applications In Geotechnical Site Characterization (Denver, CO: Geo), 1–16.

CrossRef Full Text | Google Scholar

Sherard, J. L. (1987). Lessons from the Teton Dam Failure. Eng. Geol. 24, 239–256. doi:10.1016/0013-7952(87)90064-0

CrossRef Full Text | Google Scholar

Shin, H., Santamarina, J. C., and Cartwright, J. A. (2008). Contraction-driven Shear Failure in Compacting Uncemented Sediments. Geol 36, 931–934. doi:10.1130/g24951a.1

CrossRef Full Text | Google Scholar

Shin, H., and Santamarina, J. C. (2011a). Desiccation Cracks in Saturated Fine-Grained Soils: Particle-Level Phenomena and Effective-Stress Analysis. Géotechnique 61, 961–972. doi:10.1680/geot.8.P.012

CrossRef Full Text | Google Scholar

Shin, H., and Santamarina, J. C. (2010). Fluid-driven Fractures in Uncemented Sediments: Underlying Particle-Level Processes. Earth Planet. Sci. Lett. 299, 180–189. doi:10.1016/J.EPSL.2010.08.033

CrossRef Full Text | Google Scholar

Shin, H., and Santamarina, J. C. (2009). Mineral Dissolution and the Evolution of K0. J. Geotech. Geoenviron. Eng. 135, 1141–1147. doi:10.1061/(ASCE)GT.1943-5606.0000053

CrossRef Full Text | Google Scholar

Shin, H., and Santamarina, J. C. (2011b). Open-mode Discontinuities in Soils. Géotechnique Lett. 1, 95–99. doi:10.1680/geolett.11.00014

CrossRef Full Text | Google Scholar

Sills, G. C., Wheeler, S. J., Thomas, S. D., and Gardner, T. N. (1991). Behaviour of Offshore Soils Containing Gas Bubbles. Géotechnique 41, 227–241. doi:10.1680/geot.1991.41.2.227

CrossRef Full Text | Google Scholar

Skempton, A. W., and Brogan, J. M. (1994). Experiments on Piping in Sandy Gravels. Géotechnique 44, 449–460. doi:10.1680/geot.1994.44.3.449

CrossRef Full Text | Google Scholar

Sparks, A. D. W., Gallipoli, D., Augarde, C. E., Toll, D. G., Fisher, P. C., and Congreve, A. (2012). Formation and Evolution of Water Menisci in Unsaturated Granular Media. Géotechnique 62, 1143–1144. doi:10.1680/geot.12.D.004

CrossRef Full Text | Google Scholar

Sukkarak, R., Tanapalungkorn, W., Likitlersuang, S., and Ueda, K. (2021). Liquefaction Analysis of Sandy Soil during Strong Earthquake in Northern Thailand. Soils Found. 61, 1302–1318. doi:10.1016/j.sandf.2021.07.003

CrossRef Full Text | Google Scholar

Sun, Z., Liu, Q., Benitez, M. D., and Santamarina, J. C. (2022). Invasion Patterns Induced by Nanoparticle-Coated Interfaces. Under Prep.

Google Scholar

Sun, Z., and Santamarina, J. C. (2019a). Grain‐Displacive Gas Migration in Fine‐Grained Sediments. J. Geophys. Res. Solid Earth 124, 2274–2285. doi:10.1029/2018JB016394

CrossRef Full Text | Google Scholar

Sun, Z., and Santamarina, J. C. (2019b). Haines Jumps: Pore Scale Mechanisms. Phys. Rev. E 100, 023115. doi:10.1103/physreve.100.023115

PubMed Abstract | CrossRef Full Text | Google Scholar

Valdes, J. R., and Carlos Santamarina, J. (2007). Particle Transport in a Nonuniform Flow Field: Retardation and Clogging. Appl. Phys. Lett. 90, 244101. doi:10.1063/1.2748850

CrossRef Full Text | Google Scholar

Valdes, J. R., and Santamarina, J. C. (2006). Particle Clogging in Radial Flow: Microscale Mechanisms. SPE J. 11, 193–198. doi:10.2118/88819-PA

CrossRef Full Text | Google Scholar

Van Zwieten, R., Van De Laar, T., Sprakel, J., and Schroën, K. (2018). From Cooperative to Uncorrelated Clogging in Cross-Flow Microfluidic Membranes. Sci. Rep. 8, 5687. doi:10.1038/s41598-018-24088-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Viggiani, G., Andò, E., Takano, D., and Santamarina, J. C. (2014). Laboratory X-Ray Tomography: A Valuable Experimental Tool for Revealing Processes in Soils. Geotech. Test. J. 38, 20140060–20140071. doi:10.1520/GTJ20140060

CrossRef Full Text | Google Scholar

Völtz, C., Pesch, W., and Rehberg, I. (2002). Rayleigh-Taylor Instability in a Sedimenting Suspension. Phys. Rev. E 65, 011404. doi:10.1103/PhysRevE.65.011404

CrossRef Full Text | Google Scholar

Weyl, P. K. (1959). Pressure Solution and the Force of Crystallization: a Phenomenological Theory. J. Geophys. Res. 64, 2001–2025. doi:10.1029/jz064i011p02001

CrossRef Full Text | Google Scholar

Young, T. (1805). III. An Essay on the Cohesion of Fluids. Phil. Trans. R. Soc. 95, 65–87. doi:10.1098/rstl.1805.0005

CrossRef Full Text | Google Scholar

Yun, T. S. (2005). Mechanical and Thermal Study of Hydrate Bearing Sediments. PhD Thesis.Available at: https://libproxy.kaust.edu.sa/login?url=https://www.proquest.com/dissertations-theses/mechanical-thermal-study-hydrate-bearing/docview/304999500/se-2?accountid=78788.

Google Scholar

Zhao, B., MacMinn, C. W., and Juanes, R. (2016). Wettability Control on Multiphase Flow in Patterned Microfluidics. Proc. Natl. Acad. Sci. U.S.A. 113, 10251–10256. doi:10.1073/pnas.1603387113

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, B., MacMinn, C. W., Primkulov, B. K., Chen, Y., Valocchi, A. J., Zhao, J., et al. (2019). Comprehensive Comparison of Pore-Scale Models for Multiphase Flow in Porous Media. Proc. Natl. Acad. Sci. U.S.A. 116, 13799–13806. doi:10.1073/pnas.1901619116

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, B., and Santamarina, J. C. (2020). Desiccation Crack Formation beneath the Surface. Géotechnique 70, 181–186. doi:10.1680/jgeot.18.T.019

CrossRef Full Text | Google Scholar

Glossary

A_h [J] Hamaker constant in van der Waals interaction

A [N/m] contact line adhesion

Ar [] Archimedes number

Bo [] bond number

C [mol/L] concentration

c_v [m²/s] pressure diffusion coefficient

Ca [] capillary number

d [m] diameter

D [m²/s] diffusion coefficient

D_T [m²/s] thermal diffusion coefficient

Da [] Damköhler number

e [] void ratio

F [N] force (c: capillary; b: buoyant; D: drag; sk: skeletal; W: grain weight; EI: electrical interaction; wall: wall interaction; Th: thermo-elastic)

g [m/s²] standard gravity

G [Pa/m³] stiffness (sk: skeleton)

H [m] height

k [1/s] kinetic rate of reaction

K [Pa/m³] system stiffness

k₀ [] lateral earth pressure coefficient at rest

L [m] characteristic length

L_ch [m] channel length

LL [] liquid limit

M [] viscous ratio

N_ad [] contact number

N_ec [] elastocapillary number

u [Pa] fluid pressure (w: wetting phase; n: non-wetting phase)

Pe [] Péclet number

r [m] pore radius

Stk [] Stokes number

t [s] time scale (adv: advection; diff: diffusion; r: reaction; in: inertia)

V [m³] volume

W [] water content

z [m] depth

v [m/s] fluid flow velocity

Δu [Pa] capillary pressure

$\alpha [°]$ local pore wall angle

${\alpha }_{sk} [1/°\text{C}]$ thermal expansion coefficient of the skeleton

γ [N/m] interfacial tension (VS.: vapor-solid; LS: liquid-solid; LV: liquid-vapor)

θ [°] contact angle (a: advancing; r: receding)

μ [Pa.s] viscosity (inv: invading phase; def: defending phase)

${\text{Π}}_{\text{inv}}$ [] dimensionless ratio: capillary force over skeletal force

${\text{Π}}_{drag}$ [] dimensionless ratio: drag force over skeletal force

${\text{Π}}_{THM}$ [] dimensionless ratio between thermal diffusion and pressure diffusion

ρ [kg/m³] density (b: buoyant; w: water; p: particle; f: fluid)

$\sigma$’ [Pa] effective stress

$\Gamma [\text{mol}/{\text{m}}^2]$ surface excess concentration