Life Expectancy of Evaporating Capillary Bridges Predicted by Tertiary Creep Modeling

The evaporation of capillary bridges is experimentally investigated at the microscale through a three-grain capillary cluster. This setting provides the minimum viable description of Haines jumps during evaporation, that is, capillary instabilities stemming from air entry into a saturated granular material. The displacement profile of a meniscus is obtained via digital image correlation for different grain materials, geometries, and separations. While it is well known that Haines jumps are triggered at the pore throat, we find that these instabilities are of three types depending on the separation. We also provide a temporal characterization of Haines jumps; we find that they are accurately described, as tertiary creep instabilities, by Voight’s relation, similarly to landslides and volcanic eruptions. This finding extends the description of capillary instabilities beyond their onset predicted by Laplace equilibrium. Our contribution also paves the way for a microscopically-informed description of desiccation cracks, of which Haines jumps are the precursors.

1 Introduction

Capillary bridge instabilities during evaporation fall within a multiscale problem. At the microscale, i.e. the grain scale, they result from the combined effects of capillarity and evaporation, and can therefore be described in terms of Laplace and Kelvin equilibria, respectively (Everett and Haynes, 1972). When the pore diameter is constant or decreases ahead of the meniscus (in the defending liquid phase), both equilibria are stable; otherwise, they are unstable. The onset of Haines jumps (Haines, 1930) during evaporation thus occurs when the pore diameter goes from decreasing to increasing, i.e. at pore throats. A necessary condition for this to happen is that the system be “soft” (Sun and Santamarina, 2019); for instance, in a porous system, when the grains are deformable or when the meniscii are interacting. The transient state of the bridge depends on various factors, such as the fluid viscosity, the surface tension, the humidity, the temperature, which will influence the jumps intensity. Upon neglecting the thermal effects, the latter has been shown to be inversely proportional to the Ohnesorge number $Oh={\eta }_w/\sqrt{{\rho }_w\gamma l_s}$ (Zacharoudiou and Boek, 2016), ratio of the viscous effect over the inertial and capillary effects, where η_w denotes the viscosity of the wetting fluid, ρ_w its density, γ the surface tension, and l_s a characteristic length scale of the system. When these instabilities occur serially and percolate through the mesoscale, i.e. at the multi-grain scale, one can speak of air entry (see Figure 1). To reduce the intensity of air entry, one can thus increase the Ohnesorge number by increasing the viscosity of the defending fluid, or by decreasing the surface tension. In turn, air entry is a precursor of desiccation cracks at the macroscale (Shin and Santamarina, 2011; Hueckel et al., 2014). Desiccation cracks deteriorate the mechanical strength of soils and increase their hydraulic conductivity, which can be particularly detrimental for earth embankment (Khandelwal, 2011), slope stability (Stirling, 2014) and geobarriers integrity, such as in nuclear waste disposals (Dixon et al., 2002) and landfills (Omidi et al., 1996). It is therefore paramount to better comprehend air entry and the associated Haines instabilities. In this contribution, we will focus on the temporal evolution of capillary bridges during evaporation, before and just after their rupture, by using digital image correlation and varying the separation between the grains, their material and their geometry. We consider three-grain clusters, which is the minimal number of grains to allow pore throat passage, representing air entry in the early stages of drying of geomaterials (see Figure 1). Two-grain bridges, which represent the terminal stages of drying, were already experimentally studied by Mielniczuk et al. (2014); it was found that the rupture of the bridges is accompanied by an abrupt decrease of capillary forces and cohesiveness of the granular assembly. We will show here that this abruptness can be more precisely characterized as stemming from tertiary creep, in the form of a Voight instability. Voight’s relation (Voight, 1988; Voight, 1989),

$\ddot{\mathrm{\Omega }}=A{\dot{\mathrm{\Omega }}}^{\alpha },(1)$

was empirically introduced as a general description of rate-dependent material failure under constant loading conditions; in Eq. 1, Ω is an observable quantity (here the meniscus displacement d), A > 0 and α > 0 are parameters, and the superposed dot denotes the differentiation with respect to time. This relation was first introduced by Fukuzono (1985) in the case of landslides. Following its generalization by Voight (1988), it was experimentally verified to hold for a wide range of materials, including geomaterials, metal, and ice (Voight, 1989). It proved particularly useful in predicting volcanic eruptions and landslides (see Veveakis et al. (2007) and Intrieri et al. (2019) for a recent review). Noticeably, the parameter α is found to be close to 2 in general (see Voight (1989) and Chang and Wang (2021) for more recent data).

FIGURE 1

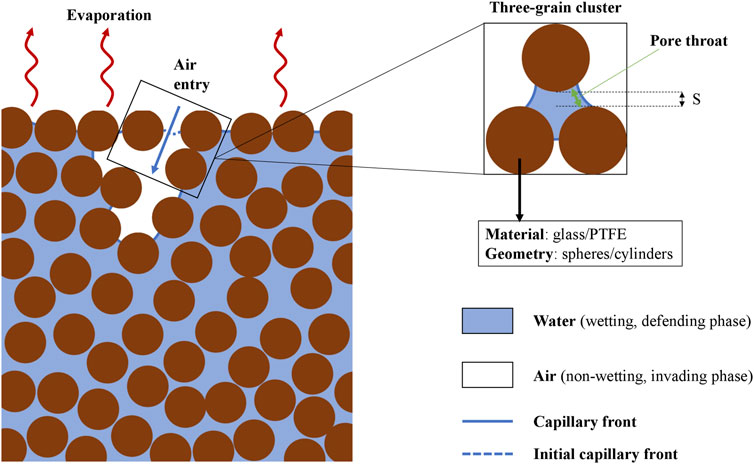
FIGURE 1. 2D representation of an assembly of grains forming a granular medium, studied through the three-gain cluster, considered as the minimum viable description of air entry at the microscale. Air entry occurs through the largest pore upon evaporation of the capillary front in contact with the environment. In the cluster, the separation S of the grains is varied as indicated, as well as the type of material (glass and PTFE) and geometry (spherical, cylindrical).

However, Voight’s relation has not yet been explored at the microscale, where macroscopic instabilities originate, especially in the case of geomaterials (see Kawamoto et al. (2018), Rattez et al. (2018a), Rattez et al. (2018b), Lesueur et al. (2020), Guével et al. (2020), Guével et al. (2022), e.g.). We suggest here that this relation, in addition to describing field-scale instabilities, may also underpin their microscopic origin. In the context of capillary instabilities, Voight’s relation is to be envisioned through the creep failure of the capillary bridge upon the constant thermal loading imposed by evaporation, due to constant environmental temperature and humidity, analogously to the constant mechanical loading due to gravity in landslides. Whereas the instability onset is due to thermal runaway in landslides (Veveakis et al., 2007), it is due here to the geometrical configuration (pore throat passage).

2 Materials and Methods

2.1 Experimental Setting

We consider four types of material configurations, where the three grains are either of spherical or cylindrical shapes, and made of either glass or polytetrafluoroethylene (PTFE). The diameters of the grains are 6,300 µm for the glass spheres, 4,000 µm for the glass cylinders, 6,000 µm for the PTFE spheres, and 3,200 µm for the PTFE cylinders, with a precision of 3 µm. The grains are immobilized with a vertical separation S between the two lower grains, which are in contact, and the upper grain varying from 100 to 1,500 µm and measured with a micrometer. This setting can be envisioned as a quasistatic description of air entry in granular materials, as the particles are displaced away from the entry point, thereby increasing S (Shin and Santamarina, 2011). Furthermore, we consider a three-grain cluster to be the minimum viable description of air entry at the microscale (see Figure 1).

The capillary bridges are created by filling the space between the grains with distilled and deionized water of surface tension 0.072 N/m, which initial volume is constant throughout the experiments for the spheres (V₀ = 20 µl) and the cylinders (V₀ = 10 µl). The experiments were performed in the apparatus presented in Figure 2, in controlled conditions in an environmental chamber, at constant relative humidity of 35 ± 2% and temperature of 21.0 ± 0.2 °C, measured in the vicinity of the system with digital sensors.

FIGURE 2

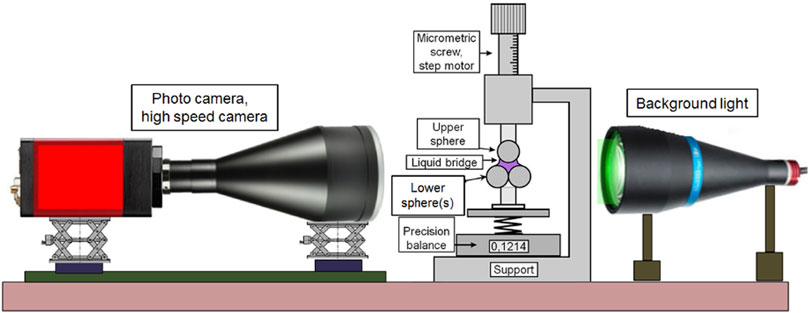
FIGURE 2. Apparatus employed for tracking the evolution of the capillary bridges for a three-grain cluster, via digital image correlation. The scale is used for measuring intergranular forces, which will be studied separately in upcoming studies from the authors. Figure reproduced from Hueckel et al. (2020).

2.2 Measurement of the Menisci Displacement

The position of the menisci was followed via digital image correlation: in time, with an acquisition frequency of 10 images per second, and in space, by measuring the position of the upper contact point (see Figure 3), with a precision of 2 pixels, corresponding here to 4 µm. More precisely, the curvilinear displacement of this contact point was converted into linear displacement through conformal mapping. A telecentric background light was used to enhance the contrast.

FIGURE 3

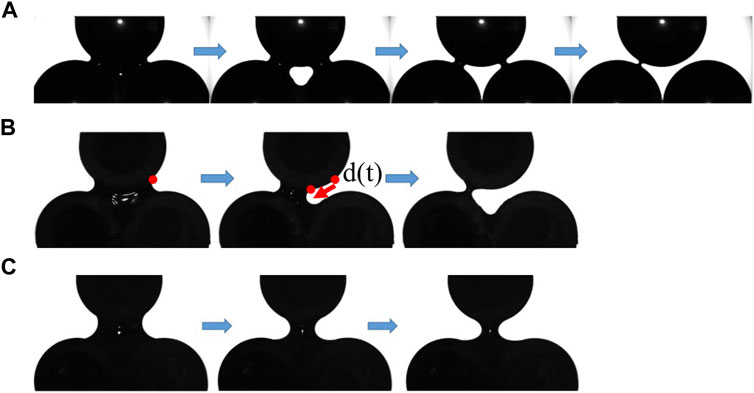
FIGURE 3. Three type of capillary instabilities with increasing separation S, shown here in the case of glass cylinders: (A) thin-sheet instability (S = 300 µm), (B) asymmetric finger instability (S = 500 µm) (C) symmetric finger instability (S = 1,000 µm). The displacement d(t) of the meniscus is defined, for the instabilities (B) and (C), by that of the upper contact point (see red dots). In the case of asymmetric instabilities (B), the displacement of the meniscus that collapses first is considered (see red arrow).

2.3 Repeatability

We found difficult to accurately assess the repeatability of our experiments, mostly because of the amplification of the manipulation errors and sensitivity to environmental conditions due to the small scale considered. For instance, while the separation of the grains could be achieved with a micrometer precision, the same distance would vary by up to 15% when measured through image processing. Sources for this error include the digital reading subject to the image resolution and creep of the glue fixing the bottom grains due to the capillary instabilities. In addition, even though the initial water volume is well controlled, its initial configuration could vary through slightly different contact angles, depending on the exact location from where it was injected. Even if the initial conditions could be perfectly implemented, the dynamic response of the capillary bridges may be subject to the environmental fluctuations such as air flow, although kept to a minimum in the environmental chamber. Therefore, our results are of qualitative rather than quantitative value. This, however, does not prevent inferring the type of law followed by the transient regime of the present setting, as shown in the next section.

3 Results

The dynamics of the capillary bridges can be decomposed into two distinct regimes. Initially, the water volume decreases quasi-statically following the evaporation rate. Then, upon reaching the pore throat, corresponding to the onset of unstable Laplace and Kelvin equilibria, the meniscus abruptly accelerates until reaching a new stable equilibrium position in the form of pendular bridges, corresponding to air entry. We observe, for three-grain clusters, three modes of air entry, depending on the separation of the grains: 1) thin-film entry for the lowest separations, 2) asymmetric finger entry for intermediate separations, and 3) symmetric finger entry for the largest separations (see Figure 3 in the case of the glass cylinders and Mielniczuk et al. (2021) in the case of five-grain clusters). We note that in the third mode, symmetric air entry was not always guaranteed as symmetry breaking could sometimes occur, owing to the sensitivity of the experiments to external perturbations. As a result, the separation threshold between the second and third modes could not be precisely identified but lies, for instance, between S = 500 µm and S = 1,000 µm for the glass cylinders. That said, far enough below this threshold (and above the threshold with the first mode), asymmetric air entry was always obtained. The bridge finally reaches a post-instability pendular configuration, which analysis is already touched upon in Mielniczuk et al. (2014) and Mielniczuk et al. (2015), and will be further studied in coming works. Fitting to the focus of this contribution, we consider the time of air entry as the final time t_f, or failure time, which is used to normalize all temporal quantities (see Table 1), so that the normalized time is t* = t/t_f ∈ [0, 1]. The duration to reach air entry is called the lifetime of the capillary bridge.

TABLE 1

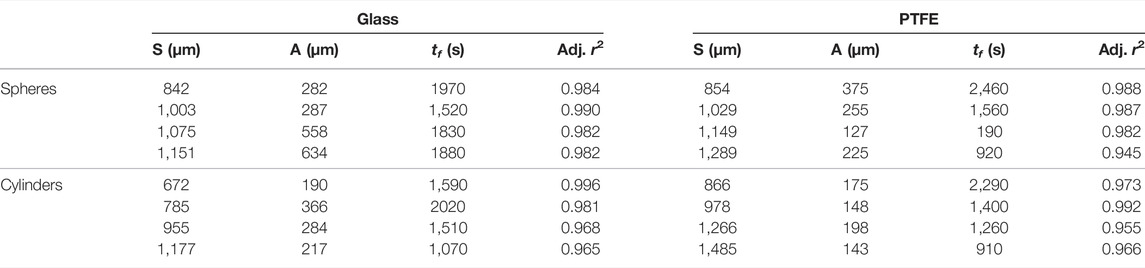
TABLE 1. Summary of the values of the parameter A found in the fitting of the experimental data with Voight’s relation, along with the corresponding adjusted r² coefficient, as well as the values of the failure time t_f.

In a given assembly of grains (see Figure 1 e.g.), air entry will occur through the largest pores, where less energy is demanded to displace the meniscus, as per Laplace’s law. Therefore, we may restrict our attention to configurations of largest grain separation, approximately S ≥ 500 μm, leading to finger-type instabilities. This assertion is verified in Figure 4 showing that the failure time t_f is a decreasing function of the separation S, which may be fitted with a power law.

FIGURE 4

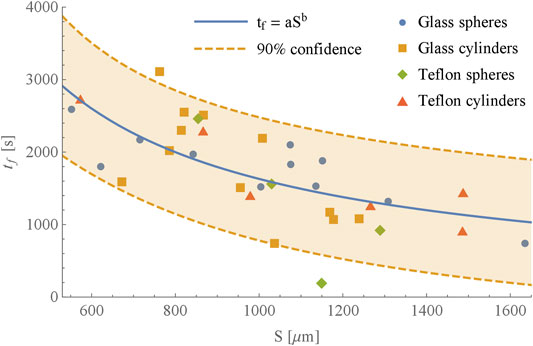
FIGURE 4. Failure time t_f vs. grain separation S for the 4 different types of clusters, fitted by a power law t_f = aS^b, with a = 9.0, ×, 10⁵ and b = −0.91 (with adequate units to have t_f in s). The 90% confidence band is also shown, indicating 2 experimental outliers.

We now proceed to characterizing air entry in time. Using the least-square method, we find that the evolution in time of the meniscus position during evaporation is well described by Voight’s relation Eq. 1 for α = 2 (see Eq. 5 in Voight (1988), with Ω₀ = 0 and t₀ = 0), regardless of the separations and type of material:

$d^{*}=-\ln \left(1-t^{*}\right),(2)$

where the distance traveled by the meniscus d is normalized for each configuration by the fitting parameter A: $d_i^{*}=d_i/A_i$, where i denotes one the 16 configurations (see Table 1). Eq. 2 can also be expressed in the more familiar form ${\dot{d}}^{*}=1/(1-t^{*})$ used in landslides prediction. The collapse of the self-similar curves onto Voight’s relation are shown in Figure 5.

FIGURE 5

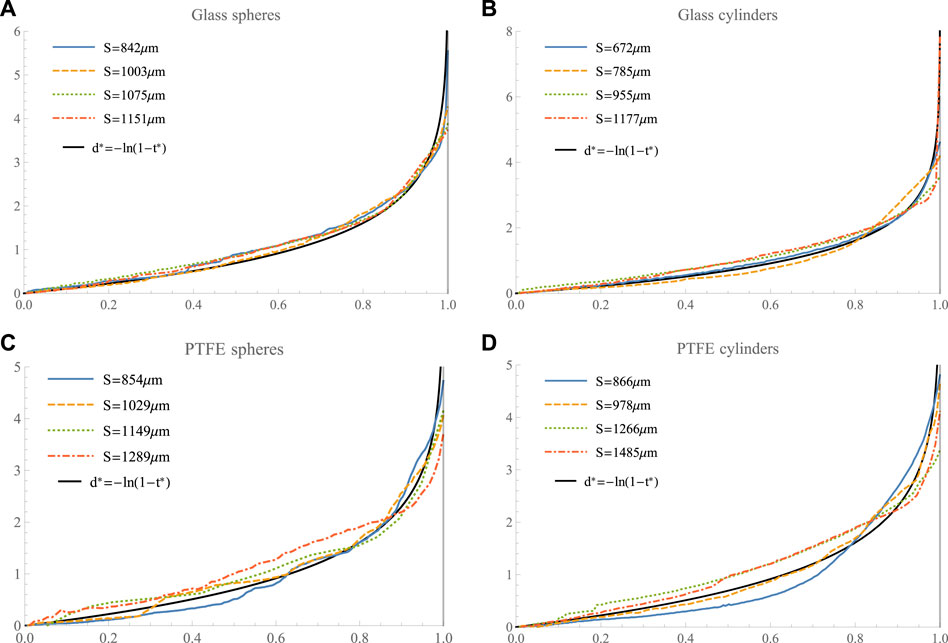
FIGURE 5. The evolution of the meniscus position during evaporation is shown against time, for different grains separations S and the four material configurations: (A) Glass spheres, (B) Glass cylinders, (C) PTFE spheres, (D) PTFE cylinders. The position is normalized by the similarity parameter A, calculated for each separation and material, while the time is normalized by the failure time. The curves are shown to collapse onto Voight’s relation for α = 2. The vertical line t* = 1 (t = t_f) is also indicated showing an asymptotic behavior at failure.

While different types of Voight’s relation are possible, depending on the value of α in Eq. 1, we found that the best fit is provided by α = 2. In particular, the case α = 1 (exponential function) yields a similar overall fitting accuracy but does not capture the asymptote for t*→ 1.

4 Discussion

4.1 Practical Use of Voight’s Relation

It is noteworthy that our fitting only requires one parameter, A, which depends, at least, on the type of material and grain geometry. In practice, A can be obtained, as in landslides prediction, through recorded data before failure. Thereupon, the failure time can be predicted with

$t_f=t_0+\frac{1}{A\dot{d}\left(t_0\right)},(3)$

obtained from Voight (1988), given a measurement of the velocity $\dot{d}$ at an instant t₀.

4.2 Meaning of α = 2

The support for finding a coefficient α = 2 in our experiments is twofold. First, this value has been found for most processes described by Voight’s relation, as previously discussed. That said, while this value has been obtained so far in macroscopic experiments, it is remarkable that it also appears at the microscale. Second, as first discussed by Voight (1989), the tendency α = 2 may imply some underlying fundamental principle. In the context of landslides, Helmstetter et al. (2004) showed that this principle could be that behind stick-slip instabilities, when assuming Dieterich–Ruina’s rate-and-state law (Dieterich, 1978; Ruina, 1983). Since the displacement of a capillary front onto a solid surface occurs through stick-slip motion as well (Gao et al., 2018), it is therefore sensible that capillary instabilities, such as the ones studied here, follow Voight’s relation with α = 2.

4.3 Tertiary Creep Failure Throughout the Scales

This microscopic characterization may motivate a similar tertiary creep characterization for the macroscopic manifestation of air entry during evaporation, namely, desiccation cracks. We speculate that the latter may be described by Voight’s relation as well, which will be the object of an upcoming experimental study. In turn, predicting desiccation cracks, which may trigger landslides (Stirling, 2014), can be seen as an intermediary buffer step towards predicting landslides a step ahead, which can also be described by Voight’s relation. In all, while it has been well known that macroscopic material failure can be described via Voight’s relation, we suggest that it originates, at least in the case of instabilities due to evaporation, at the (microscopic) grain scale, where a similar relation can be observed.

We deduce from the previous section that the physical microscopic origin of capillary instabilities may be the existence of an asperity length scale, since it is the underpinning assumption in stick-slip instability modeling and the associated rate-and-state law (Ruina, 1983). The length A appears as a natural candidate to relate to this asperity length scale. However, this correlation is not clear when comparing our results for the two different materials considered here (see Table 1). This can be explained by the restriction to qualitative conclusions due to the experimental conditions explained above, but also by the fact that different materials have different asperities but also different contact angles. Experimental studies allowing to precisely isolate the effect of the relevant parameters, perhaps at the sub-grain scale, should therefore be sought, to determine, in particular, the dependence of the fitting Voight parameter A on the materials properties.

5 Conclusion

We have proposed a temporal characterization of Haines jumps, through showing experimentally that they can be described as tertiary creep instabilities with Voight’s relation. In doing so, we adopted an engineering perspective, that encapsulates the complex mechanisms underlying capillary instabilities into a “black box” representation. A detailed physics-based analysis of these mechanisms will be pursued in upcoming works. Voight’s relation, popularized in the study of geohazards, is here extended to microscopic instabilities, suggesting surface asperities as a common origin. The multiscale validity of Voight’s law, at least for granular materials, indicates a clear coupling between the microscopic and macroscopic scales, which should be harvested to better predict and prevent material failure.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

AG wrote the paper and analyzed the experimental data. BM performed the experiments and analyzed the experimental data. MV and TH conceived the analysis of the experimental data and supervised this work.

Funding

The authors gratefully acknowledge the support of United States DOE grant DE-NE0008746.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chang, C., and Wang, G. (2022). Creep of Clayey Soil Induced by Elevated Pore-Water Pressure: Implication for Forecasting the Time of Failure of Rainfall-Triggered Landslides. Eng. Geol. 296, 106461. doi:10.1016/j.enggeo.2021.106461

CrossRef Full Text | Google Scholar

Dieterich, J. H. (1978). Time-dependent Friction and the Mechanics of Stick-Slip. Pageoph 116, 790–806. doi:10.1007/bf00876539

CrossRef Full Text | Google Scholar

Dixon, D., Chandler, N., Graham, J., and Gray, M. N. (2002). Two Large-Scale Sealing Tests Conducted at Atomic Energy of Canada's Underground Research Laboratory: the Buffer-Container experiment and the Isothermal Test. Can. Geotech. J. 39, 503–518. doi:10.1139/t02-012

CrossRef Full Text | Google Scholar

Everett, D. H., and Haynes, J. M. (1972). The Thermodynamics of Fluid Interfaces in a Porous Medium. Z. für Physikalische Chem. Neue Folge 82, 36–48. doi:10.1524/zpch.1972.82.1-4.036

CrossRef Full Text | Google Scholar

Fukuzono, T. (1985). A Method to Predict the Time of Slope Failure Caused by Rainfall Using the Inverse Number of Velocity of Surface Displacement. Landslides 22, 8–13. doi:10.3313/jls1964.22.2_8

CrossRef Full Text | Google Scholar

Gao, N., Geyer, F., Pilat, D. W., Wooh, S., Vollmer, D., Butt, H.-J., et al. (2018). How Drops Start Sliding over Solid Surfaces. Nat. Phys. 14, 191–196. doi:10.1038/nphys4305

CrossRef Full Text | Google Scholar

Guével, A., Rattez, H., and Veveakis, E. (2020). Viscous Phase-Field Modeling for Chemo-Mechanical Microstructural Evolution: Application to Geomaterials and Pressure Solution. Int. J. Sol. Struct. 207, 230–249. doi:10.1016/j.ijsolstr.2020.09.026

CrossRef Full Text | Google Scholar

Guével, A., Rattez, H., and Veveakis, E. (2022). Morphometric Description of Strength and Degradation in Porous media. Int. J. Sol. Struct. 241, 111454. doi:10.1016/j.ijsolstr.2022.111454

CrossRef Full Text | Google Scholar

Haines, W. B. (1930). Studies in the Physical Properties of Soil. V. The Hysteresis Effect in Capillary Properties, and the Modes of Moisture Distribution Associated Therewith. J. Agric. Sci. 20, 97–116. doi:10.1017/s002185960008864x

CrossRef Full Text | Google Scholar

Helmstetter, A., Sornette, D., Grasso, J.-R., Andersen, J. V., Gluzman, S., and Pisarenko, V. (2004). Slider Block Friction Model for Landslides: Application to Vaiont and La Clapière Landslides. J. Geophys. Res. 109, 1–15. doi:10.1029/2002jb002160

CrossRef Full Text | Google Scholar

Hueckel, T., Mielniczuk, B., El Youssoufi, M. S., Hu, L. B., and Laloui, L. (2014). A Three-Scale Cracking Criterion for Drying Soils. Acta Geophys. 62, 1049–1059. doi:10.2478/s11600-014-0214-9

CrossRef Full Text | Google Scholar

Hueckel, T., Mielniczuk, B., and El Youssoufi, M. S. (2020). Adhesion-force Micro-scale Study of Desiccating Granular Material. Géotechnique 70, 1133–1144. doi:10.1680/jgeot.18.p.298

CrossRef Full Text | Google Scholar

Intrieri, E., Carlà, T., and Gigli, G. (2019). Forecasting the Time of Failure of Landslides at Slope-Scale: A Literature Review. Earth Sci. Rev. 193, 333–349. doi:10.1016/j.earscirev.2019.03.019

CrossRef Full Text | Google Scholar

Kawamoto, R., Andò, E., Viggiani, G., and Andrade, J. E. (2018). All You Need Is Shape: Predicting Shear Banding in Sand with LS-DEM. J. Mech. Phys. Sol. 111, 375–392. doi:10.1016/j.jmps.2017.10.003

CrossRef Full Text | Google Scholar

Khandelwal, S. (2011). Effect of Desiccation Cracks on Earth Embankments. Ph.D. Thesis. Texas A&M University.

Google Scholar

Lesueur, M., Poulet, T., and Veveakis, M. (2020). Three-scale Multiphysics Finite Element Framework (FE3) Modelling Fault Reactivation. Comput. Methods Appl. Mech. Eng. 365, 112988. doi:10.1016/j.cma.2020.112988

CrossRef Full Text | Google Scholar

Mielniczuk, B., Hueckel, T., and Youssoufi, M. S. E. (2014). Evaporation-induced Evolution of the Capillary Force between Two Grains. Granular Matter 16, 815–828. doi:10.1007/s10035-014-0512-6

CrossRef Full Text | Google Scholar

Mielniczuk, B., Hueckel, T., and El Youssoufi, M. S. (2015). Laplace Pressure Evolution and Four Instabilities in Evaporating Two-Grain Liquid Bridges. Powder Techn. 283, 137–151. doi:10.1016/j.powtec.2015.05.024

CrossRef Full Text | Google Scholar

Mielniczuk, B., El-Youssoufi, S. M., and Hueckel, T. (2021). The Mechanics of Air Entry of Drying-Cracking Soils: Physical Models. Comput. Geotechn. 136, 104177. doi:10.1016/j.compgeo.2021.104177

CrossRef Full Text | Google Scholar

Omidi, G. H., Thomas, J. C., and Brown, K. W. (1996). Effect of Desiccation Cracking on the Hydraulic Conductivity of a Compacted clay Liner. Water Air Soil Pollut. 89, 91–103. doi:10.1007/BF00300424

CrossRef Full Text | Google Scholar

Rattez, H., Stefanou, I., and Sulem, J. (2018a). The Importance of Thermo-Hydro-Mechanical Couplings and Microstructure to Strain Localization in 3D Continua with Application to Seismic Faults. Part I: Theory and Linear Stability Analysis. J. Mech. Phys. Sol. 115, 54–76. doi:10.1016/j.jmps.2018.03.004

CrossRef Full Text | Google Scholar

Rattez, H., Stefanou, I., Sulem, J., Veveakis, M., and Poulet, T. (2018b). The Importance of Thermo-Hydro-Mechanical Couplings and Microstructure to Strain Localization in 3D Continua with Application to Seismic Faults. Part II: Numerical Implementation and post-bifurcation Analysis. J. Mech. Phys. Sol. 115, 1–29. doi:10.1016/j.jmps.2018.03.003

CrossRef Full Text | Google Scholar

Ruina, A. (1983). Slip Instability and State Variable Friction Laws. J. Geophys. Res. 88, 10359–10370. doi:10.1029/JB088iB12p10359

CrossRef Full Text | Google Scholar

Shin, H., and Santamarina, J. C. (2011). Desiccation Cracks in Saturated fine-grained Soils: Particle-Level Phenomena and Effective-Stress Analysis. Géotechnique 61, 961–972. doi:10.1680/geot.8.P.012

CrossRef Full Text | Google Scholar

Stirling, R. A. (2014). Multiphase Modelling of Desiccation Cracking in Compacted Soil. Ph.D. Thesis. Newcastle University.

Google Scholar

Sun, Z., and Santamarina, J. C. (2019). Haines Jumps: Pore Scale Mechanisms. Phys. Rev. E 100, 023115–023117. doi:10.1103/PhysRevE.100.023115

PubMed Abstract | CrossRef Full Text | Google Scholar

Veveakis, E., Vardoulakis, I., and Di Toro, G. (2007). Thermoporomechanics of Creeping Landslides: The 1963 Vaiont Slide, Northern Italy. J. Geophys. Res. 112, 1–21. doi:10.1029/2006JF000702

CrossRef Full Text | Google Scholar

Voight, B. (1988). A Method for Prediction of Volcanic Eruptions. Nature 332, 125–130. doi:10.1038/332125a0

CrossRef Full Text | Google Scholar

Voight, B. (1989). A Relation to Describe Rate-dependent Material Failure. Science 243, 200–203. doi:10.1126/science.243.4888.200

PubMed Abstract | CrossRef Full Text | Google Scholar

Zacharoudiou, I., and Boek, E. S. (2016). Capillary Filling and Haines Jump Dynamics Using Free Energy Lattice Boltzmann Simulations. Adv. Water Resour. 92, 43–56. doi:10.1016/j.advwatres.2016.03.013

CrossRef Full Text | Google Scholar