On the Development of Efficient Solvers for Real-World Coupled Hydromechanical Simulations

Linear solvers usually are the most time- and memory-demanding part of a full coupled hydromechanical simulation. The typical block structure of the linearized systems arising from a fully-implicit solution approach requires the development of specialized algorithms, ensuring both robustness and computational efficiency. In particular, the design of the preconditioner to accelerate iterative methods based on Krylov subspaces is key for the overall model effectiveness. This work introduces a unifying framework for the development of preconditioning techniques in multi-physics problems, and specifically in coupled poromechanics, with the aim to provide existing methods with a novel interpretation. Three approaches, namely explicit, implicit and reverse, are considered and compared in real-world challenging benchmarks, identifying merits and drawbacks of each strategy. The proposed framework can open the way to a systematic comparison of available preconditioning tools for coupled poromechanics and help generalize the existing methods for the introduction of additional physical processes in the simulation.

1 Introduction

Hydromechanical processes in three-dimensional porous media are governed by the coupled equations describing the matrix deformation and the fluid flow through the void spaces. Both the mechanical and the flow phenomena can be highly non-linear, including the formation of localized structures, such as fractures and channelization. Today, sophisticated real-world hydromechanical simulations are routinely required in a broad range of applications, going from geosciences, to petroleum, geotechnical, environmental and also biomedical engineering, see for instance Ferronato et al. (2010); White and Borja (2011); Hu et al. (2013); Ouchi et al. (2015); Ma et al. (2017); Gudala and Govindarajan (2021) for some applications. A key issue for the use of such models in industrial problems is the computational efficiency, which mainly relies on the properties of the resulting discrete algebraic formulation and the related linear and non-linear solvers. In this work, we focus in particular on the linear solver, which usually is by far the most time- and memory-demanding task of the entire simulation.

Several different discretization methods are available, ranging from finite difference (Gaspar et al., 2003; Boal et al., 2012) to finite volume (Chen et al., 2011; Burger et al., 2012; Asadi et al., 2014), as well as classical and mixed finite element methods (Ferronato et al., 2010; Chen Y. et al., 2018; Lee, 2018; Monforte et al., 2018; Yuan et al., 2019; Khan and Silvester, 2021; Niu et al., 2021). Despite this large variety, from the algebraic viewpoint, and independently of the actual number of physical processes accounted for, the coupled discretization of a set of partial differential equations leads to a block-structured problem that cannot be efficiently addressed by standard black-box solvers, but requires the development of specialized strategies. In 3D large-size applications, the use of sparse direct solvers is not an option, hence iterative methods must be used. In the past 15 years, a growing attention has been reserved to the iterative solution of coupled hydromechanical problems, with many works devoted to the development and implementation of both fully-algebraic approaches and discretization-based strategies. Generally speaking, solution algorithms can be grouped into two main classes: (i) sequential-implicit methods, in which the primary variables are updated one by one, iterating between the governing equations, and (ii) fully-coupled or fully-implicit methods, which solve the global system of equations simultaneously for all the primary unknowns. Sequential-implicit methods exhibit a linear convergence, but can take advantage of using distinct codes and solvers for the single-physics models. Notable examples in hydromechanics can be found in the works by Jha and Juanes (2007); Girault et al. (2016); Almani et al. (2016); Borregales et al. (2018); Dana et al. (2018), just to mention a few significant studies. One of the main numerical issues of such approaches is the stability and convergence of the overall scheme, which might not be guaranteed in any condition. In contrast, fully-coupled approaches ensure unconditional stability with a super-linear convergence, but require the design of dedicated preconditioning operators to accelerate Krylov subspace solvers such as the Generalized Minimum Residual (GMRES, Saad and Schultz (1986)) or the Bi-Conjugate Gradient Stabilized (Van der Vorst, 1992)) algorithms. This is key for the solver robustness and efficiency and has recently attracted an increasing interest from the scientific community, with the introduction of a number of different algorithms in the last years. Just to cite a few recent examples, we mention parameter-robust and spectrally-equivalent block strategies (Lee et al., 2010; Hong and Kraus, 2018), multigrid-based methods (Gaspar and Rodrigo, 2017; Chen L. et al., 2018; Bui et al., 2020), or block preconditioners based on Schur complement approximations (Castelletto et al., 2016; Frigo et al., 2021) and mixed constrained approaches (Benzi and Wathen, 2008; Bergamaschi and Martínez, 2012; Liu et al., 2016). A specific application-based technique developed for coupled poromechanics is the so-called fixed-stress split, used as both nonlinear acceleration and linear preconditioner (Castelletto et al., 2015b; Both et al., 2017; Gaspar and Rodrigo, 2017; Both et al., 2019; Hong et al., 2020).

Despite the apparent differences among the several fully-implicit algorithms, a unifying algebraic background can be recognized. Recently, Ferronato et al. (2019) have formalized a general framework to classify block preconditioners for coupled multi-physics simulations. The application of such a framework can help identify a unique basic idea underlying different strategies and make it easier to generalize the algorithms to a multiplicity of problems, possibly including an increasing number of physical processes. In this work, we aim to review from a novel and unified perspective a set of different preconditioning algorithms for coupled poromechanics, comparing their advantages and drawbacks in real-world benchmarks. The paper is organized as follows. The unifying framework developed by Ferronato et al. (2019) is first recalled and recast from a physical perspective. Then, three different approaches developed for the solution of coupled hydromechanical problems written in a mixed form, namely an approximate-inverse (Franceschini et al., 2021), a block triangular (Castelletto et al., 2016) and relaxed factorization (Frigo et al., 2019) method, are reformulated within the same framework as different variants of the same strategy. Finally, the reviewed methods are compared in a set of real-world benchmarks. A few conclusive remarks close the presentation.

2 General Framework

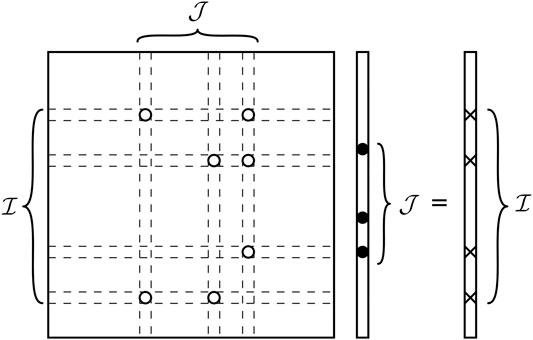
The fully-implicit simultaneous numerical simulation of different physical processes, occurring at variable time and space scales, is often a very challenging task. The discretization of coupled multi-physics problems gives rise to systems of linearized equations with an inherent block structure that reflects the nature of the underlying governing equations. Assuming that n different physical processes are simulated together, the Jacobian matrix A can be generally written as:

$\mathbf{A}=\left[\begin{array}{ccccc}\hfill A_{11}\hfill & \hfill B_{12}\hfill & \hfill B_{13}\hfill & \hfill \dots \hfill & \hfill B_{1n}\hfill \\ \hfill C_{21}\hfill & \hfill A_{22}\hfill & \hfill B_{23}\hfill & \hfill \hfill & \hfill B_{2n}\hfill \\ \hfill C_{31}\hfill & \hfill C_{32}\hfill & \hfill A_{33}\hfill & \hfill \hfill & \hfill B_{3n}\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill C_{n1}\hfill & \hfill C_{n2}\hfill & \hfill C_{n3}\hfill & \hfill \dots \hfill & \hfill A_{nn}\hfill \end{array}\right](1)$

where:

• $A_{ii}\in {\mathbb{R}}^{n_i\times n_i}$ is the square sparse diagonal block referring to the ith process described by n_i inner variables, with i = 1, … , n;

• $B_{ji}\in {\mathbb{R}}^{n_j\times n_i}$ and $C_{ij}\in {\mathbb{R}}^{n_i\times n_j}$, with i = 2, … , n and j = 1, … , i − 1, are the off-diagonal sparse rectangular blocks coupling the variables associated to the ith and jth processes.

In general, $B_{ji}\ne C_{ij}^T$ and $A_{ii}\ne A_{ii}^T$, so that A is non-symmetric and indefinite. If B_ji = 0 or C_ij = 0, then the variables associated with process j do not directly influence those associated with process i and the physics are said to be uncoupled. The numerical solution to the system of equations arising from matrix A in (1) can be very time- and memory-demanding mainly because of the coupling blocks. The basic idea underlying the development of an effective solver for A should rely on decoupling the variables associated to the different processes, so that each physics can be tackled independently of the others.

Formally, we aim to find a decoupling operator E written in the factored form:

$\mathbf{E}=\mathbf{F}\mathbf{G}(2)$

such that the matrix S:

$\mathbf{S}=\mathbf{G}\mathbf{A}\mathbf{F}(3)$

has no coupling blocks, i.e., it is block diagonal with non-zero blocks $S_i\in {\mathbb{R}}^{n_i\times n_i}$, i = 1, … , n. The operative definition of the decoupling factors can be easily obtained assuming that the block LDU decomposition of A exists. In this case, F and G are the inverse of the upper and lower unitary block triangular factors of A, while each diagonal block S_i of S is the Schur complement computed with respect to the first i physical processes. Denoting by A_i the ith leading block of A, and by B_i, C_i, F_i, G_i the ith off-block diagonal terms of the upper and lower parts of A, F, G, respectively:

$A_i=\left[\begin{array}{cccc}\hfill A_{11}\hfill & \hfill B_{12}\hfill & \hfill \dots \hfill & \hfill B_{1i}\hfill \\ \hfill C_{21}\hfill & \hfill A_{22}\hfill & \hfill \hfill & \hfill B_{2i}\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill C_{i1}\hfill & \hfill C_{i2}\hfill & \hfill \dots \hfill & \hfill A_{ii}\hfill \end{array}\right],i=1,\dots ,n-1,(4)$

$B_i=\left[\begin{array}{c}\hfill B_{1i}\hfill \\ \hfill B_{2i}\hfill \\ \hfill ⋮\hfill \\ \hfill B_{i-1,i}\hfill \end{array}\right],C_i=\left[\begin{array}{cccc}\hfill C_{i1}\hfill & \hfill C_{i2}\hfill & \hfill \dots \hfill & \hfill C_{i,i-1}\hfill \end{array}\right],i=2,\dots ,n,(5)$

$G_i=\left[\begin{array}{cccc}\hfill G_{i1}\hfill & \hfill G_{i2}\hfill & \hfill \dots \hfill & \hfill G_{i,i-1}\hfill \end{array}\right],F_i=\left[\begin{array}{c}\hfill F_{1i}\hfill \\ \hfill F_{2i}\hfill \\ \hfill ⋮\hfill \\ \hfill F_{i-1,i}\hfill \end{array}\right],i=2,\dots ,n.(6)$

the decoupling factors can be computed by solving the set of multiple right-hand side systems (Ferronato et al., 2019):

$\left\{\begin{array}{c}{A}_i{F}_{i+1}=-B_{i+1}\hfill \\ G_{i+1}{A}_i=-C_{i+1}\hfill \end{array}\right.,i=1,\dots ,n-1.(7)$

Then, the overall system with A is decoupled with each diagonal block S_i given by:

$S_i=\left[\begin{array}{cc}\hfill G_i\hfill & \hfill I\hfill \end{array}\right]\left[\begin{array}{cc}\hfill A_{i-1}\hfill & \hfill B_i\hfill \\ \hfill C_i\hfill & \hfill A_{ii}\hfill \end{array}\right]\left[\begin{array}{c}\hfill F_i\hfill \\ \hfill I\hfill \end{array}\right]=G_i{A}_{i-1}{F}_i+C_i{F}_i+G_i{B}_i+A_{ii}.(8)$

The local solution of each single-physics problem with the matrix S_i provides simultaneously the set of unknowns associated to all processes.

The general algebraic framework presented above can be also interpreted from a physical viewpoint as a block-reduction procedure, where the variables associated to each process are progressively eliminated. For example, by eliminating the variables associated to the first process the matrix A becomes:

${\mathbf{A}}^{\left(1\right)}=\left[\begin{array}{ccccc}\hfill A_{11}\hfill & \hfill B_{12}\hfill & \hfill B_{13}\hfill & \hfill \dots \hfill & \hfill B_{1n}\hfill \\ \hfill 0\hfill & \hfill A_{22}^{\left(1\right)}\hfill & \hfill B_{23}^{\left(1\right)}\hfill & \hfill \hfill & \hfill B_{2n}^{\left(1\right)}\hfill \\ \hfill 0\hfill & \hfill C_{32}^{\left(1\right)}\hfill & \hfill A_{33}^{\left(1\right)}\hfill & \hfill \hfill & \hfill B_{3n}^{\left(1\right)}\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill C_{n2}^{\left(1\right)}\hfill & \hfill C_{n3}^{\left(1\right)}\hfill & \hfill \dots \hfill & \hfill A_{nn}^{\left(1\right)}\hfill \end{array}\right](9)$

where the new blocks read:

$\begin{array}{ccc}\hfill A_{ii}^{\left(1\right)}& =\hfill & A_{ii}-C_{i1}{A}_{11}^{-1}{B}_{1i},i=2,\dots ,n\hfill \end{array}(10)$

$\begin{array}{ccc}\hfill B_{ij}^{\left(1\right)}& =\hfill & B_{ij}-C_{i1}{A}_{11}^{-1}{B}_{1j},i=2,\dots ,n,j=i+1,\dots ,n\hfill \end{array}(11)$

$\begin{array}{ccc}\hfill C_{ij}^{\left(1\right)}& =\hfill & C_{ij}-C_{i1}{A}_{11}^{-1}{B}_{1j},i=3,\dots ,n,j=2,\dots ,i-1\hfill \end{array}(12)$

Then, the procedure continues with the elimination of the variables associated to the second process:

${\mathbf{A}}^{\left(2\right)}=\left[\begin{array}{ccccc}\hfill A_{11}\hfill & \hfill B_{12}\hfill & \hfill B_{13}\hfill & \hfill \dots \hfill & \hfill B_{1n}\hfill \\ \hfill 0\hfill & \hfill A_{22}^{\left(1\right)}\hfill & \hfill B_{23}^{\left(1\right)}\hfill & \hfill \hfill & \hfill B_{2n}^{\left(1\right)}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill A_{33}^{\left(2\right)}\hfill & \hfill \hfill & \hfill B_{3n}^{\left(2\right)}\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill C_{n3}^{\left(2\right)}\hfill & \hfill \dots \hfill & \hfill A_{nn}^{\left(2\right)}\hfill \end{array}\right](13)$

and so on. At the kth step of the multi-physics reduction procedure, with k = 1, … , n − 1, Eqs. 10–12 can be easily generalized as:

$\begin{array}{ccc}\hfill A_{ii}^{\left(k\right)}& =\hfill & A_{ii}^{\left(k-1\right)}-C_{ik}^{\left(k-1\right)}{A}_{kk}^{\left(k-1\right),-1}{B}_{ki}^{\left(k-1\right)},i=k+1,\dots ,n\hfill \end{array}(14)$

$\begin{array}{ccc}\hfill B_{ij}^{\left(k\right)}& =\hfill & B_{ij}^{\left(k-1\right)}-C_{ik}^{\left(k-1\right)}{A}_{kk}^{\left(k-1\right),-1}{B}_{kj}^{\left(k-1\right)},i=k+1,\dots ,n,j=i+1,\dots ,n\hfill \end{array}(15)$

$\begin{array}{ccc}\hfill C_{ij}^{\left(k\right)}& =\hfill & C_{ij}^{\left(k-1\right)}-C_{ik}^{\left(k-1\right)}{A}_{kk}^{\left(k-1\right),-1}{B}_{kj}^{\left(k-1\right)},i=k+2,\dots ,n,j=2,\dots ,i-1\hfill \end{array}(16)$

with A⁽⁰⁾ = A. Trivially, the existence conditions for Eqs. 14–16 are the same as for (7), and the final diagonal blocks $A_{ii}^{(i-1)}$, i = 1, … , n, coincide with S_i of Eq. 8. From an engineering viewpoint, the original multi-physics problem has been reduced to a sequence of single-physics problems that can be handled one at a time.

Of course, this general framework cannot be exactly applied to real-world large-size problems, because both the decoupling factors F, G, and the diagonal blocks of S are dense. However, if their computation is carried out inexactly, we can use this approach as a preconditioner to accelerate the convergence of a non-symmetric Krylov subspace method, such as GMRES (Saad and Schultz, 1986) or Bi-CGStab (Van der Vorst, 1992). Effectiveness and computational efficiency of the preconditioner basically depend on the level of approximation for each block and the selected sequence of reductions.

3 Coupled Hydromechanics in Porous Media

Coupled hydromechanical simulations are typical examples of multi-physics problems. For the sake of simplicity, in this work we focus on a three-field mixed (displacement-velocity-pressure) formulation of the classical linear poroelasticity (Biot, 1941; Coussy, 2004), but this is not restrictive since similar procedures can be extended to other formulations as well, also including multi-phase flow and fractures. In particular, the introduction of inelastic behaviors for the porous medium does not impact on the general framework proposed herein once the structural block is replaced by the tangent stiffness matrix.

Let $\mathrm{\Omega }\subset {\mathbb{R}}^d$ (d = 2, 3) and Γ be the domain occupied by the porous medium and its Lipschitz-continuous boundary, respectively, with x the position vector in ${\mathbb{R}}^d$ and the closure $\bar{\mathrm{\Omega }}=\mathrm{\Omega }\cup \mathrm{\Gamma }$. We denote time with t, belonging to an open interval $\mathcal{I}=\left(0,t_{\max }\right)$. The boundary is decomposed as Γ = Γ_u ∪ Γ_σ = Γ_p ∪ Γ_q, with Γ_u ∩Γ_σ = Γ_p ∩Γ_q =∅, and n denotes its outer normal vector. Assuming quasi-static conditions and saturated, single-phase flow of a slightly compressible fluid, the set of governing equations consists of the conservation laws for linear momentum and mass expressed in mixed form, i.e., introducing Darcy’s velocity as an additional unknown. The strong form of the initial-boundary value problem (IBVP) consists of finding the displacement $\mathit{u}:\bar{\mathrm{\Omega }}\times \mathcal{I}\to {\mathbb{R}}^d$, the Darcy velocity $\mathit{q}:\bar{\mathrm{\Omega }}\times \mathcal{I}\to {\mathbb{R}}^d$, and the excess pore pressure $p:\bar{\mathrm{\Omega }}\times \mathcal{I}\to \mathbb{R}$ that satisfy:

$\begin{array}{ccc}\hfill \nabla \cdot \left({\mathbb{C}}_{dr}:{\nabla }^s\mathit{u}-bp\mathit{1}\right)& =\hfill & \mathit{0}\left(\text{equilibrium}\right),\hfill \end{array}(17)$

$\begin{array}{ccc}\hfill {\mu }_f{\mathit{\kappa }}^{-1}\cdot \mathit{q}+\nabla p& =\hfill & \mathit{0}\left(\text{Darcy’s\hspace{0.17em}law}\right),\hfill \end{array}(18)$

$\begin{array}{ccc}\hfill b\nabla \cdot \dot{\mathit{u}}+S_{ϵ}\dot{p}+\nabla \cdot \mathit{q}& =\hfill & f\left(\text{continuity}\right),\hfill \end{array}(19)$

with: ${\mathbb{C}}_{dr}$ the rank-four elasticity tensor, ∇^s the symmetric gradient operator, b the Biot coefficient, and 1 the rank-two identity tensor; μ_f and κ the fluid viscosity and the rank-two permeability tensor, respectively; S_ϵ the constrained specific storage coefficient, i.e., the reciprocal of Biot’s modulus, and f the fluid source term. The problem is closed by prescribing the following set of boundary and initial conditions:

$\begin{array}{ccc}\hfill \mathit{u}& =\hfill & \bar{\mathit{u}}\text{\hspace{0.17em}on\hspace{0.17em}}{\mathrm{\Gamma }}_u\times \mathcal{I},\hfill \end{array}(20)$

$\begin{array}{ccc}\hfill \left({\mathbb{C}}_{dr}:{\nabla }^s\mathit{u}-bp\mathit{1}\right)\cdot \mathit{n}& =\hfill & \bar{\mathit{t}}\text{\hspace{0.17em}on\hspace{0.17em}}{\mathrm{\Gamma }}_{\sigma }\times \mathcal{I},\hfill \end{array}(21)$

$\begin{array}{ccc}\hfill \mathit{q}\cdot \mathit{n}& =\hfill & \bar{q}\text{\hspace{0.17em}on\hspace{0.17em}}{\mathrm{\Gamma }}_q\times \mathcal{I},\hfill \end{array}(22)$

$\begin{array}{ccc}\hfill p& =\hfill & \bar{p}\text{\hspace{0.17em}on\hspace{0.17em}}{\mathrm{\Gamma }}_p\times \mathcal{I},\hfill \end{array}(23)$

$\begin{array}{ccc}\hfill p\left(\mathit{x},0\right)& =\hfill & p_0\mathit{x}\in \bar{\mathrm{\Omega }},\hfill \end{array}(24)$

where $\bar{\mathit{u}}$, $\bar{\mathit{t}}$, $\bar{q}$, and $\bar{p}$ are the prescribed boundary displacement, traction, Darcy velocity and excess pore pressure, respectively, whereas p₀ is the initial excess pore pressure. The initial displacement u₀ and Darcy’s velocity q₀ are selected so as to satisfy the equilibrium Eq. 17 and Darcy’s law (18) for p = p₀, respectively.

Let us denote with H¹(Ω) the Sobolev space of vector functions with square-integrable first derivatives, i.e., they belong to the Lebesgue space L²(Ω); and let H (div; Ω) be the Sobolev space of vector functions with square-integrable divergence. Introducing the spaces:

$\begin{array}{ccc}\hfill \mathcal{U}& =\hfill & \left\{\mathit{u}\in {\mathit{H}}^1\left(\mathrm{\Omega }\right)|\mathit{u}{|}_{{\mathrm{\Gamma }}_u}=\bar{\mathit{u}}\right\},\hfill \end{array}(25)$

$\begin{array}{ccc}\hfill {\mathcal{U}}_0& =\hfill & \left\{\mathit{u}\in {\mathit{H}}^1\left(\mathrm{\Omega }\right)|\mathit{u}{|}_{{\mathrm{\Gamma }}_u}=\mathit{0}\right\},\hfill \end{array}(26)$

$\begin{array}{ccc}\hfill \mathcal{Q}& =\hfill & \left\{\mathit{q}\in \mathit{H}\left(\text{div};\mathrm{\Omega }\right)|\mathit{q}\cdot \mathit{n}{|}_{{\mathrm{\Gamma }}_q}=\bar{q}\right\},\hfill \end{array}(27)$

$\begin{array}{ccc}\hfill {\mathcal{Q}}_0& =\hfill & \left\{\mathit{q}\in \mathit{H}\left(\text{div};\mathrm{\Omega }\right)|\mathit{q}\cdot \mathit{n}{|}_{{\mathrm{\Gamma }}_q}=0\right\},\hfill \end{array}(28)$

$\begin{array}{ccc}\hfill \mathcal{P}& =\hfill & \left\{p\in L^2\left(\mathrm{\Omega }\right)\right\},\hfill \end{array}(29)$

the weak form of the IBVP (17)–(24) reads: find $\{\mathit{u}(t),\mathit{q}(t),p(t)\}\in \mathcal{U}\times \mathcal{Q}\times \mathcal{P}$ such that $\forall t\in \mathcal{I}$:

$\begin{array}{ccc}\hfill {\left({\nabla }^s\mathit{\eta },{\mathbb{C}}_{\text{dr}}:{\nabla }^s\mathit{u}\right)}_{\mathrm{\Omega }}-{\left(\text{div}\mathit{\eta },bp\right)}_{\mathrm{\Omega }}& =\hfill & {\left(\mathit{\eta },\bar{\mathit{t}}\right)}_{{\mathrm{\Gamma }}_{\sigma }}\forall \mathit{\eta }{\in \mathcal{U}}_0,\hfill \end{array}(30)$

$\begin{array}{ccc}\hfill {\left(\mathit{\varphi },{\mu }_f{\mathit{\kappa }}^{-1}\cdot \mathit{q}\right)}_{\mathrm{\Omega }}-{\left(\text{div}\mathit{\varphi },p\right)}_{\mathrm{\Omega }}& =\hfill & -{\left(\mathit{\varphi }\cdot \mathit{n},\bar{p}\right)}_{{\mathrm{\Gamma }}_p}\forall \mathit{\varphi }{\in \mathcal{Q}}_0,\hfill \end{array}(31)$

$\begin{array}{ccc}\hfill {\left(\chi ,b\text{div}\dot{\mathit{u}}\right)}_{\mathrm{\Omega }}+{\left(\chi ,\text{div}\mathit{q}\right)}_{\mathrm{\Omega }}+{\left(\chi ,S_{ϵ}\dot{p}\right)}_{\mathrm{\Omega }}& =\hfill & {\left(\chi ,f\right)}_{\mathrm{\Omega }}\forall \chi \in \mathcal{P},\hfill \end{array}(32)$

where (⋅,⋅)_Ω denote the inner products of scalar functions in L²(Ω), vector functions in ${[L^2(\mathrm{\Omega })]}^d$, or second-order tensor functions in ${[L^2(\mathrm{\Omega })]}^{d\times d}$, as appropriate, and ${(\cdot ,\cdot )}_{{\mathrm{\Gamma }}_{*}}$ denote the inner products of scalar functions or vector functions on the boundary Γ_*.

A widely-used discrete version of the weak form Eqs. 30–32 is based on low-order elements, such as lowest-order continuous $({\mathbb{Q}}_1)$, lowest-order Raviart-Thomas $({\mathbb{RT}}_0)$, and piecewise constant $({\mathbb{P}}_0)$ spaces for the approximation of displacement, Darcy’s velocity, and fluid pore pressure, respectively. The attractive features of this choice are element-wise mass conservation and robustness with respect to highly heterogeneous hydromechanical properties, such as high-contrast permeability fields typically encountered in real-world applications. Other attractive features can arise from the hybridized version of the three-field formulation, as proposed for instance by Niu et al. (2019) and Frigo et al. (2021).

Let us consider a non-overlapping partition ${\mathcal{T}}_h$ of the domain Ω consisting of n_T quadrilateral (d = 2) or hexahedral (d = 3) elements. Let ${\mathcal{E}}_h$ be the collection of edges (d = 2) or faces (d = 3) of elements $T\in {\mathcal{T}}_h$. Denote with n_e the outer normal vector from e ∈ ∂T, where ∂T is the collection of the edges or faces belonging to T. Time integration is performed with the Backward Euler method, with the interval $\mathcal{I}$ partitioned into N subintervals ${\mathcal{I}}_n=(t_{n-1},t_n)$, n = 1, … , N, where Δt = t_n − t_n−1. With the discretization defined above, the finite dimensional counterpart of the spaces given in Eq. 25–29 read:

$\begin{array}{ccc}\hfill {\mathcal{U}}^h& =\hfill & \left\{{\mathit{u}}^h\in \mathcal{U}|{\mathit{u}}^h{|}_T\in {\left[{\mathbb{Q}}_1\left(T\right)\right]}^d,\forall T\in {\mathcal{T}}_h\right\},\hfill \end{array}(33)$

$\begin{array}{ccc}\hfill {\mathcal{U}}_0^h& =\hfill & \left\{{\mathit{u}}^h\in {\mathcal{U}}_0|{\mathit{u}}^h{|}_T\in {\left[{\mathbb{Q}}_1\left(T\right)\right]}^d,\forall T\in {\mathcal{T}}_h\right\},\hfill \end{array}(34)$

$\begin{array}{ccc}\hfill {\mathcal{Q}}^h& =\hfill & \left\{{\mathit{q}}^h\in \mathcal{Q}|{\mathit{q}}^h{|}_T\in \left[{\mathbb{RT}}_0\left(T\right)\right],\forall T\in {\mathcal{T}}_h\right\},\hfill \end{array}(35)$

$\begin{array}{ccc}\hfill {\mathcal{Q}}_0^h& =\hfill & \left\{{\mathit{q}}^h\in {\mathcal{Q}}_0|{\mathit{q}}^h{|}_T\in \left[{\mathbb{RT}}_0\left(T\right)\right],\forall T\in {\mathcal{T}}_h\right\},\hfill \end{array}(36)$

$\begin{array}{ccc}\hfill {\mathcal{P}}^h& =\hfill & \left\{p^h\in L^2|p^h{|}_T\in \left[{\mathbb{P}}_0\left(T\right)\right],\forall T\in {\mathcal{T}}_h\right\},\hfill \end{array}(37)$

with ${\mathbb{Q}}_1(T)$ the mapping to T of the space of bilinear polynomials on the unit square (d = 2) or trilinear polynomials on the unit cube (d = 3), ${\mathbb{RT}}_0(T)$ the lowest-order Raviart-Thomas space and ${\mathbb{P}}_0(T)$ the space of piecewise constant functions in T. Using the definitions above, the fully discrete weak form of the governing IBVP can be stated as follows: given {u₀, q₀, p₀}, find $\{{\mathit{u}}_n^h,{\mathit{q}}_n^h,p_n^h\}\in {\mathcal{U}}^h\times {\mathcal{Q}}^h\times {\mathcal{P}}^h$ such that for n = {1, … , N}

$\begin{array}{ccc}\hfill {\left({\nabla }^s{\mathit{\eta }}^h,{\mathbb{C}}_{\text{dr}}:{\nabla }^s{\mathit{u}}_n^h\right)}_{\mathrm{\Omega }}-{\left(\text{div}{\mathit{\eta }}^h,b{p}_n^h\right)}_{\mathrm{\Omega }}& =\hfill & {\left({\mathit{\eta }}^h,{\bar{\mathit{t}}}_n\right)}_{{\mathrm{\Gamma }}_{\sigma }}\forall {\mathit{\eta }}^h\in {\mathcal{U}}_0^h,\hfill \end{array}(38)$

$\begin{array}{ccc}\hfill {\left({\mathit{\varphi }}^h,{\mu }_f{\mathit{\kappa }}^{-1}\cdot {\mathit{q}}_n^h\right)}_{\mathrm{\Omega }}-{\left(\text{div}{\mathit{\varphi }}^h,p_n^h\right)}_{\mathrm{\Omega }}& =\hfill & -{\left({\mathit{\varphi }}^h\cdot \mathit{n},{\bar{p}}_n\right)}_{{\mathrm{\Gamma }}_p}\forall {\mathit{\varphi }}^h\in {\mathcal{Q}}_0^h,\hfill \end{array}(39)$

$\begin{array}{ccc}\hfill {\left({\chi }^h,b\text{div}{\mathit{u}}_n^h\right)}_{\mathrm{\Omega }}+\mathrm{\Delta }t{\left({\chi }^h,\text{div}{\mathit{q}}_n^h\right)}_{\mathrm{\Omega }}+{\left({\chi }^h,S_{ϵ}{p}_n^h\right)}_{\mathrm{\Omega }}& =\hfill & {\left({\chi }^h,{\tilde{f}}_n\right)}_{\mathrm{\Omega }}\forall {\chi }^h\in {\mathcal{P}}^h,\hfill \end{array}(40)$

where ${\tilde{f}}_n=b\text{div}{\mathit{u}}_{n-1}^h+S_{ϵ}{p}_{n-1}^h+\mathrm{\Delta }t{f}_n$.

It is well-known that the selected spaces do not satisfy the inf-sup stability constraint in the limit of incompressible fluid and solid constituents (S_ϵ → 0) and undrained conditions (either κ → 0 or Δt → 0). In order to restore the solvability conditions and avoid spurious pressure modes, we introduce in the discrete mass balance Eq. 40 the pressure-jump stabilization term (Frigo et al., 2021):

$J\left({\chi }^h,p^h\right)=\sum _{M\in {\mathcal{M}}_h}{\beta }_M|M|\sum _{e\in {\mathrm{\Gamma }}_M}{[[{\chi }^h]]}_e{[[p^h]]}_e(41)$

where ${\mathcal{M}}_h$ is a partition of Ω into non-overlapping macroelements M, which are generated by a patch of adjacent elements T, |M| is the macroelement measure, β_M is a stabilization term, and [ [⋅] ]_e denotes the jump across the edge/face e belonging to the internal boundary Γ_M of M. From a physical viewpoint, the stabilization contribution (41) represents a fictitious flux introduced through the inner edges of each macro-element so as to compensate the spurious fluxes induced by the non-physical pressure oscillatory modes. Appropriate values for β_M as a function of the mechanical properties of the porous medium are proposed, for instance, by Elman et al. (2014), Camargo et al. (2021) and Frigo et al. (2021).

Let ${\{{\mathit{\eta }}_i\}}_{i\in {\mathcal{N}}_u\cup {\bar{\mathcal{N}}}_u}$ be the standard vector nodal basis functions for ${\mathcal{U}}^h$, with ${\mathcal{N}}_u$ and ${\bar{\mathcal{N}}}_u$ the set of indices of basis function vanishing on Γ_u and having support on Γ_u, respectively. Let ${\{{\mathit{\varphi }}_j\}}_{j\in {\mathcal{N}}_q\cup {\bar{\mathcal{N}}}_q}$ be the edge-/face-based basis functions for ${\mathcal{Q}}^h$, with ${\mathcal{N}}_q$ and ${\bar{\mathcal{N}}}_q$ the set of indices of basis functions vanishing on Γ_q and having support on Γ_q, respectively. Notice that ${\{{\mathit{\eta }}_i\}}_{i\in {\mathcal{N}}_u}$ and ${\{{\mathit{\varphi }}_j\}}_{j\in {\mathcal{N}}_q}$ form a basis also for ${\mathcal{U}}_0^h$ and ${\mathcal{Q}}_0^h$, respectively. Let ${\{{\chi }_k\}}_{k\in {\mathcal{N}}_p}$ be the basis for ${\mathcal{P}}^h$, with χ_k the characteristic function of the kth element $T_k\in {\mathcal{T}}_h$ such that χ_k(x) = 1 if x ∈ T_k, χ_k(x) = 0 if x∉T_k. Then, discrete approximations for displacement, Darcy’s velocity, and pressure belonging to the finite-dimensional spaces (33) (35) and (37), respectively, read:

${\mathit{u}}_n^h\left(\mathit{x}\right)=\underset{≔{\mathring{\mathit{u}}}_n^h}{\underbrace{\sum _{i\in {\mathcal{N}}_u}{\mathit{\eta }}_i\left(\mathit{x}\right)u_{i,n}}}+\underset{≔{\bar{\mathit{u}}}_n^h}{\underbrace{\sum _{i\in {\bar{\mathcal{N}}}_u}{\mathit{\eta }}_i\left(\mathit{x}\right){\bar{u}}_{i,n}}},{\mathit{q}}_n^h\left(\mathit{x}\right)=\underset{≔{\mathring{\mathit{q}}}_n^h}{\underbrace{\sum _{j\in {\mathcal{N}}_q}{\mathit{\varphi }}_j\left(\mathit{x}\right)q_{j,n}}}+\underset{≔{\bar{\mathit{q}}}_n^h}{\underbrace{\sum _{j\in {\bar{\mathcal{N}}}_q}{\mathit{\varphi }}_j\left(\mathit{x}\right){\bar{q}}_{j,n}}},$

$p_n^h\left(\mathit{x}\right)=\sum _{k\in {\mathcal{N}}_p}{\chi }_k\left(\mathit{x}\right)p_{k,n}.(42)$

The unknown nodal displacement components {u_i,n}, edge-/face-centered Darcy’s velocity components {q_j,n}, and cell-centered pressures {p_k,n} at time level t_n are collected in vectors ${\mathbf{u}}_n\in {\mathbb{R}}^{n_u}$, ${\mathbf{q}}_n\in {\mathbb{R}}^{n_q}$, and ${\mathbf{p}}_n\in {\mathbb{R}}^{n_p}$. Requiring that $\{{\mathit{u}}_n^h,{\mathit{q}}_n^h,p_n^h\}$ given in Eq. 42 satisfy the fully discrete weak formulation (38)–(40) with the introduction of the stabilization (41) for each basis function of ${\mathcal{U}}_0^h$, ${\mathcal{Q}}_0^h$, and ${\mathcal{P}}^h$ yields the final matrix form of the variational problem:

$\mathbf{A}\mathbf{x}=\mathbf{b}\text{with}\mathbf{A}=\left[\begin{array}{ccc}\hfill A_{uu}\hfill & \hfill 0\hfill & \hfill A_{up}\hfill \\ \hfill 0\hfill & \hfill A_{qq}\hfill & \hfill A_{qp}\hfill \\ \hfill A_{pu}\hfill & \hfill \mathrm{\Delta }t{A}_{pq}\hfill & \hfill A_{pp}\hfill \end{array}\right],\mathbf{x}=\left[\begin{array}{c}\hfill {\mathbf{u}}_n\hfill \\ \hfill {\mathbf{q}}_n\hfill \\ \hfill {\mathbf{p}}_n\hfill \end{array}\right],\mathbf{b}=\left[\begin{array}{c}\hfill {\mathbf{f}}_u\hfill \\ \hfill {\mathbf{f}}_q\hfill \\ \hfill {\mathbf{f}}_p\hfill \end{array}\right],(43)$

where $A_{pu}=-A_{up}^T$ and $A_{pq}=-A_{qp}^T$. Note that $A_{uu}\in {\mathbb{R}}^{n_u\times n_u}$ and $A_{qq}\in {\mathbb{R}}^{n_q\times n_q}$ are symmetric and positive definite (SPD) matrices, whereas $A_{pp}\in {\mathbb{R}}^{n_p\times n_p}$ is symmetric positive semi-definite (SPSD). The explicit expressions of matrices in Eq. 43 are given below:

$\begin{array}{ccc}\hfill {\left[A_{uu}\right]}_{ij}& =\hfill & {\left({\nabla }^s{\mathit{\eta }}_i,{\mathbb{C}}_{\text{dr}}:{\nabla }^s{\mathit{\eta }}_j\right)}_{\mathrm{\Omega }},i,j=1,\dots ,n_u,\hfill \end{array}(44)$

$\begin{array}{ccc}\hfill {\left[A_{up}\right]}_{ij}& =\hfill & -{\left(\text{div}{\mathit{\eta }}_i,b{\chi }_j\right)}_{\mathrm{\Omega }},i=1,\dots ,n_u,j=1,\dots ,n_p,\hfill \end{array}(45)$

$\begin{array}{ccc}\hfill {\left[A_{qq}\right]}_{ij}& =\hfill & {\left({\mathit{\varphi }}_i,{\mu }_f{\mathit{\kappa }}^{-1}\cdot {\mathit{\varphi }}_j\right)}_{\mathrm{\Omega }},i,j=1,\dots ,n_q,\hfill \end{array}(46)$

$\begin{array}{ccc}\hfill {\left[A_{qp}\right]}_{ij}& =\hfill & -{\left(\text{div}{\mathit{\varphi }}_i,{\chi }_j\right)}_{\mathrm{\Omega }},i=1,\dots ,n_q,j=1,\dots ,n_p,\hfill \end{array}(47)$

$\begin{array}{ccc}\hfill {\left[A_{pu}\right]}_{ij}& =\hfill & {\left({\chi }_i,b\text{div}{\mathit{\eta }}_j\right)}_{\mathrm{\Omega }},i=1,\dots ,n_p,j=1,\dots ,n_u,\hfill \end{array}(48)$

$\begin{array}{ccc}\hfill {\left[A_{pq}\right]}_{ij}& =\hfill & {\left({\chi }_i,\text{div}{\mathit{\varphi }}_j\right)}_{\mathrm{\Omega }},i=1,\dots ,n_p,j=1,\dots ,n_q,\hfill \end{array}(49)$

$\begin{array}{ccc}\hfill {\left[A_{pp}\right]}_{ij}& =\hfill & {\left({\chi }_i,S_{ϵ}{\chi }_j\right)}_{\mathrm{\Omega }}+\sum _{M\in {\mathcal{M}}_h}{\beta }_M|M|\sum _{e\in {\mathrm{\Gamma }}_M}{[[{\chi }_i]]}_e{[[{\chi }_j]]}_e,i,j=1,\dots ,n_p.\hfill \end{array}(50)$

The final matrix A of Eq. 43 has the multi-physics block structure (1), where n = 3 physical processes are coupled together. According to the definitions given above, displacements and Darcy’s velocities are uncoupled processes. In the sequel, we discuss the development of effective solvers for the hydromechanical problem in the form Eq. 43. The focus is on the preconditioning technique used in a non-symmetric Krylov subspace method based on the general framework described in Section 2. According to the different strategies used to approximate the decoupling factors and the resulting Schur complements, we distinguish among three different approaches: the explicit, implicit and reverse methods.

3.1 Explicit Approach

Using the definitions introduced in Section 2, the decoupling operators G and F for the multi-physics problem Eq. 43 read:

$\mathbf{G}=\left[\begin{array}{ccc}\hfill I_u\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill G_{qu}\hfill & \hfill I_q\hfill & \hfill 0\hfill \\ \hfill G_{pu}\hfill & \hfill G_{pq}\hfill & \hfill I_p\hfill \end{array}\right],\mathbf{F}=\left[\begin{array}{ccc}\hfill I_u\hfill & \hfill F_{uq}\hfill & \hfill F_{up}\hfill \\ \hfill 0\hfill & \hfill I_q\hfill & \hfill F_{qp}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill I_p\hfill \end{array}\right],(51)$

where I_u, I_q, and I_p are the identity operators in ${\mathbb{R}}^{n_u\times n_u}$, ${\mathbb{R}}^{n_q\times n_q}$, and ${\mathbb{R}}^{n_p\times n_p}$, respectively. The application of Eq. 7 straightforwardly yields:

$\left\{\begin{array}{c}{F}_{uq}=0\hfill \\ F_{up}=-A_{uu}^{-1}{A}_{up}\hfill \\ F_{qp}=-A_{qq}^{-1}{A}_{qp}\hfill \end{array}\right.,\left\{\begin{array}{c}{G}_{qu}=0\hfill \\ G_{pu}=-A_{pu}{A}_{uu}^{-1}\hfill \\ G_{pq}=-\mathrm{\Delta }t{A}_{pq}{A}_{qq}^{-1}\hfill \end{array}\right..(52)$

Recalling from Eqs. 38–40 that $A_{pu}=-A_{up}^T$ and $A_{pq}=-A_{qp}^T$, and that A_uu and A_qq are SPD, we have $G_{pu}=-F_{up}^T$ and $G_{pq}=-\mathrm{\Delta }t{F}_{qp}^T$. Hence, Eq. 52 shows that only F_up and F_qp needs to be computed as the solution of multiple right-hand side systems with A_uu and A_qq. Here, the idea relies on computing explicit sparse approximations of F_up and F_qp.

The explicit sparse computation of the decoupling factors, say ${\tilde{F}}_{up}$ and ${\tilde{F}}_{qp}$, can be carried out by using the ideas originally introduced for the computation of sparse approximate inverses (Kolotilina and Yeremin, 1993; Grote and Huckle, 1997; Janna et al., 2010; Ferronato et al., 2014). For the sake of generality, let us consider the solution to the system Cf = b, where $C\in {\mathbb{R}}^{n\times n}$ and $\mathbf{b}\in {\mathbb{R}}^n$ are sparse. If we want to retain a prescribed sparsity for the solution vector $\mathbf{f}\in {\mathbb{R}}^n$, we can define a set $\mathcal{J}\subset \{\mathrm{1,2},\dots ,n\}$ of positions of the non-zeroes of f (Figure 1), with $|\mathcal{J}|\ll n$. Hence, only the columns of C with index $j\in \mathcal{J}$ are needed to compute the product Cf. A further restriction can be enforced to the rows where at least a non-zero entry lies in one of the selected columns. Denoting as $\mathcal{I}\subset \{\mathrm{1,2},\dots ,n\}$ the set of indices of such rows (Figure 1), the native system Cf = b can be reduced to:

$C{|}_{\mathcal{I},\mathcal{J}}\mathbf{f}{|}_{\mathcal{J}}=\mathbf{b}{|}_{\mathcal{I}},(53)$

where $C{|}_{\mathcal{I},\mathcal{J}}$, $\mathbf{f}{|}_{\mathcal{J}}$, and $\mathbf{b}{|}_{\mathcal{I}}$ are the restrictions of C, f, and b to the sets of components with indices in $\mathcal{I}$ and $\mathcal{J}$, respectively. Since $|\mathcal{J}|,|\mathcal{I}|\ll n$, the solution to system (53) is practically inexpensive if compared to the full problem Cf = b.

FIGURE 1

FIGURE 1. Schematic representation of the restriction applied to system (53).

In order to avoid the solution to over- or under-determined rectangular systems, we define the sets:

${\mathcal{K}}_r^{\left(k\right)}={\mathcal{I}}_r^{\left(k\right)}\cup {\mathcal{J}}_r^{\left(k\right)},r=u,q,k=1,\dots ,n_p,(54)$

where ${\mathcal{J}}_r^{(k)}\subset \{\mathrm{1,2},\dots ,n_r\}$ is the set of positions of the non-zero entries retained in the kth column of the sparse decoupling block ${\tilde{F}}_{rp}$, and ${\mathcal{I}}_r^{(k)}\subset \{\mathrm{1,2},\dots ,n_r\}$ is the corresponding set of row indices with at least a matrix non-zero entry in the columns $j\in {\mathcal{J}}_r^{(k)}$. With the definition (54), the sparse columns of ${\tilde{F}}_{up}$ and ${\tilde{F}}_{qp}$ can be explicitly computed as the solution to the set of independent systems:

$\left\{\begin{array}{c}{A}_{uu}{|}_{{\mathcal{K}}_u^{\left(k\right)},{\mathcal{K}}_u^{\left(k\right)}}{\tilde{F}}_{up}{|}_{{\mathcal{K}}_u^{\left(k\right)},k}=-A_{up}{|}_{{\mathcal{K}}_u^{\left(k\right)},k}\hfill \\ A_{qq}{|}_{{\mathcal{K}}_q^{\left(k\right)},{\mathcal{K}}_q^{\left(k\right)}}{\tilde{F}}_{qp}{|}_{{\mathcal{K}}_q^{\left(k\right)},k}=-A_{qp}{|}_{{\mathcal{K}}_q^{\left(k\right)},k}\hfill \end{array}\right.,k=1,\dots ,n_p,(55)$

Notice that the implementation of Eq. 55 is trivially amenable for high-performance parallel computations. Then, the diagonal blocks of S can be explicitly computed as well:

$S_u=A_{uu},S_q=A_{qq},S_p=A_{pp}+{\tilde{F}}_{up}^T{A}_{uu}{\tilde{F}}_{up}+\mathrm{\Delta }t{\tilde{F}}_{qp}^T{A}_{pp}{\tilde{F}}_{qp}.(56)$

The blocks S_u, S_q, and S_p, which can be regarded as the result of the reduction to a sequence of SPD single-physics problems, are also inverted inexactly for the sake of preconditioning by introducing three approximations $M_u^{-1}$, $M_q^{-1}$, and $M_p^{-1}$. These approximations can be obtained by using inner single-block preconditioners, such as well-established algebraic tools like incomplete factorizations, approximate inverses and multi-grid strategies. The final explicit preconditioning operator ${\mathbf{M}}_{\exp }^{-1}$ for A of Eq. 43 reads:

${\mathbf{M}}_{\exp }^{-1}=\left[\begin{array}{ccc}\hfill I_u\hfill & \hfill 0\hfill & \hfill {\tilde{F}}_{up}\hfill \\ \hfill 0\hfill & \hfill I_q\hfill & \hfill {\tilde{F}}_{qp}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill I_p\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill M_u^{-1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill M_q^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill M_p^{-1}\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill I_u\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill I_q\hfill & \hfill 0\hfill \\ \hfill -{\tilde{F}}_{up}^T\hfill & \hfill -\mathrm{\Delta }t{\tilde{F}}_{qp}^T\hfill & \hfill I_p\hfill \end{array}\right].(57)$

The key factors for the quality and effectiveness of ${\mathbf{M}}_{\exp }^{-1}$ are: (i) the choice of $M_u^{-1}$, $M_q^{-1}$ and $M_p^{-1}$, and (ii) the selection of the sets ${\mathcal{K}}_u^{(k)}$ and ${\mathcal{K}}_q^{(k)}$ for the sparse explicit computation of ${\tilde{F}}_{up}$ and ${\tilde{F}}_{qp}$, respectively. In particular, the second point turns out to be essential for building S_p as an actually representative operator of the physical properties of the pressure equation. Following the ideas introduced by Franceschini et al. (2021) and Nardean et al. (2021), we use a dynamic approach that starts from physically-based static patterns ${\mathcal{K}}_u^{(k),0}$ and ${\mathcal{K}}_q^{(k),0}$ and builds ${\mathcal{K}}_u^{(k)}$ and ${\mathcal{K}}_q^{(k)}$ by selecting and computing the most significant entries in each column.

A natural choice for ${\mathcal{K}}_u^{(k),0}$ and ${\mathcal{K}}_q^{(k),0}$ is the set of non-zero entries of the kth column of A_up and A_qp, respectively, which can be immediately derived from the grid topology and the relation tables node-to-element and face-to-element (Vassilevski, 2002). In fact, the kth column of F_up can be regarded as the discrete displacement arising in the solid body with stiffness matrix A_uu because of the loads defined in the kth column of A_up—namely, loads produced by a unit pressure change at the kth pressure degree of freedom (DoF) p_k and applied to mesh nodes associated with displacement DoFs coupled to p_k. Similarly, the kth column of F_qp is the discrete Darcy velocity in the porous volume with conductivity matrix A_qq generated by the pressure gradients defined in the kth column of A_qp—namely, pressure gradients due to a unit pressure change at p_k and applied to mesh faces associated with velocity DoFs coupled to p_k. Hence, we expect the larger entries in the kth column of F_up and F_qp to be located on the loaded nodes and faces, with progressively decaying values as we move farther in the surroundings. Possible expansions to ${\mathcal{K}}_u^{(k),0}$ and ${\mathcal{K}}_q^{(k),0}$ are topologically based, by collecting neighbors and neighbors of neighbors for a (small) given number of levels.

After setting the initial patterns, successive expansions are governed by an adaptive algorithm built on the one introduced by Janna and Ferronato (2011) and Janna et al. (2015b). We compute ${\tilde{F}}_{up}{|}_{{\mathcal{K}}_u^{(k),0},k}$ and ${\tilde{F}}_{qp}{|}_{{\mathcal{K}}_q^{(k),0},k}$ by solving systems (55) and then obtain the residuals:

$\left\{\begin{array}{c}{\mathbf{r}}_u^{\left(k\right),0}=A_{uu}{|}_{:,{\mathcal{K}}_u^{\left(k\right),0}}{\tilde{F}}_{up}{|}_{{\mathcal{K}}_u^{\left(k\right),0},k}+A_{up}{|}_{:,k}\hfill \\ {\mathbf{r}}_q^{\left(k\right),0}=A_{qq}{|}_{:,{\mathcal{K}}_q^{\left(k\right),0}}{\tilde{F}}_{qp}{|}_{{\mathcal{K}}_q^{\left(k\right),0},k}+A_{qp}{|}_{:,k}\hfill \end{array}\right.,k=1,\dots ,n_p,(58)$

The non-zero pattern ${\mathcal{K}}_r^{(k),0}$, r = u, p, is enlarged by adding ρ_r positions corresponding to the largest components of ${\mathbf{r}}_r^{(k)}$, thus obtaining the augmented pattern ${\mathcal{K}}_r^{(k),1}$. The procedure is iterated by computing the new columns ${\tilde{F}}_{rp}{|}_{{\mathcal{K}}_r^{(k),1},k}$ and the residuals (58), so as to build ${\mathcal{K}}_r^{(k),2}$, and so on. The column-wise search can be stopped when either a maximum number of entries are added or some norm of ${\mathbf{r}}_r^{(k)}$ is smaller than a prescribed tolerance. This approach has the advantage of adapting automatically column-wise the density of the decoupling factors so as to obtain a prescribed quality of the approximations. By contrast, its cost can rapidly increase with the number of computed entries, so that the need for high-quality decoupling factors and the number of enlarging steps to achieve the target are contrasting requirements that should be properly balanced.

3.2 Implicit Approach

The exact decoupling factors F_up and F_qp are dense and their explicit computation assumes that they can be well-approximated by a sparse operator. This might not be the case in complex problems, and especially where strongly coupled conditions add to grid distortion and medium heterogeneity. This limitation can be overcome by using an implicit approximation, where F_up and F_qp of Eq. 52 do not need to be formed and their application to a vector is carried out by a matrix-by-vector product and an inexact application of either $A_{uu}^{-1}$ or $A_{qq}^{-1}$, e.g., by the same operators $M_u^{-1}$ or $M_q^{-1}$ used to replace the application of $S_u^{-1}$ and $S_q^{-1}$. However, the pressure-equation Schur complement S_p now reads:

$\begin{array}{ccc}\hfill S_p& =\hfill & A_{pp}+A_{up}^T{M}_u^{-1}{A}_{uu}{M}_u^{-1}{A}_{up}+\mathrm{\Delta }t{A}_{qp}^T{M}_q^{-1}{A}_{qq}{M}_q^{-1}{A}_{qp}\hfill \\ \hfill & \simeq \hfill & A_{pp}+A_{up}^T{M}_u^{-1}{A}_{up}+\mathrm{\Delta }t{A}_{qp}^T{M}_q^{-1}{A}_{qp}=A_{pp}+S_p^{\left(u\right)}+\mathrm{\Delta }t{S}_p^{\left(q\right)},\hfill \end{array}(59)$

that can be neither computed nor inverted in simple and efficient ways. This limitation can be bypassed by defining explicit physics-based approximations ${\tilde{S}}_p^{(u)}$ and ${\tilde{S}}_p^{(q)}$ of $S_p^{(u)}$ and $S_p^{(q)}$, respectively, thus preventing from the direct use of Eq. 59.

The contribution ${\tilde{S}}_p^{(u)}$ can be computed by replacing the mass balance Eq. 19 with the flow equation in saturated porous media traditionally used in hydrogeology. The classical claim is that the medium deformation can be decoupled from the flow and lumped in a single material parameter, denoted as specific elastic storage coefficient, with no significant detrimental effects for the overall solution at large space and time scales. For example, it is well-known that decoupling takes place rigorously if the deformation evolves with no variation in time of the total volumetric stress σ_vol (Rice and Cleary, 1976):

${\dot{\sigma }}_{vol}=K_b\nabla \cdot \dot{\mathit{u}}-b\dot{p}=0(60)$

with K_b the volumetric bulk modulus. Under this hypothesis, the continuity Eq. 19 reads:

$\nabla \cdot \mathit{q}+\left(S_{ϵ}+\frac{b^2}{K_b}\right)\dot{p}=f(61)$

The same occurrence takes place if the deformation occurs in oedometric conditions with prevented lateral deformations, where we have (Verruijt, 1969):

$K_v\nabla \cdot \mathit{u}=bp(62)$

with K_v the vertical uniaxial bulk modulus. Again, we have the same expression as in (61) where K_b is replaced by K_v. Therefore, the idea is to replace the mass balance Eq. 19 with:

$\nabla \cdot \mathit{q}+\left(S_{ϵ}+\frac{b^2}{\bar{K}}\right)\dot{p}=f(63)$

for preconditioning purposes only, where $\bar{K}$ is some lumped parameter accounting for the bulk modulus. In the fully discrete weak form Eq. 40, the functional ${({\chi }^h,b\text{div}{\mathit{u}}_n^h)}_{\mathrm{\Omega }}$ is replaced by the bilinear form:

$S\left({\chi }^h,p^h\right)={\left({\chi }^h,b^2/\bar{K}{p}^h\right)}_{\mathrm{\Omega }},\forall {\chi }^h\in {\mathcal{P}}^h(64)$

Introducing in (64) the discrete approximation (42) for the pressure and the basis ${\{{\chi }_k\}}_{k\in {\mathcal{N}}_p}$ of ${\mathcal{P}}^h$, produces the matrix form:

${\left[{\tilde{S}}_p^{\left(u\right)}\right]}_{ij}={\left({\chi }_i,b^2/\bar{K}{\chi }_j\right)}_{\mathrm{\Omega }},i,j=1,\dots ,n_p.(65)$

Following the algebraic interpretation of ${\tilde{S}}_p^{(u)}$ given by Castelletto et al. (2016), $\bar{K}$ can be computed locally for every pressure DoF p_k, for instance as a measure of an appropriate sub-matrix of A_uu. Denoting as ${\mathcal{R}}_u^{(k)}$ the set of indices of the non-zero entries in the kth column of A_up, the corresponding local value ${\bar{K}}^{(k)}$ can be set to:

${\bar{K}}^{\left(k\right)}={‖A_{uu}{|}_{{\mathcal{R}}_u^{\left(k\right)},{\mathcal{R}}_u^{\left(k\right)}}‖}_2,k=1,\dots ,n_p.(66)$

The operator defined in Equation 65 was also used to obtain the so-called fixed-stress splitting scheme for the sequential solution of a finite element coupled poromechanical model (Kim et al., 2011; White et al., 2016). For this reason, ${\tilde{S}}_p^{(u)}$ is also referred to as fixed-stress matrix.

The computation of ${\tilde{S}}_p^{(q)}$ usually poses less difficulties. In fact, this issue has been already addressed in the context of the preconditioning for mixed finite element discretization of Darcy’s flow. Bergamaschi et al. (1998) propose to use a matrix derived from the discretization of the pressure Laplacian weighted by the Euclidean norm of the rows of A_qq. To this purpose, we define the diagonal matrix:

$D=\mathrm{diag}\left({\tilde{a}}_1,{\tilde{a}}_2,\dots ,{\tilde{a}}_{n_q}\right),{\tilde{a}}_i={\left(\sum _{j=1}^{n_q}{\left[A_{qq}\right]}_{ij}^2\right)}^{1/2},i=1,\dots ,n_q(67)$

The contribution $S_p^{(q)}$ is then approximated by:

${\tilde{S}}_p^{\left(q\right)}=A_{qp}^T{D}^{-1}{A}_{qp}.(68)$

The final implicit preconditioning operator ${\mathbf{M}}_{imp}^{-1}$ for A reads:

${\mathbf{M}}_{imp}^{-1}=\left[\begin{array}{ccc}\hfill I_u\hfill & \hfill 0\hfill & \hfill -M_u^{-1}{A}_{up}\hfill \\ \hfill 0\hfill & \hfill I_q\hfill & \hfill -M_q^{-1}{A}_{qp}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill I_p\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill M_u^{-1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill M_q^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill M_p^{-1}\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill I_u\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill I_q\hfill & \hfill 0\hfill \\ \hfill A_{up}^T{M}_u^{-1}\hfill & \hfill \mathrm{\Delta }t{A}_{qp}^T{M}_q^{-1}\hfill & \hfill I_p\hfill \end{array}\right],(69)$

where $M_p^{-1}$ denotes the operator that inexactly applies the inverse of $A_{pp}+{\tilde{S}}_p^{(u)}+\mathrm{\Delta }t{\tilde{S}}_p^{(q)}$. Since the application of ${\mathbf{M}}_{imp}^{-1}$ to a vector requires twice the application of $M_u^{-1}$ and $M_q^{-1}$ with respect to ${\mathbf{M}}_{\exp }^{-1}$, either the rightmost or the leftmost block triangular factors can be neglected, thus giving rise to an overall block triangular preconditioner. This kind of approximation is widely used in several problems, e.g., (Murphy et al., 2000; Benzi et al., 2005), because it reduces the application cost usually without a significant detrimental effect on the solver convergence rate.

3.3 Reverse Approach

As in any preconditioning method based on Schur complement approximations, the implicit approach requires some specific trick to define S_p in an amenable way. The main limitation of physics-based strategies, such as the one described in Section 3.2, is that they are usually very problem-dependent and do not provide the user with operative tools for improving the approximation. For example, the surrogate contributions ${\tilde{S}}_p^{(u)}$ and ${\tilde{S}}_p^{(q)}$ depend on the material and discretization properties and their accuracy cannot be controlled by the user. For this reason, we would like to develop a strategy that does not rely on accurate sparse approximations of the Schur complements.

The idea is to properly permute the block rows and columns so as to avoid the computation of S_p. This can be done, for instance, by eliminating the pressure variables first, then Darcy’s velocities, and finally reducing to a single-physics displacement problem. For this reason, we denote this strategy as a reverse preconditioning approach. Let us first permute the matrix A as:

$\bar{\mathbf{A}}=\left[\begin{array}{ccc}\hfill A_{pp}\hfill & \hfill \mathrm{\Delta }t{A}_{pq}\hfill & \hfill A_{pu}\hfill \\ \hfill A_{qp}\hfill & \hfill A_{qq}\hfill & \hfill 0\hfill \\ \hfill A_{up}\hfill & \hfill 0\hfill & \hfill A_{uu}\hfill \end{array}\right](70)$

and eliminate the pressure variables from the second and third block rows by using the multi-physics reduction procedure described in Section 2. The matrix A_pp, however, is SPSD, hence it cannot be safely inverted in any circumstances. To avoid such an inconvenience, we replace A_pp in Equation 70 with αI_p, where $\alpha \in \mathbb{R}$ is an appropriate relaxing parameter, then we eliminate the pressure variables:

${\bar{\mathbf{A}}}^{\left(1\right)}=\left[\begin{array}{ccc}\hfill \alpha I_p\hfill & \hfill \mathrm{\Delta }t{A}_{pq}\hfill & \hfill A_{pu}\hfill \\ \hfill 0\hfill & \hfill A_{qq}^{\left(1\right)}\hfill & \hfill A_{qu}^{\left(1\right)}\hfill \\ \hfill 0\hfill & \hfill A_{uq}^{\left(1\right)}\hfill & \hfill A_{uu}^{\left(1\right)}\hfill \end{array}\right],(71)$

with:

$\begin{array}{ccc}\hfill A_{qq}^{\left(1\right)}& =\hfill & A_{qq}-\mathrm{\Delta }t{\alpha }^{-1}{A}_{qp}{A}_{pq},\hfill \end{array}(72)$

$\begin{array}{ccc}\hfill A_{qu}^{\left(1\right)}& =\hfill & -{\alpha }^{-1}{A}_{qp}{A}_{pu},\hfill \end{array}(73)$

$\begin{array}{ccc}\hfill A_{uq}^{\left(1\right)}& =\hfill & -\mathrm{\Delta }t{\alpha }^{-1}{A}_{up}{A}_{pq},\hfill \end{array}(74)$

$\begin{array}{ccc}\hfill A_{uu}^{\left(1\right)}& =\hfill & A_{uu}-{\alpha }^{-1}{A}_{up}{A}_{pu}.\hfill \end{array}(75)$

The next step should include the elimination of Darcy’s velocity from the third block row, thus implying the use of the inverse of $A_{qq}^{(1)}$ and the generation of other Schur complements. A simplifying assumption that avoids the possibly troublesome computation of $A_{uu}^{(2)}=A_{uu}^{(1)}-A_{qu}^{(1)}{A}_{qq}^{(1),-1}{A}_{uq}^{(1)}$ relies on neglecting at least one of terms coupling Darcy’s velocities with displacements. For example, in their pioneering work Ferronato et al. (2010) simply neglected both the $A_{qu}^{(1)}$ and $A_{uq}^{(1)}$ blocks, with a simultaneous solution for Darcy’s velocity and displacement DoFs. More recently, Frigo et al. (2019) suggested to neglect the $A_{uq}^{(1)}$ block alone and found a robust and cheap algorithm to compute an optimal value for the relaxing parameter α. In essence, they operated a multi-physics reduction procedure on the approximate block matrix $\bar{\mathbf{A}}$:

$\bar{\mathbf{A}}=\left[\begin{array}{ccc}\hfill \alpha I_p\hfill & \hfill \mathrm{\Delta }t{A}_{pq}\hfill & \hfill A_{pu}\hfill \\ \hfill A_{qp}\hfill & \hfill A_{qq}\hfill & \hfill 0\hfill \\ \hfill A_{up}\hfill & \hfill {\tilde{A}}_{uq}\hfill & \hfill A_{uu}\hfill \end{array}\right](76)$

where ${\tilde{A}}_{uq}=\mathrm{\Delta }t{\alpha }^{-1}{A}_{up}{A}_{pq}$ and the optimal α value reads:

$\alpha =\frac{\sqrt{\mathrm{\Delta }t}}{n_p}\sqrt{\text{trace}\left[\text{diag}\left({\tilde{S}}_p^{\left(u\right)}\right)\cdot \text{diag}\left({\tilde{S}}_p^{\left(q\right)}\right)\right]}.(77)$

By permuting the sequence of variables back to the original displacement-velocity-pressure ordering, the resulting preconditioner reads:

${\mathbf{M}}_{rev}^{-1}={\left(\left[\begin{array}{ccc}\hfill I_u\hfill & \hfill 0\hfill & \hfill {\alpha }^{-1}{A}_{up}\hfill \\ \hfill 0\hfill & \hfill I_q\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill I_p\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill A_{uu}^{\left(1\right)}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill I_q\hfill & \hfill 0\hfill \\ \hfill A_{pu}\hfill & \hfill 0\hfill & \hfill I_p\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill I_u\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill A_{qq}^{\left(1\right)}\hfill & \hfill A_{qp}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \alpha I_p\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill I_u\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill I_q\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \mathrm{\Delta }t{\alpha }^{-1}{A}_{pq}\hfill & \hfill I_p\hfill \end{array}\right]\right)}^{-1},(78)$

and was denoted as Relaxed Physical Factorization in order to recall a similar strategy previously introduced for Navier-Stokes equations (Benzi et al., 2011, 2016).

The reverse preconditioning approach does not require the computation and the inversion of the classical Schur complement S_p, but needs inner solves, that are carried out inexactly, with $A_{uu}^{(1)}$ and $A_{qq}^{(1)}$. Since n_p is smaller than both n_u and n_q, $A_{uu}^{(1)}$ and $A_{qq}^{(1)}$ have the form:

$C^{\left(1\right)}=C+\beta F{F}^T,(79)$

with β > 0, C a regular SPD matrix, and FF^T a rank-deficient contribution. The inexact application of C^(1),−1 may easily become an issue for large values of β, with a progressive deterioration of the ${\mathbf{M}}_{rev}^{-1}$ effectiveness. In order to avoid this difficulty, the inexact solution to the system:

$C^{\left(1\right)}\mathbf{v}=\mathbf{b},(80)$

with C⁽¹⁾ defined as in (79), is carried by setting the auxiliary variable w = βF^Tv. System (80) then reads:

$\left[\begin{array}{cc}\hfill C\hfill & \hfill F\hfill \\ \hfill F^T\hfill & \hfill -{\beta }^{-1}{I}_p\hfill \end{array}\right]\left(\begin{array}{c}\hfill \mathbf{v}\hfill \\ \hfill \mathbf{w}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill \mathbf{b}\hfill \\ \hfill \mathbf{0}\hfill \end{array}\right).(81)$

Eliminating v from the second equation we obtain:

$\mathbf{w}=\beta {\left(I_p+\beta F^T{C}^{-1}F\right)}^{-1}{F}^T{C}^{-1}\mathbf{b},(82)$

which substituted in the first equation gives:

$\mathbf{v}=C^{-1}\left[\mathbf{b}-\beta F{\left(I_p+\beta F^T{C}^{-1}F\right)}^{-1}{F}^T{C}^{-1}\mathbf{b}\right].(83)$

Eq. 83 is nothing but the Sherman-Morrison-Woodbury formula. The use of Eq. 83 for computing the solution to system (80) is generally more stable, because it avoids the inversion of the nearly-singular matrix C⁽¹⁾. Frigo et al. (2022) suggests to use Eq. 83 for the application of ${\mathbf{M}}_{rev}^{-1}$. In particular, for the inexact solution to $A_{rr}^{(1)}{\mathbf{v}}_r={\mathbf{b}}_r$, r = u, q, we use the relationship:

${\mathbf{v}}_r=M_r^{-1}\left\{{\mathbf{b}}_r+{\beta }_r{A}_{rp}{\left[I_p+{\beta }_r\text{diag}\left({\tilde{S}}_p^{\left(r\right)}\right)\right]}^{-1}{A}_{pr}{M}_r^{-1}{\mathbf{b}}_r\right\},(84)$

where β_u = α⁻¹ and β_q = Δtα⁻¹. In this way, for the application of ${\mathbf{M}}_{rev}^{-1}$ we need the inner approximations $M_u^{-1}$ and $M_q^{-1}$ as with both the explicit and implicit approaches.

4 Numerical Results

In order to compare the proposed algorithms and assess their numerical performances, we select four real-world test cases. They are different in terms of: (i) nature of the applications, ranging from a geotechnical problem to a deep reservoir and a regional hydrogeological model; (ii) grid type, which can be either structured or unstructured; and (iii) material properties, with a variable heterogeneous and anisotropic behavior for both the intrinsic permeability and the mechanical parameters. The test cases are as follows.

• Treporti: this model is used to reproduce the consolidation conditions of shallow heterogeneous sediments due to the presence of a trial embankment in the Venice lagoon. The surface loading/unloading process lasts 5 years, with the main purpose of characterizing the geomechanical properties of the sedimentary deposits and was developed to support the analyses for the construction of the mobile barriers located at the Venice lagoon inlets (Castelletto et al., 2015a). The porous formation consists of a sequence of alternating sandy, silty and clayey layers down to 60-m depth (Figure 2A), with a vertical intrinsic permeability and Young modulus varying in the ranges [5.1 × 10^–16, 5.1 × 10^–15] m² and [2.5, 44.0] MPa, respectively. The Poisson ratio is ν = 0.15. The model represents one fourth of the embankment, thus boundary conditions are set to honour the symmetry. The only fully constrained surface is the bottom. Further details on the model can be found in Castelletto et al. (2015a).

• SPE10-16: the top 16 layers of the SPE10 Comparative Solution Project (Christie and Blunt, 2001) are used to model a compacting reservoir subject to a single-phase flow. The computational domain includes 60, ×, 220, ×, 16 hexahedral elements in the x-, y- and z-direction, respectively (Figure 2B). The reservoir is a well-known benchmark for industrial reservoir simulators, being representative of a shallow-marine Tarbert formation characterized by severe permeability and porosity variations, as shown in the figure. While the intrinsic permeability is derived from the SPE10 dataset, homogeneous mechanical properties are defined for the entire domain. In particular, we have E = 8.3 × 10³ MPa and ν = 0.3. Roller boundary conditions are imposed on all boundaries, except for the top one that is traction-free.

• SPE10-35: the model is built on top of the SPE10-16 test case by extending the simulation to the first 35 layers of the SPE10 benchmark and including the related intrinsic permeability and porosity distribution maps (Figure 2C). Mechanical properties and boundary conditions are the same as in SPE10-16.

• Chaobai: this is a regional-size hydrogeological model with the purpose of simulating land subsidence and possible ground ruptures caused by the over-exploitation of a shallow multi-aquifer system in the Chaobai River alluvial fan, North of Beijing in China. The study area has an overall extent of 1,155 km². To account for the strongly heterogeneous nature of the sediments, a statistical inverse framework in a multi-zone transition probability approach is adopted (Zhu et al., 2016, 2020). The aquifer system is confined by an irregular bedrock located at about 550 m below the top surface (Figure 2D). More details on the model implementation and porous rock parameters are provided in Ferronato et al. (2017).

FIGURE 2

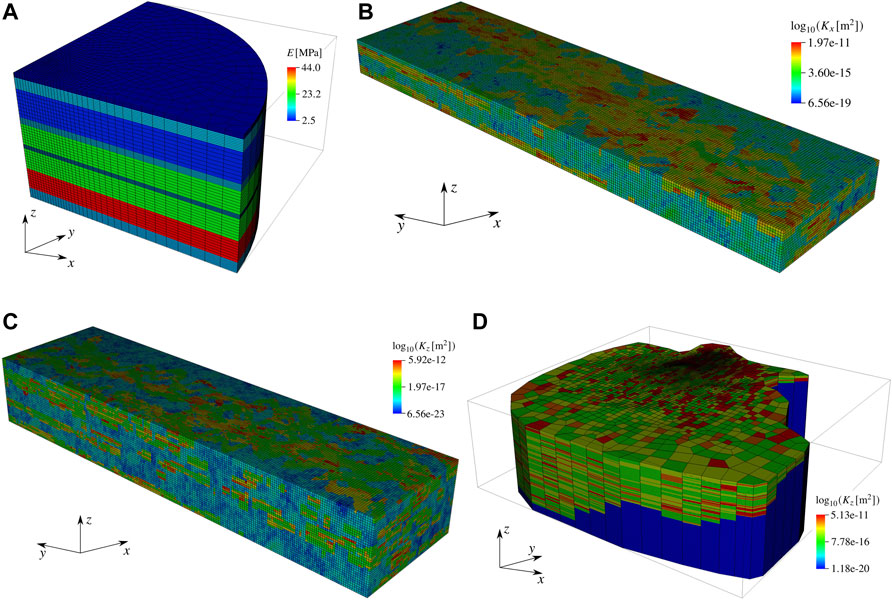
FIGURE 2. Meshes used for the numerical test cases. (A) Treporti case, showing the values of Young modulus. (B) SPE10-16, with the horizontal intrinsic permeability distribution κ_x = κ_y. (C) SPE10-35, displaying the vertical intrinsic permeability distribution κ_z. (D) Chaobai case, showing the vertical intrinsic permeability distribution K_z. For Chaobai, a vertical exaggeration factor of 25 is used.

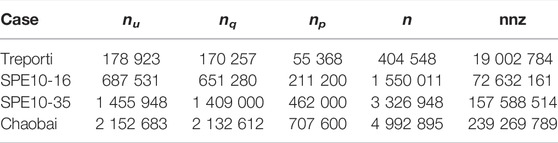
For each problem, which is generally characterized by non-linear constitutive laws, we select the Jacobian matrix arising at some representative steps of a full simulation. The objective is to test the proposed linear solvers in different regimes of a hydro-mechanical problem, so as to investigate the robustness of the proposed preconditioners and in which conditions they can work best. Moreover, the selected test cases have also a different practical nature, thus involving a wide range of mechanical and hydrological parameter values. Treporti and Chaobai test cases consider shallow environments, with the former reproducing the consolidation of a soft and very low permeable layered material lying on a lagoon deposition and the latter studying the behavior of a mostly gravel aquifer with the insertion of sand and clay lenses. By distinction, the SPE10-based problems focus on a stiff and deep rock environment, where the flow dynamics typically prevails over mechanics. Table 1 summarizes the number of displacement, Darcy’s velocity and pressure DoFs, n_u, n_q and n_p, respectively, for the four test cases. Here, n and nnz represent the total number of unknowns and the global number of non-zero entries, respectively, for the Jacobian matrix of Eq. 43. It can be noticed that the models range from about 0.5 to five million unknowns.

TABLE 1

TABLE 1. Number of unknowns and matrix size for the four test cases.

A restarted GMRES (250) has been chosen as Krylov iterative method. The iterations start from the zero initial guess and are stopped when either the residual norm is reduced by eight orders of magnitude or the iteration count exceeds 1,000. In the latter case, we assume the solver fails to converge. The right-hand side is artificially generated by computing the product of A by a random vector, so that the real solution error can be also checked for consistency. The numerical results are obtained with the original (not scaled) matrix. The code is written in Fortran90 and the simulations are run using the GNU Fortran compiler (version 9.3.0). Computational performances are evaluated on a local server equipped with an Intel(R) Xeon(R) CPU E5-2643 at3.30 GHz (quadcore) and 256 GB of DIMM RAM. For all tests, a shared-memory OpenMP paradigm is used with four computing cores.

Independently of the selected explicit, implicit or reverse approach, inner preconditioners $M_u^{-1}$ and $M_q^{-1}$ are required to apply inexactly $A_{uu}^{-1}$ and $A_{qq}^{-1}$, respectively. With the explicit and implicit approach also $M_p^{-1}$ is needed to approximate the application of $S_p^{-1}$. In order to emphasize the respective behavior of each algorithm, we use the same inner preconditioning strategy for each block. In particular, we elect to use the Adaptive Block Factorized Sparse Approximate Inverse (ABF, (Janna and Ferronato, 2011)), which is an efficient parallel black-box strategy for SPD matrices. Of course, the presented approaches are fully flexible with respect to the choice of the inner preconditioners and more effective, or specifically tailored, techniques can be used straightforwardly. For example, if a non-associative elastoplastic law is required by the mechanics, i.e., producing a non-symmetric stiffness matrix A_uu, a different inner preconditioner is required. However, the overall effectiveness of the block preconditioning framework is not affected. For the present test cases, the setup parameters for the inner ABF preconditioners are tuned following the indications provided in the original papers by Janna and Ferronato (2011) and Janna et al. (2015a). In any case, the setup parameters are tuned so as to optimize the total solution time. Typically, we observe that $M_u^{-1}$ is the most expensive inner preconditioner impacting in a more significant way on the overall algorithm performance. Some offline tests with the structural block alone A_uu might be advisable for the user to acquire some confidence about the block properties. By distinction, the inexact solves with A_qq and S_p do not create difficulties in any approach, independently of the actual heterogeneous distribution of the hydraulic parameters. Hence, $M_q^{-1}$ and $M_p^{-1}$ can be usually set as light preconditioners with no detrimental effects for the overall convergence properties.

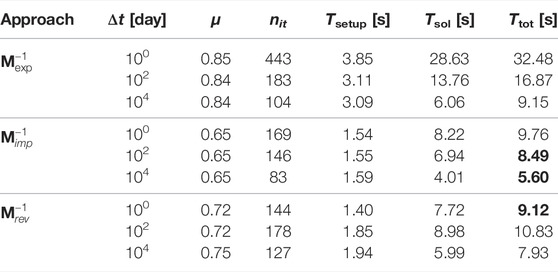
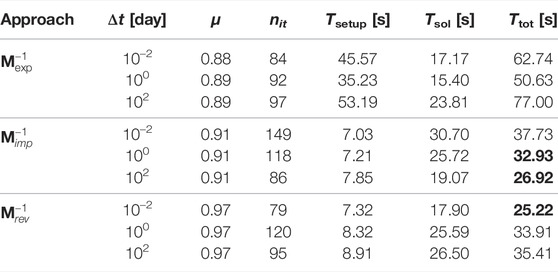
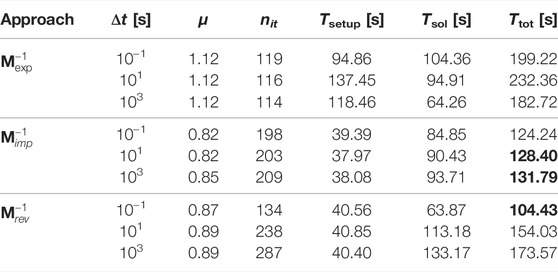
Tables 2–5 show the numerical results obtained with the four test cases. In particular, we analyze the following parameters:

• the density μ of the preconditioner, defined as the ratio between the number of non-zero entries stored for the preconditioner and the block matrix A. This number provides a measure of the memory footprint of the preconditioner and a rough estimate of the expected application cost;

• the iteration count n_it to achieve convergence. Absence of this value means that convergence was not achieved within 1,000 iterations and a failure is accounted for;

• the setup time T_setup in seconds, accounting for the cost to compute all the terms required for the preconditioner construction. This has to be taken as the maximum setup cost needed to build the full preconditioner from scratch. Of course, in a full transient simulation even significant parts of the preconditioner can be recycled with this cost largely amortized;

• the solution time T_sol in seconds, spent by preconditioned GMRES (250) to complete the iterations;

• the total time T_tot = T_setup + T_sol. This value has to be regarded as the maximum total time spent for the solution of a single system with the matrix A, neglecting the setup portion that can be recycled during a full transient simulation.

TABLE 2

TABLE 2. Treporti test case: computational performance.

TABLE 3

TABLE 3. SPE10-16 test case: computational performance.

TABLE 4

TABLE 4. SPE10-35 test case: computational performance.

TABLE 5

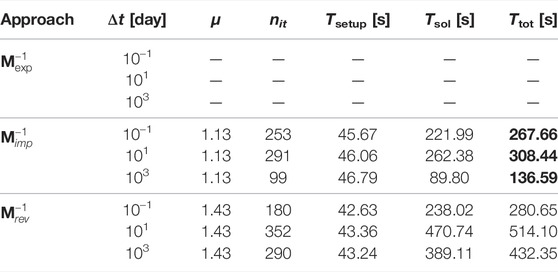
TABLE 5. Chaobai test case: computational performance. — means that convergence is not achieved within 1,000 iterations.

For each test case, three different values of the time step Δt are considered. This allows to consider the robustness and efficiency of every approach in different regimes of the hydro-mechanical problem at hand. The solver performance at each Δt value is representative of the behavior expected in three different stages of a full transient simulation. Typically, small time steps are required at the early simulation stage, so as to capture at a better detail the initial evolution, while larger and larger time steps can be safely used towards the steady state when mechanics decouples from the fluid flow. Herein we use a “small” (first line), “intermediate” (second line), and “large” (third line) time step size for each test case with respect to the characteristic consolidation time of the problem. The intermediate time step size has the order of the characteristic consolidation time, hence a time step is regarded as small or large if it is two orders of magnitude lower or higher, respectively.

In each table, bold values highlight the best performances in terms of total time. We notice that the three approaches can solve all the cases at every consolidation stage, except for the combination ${\mathbf{M}}_{\exp }^{-1}$/Chaobai. In this case, the explicit procedure fails to produce effective decoupling blocks at a workable sparsity and the convergence profile stagnates around 10^–1, without reaching convergence. In particular, the exact decoupling blocks turn out to be populated by a huge amount of (relatively small) entries having approximately the same size, so that recognizing the most significant ones is not possible. This is a typical limitation of the explicit approach, i.e., the fact that a good sparse approximation of F_up and F_qp does not exist, which can become more and more evident as the overall problem size increases. Notice also that the explicit approach is never the best method from the total time viewpoint, even if it shows in most occurrences the fastest convergence rate at a comparable, or even lower, preconditioner density with respect to the other method. The weakest point appears to be the setup time, which includes the computation of the approximate decoupling factors ${\tilde{F}}_{up}$ and ${\tilde{F}}_{qp}$ in addition to $M_u^{-1}$, $M_q^{-1}$ and $M_p^{-1}$. This task can need a cost that is comparable to that required for the three inner preconditioners and tends to increase in a super-linear way with the model size. Indeed, the sparse non-zero patterns of ${\tilde{F}}_{up}$ and ${\tilde{F}}_{qp}$ do not change too much from one time step to another, thus they can be recycled for several steps just with a coefficient update. This trick can significantly decrease the actual the setup time in a full transient simulation, with the most expensive part possibly amortized in several steps. The same does not hold for the other two approaches, thus making the explicit approach interesting anyway.

Tables 2–5 show that ${\mathbf{M}}_{imp}^{-1}$ prevails 9 times and ${\mathbf{M}}_{rev}^{-1}$ 3 times out of a total of 12 combinations. Here, the upper block triangular version of the implicit approach is used in order to have a comparable application cost with the other approaches. This implies that ${\mathbf{M}}_{imp}^{-1}$ appears to perform generally better for both shallow and deep hydro-machanical problems, as well as in different consolidation regimes, even though a clear winner does not stand. We can observe that the implicit and the reverse approaches are usually quite similar in terms of density, computational times, and convergence rate. The main advantage of the reverse approach relies on its bigger flexibility of use, which can make it preferable for the implementation in general-purpose hydro-mechanical software. Indeed, while the implicit preconditioner uses fixed physics-based approximations for ${\tilde{S}}_p^{(u)}$ and ${\tilde{S}}_p^{(q)}$, which cannot be controlled or improved by the user, the reverse approach overcomes this limitation and at the same time it is easier to setup, requiring the construction of $M_u^{-1}$ and $M_q^{-1}$ only. By distinction, this is compensated by a generally slightly larger preconditioner density to obtain a similar convergence rate.

Finally, we observe that the selected test cases are meant to provide representative information as to the linear solver performance in different consolidation regimes, physical conditions and spatial scales, but of course they cannot cover the entire spectrum of applications. However, these different situations are expected to impact more on the parameters controlling the quality associated to the inner solvers, than on the overall decoupling effectiveness of the proposed methods.

5 Conclusion

The development of robust and efficient solvers for the linearized discrete problems arising from coupled hydromechanical applications is an important field of research. In recent years, several different algorithms for preconditioning purposes have been proposed, relying on either algebraic or physical or discretization-based considerations. In this work, we attempt to introduce a unifying framework and recast apparently different approaches within similar underlying ideas. We focus, in particular, on coupled hydromechanical problems written in a mixed form.

Based on the general algebraic framework introduced by Ferronato et al. (2019) for coupled multi-physics applications, we define a decoupling operator whose action can recast a block-structured problem into a set of independent single-physics problems. The same holds true if a standard block-reduction procedure is carried out, being only a part of the overall decoupling operator computed explicitly. According to the way such a decoupling operator is approximated, different algorithms can arise. In particular, we have investigated three approaches.

• Explicit algorithm: sparse approximations of the factors of the decoupling operator are computed explicitly with the aid of techniques borrowed from approximate-inverse preconditioners. The method is flexible and able to adapt to the different features of the problem under consideration, allowing for a straightforward computation of the Schur complement matrices. Difficulties might arise, however, when sparse approximations of the decoupling factors do not exist. In these cases, the preconditioner cost and density can increase too much, also showing a possible lack of robustness.

• Implicit algorithm: the factors of the decoupling operator are not computed explicitly, but applied to a vector by a matrix-vector product and an inexact solve with an inner single-physics block. This allows for inherently keeping a much denser, hence more effective, decoupling operator, but the resulting Schur complement matrix cannot be computed explicitly. Very effective results are obtained by introducing physics-based approximations, which typically yield efficient results in a scalable and parallel-friendly environment. However, physics-based Schur complement approximations are not flexible and do not leave control to the user.

• Reverse algorithm: the reduction sequence used in the implicit approach is reversed so as to avoid the computation of troublesome Schur complement matrices. This is carried out by replacing the pressure block with a relaxed mass matrix, where the relaxation parameter is set optimally in order to cluster the eigenspectrum of the preconditioned matrix. This approach is generally more expensive and possibly prone to near-singularity of the inner single-physics blocks, but enables the user with an important flexibility and is generally more efficient than the explicit approach.

The proposed methods can integrate each other, overall proving robust and efficient in real-world challenging applications. The present work can also open the path to a more systematic interpretation and organization of other algorithms for the linear solution to coupled hydromechanical applications, yielding to a definition of common benchmarks and a thorough comparison of algorithms.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://gitlab.com/matteofrigo5/coupledporomechanicsmatrices.

Author Contributions

MFe: Conceptualization, methodology, supervision, writing (Sections 1, 2, 3, 5), review and editing. AF: Software, simulations, writing-original draft (Section 4). MFr: Software, simulations, writing-original draft (Section 4).

Conflict of Interest

MFr is employed by M3E Srl.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The Authors gratefully acknowledge Nicola Castelletto and Joshua A. White for the inspiring talks and their friendly contribution.

References

Almani, T., Kumar, K., Dogru, A., Singh, G., and Wheeler, M. F. (2016). Convergence Analysis of Multirate Fixed-Stress Split Iterative Schemes for Coupling Flow with Geomechanics. Comput. Methods Appl. Mech. Eng. 311, 180–207. doi:10.1016/j.cma.2016.07.036

CrossRef Full Text | Google Scholar

Asadi, R., Ataie-Ashtiani, B., and Simmons, C. T. (2014). Finite Volume Coupling Strategies for the Solution of a Biot Consolidation Model. Comput. Geotechnics 55, 494–505. doi:10.1016/j.compgeo.2013.09.014

CrossRef Full Text | Google Scholar

Benzi, M., Deparis, S., Grandperrin, G., and Quarteroni, A. (2016). Parameter Estimates for the Relaxed Dimensional Factorization Preconditioner and Application to Hemodynamics. Comput. Methods Appl. Mech. Eng. 300, 129–145. doi:10.1016/j.cma.2015.11.016

CrossRef Full Text | Google Scholar

Benzi, M., Golub, G. H., and Liesen, J. (2005). Numerical Solution of Saddle point Problems. Acta Numerica 14, 1–137. doi:10.1017/S0962492904000212

CrossRef Full Text | Google Scholar

Benzi, M., Ng, M., Niu, Q., and Wang, Z. (2011). A Relaxed Dimensional Factorization Preconditioner for the Incompressible Navier-Stokes Equations. J. Comput. Phys. 230, 6185–6202. doi:10.1016/j.jcp.2011.04.001

CrossRef Full Text | Google Scholar

Benzi, M., and Wathen, A. J. (2008). “Some Preconditioning Techniques for Saddle point Problems,” in Model Order Reduction: Theory, Research Aspects and Applications (Berlin, Heidelberg: Springer), 195–211. doi:10.1007/978-3-540-78841-6_10

CrossRef Full Text | Google Scholar

Bergamaschi, L., Mantica, S., and Manzini, G. (1998). A Mixed Finite Element--Finite Volume Formulation of the Black-Oil Model. SIAM J. Sci. Comput. 20, 970–997. doi:10.1137/S1064827595289303

CrossRef Full Text | Google Scholar

Bergamaschi, L., and Martínez, Á. (2012). RMCP: Relaxed Mixed Constraint Preconditioners for Saddle point Linear Systems Arising in Geomechanics. Comput. Methods Appl. Mech. Eng. 221-222, 54–62. doi:10.1016/j.cma.2012.02.004

CrossRef Full Text | Google Scholar

Biot, M. A. (1941). General Theory of Three‐Dimensional Consolidation. J. Appl. Phys. 12, 155–164. doi:10.1063/1.1712886

CrossRef Full Text | Google Scholar

Boal, N., Gaspar, F. J., Lisbona, F. J., and Vabishchevich, P. N. (2012). Finite Difference Analysis of a Double-Porosity Consolidation Model. Numer. Methods Partial Differential Eq. 28, 138–154. doi:10.1002/num.20612

CrossRef Full Text | Google Scholar

Borregales, M., Radu, F. A., Kumar, K., and Nordbotten, J. M. (2018). Robust Iterative Schemes for Non-linear Poromechanics. Comput. Geosci. 22, 1021–1038. doi:10.1007/s10596-018-9736-6

CrossRef Full Text | Google Scholar

Both, J. W., Borregales, M., Nordbotten, J. M., Kumar, K., and Radu, F. A. (2017). Robust Fixed Stress Splitting for Biot's Equations in Heterogeneous media. Appl. Math. Lett. 68, 101–108. doi:10.1016/j.aml.2016.12.019

CrossRef Full Text | Google Scholar

Both, J. W., Kumar, K., Nordbotten, J. M., and Radu, F. A. (2019). Anderson Accelerated Fixed-Stress Splitting Schemes for Consolidation of Unsaturated Porous media. Comput. Math. Appl. 77, 1479–1502. doi:10.1016/j.camwa.2018.07.033

CrossRef Full Text | Google Scholar

Bui, Q. M., Osei-Kuffuor, D., Castelletto, N., and White, J. A. (2020). A Scalable Multigrid Reduction Framework for Multiphase Poromechanics of Heterogeneous media. SIAM J. Sci. Comput. 42, B379–B396. doi:10.1137/19m1256117

CrossRef Full Text | Google Scholar

Bürger, R., Ruiz-Baier, R., and Torres, H. (2012). A Stabilized Finite Volume Element Formulation for Sedimentation-Consolidation Processes. SIAM J. Sci. Comput. 34, B265–B289. doi:10.1137/110836559

CrossRef Full Text | Google Scholar

Camargo, J. T., White, J. A., and Borja, R. I. (2021). A Macroelement Stabilization for Mixed Finite Element/finite Volume Discretizations of Multiphase Poromechanics. Comput. Geosci. 25, 775–792. doi:10.1007/s10596-020-09964-3

CrossRef Full Text | Google Scholar

Castelletto, N., Gambolati, G., and Teatini, P. (2015a). A Coupled MFE Poromechanical Model of a Large-Scale Load experiment at the Coastland of Venice. Comput. Geosci. 19, 17–29. doi:10.1007/s10596-014-9450-y

CrossRef Full Text | Google Scholar

Castelletto, N., White, J. A., and Ferronato, M. (2016). Scalable Algorithms for Three-Field Mixed Finite Element Coupled Poromechanics. J. Comput. Phys. 327, 894–918. doi:10.1016/j/jcp.2016.09.06310.1016/j.jcp.2016.09.063

CrossRef Full Text | Google Scholar

Castelletto, N., White, J. A., and Tchelepi, H. A. (2015b). Accuracy and Convergence Properties of the Fixed-Stress Iterative Solution of Two-Way Coupled Poromechanics. Int. J. Numer. Anal. Meth. Geomech. 39, 1593–1618. doi:10.1002/nag.2400

CrossRef Full Text | Google Scholar

Chen, F., Drumm, E. C., and Guiochon, G. (2011). Coupled Discrete Element and Finite Volume Solution of Two Classical Soil Mechanics Problems. Comput. Geotechnics 38, 638–647. doi:10.1016/j.compgeo.2011.03.009

CrossRef Full Text | Google Scholar

Chen, L., Wu, Y., Zhong, L., and Zhou, J. (2018a). Multigrid Preconditioners for Mixed Finite Element Methods of the Vector Laplacian. J. Sci. Comput. 77, 101–128. doi:10.1007/s10915-018-0697-7

CrossRef Full Text | Google Scholar

Chen, Y., Chen, G., and Xie, X. (2018b). Weak Galerkin Finite Element Method for Biot's Consolidation Problem. J. Comput. Appl. Math. 330, 398–416. doi:10.1016/j.cam.2017.09.019

CrossRef Full Text | Google Scholar

Christie, M. A., and Blunt, M. J. (2001). Tenth SPE Comparative Solution Project: A Comparison of Upscaling Techniques. SPE Reservoir Eval. Eng. 4, 308–317. doi:10.2118/72469-PA

CrossRef Full Text | Google Scholar

Coussy, O. (2004). Poromechanics. Chichester, UK: Wiley.

Google Scholar

Dana, S., Ganis, B., and Wheeler, M. F. (2018). A Multiscale Fixed Stress Split Iterative Scheme for Coupled Flow and Poromechanics in Deep Subsurface Reservoirs. J. Comput. Phys. 352, 1–22. doi:10.1016/j.jcp.2017.09.049

CrossRef Full Text | Google Scholar

Elman, H., Silvester, D. J., and Wathen, A. J. (2014). Finite Elements and Fast Iterative Solvers: With Applications in Incompressible Fluid Dynamics. Oxford University Press.

Google Scholar

Ferronato, M., Castelletto, N., and Gambolati, G. (2010). A Fully Coupled 3-D Mixed Finite Element Model of Biot Consolidation. J. Comput. Phys. 229, 4813–4830. doi:10.1016/j.jcp.2010.03.018

CrossRef Full Text | Google Scholar

Ferronato, M., Franceschini, A., Janna, C., Castelletto, N., and Tchelepi, H. A. (2019). A General Preconditioning Framework for Coupled Multiphysics Problems with Application to Contact- and Poro-Mechanics. J. Comput. Phys. 398, 108887. doi:10.1016/j.jcp.2019.108887

CrossRef Full Text | Google Scholar

Ferronato, M., Gazzola, L., Castelletto, N., Teatini, P., and Zhu, L. (2017). “A Coupled Mixed Finite Element Biot Model for Land Subsidence Prediction in the Beijing Area,” in Poromechanics VI (Reston, Virginia: American Society of Civil Engineers), 182–189. doi:10.1061/9780784480779.022

CrossRef Full Text | Google Scholar

Ferronato, M., Janna, C., and Pini, G. (2014). A Generalized Block FSAI Preconditioner for Nonsymmetric Linear Systems. J. Comput. Appl. Math. 256, 230–241. doi:10.1016/j.cam.2013.07.049

CrossRef Full Text | Google Scholar

Franceschini, A., Castelletto, N., and Ferronato, M. (2021). Approximate Inverse-Based Block Preconditioners in Poroelasticity. Comput. Geosci. 25, 701–714. doi:10.1007/s10596-020-09981-2

CrossRef Full Text | Google Scholar

Frigo, M., Castelletto, N., and Ferronato, M. (2019). A Relaxed Physical Factorization Preconditioner for Mixed Finite Element Coupled Poromechanics. SIAM J. Sci. Comput. 41, B694–B720. doi:10.1137/18M120645X

CrossRef Full Text | Google Scholar

Frigo, M., Castelletto, N., and Ferronato, M. (2022). Enhanced Relaxed Physical Factorization Preconditioner for Coupled Poromechanics. Comput. Math. Appl. 106, 27–39. doi:10.1016/j.camwa.2021.11.015

CrossRef Full Text | Google Scholar

Frigo, M., Castelletto, N., Ferronato, M., and White, J. A. (2021). Efficient Solvers for Hybridized Three-Field Mixed Finite Element Coupled Poromechanics. Comput. Math. Appl. 91, 36–52. doi:10.1016/j.camwa.2020.07.010

CrossRef Full Text | Google Scholar

Gaspar, F. J., Lisbona, F. J., and Vabishchevich, P. N. (2003). A Finite Difference Analysis of Biot's Consolidation Model. Appl. Numer. Math. 44, 487–506. doi:10.1016/S0168-9274(02)00190-3

CrossRef Full Text | Google Scholar

Gaspar, F. J., and Rodrigo, C. (2017). On the Fixed-Stress Split Scheme as Smoother in Multigrid Methods for Coupling Flow and Geomechanics. Comput. Methods Appl. Mech. Eng. 326, 526–540. doi:10.1016/j.cma.2017.08.025

CrossRef Full Text | Google Scholar

Girault, V., Kumar, K., and Wheeler, M. F. (2016). Convergence of Iterative Coupling of Geomechanics with Flow in a Fractured Poroelastic Medium. Comput. Geosci. 20, 997–1011. doi:10.1007/s10596-016-9573-4

CrossRef Full Text | Google Scholar

Grote, M. J., and Huckle, T. (1997). Parallel Preconditioning with Sparse Approximate Inverses. SIAM J. Sci. Comput. 18, 838–853. doi:10.1137/S1064827594276552

CrossRef Full Text | Google Scholar

Gudala, M., and Govindarajan, S. K. (2021). Numerical Investigations on Two-phase Fluid Flow in a Fractured Porous Medium Fully Coupled with Geomechanics. J. Pet. Sci. Eng. 199, 108328. doi:10.1016/j.petrol.2020.108328

CrossRef Full Text | Google Scholar

Hong, Q., Kraus, J., Lymbery, M., and Wheeler, M. F. (2020). Parameter-robust Convergence Analysis of Fixed-Stress Split Iterative Method for Multiple-Permeability Poroelasticity Systems. Multiscale Model. Simul. 18, 916–941. doi:10.1137/19M1253988

CrossRef Full Text | Google Scholar

Hong, Q., and Kraus, J. (2018). Parameter-robust Stability of Classical Three-Field Formulation of Biot's Consolidation Model. etna 48, 202–226. doi:10.1553/etna_vol48s202

CrossRef Full Text | Google Scholar

Hu, L., Winterfeld, P. H., Fakcharoenphol, P., and Wu, Y.-S. (2013). A Novel Fully-Coupled Flow and Geomechanics Model in Enhanced Geothermal Reservoirs. J. Pet. Sci. Eng. 107, 1–11. doi:10.1016/j.petrol.2013.04.005

CrossRef Full Text | Google Scholar

Janna, C., Castelletto, N., and Ferronato, M. (2015a). The Effect of Graph Partitioning Techniques on Parallel Block FSAI Preconditioning: a Computational Study. Numer. Algor 68, 813–836. doi:10.1007/s11075-014-9873-5

CrossRef Full Text | Google Scholar

Janna, C., and Ferronato, M. (2011). Adaptive Pattern Research for Block FSAI Preconditioning. SIAM J. Sci. Comput. 33, 3357–3380. doi:10.1137/100810368

CrossRef Full Text | Google Scholar

Janna, C., Ferronato, M., and Gambolati, G. (2010). A Block FSAI-ILU Parallel Preconditioner for Symmetric Positive Definite Linear Systems. SIAM J. Sci. Comput. 32, 2468–2484. doi:10.1137/090779760

CrossRef Full Text | Google Scholar

Janna, C., Ferronato, M., Sartoretto, F., and Gambolati, G. (2015b). FSAIPACK: A Software Package for High-Perfomance Factored Sparse Approximate Inverse Preconditioning. ACM Trans. Math. Softw. 41, 1–26. doi:10.1145/2629475

CrossRef Full Text | Google Scholar

Jha, B., and Juanes, R. (2007). A Locally Conservative Finite Element Framework for the Simulation of Coupled Flow and Reservoir Geomechanics. Acta Geotech. 2, 139–153. doi:10.1007/s11440-007-0033-0

CrossRef Full Text | Google Scholar

Khan, A., and Silvester, D. J. (2021). Robust A Posteriori Error Estimation for Mixed Finite Element Approximation of Linear Poroelasticity. IMA J. Numer. Anal. 41, 2000–2025. doi:10.1093/imanum/draa058

CrossRef Full Text | Google Scholar

Kim, J., Tchelepi, H. A. A., and Juanes, R. (2011). Stability, Accuracy, and Efficiency of Sequential Methods for Coupled Flow and Geomechanics. SPE J. 16, 249–262. doi:10.2118/119084-PA

CrossRef Full Text | Google Scholar

Kolotilina, L. Y., and Yeremin, A. Y. (1993). Factorized Sparse Approximate Inverse Preconditionings I. Theory. SIAM J. Matrix Anal. Appl. 14, 45–58. doi:10.1137/0614004

CrossRef Full Text | Google Scholar

Lee, J. J., Mardal, K.-A., and Winther, R. (2017). Parameter-Robust Discretization and Preconditioning of Biot's Consolidation Model. SIAM J. Sci. Comput. 39, A1–A24. doi:10.1137/15M1029473

CrossRef Full Text | Google Scholar

Lee, J. J. (2018). Robust Three-Field Finite Element Methods for Biot's Consolidation Model in Poroelasticity. Bit Numer. Math. 58, 347–372. doi:10.1007/s10543-017-0688-3

CrossRef Full Text | Google Scholar

Liu, H., Wang, K., and Chen, Z. (2016). A Family of Constrained Pressure Residual Preconditioners for Parallel Reservoir Simulations. Numer. Linear Algebra Appl. 23, 120–146. doi:10.1002/nla.2017

CrossRef Full Text | Google Scholar

Ma, T., Rutqvist, J., Oldenburg, C. M., Liu, W., and Chen, J. (2017). Fully Coupled Two-phase Flow and Poromechanics Modeling of Coalbed Methane Recovery: Impact of Geomechanics on Production Rate. J. Nat. Gas Sci. Eng. 45, 474–486. doi:10.1016/j.jngse.2017.05.024

CrossRef Full Text | Google Scholar

Monforte, L., Arroyo, M., Carbonell, J. M., and Gens, A. (2018). Coupled Effective Stress Analysis of Insertion Problems in Geotechnics with the Particle Finite Element Method. Comput. Geotechnics 101, 114–129. doi:10.1016/j.compgeo.2018.04.002

CrossRef Full Text | Google Scholar

Murphy, M. F., Golub, G. H., and Wathen, A. J. (2000). A Note on Preconditioning for Indefinite Linear Systems. SIAM J. Sci. Comput. 21, 1969–1972. doi:10.1137/S1064827599355153

CrossRef Full Text | Google Scholar

Nardean, S., Ferronato, M., and Abushaikha, A. S. (2021). A Novel Block Non-symmetric Preconditioner for Mixed-Hybrid Finite-Element-Based Darcy Flow Simulations. J. Comput. Phys. 442, 110513. doi:10.1016/j.jcp.2021.110513

CrossRef Full Text | Google Scholar

Niu, C., Rui, H., and Hu, X. (2021). A Stabilized Hybrid Mixed Finite Element Method for Poroelasticity. Comput. Geosci. 25, 757–774. doi:10.1007/s10596-020-09972-3

CrossRef Full Text | Google Scholar

Niu, C., Rui, H., and Sun, M. (2019). A Coupling of Hybrid Mixed and Continuous Galerkin Finite Element Methods for Poroelasticity. Appl. Math. Comput. 347, 767–784. doi:10.1016/j.amc.2018.11.021

CrossRef Full Text | Google Scholar

Ouchi, H., Katiyar, A., York, J., Foster, J. T., and Sharma, M. M. (2015). A Fully Coupled Porous Flow and Geomechanics Model for Fluid Driven Cracks: a Peridynamics Approach. Comput. Mech. 55, 561–576. doi:10.1007/s00466-015-1123-8

CrossRef Full Text | Google Scholar

Rice, J. R., and Cleary, M. P. (1976). Some Basic Stress Diffusion Solutions for Fluid-Saturated Elastic Porous media with Compressible Constituents. Rev. Geophys. 14, 227–241. doi:10.1029/rg014i002p00227

CrossRef Full Text | Google Scholar

Saad, Y., and Schultz, M. H. (1986). GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 7, 856–869. doi:10.1137/0907058

CrossRef Full Text | Google Scholar

Van der Vorst, H. A. (1992). Bi-CGSTAB: A Fast and Smoothly Converging Variant of Bi-CG for the Solution of Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 13, 631–644. doi:10.1137/0913035

CrossRef Full Text | Google Scholar

Vassilevski, P. S. (2002). Sparse matrix element topology with application to AMG(e) and preconditioning. Numer. Linear Algebra Appl. 9, 429–444. doi:10.1002/nla.300

CrossRef Full Text | Google Scholar

Verruijt, A. (1969). “Elastic Storage of Aquifers,” in Flow through Porous Media. Editor R. De Wiest (New York, NY, USA: Academic Press), 331–376.

Google Scholar

White, J. A., and Borja, R. I. (2011). Block-preconditioned Newton-Krylov Solvers for Fully Coupled Flow and Geomechanics. Comput. Geosci. 15, 647–659. doi:10.1007/s10596-011-9233-7

CrossRef Full Text | Google Scholar

White, J. A., Castelletto, N., and Tchelepi, H. A. (2016). Block-partitioned Solvers for Coupled Poromechanics: A Unified Framework. Comput. Methods Appl. Mech. Eng. 303, 55–74. doi:10.1016/j.cma.2016.01.008

CrossRef Full Text | Google Scholar

Yuan, W.-H., Zhang, W., Dai, B., and Wang, Y. (2019). Application of the Particle Finite Element Method for Large Deformation Consolidation Analysis. Ec 36 (9), 3138–3163. doi:10.1108/EC-09-2018-0407

CrossRef Full Text | Google Scholar

Zhu, L., Dai, Z., Gong, H., Gable, C., and Teatini, P. (2016). Statistic Inversion of Multi-Zone Transition Probability Models for Aquifer Characterization in Alluvial Fans. Stoch Environ. Res. Risk Assess. 30, 1005–1016. doi:10.1007/s00477-015-1089-2

CrossRef Full Text | Google Scholar

Zhu, L., Franceschini, A., Gong, H., Ferronato, M., Dai, Z., Ke, Y., et al. (2020). The 3‐D Facies and Geomechanical Modeling of Land Subsidence in the Chaobai Plain, Beijing. Water Resour. Res. 56, e2019WR027026. doi:10.1029/2019WR027026

CrossRef Full Text | Google Scholar