A Hybrid Multiscale Approach for Rubber Contact

Contact mechanics models based on linearity assumptions, often using the viscoelastic half space theory and numerically implemented with the boundary element method, are known to provide accurate results for small mean square slope of the surface roughness. For large mean square slope, models accounting for finite deformations, often implemented with the non-linear finite element method, are more accurate but lead to a prohibitive computational cost. We propose a new hybrid multiscale approach able to account for the finite deformations arising due to large mean square slope, while keeping a computational cost similar to that associated to linear approaches. The basic strategy is a decomposition of the surface roughness power spectrum into a discrete number of waves, whose spectral range is partitioned into a high mean square slope range and a low mean square slope range. The contact mechanics in the former is accurately solved with the kinematically non-linear model and the results averaged out at the larger wavelength scale in terms of an effective interface interaction law. This law is then applied in the linear simulation involving the scales within the low mean square slope range. The proposed approach is a more accurate alternative to fully linear and a computationally faster alternative to fully non-linear contact mechanics approaches.

1 Introduction

The mechanics of contact taking place at the interface of rough soft solids is attracting a wide scientific interest due to its implications in a number of applications, ranging from biology and biomedical devices to machine elements (Persson, 2006). As an example, passenger cars maneuverability, comfort and energy efficiency in the era of autonomous/assisted driving and novel tires design are strictly related to the ability to adopt advanced physically-based tire friction and wear models during car engineering (Farroni et al., 2017; Fortunato et al., 2017). Moreover, an accurate prediction of contact mechanics, combined with an increasingly realistic physical description of the rubber behavior, plays a key role in term of tire durability, driving safety and sustainability (Lu, 2010), as well as in the prediction of the driving range in electric vehicles (Farfan-Cabrera, 2019).

The complexity in the prediction of rubber friction arises from the multiscale nature of the physical mechanisms taking place at the contact interface (Schallamach, 1953; Grosch, 1963; Persson, 2006). Indeed, almost all man- and nature-made surfaces are covered by roughness wavelengths spanning over decades of length scales, whereas polymer dynamics typically occurs over a wide range of relaxation times. Furthermore, rubbers typically exhibit non-linear mechanical behavior as well as wear-induced graded mechanical properties (Mokhtari and Schipper, 2016). This physical scenario determines a strong non-linear coupling between length and time scales.

In the past few decades, the scientific community mostly developed rubber contact mechanics models based on the assumption of small displacements and a linear rheological behavior of the contact interface, which are combined with the further assumption of small root mean square slope roughness (so called Reynolds roughness). These contact mechanics models, stemming from the viscoelastic half-space (VHS) theory and implemented with the boundary element method (BEM) (Persson, 2001; Carbone et al., 2009; Persson, 2010; Carbone and Putignano, 2013; Carbone and Putignano, 2014; Scaraggi and Persson, 2014; Scaraggi and Persson, 2015), have the ability to consider all (mean field models (Klüppel and Heinrich, 2000; Persson, 2001; Le Gal and Klüppel, 2007)) or most (computational models (Scaraggi and Persson, 2015; Scaraggi and Persson, 2016)) of the involved roughness length scales at once with reduced computational cost. On the other hand, the models based on the formulation of the viscoelastic contact problem in the finite deformation framework, and implemented with the finite element method (FEM) (Wriggers and Reinelt, 1996; De Lorenzis and Wriggers, 2013; Wagner et al., 2015), do not have the linear kinematics limitation, and are able to predict the friction coefficient by taking into account more realistic mechanical and rheological models, but at a much higher computational cost. This induces a strong limitation in the number of roughness scales that can be involved in the computation. Moreover, the strong non-linearity resulting from the contact conditions, the large deformations and the incompressibility lead to a challenging numerical framework. Recently, viscoelastic contact models formulated in the finite deformation framework and implemented with the FEM have been proposed to tackle the multiscale nature of roughness in the calculation of rubber friction, without dealing with the random phase distribution during the roughness decomposition into sinus waves to save computational cost (Wriggers and Reinelt, 1996; Nitsche, 2011; Wagner et al., 2015). However, the random phase distribution is key in the contact mechanics of random surfaces, being responsible for specific phenomena such as the linearity of contact area vs load at small contact areas.

In previous work (Scaraggi et al., 2016; Al-Qudsi, 2020) we have shown that the square slope of a given roughness wavelength strongly affects the numerically calculated contact area and hysteretic friction coefficient corresponding to that wavelength for given pressure and sliding velocity, and that the corresponding VHS-based linear and kinematically non-linear predictions are quantitatively in agreement only up to roughness root mean square slopes (denoted as m₂) less than a threshold ≈1. Thus, for relatively large values of roughness root mean square slope (say m₂ > 1), the effect of material and contact non-linearity cannot be safely neglected and kinematically non-linear approaches should be preferred to VHS-based linear approaches. Instead, for sufficiently small values of m₂ (say, m₂ < 1), the contact mechanics models based on the linear VHS assumption can provide accurate results. This consideration is at the basis of the new approach for contact mechanics of real rough surfaces that we investigate in this paper.

Here we propose a novel hybrid non-linear FEM/linear BEM multiscale approach that can account for realistic surface statistics and for the involved non-linearities while keeping a computational cost close to that of VHS-based linear approaches. Our multiscale approach is constructed on the decomposition of the generic surface roughness power spectrum into a discrete number of waves, whose spectral range is partitioned into a low m₂ range with large roughness wavelengths (to be modeled assuming small deformations), and a high m₂ range with small wavelengths (to be modeled accounting for large deformations). The contact mechanics in the high m₂ range is solved with the kinematically non-linear model and the results averaged out at the next larger wavelength scale in terms of an effective interface interaction law, to be applied to the VHS-based linear model. Thus, the latter accounts for the low m₂ wavelength spectral domain, leading to an overall strongly reduced computational cost with respect to a full non-linear FEM model, and to a similar accuracy.

The paper is organized as follows. In Section 2 the hybrid approach is described, including the roughness partitioning procedure. The method is then validated for a simplified contact geometry in Section 3 involving a roughness with only a few scales. In Section 4 the hybrid approach is then applied to the case of a smooth rubber block in steady sliding contact against a real asphalt surface. Conclusions follow in Section 5.

2 The Hybrid Multiscale Contact Approach

2.1 General Procedure

In the schematic of Figure 1 we illustrate the concept of the proposed hybrid multiscale contact approach. We start from the typical roughness power spectral density (Figure 1C) as obtained by three-dimensional profilometry (B) of a real rough surface, such as a road asphalt surface (A). After splitting of the roughness spectral content in low (red in (C)) and high (blue in (C)) partitions, the contact mechanics problem is solved with the kinematically non-linear model on the high-slope scale range for a range of pressures and sliding velocities, and the results are averaged in terms of an effective contact interaction law (D) to be applied to the VHS-based linear model (E). Since the latter typically includes most of the roughness spectral content, the overall cost of the numerical computations is comparable to the cost of the VHS-based model computations.

FIGURE 1

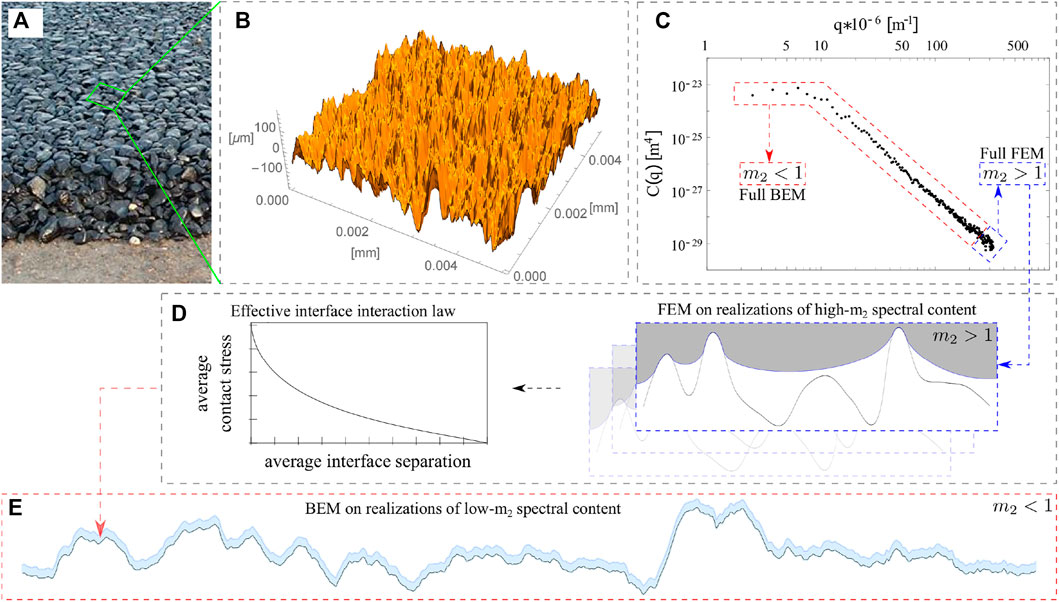
FIGURE 1. Schematic showing the basic idea behind the proposed hybrid multiscale contact approach. The typical roughness power spectral density (Figure 1.C) is obtained by three-dimensional profilometry (B) of a real rough surface, such as a road asphalt surface (A). After splitting of the roughness spectral content in low (red in (C)) and high (blue in (C)) partitions, the contact mechanics problem is solved with the kinematically non-linear model on the high-slope scale for a range of pressures and sliding velocities, and the results are averaged in terms of an effective contact interaction law (D) to be applied to the linear model (E) based on VHS theory.

More in detail, on the smallest length scales we simulate frictionless contact using the kinematically non-linear model, described in Section 2.4, for a number of applied average pressures, from which the average separation, the normalized contact area and the viscoelastic shear stress are computed. The effective contact interaction law giving the average pressure as a function of the average separation (Figure 1D) is then applied to the surface profile containing only the low-slope roughness components (E). A typical repulsive law, obtained for the adhesionless case, is shown in Figure 2 for a (two-dimensional) sinusoidal rigid roughness in sliding contact against a viscoelastic slab. The kinematically non-linear model results, reported for two different sliding speeds, show a monotonic increase of the pressure at decreasing average interface separations.

FIGURE 2

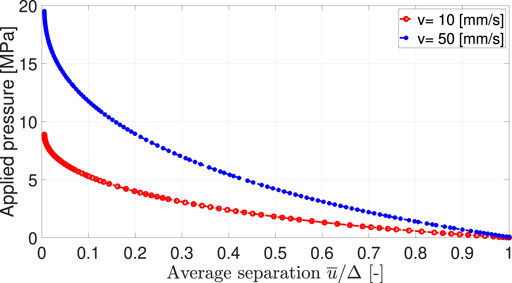
FIGURE 2. Typical average applied pressure vs separation curves (separation in dimensionless units), obtained in the case of adhesionless sliding contact between a (two-dimensional) sinusoidal rigid surface and a viscoelastic slab, for two sliding speeds. Δ is the amplitude of the sinusoidal rigid surface, however, for a generic randomly rough contact it is given by the combined root-mean-square-roughness of the interface.

We consider now a rough rigid surface in steady sliding contact against a smooth rubber sample. The rigid surface is assumed periodically rough, with periodicity L₀ in the x- and y-directions (coordinates in the average contact plane, with $\mathbf{x}=\left(x,y\right)$). The apparent projected interaction area is A₀. The surface roughness $z_{\text{r}}\left(\mathbf{x}\right)$ is decomposed, as described in Section 2.2, in the low-slope and high-slope scales, $z_{\text{ls}}\left(\mathbf{x}\right)$and $z_{\text{hs}}\left(\mathbf{x}\right)$, respectively, with $z_{\text{r}}\left(\mathbf{x}\right)=z_{\text{ls}}\left(\mathbf{x}\right)+z_{\text{hs}}\left(\mathbf{x}\right)$. First, the kinematically non-linear simulation (Section 2.4) is carried out with the surface roughness $z_{\text{hs}}\left(\mathbf{x}\right)$, at varying sliding speed v₀ (directed along the x-direction), leading to the homogenized solution fields ${\sigma }_{\text{hs}}\left(\bar{u},v_0\right)$, ${\alpha }_{\text{hs}}\left(\bar{u},v_0\right)$ and $\mathrm{\Delta }{\tau }_{\text{hs}}\left(\bar{u},v_0\right)$ depending on the sliding speed v₀ and on the average separation $\bar{u}$. Here σ_hs is the average contact pressure

${\sigma }_{\text{hs}}\left(\bar{u},v_0\right)=A_{0,\mathrm{h}\mathrm{s}}^{-1}{\int }_{A_{0,\mathrm{h}\mathrm{s}}}{d}^2\mathbf{x}{p}_{\text{hs}}\left(\mathbf{x}\right),(1)$

where $p_{\text{hs}}\left(\mathbf{x}\right)$ and A_0,hs are respectively the contact pressure field and the nominal in-plane area at the high-slope roughness scale. α_hs is the normalized projected contact area

${\alpha }_{\text{hs}}\left(\bar{u},v_0\right)=A_{0,\mathrm{h}\mathrm{s}}^{-1}{\int }_{A_{0,\mathrm{h}\mathrm{s}}}{d}^2\mathbf{x}H\left(p_{\text{hs}}\left(\mathbf{x}\right)\right),(2)$

where H denotes the Heaviside step function, and Δτ_hs is the effective average shear contact stress resulting from the asymmetric deformation of the rubber sample induced by viscoelasticity

$\mathrm{\Delta }{\tau }_{\text{hs}}\left(\bar{u},v_0\right)=A_{0,\mathrm{h}\mathrm{s}}^{-1}{\int }_{A_{0,\mathrm{h}\mathrm{s}}}{d}^2\mathbf{x}{p}_{\text{hs}}\left(\mathbf{x},\bar{u}\right)\frac{\partial z_{\text{hs}}}{\partial x}.(3)$

The VHS-based frictionless simulation (Section 2.3) is now carried out on the surface $z_{\mathrm{l}\mathrm{s}}\left(\mathbf{x}\right)$, at a given externally applied average pressure σ₀ and at sliding speed v₀, by making use of the effective interaction law computed above, ${\sigma }_{\text{hs}}\left(u_{\text{ls}}\left(\mathbf{x}\right),v_0\right)$, where $u_{\text{ls}}\left(\mathbf{x}\right)$ is the local interface separation in the BEM contact geometry. The VHS-based model provides the contact pressure ${\sigma }_{\text{ls}}\left(\mathbf{x}\right)$ and the interface separation $u_{\text{ls}}\left(\mathbf{x}\right)$. The total viscoelastic friction force F_T can thus be calculated as follows

$F_{\text{T}}\approx {\int }_{A_{0,\mathrm{l}\mathrm{s}}}{d}^2\mathbf{x}\left({\sigma }_{\text{ls}}\left(\mathbf{x}\right)\frac{\partial z_{\text{ls}}}{\partial x}+\mathrm{\Delta }{\tau }_{\text{hs\hspace{0.17em}}}\left(u_{\text{ls}}\left(\mathbf{x}\right),v_0\right)\right),(4)$

where A_0,ls is the nominal in-plane area of the low-slope scale, leading to the total viscoelastic friction coefficient

${\mu }_{\text{r}}={\mu }_{\text{ls}}+{\mu }_{\text{hs}},(5)$

with

$\begin{array}{ccc}\hfill {\mu }_{\text{hs}}& =\hfill & \frac{1}{{\sigma }_0{A}_{0,\mathrm{l}\mathrm{s}}}{\int }_{A_{0,\mathrm{l}\mathrm{s}}}{d}^2\mathbf{x}\mathrm{\Delta }{\tau }_{\text{hs}}\left(u_{\text{ls}}\left(\mathbf{x}\right),v_0\right)\hfill \end{array}(6)$

$\begin{array}{ccc}\hfill {\mu }_{\text{ls}}& =\hfill & \frac{1}{{\sigma }_0{A}_{0,\mathrm{l}\mathrm{s}}}{\int }_{A_{0,\mathrm{l}\mathrm{s}}}{d}^2\mathbf{x}{\sigma }_{\text{ls}}\left(\mathbf{x}\right)\frac{\partial z_{\text{ls}}}{\partial x}.\hfill \end{array}(7)$

The total projected contact area, from which the adhesive contribution to friction can be calculated, is

$A_{\text{c}}={\int }_{A_{0,\mathrm{l}\mathrm{s}}}{d}^2\mathbf{x}H\left({\sigma }_{\text{ls}}\left(\mathbf{x}\right)\right){\alpha }_{\text{hs}}\left(u_{\text{ls\hspace{0.17em}}}\left(\mathbf{x}\right)\right).(8)$

2.2 Surface Roughness Partitioning

It is well established that most surfaces show roughness over a broad range of wavelengths (Persson, 2006), with few exceptions belonging to nature-optimized surfaces (showing few-scale hierarchical topography arrangement). A typical example are asphalt or concrete road surfaces, which are rough over many length scales and exhibit fractality (Klüppel and Heinrich, 2000; Persson, 2001). The characterization of roughness for contact mechanics applications involves the adoption of at least two-scales profilometry, e.g. with atomic force microscopy and white light interferometry to cover the full range of roughness wavelengths. Once the roughness data are available, the statistics are fully contained in the surface power spectral density (PSD) in case of Gaussian roughness (Persson, 2006). An equivalent alternative to the PSD is the height distance correlation (HDC) function $R_{\text{zz}}\left(\lambda \right)$, introduced by Heinrich and Klüppel (Klüppel and Heinrich, 2000). Assuming a homogeneous roughness $⟨z_{\text{r}}\left(\mathbf{x}\right)⟩$, the HDC is

$\begin{array}{ccc}\hfill R_{\text{zz}}\left(\lambda \right)& =\hfill & ⟨{\left(z_{\mathrm{r}}\left(\mathbf{x}+\lambda \right)-z_{\text{r}}\left(\mathbf{x}\right)\right)}^2⟩\hfill \\ \hfill & =\hfill & 2\left(z_{\text{rms}}^2-R\left(\lambda \right)\right),\hfill \end{array}(9)$

where 〈〉 denotes the ensemble average, and where the autocorrelation (AC) function $R\left(\lambda \right)$(for homogeneous roughness) is given by

$R\left(\lambda \right)=⟨z_{\text{r}}\left(\mathbf{x}+\lambda \right)z_{\text{r}}\left(\mathbf{x}\right)⟩.(10)$

The PSD $C\left(\mathbf{q}\right)$ is given by the Fourier transform of the AC

$C\left(\mathbf{q}\right)={\left(2\pi \right)}^{-2}\int d^2\lambda R\left(\lambda \right)e^{-i\mathbf{q}\cdot \lambda }.(11)$

The simplest procedure to calculate the PSD is from the Fourier transform of the surface roughness $z_{\text{r}}\left(\mathbf{q}\right)$; in particular we observe that

$\begin{array}{ccc}\hfill ⟨z_{\text{r}}\left({\mathbf{q}}^{\prime }\right)z_{\text{r}}\left({\mathbf{q}}^{\prime \prime }\right)⟩& =\hfill & {\left(2\pi \right)}^{-4}\iint d^2\mathbf{x}{d}^2\mathbf{y}⟨z_{\text{r}}\left(\mathbf{x}\right)z_{\text{r}}\left(\mathbf{y}\right)⟩e^{i{\mathbf{q}}^{\prime }\cdot \mathbf{x}}{e}^{i{\mathbf{q}}^{\prime \prime }\cdot \mathbf{y}}\hfill \\ \hfill & =\hfill & C\left({\mathbf{q}}^{\prime }\right)\delta \left({\mathbf{q}}^{\prime }+{\mathbf{q}}^{\prime \prime }\right).\hfill \end{array}(12)$

The Fourier transform $C_{\text{zz}}\left(\mathbf{q}\right)$ of the HDC function can be easily linked to the Fourier transform $C\left(\mathbf{q}\right)$ of the AC function with

$C_{\text{zz}}\left(\mathbf{q}\right)=2\left(z_{\text{rms}}^2\delta \left(\mathbf{q}\right)-C\left(\mathbf{q}\right)\right).(13)$

We now approximate the measured surface by a finite number of sinusoidal waves, following the approach suggested by Reinelt and Wriggers (Wriggers and Reinelt, 1996) and adopted by other researchers (Falk et al., 2016). For simplicity, we focus on a two-dimensional surface roughness, however, the approach can be equally applied to the more general case of three-dimensional roughness. In particular, the single sine wave function (characterized by amplitude Δ and generic wavelength 2π/q), has the following HDC function

$R_{\text{zz}}\left(\lambda \right)=\frac{q}{2\pi }\underset{0}{\overset{2\pi /q}{\int }}dx{\left[\mathrm{\Delta }\sin \left(q\left(x+\lambda \right)\right)-\mathrm{\Delta }\sin \left(qx\right)\right]}^2=2{\mathrm{\Delta }}^2{\sin }^2\left(\frac{q\lambda }{2}\right),(14)$

which we write in the following more convenient form

$R_{\text{zz}}\left(\lambda >0\right)=\left\{\begin{array}{c}2{{\mathrm{\Delta }}^2\sin }^2\left(\frac{q\lambda }{2}\right),\lambda \le \pi /q\hfill \\ 2{\mathrm{\Delta }}^2,\text{elsewhere}\hfill \end{array}\right..(15)$

We note that the slope in the double logarithmic diagram of $R_{\text{zz}}\left(\lambda \approx 0\right)$ is 2 for any wavelength, whereas road profiles usually have slopes in range of 2.1–2.5 (Schramm, 2003). Thus, as expected, multiple sine waves with different amplitudes and wavelengths must be superimposed in order to reproduce the power law behaviour of real rough surface HDCs. The root mean square slope is defined as

$m_2=\sqrt{⟨\nabla z_{\text{r}}\cdot \nabla z_{\text{r}}⟩},(16)$

which for the sinus specializes to $m_2\left(q\right)=q\mathrm{\Delta }/\sqrt{2}$.

Finally, the measured track is approximated by a sum over a discrete number M of wavelengths

${\mathrm{z}}_{\text{r}}\left(\mathrm{x}\right)=\sum _{i=1}^M{\mathrm{\Delta }}_i\cdot \sin \left(q_i\mathrm{x}+{\varphi }_i\right),(17)$

with a uniformly distributed random shift angle ϕ_i, and q_i = 2ⁱ ⋅ q₀, where the periodicity length is 2π/q₀.

2.3 Low-Slope Scale Contact Model

The low-slope scale contact model is based on the adoption of the VHS assumption. The interaction occurs between a rigid rough surface (z_ls) and a smooth VHS, in relative steady sliding. This contact model has been first reported in (Persson and Scaraggi, 2014), and is summarized in the following with the addition of the interface contact law contribution coming from the high-slope scale roughness.

In Figure 3 we show the schematic of the low-slope scale contact interface. The local interface separation, corresponding to the local distance between the mating surfaces, measured in a reference moving with the rigid rough substrate, is

$u_{\text{ls}}\left(\mathbf{x}\right)=\bar{u}+w\left(\mathbf{x}\right)-z_{\text{ls}}\left(\mathbf{x}\right),(18)$

where $\bar{u}$ is the average interface separation, $w\left(\mathbf{x}\right)$ the surface viscoelastic normal displacement, and $z_{\text{ls}}\left(\mathbf{x}\right)$ is the low-slope surface roughness, with $⟨w\left(\mathbf{x}\right)⟩=⟨z_{\text{ls}}\left(\mathbf{x}\right)⟩=0$. We define the following Fourier transforms (q is the transformed variable of x)

$w\left(\mathbf{q}\right)={\left(2\pi \right)}^{-2}\int d^2\mathbf{x}w\left(\mathbf{x}\right)e^{-i\mathbf{q}\cdot \mathbf{x}}(19)$

and

${\sigma }_{\text{ls}}\left(\mathbf{q}\right)={\left(2\pi \right)}^{-2}\int d^2\mathbf{x}{\sigma }_{\text{ls}}\left(\mathbf{x}\right)e^{-i\mathbf{q}\cdot \mathbf{x}},(20)$

where ${\sigma }_{\text{ls}}\left(\mathbf{x}\right)$ is the distribution of contact pressures (${\sigma }_0=⟨{\sigma }_{\text{ls}}\left(\mathbf{x}\right)⟩$ is the average contact pressure). Following the discussion reported in (Persson and Scaraggi, 2014), $w\left(\mathbf{x}\right)$ can be related to ${\sigma }_{\text{ls}}\left(\mathbf{x}\right)$ through a simple equation in the Fourier space

$w\left(\mathbf{q}\right)=M_{zz}\left(\mathbf{q}\right){\sigma }_{\text{ls}}\left(\mathbf{q}\right),(21)$

where $M_{zz}\left(\mathbf{q}\right)$ is the surface response of the VHS in the frequency domain

$M_{zz}\left(\mathbf{q},\omega \right)=\frac{2}{\left|\mathbf{q}\right|E_{\text{r}}\left(\omega \right)}.(22)$

Here, $E_{\text{r}}\left(\omega \right)$ is the frequency-dependent complex reduced Young’s modulus, given by

$E_{\text{r}}\left(\omega \right)=\frac{E\left(\omega \right)}{\left(1-{\nu }^2\right)},(23)$

with ν as the Poisson’s ratio. The Poisson’s ratio undergoes only a minor variation with frequency and thus can be assumed to be constant (Persson, 2001). The linear viscoelastic modulus $E\left(\omega \right)$ can be measured using standard techniques, and its real and imaginary part are typically fitted by a generalized Maxwell model (Lorenz et al., 2014; Scaraggi and Persson, 2015). The relation between separation u_ls(x) and interaction pressure σ_ls(x) within the Derjaguin’s approximation (Derjaguin, 1934) can be written in terms of a generic interaction law (Persson and Scaraggi, 2014)

$\sigma =f\left(u\right).(24)$

Derjaguin’s approach allows to describe the force acting between close elementary portions of interacting surfaces in terms of the force per unit area acting between two planar semi-infinite walls. This approximation is typically adopted when i) the solids are separated by a distance that is much smaller than the local radius of curvature of the surfaces, and ii) the interaction decays sufficiently rapidly with distance, so that interactions between far enough elementary surface portions are negligible.

FIGURE 3

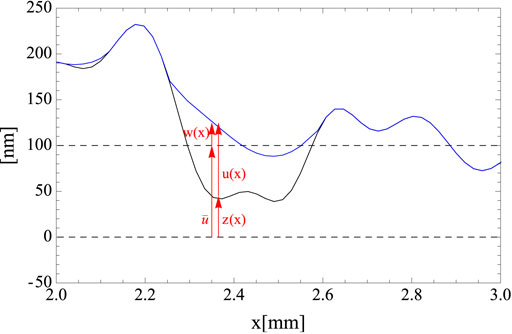
FIGURE 3. Schematic of the generic cross section of the contact geometry, used to derive Eq. 18.

In this work we integrate the repulsive term of the Lennard-Jones potential to obtain the traction due to the adhesionless interaction in (24), whereas the repulsive contribution coming from the high-slope scale is taken into account by adding to the integrated Lennard-Jones the high-slope scale traction ${\sigma }_{\text{hs}}\left(\bar{u}\right)$, calculated as described in the following.

2.4 High-Slope Scale Contact Model

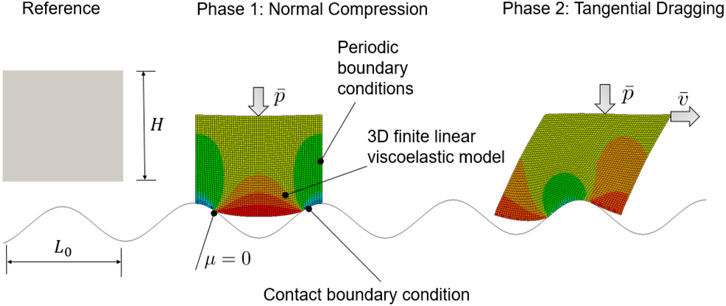
The kinematically non-linear model considers a deformable body undergoing adhesionless and frictionless contact with a superposition of rigid sinusoidal surfaces. The generic sinusoidal surface is supposed to represent one of the high-slope wavelengths belonging to the roughness spectrum of the surface. In order to compute the effective interface properties, a micromechanical numerical test is conducted, see Figure 4 (for simplicity we show only one wavelength). Because of the periodic geometry of the surface, the width of the rubber slab is taken equal to the largest wavelength of the sinusoidal spectrum; the specimen is considered as a periodic cell extracted from a long boundary layer. The specimen must have sufficient height in order to incorporate the mostly stressed material region, so that the whole amount of energy dissipation taking place at the micro-level is accounted for. In (De Lorenzis and Wriggers, 2013), a ratio H/L₀ = 0.75 was found sufficient for all analyzed dragging velocities. Thus, this ratio is also adopted in this work. From the numerical standpoint, a sufficiently fine mesh must be used in order to achieve a satisfactory resolution of the contact area and hence an accurate estimation of the contact stresses. Again exploiting results in (De Lorenzis and Wriggers, 2013), we adopt a discretization with 120 × 90 elements. At the beginning, the specimen is pressed onto the sinusoidal surface with a predetermined normal pressure of absolute value $\bar{p}$, which stays constant during the sliding process. Then, the upper side of the specimen is moved horizontally with a specified constant velocity $\bar{v}$. Since the specimen is considered as a periodic cell, periodic boundary conditions are applied on its lateral surfaces. The finite linear model for viscoelasticity proposed by Reese and Govindjee (1998) is used. The model is able to capture the large deformations arising in the contact zone of the rubber sliding over a rough surface. The model is still “linear” with respect to the evolution equation (Lion, 1997a; Lion, 1997b), i.e. it assumes small deviations from thermodynamic equilibrium. Full details can be retrieved in (Lion, 1997a) or (Reese and Govindjee, 1998), see also (De Lorenzis and Wriggers, 2013). In order to extract a single value for the macroscopic friction coefficient from each micromechanical test, time averaging is applied (Wriggers and Reinelt, 1996; De Lorenzis and Wriggers, 2013; Wagner et al., 2015).

FIGURE 4

FIGURE 4. Micromechanical testing scheme.

3 Numerical Validation of the Hybrid Multiscale Approach

In this section, we aim at verifying the proposed hybrid multiscale method on an artificial surface $z_{\text{r}}\left(\mathrm{x}\right)$ consisting in the superposition of three sinusoidal waves

$z_{\text{r}}\left(\mathrm{x}\right)=z_{\text{hs}}\left(\mathrm{x}\right)+z_{\text{ls}}\left(\mathrm{x}\right),(25)$

where the high-slope part $z_{\text{hs}}\left(\mathrm{x}\right)$ has m₂ > 1

$z_{\text{hs}}\left(\mathrm{x}\right)=0.01867\sin \frac{2\pi }{0.0625}\mathrm{x}(26)$

(lengths in mm), and where the low-slope part $z_{\text{ls}}\left(\mathrm{x}\right)$ includes the length scales with m₂ < 1

${\mathrm{z}}_{\text{ls}}\left(\mathrm{x}\right)=0.02648\sin \frac{2\pi }{0.125}\mathrm{x}+0.02939\sin \frac{2\pi }{0.25}\mathrm{x}(27)$

(lengths in mm). To describe the viscoelastic material response, a generalized Maxwell model with six relaxation times within the finite deformation formulation by (Reese and Govindjee, 1998) is used in this work, with the material parameters in Table 1.

TABLE 1

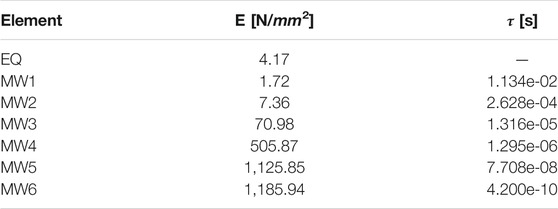
TABLE 1. Adopted constitutive parameters of a styrene-butadiene rubber (SBR) material (Wriggers and Reinelt, 1996).

In order to verify the accuracy of the hybrid multiscale approach, calculations on the artificial (full) surface using the kinematically non-linear model (resolving all three scales of the roughness) and the proposed hybrid multiscale method are compared. To do so, five different realizations of the artificial surface are taken into account by assuming the phase angle between the superimposed sine functions as a random variable with uniform distribution between 0 and 2π. In the limiting case of a large number of roughness wavelengths, a uniform phase distribution determines the resulting roughness height (random variable) to be Gaussian. The friction coefficient is then averaged over the realizations.

Figure 5 shows a comparison between all investigated approaches, i.e. the VHS-based model, the kinematically non-linear model that is used as a benchmark, and the hybrid multiscale approach, for two velocities belonging to the rubbery region and to the maximum dissipation region (Figure 5A,B, respectively). The comparison is done in terms of friction coefficient as a function of the normalized contact area. The results show a small deviation between the kinematically non-linear method and the hybrid multiscale approach. The average relative error in the friction coefficient can be estimated as follows for the hybrid multiscale method:

$e\left[\%\right]=\frac{1}{K}\sum _{k=1}^K\frac{\left|{\mu }_{\text{FEM},k}-{\mu }_{H,k}\right|}{{\mu }_{\text{FEM},k}}\ast 100,(28)$

where K is the number of considered values, ranging from a normalized contact area of 0.01–0.1 with a step size of 0.01. μ_FEM,k and μ_H,k are the friction coefficients calculated using the kinematically non-linear model and the hybrid multiscale method, respectively. The average relative error calculated from Equation 28 is 2.9% for a velocity of 10 mm/s and 7.1% for a velocity of 50 mm/s. At relatively small values of contact area, the deviation between the fully non-linear and the hybrid multiscale approaches is relatively large, and the hybrid multiscale approach underestimates the friction coefficient even more than the VHS-based model. This can be justified by the fact that the hybrid multiscale approach depends strongly on the contact pressure distribution to calculate the friction coefficient, and at small values of contact areas the number of contact patches is typically limited by the finite size effect. Thus the numerical simulations are unable to provide enough statistical content in terms of contact patches, which results in poor contact pressure statistics. When the contact area increases, the difference between the approaches decreases and the agreement between the results in terms of the rolling friction coefficient is remarkably good. This comparison confirms that the hybrid multiscale approach delivers very accurate predictions of the friction coefficient, except for the regime of low contact areas where inaccurate contact pressure statistics are obtained.

FIGURE 5

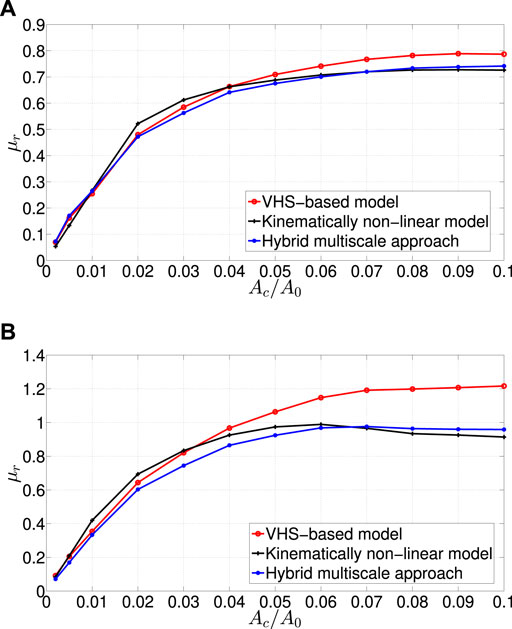
FIGURE 5. Friction coefficient as a function of the normalized contact area for a surface roughness resulting from the superposition of three sinusoidal waves at a velocity of (A) 10 [mm/s], and (B) 50 [mm/s].

4 Application to Randomly Rough Surfaces

4.1 Adopted Roughness

A confocal optical profilometer is used in this work to measure the surface roughness of asphalt specimens. In order to obtain representative data, 30 line scans in different regions of the specimen are performed using the optical profilometer in different directions. Each line scan has a measurement length of 16 mm that is consistent with the typical grain size of asphalt. The lateral resolution of the profilometer (0.05 mm) gives an acceptable degree of accuracy (within the purpose of this work). The lower cut-off is selected as 0.0625 mm. The upper cut-off is selected as the typical largest grain size of asphalt, and ranges between 5 and 20 mm. The asphalt mixture is AC-8, the measurement speed is 0.1 mm/s.

The superposed sinusoidal functions are fitted to the averaged measured surface based on their HDC functions, using the least square algorithm on a double logarithmic scale, which identifies the amplitudes Δ_i and the spatial frequencies q_i such that

${\left(\sum _{j=1}^N{\left(\sum _{i=1}^M\log \left(2{\mathrm{\Delta }}_i^2{\mathit{sin}}^2\left(\frac{q_i{\lambda }_j}{2}\right)\right)-\log \left(R_{\text{zz}}\left({\lambda }_j\right)\right)\right)}^2\right)}^{\frac{1}{2}}\to \min {\lambda }_j\le \frac{\pi }{q_i}(29)$

${\left(\sum _{j=1}^N{\left(\sum _{i=1}^M\log \left(2{\mathrm{\Delta }}_i^2\right)-\log \left(R_{\text{zz}}\left({\lambda }_j\right)\right)\right)}^2\right)}^{\frac{1}{2}}\to \min {\lambda }_j>\frac{\pi }{q_i},(30)$

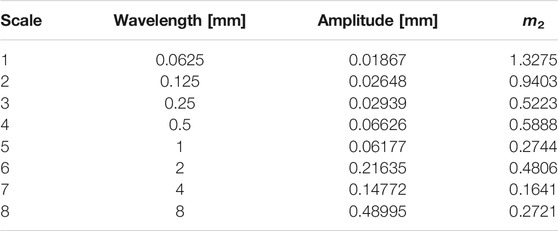
where N is the number of discrete sample points where the profile height is measured, and M is the number of superposed sine waves (each with its amplitude and wavelength) in the approximation. The approximation is carried out with different values of M. The slopes of the measured HDC and of the HDC approximated by more than eight sine waves and their cut-off-lengths were found to be identical. The HDC functions of the sine waves and of their superposition are depicted in Figure 6, where the red curve denotes the averaged measured asphalt road track. The agreement is very good. Table 2 lists the wavelengths and amplitudes of the 8 waves along with the corresponding root mean square slopes. It is important to note that only one scale has a root mean square slope larger than 1.

FIGURE 6

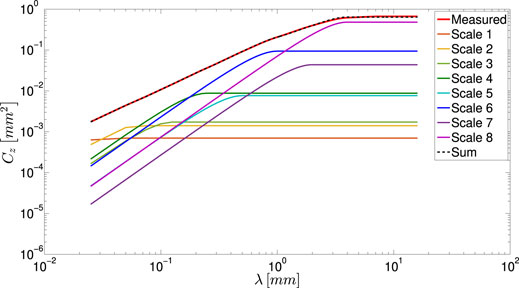
FIGURE 6. HDC function of asphalt road surface, approximated by the superposition of 8 sinusoidal waves.

TABLE 2

TABLE 2. Surface approximation for the asphalt specimen using 8 sine waves.

4.2 Intermediate Computations at the High-Slope Scale

As follows, we illustrate the results obtained for the smallest scale of the approximated rough surface. These results are obtained applying the kinematically non-linear model of Section 2.4 (and by comparison the VHS-based model of Section 2.3 to a contact problem with a sinusoidal surface with a wavelength of 0.0625 mm and an amplitude of 0.01867 mm. The root mean square slope roughness is 1.3275, see Table 2.

Figure 7A shows the obtained rolling friction coefficient as a function of the applied pressure for a sliding velocity of 10 mm/s belonging to the rubbery region. For small applied pressures, the VHS-based model only slightly underestimates the friction coefficient compared to the kinematically non-linear model. This can be justified by the fact that at very small applied pressures, the contact occurs only at the top of the asperity, so the geometric non-linearity can be neglected. A decreasing friction coefficient for high pressure values is observed for both approaches. One can note that for applied pressures larger than 2 MPa, the difference between the approaches becomes larger, as the deformation regime induced by large root mean square slope roughness significantly deviates from the small displacement assumption and thus the effect of the kinematic non-linearity comes into play. Figure 7B gives the same curve for a sliding velocity of 50 mm/s belonging to the maximum dissipation region. Similar trends as in Figure 7A are observed, with a higher maximum friction value. The deviation between the kinematically non-linear and the linear VHS-based approaches is very large in this case. These results are in agreement with the observations in (Scaraggi et al., 2016).

FIGURE 7

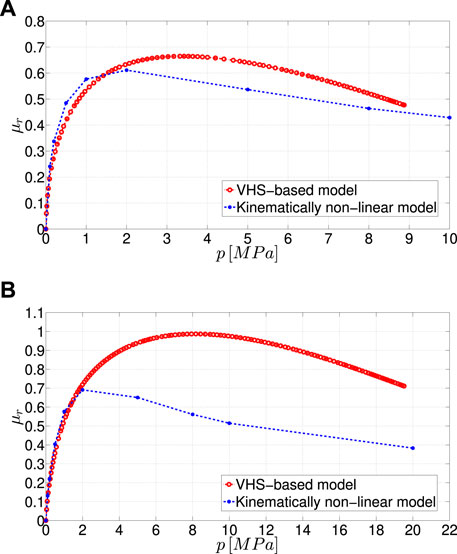
FIGURE 7. Friction coefficient as a function of the applied pressure for the high-slope wavelength, at a velocity of (A) 10 [mm/s], (B) 50 [mm/s].

4.3 Results From the Hybrid Multiscale Approach

The friction coefficient at small-slope scales (wavelength 2–8) from Table 2 is now calculated using the repulsive law deduced from the high-slope scale, which is shown in Figure 2. Figure 8 illustrates examples of the contact pressure field as a function of the dimensionless contact position for one realization of the rough surface, with dragging velocities of 10 mm/s and 50 mm/s, respectively. It should be noted that according to these contact pressures, the corresponding friction coefficients at the contact points are approximated using the results of the friction coefficients at the smallest scale, which are shown in Figures 7A,B.

FIGURE 8

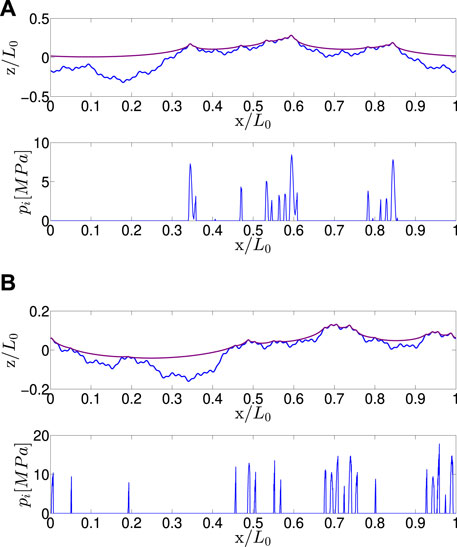
FIGURE 8. Contact pressure distribution resulting from the repulsive law as a function of the dimensioness contact position for a sliding velocity of (A) 10 [mm/s], (B) 50 [mm/s].

Figure 9 illustrates the friction coefficient predicted using the VHS-based model and the hybrid multiscale approach, for two different velocities belonging to the rubbery and the maximum dissipation regions. The discrepancy in the friction coefficient is consistent with the results in Figure 7. For a low dragging velocity of 10 mm/s, the difference between the VHS-based prediction and the results of the hybrid multiscale approach is relatively small. This can be justified by the fact that for low sliding velocities, the local contact pressures are more evenly distributed and they are small, see Figure 8A. Moreover, for small pressures, the results of the kinematically non-linear model and of the VHS-based model are comparable, see Figure 7A. However, for a dragging velocity of 50 mm/s, the difference is large, which can be ascribed to the irregular distribution of the contact pressures at larger dragging velocities and to the resulting large contact pressures, see Figure 8B. The effect of the non-linearity is remarkable, see Figure 7B. From comparison of the results in Figure 5 to those in Figure 9, one can note that in the VHS the smallest wavelengths of the roughness, ranging from 0.0625 to 0.25 mm, give the largest contribution to the friction coefficient, which seems unrealistic.

FIGURE 9

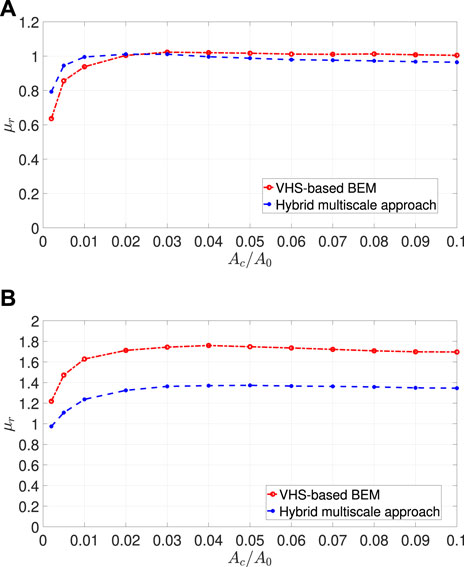
FIGURE 9. Friction coefficient as a function of the normalized contact area at a velocity of (A) 10 [mm/s], (B) 50 [mm/s].

5 Conclusion

This paper proposes a hybrid multiscale method for the prediction of rubber contact mechanics on rough surfaces. The idea of a hybrid multiscale approach stems from the observation (Scaraggi et al., 2016; Al-Qudsi, 2020) that linear models based on the viscoelastic half-space theory are able to predict the friction coefficient by accounting for all length scales of surface roughness with a low computational cost, however they are only accurate for low (less than 1) root mean square slope values; on the other hand, kinematically non-linear models are accurate also for large (large than 1) root mean square slopes, but cannot consider all length scales of roughness due to prohibitive computational cost.

The hybrid multiscale approach treats the low-slope scales with the VHS-based model and the limited number of high-slope scales with the kinematically non-linear model. The contact mechanics at the high-slope scales, predicted using the kinematically non-linear model, is transferred to the low-slope scales as a local repulsive law between the applied pressure and the average separation. This repulsive law controls the deformation behavior of the rubber according to the pressure. Depending on the local contact pressures resulting from the local repulsive law, the friction coefficient is calculated. Based on the obtained numerical results, the hybrid multiscale approach is shown to be a suitable tool to predict the friction coefficient with a degree of accuracy similar to that of the fully non-linear model, at a computational cost only marginally larger than that of the viscoelastic half-space model.

In future work, the accuracy of the approach in representative test cases should be validated through comparison with experimental results. The numerical investigation in this paper is restricted to a limited number of roughness wavelengths. In typical applications, such as tire tread vs road contact, the roughness involves several decades of length scales, whose computation is very cumbersome even with the VHS-based approach. Such cases can be handled with mean field models (Klüppel and Heinrich, 2000; Persson, 2001; Le Gal and Klüppel, 2007), which however have the same limitations as the VHS-based model in terms of linear kinematics and linear rheology. An approach similar to the hybrid multiscale approach developed in this work could help to enrich mean field contact models as well, and enable them to approach the accuracy of a fully non-linear model while handling surfaces with roughness ranging over several decades of wavelengths.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors upon reasonable request.

Author Contributions

LL and MS conceived the research idea. AA-Q and MS implemented the numerical models, and AA-Q ran the simulations. AA-Q, LL and MS wrote the paper.

Funding

MS thanks MIUR for the PRIN 2017 project support under the grant 2017948FEN (FASTire). AA-Q thanks the European Research Council (ERC starting researcher grant “INTERFACES”, No. 279439) for funding, and the North-German Supercomputing Alliance (HLRN) for providing high performance computing resources that have contributed to the research results reported in this paper.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Qudsi, A. (2020). Multiscale Modeling of Rubber Hysteretic Friction on Rough Rigid Surfaces. PhD thesis, Braunschweig, Braunschweig, Germany.

Google Scholar

Carbone, G., and Putignano, C. (2014). Rough Viscoelastic Sliding Contact: Theory and Experiments. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 89 (3), 032408. doi:10.1103/PhysRevE.89.032408

PubMed Abstract | CrossRef Full Text | Google Scholar

Carbone, G., Lorenz, B., Persson, B. N. J., and Wohlers, A. (2009). Contact Mechanics and Rubber Friction for Randomly Rough Surfaces with Anisotropic Statistical Properties. Eur. Phys. J. E 29 (3), 275–284. doi:10.1140/epje/i2009-10484-8

CrossRef Full Text | Google Scholar

Carbone, G., and Putignano, C. (2013). A Novel Methodology to Predict Sliding and Rolling Friction of Viscoelastic Materials: Theory and Experiments. J. Mech. Phys. Sol. 61 (8), 1822–1834. doi:10.1016/j.jmps.2013.03.005

CrossRef Full Text | Google Scholar

De Lorenzis, L., and Wriggers, P. (2013). Computational Homogenization of Rubber Friction on Rough Rigid Surfaces. Comput. Mater. Sci. 77, 264–280. doi:10.1016/j.commatsci.2013.04.049

CrossRef Full Text | Google Scholar

Derjaguin, B. (1934). Untersuchungen über die Reibung und Adhäsion, IV. Kolloid-Zeitschrift 69, 155–164. doi:10.1007/bf01433225

CrossRef Full Text | Google Scholar

Falk, K., Lang, R., and Kaliske, M. (2016). Multiscale Simulation to Determine Rubber Friction on Asphalt Surfaces. Tire Sci. Tech. 44 (4), 226–247. doi:10.2346/tire.16.440401

CrossRef Full Text | Google Scholar

Farfan-Cabrera, L. I. (2019). Tribology of Electric Vehicles: A Review of Critical Components, Current State and Future Improvement Trends. Tribology Int. 138, 473–486. doi:10.1016/j.triboint.2019.06.029

CrossRef Full Text | Google Scholar

Farroni, F., Sakhnevych, A., and Timpone, F. (2017). Physical Modelling of Tire Wear for the Analysis of the Influence of thermal and Frictional Effects on Vehicle Performance. Proc. Inst. Mech. Eng. L: J. Mater. Des. Appl. 231 (1-2), 151–161. doi:10.1177/1464420716666107

CrossRef Full Text | Google Scholar

Fortunato, G., Ciaravola, V., Furno, A., Scaraggi, M., Lorenz, B., and Persson, B. N. J. (2017). Dependency of Rubber Friction on Normal Force or Load: Theory and Experiment. Tire Sci. Tech. 45 (1), 25–54.

CrossRef Full Text | Google Scholar

Grosch, K. A. (1963). The Relation between the Friction and Visco-Elastic Properties of Rubber. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 274 (1356), 21–39.

Google Scholar

Klüppel, M., and Heinrich, G. (2000). Rubber Friction on Self-Affine Road Tracks. Rubber Chem. Technol. 73 (4), 578–606.

Google Scholar

Le Gal, A., and Klüppel, M. (2007). Investigation and Modelling of Rubber Stationary Friction on Rough Surfaces. J. Phys. Condens. Matter 20 (1), 015007. doi:10.1088/0953-8984/20/01/015007

CrossRef Full Text | Google Scholar

Lion, A. (1997). A Physically Based Method to Represent the Thermo-Mechanical Behaviour of Elastomers. Acta Mechanica 123 (1), 1–25. doi:10.1007/bf01178397

CrossRef Full Text | Google Scholar

Lion, A. (1997). On the Large Deformation Behaviour of Reinforced Rubber at Different Temperatures. J. Mech. Phys. Sol. 45 (11-12), 1805–1834. doi:10.1016/s0022-5096(97)00028-8

CrossRef Full Text | Google Scholar

Lorenz, B., Pyckhout-Hintzen, W., and Persson, B. N. J. (2014). Master Curve of Viscoelastic Solid: Using Causality to Determine the Optimal Shifting Procedure, and to Test the Accuracy of Measured Data. Polymer 55 (2), 565–571. doi:10.1016/j.polymer.2013.12.033

CrossRef Full Text | Google Scholar

Lu, T. (2010). The Influence of Pavement Stiffness on Vehicle Fuel consumptionPhD Thesis. Nottingham, UK: University of Nottingham.

Google Scholar

Mokhtari, M., and Schipper, D. J. (2016). Existence of a Tribo-Modified Surface Layer of BR/S-SBR Elastomers Reinforced with Silica or Carbon Black. Tribology Int. 96, 382–388. doi:10.1016/j.triboint.2014.09.021

CrossRef Full Text | Google Scholar

Nitsche, R. (2011). A Multiscale Projection Method for Contact on Rough Surfaces. PhD thesis. Hannover, Germany: Leibniz Universität Hannover.

Google Scholar

Persson, B. N. J. (2006). Contact Mechanics for Randomly Rough Surfaces. Surf. Sci. Rep. 61 (4), 201–227. doi:10.1016/j.surfrep.2006.04.001

CrossRef Full Text | Google Scholar

Persson, B. N. J. (2010). Rolling Friction for Hard cylinder and Sphere on Viscoelastic Solid. Eur. Phys. J. E 33 (4), 327–333. doi:10.1140/epje/i2010-10678-y

CrossRef Full Text | Google Scholar

Persson, B. N. J., and Scaraggi, M. (2014). Theory of Adhesion: Role of Surface Roughness. J. Chem. Phys. 141 (12), 124701. doi:10.1063/1.4895789

CrossRef Full Text | Google Scholar

Persson, B. N. J. (2001). Theory of Rubber Friction and Contact Mechanics. J. Chem. Phys. 115 (8), 3840–3861. doi:10.1063/1.1388626

CrossRef Full Text | Google Scholar

Reese, S., and Govindjee, S. (1998). A Theory of Finite Viscoelasticity and Numerical Aspects. Int. J. Sol. Structures 35 (26-27), 3455–3482. doi:10.1016/s0020-7683(97)00217-5

CrossRef Full Text | Google Scholar

Scaraggi, M., Comingio, D., Al-Qudsi, A., and Lorenzis, L. D. (2016). The Influence of Geometrical and Rheological Non-linearity on the Calculation of Rubber Friction. Tribology Int. 101, 402–413. doi:10.1016/j.triboint.2016.04.027

CrossRef Full Text | Google Scholar

Scaraggi, M., and Persson, B. N. J. (2015). Friction and Universal Contact Area Law for Randomly Rough Viscoelastic Contacts. J. Phys. Condens. Matter 27 (10), 105102. doi:10.1088/0953-8984/27/10/105102

CrossRef Full Text | Google Scholar

Scaraggi, M., and Persson, B. N. J. (2014). Rolling Friction: Comparison of Analytical Theory with Exact Numerical Results. Tribol Lett. 55 (1), 15–21. doi:10.1007/s11249-014-0327-y

CrossRef Full Text | Google Scholar

Scaraggi, M., and Persson, B. (2016). The Effect of Finite Roughness Size and Bulk Thickness on the Prediction of Rubber Friction and Contact Mechanics. Proc. Inst. Mech. Eng. C: J. Mech. Eng. Sci. 230 (9), 1398–1409. doi:10.1177/0954406216642261

CrossRef Full Text | Google Scholar

Schallamach, A. (1953). The Velocity and Temperature Dependence of Rubber Friction. Proc. Phys. Soc. B 66 (5), 386–392. doi:10.1088/0370-1301/66/5/306

CrossRef Full Text | Google Scholar

Schramm, E. J. (2003). Reibung von Elastomeren auf rauen Oberflächen und Beschreibung von Nassbremseigenschaften von PKW-Reifen. PhD thesis. Regensburg, Germany: Leibniz Universität Regensburg.

Google Scholar

Wagner, P., Wriggers, P., Klapproth, C., Prange, C., and Wies, B. (2015). Multiscale FEM Approach for Hysteresis Friction of Rubber on Rough Surfaces. Comp. Methods Appl. Mech. Eng. 296, 150–168. doi:10.1016/j.cma.2015.08.003

CrossRef Full Text | Google Scholar

Wriggers, P., and Reinelt, J. (1996). Multi-scale Approach for Frictional Contact of Elastomers on Rough Rigid Surfaces. Comp. Methods Appl. Mech. Eng. 198.

Google Scholar