Osprey optimization algorithm: A new bio-inspired metaheuristic algorithm for solving engineering optimization problems

This paper introduces a new metaheuristic algorithm named the Osprey Optimization Algorithm (OOA), which imitates the behavior of osprey in nature. The fundamental inspiration of OOA is the strategy of ospreys when hunting fish from the seas. In this hunting strategy, the osprey hunts the prey after detecting its position, then carries it to a suitable position to eat it. The proposed approach of OOA in two phases of exploration and exploitation is mathematically modeled based on the simulation of the natural behavior of ospreys during the hunting process. The performance of OOA has been evaluated in the optimization of twenty-nine standard benchmark functions from the CEC 2017 test suite. Furthermore, the performance of OOA is compared with the performance of twelve well-known metaheuristic algorithms. The simulation results show that the proposed OOA has provided superior performance compared to competitor algorithms by maintaining the balance between exploration and exploitation. In addition, the implementation of OOA on twenty-two real-world constrained optimization problems from the CEC 2011 test suite shows the high capability of the proposed approach in optimizing real-world applications.

1 Introduction

An optimization problem refers to a type of problem that has several feasible solutions. According to this definition, obtaining the best solution among these feasible solutions is called optimization (Xian et al., 2021). Every optimization problem has three main parts: decision variables, constraints, and objective function. Optimization aims to determine the values for the design variables respecting the constraints so that the value of the objective function is optimized. Numerous optimization problems in science, engineering, and real-world applications must be solved using optimization techniques (Assiri et al., 2020).

Techniques for solving optimization problems fall into two groups: deterministic and stochastic approaches. Deterministic approaches in two classes, gradient-based and non-gradient-based, have an appropriate performance in solving optimization problems of the following types: linear, convex, continuous, differentiable, and low-dimensional (Xue and Shen 2020). However, the deterministic approaches lose their capability against non-linear, non-convex, discontinuous, non-differentiable, and high-dimensional optimization problems. In this type of optimization problem, deterministic approaches provide unfavorable solutions by getting stuck in local optimal (Mirjalili et al., 2017).

The disadvantages and difficulties of deterministic approaches in solving optimization problems have led researchers to expand stochastic approaches. Metaheuristic algorithms are one of the most effective stochastic techniques based on random search in the problem-solving space using random operators and trial and error processes (Mirjalili 2015). Advantages such as efficiency in non-linear, non-convex, discontinuous, non-differentiable, NP-hard, complex, and high-dimensional problems, efficiency in non-linear and unknown search spaces, no need for differentiable information of the objective function and constraints, and no dependence on the type of problem, has led to the popularity of metaheuristic algorithms to deal with optimization problems (Cavazzuti 2013).

The nature of random search in metaheuristic algorithms means there is no guarantee to provide the global optimal using these techniques. However, the solutions obtained from metaheuristic algorithms are called quasi-optimal due to their proximity to the global optimal (Iba 1994).

Metaheuristic algorithms must be able to perform the search process well in the global and local problem-solving space to achieve a suitable solution. The search process at the global level with the concept of exploration leads to increasing the ability of the algorithm to identify the main optimal area and escape from local optima. The search process at the local level, with the concept of exploitation, leads to an increase in the ability of the algorithm to converge towards possible better solutions in promising areas (Mohar et al., 2022). The main key to the success of metaheuristic algorithms in solving optimization problems is balancing exploration and exploitation during the search process in the problem-solving space. Therefore, in comparing the performance of several metaheuristic algorithms on an optimization problem, an algorithm that provides a better quasi-optimal solution by better balancing exploration and exploitation is superior (Brunetti et al., 2022). The desire to obtain better solutions for optimization problems has led to the design of numerous metaheuristic algorithms by scientists.

The primary research question in the study of metaheuristic algorithms is, considering the numerous metaheuristic algorithms that have been introduced so far, is there still a need to introduce newer algorithms? In response to this question, the No Free Lunch (NFL) theorem (Wolpert and Macready 1997) explains that no unique metaheuristic algorithm is the best optimizer for all optimization problems. The proper performance of a metaheuristic algorithm in solving a set of optimization problems is not a guarantee for the similar performance of that algorithm in solving other optimization problems. According to the NFL theorem, an algorithm that successfully solves several optimization problems may even fail in solving another problem. Therefore, there is no assumption about the result of implementing a metaheuristic algorithm on optimization problems. Hence, the NFL theorem encourages scientists to search some more effective solutions for optimization problems by designing newer metaheuristic algorithms.

The innovation and novelty of this paper is in the design of a new metaheuristic algorithm called the Osprey Optimization Algorithm (OOA), which is used in solving optimization problems in various sciences. The main contributions of this paper are as follows:

• OOA is designed based on the simulation of osprey behavior in nature.

• The fundamental inspiration of OOA is the strategy of ospreys when hunting fish from the sea, during the steps of identifying the prey’s position, catching it, and transporting it to a suitable position for eating.

• The implementation steps of OOA in two phases of exploration and exploitation are mathematically modeled.

• OOA’s performance in optimization tasks is evaluated on twenty-nine benchmark functions from the CEC 2017 test suite.

• The performance of the proposed OOA approach is compared with the performance of twelve well-known algorithms.

• The ability of OOA to address real-world applications is tested on twenty-two constrained optimization problems from the CEC 2011 test suite.

The continuation of the paper is organized as follows: firstly, the literature review is presented in Section 2. Then, the proposed Osprey Optimization Algorithm (OOA) is introduced and mathematically modeled in Section 3. Next, simulation and evaluation studies on handling optimization tasks are presented in Section 4. The performance of the proposed OOA in solving real-world applications is evaluated in Section 5. Finally, conclusions and prospects for future studies are provided in Section 6.

2 Literature review

Various natural phenomena, animal life in nature, biological sciences, physics, rules of games, human interactions, and other evolutionary phenomena have inspired metaheuristic algorithms. Based on the inspiration’s source used in the design, metaheuristic algorithms fall into five groups: swarm-based, evolutionary-based, physics-based, human-based, and game-based approaches.

Swarm-based metaheuristic algorithms have been introduced inspired by various natural swarming phenomena, such as the natural behaviors of animals, insects, aquatic animals, birds, plants, and other living organisms. Particle Swarm Optimization (PSO) (Kennedy and Eberhart 1995), Ant Colony Optimization (ACO) (Dorigo et al., 1996), and Artificial Bee Colony (ABC) (Karaboga and Basturk 2007), are among the most famous swarm-based algorithms. The main idea in PSO design is modeling the movement of flocks of birds and fish toward the food source. The design of ACO was inspired by the ability of ants to detect the shortest path between a nest and a food source. ABC is developed based on simulating the strategy of colony bees searching for food sources. Among the natural behaviors of animals, trying to obtain food through foraging and hunting has been a source of inspiration in the design of several swarm-based algorithms such as Golden Jackal Optimization (GJO) (Chopra and Ansari 2022), Coati Optimization Algorithm (COA) (Dehghani et al., 2023), Marine Predator Algorithm (MPA) (Faramarzi et al., 2020a), African Vultures Optimization Algorithm (AVOA) (Abdollahzadeh et al., 2021), Whale Optimization Algorithm (WOA) (Mirjalili and Lewis 2016), Pelican Optimization Algorithm (POA) (Trojovský and Dehghani 2022), Honey Badger Algorithm (HBA) (Hashim et al., 2022), Reptile Search Algorithm (RSA) (Abualigah et al., 2022), Grey Wolf Optimizer (GWO) (Mirjalili, Mirjalili, and Lewis 2014), White Shark Optimizer (WSO) (Braik et al., 2022a), and Tunicate Swarm Algorithm (TSA) (Kaur et al., 2020).

Evolutionary-based metaheuristic algorithms have been developed with inspiration from biological sciences, concepts of genetics, Darwin’s theory of evolution, survival of the fittest, and natural selection. Genetic Algorithm (GA) (Goldberg and Holland 1988) and Differential Evolution (DE) (Storn and Price 1997) are among the most famous evolutionary-based methods that are designed based on modeling the reproduction process and using random operators of selection, crossover, and mutation. Modeling the human immune system against disease and microbes is employed in the design of Artificial Immune Systems (AISs) (De Castro and Timmis 2003). Some other evolutionary-based metaheuristic algorithms are: Genetic programming (GP) (Koza and Koza 1992), Evolution Strategy (ES) (Beyer and Schwefel 2002), and Cultural Algorithm (CA) (Reynolds 1994).

Phenomena, forces, laws, and other physics concepts inspire physics-based metaheuristic algorithms. Simulated Annealing (SA) (Kirkpatrick et al., 1983) is one of the most famous physics-based techniques. SA is developed based on modeling the metal annealing process in which the metal is melted under heat and then slowly heated to achieve an ideal crystal.

Newton’s laws of motion and physical forces have been a source of inspiration in designing algorithms such as the Spring Search Algorithm (SSA) (Dehghani et al., 2017) based on spring tension force and Hooke’s law, Momentum Search Algorithm (MSA) (Dehghani and Samet 2020) based on momentum force, and Gravitational Search Algorithm (GSA) (Rashedi et al., 2009) based on gravitational force.

Various physical transformations in the natural water cycle have inspired the design of the Water Cycle Algorithm (WCA) (Eskandar et al., 2012). Other physics-based metaheuristic algorithms are, e.g., Multi-Verse Optimizer (MVO) (Mirjalili et al., 2016), Archimedes Optimization Algorithm (AOA) (Hashim et al., 2021), Equilibrium Optimizer (EO) (Faramarzi et al., 2020b), Electro-Magnetism Optimization (EMO) (Cuevas et al., 2012), Nuclear Reaction Optimization (NRO) (Wei et al., 2019), and Lichtenberg Algorithm (LA) (Pereira et al., 2021).

Human-based metaheuristic algorithms have been introduced with inspiration from human interactions, communication, thinking, and interaction in social and personal life. Teaching-Learning Based Optimization (TLBO) (Rao et al., 2011) is the most widely used human-based approach. Interactions between teachers and students in the classroom environment have been a source of inspiration in the design of TLBO. The strategy of the poor and the wealthy sections of society to improve their economic conditions has been the main idea used in the design of Poor and Rich Optimization (PRO) (Moosavi and Bardsiri 2019).

Some other human-based metaheuristic algorithms are, e.g., Gaining-Sharing Knowledge-based algorithm (GSK) (Mohamed et al., 2020), War Strategy Optimization (WSO) (Ayyarao et al., 2022), Teamwork Optimization Algorithm (TOA) (Dehghani and Trojovský 2021), Coronavirus Herd Immunity Optimizer (CHIO) (Al-Betar et al., 2021), Driving Training-Based Optimization (DTBO) (Dehghani et al., 2022), and Ali Baba and the Forty Thieves (AFT) (Braik et al., 2022b).

Game-based metaheuristic algorithms have been developed inspired by the strategies of players, coaches, referees, and the rules in different games. Mathematical modeling of competitions in different game leagues has been the main idea in designing algorithms such as Soccer league competition algorithm (SLC) (Dehghani et al., 2020) and Football Game Based Optimization (FGBO) (Dehghani et al., 2020) based on football league, and Volleyball Premier League (VPL) (Moghdani and Salimifard 2018) and based on volleyball league.

Analysis of existing optimization methods has shown that no metaheuristic algorithm is based on modeling the natural behavior of osprey. A study of the osprey’s fishing behavior shows that it is an intelligent process with great potential to design a new optimizer. In this regard and in order to address this research gap, in this paper, a new swarm-based metaheuristic algorithm based on the mathematical modeling of natural behaviors of osprey is designed, which is discussed in the next section.

3 Osprey optimization algorithm

In this section, the proposed Osprey Optimization Algorithm (OOA) approach is introduced, then its mathematical modeling is presented.

3.1 Inspiration of OOA

The osprey, also known as the fish hawk, river hawk, and sea hawk, is a diurnal, fish-eating bird of prey with a cosmopolitan range. An osprey is 50–66 cm in length, 0.9–2.1 kg in weight, and 127–180 cm in wingspan. A picture of the osprey is shown in Figure 1. The appearance characteristics of the osprey are as follows (Strandberg 2013):

• The upperparts are a deep-glossy brown, while the breast is white and sometimes streaked with brown, and the underparts are pure white.

• The head is white with a black mask across the eyes, reaching to the sides of the neck.

• The irises of the eyes are golden to brown, and the transparent nictitating membrane is pale blue.

• The feet are white with black talons and bill is black with a blue cere.

• Osprey has narrow-long wings and a short tail.

FIGURE 1

FIGURE 1. Photo of a osprey; downloaded from free media Wikimedia Commons.

The osprey is a piscivorous bird, about 99% of its diet is fish (Grove et al., 2009). It usually catches alive fish weighing from 150 to 300 g and 25–35 cm in length. However, it can catch any fish from 50 g to 2 kg. Ospreys have the high vision to detect underwater objects. When the osprey is flying at a height of 10–40 m above the water’s surface, it detects the position of the fish underwater. Then it moves toward the fish, dips its feet into the water, and dives under the water to catch the fish (Poole et al., 2002). After the osprey catches its prey, it carries it to a nearby rock and begins to eat it (Szaro 1978).

The osprey’s strategy in hunting fish and carrying fish to a suitable position to eat it are intelligent natural behaviors that can be the basis of designing a new optimization algorithm. Therefore, the mathematical modeling of these intelligent osprey behaviors is employed in the design of the proposed OOA approach, which is discussed in the following part.

3.2 Mathematical modeling

In this subsection, the initialization of OOA is described first, then the process of updating the position of ospreys in the two phases of exploration and exploitation based on the simulation of natural osprey behaviors is presented.

3.2.1 Initialization

The proposed OOA is a population-based approach that can provide a suitable solution based on the search power of its population members in the problem-solving space through a repetition-based process. Each osprey, as a member of the OOA population, determines values ​​for the problem variables based on its position in the search space. Therefore, each osprey is a candidate solution to the problem, mathematically modeled using a vector. Ospreys together form the OOA population, which can be modeled using a matrix according to (1). At the beginning of OOA implementation, the position of ospreys in the search space is randomly initialized using (2).

$\mathit{X}={\left[\begin{array}{c}{\mathit{X}}_{\mathbf{1}}\\ ⋮\\ {\mathit{X}}_{\mathit{i}}\\ ⋮\\ {\mathit{X}}_{\mathit{N}}\end{array}\right]}_{\mathit{N}\times \mathit{m}}={\left[\begin{array}{ccccc}{\mathit{x}}_{\mathbf{1,1}}& \cdots & {\mathit{x}}_{\mathbf{1},\mathit{j}}& \cdots & {\mathit{x}}_{\mathbf{1},\mathit{m}}\\ ⋮& \ddots & ⋮& ⋰& ⋮\\ {\mathit{x}}_{\mathit{i},\mathbf{1}}& \cdots & {\mathit{x}}_{\mathit{i},\mathit{j}}& \cdots & {\mathit{x}}_{\mathit{i},\mathit{m}}\\ ⋮& ⋰& ⋮& \ddots & ⋮\\ {\mathit{x}}_{\mathit{N},\mathbf{1}}& \cdots & {\mathit{x}}_{\mathit{N},\mathit{j}}& \cdots & {\mathit{x}}_{\mathit{N},\mathit{m}}\end{array}\right]}_{\mathit{N}\times \mathit{m}},(1)$

${\mathit{x}}_{\mathit{i},\mathit{j}}=\mathit{l}{\mathit{b}}_{\mathit{j}}+{\mathit{r}}_{\mathit{i},\mathit{j}}\bullet \left(\mathit{u}{\mathit{b}}_{\mathit{j}}-\mathit{l}{\mathit{b}}_{\mathit{j}}\right),\mathit{i}=\mathbf{1,2},\dots ,\mathit{N},\mathit{j}=\mathbf{1,2},\dots ,\mathit{m},(2)$

where $X$ is the population matrix of ospreys’ locations, $X_i$ is the $i$ th osprey (a candidate solution), $x_{i,j}$ is its $j$ th dimension (problem variable), $N$ is the number of ospreys, $m$ is the number of problem variables, $r_{i,j}$ are random numbers in the interval $\left[\mathrm{0,1}\right]$, $l{b}_j$, and $u{b}_j$ are the lower bound and upper bound of the $j$ th problem variable, respectively

Because each osprey is a candidate solution for the problem, corresponding to each osprey, the objective function can be evaluated. The evaluated values ​​for the objective function of the problem can be represented using a vector according to (3).

$\mathit{F}={\left[\begin{array}{c}{\mathit{F}}_{\mathbf{1}}\\ ⋮\\ {\mathit{F}}_{\mathit{i}}\\ ⋮\\ {\mathit{F}}_{\mathit{N}}\end{array}\right]}_{\mathit{N}\times \mathbf{1}}={\left[\begin{array}{c}\mathit{F}\left({\mathit{X}}_{\mathbf{1}}\right)\\ ⋮\\ \mathit{F}\left({\mathit{X}}_{\mathit{i}}\right)\\ ⋮\\ \mathit{F}\left({\mathit{X}}_{\mathit{N}}\right)\end{array}\right]}_{\mathit{N}\times \mathbf{1}},(3)$

where $F$ is the vector of the objective function values and $F_i$ is the obtained objective function value for the $i$ th osprey.

The evaluated values ​​for the objective function are the main criteria for evaluating the quality of the candidate solutions. Therefore, the best value obtained for the objective function corresponds to the best candidate solution (i.e., the best member), and the worst value obtained for the objective function corresponds to the worst candidate solution (i.e., the worst member). Considering that the position of the ospreys in the search space is updated in each iteration, the best candidate solution must also be updated in each iteration.

3.2.2 Phase 1: Position identification and hunting the fish (exploration)

Ospreys are mighty hunters able to detect the location of fish underwater due to their strong eyesight. After identifying the position of the fish, they attack it and hunt the fish by going underwater. The first phase of population update in OOA is modeled based on the simulation of this natural behavior of ospreys. Modeling the osprey attack on fish leads to significant changes in the position of the osprey in the search space, which increases the exploration power of OOA in identifying the optimal area and escaping from the local optima.

In OOA design, for each osprey, the positions of other ospreys in the search space that have a better objective function value are considered underwater fishes. The set of fish for each osprey is specified using (4).

$\mathit{F}{\mathit{P}}_{\mathit{i}}=\left\{{\mathit{X}}_{\mathit{k}}|\mathit{k}\in \left\{\mathbf{1,2},\dots ,\mathit{N}\right\}\wedge {\mathit{F}}_{\mathit{k}}<{\mathit{F}}_{\mathit{i}}\right\}\cup \left\{{\mathit{X}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}\right\},(4)$

where $F{P}_i$ is the set of fish positions for the $i$ th osprey and $X_{best}$ is the best candidate solution (the best osprey).

The osprey randomly detects the position of one of these fish and attacks it. Based on the simulation of the movement of the osprey towards the fish, a new position for the corresponding osprey is calculated using (5). This new position, if it improves the value of the objective function, replaces the previous position of the osprey according to (6).

${\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{P}\mathbf{1}}={\mathit{x}}_{\mathit{i},\mathit{j}}+{\mathit{r}}_{\mathit{i},\mathit{j}}\bullet \left({\mathit{S}\mathit{F}}_{\mathit{i},\mathit{j}}-{\mathit{I}}_{\mathit{i},\mathit{j}}\bullet {\mathit{x}}_{\mathit{i},\mathit{j}}\right),$(5-a)

${\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{P}\mathbf{1}}=\left\{\begin{array}{c}{\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{P}\mathbf{1}},\mathit{l}{\mathit{b}}_{\mathit{j}}\le {\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{P}\mathbf{1}}\le \mathit{u}{\mathit{b}}_{\mathit{j}};\\ \mathit{l}{\mathit{b}}_{\mathit{j}},{\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{P}\mathbf{1}}<\mathit{l}{\mathit{b}}_{\mathit{j}};\\ \mathit{u}{\mathit{b}}_{\mathit{j}},{\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{P}\mathbf{1}}>\mathit{u}{\mathit{b}}_{\mathit{j}}.\end{array}\right.$(5-b)

${\mathit{X}}_{\mathit{i}}=\left\{\begin{array}{c}{\mathit{X}}_{\mathit{i}}^{\mathit{P}\mathbf{1}},{\mathit{F}}_{\mathit{i}}^{\mathit{P}\mathbf{1}}<{\mathit{F}}_{\mathit{i}};\\ {\mathit{X}}_{\mathit{i}},\mathit{e}\mathit{l}\mathit{s}\mathit{e},\end{array}\right.(6)$

where $X_i^{P1}$ is the new position of the $i$ th osprey based on the first phase of OOA, $x_{i,j}^{P1}$ is its $j$ th dimension, $F_i^{P1}$ is its objective function value, ${SF}_i$ is the selected fish for $i$ th osprey, ${SF}_{i,j}$ is the its $j$ th dimension, $r_{i,j}$ are random numbers in the interval $\left[\mathrm{0,1}\right]$, and $I_{i,j}$ are random numbers from the set $\left\{\mathrm{1,2}\right\}$.

3.2.3 Phase 2: Carrying the fish to the suitable position (exploitation)

After hunting a fish, the osprey carries it to a suitable (for him safe) position to eat it there. The second phase of updating the population in OOA is modeled based on the simulation of this natural behavior of osprey. The modeling of carrying the fish to the suitable position leads to the creation of small changes in the position of the osprey in the search space, which results in an increase in the exploitation power of the OOA in the local search and convergence towards better solutions near the discovered solutions.

In the design of OOA, to simulate this natural behavior of ospreys, first, for each member of the population, a new random position is calculated as a “suitable position for eating fish” using (7). Then, if the value of the objective function is improved in this new position, it replaces the previous position of the corresponding osprey according to (8).

${\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{P}\mathbf{2}}={\mathit{x}}_{\mathit{i},\mathit{j}}+\frac{\mathit{l}{\mathit{b}}_{\mathit{j}}+\mathit{r}\bullet \left(\mathit{u}{\mathit{b}}_{\mathit{j}}-\mathit{l}{\mathit{b}}_{\mathit{j}}\right)}{\mathit{t}},\mathit{i}=\mathbf{1,2},\dots ,\mathit{N},\mathit{j}=\mathbf{1,2},\dots ,\mathit{m},\mathit{t}=\mathbf{1,2},\dots ,\mathit{T},$(7-a)

${\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{P}\mathbf{2}}=\left\{\begin{array}{c}{\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{P}\mathbf{2}},\mathit{l}{\mathit{b}}_{\mathit{j}}\le {\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{P}\mathbf{2}}\le \mathit{u}{\mathit{b}}_{\mathit{j}};\\ \mathit{l}{\mathit{b}}_{\mathit{j}},{\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{P}\mathbf{2}}<\mathit{l}{\mathit{b}}_{\mathit{j}};\\ \mathit{u}{\mathit{b}}_{\mathit{j}},{\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{P}\mathbf{2}}>\mathit{u}{\mathit{b}}_{\mathit{j}},\end{array}\right.$(7-b)

${\mathit{X}}_{\mathit{i}}=\left\{\begin{array}{c}{\mathit{X}}_{\mathit{i}}^{\mathit{P}\mathbf{2}},{\mathit{F}}_{\mathit{i}}^{\mathit{P}\mathbf{2}}<{\mathit{F}}_{\mathit{i}};\\ {\mathit{X}}_{\mathit{i}},\mathit{e}\mathit{l}\mathit{s}\mathit{e},\end{array}\right.(8)$

where $X_i^{P2}$ is the new position of the $i$ th osprey based on the second phase of OOA, $x_{i,j}^{P2}$ is its $j$ th dimension, $F_i^{P2}$ is its objective function value, $r_{i,j}$ are random numbers in the interval $\left[\mathrm{0,1}\right]$, $t$ is the iteration counter of the algorithm, and $T$ is the total number of iterations.

3.3 Repetitions process, flowchart, and pseudocode of OOA

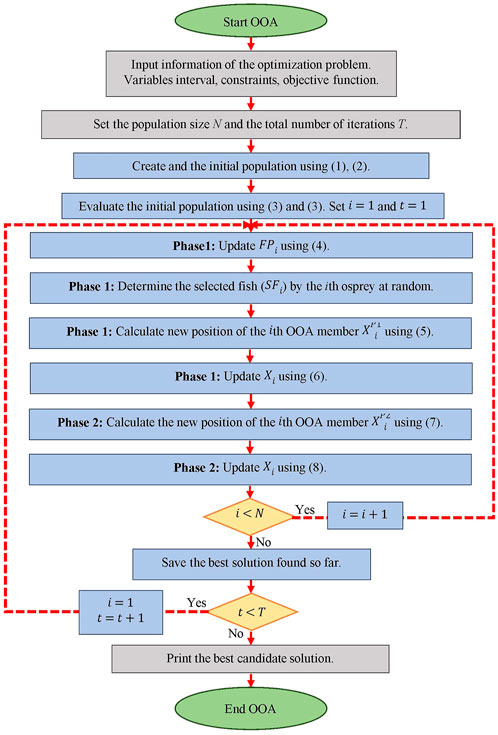
The proposed OOA is an iteration-based approach the first iteration of OOA is completed by updating all ospreys’ positions based on the first and second phases. Then, the best candidate solution is updated based on comparing the objective function values. After that, the algorithm enters the next iteration with the updated positions for the ospreys, and the algorithm update process continues until the last iteration based on (4) to (8). Finally, after the full implementation of the algorithm, OOA presents the best candidate solution stored during the iterations as a solution to the problem. The implementation steps of OOA are presented as the flowchart in Figure 2 and its pseudocode in Algorithm 1.

FIGURE 2

FIGURE 2. Flowchart of the proposed OOA.

Algorithm 1. Pseudocode of OOA.

Start OOA.

Input: The problem information (variables, objective function, and constraints).

Set OOA population size (N) and the total number of iterations (T).

Generate the initial population matrix at random using (1) and (2).

Evaluate the objective function by (3).

For $t=1$ to T

For $i=1$ to $N$

Phase 1: Position identification and hunting the fish

Update fish positions set for the $i$ th OOA member using (4). F $P_i=\left\{X_k|k\in \left\{\mathrm{1,2},\dots ,N\right\}\wedge F_k<F_i\right\}\cup \left\{X_{best}\right\}$.

Determine the selected fish by the $i$ th osprey at random.

Calculate new position of the $i$ th OOA member based on the first phase of OOA using (5-a). $x_{i,j}^{P1}\leftarrow x_{i,j}+r_{i,j}\bullet \left(S{F}_{i,j}-I_{i,j}\bullet x_{i,j}\right).$

Check the boundary conditions for the new position of OOA members using (5-b). $x_{i,j}^{P1}\leftarrow \left\{\begin{array}{c}{x}_{i,j}^{P1},l{b}_j\le x_{i,j}^{P1}\le u{b}_j;\\ l{b}_j,x_{i,j}^{P1}<l{b}_j;\\ u{b}_j,x_{i,j}^{P1}>u{b}_j.\end{array}\right.$

Update the $i$ th OOA member using (6). $X_i\leftarrow \left\{\begin{array}{c}{X}_i^{P1},F_i^{P1}<F_i;\\ X_i,else.\end{array}\right.$

Phase 2: Carrying the fish to the suitable position

Calculate new position of the $i$ th OOA member based on the second phase of OOA using (7-a). $x_{i,j}^{P2}\leftarrow x_{i,j}+\left(l{b}_j+r_{i,j}\bullet \left(u{b}_j-l{b}_j\right)\right)/t.$

Check the boundary conditions for the new position of OOA members using (7-b). $x_{i,j}^{P2}\leftarrow \left\{\begin{array}{c}{x}_{i,j}^{P2},l{b}_j\le x_{i,j}^{P2}\le u{b}_j;\\ l{b}_j,x_{i,j}^{P2}<l{b}_j;\\ u{b}_j,x_{i,j}^{P2}>u{b}_j.\end{array}\right.$

Update the $\mathrm{i}$ th OOA member using (8). $X_i\leftarrow \left\{\begin{array}{c}{X}_i^{P2},F_i^{P2}<F_i;\\ X_i,else.\end{array}\right.$

end

Save the best candidate solution found so far.

End OOA

3.4 Computational complexity

In this subsection, the computational complexity of the proposed OOA approach is evaluated. OOA initialization for a problem with dimension $m$ equals $O\left(Nm\right)$, where $m$ is the number of problem variables, and $N$ is the population size (i.e., the number of ospreys). In each iteration of the algorithm, each osprey is updated in two phases exploration and exploitation. This population update process has a complexity equal to $O\left(2NmT\right)$, where $T$ is the total number of algorithm iterations. Therefore, the total computational complexity of OOA equals $O\left(Nm\left(1+2T\right)\right)$.

4 Simulation studies and discussion

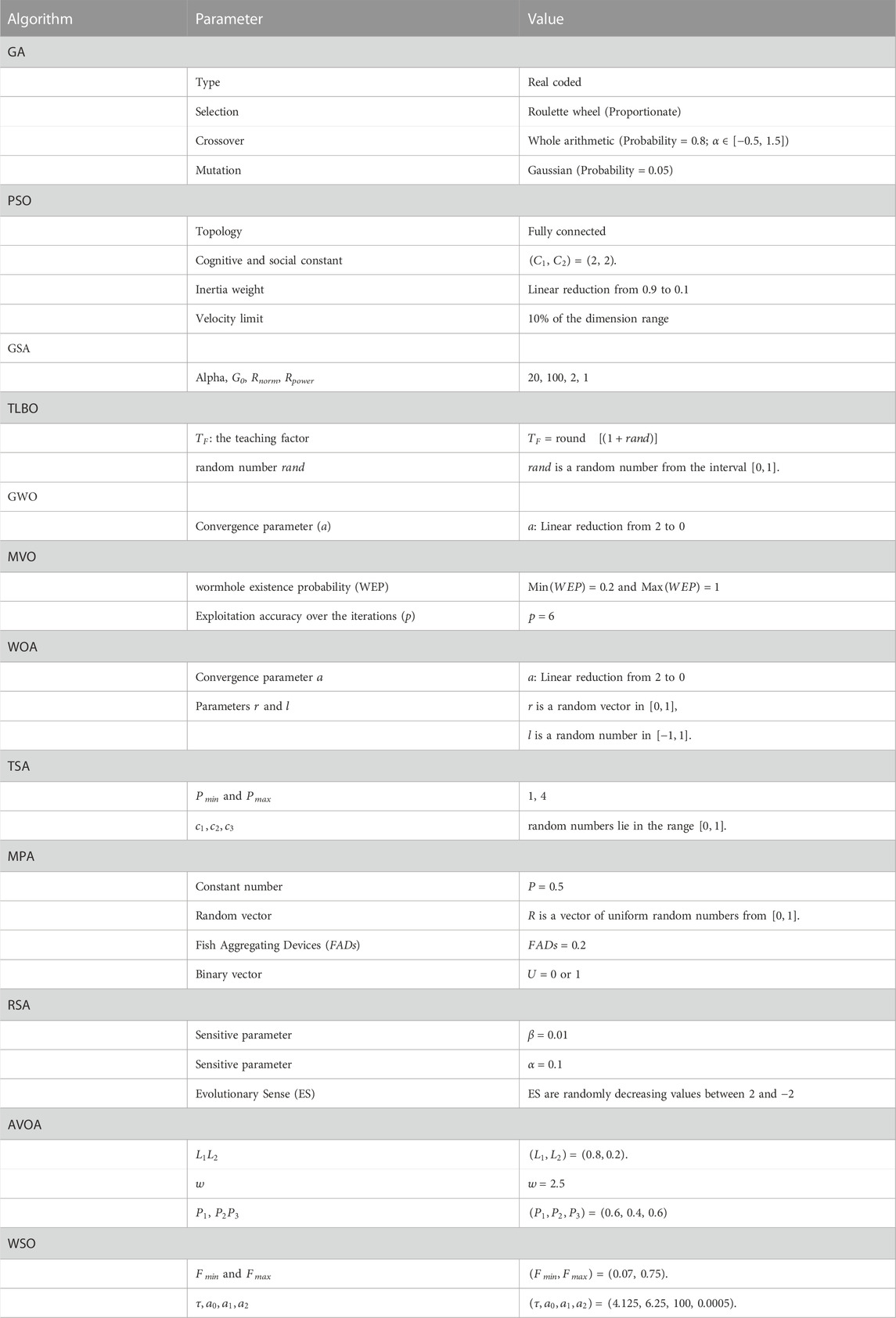
This section presents simulation studies on the performance of the proposed OOA in solving optimization problems. For this purpose, the efficiency of OOA is evaluated on the CEC 2017 test suite. Also, in order to analyze the quality of OOA in providing appropriate solutions, the results obtained from the proposed approach are compared with the performance of twelve well-known metaheuristic algorithms, including GA, PSA, GSA, TLBO, GWO, MVO, WOA, TSA, MPA, RSA, WSO, and AVOA. The values ​​of the control parameters for competitor algorithms are specified in Table 1. Simulation results are reported using six statistical indicators: mean, best, worst, standard deviation (std), and rank. The ranking criterion for metaheuristic algorithms in solving each benchmark function is to provide a better value for the mean index.

TABLE 1

TABLE 1. Parameter values for the competitor algorithms.

4.1 Evaluation of the CEC 2017 test suite

In this subsection, the OOA’s performance in solving optimization problems is evaluated on the CEC 2017 test suite. This test suite has thirty benchmark functions consisting of three unimodal functions of C17-F1 to C17-F3, seven multimodal functions of C17-F4 to C17-F10, ten hybrid functions of C17-F11 to C17-F20, and ten composition functions of C17-F21 to C17-F30. The C17-F2 function has been excluded from the simulation studies due to its unstable behavior. The full description of the CEC 2017 test suite is provided in (Awad et al., 2016). The proposed OOA approach and competitor algorithms are applied in handling the CEC 2017 test suite for dimensions equal to 10, 30, 50, and 100. For all of the functions in the CEC 2017 test suite, OOA and competitor algorithms are employed for the maximal number of function evaluations (FEs) of $10000\bullet D$, where $D$ is the number of variables (dimensions of the problem). The number of runs is 51 for each problem in each dimension, and the stop criterion is set to the maximal number of FEs.

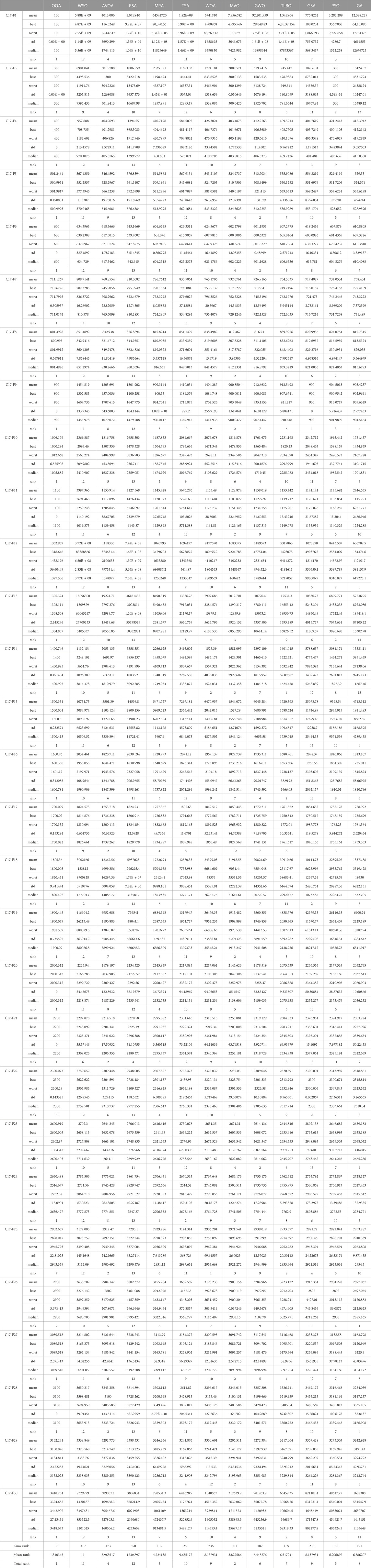
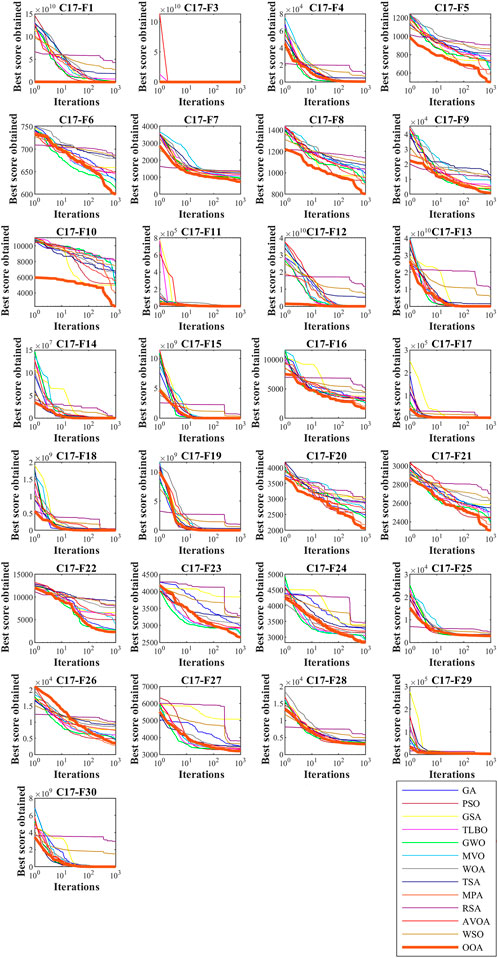
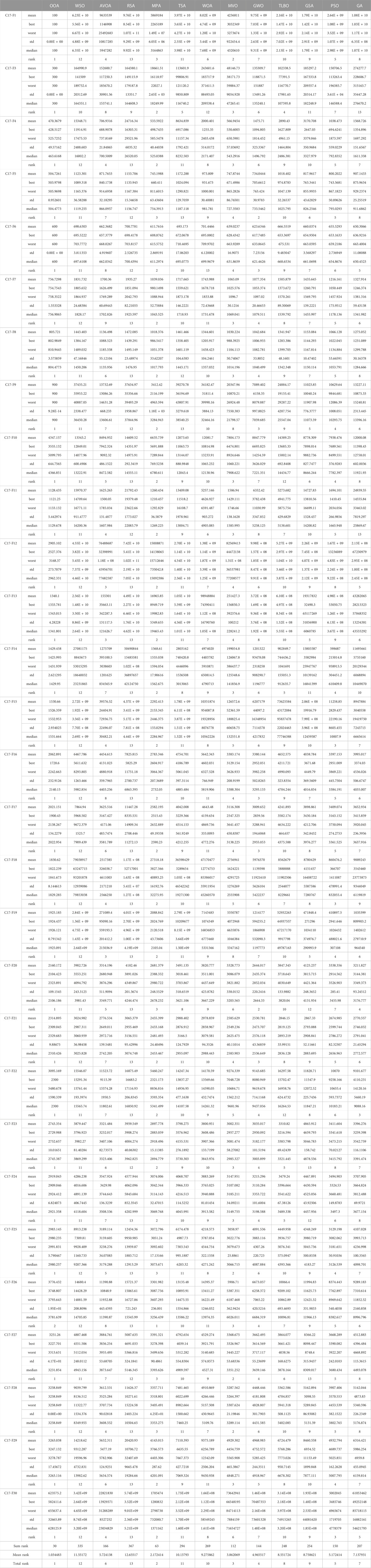
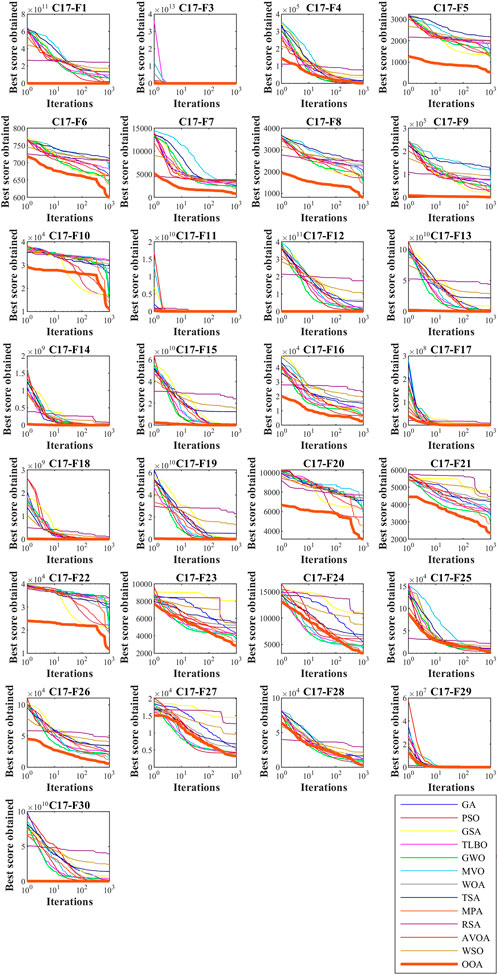
The implementation results of the proposed OOA and competitor algorithms on the CEC 2017 test suite for $D=10$ ($D$ is the dimension of the problem, i.e., the number of decision variables) are presented in Table 2. The convergence curves under this experiment for dimensions equal to 10 are plotted in Figure 3. Based on the obtained results, the proposed OOA approach is the first best optimizer for C17-F1, C17-F3 to C17-F21, C17-F23, C17-F24, and C17-F27 to C17-F30.

TABLE 2

TABLE 2. Performance of optimization algorithms on the CEC 2017 test suite ($D=10$).

FIGURE 3

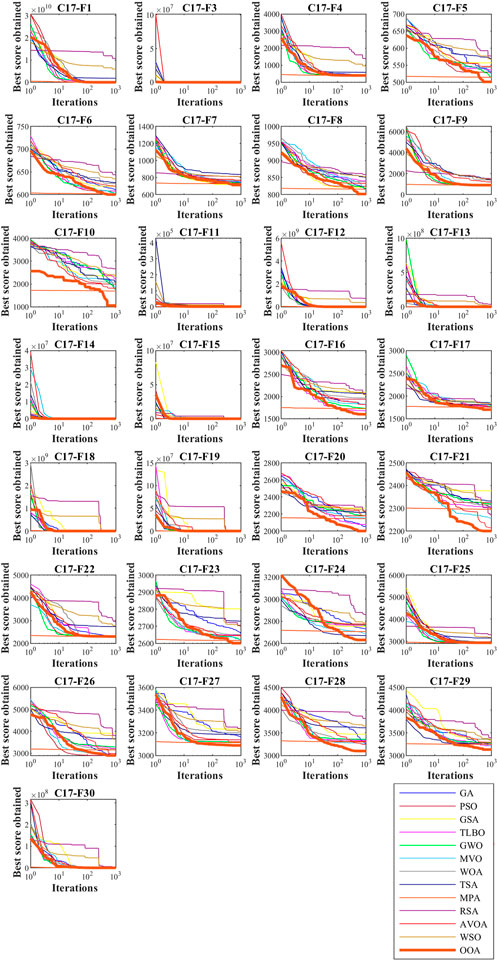
FIGURE 3. Boxplot of OOA and competitor algorithms in optimization of the CEC-2017 test suite (D = 10).

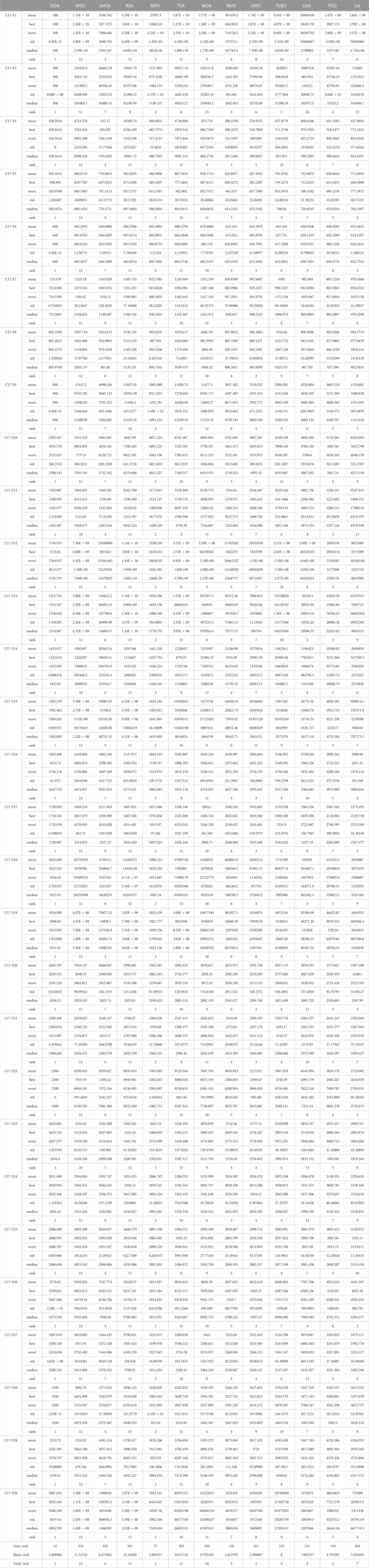
The results of employing OOA and competitor algorithms in handling the CEC 2017 test suite for $D=30$ are reported in Table 3. The convergence curves while reaching the solution for the dimension $D$ equal to 30 are shown in Figure 4. Based on the simulation results, OOA is the first best optimizer for C17-F1, C17-F3 to C17-F22, C17-F24, C17-F5, and C17-F27 to C17-F30.

TABLE 3

TABLE 3. Performance of optimization algorithms on the CEC 2017 test suite ($D=30$).

FIGURE 4

FIGURE 4. Boxplot of OOA and competitor algorithms in optimization of the CEC-2017 test suite ($\mathit{D}=\mathbf{30}$).

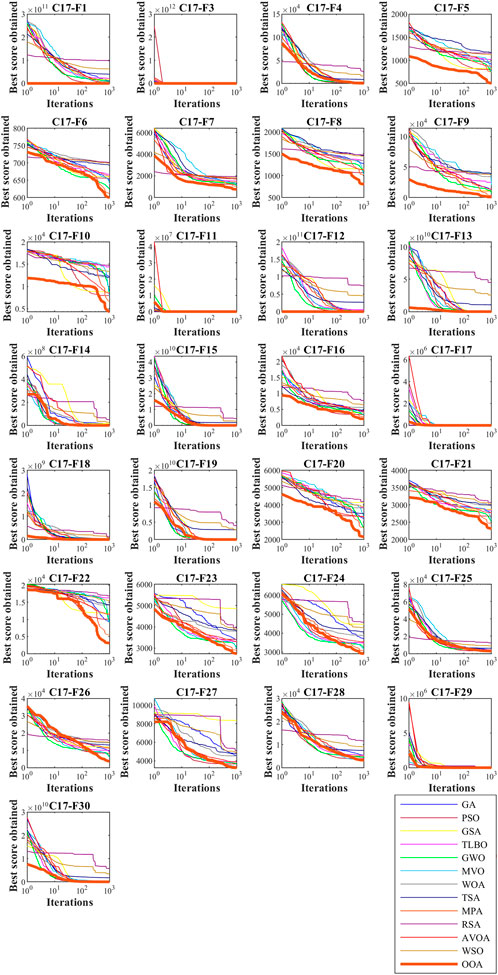
The optimization results of the CEC 2017 test suite for $D=50$, using OOA and competitor algorithms are presented in Table 4. The performance convergence curves of the algorithms on the CEC 2017 test suite for the dimension $D$ equal to 50 are drawn in Figure 5. The simulation results show that OOA is the first best optimizer for C17-F1, C17-F3 to C17-F25, and C17-F27 to C17-F30.

TABLE 4

TABLE 4. Performance of optimization algorithms on the CEC 2017 test suite ($\mathit{D}=\mathbf{50}$).

FIGURE 5

FIGURE 5. Boxplot of OOA and competitor algorithms in optimization of the CEC-2017 test suite ($\mathit{D}=\mathbf{50}$).

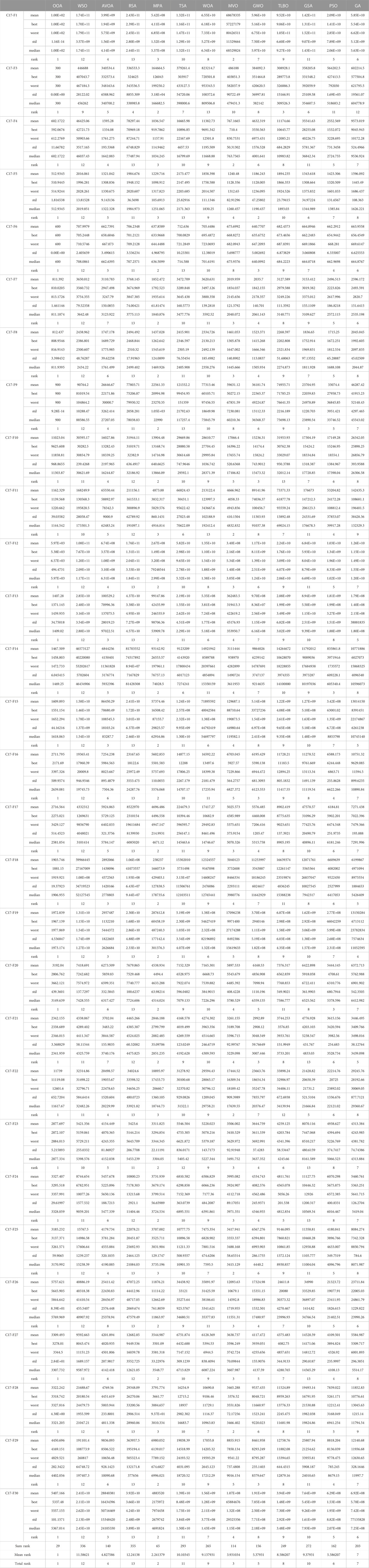
The results of using OOA and competitor algorithms in handling the CEC 2017 test suite for $D=100$ are reported in Table 5. The convergence curves under the tests of the algorithms for the dimension $D$ equal to 100 are drawn in Figure 6. Based on the obtained results, OOA is the first best optimizer for C17-F1, and C17-F3 to C17-F30.

TABLE 5

TABLE 5. Performance of optimization algorithms on the CEC 2017 test suite ($\mathit{D}=\mathbf{100}$).

FIGURE 6

FIGURE 6. Boxplot of OOA and competitor algorithms in optimization of the CEC-2017 test suite ($\mathit{D}=\mathbf{100}$).

The analysis of the simulation results shows that the proposed OOA approach has provided better results in most of the benchmark functions of the CEC 2017 test suite and for dimensions 10, 30, 50, and 100. Compared to competitor algorithms, the proposed OOA has been ranked first as the best optimizer in handling the CEC 2017 test suite.

4.2 Statistical analysis

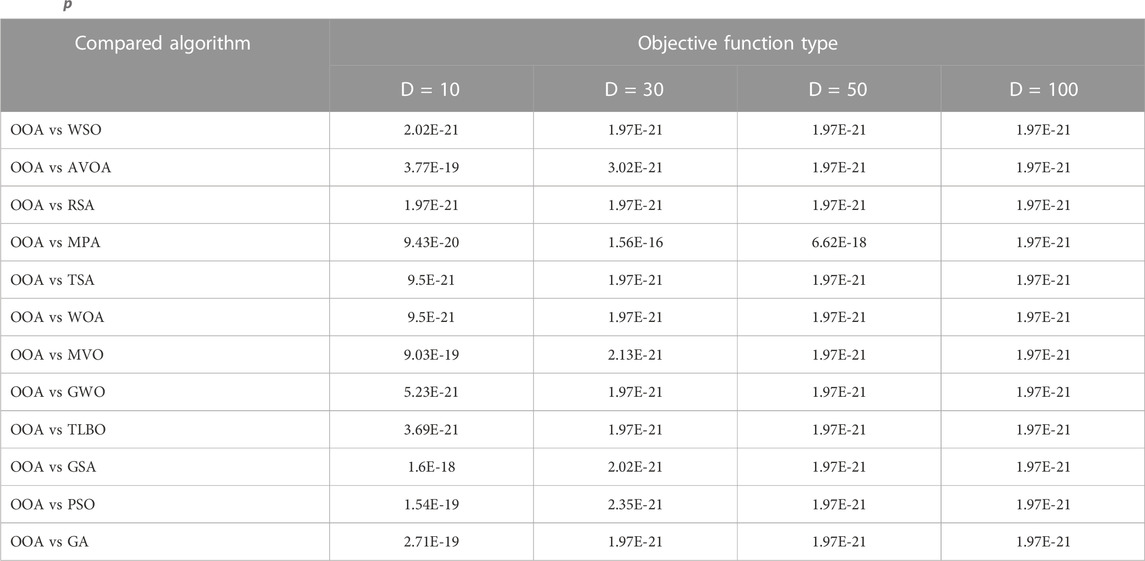
In this subsection, statistical analysis is presented on the performance of OOA and competitor algorithms to determine whether OOA has a significant statistical superiority or not. For this purpose, Wilcoxon rank sum test (Wilcoxon 1992), a non-parametric statistical test to determine the significant difference between the average of two data samples, is employed. In the Wilcoxon rank sum test, using an index called a $p$-value, it is determined whether the superiority of OOA against any of the competitor algorithms is significant from a statistical point of view.

The results of the statistical analysis on the performance of OOA and competitor algorithms are reported in Table 6. Based on these results, in cases where the $p$-value is less than 0.05, OOA has a significant statistical superiority compared to the corresponding algorithm.

TABLE 6

TABLE 6. $\mathit{p}$-values obtained from Wilcoxon rank sum test.

5 OOA for real-world applications

In this section, the effectiveness of the proposed OOA approach in solving optimization problems in real-world applications is tested. In this regard, OOA is implemented on the CEC 2011 test suite. This test suite has twenty-two up-to-date test functions for real-world constrained optimization problems. The IEEE CEC-2011 test suite details and complete information are stated in (Das and Suganthan 2010). For OOA and each competitor algorithm, the maximum number of FEs for all 22 test functions is set to 150,000, with 25 independent runs in all experiments. Furthermore, the stop criterion for the proposed OOA is set to the maximum number of function evaluations (MFEs).

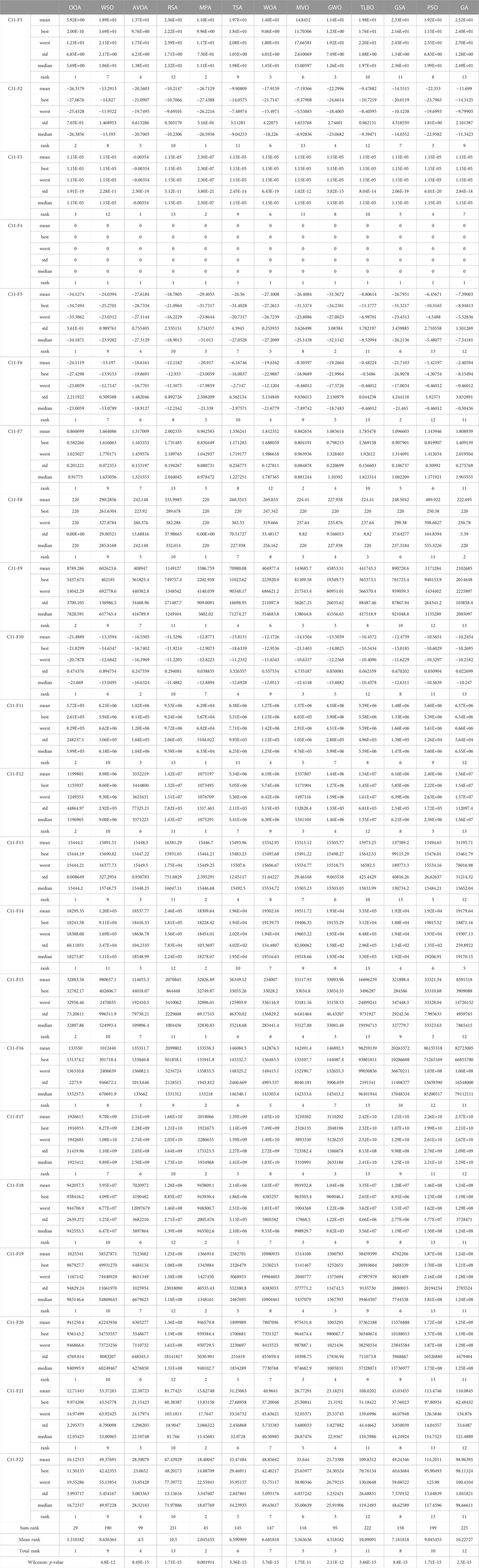
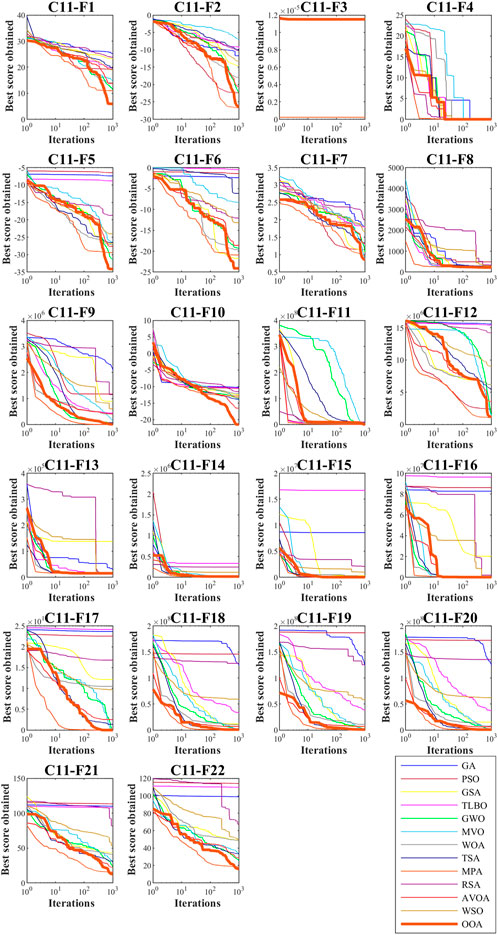
The employment results of the proposed OOA approach and competitor algorithms in solving the CEC 2011 test suite are reported in Table 7. The convergence curves of the performance of the algorithms while achieving the solution for different problems of the CEC 2011 test suite are plotted in Figure 7. Based on the simulation results, OOA is the first best optimizer for C11-F1, C11-F4 to C11-F8, C11-F10, C11-F13, C11-F14, and C11-F16 to C11-F22. What is evident from the comparison of the simulation results is that OOA has provided better results in most of the CEC 2011 test suite benchmark functions and has provided superior performance in handling this test suite compared to competitor algorithms. Also, the results obtained from the Wilcoxon sum rank test show that OOA has a significant statistical superiority in handling the CEC 2011 test suite compared to competitor algorithms.

TABLE 7

TABLE 7. Performance of optimization algorithms on the CEC 2011 test suite.

FIGURE 7

FIGURE 7. Boxplot of OOA and competitor algorithms in optimization of the CEC-2011 test suite.

6 Conclusion and future works

This paper introduced a new metaheuristic algorithm named the Osprey Optimization Algorithm (OOA) to solve real-world optimization problems. The real inspiration in the proposed OOA approach is the ospreys’ strategies when hunting fish from the sea during the steps of identifying the prey, attacking the prey in the sea, and transporting the prey to a suitable place. The proposed OOA approach theory was explained, and its implementation steps in two phases of exploration and exploitation were mathematically modeled. The effectiveness of OOA in solving optimization problems was evaluated on twenty-nine standard benchmark functions from the CEC 2017 test suite. The quality of the proposed approach was compared with the performance of twelve well-known metaheuristic algorithms. The simulation results showed that OOA had achieved better results in most of the benchmark functions by balancing exploration and exploitation during the search process, and compared to competitor algorithms, it has superior performance in optimization tasks. Also, the employment of OOA in dealing with twenty-two up-to-date real-world constrained optimization problems from the CEC 2011 test suite showed the adequate performance of the proposed approach in solving optimization problems in real-world applications.

Following the introduction of the proposed OOA approach, several research directions are activated for future studies. For example, designing binary and multi-objective versions for the proposed OOA approach is one of the central potentials of this study for further work. In addition, the employment of OOA in optimization problems in various science and real-world applications is another research proposal for further work in the future.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, PT; methodology, PT; software, MD; validation, PT and MD; formal analysis, MD; investigation, PT; resources, PT.; data curation, PT and MD; writing—original draft preparation, PT and MD; writing—review and editing, PT and MD; visualization, PT; supervision, PT; project administration, MD; funding acquisition, PT.

Funding

The research was supported by the Project of Excellence of Faculty of Science No. 2210/2023–2024, University of Hradec Králové, Czech Republic.

Acknowledgments

The authors thank Dušan Bednařík from the University of Hradec Kralove for our fruitful and informative discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdollahzadeh, B., Farhad, S. G., and Mirjalili, S. (2021). African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Industrial Eng. 158, 107408. doi:10.1016/j.cie.2021.107408

CrossRef Full Text | Google Scholar

Abualigah, L., Abd Elaziz, M., Sumari, P., Geem, Z. W., and Gandomi, A. H. (2022). Reptile search algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 191, 116158. doi:10.1016/j.eswa.2021.116158

CrossRef Full Text | Google Scholar

Al-Betar, M. A., Zaid, A. A. A., Awadallah, M. A., and Abu Doush, I. (2021). Coronavirus herd immunity optimizer (CHIO). Neural Comput. Appl. 33 (10), 5011–5042. doi:10.1007/s00521-020-05296-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Assiri, A. S., Hussien, A. G., and Amin, M. (2020). Ant lion optimization: Variants, hybrids, and applications. IEEE Access 8, 77746–77764. doi:10.1109/access.2020.2990338

CrossRef Full Text | Google Scholar

Awad, N. H., Ali, M., Liang, J., Qu, B., and Suganthan, P.Problem Definitions (2016). Evaluation criteria for the CEC 2017 special session and competition on single objective real-parameter numerical optimization. Technology Report.

Google Scholar

Ayyarao, S. V., Rama Krishna, N. S. S., Madurai Elavarasam, R., Polumahanthi, N., Rambabu, M., Saini, G., et al. (2022). War strategy optimization algorithm: A new effective metaheuristic algorithm for global optimization. IEEE Access 10, 25073–25105. doi:10.1109/access.2022.3153493

CrossRef Full Text | Google Scholar

Beyer, H. G., and Schwefel, H. P. (2002). Evolution strategies–a comprehensive introduction. Nat. Comput. 1 (1), 3–52. doi:10.1023/a:1015059928466

CrossRef Full Text | Google Scholar

Braik, M., Hammouri, A., Atwan, J., Al-Betar, M. A., and Awadallah, M. A. (2022a). White Shark optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowledge-Based Syst. 243, 108457. doi:10.1016/j.knosys.2022.108457

CrossRef Full Text | Google Scholar

Braik, M., Hashem Ryalat, M., and Al-Zoubi, H. (2022b). A novel meta-heuristic algorithm for solving numerical optimization problems: Ali Baba and the forty thieves. Neural Comput. Appl. 34 (1), 409–455. doi:10.1007/s00521-021-06392-x

CrossRef Full Text | Google Scholar

Brunetti, G., Stumpp, C., and Šimůnek, J. (2022). Balancing exploitation and exploration: A novel hybrid global-local optimization strategy for hydrological model calibration. Environ. Model. Softw. 150, 105341. doi:10.1016/j.envsoft.2022.105341

CrossRef Full Text | Google Scholar

Cavazzuti, M. (2013). “Deterministic optimization,” in Optimization methods: From theory to design scientific and technological aspects in mechanics (Berlin, Heidelberg: Springer Berlin Heidelberg), 77–102.

CrossRef Full Text | Google Scholar

Chopra, N., and Ansari, M. M. (2022). Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 198, 116924. doi:10.1016/j.eswa.2022.116924

CrossRef Full Text | Google Scholar

Cuevas, E., Oliva, D., Zaldivar, D., Pérez-Cisneros, M., and Sossa, H. (2012). Circle detection using electro-magnetism optimization. Inf. Sci. 182 (1), 40–55. doi:10.1016/j.ins.2010.12.024

CrossRef Full Text | Google Scholar

Das, S., and Suganthan, P. N. (2010). Problem definitions and evaluation criteria for CEC 2011 competition on testing evolutionary algorithms on real world optimization problems. Kolkata: Jadavpur University, Nanyang Technological University, 341–359.

Google Scholar

De Castro, L. N., and Timmis, J. I. (2003). Artificial immune systems as a novel soft computing paradigm. Soft Comput. 7 (8), 526–544. doi:10.1007/s00500-002-0237-z

CrossRef Full Text | Google Scholar

Dehghani, M., Mardaneh, M., Guerrero, J. M., Malik, O. P., and Kumar, V. (2020). Football game based optimization: An application to solve energy commitment problem. Int. J. Intelligent Eng. Syst. 13, 514–523. doi:10.22266/ijies2020.1031.45

CrossRef Full Text | Google Scholar

Dehghani, M., Montazeri, Z., Ali, D., and Seifi, A. R. (2017). “Spring search algorithm: A new meta-heuristic optimization algorithm inspired by Hooke's law,” in 2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 22-22 December 2017 (IEEE). doi:10.1109/KBEI.2017.8324975

CrossRef Full Text | Google Scholar

Dehghani, M., Montazeri, Z., Trojovská, E., and Trojovský, P. (2023). Coati optimization algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowledge-Based Syst. 259, 110011. doi:10.1016/j.knosys.2022.110011

CrossRef Full Text | Google Scholar

Dehghani, M., and Samet, H. (2020). Momentum search algorithm: A new meta-heuristic optimization algorithm inspired by momentum conservation law. SN Appl. Sci. 2 (10), 1720–1815. doi:10.1007/s42452-020-03511-6

CrossRef Full Text | Google Scholar

Dehghani, M., Trojovská, E., and Trojovský, P. (2022). A new human-based metaheuristic algorithm for solving optimization problems on the base of simulation of driving training process. Sci. Rep. 12 (1), 9924. doi:10.1038/s41598-022-14225-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Dehghani, M., and Trojovský, P. (2021). Teamwork optimization algorithm: A new optimization approach for function minimization/maximization. Sensors 21 (13), 4567. doi:10.3390/s21134567

PubMed Abstract | CrossRef Full Text | Google Scholar

Dorigo, M., Maniezzo, V., and Colorni, A. (1996). Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man, Cybern. Part B Cybern. 26 (1), 29–41. doi:10.1109/3477.484436

PubMed Abstract | CrossRef Full Text | Google Scholar

Eskandar, H., Ali, S., Bahreininejad, A., and Hamdi, M. (2012). Water cycle algorithm–A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 110, 151–166. doi:10.1016/j.compstruc.2012.07.010

CrossRef Full Text | Google Scholar

Faramarzi, A., Heidarinejad, M., Mirjalili, S., and Gandomi, A. H. (2020a). Marine predators algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 152, 113377. doi:10.1016/j.eswa.2020.113377

CrossRef Full Text | Google Scholar

Faramarzi, A., Heidarinejad, M., Stephens, B., and Mirjalili, S. (2020b). Equilibrium optimizer: A novel optimization algorithm. Knowledge-Based Syst. 191, 105190. doi:10.1016/j.knosys.2019.105190

CrossRef Full Text | Google Scholar

Goldberg, D. E., and Holland, J. H. (1988). Genetic algorithms and machine learning. Mach. Learn. 3 (2), 95–99. doi:10.1023/A:1022602019183

CrossRef Full Text | Google Scholar

Grove, R. A., Henny, C. J., and Kaiser, J. L. (2009). Osprey: Worldwide sentinel species for assessing and monitoring environmental contamination in rivers, lakes, reservoirs, and estuaries. J. Toxicol. Environ. Health, Part B 12 (1), 25–44. doi:10.1080/10937400802545078

PubMed Abstract | CrossRef Full Text | Google Scholar

Hashim, F. A., Houssein, E. H., Hussain, K., Mabrouk, M. S., and Al-Atabany, W. (2022). Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 192, 84–110. doi:10.1016/j.matcom.2021.08.013

CrossRef Full Text | Google Scholar

Hashim, F. A., Hussain, K., Houssein, E. H., Mabrouk, M. S., and Al-Atabany, W. (2021). Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 51 (3), 1531–1551. doi:10.1007/s10489-020-01893-z

CrossRef Full Text | Google Scholar

Iba, K. (1994). Reactive power optimization by genetic algorithm. IEEE Trans. power Syst. 9 (2), 685–692. doi:10.1109/59.317674

CrossRef Full Text | Google Scholar

Karaboga, D., and Basturk, B. (2007). “Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems,” in International fuzzy systems association world congress, (Berlin, Heidelberg: Springer)

Google Scholar

Kaur, S., Awasthi, L. K., Sangal, A. L., and Gaurav, D. (2020). Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 90, 103541. doi:10.1016/j.engappai.2020.103541

CrossRef Full Text | Google Scholar

Kennedy, J., and Eberhart, R. (1995). “Particle swarm optimization,” in Proceedings of ICNN'95 - International Conference on Neural Networks, Perth, WA, Australia, 27 Nov.-1 Dec. 1995.

Google Scholar

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Optimization by simulated annealing. Science 220 (4598), 671–680. doi:10.1126/science.220.4598.671

PubMed Abstract | CrossRef Full Text | Google Scholar

Koza, J. R., and Koza, J. R. (1992). Genetic programming: On the programming of computers by means of natural selection. Vol. 1. Cambridge, MA: MIT press.

Google Scholar

Mirjalili, S., Gandomi, A. H., Mirjalili, S. Z., Saremi, S., Faris, H., and Mirjalili, S. M. (2017). Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 114, 163–191. doi:10.1016/j.advengsoft.2017.07.002

CrossRef Full Text | Google Scholar

Mirjalili, S., and Lewis, A. (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008

CrossRef Full Text | Google Scholar

Mirjalili, S., Mirjalili, S. M., and Hatamlou, A. (2016). Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 27 (2), 495–513. doi:10.1007/s00521-015-1870-7

CrossRef Full Text | Google Scholar

Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey Wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007

CrossRef Full Text | Google Scholar

Mirjalili, S. (2015). The ant lion optimizer. Adv. Eng. Softw. 83, 80–98. doi:10.1016/j.advengsoft.2015.01.010

CrossRef Full Text | Google Scholar

Moghdani, R., and Salimifard, K. (2018). Volleyball premier league algorithm. Appl. Soft Comput. 64, 161–185. doi:10.1016/j.asoc.2017.11.043

CrossRef Full Text | Google Scholar

Mohamed, A. W., Hadi, A. A., and Mohamed, A. K. (2020). Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm. Int. J. Mach. Learn. Cybern. 11 (7), 1501–1529. doi:10.1007/s13042-019-01053-x

CrossRef Full Text | Google Scholar

Mohar, S. S., Goyal, S., and Kaur, R. (2022). Localization of sensor nodes in wireless sensor networks using bat optimization algorithm with enhanced exploration and exploitation characteristics. J. Supercomput. 78 (9), 11975–12023. doi:10.1007/s11227-022-04320-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Moosavi, S. H. S., and Bardsiri, V. K. (2019). Poor and rich optimization algorithm: A new human-based and multi populations algorithm. Eng. Appl. Artif. Intell. 86, 165–181. doi:10.1016/j.engappai.2019.08.025

CrossRef Full Text | Google Scholar

Pereira, J. L. J., Francisco, M. B., Diniz, C. A., Oliver, G. A., Cunha, S. S., and Ferreira Gomes, G. (2021). Lichtenberg algorithm: A novel hybrid physics-based meta-heuristic for global optimization. Expert Syst. Appl. 170, 114522. doi:10.1016/j.eswa.2020.114522

CrossRef Full Text | Google Scholar

Poole, A. F., Bierregaard, R. O., and Martell, M. S. (2002). Osprey: Pandion Haliaetus. Philadelphia, PA: Birds of North America, Incorporated, No. 683.

Google Scholar

Rao, R. V., Savsani, V. J., and Vakharia, D. P. (2011). Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Computer-Aided Des. 43 (3), 303–315. doi:10.1016/j.cad.2010.12.015

CrossRef Full Text | Google Scholar

Rashedi, E., Nezamabadi-Pour, H., and Saryazdi, S. (2009). GSA: A gravitational search algorithm. Inf. Sci. 179 (13), 2232–2248. doi:10.1016/j.ins.2009.03.004

CrossRef Full Text | Google Scholar

Reynolds, R. G. (1994). “An introduction to cultural algorithms,” in Proceedings of the third annual conference on evolutionary programming, San Diego, California, USA, 24-26 Feb 94.

Google Scholar

Storn, R., and Price, K. (1997). Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 11 (4), 341–359. doi:10.1023/a:1008202821328

CrossRef Full Text | Google Scholar

Strandberg, R. (2013). Ageing, sexing and subspecific identification of Osprey, and two WP records of American Osprey. Dutch Bird. 35 (2), 69–87.

Google Scholar

Szaro, R. C. (1978). Reproductive success and foraging behavior of the osprey at seahorse key, Florida. Wilson Bull. 1978, 112–118.

Google Scholar

Trojovský, P., and Dehghani, M. (2022). Pelican optimization algorithm: A novel nature-inspired algorithm for engineering applications. Sensors 22 (3), 855. doi:10.3390/s22030855

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, Z., Huang, C., Wang, X., Han, T., and Li, Y. (2019). Nuclear reaction optimization: A novel and powerful physics-based algorithm for global optimization. IEEE Access 7, 66084–66109. doi:10.1109/access.2019.2918406

CrossRef Full Text | Google Scholar

Wilcoxon, F. (1992). “Individual comparisons by ranking methods,” in Breakthroughs in statistics (Berlin, Germany: Springer), 196–202.

CrossRef Full Text | Google Scholar

Wolpert, D. H., and Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1 (1), 67–82. doi:10.1109/4235.585893

CrossRef Full Text | Google Scholar

Xian, H., Yang, C., Wang, H., and Yang, X. (2021). A modified sine cosine algorithm with teacher supervision learning for global optimization. IEEE Access 9, 17744–17766. doi:10.1109/access.2021.3054053

CrossRef Full Text | Google Scholar

Xue, J., and Shen, B. (2020). A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 8 (1), 22–34. doi:10.1080/21642583.2019.1708830

CrossRef Full Text | Google Scholar