Fast vibro-acoustic response computations for finite periodic metamaterial plates using a generalized Bloch Mode Synthesis based sub-structuring approach

Metamaterials have recently emerged and shown great potential for noise and vibration reduction in specific frequency ranges, called stop bands. To predict stop bands, their often periodic nature is exploited and dispersion curves are calculated based on a single representative unit cell, typically modeled using the finite element method. Since their sub-wavelength nature and often intricate design can lead to large unit cell models, model reduction methods such as the Generalized Bloch Mode Synthesis have been proposed to greatly accelerate dispersion curve calculations. In order to calculate forced vibro-acoustic responses of finite periodic elastic metamaterial plates composed of an assembly of unit cells, however, full order finite element models rapidly become computationally unaffordable. Therefore, in this work the Generalized Bloch Mode Synthesis is incorporated in a sub-structuring approach, which enables fast forced vibration response calculations of finite elastic metamaterial plates based on a single reduced order unit cell model. The main advantage as compared to a regular Craig-Bampton approach is the additional local reduction of unit cell boundary degrees of freedom, whereby a compatible basis for the identical neighboring unit cells is incorporated. In addition, by combining this Generalized Bloch Mode Synthesis based sub-structuring approach with the Elementary Radiator Approach, efficient sound transmission loss computations of finite periodic metamaterial plates are enabled. The performance of the proposed approach for fast vibro-acoustic response predictions is demonstrated for different cases.

1 Introduction

In the search for novel lightweight solutions with favourable noise and vibration attenuation performance, locally resonant metamaterials (LRMs) have gained significant attention (Liu et al., 2000; Claeys et al., 2016). Due to their stop band behaviour, arising from the addition of resonant structures on a sub-wavelength scale on or in a flexible host structure, targeted frequency ranges of strong noise and vibration attenuation can be achieved (Xiao et al., 2012, 2013; Claeys et al., 2016; Chang et al., 2018; Droz et al., 2019; Van Belle et al., 2019; de Melo Filho et al., 2020; Song et al., 2020; Pires et al., 2022; Sangiuliano et al., 2022).

Although periodicity is not strictly required, the modelling, analysis and design of LRMs typically relies on infinite periodic structure theory: a single representative unit cell (UC) model is combined with Bloch-Floquet periodicity boundary conditions in order to predict wave propagation, and thus stop bands, in the infinite periodic structure by means of dispersion curves (Hussein et al., 2014; Van Belle et al., 2017). The finite element (FE) method is often used for the UC modelling due to its versatility and high modelling flexibility. However, given the typically complex LRM structures, the amount of degrees of freedom (DOFs) in the FE UC models can become large, leading to expensive UC analyses. To accelerate dispersion curve calculations, model order reduction (MOR) techniques have been applied which reduce the amount of DOFs in the UC model: e.g. component mode synthesis (CMS) methods such as the Bloch Mode Synthesis (BMS) (Krattiger and Hussein, 2014; Aladwani et al., 2022) and Generalized Bloch Mode Synthesis (GBMS) (Krattiger and Hussein, 2018; Van Belle et al., 2020; Xi and Zheng, 2021) as well as Bloch wave based methods such as the Reduced Bloch Mode Expansion (RBME) (Hussein, 2009) and Bloch wave reduction (Boukadia et al., 2018; Palermo and Marzani, 2020) have been proposed and have been shown to lead to considerable computation time reduction.

To assess the LRM performance in real applications, however, forced vibro-acoustic responses for finite structures with realistic boundary conditions should be evaluated as opposed to considering only infinite periodic structures (Sangiuliano et al., 2020). While wave- and transfer matrix-based approaches exist for finite 1D periodic wave guides (Mencik, 2014; Mencik and Duhamel, 2021), forced response computations of finite 2D periodic structures often still rely on full order model (FOM) assemblies. However, these computations can rapidly become very expensive for an increasing amount of periodically repeating UCs contained within the finite structure. As recently shown in (van Ophem et al., 2018; Mencik, 2021) the forced vibration response of 2D periodic finite LRMs comprised of a repetition of UCs can be efficiently performed by means of dynamic sub-structuring, with the UCs constituting the individual sub-structures. To reduce the computational cost of large sub-structured FE models, MOR is often applied to the sub-structures before assembly, for which the use of CMS methods such as the Craig-Bampton method is well-established (Gruber and Rixen, 2016; Allen et al., 2020). This method reduces the interior DOFs of the sub-structures using a truncated set of eigenmodes resulting from a modal analysis before assembly, as is performed in the BMS, and was e.g. applied in (Mencik, 2021) for the analysis of finite LRM plates composed of dissimilar UCs. Alternatively to CMS, in (van Ophem et al., 2018) Krylov-based MOR was used on a single UC level in combination with sub-structuring for the analysis of finite periodic LRM plates in view of improving accuracy. In both (van Ophem et al., 2018; Mencik, 2021), an additional global MOR step was applied to the assembled system of UC reduced order models (ROMs) to further accelerate computations. Although the above MOR techniques have been developed for the vibration response of finite periodic LRM plates, the sound transmission loss (STL) predictions of 2D periodic LRM partitions are predominantly still limited to infinite periodic structure predictions, e.g. (Deckers et al., 2018; Errico et al., 2019; Boukadia et al., 2020), or accurate yet typically computationally expensive FOM finite structure predictions, e.g. (Van Belle et al., 2019; Decraene et al., 2022).

Although reducing the UC interior DOFs, the aforementioned sub-structuring-based MOR applications for finite periodic structure vibration response predictions leave the UC boundary DOFs before assembly unaltered, which can again amount to significant computational cost for the finite plate assembly, especially when many UCs and refined FE UC models are considered (Cool et al., 2022). As a consequence, substantial gains could potentially be obtained by also reducing the UC boundary DOFs before assembly, which is the purpose of this work. In (Krattiger et al., 2019), different modal boundary reduction methods for sub-structures were compared in a CMS context. Sub-structure boundary reduction based on the assembled system-level matrices was reported to be most accurate but costly, whereas local boundary reduction on the uncoupled sub-structures was found to be fast at the cost of slight accuracy loss due to the uncoupled nature of the used boundary modes. In the case of periodic LRM plates composed of a single repeating UC, particularly the local boundary reduction on a single uncoupled UC is highly interesting as it would allow obtaining a very fast sub-structured model by creating only a single UC ROM once. To achieve this, in this work, the CMS based MOR with local boundary reduction on a single UC is performed by using the GBMS methodology (Krattiger and Hussein, 2018), which can be considered as a variant of the exact-compatibility local-level characteristic constraint modes approach for sub-structure boundary reduction discussed in (Krattiger et al., 2019). This enables fast forced vibration response computations of finite periodic LRM plates. Moreover, to also enable fast STL computations of finite periodic LRM plates, the proposed GBMS-based sub-structuring approach based on a single structural FE UC model is next combined with the Elementary Radiator Approach (ERA) proposed in (Jung et al., 2017).

The rest of this paper is structured as follows. In Section 2, the problem formulation is introduced. In Section 3, the UC MOR based sub-structuring methodology and application of the ERA is explained. In Section 4, an LRM plate design and FE UC model are introduced, followed by an eigenfrequency analysis on UC and assembly level and eventually forced vibration frequency response and STL predictions of the finite LRM plate. The main outcomes are summarized in Section 5.

2 Problem formulation

In this work, 2D periodic rectangular LRM plates are considered, which are composed of an assembly of N_x × N_y identical UCs in the xy-plane (Figure 1A). Structural plate models are considered and two types of excitations and corresponding responses are of interest. On the one hand, one or more normal point forces are considered and the out-of-plane displacement response is of interest (Figure 1B). On the other hand, an acoustic plane wave incident at elevation angle θ and azimuth angle ψ excites the panel and the acoustic radiated power on the other side of the panel is of interest (Figure 1C), which enables computing the sound transmission loss (STL). The acoustic wavenumber in the acoustic medium with soundspeed c_a and density ρ_a is given by k_a = ω/c_a. The acoustic medium is air with c_a = 340 m/s and ρ_a = 1.225 kg/m³. Time harmonic behaviour with e^jωt-dependence is considered, with j² = −1, angular frequency ω and time t.

FIGURE 1

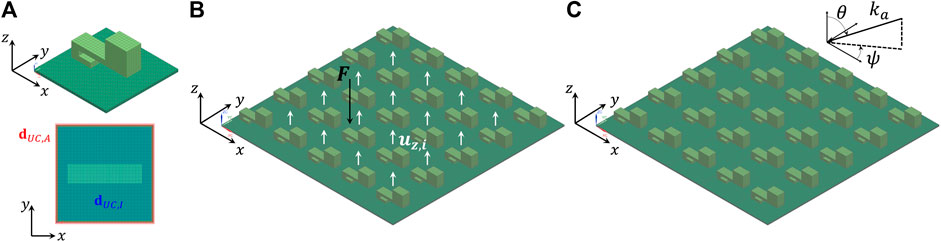
FIGURE 1. (A) LRM UC FE model (top) with highlighted interior (d_UC,I) and boundary (d_UC,A) DOFs (bottom), (B) finite LRM plate assembly composed of 5 × 5 UCs with input point force and output displacement locations and (C) with oblique acoustic plane wave excitation.

3 Methodology

In what follows, the sub-structuring approach is first recalled in Section 3.1. Next, the MOR on UC level is explained in Section 3.2, using BMS for interior modal reduction and GBMS for additional boundary modal reduction. The global modal reduction on finite plate assembly level is discussed in Section 3.3. Eventually, the application of the ERA within the sub-structuring MOR approach is explained in Section 3.4.

3.1 Sub-structured assembly of UCs

Consider a 2D periodic rectangular LRM plate composed of N_x × N_y identical UCs (Figure 1), modelled using the FE method. For the s-th UC FE model containing n_UC DOFs, the time-harmonic equations of motion of the UC FOM read as:

$\left({\mathbf{K}}_{UC}-{\omega }^2{\mathbf{M}}_{UC}\right){\mathbf{d}}_{UC}^{\left(s\right)}={\mathbf{F}}_{UC}^{\left(s\right)},(1)$

With the (n_UC × 1) UC DOF vector ${\mathbf{d}}_{UC}^{(s)}$ and generalized force vector ${\mathbf{F}}_{UC}^{(s)}$, the (n_UC × n_UC) UC mass matrix M_UC and (complex) stiffness matrix K_UC and the e^jωt-dependence omitted for readability. For sake of simplicity, only frequency-independent structural damping is considered in this work by considering a complex K_UC, although the methodology can be extended to general (viscous) damping (Rouleau et al., 2017; Allen et al., 2020; Aladwani et al., 2022). While M_UC and K_UC are identical for all UCs, this does not necessarily hold for ${\mathbf{F}}_{UC}^{(s)}$, since the periodic finite plate can be subjected to an arbitrary and distributed load. The system of equations of the 2D periodic finite rectangular LRM plate are retrieved by assembling the UC system of equations as follows (Gruber and Rixen, 2016; Allen et al., 2020; Mencik, 2021):

$\mathbf{K}=\sum _s{{\mathbf{L}}_s}^T{\mathbf{K}}_{UC}{\mathbf{L}}_s,\mathbf{M}=\sum _s{{\mathbf{L}}_s}^T{\mathbf{M}}_{UC}{\mathbf{L}}_s,\mathbf{F}=\sum _s{{\mathbf{L}}_s}^T{\mathbf{F}}_{UC}^{\left(s\right)},(2)$

with L_s the Boolean localization matrices of the N_x × N_y UCs and superscript T denoting the transpose, leading to the following system of equations for the finite LRM plate assembly FOM:

$\left(\mathbf{K}-{\omega }^2\mathbf{M}\right)\mathbf{d}=\mathbf{F}.(3)$

3.2 UC model reduction

Since the full order finite plate assembly system of equations of Eq. 3 rapidly becomes very large with increasing N_x × N_y and for fine FE UC models, model reduction is applied first on single UC level, exploiting the periodicity at hand. To this end, a single UC reduction basis V_UC is constructed, which allows expressing the original UC DOFs ${\mathbf{d}}_{UC}^{(s)}$ in terms of a reduced set of UC DOFs ${\tilde{\mathbf{d}}}_{UC}^{(s)}$ by projection, and applied to the UC FOM to set up a UC ROM as follows:

${\mathbf{d}}_{UC}^{\left(s\right)}={\mathbf{V}}_{UC}{\tilde{\mathbf{d}}}_{UC}^{\left(s\right)}\Rightarrow \left({\tilde{\mathbf{K}}}_{UC}-{\omega }^2{\tilde{\mathbf{M}}}_{UC}\right){\tilde{\mathbf{d}}}_{UC}^{\left(s\right)}={\tilde{\mathbf{F}}}_{UC}^{\left(s\right)},(4)$

with:

${\tilde{\mathbf{K}}}_{UC}={\mathbf{V}}_{UC}^T{\mathbf{K}}_{UC}{\mathbf{V}}_{UC},{\tilde{\mathbf{M}}}_{UC}={\mathbf{V}}_{UC}^T{\mathbf{M}}_{UC}{\mathbf{V}}_{UC},{\tilde{\mathbf{F}}}_{UC}^{\left(s\right)}={\mathbf{V}}_{UC}^T{\mathbf{F}}_{UC}^{\left(s\right)}.(5)$

Although ${\tilde{\mathbf{K}}}_{UC}$ and ${\tilde{\mathbf{M}}}_{UC}$ only need to be calculated once to represent all identical UCs, it is noted that ${\tilde{\mathbf{F}}}_{UC}^{(s)}$ is calculated per UC separately in case ${\mathbf{F}}_{UC}^{(s)}$ is not identical for all UCs. In particular, if a localized force input in one UC is considered, ${\tilde{\mathbf{F}}}_{UC}^{(s)}$ has to be calculated for that UC only, setting the other ${\tilde{\mathbf{F}}}_{UC}^{(s)}$ to zero. Instead, if multiple UCs are subjected to a load or if different loads apply for different frequencies, the corresponding ${\tilde{\mathbf{F}}}_{UC}^{(s)}$ can be computed simultaneously by stacking the n_f loads ${\mathbf{F}}_{UC}^{(s)}$ in the columns of an n_UC × n_f load matrix and pre-multiplying it with the UC reduction basis V_UC. To determine V_UC, the interior UC DOFs are reduced following the BMS (Krattiger and Hussein, 2014), corresponding to a classical Craig-Bampton reduction. Next, the GBMS (Krattiger and Hussein, 2018), which embeds the BMS as a first step, allows to reduce the remaining boundary UC DOFs. These steps are now explained.

3.2.1 Interior UC modal reduction using BMS

To reduce the interior UC DOFs following the BMS approach, the UC DOFs and matrices are partitioned into the n_I interior (d_UC,I) and n_A boundary (d_UC,A) DOFs (with n_UC = n_I + n_A) (Figure 1A):

$\left(\left[\begin{array}{cc}\hfill {\mathbf{K}}_{UC,II}\hfill & \hfill {\mathbf{K}}_{UC,IA}\hfill \\ \hfill {\mathbf{K}}_{UC,AI}\hfill & \hfill {\mathbf{K}}_{UC,AA}\hfill \end{array}\right]-{\omega }^2\left[\begin{array}{cc}\hfill {\mathbf{M}}_{UC,II}\hfill & \hfill {\mathbf{M}}_{UC,IA}\hfill \\ \hfill {\mathbf{M}}_{UC,AI}\hfill & \hfill {\mathbf{M}}_{UC,AA}\hfill \end{array}\right]\right)\left\{\begin{array}{c}\hfill {\mathbf{d}}_{UC,I}\hfill \\ \hfill {\mathbf{d}}_{UC,A}\hfill \end{array}\right\}=\left\{\begin{array}{c}\hfill {\mathbf{F}}_{UC,I}\hfill \\ \hfill {\mathbf{F}}_{UC,A}\hfill \end{array}\right\}.(6)$

Next, a single reduction basis V_UC is set up by representing the interior UC DOFs by a superposition of a set of fixed interface normal interior modes Φ_UC,I and a set of static constraint modes Ψ_UC,IA (Krattiger and Hussein, 2018; Krattiger et al., 2019):

${\mathbf{V}}_{UC}=\left[\begin{array}{cc}\hfill {\mathbf{\Phi }}_{UC,I}\hfill & \hfill {\mathbf{\Psi }}_{UC,IA}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{I}\hfill \end{array}\right],\left\{\begin{array}{c}\hfill {\mathbf{d}}_{UC,I}\hfill \\ \hfill {\mathbf{d}}_{UC,A}\hfill \end{array}\right\}=\left[\begin{array}{cc}\hfill {\mathbf{\Phi }}_{UC,I}\hfill & \hfill {\mathbf{\Psi }}_{UC,IA}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{I}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {\tilde{\mathbf{d}}}_{UC,I}\hfill \\ \hfill {\mathbf{d}}_{UC,A}\hfill \end{array}\right\}(7)$

where ${\tilde{\mathbf{d}}}_{UC,I}$ is a reduced set of interior modal UC DOFs corresponding to the UC interior modes and

$\left({\mathbf{K}}_{UC,II}-{\omega }_{UC,I,i}^2{\mathbf{M}}_{UC,II}\right){\varphi }_{UC,I}^i=\mathbf{0}\mathrm{a}\mathrm{n}\mathrm{d}{\mathbf{\Psi }}_{UC,IA}=-{\mathbf{K}}_{UC,II}^{-1}{\mathbf{K}}_{UC,IA},(8)$

with ${\mathbf{\Phi }}_{UC,I}=\left[{\varphi }_{UC,I}^1{\varphi }_{UC,I}^2\dots {\varphi }_{UC,I}^{n_I^{\varphi }}\right]$ and $n_I^{\varphi }\ll n_I$ is the truncated number of included interior modes, typically determined using frequency-based mode selection: e.g. the lowest-frequency modes up to twice the maximum frequency of interest. This reduction basis V_UC is next used to reduce the UC model matrices by projection:

${\mathcal{K}}_{UC}={\mathbf{V}}_{UC}^T{\mathbf{K}}_{UC}{\mathbf{V}}_{UC},{\mathcal{M}}_{UC}={\mathbf{V}}_{UC}^T{\mathbf{M}}_{UC}{\mathbf{V}}_{UC}(9)$

3.2.2 Boundary UC modal reduction using GBMS

Following the interior modal UC MOR, a large number of UC boundary DOFs n_A can potentially remain, which would still lead to large model sizes for the finite plate assembly of UC ROMs especially when using refined UC FE models. Therefore, the GBMS is used, which embeds the BMS as a first step, to also perform local boundary modal reduction on single UC level to additionally reduce the remaining UC boundary DOFs. This is done by calculating a set of normal boundary modes Φ_UC,A based on the submatrices ${\mathcal{K}}_{UC,AA}$ and ${\mathcal{M}}_{UC,AA}$ resulting from Eq. 9 as follows:

$\left({\mathcal{K}}_{UC,AA}-{\omega }_{UC,A,i}^2{\mathcal{M}}_{UC,AA}\right){\varphi }_{UC,A}^i=\mathbf{0},(10)$

with ${\mathbf{\Phi }}_{UC,A}=\left[{\varphi }_{UC,A}^1{\varphi }_{UC,A}^2\dots {\varphi }_{UC,A}^{n_A^{\varphi }}\right]$ and $n_A^{\varphi }\ll n_A$ is the truncated number of included UC boundary modes. This number is typically determined by trial and error since frequency-based truncation has been found to be less straightforward (Krattiger and Hussein, 2018). To allow compatibility between the boundaries of neighboring UCs in the finite plate assembly, augmented mode sets for the corresponding neighboring boundaries of the adjacent sub-structures would need to be considered as discussed in (Krattiger et al., 2019). However, exploiting the periodicity at hand, this can now be done using the boundary modes Φ_UC,A of the single UC alone. To this end, the GBMS approach is further followed (Krattiger and Hussein, 2018): after partitioning Φ_UC,A according to the corresponding UC DOF groups on left and right sides, bottom and top sides and bottom-left, bottom-right, top-left and top-right corners of the UC for the assembly, the corresponding UC boundary mode partitions are respectively combined and orthogonalized using a singular value decomposition (SVD) before combining them in the final boundary projection matrix B_UC,A. Eventually, the reduction basis V_UC of Eq. 7 is extended with B_UC,A to incorporate the boundary reduction (Krattiger and Hussein, 2018; Krattiger et al., 2019):

${\mathbf{V}}_{UC}=\left[\begin{array}{cc}\hfill {\mathbf{\Phi }}_{UC,I}\hfill & \hfill {\mathbf{\Psi }}_{UC,IA}{\mathbf{B}}_{UC,A}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{B}}_{UC,A}\hfill \end{array}\right],\left\{\begin{array}{c}\hfill {\mathbf{d}}_{UC,I}\hfill \\ \hfill {\mathbf{d}}_{UC,A}\hfill \end{array}\right\}=\left[\begin{array}{cc}\hfill {\mathbf{\Phi }}_{UC,I}\hfill & \hfill {\mathbf{\Psi }}_{UC,IA}{\mathbf{B}}_{UC,A}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{B}}_{UC,A}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {\tilde{\mathbf{d}}}_{UC,I}\hfill \\ \hfill {\tilde{\mathbf{d}}}_{UC,A}\hfill \end{array}\right\},(11)$

where ${\tilde{\mathbf{d}}}_{UC,A}$ is a reduced set of boundary modal UC DOFs corresponding to the UC boundary modes. The eventual UC ROM is obtained using this basis V_UC by projecting the UC FOM matrices per Eq. 5.

3.2.3 Assembly of the UC ROMs

The Boolean localization matrices ${\tilde{\mathbf{L}}}_s$ are updated according to the reduced UC DOFs and are used to create the finite plate assembly of UC ROMs as follows:

$\tilde{\mathbf{K}}=\sum _s{{\tilde{\mathbf{L}}}_s}^T{\tilde{\mathbf{K}}}_{UC}{\tilde{\mathbf{L}}}_s,\tilde{\mathbf{M}}=\sum _s{{\tilde{\mathbf{L}}}_s}^T{\tilde{\mathbf{M}}}_{UC}{\tilde{\mathbf{L}}}_s,\tilde{\mathbf{F}}=\sum _s{{\tilde{\mathbf{L}}}_s}^T{\tilde{\mathbf{F}}}_{UC}^{\left(s\right)}.(12)$

It is again noted that ${\tilde{\mathbf{K}}}_{UC}$ and ${\tilde{\mathbf{M}}}_{UC}$ are only calculated once, while for ${\tilde{\mathbf{F}}}_{UC}$ this depends on the load applied. The primal assembly of Eq. 12 enforces compatibility between the UCs by using the corresponding boundary DOFs for the adjacent sub-structures, either in terms of nodal UC boundary DOFs in case of BMS or in terms of reduced modal UC boundary DOFs in case of GBMS. The resulting system of equations for the assembly of UC ROMs reads as follows:

$\left(\tilde{\mathbf{K}}-{\omega }^2\tilde{\mathbf{M}}\right)\tilde{\mathbf{d}}=\tilde{\mathbf{F}}.(13)$

3.3 Global modal reduction of the assembly

Although applying UC MOR already allows to drastically reduce the model size of the finite plate assembly, the resulting system of equations can again become large when increasing the number of UCs. Therefore, an additional final global modal reduction step is applied by calculating a set of normal modes Φ_T for the assembly as follows, after application of boundary conditions to the plate boundaries, as in (Mencik, 2021):

$\left(\tilde{\mathbf{K}}-{\omega }_{T,i}^2\tilde{\mathbf{M}}\right){\varphi }_T^i=\mathbf{0},(14)$

with ${\mathbf{\Phi }}_T=\left[{\varphi }_T^1{\varphi }_T^2\dots {\varphi }_T^{n_T^{\varphi }}\right]$ where $n_T^{\varphi }$ is the truncated number of included global modes using a frequency-based mode selection: e.g. the lowest-frequency modes up to two times the maximum frequency of interest. Given the comparatively small size of $\tilde{\mathbf{K}}$ and $\tilde{\mathbf{M}}$, this modal calculation can be done much faster as compared to the finite plate assembly FOM. To further improve the projection basis, the set of normal modes Φ_T can be enriched with a static response for the applied load ${\mathbf{\Psi }}_T={\tilde{\mathbf{K}}}^{-1}\tilde{\mathbf{F}}$ which is afterwards mass-normalized with $\tilde{\mathbf{M}}$, leading to the global projection basis V_T = [Φ_T, Ψ_T]. In particular for localized excitations, this can enable better approximating the strong vibration attenuation inside the stop band frequency range. The system of equations of the global assembly is eventually reduced using V_T as in Eq. 5, resulting in the final globally reduced finite plate model:

$\left(\widehat{\mathbf{K}}-{\omega }^2\widehat{\mathbf{M}}\right)\widehat{\mathbf{d}}=\widehat{\mathbf{F}}.(15)$

After solving the system of equations for all frequencies of interest, the nodal responses are found via back-projection using V_T and V_UC.

3.4 Elementary radiator approach

To approximate the STL of the flat rectangular LRM plates using only structural FE models, the elementary radiator approach (ERA) proposed in (Jung et al., 2017) is applied. This method was shown to enable efficient STL approximations using structural FE models of finite, baffled flat plates, without requiring an expensive coupled vibro-acoustic analysis. Here, this method is employed in combination with the above outlined GBMS-based sub-structuring approach to accelerate STL analyses of baffled, finite periodic LRM plates based on structural UC FE models. In what follows, the method is briefly described.

Consider an oblique acoustic plane wave p_i with amplitude A = 1 Pa, which impinges upon the LRM plate, baffled in the xy-plane, along incidence angles θ and ψ (Figure 1C):

$p_i\left(x,y,z\right)=A{e}^{-\mathrm{j}\left(k_{ax}x+k_{ay}y+k_{az}z\right)},(16)$

with (k_ax, k_ay, k_az) = −k_a(sin θ cos ψ, sin θ sin ψ, cos θ) and k_a the acoustic wave number. The incident sound power on the baffled plate due to this oblique plane wave excitation is:

$P_i=\frac{S|A{|}^2}{2{\rho }_a{c}_a}\cos \theta ,(17)$

with S the area of the finite LRM plate. The acoustic plane wave excitation is applied to the structure as a blocked pressure excitation, while the radiation resistance of the acoustic medium is neglected since the mass density of the acoustic medium air is low. Corresponding to (Fahy, 2012; Yang et al., 2017), for each frequency ω, the blocked pressure is applied as lumped normal forces at the nodes of the LRM plate’s top face:

$F_{z,j}=2p_i\left(x_j,y_j,z_j\right)S_j,(18)$

with (x_j, y_j, z_j) the coordinates of node j, S_j the nodal area, and with the factor 2 arising from the blocked pressure field. This leads to the corresponding nodal external forcing vectors F(ω) for the finite LRM plate assembly FOM in Eq. 3. As shown in previous work by the authors (Van Belle et al., 2019) using a fully coupled vibro-acoustic LRM FE UC model, applying the acoustic excitation on the flat LRM plate’s top face while neglecting the presence of the sub-wavelength resonators has a negligible effect on the predicted STL and is hence applied here as such as well. In order to apply the UC model reduction, the loading vectors F(ω) for each frequency are first sub-structured into the corresponding UC force vector parts ${\mathbf{F}}_{UC}^{(s)}(\omega )$ using the L_s and stacked column-wise into one UC force matrix before being simultaneously reduced for all frequencies using the V_UC. For the global modal reduction step, the V_T is applied at once to the column-wise stacked reduced UC ROM assembly loading vectors $\tilde{\mathbf{F}}(\omega )$ for all frequencies.

After solving the reduced system of Eq. 15 for all frequencies and back-projection to obtain the LRM plate’s nodal responses d, the transmitted sound power is computed at each frequency ω of interest from the normal nodal displacement field u_z(x, y) of the flat bottom face of the LRM plate using the ERA. To this end, u_z(x, y) is first subsampled in a rectangular grid of n_p non-overlapping rectangular patches of equal dimensions, referred to as equivalent radiators, coarser than the FE mesh. The transmitted acoustic pressure p_t, evaluated at the radiating surface, is expressed as (Jung et al., 2017):

$p_t\left(x_p,y_p\right)=\sum _{q=1}^{n_p}{Z}_{pq}{v}_{z,q},(19)$

with p the index of the radiator position at which the pressure is computed, q the index of the radiators and v_z,q = v_z(x_q, y_q) = jωu_z(x_q, y_q) the normal velocity (interpolated) at the center of radiator q. Z_pq is the radiation impedance of the radiator, which is analytically computed as (Jung et al., 2017):

$Z_{pq}=\left\{\begin{array}{cc}{\rho }_a\mathrm{j}\omega \frac{e^{-\mathrm{j}{k}_a{R}_{pq}}}{2\pi R_{pq}}{S}_q\hfill & ,p\ne q\hfill \\ {\rho }_a{c}_a\left(1-e^{\text{j}{k}_a{r}_p}\right)\hfill & ,p=q\hfill \end{array}\right.\mathrm{a}\mathrm{n}\mathrm{d}{R}_{pq}=\sqrt{{\left(x_p-x_q\right)}^2+{\left(y_p-y_q\right)}^2}(20)$

with S_q the area of radiator q and $r_p=\sqrt{S_p/\pi }$ the equivalent radius of radiator p. As shown in (Jung et al., 2017, 2022), by considering a limited yet refined enough number of radiators, computing the radiated acoustic pressure this way provides a considerably more efficient yet accurate alternative to evaluating Rayleigh’s integral directly on the nodal velocity field v_z(x, y), particularly for refined FE meshes. Next, assuming identical radiator areas S₀, the transmitted sound power P_t is efficiently obtained as:

$P_t=\frac{1}{2}\sum _{p=1}^{n_p}\mathrm{R}\mathrm{e}\left\{p_t\left(x_p,y_p\right)v_z^{\ast }\left(x_q,y_q\right)\right\}{S}_p=\frac{S_0}{2}\mathrm{R}\mathrm{e}\left\{{\mathit{v}}_z^H\mathbf{Z}{\mathit{v}}_z\right\},(21)$

with superscripts * and H respectively denoting the complex conjugate and Hermitian transpose operators, Z the n_p × n_p radiation impedance matrix and ${\mathit{v}}_z={[v_{z,1}{v}_{z,2}\dots v_{z,n_p}]}^T$ the equivalent radiator velocities. With P_i and P_t known, the oblique STL at every frequency ω of interest is eventually calculated as:

$\mathrm{S}\mathrm{T}\mathrm{L}=-10{\log }_{10}\left(\tau \right)=-10{\log }_{10}\left(\frac{P_t}{P_i}\right),(22)$

with τ the sound power transmission coefficient. By considering multiple plane waves as multiple right hand sides in Eq. (14), and integrating the corresponding resulting oblique sound power transmission coefficients over the incidence angles, also the diffuse field STL can be computed. The ERA based STL results have been verified against fully coupled vibro-acoustic FE models in (Jung et al., 2017) and good agreement as well as high computational efficiency have been shown. Hence, the combination of ERA with fast structural response computations using the presented GBMS based sub-structuring approach in this work is proposed to enable further accelerating STL predictions of finite periodic LRM plates.

4 Results

In this section, the above described procedure is applied to a refined LRM UC FE model. After introducing the LRM design and finite plate configuration in Section 4.1, the eigenfrequency calculation on a UC and finite plate assembly level are compared when using the UC FOM as well as the UC ROMs obtained with BMS and GBMS in Section 4.2. Next, vibration responses are calculated for finite LRM plates for a point force excitation in Section 4.3, comparing model size, computational cost and accuracy. STL results for plane wave excitation are discussed in Section 4.4.

4.1 LRM description

The LRM design of (Van Belle et al., 2020) is considered, which consists of a 1 mm thick aluminium (Young’s modulus E = 70 GPa, mass density ρ = 2,700 kg/m³, Poisson’s ratio ν = 0.3) plate host structure with periodically added beam-shaped PMMA (Young’s modulus E = 4.85 GPa, mass density ρ = 1,188 kg/m³, Poisson’s ratio ν = 0.31) resonators with 0.03 × 0.03 m periodicity (Figure 1A). A constant damping loss factor η = 0.01 is considered for the entire structure in this work. The UC is discretized using 3,834 CHEXA8 linear solid elements, with a maximum element size of 1 mm and minimally three elements through the thickness of all parts. The UC FOM contains a total of 16,335 DOFs, with n_I = 14,871 and n_A = 1,464. As discussed in (Van Belle et al., 2020), the beam-shaped resonator is tuned with its first out-of-plane bending mode to a resonance frequency of 616 Hz and adds 39.8% mass to the host structure, which leads to a bending wave stop band between 597–656 Hz. The frequency range of interest in this work hence ranges up to a maximum frequency of 1,000 Hz.

To verify the accuracy and computational benefit of the MOR approach, a moderately sized finite LRM plate composed of 5 × 5 UCs (Figure 1B) and a larger 15 × 15 UC LRM plate are considered. A zero displacement boundary condition is imposed along the circumference of the finite plates. The resulting 5 × 5 UC plate FOM counts a total of 386,127 unknown DOFs, and the 15 × 15 UC plate FOM counts 3,497,007 unknown DOFs. The moderate 5 × 5 UC plate size allows a comparison of the ROMs with the finite LRM plate FOM within reasonable computation times, while the 15 × 15 UC plate similar to (Mencik, 2021) allows demonstrating the efficiency of the approach for larger LRM plates as compared to conventional global modal MOR.

4.2 Eigenfrequency analysis

Before assessing the vibro-acoustic forced response computations, the computation of the eigenfrequencies of the undamped UC ROMs and finite plate ROMs is first assessed for different $n_I^{\varphi }$ and $n_A^{\varphi }$ and the relative errors on these eigenfrequencies are computed against the corresponding FOMs.

4.2.1 UC level

To assess the UC ROMs, the first 20 eigenfrequencies of the free, undamped UC are computed and the non-zero eigenfrequencies are compared. First, only interior UC modal reduction is applied using the BMS, considering different amounts of interior UC modes $n_I^{\varphi }$ (Figure 2A). Choosing $n_I^{\varphi }=3$, corresponding to an interior modal frequency of 3,045.9 Hz or thus three times the maximum frequency of interest, already provides a relative error below 10⁻³ for the first three eigenfrequencies of the free UC, with f_3,FOM = 3,063.4 Hz. A further increase to $n_I^{\varphi }=10$ further decreases this error below 10⁻⁴ and is retained here and for the subsequent GBMS reduction.

FIGURE 2

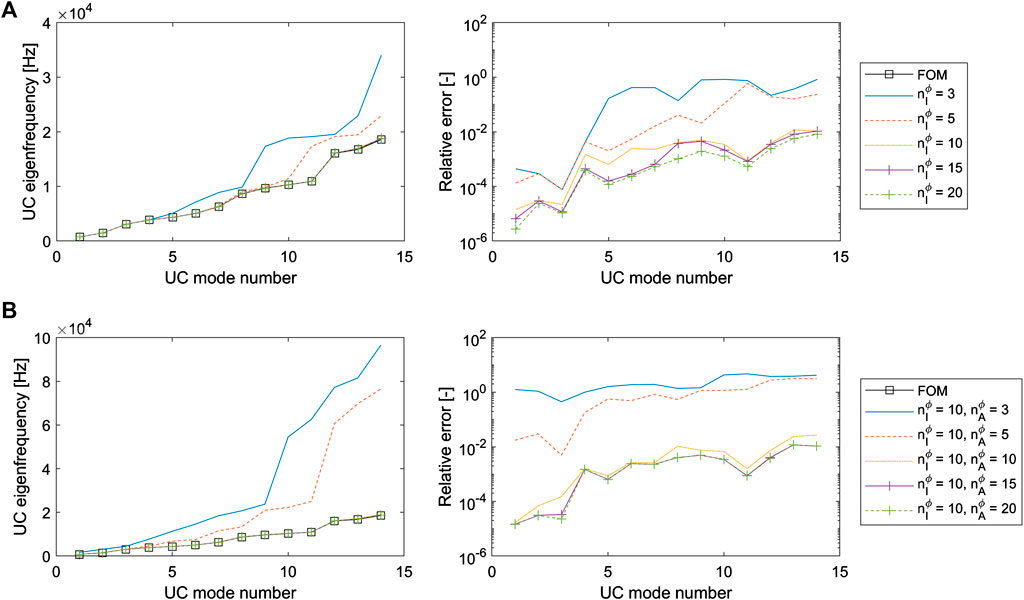
FIGURE 2. (A) Eigenfrequencies (left) and relative error of the eigenfrequencies (right) computed for the BMS reduced free UC, considering different $n_I^{\varphi }$. (B) Eigenfrequencies (left) and relative error of the eigenfrequencies (right) computed for the GBMS reduced free UC, considering $n_I^{\varphi }=10$ and different $n_A^{\varphi }$.

Next, also the UC boundary is reduced using the GBMS, considering $n_I^{\varphi }=10$ and different amounts of boundary UC modes $n_A^{\varphi }$ (Figure 2B). For $n_A^{\varphi }=3$ a high relative error is found. By increasing $n_A^{\varphi }$ to 5, the error for the first three eigenfrequencies of the free UC lowers to about 10⁻² and becomes acceptable. Eventually for $n_A^{\varphi }=15$, corresponding to a boundary modal frequency of 19,455 Hz, the error decreases further below 10⁻⁴ and approaches the error for the UC with only interior modal reduction.

4.2.2 Finite plate level

To assess the finite plate ROMs, the first 60 eigenfrequencies of the clamped, undamped finite LRM plate assembly of 5 × 5 UCs are computed, up to about twice the frequency range of interest of 1,000 Hz. This comes down to evaluating E. 14 on the assembly of UC FOMs or ROMs. Again, first only interior UC modal reduction is applied for different $n_I^{\varphi }$ before assembly and the eigenfrequencies and relative error thereof with respect to the FOM are assessed (Figure 3A). Already for $n_I^{\varphi }=3$, relative errors are achieved of around 10⁻² or lower for the eigenfrequencies below 2,000 Hz and of around 10⁻³ or lower for the eigenfrequencies below 1,000 Hz. Further increasing $n_I^{\varphi }$ to 10 further lowers this error to around 10⁻⁴ or lower below 2,000 Hz and to around 10⁻⁵ or lower below 1,000 Hz. This corresponds well to the observations in Figures 2A, 2is in line with the accuracy expected for regular Craig-Bampton based sub-structuring. It is noted that around 600 Hz and 1,200 Hz, many modes are present around the same frequency (Figure 3A left). This is due to the accumulation of modes with in-phase resonator motion which happens right before a stop band (Claeys et al., 2013, Claeys et al., 2014), with this LRM having a stop band around 600 Hz and a directional stop band around 1,200 Hz (Van Belle et al., 2017). The more localized nature of these modes due to the resonators also leads to a lower relative error on these predicted eigenfrequencies, which highlights the representativeness of the interior UC modal basis for these localized effects.

FIGURE 3

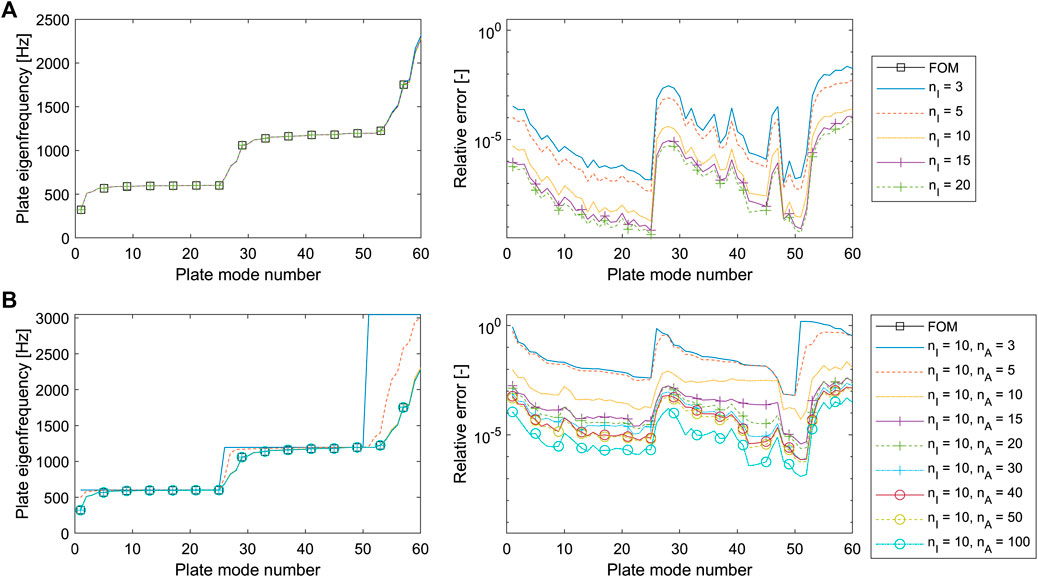
FIGURE 3. (A) Eigenfrequencies (left) and relative error of the eigenfrequencies (right) computed for the clamped finite plate assembly of 5 × 5 BMS UC ROMs, considering different $n_I^{\varphi }$. (B) Eigenfrequencies (left) and relative error of the eigenfrequencies (right) computed for the clamped finite plate assembly of 5 × 5 GBMS UC ROMs, considering $n_I^{\varphi }=10$ and different $n_A^{\varphi }$.

Next, the finite plate assembly of GBMS UC ROMs is assessed, considering $n_I^{\varphi }=10$ and different $n_A^{\varphi }$ (Figure 3B). High relative errors are found for $n_A^{\varphi }=3$ and $n_A^{\varphi }=5$. For $n_A^{\varphi }=15$, relative errors of around 10⁻³ or lower are found. These are higher than the corresponding errors found for the free UC modes (Figure 2B), which were below 10⁻⁴ for the same frequency region. This increase in error for the assembly of GBMS UC ROMs as compared to the free UC ROMs is expected, since the UC boundary modes are calculated for the uncoupled UCs and thus neglect the mass and stiffness coupling with the adjacent UCs, thereby only approximately enforcing the coupling upon assembly as explained in (Krattiger et al., 2019). Even though the error for $n_A^{\varphi }=15$ is now acceptable, $n_A^{\varphi }$ can be further increased to reduce this error, with $n_A^{\varphi }=100$ again leading to a similar error as for the free UC modes. At low frequencies and right after the (directional) stop bands, where the modes are of more global plate-level nature, higher errors are observed. This reduced accuracy can be attributed to the local nature of the UC reduction, which does not account for the system-level mass and stiffness coupling between the UCs in the finite plate assembly.

Table 1 gives an overview of the model sizes and timings for the FOM, BMS and GBMS UC based sub-structured clamped finite LRM plate’s modal calculation for the first 60 eigenmodes. All computations were performed on a Intel Xeon Gold 6240 CPU with 192 GB RAM. Where the BMS with $n_I^{\varphi }=10$ reduces the model size with a factor 26 and reduces the total computation time by half as compared to the FOM, the additional UC boundary reduction with the GBMS allows to further significantly reduce the model size and required computation time, even for an increased $n_A^{\varphi }$, with the UC boundary reduction taking only very limited additional time for the here considered case. It is noted that the ratio of interior to boundary UC dofs can have an important impact on the efficiency of the GBMS (Cool et al., 2022).

TABLE 1

TABLE 1. Overview of 5 × 5 UC finite LRM plate FOM, BMS and GBMS based model sizes and computational times required for the model reduction, assembly and eigenmodes calculation.

The additional benefit of the UC boundary reduction in the GBMS based approach is emphasized when considering a larger, 15 × 15 UC assembly and computing the first 564 eigenmodes (Table 2) up to about twice the frequency range of interest of 1,000 Hz. Where for the 5 × 5 UC assembly, the total computation time to obtain the eigenmodes up to twice the frequency range of interest is about factor 4 faster with GBMS $(n_A^{\varphi }=100)$ as compared to BMS, this speed-up increases to about a factor 12 for the 15 × 15 UC plate, despite the computation of a higher number of finite plate modes. Compared to the FOM, the GBMS $(n_A^{\varphi }=100)$ is about 24 times faster for this 15 × 15 UC plate, which is a significant speed-up as compared to the speed-up with about factor 8 for the smaller, 5 × 5 UC plate. It is noted that, although the GBMS allows increasingly faster eigenmode computations than the FOM and BMS with an increasing number of UCs in the finite plate assembly, an a priori assessment of the required $n_A^{\varphi }$ is more difficult and requires some iterations due to the absence of a clear frequency-based mode selection criterion (Krattiger and Hussein, 2018). This should be accounted for in setting up the GBMS based ROM.

TABLE 2

TABLE 2. Overview of 15 × 15 UC finite LRM plate FOM, BMS and GBMS based model sizes and computational times required for the model reduction, assembly and eigenmodes calculation.

4.3 Forced vibration response

For the forced response analysis, first the 5 × 5 UC finite LRM plate is considered. The plate is excited by a point force with magnitude F_z = 1 N in the out-of-plane direction at (x, y, z) = (4.15, 5.3, 0) cm, in the second UC along the x- and y-direction (Figure 1B). The RMS out-of-plane displacement response u_z at the UC corners of the plate’s top face is calculated for frequencies 1–1,000 Hz with a 1 Hz step and the relative errors of the RMS responses of the finite plate ROMs are computed with respect to the finite plate FOM (Figure 4). In total, six different models are considered: FOM, FOM with global MOR, BMS based ROM $(n_I^{\varphi }=10)$, BMS based ROM with global MOR, GBMS based ROM $(n_I^{\varphi }=10,n_A^{\varphi }=100)$ and GBMS based ROM with global MOR. For the global modal reduction in these models, $n_T^{\varphi }=59$ is considered, with the highest frequency 2,119 Hz corresponding to at least two times the maximum frequency of interest, and static enrichment is applied given the single point force excitation. As discussed in Section 4.2.2, due to the accumulation of modes before (directional) stop bands in the frequency range up to 2,000 Hz, the number of global modes to be included for LRM plates can be considerably higher as compared to bare plate counterparts and also increases with the amount of resonators and resonant modes in the considered frequency range (Claeys et al., 2013, 2014). The model sizes and total computation times for the forced vibration responses are listed in Table 3. The models with global MOR have the same amount of DOFs.

FIGURE 4

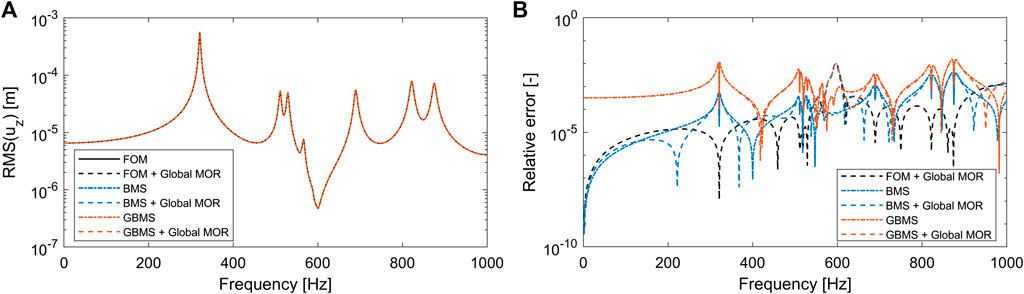
FIGURE 4. Forced vibration frequency responses (A) and relative error thereof with respect to the FOM (B) computed for the clamped finite plate assembly of 5 × 5 UCs for different ROMs. The good agreement between the results causes the frequency responses (A) to appear on top of each other.

TABLE 3

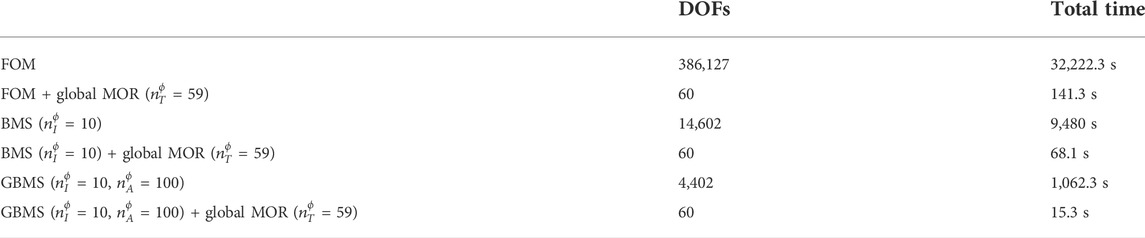
TABLE 3. Overview of FOM, BMS and GBMS UC based finite LRM plate model sizes for the clamped finite plate assembly of 5 × 5 UCs and total computational times required for the forced vibration response.

The frequency responses show very good agreement, with the stop band around 600 Hz clearly leading to vibration attenuation (Figure 4A). Overall, the BMS ROMs show good accuracy, similar to FOM with global MOR, with relative errors around 10⁻³ or lower (Figure 4B). As was observed for the finite assembly eigenfrequencies, GBMS leads to a slightly higher overall error of around 10⁻² or lower, but still shows good agreement with the other models, especially around the stop band frequency zone of interest, where the errors of around 10⁻³ are lower. At low frequencies, where the response is dominated by the plate stiffness and where the wavelengths of the subsequent vibration modes are typically large, the higher errors of the GBMS might arise from the deviation of the assembly-level stiffness due to the local UC boundary modal reduction which neglects the mass and stiffness coupling with the adjacent UCs. It is noted that, inside the stop band, applying global MOR leads to slightly lower accuracy for all models for this concentrated point force excitation. This might arise from the high attenuation inside the stop band, which could require a even higher $n_T^{\varphi }$ to better approximate the strongly spatially decaying response.

When comparing the forced response computation times of the finite plate models with global MOR applied (Table 3), the UC boundary reduction of the GBMS based UC MOR clearly allows a considerable additional computation time reduction as compared to only interior UC reduction of the BMS based UC MOR, with over a factor 4. This is attributed to the further reduced system size after assembly of the UC ROMs which hence enables a faster global reduction step, while the computation time for UC interior and consecutive boundary reduction is small (Figure 5), as also discussed in previous section. It is noted that, in all cases, the small system size after global reduction allows a fast frequency solution.

FIGURE 5

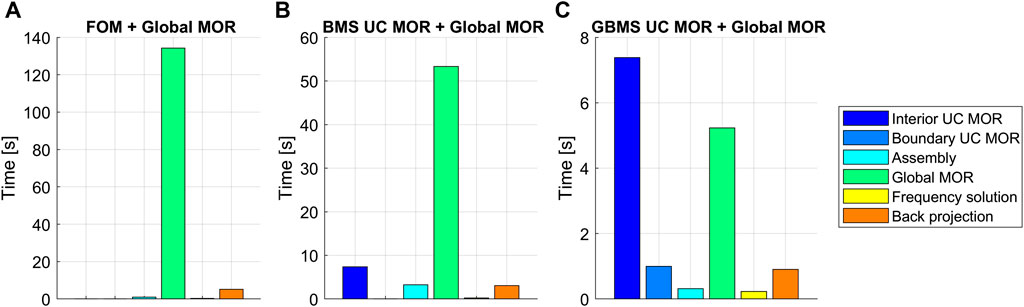
FIGURE 5. Overview of the computation times for the forced vibration response calculations of the clamped finite LRM plate assembly of 5 × 5 UCs for the FOM (A), BMS (B) and GBMS (C) based UC ROMs, all applying global MOR. The time ranges on the vertical axis differ per case for readability.

Another significant advantage of particularly the GBMS UC MOR is that, due to the smaller assembly system size, considerably less memory is required to perform the global reduction step. Especially for finite LRM plates with many UCs, this property of sub-structuring forms an important improvement and is further leveraged here by only considering a single UC. Apart from the larger system size, the typical accumulation of modes near the stop band which directly depends on the number of resonators and thus UCs also requires an increasingly higher $n_T^{\varphi }$ with increasing numbers of UCs and amount of resonant modes in the frequency range of interest.

To further illustrate the benefit of the GBMS UC MOR in combination with global modal MOR, consider the larger clamped finite LRM plate with 15 × 15 UCs. The plate is again excited by a unit point force in the out-of-plane direction, this time at (x, y, z) = (20.3, 19.15, 0) cm in the seventh UC along the x- and y-direction. The RMS out-of-plane displacement response u_z at the UC corners of the plate’s top face is calculated for frequencies 1–1,000 Hz with a 1 Hz step. To include the modes up to twice the frequency range of interest of 1,000 Hz for this LRM plate with 225 resonators, a significantly higher amount $n_T^{\varphi }=564$ is required, with a maximum frequency of 2,014 Hz. Directly applying global MOR with 564 modes and static enrichment to the FOM leads to a high computation time for the frequency response calculation (Table 4). The BMS based UC MOR with $n_I^{\varphi }=10$ and global MOR is over 2 times faster than the FOM with global MOR, which is a similar speed-up as for the 5 × 5 UC LRM plate. Instead, the GBMS based UC MOR with the same $n_I^{\varphi }=10,n_A^{\varphi }=100$ and global MOR is over 25 times faster than the FOM with global MOR, which is more than twice the speed-up as compared to the 5 × 5 UC LRM plate. These observations correspond well to the results for the eigenmode computations in Section 4.2.2, indicating that the GBMS UC MOR especially enables faster computations due to a faster global modal MOR step.

TABLE 4

TABLE 4. Overview of FOM, BMS and GBMS UC based finite LRM plate model sizes for the clamped finite plate assembly of 15 × 15 UCs and total computational times required to calculate the forced vibration responses of Figure 6.

Comparing the vibration responses for this 15 × 15 UC LRM plate computed with the FOM, BMS and GBMS, all combined with global MOR, good agreement is obtained (Figure 6A). For this larger LRM plate, a more prominent vibration attenuation is also observed around the predicted stop band. The relative errors of the vibration response (Figure 6B), this time computed with respect to the FOM with global MOR, lead to similar observations as for the 5 × 5 UC plate: the BMS with global MOR is more accurate than the GBMS with global MOR, except around the stop band where the accuracy is comparable. The considerably faster GBMS with global MOR leads to an overall error of around 10⁻² or lower, while the error in and around stop band is about 10⁻³. As expected, somewhat higher errors again occur for the GBMS at lower frequencies due to the nature of the local UC boundary mode reduction.

FIGURE 6

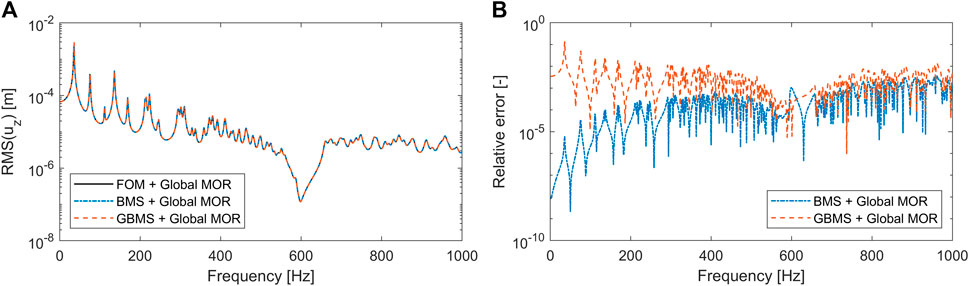
FIGURE 6. Forced vibration frequency responses (A) and relative error with respect to the FOM + global MOR (B) computed for the clamped finite plate assembly of 15 × 15 UCs for different ROMs. The good agreement between the results causes the frequency responses (A) to appear on top of each other.

4.4 Sound transmission loss

To demonstrate the fast STL computations by combining the proposed MOR approach with the ERA, first the clamped finite LRM plate composed of 5 × 5 UCs is again considered. The plate is now excited by an oblique incident plane wave at angles θ = 60°, ψ = 30° and the out-of-plane vibration response is computed for frequencies 20–1,000 Hz with a 5 Hz step. To obtain the STL, the ERA is applied, subdividing the out-of-plane nodal velocity field in a square grid of 10 × 10 square radiators with dimensions 1.5 × 1.5 cm². The latter corresponds to half the UC size in x- and y-directions, and is twice smaller than one tenth of the acoustic wavelength λ_a/10 = 3.4 cm at the maximum frequency of interest of 1,000 Hz. Although a procedure was introduced in (Jung et al., 2017) to optimize the amount of radiators depending on the frequency range, a constant and relatively fine grid was considered here for all frequencies.

For the MOR, the same settings as for the 5 × 5 UC LRM plate in Section 4.3 are applied, with exception of the static enrichment, since in this case the excitation is distributed and frequency-dependent. The latter would also lead to a different enrichment vector for each frequency, which would either result in a too large reduction basis or an inefficient frequency-dependent projection step. The STL results and corresponding relative errors as compared to the FOM are shown in Figure 7, while the model sizes and computation costs are summarized in Table 5. As expected for LRM partitions with bending wave stop bands (Van Belle et al., 2019), the STL shows a clear peak around 600 Hz, near the tuned resonator frequency, followed by a characteristic STL dip. The low-frequency STL dip around 270 Hz, corresponding to the first bending mode of the clamped plate, lies slightly below 0 dB, which is due to the underlying Rayleigh integral approximation made in the ERA in combination with the small sample size. However, despite its uncoupled nature, overall the ERA enables a representative STL prediction for the considered LRM plate configuration. As observed in previous section for the vibration response predictions, also the STL shows very good agreement between all models. This is expected, since the difference in STL between the models results from the difference in vibration responses obtained with the different ROMS. The highest absolute difference of each UC ROM based model is no larger than 0.6 dB as compared to the FOM and 0.1 dB as compared to the FOM with global MOR. The GBMS based ROMs are in good agreement with the BMS, in particular in and round the stop band frequency range of interest, but show slightly higher errors away from the stop band. All ROMs show a relative error of about 10⁻² or lower, with global MOR leading to a more outspoken accuracy reduction as compared to the vibration response. The latter might be attributed to the absence of static enrichment. Combined with reported mean errors arising from the ERA below 0.5 dB as compared to fully coupled vibro-acoustic FE modeling (Jung et al., 2017), the current MOR approach hence still enables accurate STL predictions.

FIGURE 7

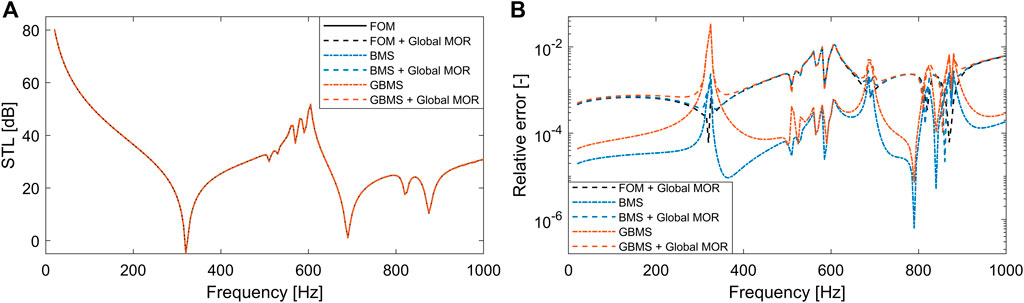
FIGURE 7. STL results (A) and relative error with respect to the FOM (B) computed for the clamped finite plate assembly of 5 × 5 UCs for different ROMs. The good agreement between the results causes the STL curves (A) to appear on top of each other.

TABLE 5

TABLE 5. Overview of FOM, BMS and GBMS UC based finite LRM plate model sizes for the clamped finite plate assembly of 5 × 5 UCs and total computational times required for the STL computations.

Comparing the model sizes and computation times in Table 5, it is again evident that the additional boundary reduction provided by the GBMS based MOR provides a significant advantage over only interior reduction in the case of BMS based MOR. In combination with global MOR, the GBMS based MOR achieves a speed-up of over a factor 3 as compared to the FOM with global MOR, and is over 2 times faster than BMS based MOR with global MOR. As illustrated in more detail in Figure 8, the apparent slightly lower speed-up of the GBMS and BMS with global MOR versus the FOM with global MOR for these STL computations as compared to the earlier vibration response computations is attributed to the fixed computation cost for the sound power evaluation using ERA, which takes about 15 s for this small 5 × 5 UC LRM plate. As no static enrichment is included for the STL computations, the global MOR step which includes the basis construction and the projection takes less time as compared to the vibration response computations for the point force loading (Figure 5). The simultaneous projection of as many loading vectors as frequencies, due to the frequency-dependency of the blocked pressure field, does not come at a high computation cost. Using the GBMS with global MOR, the cost of reducing and solving the model becomes comparable to the low cost associated with the ERA, which was already reported in detail in (Jung et al., 2017, Jung et al., 2022), while obtaining accurate predictions.

FIGURE 8

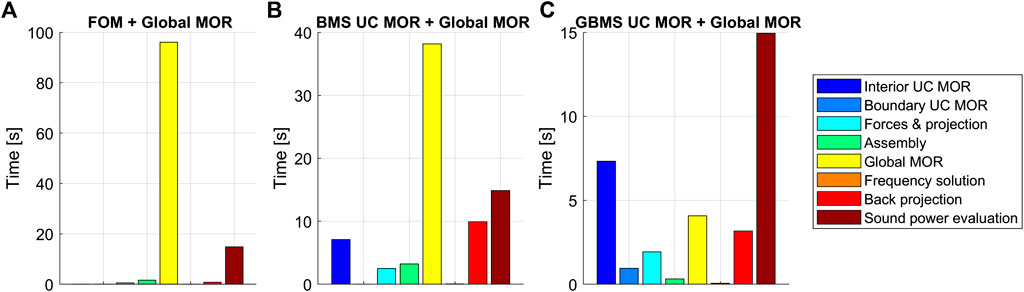
FIGURE 8. Overview of the computation times for the STL calculations of the clamped finite LRM plate assembly of 5 × 5 UCs for the FOM (A), BMS (B) and GBMS (C) based UC ROMs, all applying global MOR. The time ranges on the vertical axis differ per case for readability.

As shown earlier for the concentrated point force excitation, the acceleration of the STL predictions when using the GBMS based MOR with global reduction as compared to the BMS with global MOR and FOM with global MOR becomes even more outspoken when considering a larger 15 × 15 UC LRM plate. The STL is again computed for frequencies 20–1,000 Hz with a 5 Hz step for the same oblique plane wave excitation as before, using FOM with global MOR, BMS with global MOR and GBMS with global MOR (Figure 9). The same MOR settings as for the 15 × 15 UC LRM plate in Section 4.3 are applied, without static enrichment, and the relative error is computed against the STL results of the FOM with global MOR.

FIGURE 9

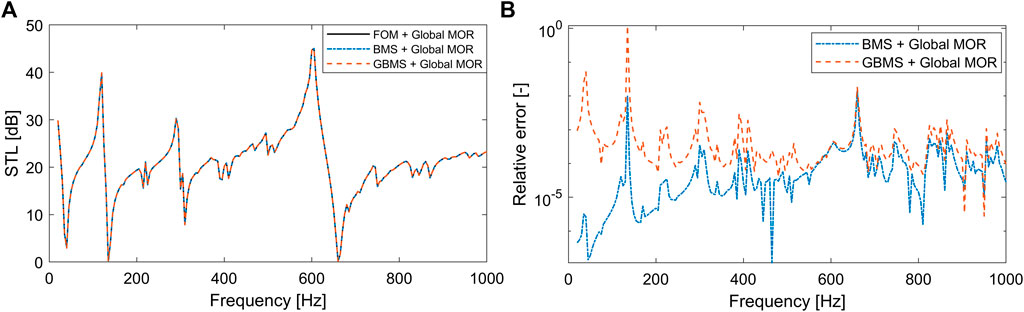
FIGURE 9. STL results (A) and relative error with respect to the FOM + global MOR (B) computed for the clamped finite plate assembly of 15 × 15 UCs for different ROMs. The good agreement between the results causes the STL curves (A) to appear on top of each other.

As expected based on the vibration response predictions, good agreement between the STL predictions of the different models is also obtained. Due to the larger plate size, the stiffness region in the STL is clearly shifted to lower frequencies, while the STL peak and dip around the stop band are more prominent. The GBMS attains an overall accuracy of around 10⁻² and lower, with some exceptions at low around global modes where the STL reaches values close to 0 dB. At low frequencies, the approximation due to the local UC boundary reduction of the GBMS again leads to somewhat higher errors. As before, the BMS is overall more accurate than the GBMS, apart from the stop band region. However, as shown in Table 6, for this larger plate assembly, the GBMS provides a substantial speed-up as compared to the BMS thanks to the additional UC boundary reduction, which is again a higher gain as compared to the smaller 5 × 5 UC LRM plate. For this 15 × 15 UC LRM plate, the ERA based sound power evaluation step takes about 155 s. Combined with the GBMS, fast and accurate STL predictions of finite periodic LRM plates are hence possible.

TABLE 6

TABLE 6. Overview of FOM, BMS and GBMS UC based finite LRM plate model sizes for the clamped finite plate assembly of 15 × 15 UCs and total computational times required to calculate the STL results of Figure 9.

It is noted that, although the GBMS with global MOR provides an advantage as compared to BMS with global MOR or FOM with global MOR for an increasing number of UCs in the finite plate assembly, the UC ROM assembly as well as the required $n_T^{\varphi }$ will also further increase. Hence, for very large finite plate assemblies composed of a large amount of UCs, further improvements of the vibration response computation might be required.

5 Conclusion

In this paper, a Generalized Bloch Mode Synthesis based sub-structuring approach was presented for fast forced vibro-acoustic response computations of finite periodic locally resonant metamaterial plates composed of periodically repeated, identical unit cells and applied to a locally resonant metamaterial design. Contrary to classical sub-structuring, the proposed method exploits the periodicity at hand by only considering a single unit cell model. By combining the structural unit cell assembly model with an Elementary Radiator Approach, also the sound transmission loss can be computed based on the forced vibration response for distributed acoustic loading. Compared to a regular Craig-Bampton based sub-structuring approach which only applies interior modal reduction to the unit cell, as also applied in the Bloch Mode Synthesis, the additional unit cell boundary modal reduction based on the Generalized Bloch Mode Synthesis was shown to enable considerable additional system size and computation time reduction for eigenmode computations and forced vibro-acoustic response computations, with only limited accuracy loss resulting from the uncoupled boundary modal computation based on just a single unit cell. The fast eigenmode computation on assembly level is particularly interesting when performing the additional global modal reduction for locally resonant metamaterials, due to the accumulation of eigenmodes around the stop band which requires a larger global modal basis. These unit cell based fast vibro-acoustic forced response computations can next be employed to accelerate the design and optimization of finite periodic locally resonant metamaterial plates, while accounting for their finite size and the boundary conditions.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

LVB has implemented the method and has run the simulations. All authors have contributed to the study conceptualization and design, analysis, manuscript writing and revision. All authors have read and approved the publication of the submitted version.

Funding

The research of LB is funded by a grant (no. 1271621N) from the Research Foundation—Flanders (FWO). Internal Funds KU Leuven were gratefully acknowledged for their support. The work leading to this publication has been partially funded by the project MOR4MDesign, which fits in the MacroModelMat (M3) research program, coordinated by Siemens (Siemens Digital Industries Software, Belgium) and funded by SIM (Strategic Initiative Materials in Flanders) and VLAIO (Flanders Innovation and Entrepreneurship Agency). The Research Foundation—Flanders (FWO) is gratefully acknowledged for its support of the FWO-FAPESP research project G0F9922N.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aladwani, A., Nouh, M., and Hussein, M. I. (2022). State-space Bloch mode synthesis for fast band-structure calculations of non-classically damped phononic materials. Comput. Methods Appl. Mech. Eng. 396, 115018. doi:10.1016/j.cma.2022.115018

CrossRef Full Text | Google Scholar

Allen, M. S., Rixen, D., Van der Seijs, M., Tiso, P., Abrahamsson, T., and Mayes, R. L. (2020). Substructuring in engineering dynamics. Heidelberg, Germany: Springer.

Google Scholar

Boukadia, R. F., Deckers, E., Claeys, C., Ichchou, M., and Desmet, W. (2020). “A rational Krylov subspace method for the unit cell modeling of 2D infinite periodic media,” in Proceedings of ISMA, September 7–9, 2020 (Leuven: KU Leuven, Mechanical Engineering, Division LMSD, Noise & Vibration Research Group).

Google Scholar

Boukadia, R. F., Droz, C., Ichchou, M. N., and Desmet, W. (2018). A Bloch wave reduction scheme for ultrafast band diagram and dynamic response computation in periodic structures. Finite Elem. Analysis Des. 148, 1–12. doi:10.1016/j.finel.2018.05.007

CrossRef Full Text | Google Scholar

Chang, K.-J., Jung, J., Kim, H.-G., Choi, D. R., and Wang, S. (2018). An application of acoustic metamaterial for reducing noise transfer through car body panels. Tech. rep. SAE Technical Paper.

CrossRef Full Text | Google Scholar

Claeys, C., Deckers, E., Pluymers, B., and Desmet, W. (2016). A lightweight vibro-acoustic metamaterial demonstrator: Numerical and experimental investigation. Mech. Syst. signal Process. 70, 853–880. doi:10.1016/j.ymssp.2015.08.029

CrossRef Full Text | Google Scholar

Claeys, C., Sas, P., and Desmet, W. (2014). On the acoustic radiation efficiency of local resonance based stop band materials. J. Sound Vib. 333, 3203–3213. doi:10.1016/j.jsv.2014.03.019

CrossRef Full Text | Google Scholar

Claeys, C., Vergote, K., Sas, P., and Desmet, W. (2013). On the potential of tuned resonators to obtain low-frequency vibrational stop bands in periodic panels. J. Sound Vib. 332, 1418–1436. doi:10.1016/j.jsv.2012.09.047

CrossRef Full Text | Google Scholar

Cool, V., Van Belle, L., Claeys, C., Deckers, E., and Desmet, W. (2022). Impact of the unit cell choice on the efficiency of dispersion curve calculations using generalized Bloch mode synthesis. J. Vib. Acoust. 144, 1-28. doi:10.1115/1.4051817

CrossRef Full Text | Google Scholar

de Melo Filho, N., Claeys, C., Deckers, E., and Desmet, W. (2020). Metamaterial foam core sandwich panel designed to attenuate the mass-spring-mass resonance sound transmission loss dip. Mech. Syst. Signal Process. 139, 106624. doi:10.1016/j.ymssp.2020.106624

CrossRef Full Text | Google Scholar

Deckers, E., Jonckheere, S., Van Belle, L., Claeys, C., and Desmet, W. (2018). Prediction of transmission, reflection and absorption coefficients of periodic structures using a hybrid wave based–finite element unit cell method. J. Comput. Phys. 356, 282–302. doi:10.1016/j.jcp.2017.12.001

CrossRef Full Text | Google Scholar

Decraene, C., Lombaert, G., and Reynders, E. P. (2022). Prediction of diffuse sound transmission through finite-sized periodic structures. J. Sound Vib. 528, 116851. doi:10.1016/j.jsv.2022.116851

CrossRef Full Text | Google Scholar

Droz, C., Robin, O., Ichchou, M., and Atalla, N. (2019). Improving sound transmission loss at ring frequency of a curved panel using tunable 3D-printed small-scale resonators. J. Acoust. Soc. Am. 145, EL72–EL78. doi:10.1121/1.5088036

PubMed Abstract | CrossRef Full Text | Google Scholar

Errico, F., Tufano, G., Robin, O., Guenfoud, N., Ichchou, M., and Atalla, N. (2019). Simulating the sound transmission loss of complex curved panels with attached noise control materials using periodic cell wavemodes. Appl. Acoust. 156, 21–28. doi:10.1016/j.apacoust.2019.06.027

CrossRef Full Text | Google Scholar

Fahy, F. J. (2012). Sound and structural vibration: Radiation, transmission and response. Massachusetts, United States: Academic Press.

Google Scholar

Gruber, F. M., and Rixen, D. J. (2016). Evaluation of substructure reduction techniques with fixed and free interfaces. Strojniški vestnik-Journal Mech. Eng. 62, 452–462. doi:10.5545/sv-jme.2016.3735

CrossRef Full Text | Google Scholar

Hussein, M. I., Leamy, M. J., and Ruzzene, M. (2014). Dynamics of phononic materials and structures: Historical origins, recent progress, and future outlook. Appl. Mech. Rev. 66, 040802. doi:10.1115/1.4026911

CrossRef Full Text | Google Scholar

Hussein, M. I. (2009). Reduced Bloch mode expansion for periodic media band structure calculations. Proc. R. Soc. A 465, 2825–2848. doi:10.1098/rspa.2008.0471

CrossRef Full Text | Google Scholar

Jung, J., Kook, J., and Goo, S. (2022). Maximizing sound transmission loss using thickness optimization based on the elementary radiator approach. Struct. Multidiscipl. Optim. 65 (4), 1–13. doi:10.1007/s00158-022-03228-7

CrossRef Full Text | Google Scholar

Jung, J., Kook, J., Goo, S., and Wang, S. (2017). Sound transmission analysis of plate structures using the finite element method and elementary radiator approach with radiator error index. Adv. Eng. Softw. 112, 1–15. doi:10.1016/j.advengsoft.2017.06.001

CrossRef Full Text | Google Scholar

Krattiger, D., and Hussein, M. I. (2014). Bloch mode synthesis: Ultrafast methodology for elastic band-structure calculations. Phys. Rev. E 90, 063306. doi:10.1103/physreve.90.063306

PubMed Abstract | CrossRef Full Text | Google Scholar

Krattiger, D., and Hussein, M. I. (2018). Generalized Bloch mode synthesis for accelerated calculation of elastic band structures. J. Comput. Phys. 357, 183–205. doi:10.1016/j.jcp.2017.12.016

CrossRef Full Text | Google Scholar

Krattiger, D., Wu, L., Zacharczuk, M., Buck, M., Kuether, R. J., Allen, M. S., et al. (2019). Interface reduction for Hurty/Craig-Bampton substructured models: Review and improvements. Mech. Syst. Signal Process. 114, 579–603. doi:10.1016/j.ymssp.2018.05.031

CrossRef Full Text | Google Scholar

Liu, Z., Zhang, X., Mao, Y., Zhu, Y., Yang, Z., Chan, C. T., et al. (2000). Locally resonant sonic materials. science 289, 1734–1736. doi:10.1126/science.289.5485.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

Mencik, J.-M., and Duhamel, D. (2021). “Dynamic analysis of periodic structures and metamaterials via wave approaches and finite element procedures,” in 8th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, June 28–30, 2021 (Athens, Greece: Institute of Structural Analysis and Antiseismic Research School of Civil Engineering, National Technical University of Athens (NTUA)).

CrossRef Full Text | Google Scholar

Mencik, J.-M. (2021). Model reduction based on matrix interpolation and distorted finite element meshes for dynamic analysis of 2D nearly periodic structures. Finite Elem. Analysis Des. 188, 103518. doi:10.1016/j.finel.2021.103518

CrossRef Full Text | Google Scholar

Mencik, J.-M. (2014). New advances in the forced response computation of periodic structures using the wave finite element (WFE) method. Comput. Mech. 54, 789–801. doi:10.1007/s00466-014-1033-1

CrossRef Full Text | Google Scholar

Palermo, A., and Marzani, A. (2020). A reduced Bloch operator finite element method for fast calculation of elastic complex band structures. Int. J. Solids Struct. 191, 601–613. doi:10.1016/j.ijsolstr.2019.12.011

CrossRef Full Text | Google Scholar

Pires, F. A., Wandel, M., Thomas, C., Deckers, E., Desmet, W., and Claeys, C. (2022). Improving the sound transmission loss of an aircraft ceiling panel by locally resonant metamaterials. Tech. rep. SAE Technical Paper.

Google Scholar

Rouleau, L., Deü, J.-F., and Legay, A. (2017). A comparison of model reduction techniques based on modal projection for structures with frequency-dependent damping. Mech. Syst. Signal Process. 90, 110–125. doi:10.1016/j.ymssp.2016.12.013

CrossRef Full Text | Google Scholar

Sangiuliano, L., Claeys, C., Deckers, E., and Desmet, W. (2020). Influence of boundary conditions on the stop band effect in finite locally resonant metamaterial beams. J. Sound Vib. 473, 115225. doi:10.1016/j.jsv.2020.115225

CrossRef Full Text | Google Scholar

Sangiuliano, L., Reff, B., Palandri, J., Wolf-Monheim, F., Pluymers, B., Deckers, E., et al. (2022). Low frequency tyre noise mitigation in a vehicle using metal 3D printed resonant metamaterials. Mech. Syst. Signal Process. 179, 109335. doi:10.1016/j.ymssp.2022.109335

CrossRef Full Text | Google Scholar

Song, Y., Wen, J., Tian, H., Lu, X., Li, Z., and Feng, L. (2020). Vibration and sound properties of metamaterial sandwich panels with periodically attached resonators: Simulation and experiment study. J. Sound Vib. 489, 115644. doi:10.1016/j.jsv.2020.115644

CrossRef Full Text | Google Scholar

Van Belle, L., Claeys, C., Deckers, E., and Desmet, W. (2017). On the impact of damping on the dispersion curves of a locally resonant metamaterial: Modelling and experimental validation. J. Sound Vib. 409, 1–23. doi:10.1016/j.jsv.2017.07.045

CrossRef Full Text | Google Scholar

Van Belle, L., Claeys, C., Deckers, E., and Desmet, W. (2019). The impact of damping on the sound transmission loss of locally resonant metamaterial plates. J. Sound Vib. 461, 114909. doi:10.1016/j.jsv.2019.114909

CrossRef Full Text | Google Scholar

Van Belle, L., de Melo Filho, N., Claeys, C., Deckers, E., Naets, F., Desmet, W., et al. (2020). Fast metamaterial design optimization using reduced order unit cell modeling. Proceedings of ISMA.

Google Scholar

van Ophem, S., Deckers, E., and Desmet, W. (2018). Efficient assembly of unit cells with Krylov based model order reduction. Proceedings of ISMA, September 17–19, 2018 (Leuven: KU Leuven, Mechanical Engineering), 445–456.

Google Scholar

Xi, C., and Zheng, H. (2021). Improving the generalized Bloch mode synthesis method using algebraic condensation. Comput. Methods Appl. Mech. Eng. 379, 113758. doi:10.1016/j.cma.2021.113758

CrossRef Full Text | Google Scholar

Xiao, Y., Wen, J., Wang, G., and Wen, X. (2013). Theoretical and experimental study of locally resonant and Bragg band gaps in flexural beams carrying periodic arrays of beam-like resonators. J. Vib. Acoust. 135, 041006. doi:10.1115/1.4024214

CrossRef Full Text | Google Scholar

Xiao, Y., Wen, J., and Wen, X. (2012). Sound transmission loss of metamaterial-based thin plates with multiple subwavelength arrays of attached resonators. J. Sound Vib. 331, 5408–5423. doi:10.1016/j.jsv.2012.07.016

CrossRef Full Text | Google Scholar

Yang, Y., Mace, B. R., and Kingan, M. J. (2017). Prediction of sound transmission through, and radiation from, panels using a wave and finite element method. J. Acoust. Soc. Am. 141, 2452–2460. doi:10.1121/1.4977925

PubMed Abstract | CrossRef Full Text | Google Scholar