Gear fault detection in gearboxes operated in non-stationary conditions based on variable sideband analysis without a tachometer

Introduction

Gearboxes are commonly used in mechanical drive systems, elevators, wind turbine systems, etc. In the industry, fault diagnosis of gearboxes plays an important role because of decreasing the downtime for production equipment and the extent of damages caused by failures. In recent advances, signal processing methods and measuring techniques have been applied to analyze vibrations to detect fault machine elements early in complicated systems, i.e., gearboxes. Signal processing methods include categories as follows: 1) the conventional method has been successfully applied in the industry with spectral analysis (Newland, 1993), cepstrum analysis (Randall, 2016), vibrational mode decomposition method (Wang et al., 2020), and morphological filtering (Yan et al., 2019); 2) several methods used the time–frequency analysis (Thakur et al., 2013) or the singular spectrum decomposition (Yan et al., 2020; Yan et al., 2021) that has been applied effectively to diagnosis machines in recent times; 3) the third group comprises new and complicated methods but has not yet been carried out in many experiments (Li and Liang, 2012). These methods are generally used to diagnose the failure of a gearbox operating with a steady or small change of rotational speed. Generally, gearboxes operate under fluctuating loads and variable rotational speeds, so traditional methods are unsuitable for applying these situations. Therefore, in recent years, time synchronous averaging (TSA) (Braun, 2011) has been commonly used to overcome these drawbacks. In this method, a measured vibration signal is split in each cycle; thus, the asynchronous component with the rotational speed of the shaft is removed, and the synchronous signal components are retained (Zhang and Hu, 2019). However, in this method, eliminating asynchronous components can mistakenly remove important information about these components. To overcome this, an order tracking method that removes asynchronous components without losing essential information is a better improvement based on resampling in the angular domain (Dien and Du, 2020). However, this technique requires a reference phase signal measured using a tachometer. It not only increases the cost of the system and causes inconvenience but also cannot set up the tachometer in the system in some individual cases.

This study proposes a simple cost-saving method by enhancing variable sidebands in time–frequency distribution to improve the diagnostic quality in non-stationary conditions. The proposed method is combined with many different methods and implemented in two steps as follows: 1) the damaged symptoms of the gearbox operating in unstable conditions are proposed, and the diagnostic solutions on the basis of the generalized Fourier transform are provided; 2) the wavelet synchronous compression method is used to sharpen the frequency–time distribution of the signal. Moreover, the proposed method has been verified by simulation and experiment, which shows good results and can be applied in the industry to reduce costs and quickly provide diagnostic results. Compared to the earlier works, the proposed method contains the following merits and novelties: 1) modeling the gearbox with failure operating in unstable conditions and providing diagnostic solutions; 2) combining several methods to find fault symptoms based only on the frequency–time distribution of the signal, and there is no need to use additional phase signals; and 3) providing a diagnostic process that uses less measuring equipment to predict failure of gears and obtaining quick and accurate results.

The remaining sections of this work are the following: the Fault symptoms of the gearbox operated in non-stationary conditions and solutions section presents fault symptoms and the solution to the gearbox operated in non-stationary conditions. The Principle of the proposed method section gives the principle of the proposed method. The Experiment evaluation section shows the verification of the proposed method by the experiment. Finally, conclusions are drawn in the Conclusion section.

Fault symptoms of the gearbox operated in non-stationary conditions and solutions

Amplitude modulation–frequency modulation (AM–FM) components are used to create a complex vibration signal measured on damaged gearboxes. A sine family, denoted by $x\left(t\right)$, is considered to illustrate the AM–FM signal, which is expressed as the following equation (Peng et al., 2011):

$x\left(t\right)=A\left(t\right)\cos \left(\phi \left(t\right)\right),(1)$

where $A\left(t\right)=A\left(1+B\cos \left(2\pi f_n\left(t\right)t\right)\right)$ presents the instantaneous amplitude and $\phi \left(t\right)=2\pi .Z.f_n\left(t\right)t+\varphi \left(t\right)$ is presentative for the instantaneous phase. In this case, $Z$ is the number of the tooth, and $\varphi \left(t\right)$ presents the FM function; f_n(t) is the shaft variable rotational frequency. Instantaneous frequency (IF) is expressed as the following equation (Peng et al., 2011):

$f\left(t\right)=\frac{1}{2\pi }\frac{d}{dt}\phi \left(t\right).(2)$

From Eqs 1, 2, the vibration signal is modulated as follows:

$x\left(t\right)=\underset{x_1\left(t\right)}{\underbrace{A\cos \left(2\pi .Z.f_n+\varphi \left(t\right)\right)}}+\underset{x_2\left(t\right)}{\underbrace{\frac{1}{2}AB\cos \left(2\pi \left(Z+1\right)f_{n}t+\varphi \left(t\right)\right)}}+\underset{x_3\left(t\right)}{\underbrace{\frac{1}{2}AB\cos \left(2\pi \left(Z-1\right)f_{n}t+\varphi \left(t\right)\right)}}$

$x\left(t\right)=x_1\left(t\right)+x_2\left(t\right)+x_3\left(t\right),(3)$

in which $x_1\left(t\right),x_2\left(t\right),{\mathrm{a}\mathrm{n}\mathrm{d}x}_3\left(t\right)$ are component signals. The IF profiles of these component signals are f₁(t) (the meshing frequency), f₂(t) (the upper sideband), and f₃(t) (the lower sideband), respectively. They are calculated as follows:

$\left\{\begin{array}{c}{f}_1\left(t\right)=Z{f}_n+{\varphi }^{\prime }\left(t\right),\\ f_2\left(t\right)=\left(Z+1\right)f_n+{\varphi }^{\prime }\left(t\right),\\ f_3\left(t\right)=\left(Z-1\right)f_n+{\varphi }^{\prime }\left(t\right).\end{array}\right.(4)$

For the aforementioned discussion, in the case of a fault gearbox, sidebands will be around the meshing frequency; otherwise, there will be no sidebands. Separating the sidebands in case of the non-overlapping frequency is simple, as shown in Figure 1A; however, when the frequency is varied, frequency overlap will appear, as shown in Figure 1B, and then, it will be challenging to extract. This work applies the generalized Fourier transform (GFT) by Olhede and Walden (2005) to convert the varying frequency to a constant frequency to avoid overlap. The GFT is applied by multiplying a mapping function $e^{-i2\pi x_0\left(t\right)}$ with the analytical form of the original signal x(t) to make a signal-straightened frequency (Zhu et al., 2009):

$\stackrel{\sim }{x}\left(t\right)=Hilbert\left(x\left(t\right)\right).(5)$

FIGURE 1

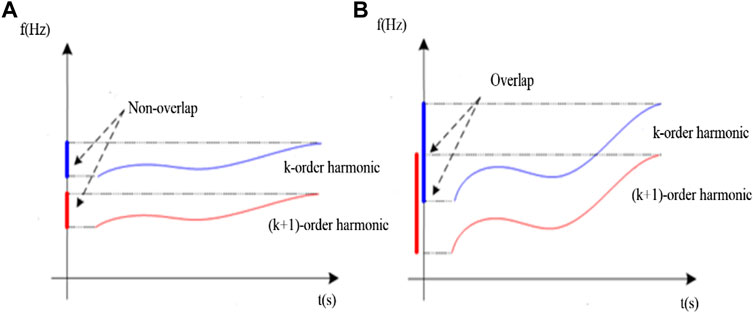
FIGURE 1. Description of the frequency overlap: (A) no overlap; (B) overlap (Wang et al., 2017).

For a signal x, the GFT is defined as the following expression:

$X_g\left(f\right)=\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\stackrel{\sim }{x}\left(t\right)e^{-j2\pi \left[ft+x_0\left(t\right)\right]}dt,(6)$

where x₀(t) presents a real value function; this function only depends on time and relates to the phase of the signal (Olhede and Walden, 2005).

Setting $u\left(t\right)=\stackrel{\sim }{x}\left(t\right)e^{-j2\pi x_0\left(t\right)}$, Eq. 6 can be rewritten as the Fourier transform:

$X_G\left(f\right)={\int }_{-\infty }^{+\infty }u\left(t\right)e^{-j2\pi ft}dt.(7)$

The inverse GFT (iGFT) based on the Fourier transform can be expressed as the following expression:

$u\left(t\right)=\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}{X}_G\left(f\right)e^{j2\pi ft}df(8)$

and

$x\left(t\right)=e^{j2\pi x_0\left(t\right)}\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}{X}_G\left(f\right)e^{j2\pi ft}df.(9)$

Neglecting amplitudes, we have $X_G\left(f\right)=\delta \left(f-f_0\right)$. The aforementioned equation can be rewritten as follows:

$x\left(t\right)=e^{j2\pi \left[f_{0}t+x_0\left(t\right)\right]}.(10)$

This means that the original signal x(t) with IF f(t) will be mapped to another signal $y\left(t\right)=x\left(t\right)e^{-j2\pi x_0\left(t\right)}$ with a constant frequency f₀, as long as the following equation is satisfied:

$f\left(t\right)=\frac{d{x}_0\left(t\right)}{dt}+f_0.(11)$

The aforementioned equation proves that the signal x(t) with the time-varying frequency can be straightened using the mapping function $e^{-j2\pi x_0\left(t\right)}$ with the phase x₀(t) determined by (Eq. 11).

When the signal x(t) has the original frequency f(t) after applying the GFT, it is converted into another signal with a time-constant frequency f₀. Otherwise, if applying iGFT, it is the reconstructed original frequency.

An example to demonstrate the application of the GFT is shown in Figure 2. Using the GFT, we can take the time-varying frequency component f(t) to the time-constant frequency component f₀. In other words, we have “straightened” the harmonic frequency component of the $k$-order of the signal, as shown in Figure 2B. After that, when band-pass filtering is performed, it will generate separated instantaneous frequency harmonics, as shown in Figure 2C. Finally, the original frequency will be reconstructed based on the iGFT by multiplying a mapping function $e^{j2\pi x_0\left(t\right)}$. In order to simulate the aforementioned theory, an experiment is carried out with a couple of gears, in which the number of the tooth is 10 for the fault gear. The formula vibration signal can be expressed as follows:

$x\left(t\right)=1.1\left(1+0.6\cos \left(2\pi f_n\left(t\right)t\right)\right).\cos \left(2\pi .10.f_n\left(t\right)t+\varphi \left(t\right)\right),(12)$

where $f_n\left(t\right)=-4.3t^2+10t+12,\varphi \left(t\right)=1.6\cos \left(0.3\pi t\right)$ and $t\in \left[\mathrm{0.1,1.1}\right]$.

FIGURE 2

FIGURE 2. Simulation generalized Fourier transform for a component frequency.

The IF profiles of the sub-signals can be calculated from Eq. 4. Figure 3 shows the analysis of the signal x(t) in the time and frequency domains, where f_n(t) and A(t) are not constant. It is clearly seen in this signal that all frequency spectra do not provide any information due to variable frequency, as shown in Figure 3B. Based on the aforementioned argument, to separate the sidebands around the meshing frequency in case the gearbox operates in non-stationary conditions, it is necessary to determine the meshing frequency f(t) and select the frequency f₀, as shown in Eq. 11. There are two ways to look for the meshing frequency f(t), that is, through phase information and the direct estimation on the time–frequency distribution. The machine must stop to set up the tachometer on gearbox housing to achieve phase information. However, this is unwanted since it affects the production process. In addition, using a tachometer is not feasible in some unique working environments with a lot of light and dust, and it also increases the cost and time of measurement. Therefore, in this paper, we will directly estimate the instantaneous meshing frequency and propose a novel approach to detect upper and lower sidebands, as shown in Figure 3C. This novel approach combines WSST and GFT to achieve a set goal. It would be consistent with the diagnostic symptom for the gearbox operating in non-stationary conditions described in the previous sections.

FIGURE 3

FIGURE 3. Time domain signal (A), spectrum (B), and time–frequency distribution based on a novel approach (C).

Principle of the proposed method

As discussed in the previous section, the frequency components are straightened by the generalized Fourier transform based on two input parameters: the meshing frequency f(t) and the constant f₀. In order to estimate the matching frequency, this study used the two-step method found in Urbanek et al. (2013). After straightening the frequency components, the signal must be cleaned to remove the effect of noise and sharpen the frequency–time distribution. Then, the signal is reconstructed by the inverse generalized Fourier transform.

Wavelet-based synchrosqueezing transform

The continuous wavelet transform (CWT), known as the most popular signal transform in the time–frequency domain, belongs to the class of traditional time–frequency transforms. The CWT provides a good frequency resolution at low frequencies and a good time resolution at high frequencies (Mallat, 1999). Therefore, the CWT is an effective method for analyzing vibration signals with rapidly time-varying frequencies and detecting transient components in noisy signals (Zhu et al., 2009).

The CWT, denoted by $W_x$, is defined by the following expression:

$W_x\left(\tau ,s\right)={\left|s\right|}^{-\frac{1}{2}}\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}x\left(t\right){\psi }^{*}\left(\frac{t-\tau }{s}\right)dt,(13)$

in which * is the complex conjugate of the basis wavelet function, x(t) is presentative for a continuous-time signal, s is a scale, and t is the localized time. Based on the change of s and translation t, wavelet coefficients $\left|W_x\left(\tau ,s\right)\right|$ can construct a wavelet amplitude map to indicate a distribution of the signal amplitude versus s and t. The FFT algorithm is used to calculate the CWT using a sinusoidal function modulated by a Gaussian curve, which is applied to compute the wavelet, as shown in the following expression:

$\psi \left(t\right)={\pi }^{-1/4}{e}^{i{\omega }_{0}t}{e}^{-t^2/2},(14)$

where ${\omega }_0$ is a constant. The relationship between the frequency f and the scale s is given by the following expression:

$f=\frac{{\omega }_0+\sqrt{2+{\omega }_0^2}}{\begin{array}{c}4\pi s\end{array}}.(15)$

The advantage of the wavelet transform is that it quickly gives a vibration signal in the time–frequency domain, as shown in Figure 5A. However, the frequency resolution is not good in the low-frequency zone. Thus, Daubechies et al. (2010) have proposed the advanced mathematical theory called the wavelet-based synchrosqueezing transform (WSST) to increase the frequency resolution in the wavelet amplitude map. WSST transforms a vibration signal, as found in the following equation (Daubechies et al., 2011):

$T_x^{\gamma }\left(\tau ,\omega \right)=\underset{A_{\gamma ,x}\left(\tau \right)}{{\displaystyle \int }}W{T}_x\left(\tau ,s\right)\delta \left(\omega -{\omega }_x\left(\tau ,s\right)\right)s^{-3/2}ds,(16)$

where $\delta \left(t\right)=\frac{1}{\pi }{e}^{-t^2}$ is the Dirac delta function; $A_{\gamma ,x}\left(\tau \right)$ is the WSST coefficient of the signal x(t) at a time t and instantaneous angular frequency ωwith the threshold g. It can be expressed as the following equation:

$A_{\gamma ,x}\left(\tau \right)=\left\{s\in R^{+};\left|W{T}_x\left(\tau ,s\right)\right|>\gamma \right\},T_x^{\gamma }\left(\tau ,\omega \right).(17)$

The instantaneous angular frequency, ${\omega }_x\left(\tau ,s\right)$ in Eq. 5, can be computed by the following equation:

${\omega }_x\left(\tau ,s\right)=\left\{\begin{array}{c}\begin{array}{cc}\begin{array}{c}\frac{-j}{W{T}_x\left(\tau ,s\right)}\frac{\partial \left(W{T}_x\left(\tau ,s\right)\right)}{\partial \tau }\end{array}& \left|W{T}_x\left(\tau ,s\right)\right|>0,\\ \infty & \left|W{T}_x\left(\tau ,s\right)\right|=0.\end{array}\end{array}\right.(18)$

The flowchart of WSST using the signal x(t) and the base wavelet is shown in Figure 4. In WSST, the information is moved from the time–scale space to the time–frequency space in the map $\tau ,s\to \left(\tau ,{\omega }_x\right)$. Figure 5 shows that the frequency resolution in both CWT and WSST spreads along the time dimension. In CWT, the frequency lines are blurred (see Figure 5A), and the width of the frequency lines is larger than that of WSST. Thus, it is difficult to detect the sidebands; meanwhile, the frequency resolution of WSST can be more clearly seen (Figure 5B).

FIGURE 4

FIGURE 4. Flowchart of the wavelet synchrosqueezing transform.

FIGURE 5

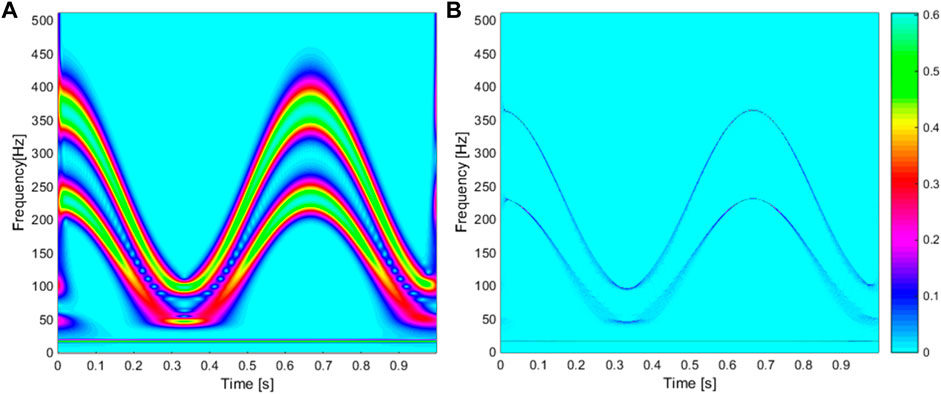
FIGURE 5. Comparison of the frequency resolution: (A) CWT and (B) WSST (Thakur et al., 2013).

Flowchart of the proposed method

The measured vibration signal is fed into the continuous wavelet transform to obtain the time–frequency distribution. Then, the meshing frequency from this distribution is estimated using the two-step method (Urbanek et al., 2013). To calculate the real phase x₀(t) in Eq. 11, an optional frequency f₀ must be defined, and the value of f₀ is selected equal to 30 to ensure the best frequency resolution. As mentioned in the previous sections, it is necessary to use the sideband extract method around the meshing frequency to detect the fault of the gearbox operated in non-stationary conditions. First, the GFT method is used for the efficient separation of sidebands, and then, the WSST method is used to sharpen the time–frequency distribution, as shown in Figure 5.

After looking for a real phase and putting it into the GFT, the meshing frequency and sidebands are straightened. Thus, band-pass filtering is performed around the straightened meshing frequency to separate sidebands. The WSST method is then practiced to sharpen separated sidebands around the meshing frequency. Finally, the iGFT is used to recover the meshing frequency and sidebands. The proposed method is briefly described in Figure 6. A fault is detected when there are sidebands around the meshing frequency.

FIGURE 6

FIGURE 6. Flowchart of the proposed method.

Experiment evaluation

The experiment was carried out at the Hanoi University of Science and Technology. The vibration KIT consists of 1Kw of a 3-phase asynchronous motor, a spur-gear gearbox with a transmission ratio of 2:1, a controllable magnetic brake, an inverter for controlling the motor speed, accelerometer, and a signal acquisition and processing unit. The PID controller can control the torque and motor speed.

The high-resolution encoder enables continuous measurement and interpolation of shaft torque. Furthermore, the gearbox can easily change the driving gear position, according to the fault patterns of the driven gear. The signal acquisition and processing unit has a continuous sampling rate up to 30 khz; the SNR parameter is 98 dB; the resolution is 18 bits. The pre-sampled signal is anti-aliased and low-pass filtered. The analyzer is integrated with signal analysis methods such as the fast Fourier transform, wavelet transform, and FIR digital filters. It can alert users according to the ISO-10816 vibration standard; moreover, a history graph can show the trend of the RMS vibration, RMS value, and the trend of changes in the vibration spectrum. With this, users can detect potential failures sooner in the future. The experimental model is depicted in Figure 7. In the model, the gearbox is driven by a motor with speed control. Some types of cracks in the gear teeth are intentionally created to test the effectiveness of the proposed method.

FIGURE 7

FIGURE 7. Actual experimental model.

The qualitative analysis indicates the efficiency of the WSST compared to traditional methods such as the short-time Fourier transform (STFT). STFT is used to generate the time–frequency distribution of the measured vibration signal, as shown in Figure 8A. In this figure, the color scale is arranged from the bottom to the top, which corresponds to the ascending arrangement of the STFT coefficient magnitudes. Figure 8B shows the frequency–time distribution by the WSST. It is seen that when using the WSST, white noise has been significantly eliminated.

FIGURE 8

FIGURE 8. Comparison of the time–frequency distribution based on the STFT (A) and và WSST (B).

The meshing frequency extracted from the time–frequency distribution in Figure 8B is shown in Figure 9A based on the WSST. The result of frequency separation using the proposed method is compared to the computed order tracking (COT) method (see Figure 9B) to evaluate quantitatively. It can be seen that the result showing the separation of the meshing frequency obtained from the proposed method is similar to the result achieved by the COT method. For this, the proposed method effectively diagnoses faults in the gearbox, which operates in non-stationary conditions. This problem is a new point of this study that previous works have not clarified. When applying this method in practice, we can completely build an online diagnostic system without using much measuring equipment; moreover, accurate results can also be achieved.

FIGURE 9

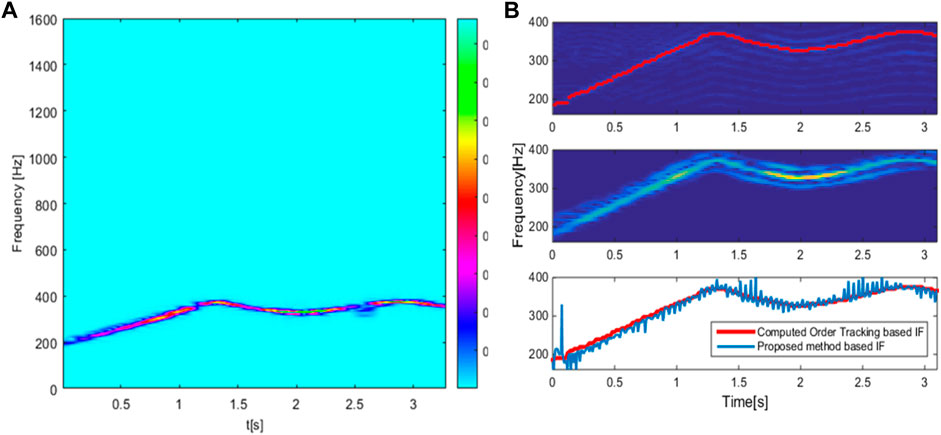
FIGURE 9. Meshing frequency extracted from the proposed method (A) and comparison with the COT method (B).

In order to eliminate the frequency overlap, the GFT is used to straighten the frequency component of the first-order meshing harmonic. Figure 8B depicts the estimated meshing frequency extracted from the time–frequency distribution. This frequency is input for the GFT to extract information on the sideband around a surveyed meshing frequency after applying the WSST to clear noise and sharpness of the time–frequency distribution. Finally, the inverse GFT is then used to reconstruct the initial frequency components. Figure 10 presents the time–frequency distribution around the meshing frequency harmonic where the sidebands are detected clearly. For this, a gear fault has occurred in the gearbox. This demonstrates that the proposed method and the experimental model have coincided.

FIGURE 10

FIGURE 10. Time–frequency representation.

Conclusion

There are many methods of gearbox vibration analysis. Traditional techniques, such as spectral analysis based on FFT or TSA, have become influential in detecting gear faults in stationary operating conditions; however, it is inefficient in the case of time-varying speeds. Applying advanced and sophisticated signal processing tools such as time–frequency analysis using the CWT and WSST can get us more information on the gear fault condition from vibration signals. This paper proposes a novel approach based on combining many advanced modern methods to detect a symptom of gear faults in the gearbox in non-stationary conditions based on sideband analysis. When using this proposed method, no additional measuring equipment is required. In particular, it is necessary to build an online diagnostic system for machines and equipment. This can be studied by using the least number of measuring devices in the near future, which does not affect the diagnostic accuracy. For this, further research can apply artificial intelligence to classify damage in gearboxes operating in unstable conditions, which only uses one measuring head.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors contributed to the paper. NTD: conceptualization, methodology, investigation, resources, software, writing—original draft. NPD: conceptualization, methodology, review, and supervision. NTTN: writing—original draft, review, and edit.

Acknowledgments

This research is funded by Hanoi University of Science and Technology (HUST) under project number T2022-PC-027.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Braun, S. (2011). The synchronous (time domain) average revisited. Mech. Syst. Signal Process. 25 (4), 1087–1102. doi:10.1016/j.ymssp.2010.07.016

CrossRef Full Text | Google Scholar

Daubechies, I., Lu, J. F., and Wu, H. T. (2011). Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Analysis 30, 243–261. doi:10.1016/j.acha.2010.08.002

CrossRef Full Text | Google Scholar

Daubechies, I., Lu, J., and Wu, H.-T. (2010). Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Analysis 30, 243–261. doi:10.1016/j.acha.2010.08.002

CrossRef Full Text | Google Scholar

Dien, N. P., and Du, N. T. (2020). “fault detection for rotating machines in non-stationary operations using order tracking and cepstrum,” in Advances in engineering research and application, 349–356.

CrossRef Full Text | Google Scholar

li, C., and Liang, M. (2012). Time-Frequency signal analysis for gearbox fault diagnosis using a generalized synchrosqueezing transform. Mech. Syst. Signal Process. 26, 205–217. doi:10.1016/j.ymssp.2011.07.001

CrossRef Full Text | Google Scholar

Mallat, S. (1999). A wavelet tour of signal processing. New York: Academic Press.

Google Scholar

Newland, D. E. (1993). An introduction to random vibrations, spectral and wavelet analysis. John Wiley & Sons.

Google Scholar

Olhede, S., and Walden, A. T. (2005). A generalized demodulation approach to time-frequency projections for multicomponent signals. Proc. R. Soc. A 461, 2159–2179. doi:10.1098/rspa.2005.1455

CrossRef Full Text | Google Scholar

Peng, F. Q., Yu, D. J., and Luo, J. S. (2011). Sparse signal decomposition method based on multi-scale chirplet and its application to the fault diagnosis of gearboxes. Mech. Syst. Signal Process. 25, 549–557. doi:10.1016/j.ymssp.2010.06.004

CrossRef Full Text | Google Scholar

Randall, R. B. (2016). A history of cepstrum analysis and its application to mechanical problems. Mech. Syst. Signal Process. 97, 3–19. doi:10.1016/j.ymssp.2016.12.026

CrossRef Full Text | Google Scholar

Thakur, G., Brevdo, E., Fučkar, N. S., and Wu, H.-T. (2013). The Synchrosqueezing algorithm for time-varying spectral analysis: Robustness properties and new paleoclimate applications. Signal Process. 93 (5), 1079–1094. doi:10.1016/j.sigpro.2012.11.029

CrossRef Full Text | Google Scholar

Urbanek, J., Barszcz, T., and Antoni, J. (2013). A two-step procedure for estimation of instantaneous rotational speed with large fluctuations. Mech. Syst. Signal Process. 38 (1), 96–102. doi:10.1016/j.ymssp.2012.05.009

CrossRef Full Text | Google Scholar

Wang, X., Liu, Y., Zhang, W., and Jia, M. (2020). Research on a novel improved adaptive variational mode decomposition method in rotor fault diagnosis. Appl. Sci. 10 (1696), 1696–1727. doi:10.3390/app10051696

CrossRef Full Text | Google Scholar

Wang, Y., Xie, Y., Xu, G., Zhang, S., and Hou, C. (2017). Tacholess order-tracking approach for wind turbine gearbox fault detection. Front. Mech. Eng. 12, 427–439. doi:10.1007/s11465-017-0452-z

CrossRef Full Text | Google Scholar

Yan, X., Liu, Y., and Jia, M. (2019). Research on an enhanced scale morphological-hat product filtering in incipient fault detection of rolling element bearings. Measurement 147, 106856. doi:10.1016/j.measurement.2019.106856

CrossRef Full Text | Google Scholar

Yan, X., Liu, Y., Xu, Y., and Jia, M. (2021). Multichannel fault diagnosis of wind turbine driving system using multivariate singular spectrum decomposition and improved Kolmogorov complexity. Renew. Energy 170, 724–748. doi:10.1016/j.renene.2021.02.011

CrossRef Full Text | Google Scholar

Yan, X., Liu, Y., Xu, Y., and Jia, M. (2020). Multistep forecasting for diurnal wind speed based on hybrid deep learning model with improved singular spectrum decomposition. Energy Convers. Manag. 225 (113456), 113456. doi:10.1016/j.enconman.2020.113456

CrossRef Full Text | Google Scholar

Zhang, L., and Hu, N. (2019). Time domain synchronous moving average and its application to gear fault detection. IEEE Access 7, 93035–93048. doi:10.1109/access.2019.2927762

CrossRef Full Text | Google Scholar

Zhu, Z. K., Yan, R., Luo, L., Feng, Z. H., and Kong, F. R. (2009). Detection of signal transients based on wavelet and statistics for machine fault diagnosis. Mech. Syst. Signal Process. 23, 1076–1097. doi:10.1016/j.ymssp.2008.06.012

CrossRef Full Text | Google Scholar