Kinematics of Articulated Planar Linkages

This paper proposes a kinematics algorithm in screw coordinates for articulated linkages. As the screw consists of velocity and position variables of a joint, the solutions of the forward and inverse velocities are the functions of position coordinates and their time derivatives. The most prominent merit of this kinematic algorithm is that we only need the first order numerical differential interpolation for computing the acceleration. To calculate the displacement, we also only need the first order numerical integral of the velocity. This benefit stems from the screw the coordinates of which are velocity components. Both the forward and the inverse kinematics have the similar calculation process in this method. Through examples of planar open-chain linkage, single closed-chain linkage and multiple closed-chain linkage, the kinematics algorithm is validated. It is particularly fit for developing numerical programmers for forward and inverse kinematics in the same procedures, including the velocity, displacement and acceleration which provide the fundamental information for dynamics of the linkage.

Introduction

Kinematics of a linkage aims at studying its motion without regard to forces (Norton, 2004) for the synthesis of a mechanism (Suh and Radcliffe, 1978) or to accomplish the desired motion (Shigley and Uicher, 1980) and determine its rigid-body dynamic behavior (Bottema and Roth, 1979; Waldron and Kinematics, 2004). Kinematic geometry (Hunt, 1978), geometric design (McCarthy and Soh, 2011), theoretical kinematics of robotic mechanisms (McCarthy, 1990; Duffy, 1996; Davidson and Hunt, 2004; Dai, 2014), and the analysis, synthesis and optimization of spatial kinematic chains (Angeles, 1982) are elaborated in previous works in the past decades. Kinematic analysis of a linkage requires the algebraic equations that might be iterated numerically. Computational kinematic analysis plays a vital role in the study of a mechanical system (Saura et al., 2019). It is the most straightforward procedure for kinematics and dynamics to select the absolute coordinates of the reference point as the variables (García de Jalón and Bayo, 1994). This selection has the advantage of normally leading to a facilitated expression for the constraints and Jacobian matrices of a multi-body system (García de Jalón and Bayo, 1994). The forward kinematics of a serial linkage is easier than its inverse kinematics while the forward kinematics of a parallel linkage is more complex than its inverse kinematics (Suh and Radcliffe, 1978; Bottema and Roth, 1979; Duffy, 1980; Shigley and Uicher, 1980; Angeles, 1982; García de Jalón and Bayo, 1994; Duffy, 1996).

In the past half century, parallel manipulators witnessed very quick development. Parallel manipulators have been attracted a great attention ever since the industry application of Gough’s tire testing machine and Stewart’s platform for its superior performance over its serial counterparts in terms of loading capacity, rigidity and accuracy (Gough and Whitehall, 1962; Stewart, 1965). However, the forward kinematics usually contains a group of nonlinear algebraic equations that are complexly coupled and there are no general methods to solve them analytically (Chapelle and Bidaud, 2004; Wu et al., 2009). It has been recognized as the general purpose of a software that standardized procedures should be proposed for reducing the kinematic analysis of mechanism to simplify the problem (Kong et al., 2016). Different procedures were developed to establish the restriction equations to solve their time derivatives of first and second orders (Zhao et al., 2016). Actually, such procedures can be accomplished through vector-loop processing for planar linkages (Brát and Lederer, 1973; Kong et al., 2018). The forward kinematics are either established in the functions of structure parameters and input variables numerically (Yang et al., 2018) or presented in algebraic coordinates (Wu et al., 2013; Kong et al., 2019). The inverse kinematic problem consists of finding the joint variables to achieve a desired configuration of a mechanism (Chapelle and Bidaud, 2004; Wu et al., 2013).

To understand the kinematic performance of a linkage, many scholars have been proposing different theories (McCarthy, 1990; Duffy, 1996; Davidson and Hunt, 2004; Dai, 2014; Zhao et al., 2016; Amiri and Mazaheri, 2020; Faghidian and Mohammad-Sedighi, 2020), methods (Angeles, 1982; Kong et al., 2018; Yang et al., 2018; Kong et al., 2019; Shen et al., 2020), algorithms (García de Jalón and Bayo, 1994; Kong et al., 2016; Saura et al., 2019) and software (Brát and Lederer, 1973; García de Jalón and Bayo, 1994; Wu et al., 2009; Wu et al., 2017). This paper focuses on an algorithm in the screw coordinates to solve the velocity of articulated planar linkage and investigates the displacement and acceleration. A screw is a line vector accompanied by a secondary vector attached with a pitch. As the geometrical element, a screw with six components plays a vital role in kinematics and mechanics of a mechanism (Barus, 1900). The paper develops an algorithm to analyze the displacement, velocity and acceleration of articulated planar mechanisms in twist coordinates of each joint. This is the first try to use screw coordinates to completely study the displacement, velocity and acceleration of linkages in a general systematic way. Because the kinematics analysis starts from the velocity, the solutions of forward and inverse kinematics of a mechanism have the same form in expression which facilitates the programming and calculation. The discussion is not restricted to the kinematics of revolute jointed planar linkages, and the similar principles also apply to spatial mechanisms.

Instantaneous Twist of the End Effector of a Series Mechanism

Definition of Twist

Table 1 is the definition of parameters in this paper.

TABLE 1

TABLE 1. Definition of parameters.

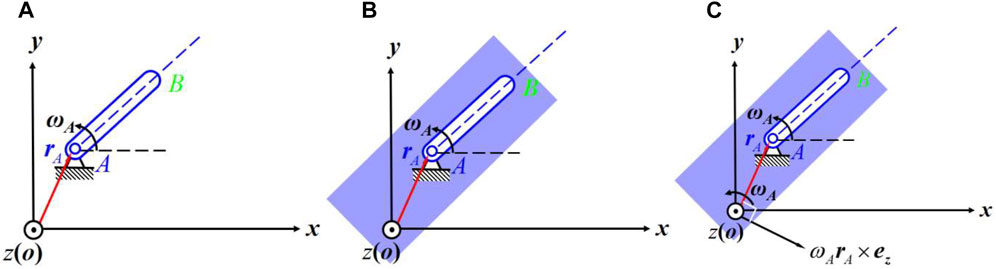
Figure 1A shows an articulated link $\mathrm{AB}$ that is rotating around a fixed revolute joint $A$ with angular velocity of ${\omega }_A$ around the $z$ -axis. The velocity of any point $P$ attached to the rigid link $\mathrm{AB}$ can be expressed by ${\mathit{v}}_P={\mathit{\omega }}_A\times {\mathit{r}}_{AP}$. As a result, the velocity of point $P$ on the extended rigid body of link $\mathrm{AB}$ that is overlapped with the origin of the coordinate frame is ${\mathit{v}}_o={\mathit{\omega }}_A\times {\mathit{r}}_{Ao}$ where ${\mathit{r}}_{Ao}=-{\mathit{r}}_A$ which is illustrated in Figure 1B.

FIGURE 1

FIGURE 1. Twist of a revolute jointed link.

Also, there is ${\mathit{v}}_o={\mathit{\omega }}_A\times \left(-{\mathit{r}}_A\right)={\mathit{r}}_A\times {\mathit{\omega }}_A$ which is illustrated in Figure 1C. The dual 3-dimensional vectors ${\mathit{\omega }}_A$ and ${\mathit{v}}_o$ can fully determine the rotation of link $\mathrm{AB}$. So, a dual vector can be defined as

${\hspace{0.17em}}_o{\mathit{\$}}_A=\left[\begin{array}{c}{\mathit{\omega }}_A\\ r_A\times {\mathit{\omega }}_A\end{array}\right](1)$

where ${\hspace{0.17em}}_o{\mathit{\$}}_A$ is a screw that expresses the twist of link $\mathrm{AB}$ that is rotating around joint $A$ with a marking point superimposing with the origin $o$ of the coordinate system. Supposing that ${\mathit{e}}_{\mathit{z}}={\left[\begin{array}{ccc}\text{0}& \text{0}& 1\end{array}\right]}^T$, Equation 1 can be rewritten as

${\hspace{0.17em}}_o{\mathit{\$}}_A={\omega }_A\left[\begin{array}{c}{\mathit{e}}_{\mathit{z}}\\ {\mathit{r}}_A\times {\mathit{e}}_{\mathit{z}}\end{array}\right](2)$

where ${\omega }_A$ is the angular speed of the rotation about joint $A$. Let

${\hspace{0.17em}}_o{\mathit{\$}}_{\mathit{Au}}=\left[\begin{array}{c}{\mathit{e}}_{\mathit{z}}\\ {\mathit{r}}_A\times {\mathit{e}}_{\mathit{z}}\end{array}\right](3)$

where $o{\mathit{\$}}_{Au}$ is called unit screw because the norm of ${\mathit{e}}_{\mathit{z}}$ is $\Vert {\mathit{e}}_{\mathit{z}}\Vert =1$ (35].

In Equation 3, the first three components indicate the unit direction of a rotation and the last three components present implicitly the position of the axis of rotation with respect to the origin of the coordinate system (Zhao et al., 2014). Therefore, Equation 2 can be denoted by

${\hspace{0.17em}}_o{\mathit{\$}}_A={\omega }_A{\hspace{0.17em}}_o{\mathit{\$}}_{\mathit{Au}}(4)$

Twist Matrix of a Series Pivoted Kinematic Chain

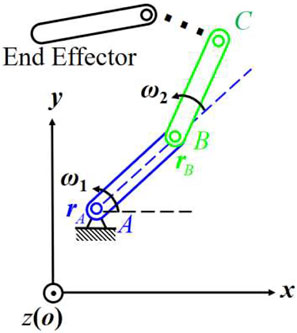
When a second link $BC$ is jointed with $AB$ at $B$(see Figure 2A), the relative twist of $BC$ with respect to $AB$ can be analyzed by fixing $AB$ with the ground which is indicated by Figure 2B.

FIGURE 2

FIGURE 2. Twist of link $BC$with respect to the fixed coordinate frame.

With the similar procedure mentioned above, we get

${\hspace{0.17em}}_o{\mathit{\$}}_B={\omega }_B{\hspace{0.17em}}_o{\mathit{\$}}_{\mathit{Bu}}(5)$

where ${\omega }_B$ is the relative speed of link $BC$with respect to $AB$ rotating around the revolute joint $B$, and

${\hspace{0.17em}}_o{\mathit{\$}}_{\mathit{Bu}}=\left[\begin{array}{c}{\mathit{e}}_{\mathit{z}}\\ {\mathit{r}}_B\times {\mathit{e}}_{\mathit{z}}\end{array}\right](6)$

According to the principle of linear superposition, the absolute angular velocity of link $BC$ is (Zhao et al., 2014)

${\mathit{\omega }}_{\mathit{BC}}={\mathit{\omega }}_A+{\mathit{\omega }}_B(7)$

and the absolute velocity of link $BC$ with the marking point that is superimposed with the origin at the moment is

${\hspace{0.17em}}_o{\mathit{v}}_{\mathit{Bc}}={\omega }_A\left({\mathit{r}}_A\times {\mathit{e}}_{\mathit{z}}\right)+{\omega }_B\left({\mathit{r}}_B\times {\mathit{e}}_{\mathit{z}}\right)(8)$

where ${\hspace{0.17em}}_o{\mathit{v}}_{\mathit{BC}}$ indicates the velocity of a point on link $BC$ that is at this instant superimposed with the origin illustrated in Figure 2C.

As a result, the twist of link $BC$ with respect to the coordinate system is

${\hspace{0.17em}}_o{\mathit{\$}}_{\mathit{BC}}=\left[\begin{array}{c}{\mathit{\omega }}_{\mathit{BC}}\\ {\hspace{0.17em}}_o{\mathit{v}}_{\mathit{BC}}\end{array}\right]=\left[\begin{array}{c}{\omega }_A{\mathit{e}}_{\mathit{z}}+{\omega }_B{\mathit{e}}_{\mathit{z}}\\ {\omega }_A{\mathit{r}}_A\times {\mathit{e}}_{\mathit{z}}+{\omega }_B{\mathit{r}}_B\times {\mathit{e}}_{\mathit{z}}\end{array}\right](9)$

Equation (9) can be rewritten as

${\hspace{0.17em}}_o{\mathit{\$}}_{\mathit{BC}}={\omega }_A{\hspace{0.17em}}_o{\mathit{\$}}_{\mathit{Au}}+{\omega }_B{\hspace{0.17em}}_o{\mathit{\$}}_{\mathit{Bu}}(10)$

which can be expressed in matrix multiplication form:

${\hspace{0.17em}}_o{\mathit{\$}}_{\mathit{BC}}={\mathbf{S}}_{\mathit{BC}}{\mathit{\omega }}_{\mathit{BC}}(11)$

where ${\mathbf{S}}_{BC}\mathbf{=}\left[\begin{array}{cc}{\mathit{e}}_{\mathit{z}}& {\mathit{e}}_{\mathit{z}}\\ {\mathit{r}}_A\times {\mathit{e}}_{\mathit{z}}& {\mathit{r}}_B\times {\mathit{e}}_{\mathit{z}}\end{array}\right]$ and ${\mathit{\omega }}_{BC}=\left[\begin{array}{c}{\omega }_A\\ {\omega }_B\end{array}\right]$.

Similarly, the twist of the end effector, denoted by${\hspace{0.17em}}_o{\mathit{\$}}_E$, of a kinematic chain in series illustrated by Figure 3 can be expressed as.

${\hspace{0.17em}}_o{\mathit{\$}}_E=\mathit{S}\mathit{\omega }(12)$

where

$\mathrm{S}=\left[\begin{array}{cccc}{\hspace{0.17em}}_o{\mathit{\$}}_1& {\hspace{0.17em}}_o{\mathit{\$}}_2& \cdots & {\hspace{0.17em}}_o{\mathit{\$}}_n\end{array}\right](13)$

and

$\mathit{\omega }={\left[\begin{array}{cccc}{\omega }_1& {\omega }_2& \cdots & {\omega }_n\end{array}\right]}^T(14)$

FIGURE 3

FIGURE 3. A series kinematic chain.

Eq. 13 is called the unit twist matrix of a serial linkage while Equation 14 presents a vector including all relative angular speeds of each joint relative to its previous neighbor in the kinematic chain. Screw matrix 13) is made up of the geometry parameters of the mechanism. It can be programmed in the computer software. This procedure offers an explicit inference of kinematic attributes for velocities in the mechanisms that have the same topology.

Kinematics of a Revolute Jointed Mechanism With Serial Open Chain

From Equation 12, we know that the twist of the end effector with a marking point of the origin of the coordinate frame can be directly obtained when ${\omega }_i(i=\mathrm{1,2},\cdots n)$ are all prescribed. Denote the twist by

${\hspace{0.17em}}_o{\mathit{\$}}_E=\left[\begin{array}{c}{\mathit{\omega }}_E\\ {\hspace{0.17em}}_o{\mathit{v}}_E\end{array}\right](15)$

We know that ${\mathit{\omega }}_E$ is the absolute angular velocity of the end effector and ${\mathit{v}}_E\left(o\right)$ is the velocity of the point attached with the end effector that is superimposed with the origin of the coordinate system at this moment. The velocity of the geometry center of the end effector is therefore denoted by

${\hspace{0.17em}}_C{\mathit{v}}_E={\hspace{0.17em}}_o{\mathit{v}}_E+{\mathit{\omega }}_E\times {\mathit{r}}_C(16)$

where ${\mathit{r}}_C$ is the position vector of the geometry center of the end effector in the absolute ground coordinate system. As a result, we get the twist of the end effector at its central coordinate frame whose axes are parallel with the corresponding absolute ones at this instant:

${\hspace{0.17em}}_C{\mathit{\$}}_E=\left[\begin{array}{c}{\mathit{\omega }}_E\\ {\hspace{0.17em}}_{\mathit{C}}{\mathit{v}}_E\end{array}\right]=\left[\begin{array}{c}{\mathit{\omega }}_E\\ {\hspace{0.17em}}_o{\mathit{v}}_E+{\mathit{\omega }}_E\times {\mathit{r}}_C\end{array}\right](17)$

where ${\mathit{\omega }}_E$ is the absolute angular velocity of the end effector and ${\hspace{0.17em}}_C{\mathit{v}}_E$ is the absolute linear velocity of the center of the end effector. Eq. 17 is the forward kinematics of a serial linkage in screw form which provides all necessary parameters for developing the dynamics of the linkage.

After knowing the twist of the end effector with a marking point of the origin $o$ of the coordinate frame, we can left multiply ${\mathbf{S}}^T$ at both sides of Equation 15:

${\mathbf{S}}^T\mathbf{S}\mathit{\omega }={\mathbf{S}}^T{\hspace{0.17em}}_o{\mathit{\$}}_E(18)$

where ${\mathbf{S}}^T$ is the transpose of matrix $\mathbf{S}$.

When $\left|{\mathbf{S}}^T\left(o\right)\mathbf{S}\left(o\right)\right|=\text{0}$, the serial linkage is either redundantly actuated or in its singularity configuration. Otherwise, we get:

$\mathit{\omega }={\left[{\mathbf{S}}^T\mathbf{S}\right]}^{-1}{\mathbf{S}}^T{\hspace{0.17em}}_o{\mathit{\$}}_E(19)$

where ${\left[{\mathbf{S}}^T\mathbf{S}\right]}^{-1}{\mathbf{S}}^T$ is called the pseudo inverse of the unit twist matrix $\mathbf{S}$. Eq. 19 represents the inverse kinematics for the serial mechanism.

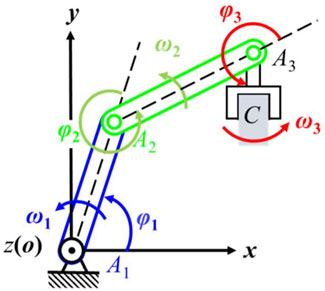
Figure 4 shows a planar linkage in series. In the absolute coordinate system, we gain the twist of the end effector:

${\hspace{0.17em}}_o{\mathit{\$}}_E=\mathbf{S}\mathit{\omega }(20)$

where

$\mathbf{S}={\left[\begin{array}{cccccc}0& 0& 1& y_1& -x_1& 0\\ 0& 0& 1& y_2& -x_2& 0\\ 0& 0& 1& y_3& -x_3& 0\end{array}\right]}^T(21)$

and

$\mathit{\omega }={\left[\begin{array}{ccc}{\omega }_1& {\omega }_2& {\omega }_3\end{array}\right]}^T(22)$

FIGURE 4

FIGURE 4. A planar open chain linkage of 3 degrees of freedom.

Supposing the length of the links are $l_1$, $l_2$ and $l_3$, the coordinates of each revolute joint can be expressed by $x_1=0$, $y_1=0$, $x_2=l_1\cos {\phi }_1$, $y_2=l_1\sin {\phi }_1$, $x_3=l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)$, $y_3=l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)$, respectively. So the unit twist matrix 18) is

$\mathbf{S}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 1& 1& 1\\ 0& l_1\sin {\phi }_1& l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)\\ 0& -l_1\cos {\phi }_1& -l_1\cos {\phi }_1-l_2\cos \left({\phi }_1+{\phi }_2\right)\\ 0& 0& 0\end{array}\right](23)$

In accordance to Equation 17, we know that the twist of the end effector with the marking point on its center is

${\hspace{0.17em}}_C{\mathit{\$}}_E=\left[\begin{array}{c}{\mathit{\omega }}_E\\ {\hspace{0.17em}}_C{\mathit{v}}_E\end{array}\right]=\left[\begin{array}{c}{\mathit{\omega }}_1+{\mathit{\omega }}_2+{\mathit{\omega }}_3\\ {\hspace{0.17em}}_o{\mathit{v}}_E+\left({\mathit{\omega }}_1+{\mathit{\omega }}_2+{\mathit{\omega }}_3\right)\times {\mathit{r}}_C\end{array}\right](24)$

where ${\mathit{r}}_C=\left[\begin{array}{c}{l}_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)+\frac{1}{2}{l}_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)\\ l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)+\frac{1}{2}{l}_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)\\ 0\end{array}\right]$.

By programming with the numerical algorithms, we obtain the forward kinematics of the linkage. With the initial conditions of ${\phi }_1\left(\text{0}\right)$, ${\phi }_2\left(\text{0}\right)$ and ${\phi }_3\left(\text{0}\right)$, and ${\omega }_1$, ${\omega }_2$ and ${\omega }_3$, we get the first set of parameters, $\mathit{\omega }\left(1\right)$ from equation (22). And then we gain the first twist of the end effector from equation (20) and $\mathbf{S}\left(1\right)$ from equation (23) and $\mathrm{c}{\mathit{\$}}_E\left(1\right)$ from equation (24)

Then we get the successive parameters of $\mathbf{S}\left(i\right)$ from Equation 23 and $\mathrm{c}{\mathit{\$}}_E\left(i\right)$ from Equation 24 by updating the data:

$\{\begin{array}{l}{\phi }_1\left(i\right)={\phi }_1\left(0\right)+i\Delta t{\omega }_1\\ {\phi }_2\left(i\right)={\phi }_2\left(0\right)+i\Delta t{\omega }_2\\ {\phi }_3\left(i\right)={\phi }_3\left(0\right)+i\Delta t{\omega }_3\end{array}(25)$

where $i=\mathrm{1,2},\cdots$ and $\Delta t$ is a finite small time increment. The absolute angular displacement of the end effector is

${\phi }_E\left(i\right)={\phi }_1\left(i\right)+{\phi }_2\left(i\right)+{\phi }_3\left(i\right)(26)$

The angular accelerations of each joint can be numerically calculated by

${\alpha }_j\left(i\right)=\frac{{\omega }_j\left(i+1\right)-{\omega }_j\left(i-1\right)}{2\Delta t}(27)$

where $j=\mathrm{1,2},\cdots ,n$ represents the jth joint.

In forward kinematic, we let the angular velocity of screw joint $O_1$ be $3\sin \pi t$_, the angular velocity of screw joint $O_2$ be $2\sin \frac{3\pi t}{2}$_, the angular velocity of screw joint $O_3$ be $\sin 2\pi t$_.with the structure parameters and initial conditions in Table 2, we programmed the above process in MATLAB and drew the forward displacement, velocity and acceleration for each joint (see Figure 5) by numerical methods based on Equations 25–27.

TABLE 2

TABLE 2. Structure parameters and initial conditions.

FIGURE 5

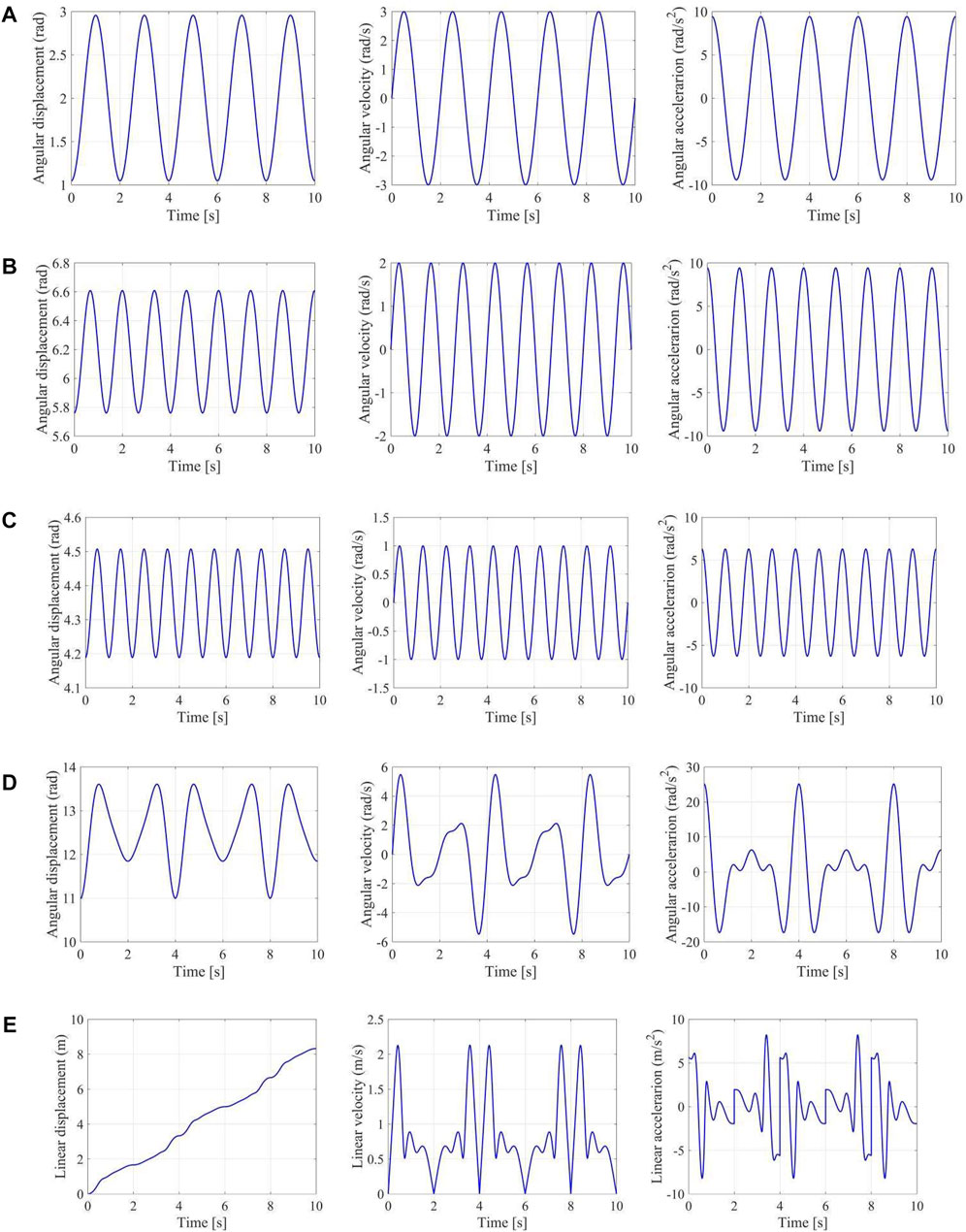
FIGURE 5. Forward kinematics of a planar 4-bar mechanism. (A) Angular displacement, velocity and acceleration of joint A₁; (B) Angular displacement, velocity and acceleration of joint A₂; (C) Angular displacement, velocity and acceleration of joint A₃; (D) Angular displacement, velocity and acceleration of end effector; (E) Linear velocity and acceleration of the center of end effector.

Kinematics of Pivoted Linkages of Closed Chain

Kinematics of the 4-bar Linkage

Figure 6 1) shows a planar 4-bar linkage in series and 2) a 4-bar mechanism with closed loop. The twist of the end effector of the 4-bar linkage in series can be gained from Equation 12:

${\hspace{0.17em}}_o{\mathit{\$}}_E=\mathbf{S}\mathit{\omega }$

where $\mathbf{S}=\left[\begin{array}{cccc}{\mathit{\$}}_1& {\mathit{\$}}_2& {\mathit{\$}}_3& {\mathit{\$}}_4\end{array}\right]$, $\mathit{\omega }={\left[\begin{array}{cccc}{\omega }_1& {\omega }_2& {\omega }_3& {\omega }_4\end{array}\right]}^T$ and ${\mathit{\$}}_1={\left[\begin{array}{cccccc}0& 0& 1& y_1& -x_1& 0\end{array}\right]}^T$, ${\mathit{\$}}_2={\left[\begin{array}{cccccc}0& 0& 1& y_2& -x_2& 0\end{array}\right]}^T$, ${\mathit{\$}}_3={\left[\begin{array}{cccccc}0& 0& 1& y_3& -x_3& 0\end{array}\right]}^T$, ${\mathit{\$}}_4={\left[\begin{array}{cccccc}0& 0& 1& y_4& -x_4& 0\end{array}\right]}^T$.

FIGURE 6

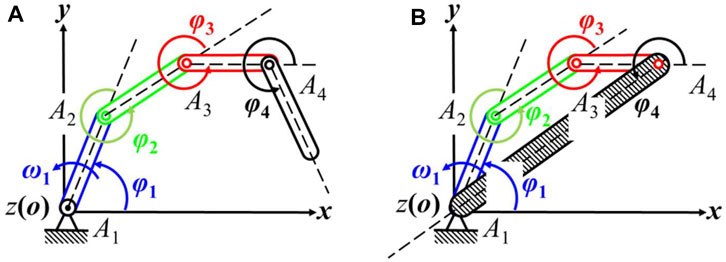
FIGURE 6. Planar 4-bar linkages. (A) A 4-bar linkage in series; (B) A 4-bar linkage with closed loop.

Eq. 12 indicates that the kinematic chain forms a closed loop when the end effector is fixed with the frame (see Figure 6B). And therefore, there must be

${\hspace{0.17em}}_o{\mathit{\$}}_E=\text{0}(28)$

Eq. 28 is called the loop equation of the mechanism which can be used to solve all angular velocities by taking other known conditions into account. In the coordinate frame shown in Figure 6, $x_1=0$, $y_1=0$, $x_2=l_1\cos {\phi }_1$, $y_2=l_1\sin {\phi }_1$, $x_3=l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)$, $y_3=l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)$, $x_4=l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)+l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)$ and $y_4=l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)+l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)$, we get that

$o{\mathit{\$}}_E=\left[\begin{array}{c}0\\ 0\\ o{\mathit{\$}}_E\left(\mathrm{3,1}\right)\\ o{\mathit{\$}}_E\left(\mathrm{4,1}\right)\\ o{\mathit{\$}}_E\left(\mathrm{5,1}\right)\\ 0\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right](29)$

where $o{\mathit{\$}}_E\left(\mathrm{3,1}\right)={\omega }_1+{\omega }_2+{\omega }_3+{\omega }_4$, $o{\mathit{\$}}_E\left(\mathrm{4,1}\right)={\omega }_2{l}_1\sin {\phi }_1+{\omega }_3\left[l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)\right]+{\omega }_4\left[l_1\sin {\phi }_{11}+l_2\sin \left({\phi }_1+{\phi }_2\right)+l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)\right]$, $o{\mathit{\$}}_E\left(\mathrm{5,1}\right)=-{\omega }_2{l}_1\cos {\phi }_1-{\omega }_3\left[l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)\right]-{\omega }_4\left[l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)+l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)\right]$.

Rearranging equation (29) presents

$\{\begin{array}{l}{\omega }_2+{\omega }_3+{\omega }_4=-{\omega }_1\\ {\omega }_2{l}_1\sin {\phi }_1+{\omega }_3\left[l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)\right]+{\omega }_4\left[l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)+l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)\right]=0\\ -{\omega }_2{l}_1\cos {\phi }_1-{\omega }_3\left[l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)\right]-{\omega }_4\left[l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)+l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)\right]=0\end{array}$

Therefore, we gain the forward kinematics of the closed-chain 4-bar linkage (Figure 6B):

${\mathit{\omega }}_F={\mathbf{A}}^{-1}{\mathit{v}}_1(30)$

where

$\mathbf{A}=\left[\begin{array}{ccc}1& 1& 1\\ l_1\sin {\phi }_1& l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)& l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)+l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)\\ -l_1\cos {\phi }_1& -l_1\cos {\phi }_1-l_2\cos \left({\phi }_1+{\phi }_2\right)& -l_1\cos {\phi }_1-l_2\cos \left({\phi }_1+{\phi }_2\right)-l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)\end{array}\right],$

${\mathit{\omega }}_F=\left[\begin{array}{c}{\omega }_2\\ {\omega }_3\\ {\omega }_4\end{array}\right]\text{and}{\mathit{v}}_1=\left[\begin{array}{c}-{\omega }_1\\ 0\\ 0\end{array}\right].$

When the output of ${\omega }_4$ is known, we can also get that

$\{\begin{array}{l}{\omega }_1+{\omega }_2+{\omega }_3=-{\omega }_4\\ {\omega }_2{l}_1\sin {\phi }_1+{\omega }_3\left[l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)\right]=-{\omega }_4\left[l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)+l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)\right]\\ -{\omega }_2{l}_1\cos {\phi }_1-{\omega }_3\left[l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)\right]={\omega }_4\left[l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)+l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)\right]\end{array}$

Consequently, the inverse kinematics of the 4 bar mechanism is now rewritten as

${\mathit{\omega }}_I={\mathbf{B}}^{-1}{\mathit{v}}_4(31)$

where $\mathbf{B}=\left[\begin{array}{ccc}1& 1& 1\\ \text{0}& l_1\sin {\phi }_1& l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)\\ \text{0}& -l_1\cos {\phi }_1& -l_1\cos {\phi }_1-l_2\cos \left({\phi }_1+{\phi }_2\right)\end{array}\right]$, ${\mathit{\omega }}_I=\left[\begin{array}{c}{\omega }_1\\ {\omega }_2\\ {\omega }_3\end{array}\right]$ and ${\mathit{v}}_4=\left[\begin{array}{c}-{\omega }_4\\ -{\omega }_4\left[l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)+l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)\right]\\ {\omega }_4\left[l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)+l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)\right]\end{array}\right]$.

In this regard, the forward velocity and inverse velocity have the same form in mathematical expressions which is one of the advantages of this algorithm. Then, we get the successive parameters of ${\mathit{\omega }}_F$ from Equation 30 or ${\mathit{\omega }}_I$ from Equation 31 by updating the data of $\mathbf{A}$, $\mathbf{B}$ and ${\mathit{v}}_4$ with the interactions below:

$\{\begin{array}{l}{\phi }_1\left(i+1\right)={\phi }_1\left(i\right)+\Delta t{\omega }_1\left(i\right)\\ {\phi }_2\left(i+1\right)={\phi }_2\left(i\right)+\Delta t{\omega }_2\left(i\right)\\ {\phi }_3\left(i+1\right)={\phi }_3\left(i\right)+\Delta t{\omega }_3\left(i\right)\end{array}(32)$

where $i=\mathrm{1,2},\cdots$ represents the ith iteration and $\Delta t$ is a finite small time increment.

Compared with the Denavit-Hartenberg notation for a closed loop (Craig, 1986), the kinematics algorithm in screw form here only requires to implement one numerical integration 32) for displacement and one numerical differential 27) for acceleration in the absolute coordinate frame. This provides a more convergent algorithm to develop computational kinematics of a linkage. We let the angular velocity of joint $O_1$ is 2 rad/s and with the structure parameters and initial conditions in Table 3, we programmed the method in MATLAB and obtained the forward displacement, velocity and acceleration for each joint (see Figure 7) by numerical methods based on Equations 32, 27 for validating the method.

TABLE 3

TABLE 3. Structure parameters and initial conditions.

FIGURE 7

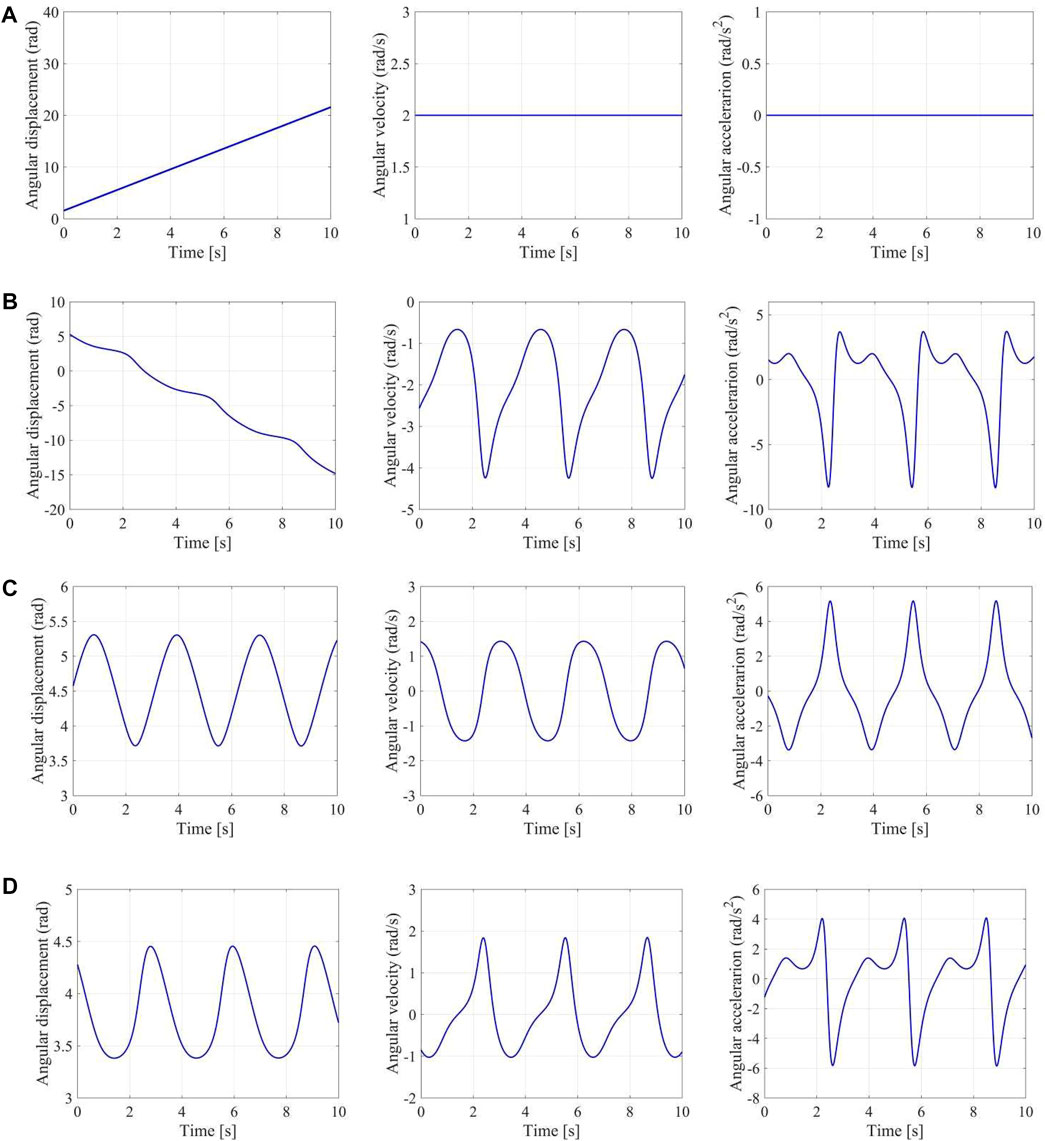
FIGURE 7. Forward kinematics of a planar 4-bar linkage. (A) Angular displacement, velocity and acceleration of joint A₁; (B) Angular displacement, velocity and acceleration of joint A₂; (C) Angular displacement, velocity and acceleration of joint A₃; (D) Angular displacement, velocity and acceleration of joint A₄.

Kinematics of an Articulated Linkage of 1 degree of Freedom With Multiple Closed Chains

Figure 8 illustrates a planar multi-closed-chain 6-bar linkage 1) in which there are two independent closed chains (b). For the first closed chain of a 4-bar linkage (Figure 8 (c)), the loop equation can be found from Equation 27:

$\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 1& 1& 1& 1\\ y_{A_1}& y_{A_2}& y_{A_3}& y_{A_4}\\ -x_{A_1}& -x_{A_2}& -x_{A_3}& -x_{A_4}\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}\underset{¯}{{\omega }_{A_1}}\\ {\omega }_{A_2}\\ {\omega }_{A_3}\\ {\omega }_{A_4}\end{array}\right]=0$

where $\underset{¯}{{\omega }_{A_1}}$ is the input. Rearranging this loop equation yields:

$\left[\begin{array}{ccc}1& 1& 1\\ y_{A_2}& y_{A_3}& y_{A_4}\\ -x_{A_2}& -x_{A_3}& -x_{A_4}\end{array}\right]\left[\begin{array}{c}{\omega }_{A_2}\\ {\omega }_{A_3}\\ {\omega }_{A_4}\end{array}\right]=\left[\begin{array}{c}-\underset{¯}{{\omega }_{A_1}}\\ -\underset{¯}{{\omega }_{A_1}}{y}_{A_1}\\ \underset{¯}{{\omega }_{A_1}}{x}_{A_1}\end{array}\right](33)$

FIGURE 8

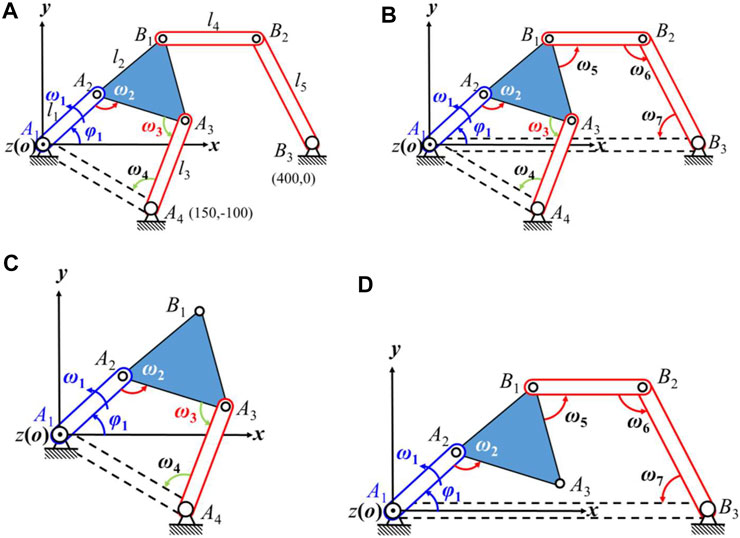
FIGURE 8. A planar 6-bar linkage. (A) Structure of a planar 6-bar linkage; (B) Two independent closed-chain 6-bar linkages; (C) A 4-bar linkage of closed chain; (D) Closed chain of a coupled 5-bar linkage.

Similarly, we get the loop equation of the second coupled 5-bar closed chain linkage (Figure 8 (d)) from Equation 28:

$\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 1& 1& 1& 1& 1\\ y_{A_1}& y_{A_2}& y_{B_1}& y_{B_2}& y_{B_3}\\ -x_{A_1}& -x_{A_2}& -x_{B_1}& -x_{B_2}& -x_{B_3}\\ 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}\underset{¯}{{\omega }_{A_1}}\\ {\omega }_{A_2}\\ {\omega }_{B_1}\\ {\omega }_{B_2}\\ {\omega }_{B_3}\end{array}\right]=0$

Rearranging this loop equation presents:

$\left[\begin{array}{cccc}1& 1& 1& 1\\ y_{A_2}& y_{B_1}& y_{B_2}& y_{B_3}\\ -x_{A_2}& -x_{B_1}& -x_{B_2}& -x_{B_3}\end{array}\right]\left[\begin{array}{c}{\omega }_{A_2}\\ {\omega }_{B_1}\\ {\omega }_{B_2}\\ {\omega }_{B_3}\end{array}\right]=\left[\begin{array}{c}-\underset{¯}{{\omega }_{A_1}}\\ -\underset{¯}{{\omega }_{A_1}}{y}_{A_1}\\ \underset{¯}{{\omega }_{A_1}}{x}_{A_1}\end{array}\right](34)$

So the forward kinematics of the multiple closed chain linkage can be obtained by associating these double-loop Equations 33, 34:

$\mathit{\omega }={\mathbf{M}}^{-1}\mathit{v}(35)$

where $\mathbf{M}=\left[\begin{array}{cccccc}1& 1& 1& 0& 0& 0\\ y_{A_2}& y_{A_3}& y_{A_4}& 0& 0& 0\\ -x_{A_2}& -x_{A_3}& -x_{A_4}& 0& 0& 0\\ 1& 0& 0& 1& 1& 1\\ y_{A_2}& 0& 0& y_{B_1}& y_{B_2}& y_{B_3}\\ -x_{A_2}& 0& 0& -x_{B_1}& -x_{B_2}& -x_{B_3}\end{array}\right]$, $\mathit{\omega }=\left[\begin{array}{c}{\omega }_{A_2}\\ {\omega }_{A_3}\\ {\omega }_{A_4}\\ {\omega }_{B_1}\\ {\omega }_{B_2}\\ {\omega }_{B_3}\end{array}\right]$ and $\mathit{v}=\left[\begin{array}{c}-\underset{¯}{{\omega }_{A_1}}\\ -\underset{¯}{{\omega }_{A_1}}{y}_{A_1}\\ \underset{¯}{{\omega }_{A_1}}{x}_{A_1}\\ -\underset{¯}{{\omega }_{A_1}}\\ -\underset{¯}{{\omega }_{A_1}}{y}_{A_1}\\ \underset{¯}{{\omega }_{A_1}}{x}_{A_1}\end{array}\right]$.

We let the angular velocity of joint $O_1$ is 2 rad/s and with the structure parameters and initial conditions in Table 4, we programmed the method in MATLAB and gained the forward displacement, velocity and acceleration for each joint (see Figure 9) by numerical methods with Equation 35.

TABLE 4

TABLE 4. Structure parameters and initial conditions.

FIGURE 9

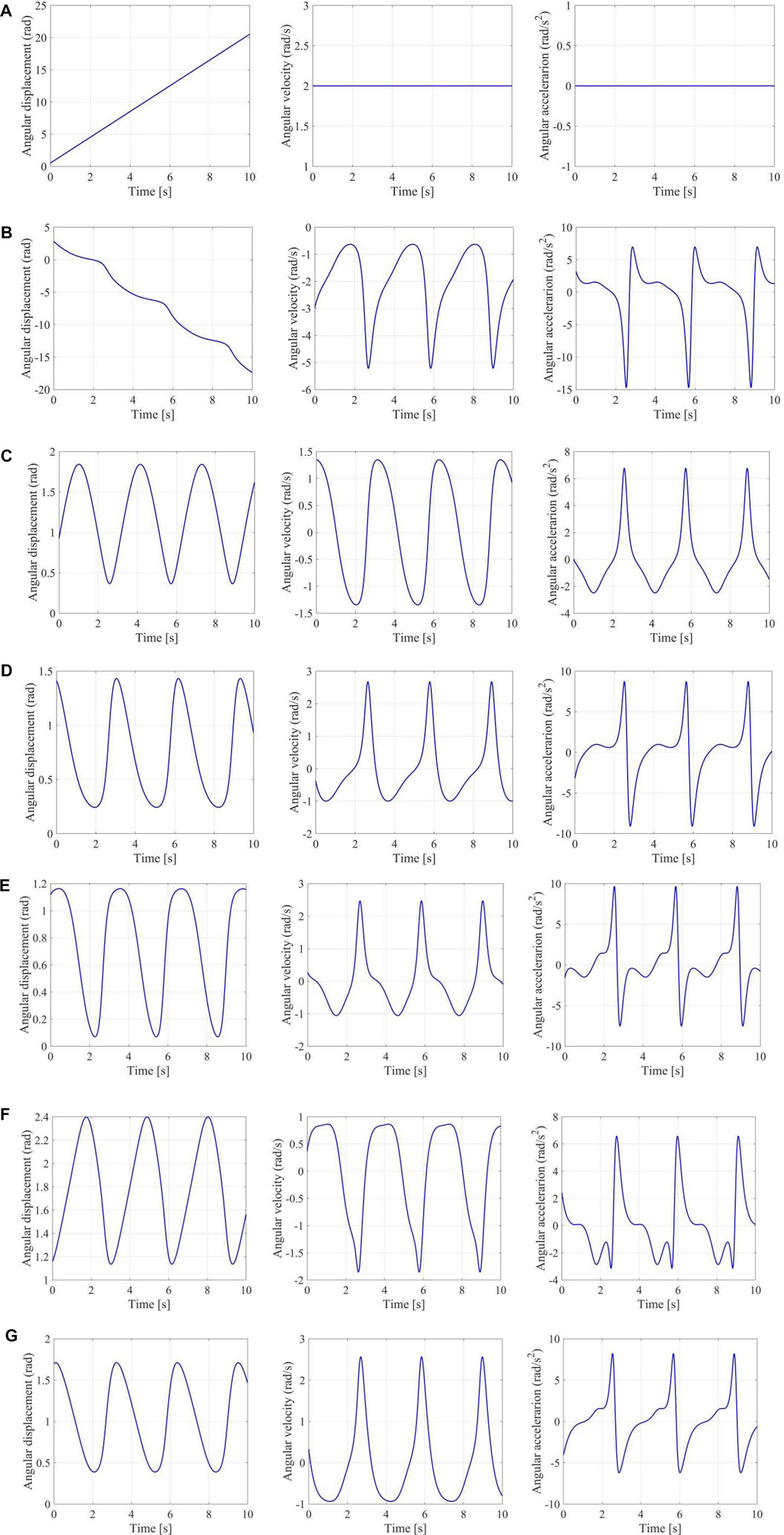
FIGURE 9. Forward kinematics of a multiple closed chain linkage. (A) Angular displacement, velocity, and acceleration of joint A₁; (B) Angular displacement, velocity, and acceleration of joint A₂; (C) Angular displacement, velocity, and acceleration of joint A₃; (D) Angular displacement, velocity, and acceleration of joint A₄; (E) Angular displacement, velocity, and acceleration of joint B₁; (F) Angular displacement, velocity, and acceleration of joint B₂; (G) Angular displacement, velocity, and acceleration of joint B₃.

Kinematics of a Planar Mechanism of More Degrees of Freedom With Single Closed Chain

Figure 10 illustrates 1) a planar 5-bar linkage in series and 2) a 5-bar linkage of closed loop. The twist of the end effector of the 5-bar linkage in series can be gained by Equation 12:

${\hspace{0.17em}}_o{\mathit{\$}}_E=\mathbf{S}\mathit{\omega }$

where $\mathbf{S}=\left[\begin{array}{ccccc}{\mathit{\$}}_1& {\mathit{\$}}_2& {\mathit{\$}}_3& {\mathit{\$}}_4& {\mathit{\$}}_5\end{array}\right]$, $\mathit{\omega }={\left[\begin{array}{ccccc}{\omega }_1& {\omega }_2& {\omega }_3& {\omega }_4& {\omega }_5\end{array}\right]}^T$ and ${\mathit{\$}}_1={\left[\begin{array}{cccccc}0& 0& 1& y_1& -x_1& 0\end{array}\right]}^T$, ${\mathit{\$}}_2={\left[\begin{array}{cccccc}0& 0& 1& y_2& -x_2& 0\end{array}\right]}^T$, ${\mathit{\$}}_3={\left[\begin{array}{cccccc}0& 0& 1& y_3& -x_3& 0\end{array}\right]}^T$, ${\mathit{\$}}_4={\left[\begin{array}{cccccc}0& 0& 1& y_4& -x_4& 0\end{array}\right]}^T$, ${\mathit{\$}}_5={\left[\begin{array}{cccccc}0& 0& 1& y_5& -x_5& 0\end{array}\right]}^T$.

FIGURE 10

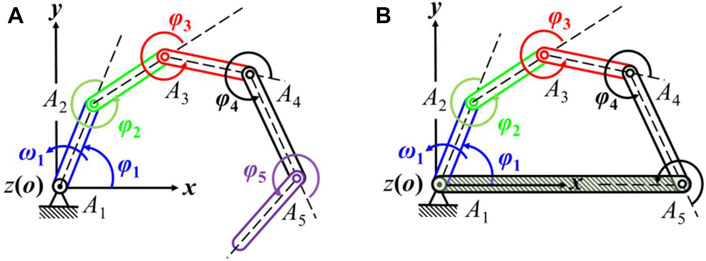
FIGURE 10. Planar 5-bar linkages. (A) A 5-bar linkage in series; (B) A 5-bar linkage of closed chain.

From Equation 12, we know that the kinematic chain forms a closed loop when the end effector is fixed with the frame (Figure 10B). Therefore, there must be ${\hspace{0.17em}}_o{\mathit{\$}}_E=\text{0}$. In the coordinate frame shown in Figure 10, $x_1=0$, $y_1=0$, $x_2=l_1\cos {\phi }_1$, $y_2=l_1\sin {\phi }_1$, $x_3=l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)$, $y_3=l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)$, $x_4=l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)+l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)$, $y_4=l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)+l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)$, and $x_5=l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)+l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)+l_4\cos \left({\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4\right)$, and $y_5=l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)+l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)+l_4\sin \left({\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4\right)$, we get that

$o{\mathit{\$}}_E=\left[\begin{array}{c}0\\ 0\\ \begin{array}{l}{\omega }_1+{\omega }_2+{\omega }_3+{\omega }_4+{\omega }_5\end{array}\\ {\omega }_2{l}_1\sin {\phi }_1+{\omega }_3\left[l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)\right]+{\omega }_4\left[l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)+l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)\right]\\ +{\omega }_5\left[l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)+l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)+l_4\cos \left({\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4\right)\right]\\ -{\omega }_2{l}_1\cos {\phi }_1-{\omega }_3\left[l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)\right]-{\omega }_4\left[l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)+l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)\right]\\ -{\omega }_5\left[l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)+l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)+l_4\cos \left({\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4\right)\right]\\ 0\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right](36)$

Then there is

$\{\begin{array}{l}{\omega }_2+{\omega }_3+{\omega }_4=-{\omega }_1-{\omega }_5\\ {\omega }_2{l}_1\sin {\phi }_1+{\omega }_3\left[l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)\right]+{\omega }_4\left[\begin{array}{l}{l}_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)\\ +l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)\end{array}\right]=-{\omega }_5\left[\begin{array}{l}{l}_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)\\ +l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)\\ +l_4\sin \left({\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4\right)\end{array}\right]\\ -{\omega }_2{l}_1\cos {\phi }_1-{\omega }_3\left[l_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)\right]-{\omega }_4\left[\begin{array}{l}{l}_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)\\ +l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)\end{array}\right]={\omega }_5\left[\begin{array}{l}{l}_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)\\ +l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)\\ +l_4\cos \left({\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4\right)\end{array}\right]\end{array}$

Therefore, we get the forward kinematics of the closed-chain 5-bar linkage (Figure 10B):

${\mathit{\omega }}_F={\mathbf{A}}^{-1}{\mathit{\omega }}_1(37)$

where $\mathbf{A}=\left[\begin{array}{ccc}1& 1& 1\\ l_1\sin {\phi }_1& l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)& l_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)+l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)\\ -l_1\cos {\phi }_1& -l_1\cos {\phi }_1-l_2\cos \left({\phi }_1+{\phi }_2\right)& -l_1\cos {\phi }_1-l_2\cos \left({\phi }_1+{\phi }_2\right)-l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)\end{array}\right]{\mathit{\omega }}_F=\left[\begin{array}{c}{\omega }_2\\ {\omega }_3\\ {\omega }_4\end{array}\right]$and ${\mathit{\omega }}_1={\left[\begin{array}{ccc}-{\omega }_1-{\omega }_5& -{\omega }_5\left[\begin{array}{l}{l}_1\sin {\phi }_1+l_2\sin \left({\phi }_1+{\phi }_2\right)\\ +l_3\sin \left({\phi }_1+{\phi }_2+{\phi }_3\right)\\ +l_4\sin \left({\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4\right)\end{array}\right]& {\omega }_5\left[\begin{array}{l}{l}_1\cos {\phi }_1+l_2\cos \left({\phi }_1+{\phi }_2\right)\\ +l_3\cos \left({\phi }_1+{\phi }_2+{\phi }_3\right)\\ +l_4\cos \left({\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4\right)\end{array}\right]\end{array}\right]}^T$.

Eq. 37 represents the forward velocity of the planar 5-bar mechanism of 2 degrees of freedom. In accordance to the numerical Eq. 32, 27, we obtain the forward displacement and acceleration of the mechanism with a single closed chain. We let the angular velocity of joint $O_1$ is 3 rad/s, the angular velocity of joint $O_2$ is 4 rad/s, and with the structure parameters in Table 5, the displacement, velocity and acceleration curves for each joint are illustrated in Figure 11 by numerical formulas of Eq. 32, 27 in accordance to Equation 37.

TABLE 5

TABLE 5. Initial conditions and structure parameters.

FIGURE 11

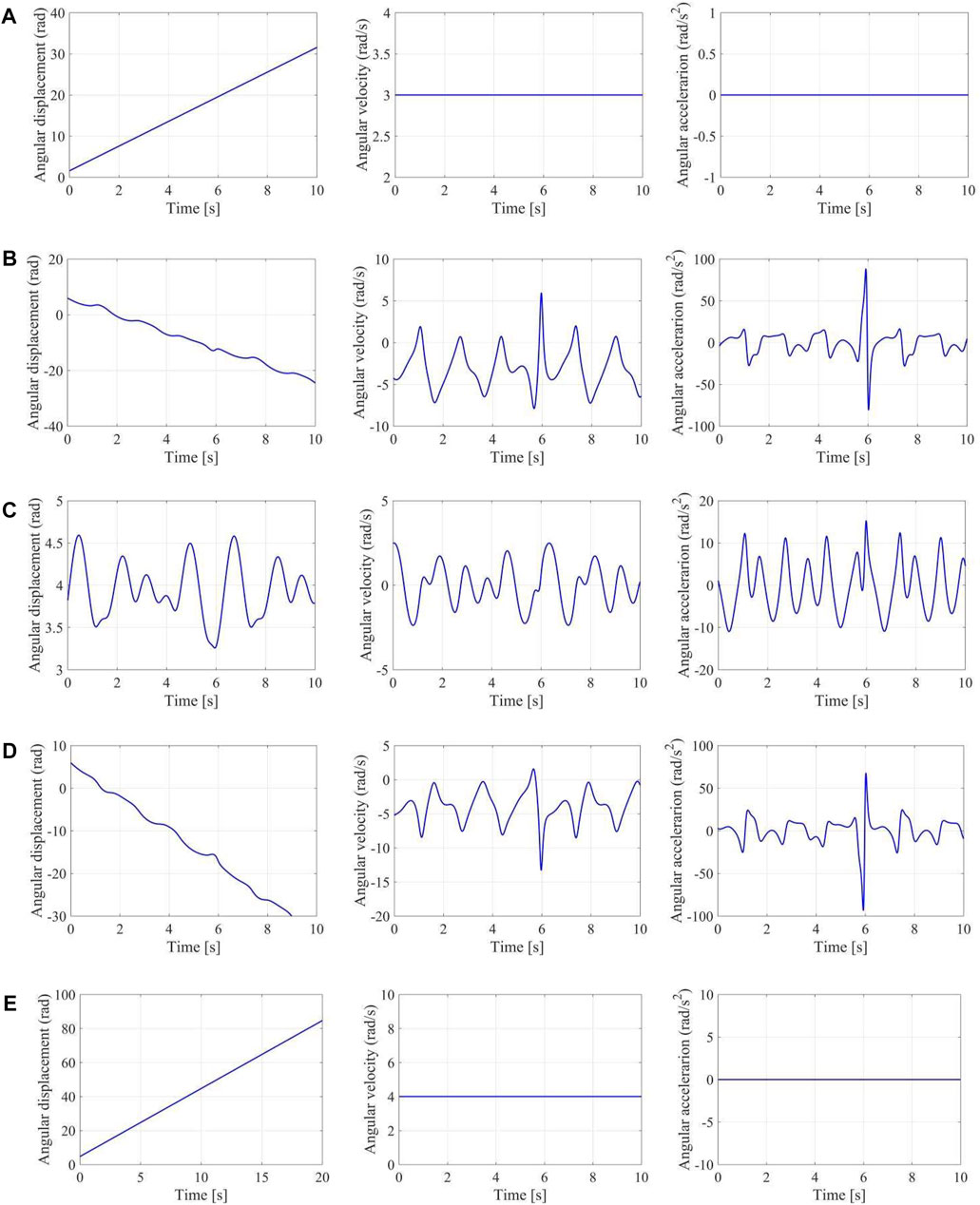
FIGURE 11. Forward kinematics of a 5-bar linkage. (A) Angular displacement, velocity, and acceleration of joint A₁; (B) Angular displacement, velocity, and acceleration of joint A₂; (C) Angular displacement, velocity, and acceleration of joint A₃; (D) Angular displacement, velocity, and acceleration of joint A₄; (E) Angular displacement, velocity, and acceleration of joint A₅.

Conclusion

This paper proposed a method to investigate the displacement, velocity and acceleration of a mechanism in screw coordinates in a general systematic way. As the twist of an articulated rigid body includes the angular velocity and linear velocity, the corresponding displacements of all joints are obtained through one-order integration of the velocity solutions and the accelerations are represented by the first order numerical differential interpolation. Compared to the traditional methods in which the displacement parameters are the only variables that will surely lead to the second order differential interpolations for the accelerations, the advantages of this method is that both the forward and inverse kinematics of a mechanism can be expressed in a same way and only one-order differential interpolation is needed to get the acceleration and one-order integral is required to calculate the displacement. This method is validated by planar mechanisms in series, single closed loop and multiple closed loops. This method is particularly suitable for programming the computational software for forward and inverse kinematics of a mechanism, covering the velocity, displacement and acceleration. Although this paper discusses the kinematics of revolute jointed planar mechanisms, the same principles may apply to any spatial linkages.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

methodology, J-SZ; software, S-TW; validation, J-SZ, S-TW; formal analysis, J-SZ; investigation, J-SZ, S-TW; resources, J-SZ; data curation, S-TW; writing—original draft preparation, J-SZ; writing—review and editing, J-SZ, S-TW; visualization, J-SZ, S-TW; supervision, J-SZ; project administration, J-SZ; funding acquisition, J-SZ All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Natural Science Foundation of China under Grant 51575291.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2021.774814/full#supplementary-material

References

Amiri, A., and Mazaheri, H. (2020). Study on the Behavior of a Temperature-Sensitive Hydrogel Micro-channel via FSI and Non-FSI Approaches. Acta Mech. 231, 2799–2813. doi:10.1007/s00707-020-02673-z

CrossRef Full Text | Google Scholar

Angeles, J. (1982). Spatial Kinematic Chains: Analysis, Synthesis, and Optimization. Berlin: Springer-Verlag, 55–76.

Google Scholar

Barus, C. (1900). A Treatise on the Theory of Screws. Cambridge: Cambridge University Press, 1001–1003. doi:10.1126/science.12.313.1001

CrossRef Full Text | Google Scholar

Bottema, O., and Roth, B. (1979). Theoretical Kinematics. New York, Jan: North-Holland, 35–56.

Google Scholar

Brát, V., and Lederer, P. (1973). KIDYAN: Computer-Aided Kinematic and Dynamic Analysis of Planar Mechanisms. Mechanism Machine Theor. 8 (4), 457–467. doi:10.1016/0094-114X(73)90020-7

CrossRef Full Text | Google Scholar

Chapelle, F., and Bidaud, P. (2004). Closed Form Solutions for Inverse Kinematics Approximation of General 6R Manipulators. Mechanism Machine Theor. 39 (3), 323–338. doi:10.1016/j.mechmachtheory.2003.09.003

CrossRef Full Text | Google Scholar

Craig, J. (1986). Introduction to Robotics, Mechanics and Control. New York, Jan: Addison-Wesley, 33–137.

Google Scholar

Dai, J. (2014). Screw Algebra and Lie Groups and Lie Algebras. 2nd Edition. Beijing: Higher Education Press, 123–140.

Google Scholar

Davidson, J. K., and Hunt, K. H. (2004). Robots and Screw Theory: Applications of Kinematics and Statics to Robotics. New York: Oxford University Press, 56–78.

Google Scholar

Duffy, J. (1980). Analysis of Mechanisms and Robot Manipulators. London: Edward Arnold, 123–135.

Google Scholar

Duffy, J. (1996). Statics and Kinematics with Applications to Robotics. New York: Cambridge University Press, 46–78.

Google Scholar

Faghidian, S. A., and Mohammad-Sedighi, H. (2020). Dynamics of Nonlocal Thick Nano-Bars. Eng. Comput. doi:10.1007/s00366-020-01216-3

CrossRef Full Text | Google Scholar

García de Jalón, J., and Bayo, E. (1994). Kinematic and Dynamic Simulation of Multibody Systems: The Real-Time Challenge. New York, Jan: Springer-Verlag, 220–254.

Google Scholar

Gough, V. E., and Whitehall, S. G. (1962). “Universal Tyre Test Machine,” Proceedings of the International Technical Congress FISITA. UK: Institution of Mechanical Engineers, 117.

Google Scholar

Hunt, K. H. (1978). Kinematic Geometry of Mechanisms. New York, Jan: Oxford University Press, 66–85.

Google Scholar

Kong, K., Chen, G., and Hao, G. (2019). Kinetostatic Modeling and Optimization of a Novel Horizontal-Displacement Compliant Mechanism. J. Mech. Robotics 11 (6), 1. doi:10.1115/1.4044334

CrossRef Full Text | Google Scholar

Kong, X., He, X., and Li, D. (2018). A Double-Faced 6R Single-Loop Overconstrained Spatial Mechanism. J. Mech. robotics 10 (3). 031013 doi:10.1115/1.4039224

CrossRef Full Text | Google Scholar

Kong, X., Yu, J., and Li, D. (2016). Reconfiguration Analysis of a Two Degrees-Of-Freedom 3-4R Parallel Manipulator with Planar Base and Platform1. J. Mech. Robotics 8 (17). 011019 doi:10.1115/1.4031027

CrossRef Full Text | Google Scholar

McCarthy, J. M. (1990). An Introduction to Theoretical Kinematics. London, Mar: The MIT Press, 33–45.

Google Scholar

McCarthy, J. M., and Soh, G. S. (2011). Geometric Design of Linkages. New York, Jan: Springer, 13–46.

Google Scholar

Norton, R. L. (2004). Design of Machinery—An Introduction to the Synthesis and Analysis of Mechanisms and Machines. 3rd ed. New York, Jan: McGraw-Hill Companies, Inc., 30–81.

Google Scholar

Saura, M., Segado, P., and Dopico, D. (2019). Computational Kinematics of Multibody Systems: Two Formulations for a Modular Approach Based on Natural Coordinates. Mechanism Machine Theor. 142 (12). 103602 doi:10.1016/j.mechmachtheory.2019.103602

CrossRef Full Text | Google Scholar

Shen, H., Chablat, D., Zeng, B., Li, J., Wu, G., and Yang, T.-L. (2020). A Translational Three-Degrees-Of-Freedom Parallel Mechanism with Partial Motion Decoupling and Analytic Direct Kinematics. J. Mech. Robotics 12 (2). 021112 doi:10.1115/1.4045972

CrossRef Full Text | Google Scholar

Shigley, J. E., and Uicher, J. J. (1980). Theory of Machines and Mechanisms. New York, Jan: McGraw-Hill Companies, Inc.

Google Scholar

Stewart, D. (1965). A Platform with Six Degrees of freedom. Proc. Inst. Mech. Eng. 180 (1), 371–386. doi:10.1243/pime_proc_1965_180_029_02

CrossRef Full Text | Google Scholar

Suh, C. H., and Radcliffe, C. W. (1978). Kinematics and Mechanisms Design. New York: Wiley

Google Scholar

Waldron, K. J., and Kinematics, G. L. Kinzel. (2004). Dynamics, and Design of Machinery. Hamilton PrintingNew York: John Wiley & Sons, 5–16.

Google Scholar

Wu, J., Gao, Y., Zhang, B., and Wang, L. (2017). Workspace and Dynamic Performance Evaluation of the Parallel Manipulators in a spray-painting Equipment. Robotics and Computer-Integrated Manufacturing 44 (4), 199–207. doi:10.1016/j.rcim.2016.09.002

CrossRef Full Text | Google Scholar

Wu, J., Li, T., Wang, J., and Wang, L. (2013). Performance Analysis and Comparison of Planar 3-DOF Parallel Manipulators with One and Two Additional Branches. J. Intell. Robot Syst. 72 (1), 73–82. doi:10.1007/s10846-013-9824-8

CrossRef Full Text | Google Scholar

Wu, J., Wang, J., Wang, L., and Li, T. (2009). Dynamics and Control of a Planar 3-DOF Parallel Manipulator with Actuation Redundancy. Mechanism and Machine TheoryApr 44 (4), 835–849. doi:10.1016/j.mechmachtheory.2008.04.002

CrossRef Full Text | Google Scholar

Yang, T.-L., Liu, A., Shen, H., Hang, L., and Jeffery Ge, Q. (2018). Composition Principle Based on Single-Open-Chain Unit for General Spatial Mechanisms and its Application-In Conjunction with a Review of Development of Mechanism Composition Principles. J. Mech. Robotics 10 (5). 051005 doi:10.1115/1.4040488

CrossRef Full Text | Google Scholar

Zhao, D.-J., Zhao, J.-S., and Yan, Z.-F. (2016). Planar Deployable Linkage and its Application in Overconstrained Lift Mechanism. J. Mech. Robotics 8 (29). 021022 doi:10.1115/1.4032096

CrossRef Full Text | Google Scholar

Zhao, J., Feng, Z., Chu, F., and Ma, N. (2014). Advanced Theory of Constraint and Motion Analysis for Robot Mechanisms. Elsevier, 113–157. doi:10.1016/B978-0-12-420162-0.00014-X10.1016/b978-0-12-420162-0.00004-7Free Motion of the End Effector of a Robot Mechanism

CrossRef Full Text | Google Scholar