Ab-Initio Predictions of the Energy Harvesting Performance of L-Arginine and L-Valine Single Crystals

Biological piezoelectric materials are beginning to gain attention for their huge potential as eco-friendly energy harvesting materials. In particular, simple amino acid and peptide crystal assemblies are demonstrating large voltage outputs under applied force, and high sensitivity when detecting vibrations. Here we utilise Density Functional Theory (DFT) calculations to quantitatively predict the energy harvesting properties of two understudied proteinogenic amino acid crystals: L-Arginine and L-Valine. The work highlights the ability of quantum mechanical calculations to screen crystals as high-performance energy harvesters, and demonstrates the capability of small biological crystals as eco-friendly piezoelectric materials. L-Arginine is predicted to have a maximum piezoelectric voltage constant of g_ij = 274 mV m/N, with a Young’s Modulus of E = 17.1 GPa. L-Valine has a maximum predicted piezoelectric voltage constant of g_ij = 62 mV m/N, with a calculated Young’s Modulus of E = 19.8 GPa.

Introduction

Piezoelectric materials have long been utilised for their ability to linearly interconvert electrical and mechanical energy. In recent years, there has been a large increase in the number of biomolecule-based materials demonstrating this phenomenon, from amino acids (Lemanov, 2000; Guerin et al., 2018a) and peptides (Baptista et al., 2019; Gayatri and Hutchison, 2019; Basavalingappa et al., 2020) to globular (Stapleton et al., 2017) and transmembrane proteins (O'Donnell et al., 2021), viruses (Lee et al., 2012), plants (Alluri et al., 2020), and food waste (Ghosh and Mandal, 2017; Ghosh et al., 2021). While a number of these materials rival established inorganic piezoelectrics such as aluminium nitrate (AlN) (Supryadkina et al., 2014) and zinc oxide (ZnO) (Kobiakov, 1980), few have demonstrated piezoelectric strain constants that can rival ceramics such as barium titanate (BaTiO3), lead zirconium titanate (PZT), and lead-free counterparts (Panda and Sahoo, 2015; Bell and Deubzer, 2018) for traditional sensing and actuating applications. More recently, biomolecular crystals have been shown to outperform PZT and KNN films (Zhou et al., 2011; Basavalingappa et al., 2020), as well as PVDF polymer films (Okosun et al., 2021).

The more natural application avenue for biomolecular crystal piezoelectrics is in energy harvesting. For years this field has successfully utilised many techniques to modulate the dielectric constants of inorganic piezoelectric materials and increase their energy harvesting performance (Trolier-McKinstry et al., 2011; Roscow et al., 2019; Wang et al., 2021). The lower the dielectric constant of a material the higher its piezoelectric voltage constant g_ij, and the higher the electric field generated per unit force. Biomolecular crystals have an average dielectric constant of 3, two orders of magnitude lower than ceramics (Zhang et al., 2007; Guerin et al., 2019). This means that even “weak” organic piezoelectrics can outperform ceramics and polymers in both output per unit force and sensitivity. We have recently demonstrated this using a flexible glycine-based energy harvester that can be used as a structural health monitor to detect leaks in water infrastructure networks (Okosun et al., 2021). Amino acids have also been utilised to detect ultra-low mechanical pressures (Bishara et al., 2020).

In this work, we add to the database of biomolecular crystals that can be used as low-cost, eco-friendly, high-performance energy harvesters, by predicting the electromechanical properties of the amino acids L-Arginine and L-Valine. We report the elastic, piezoelectric, and dielectric properties of these crystals, and rationalise their anisotropic response via supramolecular packing analysis. This methodology can be used to screen biomolecular crystals such as these for desirable electromechanical properties, which can then be experimentally validated using techniques such as impedance spectroscopy, scanning probe microscopy, nanoindentation, or the Berlincourt method.

L-Arginine is one of the most underutilised amino acids, with the molecule being used as a ligand in 1D-copper (II) coordination polymers (Alikhani et al., 2020). Arginine has been crystallized as L-arginine 4-nitrophenolate 4-nitrophenol dehydrate (LAPP) (Wang et al., 2011), L-arginine hydrofluoride (Pal and Kar, 2002), and L-arginine hydrochloride monohydrate (Kalaiselvi et al., 2008) for non-linear optical applications, as has L-Valine (Moitra and Kar, 2010). These biomolecular-crystal assemblies can be grown at room temperature with no by-products, and do not require an external electric field to induce piezoelectricity, unlike PZT and other piezoceramics. Both the raw material and fabrication cost of arginine and valine are a tiny fraction of that of current commercial piezoelectrics which rely on heavy processing of heavy metals and their oxides, which carries a large financial and environmental burden (Ibn-Mohammed et al., 2018).

Results and Discussion

L-Arginine crystallises in the monoclinic space group P2₁, allowing for eight non-zero piezoelectric tensor components. The predicted piezoelectric charge constants (Table 1), denoted e_ij, range from a minimum of e₁₄ = 0.0041 C/m² to a maximum of e₂₂ = 0.1031 C/m². Dividing the charge tensor by the calculated elastic stiffness tensor (Table 2) gives the piezoelectric strain constants d_ij (Table 3), which for Arginine range from d₁₄ = 0.28 pC/N to d₁₆ = 6.52 pC/N. The elastic stiffness tensor itself shows high elastic anisotropy, with increased stability along the crystallographic a axis (c₁₁ = 29 GPa, c₄₄ = 14 GPa). The bulk Young’s Modulus is predicted to be 17.1 GPa.

TABLE 1

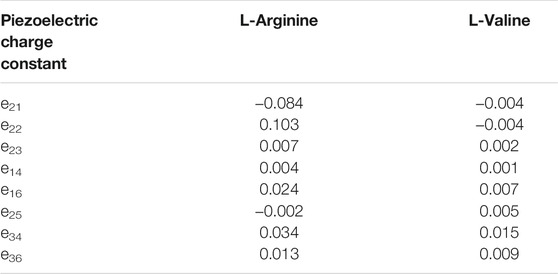
TABLE 1. DFT-predicted piezoelectric charge tensor components of L-Arginine and L-Valine single crystals. All values are in C/m².

TABLE 2

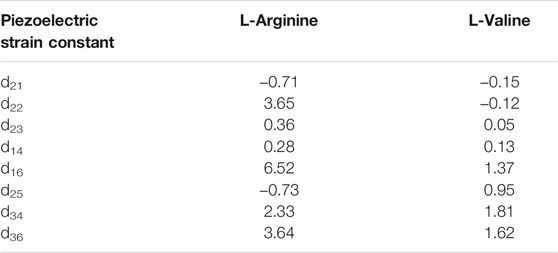
TABLE 2. DFT-predicted piezoelectric strain tensor components of L-Arginine and L-Valine single crystals. All values are in pC/N.

TABLE 3

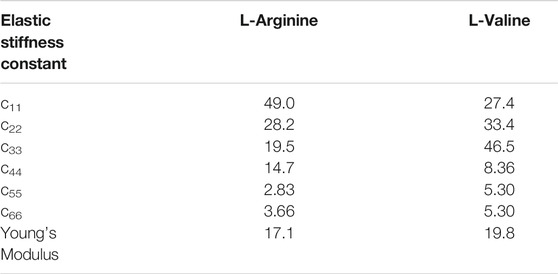
TABLE 3. DFT-predicted elastic stiffness tensor components and elastic moduli of L-Arginine and L-Valine single crystals. All values are in GPa.

As mentioned, the key energy harvesting figures of merit (FoMs) are the piezoelectric voltage constants g_ij (Table 4). The predicted bulk dielectric constant of L-Arginine is 2.54, resulting in predicted voltage constants ranging from 12 mV m/N to 274 mV m/N. L-Arginine is predicted to have five voltage constants that exceed both the 40 mV/m N value for KNN ceramics (Zhang et al., 2007), and the 64 mV m/N of organic polymer PVDF (Bernard et al., 2017).

TABLE 4

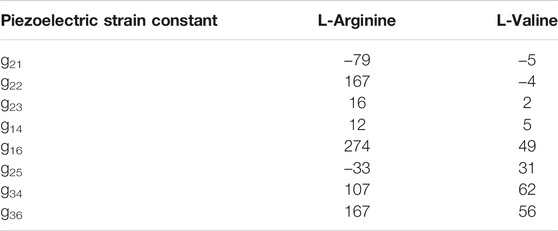
TABLE 4. DFT-predicted piezoelectric voltage tensor components of L-Arginine and L-Valine single crystals. All values are in mV m/N.

L-Valine is predicted to have a low piezoelectric response compared to other biological crystals. It too crystallises in the monoclinic P2₁ space group, with eight piezoelectric constants in each tensor. The piezoelectric charge constants of valine range from 0.0024 to 0.0151 C/m². It is unique amongst biomolecular crystals in that the predicted electronic and ionic contributions to the piezoelectric tensor are both high but of opposite polarity, resulting in these reduced values. This also explains why valine has a low piezoelectric response, but high non-linear optical performance (Moitra and Kar, 2010), as we have recently demonstrated that the second harmonic generation capabilities of small biomolecular crystals correlates to the electronic contribution to the piezoelectric tensor only (Gleeson et al., 2020).

L-Valine is predicted to have lower elastic anisotropy than L-Arginine, but does demonstrate increased longitudinal stiffness along the crystallographic c axis (c₃₃ = 46.5 GPa). Its piezoelectric strain constants range from d₂₃ = 0.05 pC/N to d₃₄ = 1.8 pC/N, of similar value to quartz crystals. Still, we see that the predicted dielectric constant of 3.31 results in four piezoelectric voltage constants that exceed that of PZT (25 mV m/N), though they are all shear, i.e. voltage can only be produced under application of a shearing force. The predicted piezoelectric voltage constants of L-Valine range from 2 to 62 mV m/N.

Looking at the supramolecular packing of the L-Arginine unit cell (Figure 1), we can see that the high stiffness along the crystallographic a axis is due to both continuous directional hydrogen bonding and the molecular backbone, which runs perpendicular to the axis increasing mechanical stability. By symmetry and the presence of a 22 piezoelectric constant, the net dipole in the crystal will be predominantly in line with the b axis, which also contains a continuous directional hydrogen bond network. The zwitterionic molecules create this 2D hydrogen bond network in the ab plane, enhancing the piezoelectric polarisation both in equilibrium and under an applied longitudinal (along b only) or shear force.

FIGURE 1

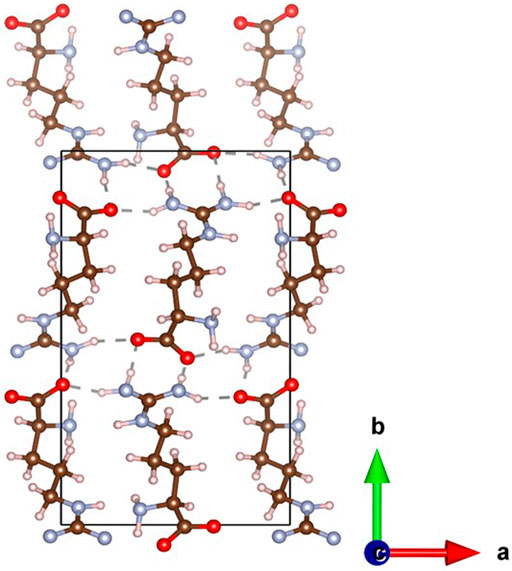
FIGURE 1. Crystal structure of L-Arginine, with molecules shown in CPK representation. Nitrogen atoms are coloured red, carbons are brown, hydrogens are white, and nitrogens are blue. Intermolecular hydrogen bonds are shown in dark grey.

L-Arginine has many features of a moderately piezoelectric molecular crystal, with medium to high density, small functional groups, low molecular weight, and a monoclinic angle of 97.4°. Comparing the response to other materials we see that the maximum piezoelectric strain constant of both crystals is low compared to many inorganic single crystals and ceramics (Figure 2).

FIGURE 2

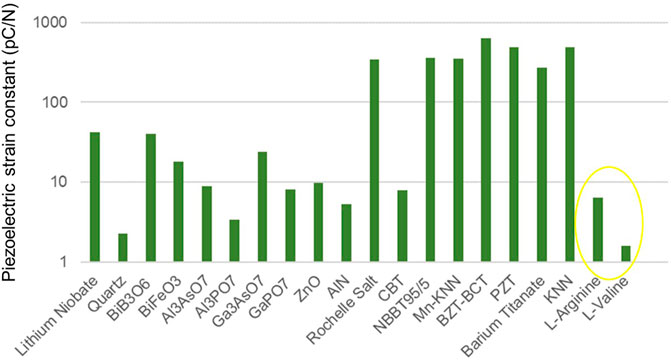
FIGURE 2. Graph placing the piezoelectric charge constants of L-Arginine and L-Valine (circled in yellow) in the context of common inorganic single crystals and ceramics c).

However Figure 3 shows that both crystals dramatically outperform ceramics in their energy harvesting responses, with the maximum piezoelectric voltage constants of L-Valine matching those of organic polymers PVDF and PLLA.

FIGURE 3

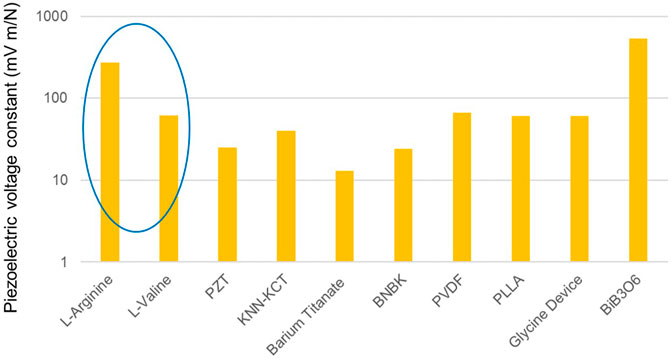
FIGURE 3. Graph placing the piezoelectric voltage constants of L-Arginine and L-Valine (circled in dark blue) in the context of other energy harvesting materials and devices.

Examining the crystal structure of L-Valine (Figure 4), it can be seen that the low piezoelectric response is due to inhibited hydrogen bonding along the b axis (the only axis that can allow a longitudinal piezoelectric response by symmetry). The molecules pack as distinct sheets, with two layers of molecules forming hydrogen bonds along the a and c axes between NH₂⁺ and COO- termini. However the molecular sheets are separated by the valine methyl side chains, which cannot form hydrogen bonds and thus disrupt the formation of a long-range hydrogen bonding network that would increase the net polarisation in the unit cell and thus the piezoelectric response and energy harvesting performance.

FIGURE 4

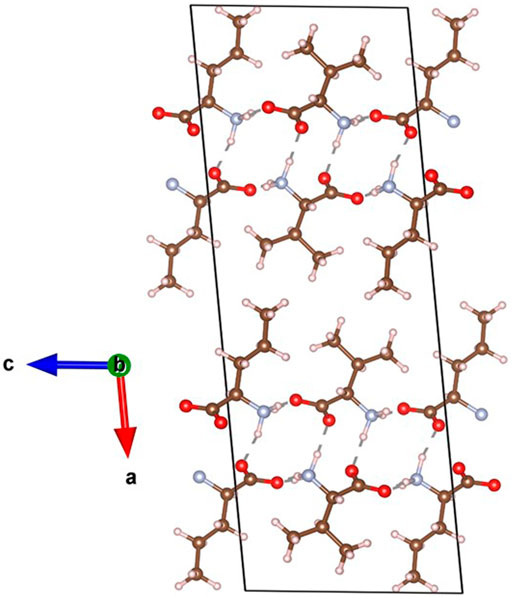
FIGURE 4. Crystal structure of L-Valine, with molecules shown in CPK representation. Nitrogen atoms are coloured red, carbons are brown, hydrogens are white, and nitrogens are blue. Intermolecular hydrogen bonds are shown in dark grey.

Similarly to the L-Arginine single crystal, maximum mechanical stability is observed in the direction of the continuous hydrogen bond network that does form along the c axis, as well as perpendicular to the molecular backbone. The L-Valine unit cell also has a lower monoclinic angle than L-Arginine of 96°, which results in increased shear stiffness (c₅₅ = c₆₆ = 5.3 GPa) and reduces the amount of ionic displacement that can occur under an applied force. This is also reflected in the larger predicted Young’s Modulus of L-Valine of 19.8 GPa. Figure 5 shows that despite the low response of valine compared to the whole spectrum of piezoelectrics, the responses of both valine and arginine are average for biological materials overall, and far exceed the piezoelectric response of materials such as bone, tendon, calcite, wool, wood, and so on.

FIGURE 5

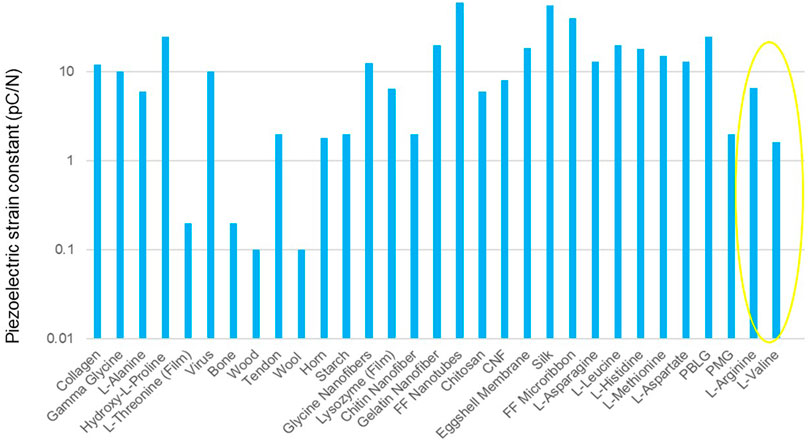
FIGURE 5. Graph placing the piezoelectric charge constants of L-Arginine and L-Valine (circled in yellow) in the context of other biological materials.

Conclusion

In this work, it is shown that both L-Arginine and L-Valine single crystals are predicted to have piezoelectric voltage constants that exceed those of piezoelectric ceramics, with L-Arginine having voltage constants that also far exceed piezoelectric polymers. This highlights that both crystals would be suitable as energy harvesting materials, with substantially reduced cost and environmental impact than currently used candidates. The higher response of L-Arginine is attributed to its continuous hydrogen bond network along the axis of polarisation and larger monoclinic angle, while the lower response of L-Valine is caused by inhibited long-range hydrogen bonding and higher shear stiffness. The predicted elastic constants indicate that these amino acids could be used as rigid single crystal components, or as flexible thin films for a variety of energy harvesting applications.

Computational Details

Classical piezoelectricity manifests itself in both a direct and a converse effect. The direct piezoelectric effect is a linear coupling between mechanical stress and electrical polarization. The converse piezoelectric effect is a linear coupling between mechanical strain and an applied electric field. Both behaviours are described by the same set of piezoelectric constants, most commonly the piezoelectric strain constant d_ij, which is measured in pC/N for the direct piezoelectric effect, and pm/V for the converse piezoelectric effect.

Mathematically, this piezoelectric response can be described by a third rank tensor in the form of a 3 × 6 matrix:

$\left(\begin{array}{ccc}{d}_{11}& d_{12}& d_{13}\\ d_{21}& d_{22}& d_{23}\\ d_{31}& d_{32}& d_{33}\end{array} \begin{array}{ccc}{d}_{14}& d_{15}& d_{16}\\ d_{24}& d_{25}& d_{26}\\ d_{34}& d_{35}& d_{36}\end{array}\right)(1)$

Here d₁₁, d₂₂, and d₃₃ are defined as the longitudinal piezoelectric strain coefficients, with the final three columns containing the shear piezoelectric strain coefficients. The remaining matrix components represent the transverse piezoelectric strain coefficients, defined according to the direction of the applied stimulus and the direction of the resulting response.

Electromechanical properties were predicted from periodic Density Functional Theory (DFT) (Argaman and Makov, 2000) calculations on single crystals using the VASP (Hafner, 2007) code. For a full overview on DFT readers are directed to more thorough overviews (Fiolhais et al., 2003; Koch and Holthausen, 2015). A number of multiscale modelling techniques can be used to evaluate and simulate electromechanical properties (Sass et al., 2004), and within DFT other suitable softwares include CP2K (Kühne et al., 2020), ABINIT (Gonze et al., 2016), and CASTEP (Clark et al., 2005). Alternative methods to DFT for prediction and calculation of material properties without requiring higher-order parameters include deterministic artificial intelligence, which has recently been proposed for material property utilization in control (Sands, 2020). Whiplash compensation, as applied to flexible space robotics has also been used for stiffness estimation (Sands, 2019), stemming from a similar problem formulation utilizing the Hamiltonian-akin to the many-electron time-independent Schrödinger equation used for piezoelectric constant estimation in DFT.

Electronic structures were calculated using the PBE functional (Perdew et al., 1992) with Grimme-D3 dispersion corrections (Grimme et al., 2010) and projector augmented wave (PAW) pseudopotentials (Kresse and Joubert, 1999). Calculations were carries out using Gaussian smearing, and a plane wave cut-off of 600 eV. Piezoelectric charge constants, e_ij, were calculated using density functional perturbation theory (DFPT) (Wu et al., 2005). For this a 2 × 2 × 2 Γ-centred k-point grid was also used,

The theoretical methodology herewith consists of four steps:

- Geometry optimisation

- Calculation of piezoelectric charge tensor

- Calculation of elastic constants

- Calculation of static dielectric tensor

Geometry Optimisation

The first step is to take the experimental crystal structures of interest, and allow their lattice parameters and atomic positions to relax in order to obtain ideal ground state structures. Experimental structures were downloaded from the Cambridge Crystallographic Data Centre (CCDC). All crystal structures were optimised using the conjugate gradient algorithm (Štich et al., 1989). For a periodic system, integrals in real space over the infinitely extended system are replaced by integrals over the finite first Brillouin zone in reciprocal space, in accordance with Bloch’s theorem. These integrals are performed at a finite number of points in the Brillouin zone, called the k-point mesh, or grid. A 4 × 4 × 4 Γ-centred k-point grid was used for geometry optimisations; with a plane wave energy cut-off of 600 eV (all plane waves with a kinetic energy less than this are included in the basis set). Γ-centred k-point grids are generally recommended for non-centrosymmetric unit cells. These values were obtained after energy convergence tests with respect to N (where N = number of subdivisions of the reciprocal lattice vector), and plane wave cut off energy. Minimum converged are chosen to balance calculation accuracy with computational expense.

Elastic Constants

The elastic stiffness constants c_kj, are required to calculate the piezoelectric strain constants d_ik. The elastic constants are also important experimentally. The elastic compliance can easily be derived from the stiffness and measured using impedance spectroscopy or nanoindentation, as can the Young’s Modulus, which is important for device applications. Using the piezoelectric charge coefficients, e_ij, which are calculated directly by VASP, and the elastic stiffness constants, c_kj, we can calculate the more useful piezoelectric strain coefficient, d_ik, using the relationship

$d_{ik}=\raisebox{1ex}{$e_{ij}$}\!\left/ \!\raisebox{-1ex}{$c_{kj}$}\right.(2)$

The elastic constants are calculated in the form of the stiffness tensor, C, presented as a 6 × 6 matrix. VASP outputs this tensor in Voigt notation in kB, so post analysis is required to produce C in matrix notation in GPa.

$C=\left(\begin{array}{cccccc}{\mathit{c}}_{11}& c_{12}& c_{13}& c_{14}& c_{15}& c_{16}\\ c_{21}& {\mathit{c}}_{22}& c_{23}& c_{24}& c_{25}& c_{26}\\ c_{31}& c_{32}& {\mathit{c}}_{33}& c_{34}& c_{35}& c_{36}\\ c_{41}& c_{42}& c_{43}& {\mathit{c}}_{44}& c_{45}& c_{46}\\ c_{51}& c_{52}& c_{53}& c_{54}& {\mathit{c}}_{55}& c_{56}\\ c_{61}& c_{62}& c_{63}& c_{64}& c_{65}& {\mathit{c}}_{66}\end{array}\right)(3)$

For this work, it is only necessary to extract the six primary diagonal matrix components, shown in bold in Eq. (2). The number of non-zero elements in both the elastic and piezoelectric matrices will vary according to the symmetry of the crystal being studied. Young’s Moduli were derived from the stiffness and its inverse compliance matrix components. Values are presented as Voigt-Reuss-Hill averages (Chung and Buessem, 1967; Zuo et al., 1992) as calculated by the ELATE software tool (Gaillac et al., 2016). Crystal structures were visualised using VESTA (Momma and Izumi, 2011). Currently, VASP only supports the calculation of the ionic contribution to the elastic stiffness constants using DFPT, and so cannot be used to derive the full elastic stiffness tensor. For more information on these constants, their matrix representations and their units, readers are directed to Nye (Nye, 1985).

Dielectric Tensor

DFPT calculations can also predict the static dielectric tensor of the crystal being studied. Using the dielectric tensor we can extract the final piezoelectric constant: the voltage constant, g_ik. This is an important figure of merit (FoM) for energy harvesting applications, and in motion and pressure sensing. To obtain these g_ik values we divide the corresponding piezoelectric strain constant, d_ik, by the relevant dielectric constant ε_ii, as shown in Eq. (3). These constants are measured in V m/N.

$g_{ik}=\raisebox{1ex}{$d_{ik}$}\!\left/ \!\raisebox{-1ex}{${\mathbf{\epsilon }}_{\mathit{i}\mathit{i}} {\mathit{\epsilon }}_{\mathit{o}}$}\right.(4)$

The accuracy of the computational methods used in the simulation of permittivity, elastic stiffness, and piezoelectricity, has been extensively benchmarked and validated in previous publications. Initially the methodology was benchmarked with respect to three well-known inorganic piezoelectric materials; namely aluminium nitride (AlN), zinc oxide (ZnO) and α-quartz (SiO₂). This was then extended to the proteinogenic amino acids (Guerin et al., 2018a), biominerals (Guerin et al., 2018b), co-crystals (Ji et al., 2020) and peptides (Bera et al., 2021), with deviations from experiment ranging from 1–20%, which is highly accurate for identifying high-performance materials. The upper limit is observed in highly flexible materials with individual stiffness constants of less than 5 GPa.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SG carried out the calculations and analysis and compiled the manuscript including Figures and Tables.

Funding

This work was supported by Science Foundation Ireland (SFI) under award number 12/RC/2275_P2.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

SG acknowledges supercomputing resources at the SFI/Higher Education Authority Irish Center for High-End Computing (ICHEC).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2021.738446/full#supplementary-material

References

Alikhani, M., Hakimi, M., Moeini, K., Eigner, V., and Dusek, M. (2020). Synthesis, Characterization and Thermal Studies of a Nanosized 1D l-Arginine/Copper(II) Coordination Polymer by Sonochemical Method: A New Precursor for Preparation of Copper(II) Oxide Nanoparticles. J. Inorg. Organomet. Polym. 30 (8), 2907–2915. doi:10.1007/s10904-020-01442-8

CrossRef Full Text | Google Scholar

Alluri, N. R., Maria Joseph Raj, N. P., Khandelwal, G., Vivekananthan, V., and Kim, S.-J. (2020). Aloe Vera: A Tropical Desert Plant to Harness the Mechanical Energy by Triboelectric and Piezoelectric Approaches. Nano Energy 73, 104767. doi:10.1016/j.nanoen.2020.104767

CrossRef Full Text | Google Scholar

Argaman, N., and Makov, G. (2000). Density Functional Theory: An Introduction. Am. J. Phys. 68 (1), 69–79. doi:10.1119/1.19375

CrossRef Full Text | Google Scholar

Baptista, R. M. F., de Matos Gomes, E., Raposo, M. M. M., Costa, S. P. G., Lopes, P. E., Almeida, B., et al. (2019). Self-assembly of Dipeptide Boc-Diphenylalanine Nanotubes inside Electrospun Polymeric Fibers with strong Piezoelectric Response. Nanoscale Adv. 1 (11), 4339–4346. doi:10.1039/c9na00464e

CrossRef Full Text | Google Scholar

Basavalingappa, V., Bera, S., Xue, B., O'Donnell, J., Guerin, S., Cazade, P.-A., et al. (2020). Diphenylalanine-Derivative Peptide Assemblies with Increased Aromaticity Exhibit Metal-like Rigidity and High Piezoelectricity. ACS Nano 14, 7025–7037. doi:10.1021/acsnano.0c01654

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, A. J., and Deubzer, O. (2018). Lead-free Piezoelectrics-The Environmental and Regulatory Issues. MRS Bull. 43 (8), 581–587. doi:10.1557/mrs.2018.154

CrossRef Full Text | Google Scholar

Bera, S., Guerin, S., Yuan, H., O'Donnell, J., Reynolds, N. P., Maraba, O., et al. (2021). Molecular Engineering of Piezoelectricity in Collagen-Mimicking Peptide Assemblies. Nat. Commun. 12 (1), 2634–2712. doi:10.1038/s41467-021-22895-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernard, F., Gimeno, L., Viala, B., Gusarov, B., and Cugat, O. (2017). Direct Piezoelectric Coefficient Measurements of PVDF and PLLA under Controlled Strain and Stress, 1. Multidisciplinary Digital Publishing Institute Proceedings, 335. doi:10.3390/proceedings1040335

CrossRef Full Text

Bishara, H., Nagel, A., Levanon, M., and Berger, S. (2020). Amino Acids Nanocrystals for Piezoelectric Detection of Ultra-low Mechanical Pressure. Mater. Sci. Eng. C 108, 110468. doi:10.1016/j.msec.2019.110468

PubMed Abstract | CrossRef Full Text | Google Scholar

Chung, D. H., and Buessem, W. R. (1967). The Voigt‐Reuss‐Hill Approximation and Elastic Moduli of Polycrystalline MgO, CaF2, β‐ZnS, ZnSe, and CdTe. J. Appl. Phys. 38 (6), 2535–2540. doi:10.1063/1.1709944

CrossRef Full Text | Google Scholar

Clark, S. J., Segall, M. D., Pickard, C. J., Hasnip, P. J., Probert, M. I., Refson, K., et al. (2005). First Principles Methods Using CASTEP. Z. für kristallographie-crystalline Mater. 220 (5-6), 567–570. doi:10.1524/zkri.220.5.567.65075

CrossRef Full Text | Google Scholar

Fiolhais, C., Nogueira, F., and Marques, M. A. (2003). A Primer in Density Functional Theory, Vol. 620. Berlin, Germany: Springer-Verlag.

Gaillac, R., Pullumbi, P., and Coudert, F.-X. (2016). ELATE: an Open-Source Online Application for Analysis and Visualization of Elastic Tensors. J. Phys. Condens. Matter 28 (27), 275201. doi:10.1088/0953-8984/28/27/275201

CrossRef Full Text | Google Scholar

Gayatri, N. N. D., and Hutchison, G. (2019). Origins of Negative and Positive Electromechanical Response of Oligopeptide Piezoelectrics. Available at: https://chemrxiv.org/engage/chemrxiv/article-details/60c7453b9abda2623df8c4ec

Ghosh, S. K., and Mandal, D. (2017). Bio-assembled, Piezoelectric Prawn Shell Made Self-Powered Wearable Sensor for Non-invasive Physiological Signal Monitoring. Appl. Phys. Lett. 110 (12), 123701. doi:10.1063/1.4979081

CrossRef Full Text | Google Scholar

Ghosh, S. K., Park, J., Na, S., Kim, M. P., and Ko, H. (2021). A Fully Biodegradable Ferroelectric Skin Sensor from Edible Porcine Skin Gelatine. Adv. Sci. 8, 2005010. doi:10.1002/advs.202005010

PubMed Abstract | CrossRef Full Text | Google Scholar

Gleeson, M., O'Dwyer, K., Guerin, S., Rice, D., Thompson, D., Tofail, S. A. M., et al. (2020). Quantitative Polarization‐Resolved Second‐Harmonic‐Generation Microscopy of Glycine Microneedles. Adv. Mater. 32 (46), 2002873. doi:10.1002/adma.202002873

PubMed Abstract | CrossRef Full Text | Google Scholar

Gonze, X., Jollet, F., Abreu Araujo, F., Adams, D., Amadon, B., Applencourt, T., et al. (2016). Recent Developments in the ABINIT Software Package. Comput. Phys. Commun. 205, 106–131. doi:10.1016/j.cpc.2016.04.003

CrossRef Full Text | Google Scholar

Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 132 (15), 154104. doi:10.1063/1.3382344

CrossRef Full Text | Google Scholar

Guerin, S., Stapleton, A., Chovan, D., Mouras, R., Gleeson, M., McKeown, C., et al. (2018). Control of Piezoelectricity in Amino Acids by Supramolecular Packing. Nat. Mater. 17 (2), 180–186. doi:10.1038/nmat5045

PubMed Abstract | CrossRef Full Text | Google Scholar

Guerin, S., Tofail, S. A. M., and Thompson, D. (2018). Longitudinal Piezoelectricity in Natural Calcite Materials: Preliminary Studies. IEEE Trans. Dielect. Electr. Insul. 25 (3), 803–807. doi:10.1109/tdei.2017.007045

CrossRef Full Text | Google Scholar

Guerin, S., Tofail, S. A., and Thompson, D. (2019). Organic Piezoelectric Materials: Milestones and Potential. NPG Asia Mater. 11 (1), 1–5. doi:10.1038/s41427-019-0110-5

CrossRef Full Text | Google Scholar

Hafner, J. (2007). Materials Simulations Using VASP—A Quantum Perspective to Materials Science. Comput. Phys. Commun. 177 (1), 6–13. doi:10.1016/j.cpc.2007.02.045

CrossRef Full Text | Google Scholar

Ibn-Mohammed, T., Reaney, I. M., Koh, S. C. L., Acquaye, A., Sinclair, D. C., Randall, C. A., et al. (2018). Life Cycle Assessment and Environmental Profile Evaluation of lead-free Piezoelectrics in Comparison with lead Zirconate Titanate. J. Eur. Ceram. Soc. 38 (15), 4922–4938. doi:10.1016/j.jeurceramsoc.2018.06.044

CrossRef Full Text | Google Scholar

Ji, W., Xue, B., Bera, S., Guerin, S., Shimon, L. J., Ma, Q., et al. (2020). Tunable Mechanical and Optoelectronic Properties of Organic Cocrystals by Unexpected Stacking Transformation from H-to J-and X-Aggregation. ACS nano 14 (8), 10704–10715. doi:10.1021/acsnano.0c05367

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalaiselvi, D., Kumar, R. M., and Jayavel, R. (2008). Single crystal Growth and Properties of Semiorganic Nonlinear Optical L-Arginine Hydrochloride Monohydrate Crystals. Cryst. Res. Technol. 43 (8), 851–856. doi:10.1002/crat.200711133

CrossRef Full Text | Google Scholar

Kobiakov, I. B. (1980). Elastic, Piezoelectric and Dielectric Properties of ZnO and CdS Single Crystals in a Wide Range of Temperatures. Solid State. Commun. 35 (3), 305–310. doi:10.1016/0038-1098(80)90502-5

CrossRef Full Text | Google Scholar

Koch, W., and Holthausen, M. C. (2015). A Chemist's Guide to Density Functional Theory. Weinheim: John Wiley & Sons.

Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59 (3), 1758–1775. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

Kühne, T. D., Iannuzzi, M., Del Ben, M., Rybkin, V. V., Seewald, P., Stein, F., et al. (2020). CP2K: An Electronic Structure and Molecular Dynamics Software Package - Quickstep: Efficient and Accurate Electronic Structure Calculations. J. Chem. Phys. 152 (19), 194103. doi:10.1063/5.0007045

CrossRef Full Text | Google Scholar

Lee, B. Y., Zhang, J., Zueger, C., Chung, W.-J., Yoo, S. Y., Wang, E., et al. (2012). Virus-based Piezoelectric Energy Generation. Nat. Nanotech 7 (6), 351–356. doi:10.1038/nnano.2012.69

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemanov, V. V. (2000). Piezoelectric and Pyroelectric Properties of Protein Amino Acids as Basic Materials of Soft State Physics. Ferroelectrics 238 (1), 211–218. doi:10.1080/00150190008008786

CrossRef Full Text | Google Scholar

Moitra, S., and Kar, T. (2010). Growth and Characterization of L-Valine - a Nonlinear Optical crystal. Cryst. Res. Technol. 45 (1), 70–74. doi:10.1002/crat.200900447

CrossRef Full Text | Google Scholar

Momma, K., and Izumi, F. (2011). VESTA 3for Three-Dimensional Visualization of crystal, Volumetric and Morphology Data. J. Appl. Cryst. 44 (6), 1272–1276. doi:10.1107/s0021889811038970

CrossRef Full Text | Google Scholar

Nye, J. F. (1985). Physical Properties of Crystals: Their Representation by Tensors and Matrices. New York: Oxford University Press.

O'Donnell, J., Cazade, P. A., Guerin, S., Djeghader, A., Haq, E. U., Tao, K., et al. (2021). Piezoelectricity of the Transmembrane Protein Ba3 Cytochrome C Oxidase. Adv. Funct. Mater. 31 (28), 1272. doi:10.1002/adfm.202100884

CrossRef Full Text | Google Scholar

Okosun, F., Guerin, S., Celikin, M., and Pakrashi, V. (2021). Flexible Amino Acid-Based Energy Harvesting for Structural Health Monitoring of Water Pipes. Cel Rep. Phys. Sci. 2 (5), 100434. doi:10.1016/j.xcrp.2021.100434

CrossRef Full Text | Google Scholar

Pal, T., and Kar, T. (2002). Single crystal Growth and Characterization of the Nonlinear Optical crystal L-Arginine Hydrofluoride. J. Cryst. Growth 234 (1), 267–271. doi:10.1016/s0022-0248(01)01662-1

CrossRef Full Text | Google Scholar

Panda, P. K., and Sahoo, B. (2015). PZT to lead Free Piezo Ceramics: a Review. Ferroelectrics 474 (1), 128–143. doi:10.1080/00150193.2015.997146

CrossRef Full Text | Google Scholar

Perdew, J. P., Chevary, J. A., Vosko, S. H., Jackson, K. A., Pederson, M. R., Singh, D. J., et al. (1992). Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 46 (11), 6671–6687. doi:10.1103/physrevb.46.6671

CrossRef Full Text | Google Scholar

Roscow, J. I., Pearce, H., Khanbareh, H., Kar-Narayan, S., and Bowen, C. R. (2019). Modified Energy Harvesting Figures of merit for Stress- and Strain-Driven Piezoelectric Systems. Eur. Phys. J. Spec. Top. 228 (7), 1537–1554. doi:10.1140/epjst/e2019-800143-7

CrossRef Full Text | Google Scholar

Sands, T. (2019). Optimization Provenance of Whiplash Compensation for Flexible Space Robotics. Aerospace 6 (9), 93. doi:10.3390/aerospace6090093

CrossRef Full Text | Google Scholar

Sands, T. (2020). Development of Deterministic Artificial Intelligence for Unmanned Underwater Vehicles (UUV). Jmse 8 (8), 578. doi:10.3390/jmse8080578

CrossRef Full Text | Google Scholar

Sass, L., McPhee, J., Schmitke, C., Fisette, P., and Grenier, D. (2004). A Comparison of Different Methods for Modelling Electromechanical Multibody Systems. Multibody Syst. Dyn. 12 (3), 209–250. doi:10.1023/b:mubo.0000049196.78726.da

CrossRef Full Text | Google Scholar

Stapleton, A., Noor, M. R., Sweeney, J., Casey, V., Kholkin, A. L., Silien, C., et al. (2017). The Direct Piezoelectric Effect in the Globular Protein Lysozyme. Appl. Phys. Lett. 111 (14), 142902. doi:10.1063/1.4997446

CrossRef Full Text | Google Scholar

Štich, I., Car, R., Parrinello, M., and Baroni, S. (1989). Conjugate Gradient Minimization of the Energy Functional: A New Method for Electronic Structure Calculation. Phys. Rev. B Condens Matter 39 (8), 4997–5004. doi:10.1103/physrevb.39.4997

PubMed Abstract | CrossRef Full Text | Google Scholar

Supryadkina, I., Abgaryan, K., Bazhanov, D., and Mutigullin, I. (2014). Ab Initio study of Macroscopic Polarization of AlN, GaN and AlGaN. Phys. Status Solidi C 11 (2), 307–311. doi:10.1002/pssc.201300756

CrossRef Full Text | Google Scholar

Trolier-McKinstry, S., Griggio, F., Yaeger, C., Jousse, P., Dalong Zhao, D., Bharadwaja, S. S. N., et al. (2011). Designing Piezoelectric Films for Micro Electromechanical Systems. IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 58 (9), 1782–1792. doi:10.1109/tuffc.2011.2015

CrossRef Full Text | Google Scholar

Wang, L. N., Wang, X. Q., Zhang, G. H., Liu, X. T., Sun, Z. H., Sun, G. H., et al. (2011). Single crystal Growth, crystal Structure and Characterization of a Novel crystal: L-Arginine 4-nitrophenolate 4-nitrophenol Dehydrate (LAPP). J. Cryst. Growth 327 (1), 133–139. doi:10.1016/j.jcrysgro.2011.05.010

CrossRef Full Text | Google Scholar

Wang, H. L., Guo, Z. H., Zhu, G., Pu, X., and Wang, Z. L. (2021). Boosting the Power and Lowering the Impedance of Triboelectric Nanogenerators through Manipulating the Permittivity for Wearable Energy Harvesting. ACS nano 15 (4), 7513–7521. doi:10.1021/acsnano.1c00914

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, X., Vanderbilt, D., and Hamann, D. (2005). Systematic Treatment of Displacements, Strains, and Electric fields in Density-Functional Perturbation Theory. Phys. Rev. B 72 (3), 035105. doi:10.1103/physrevb.72.035105

CrossRef Full Text | Google Scholar

Zhang, S., Xia, R., and Shrout, T. R. (2007). Lead-free Piezoelectric Ceramics vs. PZT? J. Electroceram. 19 (4), 251–257. doi:10.1007/s10832-007-9056-z

CrossRef Full Text | Google Scholar

Zhou, Q., Lau, S., Wu, D., and Kirk Shung, K. (2011). Piezoelectric Films for High Frequency Ultrasonic Transducers in Biomedical Applications. Prog. Mater. Sci. 56 (2), 139–174. doi:10.1016/j.pmatsci.2010.09.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Zuo, L., Humbert, M., and Esling, C. (1992). Elastic Properties of Polycrystals in the Voigt-Reuss-Hill Approximation. J. Appl. Cryst. 25 (6), 751–755. doi:10.1107/s0021889892004874

CrossRef Full Text | Google Scholar