- 1College of Engineering, University of Georgia, Athens, GA, United States
- 2Department of Chemistry, University of Georgia, Athens, GA, United States
Abstraction of hydrogen by ȮH is the dominant initiation step in low-temperature oxidation of biofuels. Theoretical chemical kinetics calculations for such reactions provide a direct means of quantifying rates of abstraction, which are critical to modeling biofuel combustion. However, in several cases and despite agreement on total rate coefficients, branching fractions (i.e. the distribution of initial radicals) can vary depending on the level of theory, which leads to variations in ignition delay time predictions. To examine the connection between branching fractions and ignition delay time predictions, simulations were conducted for 1-butanol, cyclopentanone, and methyl propanoate at 10 atm and from 500–1000 K. For each case, the simulations utilized recent combustion mechanisms to produce an initial set of ignition delay time trends. H-abstraction rates were then replaced using rates from the literature to examine the effects of ȮH-initiated branching fractions on ignition chemistry. Branching fractions were found to significantly influence ignition chemistry, specifically in the case of 1-butanol, even when total rate coefficients were relatively consistent. From comparison of site-specific rates in the literature, branching fractions for initiation of 1-butanol and methyl propanoate are not consistent, which resulted in ignition delay times differing by factors of up to 6.3 and 1.2 respectively. Conversely, in the case of cyclopentanone, for which both the total and the site-specific rate coefficients agree, ignition delay times were unaffected. From the observed dependence of ignition delay times on ȮH-initiated branching fractions, an intermediate step in the development of combustion mechanisms is necessary to validate site-specific rate coefficients and ensure accurate model predictions. Speciation measurements are one example that can provide a critical link to radical-specific, fundamental chemical pathways and determine accurate branching fractions.
Introduction
Ignition delay times are an important metric necessary for the development of predictive combustion models, which depend on accurate chemical kinetics, including reaction mechanisms and rates for elementary steps including abstraction, addition, isomerization, and disproportionation. The chemistry leading to ignition, defined here as the time where the rate of change in the mole fraction of ȮH reaches a local maximum, results from a chain-branching step that is governed by a balance of temperature- and pressure-dependent reactions. For low-temperature combustion, occurring below 1000 K and where ignition occurs via hydroperoxyalkyl (Q̇OOH)-mediated chain-branching (Zádor et al., 2011; Savee et al., 2015), the initiation step is particularly important because the radical isomers formed via H-abstraction each follow a unique set of reactions that compete with chain-branching–propagating (ȮH forming) or inhibiting (HOȮ forming). The propensity of a radical isomer to react with O2, form Q̇OOH, then undergo second-O2-addition ultimately determines the contribution of that isomer to chain-branching, which is derived from decomposition of ketohydroperoxide species and results in the net production of two radicals (ȮH + carbonyl-oxy radical). Understanding the connections between ignition delay times and the initiation step, particularly the branching fractions of initial radicals and species related directly to Q̇OOH, is critical.
OH-initiated H-abstraction is the dominant step below 1000 K for all types of biofuels (Rotavera and Taatjes, 2021). Oxygenated functional groups affect branching fractions of ȮH + RH → H2O+ Ṙ due to a reduction in adjacent C–H bond energy and from hydrogen bonding in the transition state with the H atom of the hydroxyl radical (Rotavera and Taatjes, 2021); the label RH is used to designate an arbitrary biofuel, such as 1-butanol. Figure 1 shows the radical isomers of 1-butanol formed via H-abstraction by ȮH. As an example of the–OH functional group influence, reaction of the α isomer, formed in (ii), with O2 exclusively produces butanal + HOȮ in a chain-inhibiting step, while Q̇OOH-mediated reactions are possible for other radicals (Rotavera and Taatjes, 2021). In part, because selectivity towards α radicals in alcohols is favored, ignition delay times of 1-butanol below 1000 K are longer when compared to n-butane (Rotavera and Taatjes, 2021). Similarly, radicals formed in biofuels with different functional groups, such as R–C (=O)–R (ketones) and R–C (=O)–O–R (esters) exert significant influence over the distribution of initial radicals and subsequent reaction mechanisms connected to each. In some cases, to the extent that branching fractions vary significantly, site-specific rate coefficients employed in chemical kinetics mechanisms may skew the reliability of ignition predictions.
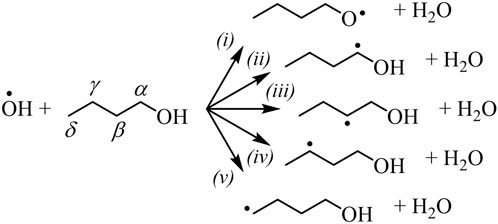
FIGURE 1. Radicals produced from ȮH-initiated H-abstraction from 1-butanol. The–OH functional group predisposes each isomer to undergo a unique set of reactions that compete with chain-branching. Similar effects are created by other oxygenated functional groups.
While site-specific rate coefficient measurements are not common, for some species, theoretical rate calculations are available from multiple studies that employ high-level methods. In such cases, the correct k(T) to select for inclusion in a mechanism is often unclear, particularly when total rate coefficients are consistent with one another and with experiment. Moreover, as discussed in the present work, branching fractions can differ substantially even when total rate coefficients are similar.
Rate coefficients that are included in a given chemical kinetics mechanism are derived from measurements or theoretical chemical kinetics computations. In absence of both, rate rules are adopted as a means of approximation, yet are typically incapable of capturing functional group effects over broad ranges of temperature and pressure. Fenard et al. (Fenard et al., 2018) employed transition state theory to compute ROȮ isomerization rates in tetrahydrofuran oxidation, which differed up to 102 s−1 at 600 K compared with rates from alkane-based rate rules. Additionally, Al Rashidi et al. (Al Rashidi et al., 2015) showed that the use of rate rules predicted C–C and C–O bond-scission rates significantly lower than analogous reactions in di-n-butyl ether and over a broad range of temperature.
The initiation step is important because of the direct impact on the balance of chain reactions that precede ignition. Connections between the initial radical pool and ignition are described cogently in the theoretical calculations of Ji et al. (Ji et al., 2016) for alkyl radical oxidation in the context of identifying turnover states, i.e. the inflection point in the negative-temperature coefficient (NTC) region near the high-temperature regime where ignition times exhibit a local maximum. In addition, site-specific initiation reactions often appear in sensitivity analysis, such as in Jacobs et al. (Jacobs et al., 2019) for dimethoxymethane, Vranckx et al. (Vranckx et al., 2011) for 1-butanol, Burke et al. (Burke et al., 2016) for butanone, among others. The present work expands on the basic concept that bridges an initial radical pool of arbitrary composition, e.g. Ṙ, ROȮ, and Q̇OOH as in Ji et al. (Ji et al., 2016), with the dynamics that subsequently unfold and lead to ignition. Specifically, the dependence of ignition predictions on branching fractions of the initiation step is examined quantitatively using several sets of rate parameters for ȮH + RH → H2O+ Ṙ where total rate coefficients agree, yet site-specific rate coefficients differ.
To examine the influence of branching fractions on ignition delay times, a series of ChemKin simulations was conducted for 1-butanol, cyclopentanone, and methyl propanoate. For all three species, recent chemical kinetics mechanisms were utilized to produce an initial, baseline set of simulations. Additional ignition simulations were then conducted using all available sets of site-specific rate coefficients from the literature for OH-initiated H-abstraction, which effectively alters the branching fractions of the initiation step.
The most pronounced effects were observed for 1-butanol. As a result, additional simulations were conducted to examine the underlying details. First, to complement the simulations where branching fractions were varied, additional ignition simulations were conducted to account for uncertainties in the rate coefficients in order to quantify the impact on the model predictions. Second, rate-of-production and sensitivity analysis simulations were conducted to assess the impact on reactions involving ȮH from changing the branching fractions. Third, species profile simulations were conducted to assess the dependence of species produced from Ṙ + O2 reactions on branching fractions of the initiation step.
The sections below provide an overview of the approach taken for the chemical kinetics modeling, a comparison of branching fractions from several theoretical computations, and the effect of using different site-specific rates for H-abstraction by ȮH on ignition predictions. Basic analysis is then applied to provide some clarity on the results, interpreted in the context of the selectivity towards one radical isomer or another produced in the initiation step. Subsequent analysis is also discussed as to what experimental measurements may provide for a more reliable validation assessment to determine the most appropriate set of rate parameters to incorporate in a chemical kinetics mechanism.
Ignition delay time measurements exist for 1-butanol (Vranckx et al., 2011; Weber et al., 2011), cyclopentanone (Zhang et al., 2019), and methyl propanoate (Akih-Kumgeh and Bergthorson, 2011; Zhang et al., 2014; Kumar et al., 2018), and cover a broad range of conditions. For simplicity in examining the basic premise herein, the simulations were restricted to stoichiometric conditions, a pressure of 10 atm, and temperatures from 675–1000 K. Moreover, the objective of the present work is to quantify the effect of differences in branching fraction predictions of the initiation step on ignition delay times–for the specific case when total rate coefficients agree–rather than drawing contrast between mechanisms or proposing revised rate parameters.
Approach
Using ChemKin (v19.0), simulations were conducted using the closed 0-D homogenous batch reactor module to determine ignition delay times under isobaric conditions at 10 atm over a temperature range of 650–1000 K at an equivalence ratio of ϕ = 1 and with ∼76% N2 to represent practical combustion conditions. Ignition delay times were defined from the model simulations using ȮH time profiles; a representative example is shown in the Supplemental Material S1. Ignition delay times were defined as the time where the rate of change in the mole fraction of ȮH reaches a local maximum, indicating chain-branching, and times longer than ∼1,000 ms were neglected. Table 1 lists the chemical kinetics mechanisms used for each species. In the case of cyclopentanone, two mechanisms that contain peroxy radical chemistry exist in the literature. To examine the effects of differing branching fractions for site-specific H-abstractions, initiation steps of RH + ȮH were replaced using all sets of rate parameters available in literature (Table 2). Importantly, for 1-butanol and methyl propanoate, the total rate coefficients are similar, yet the site-specific branching fractions differ as discussed in Chemical Kinetics Modeling.

TABLE 2. References for rate coefficients for ȮH-initiated H-abstraction from 1-butanol, cyclopentanone, and methyl propanoate.
In addition to ignition delay time modeling, ChemKin simulations were also conducted on 1-butanol oxidation to examine the effects of differing branching fractions on combustion intermediates. Using the perfectly-stirred reactor module, simulations were conducted under stoichiometric conditions with ∼95% N2, 0.71% (7,100 ppm) 1-butanol and 4.29% O2. The conditions of the simulations were a 2000 ms residence time, pressure of 10 atm, and temperature range of 500–1000 K where peroxy radical chemistry is dominant. Four sets of simulations were conducted using the detailed chemical kinetics mechanism of Sarathy et al. (Sarathy et al., 2012). Subsequent modifications to the Sarathy et al. (Sarathy et al., 2012) mechanism employed site-specific rates for ȮH + 1-butanol → Ṙ + H2O from Zhou et al. (Zhou et al., 2011), McGillen et al. (McGillen et al., 2013), and Seal et al. (Seal et al., 2013). Vranckx et al. (Vranckx et al., 2011) also developed a mechanism for 1-butanol, yet low-temperature peroxy chemistry is treated with a simplified model that includes a lumped approach for Q̇OOH reactions, as opposed to Sarathy et al. (Sarathy et al., 2012) in which radical-specific pathways are defined explicitly.
For 1-butanol, simulations were conducted using rate parameters from Zhou et al. (Zhou et al., 2011), McGillen et al. (McGillen et al., 2013), and Seal et al. (Seal et al., 2013) to replace the parameters in the base mechanism of Sarathy et al. (Sarathy et al., 2012). Seal et al. (Seal et al., 2013) utilized a four-parameter non-Arrhenius equation for fitting calculated rates over the temperature range 200–2400 K. To obtain the format necessary for ChemKin, the rates computed in Seal et al. (Seal et al., 2013) were fit to a conventional three-parameter modified Arrhenius equation over the temperature range of 500–1000 K Supplemental Material S2. To make the modifications for the cyclopentanone simulations, initiation rates were switched between the two mechanisms, i.e. the Thion et al. (Thion et al., 2016) modification employed rates from the mechanism of Zhang et al. (Zhang et al., 2019) and vice versa. The Zhang et al. (Zhang et al., 2019) mechanism uses OH-initiation rates from Zhou et al. (Zhou et al., 2016). For methyl propanoate, one modification was made using rates from Mendes et al. (Mendes et al., 2014). The mechanism of Felsmann et al. (Felsmann et al., 2017) uses rates from Tan et al. (Tan et al., 2016). A complete list of the rate parameters used for each simulation is in Supplemental Material S3.
To assess the influence of uncertainty in site-specific rate coefficients on ignition times, simulations were conducted for 1-butanol using the upper and lower bounds provided in Zhou et al. (Zhou et al., 2011), McGillen et al. (McGillen et al., 2013), and Seal et al. (Seal et al., 2013). Zhou et al. (Zhou et al., 2011) utilized the G3 method for the potential energy surface computations, which inherit an uncertainty of ∼1 kcal/mol (Curtiss et al., 1998). The rate parameters in McGillen et al. (McGillen et al., 2013) were produced from fits to experimental product yields (Cavalli et al., 2002; Hurley et al., 2009), which were reported with an uncertainty of ±10%. Barrier heights in Seal et al. (Seal et al., 2013) were reported with a mean unsigned error of ±0.28 kcal/mol. All site-specific rate parameters with upper and lower bounds of uncertainties are listed in Supplemental Material S3 along with a tabulation of the resultant effects on ignition delay times Supplemental Material S4.
Chemical Kinetics Modeling
Total rate coefficients and branching fractions for site-specific H-abstraction of each reaction in Table 2 are compared in the sections below for 1-butanol (Butanol), cyclopentanone (Cyclopentanone), and methyl propanoate (Methyl Propanoate). Subsequently, results from the ignition delay time simulations using modified versions of the mechanisms in Table 1 are compared. The most salient observation from the results is that variation in branching fractions for ȮH + RH → H2O+ Ṙ leads directly to non-negligible variations in ignition delay times for two species. Significant effects are shown for 1-butanol and moderate effects for methyl propanoate. Conversely, variations are negligible in the branching fractions for cyclopentanone, which resulted in negligible effects on ignition delay times. Consistency in the dependence on branching fractions across the three species underscores the importance of site-specific rate coefficients on accurately predicting ignition delay times, as well as species profiles (Discussion).
1-Butanol
Total rate coefficients for H-abstraction from 1-butanol by hydroxyl are shown in Figure 2A from 500 to 1000 K. The largest disparity, occurring at 500 K, is a factor of 3.2 between rates from Seal et al. (Seal et al., 2013) and Zhou et al. (Zhou et al., 2011). At 1000 K, disagreement decreases to a factor of 1.6. Despite the relative agreement in the total rates, site-specific rates vary considerably (Figure 2B,F). At 500 K, branching fractions vary up to factors of 1.4 for α radicals, 3.4 for β radicals, 2.7 for γ radicals, 2.7 for δ radicals, and 12.8 for RȮ radicals. At 1000 K, branching fractions vary up to factors of 1.5 for α radicals, 3.0 for β radicals, 1.8 for γ radicals, 2.7 for δ radicals, and 6.5 for RȮ radicals. Predictions of branching fractions as a function of temperature vary considerably as well. Branching fractions follow either a weak or strong dependence on temperature, as illustrated in Figure 2B, where Sarathy et al. (Sarathy et al., 2012) predicts weak temperature dependence for the α radical while the other three rates do not.
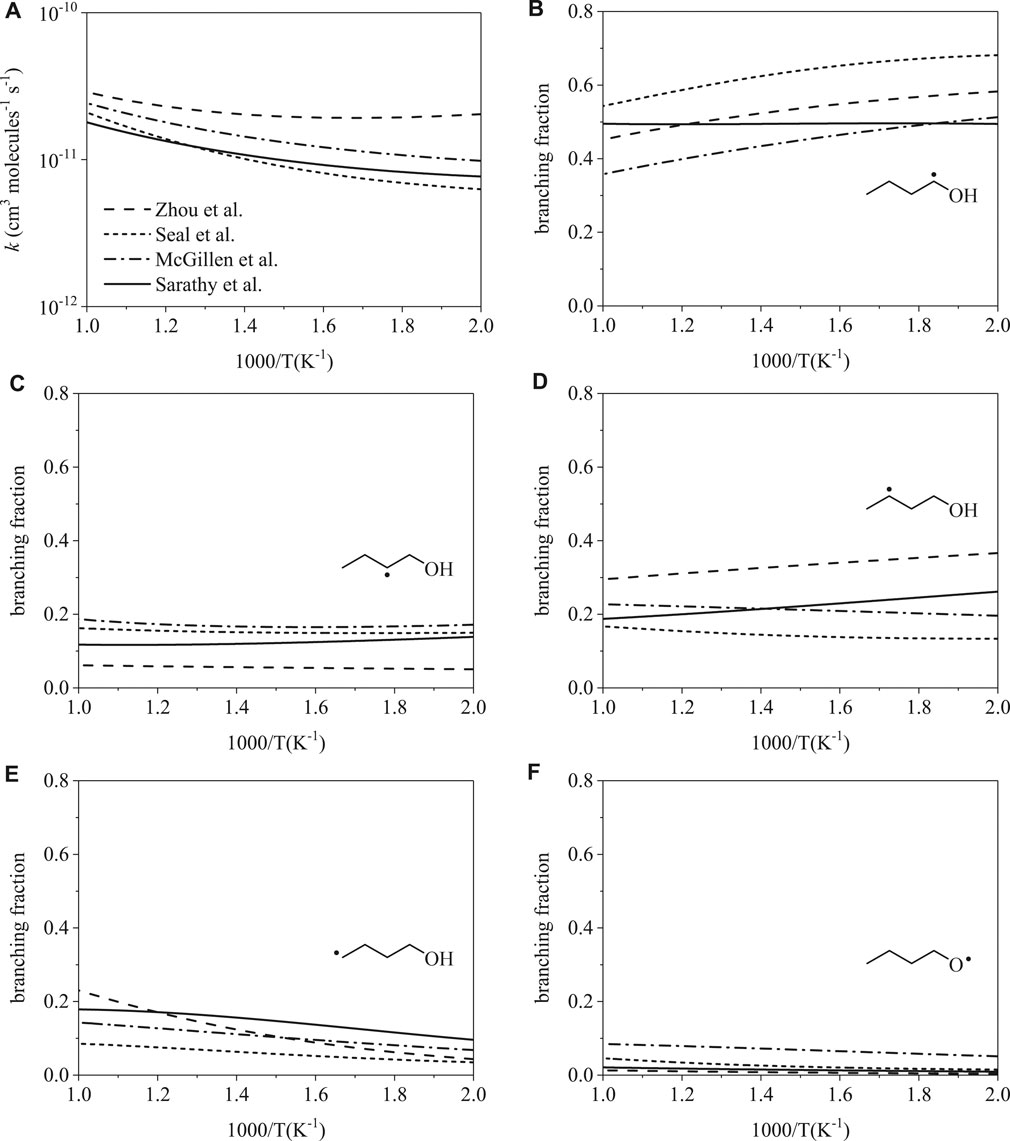
FIGURE 2. Rate coefficients from Sarathy et al. (Sarathy et al., 2012), Zhou et al. (Zhou et al., 2011), Seal et al. (Seal et al., 2013), McGillen et al. (McGillen et al., 2013): (A) total, (B–F) site-specific. Despite relative consistency in total rate coefficients, branching fractions for OH-initiated H-abstraction differ substantially.
Figure 3 compares ignition delay times as a function of temperature for the mechanism of 1-butanol from Sarathy et al. (Sarathy et al., 2012) and the rate modifications in Table 2. Three of the mechanisms predicted 675 K as the first temperature to yield an ignition delay time below 1,000 ms. The modification using rates from Seal et al. (Seal et al., 2013) predicted an ignition delay time of 1,070 ms at 675 K. Disagreement between the four mechanisms is highest at 675 K–a factor of 6.3 difference between predictions using rates from Zhou et al. (Zhou et al., 2011) and Seal et al. (Seal et al., 2013). The predictions converge at 1000 K to ∼3.2 ms with a maximum difference of 0.20 ms, which indicates that low-temperature chemistry is more sensitive to branching fractions. In addition, for a given mechanism, the effects of uncertainty in site-specific rate coefficients increases towards lower temperatures (S4). However, for the simulations in Figure 3 produced using the modifications, uncertainties in the rate coefficients translated to negligible differences in ignition delay times from 675–1000 K (<5% in nearly all cases). The latter observation indicates that uncertainty in branching fractions does not explain the appreciable differences towards lower temperatures, which implies that the composition of the initial radical pool is the main driver.
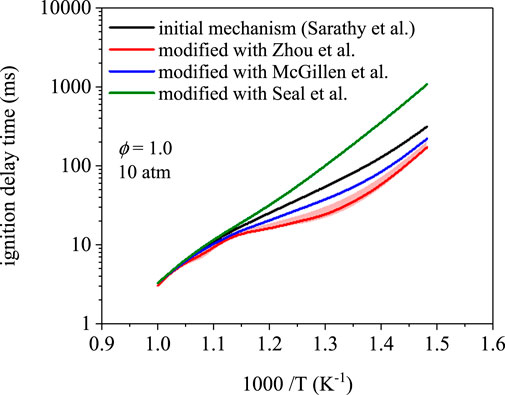
FIGURE 3. Ignition delay time simulations using the mechanism from Sarathy et al. (Sarathy et al., 2012) and site-specific rate modifications from Zhou et al. (Zhou et al., 2011), Seal et al. (Seal et al., 2013), and McGillen et al. (McGillen et al., 2013). Ignition delay times are nearly identical at 1000 K; however, ignition delay times differ towards lower temperature, where peroxy radical chemistry dominates, up to a factor of 6.3 at 675 K.
Cyclopentanone
Total rate coefficients for cyclopentanone initiation by ȮH are shown in Figure 4A. The two rates are remarkably consistent with one another, with the largest difference being a factor of 1.5 at 500 K. Branching fractions for cyclopentanone are shown in Figure 4B. While the difference appears large at the extrema, the branching fractions are similar. Branching fractions reach the largest disagreement of factors of 1.4 and 1.2 at 1000 K for the α radical and β radical respectively. The average disagreement from 500–1000 K is only 1.2 for the α radical and 1.1 for the β radical.
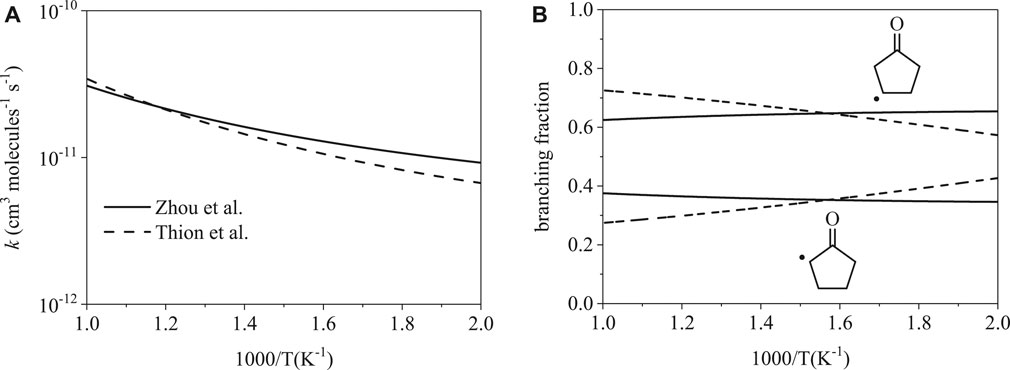
FIGURE 4. Rate coefficients from Thion et al. (Sarathy et al., 2012) and Zhou et al. (Zhou et al., 2016): (A) total, (B) site-specific. The total and site-specific rates are both similar from 500–1000 K.
Ignition delay time predictions as a function of temperature are shown in Figure 5 for cyclopentanone and are mechanism-dependent. The mechanism of Zhang et al. (Zhang et al., 2019) predicts shorter ignition delay times overall. However, modifications made to each mechanism did not affect ignition delay times. To reiterate, modification to the mechanism of Thion et al. (Thion et al., 2016) involved replacing initiation rate parameters with those from Zhou et al. (Zhou et al., 2016). The Zhang et al. (Zhang et al., 2019) mechanism uses initiation rates from Zhou et al. (Zhou et al., 2016). Modification of the mechanism from Zhang et al. (Zhang et al., 2019) involved replacing its initiation rate parameters with those of the mechanism from Thion et al. (Thion et al., 2016). As shown in Figures 5A,B, predictions using the initial and modified mechanism overlap each other. Despite the relative difference in ignition delay times between the two mechanisms, interchanging the initiation rates resulted in no effect on the predictions, which is potentially due to the similarity in branching fractions between the α and β isomers.
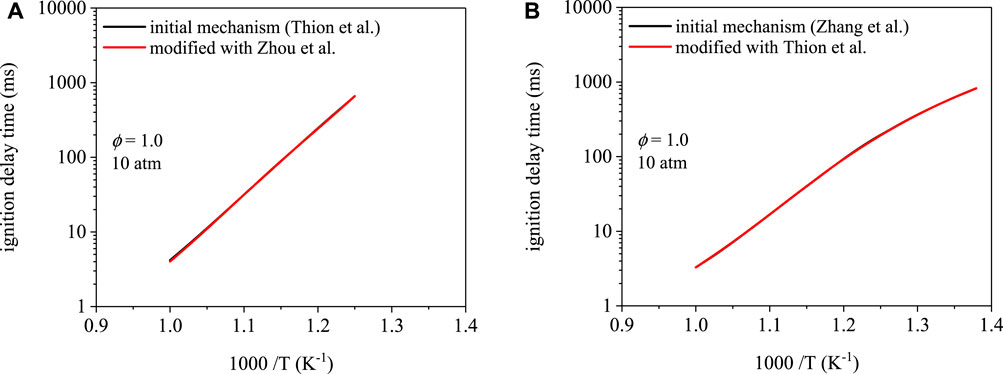
FIGURE 5. Ignition delay time simulations for cyclopentanone: (A) Thion et al. (Thion et al., 2016) mechanism, (B) Zhang et al. (Zhang et al., 2019) mechanism. Modifications to each mechanism result in indiscernible ignition delay time predictions.
Methyl Propanoate
Figure 6A shows total rate coefficients of ȮH-initiation for methyl propanoate. The calculations of Mendes et al. (Mendes et al., 2014) and Tan et al. (Tan et al., 2016) are largely consistent; disparities of factors 1.5 and 1.4 occur at 500 and 1000 K. Despite agreement on the total rate coefficient, branching fractions vary significantly: radical isomers α (Figure 6B), α′ (Figure 6B), and β ′ (Figure 6C) differ by factors of up to 1.5, 1.7, and 1.6, respectively, at 500 K and by factors of up to 1.4, 2.6, and 2.1, respectively, at 1000 K. The prime notation (α′ and β ′) is used to indicate abstraction sites on the ethyl group, the carboxylic acid side of the ester, while α is used to indicate the methyl group on the alcohol-derived side of the ester.
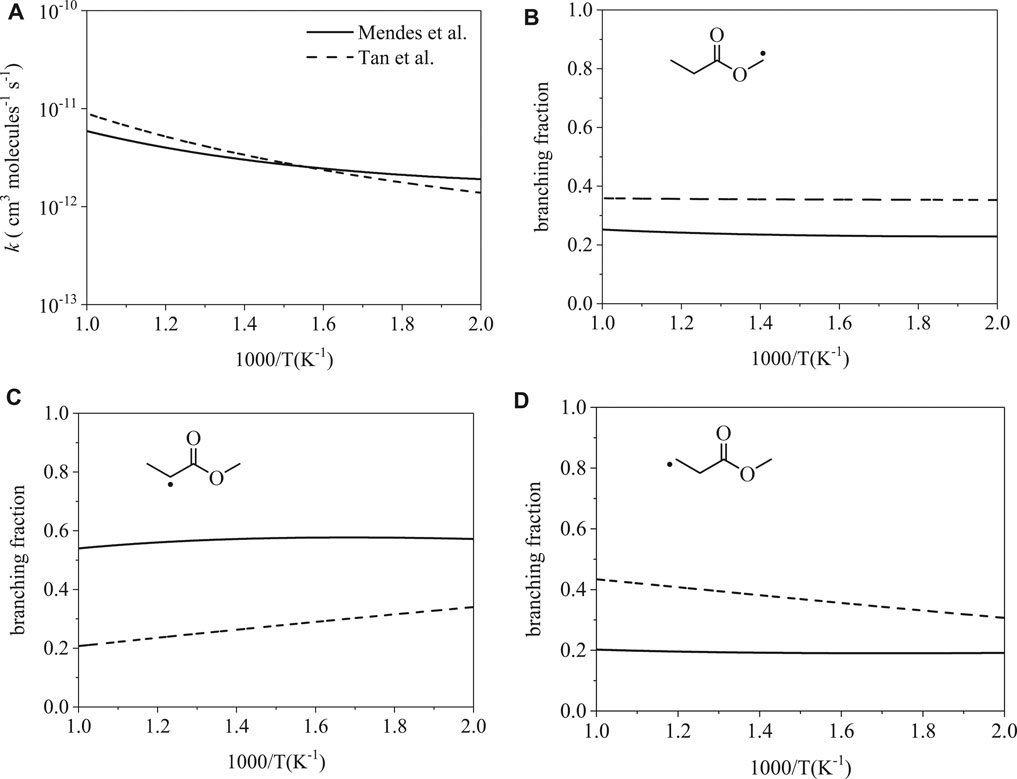
FIGURE 6. Rate coefficients from Mendes et al. (Mendes et al., 2014) and Tan et al. (Tan et al., 2016): (A) total, (B–D) site-specific. Despite the similarity between the total rate coefficients, branching fractions for ȮH-initiated H-abstraction differ up to a factor of 2.6.
Figure 7 shows the ignition delay times for methyl propanoate using the Felsmann et al. (Felsmann et al., 2017) mechanism, which uses rates from Tan et al. (Tan et al., 2016). Low-temperature chain-branching is limited in methyl propanoate oxidation in part because of resonance-stabilization of the α and α′ sites, which inhibits O2-addition (Rotavera and Taatjes, 2021). As a result, ignition delay times below 1,000 ms were only observed at temperatures higher than 850 K. Over the temperature range covered, the differences in ignition delay times are within typical experimental uncertainty. The two trends are within 20% at 850 K (651 ms for the initial mechanism, 769 ms for the modification). At higher temperature, the difference decreases to ∼10% at 1000 K (22 vs 24 ms).
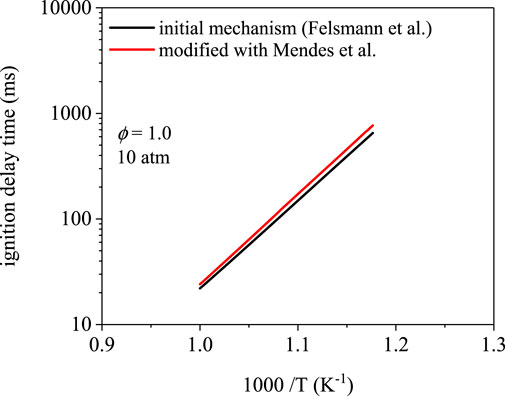
FIGURE 7. Ignition delay time simulations using the mechanism from Felsmann et al. (Felsmann et al., 2017) and a modification using site-specific rates from Mendes et al. (Mendes et al., 2014). Ignition delay times differ by nearly 20% at 850 K and 10% 500 K.
Discussion
Despite the relative consistency among total rate coefficients, ignition delay times can vary substantially when branching fractions differ. At 675 K, ignition delay time predictions for 1-butanol range from roughly 170–1,070 ms depending on the choice of rate parameters. At 850 K, the lowest temperature included for methyl propanoate, ignition delay times varied from 651 to 769 ms. As shown for 1-butanol and methyl propanoate, changes in branching fractions clearly affected ignition delay times. Variations of branching fractions led to differences of up to ∼20% for methyl propanoate, which is within the typical range of experimental error. Conversely, variations in branching fractions led to differences of over 600% for 1-butanol. The effects were more pronounced for 1-butanol than for methyl propanoate most likely due to the limited role of peroxy radicals in oxidation of the latter species owing to resonance-stabilization of the initial radical. As shown in 1-butanol, ignition delay times predictions are not always a reflection of differences in the total rate coefficient for 1-butanol, which implies that branching fractions play a significant role in the simulation results.
As shown in Figure 2B, Seal et al. (Seal et al., 2013) predicts the largest flux of 1-butanol towards α radicals, and the modification of the Sarathy et al. (Sarathy et al., 2012) mechanism using rates from Seal et al. (Seal et al., 2013) produced the longest ignition delay times in Figure 3. As the α isomer exclusively reacts with O2 in a chain-inhibiting step to form butanal and HOȮ, the prediction of higher flux towards the α isomer is consistent with longer ignition delay times as a result of using the Seal et al. (Seal et al., 2013) rates.
Ignition delay time simulations for cyclopentanone provide additional confirmation on the effects of branching fractions on ignition predictions. Within the low-temperature region, branching fractions were remarkably similar, reaching the largest disagreement of factors of 1.4 and 1.2 at 1000 K for the α radical and β radical, respectively. With notable agreement from both the total rate coefficients and the site-specific rate coefficients, both mechanisms yielded nearly identical ignition delay times when rates from Zhou et al. (Zhou et al., 2016) and Thion et al. (Thion et al., 2016) were switched between the mechanisms listed in Table 1.
The results herein indicate that branching fractions of ȮH-initiated H-abstraction reactions are of significant importance, which is because each initial radical follows unique oxidation chemistry, some of which directly influences the degree to which low-temperature chain-branching occurs. To the extent that a functional group affects the rate and mechanism of reaction with ȮH, branching fractions are potentially most important for molecules in which more distinct sites for H-abstractions exist. As an example, in the present work the disparity between ignition delay times was negligible for cyclopentanone, yet within typical experimental uncertainty in the case of methyl propanoate, and pronounced for 1-butanol.
Accordingly, direct and radical-specific experimental measurements of species profiles are needed to provide benchmark validation targets for site-specific rate coefficients and to bridge the gap in model sensitivity between initiation steps and ignition delay times. Ideally, such targets must form from a specific isomer of the initial radical pool to accurately develop a connection between the predicted yield of that radical, i.e. the calculated branching fraction, and products formed via subsequent oxidation. Species produced via chain-propagation from Ṙ + O2 → products and Q̇OOH → products are examples of validation targets that are often isomer-dependent and may serve as unique identifiers for determining correct branching fractions to utilize in combustion models.
Validation targets for 1-butanol include butanal, 3-hydroxybutanal, and 2-hydroxytetrahydrofuran, among other species. Because of the impact of the alcohol group, butanal is a validation target exclusively for the α radical isomer of 1-butanol, CH3CH2CH2ĊHOH. Similarly, 3-hydroxybutanal is a validation target for the γ radical isomer of 1-butanol, CH3ĊHCH2CH2OH. The peroxy radical formed via O2-addition, γ-ROȮ, can isomerize to form Q̇OOH via a favorable six-membered transition state. 2-hydroxytetrahydrofuran is a validation target for the δ isomer of 1-butanol. δ-ROȮ follows a similar reaction sequence to γ-ROȮ, yet involving a seven-membered ring transition state to form 2-hydroxytetrahydrofuran.
To illustrate the dependence of species profiles on branching fractions, Figure 8 shows mole fractions of butanal and 2-hydroxytetrahydrofuran from PSR simulations using the mechanism of Sarathy et al. (Sarathy et al., 2012) and the three mechanism modifications discussed in Approach. The PSR module in ChemKin is the most common and appropriate model for simulating steady-state homogeneous reacting systems from which species profiles are measured, e.g. jet-stirred reactors (Herbinet et al., 2013). Despite being a major product of 1-butanol combustion, the predicted yields of butanal from the four simulations vary significantly. Notably, the differences are consistent with the ignition delay time results, in terms of a dependence on branching fractions, and stem from differences in predictions of selectivity towards α radicals. The rates from Seal et al. (Seal et al., 2013) predict the largest branching fraction towards α radicals and, consistent with that result, the simulation in Figure 8A produced from modifying the Sarathy et al. (Sarathy et al., 2012) mechanism with the rates from Seal et al. (Seal et al., 2013) predicts the highest yield of butanal.
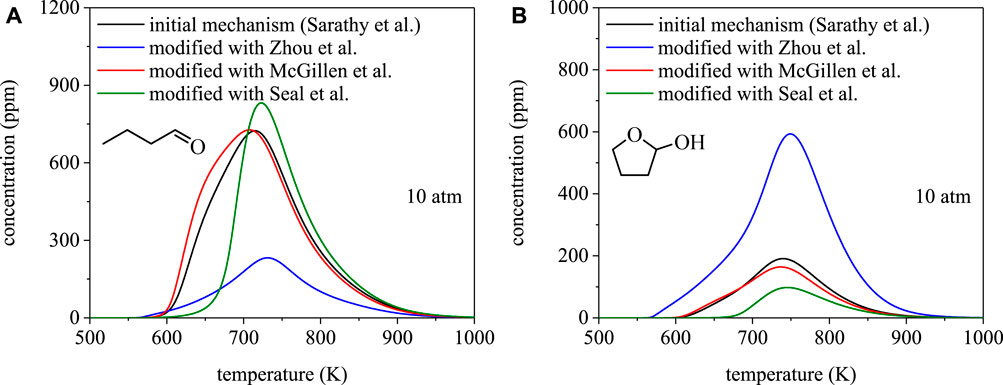
FIGURE 8. Speciation simulations for 1-butanol using the mechanism from Sarathy et al. (Sarathy et al., 2012) and site-specific rate modifications using Zhou et al. (Zhou et al., 2011), Seal et al. (Seal et al., 2013), McGillen et al. (McGillen et al., 2013): (A) butanal, (B) 2-hydroxytetrahydrofuran. Despite agreement between total rate coefficients, disagreements in predicted branching fractions can result in significantly different projections for combustion products.
Cyclic ethers, such as 2-hydroxytetrahydrofuran, are also major chain-propagation products of 1-butanol combustion. As shown in Figure 8B, the four simulations predict comparable concentrations of 2-hydroxytetrahydrofuran to butanal and, similarly, the temperature dependence varies with the set of site-specific rate coefficients used in the mechanism. Despite being predicted to form in comparable concentrations to butanal, no experimental measurements of 2-hydroxytetrahydrofuran (or any other OH-substituted cyclic ethers from 1-butanol), exist. The lack of such measurements highlights a need for speciation measurements in order to provide a direct connection to validating site-specific rate coefficients used in biofuel combustion mechanisms to ultimately enable robust ignition delay time predictions.
Rate-of-production calculations Supplemental Material S5 were conducted on ȮH using each of the four 1-butanol mechanisms at 675 K, the temperature at which the largest observable change occurred. Radical-specific pathways were unchanged despite variations in branching fractions of the initiation step. Instead, changes in the flux towards specific initial radicals only affected the rate of ȮH formation/consumption through a common set of oxidation pathways, which in turn controlled the overall yield of ȮH. As reflected in the ignition delay time trends (cf. Figure 3), the Zhou et al. (Zhou et al., 2011) modification yielded the highest net production rate of ȮH (∼10−2 mol cm3 s−1) at the predicted ignition time, 170 ms, while the Seal et al. (Seal et al., 2013) modification produced the lowest (∼10−12 mol cm3 s−1) at the predicted ignition time, 1,070 ms. The only outlier is the dissociation reaction ȮH + M → Ö + Ḣ + M in the modification using the Seal et al. (Seal et al., 2013) rate parameters Supplemental Material S5, which replaces CH2O+ ȮH → HĊO + H2O that appears in the results using the other mechanisms. However, the predicted rate of dissociation is the lowest of the ten reactions for ȮH.
Sensitivity analysis calculations were also conducted to determine the ten reactions to which ȮH is most sensitive Supplemental Material S6. The reactions are mostly categorized into five classes: initiation/H-abstraction, first-O2-addition, second-O2-addition, ROȮ → Q̇OOH isomerization, or HOO-elimination. The relative importance of one reaction over another varies depending on the mechanism and no clear trend is apparent. However, the dominance of peroxy radical chemistry mediating ȮH underscores the role that isomer-resolved speciation measurements may play in identifying proper branching fractions of initial radical isomers.
Conclusion
Several sets of ignition delay times simulations were conducted at 10 atm for 1-butanol, cyclopentanone, and methyl propanoate using recent combustion mechanisms in the literature. Results were produced from the initial, unmodified mechanisms, followed by additional simulations wherein site-specific rates for ȮH-initiated H-abstraction were replaced in each mechanism using rates from the literature. The main objective of the simulations was to determine the impact of varying branching fractions in the initiation step on ignition delay time simulations for the specific case when total rate coefficients agree.
For both 1-butanol and methyl propanoate, branching fractions in the literature vary non-negligibly and, when incorporated into chemical kinetics mechanisms, led to appreciable differences in ignition delay times below 1000 K for 1-butanol. Relatively minor differences were shown for methyl propanoate predictions. Conversely, site-specific abstraction rates for ȮH + cyclopentanone → Ṙ + H2O are similar and ignition delay time predictions show no dependence on the choice of rates. In the case of 1-butanol, for which multiple rate coefficient studies exist, no significant effects on ignition delay time predictions were observed from uncertainties in the site-specific rate coefficients.
The effects of varying branching fractions were analyzed on three different biofuels for which multiple sets of rate coefficients are available along with detailed chemical kinetics mechanisms that include peroxy radical chemistry. Incidentally, for the present conditions, none of the three biofuels exhibit significant NTC behavior. The dependence of ignition predictions on branching fractions shown herein may also apply in a more general sense to biofuels that undergo NTC behavior, such as diethyl ether, 2-pentanone, or 3-pentanone. To more accurately model combustion of biofuels at low temperature, more stringent and direct validation targets are needed to determine proper branching fractions for initiation reactions. One example of such a target are speciation profiles that provide a direct connection to quantifying isomer-dependent products of combustion reactions, particularly Ṙ + O2 → products and Q̇OOH → products.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
SH contributed computational modeling, analysis, and manuscript preparation; BR contributed analysis and manuscript review.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2021.718598/full#supplementary-material
References
Akih-Kumgeh, B., and Bergthorson, J. M. (2011). Structure-reactivity Trends of C1-C4 Alkanoic Acid Methyl Esters. Combust. Flame 158, 1037–1048. doi:10.1016/j.combustflame.2010.10.021
Al Rashidi, M. J., Davis, A. C., and Sarathy, S. M. (2015). Kinetics of the High-Temperature Combustion Reactions of Dibutylether Using Composite Computational Methods. Proc. Combust. Inst. 35, 385–392. doi:10.1016/j.proci.2014.05.109
Burke, U., Beeckmann, J., Kopp, W. A., Uygun, Y., Olivier, H., Leonhard, K., et al. (2016). A Comprehensive Experimental and Kinetic Modeling Study of Butanone. Combust. Flame 168, 296–309. doi:10.1016/j.combustflame.2016.03.001
Cavalli, F., Geiger, H., Barnes, I., and Becker, K. H. (2002). FTIR Kinetic, Product, and Modeling Study of the OH-Initiated Oxidation of 1-Butanol in Air. Environ. Sci. Technol. 36, 1263–1270. doi:10.1021/es010220s
Curtiss, L. A., Raghavachari, K., Redfern, P. C., Rassolov, V., and Pople, J. A. (1998). Gaussian-3 (G3) Theory for Molecules Containing First and Second-Row Atoms. J. Chem. Phys. 109, 7764–7776. doi:10.1063/1.477422
Felsmann, D., Zhao, H., Wang, Q., Graf, I., Tan, T., Yang, X., et al. (2017). Contributions to Improving Small Ester Combustion Chemistry: Theory, Model and Experiments. Proc. Combust. Inst. 36, 543–551. doi:10.1016/j.proci.2016.05.012
Fenard, Y., Gil, A., Vanhove, G., Carstensen, H.-H., Van Geem, K. M., Westmoreland, P. R., et al. (2018). A Model of Tetrahydrofuran Low-Temperature Oxidation Based on Theoretically Calculated Rate Constants. Combust. Flame 191, 252–269. doi:10.1016/j.combustflame.2018.01.006
Herbinet, O., and Dayma, G. (2013). “Jet-Stirred Reactors,” in Cleaner Combustion: Developing Detailed Chemical Kinetic Models. Editors F. Battin-Leclerc, J. M. Simmie, and E. Blurock (London: Springer London), 183–210. doi:10.1007/978-1-4471-5307-8_8
Hurley, M. D., Wallington, T. J., Laursen, L., Javadi, M. S., Nielsen, O. J., Yamanaka, T., et al. (2009). Atmospheric Chemistry of N-Butanol: Kinetics, Mechanisms, and Products of Cl Atom and OH Radical Initiated Oxidation in the Presence and Absence of NOx. J. Phys. Chem. A. 113, 7011–7020. doi:10.1021/jp810585c
Jacobs, S., Döntgen, M., Alquaity, A. B. S., Kopp, W. A., Kröger, L. C., Burke, U., et al. (2019). Detailed Kinetic Modeling of Dimethoxymethane. Part II: Experimental and Theoretical Study of the Kinetics and Reaction Mechanism. Combust. Flame 205, 522–533. doi:10.1016/j.combustflame.2018.12.026
Ji, W., Zhao, P., He, T., He, X., Farooq, A., and Law, C. K. (2016). On the Controlling Mechanism of the Upper Turnover States in the NTC Regime. Combust. Flame 164, 294–302. doi:10.1016/j.combustflame.2015.11.028
Kumar, K., Sung, C.-J., Weber, B. W., and Bunnell, J. A. (2018). Autoignition of Methyl Propanoate and its Comparisons with Methyl Ethanoate and Methyl Butanoate. Combust. Flame 188, 116–128. doi:10.1016/j.combustflame.2017.09.027
McGillen, M. R., Baasandorj, M., and Burkholder, J. B. (2013). Gas-Phase Rate Coefficients for the OH + N-, I-, S-, and T-Butanol Reactions Measured between 220 and 380 K: Non-arrhenius Behavior and Site-specific Reactivity. J. Phys. Chem. A. 117, 4636–4656. doi:10.1021/jp402702u
Mendes, J., Zhou, C.-W., and Curran, H. J. (2014). Theoretical Study of the Rate Constants for the Hydrogen Atom Abstraction Reactions of Esters with OH Radicals. J. Phys. Chem. A. 118, 4889–4899. doi:10.1021/jp5029596
Sarathy, S. M., Vranckx, S., Yasunaga, K., Mehl, M., Osswald, P., Metcalfe, W. K., et al. (2012). A Comprehensive Chemical Kinetic Combustion Model for the Four Butanol Isomers. Combust. Flame 159, 2028–2055. doi:10.1016/j.combustflame.2011.12.017
Savee, J. D., Papajak, E., Rotavera, B., Huang, H., Eskola, A. J., Welz, O., et al. (2015). Direct Observation and Kinetics of a Hydroperoxyalkyl Radical (QOOH). Science 347, 643–646. doi:10.1126/science.aaa1495
Seal, P., Oyedepo, G., and Truhlar, D. G. (2013). Kinetics of the Hydrogen Atom Abstraction Reactions from 1-Butanol by Hydroxyl Radical: Theory Matches Experiment and More. J. Phys. Chem. A. 117, 275–282. doi:10.1021/jp310910f
Tan, T., Yang, X., Ju, Y., and Carter, E. A. (2016). Ab Initio kinetics Studies of Hydrogen Atom Abstraction from Methyl Propanoate. Phys. Chem. Chem. Phys. 18, 4594–4607. doi:10.1039/c5cp07282d
Thion, S., Togbé, C., Dayma, G., Serinyel, Z., and Dagaut, P. (2016). Experimental and Detailed Kinetic Modeling Study of Cyclopentanone Oxidation in a Jet-Stirred Reactor at 1 and 10 Atm. Energy Fuels 31, 2144–2155. doi:10.1021/acs.energyfuels.6b02061
Vranckx, S., Heufer, K. A., Lee, C., Olivier, H., Schill, L., Kopp, W. A., et al. (2011). Role of Peroxy Chemistry in the High-Pressure Ignition of N-Butanol - Experiments and Detailed Kinetic Modelling. Combust. Flame 158, 1444–1455. doi:10.1016/j.combustflame.2010.12.028
Weber, B. W., Kumar, K., Zhang, Y., and Sung, C.-J. (2011). Autoignition of N-Butanol at Elevated Pressure and Low-To-Intermediate Temperature. Combust. Flame 158, 809–819. doi:10.1016/j.combustflame.2011.02.005
Zádor, J., Taatjes, C. A., and Fernandes, R. X. (2011). Kinetics of Elementary Reactions in Low-Temperature Autoignition Chemistry. Prog. Energ. Combust. Sci. 37, 371–421. doi:10.1016/j.pecs.2010.06.006
Zhang, Z., Hu, E., Pan, L., Chen, Y., Gong, J., and Huang, Z. (2014). Shock-Tube Measurements and Kinetic Modeling Study of Methyl Propanoate Ignition. Energy Fuels 28, 7194–7202. doi:10.1021/ef501527z
Zhang, K., Lokachari, N., Ninnemann, E., Khanniche, S., Green, W. H., Curran, H. J., et al. (2019). An Experimental, Theoretical, and Modeling Study of the Ignition Behavior of Cyclopentanone. Proc. Combust. Inst. 37, 657–665. doi:10.1016/j.proci.2018.06.097
Zhou, C.-W., Simmie, J. M., and Curran, H. J. (2011). Rate Constants for Hydrogen-Abstraction by O˙H from N-Butanol. Combustion and Flame 158, 726–731. doi:10.1016/j.combustflame.2010.11.002
Zhou, C.-W., Simmie, J. M., Pitz, W. J., and Curran, H. J. (2016). Toward the Development of a Fundamentally Based Chemical Model for Cyclopentanone: High-Pressure-Limit Rate Constants for H Atom Abstraction and Fuel Radical Decomposition. J. Phys. Chem. A 120 (36), 7037–7044. doi:10.1021/acs.jpca.6b03994
Keywords: biofuel, low-temperature combustion, branching fraction, alcohol, ketone, ester
Citation: Hartness SW and Rotavera B (2021) Dependence of Biofuel Ignition Chemistry on OH-Initiated Branching Fractions. Front. Mech. Eng 7:718598. doi: 10.3389/fmech.2021.718598
Received: 01 June 2021; Accepted: 30 July 2021;
Published: 19 August 2021.
Edited by:
Ruben Van De Vijver, Ghent University, BelgiumReviewed by:
Charles McGill, Massachusetts Institute of Technology, United StatesMalte Döntgen, RWTH Aachen University, Germany
Copyright © 2021 Hartness and Rotavera. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Brandon Rotavera, Um90YXZlcmFAdWdhLmVkdQ==
 Samuel W. Hartness1
Samuel W. Hartness1 Brandon Rotavera
Brandon Rotavera