- Department of Physics, University of Cagliari, Monserrato, Italy
Thermal conductivity of bulk Si0.5 Ge0.5 at room temperature has been calculated using density functional perturbation theory and the phonon Boltzmann transport equation. Within the virtual crystal approximation, second- and third-order interatomic force constants have been calculated to obtain anharmonic phonon scattering terms. An additional scattering term is introduced to account for mass disorder in the alloy. In the same way, mass disorder resulting from n- and p-type dopants with different concentrations has been included, considering doping with III-group elements (p-type) such as B, Al, and Ga, and with V-group elements (n-type) such as N, P, and As. Little effect on the thermal conductivity is observed for all dopants with a concentration below 1021 cm−3. At higher concentration, reduction by up to 50% is instead observed with B-doping in agreement with the highest mass variance. Interestingly, the thermal conductivity even increases with respect to the pristine value for dopants Ga and As. This results from a decrease in the mass variance in the doped alloy, which can be considered a ternary system. Results are compared to the analogous effect on the thermal conductivity in doped Si.
1 Introduction
A detailed understanding of the mechanisms ruling over thermal transport is of great importance for many technological applications. In microelectronics, for example, fast dissipation of heat is desired (Cahill et al., 2003), translating into a high thermal conductivity. On the other hand, low thermal conductivity is sought for in thermoelectric devices which are of great environmental interest for their ability to transform waste heat into electrical energy. A lower thermal conductivity results in an increased figure of merit, which is the key indicator for the efficiency of heat-to-current conversion (Dresselhaus et al., 2007; Snyder and Toberer, 2008; Hahn et al., 2021).
In fact, a common strategy to optimize the performance of such materials is the reduction of their thermal conductivity while keeping the electrical conductivity mostly unaffected (Snyder and Toberer, 2008; Yu et al., 2010). A promising approach in this respect is nanostructuration (Minnich et al., 2009; He, Donadio, and Galli, 2011; Ferre Llin et al., 2013; Savic et al., 2013). Another efficient way to reduce the thermal conductivity is through introduction of mass disorder, which can be achieved by alloying as successfully shown, for example, in SiGe materials (Steele and Rosi, 1958; Abeles, 1963; Garg et al., 2011; Melis and Colombo, 2014). Already at a Ge content as low as 3%, the thermal conductivity is reduced by a remarkable 84% with respect to pure Si (Garg et al., 2011).
In a similar way, doping of semiconducting materials (essential in most technological applications) introduces mass disorder and can lead to a reduced thermal conductivity. Besides mass disorder, the addition of dopants deeply affects the crystalline state in many respects, including the variation of chemical bonds, the charge distribution, and a possible alteration of the electronic band structure. Different methods have been proposed recently to address such phenomena within the framework of first-principles calculations (Lindsay et al., 2019; McGaughey et al., 2019) and their effect on the thermal conductivity (Liao et al., 2015; Wang et al., 2016).
Recent progress in theoretical methods gave rise to a detailed description of various scattering mechanisms affecting the thermal conductivity in doped materials. However, it is almost impossible to verify single scattering contributions on an experimental level. It is therefore of great interest to elaborate each scattering mechanism as detailed as possible while keeping in mind all other possible scattering mechanisms when comparing theoretical results to experimental data. This state of affairs defines the scenario in which this investigation is framed in.
A first important issue to consider when addressing thermal transport in doped materials is the phonon–electron interaction. It can be invoked using Fermi’s golden rule for phonon–electron scattering (Ziman, 1960). In semiconductors, however, carrier concentrations are typically low with respect to metals, and the effect of phonon–electron interaction on the thermal conductivity can be neglected to a good extent (Liao et al., 2015; Wang et al., 2016).
Next, structural and chemical differences resulting in a change of the interatomic force constants (IFC) can be described using Green’s function method based on the construction of the T-matrix (Mingo et al., 2010; Polanco and Lindsay, 2018). The T-matrix is derived from Green’s function and the perturbation to the dynamical matrix of the defect-free system caused by the system with defect. In the dilute limit, the scattering from such perturbation in the IFC force constants linearly depends on the number of defects.
Several studies have addressed the contributions of different effects. It has been shown, for example, that acoustic phonons in doped InN are represented well considering only mass disorder as the perturbing scattering mechanism for almost all dopants, except for As substitution of N, having the highest mass variance (Polanco and Lindsay, 2018). For optical phonon scattering rates, perturbation of the IFC, however, adds a relevant contribution. Unfortunately, verification with experimental data has not been provided. Another study provided evidence that the IFC disorder is essential in alloys consisting of III–V or II–VI group elements, while thermal transport in IV-group alloys, such as Si1-xGex, is described well taking into account only mass disorder (Arrigoni et al., 2018). Recently, the effect of phonon–electron interaction on the thermal conductivity in Si1-xGex has been analyzed, showing a notable effect for carrier concentration above 1019 cm−3 (Xu et al., 2019). However, mass disorder from the dopant species has not been considered.
The effect of mass disorder was evaluated in multicomponent semiconductors where phonon spectrum and thermal conductivity have been calculated for ZnS, CuGaS2, and Cu2ZnGeSn4 (Shibuya et al., 2016). Zn isotopes were introduced in ZnS resembling the mass disorder of the other materials, that is, Cu + Ga and Cu2+Zn + Ge. A direct comparison to the real systems, however, is difficult, since the crystal structure and chemical composition of ZnS and the respective ternary and quaternary systems are different.
First-principles calculations were used as well to analyze the effect of Na- and Ga-doping in CaMnO3 by explicitly introducing the dopants into a supercell, resulting in a dopant concentration of 2.5% (Zhang et al., 2011). The thermal conductivity was approximated from the mean free path based on the Debye temperature, neglecting anharmonic phonon scattering. This, however, has been shown to be critical for systems with components of different masses. A comparative study of the thermal properties in GaN confronting the latter approach with a fitted parameter for anharmonic scattering with the explicit calculation of three-phonon scattering events based on the third-order IFC revealed the importance of optical phonons in scattering processes which are poorly captured using a fitted parameter for anharmonic scattering (Albar and Donmezer, 2020).
While previous studies have often focused on IFC disorder and phonon–electron scattering for the determination of thermal transport, less attention has been paid to the effect of mass disorder induced by doping with different materials. Therefore, here, we focus on scattering events resulting from different mass variances and their effect on the lattice thermal conductivity in the Si0.5Ge0.5 alloy, which is of technological interest for thermoelectric applications. Several dopants of group III and V elements have been considered, including B, N, Al, P, Ga, and As, and their concentration has been changed from 1019 to 1022 cm−3. Results have been compared to the same kind of doping in bulk Si.
2 Theoretical Framework
The phonon transport processes have been evaluated by density functional (perturbation) theory (DF(P)T) calculations as implemented in the D3Q plug-in of the Quantum Espresso program package (Giannozzi et al., 2009). In this approach, third-order force constants are calculated applying the “2n+1” theorem (Debernardi and Baroni, 1994; Debernardi et al., 1995), which basically states that the “2n+1”-th order variation of the total energy can be obtained from the nth order variation of the charge density. Knowledge of the third-order force constants allows for the determination of three phonon scattering processes and eventually the calculation of thermal conductivity (Ziman, 1960; Fugallo et al., 2013; Paulatto et al., 2013) given by
where
Group velocities and vibrational frequencies are obtained from the dynamical matrix, whose entries are the second-order interatomic force constants. Without the contribution of scattering events that are captured in the relaxation time
Here, the single-mode relaxation time approximation (SMA) has been applied to account for scattering rates due to anharmonicity. At temperatures >100 K, Umklapp processes dominate the phonon scattering which justifies the use of the SMA. The thermal conductivity in Si0.5Ge0.5 at 300 K has been calculated as well using the exact solution (variational approach) (Fugallo et al., 2013), showing no notable difference with respect to the SMA results. Within the relaxation time approximation, scattering rates
where the label i runs over all possible scattering mechanisms. In this work, we consider both the material intrinsic scattering due to anharmonicity of lattice vibrations and scattering from mass disorder. The anharmonic scattering rate, resulting from three-phonon events, is described by Paulatto et al. (2013):
where
where
where
with
For a realistic description of the lattice thermal conductivity of SiGe alloys, an additional scattering term resulting from mass disorder needs to be considered. This scattering term was first introduced by Tamura (Tamura, 1984) for isotope scattering and has been proven to adequately describe mass disorder scattering in several alloy materials (Li et al., 2012; Tian et al., 2012), including Si0.5Ge0.5 (Garg et al., 2011). The mass disorder scattering rate is described by
with
From the
The aim of this study was to evaluate the effect of mass disorder resulting from various dopants in the Si0.5Ge0.5 alloy and to compare it to the effect in doped Si. For this purpose, mass disorder from dopants has been introduced into the calculations in the same way as mass disorder from alloys according to Eq. 7.
3 Computational Details
DFT calculations have been carried out using the Quantum Espresso suite of programs (Giannozzi et al., 2009) within the local density approximation for exchange–correlation interaction (Kohn and Sham, 1965). Norm-conserving, Trouiller–Martins type pseudopotentials (Troullier and Martins, 1991) have been applied to describe the core electrons, while four valence electrons have been treated explicitly for both Si and Ge atoms. An energy cutoff of 50 and 200 Ry, respectively, has been found to be sufficient for the wave function basis set and charge density.
Calculations have been performed using the primitive cell of the face-centered cubic crystal structure containing two atoms. The structure of all systems has been optimized using a
The virtual crystal approximation (VCA) has been applied for DFT calculations of the SiGe alloy. For this purpose, a virtual crystal pseudopotential has been generated from the pseudopotentials of Si and Ge using the tools provided in Quantum Espresso (Hahn et al., 2021).
For the calculation of phonon dispersion, a
We remark an important technical issue often overlooked. The finite value applied for
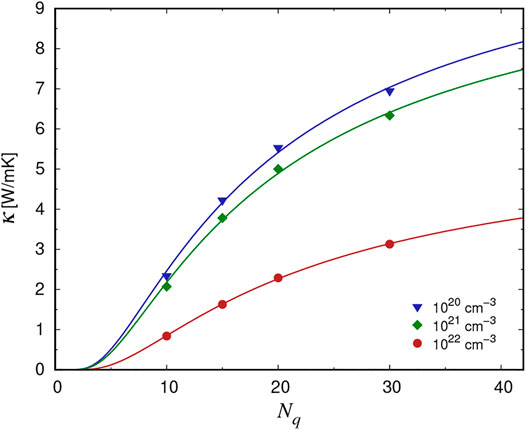
FIGURE 1. Thermal conductivity in B-doped Si0.5Ge0.5 as a function of the integration grid for different concentrations of B. Solid lines represent the exponential function
The linewidth, or inverse relaxation time (Eq. 2), has been calculated on a
4 Results
The effect of mass disorder caused by dopants in SiGe has been investigated for the p-type dopants such as B, Al, and Ge as well as for the n-type dopants such as N, P, and As. Since we focus on the influence of mass disorder without considering phonon–carrier interactions or effects from changes in chemical bonds, no further distinction is made between n- and p-type materials.
The concentration of dopants has been changed from 1019 to 1022 cm−3. We duly remark that a concentration of 1022 cm−3 corresponds to an atomic percentage of 41% of dopant in Si0.5Ge0.5, thus transforming the material into a ternary system (or binary system in the case of Si) where the dopant would have to be considered as part of the alloy rather than just a perturbation. In fact, the electronic structure and phonon dispersion would have to be recalculated since such high dopant concentrations can lead to a shift from semiconducting to metallic properties (Zhang et al., 2011). Nevertheless, the concentrations 5.1021 and 1022 cm−3 have been added to this study to provide a magnification of the trends at lower concentrations rather than to give accurate quantitative behavior.
It has been shown that phonon–electron interactions can notably reduce the thermal conductivity in silicon for carrier concentrations above 1013 cm−3 (Liao et al., 2015). Phonon–electron interactions are not considered in this study. The calculated values can therefore be regarded an upper limit for the lattice thermal conductivity.
4.1 Effect of Mass Disorder in Si0.5Ge0.5
The thermal conductivity as a function of doping concentration is shown in Figure 2. For doping concentrations of
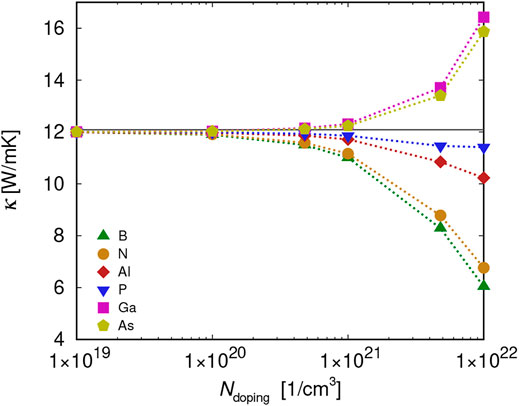
FIGURE 2. Thermal conductivity in Si0.5Ge0.5 as a function of the doping level for various dopants. The horizontal gray line indicates the thermal conductivity in undoped Si0.5Ge0.5.
Interestingly, for Ga and As, the opposite trend is observed: thermal conductivity in fact increases with respect to undoped Si0.5Ge0.5. We attribute this unexpected behavior to a decrease in the mass variance
where
In fact, we have verified this behavior for a fictitious dopant of mass 60.217 a. u. resulting in an increase of the thermal conductivity by 2.2% at a doping concentration of 1021 cm−3 (see Figures 3, 4). A slightly smaller increase of κ by 1.8% is found when the doping mass is set to the average mass of the Si0.5Ge0.5 alloy (50.354 a. u.).
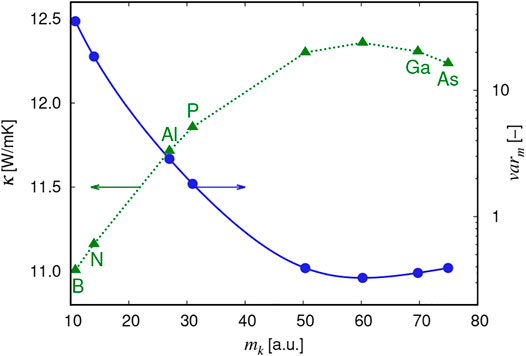
FIGURE 3. Thermal conductivity (green triangles) in Si0.5Ge0.5 as a function of the atomic mass
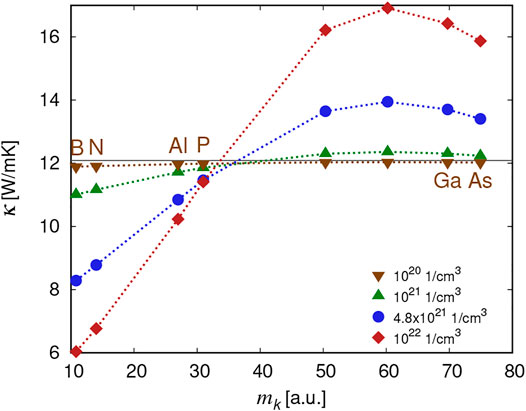
FIGURE 4. Thermal conductivity in Si0.5Ge0.5 as a function of the atomic mass
This result is very interesting and of great technological importance since it provides evidence that in ternary systems, a maximum thermal conductivity can be engineered by reducing the mass variance. Reduction in the mass variance can possibly be obtained as well from a controlled distribution of isotopes.
For the sake of completeness, in Figure 4, we show the thermal conductivity as a function of dopant mass for several doping concentrations up to 1022 cm−3. At high doping concentration, the maximum of κ at
The scattering spectrum in doped and undoped SiGe has been analyzed calculating the linewidth, that is, the inverse scattering time (Eq. 2), at different wave vectors along high symmetric directions. It is presented in Figure 5 as a function of the phonon dispersion. Upon doping with a fictitious material of mass
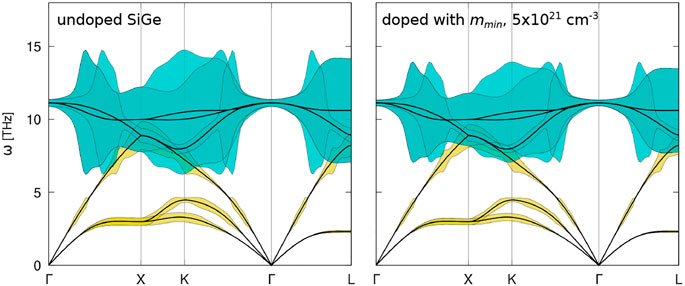
FIGURE 5. Phonon dispersion of SiGe undoped (left) and doped with fictitious species of mass 60.217 a. u. (right). The linewidth (inverse relaxation time) of acoustic and optical modes is represented in yellow and cyan, respectively. For better visual presentation, the value of the linewidth of optical modes has been divided in half.
Figure 6 shows the thermal conductivity in undoped SiGe and SiGe doped with B and with a fictitious species of mass
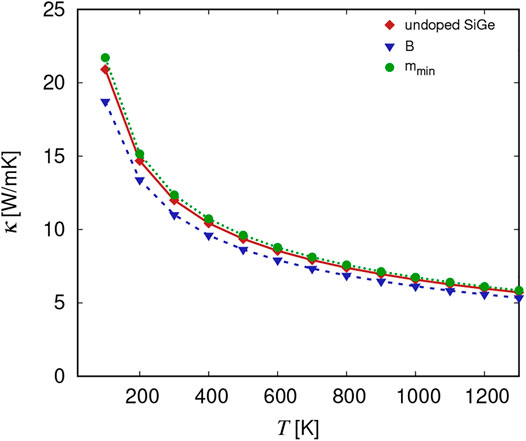
FIGURE 6. Thermal conductivity in undoped Si0.5Ge0.5 (red diamonds) and doped with B (blue triangles) and a fictitious species with mass
4.2 Effect of Mass Disorder in Si
In the case of pure hosts, such as Si, introduction of dopants always results in an increase of mass variance. As a result, the thermal conductivity is highest in the undoped material and decreases with increasing difference between dopant and host mass (Figure 7).
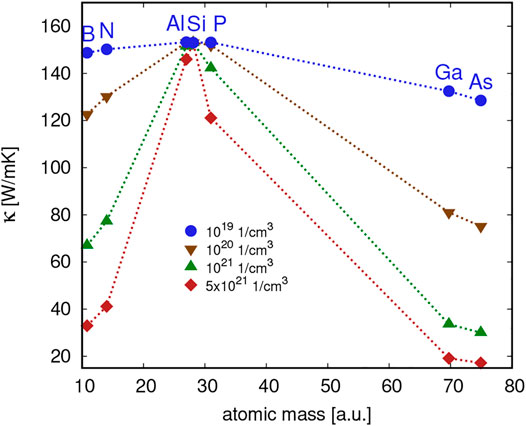
FIGURE 7. Thermal conductivity in Si as a function of the atomic mass of the dopant for various doping concentrations.
Different to Si0.5Ge0.5, the thermal conductivity is notably reduced already at a doping concentration of 1019 cm−3 when the introduced dopants lead to a high mass variance (Ga and As). This effect is most pronounced for As, resulting in a reduction of 16%. At
Figure 8 shows the thermal conductivity as a function of doping concentration. For a high mass variance, as it is the case for Ga and As, the thermal conductivity drops fast by roughly 90% at a doping concentration of 5.1021 cm−3. Further increase to 1022 cm−3, however, does not alter the thermal conductivity any further. For doping with elements of the second period, B and N, the thermal conductivity continues to decrease from 33 to 23 W/mK and from 41 to 30 W/mK, respectively. The relative mass variance in doped Si0.5Ge0.5 (compared to undoped Si0.5Ge0.5) is in general lower with respect to doped Si. Therefore, the behavior of κ as a function of dopant concentration in Si0.5Ge0.5 (Figure 2) can only be compared to the behavior in doped Si with low mass variance. In fact, a similar trend is found for Al- and P-doping of Si and all doping types in Si0.5Ge0.5.
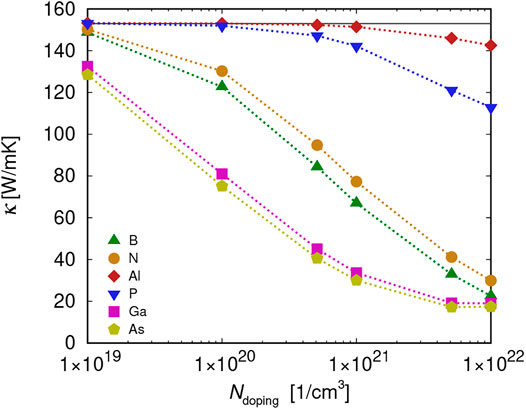
FIGURE 8. Thermal conductivity in Si as a function of the doping level for various dopants. The horizontal gray line indicates the thermal conductivity in pure Si.
Experimental studies have reported a lower thermal conductivity in B-doped Si than in P-doped samples (Slack, 1964; McConnell et al., 2001), which is in good agreement with our results. Scattering events resulting from electron–phonon and hole–phonon interactions could additionally reduce the thermal conductivity in Si as it had been shown previously by first-principles calculations (Liao et al., 2015). In fact, hole–phonon scattering has been shown to be stronger than electron–phonon scattering, resulting in a lower thermal conductivity of p-type Si (Liao et al., 2015). This effect adds to the mass–variance one above discussed, thus justifying the comparatively lower thermal conductivity experimentally found in B-doped Si (p-type).
Scattering rates in undoped Si (Figure 9) are remarkably smaller with respect to the ones in SiGe. Introduction of mass disorder by dopants already at medium concentrations (here shown for 1020 cm−3) drastically increases the linewidth of optical phonons, for B-doping. Note that for better visualization, the linewidth in Figure 9 has been multiplied by a factor of 20. The highest increase of the linewidth of acoustic phonons is observed at K for longitudinal modes. Even though low-frequency acoustic phonons are known to be the main carriers for thermal transport, increase of the phonon linewidth of optical modes increases scattering, with the former explaining the notable reduction of thermal conductivity in doped Si.
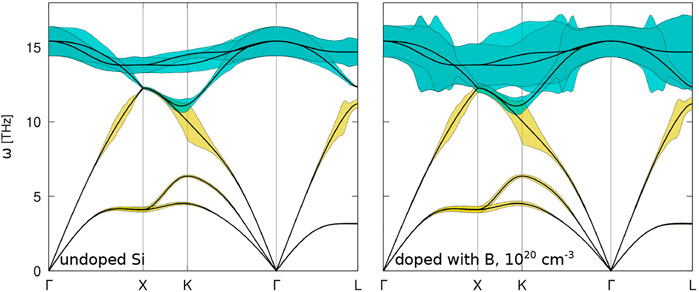
FIGURE 9. Phonon dispersion of Si undoped (left) and doped with B (right). The linewidth (inverse relaxation time) of acoustic and optical modes is represented in yellow and cyan, respectively. For better visual presentation, the value of the linewidth has been multiplied by 20.
In agreement with the literature, the thermal conductivity of Si decreases with increasing temperature (Figure 10) as a result of increased Umklapp scattering processes. Similar to SiGe, the effect of mass disorder is higher at low temperatures and decreases steadily with increasing temperatures. At a doping concentration of 1020 cm−3 with As, the thermal conductivity is reduced with respect to pristine Si by 81 and 27% at 100 and 1200 K, respectively. This demonstrates that scattering from mass disorder is more pronounced at low temperatures, while other scattering effects (e.g., Umklapp scattering) become more important at higher temperature.
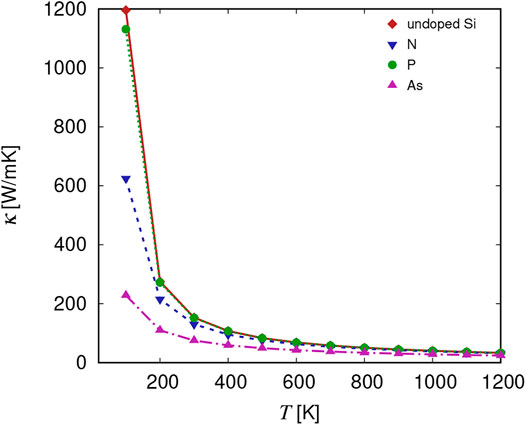
FIGURE 10. Thermal conductivity in undoped Si (red diamonds) and doped with N (blue triangles), p (green circles), and As (pink triangles) at a concentration of 1020 cm−3 as a function of temperature.
The general trend of decreasing thermal conductivity with increasing carrier concentration in both Si0.5Ge0.5 and Si is in agreement with experimental data (Dismukes et al., 1964; Slack, 1964; McConnell et al., 2001). Since most theoretical studies so far have focused on the contribution of phonon–electron interaction in doped materials (Liao et al., 2015; Xu et al., 2019), the role of mass disorder and variance is still unclear. With this study, we have shown that mass disorder does play a role at high doping concentrations and suggest that both mechanisms should be investigated simultaneously in a future study.
5 Conclusion
The effect of mass disorder due to dopants on the thermal conductivity in Si0.5Ge0.5 has been investigated by first-principles calculations. III-group elements such as B, Al, and Ga have been considered for p-type doping and V-group elements such as N, P, and As for n-type doping with concentrations ranging from 1019 to 1022 cm−3.
Scattering from mass disorder is already present in the undoped Si0.5Ge0.5 alloy. Notable effects on the thermal conductivity from doping-induced mass disorder are therefore observed only at concentrations of 5.1020 cm−3 and higher. Doping with B generates the highest mass variance in the Si0.5Ge0.5 system, resulting in the most pronounced reduction of the thermal conductivity, namely, 9% at a concentration of 1021 cm−3. Slightly lower reduction is found for N-doping. At this concentration, for dopants P, Ga, and As, the effect on the thermal conductivity is less than 2%.
Interestingly, for Ga and As, an increase in the thermal conductivity is observed. This results from a reduced mass variance with respect to the undoped Si0.5Ge0.5. In fact, the minimal mass variance in doped Si0.5Ge0.5 is given for a dopant with
In contrast to Si0.5Ge0.5, doping in Si always leads to a reduction of the thermal conductivity. Notable decrease is already observed at a concentration of 1019 cm−3 and is most pronounced for As in agreement with the highest mass variance.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
KH carried out the calculations and analysis of the data, and prepared the first draft of the manuscript. All authors equally contributed to the design of the study, manuscript revision, reading, and approved the submitted version.
Funding
This work was financed by Ministero dell’Università e Ricerca (MIUR) under the Piano Operativo Nationale 2014–2020 asse I, action I.2 “Mobilità dei Ricercatori” (PON 2014–2020, AIM), through project AIM1809115-1.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abeles, B. (1963). Lattice Thermal Conductivity of Disordered Semiconductor Alloys at High Temperatures. Phys. Rev. 131, 1906–1911. doi:10.1103/physrev.131.1906
Albar, I., and Donmezer, N., Mean Free Path-Thermal Conductivity Accumulation Calculations for Wurtzite Gallium Nitride: Two Approaches,” Nanoscale Microscale Thermophysical Eng. 24, 80, 93. (2020). doi:10.1080/15567265.2020.1744777
Arrigoni, M., Carrete, J., Mingo, N., and Madsen, G. K. H. (2018). First-principles Quantitative Prediction of the Lattice thermal Conductivity in Random Semiconductor Alloys: The Role of Force-Constant Disorder. Phys. Rev. B 98, 115205. arXiv:1712.02577. doi:10.1103/physrevb.98.115205
Cahill, D. G., Ford, W. K., Goodson, K. E., Mahan, G. D., Majumdar, A., Maris, H. J., et al. (2003). Nanoscale Thermal Transport. J. Appl. Phys. 93 (2), 793–818. doi:10.1063/1.1524305
Cepellotti, A., Fugallo, G., Paulatto, L., Lazzeri, M., Mauri, F., and Marzari, N. (2015). Phonon Hydrodynamics in Two-Dimensional Materials. Nat. Commun. 6, 6400. doi:10.1038/ncomms7400
Debernardi, A., Baroni, S., and Molinari, E. (1995). Anharmonic Phonon Lifetimes in Semiconductors from Density-Functional Perturbation Theory. Phys. Rev. Lett. 75, 1819–1822. doi:10.1103/physrevlett.75.1819
Debernardi, A., and Baroni, S., “Third-order Density-Functional Perturbation Theory: A Practical Implementation with Applications to Anharmonic Couplings in Si,” Solid State. Commun. 91, 813, 816. (1994). doi:10.1016/0038-1098(94)90654-8
Dismukes, J. P., Ekstrom, L., Steigmeier, E. F., Kudman, I., and Beers, D. S. (1964). Thermal and Electrical Properties of Heavily Doped Ge‐Si Alloys up to 1300°K. J. Appl. Phys. 35, 2899–2907. doi:10.1063/1.1713126
Dresselhaus, M. S., Chen, G., Tang, M. Y., Yang, R. G., Lee, H., Wang, D. Z., et al. (2007). New Directions for Low-Dimensional Thermoelectric Materials. Adv. Mater. 19, 1043–1053. doi:10.1002/adma.200600527
Ferre Llin, L., Samarelli, A., Cecchi, S., Etzelstorfer, T., Müller Gubler, E., Chrastina, D., et al. (2013). The Cross-Plane Thermoelectric Properties of p-Ge/Si0.5Ge0.5 Superlattices. Appl. Phys. Lett. 103, 143507. doi:10.1063/1.4824100
Fugallo, G., Cepellotti, A., Paulatto, L., Lazzeri, M., Marzari, N., and Mauri, F. (2014). Thermal Conductivity of Graphene and Graphite: Collective Excitations and Mean Free Paths. Nano Lett. 14, 6109–6114. doi:10.1021/nl502059f
Fugallo, G., Lazzeri, M., Paulatto, L., and Mauri, F. (2013). Ab Initio variational Approach for Evaluating Lattice thermal Conductivity. Phys. Rev. B - Condensed Matter Mater. Phys. 88, 045430. doi:10.1103/physrevb.88.045430
Garg, J., Bonini, N., Kozinsky, B., and Marzari, N. (2011). Role of Disorder and Anharmonicity in the Thermal Conductivity of Silicon-Germanium Alloys: A First-Principles Study. Phys. Rev. Lett. 106, 045901. doi:10.1103/PhysRevLett.106.045901
Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). QUANTUM ESPRESSO: a Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 21, 395502. doi:10.1088/0953-8984/21/39/395502
Hahn, K. R., Melis, C., Bernardini, F., and Colombo, L. (2021). Intrinsic Thermoelectric Figure of merit of Bulk Compositional SiGe Alloys: A First-Principles Study. Phys. Rev. Mater. 5, 065403. doi:10.1103/physrevmaterials.5.065403
He, Y., Donadio, D., and Galli, G. (2011). Heat Transport in Amorphous Silicon: Interplay between Morphology and Disorder. Appl. Phys. Lett. 98, 144101. doi:10.1063/1.3574366
Kohn, W., and Sham, L. J., “Self-Consistent Equations Including Exchange and Correlation Effects,” Phys. Rev. 140, A1133, A1138. (1965). doi:10.1103/physrev.140.a1133
Lazzeri, M., Calandra, M., and Mauri, F. (2003). Anharmonic Phonon Frequency Shift inMgB2. Phys. Rev. B 68 (R), 220509. doi:10.1103/physrevb.68.220509
Li, W., Lindsay, L., Broido, D. A., Stewart, D. A., and Mingo, N. (2012). Thermal Conductivity of Bulk and Nanowire Mg2SixSn1−xalloys from First Principles. Phys. Rev. B 86, 174307. doi:10.1103/physrevb.86.174307
Liao, B., Qiu, B., Zhou, J., Huberman, S., Esfarjani, K., and Chen, G. (2015). Significant Reduction of Lattice thermal Conductivity by the Electron-Phonon Interaction in Silicon with High Carrier Concentrations: A First-Principles Study. Phys. Rev. Lett. 114, 115901. arXiv:1409.1268. doi:10.1103/physrevlett.114.115901
Lindsay, L., Katre, A., Cepellotti, A., and Mingo, N. (2019). Perspective on Ab Initio Phonon thermal Transport. J. Appl. Phys. 126, 11305. doi:10.1063/1.5108651
McConnell, A. D., Uma, S., and Goodson, K. E. (2001). Thermal Conductivity of Doped Polysilicon Layers. J. Microelectromech. Syst. 10, 360–369. doi:10.1109/84.946782
McGaughey, A. J., Jain, A., Kim, H. Y., and Fu, B. (2019). Phonon Properties and thermal Conductivity from First Principles, Lattice Dynamics, and the Boltzmann Transport Equation. J. Appl. Phys. 125, 11101. doi:10.1063/1.5064602
Melis, C., and Colombo, L. (2014). Lattice thermal Conductivity of Si(1-x)Ge(x) Nanocomposites,” Phys. Rev. Lett. 112, 065901 doi:10.1103/PhysRevLett.112.065901
Mingo, N., Esfarjani, K., Broido, D. A., and Stewart, D. A. (2010). Cluster Scattering Effects on Phonon Conduction in Graphene. Phys. Rev. B - Condensed Matter Mater. Phys. 81, 045408. doi:10.1103/physrevb.81.045408
Minnich, A. J., Lee, H., Wang, X. W., Joshi, G., Dresselhaus, M. S., Ren, Z. F., et al. (2009). Modeling Study of Thermoelectric SiGe Nanocomposites. Phys. Rev. B 80, 155327. doi:10.1103/physrevb.80.155327
Monkhorst, H. J., and Pack, J. D., “Special Points for Brillouin-Zone Integrations,” Phys. Rev. B 13, 5188, 5192. (1976). doi:10.1103/physrevb.13.5188
Paulatto, L., Mauri, F., and Lazzeri, M. (2013). Anharmonic Properties from a Generalized Third-Orderab Initioapproach: Theory and Applications to Graphite and Graphene. Phys. Rev. B 87, 214303. doi:10.1103/physrevb.87.214303
Polanco, C. A., and Lindsay, L., “Thermal Conductivity of InN with point Defects from First Principles,” Phys. Rev. B 98, 014306. (2018). doi:10.1103/physrevb.98.014306
Savic, I., Donadio, D., Gygi, F., and Galli, G. (2013). Dimensionality and Heat Transport in Si-Ge Superlattices. Appl. Phys. Lett. 102, 073113.
Shibuya, T., Skelton, J. M., Jackson, A. J., Yasuoka, K., Togo, A., Tanaka, I., et al. (2016). Suppression of Lattice thermal Conductivity by Mass-Conserving Cation Mutation in Multi-Component Semiconductors. APL Mater. 4, 104809. doi:10.1063/1.4955401
Slack, G. A. (1964). Thermal Conductivity of Pure and Impure Silicon, Silicon Carbide, and diamond. J. Appl. Phys. 35, 3460–3466. doi:10.1063/1.1713251
Snyder, G. J., and Toberer, E. S., “Complex Thermoelectric Materials,” Nat. Mater 7, 105, 114. (2008). doi:10.1038/nmat2090
Steele, M. C., and Rosi, F. D., “Thermal Conductivity and Thermoelectric Power of Germanium‐Silicon Alloys,” J. Appl. Phys. 29, 1517, 1520. (1958). doi:10.1063/1.1722984
Tamura, S.-i. (1984). Isotope Scattering of Large-Wave-Vector Phonons in GaAs and InSb: Deformation-Dipole and Overlap-Shell Models. Phys. Rev. B 30, 849–854. doi:10.1103/physrevb.30.849
Tian, Z., Garg, J., Esfarjani, K., Shiga, T., Shiomi, J., and Chen, G. (2012). Phonon Conduction in PbSe, PbTe, and PbTe1−xSexfrom First-Principles Calculations. Phys. Rev. B 85, 184303. doi:10.1103/physrevb.85.184303
Troullier, N., and Martins, J. L., “Efficient Pseudopotentials for Plane-Wave Calculations,” Phys. Rev. B 43, 1993, 2006. (1991). doi:10.1103/physrevb.43.1993
Wang, Y., Lu, Z., and Ruan, X. (2016). First Principles Calculation of Lattice thermal Conductivity of Metals Considering Phonon-Phonon and Phonon-Electron Scattering. J. Appl. Phys. 119, 225109. doi:10.1063/1.4953366
Xu, Q., Zhou, J., Liu, T. H., and Chen, G. (2019). Effect of Electron-Phonon Interaction on Lattice thermal Conductivity of SiGe Alloys. Appl. Phys. Lett. 115, 23903. doi:10.1063/1.5108836
Yu, J.-K., Mitrovic, S., Tham, D., Varghese, J., and Heath, J. R. (2010). Reduction of thermal Conductivity in Phononic Nanomesh Structures. Nat. Nanotech 5, 718–721. doi:10.1038/nnano.2010.149
Keywords: thermoelectric, mass disorder, first-principles analysis, doped SiGe, thermal conductivity
Citation: Hahn KR, Melis C, Bernardini F and Colombo L (2021) Engineering the Thermal Conductivity of Doped SiGe by Mass Variance: A First-Principles Proof of Concept. Front. Mech. Eng 7:712989. doi: 10.3389/fmech.2021.712989
Received: 21 May 2021; Accepted: 28 June 2021;
Published: 28 July 2021.
Edited by:
Sukwon Choi, The Pennsylvania State University (PSU), United StatesReviewed by:
Zlatan Aksamija, University of Massachusetts Amherst, United StatesNazli Donmezer, Boğaziçi University, Turkey
Copyright © 2021 Hahn, Melis, Bernardini and Colombo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Konstanze R. Hahn, a29uc3RhbnplLmhhaG5AZHNmLnVuaWNhLml0
 Konstanze R. Hahn
Konstanze R. Hahn Claudio Melis
Claudio Melis Fabio Bernardini
Fabio Bernardini