Assessing the Mechanisms Thought to Govern Ice and Snow Friction and Their Interplay With Substrate Brittle Behavior

Sliding friction on ice and snow is characteristically low at temperatures common on Earth’s surface. This slipperiness underlies efficient sleds, winter sports, and the need for specialized tires. Friction can also play a micro-mechanical role affecting ice compressive and crushing strengths. Researchers have proposed several mechanisms thought to govern ice and snow friction, but directly validating the underlying mechanics has been difficult. This may be changing, as instruments capable of micro-scale measurements and imaging are now being brought to bear on friction studies. Nevertheless, given the broad regimes of practical interest (interaction length, temperature, speed, pressure, slider properties, etc.), it may be unrealistic to expect that a single mechanism accounts for why ice and snow are slippery. Because bulk ice, and the ice grains that constitute snow, are solids near their melting point at terrestrial temperatures, most research has focused on whether a lubricating water film forms at the interface with a slider. However, ice is extremely brittle, and dry-contact abrasion and wear at the front of sliders could prevent or delay a transition to lubricated contact. Also, water is a poor lubricant, and lubricating films thick enough to separate surface asperities may not form for many systems of interest. This article aims to assess our knowledge of the mechanics underlying ice and snow friction. We begin with a brief summary of the mechanical behavior of ice and snow substrates, behavior which perhaps has not received sufficient attention in friction studies. We then assess the strengths and weaknesses of five ice- and snow-friction hypotheses: pressure-melting, self-lubrication, quasi-liquid layers, abrasion, and ice-rich slurries. We discuss their assumptions and review evidence to determine whether they are consistent with the postulated mechanics. Lastly, we identify key issues that warrant additional research to resolve the specific mechanics and the transitions between them that control ice and snow friction across regimes of practical interest.

Introduction

Sliding friction on ice and snow is remarkably low at temperatures common on Earth’s surface. This slipperiness underlies efficient sleds for polar transport, competitive and recreational winter sports, and specialized vehicle tires (e.g., De Koing et al., 1992; Higgins et al., 2008; Scherge et al., 2013; Nachbauer et al., 2016a; Lever et al., 2016). Friction can also play a micro-mechanical role affecting ice compressive and crushing strengths (e.g., Schulson, 2001). Researchers have proposed several plausible mechanisms that focus on the properties of ice near its melting point. Kietzig et al. (2010) and Colbeck (1992) provided comprehensive reviews of these hypothesized mechanisms for ice and snow substrates, respectively. However, directly validating these mechanisms has been difficult owing to the small length scales and time intervals of surface interactions. Nevertheless, recent advances in imaging and surface-measurement technology have provided new insight and the potential to discern between hypothesized mechanisms governing friction on ice and snow.

This article aims to assess our knowledge of the mechanics underlying ice and snow friction. Our focus is on kinetic friction relevant to dynamic systems rather than slower motion relevant to glaciers or stationary structures. Owing to competitive or safety interests, much research has aimed to understand friction governing sports equipment (e.g., skis, skates, sled-runners) and vehicles (e.g., tires, cargo sleds), largely relying on the tenets of self-lubrication theory. This approach is slowly changing as more observational evidence emerges on the roles of other mechanisms.

We begin with a review of the mechanical properties of ice and snow (Ice and Snow Mechanical Behavior) and discuss how those properties influence friction mechanics. We then summarize five ice- and snow-friction hypotheses and assess their strengths and weaknesses:

• Pressure melting—the reduction in phase-transition temperature by slider pressure

• Self-lubrication by a melt-water film produced by frictional heating

• Quasi-liquid surface layers on ice that display increased molecular mobility compared with the bulk crystal structure

• Abrasion of ice or snow-grains by slider asperities and the role of the resulting wear particles as dry lubricants

• Ice-rich slurries formed by crushing or abrasion that act as lubricating layers with viscoelastic rheology

In Evidence of Ice- and Snow-Friction Mechanics, we summarize observations that support or challenge these hypotheses. Lastly, we identify key issues that warrant additional research to resolve the specific mechanics and the transitions between them that control ice and snow friction across regimes of practical interest.

Ice and Snow Mechanical Behavior

Ice and bulk snow show complex mechanical behavior that can vary with temperature, load rate, microstructure and morphology (Petrovic, 2003). We focus here on relatively rapid loading that induces elastic deformation and brittle failure within the ice or snow, a regime that governs most kinetic-friction scenarios. For example, interactions between micron-scale asperities would occur on ms time scales for 1 mm s⁻¹ sliding speeds. Rapid macro-scale indentation of bulk ice or natural snow also causes brittle fracture of the substrate. The cited studies also provide guidance on substrate behavior at lower interaction rates, should those conditions be relevant to the sliding-system of interest.

Ice Under Compression and Tension

Solid ice is remarkably brittle right up to its melting point (Schulson, 2001). Under uniaxial compression, brittle failure occurs at strain rates above 10^–4—10^–3 s⁻¹ and at strengths of about 10 MPa at −10°C (Hawkes and Mellor, 1972; Gold, 1977; Schulson, 2001). Strain at failure is on the order of 10^–3. The strain rate for transition from ductile to brittle failure decreases, and compressive strength increases, with decreasing temperature (Arakawa and Maeno, 1997; Schulson, 2001). Young’s modulus for rapidly loaded ice ranges 6–10 GPa, increasing with loading rate, and Poisson’s ratio ranges about 0.28–0.36 (Gold, 1977; Gold, 1988).

For ice specimens well bonded to the platens, compressive failure usually occurs through shear faulting. In this mode, wing cracks form at the tips of sliding cracks and open in tension, at rates controlled by the sliding friction of opposing faces of the main cracks. The material strain-softens but continues to carry load. Friction coefficients of these sliding cracks range μ ∼ 0.3–0.8, increasing with decreasing temperature (Schulson, 2001). Interestingly, Schulson (1990) noted that this sliding can produce powdered ice on the fractured surfaces from localized failures. Confinement increases failure stresses, and the ice becomes more ductile at high confining pressures; the reduction in melting point limits the increase in deviatoric stress at failure (Schulson, 2001).

In tension, brittle fracture dominates ice failure at strain rates higher than about 10^–3 s⁻¹. Uniaxial tensile strength is about 1–2 MPa for granular ice under brittle failure and is nearly independent of temperature from −40 to 0°C. (Hawkes and Mellor, 1972; Gold, 1977; Schulson, 2001). Strain at failure is on the order of 10^–4. Fracture processes (crack initiation and propagation) govern brittle tensile strength. Even as warm as −2°C, freshwater ice at high loading rates is more brittle than rocks and ceramics, with fracture energy ∼0.5 Jm⁻² or just 2.5 times higher than the surface energy required to create two new surfaces (Nixon and Schulson, 1987). This extreme brittleness also influences the response of ice to rapid indentation and shear.

Ice Indentation

Hardness, or average indentation pressure, is often considered a material property, and hardness under spherical indentation relates to tensile yield stress for ductile materials (Bowden and Tabor, 1954; Bhushan, 2013). However, brittle failure can introduce important variations in indentation resistance with indenter geometry and rate. Considerable research effort has sought to understand the mechanics of ice indentation to aid safe design of bridge piers, ships and offshore structures exposed to ice loads. Here, we review some of this research relevant to ice friction on skate blades, sled runners or, potentially, surface asperities. Note that with μ < 0.1 common for these systems, the vast majority of the applied load is compressive.

Schulson (1999) estimated the effective strain rate in an indentation contact zone as

$\dot{\in }\sim \frac{u}{2w}(1)$

where u is the indentation velocity and w is the indenter width. Eq. 1 predicts high effective strain rates under narrow indenters. For example, hockey- or speed-skate forward speeds greater than about 1 mm/s would cause brittle ice behavior at the front of the contact zone. Furthermore, Hertzian (elastic) stresses are unbounded at sharp blade edges, essentially guaranteeing brittle failure beneath some fraction of the blade’s width.

Under brittle failure, average ice-indentation pressure decreases with increasing contact area and varies with indenter geometry and the state of confinement (Masterson and Frederking, 1993; Sodhi, 2001; Jordaan, 2001). Consequently, ice hardness is not a uniquely defined material property. Importantly, isolated high-pressure zones (HPZs) occur during ice indentation tests (Figure 1), with measured pressures approaching the pressure-melting point for the ambient ice temperatures (Gagnon, 1994a; Wells et al., 2011; Kim et al., 2012; Browne et al., 2013). This last point bears emphasis. Kheisin and Cherepano (1973) and Kurdyumov and Kheisin (1979) investigated the mechanics of ice indentation during drop-ball tests. They identified a layer of shattered ice particles with water present under pressure. Kurdyumov and Kheisin (1979) stated that “Depending on the quantity of liquid phase, the intermediate layer can be represented as a pasty or powdery substance. Such a substance may possess both viscous and plastic properties …”

FIGURE 1

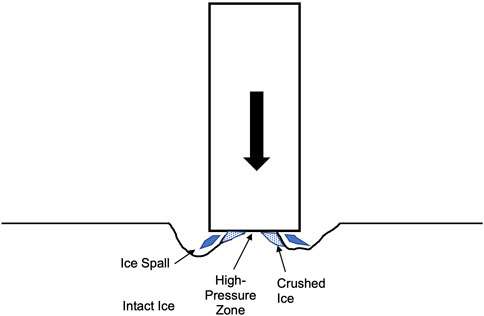
FIGURE 1. Schematic of ice-indentation processes as they occur under a narrow indenter, based on concepts by Gagnon and Molgaard (1991), Jordaan (2001) and Wells et al. (2011). Similar processes might occur at slider or ice asperities.

Gagnon and Molgaard (1991), using video and strobe light, documented HPZs during rapid ice-indentation tests. They calculated peak pressures averaging 90 ± 24 MPa and identified evidence of pressure-melting and extrusion of ice-water slurries consisting of about 20% liquid. They estimated that extrusion consumed at least 50% of the indentation energy and suggested that these processes could be important at asperity contacts and under sled runners and skate blades. Gagnon (1994b) used a combined pressure/capacitive sensor to measure slurry thicknesses of several microns under HPZs, and Gagnon (2010) used high-speed video (30,000 frames s⁻¹) to capture the flow of ice-water jets exiting HPZs. These crushing and slurry-creation and -extrusion processes could play important roles at local slider-ice contacts, either from overall slider geometry or from surface asperities.

Snow Under Compression and Tension

Snow is a porous aggregate of fairly weakly bonded grains of ice. Its strength varies with density, sintering time and loading rate (Mellor, 1964; Mellor, 1975; Abele and Gow, 1975; Salm, 1982; Shapiro et al., 1997; Marshall and Johnson, 2009). Compressive, tensile and shear strengths under rapid loading (brittle failure, strain rates greater than ∼10^–4 s⁻¹) range 10 kPa–1 MPa, generally increasing with density across a range 100–600 kg m⁻³. Failure strain is on the order of 10^–3. Young’s modulus increases from roughly 0.1 MPa to 1 GPa across this density range, whereas Poisson’s ratio ranges about 0.23–0.30, showing a slight increase with density (Mellor, 1964; Mellor, 1975). The specific fracture energy of snow can range 0.1–1 J m⁻² (Reuter et al., 2019). Temperature has less influence on snow strength, especially under brittle failure. Although snow mechanical properties vary strongly with density, variations at a given density are significant and reflect the development of intergranular bonds as the constituent ice grains sinter together. This is especially noticeable for mechanically worked snow used to create roads and runways (Fukue, 1979; Abele, 1990). Snow can also lose strength over time as metamorphism produces layers of large, weakly bonded grains (Schweizer et al., 2003; Blackford 2007; Reuter et al., 2019).

Combined Compression and Shearing of Snow

Researchers have long recognized that sliders (e.g., skis or sleds) perform work to compact snow to support slider weight (Nakaya et al., 1936; Bekker, 1956; Wong, 1989; Colbeck, 1992). This compaction begins as dry contact at the front of a slider and is rapid enough to cause brittle failure of the snow through rupture of intergranular bonds. Even well-sintered snow can fail in this manner. The concurrent response of the snow to slider shear has not received much attention, yet the resulting snow-grain motion can produce low slider friction. Nakaya et al. (1936) used thin planes of soot and red ochre to track the displacement of natural snow beneath the tracks of skis and sleds for common alpine skiing speeds and normal loads. They found that the slider often displaced the snow at the slider-contact surface several meters longitudinally (down-track), and the sub-track displacements formed a parabolic shape suggestive of fluid-like shear of the powdery snow, despite its compaction by the slider (Figure 2). Kuroiwa (1977) observed similar down-track shearing profiles of snow compacted under a ski. Mellor (1975) suggested that shearing of fluidized snow imparts friction on the solid boundary similar to turbulent flow.

FIGURE 2

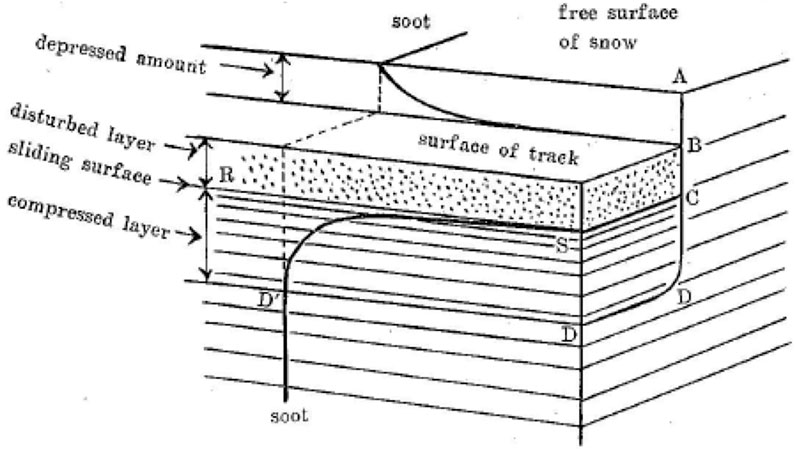
FIGURE 2. Schematic of snow deformation after passage by a ski or sled on natural snow (reproduced from Nakaya et al., 1936, with the permissions of Hokkaido University Collection of Scholarly and Academic Papers). A plane of soot placed across the path revealed the subsurface compression (Points A-D) and concurrent shearing (Points D’-S) of the snow beneath the slidling plane R-S-C. The slider also fractured and lofted some snow crystals to form disturbed layer R on top of the sliding plane.

Rapid compression can also produce pore-pressure lift on a ski or snowboard by pumping air through the dynamically compressed porous snow (Feng and Weinbaum, 2000; Wu et al., 2005; Wu et al., 2006). For moderate snow density (400 kg m⁻³) and slider speed >10 m s⁻¹, predicted pore-pressure lift can exceed the vertical support of the solid matrix and thereby reduce contact forces on the snow grains and thus contact friction. The resulting “aerodynamic” drag then becomes important. While Wu and Sun (2011) examined the role of snow-slider friction on pore-pressure lift, the interplay between this lift mechanism and the mechanics of contact friction has not been explored. Additionally, the porous-flow theory as formulated omits longitudinal movement of the fractured grains in response to slider shear.

It seems unlikely that sintering can reform intergranular bonds to arrest snow-grain motion under a slider, although some evidence exists that sintering can proceed quickly. Gubler (1982) measured the development of tensile strength of two ice cones after contact times of 1–500 s. Federolf et al. (2004) observed densified bulbs of snow fragments at the front of an indenter under rapid penetration (up to 2 m s⁻¹) and suggested that the fragments sintered quickly. Szabo and Schneebeli (2007) demonstrated sub-second sintering of two ice specimens during brief contact. However, none of these tests imposed concurrent shear motion. If snow-grain translation or rotational motion prevents intergranular bonds from reforming, the snow fragments essentially form a cohesionless granular material. Lever et al. (2018), Lever et al. (2019) noted that snow friction can be quite low under these conditions.

Summary of Ice and Snow Mechanical Behavior

The mechanical behavior of ice and snow can strongly influence contact mechanics on these substrates. Micro-scale asperity interactions, and most macro-scale slider interactions, occur at strain rates sufficient to produce brittle substrate behavior. Ice is extremely brittle right up to its melting temperature. Ice hardness varies with indenter geometry and speed, and brittle crushing can produce ice-rich slurries at the interface that govern contact processes. Slider normal and shear loads can cause snow intergranular bonds to fail, which can prevent warming and melting of persistent contacts. Snow-grain sintering is unlikely to reform these bonds until after the slider has passed. The brittle behavior of ice and snow warrants thorough consideration for its role in influencing friction on these substrates.

Postulated Ice and Snow Friction Mechanisms

Pressure Melting

On Earth’s surface, water is denser than ice (hexagonal-structure ice Ih). Consequently, increased hydrostatic pressure aids the phase change from ice to water. Pressure depresses the melting temperature of ice from the ice Ih-liquid-vapor triple point (0.01°C, 611.7 Pa) to the ice Ih-ice III-liquid triple point at −21.985°C and 208.6 MPa (Wagner et al., 2011; Figure 3). The effect is weak: pressure depresses the melting point by only −0.074°C MPa⁻¹ near 0°C. The system must also provide the change in enthalpy (latent heat) needed to melt ice, dH:

$dH=dE+PdV(2)$

Work done through the volume change, PdV, reduces the required change in internal energy, dE, by less than 10% (Bridgman, 1912); heat transfer from the surroundings must provide the remainder.

FIGURE 3

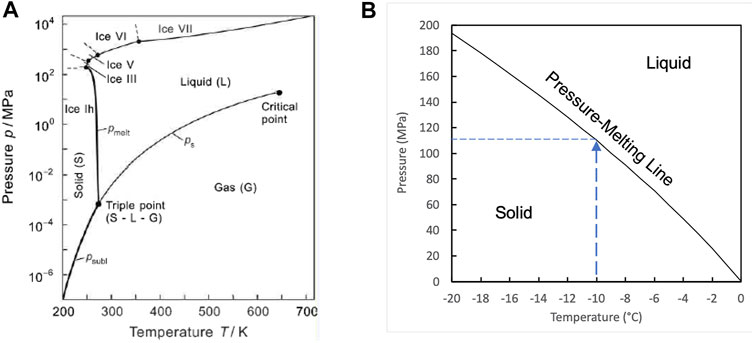
FIGURE 3. (A)P(T) phase daigram for water (reproduced from Wagner et al., 2011, with the permission of AIP Publishing). Hexagonal-structure Ice Ih is the only ice phase stable on Earth's surface. (B) Equilibrium pressure-melting line for Ice Ih (from Eq. 6 in Wagner et al., 2011). For example, inceasing pressure to 110 MPa will cause ice to melt at −10°C with the requisite addition of heat.

Reynolds (1899) postulated that a thin water film formed by pressure melting could account for the slipperiness of ice during skating or walking. Most subsequent researchers dismissed this mechanism owing to the high contact-pressures needed and the requirement of a heat source (Bowden and Hughes, 1939; Colbeck, 1995; Kietzig et al., 2010). Frictional heating from slider motion seemed a direct way to create a lubricating film and did not require high pressures (see Self-Lubrication).

Niven (1959) argued that both pressure and heating could produce water films at contacting ice asperities, citing steel-on-ice tests that showed the friction force approaching a constant value with increasing normal load. However, Niven envisioned plastic deformation during asperity interactions and did not consider that the ice asperity could fracture and fail during such short interactions.

Colbeck (1995) specifically dismissed pressure melting as an important process during ice skating. He argued that pressures needed significantly to reduce the melting point exceeded the crushing strength of ice. While Colbeck noted that failure pressures depended on the state of confinement, he stated that “Indentation hardness experiments [Barnes et al. (1971)] also show that pressure melting is not one of the failure mechanisms when ice is rapidly loaded …” However, drop-ball experiments by Kheisin and Cherepano (1973) and Kurdyumov and Kheisin (1979), and indentation tests by Gagnon and Molgaard (1991), showed that pressure melting could play a role by lowering the temperature at which ice melts via energy supplied by the indenter. Ice-rich viscous slurries could consequently form under the indenter.

Colbeck (1995) made two other arguments refuting pressure melting during ice skating: 1) that heat conduction from the ambient to the interface is required and is weak compared with frictional heat generated at the interface, and 2) that any liquid-water films would be squeezed to small thicknesses by the high pressures required for pressure melting. Both arguments warrant reconsideration if the fluid at the interface consists of an ice-rich slurry. This appears to be the case for some ice-friction scenarios.

Certainly, snow is far too weak to support high contact pressures. However, ice is much stronger, and ice-indention research has revealed that HPZs can reach the pressure-melting point. Furthermore, the slider/indenter can provide the energy needed to melt some fraction of the ice through crushing, shearing and extrusion processes. Localized HPZs could also arise at slider-ice contacting asperities. That is, frictional heat generated by the viscous flow of ice-rich slurries could operate together with pressure-driven lowering of the melting point to provide an efficient lubrication layer between a slider and ice (see Ice-Rich Slurries).

Self-Lubrication

Background

We define the self-lubrication hypothesis as one that attributes the slipperiness of ice and snow to a lubricating melt-water film generated by heat from viscous shearing of that film (Figure 4). This hypothesis allows one to calculate the friction coefficient and heat flux by assuming low Reynolds number (Couette) flow in the sliding direction:

$\tau =\eta \frac{dv}{dz}=\eta \frac{v}{h}(3)$

$\mu =\frac{\tau }{\sigma }=\frac{\eta v}{h\sigma }(4)$

$q_f=\tau v=\eta \frac{v^2}{h}(5)$

where $\tau$ is the shear stress, $\eta$ is the viscosity of water (usually at 0°C), v is slider speed, h is water-film thickness, $\sigma$ is normal pressure, and $q_f$ is frictional heat flux (W m⁻²).

FIGURE 4

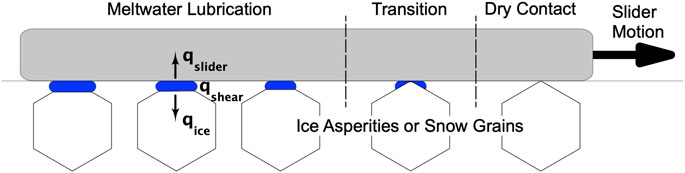
FIGURE 4. Schematic of the self-lubrication hypothesis, which posits that low friction on ice and snow results from a lubricating water film generated by frictional heat via shearing of that film ($q_f={\text{q}}_{\text{shear}}$, Eq. 5). Most self-lubrication formulations do not describe the mechanics of how dry contact at the front of a slider transitions to lubricated contact as sliding proceeds.

In its fullest form, the mechanics split $q_f$ into the slider, $q_s$, and into the ice, $q_i$, by equating the contact temperature on each surface to the melting temperature (usually 0°C). Any excess heat melts the contacting ice. The unknown h derives from a mass balance between melt-water production and water-loss from squeezing or shearing of the film by slider normal pressure or forward motion. Because the ice or snow substrate experiences frictional heat for a short duration, t = l/v, where l is slider length, most formulations compute the substrate temperature rise using the 1D transient heat-conduction equation (e.g., Carslaw and Jaeger 1959):

$\text{Δ}{T}_i=\frac{2q_i}{k_i}{\left(\frac{{\text{Κ}}_{i}t}{\pi }\right)}^{1/2}(6)$

where $\text{Δ}{T}_i$ is ice temperature rise, k_i and K_i are ice thermal conductivity and diffusivity, respectively, and $q_i$ is the portion of frictional heat flux that flows into the ice, assumed constant. Eq. 6 can also apply to bulk snow by changing the thermal properties. A transient or a steady-state conduction equation can be used for the slider, depending on the duration of sliding.

Self-lubrication can quantitatively connect μ to ambient temperature and slider speed, normal pressure and thermal properties. However, it generally does not account for slider surface properties or substrate (ice, snow) mechanical properties. Determining the real area of contact also poses problems, especially at ice asperities and for sliding on snow where contact area evolves. Importantly, it assumes that a self-generated water film forms during sliding without describing how dry contact at the front of a slider or at the start of motion transitions to lubricated contact. Direct asperity contact must occur until the film thickens sufficiently to separate the surfaces.

Bhushan (2013) delineated lubrication regimes based on the ratio of film thickness to roughness:

$\frac{h}{R_c}<1\hspace{1em}\text{boundary}(\mathrm{7a})$

$1<\frac{h}{R_c}<5\hspace{1em}\text{mixed-mode}(\mathrm{7b})$

$\frac{h}{R_c}>6\text{hydrodynamic}(\mathrm{7c})$

where R_c is the composite standard deviation of roughness heights. Friction and wear rates can be high under boundary lubrication, and appreciable solid-solid interactions occur, mediated by molecular-scale films (Jones, 1982; Bhushan, 2013). Within the mixed-mode regime, some solid-solid contacts occur, producing contact friction and wear particles, along with partial hydrodynamic lubrication. For full hydrodynamic lubrication to prevail, the surfaces must be smooth relative to the film thickness to avoid solid-solid contact and for roughness to have negligible effect on squeeze flow (Moore, 1965; Bhushan, 2013). Most self-lubrication formulations fail this test.

Despite these potential drawbacks, self-lubrication remains widely accepted as an explanation for why ice and snow are slippery. Here, we review its development as a friction hypothesis and identify some of its shortcomings.

Self-Lubrication on Ice

Bowden and Hughes (1939) conducted the first systematic tribometer experiments of sliders on solid ice and compacted-snow and suggested that a lubricating film of melt-water from frictional heat could account for low friction on both substrates. They noted that high static friction argued against pressure melting, whereas system changes that increased interface temperatures (e.g., higher ambient temperatures, heat conducted to or trapped at the interface) reduced friction, consistent with their hypothesis. Furthermore, they suggested that the higher friction on snow compared to ice was “… almost certainly due to the extra mechanical work of displacing and compacting the snow” and noted that outdoor tests on actual skis produced lower friction after several repeated passes over the same tracks. While not stated, these snow-friction observations are consistent with intergranular-bond failure and grain movement that would impede persistent heating and melting of individual snow-slider contacts. Later, Bowden (1953) conducted static-friction tests of skis on compacted snow and compared the results with kinetic friction measured using coupons of the same surface treatments contacting a rotating ice disk at 5 m s⁻¹. Bowden interpreted the large drop in kinetic vs. static friction as evidence supporting self-lubrication theory. Indeed, post-test freezing of an aluminum coupon to the ice confirmed some friction-induced melting, although Bowden did not report the duration of sliding for these tests.

Evans et al. (1976) accepted the self-lubrication hypothesis and used it to explain the dependence of ice friction on ambient temperature, sliding speed and thermal conductivity. They tested acrylic, steel and copper rods sliding against a rotating ice cylinder. For theory, they formulated an equation for the heat sinks to estimate friction and its dependence on system parameters. Notably, they did not equate these sinks to the heat from viscous shearing of a water film. Their equation tracked heat conduction into the rods and into the ice and the latent heat needed to form a melt layer, assuming that the contacting area was at the pressure-adjusted melting temperature, T_m. Because they modeled q_i as a transient heat flux (Eq. 6), they obtained a v^−1/2 dependence of friction on slider speed that agreed well with their measurements for cases of low rod thermal conductivity. They concluded that “Our results are consistent with the view ofBowden and Hughes (1939)that water is formed at the area of contact and that it serves to lubricate the surfaces.”

However, Evans et al. (1976) also presented evidence that other mechanisms could be important:

• Friction values were lower during the first few revolutions of the ice cylinder, then rose to steady-state values. Lower initial values likely resulted from dry-contact shearing or pressure-melting at ice asperities.

• They noted that “At lower temperatures [<−2°C] wear was rapid at first, as the pressure exceeded the hardness of the ice, but after a few hundred traversals of the surface it quickly decreased.” This observation is also consistent with dry-contact abrasion or pressure-melting at ice asperities.

• “After a run the rods showed definite signs of abrasion at the areas of contact.” “Abrasion was visible on rods of all the different materials …”

• They noted that if viscous shearing accounted for their measured friction values, h would only be 5 nm or “… much smaller than the surface roughness, and therefore viscous shearing of the water film cannot be the mechanism that produces the friction.”

• “It is clear that mixed lubrication exists: the lubricant supports much of the load between the two surfaces, but at high points the surfaces come into contact or are separated by a film of only a few molecules thick, and these are the sources of most of the frictional force.”

In effect, Evans et al. (1976) analyzed the heat flows from the slider-ice interface without identifying the mechanism that generated the frictional heat. They noted evidence of abrasion and direct slider-ice contact. Nevertheless, they concluded that “… in the range of our experiments, the main contribution to the observed friction comes from a large lubricated area at the melting point rather than a small dry area in front.”

Oksanen and Keinonen (1982) extended self-lubrication theory by assuming that viscous shear of the water film generated the frictional heat. They modeled transient heat flows into both slider and ice, although they independently set the interface melting temperature, T_m, and ice hardness, H_i (to establish contact area). Notably, they did not include squeeze flow to balance water production and loss with applied normal load. Their model predicted $\mu \propto v^{-1/2}$ and $\mu \propto v^{1/2}$ at low temperatures and high temperatures, respectively, and model predictions agreed well with their ice-on-ice friction measurements and with those of Evans et al. (1976), with the caveat that they selected rather than calculated T_m and H_i.

The Oksanen and Keinonen (1982) model raises several concerns:

• It predicted h ∼ 0.4–6 nm at −15°C and 40–90 nm at −1°C, yet they did not note that solid-solid contact was likely for such thin films.

• The model did not include water loss from squeeze flow and its consequent reduction of h.

• Although the authors extended the model to include a slider steady-state conduction term, that term introduced another independent variable, the thermal-disturbance thickness, to be selected.

• The model did not rigorously predict the interface temperature but rather assumed independent temperature differentials for heat flows into the two bodies.

Stiffler (1984) formulated a first-principles, self-lubrication model by coupling the Reynolds’ equation for hydrodynamic lubrication with an energy equation wherein the source was viscous shearing of a water film and the sinks were transient heat flow into the two bodies and latent heat needed to melt one surface. He recognized that, even for parallel surfaces, steady melting would compensate for mass-loss by squeeze flow to provide normal pressure to support the slider. The model matched surface temperatures to determine the heat flow into each surface and offered two end cases: all the frictional heat flowed into the non-melting surface, or all the heat flowed into the melting surface. The former gave $\mu \propto v^{-1/2}$ while the latter $\mu \propto v^{1/2}$. Applied to an ice skate (−2°C, 1 MPa normal pressure, 1 m s⁻¹ speed), Stiffler predicted μ = 0.011 and film thickness h = 0.17 μm. Because the formulation required that h be larger than the combined peak roughness of the surfaces, he concluded that “A skater on typical ice would probably fail the test.” Nevertheless, the model formally included all the components of self-lubrication theory.

Makkonen and Tikanmäki (2014) formulated a self-lubrication model that considered n slider-ice contact regions, each of size a, assumed that viscous shearing of the water film at each contact generated the frictional heat, and assumed that transient heat conduction governed heat flow into both bodies. They also iteratively included water loss by squeeze-flow to reduce h. A major assumption was that each contact was a constant, 1-mm square, with n increasing with normal load such that normal pressure in each contact equaled H_i. This resulted in $\mu \propto a^{-1/2}$. Here, a concern is that μ depends fairly strongly on the choice of a, and 1 mm seems much too large to represent slider asperities. As with other self-lubrication models, the Makkonen and Tikanmäki model predicted very thin water films: h < 0.1 μm for 1 m s⁻¹ speeds at temperatures below −2°C. They did not note the difficulties such thin films pose to the formulation.

Lozowski and Szilder (2013) and Lozowski et al. (2013) formulated a friction model for speed skates that included crushing and self-lubrication components. They assumed that the blade crushed ice at constant pressure, equal to drop-ball hardness (Poirier et al., 2011), to support the skater’s weight. The model calculated the crushing power dissipated, but it did not consider the role of the crushed particles along the interface and instead assumed that a hydrodynamic film began at the front of the contact zone. The formulation included squeeze flow but neglected heat flow into the skate blade. Overall, the model gave excellent agreement with measured speed-skate friction (De Koing et al., 1992), including variations caused by blade tilt during actual skating strides. However, the model predicted h < 0.5 μm for v < 12 m s⁻¹ at −5°C, with thinner films at the front of the blade and at lower speeds and temperatures. Although Lozowski and Szilder (2013) noted that polished speed skates can have low roughness (0.05 μm), such thin films cast doubt on whether hockey and recreational skates at most speeds and temperatures would satisfy Eq. 7c. Moreover, Lever et al. (2021) documented hockey- and speed-skate ice interactions during actual skating, using infrared thermography, high-speed video, confocal profilometry and optical microscopy. Their results were inconsistent with the presence of supporting water films and favored the presence of ice-rich slurries at discontinuous HPZs, with brittle ice failure playing an important role. Seymore-Pierce et al. (2017) and Scherge et al. (2013) also observed a dominate role of brittle ice failure beneath sliders on ice during tests aimed to reveal friction mechanics relevant to the sports of skeleton and bobsled, respectively.

Self-Lubrication on Snow

Researchers have also proposed that self-lubrication can account for low friction on snow despite important mechanical and structural differences with ice. The front of a slider simultaneously compacts and shears natural snow. Even well-sintered snow can deform and fail in response to frictional shear before contact points warm to 0°C. Assuming persistent snow-grain contacts form, real contact area must increase during sliding either by melting or abrading contacting grains. This process is central to quantifying snow friction but is largely unknown and potentially quite different from contact evolution on ice. If meltwater films form, pore spaces in snow allow water loss through squeezing, shearing and plowing by slider asperities, processes also very different from those on ice.

Colbeck (1988), Colbeck (1992) attributed to Klein (1947) the concept of three snow-friction mechanisms: solid-solid, lubricated and capillary suction. Colbeck (1988) focused on self-lubrication, then Colbeck (1992) more thoroughly considered the role of other friction mechanisms. For self-lubrication, he envisioned grain-scale (mm) lubricated contacts. At each of n contacts (assumed equal in size), viscous shearing of the water film provided the heat to melt the grains and to conduct into the slider and the snow. He included two water-loss mechanisms: squeeze-flow from normal pressure and shearing-flow from slider forward motion, and argued that shearing-flow dominated. He treated heat flow into the snow grains as 1D transient conduction, and he considered several cases of heat flow into the slider: fully insulated, and transient, steady-state and periodic conduction, with the latter preferred qualitatively. The resulting model predicted $\mu \propto v^{-1/2}$ at low speeds and $\mu \propto v^{1/2}$ at high speeds, with high slider conductivity increasing friction at all speeds.

The model predicted h < 0.1 μm for downhill-skiing conditions (v = 10 m s⁻¹, plastic ski) across the temperature range −40°C to −0.5°C, assuming a relatively large grain-contact diameter of 2 mm (Colbeck, 1988). Because squeeze-flow rates increase as $d^{-2}$, smaller grain-contact areas would produce thinner films. Even after weakening the water-loss mechanism for hydrophobic sliders, Colbeck (1992) concluded that “… the calculated value for film thickness is probably too small to separate the solids under most conditions of interest, even when only squeeze occurs, and this suggests that there is solid-to-solid interaction as well as meltwater lubrication”.

Colbeck (1992) expanded his consideration of snow-friction mechanisms while cautioning that “… there is not enough information about them to combine them into a theory of snow friction for application.” He discussed surface properties of snow relevant to friction, the “polishing” effect of repeated passes, and noted that “… it is especially difficult to estimate the actual contact area during sliding.” He then introduced and discussed several snow-friction mechanisms: “plowing and compaction of snow in front of the slider, snow deformation below the slider, deformation or fracture of asperities, shearing of the water films that support the slider’s weight, capillary attraction from other water attachments, and drag by surface dirt.” He mentioned but did not treat snow disaggregation (i.e., grain-bond failure) as a mechanism, noting that it “… might be important since snow grains seem to release by rebound after rapid ski passage.” To add to this daunting task, Colbeck noted that these mechanisms often interact.

Colbeck (1992) extensively discussed dry contact mechanics and the transition to melt-water lubrication, and he noted that lack of important details impedes understanding of dry-contact friction. To estimate the relative importance of the two, he predicted the dry-contact length, l_d, to raise the snow ambient temperature to 0°C, based on Eq. 6 and assuming an insulated slider:

$l_d=\frac{\pi k_i^2{T}_s^2{\left(\raisebox{1ex}{$A_c$}\!\left/ \!\raisebox{-1ex}{$A_n$}\right.\right)}^2}{4{\text{Κ}}_{i}v{\mu }_d^2{p}_n^2}(8)$

where T_s is snow ambient temperature, and p_n is slider nominal pressure. Heat flow into the slider increases l_d. The predicted length depends strongly on the actual contact area and the dry-contact friction coefficient, μ_d, both assumed to be constant. However, dry-contact abrasion should increase A_c as grains wear, and many friction studies indicate that μ_d can initially be quite low and increases as the slider shears snow-grain or ice asperities. These changing conditions invalidate the assumptions embedded in Eq. 8. Furthermore, if the slider fails the snow intergranular bonds and the grains move, persistent heating does not occur. That is, Eq. 8 may not provide reasonable predictions for the dry-contact length under a slider and thus the relative importance of dry vs. lubricated friction mechanics. Also, Colbeck’s self-lubrication model assumed that $n{d}^2=const$, so that the size of each contact would reduce as more grains came into contact. This seems counterintuitive, as both the size and number of contacts should increase as the slider melts or abrades the contacting grains.

Lehtovaara (1989) developed a similar self-lubrication model for ski-snow friction but neglected heat flow into the ski. He also derived Eq. 8 to estimate the length of the dry-contact region. Lehtovaara included only squeeze flow (no shear flow) to account for water loss at the contacts, but did describe mixed dry/lubricated friction, with a transition to fully lubricated at h > 3 R_c, half of the value recommended by Bhushan (2013); Eq. 7c). Wet friction followed Eq. 4, and the dry-friction coefficient was assumed to be 0.06. To assess the model, Lehtovaara tested short sliders against flat ice using a rotary tribometer. He allowed a long (3 km) run-in distance for each test specimen “… to ensure that a steady-state friction process was achieved.” Interestingly, measured roughness of each slider decreased during the tests, suggesting that dry-contact polishing was an important process.

Bäurle at al (2007) formulated a numerical model for sliding on ice and snow that included dry and lubricated contact. Importantly, they attempted to account for the evolution of real contact area as sliding progressed. After compacting snow samples, they measured static contact areas (A_c/A_n ∼ 0.01–0.1) using micro-computed tomography. They also used scanning electron microscopy (SEM) to examine the surface of snow samples subjected to repeated passes of a small ski and suggested that the flattened grain contacts showed evidence of melting. The model assumed constant dry-contact friction (μ_d = 0.3) at the start of sliding until the water film thickened sufficiently to equal that friction, after which the model used wet friction. In its full form, their self-lubrication model included heat flows into both surfaces and water loss by squeeze flow. They accounted for 3D heat transfer at the contact areas by altering ice thermal conductivity with contact-area ratio, although most researchers view 1D heat flow as a reasonable assumption at sliding contacts (Blok, 1937; Archard, 1959; Carslaw and Jaeger, 1959). They also heuristically attempted to account for slider roughness, although they did not treat its effect of increasing squeeze-flow (Moore, 1965). Nevertheless, the model posed a fairly complete implementation of self-lubrication theory for snow.

In lieu of testing on snow, Bäurle at al (2007) measured friction and surface-temperature rise of a 40-mm-long polyethylene slider pressed against a rotating ice ring. Their data and numerical results revealed several interesting features:

• Measured friction coefficients (shown for −5°C) started below μ = 0.007 and smoothly rose to μ ∼ 0.053 after 1 s of sliding before increasing more gradually.

• Even after 10 s of sliding, measured interface temperatures were below −2°C near the front of the slider and below −3°C at the center and rear of the slider. The model also predicted average interface temperatures below −2°C.

• Predicted h increased along the slider but remained below 0.25 μm at −5°C and 1.3 μm at −0.5°C ambient temperatures. The roughness of the slider was R_a = 2 μm.

The very low starting friction probably resulted from shearing of ice asperities (dry-contact), and the thin predicted films relative to slider roughness suggest that dry or mixed contact probably occurred throughout the tests. Measured sub-freezing interface temperatures are consistent with dry-contact abrasion (see Abrasion and Dry Lubrication), so lubricated contact may not have governed their tribometer tests.

Summary of Self-Lubrication

Self-lubrication, the prevailing hypothesis for the slipperiness of ice and snow for over 80 years, has some significant shortcomings despite offering helpful insights. On both ice and snow, the supporting water films must be substantially thicker than the combined roughness of the surfaces, a test that most self-lubrication models fail. Many studies have overlooked or poorly represented slider topography and roughness and their influence on interface mechanics. For sliders on ice, many studies have observed abrasion of the sliders and ice surfaces but have not described the mechanics of transition from dry to lubricated contact. For sliders on snow, it is difficult to rationalize persistent heating and melting of contacts owing to snow’s susceptibility to intergranular bond breakage and movement during sliding. On both substrates, lower startup friction compared with steady-state friction suggests that hydrodynamic lubrication may not be the slipperiest friction mode. These issues warrant more attention if self-lubrication is to continue as the prevailing theory.

Quasi-Liquid Layers

Surfaces are inherently disordered, with unsatisfied bonds that present a higher-energy state than the bulk substrate. Species from the surrounding environment readily adsorb to surfaces to lower the overall system energy. This process is inherently dynamic and can involve ongoing rearrangements of the surface atoms or molecules as well as exchanges with the adjacent phase (Myers, 1991). Ice surfaces are no exception.

Quasi-Liquid Layers on Ice and Snow

Water molecules on ice and snow surfaces have properties intermediate to those of the bulk ice and liquid: unsatisfied hydrogen bonds cause the surface water molecules to be more mobile than those within the bulk ice (Glen, 1968; Neshyba et al., 2009; Louden and Gezelter, 2018; Weber et al., 2018; Nagata et al., 2019), imparting liquid-like properties at the molecular scale. A quasi-liquid layer (QLL) on ice, at temperatures below the bulk-melting point, can reduce surface energy at a vapor or solid boundary. The layer thickness represents an energy minimum, balancing energy to melt the layer with the reduction in surface energy (Dash et al., 1995; Dash et al., 2006).

Recent advances in measurement techniques and molecular-dynamics simulations (MDS) have provided remarkable insight into the nature and emergence of QLLs on the surface of ice. These efforts show large variations in QLL thickness vs. temperature, but values generally vary from a few nanometers near −40°C to tens of nanometers near 0°C (Doppenschmidt and Butt, 2000; Pittenger et al., 2001; Rosenberg, 2005; Li and Somorjai, 2007; Slater and Michaelides, 2019). Paesani and Voth (2008) conducted MDS using a quantum-mechanical, rather than classical, model of water molecules and concluded that quantum effects can account for some discrepancies between measurements and predictions of QLL thickness.

Different regimes of QLL appear to exist. Sazaki et al. (2012) used advanced, laser confocal microscopy combined with differential interference contrast microscopy to observe the emergence of two immiscible phases of QLLs, droplets and thin films, directly on the surface of ice at temperatures −1.5–0.1°C. Nagata et al (2019) summarized the transition of homogeneous disordered surface layers, an equilibrium process that begins at about −90°C, through to the emergence of inhomogeneous, non-equilibrium QLL droplets and films near the bulk-melting point.

Quasi-Liquid Layer Role in Ice Friction

Weber et al. (2018) provided direct evidence that QLLs can play an important role in ice friction (Figure 5). They combined MDS with steel sphere-on-ice friction tests to reveal a strong correlation of measured friction with calculated surface mobility (diffusion) of water molecules over the temperature range -10°C to -100°C and sliding speeds 10^–6–10^–1 m s⁻¹. The Arrhenius dependence (exponential-decay) of measured μ(T) below about −7°C had the same activation energy as the lateral self-diffusion constant of surface water molecules from the MDS, ∼ 11.5 kJ mol⁻¹ or about ½ of the hydrogen-bonding energy. This correlation encouraged them to conclude “…that slippery ice arises from the high mobility of its surface molecules, making the ice surface smooth and the shearing of the weakly bonded surface molecules easy.” Weber et al. (2018) also found that friction was independent of sliding speed for tests at −7°C and −12°C, which they interpreted as indicating that “… frictional heating does not play an important role in the experiments.”

FIGURE 5

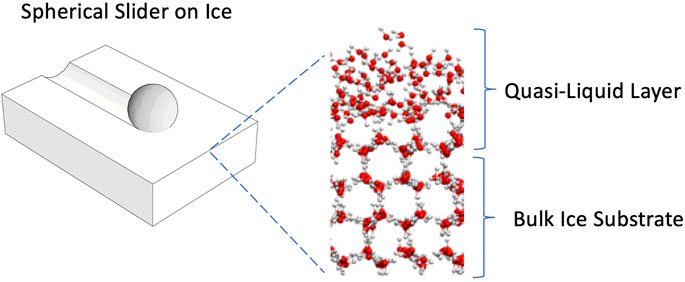
FIGURE 5. Schematic illustrating the role of the quasi-liquid layer on ice friction (based on Weber et al., 2018; Nagata et al., 2019). Friction on a smooth slider decreases with increasing mobility of the surface water molecules, provided that the bulk-ice substrate responds elastically.

Louden and Gezelter (2018) used MDS to map the reduction in viscosity of the QLL molecules with distance from the bulk substrate and agreed with Weber et al. (2018) “…that the small coefficients of friction commonly associated with ice surfaces are due almost entirely to the shear viscosity of water molecules near the QLL/vapor interface.” Nagata et al. (2019) went further to suggest that “… the disordering of the topmost ice surface governs the slipperiness of the ice surface, allowing for ice skating.” and that “The observation of velocity-independent friction is inconsistent with the frictional melting hypothesis …”

Despite identifying an important ice-friction role for QLLs, Weber et al. (2018) also showed that deformation of the bulk-ice substrate played a role in their tests. They modeled ploughing of the steel sphere through the ice as a plastic-deformation process at pressures equal to separately measured H_i(T). This ploughing term accounted for their measured rise of friction near 0°C.

Liefferink et al. (2021), expanding on Weber et al. (2018), clarified the role of ice deformation on measured friction. Testing spheres of differing roughness and normal load, friction from ploughing became important above ∼ −20°C as contact pressures, including from increased roughness, exceeded measured hardness. Indeed, rms roughness played a role above R_q ∼ 0.2 μm, even for ice at −50°C, and the roughest sphere (R_q ∼ 3 μm) left μm-deep striations in the ice. Clearly, the QLLs did not prevent direct ice contact by slider asperities. Also, Liefferink et al. (2021) measured a non-monotonic velocity-dependence of friction at −20°C, which they attributed to velocity effects on penetration hardness and thus ploughing friction. They noted that the ice substrate responded elastically in the low-temperature region that displayed the diffusion-correlated Arrhenius dependence of μ(T), and that “… friction on ice increases exponentially with the local contact pressure, suggesting that this pressure frustrates the mobility of the lubricating layer.”

Bluhm et al. (2000) measured friction on ice of μ ∼ 0.6 over temperatures −24°C to −40°C using an atomic-force microscope tip scanned at 5 μm/s. They concluded that the tip moved sufficiently slowly to displace the quasi-liquid film and consequently measured dry friction. This result also indicates that the QLLs did not continuously reform under the tip, and may not reform under slider asperities, to facilitate low friction.

Quasi-Liquid Layer Summary

The high mobility of QLL water molecules can account for the slipperiness of ice provided the bulk substrate responds elastically. However, the results of Weber et al. (2018), Liefferink et al. (2021) and Bluhm et al. (2000) limit the role of QLLs on ice friction: QLLs do not prevent macro-scale deformation of the bulk-ice substrate, and micron-scale slider asperities can directly gouge the substrate. Depending on slider geometry, normal load and speed, bulk-ice brittle crushing could occur. Importantly, rapid micron-scale asperity interactions should induce local brittle failure and thus generate wear particles. Crushed ice and wear particles could play important roles in ice-slider interaction despite the presence of QLLs.

Abrasion and Dry Lubrication

Abrasion and wear are ubiquitous on unlubricated sliding surfaces. The extreme brittleness of ice makes it susceptible to brittle wear by slider asperities or fracture at ice and snow-grain asperities. Bulk-snow intergranular bonds are also susceptible to brittle fracture, allowing the grains to move in response to slider shear. These processes could prevent warming and melting of persistent contacts (self-lubrication) and limit the role of nano-scale QLLs to govern friction. Here, we summarize theory and evidence that dry-contact abrasion and wear could play important roles in ice and snow friction (Figure 6).

FIGURE 6

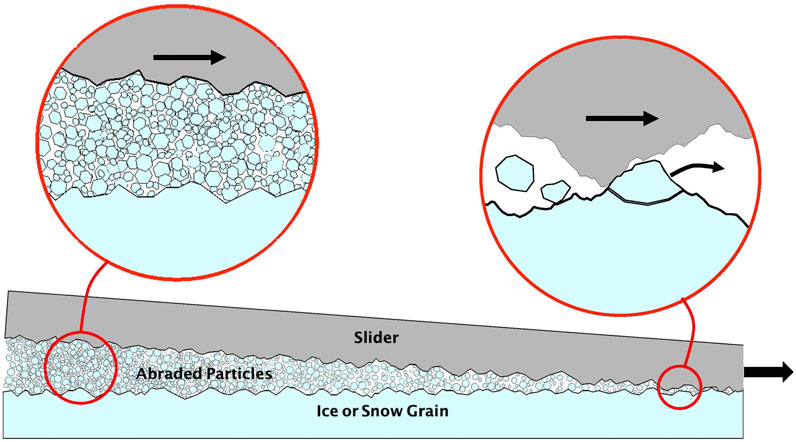
FIGURE 6. Schematic of dry-contact abrasion as a friction hypothesis. Direct contact by slider asperities causes brittle fracture of ice or snow-grain asperities to produce a layer of wear particles that seperates the surfaces and acts as dry lubricant.

Abrasion on Ice

Akkok et al. (1987) formulated a simple model that considered the flash-temperature rise (Blok, 1937; Archard, 1959) for a contact sliding on flat ice or for an ice contact sliding on a flat material. They solved for the friction coefficient that would cause the contact temperature to rise to an upper-bound temperature, T_f < T_m and explained that “Essentially T_fmust be that surface temperature above which the material at the immediate surface cannot remain in the contact since it is easily abraded and removed by shear.” Similar to Evans et al. (1976), this approach allowed them to predict friction coefficients and their variations with system parameters without identifying the friction mechanism, except to note that it was not viscous shearing of a melt-water film. They then compared model predictions with their own friction measurements and those of Evans et al. Quantitative agreement was not strong, but the model predicted the dominant speed effect, $\mu \propto v^{-1/2}$. This dependence falls out of the assumption of transient heat-conduction into the ice by combining Eqs (4–6) with t = l/v, where l is slider length:

$\text{μ}=\frac{\text{Δ}{T}_i{k}_i}{2\sigma }{\left(\frac{\pi }{{\text{Κ}}_{i}lv}\right)}^{1/2}(9)$

An important assumption embedded in Eq. 9 is that μ (or heat flux q_f) is constant, which may not be true along a slider as friction mechanics and contact area change. However, the general $\mu \propto v^{-1/2}$ does not require that $\text{Δ}{T}_i$ raise the ice temperature to melting or that friction results from viscous shearing of a water film.

Tusima (2011) formulated a dry-contact model for ice friction, $\mu =\tau /\sigma$, with τ attributed to adhesion between the ice and the slider. The model correlated well with ice-friction tests by adding a ploughing term to the shear stress. These were mostly low-speed tests (7 × 10^–5 m s⁻¹) where plastic yielding of the ice could have governed its behavior for both the adhesion and ploughing terms. Nevertheless, Tusima photographed tracks left by the spherical sliders that showed striations and noted abraded particles, recrystallization and cracks, with higher μ correlating with more surface damage. Importantly, he measured lower friction on ice basal planes compared with prism planes, which he attributed to lower shear strength and higher normal strength on basal planes. Tusima (2011) reported similar reductions in friction of speed-skate blades at ∼1 m s⁻¹on an ice rink consisting entirely of basal-plane ice (μ = 0.0038) compared with polycrystalline ice on a standard rink (μ = 0.0045), although the slightly colder polycrystalline ice could have accounted for some of the difference. He concluded that the dependence of ice friction on crystallographic plane supported his theory of pure solid friction without lubrication from melt-water.

Makkonen and Tikanmäki (2014) formulated a dry-contact ice-friction model to supplement their self-lubrication model. They related friction in the dry-contact regime to the change in surface area at a nano-scale sliding contact:

$\mu =\frac{\gamma +{\gamma }_s-{\gamma }_{s,i}}{2d{H}_i}(10)$

where $\gamma$, ${\gamma }_s$ and ${\gamma }_{s,i}$ are the surface energies of the ice, slider and ice-slider interface, respectively, and d is a characteristic nano-scale contact length, assumed to be 2 nm. A concern with this formulation is that the surface area of ice created during dry-contact sliding should include any wear particles formed by brittle failure at the asperities, which would increase the area associated with the $\gamma$ term. The selection of d = 2 nm also differs from the contact length for their wet-contact model (1 mm) with no discussion of the mechanics of transition between the two.

Abrasion on Snow

Lever et al. (2018) sought to document the transition from dry to lubricated contact for a ring of polyethylene sliding on compacted snow, using a high-resolution IR camera to measure evolving snow-grain contact area and temperature. Unexpectedly, they obtained evidence that contradicted self-lubrication theory. Measured friction was low (μ < 0.03) for cases where slider shear caused widespread intergranular bond failure with no persistent contacts to melt. When the snow grains did not move, the slider abraded but did not melt the evolving contacts yet still produced low friction (μ < 0.05). Lever et al. (2019) obtained additional evidence that abrasion could govern snow friction by coordinating IR, optical microscope and SEM images of the contacting snow grains. IR thermography again showed no melting, while coordinated images revealed that wear particles abraded from stationary grains deposited and sintered together in the snow’s pore spaces to produce lacy structures that could completely fill the pore spaces to the plane of the slider.

Lever et al. (2019) formulated a partial snow-friction model based on dry-contact abrasion and heat transfer to account for and extend their observations. They applied the Archard (1953) model of abrasive wear, and it reasonably predicted the evolution of snow-grain contact area. They also applied an extension of sliding-heat-source theory (Tian and Kennedy, 1993; Tian and Kennedy, 1994) to account for multiple contacts sliding across finite bodies, which predicted that contact temperatures would not reach 0°C during their tribometer tests. Importantly, the thermal model predicted that flash temperatures would be small on typical 10–100 μm-diameter snow-grain contacts. Consequently, they asserted that existing field measurements of interface temperatures on skis and sleds closely approximated actual contact temperatures. Measurements on skis (Colbeck and Warren 1991; Colbeck and Perovich 2004; Schindelwig et al., 2014) and sleds (Lever and Weale 2012; Lever et al., 2016) have consistently shown that interface temperatures remained well below 0°C under the action of sliding friction. Self-lubrication may not occur for sliders on snow at common field conditions.

Abrasion and Dry-Lubrication Summary

Lever et al. (2019) suggested that dry-contact abrasion and heat flow can prevent the formation of lubricating water films for snow-friction scenarios of practical interest and speculated that the wear particles could serve as a dry lubricant to account for why snow is slippery. Third-body tribology theories attempt to account for the production, loss and shearing of wear particles at sliding interfaces (Godet, 1984; Iordanoff et al., 2002; Fillot et al., 2007), and these ideas could guide formulation of dry-lubrication theory for ice and snow. One mode of dry lubrication is that a layer of fine wear particles can act as a viscous fluid (Heshmat, 1991; Heshmat, 1995; Wornyoh et al., 2007). However, Lever et al. (2019) did not directly observe the presence of wear particles at the contacting interfaces owing to their small size and rapid post-test sintering. Thus, this dry-lubrication hypothesis remains unproven, and it is unclear whether it plays an important role in ice friction, where abraded particles may be trapped at the interface and melt under further sliding rather than deposit into voids between snow grains.

Ice-Rich Slurries

Ice-rich slurries can form beneath an indenter during rapid indentation of ice (see Ice Indentation), including with concurrent sliding motion. It is also possible for ice-rich slurries to form by sliding friction, as abraded wear particles partially melt (Figure 7). The viscoelastic properties of the resulting slurry film could account for why ice and snow are slippery, with dry and fully liquid lubrication as the two end states based on the film’s water content.

FIGURE 7

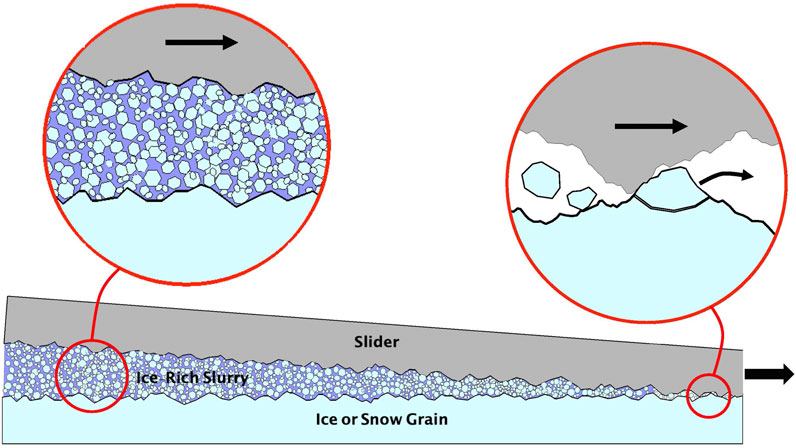
FIGURE 7. Schematic of ice-rich slurry as a friction hypothesis. Crushing or abrasion by the slider produces ice fragments, which partially melt under contact pressure and shear motion to generate a viscoelastic, ice-rich slurry that separates and lubricates the two surfaces.

Ice Friction With Micro-scale Ice-Rich Slurries

Gagnon and Molgaard (1989) measured kinetic friction with concurrent crushing of freshwater ice against a rotating steel wheel. Crushing rate was constant at 5.5 mm s⁻¹, temperatures ranged −5°C to −19°C and sliding speeds 0.06–0.82 m s⁻¹. Friction during crushing was generally low (μ ∼ 0.02–0.1) and decreased with increasing temperature or wheel speed. The tests produced periodic crushing and extrusion of pulverized ice, similar to ice-indentation tests without sliding motion. Video records revealed mm-thick layers of pulverized ice at the contact zone along with some melt-water.

Gagnon and Molgaard (1991) and Gagnon (1994a), Gagnon (1994b), Gagnon (2010) conducted follow-up ice-indentation tests that revealed important features relevant to crushing-friction mechanics: isolated HPZs of intact ice could apply pressures approaching the melting pressure; micron-scale ice-rich slurries (liquid content <20%) existed at the interfaces between HPZs and the slider/indenter; these HPZs could support nearly 90% of the normal load; energy expended in the viscous squeeze-flow of the slurries could consume >60% of the mechanical work supplied by the system.

Returning to ice friction, Gagnon (2016) crushed ice against high-roughness surfaces with concurrent sliding motion. Tests were at −10°C and covered a range of crushing and sliding rates ∼4–30 mm s⁻¹. Friction coefficients were remarkably low (μ ∼ 0.02–0.14) given the mm-scale surface roughness. High-speed video identified ice-rich slurries separating the intact-ice zones from the contacting slider elements. Pressure across the slurries reached 55 MPa, or about half of the pressure-melting value. Gagnon suggested that the formation and extrusion of ice-rich slurries controlled the friction mechanics: “The squeeze-film slurry dissipates the majority of the actuator energy supplied to the system because the load is mostly borne on the hard-zone ice (∼88%,Gagnon, 1994a), where the slurry is generated and flows.” He noted that “The layer may be thought of as a self-generating squeeze film that is powered by the energy supplied by the loading system that causes the ice crushing.” Gagnon noted that these processes should be considered to explain the friction on ice of skate blades, sled runners and curling stones, where ploughing or local crushing of ice asperities occurs. He also noted that high-roughness surfaces such as tracks or wheels could unexpectedly experience low friction on ice when crushing occurs.

Ice Friction With Sub-micron Ice-Rich Slurries

Canale et al. (2019) measured the nano-scale tribology and rheology of ice-slider interfaces using a novel “stroke-probe” tribometer consisting of a mm-scale smooth glass bead (R_q ∼ 0.4 nm) mounted to a double-mode tuning fork. Horizontal vibration against the ice revealed the frictional behavior, and vertical vibration during retract of the probe revealed the rheological behavior of the interfacial film. Tests covered 0°C to −16°C with peak oscillatory speeds to 0.09 m s⁻¹. Each test began with a run-in period after reaching the target normal force, during which the friction force steadily increased, indicating some development of the interfacial film. The authors noted that “… during the retract the normal conservative impedance does not exhibit a square root dependence with the indentation as it would be expected for a Hertzian deformation; it rather exhibits a hydrodynamic behavior, pointing to a fluidized interface.” Friction varied as $\mu \propto v^{-\gamma }$ with γ ∼ 0.3–0.5, in common with many macro-scale tests, and was independent of normal load, suggesting solid-like friction behavior with μ ∼ 0.015. Friction and film thickness both increased with temperature above −10°C, with h ranging 0.1–0.4 μm.

Canale et al. (2019) measured lubricating films that were much thicker than QLLs and displayed viscoelastic behavior, with viscosity up to two orders-of-magnitude greater than liquid water. Higher normal loads produced greater viscosity, and extrapolation of measured viscosity to zero normal load matched the viscosity of supercooled water at the test temperature. Elastic modulus averaged about 100 Pa. They suggested that the high viscosity of the film “… points to an unexpected rationale for the exceptional friction properties of ice, contrasting with the bad lubricant behavior of bare liquid water. Indeed, a viscous film is a prerequisite to properly lubricate the contact: it limits squeeze-out, thereby avoiding direct solid-on-solid contact.” They concluded that “… a tempting explanation for the observed response is accordingly that, under abrasive wear, a suspension of liquid and submicron … debris is formed, hence resulting in composite lubrification of the contact.” The observed increase in friction and viscosity with temperature “… may be interpreted as an increasing density of ice fragments when the ice becomes softer close to the melting point.”

Summary of Ice-Rich Slurries

Ice-rich slurries can result from crushing or abrasion by slider motion, with water fraction dependent on confining pressure and heat generated by shearing of the particle layer. Ice-rich slurry films could potentially form on both ice and snow substrates, and their high viscosity and elastic properties could separate and lubricate the slider. The mechanics of such slurries could explain how dry contact at the front of a slider transitions to fully lubricated contact and help to map the regimes where each end state governs system friction.

Evidence of Ice- and Snow-Friction Mechanics

Researchers have undertaken tribometer studies on ice and snow for various purposes: to investigate the underlying mechanisms, to understand the role of system properties, or to minimize (e.g., winter sports) or maximize (e.g., vehicle tires) friction. Test variables include slider geometry (e.g., flat, spherical) and motion (e.g., unidirectional, reciprocating) plus slider material properties, ice crystal structure or snow morphology. Given these differences, it can be difficult to compare tribometer results or to infer underlying mechanics using only the dependence of μ on system variables.

A fundamental difficulty is that the friction mode (dry, boundary, mixed, lubricated) can vary with position along a slider and duration of sliding. The existence of different modes introduces a scaling requirement not generally acknowledged for laboratory ice- and snow-friction tests: to isolate and separately scale the contributions from each mode to extrapolate to full-scale systems (Glenne 1987; Colbeck 1992). Nachbauer et al. (2016a) and Hasler et al. (2016) developed a 24-m-long linear tribometer to test full-scale skis in part to avoid this scaling requirement. Nachbauer et al. (2016b) highlighted systematic variations in friction along a ski by testing sliders of increasing length.

Another difficulty involves the common use of a “run-in” period to seek steady-state conditions. As noted, friction on ice and snow often rises from very low levels during run-in. If the goal is to understand why they are slippery, it seems counterintuitive to omit the slipperiest portion of the tests. Also, the field application matters: for skis, sleds, tires and other systems of interest, the ice or snow experiences brief, one-pass contact by the slider. The substrate’s initial response should be of particular interest, and the friction mechanics could be quite different from those governing after repeated passes (Hsia et al., 2020).

We summarize here evidence of the mechanics underlying ice and snow friction obtained through direct observations, beyond efforts noted in Postulated Ice and Snow Friction Mechanisms.

Evidence of Ice-Friction Mechanics

Tusima and Yosida (1969) continuously rotated a disc of ice against a thick ring of acrylic. They intentionally ran long-duration tests and observed water droplets flying off the disc after 30–60 s at 10.5 m s⁻¹ and −35°C. They estimated film-thickness of 10–50 μm for these tests. At 0.155 m s⁻¹ and warmer temperatures, they observed transparent, mm-scale spots rotating with the ice, which they interpreted as melt-water at the real-contact areas. The size of the spots decreased with decreasing temperature, and they did not observe spots below −15°C. Although they suggested that the melt-layers formed right away, a plot of friction force at 10.5 m s⁻¹ and −19°C showed ∼1 s rise from very low values followed by a slow decrease. If the rise occurred at constant normal load, initial dry-contact produced lower friction. Also, abrasion can polish ice contacts and may have produced the transparent spots observed during the low-speed tests. If the spots had been melt-water films, Tusima and Yosida should have seen smearing in the direction of motion, but none was reported.

Strausky et al. (1998) used fluorescence spectroscopy to measure water-layer thickness separating an acrylic slider on a rotating ice disc. Contact pressure was 5 MPa and speed ranged 0.005–0.1 m s⁻¹. After ∼60 s of run-in, they measured μ = 0.03 at −2°C but observed no water films thicker than their detection limit of 50 nm. They noted that this result “… supports some suggestions in the literature, in which the interface is described as … ‘a liquidlike layer being several hundred molecules thick’“. Indeed, these findings could support the QLL hypothesis, although Weber et al. (2018) and Liefferink et al. (2021) found that ploughing dominated friction at −2°C. Alternatively, the lack of a detectable water film could be consistent with abrasion/dry-lubrication or the ice-rich slurry hypothesis, depending on the sensitivity of the spectrometer to low water fraction in a slurry.

Marmo et al. (2005) used a reciprocating linear tribometer to generate a friction map of ice hemispheres sliding against steel. The map plotted 449 friction values spanning −27°C to −0.5°C, 0.008–0.37 m s⁻¹ and two normal loads. They used 60-grit silicon-carbide paper to finish the steel surface, which suggests R_a ∼ 2–3 μm. They conducted companion tests to obtain specimens for low-temperature SEM imaging of the wear surfaces in three regimes of the friction map. The resulting images show fine detail in the wear surfaces and adjacent debris bands. They carefully described features suggesting refrozen melt-water on the two specimens that produced low friction (μ = 0.06–0.07), for example: “… concave grooves in the wear surface separated by sausage-shaped ridges that display no evidence of brittle deformation … The grooves are filled with fine, rounded interconnecting ridges that appear to be the remnants of liquid water.”

Conversely, they describe features of the high-friction sample (μ = 0.16) consistent with dry contact: “The worn surface shows signs of brittle deformation with microcracks and scuffing … Scuffing is a common wear morphology produced by failure when the sliding interfaces become welded together …”

While it can be difficult to link SEM-observed features unambiguously to processes, Marmo et al. (2005) stated their interpretations clearly. The images show striations from the rough steel surface, so mixed-mode friction was likely even if liquid formed at the wear surface. The authors calculated water-film thickness as (0.88–6.97) x 10^–11 m for the low-friction tests (viaEq. 4 here). These values are thinner than the diameter of a water molecule (∼0.3 nm). Perhaps the evidence of refrozen liquid related to QLLs rather than micron-scale melt-films, but that raises the question of how it could be observed hundreds of microns away from the wear surface. Studies that couple SEM with other diagnostic modes could help resolve these issues.

Higgins et al. (2008) pressed ice hemispheres against a rotating disc of rubber and produced a friction map consisting of 225 measurements spanning −33°C to −1.0°C and 0.003–2.6 m s⁻¹. They also conducted five similar tests to provide samples for SEM imaging using the same methods as Marmo et al. (2005) and clearly stated their interpretations of features linked to dry and lubricated contact. For example, they described evidence of dry-contact friction at −25°C and 0.005 m s⁻¹ that produced μ = 0.85: “The smeared, multi-layered features … demonstrate successive layers of this slurry mixture being deposited at intervals during sliding and indicate deformation of entrained ice debris.” Interestingly, for two tests at low speeds that produced the same friction (μ = 0.30), they described features that suggested melt-water formation at −5°C and dry-contact friction at −33°C. They also identified melt-features for a −20°C test (μ = 0.35, 2.1 m s⁻¹): “The wear surface shows signs of melting with “sausage-shaped” ridges present, identified inMarmo et al., 2005as being formed by refreezing of liquid.” These diagnostic efforts suggest that friction mechanics can change significantly yet produce similar friction values. For the lubricated-friction cases above, Eq. 4 would predict h ∼ 0.2–50 nm, which again are too small to be realistic water films. Mixed-mode friction was likely.

Klein-Paste and Sinha (2010) examined ice surfaces before and after single-pass, short-duration (∼40 ms) sliding by rubber. They used a traditional etching and replicating technique to create thin-plastic casts of the ice surfaces that revealed grain boundaries, dislocations, and “… most importantly, deformation related features like tilt boundaries, dislocation cells and pileups.” For all tests, the casts captured ploughing tracks and rows of dislocation etch pits consistent with deformation by the rubber slider. They saw no evidence of melt-water even for tests at −0.1°C and high-speed sliding (3 ms⁻¹) that produced low friction (μ = 0.08). They suggested that their results contradicted Higgins et al. (2008) owing to the longer duration (15 s) sliding used in those earlier tests. Although they allowed that etching could have removed very thin water layers (<0.1 μm), they noted that ice deformation occurred even close to the melting point and that “… deformation processes during ice friction are not strictly confined to viscous shearing of a melt water film at the interface.” As a minimum, mixed-mode friction occurred.

Tuononen et al. (2016) sought to clarify the mechanics of rubber-ice sliding via observations guided by multi-scale friction theory (Perrson, 2015). They conducted repeated, unidirectional sweeps of rubber on ice and measured the resulting changes in surface topography at three magnifications using white-light interferometry. Even after the first sweep (∼0.3 m long), they observed scratches in the ice surface at the lowest magnification, which they attributed to silica filler particles in the rubber. The number of scratches increased with the number of sweeps. They used the number of scratches and their average cross-sectional area to determine that ploughing friction was a negligible contribution, with viscoelastic energy dissipation of the rubber and heat flow into the ice contributing about equally to the measured friction.

At the highest magnification, Tuononen et al. (2016) observed isolated droplets of refrozen water, similar in dimensions to the QLL droplets observed by Sazaki et al. (2012) but aligned with the direction of sliding, “… which indicates that the meltwater freezes rather quickly, or is only in a quasi-liquid state.” They also noted “No ‘sausage-shaped’ meltwater features … were observed …” Also, “The droplets … may originate from melted virgin ice asperities and/or from a liquid-like layer of premelted ice which may become more liquid-like as a result of the frictional heating of the ice surface.” Interestingly, at the start of the first sweep, friction increased from low levels to a maximum after ∼1 mm of sliding. They argued that the subsequent decrease was “… at least in part, related to frictional heating and the softening or melting of the ice in the asperity contact regions …“. This work makes a convincing case for the need to consider ice friction as different processes acting on different spatial and temporal scales.

Evidence of Snow-Friction Mechanics

Huzioka (1962) continuously rotated a glass disc against a block of compacted snow, and from microphotographs taken after 5 min of sliding (69 mm s⁻¹, −4°C and 4.6 kPa), measured the area of the 190 contacting grains as 1.4% of the nominal area. Huzioka (1963) conducted similar experiments that revealed differences in contact mechanics for glass and acrylic discs. For snow against bare glass (−2°C for 5 min), “The glass plate rubbed off the projections of the ice grains of snow and left scobs (ice particles) to the right (downstream) side of the actual contact areas …” When the glass was coated with a film of lacquer, “… the actual contact areas became wider and more scobs were produced … Almost all the ice grains are rubbed off and the spaces between them are filled up by the scobs.” The respective friction coefficients were μ = 0.30 and 0.13 for the bare and lacquer-coated glass. Apparently, the higher rate of dry-contact abrasion reduced sliding friction. Conversely, when the snow was rubbed by acrylic, the microphotographs showed “… ice sticks extending in the direction of motion” from several contacting grains, consistent with refrozen melt-water. Huzioka (1963) reported μ = 0.61 for this test, noting that the higher friction contradicted the belief that meltwater plays the role of a lubricant. Kuroiwa (1977) noted that these microphotographs also showed “filings” (i.e., wear particles) produced by friction, indicating mixed-mode contact.

Ambach and Mayr (1981) used a capacitive probe to measure the thickness of water films between a ski and snow during downhill skiing. They calibrated the probe using static measurements of water-film thickness. Two runs of varying speed 0–17 m s⁻¹ on −5°C and −10°C snow gave film thickness ∼4–20 μm, with thickness increasing with speed down the course. A run at constant speed on alternate sections of piste (compacted snow) and deep snow showed thicker films on the deep snow. This casts some doubt on the measurements, because snow grains fracture and move down-track under the action of a ski on natural snow (Nakaya et al., 1936; Kuroiwa, 1977), reducing the opportunity for friction to warm and melt persistent contacts. Also, modeling by Colbeck (1988) and Bäurle et al. (2007) predicted film thickness less than 1 μm for skiing conditions. It’s possible that friction-generated electric charge (Petrenko and Colbeck 1995) affected the Ambach and Mayr capacitive probe.

Lever et al. (2019) demonstrated that, for realistic values of A_c/A_n, flash temperatures on snow make small contributions, and thus nominal temperatures measured by flush-mounted thermocouples approximate snow-grain contact temperatures. Colbeck and Warren (1991) measured ski-snow contact temperatures on hard-packed snow that rose 3–5°C but remained well below 0°C. Interestingly, they measured the warmest contact temperatures on soft, fresh snow where intergranular bond failure would likely have impeded the formation of persistent contacts. Colbeck and Perovich (2004) showed that sunlight absorption can bring contact temperatures closer to 0°C, but ski runs at night raised contact temperatures from −9.2°C to only -7.8°C. Lever and Weale (2012) and Lever et al. (2016) measured contact temperatures of flexible sleds towed at 2–3 m s⁻¹ over natural snow in Antarctica and Greenland. Towing resistance (dominated by sliding friction) dropped significantly with increasing contact temperatures, both during startup and at steady-state, but temperatures remained well below 0°C. The sleds also developed low steady-state friction, μ ∼ 0.03–0.08, at ambient temperatures −5°C to −30°C. Overall, contact temperatures measured to date contradict the self-lubrication hypothesis for skis and sleds on snow.

Conclusion

Why are ice and snow slippery? For the last 80 years, the prevailing hypothesis has been self-lubrication: rapid formation of a lubricating melt-water film by frictional heat arising from shearing of that film. However, it predicts water films that are too thin to separate surfaces with micron-scale roughness, and new diagnostic tools have revealed that sliders may not melt the ice asperities or snow-grain contacts despite low friction values. Importantly, an expectation that dry contact at the front of a slider transitions to lubricated contact warrants a description of the mechanics linking the two regimes: specifically, how does that transition occur? Furthermore, the mechanical behavior of the ice or snow substrate plays an important and largely overlooked role in governing the friction regime for practical systems.

The brittle behavior of ice and the weak bulk-strength of snow have not been included in most friction theories. Ice is brittle at temperatures close to its melting point and at strain rates relevant to most asperity and macro-slider interactions. Additionally, ice hardness is not a material property, and high-pressure zones accompanied by ice-rich slurries exist during combined indentation and sliding that influence the friction mechanics. The fracture of ice asperities, generation of wear particles, and their role as third bodies between the slider and the ice all warrant attention, preferably through observations at the sub-micron scale. It is possible that wear particles can act as dry lubricants to reduce sliding friction and prevent fully lubricating water films from forming except during long-duration, repeated sliding over the same ice substrate. When slider asperities interact with those on the ice, can pressure-melting, partial melt-water films or QLLs prevent fracture and generation of wear particles? This seems unlikely given the brittle behavior of ice.

Natural snow deforms easily, and even well-sintered intergranular bonds can fail in response to slider normal and shear stresses. The mechanics of snow friction should include the substrate’s response to these combined stresses, where the resulting snow-grain motion or asperity fracture can prevent persistent heating of contacts. Lift from pressurized porous flow under skis and snowboards, which reduces normal stresses at the contacts, also warrants more attention. The common test technique to “run-in” a snow substrate through repeated slider passes should be reconciled with the full-scale system of interest: does the full-scale slider encounter strong, compacted snow previously exposed to repeated passes, or does the slider engage the snow on a single pass that could deform and fracture it, locally or in bulk?

As instrumentation has improved, researchers have undertaken micro- and nano-scale observations of friction mechanics at ice and snow interfaces. Ample evidence reveals direct slider-ice contact in the form of slider abrasion, substrate striations, lines of nano-scale melt features, dislocation etch lines, sintered wear particles, etc. Even if melting or temperature-dependent softening occurs, most systems must experience mixed-mode friction with contributions that vary with contact duration and roughness-dependent pressures. While QLLs can govern ice friction when the substrate responds elastically, QLLs are too thin to prevent micron-scale asperities from directly interacting with the substrate.

Ice-rich slurries potentially offer a unifying hypothesis for ice and snow friction by relating the transition from dry to fully-lubricated contact through increasing water-content. Local crushing and dry-contact abrasion can provide the ice particles, and the slurry’s viscoelastic rheology can support and lubricate the slider. Such slurries can even support pressures sufficient to decrease the interface melting temperature by several degrees. Furthermore, QLLs would exist on the surfaces of ice wear particles and thereby establish the minimum effective water contact of a slurry. System characteristics and the duration of sliding would then govern the slurry’s spatial and temporal evolution.

Future high-resolution observations should aim to illuminate the actual contact physics occurring at interaction scales relevant to snow and ice friction. Researchers must somehow document the transitions in governing modes as contact temperatures increase with position along a slider or sliding duration, and then account for these varying modes when interpreting mechanics or scaling the results of tribometer tests to full-scale systems. These are demanding but necessary tasks to account for why ice and snow are slippery across systems of practical interest.

Author Contributions

JL structured the review. JL, EA-S, ST, and AL all contributed to assessing hypothesized friction mechanics relative to available observations, with EA-S providing additional background on measurement and modeling techniques for quasi-liquid layers.

Funding

The US Army Engineer Research and Development Center, Military Engineering Program under the Basic Research Portfolio, funded this work under Work Item A1000 “The Role of Abrasion in Snow and Ice Friction”.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank the ERDC 6.1 Basic Research program for providing multi-year funding to investigate the mechanics underlying ice and snow friction. We also thank Garrett Hoch for his ideas and hands-on contributions to our earlier studies of snow friction. We are grateful for permissions granted by Hokkaido University Collection of Scholarly and Academic Papers, AIP Publishing and ACS Publications to reproduce images here.

References

Abele, G., and Gow, A. J. (1975). Compressibility Characteristics of Compacted Snow. Research Report 336. U.SHanover, NH: Army Cold Regions Research and Engineering Laboratory. doi:10.21236/ada013139

CrossRef Full Text

Abele, G. (1990). Snow Roads and runwaysCRREL Monograph 90-3. Hanover, NH: Cold Regions Research and Engineering Laboratory.

Akkok, M., Ettles, C. M. M. S. J., and Calabrese, S. J. (1987). Parameters Affecting the Kinetic Friction of Ice. J. Tribology 109, 552–559. doi:10.1115/1.3261503

CrossRef Full Text | Google Scholar

Ambach, W., and Mayr, B. (1981). Ski Gliding and Water Film. Cold Regions Sci. Technol. 5, 59–65. doi:10.1016/0165-232x(81)90040-9

CrossRef Full Text | Google Scholar

Arakawa, M., and Maeno, N. (1997). Mechanical Strength of Polycrystalline Ice under Uniaxial Compression. Cold Regions Sci. Technol. 26, 215–229. doi:10.1016/s0165-232x(97)00018-9

CrossRef Full Text | Google Scholar

Archard, J. F. (1953). Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 24 (8), 981–988. doi:10.1063/1.1721448

CrossRef Full Text | Google Scholar

Archard, J. F. (1959). The Temperature of Rubbing Surfaces. Wear 2, 438–455. doi:10.1016/0043-1648(59)90159-0

CrossRef Full Text | Google Scholar

Barnes, P., Tabor, D., and Walker, J. C. F. (1971). The Friction and Creep of Polycrystalline Ice. Proc. R. Soc. Lond. A 324, 127–155.

CrossRef Full Text | Google Scholar

Bäurle, L., Kaempfer, T. U., Szabó, D., and Spencer, N. D. (2007). Sliding Friction of Polyethylene on Snow and Ice: Contact Area and Modeling. Cold Regions Sci. Technol. 47, 276–289. doi:10.1016/j.coldregions.2006.10.005

CrossRef Full Text | Google Scholar

Bekker, M. G. (1956). Theory of Land Locomotion – the Mechanics of Vehicle Mobility. Ann Arbor, (Michigan): University of Michigan Press.

Bhushan, B. (2013). Introduction to Tribology. 2nd Edition. New York: Wiley. doi:10.1002/9781118403259

CrossRef Full Text

Blackford, J. R. (2007). Sintering and Microstructure of Ice: a Review. J. Phys. D: Appl. Phys. 40 (2007), R355–R385. doi:10.1088/0022-3727/40/21/R02

CrossRef Full Text | Google Scholar

Blok, H. (1937). “Theoretical Study of Temperature Rise at Surfaces of Actual Contact under Oiliness Conditions,” in Proc Institution of Mechanical Engineers General Discussion of Lubrication (London: Institution of Mechanical Engineers), 2, 222–235.

Google Scholar

Bluhm, H., Inoue, T., and Salmeron, M. (2000). Friction of Ice Measured Using Lateral Force Microscopy. Phys. Rev. B 61 (11), 7760–7765. doi:10.1103/physrevb.61.7760

CrossRef Full Text | Google Scholar

Bowden, F. P. (1953). Friction on Snow and Ice. Proc. R. Soc. Lond. A217, 462–478. doi:10.1098/rspa.1953.0074

CrossRef Full Text | Google Scholar

Bowden, F. P., and Hughes, T. P. (1939). The Mechanism of Sliding on Snow and Ice. Proc. R. Soc. Lond. (172), 280–298. Series A.

CrossRef Full Text | Google Scholar

Bowden, F. P., and Tabor, D. (1954). The Friction and Lubrication of Solids. Oxford: Oxford University Press.

Bridgman, P. W. (1912). Water, in the Liquid and Five Solid Forms, under Pressure. Proc. Am. Acad. Arts Sci. 47 (No. 13), 441–558. doi:10.2307/20022754

CrossRef Full Text | Google Scholar

Browne, T., Taylor, R., Jordaan, I., and Gürtner, A. (2013). Small-scale Ice Indentation Tests with Variable Structural Compliance. Cold Regions Sci. Technol. 88 (2013), 2–9. doi:10.1016/j.coldregions.2012.12.006

CrossRef Full Text | Google Scholar

Canale, L., Comtet, J., Niguès, A., Cohen, C., Clanet, C., Siria, A., et al. (2019). Nanorheology of Interfacial Water during Ice Gliding. Phys. Rev. X 9, 041025. doi:10.1103/PhysRevX.9.041025

CrossRef Full Text | Google Scholar

Carslaw, H. S., and Jaeger, J. C. (1959). Conduction of Heat in Solids. Second Edition. London: Oxford University Press.

Colbeck, S. C. (1992). A Review of the Processes that Control Snow Friction. CRREL report 92–2. Hanover, NH: Cold Regions Research and Engineering Laboratory.

Colbeck, S. C. (1988). The Kinetic Friction of Snow. J. Glaciology 34 (No. 116), 78–86. doi:10.3189/s0022143000009096

CrossRef Full Text | Google Scholar

Colbeck, S. C., and Perovich, D. K. (2004). Temperature Effects of Black versus white Polyethylene Bases for Snow Skis. Cold Regions Sci. Technol. 39, 33–38. doi:10.1016/j.coldregions.2003.12.004

CrossRef Full Text | Google Scholar

Colbeck, S. C. (1995). Pressure Melting and Ice Skating. Am. J. Phys. 63, 888–890. doi:10.1119/1.18028

CrossRef Full Text | Google Scholar

Colbeck, S. C., and Warren, G. C. (1991). The thermal Response of Downhill Skis. J. Glaciol. 37 (126), 228–235. doi:10.1017/s0022143000007243

CrossRef Full Text | Google Scholar

Dash, J. G., Fu, H., and Wettlaufer, J. S. (1995). The Premelting of Ice and its Environmental Consequences. Rep. Prog. Phys. 58, 115–167. doi:10.1088/0034-4885/58/1/003

CrossRef Full Text | Google Scholar

Dash, J. G., Rempel, A. W., and Wettlaufer, J. S. (2006). The Physics of Premelted Ice and its Geophysical Consequences. Rev. Mod. Phys. 78, 695–741. doi:10.1103/revmodphys.78.695

CrossRef Full Text | Google Scholar

De Koing, J. J., De Groot, G., and Van Ingren Schenau, G. J. (1992). Ice Friction during Speed Skating. J. Biomech. 25 (6), 565–571.

PubMed AbstractGoogle Scholar

Döppenschmidt, A., and Butt, H.-J. (2000). Measuring the Thickness of the Liquid-like Layer on Ice Surfaces with Atomic Force Microscopy. Langmuir 16, 6709–6714. doi:10.1021/la990799w

CrossRef Full Text | Google Scholar

Evans, D. A., Nye, J. F., and Cheeseman, K. J. (1976). Immunology of Bronchial Carcinoma. Thorax 31, 493–506. doi:10.1098/rspa.1976.001310.1136/thx.31.5.493

PubMed Abstract | CrossRef Full Text | Google Scholar

Federolf, P., Fauve, M., Szabó, D., Lüthi, A., Rhyner, H., Schneebeli, M., et al. (2004). Mechanical Properties of Snow during Rapid Impacts in Snow Engineering V. Editors P. Bartelt, E. Adams, M. Christen, R. Sack, and A. Sato (London: Taylor & Francis Group).

Google Scholar

Feng, J., and Weinbaum, S. (2000). Lubrication Theory in Highly Compressible Porous media: the Mechanics of Skiing, from Red Cells to Humans. J. Fluid Mech. 422, 282–317. doi:10.1017/s0022112000001725

CrossRef Full Text | Google Scholar

Fillot, N., Iordanoff, I., and Berthier, Y. (2007). Wear Modeling and the Third Body Concept. Wear 262, 949–957. doi:10.1016/j.wear.2006.10.011

CrossRef Full Text | Google Scholar

Fukue, M. (1979). Mechanical Performance of Snow under Loading. Tokyo, Japan: Tokai University Press.

Gagnon, R. E. (2010). “Liquid/solid Jets from Ice Crushing Experiments and Implications for Plumes on Enceladus,” in 12th International Conference on the Physics and Chemistry of Ice, Sapporo, Japan, 2010-09-05.

Google Scholar

Gagnon, R. E., and Mølgaard, J. (1989). “Crushing Friction Experiments on Freshwater Ice,” in Proceedings of the IUTAM/IAHR Symposium on Ice/Structure Interaction (St, John’s, Newfoundland, Canada), 405–421.

Google Scholar

Gagnon, R. E., and Molgaard, J. (1991). Evidence for Pressure Melting and Heat Generation by Viscous Flow of Liquid in Indentation and Impact Experiments on Ice. Ann. Glaciology 15, 245–260. doi:10.1017/s0260305500009824

CrossRef Full Text | Google Scholar

Gagnon, R. E. (1994a). Generation of Melt during Crushing Experiments on Freshwater Ice. Cold Regions Sci. Technol. 22 (4), 385–398. doi:10.1016/0165-232x(94)90022-1

CrossRef Full Text | Google Scholar

Gagnon, R. E. (1994b). Melt-layer Thickness Measurements during Crushing Experiments on Fresh-Water Ice. J. Glaciol. 40 (134), 119–124. doi:10.3189/s0022143000003877

CrossRef Full Text | Google Scholar

Gagnon, R. E. (2016). New Friction Mechanisms Revealed by Ice Crushing-Friction Tests on High-Roughness Surfaces. Cold Regions Sci. Technol. 131, 1–9. doi:10.1016/j.coldregions.2016.08.002

CrossRef Full Text | Google Scholar

Glen, J. W. (1968). The Effect of Hydrogen Disorder on Dislocation Movement and Plastic Deformation of Ice. Phys. Kondens. Materie 7, 43–51. doi:10.1007/bf02422799

CrossRef Full Text | Google Scholar

Glenne, B. (1987). Sliding Friction and Boundary Lubrication of Snow. J. Tribology 109, 614–617. doi:10.1115/1.3261520

CrossRef Full Text | Google Scholar

Godet, M. (1984). The Third-Body Approach: a Mechanical View of Wear. Wear 100, 437–452. doi:10.1016/0043-1648(84)90025-5

CrossRef Full Text | Google Scholar

Gold, L. W. (1977). Engineering Properties of Fresh-Water Ice. J. Glaciol. 19 (81), 197–212. doi:10.3189/s0022143000215608

CrossRef Full Text | Google Scholar

Gold, L. W. (1988). On the Elasticity of Ice Plates. Can. J. Civ. Eng. 15, 1080–1084. doi:10.1139/l88-140

CrossRef Full Text | Google Scholar

Gubler, H. (1982). Strength of Bonds between Ice Grains after Short Contact Times. J. Glaciol. 28, 457–473. doi:10.3189/s0022143000005050

CrossRef Full Text | Google Scholar

Hasler, M., Schindelwig, K., Mayr, B., Knoflach, Ch., Rohm, S., van Putten, J., et al. (2016). A Novel Ski-Snow Tribometer and its Precision. Tribology Lett. 66, 33. doi:10.1007/s11249-016-0719-2

CrossRef Full Text | Google Scholar

Hawkes, I., and Mellor, M. (1972). Deformation and Fracture of Ice under Uniaxial Stress. J. Glaciol. 11 (61), 103–131. doi:10.3189/S002214300002253X10.1017/s002214300002253x

CrossRef Full Text | Google Scholar

Heshmat, H. (1995). The Quasi-Hydrodynamic Mechanism of Powder Lubrication-Part III: On Theory and Rheology of Triboparticulates. Tribology Trans. 38 (2), 269–276. doi:10.1080/10402009508983404

CrossRef Full Text | Google Scholar

Heshmat, H. (1991). The Rheology and Hydrodynamics of Dry Powder Lubrication. Tribology Trans. 34 (3), 433–439. doi:10.1080/10402009108982054

CrossRef Full Text | Google Scholar

Higgins, D. D., Marmo, B. A., Jeffree, C. E., Koutsos, V., and Blackford, J. R. (2008). Morphology of Ice Wear from Rubber-Ice Friction Tests and its Dependence on Temperature and Sliding Velocity. Wear 265 5–6, 634–644. doi:10.1016/j.wear.2007.12.015

CrossRef Full Text | Google Scholar

Hsia, F.-C., Elam, F. M., Bonn, D., Weber, B., and Franklin, S. E. (2020). Wear Particle Dynamics Drive the Difference between Repeated and Non-repeated Reciprocated Sliding. Tribology Int. 142, 105983. doi:10.1016/j.triboint.2019.105983

CrossRef Full Text | Google Scholar

Huzioka, T. (1963). Studies on the Resistance of Snow Sledge. V. Friction between Snow and a Plate of Glass or Plastics. Low Temperature Science, Ser. A. 21, 31–44. with English summary.

Google Scholar

Huzioka, T. (1962). Studies on the Resistance of Snow Sledge. VI. Friction between Snow and a Plastic Plate. Low Temperature Science, Ser. A. 20, 159–179. with English summary.

Google Scholar

Iordanoff, I., Berthier, Y., Descartes, S., and Heshmat, H. (2002). A Review of Recent Approaches for Modeling Solid Third Bodies. J. Tribology 124, 725–735. doi:10.1115/1.1467632

CrossRef Full Text | Google Scholar

Jones, W. R. (1982). Boundary Lubrication RevisitedNASA Technical Memorandum 82858. Cleveland, OH: Lewis Research Center. doi:10.1109/fie.1982.715887

CrossRef Full Text

Jordaan, I. J. (2001). Mechanics of Ice-Structure Interaction. Eng. Fracture Mech. 68, 1932–1960. doi:10.1016/s0013-7944(01)00032-7

CrossRef Full Text | Google Scholar

Kheisin, D. E., and Cherepano, N. V. (1973). Change of Ice Structure in the Zone of Impact of a Solid Body against the Ice Cover Surface. In Problems of the Arctic and Antarctic. Editors A. F. Treshnikov 33-35. Washington, D.C.: National Science Foundation by the Israel Program for Scientific Translation, 239–245.

Google Scholar

Kietzig, A-M., Hatzikiriakos, S. G., and Englezos, P. (2010). Physics of Ice Friction. J. Appl. Phys. 107, 081101. doi:10.1063/1.3340792

CrossRef Full Text | Google Scholar

Kim, E., Golding, N., Schulson, E. M., Løset, S., and Renshaw, C. E. (2012). Mechanisms Governing Failure of Ice beneath a Spherically-Shaped Indenter. Cold Regions Sci. Technol. 78, 46–63. doi:10.1016/j.coldregions.2012.01.011

CrossRef Full Text | Google Scholar

Klein, G. J. (1947). The Snow Characteristics of Aircraft Skis. Aeronautical Report AR-2. Ottawa: National Research Council of Canada.

Klein-Paste, A., and Sinha, N. K. (2010). Microstructural Investigation of Ice Surfaces after Rubber-Ice and Sand-Ice Sliding Friction Tests. Tribology Int. 43, 1151–1157. doi:10.1016/j.triboint.2009.12.036

CrossRef Full Text | Google Scholar

Kurdyumov, V. A., and Kheisin, D. E. (1979). Hydrodynamic Model of the Impact of a Solid on Ice. Prikladnaya Mekhanika 12 (10), 103–109. Transl.

CrossRef Full Text | Google Scholar

Kuroiwa, D. (1977). The Kinetic Friction on Snow and Ice. J. Glaciol. 19 (81), 141–152. doi:10.3189/s0022143000029233

CrossRef Full Text | Google Scholar

Lehtovaara, A. (1989). Kinetic Friction between Ski and Snow. Acta Polytechnica Scand. Mech. Eng. Ser. 93, 52.

Google Scholar

Lever, J. H., Lines, A. P., Taylor, S., Hoch, G. R., Asenath-Smith, E., and Sodhi, D. S. (2021). Investigation of the Mechanics Underlying Ice-Skate Friction. J. Glaciology. in press. doi:10.5194/egusphere-egu2020-1468

CrossRef Full Text | Google Scholar

Lever, J. H., Weale, J. C., Kaempfer, T. U., and Preston, M. J. (2016). Advances in Antarctic Sled Technology. Hanover, NH, United States: Army Engineer Research and Development Center. ERDC/CRREL TR-16-4.

Lever, J. H., Taylor, S., Hoch, G. R., and Daghlian, C. (2019). Evidence that Abrasion Can Govern Snow Kinetic Friction. J. Glaciol. 65 (249), 68–84. doi:10.1017/jog.2018.97

CrossRef Full Text | Google Scholar

Lever, J. H., Taylor, S., Song, A. J., Courville, Z. R., Lieblappen, R., and Weale, J. C. (2018). The Mechanics of Snow Friction as Revealed by Micro-scale Interface Observations. J. Glaciol. 64 (243), 27–36. doi:10.1017/jog.2017.76

CrossRef Full Text | Google Scholar

Lever, J. H., and Weale, J. C. (2012). High Efficiency Fuel Sleds for Polar Traverses. J. Terramechanics 49, 207–213. doi:10.1016/j.jterra.2012.05.001

CrossRef Full Text | Google Scholar

Li, Y., and Somorjai, G. A. (2007). Surface Premelting of Ice. J. Phys. Chem. C 111 (27), 9631–9637. doi:10.1021/jp071102f

CrossRef Full Text | Google Scholar

Liefferink, R. W., Hsia, F.-C., Weber, B., and Bonn, D. (2021). Friction on Ice: How Temperature, Pressure, and Speed Control the Slipperiness of Ice. Phys. Rev. X 11, 011025. doi:10.1103/PhysRevX.11.011025

CrossRef Full Text | Google Scholar

Louden, P. B., and Gezelter, J. D. (2018). Why Is Ice Slippery? Simulations of Shear Viscosity of the Quasi-Liquid Layer on Ice. J. Phys. Chem. Lett. 9, 3686–3691. doi:10.1021/acs.jpclett.8b01339

PubMed Abstract | CrossRef Full Text | Google Scholar

Lozowski, E. P., and Szilder, K. (2013). Derivation and New Analysis of a Hydrodynamic Model of Speed Skate Ice Friction. Int. J. Offshore Polar Eng. 23 (No. 2), 104–111.

Google Scholar

Lozowski, E., Szilder, K., and Maw, S. (2013). A Model of Ice Friction for a Speed Skate Blade. Sports Eng. 16, 239–253. doi:10.1007/s12283-013-0141-z

CrossRef Full Text | Google Scholar

Makkonen, L., and Tikanmäki, M. (2014). Modeling the Friction of Ice. Cold Regions Sci. Technol. 102, 84–93. doi:10.1016/j.coldregions.2014.03.002

CrossRef Full Text | Google Scholar

Marmo, B. A., Blackford, J. R., and Jeffree, C. E. (2005). Ice Friction, Wear Features and Their Dependence on Sliding Velocity and Temperature. J. Glaciol. 51 (174), 391–398. doi:10.3189/172756505781829304

CrossRef Full Text | Google Scholar

Marshall, H.-P., and Johnson, J. B. (2009). Accurate Inversion of High-Resolution Snow Penetrometer Signals for Microstructural and Micromechanical Properties. J. Geophys. Res. 114, F04016. doi:10.1029/2009JF001269

CrossRef Full Text | Google Scholar

Masterson, D. M., and Frederking, R. M. W. (1993). Local Contact Pressures in Ship/ice and Structure/ice Interactions. Cold Regions Sci. Technol. 21, 169–185. doi:10.1016/0165-232x(93)90005-s

CrossRef Full Text | Google Scholar

Mellor, M. (1975). A Review of Basic Snow Mechanics 114. IAHS-AISH Publ Symposium at Grindelwald 1974 – Snow Mechanics, 251–291.

Mellor, M. (1964). Properties of Snow CRREL Monograph III-A1. Hanover, NH: Cold Regions Research and Engineering Laboratory.

Moore, D. F. (1965). A Review of Squeeze Films. Wear 8, 245–263. doi:10.1016/0043-1648(65)90001-3

CrossRef Full Text | Google Scholar

Myers, D. (1991). Surfaces, Interfaces, and Colloids: Principles and Applications. New York: VCH Publishers.

Nachbauer, W., Kaps, P., Hasler, M., and Mossner, M. (2016a). Friction between Ski and Snow. In The Engineering Approach to Winter Sports, Editors F. Braghin. New York: Springer-Verlag.

Google Scholar

Nachbauer, W., Rohm, S., Knoflach, C., van Putten, J., and Hasler, M. (2016b). “Friction along a Slider on Snow,” in Proceedings of the 8th International Conference on Snow Engineering, Nantes, France, 125–126. Available at: https://hal-cstb.archives-ouvertes.fr/hal-01426073v2.

Google Scholar

Nagata, Y., Hama, T., Backus, E. H. G., Mezger, M., Bonn, D., Bonn, M., et al. (2019). The Surface of Ice under Equilibrium and Nonequilibrium Conditions. Acc. Chem. Res. 52 (4), 1006–1015. doi:10.1021/acs.accounts.8b00615

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakaya, U., Tada, M., Sekido, Y., and Takano, T. (1936). Physics of Skiing, the Preliminary and General Survey. Hokkaido University Collection of Scholarly and Academic Papers. J. Fac. Sci. 1 (9), 265–288. Available at: http://hdl.handle.net/2115/34460.

Google Scholar

Neshyba, S., Nugent, E., Roeselová, M., and Jungwirth, P. (2009). Molecular Dynamics Study of Ice−Vapor Interactions via the Quasi-Liquid Layer. J. Phys. Chem. C 113, 4597–4604. doi:10.1021/jp810589a

CrossRef Full Text | Google Scholar

Niven, C. D. (1959). A Proposed Mechanism for Ice Friction. Can. J. Phys. 37, 247–255. doi:10.1139/p59-029

CrossRef Full Text | Google Scholar

Nixon, W. A., and Schulson, E. M. (1987). A Micromechanical View of the Fracture Toughness of Ice. J. Phys. Colloques 48, C1–C313. doi:10.1051/jphyscol:1987144

CrossRef Full Text | Google Scholar

Oksanen, P., and Keinonen, J. (1982). The Mechanism of Friction of Ice. Wear 78, 315–324. doi:10.1016/0043-1648(82)90242-3

CrossRef Full Text | Google Scholar

Paesani, F., and Voth, G. A. (2008). Quantum Effects Strongly Influence the Surface Premelting of Ice. J. Phys. Chem. C 112, 324–327. doi:10.1021/jp710640e

CrossRef Full Text | Google Scholar

Perrson, B. N. J. (2015). Ice Friction: Role of Non-uniform Frictional Heating and Ice Premelting. J. Chem. Phys. 143, 224701. doi:10.1063/1.4936299

PubMed Abstract | CrossRef Full Text | Google Scholar

Petrenko, V. F., and Colbeck, S. C. (1995). Generation of Electric fields by Ice and Snow Friction. J. Appl. Phys. 77 (9), 4518–4521. doi:10.1063/1.359448

CrossRef Full Text | Google Scholar

Petrovic, J. J. (2003). Review Mechanical Properties of Ice and Snow. J. Mater. Sci. 38, 1–6. doi:10.1023/a:1021134128038

CrossRef Full Text | Google Scholar

Pittenger, B., Fain, S. C., Cochran, M. J., Donev, J. M. K., Robertson, B. E., Szuchmacher, A., et al. (2001). Premelting at Ice-Solid Interfaces Studied via Velocity-dependent Indentation with Force Microscope Tips. Phys. Rev. B 63, 134102. doi:10.1103/PhysRevB.63.134102

CrossRef Full Text | Google Scholar

Poirier, L., Thompson, R. I., Lozowski, E. P., and Maw, S. (2011). “Getting a Grip on Ice Friction,” in 21st Int Offshore and Polar Eng Cong (Maui, USA: ISOPE), 3, 1071–1077.

Google Scholar

Reuter, B., Proksch, M., Löwe, H., Van Herwijnen, A., and Schweizer, J. (2019). Comparing Measurements of Snow Mechanical Properties Relevant for Slab Avalanche Release. J. Glaciol. 65 (249), 55–67. doi:10.1017/jog.2018.93

CrossRef Full Text | Google Scholar

Reynolds, O. (1899). On the Slipperiness of Ice. Manchester Mem. xlii (5), 1 – 7.

Google Scholar

Rosenberg, R. (2005). Why Is Ice Slippery? Phys. Today 58, 50–54. doi:10.1063/1.2169444

CrossRef Full Text | Google Scholar

Salm, B. (1982). Mechanical Properties of Snow. Rev. Geophys. 20 (1), 1–19. doi:10.1029/rg020i001p00001

CrossRef Full Text | Google Scholar

Sazaki, G., Zepeda, S., Nakatsubo, S., Yokomine, M., and Furukawa, Y. (2012). Quasi-liquid Layers on Ice crystal Surfaces Are Made up of Two Different Phases. Proc. Natl. Acad. Sci. 109, 1052–1055. doi:10.1073/pnas.1116685109

PubMed Abstract | CrossRef Full Text | Google Scholar

Scherge, M., Böttcher, R., Richter, M., and Gurgel, U. (2013). High-speed Ice Friction Experiments under Lab Conditions: on the Influence of Speed and normal Force. ISRN Tribology, 2013. Article ID 703202, 1, 6. doi:10.5402/2013/703202

CrossRef Full Text | Google Scholar

Schindelwig, K., Hasler, M., Van Putten, J., Rohm, S., and Nachbauer, W. (2014). Temperature below a Gliding Cross Country Ski. Proced. Eng. 72, 380–385. doi:10.1016/j.proeng.2014.06.065

CrossRef Full Text | Google Scholar

Schulson, E. M. (1990). The Brittle Compressive Fracture of Ice. Acta Metallurgica et Materialia 38 (10), 1963 – 1976.

CrossRef Full Text | Google Scholar

Schulson, E. M. (2001). Brittle Failure of Ice. Eng. Fracture Mech. 68, 1839–1887. doi:10.1016/s0013-7944(01)00037-6

CrossRef Full Text | Google Scholar

Schulson, E. M. (1999). The Structure and Mechanical Behavior of Ice. Jom 51 (2), 21–27. doi:10.1007/s11837-999-0206-4

CrossRef Full Text | Google Scholar

Schweizer, J., Jamieson, J. B., and Schneebeli, M. (2003). Snow Avalanche Formation. Rev. Geophys. 41 (4), 1016. doi:10.1029/2002RG000123

CrossRef Full Text | Google Scholar

Seymour-Pierce, A., Lishman, B., and Sammonds, P. (2017). Recrystallization and Damage of Ice in winter Sports. Phil. Trans. R. Soc. A. 375, 20150353. doi:10.1098/rsta.2015.0353

PubMed Abstract | CrossRef Full Text | Google Scholar

Shapiro, L. H., Johnson, J. B., Sturm, M., and Blaisdell, G. L. (1997). Snow Mechanics: Review of the State of Knowledge and Applications. CRREL Report 97-3. Hanover, NH: Cold Regions Research and Engineering Laboratory.

Slater, B., and Michaelides, A. (2019). Surface Premelting of Water Ice. Nat. Rev. Chem. 3, 172–188. doi:10.1038/s41570-019-0080-8

CrossRef Full Text | Google Scholar

Sodhi, D. S. (2001). Crushing Failure during Ice-Structure Interaction. Eng. Fracture Mech. 68, 1889–1921. doi:10.1016/s0013-7944(01)00038-8

CrossRef Full Text | Google Scholar

Stiffler, A. K. (1984). Friction and Wear with a Fully Melting Surface. J. Tribology 106, 416–419. doi:10.1115/1.3260949

CrossRef Full Text | Google Scholar

Strausky, H., Krenn, J. R., Leitner, A., and Aussenegg, F. R. (1998). Sliding Plastics on Ice: Fluorescence Spectroscopic Studies on Interfacial Water Layers in the μm Thickness Regime. Appl. Phys. B 66, 599–602. doi:10.1007/s003400050442

CrossRef Full Text | Google Scholar

Szabo, D., and Schneebeli, M. (2007). Subsecond Sintering of Ice. Appl. Phys. Lett. 90, 151916. doi:10.1063/1.2721391

CrossRef Full Text | Google Scholar

Tian, X., and Kennedy, F. E. (1994). Maximum and Average Flash Temperatures in Sliding Contacts. J. Tribology 116, 167–174. doi:10.1115/1.2927035

CrossRef Full Text | Google Scholar

Tian, X., and Kennedy, F. E. (1993). Contact Surface Temperature Models for Finite Bodies in Dry and Boundary Lubricated Sliding. J. Tribology 115, 411–418. doi:10.1115/1.2921652

CrossRef Full Text | Google Scholar

Tuononen, A. J., Kriston, A., and Persson, B. (2016). Multiscale Physics of Rubber-Ice Friction. J. Chem. Phys. 145, 114703. doi:10.1063/1.4962576

CrossRef Full Text | Google Scholar

Tusima, K. (2011). Adhesion Theory for Low Friction on Ice. New Tribological Ways, Editors Dr. Taher Ghrib. ISBN: 978-953-307-206-7, InTech, Available from: http://www.intechopen.com/books/new-tribologicalways/adhesion-theory-for-low-friction-on-ice doi:10.5772/15085

CrossRef Full Text | Google Scholar

Tusima, K., and Yosida, Y. (1969). Melting of Ice by Friction. Low Temperature Science, Ser. A. 27, 17–30. with English summary.

Google Scholar

Wagner, W., Riethmann, T., Feistel, R., and Harvey, A. H. (2011). New Equations for the Sublimation Pressure and Melting Pressure of H2O Ice Ih. J. Phys. Chem. Reference Data 40, 043103. doi:10.1063/1.3657937

CrossRef Full Text | Google Scholar

Weber, B., Nagata, Y., Ketzetzi, S., Tang, F., Smit, W. J., Bakker, H. J., et al. (2018). Molecular Insight into the Slipperiness of Ice. J. Phys. Chem. Lett. 9, 2838–2842. doi:10.1021/acs.jpclett.8b01188

PubMed Abstract | CrossRef Full Text | Google Scholar

Wells, J., Jordaan, I., Derradji-Aouat, A., and Taylor, R. (2011). Small-scale Laboratory Experiments on the Indentation Failure of Polycrystalline Ice in Compression: Main Results and Pressure Distribution. Cold Regions Sci. Technol. 65, 314–325. doi:10.1016/j.coldregions.2010.11.002

CrossRef Full Text | Google Scholar

Wong, J. Y. (1989). Terramechanics and Off-Road Vehicles. Amsterdam: Elsevier.

Wornyoh, E. Y. A., Jasti, V. K., and Fred Higgs, C. (2007). A Review of Dry Particulate Lubrication: Powder and Granular Materials. J. Tribology 129, 438–449. doi:10.1115/1.2647859

CrossRef Full Text | Google Scholar

Wu, Q., Andreopoulos, Y., Xanthos, S., and Weinbaum, S. (2005). Dynamic Compression of Highly Compressible Porous media with Application to Snow Compaction. J. Fluid Mech. 542, 281–304. doi:10.1017/s0022112005006294

CrossRef Full Text | Google Scholar

Wu, Q., Igci, Y., Andreopoulos, Y., and Weinbaum, S. (2006). Lift Mechanics of Downhill Skiing and Snowboarding. Med. Sci. Sports Exerc. 38 (6), 1132–1146. doi:10.1249/01.mss.0000222842.04510.83

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Q., and Sun, Q. (2011). A Comprehensive Skiing Mechanics Theory with Implications to Snowboard Optimization. Med. Sci. Sports Exerc. 43, 1955–1963. doi:10.1249/MSS.0b013e318219480c

PubMed Abstract | CrossRef Full Text | Google Scholar