Bone Stress-Strain State Evaluation Using CT Based FEM

Nowadays, the use of a digital prototype in numerical modeling is one of the main approaches to calculating the elements of an inhomogeneous structure under the influence of external forces. The article considers a finite element analysis method based on computed tomography data. The calculations used a three-dimensional isoparametric finite element of a continuous medium developed by the authors with a linear approximation, based on weighted integration of the local stiffness matrix. The purpose of this study is to describe a general algorithm for constructing a numerical model that allows static calculation of objects with a porous structure according to its computed tomography data. Numerical modeling was carried out using kinematic boundary conditions. To evaluate the results obtained, computational and postprocessor grids were introduced. The qualitative assessment of the modeling data was based on the normalized error. Three-point bending of bone specimens of the pig forelimbs was considered as a model problem. The numerical simulation results were compared with the data obtained from a physical experiment. The relative error ranged from 3 to 15%, and the crack location, determined by the physical experiment, corresponded to the area where the ultimate strength values were exceeded, determined by numerical modeling. The results obtained reflect not only the effectiveness of the proposed approach, but also the agreement with experimental data. This method turned out to be relatively non-resource-intensive and time-efficient.

Introduction

At the moment, numerical modeling is the main calculation method in various fields of scientific research. And the use of data from experimental samples’ images is the most promising approach to describing the behavior of elements of inhomogeneous structures under external the influence (Mithun and Mohammad, 2014; Marwa et al., 2018). This approach allows us to consider problems with multi-connected porous or inhomogeneous materials (Kayumov, 1999; Alberich-Bayarri et al., 2008; Kharin et al., 2019). This is especially true in clinical practice since it can significantly affect the quality of treatment (Kichenko et al., 2008; Kichenko et al., 2011; Maquer et al., 2015). Stress-strain state is important in tasks to estimate bone remodeling, especially in the case of patient-based implant design (Maslov, 2017; Borovkov et al., 2018; Maslov, 2020). There are several image-based approaches to determining the mechanical parameters of the model. One of them is based on approximating the inhomogeneity by constructing a distribution using the mean intercept length method. With this approach, the physical relations are expressed in terms of the tensor of elastic constants and the fabric tensor (Sachenkov et al., 2016; Kayumov et al., 2018; Yaikova et al., 2019). The next approach is based on reducing the material anisotropy to orthotropy by calculating constants from numerical experiments (Ruess et al., 2012; Ridwan-Pramana et al., 2017; Chikova et al., 2018). Finally, the work presents a third approach based on taking into account the material properties by weighted integration of the global stiffness matrix of the finite element mesh.

Computed tomography is the main approach to reconstructing images of the investigated domain. Such a process implies the creation of its digital prototype, which is a three-dimensional array of numbers corresponding to the material permeability in each microelement (voxel) of the volume. These values can be interpreted according to Hounsfield’s quantitative scale of X-ray density. Modern computed tomography (CT) allows getting detailed information not only about bone tissue state but also its interaction with implants (Stock et al., 2002; Jones et al., 2007; Vanlenthe et al., 2007). Using CT data the segmentation can be performed. It’s a complicated process because it’s important to restore not only geometry but also the inner structure of the organ (Supplementary Material). Wherein restored geometry should be meshed for simulation. The quality of mesh influences a lot on simulation quality. A common approach is to use stratified segmentation. E.g., separate geometry for cortical and cancellous bone tissue in whole bone (Marcián et al., 2018; Carniel et al., 2019). Then, in simulation, each geometry can be taken into account with different mechanical properties (Marcian et al., 2017; Hettich et al., 2018; Kuchumov and Selyaninov, 2020). But these actions are laborious and modern research focused on ways to facilitate the segmentation (Moriya et al., 2018). On other hand, the highest calculation accuracy is achieved by modeling each microvolume of a continuous medium with one finite element (Prez et al., 2014; Tveito et al., 2017). However, in this case, the computational intensity increases excessively. In this regard, it makes sense to increase the finite element size so that it contains a certain amount of microvolumes (Nadal et al., 2013; Marco et al., 2015; Giovannelli et al., 2017). In this case, each voxel can be considered as a neighborhood of the integration point of the local stiffness matrix. However, the question of the number of voxels in the element volume is still open. The same question is open for applicability of finite element method (FEM) in casual clinic practice (Viceconti et al., 2018).

The purpose of the study is to implement the method of static calculation of problems based on samples of a porous structure. A three-dimensional isoparametric linear element of a continuous medium, built on the basis of computed tomography data, was used as a finite element of the grid.

Materials and Methods

Computed Tomography Based Finite Element

Let’s consider the region describing the volume of an object. Additionally, there is digital data of the object. In the research computed tomography data is understood as a digital prototype. The data consists of a number of microvolumes with an average value of the Hounsfield unit. Usually, such data illustrated by a greyscale three-dimensional image. Each microvolumes (voxel) has dimensions Δx, Δy, Δz. Usually, a voxel is equal to a cube and the size depends on computed tomography resolution. The mechanical behavior of the object will be investigated by the finite element methods. In this case, the volume is consists of a number of finite element. To simulate the inhomogeneity continuum three-dimensional eight-node finite element with bilinear interpolation was built. Using shape functions N_n in the local coordinate system of the element (ξ_n, η_n, ζ_n) the displacement can be presented as follows:

$\left\{\vartheta \right\}=\left\{\begin{array}{c}u\\ v\\ w\end{array}\right\}={\displaystyle \sum }_{i=1}^8\left\{\begin{array}{c}{u}_n\\ v_n\\ w_n\end{array}\right\}{N}_n\left({\xi }_n,{\eta }_n,{\zeta }_n\right)$(2.1.1)

where u, v, w are components of a displacement vector in global coordinate system x, y, z, and shape function looks like N_n(ξ, η, ζ) = (1 + ξ ∙ ξ_n) (1 + η∙η_n) (1 + ζ∙ζ_n)/8.

The equations can be presented in matrix from:

$\left\{\vartheta \right\}=\left[N\right]\left\{{\vartheta }^E\right\}$(2.1.2)

where {ϑ^E}—vector of the node displacements, [N]—matrix of the shape functions.

Let’s introduce strain and stress vectors:

$\left\{\epsilon \right\}=\left({\epsilon }_{xx},{\epsilon }_{yy},{\epsilon }_{zz},{\epsilon }_{xy},{\epsilon }_{yz},{\epsilon }_{zx}\right)$(2.1.3)

$\left\{\sigma \right\}=\left({\sigma }_{xx},{\sigma }_{yy},{\sigma }_{zz},{\sigma }_{xy},{\sigma }_{yz},{\sigma }_{zx}\right)$(2.1.4)

Using strain-displacement equations strain vector can be determined (Zienkiewicz and Zhu, 1987):

$\left\{\epsilon \right\}=\left[L\left(\xi ,\eta ,\zeta \right)\right]\left\{\vartheta \right\}$(2.1.5)

where [L]—differentiation matrix.

Using Hooke's law stress vector can be found:

$\left\{\sigma \right\}=\left[D\left(\left\{r\right\}\right)\right]\left\{\epsilon \right\}$(2.1.6)

where [D]—elasticity matrix, {r}—vector in a point where elasticity matrix set.

In case of inhomogeneous media elasticity matrix can be rewritten in form:

$\left[D\left(\left\{r\right\}\right)\right]=\left[D^B\right]\cdot \omega \left(\left\{r\right\}\right)$(2.1.7)

where [D^B]—elasticity matrix of pure material, ω{r}—scalar function which determines inhomogeneity by digital prototype data.

The ω{r} function can be calculated using Hounsfield unit (HU) from CT data. And then strain vector can be rewritten as follow:

$\left\{\epsilon \right\}=\left[B\left(\xi ,\eta ,\zeta \right)\right]\cdot \omega \left(\left\{r\right\}\right)\cdot \left\{\vartheta \right\}$(2.1.8)

where matrix [B] is equal to [D^B]∙[L(ξ, η, ζ)].

So stiffness matrix for an element can be denoted (Zienkiewicz and Zhu, 1987):

$\left[K^E\right]={\displaystyle \iiint \underset{-1}{\overset{1}{}}{\left[B\left(\xi ,\eta ,\zeta \right)\right]}^T\left[D\right]\left[B\left(\xi ,\eta ,\zeta \right)\right]\left|J\left(\xi ,\eta ,\zeta \right)\right|\omega \left(\xi ,\eta ,\zeta \right)d\xi d\eta d\zeta }$(2.1.9)

where |J(ξ,η,ζ)| is the Jacobian determinant of coordinate transformation.

When node displacements are found using differentiation matrix and elasticity matrix strain and stress vectors can be found. Using shape functions for every element stress function can be approximated:

${\sigma }^E\left(\xi ,\eta ,\zeta \right)={\displaystyle {\iiint }_{V^E}\left({\left\{N\right\}}^T\left\{{\sigma }_0^E\right\}-{\sigma }^i\right)dV\to min}$(2.1.10)

where σⁱ—node value of stress, {σ^E₀}—vector if approximation coefficients.

So average stress in each element can be found:

${\overline{\sigma }}^E=V_E^{-1}{\displaystyle {\iiint }_{V^E}{\left\{N\right\}}^T\left\{{\sigma }_0^E\right\}dV}$(2.1.11)

where V_E—element’s volume.

To estimate computational error the energy norm should be calculated. For this purpose at every element stress error should be calculated:

$\left\{\Delta {\sigma }_n^i\right\}=\left\{{\sigma }_n^a\right\}-\left\{{\sigma }_n^i\right\}$(2.1.12)

where {σ^a_n}—average stress vector at node n, {σⁱ_n}—stress vector of node n of finite element i.

Then, for each element, the energy error is calculated as follows (Grassi et al., 2012; Giovannelli et al., 2017):

${\overline{\mathit{E}}}^i=\frac{1}{2}{\displaystyle {\iiint }_{V^E}{\left\{\Delta \sigma \right\}}^T{\left[D\right]}^{-1}{\omega }^{-1}\left\{\Delta \sigma \right\}d{V}^E}$(2.1.13)

Strain energy of the element can be calculated by equation:

${\overline{U}}^i=\frac{1}{2}{\displaystyle {\iiint }_{V^{\mathit{E}}}{\left\{\sigma \right\}}^T\left\{\epsilon \right\}d{V}^E}$(2.1.14)

Finally, the energy error can be normalized according to the strain energy:

${\tilde{E}}^i=\sqrt{\frac{{\overline{E}}^i}{{\overline{U}}^i+{\overline{E}}^i}\cdot }100\%$(2.1.15)

So, the described approach allows taking into account the inhomogeneity of media in terms of the stiffness matrix. Analyses of stress-strain state should be held in terms of average stress and strain. The quality of results can be judged by normalized energy error value. A more detailed description of the method and evaluation of element convergence depending on voxel number is given in the previous publications (Gerasimov et al., 2019; Gerasimov et al., 2021).

Meshing and Segmentation

Consider the global algorithm of the analysis of the bone. Input data is presented as CT, where each value of HU can be interpreted as optical density and even can be recalculated to elastic constants, and ultimate stress using equations (Rho et al., 1995):

$\rho =a_{\rho }+b_{\rho }\cdot HU$(2.2.1)

$E=a_E{\rho }^{b_E}$(2.2.2)

$\left[\sigma \right]=a_{\sigma }{\rho }^{b_{\sigma }}$(2.2.3)

where coefficients a and b with the corresponding indices are determined from experiments or literature and can vary depending on the type of bone tissue or organ.

Bone is a heterogeneous porous material with an irregular structure. The process of constructing a finite element mesh over the selected area implies segmentation of the initial CT data. In this case, each finite element is associated with a certain area of the bone. Such subregions are characterized by a different distribution of bone substance, which can include both the cortical plate and the spongy substance. Thus, the proposed method for constructing the finite element mesh makes it possible to take into account the material anisotropy at the level of modeling an individual finite element based on its CT data. Figure 1 sequentially shows subvolumes with different levels of porosity. On the left side is the area with a highest porosity (cancellous zone), on the right one is the part corresponding to a cortical plate. A popular approach is to use segmentation to restore the geometry of an organ. But researchers face difficulty when investigating organs with irregular geometry and complicated inner structure, e.g., femur, where there are cortical and cancellous regions. The proposed method allows taking into account such anisotropy properties indirectly. Based on the developed FE it is offered to use regular mesh for the whole CT space. Using a threshold filter for porosity the mesh can be clarified. Let’s call such a mesh computational grid. Then kinematic or/and static boundary conditions can be applied. Then all local stiffness matrixes can be calculated using CT data. Assembling the global stiffness matrix is a casual task. After nodal displacements are found average stress and strain vector for each element can be found. Principal values, directions, and von Mises yield was calculated for average stress and strain in each element. To juxtapose stress-strain state and CT data additional mesh was build. Let’s call such a mesh post-processing grid. Such a grid can be built as a contour of binarized CT data. So, results from the computational grid can be interpolated to the post-processing grid.

FIGURE 1

FIGURE 1. Three-dimensional visualization of CT data corresponding to different areas of the bone: porosity decreases from left to right, which, accordingly, leads to an increase in the bone volume fraction.

General algorithm

Input: CT data, boundary conditions

Output: Post processing grid, nodal and element solutions

1: generate regular mesh for hole CT space with given element size

2: for each element in regular mesh

3:  if bone tissue relative content < bone threshold

4:  then delete element

4:  else compute local stiffness matrix according to CT data

4: End for

5: Save mesh as a computational grid

6: Assembling the global stiffness matrix, apply boundary conditions and solve

7: Calculate stress and strain in elements

8: Generate post-processing grid using given HU threshold with given tolerance

9: Interpolate solution to post-processing grid

FEM software was implemented using C++ (g++ compiler). An Eight-node finite element with three degrees of freedom in each node was realized. The algorithm was parallelized using OpenMP technology because of the high labor costs of integrating the local stiffness matrix. The solution of problems was carried out on a computer with the following configuration: CPU—AMD Ryzen 7 1700 with 8 physical and 16 logical cores with a frequency of 3.7 GHz, RAM—G. Skill Aegis 16 GB DDR4 3000 16GISB K2 C16 with a frequency of 2933 MHz, motherboard—MSI B350M MORTAR. Post-processing was carried out using the ParaView software (Ahrens et al., 2005; Ayachit, 2015).

Bending Test

Experiments were performed on six 15–20 kg male Vietnamese swine. Animals were placed in individual cages under standard laboratory conditions with unlimited access to food and water and a 12 h day/night cycle. The protocol of the experiment, including anesthesia, surgery, postoperative care, testing, and euthanasia, was approved by the Animal Care Committee of Kazan State Medical University (protocol #5 of 20 May 2020). All experimental procedures were performed in accordance with the standards to minimize animal suffering and the size of experimental groups. Animals were included in experiments after a period of adaptation of at least 7 days. In experiments bones of animals after contusion spinal injury were used. The animals were sacrificed on the 8th week after a spinal cord injury (SCI). The euthanasia was performed under deep anesthesia by overdosing on an inhalational narcosis agent (Isoflurane) (Fadeev et al., 2020). The bones of the fore and hind limbs were extracted.

Bones were scanned by CT. Micro/nanofocal X-ray inspection system for CT and 2D inspections of Phoenix V | tome | X S240 was used for scanning. The system is equipped with two X-ray tubes: microfocus with a maximum accelerating voltage of 240 kV power of 320 W and nanofocus with a maximum accelerating voltage of 180 kV power of 15 W. For primary data processing and creating a volume (voxel) model of the sample based on x-ray images, the datos|x reconstruction software was used. The sample fixed in the holder was placed on the rotating table of the X-ray computed tomography chamber at the optimum distance from the X-ray source. The survey was carried out at an accelerating voltage of 90–100 kV and a current 140–150 mA. After that three-point bending tests were carried out.

CT data was about 800–900 Mb, voxel size in the direction of three Cartesian coordinate axes was equal to 0.2 mm. The data dimension was equal to 7523. Based on CT data, an initial regular finite element mesh was constructed. The computational grid generation was based on the removal of elements with a bone substance content of less than 5%. In this case, the initial CT data was pre-binarized according to the specified threshold value: values less than the threshold value were equated to zero, larger or equal—to one. Determination of the mechanical properties of bone tissue was based on the use of a similar binarization function. Young’s modulus for pure bone tissue can be calculated by Eq. 2.2.2 and was equal to 30 GPa and Poisson’s ratio equal to 0.3. In calculations three-point bending simulation. The top and the bottom surfaces of the distal and the proximal regions were fixed (marked by black lines in Figures 2A,C). Displacements in y negative direction were applied on the top surface of the medial region (marked by red arrows in Figures 2A,C) and were equal to 2, 3, and 4 mm, respectively. To verify the simulation results equivalent force was calculated. All steps of calculations from reading CT data to interpolate nodal and element solution to the post-processing grid took about 15 min.

FIGURE 2

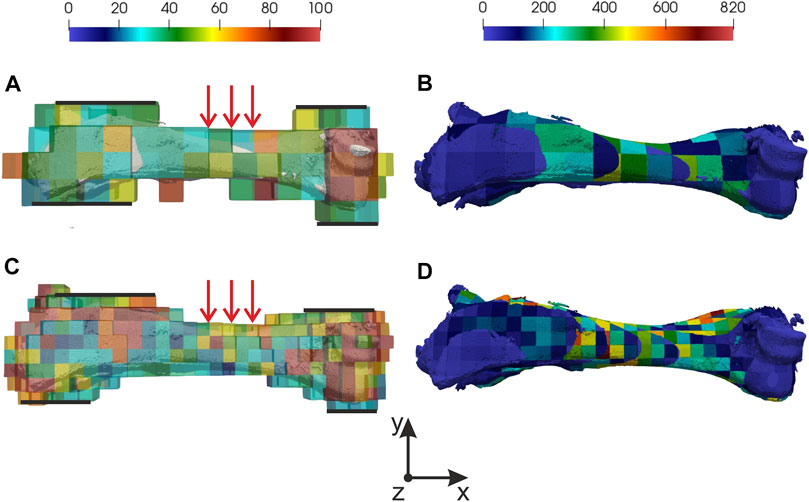
FIGURE 2. Distribution of normalized error and Von Mises stress: (A) normalized error for 10 mm mesh, (B) Von Mises stress for 10 mm mesh, (C) normalized error for 5 mm mesh, (D) Von Mises stress for 5 mm mesh. In (A,C) fixed regions marked by black lines and region where displacements were applied marked by red arrows.

Results and Discussion

Two initial meshes with 10 and 5 mm element sizes were used. Normalized errors were analyzed for each result. Special attention was paid to the value of normalized errors in elements where maximum Von Mises stress appears. In Figure 2 distribution of normalized error (on computational grid) and Von Mises stress (on post processing grid) in forelimb is shown. It’s important to understand correctly the meaning of the Von Mises stress in results. Averaging in element according to corresponding CT data change the understanding of the received value. In this case, we consider the element as a subvolume of the digital prototype with unknown stress spatial distribution but a known mean value. It means that falsely high and falsely low values can appear, that’s why normalized errors should be checked in the element. For both meshes maximum of normalized error appears in border elements where relative bone tissue content is low. It can be explained by the stiffness matrix decrease in stiffness. It’s important to notice that values of normalized error in regions of interest are below 50%. The maximum value of 50% is reached in the location of kinematics boundary conditions are applied. In other regions, the normalized error is below 25%.

Let’s focus on the task with 4 mm displacement applied and consider the mesh with a 5 mm element size. The minimum of normalized error (20%) and maximum of Von Mises (500 MPa) stress was in the region near applied loading (see Figures 2C,D). For more detailed analyses principal stresses and directions were found, which are shown in Figure 3. To estimate equivalent force in displacements’ applied region 2nd principal stresses were used (see Figures 3C,D). The integral of the stress vector in the region multiplied by the area will consider as a reaction to equivalent force. 1st and 3 days principal stresses describe the stress state of the bone (see Figures 3A,B,E,F). Corresponding streamlines form an orthogonal system. It should be noticed that in the region of Von Mises maximum first principal stresses reach a maximum value 400 MPa and 3 days principal—minimum −400 MPa. It explains the crack that appears in an experiment, cause the values exceed yield strength (Crenshaw et al., 1981; Imai, 2015).

FIGURE 3

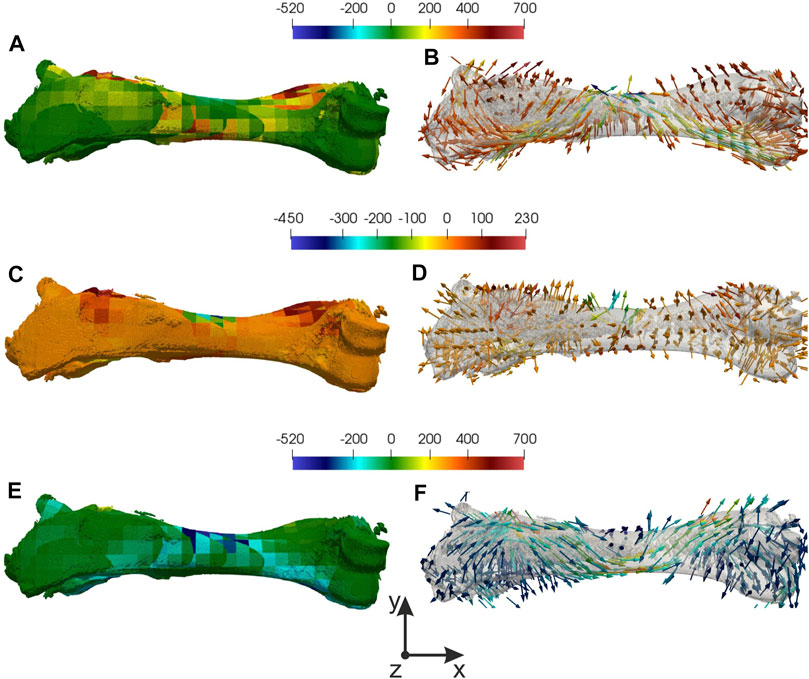
FIGURE 3. Distribution of principal stresses and directions: (A), (B) 1st principal stress and direction, (C,D) 2nd principal stress and direction, (E,F) 3rd principal stress and direction.

To verify simulation results equivalent force was compared with force from three-point bending experiments. In Figure 4A force-displacement curve is shown. On curve marked values of equivalent force (green markers in Figure 4A) and values of applied force in the same displacements (red markers in Figure 4A). The relative error was from 3 to 15%. The region a crack appears in experiments matches the region in simulation. Of course, there were some deviations, which can be explained by not accurate boundary conditions.

FIGURE 4

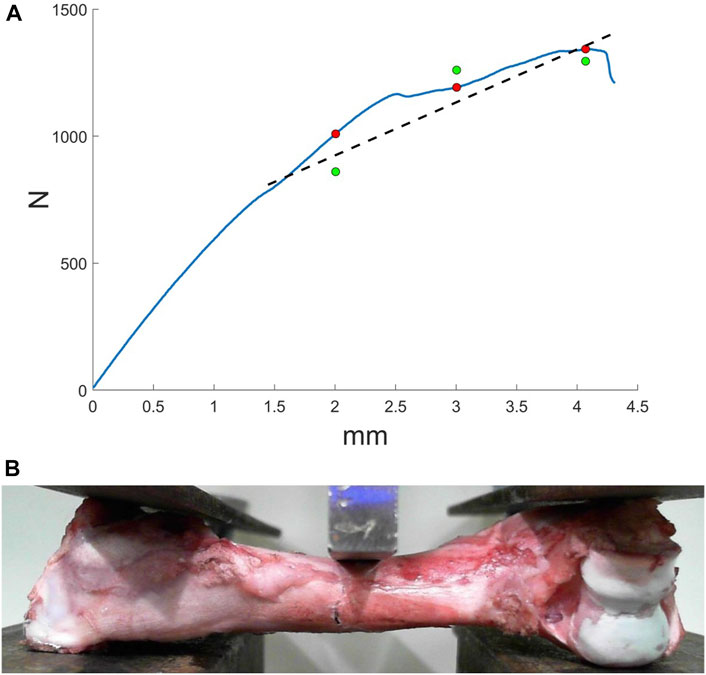
FIGURE 4. Results of three-point bending experiments: (A) force-displacement curve, where green markers indicate the equivalent force from the simulation, red markers correspond to the force form the experiment, dashed line—approximation of the equivalent force: (B) bone fracture formation.

Despite the simple function for mechanical properties (binarization by threshold), adequate results were achieved. It can be explained by the stiffness matrix integration way. It proposes a method to consider the bone tissue structure. In this case, nodal displacement in element conditioned not only by mechanical properties but by material distribution. Previously it was shown that bone volume fraction and material distribution influence much greater on mechanical properties than other morphological variables (Maquer et al., 2015). To estimate the distribution approximation by tensor is popular. But in practice, it means that at the first step such tensor should be calculated, and then the tensors should be taken into account in mechanical model and simulation. The described method allows taking into account structural properties indirectly by stiffness matrix integration way. Add it costs less laborious.

More than that, the proposed method allows using part of the CT data space. In this case, the corresponding dimensions of the initial mesh should be set. From a practical point of view after the region of interest is chosen boundary conditions should be applied. So bone can be checked for strength. Typical loading cases can be simulated. The quality of the solution can be estimated by normalized error. And analyses can be automated in terms of the normalized error and the stress invariants, e.g., Von Mises stress.

Conclusion

The CT-based FEM method is introduced. A three-dimensional isoparametric linear element of a continuous medium, built on the basis of computed tomography data, presented. The general algorithm to get the FE model is presented. For this purpose computational and post-processing grids were introduced. To estimate the quality of simulation normalized error was used. Three-point bending was simulated by the method and results were compared with provided experiments. Received results illustrate the effectiveness of the method.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics Statement

The animal study was reviewed and approved by the Animal Care Committee of Kazan State Medical University.

Author Contributions

OG, NK, PB, TB, and OS design method, realized it on programming language and wrote the manuscript. AF, MB, OS, FF, RI, ES, and TB conducted experimental data for numerical calculation and contributed to manuscript writing. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Russian Science Foundation (RSF grant No. 18-75-10027).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Special thanks to Interdisciplinary center for analytical microscopy of Kazan Federal University.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2021.688474/full#supplementary-material

References

Ahrens, J., Geveci, B., and Law, C. (2005). ParaView: An End-User Tool for Large Data Visualization, Visualization Handbook. Elsevier. ISBN-13: 978-0123875822.

Alberich-Bayarri, A., Marti-Bonmati, L., Sanz-Requena, R., Belloch, E., and Moratal, D. (2008). In Vivo Trabecular Bone Morphologic and Mechanical Relationship Using High-Resolution 3-T MRI. Am. J. Roentgenology 191 (3), 721–726. doi:10.2214/AJR.07.3528

PubMed Abstract | CrossRef Full Text | Google Scholar

Ayachit, U. (2015). The ParaView Guide: A Parallel Visualization Application. Kitware. ISBN 978-1930934306. doi:10.1145/2828612.2828624

CrossRef Full Text

Borovkov, A. I., Maslov, L. B., Zhmaylo, M. A., Zelinskiy, I. A., Voinov, I. B., Keresten, I. A., et al. (2018). Finite Element Stress Analysis of a Total Hip Replacement in Two-Legged Standing. Russ. J. Biomech. 22 (4), 382–400. doi:10.15593/RJBiomech/2018.4.02

CrossRef Full Text | Google Scholar

Carniel, T. A., Klahr, B., and Fancello, E. A. (2019). On Multiscale Boundary Conditions in the Computational Homogenization of an RVE of Tendon Fascicles. J. Mech. Behav. Biomed. Mater. 91, 131–138. doi:10.1016/j.jmbbm.2018.12.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Chikova, T. N., Kichenko, A. A., Tverier, V. M., and Nyashin, Y. I. (2018). Biomechanical Modelling of Trabecular Bone Tissue in Remodelling Equilibrium. Russ. J. Biomech. 22 (3), 245–253. doi:10.15593/RJBiomeh/2018.3.01

CrossRef Full Text | Google Scholar

Crenshaw, T. D., Peo, Jr. E. R., Lewis, A. J., and Moser, B. D. (1981). Bone Strength as a Trait for Assesing Mineralization in Swine: A Critical Review of Techniques Involved. J. Ani Sci. 53 (3), 827–835. doi:10.2527/JAS1981.533827X

CrossRef Full Text | Google Scholar

Fadeev, F., Eremeev, A., Bashirov, F., Shevchenko, R., Izmailov, A., Markosyan, V., et al. (2020). Combined Supra- and Sub-lesional Epidural Electrical Stimulation for Restoration of the Motor Functions after Spinal Cord Injury in Mini Pigs. Brain Sci. 10 (10), 744. doi:10.3390/brainsci10100744

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerasimov, O., Kharin, N., Statsenko, E., Mukhin, D., Berezhnoi, D., and Sachenkov, O. (2021). Patient-Specific Bone Organ Modeling Using CT Based FEM. Lecture Notes Comput. Sci. Eng. in press.

Google Scholar

Gerasimov, O. V., Berezhnoi, D. V., Bolshakov, P. V., Statsenko, E. O., and Sachenkov, O. A. (2019). Mechanical Model of a Heterogeneous Continuum Based on Numerical-Digital Algorithm Processing Computer Tomography Data. Russ. J. Biomech. 23 (1), 87–97.

Google Scholar

Giovannelli, L., Ródenas, J. J., Navarro-Jiménez, J. M., and Tur, M. (2017). Direct Medical Image-Based Finite Element Modelling for Patient-specific Simulation of Future Implantsfic Simulation of Future Implants. Finite Elem. Anal. Des. 136, 37–57. doi:10.1016/j.finel.2017.07.010

CrossRef Full Text | Google Scholar

Grassi, L., Schileo, E., Taddei, F., Zani, L., Juszczyk, M., Cristofolini, L., et al. (2012). Accuracy of Finite Element Predictions in Sideways Load Configurations for the Proximal Human Femurfinite Element Predictions in Sideways Load Configurations for the Proximal Human Femur. J. Biomech. 45 (2), 394–399. doi:10.1016/j.jbiomech.2011.10.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Hettich, G., Schierjott, R. A., Ramm, H., Graichen, H., Jansson, V., Rudert, M., et al. (2018). Method for Quantitative Assessment of Acetabular Bone Defects. J. Orthop. Res. 37 (1), 181–189. doi:10.1002/jor.24165

PubMed Abstract | CrossRef Full Text | Google Scholar

Imai, K. (2015). Computed Tomography-Based Finite Element Analysis to Assess Fracture Risk and Osteoporosis Treatment. Wjgem 5 (3), 182–187. doi:10.5493/wjem.v5.i3.182

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, A., Arns, C., Sheppard, A., Hutmacher, D., Milthorpe, B., and Knackstedt, M. (2007). Assessment of Bone Ingrowth into Porous Biomaterials Using MICRO-CT. Biomaterials 28 (15), 2491–2504. doi:10.1016/j.biomaterials.2007.01.046

PubMed Abstract | CrossRef Full Text | Google Scholar

Kayumov, R. A., Muhamedova, I. Z., Tazyukov, B. F., and Shakirzjanov, F. R. (2018). Parameter Determination of Hereditary Models of Deformation of Composite Materials Based on Identification Methodfication Method. J. Phys. Conf. Ser. 973 (1), 012006. doi:10.1088/1742-6596/973/1/012006

CrossRef Full Text | Google Scholar

Kayumov, R. A. (1999). Structure of Nonlinear Elastic Relationships for the Highly Anisotropic Layer of a Nonthin Shell. Mech. Compos. Mater. 35 (5), 409–418. doi:10.1007/BF02329327

CrossRef Full Text | Google Scholar

Kharin, N., Vorob’yev, O., Bolshakov, P., and Sachenkov, O. (2019). Determination of the Orthotropic Parameters of a Representative Sample by Computed Tomography. J. Phys. Conf. Ser. 1158 (3), 032012. doi:10.1088/1742-6596/1158/3/032012

CrossRef Full Text | Google Scholar

Kichenko, A. A., Tverier, V. M., Nyashin, Y. I., Simanovskaya, E. Y., and Elovikova, A. N. (2008). Formation and Elaboration of the Classical Theory of Bone Tissue Structure Description. Russ. J. Biomech. 12 (1), 66–85.

Google Scholar

Kichenko, A. A., Tverier, V. M., Nyashin, Y. I., and Zaborskikh, A. A. (2011). Experimental Determination of the Fabric Tensor for Cancellous Bone Tissue. Russ. J. Biomech. 15 (4), 66–81.

Google Scholar

Kuchumov, A. G., and Selyaninov, A. (2020). Application of Computational Fluid Dynamics in Biofluids Simulation to Solve Actual Surgery Tasks. Adv. Intell. Syst. Comput. 1018, 576–580. doi:10.1007/978-3-030-25629-6_89

CrossRef Full Text | Google Scholar

Maquer, G., Musy, S. N., Wandel, J., Gross, T., and Zysset, P. K. (2015). Bone Volume Fraction and Fabric Anisotropy Are Better Determinants of Trabecular Bone Stiffness Than Other Morphological Variablesffness Than Other Morphological Variables. J. Bone Miner. Res. 30 (6), 1000–1008. doi:10.1002/jbmr.2437

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcian, P., Florian, Z., Horačkova, L., Kaiser, J., and Borak, L. (2017). Microstructural FIfinite-Element Analysis of Influence of Bone Density and Histomorphometric Parameters on Mechanical Behavior of Mandibular Cancellous Bone Structure. Solid State Phenom 258, 362–365. doi:10.4028/www.scientific.net/SSP.258.362

CrossRef Full Text | Google Scholar

Marcián, P., Horáčková, J. L. J., ZikmundKaiser, T., Borák, L., Zikmund, T., and Borak, L. (2018). Micro Finite Element Analysis of Dental Implants under Different Loading Conditionsfinite Element Analysis of Dental Implants under Different Loading Conditions. Comput. Biol. Med. 96, 157–165. doi:10.1016/j.compbiomed.2018.03.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Marco, O., Sevilla, R., Zhang, Y., Ródenas, J. J., and Tur, M. (2015). Exact 3D Boundary Representation in Finite Element Analysis Based on Cartesian Grids Independent of the Geometryfinite Element Analysis Based on Cartesian Grids Independent of the Geometry. Int. J. Numer. Meth. Engng 103 (6), 445–468. doi:10.1002/nme.4914

CrossRef Full Text | Google Scholar

Marwa, F., Wajih, E. Y., Philippe, L., and Mohsen, M. (2018). Improved USCT of Paired Bones Using Wavelet-Based Image Processing. IJIGSP 10 (9), 1–9. doi:10.5815/ijigsp.2018.09.01

CrossRef Full Text | Google Scholar

Maslov, L. B. (2020). Biomechanical Model and Numerical Analysis of Tissue Regeneration within a Porous Scaffold. Mech. Sol. 55 (7), 1115–1134. doi:10.3103/S0025654420070158

CrossRef Full Text | Google Scholar

Maslov, L. B. (2017). Mathematical Model of Bone Regeneration in a Porous Implant. Mech. Compos. Mater. 53 (3), 399–414. doi:10.1007/s11029-017-9671-y

CrossRef Full Text | Google Scholar

Mithun, K. P. K., and Mohammad, M. R. (2014). Metal Artifact Reduction from Computed Tomography (CT) Images Using Directional Restoration Filter. IJITCS 6 (6), 47–54. doi:10.5815/ijitcs.2014.06.07

CrossRef Full Text | Google Scholar

Moriya, T., Roth, H. R., Nakamura, S., Oda, H., Nagara, K., Oda, M., et al. (2018). Unsupervised Segmentation of 3D Medical Images Based on Clustering and Deep Representation Learning. Prog. Biomed. Opt. Imaging - Proc. SPIE 10578, 1057820. doi:10.1371/journal.pone.0188717

CrossRef Full Text | Google Scholar

Nadal, E., Ródenas, J. J., Albelda, J., Tur, M., Tarancón, J. E., and Fuenmayor, F. J. (2013). Efficient Finite Element Methodology Based on Cartesian Grids: Application to Structural Shape Optimizationfficient FIfinite Element Methodology Based on Cartesian Grids: Application to Structural Shape Optimization. Abstract Appl. Anal. 2013, 1–19. doi:10.1155/2013/953786

CrossRef Full Text | Google Scholar

Prez, M., Vendittoli, P-A., Lavigne, M., and Nuo, N. (2014). Bone Remodeling in the Resurfaced Femoral Head: Effect of Cement Mantle Thickness and Interface Characteristic. Med. Eng. Phys. 36 (2), 185–195. doi:10.1016/j.medengphy.2013.10.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Rho, J. Y., Hobatho, M. C., and Ashman, R. B. (1995). Relations of Mechanical Properties to Density and CT Numbers in Human Bone. Med. Eng. Phys. 17 (5), 347–355. doi:10.1016/1350-4533(95)97314-f

PubMed Abstract | CrossRef Full Text | Google Scholar

Ridwan-Pramana, A., Marcián, P., Borák, L., Narra, N., Forouzanfar, T., and Wolff, J. (2017). Finite Element Analysis of 6 Large PMMA Skull Reconstructions: A Multi-Criteria Evaluation Approach. PLoS ONE 12, e0179325. doi:10.1371/journal.pone.0179325

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruess, M., Tal, D., Trabelsi, N., Yosibash, Z., and Rank, E. (2012). The Finite Cell Method for Bone Simulations: Verification and Validationfinite Cell Method for Bone Simulations: Verification and Validation. Biomech. Model. Mechanobiol. 11 (3-4), 425–437. doi:10.1007/s10237-011-0322-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Sachenkov, O., Hasanov, R., Andreev, P., and Konoplev, Y. (2016). Determination of Muscle Effort at the Proximal Femur Rotation Osteotomy. IOP Conf. Ser. Mater. Sci. Eng. 158 (1), 012079. doi:10.1088/1757-899x/158/1/012079

CrossRef Full Text | Google Scholar

Stock, S. R., Naik, N. K., Wilkinson, A. P., and Kurtis, K. E. (2002). X-ray Microtomography (microCT) of the Progression of Sulfate Attack of Cement Paste. Cement Concrete Res. 32 (10), 1673–1675. doi:10.1016/S0008-8846(02)00814-1

CrossRef Full Text | Google Scholar

Tveito, A., Jæger, K. H., Kuchta, M., Mardal, K.-A., and Rognes, M. E. (2017). A Cell-Based Framework for Numerical Modeling of Electrical Conduction in Cardiac Tissue. Front. Phys. 5, 48. doi:10.3389/fphy.2017.00048

CrossRef Full Text | Google Scholar

Vanlenthe, G., Hagenmüller, H., Bohner, M., Hollister, S., Meinel, L., and Müller, R. (2007). Nondestructive Micro-computed Tomography for Biological Imaging and Quantification of Scaffold-Bone Interaction In Vivo. Biomaterials 28 (15), 2479–2490. doi:10.1016/j.biomaterials.2007.01.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Viceconti, M., Qasim, M., Bhattacharya, P., and Li, X. (2018). Are CT-Based Finite Element Model Predictions of Femoral Bone Strengthening Clinically Useful?. Curr. Osteoporos. Rep. 16, 216–223. doi:10.1007/s11914-018-0438-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Yaikova, V. V., Gerasimov, O. V., Fedyanin, A. O., Zaytsev, M. A., Baltin, M. E., Baltina, T. V., et al. (2019). Automation of Bone Tissue Histology. Front. Phys. 7, 91. doi:10.3389/fphy.2019.00091

CrossRef Full Text | Google Scholar

Zienkiewicz, O. C., and Zhu, J. Z. (1987). A Simple Error Estimator and Adaptive Procedure for Practical Engineerng Analysis. Int. J. Numer. Meth. Engng. 24 (2), 337–357. doi:10.1002/nme.1620240206

CrossRef Full Text | Google Scholar