- 1Department of Mechanics, Mathematics and Management, Polytechnic University of Bari, Bari, Italy
- 2Soft Matter Science and Engineering Laboratory (SIMM), PSL Research University, UPMC Univ Paris 06, Sorbonne Universités, ESPCI Paris, CNRS, Paris, France
A closed-form solution for the adhesive contact of soft spheres of linear elastic material is available since 1971 thanks to the work of Johnson, Kendall, and Roberts (JKR). A similar solution for viscoelastic spheres is still missing, though semi-analytical and numerical models are available today. In this note, we propose a closed-form analytical solution, based on JKR theory, for the detachment of a rigid sphere from a viscoelastic substrate. The solution returns the applied load and contact penetration as functions of the contact radius and correctly captures the velocity-dependent nature of the viscoelastic pull-off. Moreover, a simple approach is provided to estimate the stick time, i.e., the delay between the time the sphere starts raising from the substrate and the time the contact radius starts reducing. A simple formula is also suggested for the viscoelastic pull-off force. Finally, a comparison with experimental and numerical data is shown.
1. Introduction
Velocity-induced increase of adhesion may be observed when detaching two viscoelastic media, due to their rate-dependent behavior (Baek et al., 2017, 2018; Violano and Afferrante, 2019a). Adhesion is of paramount importance in several applications. For example, in printing industry, kinetically controlled adhesion has been exploited to transfer solid print objects from one elastomeric stamp to another (Metil et al., 2006). In biomedical field, experimental investigations effectively provided the rate-dependence of adhesion of articular cartilage tissue over a wide range of unloading velocities (Han et al., 2020). In tapes industry, structural adhesives (Blackman et al., 2009) and pressure-sensitive adhesives (Villey et al., 2015) often show rate-dependent behavior. Moreover, in Goryacheva et al. (1996) and Menga et al. (2018) it has been shown that contact pressure and internal stress distributions are significantly affected by viscoelastic properties.
In the “basic” adhesive contact between a rigid sphere and an elastic soft half-space, analytical closed-form solution is available thanks to the work of Johnson, Kendall, and Roberts (JKR) (Johnson et al., 1971). JKR theory returns simple expressions relating applied load F, contact penetration δ, and contact radius a. A similar solution is not available in the viscoelastic case, and one must use numerical or semi-analytical approaches to deal with this problem.
Exploiting the analogy between the rupture of adhesive bond and crack propagation, Maugis and Barquins (MB) first studied the detachment of a sphere from a soft substrate (Maugis and Barquins, 1980). According to Gent and Schultz (GS) findings (Gent and Schultz, 1972), they assumed that viscous dissipation is mainly located in the vicinity of the contact line. In their experiments, MB measured a surface energy greater than the quasi-static value predicted by JKR theory.
Inspired by MB work, Muller (1999) proposed a semi-analytical approach, based on the numerical solution of a first order differential equation, to obtain the contact radius in terms of the penetration of the sphere in the half-space. More elaborated strategies were proposed in Greenwood and Johnson (1981), Barthel and Haiat (2002), Lin et al. (2002), and Haiat et al. (2003).
All above methods do not return simple relations between load, penetration and contact radius. Moreover, an immediate estimate of the pull-off force, i.e., the maximum tensile force required for detachment, is not possible. Here, we instead propose a closed-form analytical solution based on JKR theory. Simple expressions are derived for F(a) and δ(a). Furthermore, empirical formulas are obtained for pull-off force and stick-time, which is the delay between the time the sphere starts raising from the substrate and the time the contact radius starts reducing. The proposed solution is validated on experimental and numerical data.
2. Formulation
Figure 1 shows the geometry of the problem under investigation: a rigid sphere of radius R is pulled apart from a viscoelastic half-space at a driving velocity V.
Figure 1. The problem under investigation: a rigid sphere is pulled apart from a viscoelastic half-space.
For an elastic substrate, the applied load FE and the penetration δE can be determined in terms of the contact radius a by JKR theory (Johnson et al., 1971)
where E* is the equivalent elastic modulus and Δγ is the adiabatic surface energy, which depends on the adhesive properties of the contacting interfaces.
In the presence of a viscoelastic substrate, viscous dissipation occurs during detachment. Gent and Schultz (1972), in order to take into account such dissipation, introduced an effective velocity-dependent surface energy Δγeff. Maugis and Barquins (1978) and Charmet et al. (1999) observed that viscoelastic losses are proportional to the adiabatic work of adhesion Δγ and are only localized at the crack tip. Consequently, the dissipation function can be written in terms of proportionality of Δγ and a dimensionless function φ(aTV) of the contact line speed vc = −da/dt and of the temperature through the William-Landel-Ferry (WLF) factor aT (Williams et al., 1955). Such dissipation function is characteristic of the viscoelastic material and is independent of the geometry of contact. These observations can be traduced in the following equation (Gent and Schultz, 1972; Maugis and Barquins, 1978)
whose application entails “that gross displacements are purely elastic, with Δγeff computed from the relaxed elastic modulus E and that the frequency dependence of E only appears at the crack tip where deformation velocities are high” (Charmet et al., 1999).
Therefore, the loss factor Re(E)/Im(E) and its dependence on the frequency are taken into account in the function φ (Ramond et al., 1985). Specifically, for elastomers, the function φ can be expressed in terms of a power law of the contact line velocity
where v* takes account of the dependence on the temperature.
Finally, substituting (4) in (3),
In the above equation, the viscoelastic constants v* and n can be measured experimentally (Gent and Schultz, 1972; Muller, 1999; Violano and Afferrante, 2019a). Notice the exponent n is not a universal number but takes different values depending on the viscoelastic modulus (Lorenz et al., 2013). Moreover, we have to mention that Persson et al. developed a theoretical approach to relate the dissipation function φ(aTvc) to the bulk viscoelastic modulus E(ω) (Carbone and Persson, 2005; Persson and Brener, 2005; Persson et al., 2005). In this regard, we could calculate the effective surface energy Δγeff from the bulk parameters and then find the values of v* and n of Equation (5). However, to do this, we should accurately know E(ω) in a wide interval of frequencies ω (ranging from the rubbery region to the glassy one), which is not the case.
To describe the detachment behavior of the sphere, one should know the exact law vc(a). As the pulling velocity is V = −dδ/dt, it is straightforward to observe that vc = V · da/dδ. The derivative da/dδ can be numerically calculated by solving the differential equation given in Muller (1999). Alternatively, we can estimate da/dδ from JKR solution, so that
Of course, we expect that such approximation works well at low pulling velocities V and progressively gets worse increasing V.
Therefore, inspired by a similar approach proposed in Barthel and Roux (2000), Equations (1) and (2) can be then used to determine the applied load F and the penetration δ in the viscoelastic substrate by replacing Δγ with the effective surface energy Δγeff
Notice (7) and (8) return JKR solution when viscous effects are neglected.
Introducing the following dimensionless quantities
the above relations can be rewritten as
being and .
2.1. The Stick Zone
If we denote with amax the contact radius reached at the end of the loading phase, the corresponding penetration δmax and compressive force Fmax can be calculated by Equations (1) and (2).
Many experimental (Deruelle et al., 1998; Morishita et al., 2008; Baek et al., 2017, 2018; Violano et al., 2020a) and numerical (Lin et al., 2002; Haiat et al., 2003) works showed the contact radius amax remains almost constant (contact line velocity vc ≈ 0) during the initial phase of the unloading process. Only when a critical penetration δc is reached, the contact radius starts to decrease and consequently vc increases. The zone where the contact radius is constant and the penetration reduces from the initial value δmax to δc (see Figure 2) is usually identified as stick zone. The corresponding time interval is the stick time. This sticking effect is one of the main causes of adhesion hysteresis (Chaudhury and Whitesides, 1991; Violano and Afferrante, 2019a), which is the difference between the work spent bringing into contact two media and the one required for detaching them.
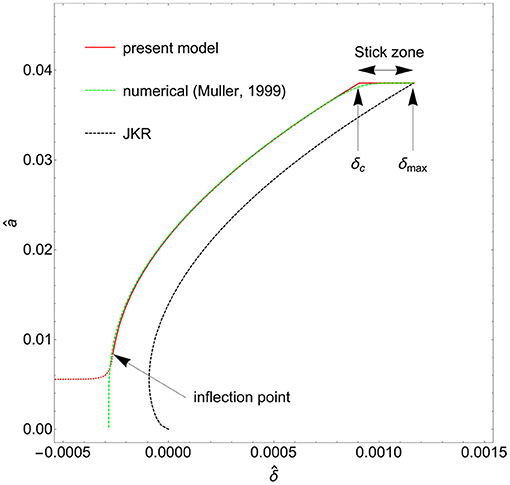
Figure 2. The dimensionless contact radius â = a/R in terms of the dimensionless penetration . Curves are shown for JKR theory (black dashed line), Muller's numerical model (green dashed line), and proposed model (red solid line).
The origin of the stick zone was explained by Maugis and Barquins (1980) exploiting an analogy with the linear elastic fracture mechanics. In the framework of the detachment of a circular flat punch from a viscoelastic substrate, they showed that the spontaneous rupture of the contact occurs when the energy release rate exceeds the surface energy. This occurs when the penetration is reduced at a critical value δc.
To include the effect of sticking in our solution, we observe that in the stick zone the problem resembles the detachment of a circular flat punch of radius amax. As a result, we can assume Equations (10) and (11) working for , and the flat punch solution (12) working for , i.e.,
The critical penetration is hence obtained substituting âmax in (11). As a result, the stick zone and stick time can be easily estimated as
where .
2.2. Pull-Off
In the elastic case, contact break-up occurs at if the process of detachment is displacement controlled. In the presence of dissipation, Figure 2 shows that a very good estimate of the pull-off point can be empirically obtained at the inflection point of the red curve where
Thus solution of Equation (15) returns an estimate of the contact radius at pull-off aVD, while Equation (8) allows to calculate the critical penetration at the contact break-up.
Under load controlled conditions, JKR theory predicts contact rupture at . Similarly, the contact radius at pull-off aVL in the viscoelastic case can be calculated recalling that
The pull-off force, i.e., the maximum tensile force required to detach the sphere, is, therefore (see also Lorenz et al., 2013),
To obtain a closed-form expression for aVL, we consider the zeroth order expansion of (5) around aEL, and then solve Equation (16) obtaining, in terms of the dimensionless quantities,
Finally, the pull-off force is
3. Results
In this section, the theoretical predictions are compared with experimental data and numerical calculations in terms of contact radius a, pulled force F, and penetration δ.
Experimental data are taken from Violano et al. (2020a), where JKR-like tests were carried out between an optical spherical glass lens with radius of curvature R = 103.7 mm and smooth rubber substrates made of PolyDiMethylSiloxane (PDMS) silicones (more details on the experimental set-up can be found in that work).
Loading tests were performed increasing the force step by step and maintaining the contact at each step for a long time to ensure complete relaxation of the viscoelastic material (as suggested in Acito et al., 2019).
Unloading tests were carried out starting from a maximum load Fmax = 0.02 N and for different driving velocities V = 0.2, 2, 20 μm/s. Moreover, three contact realizations were considered for each velocity. Experimental data of unloading tests were also used to calculate the viscoelastic parameters n = 0.25 and v* = 1.08281 × 10−6 m/s by fitting with Equation (5) the values of the quantity (Δγeff − Δγ)/Δγ.
The equivalent elastic modulus (E* = 0.83 MPa) and the adiabatic surface energy (Δγ = 37 mJ/m2) were obtained by fitting, with JKR model (Johnson et al., 1971), the contact radius vs. load data of the loading curve.
The actual pulling velocity Vact of the lens was found to be quite different from the imposed value V as the spherical indenter was fixed to a motorized vertical translation stage by means of a double cantilever beam of finite stiffness. For this reason, a laser displacement sensor was used to monitor the actual position of the lens and measure Vact. Furthermore, the contact line velocity vc = −da/dt was also monitored since pictures of contact radius a and corresponding time steps t were collected during unloading.
Therefore, the law vc(a) required to evaluate the velocity-dependent surface energy Δγeff given in Equation (5) can be determined by fitting the experimental data relating vc with a. Alternatively, when experimental data are not available, vc can be estimated by Equation (6).
Figure 3 shows the dimensionless contact line velocity as a function of the dimensionless contact radius â at different pulling velocities. Markers refer to experimental measurements, while solid lines to Equation (6) with V replaced with the actual pulling velocity Vact.
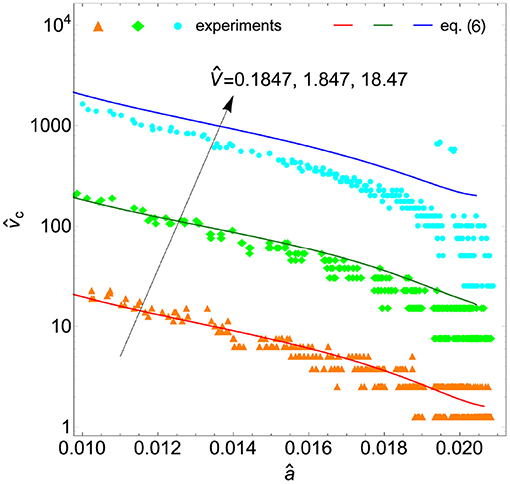
Figure 3. The dimensionless contact line velocity as a function of the dimensionless contact radius â for different pulling velocities 18.47 (V = 0.2, 2, 20 μm/s). Markers denote experimental data, while solid lines refer to the prediction given by Equation (6) with the actual pulling velocity Vact.
The idea to derive the contact line velocity from JKR solution seems to work well enough as the agreement with experimental results is acceptable in the whole range of variation of the contact radius, although at the highest pulling velocity our approximation is less accurate.
Figures 4A,B show the curves relating the dimensionless contact radius â, contact penetration , and contact force for different driving velocities . Markers denote experimental data obtained from three replications of unloading tests performed for each value of .
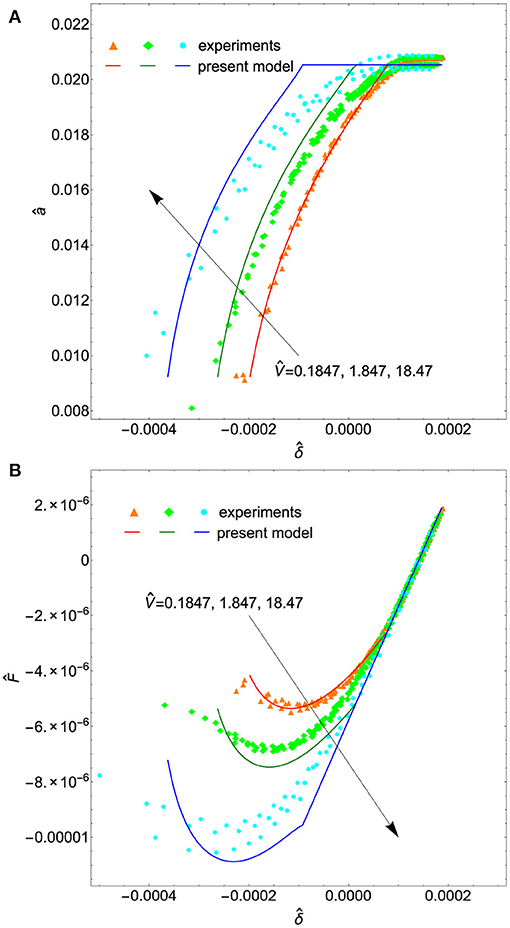
Figure 4. Dimensionless contact radius â (A) and contact force (B) as functions of the dimensionless approach for different driving velocities 1.847, 18.47 (V = 0.2, 2.0, 20 μm/s). Experimental data are plotted with colored markers, while solid lines are the theoretical predictions.
Theoretical predictions (solid lines) almost agree with experimental outcomes even if small deviations occur at the highest velocity, where the analytical solution seems to overestimate viscoelastic dissipation as Equation (6) gives a slightly larger contact line velocity.
The pull-off force , normalized with respect to JKR value (), is shown in Figure 5 in terms of the driving velocity . Predictions of the present model (red circles) almost agree with the experimental values. Moreover, the approximate formula (19) (black dashed line) works equally well even if we use the imposed value of the driving velocity V and not the actual one Vact. In the range of velocities here considered [which are typical of adhesive contact experiments (Guduru and Bull, 2007; Baek et al., 2017)], differences at the higher velocities between analytical predictions and experimental data are of the same order of experimental scatter.
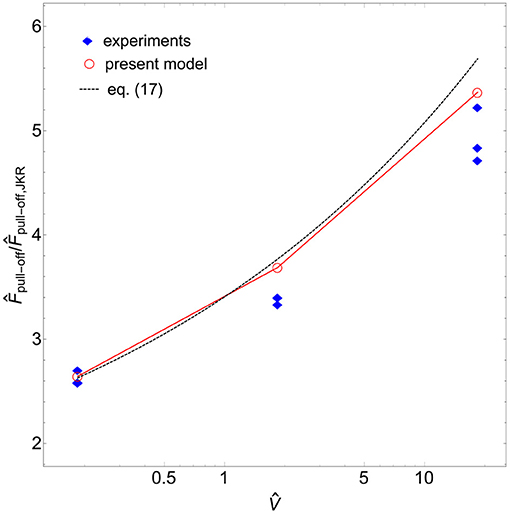
Figure 5. The predicted pull-off force , normalized with respect to JKR's one (), as a function of the dimensionless driving velocity . Blue diamonds refer to experimental data, while red circles to theoretical predictions. Black dashed line denotes the predictions of the empirical Equation (19).
Figure 6 shows a comparison of the proposed analytical solution with the numerical results by Muller's model (Muller, 1999), which showed to be quite accurate in predicting the pull-off process of viscoelastic spheres (see Violano and Afferrante, 2019a; Violano et al., 2020a). The curves are obtained assuming the same values of the parameters (R = 103.7 mm, Δγ = 37 mJ/m2, E* = 0.83 MPa, n = 0.25, and v* = 1.08281 × 10−6 m/s) but changing the maximum force reached at the end of the loading phase, which is assumed to be performed at sufficiently slow velocity to make working JKR theory.
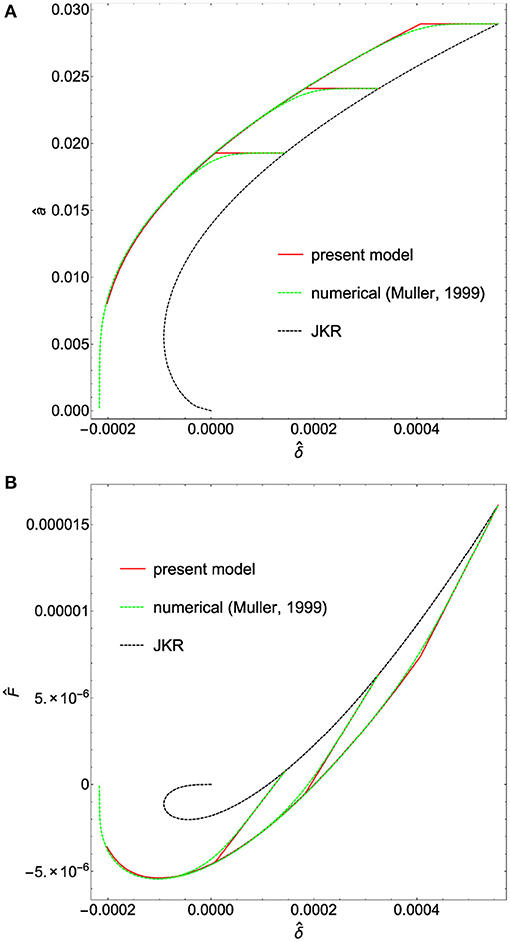
Figure 6. Dimensionless contact radius â (A) and contact force (B) as functions of the dimensionless penetration for (V= 0.2 μm/s). Results are given for different initial points of unloading. Loading curve (blach dashed line) is obtained with JKR's model, while unloading curves are obtained with the proposed solution (red solid line) and Muller's numerical one (green dashed line).
Specifically, Figures 6A,B show the dependence of the contact radius and contact force on the contact penetration for different values of the maximum force and (V = 0.2 μm/s). Black dashed lines refer to the loading phase and are obtained by using JKR theory, while red solid and green dashed lines refer to the unloading phase. The former are obtained through Equations (10) and (11), the latter by numerically integrating the differential equation proposed in Muller (1999). Notice our predictions closely match the numerical ones.
Moreover, we observe that the stick zone, i.e., the zone at constant contact radius, is almost independent of the point at which unloading starts in agreement with experimental findings given in Baek et al. (2017, 2018) and Deruelle et al. (1998). Finally, Figure 6B shows all curves collapse on the same path entailing that the pull-off force is independent of the initial point of unloading.
4. Conclusions
In this work, we propose a simple analytical solution for the problem of detachment of a rigid sphere from a viscoelastic substrate. The solution is formulated under the assumption that viscoelastic dissipation is localized at the edge of the contact line. Specifically, closed-form equations are proposed for pull-off force and stick zone. The model is based on the assumption the contact line velocity vc can be derived from JKR theory. An extensive comparison with experimental data and numerical calculations shows such assumption works quite well in a wide range of contact radii and pulling velocities.
The proposed solution could be exploited in multiasperity models (see, e.g., Afferrante et al., 2012, 2018; Violano and Afferrante, 2019b; Violano et al., 2020b) to take into account dissipation effects occurring during the detachment of rigid spheres from soft rough substrates.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
GV and LA designed the theoretical model. GV and AC elaborated the experimental data. GV wrote the first draft of the manuscript. LA wrote the final version of the manuscript. All authors equally contributed in revising the final version.
Funding
This work was supported by the project FASTire (Foam Airless Spoked Tire): Smart Airless Tyres for Extremely-Low Rolling Resistance and Superior Passengers Comfort funded by the Italian MIUR Progetti di Ricerca di Rilevante Interesse Nazionale (PRIN) call 2017—grant no. 2017948FEN.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
LA and GV acknowledge support from the Italian Ministry of Education, University and Research (MIUR) under the program Departments of Excellence (L.232/2016).
References
Acito, V., Ciavarella, M., Prevost, A. M., and Chateauminois, A. (2019). Adhesive contact of model randomly rough rubber surfaces. Tribol. Lett. 67:54. doi: 10.1007/s11249-019-1164-9
Afferrante, L., Bottiglione, F., Putignano, C., Persson, B. N. J., and Carbone, G. J. T. L. (2018). Elastic contact mechanics of randomly rough surfaces: an assessment of advanced asperity models and Persson's theory. Tribol. Lett. 66, 1–13. doi: 10.1007/s11249-018-1026-x
Afferrante, L., Carbone, G., and Demelio, G. (2012). Interacting and coalescing Hertzian asperities: a new multiasperity contact model. Wear 278, 28–33. doi: 10.1016/j.wear.2011.12.013
Baek, D., Hemthavy, P., Saito, S., and Takahashi, K. (2017). Evaluation of energy dissipation involving adhesion hysteresis in spherical contact between a glass lens and a PDMS block. Appl. Adhes. Sci. 5, 1–11. doi: 10.1186/s40563-017-0082-z
Baek, D., Saito, S., and Takahashi, K. (2018). Estimating work of adhesion using spherical contact between a glass lens and a PDMS block. J. Adhes. Sci. Technol. 32, 158–172. doi: 10.1080/01694243.2017.1343519
Barthel, E., and Haiat, G. (2002). Approximate model for the adhesive contact of viscoelastic spheres. Langmuir 18, 9362–9370. doi: 10.1021/la025959+
Barthel, E., and Roux, S. (2000). Velocity-dependent adherence: an analytical approach for the JKR and DMT models. Langmuir 16, 8134–8138. doi: 10.1021/la000474b
Blackman, B. R. K., Kinloch, A. J., Sanchez, F. R., Teo, W. S., and Williams, J. G. (2009). The fracture behaviour of structural adhesives under high rates of testing. Eng. Fract. Mech. 76, 2868–2889. doi: 10.1016/j.engfracmech.2009.07.013
Carbone, G., and Persson, B. N. J. (2005). Crack motion in viscoelastic solids: the role of the flash temperature. Eur. Phys. J. E 17, 26–281. doi: 10.1140/epje/i2005-10013-y
Charmet, J. C., Vallet, D., and Barquins, M. (1999). “Chapter 3: Surface and bulk properties in adherence of elastic-viscoelastic solids,” in Microstructure and Microtribology of Polymer Surfaces, eds V. V. Tsukruk and K. J. Wahl (American Chemical Society). doi: 10.1021/bk-2000-074
Chaudhury, M. K., and Whitesides, G. M. (1991). Direct measurement of interfacial interactions between semispherical lenses and flat sheets of poly (dimethylsiloxane) and their chemical derivatives. Langmuir 7, 1013–1025. doi: 10.1021/la00053a033
Deruelle, M., Hervet, H., Jandeau, G., and Léger, L. (1998). Some remarks on JKR experiments. J. Adhes. Sci. Technol. 12, 225–247. doi: 10.1163/156856198X00074
Gent, A. N., and Schultz, J. (1972). Effect of wetting liquids on the strength of adhesion of viscoelastic material. J. Adhes. 3, 281–294. doi: 10.1080/00218467208072199
Goryacheva, I., Sadeghi, F., and Nickel, D. A. (1996). Internal stresses in contact of a rough body and a viscoelastic layered semi-infinite plane. J. Tribol. 118, 131–136. doi: 10.1115/1.2837068
Greenwood, J. A., and Johnson, K. L. (1981). The mechanics of adhesion of viscoelastic solids. Philos. Mag. A 43, 697–711. doi: 10.1080/01418618108240402
Guduru, P. R., and Bull, C. (2007). Detachment of a rigid solid from an elastic wavy surface: experiments. J. Mech. Phys. Solids 55, 473–488. doi: 10.1016/j.jmps.2006.09.007
Haiat, G., Huy, M. P., and Barthel, E. (2003). The adhesive contact of viscoelastic spheres. J. Mech. Phys. Solids 51, 69–99. doi: 10.1016/S0022-5096(02)00059-5
Han, G., Eriten, M., and Henak, C. R. (2020). Rate-dependent adhesion of cartilage and its relation to relaxation mechanisms. J. Mech. Behav. Biomed. Mater. 102:103493. doi: 10.1016/j.jmbbm.2019.103493
Johnson, K. L., Kendall, K., and Roberts, A. (1971). Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A Math. Phys. Sci. 324, 301–313. doi: 10.1098/rspa.1971.0141
Lin, Y. Y., and Hui, C. Y. (2002). Mechanics of contact and adhesion between viscoelastic spheres: an analysis of hysteresis during loading and unloading. J. Polym. Sci. B Polym. Phys. 40, 772–793. doi: 10.1002/polb.10140
Lorenz, B., Krick, B. A., Mulakaluri, N., Smolyakova, M., Dieluweit, S., Sawyer, W. G., et al. (2013). Adhesion: role of bulk viscoelasticity and surface roughness. J. Phys. Condens. Matter 25:225004. doi: 10.1088/0953-8984/25/22/225004
Maugis, D., and Barquins, M. (1978). Fracture mechanics and the adherence of viscoelastic bodies. J. Phys. D Appl. Phys. 11, 1989–2023. doi: 10.1088/0022-3727/11/14/011
Maugis, D., and Barquins, M. (1980). “Fracture mechanics and adherence of viscoelastic solids,” in Adhesion and Adsorption of Polymers, ed L.-H. Lee (Boston, MA: Springer), 203–277. doi: 10.1007/978-1-4613-3093-6_17
Meitl, M. A., Zhu, Z. T., Kumar, V., Lee, K. J., Feng, X., Huang, Y. Y., et al. (2006). Transfer printing by kinetic control of adhesion to an elastomeric stamp. Nat. Mater. 5, 33–38. doi: 10.1038/nmat1532
Menga, N., Afferrante, L., Demelio, G. P., and Carbone, G. (2018). Rough contact of sliding viscoelastic layers: numerical calculations and theoretical predictions. Tribol. Int. 122, 67–75. doi: 10.1016/j.triboint.2018.02.012
Morishita, Y., Morita, H., Kaneko, D., and Doi, M. (2008). Contact dynamics in the adhesion process between spherical polydimethylsiloxane rubber and glass substrate. Langmuir 24, 14059–14065. doi: 10.1021/la8024155
Muller, V. M. (1999). On the theory of pull-off of a viscoelastic sphere from a flat surface. J. Adhes. Sci. Technol. 13, 999–1016. doi: 10.1163/156856199X00479
Persson, B. N. J., Albohr, O., Heinrich, G., and Ueba, H. (2005). Crack propagation in rubber-like materials. J. Phys. Condens. Matter 17, R1071–R1142. doi: 10.1088/0953-8984/17/44/R01
Persson, B. N. J., and Brener, E. A. (2005). Crack propagation in viscoelastic solids. Phys. Rev. E 71:036123. doi: 10.1103/PhysRevE.71.036123
Ramond, G., Pastor, M., Maugis, D., and Barquins, M. (1985). Mesure du module complexe par poinçonnement. Cahiers Groupe Franç. Rhéol. 6, 3–3.
Villey, R., Creton, C., Cortet, P. P., Dalbe, M. J., Jet, T., Saintyves, B., et al. (2015). Rate-dependent elastic hysteresis during the peeling of pressure sensitive adhesives. Soft Matter 11, 3480–3491. doi: 10.1039/C5SM00260E
Violano, G., and Afferrante, L. (2019a). Adhesion of compliant spheres: an experimental investigation. Proc. Struct. Integr. 24, 251–258. doi: 10.1016/j.prostr.2020.02.022
Violano, G., and Afferrante, L. (2019b). Modeling the adhesive contact of rough soft media with an advanced asperity model. Tribol. Lett. 67, 1–7. doi: 10.1007/s11249-019-1232-1
Violano, G., Chateauminois, A., and Afferrante, L. (2020a). Rate-dependent adhesion of viscoelastic contacts. Part I: contact area and contact line velocity within model multi-asperity contacts with rubber. arXiv 2012.07779.
Violano, G., Chateauminois, A., and Afferrante, L. (2020b). Rate-dependent adhesion of viscoelastic contacts. Part II: numerical model and hysteresis dissipation. arXiv 2012.07799.
Keywords: rate-dependent adhesion, viscoelasticity, JKR theory, soft matter, pull-off force
Citation: Violano G, Chateauminois A and Afferrante L (2021) A JKR-Like Solution for Viscoelastic Adhesive Contacts. Front. Mech. Eng. 7:664486. doi: 10.3389/fmech.2021.664486
Received: 05 February 2021; Accepted: 18 March 2021;
Published: 13 April 2021.
Edited by:
Martin H. Müser, Saarland University, GermanyReviewed by:
Yulia Makhovskaya, Institute for Problems in Mechanics (RAS), RussiaLinmao Qian, Southwest Jiaotong University, China
Copyright © 2021 Violano, Chateauminois and Afferrante. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guido Violano, Z3VpZG8udmlvbGFubyYjeDAwMDQwO3BvbGliYS5pdA==
 Guido Violano
Guido Violano Antoine Chateauminois2
Antoine Chateauminois2 Luciano Afferrante
Luciano Afferrante