- 1Ray W. Herrick Laboratories, Department of Mechanical Engineering, Purdue University, West Lafayette, IN, United States
- 2Cummins Inc., Columbus, IN, United States
This paper outlines a novel sensor selection and observer design algorithm for linear time-invariant systems with both process and measurement noise based on H2 optimization to optimize the tradeoff between the observer error and the number of required sensors. The optimization problem is relaxed to a sequence of convex optimization problems that minimize the cost function consisting of the H2 norm of the observer error and the weighted l1 norm of the observer gain. An LMI formulation allows for efficient solution via semi-definite programing. The approach is applied here, for the first time, to a turbo-charged spark-ignited engine using exhaust gas circulation to determine the optimal sensor sets for real-time intake manifold burnt gas mass fraction estimation. Simulation with the candidate estimator embedded in a high fidelity engine GT-Power model demonstrates that the optimal sensor sets selected using this algorithm have the best H2 estimation performance. Sensor redundancy is also analyzed based on the algorithm results. This algorithm is applicable for any type of modern internal combustion engines to reduce system design time and experimental efforts typically required for selecting optimal sensor sets.
1 Introduction
The control of fuel and air in spark-ignited engines has increasingly become a challenge with the incorporation of turbo-charging, exhaust gas recirculation (EGR), valvetrain flexibility, and more stringent emission regulations. To enable effective stoichiometric air-to-fuel ratio control, the engine flow and composition must be accurately and robustly measured or estimated. The only viable option is to use algorithms to estimate the engine mass flow and composition. Five difficulties have to be taken into consideration for the engine air handling sensor and observer (i.e. estimator) design problem: 1) nonlinear system dynamics; 2) measurement uncertainties, including sensor delays and noise; 3) multivariate interactions; 4) engine variability for different operation conditions and 5) the trade-off between estimation accuracy and sensor costs.
Previous studies in the field of engine air handling system management have focused on the observer design based on pre-selected sensor sets (Wang, 2008; Simon and Garg, 2010; Chen and Wang, 2012; Rengarajan et al., 2018). However, considering the increasing complexity of today’s engine systems and sensor characteristics, the choice of optimal air handling sensor set is not obvious; and it can be time-consuming and error prone if ‘guess and check’ experimental or simulation approaches are used. With the increasing variety of available sensors, the possible combinations of sensors will grow quickly. Brute-force experimentation with different sensors is very expensive and time-consuming, and may need to be redone even when there are minor changes to the engine system or control strategies. In order to effectively solve the problem, an algorithm for optimal sensor selection and observer design for the engine air handling system is outlined and demonstrated in this paper.
As described in more detail in the following paragraphs, several mathematical methods have been developed to solve the sensor selection problem, including greedy algorithms and convex optimization. Greedy algorithms aim to find a global optimum by making the locally optimal choice at each stage. The solution computed by the greedy algorithm is not always globally optimal. Convex optimization problems have the property that any found local optimal will also be global. While most formulations are nonconvex, sometimes it is possible to convexify them with minimum or no impact on the solution to take advantage of the solution properties as well as of available solvers (Joshi and Boyd, 2008; Tropp, 2006; Luo et al., 2010).
Sensor selection methods have been applied to various areas. In Kalandros and Pao (1998), the authors proposed three sensor selection algorithms for signal target tracking problems based on different resource and performance metrics. In another paper Kalandros et al. (1999), the authors explored the use of randomization and a super-heuristic in multiple targets tracking problem to improve any given sensor set solution via random perturbation. That approach is more suitable for systems with little structure and for which the cost of solution evaluation is not high. In Hashemi et al. (2018), the authors studied a randomized greedy algorithm for near-optimal sensor scheduling in large-scale sensor networks. In Rao et al. (2015), a greedy algorithm based on two submodular cost functions, the weighted frame potential and the weighted log-det, was developed for the sensor selection problem in non-linear measurement models with additive normally distributed noise. Several sensor selection algorithms based on convex optimization or relaxation have also been applied to flexible structures. In Fardad et al. (2011), Münz et al. (2014), Zare and Jovanović (2018), and Dhingra et al. (2014), the weighed l1 norm (without considering measurement noise) or l2 norm of the observer gain was used to represent the sensor number, and minimized along with the H2 norm of the estimation error. The optimization problem was solved via SDP (Fardad et al., 2011; Münz et al., 2014), alternating direction method of multipliers (ADMM) (Zare and Jovanović, 2018) and proximal methods (Dhingra et al., 2014). In Chepuri and Leus (2014), several functions of the Cramer–Rao bound (CRB) were used as a performance measure and the sensor selection problem was formulated to minimize the CRB functions and a sparse selection vector. In Joshi and Boyd (2008), the authors computed the optimal sensor set among candidate linear measurements corrupted with normally distributed noises. The maximum-likelihood estimation errors were used as the performance evaluations.
In the application of engine sensor selection, methods include experimentation-based sensor selection and algorithm-based sensor selection. In Pekař et al. (2012), the best sensor configuration for a heavy-duty engine was found based on experimental results by testing each sensor design. In Mushini and Simon (2005), the authors implemented a sensor selection algorithm for aircraft gas turbine engine healthy parameter estimation by minimizing the cost function of the estimation error and financial cost via a greedy algorithm. In Suard et al. (2008), the authors determined the best sensor configurations among three candidate sensor configurations for air-fuel-ratio control in a spark ignited engine. Different controllers were designed for candidate sensor configurations. An objective function incorporating the overall system cost and controller performance as the optimization target was used, with solution via a genetic algorithm. In Palmer et al. (2018), the authors proposed a methodology for fault diagnosis sensor selection based on Ds optimal FDI test design that maximized the sensitivity of outputs to anticipated faults and applied it in a diesel engine air handling system. The problem was solved using a heuristic method.
In the work described here, a simultaneous, coupled sensor selection and observer design method for the air handling system of the turbo-charged SI engine with EGR is proposed. In a manner similar to the approach taken in (Fardad et al., 2011; Münz et al., 2014), the strategy uses H2 optimization and accounts for both process and measurement noise. The goal of this algorithm is to definitively, and accurately, determine the tradeoff between the necessary sensor number and the accuracy of intake manifold oxygen fraction estimation. The implemented cost function consists of the H2 norm of the observer error and the weighted l1 norm of the observer gain. The problem, once formulated, can be solved efficiently via semi-definite programming (SDP). After selecting the optimal sensor set, the algorithm computes the corresponding Kalman-filter gain based on the selected sensor set. A method to estimate the modeling errors based on the comparison of reference data and modeling data is also proposed in this paper, enabling the application of the sensor selection framework to physical systems.
The rest of the paper is organized as follows: The statement of the sensor selection problem and its convex formulation; The application of the algorithm on a spark-ignited (SI) engine for intake manifold burnt gas mass fraction estimation for medium/high-speed operating conditions; Conclusions; Future work.
2 Sensor Selection Algorithm Based on H2 Optimization
Considering the following linear continuous state space model:
with the state variables
A Luenberger observer then takes the form:
where
By introducing the following two matrices:
the weighted error z can be formulated as:
where the error system G is the transfer function matrix between
2.1 Cost Function
For MIMO systems, the H2 norm is the impulse-to-energy gain or steady-state variance of outputs in response to white noise (Arzelier, 2008). Therefore, by minimizing the H2 norm of the error system (4), the expected root-mean-square error (RMSE) of the observer in response to white noise input excitation is minimized. The H2 norm of the error system G in Eq. 4 is expressed as:
where
Considering the observer gain matrix L, the corresponding jth sensor measurement does not contribute to the state estimation results if every element in the jth column of L is zero. In this case, the absolute sum of the elements in jth column of L is also zero. The number of sensors can be reduced by minimizing the non-zero columns in L, which is the
In order to optimize the tradeoff between the observer estimation error and the number of required sensors, a cost function is defined as following:
where
2.2 H2 Norm of the Observer Error
From Peet (2016), for a LTI system with a transfer function
(1) A is Hurwitz and
(2) There exists a positive definite matrix P (i.e.,
where the symbol
By applying Eq. 7 to system (4), the optimization problem for the first target
The optimization target and the first constraint in (8) are bilinear matrix inequalities (BMI) and is thus not a convex optimization problem. Therefore, they need to be converted to linear matrix inequalities (LMI). A matrix
Via the Schur complement condition for positive semi-definiteness (Chong and Zak, 2013), the following two statements are equivalent:
(1) Symmetric matrix
(2)
To apply the Schur complement condition to the optimization target Eq. 8, we introduce a positive semi-definite matrix T, i.e.,
iff
The inequality in Eq. 11 can be rewritten as:
Therefore, the following statement holds if condition (10) meets:
Therefore, the optimization problem in (8) can be rewritten as:
where the root of
2.3 Weighted l1 Norm of the Observer Gain Matrix
The second optimization target
2.4 Optimization Problem
Using the lemma which is used and proved in Polyak et al. (2013): given a matrix
(1) The jth column of L is zero.
(2) The jth column of
Combine the above lemma with (14) and weighted
The optimization problem (15) can be solved by the CVX toolbox (Grant and Boyd, 2015) iteratively. At each iteration, the algorithm updates the weight factor
Ideally, the jth sensor signal is not utilized for the state estimation and should be removed if the jth column of the observer gain matrix L is zero (Münz et al., 2014). Similarly, for a properly scaled system, the signal from sensor(s) j with small
After computing the optimal sensor set, set α to 0 and remove the rows in C corresponding to unneeded sensors. Substitute
3 Algorithm Application on a Turbo-Charged SI Engine Model for Air Handling System Sensor Designs
In this section, the proposed sensor selection algorithm is applied to a turbo-charged SI engine utilizing EGR. The goal of the sensor design is to choose the optimal sensor combination for accurately estimating the intake manifold gas composition. More specifically, the desired outcome is to quickly be able to determine the tradeoff between estimated intake manifold gas composition estimation error and the number of sensors.
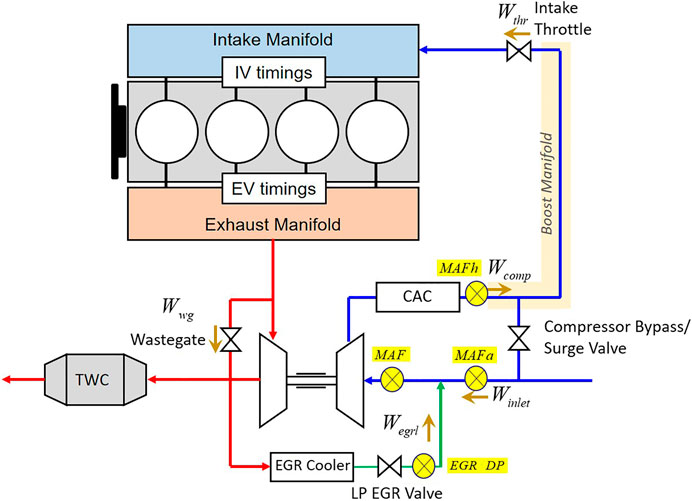
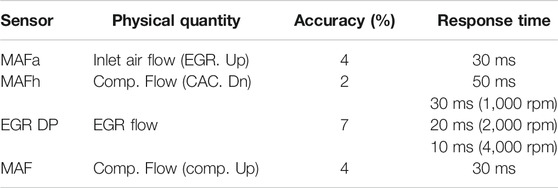
The engine architecture is shown in Figure 1. For illustrative purposes, four available sensors are considered as candidates as shown in Table 1. A mass air flow sensor for inlet air (MAFa) can be placed upstream of the air and low pressure (LP) EGR confluence point, to measure the inlet air. A mass air flow sensor for high pressure flow (MAFh) can be placed downstream of the charge air cooler (CAC) to measure the cooled compressor mass flow rate. An EGR delta pressure sensor (EGR DP) can be located in the LP EGR valve to measure the LP EGR mass flow rate. Another option is a mass air flow sensor (MAF) put downstream of the air and LP EGR confluence point, but before the compressor, to measure total compressor inlet mass flow rate.
3.1 Control-Oriented State-Space Engine Model
The model is a mean-value engine model based on Eriksson and Nielsen (2014), Kocher et al. (2012), Van Alstine et al. (2013), Stricker et al. (2014).
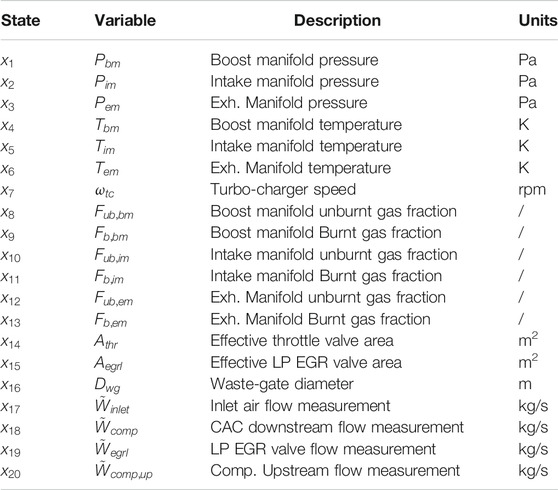
The model has 8 inputs, 1 disturbance input and 20 states as shown in Table 2–4, respectively. The nonlinear dynamic model equations can be written as follows and the detailed governing equations are listed in the Supplemental Material
Taking the actuator and sensor response times into consideration, states
where
In this engine model, the valve mass flow rate outputs are modeled by the following orifice equation (Eriksson and Nielsen, 2014):
where γ is the gas specific heat ratio,
The nonlinear model is linearized at the steady-state
The nominal model is linearized into the following format:
where
An observer is designed from the linear state-space model as follows. The state-space representation is a well-known practice to capture the system dynamics for its effective computation and real-time implementation. The observer is a linear dynamic system to correct the model estimation errors from measurements of the inputs and outputs of the real system.
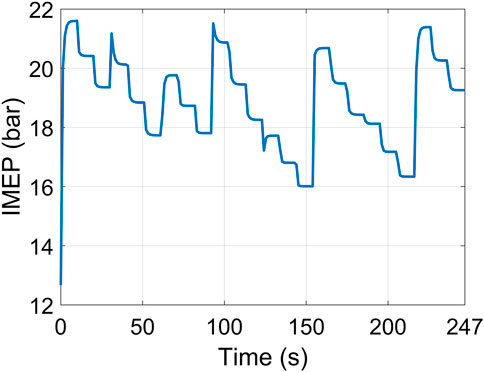
In simulation results that follow, the commanded engine throttle angle and number of firing cylinders are fixed as their linearization points. As studied in Rivas Perea (2016), a 11.5% brake˗specific fuel consumption (BSFC) reduction and 4.5% absolute indicated efficiency improvement can be achieved by introducing 10% cooled EGR in a 2L, 4-cylinder, turbo-charged, direct injected SI engine at 3000 RPM part load conditions. Considering the fact that EGR tolerance decreases with the increasing engine speed (Francqueville and Michel, 2014), for an engine operation speed range of 2,400–4000 RPM, the waste-gate and LP EGR valve are operated as shown in Figure 3, to vary the EGR ratio within 1.5–11%, which is a helpful level for the SI engine to improve fuel efficiency and keep combustion stability. Figure 4 shows the indicated mean effective pressure (IMEP) of the engine for the drive cycle (per Figure 3), which demonstrates the implementation of the proposed sensor selection algorithm for medium/high-speed operating conditions.
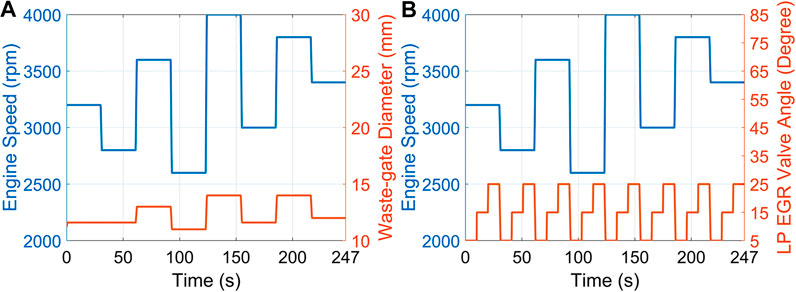
FIGURE 3. Engine operation conditions (A): engine speed and waste-gate (B): engine speed and LP EGR valve.
3.2 Unknown Disturbance
The process noise
To implement the proposed sensor selection algorithm, the actual system is expressed as a linear state-space model with uncertainty represented by additive errors:
where w is zero-mean unitary white noise and
The modeling error
where the values of the variables (
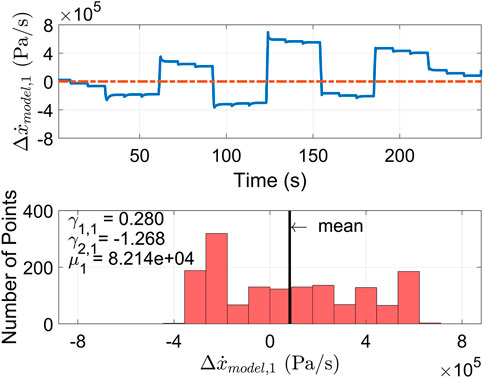
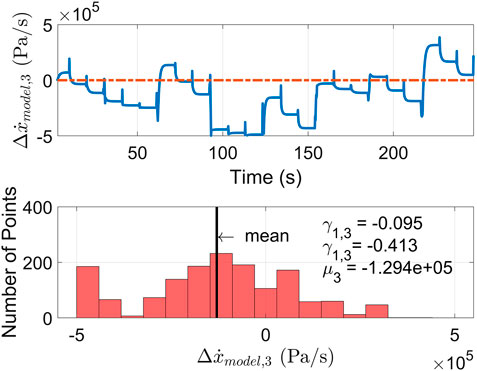
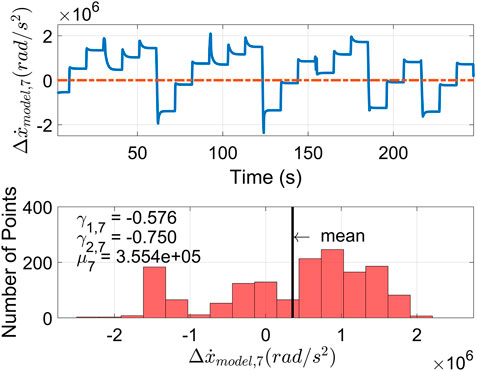
Figures 5–7 show the unknown disturbance plots for boost manifold pressure x1, exhaust manifold pressure x3 and turbocharger speed x7, respectively. The errors
An initial estimation of the process noise is the standard deviation of
3.2.1 Skewness Correction for Unknown Disturbance Estimation
The skewness
where
where N is the number of sampled points.
The positive skewness values mean that the data is skewed to the right (right-tail), and negative values suggest skewing to the left (left-tail) (Blanca et al., 2013). The larger the absolute skewness value is, the more significant the asymmetry is. For the states where the error
For the states where the error
3.2.2 Kurtosis Correction for Unknown Disturbance Estimation
The excess kurtosis
For the states which have negative excess kurtosis, the unknown disturbances have more data distributed outside the region of the peak than a normal distribution. The more negative the excess kurtosis is, the more outliers the distributions will have. When the excess kurtosis is large, Eqs 25, 26 without considering the extreme error distributions may not be a proper way to estimate the unknown disturbance. Therefore, a correction is made to the unknown disturbance estimations of the states which have excess kurtosis lower than
where
For the states
3.3 Measurement Noise
The diagonal measurement noise covariance matrix H is defined as:
where sensor accuracy data comes from Table 1 and
3.4 Sensor Selection Results
The sensor selection algorithm is applied to the scaled linear system. This is to eliminate the effect of magnitude differences of measurements.
Table 5 shows the optimal sensor set computed by the sensor selection algorithm (per Section 2) for different sensor number constraints. The iterative parameter ɛ is set as
where
The algorithm identifies the EGR DP sensor as the best sensor if only one single can be used. When two sensors are used, the optimal sensor set becomes EGR DP and MAFa, which measures the inlet air mass flow rate before the EGR joint (per Figure 1). The optimal three-sensor set combines EGR DP, MAFa and MAFh.
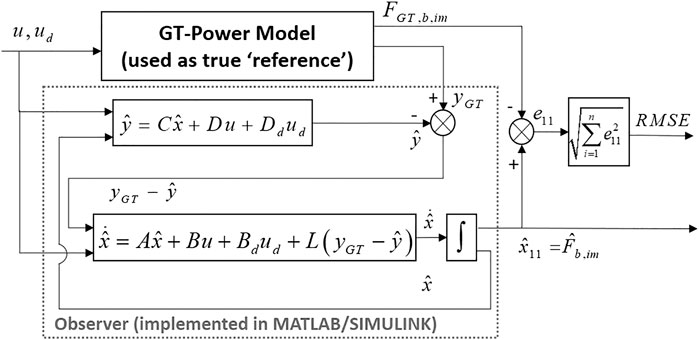
Different sensor sets with their corresponding observers are tested on the reference engine model in GT-Power. The four candidate sensors (per Table 1 and Figure 1) are placed in the GT-Power model. Per Table 1 data, these four GT-Power outputs are filtered with first-order functions described in Eq. 17 and corrupted by measurement noise before being sent to the observers to account for sensor noise. The GT-Power and observer simulation structure is shown in Figure 8. The observer gain for each sensor set is computed by the optimization (15) with
3.4.1 Single Sensor Sets
Figure 9 shows the estimation results of intake manifold burnt gas mass fraction when using different single sensor sets. As shown in Figure 9A, the EGR DP sensor has the most accurate estimation results at every step. Considering the overall estimation performance, the EGR DP sensor is the most accurate single-sensor option since it has the smallest root-mean-square error (RMSE), 0.498%, over the entire simulation. Without using any sensor, the maximum absolute estimation error is 1.744%. With the computed optimal sensor EGR DP, the maximum error is reduced to 1.014%, which is a 42% improvement compared to the model-only estimated result. The maximum errors for single MAFa sensor, MAFh sensor and MAF sensor are 1.684, 1.724 and 1.724%, respectively. Figure 9B shows the transient tracking performance of intake manifold burnt gas mass fraction when using different single sensor sets. Per Figure 9B, EGR DP sensor has the best tracking performance during the transient change. MAFa sensor is slightly better than MAFh sensor and MAF sensor. Even though the upstream compressor flow sensor MAF has a shorter response time than the downstream compressor flow sensor MAFh (per Table 1), there is few difference between the tracking transient performance of these two sensors (per Figure 9B).
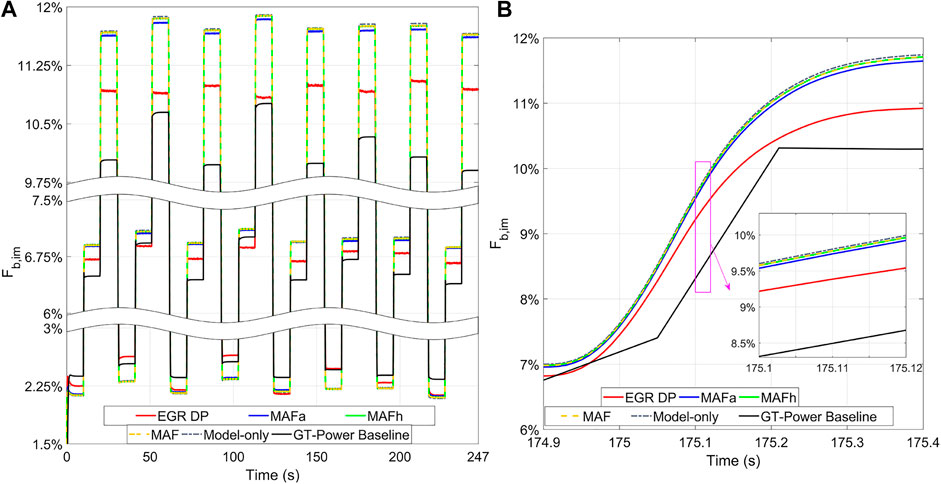
FIGURE 9. Intake manifold burnt gas mass fraction estimation when only using one sensor (A): the entire drive cycle (B): transient performance (500 ms zoomed).
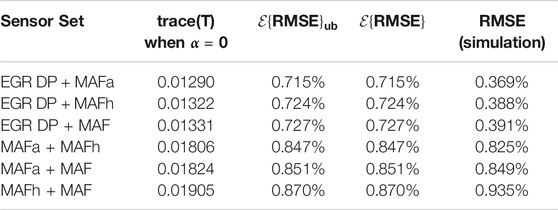
As shown in Table 6, the RMSE for a single MAFa sensor, a single MAFh sensor and a single MAF sensor are 0.909, 0.935 and 0.935%, respectively. This indicates that if the EGR DP sensor fails, the next sensor the engine should select is the MAFa sensor based on their trace (T) and
Figure 10 shows the histograms of different single sensor sets’ estimation errors. Compared to the optimal sensor EGR DP, the error distributions of the other three sensors are more spread out.
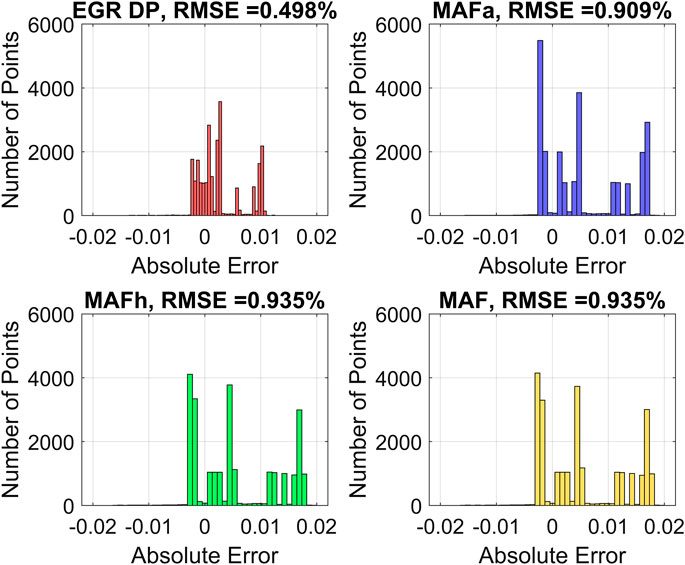
FIGURE 10. Histograms of Intake manifold burnt gas mass fraction estimation error when only using one sensor.
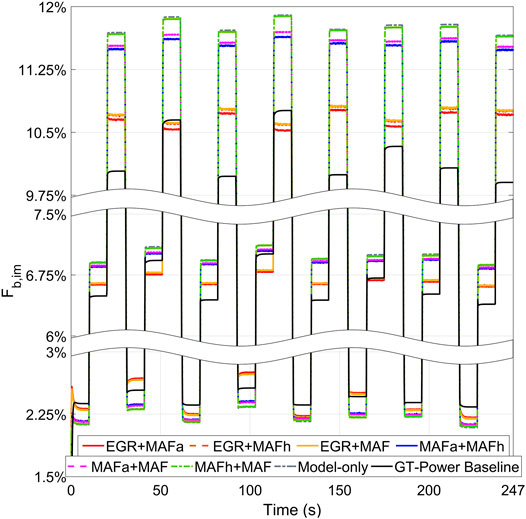
3.4.2 Two-Sensor Sets
The optimal two-sensor set computed by the sensor selection algorithm (per Section 2) is the combination of the EGR DP and MAFa sensors. This is verified in the coupled GT-Power/Observer simulation (per Figure 8). As shown in Figure 11, the computed optimal sensor set has the smallest estimation error for almost every step. Comparing the overall estimation performance of the optimal sensor set with the other five combinations, the optimal one has the lowest RMSE. With the computed optimal sensor set, the maximum error is reduced to 0.754%, which is 57% improvement compared to the model estimated result. The maximum estimation error is 0.794% for the combination of EGR DP sensor and upstream compressor flow sensor MAFh, and is 0.804% for the combination of EGR DP sensor and downstream compressor flow sensor MAF. For the combinations of MAFa sensor + MAFh sensor, MAFa sensor + MAF sensor, the maximum estimation errors are both 1.564 and 1.594%. When only two compressor flow sensors are used, the maximum error is up to 1.724%.
In Table 7 and Figure 12, the simulated RMSE for different two-sensor set combinations monotonically increases with increasing
Figure 13 shows the histograms of different two-sensor combinations estimation errors. As shown, the best three two-sensor combinations have the estimation errors distributions closer to 0.
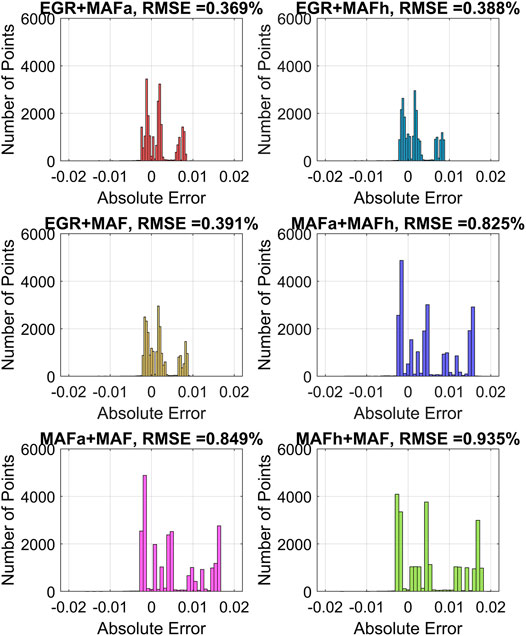
FIGURE 13. Histograms of intake manifold burnt gas mass fraction estimation error when using two sensors.
3.4.3 Optimal Sensor Sets
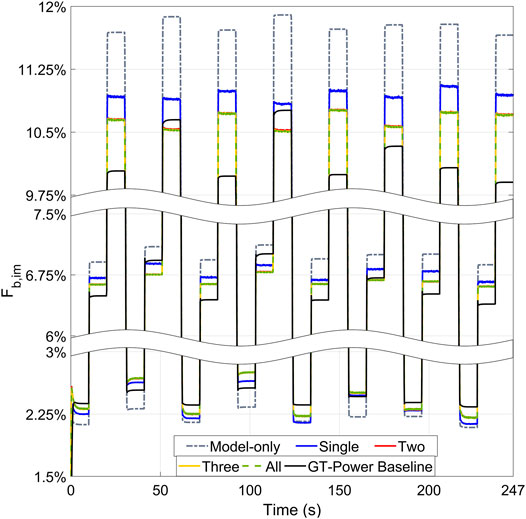
Figure 14 show the estimation results of intake manifold burnt gas mass fraction
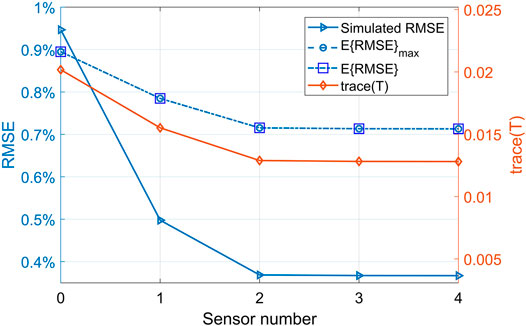
The sensor selection results indicates that though increasing sensor number reduces RMSE, the added sensor(s) brings in very small improvements of the estimation performance when number of sensors is higher than two. Based on the estimation error requirement, it may be worth using a single EGR DP sensor or adding a second sensor MAFa in addition to a single EGR DP sensor, but it may not be worth spending more money on adding the third or fourth sensor for the intake manifold gas composition estimation.
Figure 16 shows the histograms of different optimal sensor combinations estimation errors. It can be seen that with the increasing of sensor number, the RMSE distribution is narrowed down and has smaller peaks at large errors.
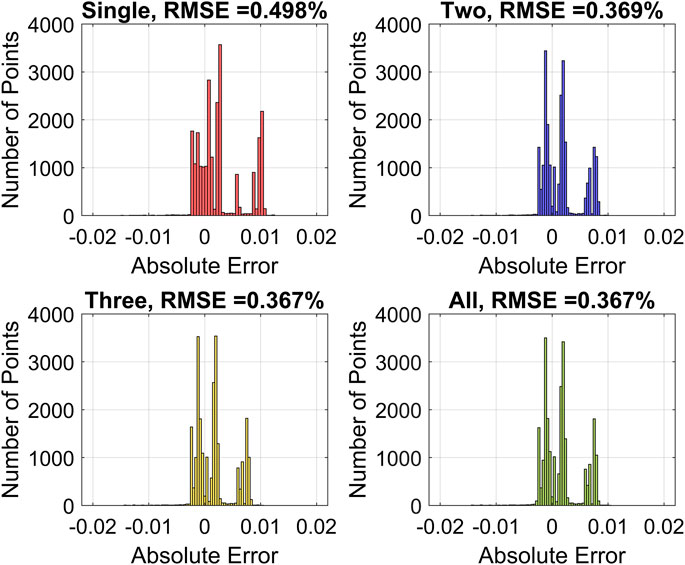
FIGURE 16. Histograms of intake manifold burnt gas mass fraction estimation error when using optimal sensor sets.
3.4.4 Additional Discussion
The difference between the expected RMSE
4 Conclusion
This paper outlines a sensor selection and observer deign algorithm based on H2 optimization while considering process and measurement noise. The approach is (1) implemented to an advanced turbo-charged spark-ignited engine architecture using exhaust gas circulation; and (2) validated on a high fidelity engine simulation in GT-Power. The objective of the sensor selection + observer design algorithm is to minimize the estimation error and the required sensor numbers. The optimization problem is convexified and solved via SDP. A method to estimate the unknown model uncertainties was also developed. The high fidelity simulation results verified that the optimal sensor sets computed by the algorithm had the best estimation performances. Sensor redundancy was also analyzed based on the computation results. This algorithm reduces the computation time and experimental efforts of selecting optimal sensor sets.
5 Future Work
The future work of this algorithm study can involve the estimation of other engine key parameters and observer designs; other engine operation conditions analysis.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
XZ and GS developed the theory, performed the computations and planned the simulations. XZ carried out the simulations. XZ and GS wrote the manuscript with support from CL, DG, and DaL. DL supervised the project.
Conflict of Interest
CL, DG, DaL and DL were employed by the company Cummins Inc.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This material is based upon work supported by the U.S. Department of Energy.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2021.611992/full#supplementary-material.
References
Arzelier, D. (2008). “LMIs in systems control state-space methods performance analysis and synthesis”, in Lecture Notes of LAAS course on LMIs optimization with application in control Part II.
Blanca, M. J., Arnau, J., López-Montiel, D., Bono, R., and Bendayan, R. (2013). Skewness and kurtosis in real data samples. Methodol. Eur. J. Res. Methods Behav. Soc. Sci. 9, 78–74. doi:10.1027/1614-2241/a000057
Candes, E. J., Wakin, M. B., and Boyd, S. P. (2008). Enhancing sparsity by reweighted minimization. J. Fourier Anal. Appl. 14, 877–905. doi:10.1007/s00041-008-9045-x
Chen, P., and Wang, J. (2012). Oxygen concentration dynamic model and observer-based estimation through a diesel engine aftertreatment system. J. Dyn. Syst. Meas. Control. 134, 031008. doi:10.1115/1.4005508
Chepuri, S. P., and Leus, G. (2014). Sparsity-promoting sensor selection for non-linear measurement models. IEEE Trans. Signal Process. 63, 684–698. doi:10.1109/TSP.2014.2379662
Chong, E. K., and Zak, S. H. (2013). An introduction to optimization, 4th Edn. Vol. 76. Hoboken, NJ: John Wiley & Sons.
Dhingra, N. K., Jovanović, M. R., and Luo, Z.-Q. (2014). “An ADMM algorithm for optimal sensor and actuator selection,” in 53rd IEEE conference on decision and control (IEEE), Los Angeles, CA, 15–17 Dec. 2014 (IEEE), p. 4039–4044.
Duník, J., Straka, O., Kost, O., and Havlík, J. (2017). Noise covariance matrices in state-space models: A survey and comparison of estimation methods-Part I. Int. J. Adapt Control. Signal. Process. 31, 1505–1543. doi:10.1002/acs.2783
Eriksson, L., and Nielsen, L. (2014). Modeling and control of engines and drivelines. 1st edn, Hoboken, NJ: John Wiley & Sons.
Fardad, M., Lin, F., and Jovanović, M. R. (2011). “Sparsity-promoting optimal control for a class of distributed systems,” in Proceedings of the 2011 American control conference, San Francisco, CA. 29 June–1 July 2011 (IEEE).
Francqueville, L., and Michel, J.-B. (2014). On the effects of egr on spark-ignited gasoline combustion at high load. SAE Int. J. Eng. 7, 1808–1823. doi:10.4271/2014-01-2628
Grant, M. C., and Boyd, S. P. (2015). The CVX users™ guide release, 2.1. Austin, TX: CVX Research Inc.,
Hashemi, A., Ghasemi, M., Vikalo, H., and Topcu, U. (2018). “A randomized greedy algorithm for near-optimal sensor scheduling in large-scale sensor networks,” in 2018 Annual American control conference. (ACC), Milwaukee, WI, 27–29 June 2018 (IEEE), p. 1027–(1032.).
Joshi, S., and Boyd, S. (2008). Sensor selection via convex optimization. IEEE Trans.Signal Process. 57, 451–462. doi:10.1109/TSP.2008.2007095
Kalandros, M., and Pao, L. Y. (1998). “Controlling target estimate covariance in centralized multisensor systems,” in Proceedings of the 1998 American control conference ACC (IEEE Cat. No. 98ch36207) (IEEE), Philadelphia, PA, 26–26 June 1998, 2749–2753.
Kalandros, M., Pao, L. Y., and Ho, Y.-C. (1999). “Randomization and super-heuristics in choosing sensor sets for target tracking applications,” in Proceedings of the 38th IEEE conference on decision and control (cat No. 99CH36304) (IEEE), Phoenix, AZ, 7–10 Dec. 1999, 2, 1803–1808.
Kocher, L., Koeberlein, E., Van Alstine, D., Stricker, K., and Shaver, G. (2012). Physically based volumetric efficiency model for diesel engines utilizing variable intake valve actuation. Int. J. Eng. Res. 13, 169–184. doi:10.1177/1468087411424378
Kost, O., Duník, J., and Straka, O. (2018). Noise moment and parameter estimation of state-space model. IFAC-POL 51, 891–896. doi:10.1016/j.ifacol.2018.09.107
Luo, Z.-Q., Chang, T.-H., Palomar, D., and Eldar, Y. (2010). SDP relaxation of homogeneous quadratic optimization: approximation. Convex Optimi. Signal. Process. Commun. 117. doi:10.1017/CBO9780511804458.005
Miran, S., Simon, J. Z., Fu, M. C., Marcus, S. I., and Babadi, B. (2019). “Estimation of state-space models with Gaussian mixture process noise,” in 2019 IEEE Data Science Workshop (DSW), Minneapolis, MN, 2–5 June 2019 (IEEE).
Münz, U., Pfister, M., and Wolfrum, P. (2014). Sensor and actuator placement for linear systems based on and optimizationsensor and actuator placement for linear systems based on H2 and H∞ optimization. IEEE Trans. Automat. Contr. 59, 2984–2989. doi:10.1109/tac.2014.2351673
Mushini, R., and Simon, D. (2005). “On optimization of sensor selection for aircraft gas turbine engines,” in 18th international conference on systems engineering (ICSEng’05), Las Vegas, NV, 16–18 Aug. 2005, 9–1.
Palmer, K. A., Hale, W. T., and Bollas, G. M. (2018). “Active fault diagnosis with sensor selection in a diesel engine air handling system,” in 2018 Annual American control conference (ACC), Milwaukee, WI, 27–29 June 2018 (IEEE), 4995–(5000.)
Peet, M. M. (2016). LMI methods in optimal and robust control. Lecture Notes, Department of Mechanical and Aerospace Engineering ((Tempe, AZ: Arizona State University).
Pekař, J., Garimella, P., Germann, D., and Stewart, G. E. (2012). Experimental results for sensor selection and multivariable controller design for a heavy-duty diesel engine. IFAC Proc. Vol. 45, 122–129.
Polyak, B., Khlebnikov, M., and Shcherbakov, P. (2013). “An LMI approach to structured sparse feedback design in linear control systems,” in 2013 European control conference (ECC). Zurich, 17–19 July 2013(IEEE), 833–838.
Rao, S., Chepuri, S. P., and Leus, G. (2015). “Greedy sensor selection for non-linear models,” in 2015 IEEE 6th international workshop on computational advances in multi-sensor adaptive processing (CAMSAP). Cancun, CUN, 13–16 Dec. 2015 (IEEE), 241–244.
Rengarajan, S. B., Sarlashkar, J., Roecker, R., and Anderson, G. (2018). Estimation of intake oxygen mass fraction for transient control of EGR engines, SAE Technical Paper, Tech. Rep.
Rivas Perea, M. E. (2016). Assessment of fuel consumption reduction strategies on a gasoline turbocharged direct injection engine with a cooled EGR system. Ph.D. Thesis. Valencia, Spain Universitat Politècnica de València.
Simon, D. L., and Garg, S. (2010). Optimal tuner selection for kalman filter-based aircraft engine performance estimation. J. Eng. Gas Turbin. Power 132. 031601‐1–031601‐10. doi:10.1115/1.3157096
Solonen, A., Hakkarainen, J., Ilin, A., Abbas, M., and Bibov, A. (2014). Estimating model error covariance matrix parameters in extended kalman filtering. Nonlin. Process. Geophys. 21, 919–927. doi:10.5194/npg-21-919-2014
Stricker, K., Kocher, L., Koeberlein, E., Van Alstine, D., and Shaver, G. M. (2014). Turbocharger map reduction for control-oriented modeling. J. Dyn. Syst. Meas. Control. 136, 041008. doi:10.1115/1.4026532
Suard, R., Onder, C. H., and Guzzella, L. (2008). Optimal sensor selection and configuration, case study spark ignited engine. SAE Int. J. Passeng Cars Electron. Electr. Syst. 1, 382–392. doi:10.1109/tit.2005.864420
Tropp, J. A. (2006). Just relax: convex programming methods for identifying sparse signals in noise. IEEE Trans. Inform. Theor. 52, 1030–1051. doi:10.1109/tit.2005.864420
Van Alstine, D. G., Kocher, L. E., Koeberlein, E., Stricker, K., and Shaver, G. M. (2013). Control-oriented premixed charge compression ignition combustion timing model for a diesel engine utilizing flexible intake valve modulation. Int. J. Eng. Res. 14, 211–230. doi:10.1016/j.conengprac.2008.04.007
Wang, J (2008). Air fraction estimation for multiple combustion mode diesel engines with dual-loop egr systems. Control. Eng. Pract. 16, 1479–1486. doi:10.1016/j.conengprac.2008.04.007
Keywords: engine, sensor selection, observer design, H2 optimization, semi-definite programming, turbo-charged, exhaust gas recirculation, air management
Citation: Zhang X, Shaver GM, Lana CA, Gosala D, Le D and Langenderfer D (2021) Sensor System and Observer Algorithm Co-Design For Modern Internal Combustion Engine Air Management Based on H2 Optimization. Front. Mech. Eng 7:611992. doi: 10.3389/fmech.2021.611992
Received: 29 September 2020; Accepted: 09 February 2021;
Published: 15 April 2021.
Edited by:
Carrie Hall, Illinois Institute of Technology, United StatesReviewed by:
Junfeng Zhao, General Motors (United States), United StatesThomas Leroy, IFP Energies nouvelles, France
Copyright © 2021 Zhang, Shaver, Lana, Gosala, Le and Langenderfer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gregory M. Shaver, Z3NoYXZlckBwdXJkdWUuZWR1
 Xu Zhang
Xu Zhang Gregory M. Shaver
Gregory M. Shaver Carlos A. Lana
Carlos A. Lana Dheeraj Gosala
Dheeraj Gosala Dat Le2
Dat Le2