Artificial Neural Network Architecture for Prediction of Contact Mechanical Response

Predicting the contact mechanical response for various types of surfaces is and has long been a subject, where many researchers have made valuable contributions. This is because the surface topography has a tremendous impact on the tribological performance of many applications. The contact mechanics problem can be solved in many ways, with less accurate but fast asperity-based models on one end to highly accurate but not as fast rigorous numerical methods on the other. A mathematical model as fast as an asperity-based, yet as accurate as a rigorous numerical method is, of course, preferred. Artificial neural network (ANN)–based models are fast and can be trained to interpret how in- and output of processes are correlated. Herein, 1,536 surface topographies are generated with different properties, corresponding to three height probability density and two power spectrum functions, for which, the areal roughness parameters are calculated. A numerical contact mechanics approach was employed to obtain the response for each of the 1,536 surface topographies, and this was done using four different values of the hardness per surface and for a range of loads. From the results, 14 in situ areal roughness parameters and six contact mechanical parameters were calculated. The load, the hardness, and the areal roughness parameters for the original surfaces were assembled as input to a training set, and the in situ areal roughness parameters and the contact mechanical parameters were used as output. A suitable architecture for the ANN was developed and the training set was used to optimize its parameters. The prediction accuracy of the ANN was validated on a test set containing specimens not seen during training. The result is a quickly executing ANN, that given a surface topography represented by areal roughness parameters, can predict the contact mechanical response with reasonable accuracy. The most important contact mechanical parameters, that is, the real area of contact, the average interfacial separation, and the contact stiffness can in fact be predicted with high accuracy. As the model is only trained on six different combinations of height probability density and power spectrum functions, one can say that an output should only be trusted if the input surface can be represented with one of these.

1 Introduction

Surface topography plays an extremely important role in processes such as wear, friction, lubrication, sealing, contact resistance, and heat conduction. This is due to that the roughness causes local contacts between the surfaces, as in mixed lubrication, thus governing how the surface deforms and behaves in contact and defining the boundary friction and the real area of contact. The surface topography may be characterized by a number of areal roughness parameters defined in ISO 25178, see ISO Central Secretary (2012). These parameters have, however, limited correlation to the real area of contact, as well as to friction and wear processes, especially if only a few out of the complete set of field parameters are considered.

By using computational contact mechanics, we can estimate the real area of contact for a surface with given topography and also show how the areal roughness parameters change inside the contact. Notice that, an accurate and reliable result requires a highly resolved surface topography measurement. Thereby, the mesh considered in the numerical solution procedure will have to be of equal resolution, which, in turn, increases the computational time significantly. From an engineering point of view, a non-iterative model that swiftly yields relatively exact predictions of contact mechanics parameters, such as the real area of contact, would therefore be highly desired.

The Greenwood and Williamson (GW) theory (Greenwood and Williamson, 1966; Greenwood and Tripp, 1970) has been and still is very frequently used. Note that it was Archard (1957) who laid the foundation for most of the (multi)asperity-based type of models known of today (Nayak, 1971; Onions and Archard, 1973; Bush et al., 1975; Bush et al., 1979; Carbone, 2009; Greenwood et al., 2011). The Persson contact mechanics theory (Persson, 2006; Yang and Persson, 2008) is also a frequently used tool. Although being highly useful models that provide insight and yield rapid predictions, they are based on assumptions, making them not always very accurate. The GW theory assumes that the asperities at the surfaces exhibit Gaussian probability distributions. The asperities are also assumed to deform independently of each other which leads to that GW theory is applicable only when the contact area is small (compared with the nominal contact area). Persson’s theory assumes that the surfaces exhibit Gaussian height probability distributions and it considers interasperity coupling. Although Persson’s theory might not be very accurate for small real area of contact, it applies well to study the complete contact (see e.g. (Almqvist et al., 2011)). The study by Müser et al. (2017) summarizes findings obtained with various kinds of models, including asperity-based ones and Persson’s theory. Moreover, results from numerical brute force methods, all-atoms–based models, and experiments were presented as well. It was concluded that 1) rigorous numerical brute force approaches yield almost identical results on all properties, 2) Persson’s theory, all-atom simulations, and experiments could be used to identify the correct trends, and almost exact numbers for some properties, and 3) asperity models predicted the real area of contact rather well and provided alternative interpretations for other properties. It would be very useful if it was possible to obtain a mathematical model for fast calculation, which is as accurate as the rigorous models are, when predicting contact mechanics parameters such as real area of contact.

The ideal situation would be to describe surface topography by its height probability distribution and its power spectrum, which constitute the complete description. However, this complicates the analysis, and if a subset of the areal roughness parameters ISO Central Secretary (2012) would be sufficient, it would facilitate the analysis tremendously. In this study, we will present an artificial neural network (ANN)–based model. This model acts as a transfer function, taking areal roughness parameters as input and predicts the real area of contact and other contact mechanics parameters. A similar ANN-based approach has been used in contact mechanics before (see (Rapetto et al., 2009)). Other examples where ANN-based approaches have been used in tribology are Nasir et al. (2010), Nirmal (2010), Ćirović et al. (2012), and Moder et al. (2018). If an ANN, which executes much faster than a computational contact mechanics approach, is well designed, trained, and tested, it can thus provide reasonably accurate predictions of tribological performance parameters very rapidly.

The idea with the present work is to generate thousands of surfaces by means of the method developed by Pérez-Ràfols and Almqvist (2019), and to compute parameters, such as the real area of contact and areal roughness parameters when these surfaces are pressed into contact with a flat rigid counter surface. To this end, we will use the computational contact mechanics approach presented by Almqvist et al.( 2007), which was further developed by Sahlin et al. (2010).

The ANN is trained to find the relationship between the surfaces’ original, the in-contact, that is, in situ areal roughness parameters and the contact mechanics parameters, for a range of loads, spanning from no load at all to a load that causes nearly as much as 50% real area of contact.

2 Methods

This section presents, in a workflow order, the implementation of the ANN. It starts with describing surface topography generation, followed by preprocessing and a brief description of the contact mechanics approach adopted, and it ends with a presentation of the architecture of artificial neural network that was developed herein.

2.1 Surface Topography Generation

Training neural networks requires large data sets. Therefore, it is necessary to generate a wide range of different surface topographies. The surface randomization algorithm developed by Pérez-Ràfols and Almqvist (2019) was employed to randomly generate 2,022 surfaces topographies with given height probability distribution (HPD) and a power spectrum (PS). The HPD and PS can be mathematically modeled by classical distribution and spectrum functions, but they may also be obtained (and adapted) from measured surface topographies. In this work, mathematical models for Gaussian, bi-Gaussian and Weibull functions, and self-affine and exponential PS functions were used. The reader is referred to Pérez-Ràfols and Almqvist (2019) for a precise description of these HPD and PS. A surface topography generation selection scheme is depicted in Figure 1, where one type of HPD and PS is selected together with the corresponding shape-defining parameters, that is, c, k, H, β, α, q₀, and q₁. Remark that the HPDs are defined with zero mean value and unit standard deviation. With these constrains, the Gaussian HPD requires no input, while the bi-Gaussian and the Weibull distributions may be defined using one parameter, that is, c and k, respectively. Specifying the PS requires four parameters, that is, the Hurst exponent H for the self-affine and the parameter β, which defines the autocorrelation length $1/\beta$, for the exponential function, plus α for the anisotropy and the wave numbers $\left(q_0,q_1\right)$ that specify the frequency bandwidth. A 256 × 256 mesh was considered affordable for the grand total of 7,602 elastoplastic contact mechanics simulations performed. The mesh limits the choice of the high frequency cutoff, and in order to resolve the shortest wavelength with at least eight nodes, it was chosen as $q_1=32$ (in terms of its wave number). This parameter was also kept constant when generating the sets of surfaces for training, testing, and validation. Thus, each surface is generated based on a pair of HPD and PS functions and five corresponding numerical parameters, except for the Gaussian which needs four.

FIGURE 1

FIGURE 1. Surface topography generation scheme.

Figure 2 shows an example of a generated surface, using the bi-Gaussian HPD model and the self-affine PS model. The corresponding parameter settings are displayed to the right.

FIGURE 2

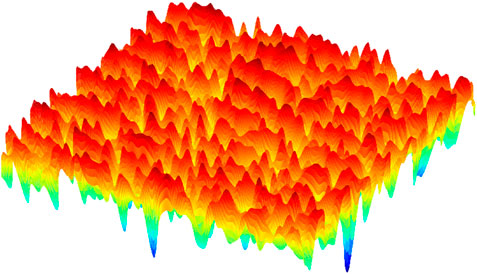
FIGURE 2. A randomized surface, generated by following the scheme in Figure 1, using the settings presented to the right.

The parameter space for the surface dataset used for training was defined by four equidistantly spaced values for each of the seven parameters ($q_1$ was kept constant). In this way, a wide and dense dataset range was obtained. A surface dataset for testing is also needed, and it is important that it is different from, but still within, the same parameter space as the training set. Notice that the validation set is a subset of the training set. The training and test sets, for a pair of parameters (k and H), are schematically illustrated in Figure 3. As the figure shows, the parameters in the test set are shifted a half step to be placed in the void of the training set. This ensures that the test set is located at the maximum Euclidean distance to the training set. The parameter space for the training range is specified in the table shown to the right in the figure. The training set contains 1,536 unique surfaces and the test set contains 486 unique surfaces. From the training set, 20% of the surfaces are transferred to a validation set, which is used to detect overfitting during training.

FIGURE 3

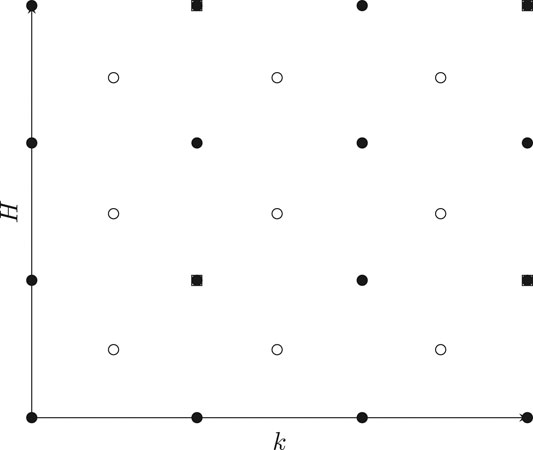
FIGURE 3. The parameter space for the $•$ Training-/⁃Validation set and $\circ$ Test set, illustrating how the $\circ$ Test set was positioned in the voids of the $•$ Training-/⁃Validation set.

2.2 Preprocessing and Contact Mechanics

The areal roughness parameters in Table 1 are calculated for all of the 2,022 surfaces, which are made dimensionless by scaling to exhibit unit rms roughness, that is, $S_q=1$. This is done, in connection with the non-dimensionalization of the contact mechanics model Almqvist and Pérez-Ràfols (2019), to increase the applicability of the ANN. The areal roughness parameters are, in fact, also calculated for the scaled surfaces in situ, that is, as the surfaces are loaded against a flat counter surface for a range of loads, spanning from no load at all to a load that causes up to 50% real area of contact. The loading sequence was defined in terms of the dimensionless nominal contact pressure ${\overline{p}}_c$, and the contact mechanics simulations were performed using the method presented by Almqvist et al. (2007); Sahlin et al. (2010) and the then utilized by Almqvist et al. (2011), Spencer et al. (2011), Spencer et al. (2013), Pérez-Ràfols et al. (2016), and Pérez-Ràfols et al. (2018).

TABLE 1

TABLE 1. Areal roughness parameters calculated according to ISO Central Secretary (2012).

The dimensionless areal roughness parameters (for the scaled surfaces) in Table 1 are calculated according to ISO Central Secretary (2012). They are grouped as parameters of field type and of Bearing Area Curve (BAC) type. These parameters are the input for the ANN described in Section 2.3, with architecture illustrated in Figure 4. For more details on how to calculate the areal roughness parameters according to the standard, see Blateyron (2013). As a result of the contact mechanics simulations, the surfaces may be plastically deformed, and it is the hardness $p_p$ that limits the maximum pressure the surface can exhibit before it yields plastically. Therefore, four equidistantly spaced values for ${\overline{p}}_p$ in the range $\left[\mathrm{20,100}\right]$ were used for the training set and three different values were chosen for the test set, in the same way as described for H and k in Figure 3. Thereby, there are in total 7,602 contact mechanics calculations performed. Out of these, 6,144 were used to train the ANN and 1,458 were used for testing.

FIGURE 4

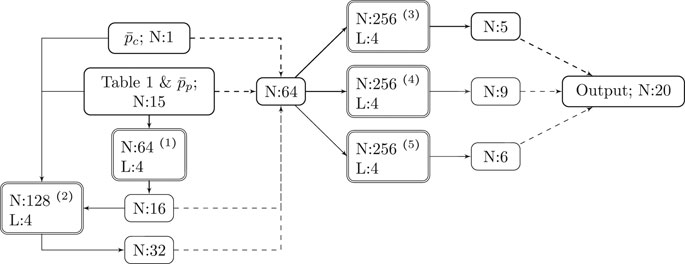
FIGURE 4. Multitask neural network architecture, with ${\overline{p}}_c$ and the 14 original areal roughness parameters as input and with the 14 in situ areal roughness parameters and six the contact mechanics parameters as output.

The output from the contact mechanics calculations are the in situ, areal roughness parameters, and the six contact mechanics parameters in Table 2. These are the real area of contact to nominal contact area ratio $A_r=A_e+A_p$, the elastic- $A_e$ and plastic contributions $A_p$ to it, the dimensionless maximum contact pressure ${\overline{p}}_{\max }=p_{\max }/E$, the dimensionless average interfacial separation $\overline{u}=u/h_r$, and the dimensionless contact stiffness $\overline{K}=K{h}_r/E$.

TABLE 2

TABLE 2. Contact mechanics parameters.

2.3 The Artificial Neural Network

Here, the ANN architecture depicted in Figure 4, which is engineered to predict the contact mechanical response of surfaces represented by the areal roughness parameters (given in Table 1), will be described. The areal roughness parameters in Table 1 and the dimensionless hardness ${\overline{p}}_p$ are used as input for the ANN and it outputs the corresponding, in situ, areal roughness parameters and the six contact mechanics parameters in Table 2. As emphasized with double borders in Figure 4, the ANN consists of five subnetworks. These all have four fully connected layers, but a different amount of neurons per layer. The arrows with continuous lines indicate connections that are fully connected with weights, whereas arrows with dashed lines indicate just passing the data from one part of the network to another. A regular MSE loss function was adopted for the training procedure.

The first subnetwork⁽¹⁾, with 64 neurons, has rectifier (ReLU) activation functions $\left(f\left(x\right)=\max \left(0,x\right)\right)$, and it takes the 14 areal roughness parameters in Table 1 and the value of the hardness as input. The purpose of this network is to process the areal roughness parameters, without the influence of the contact pressure, to extract suitable input for the second subnetwork⁽²⁾ with 128 neurons. This subnetwork has sigmoid activation functions $\left(f\left(x\right)=1/\left(1+e^{-x}\right)\right)$, and it is fully connected to the 14 areal roughness parameters, the hardness, the dimensionless contact pressure, and the output of the first subnetwork.

The input to the first and second subnetworks and their output are assembled into one vector with 64 values. This vector is the input to each of the three parallel subnetworks^(3)–(5), which have softplus (smooth rectifying) activation functions $\left(f\left(x\right)=\text{ln}\left(1+e^x\right)\right)$ and 256 nodes each. As mentioned previously, the purpose of the ANN is to predict the 14 in situ areal roughness parameters as well as the six contact mechanics parameters in Table 2. To this end, each of the three parallel subnetworks output parameters grouped by its origin, that is, the five in situ areal roughness parameters of field type, the nine in situ areal roughness parameters related to the bearing area (or Abbott-Firestone) curve, and the six contact mechanics parameters.

3 Results and Discussion

First, in Section 3.1, the performance of the ANN model will be evaluated with linear regression between predicted values and the output in the test dataset. Then, in Section 3.2, examples of how the predictions changes with the load will be presented and compared to the correct values.

3.1 Predicting Contact Mechanical Response

Herein, the test set, which contains 1,458 specimens that it has never seen before, is used to evaluate the ANN’s predictive performance on surfaces for a whole range of loads. Depicted in Figures 5, 6 are linear regression of all the predicted parameter values and the $R^2$-value, that is,

$R^2=1-{\displaystyle {\sum }_i{\left(y_i-{\widehat{y}}_i\right)}^2}/{\displaystyle {\sum }_i{\left(y_i-\overline{y}\right)}^2},$

where y is the target output, $\widehat{y}$ is the predicted output, and $\overline{y}$ is the mean target output, is used as a measure of the accuracy. Overall, one can see that some parameters are predicted with extraordinary high accuracy, whereas a few are predicted with less precision. Figure 5 reveals that there is a systematic error for the predictions of ${\overline{S}}_a$ and ${\overline{S}}_q$, which both have relatively low $R^2$-values. The reason for the low $R^2$-values is because the absolute majority of predictions (for both ${\overline{S}}_a$ and ${\overline{S}}_q$) are underestimated. Among the output shown in Figure 5, the one with highest accuracy is the mean quadratic slope parameter ${\overline{S}}_{dq}$. Visually, the bearing area curve parameter $S_{mr1}$ shows a quite large spread, while the $R^2$-value is rather high. This is caused by a relatively small percentage predictions with large errors.

FIGURE 5

FIGURE 5. Linear regression of target (x-axis) and predicted (y-axis) outputs.

FIGURE 6

FIGURE 6. Linear regression of target (x-axis) and predicted (y-axis) outputs.

There is much that can be said about the results presented in Figure 6. One thing, which is nearly impossible not to notice, is the regression for the dimensionless maximum pressure ${\overline{p}}_{\max }$, with wide-spread and a low $R^2$-value. The reason for this is that the ${\overline{p}}_{\max }$ is a local event, while areal roughness parameters are averaged in some sense. In other words, prediction of a local quantity based on average terms is a complicated task, and the low accuracy is, therefore, to be expected. The more important outputs $A_r$, $A_{re}$, $A_{rp}$, $\overline{u}$, and $\overline{K}$ are, fortunately, predicted with higher accuracy. For more details on the ANN’s predictability, the reader is referred to next section.

3.2 Application

In this section, the accuracy of the predictions of the ANN for three different test specimens, taken from the test set that the network never has seen before, will be investigated over the whole range of loads considered when the test set was generated with the contact mechanics simulations. The test specimens are listed in Tables 3, 4, and they consist of the areal roughness parameters, corresponding to the surfaces topographies presented in Figure 7, combined with a value of the dimensionless hardness.

TABLE 3

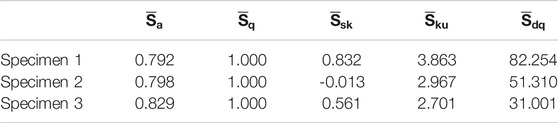
TABLE 3. Test specimens containing the dimensionless areal roughness parameters, corresponding to the topographies depicted in Figure 7 and a value of the dimensionless hardness: part 1—field type parameters.

TABLE 4

TABLE 4. Test specimens containing the dimensionless areal roughness parameters, corresponding to the topographies depicted in Figure 7 and a value of the dimensionless hardness: part 2—BAC type parameters and dimensionless hardness.

FIGURE 7

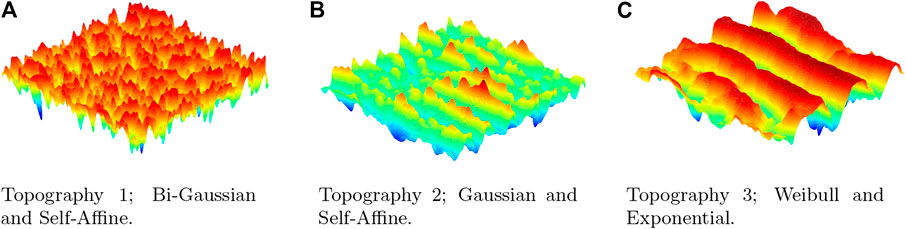
FIGURE 7. Surface topographies for the three test specimens (A–C) with dimensionless areal roughness paraeters and hardness, listed in Tables 3, 4.

The predictions of the in situ dimensionless mean square height ${\overline{S}}_q$ and skewness ${\overline{S}}_{sk}$ are depicted in Figure 8, which also shows the correct values. This figure and Figures 9–12 share the same legend in which the lines (continuous blue, dashed red, and dotted turquoise) are for the predictions, and the correct values are represented with the markers (round blue, round red, and cross turquoise). The ANN predicts both the ${\overline{S}}_q$ and ${\overline{S}}_{sk}$ output parameters for Specimen 1 (bi-Gaussian and self-affine) with best accuracy. The lowest accuracy was observed when predicting ${\overline{S}}_q$ for Specimen 2 (Gaussian and self-affine), and the lowest accuracy was observed when predicting ${\overline{S}}_{sk}$ for Specimen 3 (Weibull and exponential).

FIGURE 8

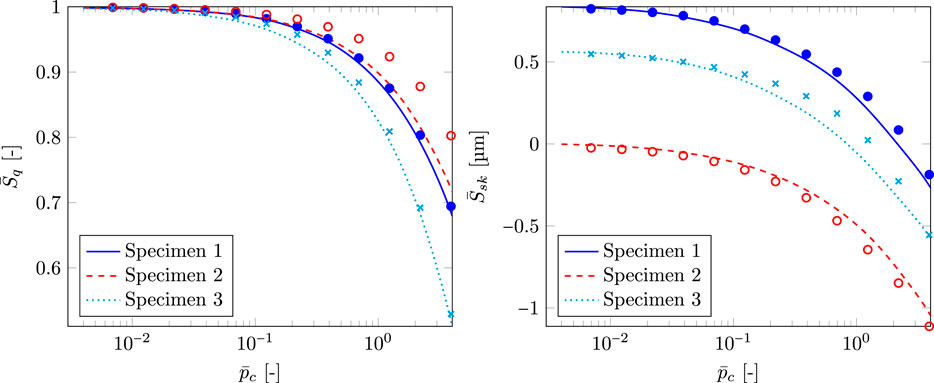
FIGURE 8. Dimensionless root mean square height ${\overline{S}}_q$(left) and skewness ${\overline{S}}_{sk}$(right) for varying dimensionless nominal pressure ${\overline{p}}_c$, predicted (line) and real value (marker).

FIGURE 9

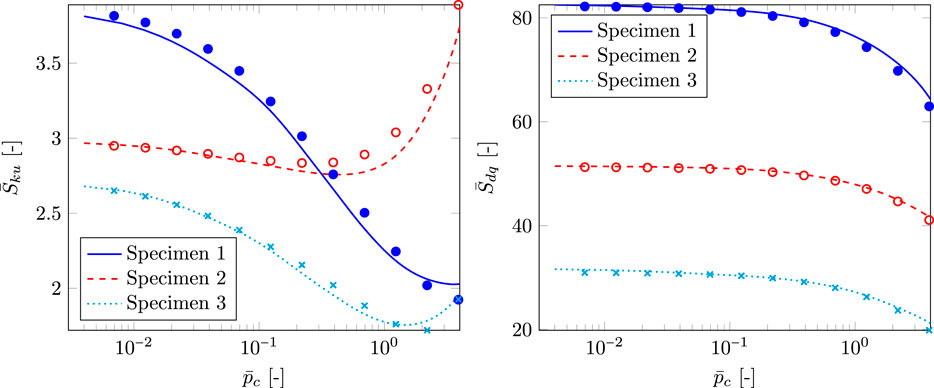
FIGURE 9. Dimensionless kurtosis ${\overline{S}}_{ku}$(left) and mean quadratic slope ${\overline{S}}_{dq}$(right) for varying dimensionless nominal pressure ${\overline{p}}_c$, predicted (line) and real value (marker).

FIGURE 10

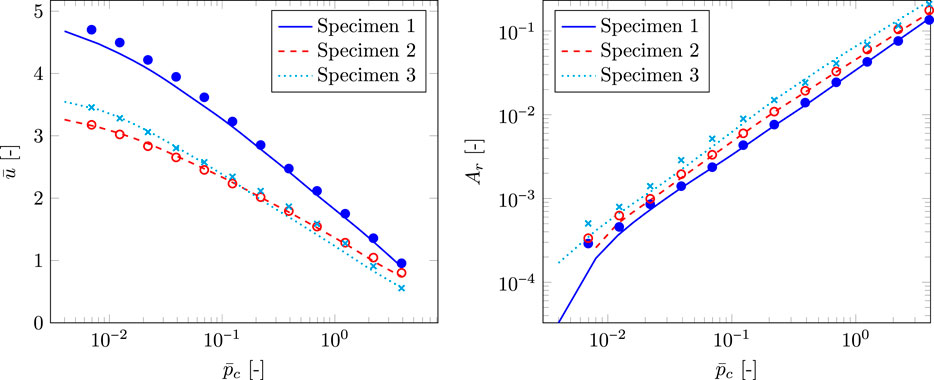
FIGURE 10. Dimensionless average interfacial separation $\overline{u}$(left) and real area of contact ratio ${\overline{A}}_r$(right) for varying dimensionless nominal pressure ${\overline{p}}_c$, predicted (line) and real value (marker).

FIGURE 11

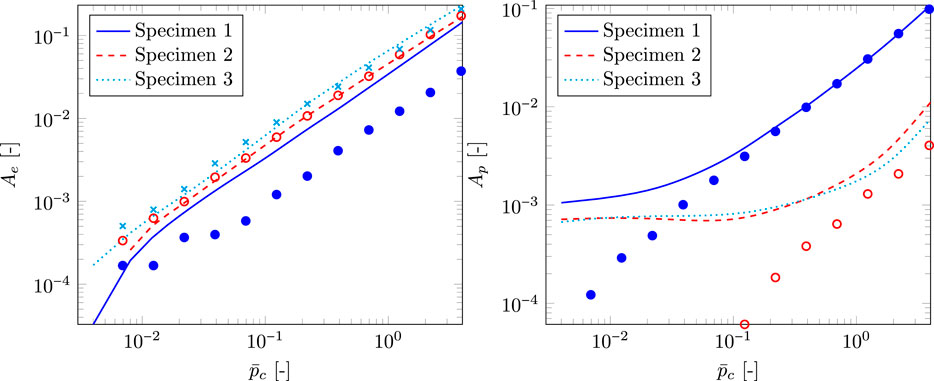
FIGURE 11. Real area of elastic contact ratio $A_e$(left) and real area of plastic contact ratio $A_p$(right) for varying dimensionless nominal pressure ${\overline{p}}_c$, predicted (line) and real value (marker). Note that the correct values for ${\overline{A}}_p$ for Specimen 3 is zero for all loads.

FIGURE 12

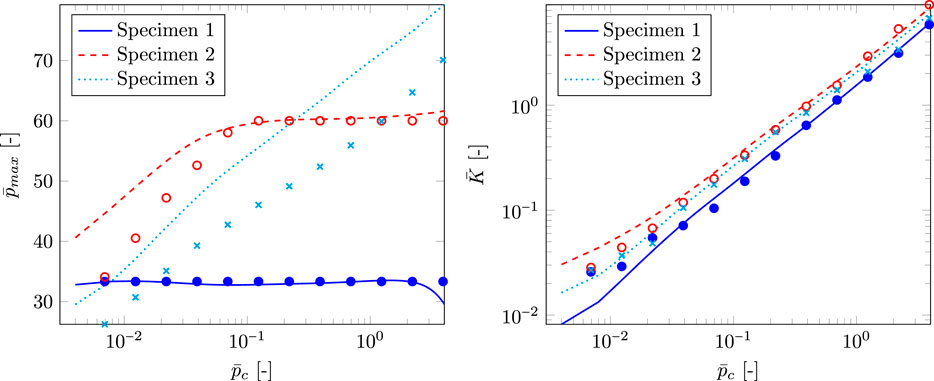
FIGURE 12. Dimensionless maximum pressure ${\overline{p}}_{\max }$(left) and contact stiffness $\overline{K}$(right) for varying dimensionless nominal pressure ${\overline{p}}_c$, predicted (line) and real value (marker).

The predictions of the in situ dimensionless kurtosis ${\overline{S}}_{ku}$ and mean quadratic slope ${\overline{S}}_{dq}$ are depicted in Figure 9. For ${\overline{S}}_{ku}$, to the left in Figure 9, the accuracy is rather high and approximately the same for all three specimens. The variation of the in situ kurtosis is very complex, but still accurately captured by the ANN. To the right in Figure 9, it can be seen that the predictions of the in situ${\overline{S}}_{dq}$ are of very high accuracy, and this can be understood from the linear regression analysis presented in Figure 5.

The predictions of the dimensionless average interfacial separation $\overline{u}$ and real area of contact ratio $A_r$ are depicted in Figure 10. It is observed that the ANN very accurately predicts $\overline{u}$ for Specimen 2 over the whole range of loads tested. The accuracy for Specimen 1 is not so high at low loads but really good for moderate and high loads, and it is vice versa for Specimen 3. Overall, the ANN’s accuracy in predicting $\overline{u}$ is good, which is required if the ANN would be employed in a mixed lubrication model like the one in Sahlin et al. (2010). As displayed in the right of Figure 10, the real area of contact ratio can be predicted with satisfactory accuracy for all but the lowest load, where it ideally should extrapolate $A_r\to 0$ as ${\overline{p}}_c\to 0$. Better performance could (most likely) have been obtained, by extending the training set to include more results for lower loads. Note that this would also require a higher mesh density than the 256 × 256 used presently. The ANN is trained such that the areal roughness parameters for ${\overline{p}}_c=0$ remains unchanged. The ANN is also trained such that the contact mechanics parameters are zero for ${\overline{p}}_c=0$, except for the average interfacial separation, which is specified as the surface’s maximum peak height.

The predictions of the elastic part of the real area of contact ratio ${\overline{A}}_e$ (left) and plastic part of the real area of contact ratio $A_p$ (right) are depicted in Figure 11. When looking at the predictions for ${\overline{A}}_e$, it is noticeable that there is a large error for Specimen 1; however, the other specimens are predicted with acceptable accuracy. From the results for ${\overline{A}}_p$ presented to the right in Figure 11, it seems as if the ANN has qualitatively learned what the variation of ${\overline{A}}_p$ would be. More precisely, that it is constant for low loads but that it starts to increase at some point. The reason for that it does not quantitatively capture the variation correctly has probably to do with that a relative error for a large ${\overline{A}}_p$ is much more significant than it is for a small ${\overline{A}}_p$, during the training procedure. Notice that the ANN predicts that Specimen 3 exhibits plastic deformation, but that the correct result is that the deformations are purely elastic for all loads considered (${\overline{A}}_p=0$ is not displayed on the log-scaled axis).

The predictions of the dimensionless maximum pressure ${\overline{p}}_{\max }$ (left) and contact stiffness $\overline{K}$ (right) are depicted in Figure 12. When looking at the predictions for ${\overline{p}}_{\max }$, one can see that there is a quite large error. This was also brought up in connection to the presentation of Figure 6. Most surfaces will be plastically deformed, and it seems as it would be fairly easy for the ANN to learn that the ${\overline{p}}_{\max }$ will saturate at ${\overline{p}}_p$. Indeed, by looking at the predictions for Specimen 1 and 2, it is also clear that it has learned this. Specimen 1 that has the lowest ${\overline{p}}_p$ is already plastically deformed at the smallest load in the range and Specimen 3 with the highest ${\overline{p}}_p$ is not plastically deformed at all. Specimen 2 does, however, exhibit ${\overline{p}}_{\max }$ for an intermediate load in the range, and it can be observed that the ANN is able to predict that it will and that it is capable of capturing the position where it occurs. From Figure 12, it can also be observed that the contact stiffness, for all three specimens, can be predicted with quite high accuracy for moderate and high loads but that the accuracy decreases for lower loads.

4 Concluding Remarks

Two datasets containing a total of 2,022 different surface topographies were generated using the algorithm developed by Pérez-Ràfols and Almqvist (2019). Three different HPD functions and two different PS functions were obtained from Gaussian, bi-Gaussian, and Weibull HPD functions and self-affine and exponential PS functions, described with as few shape-defining parameters as possible. Fourteen areal roughness parameters were calculated for all surfaces in the dataset. Together with the surface indentation hardness and a given applied load, these 14 areal roughness parameters were used as input for the ANN.

A numerical elastoplastic contact mechanics approach, in which the hardness limits the maximum pressure the surface can exhibit before it yields plastically, was then employed to perform simulations of pressing each of the generated surfaces against a flat rigid counter surface for a sequence of loads. Since four values for the hardness were considered for the training set with 1,536 different surface topographies and three were considered for the test set with 486 topographies, a grand total of $4\times 1536+3\times 486=7602$ realizations were conducted. Out of these, 6,144 specimens were used for training and 1,458 were left for testing and validation. For each of the these specimens, 14 in situ areal roughness parameters and six contact mechanics parameters were calculated for the sequence of loads that was also used as input for the ANN.

An architecture for an artificial neural network (ANN), which consisted of five different subnetworks, was designed and trained on the dataset. Linear regression was applied, and the $R^2$-value was used to appreciate the correlation between the network prediction and the correct data. A few parameters were almost perfectly predicted, whereas other were predicted with large errors. According to the $R^2$-values, the most important parameters, that is, the real area of contact ratio $A_r$, the dimensionless average interfacial separation $\overline{u}$, and contact stiffness $\overline{K}$ were all predicted accurately by the ANN.

Summing up, the ANN can be used to roughly appreciate the in situ behavior of various kinds of surface topographies, if the areal roughness parameters, the indentation hardness, and the nominal contact pressure are known. Some parameters, that is, the real area of contact ratio, the dimensionless average interfacial separation, and contact stiffness can actually be predicted with high accuracy.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

KK has performed the main part of the development of the ANN-based model and has been coordinating the writing. RL contributed with expertise, to the discussions and was engaged in the writing. FR has been engaged in surface generation and contact mechanics and contributed to the writing. ML contributed with expertise, particularly regarding AI and machine learning, contributed to discussions and to the writing. AA has initiated the work and has been involved in all parts of it.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to acknowledge the support from VR (The Swedish Reseach Council): DNR 2019-04293.

Nomenclature

$\alpha$ anisotropy coefficient

$S_a$ arithmetic mean height $\left(\text{μm}\right)$

$1/\beta$ auto-correlation length

$u$ average interfacial separation $\left(\text{μm}\right)$

$c$ bimodal shape parameter

$K$ contact stiffness (N/m)

$V_{mc}$ core material volume $\left({\text{μm}}^3/{\text{μm}}^2\right)$

$S_k$ core roughness depth $\left(\text{μm}\right)$

$V_{vc}$ core void volume $\left({\text{μm}}^3/{\text{μm}}^2\right)$

${\overline{S}}_a$ dimensionless arithmetic mean height $S_a/h_r$

$\overline{u}$ dimensionless average interfacial separation $u/h_r$

$\overline{K}$ dimensionless contact stiffness $K{x}_r/E$

${\overline{V}}_{mc}$ dimensionless core material volume $V_{mc}/h_r$

${\overline{S}}_k$ dimensionless core roughness depth $S_k/h_r$

${\overline{V}}_{vc}$ dimensionless core void volume $V_{vc}/h_r$

${\overline{p}}_p$ dimensionless hardness $p_p/\left(E{h}_r/x_r\right)$

${\overline{S}}_{ku}$ dimensionless kurtosis $S_{ku}/h_r$

${\overline{p}}_{\max }$ dimensionless maximum pressure $p_{\max }/\left(E{h}_r/x_r\right)$

${\overline{S}}_{dq}$ dimensionless mean quadratic slope $S_{dq}{x}_r/h_r$

${\overline{p}}_c$ dimensionless nominal pressure $p_c/\left(E{h}_r/x_r\right)$

${\overline{V}}_{mp}$ dimensionless peak material volume $V_{mp}/h_r$

${\overline{S}}_{pk}$ dimensionless reduced peak height $S_{pk}/h_r$

${\overline{S}}_{vk}$ dimensionless reduced valley depth $S_{vk}/h_r$

${\overline{S}}_q$ dimensionless root mean square height $S_q/h_r$

${\overline{S}}_{sk}$ dimensionless skewness $S_{sk}/h_r$

${\overline{V}}_{vv}$ dimensionless valley void volume $V_{vv}/h_r$

$p_p$ hardness MPa

$H$ Hurst exponent

$S_{ku}$ kurtosis $\left(\text{μm}\right)$

$q_0$ long wavelength cutoff

$S_{mr1}$ material ratio 1 –

$S_{mr2}$ material ratio 2

$p_{\max }$ maximum pressure MPa

$S_{dq}$ mean quadratic slope $\left(\text{μm}/\text{mm}\right)$

$p_c$ nominal pressure MPa

$V_{mp}$ peak material volume $\left({\text{μm}}^3/{\text{μm}}^2\right)$

$A_r$ real area of contact ratio

$A_e$ real area of elastic contact ratio

$A_p$ real area of plastic contact ratio

$S_{pk}$ reduced peak height $\left(\text{μm}\right)$

$S_{vk}$ reduced valley depth $\left(\text{μm}\right)$

$h_r$ reference height $S_q$$\left(\text{μm}\right)$

$x_r$ reference length (mm)

$S_q$ root mean square height$\left(\text{μm}\right)$

$q_1$ short wavelength cutoff

$S_{sk}$ skewness $\left(\text{μm}\right)$

$V_{vv}$ valley void volume $\left({\text{μm}}^3/{\text{μm}}^2\right)$

$k$ Weibull shape parameter

$t$ worn shape parameter

References

Almqvist, A., and Pérez-Ràfols, F. (2019). Scientific Computing with Applications in Tribology: A Course Compendium. Luleå, Sweden: Luleå University of Technology

Almqvist, A., Campañá, C., Prodanov, N., and Persson, B. N. J. (2011). Interfacial Separation between Elastic Solids with Randomly Rough Surfaces: Comparison between Theory and Numerical Techniques. J. Mech. Phys. Sol. 59 (11), 2355–2369. doi:10.1016/j.jmps.2011.08.004

CrossRef Full Text | Google Scholar

Almqvist, A., Sahlin, F., Larsson, R., and Glavatskih, S. (2007). On the Dry Elasto-Plastic Contact of Nominally Flat Surfaces. Tribology Int. 40 (4), 574–579. doi:10.1016/j.triboint.2005.11.008

CrossRef Full Text | Google Scholar

Archard, J. F. (1957). Elastic Deformation and the Laws of Friction. Proc. R. Soc. Lond. A 243 (1233):190–205. doi:10.1098/rspa.1957.0214

CrossRef Full Text | Google Scholar

Blateyron, F. (2013). The Areal Field Parameters. Berlin, Heidelberg: Springer Berlin Heidelberg, 15–43. doi:10.1007/978-3-642-36458-7_2

CrossRef Full Text

Bush, A. W., Gibson, R. D., and Keogh, G. P. (1979). Strongly Anisotropic Rough Surfaces. Trans. ASME. J. Lubrication Tech. 101 (1), 15–20. doi:10.1115/1.3453271

CrossRef Full Text | Google Scholar

Bush, A. W., Gibson, R. D., and Thomas, T. R. (1975). The Elastic Contact of a Rough Surface. Wear 35 (1), 87–111. doi:10.1016/0043-1648(75)90145-3

CrossRef Full Text | Google Scholar

Ćirović, V., Aleksendrić, D., and Mladenović, D. (2012). Braking Torque Control Using Recurrent Neural Networks. Proc. Inst. Mech. Eng. D: J. Automobile Eng. 226 (6), 754–766. doi:10.1177/0954407011428720

CrossRef Full Text | Google Scholar

Carbone, G. (2009). A Slightly Corrected Greenwood and Williamson Model Predicts Asymptotic Linearity between Contact Area and Load. J. Mech. Phys. Sol., 57(7):1093–1102. doi:10.1016/j.jmps.2009.03.004

CrossRef Full Text | Google Scholar

ISO Central Secretary (2012). Geometrical Product Specifications (Gps)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters. Geneva, CH: International Organization for StandardizationAvailable at: https://www.iso.org/standard/42785.html

Greenwood, J. A., Putignano, C., and Ciavarella, M. (2011). A Greenwood & Williamson Theory for Line Contact. Wear 270, 332–334. doi:10.1016/j.wear.2010.11.002

CrossRef Full Text | Google Scholar

Greenwood, J., and Tripp, J. (1970). The Contact of Two Nominally Flat Rough Surfaces. Proc. Inst. Mech. Eng. 185, 625–634. doi:10.1243/pime_proc_1970_185_069_02

CrossRef Full Text | Google Scholar

Greenwood, J., and Williamson, J. (1966). Contact of Nominally Flat Surfaces. Proc. R. Soc. Lond. A 295, 300–319. doi:10.1098/rspa.1966.0242

CrossRef Full Text | Google Scholar

Müser, M. H., Dapp, W. B., Bugnicourt, R., Sainsot, P., Lesaffre, N., Lubrecht, A. A., et al. (2017). Meeting the Contact-Mechanics Challenge. Tribology Lett. 65 (4), 118. doi:10.1007/s11249-017-0900-2

CrossRef Full Text | Google Scholar

Moder, J., Bergmann, P., and Grün, F. (2018). Lubrication Regime Classification of Hydrodynamic Journal Bearings by Machine Learning Using Torque Data. Lubricants 6 (4). 108. doi:10.3390/lubricants6040108

CrossRef Full Text | Google Scholar

Nasir, T., Yousif, B. F., McWilliam, S., Salih, N. D., and Hui, L. T. (2010). An Artificial Neural Network for Prediction of the Friction Coefficient of Multi-Layer Polymeric Composites in Three Different Orientations. Proc. Inst. Mech. Eng. C: J. Mech. Eng. Sci. 224 (2), 419–429. doi:10.1243/09544062jmes1677

CrossRef Full Text | Google Scholar

Nayak, P. R. (1971). Random Process Model of Rough Surfaces. J. Lubrication Tech. 93 (3), 398–407. doi:10.1115/1.3451608

CrossRef Full Text | Google Scholar

Nirmal, U. (2010). Prediction of Friction Coefficient of Treated Betelnut Fibre Reinforced Polyester (T-bfrp) Composite Using Artificial Neural Networks. Tribology Int. 43 (8), 1417–1429. doi:10.1016/j.triboint.2010.01.013

CrossRef Full Text | Google Scholar

Onions, R. A., and Archard, J. F. (1973). The Contact of Surfaces Having a Random Structure. J. Phys. D: Appl. Phys. 6 (3), 289–304. doi:10.1088/0022-3727/6/3/302

CrossRef Full Text | Google Scholar

Persson, B. N. J. (2006). Contact Mechanics for Randomly Rough Surfaces. Surf. Sci. Rep. 61, 201–227. doi:10.1016/j.surfrep.2006.04.001

CrossRef Full Text | Google Scholar

Pérez-Ràfols, F., and Almqvist, A. (2019). Generating Randomly Rough Surfaces with Given Height Probability Distribution and Power Spectrum. Tribology Int. 131, 591–604. doi:10.1016/j.triboint.2018.11.020

CrossRef Full Text | Google Scholar

Pérez-Ràfols, F., Larsson, R., and Almqvist, A. (2016). Modelling of Leakage on Metal-To-Metal Seals. Tribology Int. 94, 421–427. doi:10.1016/j.triboint.2015.10.003

CrossRef Full Text | Google Scholar

Pérez-Ràfols, F., Larsson, R., van Riet, E. J., and Almqvist, A. (2018). On the Loading and Unloading of Metal-To-Metal Seals: A Two-Scale Stochastic Approach. Proc. Inst. Mech. Eng. Part J: J. Eng. Tribology 232 (12), 1525–1537. doi:10.1177/1350650118755620

CrossRef Full Text | Google Scholar

Rapetto, M. P., Almqvist, A., Larsson, R., and Lugt, P. M. (2009). On the Influence of Surface Roughness on Real Area of Contact in Normal, Dry, Friction Free, Rough Contact by Using a Neural Network. Wear 266 (5), 592–595. doi:10.1016/j.wear.2008.04.059

CrossRef Full Text | Google Scholar

Sahlin, F., Larsson, R., Marklund, P., Lugt, P. M., and Almqvist, A. (2010). A Mixed Lubrication Model Incorporating Measured Surface Topography. Part 1: Theory of Flow Factors. Proc. Inst. Mech. Eng. Part J: J. Eng. Tribology 224 (4), 335–351. doi:10.1243/13506501jet658

CrossRef Full Text | Google Scholar

Spencer, A., Almqvist, A., and Larsson, R. (2011). A Semi-deterministic Texture-Roughness Model of the Piston Ring-Cylinder Liner Contact. Proc. Inst. Mech. Eng. Part J: J. Eng. Tribology 225 (6), 325–333. doi:10.1177/1350650110396279

CrossRef Full Text | Google Scholar

Spencer, A., Avan, E. Y., Almqvist, A., Dwyer-Joyce, R. S., and Larsson, R. (2013). An Experimental and Numerical Investigation of Frictional Losses and Film Thickness for Four Cylinder Liner Variants for a Heavy Duty Diesel Engine. Proc. Inst. Mech. Eng. Part J: J. Eng. Tribology 227 (12), 1319–1333. doi:10.1177/1350650113491244

CrossRef Full Text | Google Scholar

Yang, C., and Persson, B. N. J. (2008). Contact Mechanics: Contact Area and Interfacial Separation from Small Contact to Full Contact. J. Phys. Condensed Matter 20, 1–13. doi:10.1088/0953-8984/20/21/215214

CrossRef Full Text | Google Scholar