- 1Department of Engineering Mechanics, SVL, Xi'an Jiaotong University, Xi'an, China
- 2Institute of Mechanics, Technical University of Berlin, Berlin, Germany
This work considers the non-adhesive frictionless contact problem of soft materials with surface being tensed by equi-biaxial tension. The boundary element method (BEM) based on Fast Fourier Transform and conjugate gradient algorithm is extended to deal with this problem. By comparing with existing analytical solutions for the axisymmetric contact between a rigid parabolic indenter and an elastic half space, our numerical simulations are validated having great accuracy. Moreover, the developed BEM algorithm is applied on the calculations of elastic responses of a soft substrate indented by a smooth indenter with general quadric profile and a rough indenter with self-affine fractal surface, respectively. Some essential contact behaviors resulted from the presence of membrane tension are presented and discussed.
Introduction
Many physiological systems can be modeled as the layer-foundation structure, and generally, the mechanical properties of surface layer differ from those of bulk interior. Early in 1978, Hajji (1978) investigated the indentation of lung under uniform pressure by considering the sample as an isotropic elastic half space ideally adhered with a tensed membrane. It is assumed that the surface membrane thickness is ultimately small so that its bending rigidity can be neglected. Besides, for small deformation, the membrane tension is assumed keeping constant. With the same assumptions, Kim and Gouldstone (2008) addressed the axisymmetric spherical indentation of elastic solid with strain-independent membrane tension. Moreover, the surface layer of some soft tissues and single cells can be regarded as pre-tensed “plate” or “shell” with finite thickness, which can also resist bending deformation (Zamir and Taber, 2004; Zhang and Zhang, 2009). Recently, Argatov and Sabina (2012) treated the surface layer as a reinforced membrane under generalized plane stress state. They hypothesized that no pre-tension exists in the membrane, and the flexural stiffness is negligible compared with the in-plane tensile stiffness. Such modeling method was employed in the deformation analysis of anisotropic articular cartilage (Argatov and Mishuris, 2016).
It is interesting to note that the above models originally developed for the biological materials are analogous to the well-known surface elasticity theory of Gurtin and Murdoch (1975), which characterizes the material surface with surface tension and surface elasticity. As Hajji stated (Hajji, 1978), the mathematical expressions are basically consistent, although they have completely different physical natures. The constant membrane tension in Hajji (1978) and Kim and Gouldstone (2008) is corresponding to the residual surface tension, and the superficial layer modeled in Argatov and Sabina (2012) and Argatov and Mishuris (2016) can be considered as a solid surface with surface elasticity. Recently, problems of surface loadings and contacts have been widely studied based on the surface elasticity theory (He and Lim, 2006; Wang and Feng, 2007; Zhou and Gao, 2013; Long et al., 2017; Li et al., 2020). It is found that the deformation behavior would be distinctly different from classical models when the size of loading is comparable or even smaller than a critical length, usually at nano/microscale. However, these analytical works are usually limited to simple cases under a given surface pressure or for the symmetric situations.
Physically, the surface elasticity theory is based on the concept of solid surface energy (Gurtin and Murdoch, 1975). For the general contact between two solid bodies, the surface energy of each free surface (γ1, γ2) and contacting interface (γ12) should be taken into account simultaneously. Two simplified cases can be recognized according to values of these surface energies. When the energy difference w = γ1+γ2-γ12 (called work of adhesion) is appreciable and the effect of surface energy outside the contact can be neglected, adhesive contact model with specific work of adhesion would be appropriate (Johnson et al., 1971). On the other hand, if the energy difference equals to zero (w = 0) but the surface energy of one contact body is much larger than the other (i.e., γ1 >> γ2 and γ1 ≈ γ12), the contact problem can be addressed in the framework of surface elasticity theory (He and Lim, 2006; Wang and Feng, 2007; Zhou and Gao, 2013; Long et al., 2017; Li et al., 2020). In this work, we consider the latter circumstance with constant surface tension or, equivalently, the non-adhesive contact of solids with tensed surface membrane.
The Fast Fourier Transform (FFT) based methods have been widely employed to solve the elastic contact problems for its great advantage on reducing the computation cost. For the efficient Green's function molecular dynamics (GFMD) (Campañá and Müser, 2006; Prodanov et al., 2014), the FFT technique plays an important role in the determination of substrate elastic response to external surface forces. In addition, the boundary element method (BEM) that exploits FFT to accelerate the calculation of displacements induced by given surface forces has been also proved fast and robust for the analysis of various contact problems (Nogi and Kato, 1997; Liu et al., 2000; Polonsky and Keer, 2000; Pohrt and Popov, 2012, 2015; Pohrt and Li, 2014; Rey et al., 2017; Bugnicourt et al., 2018). The basic principle of the FFT-based BEM is to evaluate the linear convolution of fundamental solution and pressure distribution based on the convolution theorem. For the classical elastic problem with half space approximation, the simple Boussinesq's fundamental solution or its form in Fourier space is commonly used in the BEM for normal contact problems. However, when the surface of elastic half space is equi-biaxially tensed, things will be different.
This paper aims to extend the mature FFT-based BEM for the calculation of normal contact of material with membrane/surface tension. Several calculation examples are implemented to demonstrate the validity and usefulness of this method. This method provides a potential numerical approach for the study of contact behavior of some soft structures, which is of particular interest for the measurement of mechanical properties of biological tissues (Zhang et al., 2014).
Numerical Method
We consider an ideally smooth elastic substrate. The surface is tensed by a constant, strain-independent tension τ0, and the bulk material is homogeneous having elastic modulus E and Poisson's ratio ν. The origin of the Cartesian coordinate system (o-xyz) is located at the surface of half space, and the z-axis is perpendicular to the surface, as shown in Figure 1A.
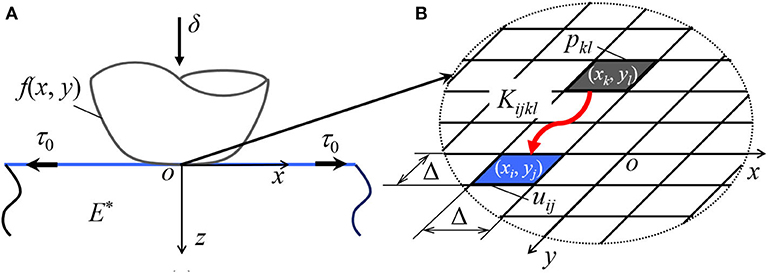
Figure 1. (A) Normal contact between a rigid indenter and an elastic half space with tensed surface membrane, and (B) the schematic of surface discretization used in BEM.
With some specified external pressure applied on the surface, the boundary value problem can be solved in the framework of classical linear elastic theory, provided that the unconventional boundary condition associated with surface tension is employed (Hajji, 1978; He and Lim, 2006; Wang and Feng, 2007; Zhou and Gao, 2013). For the axisymmetric situation under a uniform normal pressure p0 within a circular region of radius a, the boundary condition reads,
where u(r) is the vertical displacement on the surface, σzz and σzr are the bulk normal stress and shear stress at z = 0, respectively, and H is the Heaviside step function.
By using Hankel integral transform and substituting the boundary condition into the general solutions, the vertical displacement caused by the uniform pressure p0 can be derived (Hajji, 1978). Moreover, by implementing a limiting process in which the radius a decreases to zero with the resultant force held constant unity πa2p0 = 1, the fundamental solution that is the vertical displacement at the point (x, y) induced by unit concentrate force acting at the coordinate origin can be derived as,
where s = 2τ0/E* is the characteristic length, E* = E/(1–ν2) is the reduced modulus, Hn and Yn are the Struve function and the Bessel function of second kind of order n, respectively.
The FFT of this fundamental solution, , is plotted in Figure 2, where is the magnitude of wave vector (ωx is the angular frequency in the x-direction and ωy is the angular frequency in the y-direction). It is found that the results are consistent with the theoretical prediction (Li and Popov, 2020),
which reduces to the Boussinesq's solution in Fourier space when the characteristic length s decreases to zero, .
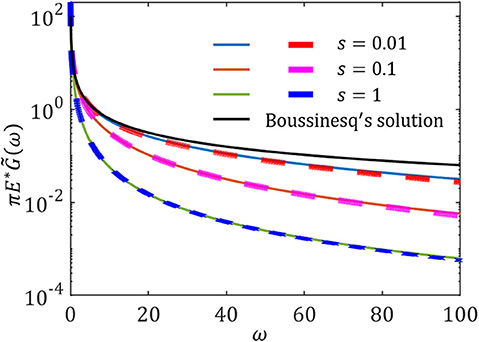
Figure 2. The fundamental solutions in Fourier space with different values of s. Thick dashed lines are the numerical results of the FFT of Equation (2), and thin solid lines are the theoretical predictions of Equation (3). Note the unit of s is same as 1/ω.
For the indentation of a rigid body with known profile f (x, y) into a depth δ, see Figure 1A, the vertical displacement on the surface u(x, y) has to fulfill the following condition:
where Ω is the domain of contact.
Assume that the positive contact pressure between the substrate and the indenter distributes as p(x, y). Then, according to the superposition principle, the vertical displacement generated by p(x, y) can be expressed by
which is exactly a two dimensional continuous convolution of fundamental solution and contact pressure distribution. As a result, substitution of Equation (5) into the displacement boundary condition Equation (4) leads to
Note that the inequality characterizing the non-overlapping condition outside the contact region is always accompanied with Equation (6) no matter which expression form is utilized. The resultant load P acting on the rigid indenter equals to the summation of the contact pressure over entire contact area. For a given indentation depth, the corresponding contact area and contact pressure are to be determined.
Next, this problem will be solved in the light of FFT based boundary element method. In contrast to finite element method, only part of substrate surface needs to be discretized. As shown in Figure 1B, squared elements with side length Δ are used to mesh the surface. Assuming that the pressure within each single element distributes uniformly, Equation (6) can be transformed into linear algebraic equations,
where
Note that the computational domain that is discretized into surface elements should include all potential contact region. If the computational domain contains N×N elements, the influence coefficients Kijkl have N4 values. Using direct multiplication method has the complexity of O(N4). Instead, we prefer to apply the FFT technique to evaluate the vertical displacement for a given pressure, i.e., the left side of Equation (7). The complexity is then reduced to O(N2logN). It is worth mentioning that the multilevel multi-integration method suggested by Brandt and Lubrecht (1990) allows for the same computation acceleration.
The basic idea of the FFT based speed-up method is to interpret the left side of Equation (7) as a two-dimensional discrete convolution and applying the circular convolution theorem (Liu et al., 2000; Pohrt and Li, 2014). In this work, the influence coefficient matrix (Kkl)N×N is first prepared in real space by performing numerical integration of Equation (8) with xi = yj = 0. It should be pointed out that appropriate zero padding and wrap-around order operations to the original influence coefficient matrix (Kkl)N×N and pressure matrix (pkl)N×N are necessary for the proper application of circular convolution theorem, which can avoid the periodic error (Liu et al., 2000). Next, FFT is implemented on the two matrices. The results can be easily obtained through element-wise multiplication of the influence coefficient matrix and pressure matrix in Fourier space. Then, performing an inverse FFT (IFFT) yields the vertical displacement caused by the pressure distribution (pkl)N×N in real space. As a result, the problem becomes,
where ∘ represents the element-wise product, and h is given by the indenter shape and the indentation depth, hij = δ +f (xi, yj).
With the FFT based acceleration technique, this inverse problem can be solved using an iteration scheme based on conjugate gradient method (Liu et al., 2000; Polonsky and Keer, 2000; Pohrt and Li, 2014). The final obtained contact pressure (pkl)N×N should be positive at all contact elements where the induced vertical displacement matches with the given rigid profile, and equal to zero in the non-contact region where the non-overlapping condition is always satisfied. Finally, the overall contact responses under a specified indentation loading δ are ready to be evaluated. The resultant force P applied on the indenter is obtained by summing up the forces at all discrete contacting elements. The real contact area A is computed by multiplying the number of contacting elements with the area of a single element Δ2. It should be pointed out that the contact area obtained by this direct summation method can be only accurate when the contacting surface is discretized by sufficiently refined grids. Area correction to continuum limit as done by Prodanov et al. (2014) is necessary. Inevitably, the BEM calculation with finer surface discretization would require more time cost. In addition, it is worth mentioning that Yastrebov et al. (2017) presented a correction route to compute accurate contact area with relatively coarse discretization for such kind of numerical method.
Calculation Examples
Contact With an Axisymmetric Parabolic Indenter
To validate the capability of the FFT-based BEM described in section Numerical method, we first consider a simple case that an axisymmetric parabolic indenter is pressed into a half space by a displacement δ. Numerical simulations are carried out for a soft material (E* = 10 kPa), of which the surface is pre-tensed by a constant tension τ0 = 1 N/m (with negligible bending rigidity and in-plane stiffness). A square surface domain of edge length 2aH, where aH is the contact radius predicted by Hertz theory, is meshed by N×N elements. The profile of the rigid indenter of curvature radius R = 1 mm is given by
At first, the area in contact under different discretization level is examined to check the meshing dependent error in this BEM. In Figure 3, the contact area under a normal displacement δ = 0.05 mm is plotted as a function of surface element number. It can be found that the area converges to a stable limit (i.e., the continuum limit) as the element number N increases. In this case, the maximum error is about 4% for the coarsest grid N = 32. The error gets sufficiently small (< 0.5%) when N is larger than 256. Moreover, by using the correction method proposed by Yastrebov et al. (2017), it is found that the grid can be coarser to achieve same accuracy as that of finer meshing without correction. For convenience, we use the meshing grid of N = 256 to simulate the contacts of single asperity, which is already enough to get accurate results even without correction.
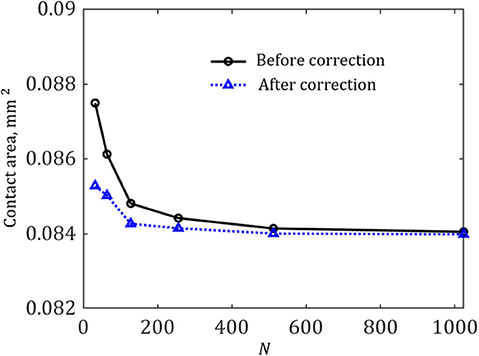
Figure 3. The contact area for δ = 0.05 mm with and without correction as a function of element number.
The influence of membrane/surface tension can be reflected by a dimensionless ratio of the characteristic length s (defined by 2τ0/E*) to the contact radius a. Figure 4 displays the distributions of contact pressure for the cases of different ratio s/a. The variations of indentation load and indentation depth with respect to the ratio s/a are plotted in Figures 5A,B, respectively. It is seen that our numerical results obtained from BEM calculations coincide well with existing semi-analytical solutions (Kim and Gouldstone, 2008; Long et al., 2017). The size dependent contact behavior is reproduced. Apparently, when the contact size a is comparable or smaller than the characteristic length, the contact response will essentially deviate from the classical Hertz contact theory. Compared with the prediction of Hertz theory, a higher indentation load or a larger indentation depth is needed to achieve a specific contact area because of the presence of membrane/surface tension.
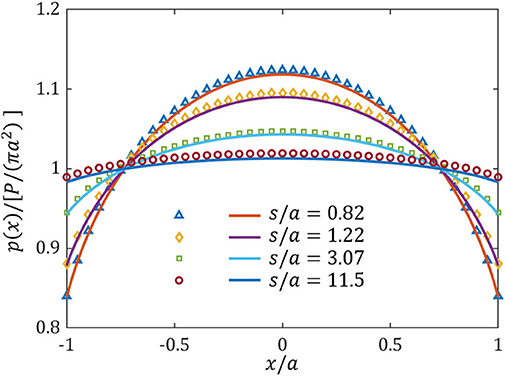
Figure 4. Contact pressure distribution along x-axis direction. Solid lines are the semi-analytical solution from Kim and Gouldstone (2008), and scatter symbols are the numerical results from BEM.
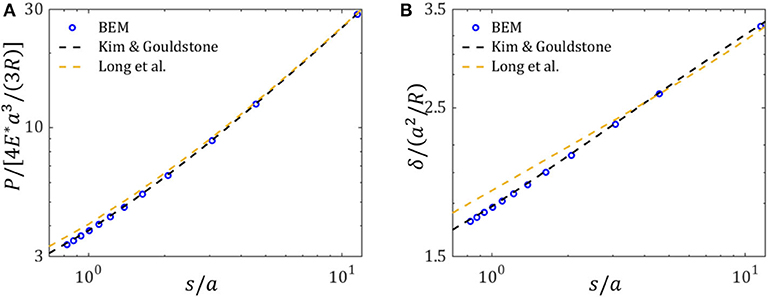
Figure 5. Dependences of contact responses (normalized by the prediction of Hertz theory) on the ratio s/a: (A) indentation load; (B) indentation depth.
Contact With an Elliptical Indenter
Let us further consider a smooth indenter with quadric surface, of which the principle curvatures (R1, R2) are unequal. By adjusting the x-axis and y-axis along the axes of principle curvature, the indenter shape can be expressed by
For a given displacement δ = 0.05 mm exerted on the rigid indenter of R1 = 1 mm and R2 = 2 mm, the distributions of normal pressure on the half space with different membrane/surface tension are shown in Figure 6. Based on the pressure distribution, the contact region can be determined, which is identified as an ellipse with semi-minor axis a1 and semi-major axis a2. With the membrane/surface tension increasing, the elliptical contact area shrinks, and the distribution of contact pressure tends to be more uniform. According to the classical Hertz theory, the ratio of a1/a2 depends only on the ratio of principle curvatures of the indenter R1/R2. However, it is noticed that the value of a1/a2 no longer keeps constant for a given indenter, but declines as the membrane/surface tenion increases. In other words, the contact ellipse will be somewhat slender if the surface membrane is equi-biaxially tensed. This phenomenon can be explained by the size-dependent behavior caused by membrane/surface tension. Because the length along the minor axis of contact ellipse is smaller than that along major axis, the size effect on the reduction of contact dimension nearby minor axis would be relatively more remarkbale.
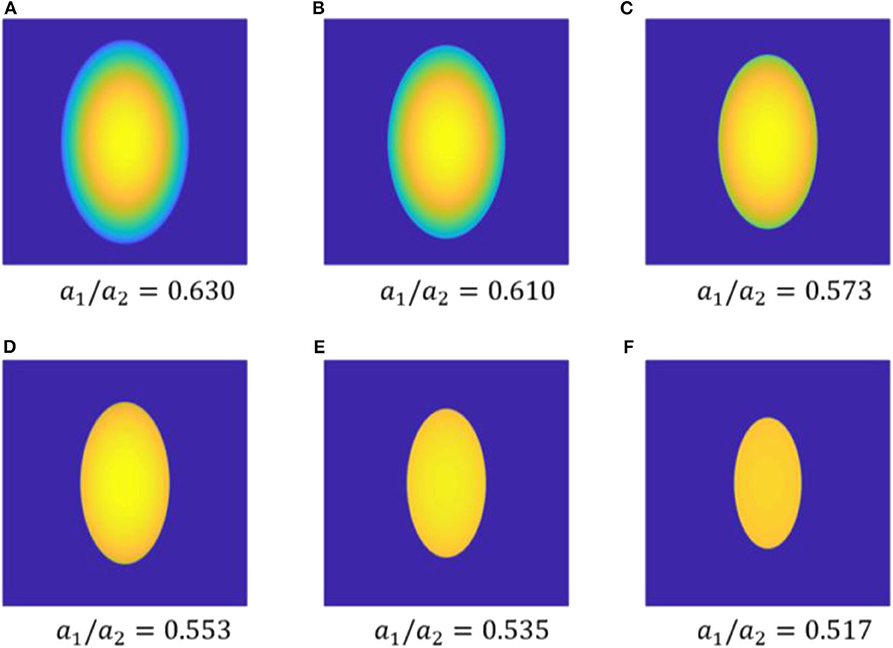
Figure 6. Distributions of normal pressure of the contact between an elliptical indenter and a soft substrate with modulus E* = 10 kPa and different membrane/surface tension: (A) τ0 = 0 N/m, (B) τ0 = 0.1 N/m, (C) τ0 = 0.5 N/m, (D) τ0 = 1 N/m, (E) τ0 = 2 N/m and (F) τ0 = 5 N/m.
Contact With a Rough Surface
With the validated BEM, we are also able to calculate the response of rough surface contact in the presence of membrane/surface tension. As illustrated in Figure 7, we consider the normal contact between a square rigid random rough surface and a soft elastic half space with tensed surface membrane. Assume that the rough surface is self-affine fractal and has the following power spectral density (PSD),
where C0 is a constant, H is the Hurst exponent, q is the wave vector, q0 = 2π/L and qs are the roll-off and cutoff wavenumbers, respectively.
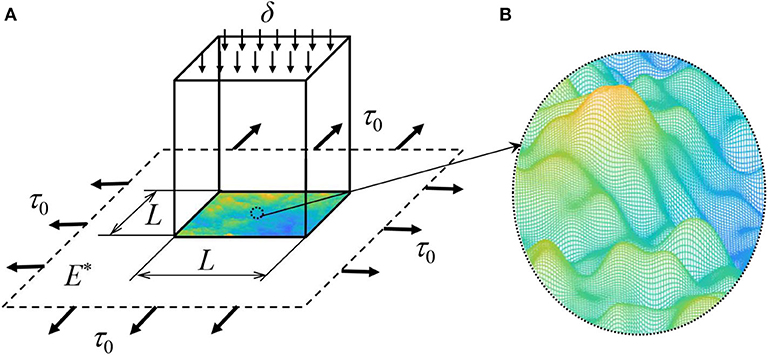
Figure 7. (A) Indentation on the elastic half space by a square punch with fractal rough surface, and (B) the detail of generated rough surface.
Based on this power spectrum, a discrete rough surface can be generated by using the inverse Fast Fourier Transform (Pohrt and Popov, 2012). Then, the surface height data f (xi, yj) over a uniform N×N grid are superimposed onto the bottom of a square flat-ended indenter with length L. Note that the highest point of rough surface is initially put on the surface of half space. Accordingly, a square surface region on the half space A0 = L×L that is corresponding to the projected area of indenter is meshed by N×N surface elements. Partial contact happens when the indenter moves downward by a displacement δ.
In general, the elastic contact response of rough surface should be dependent on the material property E* and the surface topography parameters including the root mean square (RMS) roughness σ, Hurst exponent H, the system size L = 2π/q0, and the cut-off wavenumbers qs. In this case with membrane/surface tension τ0, the contact response ϕ for a given indentation depth δ should be a function of these variables, ϕ = ϕ(τ0, E*, σ, H, L, qs, δ). Dimensional analysis reveals that the effects of membrane/surface tension can be reflected by a dimensionless parameter, (τ0/E*)/(σ2/L). In this work, we would lay aside the role of surface topography property, which is controlled by the dimensionless parameters including σ/L, H, and σqs, and just display the effects of membrane/surface tension.
An artificial rough surface (N = 1,024, L = 1 mm) with RMS roughness σ = 0.01 mm, H = 0.7, q0 = 2π/L and qs = 2π/(16L/N) is considered. Calculation examples are carried out for this rough surface in contact with a soft substrate with reduced modulus E* = 10 kPa and different membrane tensions τ0 = 0, 10, 50, 100 mN/m. The real contact area A/A0 and indentation load P/(E*σL) are obtained for different indentation depth δ/σ.
Figure 8A shows the dependence of A/A0 on δ/σ for the cases of different membrane/surface tension. For a given indenter displacement, the contact area significantly declines with the increasing of applied membrane/surface tension. For instance, when the indenter displacement δ = 10σ, the fraction area of contact drops from 43.5% for a substrate with un-tensed surface to 7.95% for that having membrane/surface tension of 100 mN/m. The configurations of contact regions for δ = 10σ are exhibited in Figure 8B. Note that the real contact area computed by direct summation of contacting elements has been compared with that evaluated by the correction technique of Yastrebov et al. (2017). As shown in Figure 8A, the difference is small. Therefore, the contact area calculation for this level of discretization should be proper and accurate. In addition, the variation of A/A0 with respect to P/(E*σL) is displayed in Figure 9. The slope of the curve decreases as the value of τ0 increases, which means that to generate a specified contact area needs a higher external indentation load for the case of larger membrane/surface tension. As a result, for a given substrate with determined modulus indented by a specific rough surface, the mean contact stress defined by the ratio of indentation load to the real contact area, P/A, can be increased by applying a certain membrane/surface tension on the substrate surface.
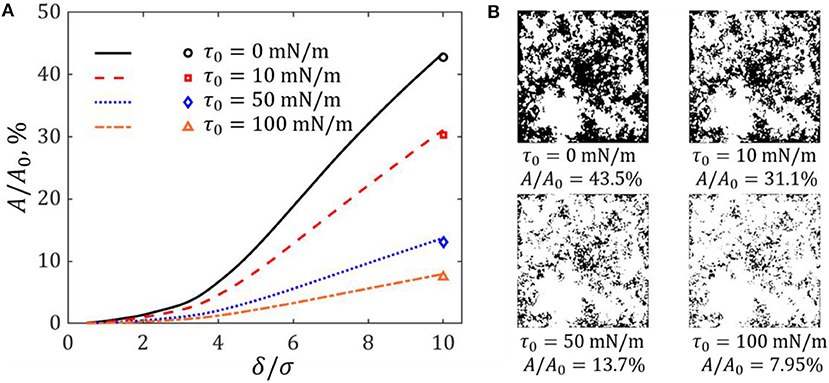
Figure 8. (A) Variations of real contact area with respect to the indentation depth for the cases of different membrane/surface tension. Scatter symbols are the real contact area after correction operation for a specified displacement δ = 10σ. (B) Images of contact regions under the displacement δ = 10σ (black zone is the contact region).
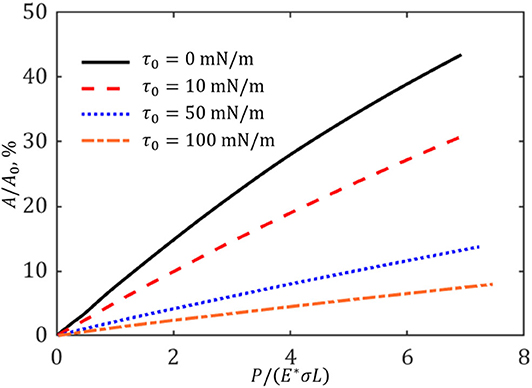
Figure 9. Variations of real contact area with respect to the resultant load for the cases of different membrane/surface tension.
For this problem of rough surface contact, it should be pointed out that the analytical relations between the contact response and the properties of substrate material and indenter rough surface have not been generalized in this paper. More numerical calculations for different rough surface and different substrate with different membrane/surface tension are required in order to achieve this point, which will be conducted in the future.
Conclusion
In summary, the FFT-based boundary element method is extended for normal contact of soft material, of which the surface is tensed by equi-biaxial tension. Three type of indenters compressing on the elastic half space with constant membrane/surface tension are considered. The calculation results show excellent agreement with related available solutions. Typical size-dependent contact behavior is demonstrated. In particular, due to the presence of membrane/surface tension, the eccentricity of contact ellipse will be slightly increased for the contact with a rigid elliptical indenter. For a given substrate indented by a specific rigid indenter, the mean contact pressure defined by the ratio of indentation load to the real contact area can be increased by increasing membrane/surface tension on the substrate surface. This numerical method would be helpful for the deformation analysis of some soft systems with membrane/surface tension.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
WY and GW conceived the study. WY carried out numerical simulations. All authors drafted and reviewed the manuscript.
Funding
This financial support from the National Natural Science Foundation of China (Grant No.11525209) was acknowledged. WY also thanks the support from the China Scholarship Council (CSC).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors are grateful to Dr. Q. Li and Prof. V. L. Popov for helpful discussions on the BEM and providing results from a non-published manuscript.
References
Argatov, I., and Mishuris, G. (2016). An asymptotic model for a thin bonded elastic layer coated with an elastic membrane. Appl. Math. Modell. 40, 2541–2548. doi: 10.1016/j.apm.2015.09.109
Argatov, I. I., and Sabina, F. J. (2012). Spherical indentation of a transversely isotropic elastic half-space reinforced with a thin layer. Int. J. Eng. Sci. 50, 132–143. doi: 10.1016/j.ijengsci.2011.08.009
Brandt, A., and Lubrecht, A. A. (1990). Multilevel matrix multiplication and fast solution of integral equations. J. Comput. Phys. 90:348–70. doi: 10.1016/0021-9991(90)90171-V
Bugnicourt, R., Sainsot, P., Dureisseix, D., Gauthier, C., and Lubrecht, A. A. (2018). FFT-based methods for solving a rough adhesive contact: description and convergence study. Tribol. Lett. 66:29. doi: 10.1007/s11249-017-0980-z
Campañá, C., and Müser, M. H. (2006). Practical Green's function approach to the simulation of elastic semi-infinite solids. Phys. Rev. B. 74:075420. doi: 10.1103/PhysRevB.74.075420
Gurtin, M. E., and Murdoch, A. I. (1975). A continuum theory of elastic material surfaces. Arch. Rat. Mech. Anal. 57, 291–323. doi: 10.1007/BF00261375
Hajji, M. A. (1978). Indentation of a membrane on an elastic half space. ASME J. Appl. Mech. 45, 320–324. doi: 10.1115/1.3424295
He, L. H., and Lim, C. W. (2006). Surface green function for a soft elastic half-space: influence of surface stress. Int. J. Solids Struct. 43, 132–143. doi: 10.1016/j.ijsolstr.2005.04.026
Johnson, K. L., Kendall, K., and Roberts, A. D. (1971). Surface energy and the contact of elastic solids. Proc. R. Soc. London A 324, 301–313. doi: 10.1098/rspa.1971.0141
Kim, J. H., and Gouldstone, A. (2008). Spherical indentation of a membrane on an elastic half-space. J. Mater. Res. 23, 2212–2220. doi: 10.1557/JMR.2008.0278
Li, M., Zhang, H. X., Zhao, Z. L., and Feng, X. Q. (2020). Surface effects on cylindrical indentation of a soft layer on a rigid substrate. Acta Mech. Sinica. 36, 422–429. doi: 10.1007/s10409-020-00941-8
Li, Q., and Popov, V. L. (2020). Non-adhesive contacts with different surface tension inside and outside the contact area. Front. Mech. Eng. doi: 10.3389/fmech.2020.00063
Liu, S., Wang, Q., and Liu, G. (2000). A versatile method of discrete convolution and FFT (DC-FFT) for contact analyses. Wear. 243, 101–111. doi: 10.1016/S0043-1648(00)00427-0
Long, J. M., Ding, Y., Yuan, W. K., Chen, W., and Wang, G. F. (2017). General relations of indentations on solids with surface tension. ASME J. Appl. Mech. 84:051007. doi: 10.1115/1.4036214
Nogi, T., and Kato, T. (1997). Influence of a hard surface layer on the limit of elastic contact - Part I: Analysis using a real surface model. J. Tribol. 119, 493–500. doi: 10.1115/1.2833525
Pohrt, R., and Li, Q. (2014). Complete boundary element formulation for normal and tangential contact problems. Phys. Mesomech. 17, 334–340. doi: 10.1134/S1029959914040109
Pohrt, R., and Popov, V. L. (2012). Normal contact stiffness of elastic solids with fractal rough surfaces. Phys. Rev. Lett. 108:104301. doi: 10.1103/PhysRevLett.108.104301
Pohrt, R., and Popov, V. L. (2015). Adhesive contact simulation of elastic solids using local mesh-dependent detachment criterion in boundary element method. Facta Universitatis. 13, 3–10.
Polonsky, I. A., and Keer, L. M. (2000). Fast methods for solving rough contact problems: a comparative study. ASME. J. Tribol. 122, 36–41. doi: 10.1115/1.555326
Prodanov, N., Dapp, W. B., and Müser, M. H. (2014). On the contact area and mean gap of rough, elastic contacts: dimensional analysis, numerical corrections, and reference data. Tribol. Lett. 53, 433–448. doi: 10.1007/s11249-013-0282-z
Rey, V., Anciaux, G., and Molinari, J. F. (2017). Normal adhesive contact on rough surfaces: efficient algorithm for FFT-based BEM resolution. Comput. Mech. 60, 69–81. doi: 10.1007/s00466-017-1392-5
Wang, G. F., and Feng, X. Q. (2007). Effects of surface stresses on contact problems at nanoscale. J. Appl. Phys. 101:013510. doi: 10.1063/1.2405127
Yastrebov, V. A., Anciaux, G., and Molinari, J. F. (2017). On the accurate computation of the true contact-area in mechanical contact of random rough surfaces. Tribol. Int. 114, 161–171. doi: 10.1016/j.triboint.2017.04.023
Zamir, E. A., and Taber, L. A. (2004). On the effects of residual stress in microindentation tests of soft tissue structures. ASME J. Biomech. Eng. 126, 276–283. doi: 10.1115/1.1695573
Zhang, C. Y., and Zhang, Y. W. (2009). Extracting elastic properties and prestress of a cell using atomic force microscopy. J. Mater. Res. 24, 1167–1171. doi: 10.1557/jmr.2009.0121
Zhang, M. G., Cao, Y. P., Li, G. Y., and Feng, X. Q. (2014). Spherical indentation method for determining the constitutive parameters of hyperelastic soft materials. Biomech. Model. Mechanobiol. 13, 1–11. doi: 10.1007/s10237-013-0481-4
Keywords: boundary element method, membrane/surface tension, contact mechanics, elliptical indenter, rough surface
Citation: Yuan W and Wang G (2020) Boundary Element Calculations for Normal Contact of Soft Materials With Tensed Surface Membrane. Front. Mech. Eng. 6:57. doi: 10.3389/fmech.2020.00057
Received: 26 March 2020; Accepted: 19 June 2020;
Published: 29 July 2020.
Edited by:
Irina Goryacheva, Institute for Problems in Mechanics (RAS), RussiaCopyright © 2020 Yuan and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Weike Yuan, dy55dWFuQGNhbXB1cy50dS1iZXJsaW4uZGU=; Gangfeng Wang, d2FuZ2dmQHhqdHUuZWR1LmNu
 Weike Yuan
Weike Yuan Gangfeng Wang1*
Gangfeng Wang1*