Contacts With Negative Work of “Adhesion” and Superlubricity

Introduction

Van der Waals forces between solids in vacuum are always attractive and are considered as the main source of adhesion. However, in the presence of an intermediate medium, they can also be repelling (Dzyaloshinskii et al., 1961) which means that the “work of adhesion” becomes negative. Similarly to the case of adhesion, the interaction range of these forces can be either comparable (or larger) than the minimum characteristic length scale of the contact problem or it can be negligible compared with all characteristic length scales. We call this latter case the “JKR-approximation,” as the JKR theory of adhesion (Johnson et al., 1971) is also valid in this limit. The repelling interaction can also be due to the presence (and squeezing out) of a thin fluid layer between solids as considered in Müser (2014). In the papers Popov and Hess (2018) and Heß and Popov (2019), it was shown that the contact of two oppositely charged surfaces at a constant voltage is equivalent to the adhesive contact with an effective van der Waals interaction. Similarly, the contact of the bodies with the same charge would be equivalent to repelling van der Waals forces with a negative work of adhesion. Further kinds of repelling forces may be solvation, structural, and hydration forces (Israelachvili, 2011). In the following, we speak about van der Waals forces, but they are thought as representative for a larger class of long range repelling forces.

We argue that in the JKR approximation, the Hertz' solution of the contact problem with a repelling van der Waals interaction, remains practically unchanged. However, the contact area falls apart into the area of “weak (van der Waals) interaction” and “strong (rigid wall) interaction.” It is speculated that if the normal force is smaller than a critical value at which the core region of strong interaction disappears, a macroscopic superlubricity state of the contact may be observed.

Attractive and Repelling van der Waals Forces

The interaction force between neutral molecules is often modeled as a superposition of the very sharp increasing “core repulsion” ∝ 1/r¹³ and a weaker van der Waals “tail” ∝ r⁻⁷ (the corresponding potential is known as Lennard-Jones-Potential), Figure 1A, left:

$\begin{array}{ll}F(r)=\frac{12·w}{r_0}\left[{\left(\frac{r_0}{r}\right)}^{13}-{\left(\frac{r_0}{r}\right)}^7\right]\text{ for attractive van der Waals forces},& (1)\end{array}$

where r₀ is the equilibrium distance, at which the core force and the van der Waals force become equal and w is the work of adhesion (the work needed to separate the molecules starting with their equilibrium position).

FIGURE 1

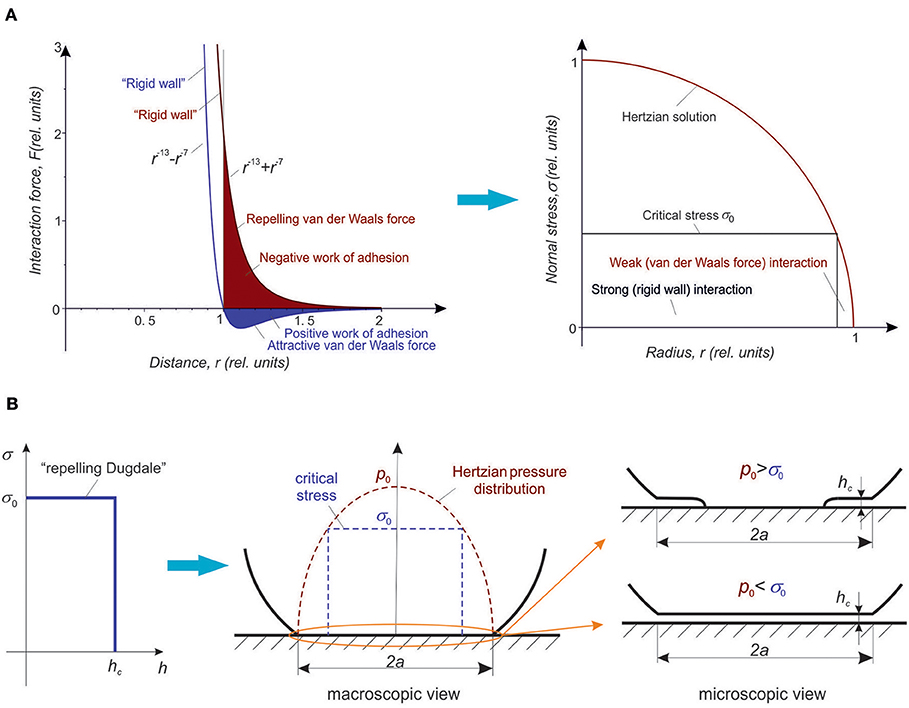
Figure 1. (A) Left: Model intermolecular force in the case of attractive van der Waals force (blue line) and repelling van der Waals force (red line), in relative units. The distance r = 1 corresponds to the equilibrium in the case of attractive van der Waals forces. At distances smaller than r = 1 the repelling force increases steeply: At these distances, one can qualitatively speak about a “rigid wall.” At distances r > 1, there exist weak long-range van der Waals force, either positive or negative. The work needed to separate the surfaces starting from the “rigid wall” position r = 1 are shown by filled areas (blue filled area—positive work of adhesion in an adhesive contact, red filled area—“negative work of adhesion” in the repelling case). (A) Right: The normal stress (pressure) distribution in a Hertzian contact. If the range of action of both core “rigid wall” force and van der Waals force are negligible compared with all characteristic length scales of the contact problem, the repelling van der Waals forces do not influence the contact problem and do not change the stress distribution. However, on the microscopic scale, in the regions where the stress is larger then a critical stress σ₀ (see the text of paper for details), the surfaces are in “direct rigid wall contact” and feel strong atomic corrugation potential. In the regions where the stress is smaller than σ₀, they “levitate” due to van der Waals force and see only weak corrugation. By decreasing the normal force, one can achieve the state in which the normal stress is smaller than σ₀ in the whole contact area. This state corresponds to the state of superlubricity. (B) Schematic illustration of the contact configuration on the example of a simple model adhesive stress of “Dugdale type” (Dugdale, 1960) with a constant repelling stress σ₀ up to the distance h_c (scheme on the left). In the center: Macroscopic shape of a soft sphere in contact with a rigid surface (black line) and the Hertzian stress distribution (brown dashed line). On the right: Microscopic view of the contact gap in the undercritical and overcritical cases. From the macroscopic point of view, the gap in both cases is zero, from the micrsocopic point of view, the bodies can be either in direct rigid wall contact (where the local Hertzian pressure is larger σ₀ or “levitate” in the distance h_c where the Hertzian pressure is smaller σ₀.

For two bodies with a plane surface at distance z, Equation (1) is modified to an equation of the interaction stress:

$\begin{array}{ll}\sigma (z)=\frac{8·\Delta \gamma }{3z_0}\left[{\left(\frac{z_0}{z}\right)}^9-{\left(\frac{z_0}{z}\right)}^3\right]\text{ for attractive van der Waals forces}& (2)\end{array}$

where z₀ is the equilibrium distance between the bodies (of the order of r₀), and Δγ is the (positive) specific work of adhesion (work of separation of two surfaces per unit area).

While in vacuum the van der Waals forces are always attractive, in the presence of an intermediate medium between two bodies, they can also become repelling—if the dielectric constant of the intermediate medium lies between the dielectric constants of the contacting bodes (Dzyaloshinskii et al., 1961). In this case, Equation (1) for the interaction force is modified by changing the sign of the van der Waals force, Figure 1A, left:

$\begin{array}{l}F(r)=\frac{12·w}{r_0}\left[{\left(\frac{r_0}{r}\right)}^{13}+{\left(\frac{r_0}{r}\right)}^7\right]\\ \text{ for repelling van der Waals forces}.& (3)\end{array}$

In this equation, r₀ loses its meaning of the equilibrium position (which without external force does not exist anymore), but can still be considered as a distance characterizing the transition from the “core potential” to the “van der Waals potential.” At smaller distances, the repelling force increase very steeply and can be qualitatively considered as a “rigid wall,” while at larger distances it describes long range repelling van der Waals force. For bodies with plane surfaces, the corresponding modification of Equation (2) reads

$\begin{array}{l}\sigma (z)=\frac{8·\Delta \gamma }{3z_0}\left[{\left(\frac{z_0}{z}\right)}^9+{\left(\frac{z_0}{z}\right)}^3\right]\\ \text{ for repelling van der Waals forces}.& (4)\end{array}$

Therein, Δγ is not the work of adhesion anymore but has to be considered just formally as a coefficient determining the amplitude of the interaction. However, if we calculate the “work needed to separate” the bodies starting with the distance z₀ (the presumable position of the “rigid wall”), we get the specific “negative work of adhesion”

$\begin{array}{ll}\Delta {\gamma }_{repelling}=-(5/3)\Delta \gamma .& (5)\end{array}$

In the past, there were only a few attempts to study contact mechanics in the presence of explicit surface interaction potential (“soft walls”) (e.g., Hughes and White, 1979; Vinogradova and Feuillebois, 2003; Müser, 2014). However, these works were focused on the normal interaction while we would like to discuss the implications of the surface interactions to the tangential force (friction).

Influence of Repelling van der Waals Forces on Contact and Friction

As Martin Müser writes in Müser (2014), “For repulsive contacts,…, there is obviously no finite contact radius at zero normal load …The repelled rigid tip simply “hovers” at (infinitely) large distance over an undeformed elastic manifold …”. Let us consider this absolutely correct statement more closely. It is correct that the repelling van der Waals forces will keep the surfaces at “infinite large distance” which physically means at “very large distance.” However, from the macroscopic point of view, this “very large distance” may be smaller than any other characteristic length of the contact problem and thus can be considered as being zero (JKR-approximation). In the contact with repelling forces, the smallest characteristic length is the indentation depth, so the range of van der Waals interactions is assumed to be smaller than the indentation depth.

Whether the “very large distance” is zero or infinite—depends on the quantities, which we are interested in. If we consider the contact problem itself and the range of repelling van der Waals forces can be neglected, then they have no influence on the contact problem at all. In particular, all displacements and stress distributions will remain the same as in the classical “rigid wall” Hertz contact problem. However, if we consider the tangential forces (caused by the microscopic tangential corrugation potential), the “very large distance” can again be considered as infinite which leads to a vanishing force of friction. In order for the macroscopic frictional force to disappear, it is not even necessary that the tangential corrugation potential becomes zero; it is enough that it becomes smaller than some critical value, as has been shown theoretically and experimentally in Socoliuc et al. (2004).

When two surfaces approach each other, the interaction stress (4) increases monotonously and accepts at the distance z = z₀ the value σ₀ = (16/5)(Δγ_repelling/z₀). If the local elastic stress in the material is larger than this critical stress, then, roughly speaking, the bodies are in “rigid wall contact.” If the local stress is much smaller than this critical stress, then the surfaces “hover” at “infinitely large distance.” In a Hertzian contact, all parts of the contact where the stress is larger than the critical one, will be in “direct rigid wall contact,” and feel strong corrugation potential, while the areas where the stress is essentially smaller then σ₀ will be held apart by the repelling van der Waals forces and feel only a very weak corrugation potential. This is illustrated in Figure 1A, right for the example of a Hertzian contact. The contact area is divided into two parts: the inner part of “rigid wall contact” and high friction and the outer part of levitation due to repelling van der Waals forces and a weak (or zero) friction force. Figure 1B schematically illustrates the macroscopic and microscopic views of the contact for the case of a simplified repelling stress of “Dugdale type” (Dugdale, 1960).

The most interesting conclusion is that if the Hertzian stress is smaller than the critical stress needed to bring the surfaces into the “rigid wall contact,” then they “levitate” in the whole contact area. This inevitably should lead to a small or vanishing macroscopic frictional force—the macroscopic state of superlubricity. The critical stress depends on particular mechanism of repulsion force. A very rough estimation can be made by assuming the value of Δγ ~ 4 · 10⁻² J/m² for the surface energy [which is “typical” for polymers and fluids (Popov, 2017)] and Δl ~ 10⁻⁹ m as the “levitation” distance needed for suppressing the tangential corrugation potential. The critical stress will then be on the order of σ_c ~ Δγ/Δl ≈ 40 MPa. In Ge et al. (2019a), the values up to 600 MPa were reported.

Conclusion

Let us briefly summarize the main points of the above-sketched picture:

1. If one does not look at the contact so closely, the “adhesive” repulsion looks just like a hard wall, similarly to the actual hard wall of the Pauli principle.

2. Therefore, in this “JKR-limit” nothing changes in the solution of the contact problem.

3. Nevertheless, if one looks more closely, the adhesive repulsion (as opposed to the hard wall) has some reach, so this long-range tail of the repelling force can hold the surfaces apart.

4. There is (almost) no friction in the areas that are levitating due to “negative adhesion.”

5. If the maximum stress in the whole contact area is smaller then the “critical stress of levitation,” the system transits into the state of very low (or vanishing) friction—state of superlubricity.

The key prerequisite of the described mechanism of superlubricity is the presence of repelling long range interaction forces which are able to hold the surfaces apart so that they do not feel the corrugation potential. This repulsion can be achieved in different ways:

- As repelling van der Waals force due to an intermediate medium with dielectric constant lying between the dielectric constancies of both contacting bodies. This mechanics can only be active for a contact of two bodies having different dielectric constants.

- As thermodynamic repulsion due to a layer of free or grafted macromolecules between the bodies so that the entropy of the intermediate layer decreases at small distances due to stronger confinement.

- As electrical repulsion due to external electrical voltage (so that both surfaces receive the charge of the same sign).

- As repulsion due to electrical double layer (Guldbrand et al., 1984).

- Possible is also an effective repulsion due to thermal fluctuations (Müser et al., 2019).

The necessity of an intermediate layer for achieving negative work of adhesion leads to the conclusion that the kinetic friction will also be essentially dependent on the rheology or viscosity of this intermediate medium. The importance of the local pressure brings the problematics of the surface roughness in play. The flattening of roughness and lowering local stresses may be one of the reasons of the necessity of the wearing-in process for achieving the superlubricity state (Ge et al., 2019a).

In my opinion, the above simple picture can help a lot for both qualitative and quantitative physical understanding of the transition into the superlubricity state—both in the case of fluid superlubricity (Ge et al., 2019b) and solid state superlubricity (Erdemir and Eryilmaz, 2014) as well of the tuning of friction by electric fields (Krim, 2019; Figure 1).

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was funded by the German Research Foundation (DFG PO 810/55-1).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I am grateful to Emanuel Willert and Qiang Li for discussions. I acknowledge support from the German Research Foundation and the Open Access Publication Funds of TU Berlin.

References

Dugdale, D. S. (1960). Yielding of steel sheets containing slits. J. Mech. Phys. Solids 8, 100–104. doi: 10.1016/0022-5096(60)90013-2

CrossRef Full Text | Google Scholar

Dzyaloshinskii, I. E., Lifshitz, E. M., and Pitaevskii, L. P. (1961). General theory of van der Waals' forces. Sov. Phys. Usp. 4, 153–176. doi: 10.1070/PU1961v004n02ABEH003330

CrossRef Full Text | Google Scholar

Erdemir, A., and Eryilmaz, O. (2014). Achieving superlubricity in DLC films by controlling bulk, surf ace, and tribochemistry. Friction 2, 140–155. doi: 10.1007/S40544-014-0055-1

CrossRef Full Text | Google Scholar

Ge, X., Li, J., and Luo, J. (2019b). Macroscale superlubricity achieved with various liquid molecules: a review. Front. Mech. Eng. 5:2. doi: 10.3389/fmech.2019.00002

CrossRef Full Text | Google Scholar

Ge, X., Li, J., Wang, H., Zhang, C., Liu, Y., and Luo, J. (2019a). Macroscale superlubricity under extreme pressure enabled by the combination of graphene-oxide nanosheets with ionic liquid. Carbon 151, 76–83 doi: 10.1016/j.carbon.2019.05.070

CrossRef Full Text | Google Scholar

Guldbrand, L., Jönsson, B., Håkan Wennerström, H., and Linse, P. (1984). Electrical double layer forces. A Monte Carlo study. J. Chem. Phys. 80:2221. doi: 10.1063/1.446912

CrossRef Full Text | Google Scholar

Heß, M., and Popov, V. L. (2019). Voltage-induced friction with application to electrovibration. Lubricants 7:102. doi: 10.3390/lubricants7120102

CrossRef Full Text | Google Scholar

Hughes, B. D., and White, L. R. (1979). ‘Soft' contact problems in linear elasticity, Q. J. Mech. Appl. Math. 32, 445–471. doi: 10.1093/qjmam/32.4.445

CrossRef Full Text | Google Scholar

Israelachvili, J. N. (2011). Intermolecular and Surface Forces, 3rd Edn. Waltham, MA; San Diego, CA; Oxford; Amsterdam: Elsevier. doi: 10.1016/C2009-0-21560-1

CrossRef Full Text | Google Scholar

Johnson, K. L., Kendall, K., and Roberts, A. D. (1971). Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A 324, 301–313. doi: 10.1098/rspa.1971.0141

CrossRef Full Text | Google Scholar

Krim, J. (2019). Controlling friction with external electric or magnetic fields: 25 examples. Front. Mech. Eng. 5:22. doi: 10.3389/fmech.2019.00022

CrossRef Full Text | Google Scholar

Müser, M. H. (2014). Single-asperity contact mechanics with positive and negative work of adhesion: influence of finite-range interactions and a continuum description for the squeeze-out of wetting fluids, Beilstein J. Nanotechnol. 5, 419–437. doi: 10.3762/bjnano.5.50

PubMed Abstract | CrossRef Full Text | Google Scholar

Müser, M. H., Zhou, Y., and Wang, A. (2019). How thermal fluctuations affect hard-wall repulsion and thereby Hertzian contact mechanics. Front. Mech. Eng. 5:67. doi: 10.3389/fmech.2019.00067

CrossRef Full Text | Google Scholar

Popov, V. L. (2017). Contact Mechanics and Friction: Physical Principles and Applications, 2nd Edn. Berlin; Heidelberg: Springer. doi: 10.1007/978-3-642-10803-7

CrossRef Full Text | Google Scholar

Popov, V. L., and Hess, M. (2018). Voltage induced friction in a contact of a finger and a touchscreen with a thin dielectric coating. arXiv[Preprint].arXiv:1805.08714

Google Scholar

Socoliuc, A., Bennewitz, R., Gnecco, E., and Meyer, E. (2004). Transition from stick-slip to continuous sliding in atomic friction: entering a new regime of ultralow friction. Phys. Rev. Lett. 92:134301. doi: 10.1103/PhysRevLett.92.134301

PubMed Abstract | CrossRef Full Text | Google Scholar

Vinogradova, O. I., and Feuillebois, F. J. (2003). Interaction of elastic bodies via surface forces 2. Exponential decay. Colloid Interface Sci. 268, 464–475. doi: 10.1016/j.jcis.2003.09.00

PubMed Abstract | CrossRef Full Text | Google Scholar