Firebrand Generation From Thermally-Degraded Cylindrical Wooden Dowels

Introduction

Over the past few decades, wildland fires have been increasing in size, frequency, and severity (Caton et al., 2016; Balch et al., 2017). These fires result in many large-scale disasters, in particular at the Wildland-Urban Interface (WUI), where human development and unoccupied land intermingle. This trend is projected to increase due to fire management policies, an increase in land development adjacent to wildlands, and climate change (Howard, 2014; Tohidi, 2016; Tohidi and Kaye, 2017a). In order to improve land development and wildfire management policies, map the risks from wildfires, and improve the resilience of WUI communities, it is imperative to understand and model the mechanisms by which fires ignite communities and pose serious threats to people, properties, infrastructure, and ecosystems.

Three pathways for wildland fire spread and ignition in WUI communities have been identified. These include direct flame impingement on fuel sources, radiation, and firebrand showers. Firebrands are combusting pieces of vegetation or structural elements that break off of burning elements during wildfires or other large conflagrations. During many of these fires, a large number of firebrands are formed creating a “shower” of brands lofted into the fire plume. These lofted firebrands travel downwind and upon landing eventually ignite spot fires far ahead of the main fire front (Koo et al., 2010; Tohidi and Kaye, 2017a,b) (Figure 1). Investigations of several past WUI fires have revealed that firebrand showers are often responsible for more than half of the reported ignitions (Manzello et al., 2008; Caton et al., 2016).

FIGURE 1

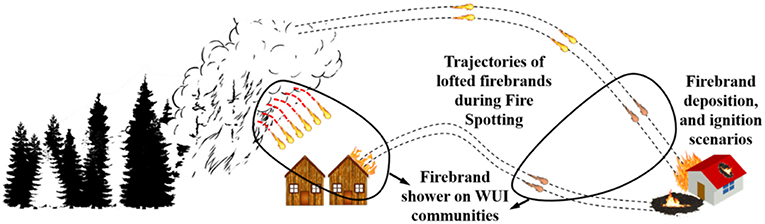
Figure 1. Schematic of a firebrand shower scenario in the wildland-urban interface (WUI); excerpted from Tohidi and Kaye (2017c) with permission.

Among the three phases important for firebrand showers: generation, transport and ignition, firebrand transport has received the most attention both experimentally and numerically (Albini, 1979; Sardoy et al., 2007; Tohidi and Kaye, 2017b,c). Numerous studies have collected data on the general characteristics of firebrands, i.e., the mass, surface area, and shape, that are formed from trees (Manzello et al., 2006a, 2008, 2009, 2007a; Mell et al., 2009), structural elements (Suzuki et al., 2012a,b), and during small prescribed fires (El Houssami et al., 2016). Studies on the ignition of fuel beds and some structural components have also been reported (Manzello et al., 2006b; Hadden et al., 2010), however very few works on the actual formation processes of firebrands from thermally-degraded vegetative elements can be found in the literature (Barr and Ezekoye, 2013; Tohidi et al., 2015);(Chen et al., 2017).

Barr and Ezekoye (2013) proposed a thermo-mechanical breakage model for firebrands formed from a fractal tree. Later, Tohidi et al. (2015) presented a mechanical break-off model for firebrand formation from cylindrical twigs and tree branches with relatively high aspect ratios, i.e., length over diameter (η = L/D). Chen et al. (2017) also recently investigated, both experimentally and numerically, the burning rate and burning lifetime of wooden particles of different ellipsoid shapes and, similar to Tohidi et al. (2015) concluded that the aspect ratio of the elements is an important factor in material failure. Although findings from these studies lay the foundation of break-off analysis, the effects of thermal-degradation of the material under external loading is not directly addressed.

Therefore, the present study focuses on the behavior of thermally-degraded cellular solids (wooden elements) under subsequent external loading. With the lack of current knowledge in the area, this work is meant to propose a framework and a model to understand the behavior of thermally-degraded wooden elements with a cylindrical shape under external loading such as wind-induced drag. Beyond its importance in wildland and WUI fires, wood is the most widely used structural material (Gibson and Ashby, 1999), however there are few studies on the behavior of thermally-degraded wooden elements under external loading. After a review of the processes applied to this problem, a series of experiments are presented which capture the effects of thermal-degradation on failure mechanisms of wooden dowels that are exposed to flames and subsequently subjected to external loading. Utilizing the collected data during experiments, a dimensional analysis is conducted on the parameter space. The results of the scaling analysis suggest that there are two distinct failure regimes dominating the breakage and ultimately the formation of firebrands from thermally-degraded wooden elements.

Formation Mechanisms (Evolution) of Firebrands

The mechanisms that lead to firebrand formation from wooden elements may be related to the physical properties of the materials both prior and after thermal-degradation. Previous studies have proposed mechanical break-off models which relates the physical properties to the failure mechanism of the samples. For instance, Barr and Ezekoye (2013) report a linear correlation between the flexural stress (corresponding to the critical fracture load) and the density of pyrolyzed firebrands (wooden cylinders) in three-point-bending tests. This is similar to Easterling et al. (1982) results from balsa wood samples, where the collapse stress $({\sigma }_L^c)$ was found to be linearly proportional to the relative density of the wood,

$\begin{array}{ll}{\sigma }_L^c\propto (\frac{\rho }{{\rho }_s}).& (1)\end{array}$

Here, ${\sigma }_L^c$ is the stress recorded at the point of collapse in the longitudinal direction (parallel to the grain), ρ is the density of the wood species, and ρ_s is the density of the wood cell-wall material. Following this, Tohidi et al. (2015) assumed that failure occurs once the distortion energy of the wood from bending moment-induced shear exceeds the yield energy of the wood. This is assuming the maximum allowable stress of the wood sample remains constant during the generation process. While this is a simplified mechanical model, decoupled from combustion effects, it incorporates the effects of mass in addition to drag forces due to vertical and horizontal velocities in the fire plume to calculate the bending moments of tree branches. A non-dimensional parameter was also introduced that quantifies the relative importance of firebrand weight and vertical drag on the bending moment that connects individual branches to the main element. Using this parameter, it was shown that drag-driven (wind-driven) firebrand formation is the dominant formation mechanism and that firebrands with large aspect ratios (η > 3) are more likely to form and be lofted through the fire plume. These results are consistent with experimental observations from burning trees by Manzello et al. (2007b). In addition, results presented by Chen et al. (2017) support previous models as it concludes that the larger aspect ratio firebrands decompose faster, which makes them more susceptible to failure due to external loading.

The micro-structure of wood plays a critical role in its physical degradation and failure (Gibson and Ashby, 1999). At fine scales, wood is a cellular composite with different geometric configurations that depend on the type and species of the wood. Generally, wood species can be categorized as hardwoods (dense) and softwoods (light) (Easterling et al., 1982). Hardwoods are deciduous angiosperms with pores and vessels in their micro-structure, whereas softwoods are gymnosperms (conifers) that do not have pores and vessels (Dinwoodie, 2000). In angiosperms (hardwood), more than 90% of the wood is aligned in the longitudinal direction, whereas in gymnosperms (softwoods), this cell distribution varies between 80 and 90%. The rest of the material is distributed through rays in radial and tangential directions, which implies a high degree of anisotropy in wood structure (Dinwoodie, 2000). Figure 2 illustrates a typical wood structure from a full tree down to the micro-scale structures within. While the behavior of composite or tapered wood samples are also of interest in firebrand formation, their physical and chemical properties might be different and are not included in this work. This also holds true for samples with a shell-type geometry, such as tree bark, although the introduced framework may be applicable to their study in the future.

FIGURE 2

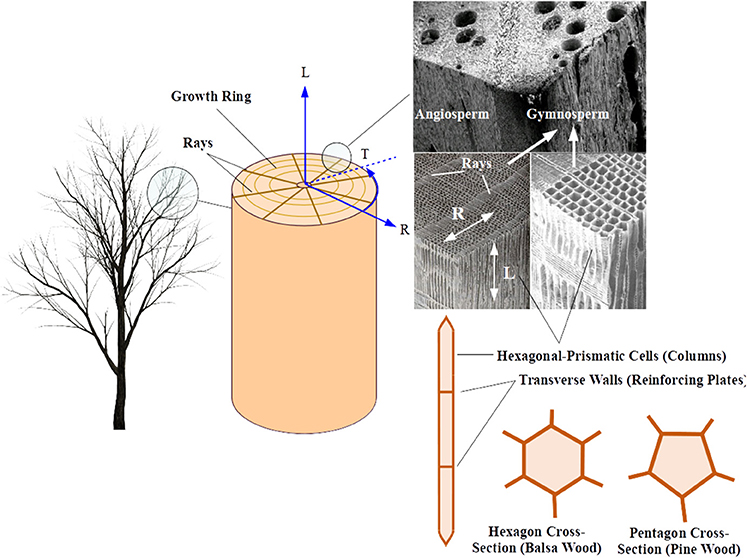
Figure 2. Schematic of wood structure at different scales; shown are the customary coordinates aligned with rays, growth rings and fibers (grain), i.e., Radial, Tangential, and Longitudinal (RTL), along with a Scanning Electron Microscopy (SEM) image of typical angiosperm and gymnosperm wood species, here, Pinus and Balsa wood. The SEM images show the general micro-structure of the hardwood (top) and softwood (bottom) which are, respectively, excerpted from Wikipedia and raw materials of Koch (1972a,b).

A framework for understanding firebrand formation is first presented here, as such a description does not yet exist in the literature. The process is viewed in three phases which occur across different scales. First, a thermo-mechanical instability (buckling) develops at the micro-scale, leading to crack formation. Second, a series of physiochemical degradation processes that involve pyrolysis and oxidation occurs through which the material losses its structural integrity, and finally thermo-mechanical break-off due to external loading, most likely via wind or body forces such as gravity occurs at the macro-scale. In a real scenario, these three phases occur sequentially or, more likely, simultaneously depending on the intensity of heat exposure and mechanical loading scenarios.

At the micro-scale, natural wood is a fiber-reinforced composite made up of crystalline cellulose fibers embedded in a matrix of (amorphous) hemicellulose and lignin (Easterling et al., 1982; Gibson and Ashby, 1999) (see Figure 2). Previous studies, i.e., Gibson and Ashby (1999), Easterling et al. (1982) and Ashby (1983) have shown that the material's density, dimensions, and shape of the cell walls at the microscale determine the anisotropy and mechanical properties of the wood in macroscale (RTL coordinates), that is the modulus of elasticity, bending, buckling, plastic collapse, and fracture mechanisms (Easterling et al., 1982; Ashby, 1983; Gibson and Ashby, 1999). If the samples of wood are extracted at sufficient distance from the pith where the curvature of the growth rings are relatively small (i.e., a large radius), it is reasonable to assume that wood in the tangential (T) and radial (R) directions is orthotropic, i.e., E_L ∝ ρ/ρ_s, $E_{RT}\propto {(\rho /{\rho }_s)}^3$, ${\nu }_{TL}={\nu }_{RL}\approx {O}(0.01)$, and ${\nu }_{TR}={\nu }_{RT}\approx {O}(0.5)$ (Easterling et al., 1982; Gibson et al., 1982) where E is the module of elasticity, ν is Poisson's ratio, and subscripts show the directions in RTL coordinates system. This is consistent with the fact that, as a tree grows, pores and vessels in the outer layers (latewood) get smaller relative to the ones in the center (earlywood) (Dinwoodie, 2000). The longitudinal direction (L) would be different as the microfibrils of cellulose in the cells are mostly aligned in the L-direction and prismatic cells are stiffer under tension and compression in the L-direction in relation to bending in the R and T directions. Other factors such as age and moisture content play an influential yet secondary role on the mechanical properties of the wood.

It should be noted that the orthotropic assumption could be violated in this study due to the small diameter of samples used. However, samples are oven-dried and deliberately chosen such that the grains are aligned with the longitudinal direction (length of the samples). Therefore, as demonstrated in the experimental results, the differences between physical properties in the longitudinal direction compared to the ones in the radial/tangential direction are significant, which suggests that the orthotropic assumption is still valid and appropriate. For a detailed description of the mechanical properties, deformation, and behavior of wood, refer to either Gibson and Ashby (1999) or Dinwoodie (2000). Having reviewed the micro-structure of wooden elements, a three-phase thermal-degradation mechanism can now be described.

Phase I: Thermo-Mechanical Instability (Buckling)

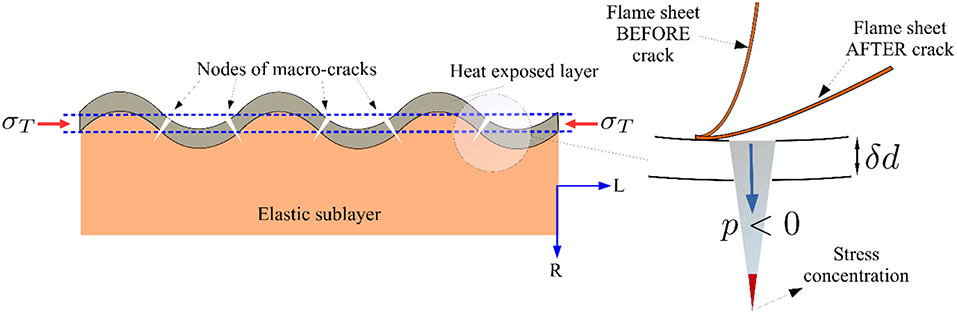
Burning cellulosic materials, such as wood, forms a layer of char that significantly reduces heat conduction to virgin wood at the inner layers and subsequently reduces the burning rate of the uncharred material. However, the charred layer may shrink and crack, which notably affects the pyrolysis and oxidation of the sample material (Bryden and Hagge, 2003; Li et al., 2014). It was initially thought that pyrolysis and oxidation were the primary mechanisms of crack formation for heat-exposed wood samples. However, recent work by Baroudi et al. (2017) showed that, due to a global thermo-mechanical instability in the heat-exposed layer at temperatures below the pyrolysis temperature $(T_p\approx 573{}^{◦}K),$macro-crack patterns are established before physiochemical processes dominate.

External heating of wood samples, either through radiation or direct flame exposure (convection), not only boils entrapped water within the virgin wood, but also leads to the transformation of some of the chemical components of the material to gases (pyrolysis). Accumulation of the water vapor and gases builds up a hydrostatic pressure inside the material and increases the internal pressure, shown illustratively in Figure 3.

FIGURE 3

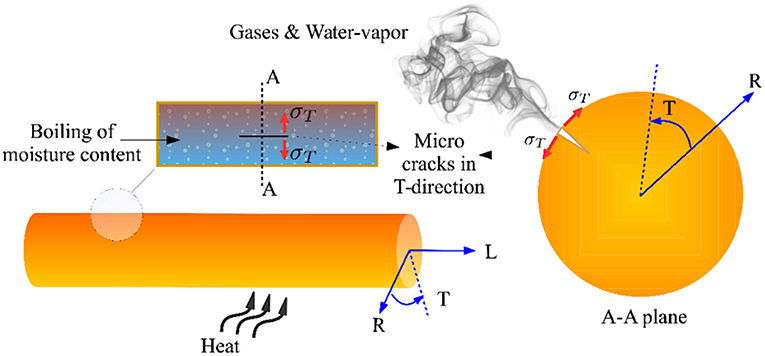
Figure 3. Schematic of the evolution of micro-crack patterns through the heat-exposed wooden material.

As the internal hydrostatic pressure increases, preliminary micro-cracks evolve in the tangential direction, eventually leading to the rupture and exit of gases, shown in Figure 3. This is expected as the tangential moduli (E_T) of the wood varies with the cube of the relative density as opposed to the linear relation of E_L with relative density; wood is a much stronger and stiffer material in the longitudinal direction than the transverse (tangential/radial) direction (Easterling et al., 1982; Ennos and Van Casteren, 2010). This is partly due to the fact that more than 80% of the microfibrils in the cell walls lie along the longitudinal direction, which makes the cell walls stiffest in that direction (Mark, 1907; Dinwoodie, 2000), and partly due to the prismatic shape of the cell walls that are stiff axially and less stiff transversely (Gibson and Ashby, 1999). Depending on the age of the wood, its moisture content, and species type, this process is likely to continue even at the macro-scale and leads to a crack in the longitudinal direction. In addition, after release of water vapor and gasses the material shrinks due to lower external ambient pressure which increases the opening of micro-cracks. As shown in Figure 4-right, the evolution of micro and macro cracks on the surface of the heat-exposed layer not only generates a temporary path for the discharge of gases and water vapor, but also induces a negative pore pressure which may pull the flame sheet closer to the wood surface (Li et al., 2015). After the release of water vapor and gases from the sample and generation of a negative pressure field, the material starts to shrink at the micro-scale, exacerbating the effects of micro-cracks.

FIGURE 4

Figure 4. Development of global macro-crack patterns.

In addition to the previously-described effects, the negative-pressure increases the heat feedback from the flame to the fuel surface and amplifies thermomechanical effects. With persistent heat exposure, wood enters a rubber-like state and softens as the temperature exceeds the sample's glass transition temperature; here denoted by T_g. For dry wood with 10% moisture content, T_gis about 373 K, which is well-below the pyrolysis temperature of the wood (Salmén, 1984, 2004; Bažant, 1985; Antoniow et al., 2012; Baroudi et al., 2017). Because wood is an elasto-viscoplastic natural composite consisting of cellulose and hemicellulose-lignin matrices, e.g., polyermic materials, the elasticity modulus in all directions decreases around close to the glass transition temperature, while the thermal expansion coefficient of the wood increases dramatically (Li et al., 2016; Baroudi et al., 2017). This behavior induces substantial thermal stresses on the surface of the heat-exposed layer (hot-layer) before the formation of any char layer (Baroudi et al., 2017; Tohidi et al., 2017). Baroudi et al. (2017) showed that the thermal stresses, indicated as σ_T in Figure 4-left, are due to resistance against thermal expansion from the cold elastic sublayer (virgin wood). Assuming a thin-plate approximation for cases when T_g < T < T_p and utilizing the Kirchhoff-Love theory of plates (Ventsel and Krauthammer, 2001; Li et al., 2016; Baroudi et al., 2017), it can be shown that by increasing thermal stresses, buckling occurs during transition from a membrane bi-axial state (flat plate) to a post-critical membrane and bending state (wrinkle-shaped plate), see Figure 4-left. At nodes of the buckled plate in a post-critical state, principal tension stresses exist which may lead to the development of macro-crack patterns perpendicular to the grains (Baroudi et al., 2017) as well as elongating and deepening existing cracks. Importantly, macro-crack patterns appear to emerge before char formation (Baroudi et al., 2017). Figure 5 shows evidence of the development of global macro-crack patterns on birch dowels exposed to a propane flame at different times in this study; the experimental methods shall be discussed in section Experimental Methodology. Concepts of this framework may apply to shell-type wooden elements, e.g., tree bark, however this is beyond the scope of this study.

FIGURE 5

Figure 5. Shown are the of the global periodic macro-crack patterns due to thermo-mechanical instabilities. From top to bottom the flame exposure times are 10, 15, and 20 s for the 6.35 mm diameter birch dowels.

Phase II: Physiochemical Processes (Pyrolysis and Oxidation)

During pyrolysis, elevated temperatures initiate reactions within the organic material that changes its chemical composition and primarily forms char (Turns, 2000). Several studies (Ragland et al., 1991; Spearpoint and Quintiere, 2001; Haas et al., 2009; Liu et al., 2013; Sedighi Gilani et al., 2013; Li et al., 2016), however, have shown that the micro-structure of charred wood has a cellular form and wood charring due to pyrolysis does not change the micro-structure of the wood. Despite the fact that a consensus on this behavior does not exist, Hagge et al. (2004) argues that this is primarily due to reconstruction of chemical bonds and carbon atom connections. Thermal decomposition under pyrolysis transforms the material to char which produces a considerable amount of gas and leaves behind a porous media (Shen et al., 2009; Li et al., 2016). This porous media shrinks considerably under ambient pressure. Non-uniform shrinkage may lead to the generation of internal stress and, subsequently, unbalanced penetration of developed cracks in previous phases through the affected (char) layer; see Figure 5. As pyrolysis transforms a wooden element into a porous medium, its surface density and subsequently its stiffness will significantly decrease. Hence, the combined effects of the stress concentration at the tip of the already developed cracks (see Figure 4-right) and loss of structural stiffness (integrity), help the cracks gain sufficient depth through the charred layer. Once these macro-cracks or fissures are established, their number and path generally does not change (Li et al., 2016). It is also shown that the length of the crack is directly proportional to the square root of the heating time (Li et al., 2016). This is consistent with the findings of Nguyen et al. (2017) on crack morphology, where it is shown that short cracks develop after long fissures are established. Eventually, short and long cracks converge and, so long as a heat source exists, pyrolysis continues until full degradation of the wooden element's cross section.

With the presence of ambient oxygen, oxidation of the surface material also occurs, during which the surface of the solid material reduces without a significant change in density and remaining strength (Barr and Ezekoye, 2013). This process is associated with the formation of oxides from oxygen molecules (formation of ash over the charred layer). Continuation of pyrolysis and oxidation leads to the full thermal degradation of the material. As a result, established macro-cracks penetrate throughout the entire depth of the material thickness and cause brittle failure/break-off from the main wooden branches that are not yet fully degraded (Tohidi et al., 2017).

Phase III: Presence of External Loading or Constraints

While thermal degradation of the wooden elements alone can cause failure, during a typical fire scenario external loading of the elements will also contribute to failure. External loading is often applied due to a buoyancy-driven updraft flow in the fire plume, wind or entrainment-driven horizontal flow, and the weight of the wooden branches. These are considered in a simple mechanical break-off model by Tohidi et al. (2015). In a real fire scenario, the flame exposure and consequently heat conduction are not uniform throughout heated samples. The resulting temperature gradient leads to non-uniform thermal expansion and compression, as shown in Figure 6.

FIGURE 6

Figure 6. Observations of the combined effect of thermal rolling and thermal degradation in firebrand formation from a burning Leyland Cypress tree performed under wind at the IBHS wind tunnel.

The thermal effects due to this temperature gradient will be manifested as either internal stresses, if the element is restrained, or displacement, if the element is unrestrained (Usmani et al., 2001). Most tree branches and twigs can be considered cantilever beams where there is at least one boundary constraint at the joints. These restraints play a major role in determining the response of wooden elements to fire (heat) exposure. In fact, for branches at the top of what could be considered a fractal chain, the induced thermal strains lead to continuous rolling of the branch as it is simultaneously being thermally-degraded. We call this phenomenon thermal rolling. Upon close investigation of burn scenarios with various fuels, this behavior can be directly observed. Figure 6 shows some evidence of thermal degradation and subsequent rolling along a single branch during combustion of a Leyland Cypress tree at the Insurance Institute for Business & Home Safety's (IBHS) wind tunnel.

In real fire scenarios, thermal rolling occurs when branches experience non-uniform heating as the fire (flame) approaches and heats them more from one side than the other, often upwind. This temperature gradient most likely causes thermal expansion of the lee side and, since one end of the branch is constrained, the cooler material above the neutral axis experiences compression. Therefore, assuming a constant and linear temperature gradient, Hookean-Orthotropic behavior, and a circular cross section, the equivalent uniform moment that develops at the cross-section due to thermal rolling may be characterized as

$\begin{array}{ll}{M}_{r,R}=\left(\frac{3\pi }{128}\right)\beta E_L\frac{\partial T}{\partial z}{D}^5,& (2)\end{array}$

where β is the thermal expansion coefficient, T is temperature, and z is the distance from the neutral axis of the circular cross section. The bending moment in Equation (2) is time-dependent and applies to cylindrical dowels in which the temperature gradient can be resolved. However, this still applies to cylindrical dowels with a relatively small diameter as tree branches show fractal behavior (Barr and Ezekoye, 2013) and only the time scale for the presence of the gradient would be shorter. Due to the time-dependent nature and difficulties of capturing temperature gradients across the cross section of samples within our current experimental setup, the thermal-rolling induced bending moments are not measured in this study. Nevertheless, based on our experimental observations, the time-varying bending moment causes small deflections in elements where thermal degradation is not dominant yet. As time passes, E_L will decrease, but β will increase, and micro and macro cracks will develop throughout the wooden elements. This may further increase the temperature gradient and subsequently the thermal rolling moment, see Equation (2). Hence, the softened element starts to bend, as shown in Figure 6 where thermal rolling is acting simultaneously during the softening of the branch that eventually leads to the brittle failure and detachment or lofting of the firebrand through the wind field. To summarize these processes, the thermo-mechanical failure cycle for a cylindrical wooden element under persistent heat exposure and external mechanical loading is shown in Figure 7.

FIGURE 7

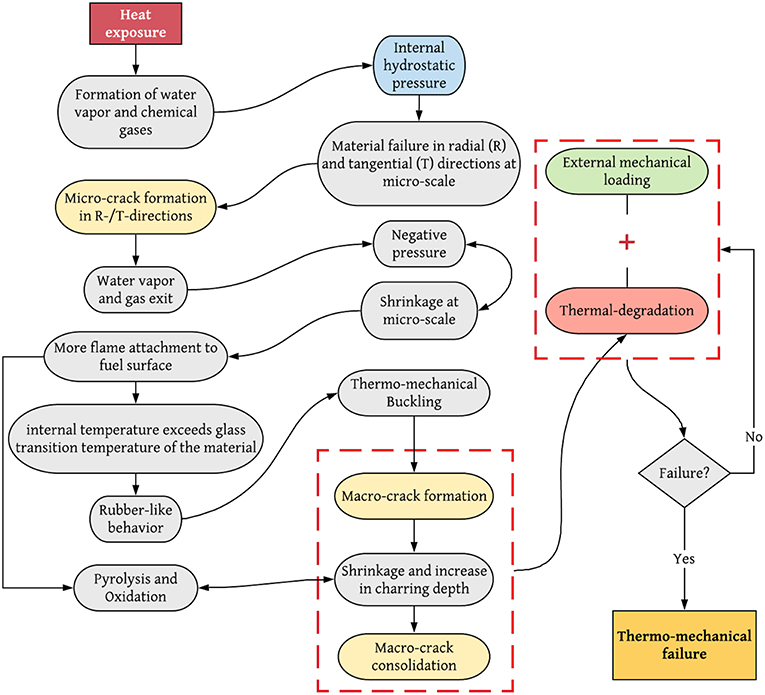
Figure 7. Thermo-mechanical failure cycle for a cylindrical wooden element under continuous heat exposure. Here, arrows with two heads show concurrent processes.

In a real scenario, thermal-degradation of the material occurs concurrently with a variety of dynamic loading combinations. These are primarily due to thermal rolling, traction forces, and body forces which depending on the extent of degradation and magnitude of loading, one of the failure modes in tree branches could occur. The failure modes are (1) diffuse fracture (greenstick), (2) fibrous (clean) fracture, (3) transverse buckling, and (4) brittle rupture. For a detailed explanation of the failure modes in tree branches refer to Ennos and Van Casteren (2010); Casteren et al. (2012).

The process of firebrand generation includes heat transfer in cellular solids, pyrolysis, elastic and elastoplastic deformation, and eventually crack formation and failure. Previous studies (Wichman and Atreya, 1987; Baroudi et al., 2017; Nguyen et al., 2017) are available where the governing equations are presented and numerical simulations of wood charring and crack propagation are conducted. However, very few works discuss the dominant parameters, processes, and failure modes in thermally-degraded wooden elements that lead to firebrand generation. Given this and the detailed explanatory framework of the processes, an experimental methodology along with a series of experiments are devised to investigate the dominant modes of firebrand generation from thermally degraded wooden dowels.

Experimental Methodology

Previous studies (Manzello et al., 2006b) have shown that many firebrands generated from burning vegetation (e.g., conifers) are in cylindrical form. Thus, cylindrical wooden dowels of three different wood species, i.e., birch, oak, and poplar, were chosen for testing. This provides a range of material properties as well as allowing for testing of smaller wooden dowels. The average initial densities measured before testing were 610, 700, and 540 kg/m³ for the birch, oak, and poplar, respectively. Since Barr and Ezekoye (2013) found a relationship between strength and density, a range of initial densities was studied to better understand the role of density in firebrand generation. The density of Douglas fir and pine species, which are more typical species in WUI fires, overlap with the lower range of densities tested in this study. Due to an inability to source hardwoods such as pines in the desired diameter ranges, we chose to use birch, oak, and poplar as surrogates which could be readily supplied for experiments.

The diameter of dowels tested range from about 3 mm to 13 mm (1/8 in to 1/2 in). Previous works (Albini, 1979; Suzuki et al., 2012a,b) have found that the average firebrand diameter ranges from 3 to 5 mm, which motivated the dowel sizes used in these experiments. All of the dowels were cut to 10.16 cm (4 in) in length for the three-point bending tests. Moisture contents were measured with a moisture content analyzer which dried the fuel over a load cell. The moisture content ranged from 5 to 8% on a dry basis for all three species. Drying the dowels to lower moisture contents was tested but did not have an effect on the results of the bending tests.

Dowels were weighed and then exposed to a propane flame created by a large Bunsen-type burner to induce flaming combustion. While the temperatures produced by this burner were likely higher than those produced in a real wildland fire, they were much more representative of the temperatures and heating rates expected compared to the other heating methods tried in preliminary tests, such as a hot plate and oven (Caton, 2016). The effect of the flaming time on degradation was determined by increasing the exposure time in 5 s intervals from 10 to 20 s. It should be noted that the exposure times are corroborated with the charring depth that is estimated from image processing of the cross section of the extinguished samples. In order to ensure that all pyrolysis and combustion reactions stopped, and that the heating times were as accurate as possible, the dowels were placed in a 22.9 × 33 × 6.35 cm aluminum box after each exposure time. The box was lined with Kaowool ceramic insulation fiber, such that the dowels would not fracture when placed inside. Then, nitrogen gas (N₂) was injected through an inlet hole in the top of the enclosure box. N₂ acted as an inert to extinguish any combustion processes, flaming or smoldering, that were still occurring. After ensuring the combustion reactions cease, the samples were weighed again in order to calculate the mass loss rate.

Finally, three-point bending tests were performed using a PASCO Materials Testing System with the bending accessory on all of the heated dowels. There was also a set of three-point bending tests conducted with virgin dowels of all the species to produce data on initial mechanical properties. The length span between the supports, L₀, was 8.65 cm, with supports located 0.76 cm from the edge of the 10.16 cm long dowel. The Materials Testing System's software measured the force applied to the specimen through the plunger by a 7,100 N load cell in the base of the machine, and the position of the tip of the plunger was measured when the software was recording data by an optical encoder. The loading history of the bending force as well as the associated strain, measured based on the location of the plunger's tip, were collected for each sample until it failed.

Results

The maximum force that each dowel could withstand prior to breakage was measured based on the three-point-bending tests. Ten dowels were tested for each scenario and the mean of the maximum force for each condition was calculated. In the birch tests, the maximum force decreased with increasing time for each diameter. The results of the oak tests demonstrate that increasing the exposure time from 15 to 20 s did not significantly change the maximum force measured for any of the sizes. The poplar dowels lost a significant amount of strength after burning for 10 s but increasing the exposure time beyond 10 s only created small decreases in the ultimate force. Figure 8 shows the observed breakage modes for birch dowels of the same diameter but with different flame exposure times. This trend has been consistently observed for other species as well.

FIGURE 8

Figure 8. Birch dowels with a diameter of 6.35 mm (1/4 in) heated in the flame for 10 s (left) and 20 s (right) which, respectively, show fibrous and brittle fracture modes. This result provides evidence that the breakage mechanisms are dependent on the heating exposure time.

On the left-hand side of Figure 8, samples with shorter flame exposure times (10 s) are shown. Fibrous failure can be observed which implies that the stiffness of the thermally degraded material is the dominating mode of failure. In addition, the presence of the common 45-degrees angle cracks, which show propagation along the longitudinal direction, supports this. By increasing the exposure time (20 s), a change in the crack propagation mode and form of the failure can be observed, shown in Figure 8-right. This type of failure, namely a sudden 90-degree crack, suggests failure of the material in a brittle form. Due to prolonged exposure to the propane flame, the material's cross-section is thermally degraded such that the stiffness of the cross-section is no longer sufficient to withstand the load. Therefore, it suddenly ruptures. These modes of mechanical behavior are effects of the combustion process, which increases the proportion of char within the sample.

The maximum forces that each dowel could withstand prior to breakage were studied as a function of the initial diameter of the dowels for all the tests. Ten dowels were tested for each scenario and the mean of the maximum force for each testing condition was calculated to find the average value associated with the test parameters. The results for the flaming tests are shown in Figure 9 for all three species to demonstrate the differences between the species tested. In the birch tests, the maximum forces decreased with increasing time for each diameter. The results of the oak tests demonstrate that increasing the exposure time from 15 to 20 s did not significantly change the maximum force measured for any of the sizes. The poplar dowels lost a significant amount of strength after burning for 10 s but increasing the exposure time beyond 10 s only resulted in small decreases in the ultimate force. To capture the underlying physics, influential parameters of the experiment are summarized using dimensional analysis in the next section.

FIGURE 9

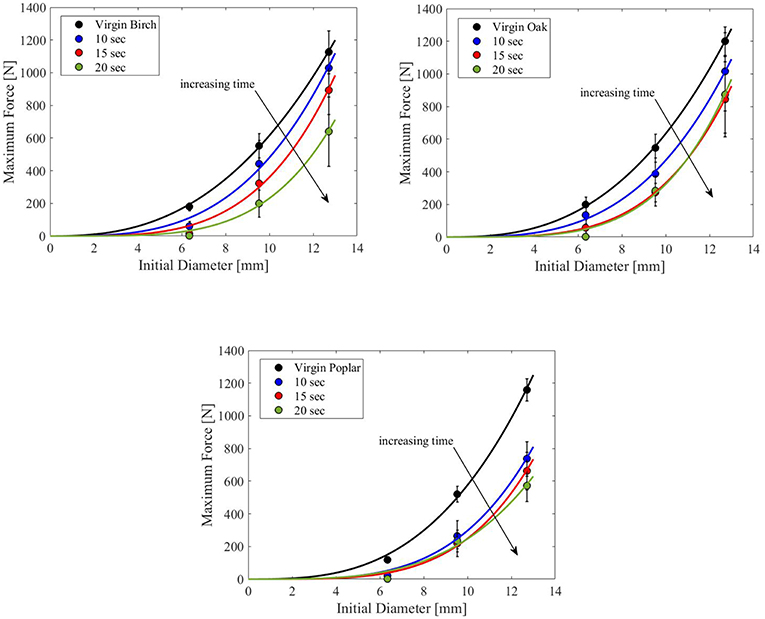
Figure 9. Variation of the maximum force as a function of initial diameter for the birch (top left), oak (top right), and poplar (bottom) in the flaming tests.

Dimensional Analysis

The three-point bending tests provide valuable knowledge about the effects of the combustion processes on breakage mechanisms of cylindrical wooden dowels; however, due to the specificity of the results to the species and size of the dowels, it is beneficial to use non-dimensional analysis to extend and generalize the observations. This approach extracts relationships between a variety of physical quantities based on the identified independent variables and their base physical units (e.g., mass, length, time, etc.), and represents the dependent variables as a function of them. One of the common methods of using this technique is the Buckingham-Π theorem; for details of this method refer to Kundu et al. (2002). As one of the dependent variables, the critical breakage force should be scaled in the parameter space of the experiments. This can be shown by summarizing the parameter space as

$\begin{array}{ll}\psi (F_{max},P_{\infty },{\rho }_s,{\rho }_{\infty },L_0,{\nu }_{RT},E_L,\alpha |\dot{m},{\rho }_0,D_0)=0& (3)\end{array}$

where F_max is the maximum (critical) force before breakage, ρ₀ the initial species' density, L₀ is the length span between the supports of the three-point bending test, D₀ denotes the initial dowel diameter, ν_RT is Poisson's ratio in the radial plane R and in transverse direction T in the RTL coordinate system, α is species' thermal diffusivity, ṁ is the mass loss rate, E_L is the modulus of elasticity in the longitudinal direction, ρ_s is the density of wood cell wall material, and P_∞ and ρ_∞ are the ambient pressure and density, respectively. In Equation 3, respectively from left to right, the dependent variables are separated from the independent variables with a vertical line. Also, the mass loss rate represents the time dependent effects of the flame exposure time. Here, it is assumed that wooden dowels follow Hookean-Orthotropic behavior, i.e., having material properties that differ along three mutually-orthogonal 2-fold axes of rotational symmetry. By utilizing the Buckingham-Π theorem, two governing non-dimensional parameters can be obtained,

$\begin{array}{ll}{\Pi }_1=\left(\frac{\alpha \dot{m}{\rho }_{\infty }}{P_{\infty }{D}_0^3{\rho }_0}\right),{\Pi }_2=\left(\frac{F_{max}{L}_0{\nu }_{RT}}{E_L{D}_0^3}\right)\left(\frac{{\rho }_0}{{\rho }_s}\right)& (4)\end{array}$

Π₁ can be interpreted as the ratio of the average burning rate of the material to its scaled mechanical stiffness and Π₂ is a non-dimensional representation of the recoverable plastic strain in the transverse direction of the dowels. Figure 10 illustrates the variation of these non-dimensional groups under the parameter space of the experiments. As the ratio of the burning rate to the scaled stiffness increases (combustion intensifies), the recoverable transverse strain remains relatively constant until it exceeds the maximum plasticity potential of the wooden dowels, where the failure occurs. Once the magnitude of the recoverable strain tends toward zero, the failure strain tends toward infinity, which effectively causes rupture of the dowels.

FIGURE 10

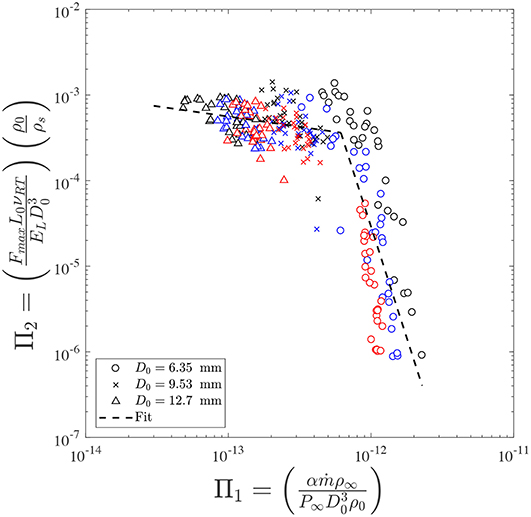
Figure 10. Non-dimensional analysis of the effects of combustion on the breakage mechanisms of wooden dowels of different species. Two distinct failure regimes are shown that control the failure mechanism regardless of the species type and initial physical properties. The exponential fits for the first and second failure modes are ${\Pi }_2=e^{-13.51}{\Pi }_1^{-0.21}$ (approximately horizontal fit) and ${\Pi }_2=e^{-131.51}{\Pi }_1^{-4.38}$ (steep line). (Colored version) Black, blue, and red symbols correspond to 10, 15, and 20 s heat exposure, respectively.

Based on the results shown in Figure 10, two distinct regimes describe the effects of combustion on the breakage mechanism of dowels. The first regime can be shown by an approximately horizontal exponential fit, i.e., ${\Pi }_2=e^{-13.51}{\Pi }_1^{-0.21}$, which demonstrates that the recoverable plastic strain is weakly affected by the burning rate parameter Π₁. This shows that, for cylindrical samples with either short flame exposure times or large (residual) diameters, the stiffness of the material cross section is the dominant parameter in describing the failure mechanism of the sample during bending tests.

The second regime, fitted by the vertical steep line in Figure 10, i.e., ${\Pi }_2=e^{-131.51}{\Pi }_1^{-4.38}$, shows that material strain is strongly affected by changes in the burning rate. Throughout the second regime, the critical breakage force drops significantly, which indicates that samples were more susceptible to failure by a slight increase in the burning rate parameter. This is indicative of the fact that, for samples with either longer exposure times or smaller (residual) diameters, the dominant factor that accounts for the failure is thermal degradation, as the stiffness of the cross section is not sufficient to overcome the thermal degradation effects. Further, it is evident that the diameter, size, and plasticity of the samples are the controlling factors for the observed transition between the failure regimes. The flaming time (shown by the changing colors of the symbols) which to some extent represents variations in the plasticity of the thermally degraded samples, shows that the exposure time is another controlling parameter as well since the dowels with longer exposure time were more susceptible to fracture. Moreover, the presented analysis is invariant with respect to the species type.

Conclusions

With the eventual goal of modeling the generation of firebrands from diverse vegetative species, a phenomenological framework was presented to understand thermal-degradation and failure of cylindrical wooden elements under simultaneous external loading. Depending on the state of thermal degradation and extent of external loading, four failure modes are possible: (1) diffuse fracture (greenstick), (2) fibrous (clean) fracture, (3) transverse buckling, and (4) brittle rupture. To further investigate the dominant modes, an experimental methodology for testing the effects of combustion on the strength of small cylindrical wooden dowels in the laboratory utilizing a propane flame, nitrogen extinction, and three-point bending tests is presented. Scaling analysis of the experimental results suggests that the fracture mode, i.e., fibrous or brittle, primarily depends on the ratio of burning rate to initial stiffness, regardless of species type and initial physical properties. These two regimes summarize the thermal degradation of the wooden dowels in terms of the recoverable transverse strain. Despite these preliminary results, more detailed experiments and analysis are needed in order to extend the observed results, including development of an improved plasticity model and testing of more species, diameters and lengths so that results can eventually be incorporated into a time-dependent firebrand release model for different species.

Author Contributions

SC-K did the experiments, some initial analysis, and visualization of the experimental results. AT provided the description of firebrand generation from thermally-degraded material and did the dimensional analysis of the experimental results. MG advised the work and edited the manuscript.

Funding

This work was partially performed with support from financial assistance awards 70NANB15H176 and 70NANB16H284 from the U.S. Department of Commerce, National Institute of Standards & Technology, Fire Research Grants Program. SC-K was employed by NIST as a Pathways Intern during the course of this research. Additional support is also acknowledged from the USDA Forest Service through cooperative agreement 15-CA-11272167-058 funded through the Joint Fire Science Program award 15-1-04-4 for tests conducted at IBHS.

Conflict of Interest Statement

SC-K was employed by the company Jensen Hughes and AT was employed by the company One Concern Inc.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Nelson Bryner of NIST for multiple suggestions which have contributed to this work, Stephen Quarles and the rest of the staff at IBHS for running the experiments demonstrated in Figure 6 and Raquel Hakes for her assistance in laboratory experiments.

References

Albini, F. A. (1979). Spot Fire Distance From Burning Trees—A Predictive Model. Ogden: Intermountain Forest and Range Experiment Station, Forest Service; US Department of Agriculture.

Google Scholar

Antoniow, J. S., Maigret, J.-E., Jensen, C., Trannoy, N., Chirtoc, M., and Beaugrand, J. (2012). Glass-transition temperature profile measured in a wood cell wall using scanning thermal expansion microscope (SThEM). Int. J. Thermophy 33, 2167–2172. doi: 10.1007/s10765-012-1313-y

CrossRef Full Text | Google Scholar

Ashby, M. F. (1983). The mechanical properties of cellular solids. Metall. Trans. A 14, 1755–1769. doi: 10.1007/BF02645546

CrossRef Full Text | Google Scholar

Balch, J. K., Bradley, B. A., Abatzoglou, J. T., Nagy, R. C., Fusco, E. J., and Mahood, A. L. (2017). Human-started wildfires expand the fire niche across the United States. Proc. Natl. Acad. Sci. U.S.A. 11, 2946–2951. doi: 10.1073/pnas.1617394114

CrossRef Full Text | Google Scholar

Baroudi, D., Ferrantelli, A., Li, K. Y., and Hostikka, S. A. (2017). thermomechanical explanation for the topology of crack patterns observed on the surface of charred wood and particle fibreboard. Combust. Flame 182, 206–215. doi: 10.1016/j.combustflame.2017.04.017

CrossRef Full Text | Google Scholar

Barr, B. W. W., and Ezekoye, O. A. (2013). Thermo-mechanical modeling of firebrand breakage on a fractal tree. Proc. Combust. Inst. 2, 2649–2656. doi: 10.1016/j.proci.2012.07.066

CrossRef Full Text | Google Scholar

Bažant, Z. P. (1985). Constitutive equation of wood at variable humidity and temperature. Wood Sci. Technol. 2, 159–177. doi: 10.1007/BF00353077

CrossRef Full Text | Google Scholar

Bryden, K. M., and Hagge, M. J. (2003). Modeling the combined impact of moisture and char shrinkage on the pyrolysis of a biomass particle. Fuel 82, 1633–1644. doi: 10.1016/S0016-2361(03)00108-X

CrossRef Full Text | Google Scholar

Casteren, A. V., Sellers, W. I., Thorpe, S. K. S., Coward, S., Crompton, R. H., and Ennos, A. R. (2012). Why don't branches snap? The mechanics of bending failure in three temperate angiosperm trees. Trees 26, 789–797. doi: 10.1007/s00468-011-0650-y

CrossRef Full Text | Google Scholar

Caton, S. (2016). Laboratory Studies on the Generation of Firebrands From Cylindrical Wooden Dowels.

Google Scholar

Caton, S. E., Hakes, R. S. P., Gorham, D. J., Zhou, A., and Gollner, M. J. (2016). Review of pathways for building fire spread in the wildland urban interface part I: exposure conditions. Fire Technol. 53, 1–45. doi: 10.1007/s10694-016-0589-z

CrossRef Full Text | Google Scholar

Chen, Y., Aanjaneya, K., and Atreya, A. (2017). A study to investigate pyrolysis of wood particles of various shapes and sizes. Fire Saf. J. 91, 820–827. doi: 10.1016/j.firesaf.2017.03.079

CrossRef Full Text | Google Scholar

Dinwoodie, J. M. (2000). Timber; Its Nature and Behaviour, 2nd Edn. London: Taylor & Francis.

Google Scholar

Easterling, K. E., Harrysson, R., Gibson, L. J., and Ashby, M. F. (1982). On the Mechanics of Balsa and Other Woods. Proc. R. Soc. A Math. Phys. Eng. Sci. 1784, 31–41. doi: 10.1098/rspa.1982.0118

CrossRef Full Text | Google Scholar

El Houssami, M., Mueller, E., Filkov, A., Thomas, J. C., Skowronski, N., Gallagher, M. R., et al. (2016). Experimental procedures characterising firebrand generation in wildland fires. Fire Technol. 3, 731–751. doi: 10.1007/s10694-015-0492-z

CrossRef Full Text | Google Scholar

Ennos, A. R., and Van Casteren, A. (2010). Transverse stresses and modes of failure in tree branches and other beams. Proc Biol Sci. 277, 1253–1258. doi: 10.1098/rspb.2009.2093

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibson, L. J., and Ashby, M. F. (1999). Cellular Solids: Structure and Properties, 2nd Edn. Cambridge: Cambridge University Press.

Google Scholar

Gibson, L. J., Ashby, M. F., Schajer, G. S., and Robertson, C. I. (1982). The mechanics of two-dimensional cellular materials. Proc. R. Soc. London A Math. Phys. Eng. Sci. 382:1782. doi: 10.1098/rspa.1982.0087

CrossRef Full Text | Google Scholar

Haas, T. J., Nimlos, M. R., and Donohoe, B. S. (2009). Real-time and post-reaction microscopic structural analysis of biomass undergoing pyrolysis. Energy Fuels 23, 3810–3817. doi: 10.1021/ef900201b

CrossRef Full Text | Google Scholar

Hadden, R. M., Scott, S., Lautenberger, C., and Fernandez-Pello, A. C. (2010). Ignition of combustible fuel beds by hot particles: an experimental and theoretical study. Fire Technol. 2, 341–355. doi: 10.1007/s10694-010-0181-x

CrossRef Full Text | Google Scholar

Hagge, M. J., Bryden, K. M., and Dietenberger, M. A. (2004). “Effects of backing board materials on wood combustion performance,” in Wood & Fire Safety: Proceedings, 5th International Scientific Conference. Svolen, Slovakia: Faculty of Wood Sciences and Technology; Technical University of Zvolen, 51–58. Available online at: https://www.fs.usda.gov/treesearch/pubs/7019

Google Scholar

Howard, P. (2014). Flammable Planet: Wildfires and the Social Cost of Carbon. New York, NY: Institute for Policy Integrity; New York University School of Law.

Google Scholar

Koch, P. (1972a). “Utilization of the Southern pines, Vol. 1,” in Agricultural Handbook SFES-AH-420 (Asheville, NC: USDA-Forest Service, Southern Forest Experiment Station), 1–734.

Google Scholar

Koch, P. (1972b). “Utilization of the Southern pines, Vol. 2,” in Agricultural Handbook SFES-AH-420 (Asheville, NC: USDA-Forest Service, Southern Forest Experiment Station), 735–1663.

Google Scholar

Koo, E., Pagni, P. J., Weise, D. R., and Woycheese, J. P. (2010). Firebrands and spotting ignition in large-scale fires. Int. J. Wildl. Fire 19:818. doi: 10.1071/WF07119

CrossRef Full Text | Google Scholar

Kundu, P. K., Cohen, I. M., Hu, H. H., and Publishers, E. S. (2002). Fluid Mechanics. San Diego, CA: Academic Press.

Google Scholar

Li, K., Hostikka, S., Dai, P., Li, Y., Zhang, H., and Ji, J. (2016). Charring shrinkage and cracking of fir during pyrolysis in an inert atmosphere and at different ambient pressures. Proc. Combust. Inst. 36, 3185–3194. doi: 10.1016/j.proci.2016.07.001

CrossRef Full Text | Google Scholar

Li, K., Pau, D. S. W., Wang, J., and Ji, J. (2015). Modelling pyrolysis of charring materials: determining flame heat flux using bench-scale experiments of medium density fibreboard (MDF). Chem. Eng. Sci. 123, 39–48. doi: 10.1016/j.ces.2014.10.043

CrossRef Full Text | Google Scholar

Li, K. Y., Cheng, X., and Zhang, H. A. (2014). simplified model on vertical density profile and shrinkage ratio of virgin and charred medium density fibreboard. Fire Mater 6, 659–672. doi: 10.1002/fam.2207

CrossRef Full Text | Google Scholar

Liu, Q., Shen, D., Xiao, R., and Fang, M. (2013). Thermal behavior of wood slab under a truncated-cone electrical heater: experimental observation. Combust. Sci. Technol. 5, 848–862. doi: 10.1080/00102202.2012.760548

CrossRef Full Text | Google Scholar

Manzello, S. L., Cleary, T. G., Shields, J. R., Maranghides, A., Mell, W., and Yang, J. C. (2008). Experimental investigation of firebrands: generation and ignition of fuel beds. Fire Saf. J. 3, 226–233. doi: 10.1016/j.firesaf.2006.06.010

CrossRef Full Text | Google Scholar

Manzello, S. L., Cleary, T. G., Shields, J. R., and Yang, J. C. (2006b). On the ignition of fuel beds by firebrands. Fire Mater. 1, 77–87. doi: 10.1002/fam.901

CrossRef Full Text | Google Scholar

Manzello, S. L., Maranghides, A., Shields, J. R., Mell, W. E., Hayashi, Y., and Nii, D. (2007a). Measurement of firebrand production and heat release rate (HRR) from burning Korean pine trees. Fire Saf. Sci. 7:108. Available online at: https://www.iafss.org/publications/aofst/7/108

Google Scholar

Manzello, S. L., Maranghides, A., and Mell, W. E. (2007b). Firebrand generation from burning vegetation. Int. J. Wildl. Fire 16:4. doi: 10.1071/WF06079

CrossRef Full Text | Google Scholar

Manzello, S. L., Maranghides, A., Mell, W. E., Cleary, T. G., and Yang, J. C. (2006a). Firebrand production from burning vegetation. For. Ecol. Manag. 234:S119. doi: 10.1016/j.foreco.2006.08.160

CrossRef Full Text | Google Scholar

Manzello, S. L., Maranghides, A., Shields, J. R., Mell, W. E., Hayashi, Y., and Nii, D. (2009). Mass and size distribution of firebrands generated from burning Korean pine (Pinus koraiensis) trees. Fire Mater. 33:1. doi: 10.1002/fam.977

CrossRef Full Text | Google Scholar

Mark, R. E. (1907). Cell Wall Mechanics of Tracheids. New Haven, CT: Yale University Press.

Google Scholar

Mell, W., Maranghides, A., McDermott, R., and Manzello, S. L. (2009). Numerical simulation and experiments of burning douglas fir trees. Combust. Flame 156, 2023–2041. doi: 10.1016/j.combustflame.2009.06.015

CrossRef Full Text | Google Scholar

Nguyen, Y., Pence, T. J., and Wichman, I. S. (2017). “Crack formation during material thermal degradation in combustion,” in 10th U.S. National Combustion Meeting (College Park, MD).

Google Scholar

Ragland, K. W., Aerts, D. J., and Baker, A. J. (1991). Properties of wood for combustion analysis. Bioresour. Technol. 2, 161–168. doi: 10.1016/0960-8524(91)90205-X

CrossRef Full Text | Google Scholar

Salmén, L. (1984). Viscoelastic properties of in situ lignin under water-saturated conditions. J. Mater. Sci. 9, 3090–3096. doi: 10.1007/BF01026988

CrossRef Full Text | Google Scholar

Salmén, L. (2004). Micromechanical understanding of the cell-wall structure. Comptes Rendus Biol. 9–10, 873–880. doi: 10.1016/j.crvi.2004.03.010

CrossRef Full Text | Google Scholar

Sardoy, N., Consalvi, J.-L., Porterie, B., and Fernandez-Pello, A. (2007). Modeling transport and combustion of firebrands from burning trees. Combust. Flame 150, 151–169. doi: 10.1016/j.combustflame.2007.04.008

CrossRef Full Text | Google Scholar

Sedighi Gilani, M., Fife, J. L., Boone, M. N., and Ghazi Wakili, K. (2013). Dynamics of microcrack propagation in hardwood during heat treatment investigated by synchrotron-based X-ray tomographic microscopy. Wood Sci. Technol. 5, 889–896. doi: 10.1007/s00226-013-0545-8

CrossRef Full Text | Google Scholar

Shen, D. K., Gu, S., Luo, K. H., and Bridgwater, A. K. (2009). Analysis of wood structural changes under thermal radiation. energy fuels. Am. Chem. Soc. 23, 1081–1088. doi: 10.1021/ef800873k

CrossRef Full Text | Google Scholar

Spearpoint, M. J., and Quintiere, J. G. (2001). Predicting the piloted ignition of wood in the cone calorimeter using an integral model—effect of species, grain orientation and heat flux. Fire Saf. J. 4, 391–415. doi: 10.1016/S0379-7112(00)00055-2

CrossRef Full Text | Google Scholar

Suzuki, S., Manzello, S. L., and Hayashi, Y. (2012a). The size and mass distribution of firebrands collected from ignited building components exposed to wind. Proc. Combust. Inst. 3, 2479–2485. doi: 10.1016/j.proci.2012.06.061

CrossRef Full Text | Google Scholar

Suzuki, S., Manzello, S. L., Lage, M., and Laing, G. (2012b). Firebrand generation data obtained from a full-scale structure burn. Int. J. Wildl. Fire. 21, 961–968. doi: 10.1071/WF11133

CrossRef Full Text | Google Scholar

Tohidi, A. (2016). Experimental and Numerical Modeling of Wildfire Spread via Fire Spotting. Boston, MA: Northeastern University.

Google Scholar

Tohidi, A., Caton, S., Gollner, M., and Bryner, N. (2017). “Thermo-mechanical breakage mechanism of firebrands,” in 10th US National Combustion Meeting (College Park, MD: University of Maryland College Park).

Google Scholar

Tohidi, A., Kaye, N., and Bridges, W. (2015). Statistical description of firebrand size and shape distribution from coniferous trees for use in Metropolis Monte Carlo simulations of firebrand flight distance. Fire Saf. J. 77, 21–35. doi: 10.1016/j.firesaf.2015.07.008

CrossRef Full Text | Google Scholar

Tohidi, A., and Kaye, N. B. (2017a). Aerodynamic characterization of rod-like debris with application to firebrand transport. J. Wind Eng. Ind. Aerodyn. 168, 297–311. doi: 10.1016/j.jweia.2017.06.019

CrossRef Full Text | Google Scholar

Tohidi, A., and Kaye, N. B. (2017b). Comprehensive wind tunnel experiments of lofting and downwind transport of non-combusting rod-like model firebrands during firebrand shower scenarios. Fire Saf. J. 90, 95–111. doi: 10.1016/j.firesaf.2017.04.032

CrossRef Full Text | Google Scholar

Tohidi, A., and Kaye, N. B. (2017c). Stochastic modeling of firebrand shower scenarios. Fire Saf. J. 91, 91–102. doi: 10.1016/j.firesaf.2017.04.039

CrossRef Full Text | Google Scholar

Turns, S. R. (2000). An Introduction to Combustion. Boston, MA: MacGraw Hill.

Google Scholar

Usmani, A. S., Rotter, J. M., Lamont, S., Sanad, A. M., and Gillie, M. (2001). Fundamental principles of structural behaviour under thermal effects. Fire Saf. J. 8, 721–744. doi: 10.1016/S0379-7112(01)00037-6

CrossRef Full Text | Google Scholar

Ventsel, E., and Krauthammer, T. (2001). Thin Plates and Shells: Theory: Analysis, and Applications. New York, NY: CRC press.

Google Scholar

Wichman, I. S., and Atreya, A. A. (1987). Simplified model for the pyrolysis of charring materials. Combust. Flame 68, 231–247. doi: 10.1016/0010-2180(87)90002-2

CrossRef Full Text | Google Scholar