- 1Department of Mechanical Engineering, George Mason University, Fairfax, VA, United States
- 2Optical Sciences Division, United States Naval Research Laboratory, Washington, DC, United States
The problem of determining the strength of the infrared radiation from an air-water interface has been addressed analytically. The approach taken here is to express the Planck spectrum as a linear function of the temperature, an approximation valid for small variations of the temperature from the surface temperature, and to assume a linear temperature profile across the thermal boundary layer. The main result shows that the deviation of the surface radiation intensity from the Planck spectrum due solely to thermal stratification, is linearly proportional to the temperature change across the thermal boundary layer and the optical depth, but is inversely proportional to the thermal boundary layer thickness. This signal was shown to be about one order of magnitude greater than the noise level expected from modern CCD IR sensors at a wavelength of about 3.8 μm. It is suggested that controlled laboratory experiments be conducted to verify these theoretical estimates.
Introduction
The accurate prediction of momentum, heat and gas transport across the air-sea interface is of obvious importance in determining the long term global climate. This need has motivated a number of field, modeling, simulation, and experimental efforts aimed at quantifying these fluxes. Bulk parametrizations of momentum and heat flux have been determined in field experiments (Fairall et al., 1996), while the dependence of carbon dioxide transport on wind speed has been modeled by Wanninkhof (1992, 2014). Additional work under controlled laboratory conditions has explored the microphysics responsible for gas flux at an air-water interface (Katsaros et al., 1977; Jahne et al., 1987; Handler et al., 2001; Handler and Smith, 2011).
More recently, advances in infrared (IR) sensors have been used by a number of researchers to develop novel methods for obtaining these fluxes through the use of advanced image processing (Garbe et al., 2004). These efforts also include the use of active methods (Jahne et al., 1989; Atmane et al., 2004) as well as the modeling of these methods (Zhang and Handler, 2014). Numerical simulations have also provided further insight regarding the small-scale turbulent dynamics responsible for determining these fluxes (Handler et al., 1999; Leighton et al., 2003; Nagaosa and Handler, 2003, 2012; Handler and Zhang, 2013; Herlina and Wissink, 2014; Fredriksson et al., 2016a,b).
The remote determination of oceanic heat flux from aircraft or satellites has also been considered. This has the obvious advantage of enabling a rapid large scale mapping of oceanic heat flux, and since heat flux can be considered a proxy for gas flux (Jahne et al., 1987), a mapping of gas flux can also be obtained. In fact, a limited effort has been made in this direction. The approach is based upon the existence of a thin thermal boundary layer at the air-sea interface, sometimes referred to as the cool-skin the ocean surface. This layer is typically between 0.1 and 1 mm in thickness, and the temperature difference across the layer can as much a 1 K (Katsaros et al., 1977). In addition, the optical depth of infrared radiation in wavelength bands transparent to the atmosphere can vary as much one order of magnitude (Downing and Williams, 1975). This has motivated the early attempts of McAlister and McLeish (1970) and McAlister et al. (1971) to use IR sensors mounted on aircraft, sensitive to radiation in differing wavelength bands, to probe the thermal layer at the air-sea interface. Using this approach, they claim to have obtained estimates of oceanic heat flux remotely. This idea was revisited by McKeown et al. (1995) and McKeown and Leighton (1999), who performed laboratory experiments using an IR imaging system.
The relatively little attention payed to the remote sensing of oceanic heat flux has motivated us to reconsider this approach. We are especially interested in using solutions of the radiation transport equation to develop an estimate for the strength of the radiation emerging from a thermally stratified medium. In this approach we choose to ignore the complicating effects of scattering in the water and atmosphere, surface waves, and atmospheric absorption. Furthermore, we consider a fluid layer in which the stratification is linear with depth, and we use a truncated expansion of the Planck spectrum about the surface temperature to obtain an expression for the radiation source that can be integrated exactly. This allows us to obtain a simple expression for the strength of the signal which results purely from stratification. Finally, we obtain estimates for the signal-to-noise ratio that that can be expected from current infrared focal plane array sensors.
Radiation Transport Equations in a Stratified Medium
The General Form of the Radiation Transport Equation
The radiation transport equation (Chandrasekhar, 1960; Thomas and Stamnes, 1999) for a radiating and absorbing medium following a ray in a direction associated with the coordinate s, a coordinate associated with any direction in space, is:
where I is the radiation intensity, k is the opacity, ρ is the density of the medium, and j is the emission coefficient. Local thermodynamic equilibrium implies:
where the Planck spectrum B(T, λ) is given by:
Here , , h is Plank's constant, c is the speed of light, λ is the wave length of the radiation, kb is Boltzmann's constant, and T is the temperature. From here on, we will suppress the dependence of B(T, λ) and C2(λ) on wavelength and will write them instead as B(T) and C2. Now referring to Figure 1, we consider a radiation field which is stratified in planes parallel to the top surface defined by y = 0, and we further choose outer and inner length scales D and d respectively. For simplicity, we chose the linearly varying temperature field given by:
where ΔT = (Td − T0), T0 is the temperature at the air-water interface (y = 0), and Td = T(d). We choose a coordinate system as shown in which y = D − s cos(θ). Applying this coordinate transformation to Equation (1) gives:
where β = ρk is the wavelength dependent absorption coefficient. The boundary condition for equation 5 is:
where ID is assumed to be known. The exact solution to Equation (5) with the boundary condition given by Equation (6) is:
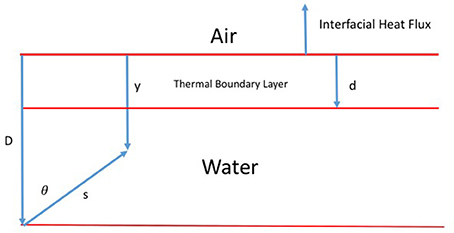
Figure 1. The geometry associated with a radiation field at an air-water interface stratified in planes parallel to the water surface. The thermal boundary layer thickness is d, and the domain depth is D. Radiation propagates along a ray whose path length is s in direction θ.
Approximate Solution of the RTE in a Stratified Medium
In general, there is no closed form expression for the integral in Equation (7) for the temperature profile given by Equation (4). Although this integral can be treated numerically, it is useful to obtain an approximate solution since this can expose the parameters and length scales that are most important in understanding the nature of the problem. This kind of understanding is critical in gaining insight into the physical phenomena involved and may aid in the design of experiments. For this purpose we now expand B(T) about the surface temperature T0 in a Taylor series as follows:
where we have truncated the series after the first two terms. This linear approximation should be accurate for cases in which the temperature change across the surface layer Δ T = T(d) − T0 is small compared to the surface temperature, such that ΔT/T0 < < 1. In view of Equation (4), it is convenient to write Equation (8) as:
where , F(T0) = B(T0)G(T0), and . Substitution of Equation (9) into Equation (7) with y = 0 gives the radiation intensity at the air-water interface, I(0), as follows:
where . The integrals in Equation (10) can now be evaluated yielding:
Results
In the expressions to follow, we let β = 1/lopt, where lopt is the optical depth of the medium, so that . We choose here to examine the radiation in the 3 − 5 μm wavelength band, one of bands for which the atmosphere is relatively transparent (McKeown et al., 1995). In this wavelength range, Downing and Williams (1975) found that optical depth of water varied from 1−90 μm. Given these values for the optical depth, it is justified to assume that since the thermal boundary layer thickness is on the order d = 1 mm. In addition, for T0 = 300K, eq ≫ 1 where at these wavelengths. Furthermore, since we are concerned with effectively infinite water depths, we will assume .
Applying these limits to Equation (11) the deviation of the surface radiation intensity from the Planck spectrum, normalized with the Planck spectrum, can be expressed in terms of three non-dimensional numbers: , and as follows:
We will refer to the quantity defined above, , the radiation emitted from the surface due solely to thermal stratification, as the signal. This result shows that when θ = 0, in which radiation is observed in directions perpendicular to the interface, the signal is maximal, consistent with the results of Zel'dovich and Raizer (1966). In addition, for a fixed surface temperature T0, the signal increases in proportion to the temperature change across the surface layer, ΔT, and the optical depth, lopt, but inversely with the layer depth, d. The signal is also seen via equation 12 to be proportional to the heat flux, , directed from the water to the atmosphere when Δ T > 0, where k is the thermal conductivity of water.
It is of interest also to estimate the noise level of a typical IR sensing device by observing from Equation (9) that:
where the system noise, , represents the normalized change in the Planck spectrum due to a change in temperature. In this case, it is appropriate to identify ΔT as the noise-equivalent-differential-temperature (NEDT) of the sensing device. At the present time, the most sensitive IR CCD arrays are found to have an NEDT of about 10−2K.
The results of the calculations for both the signal, Srad, and the noise, Nrad, are shown in Figure 2A in which the signal is obtained from Equation (12) with θ = 0 using optical depth data from Downing and Williams (1975) in the 3 − 5 μm band, T0 = 300 K, d = 1 mm, and ΔT = 1K. The noise level shown in Figure 2A was obtained using ΔT = 10−2K in equation 13. The signal to noise ratio, , is shown in Figure 2B. These results indicate that, over most of the wavelength range, the signal to noise ratio is above one, with a maximum occurring at a wavelength of about 3.8 μm.
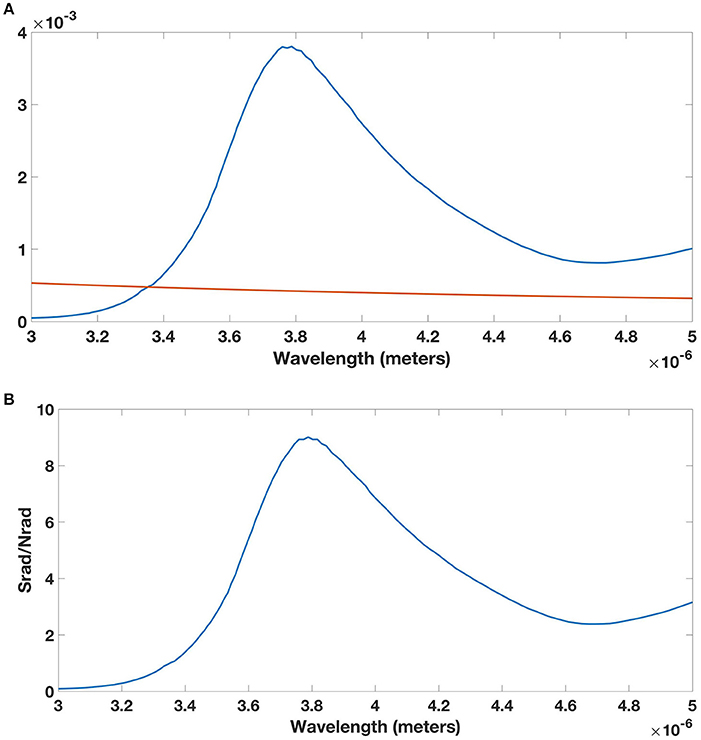
Figure 2. (A) The signal (blue) obtained from Equation (12) with θ = 0, and the noise (red) from Equation (13). The signal was obtained using T0 = 300 K, ΔT = 1 K, and d = 1 mm, and using the optical depth data from Downing and Williams (1975). This represents heat flux from the water layer to the atmosphere of , which is nearly equivalent to the heat flux obtained in experiments (Handler and Smith, 2011) for a wind speed of about 3 ms−1. The noise was obtained for a sensor with a thermal resolution of 10−2K. (B) The signal to noise ratio obtained from the results in (A).
Summary and Conclusions
The problem of determining the strength of infrared radiation from an air-water interface has been addressed analytically. This is essentially a special case of determining the radiation intensity from a radiating and absorbing thermally stratified medium. The approach taken here is to express the Planck spectrum as a linear function of the temperature, an approximation valid for small variations of the temperature from the surface temperature, and to assume a linear temperature profile across the thermal boundary layer. This allows the radiation transport equation to be integrated exactly. The resulting expression for the surface radiation intensity can be simplified by making the further approximation that the optical depth is small compared to the thermal boundary layer thickness, and that the depth of the domain is effectively infinite. The main result shows that the signal given by Equation (12), the deviation from the surface intensity from the Planck spectrum due solely to thermal stratification, is linearly proportional to the temperature change across the thermal boundary layer and the optical depth, but is inversely proportional to the thermal boundary layer thickness. This signal was shown to be about one order of magnitude greater than the noise level expected from modern CCD IR sensors at a wavelength of about 3.8 μm for a realistic interfacial heat flux (Handler and Smith, 2011).
This result would suggest, as has been previously claimed (McAlister and McLeish, 1970; McAlister et al., 1971; McKeown et al., 1995; McKeown and Leighton, 1999), that it may be possible to remotely detect the thermal stratification at the air-sea interface. However, this estimate assumes nearly perfect conditions: (1) The air-water interface is flat (no surface waves), (2) No scattering of radiation by particulates in the air or water, and (3) A surface emissivity of one. Given these significant potential sources of noise and non-ideality, and most likely others that we cannot now anticipate, our analysis suggests that it is unlikely in the near future that such a signal will be easily detected. On the other, we feel that the result embodied in equation 12 gives a theoretical basis for the design of future experiments, particularly in a controlled laboratory setting. A follow-on paper will extend these results to more realistic cases which include relaxing the linearity assumptions, and using a more realistic thermal boundary layer profile (Smith et al., 2001).
Author Contributions
All authors listed, have made substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Atmane, M. A., Asher, W. E., and Jessup, A. T. (2004). On the use of the active infrared technique to infer heat and gas transfer velocities at the air-water free surface. J. Geophys. Res. 109:C08S14. doi: 10.1029/2003JC001805
Downing, H. D., and Williams, D. (1975). Optical Constants of Water in the Infrared. J. Geophys. Res. 80, 1656–1661. doi: 10.1029/JC080i012p01656
Fairall, C. W., Bradley, E. F., Rogers, D. P., Edson, J. B., and Young, G. S. (1996). Bulkparameterization of air-sea fluxes for Tropical Ocean-Global Atmosphere Coupled-Ocean–Atmosphere Response Experiment. J. Geophys. Res. 101, 3747–3764.
Fredriksson, S. T., Arneborg, L., Nilsson, H., and Handler, R. A. (2016b). Surface shear stress dependence of gas transfer velocity parameterizations using DNS. J. Geophys. Res. 121, 7369–7389. doi: 10.1002/2016JC011852
Fredriksson, S. T., Arneborg, L., Nilsson, H., Zhang, Q., and Handler, R. A. (2016a). An evaluation of gas transfer velocity parameterizations during natural convection using DNS. J. Geophys. Res. 121, 1400–1423. doi: 10.1002/2015JC011112
Garbe, C. S., Schimpf, U., and Jahne, B. (2004). A surface renewal model to analyze infrared image sequences of the ocean surface for the study of air-sea heat and gas exchange. J. Geophys. Res. 109:C08S15. doi: 10.1029/2003JC001802
Handler, R. A., Saylor, J. R., Leighton, R. I., and Rovelstad, A. L. (1999). Transport of a passive scalar at a shear-free boundary in fully developed turbulent open channel flow. Phys. Fluids 11, 2607–2625. doi: 10.1063/1.870123
Handler, R. A., and Smith, G. B. (2011). Statistics of the temperature and its derivatives at the surface of a wind-driven air-water interface. J. Geophys. Res. Oceans 116:C06021. doi: 10.1029/2010JC006496
Handler, R. A., Smith, G. B., and Leighton, R. I. (2001). The thermal structure of an air-water interface at low wind speeds. Tellus A 53, 233–244. doi: 10.3402/tellusa.v53i2.12187
Handler, R. A., and Zhang, Q. (2013). Direct numerical simulations of a sheared interface at low wind speeds with applications to infrared remote sensing. IEEE J. Select. Top. Appl. Earth Observ. Remote Sens. 6, 1086–1091. doi: 10.1109/JSTARS.2013.2241736
Herlina, H., and Wissink, J. G. (2014). Direct numerical simulation of turbulent scalar transport across a flat surface. J. Fluid Mech. 744, 217–249. doi: 10.1017/jfm.2014.68
Jahne, B., Libner, P., Fischer, R., Billen, T., and Plate, E. J. (1989). Investigating the transfer processes across the free aqueous boundary layer by the controlled flux method. Tellus 41B, 177–195. doi: 10.3402/tellusb.v41i2.15068
Jahne, B., Munnich, K. O., Bosinger, A. D., Huber, W., and Libner, P. (1987). On the parameters influencing air-water gas exchange. J. Geophys. Res. 92, 1937–1949. doi: 10.1029/JC092iC02p01937
Katsaros, K. B., Liu, W. T., Businger, J. A., and Tillman, J. E. (1977). Heat transport and thermal structure in the interfacial boundary layer measured in an open tank of water in turbulent free convection. J. Fluid Mech. 83, 311–335.
Leighton, R. I., Smith, G. B., and Handler, R. A. (2003). Direct numerical simulations of free convection beneath an air–water interface at low Rayleigh numbers, Phys. Fluids 15, 3181–3193. doi: 10.1063/1.1606679
McAlister, E. D., and McLeish, W. (1970). A Radiometric System for Airborne Measurement of the Total Heat Flow from the Sea. Appl. Optics 9, 2697–2705. doi: 10.1364/AO.9.002697
McAlister, E. D., McLeish, W., and Corduan, E. A. (1971). Airborne Measurements of the Total Heat Flux from the Sea during Bomex. J. Geophys. Res. 76, 4172–4180. doi: 10.1029/JC076i018p04172
McKeown, W., Bretherton, F., Huang, H. L., Smith, W. L., and Revercomb, H. L. (1995). Sounding the skin of water: sensing air/water interface temperature gradients with interferometry. J. Atmos. Oceanic Technol. 12, 1313–1327. doi: 10.1175/1520-0426(1995)012<1313:STSOWS>2.0.CO;2
McKeown, W., and Leighton, R. (1999). Mapping heat flux. J. Atmos. Ocean Tech. 16, 80–91. doi: 10.1175/1520-0426(1999)016<0080:MHF>2.0.CO;2
Nagaosa, R., and Handler, R. A. (2003). Statistical analysis of coherent vortices near a free surface in a fully developed turbulence. Phys. Fluids 15, 375–394. doi: 10.1063/1.1533071
Nagaosa, R., and Handler, R. A. (2012). Characteristic time scales for predicting the scalar flux at a free surface in turbulent open-channel flows. AIChE J. 58, 3867–3877. doi: 10.1002/aic.13773
Smith, G. B., Volino, R. J., Handler, R. A., and Leighton, R. I. (2001). The thermal signature of a vortex pair impacting a free surface. J. Fluid Mech. 444, 49–78. doi: 10.1017/S0022112001005304
Thomas, G. E., and Stamnes, K. (1999). Radiative Transfer in the Atmosphere and the Ocean. Cambridge: Cambridge University Press.
Wanninkhof, R. (1992). Relationship between wind speed and gas exchange over the ocean. J. Geophys. Res. 97, 7373–7382. doi: 10.1029/92JC00188
Wanninkhof, R. (2014). Relationship between wind speed and gas exchange over the ocean revisited. Limnol. Oceanogr. Methods 12, 351–362. doi: 10.4319/lom.2014.12.351
Zel'dovich, Y. B., and Raizer, Y. P. (1966). Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena. New York, NY: Academic Press.
Keywords: infrared radiation, air-sea heat flux, radiation transport equation, air-sea gas flux, remote sensing technology
Citation: Handler RA and Judd KP (2018) Analysis of Infrared Radiation at an Air-Water Interface. Front. Mech. Eng. 4:5. doi: 10.3389/fmech.2018.00005
Received: 11 December 2017; Accepted: 03 April 2018;
Published: 08 May 2018.
Edited by:
Md Anwar Hossain, University of Dhaka, BangladeshReviewed by:
Michael John Gollner, University of Maryland, College Park, United StatesSadia Siddiqa, COMSATS Institute of Information Technology, Pakistan
Copyright © 2018 Handler and Judd. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Robert A. Handler, cmhhbmRsZXJAZ211LmVkdQ==
 Robert A. Handler
Robert A. Handler K. Peter Judd
K. Peter Judd