
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mech. Eng., 07 December 2017
Sec. Thermal and Mass Transport
Volume 3 - 2017 | https://doi.org/10.3389/fmech.2017.00015
This article is part of the Research TopicDirect Thermal Energy Conversion and UtilizationView all 8 articles
A first-principles study using density functional theory and Boltzmann transport theory has been performed to evaluate the thermoelectric (TE) properties of a series of single-layer 2D materials. The compounds studied are SnSe, SnS, GeS, GeSe, SnSe2, and SnS2, all of which belong to the IV–VI chalcogenides family. The first four compounds have orthorhombic crystal structures, and the last two have hexagonal crystal structures. Solving a semi-empirical Boltzmann transport model through the BoltzTraP software, we compute the electrical properties, including Seebeck coefficient, electrical conductivity, power factor, and the electronic thermal conductivity, at three doping levels corresponding to 300 K carrier concentrations of 1018, 1019, and 1020 cm−3. The spin orbit coupling effect on these properties is evaluated and is found not to influence the results significantly. First-principles lattice dynamics combined with the iterative solution of phonon Boltzmann transport equations are used to compute the lattice thermal conductivity of these materials. It is found that these materials have narrow band gaps in the range of 0.75–1.58 eV. Based on the highest values of figure-of-merit ZT of all the materials studied, we notice that the best TE material at the temperature range studied here (300–800 K) is SnSe.
Thermoelectric (TE) materials have attracted significant attention, especially in the past two decades, for their capacity to convert heat directly into electricity without the need of moving components (Ioffe, 1957; Sootsman et al., 2009; Vineis et al., 2010). They are expected to play important roles in the development of a more sustainable energy landscape worldwide (Kraemer et al., 2011; Barma et al., 2015; Favarel et al., 2015; Mehdizadeh Dehkordi et al., 2015; Moraes et al., 2015; Gayner and Kar, 2016), and there are also opportunities for using them for onboard power for wearable electronics (Leonov and Vullers, 2009; Kim et al., 2014; Du et al., 2015), sensors, or systems for disaster mitigations (Chen et al., 2016; Rais et al., 2016). However, the practical applications of TE devices has been largely impeded by the usually low energy conversion efficiency. The efficiency of TE materials depends on their dimensionless figure-of-merit ZT defined as ZT = S2σ T/k, where S is the Seebeck coefficient, σ is the electrical conductivity, T is the absolute temperature, and k is the total thermal conductivity, including the electronic and lattice contributions. Identifying TE materials with high values of ZT has been the research focus of this field for decades (Mahan and Sofo, 1996; Dresselhaus et al., 2007; Snyder and Toberer, 2008; Tian et al., 2013; Cahill et al., 2014; Liao and Chen, 2015). However, simultaneously optimizing these individual parameters to improve ZT is a challenging task since they are inter-correlated. There is a number of related reviews that describe different mechanisms to improve these properties and thus increase the ZT (Nolas et al., 1999; Snyder and Toberer, 2008; Sootsman et al., 2009; Heremans et al., 2012; Wang et al., 2013).
The discovery of 2D materials, exemplified by graphene (Novoselov et al., 2005; Geim and Novoselov, 2007; Geim, 2009; Jin et al., 2015) and transition metal dichalcogenides (TMDCs) (Gu and Yang, 2014; Wu and Luo, 2014; Yan et al., 2014; Jin et al., 2015; Kumar and Schwingenschlögl, 2015; Pu et al., 2016), has stimulated much research interests due to their unique structural, mechanical, optical, electrical, and thermal properties (Fiori et al., 2014; Zhang and Zhang, 2015; Singh and Hennig, 2016; Bernardi et al., 2017), and potential applications in photovoltaics (Britnell et al., 2013), transistors (Fang et al., 2012; Larentis et al., 2012; Liu et al., 2013; Li et al., 2014a), optoelectronics (Tritsaris et al., 2013), photodetector and molecular sensing (Wang et al., 2012), and wearable heating and cooling (Zhang and Zhang, 2017). Moreover, due to their intrinsic band gaps, TMDC monolayers have better potential in nanoelectronics applications compared to graphene (Guo and Zhang, 2016). In addition, TMDC materials have relatively high electrical properties such as Seebeck coefficient and electrical conductivity, positioning it as good candidates for TE applications. Although a large range of thermal conductivity have been reported for TMDCs, mostly with values higher than 30 W mK−1, values for suspended monolayer in the order of 15 W mK−1 or less have been observed recently (Adessi et al., 2017; Zhang and Zhang, 2017). It has been reported that the TE properties of 2D materials can also be unique because any modification to their environment or chemical functionalization, which play significant roles in thermal and electronic transport, can greatly impact their TE properties (Kim and Grossman, 2015).
In this work, we study and compare the electronic behavior and TE properties, including Seebeck coefficient, electrical conductivity, power factor, electronic thermal conductivity, and lattice thermal conductivity of a series of single-layer 2D materials belonging to the IV–VI Chalcogenides family. These include SnSe, GeSe, SnS, GeS, SnS2, and SnS2. We evaluate the importance of the spin orbit coupling (SOC) due its potential relevance in the electronic transport in TEs (Guan et al., 2015; Guo and Wang, 2017). To compute TE properties, we solve the semi-empirical Boltzmann transport model, through the BoltzTraP software (Madsen and Singh, 2006), and for thermal properties, we used first-principles lattice dynamics combined with the iterative solution of phonon Boltzmann transport equations (BTEs) using the ShengBTE software (Li et al., 2014b). For the electronic properties, three doping levels corresponding to 300 K carrier concentrations of 1018, 1019, and 1020 cm−3 are studied. A temperature range from 300 to 800 K has been investigated. The results reveal a clear increasing trend of the temperature dependence of Seebeck coefficient (in absolute values), power factor, and ZT for all materials studied, be they p-type or n-type. Our calculations show that the compounds with orthorhombic crystal structures (i.e., GeS, GeSe, SnS, and SnSe) have much lower thermal conductivity values than those with hexagonal crystal structures (i.e., SnS2 and SnSe2), leading to a larger ZT values for the orthorhombic crystals. Based on the calculated ZT, we found that the most promising 2D TE materials at low and high temperature is SnSe at the three doping levels, respectively.
This paper is organized as follows: Section “Computational Details” includes a description of the computational details with emphasis in simulation processes used for different types of calculations. Section “Results and Discussion” includes the results and discussion of the TE properties obtained from the calculations. Section “Conclusion” outlines the main conclusions of this work.
The methodology used for our calculations is based on first-principles density functional theory (DFT) (Zhou et al., 2016) calculations and Boltzmann transport theory. The structures of the studied 2D materials are first optimized using DFT calculations and then the electron transport properties are calculated using DFT program Quantum Espresso (Giannozzi et al., 2009) and the semi-classical Boltzmann transport approach implemented in BoltzTraP (Madsen and Singh, 2006). The thermal conductivity values are calculated using the iterative solution of phonon BTE using the ShengBTE (Li et al., 2014b) code with force constants calculated from Quantum Espresso.
For all DFT calculations, the generalized gradient approximation of Perdew, Burke, and Ernzerhof are used for the exchange-correlation functional (Perdew et al., 1996). The kinetic energy cutoff of the wave functions is set to 50 Ry for all calculations. The Monkhorst–Pack k-mesh of 8 × 8 × 1 is used to sample the first Brillouin Zone. In the electronic band structure calculation, a finer mesh of 25 × 25 × 1 is used. To simulation monolayers, a large vacuum space of at least 10 Å is left in the z-direction to prevent the interactions between the layer and its periodic images in the cross-plane direction.
The optimized lattice parameters and their comparison to values reported in the literature are presented in Table 1.
Once the structures are optimized, we continue to calculate the electronic transport properties and the lattice thermal conductivity. The flow chart of these calculations, their corresponding input and output parameters and the programs used are schematically shown in Figure 1.
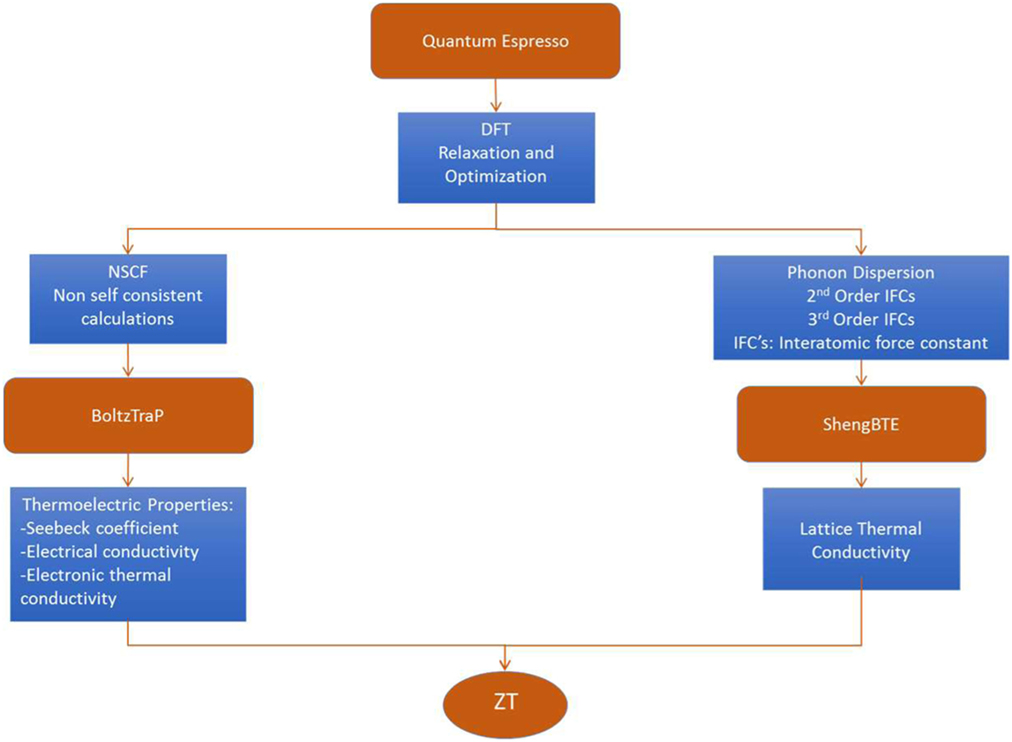
Figure 1. Schematic of the flow chart for TE properties and lattice thermal conductivity calculations.
To obtain the electronic transport properties, including electrical conductivity, Seebeck coefficient, and electronic thermal conductivity, the electron band structure and density of states are first calculated in the DFT framework. Then, the band structures are then input into the BoltzTraP package (Løvvik and Prytz, 2004; Madsen and Singh, 2006), which uses a Fourier expansion scheme to fit the band structures for transport property calculations. In the semi-classical transport theory, the Seebeck coefficient, electrical conductivity, and electronic thermal conductivity transport tensors are expressed as (Madsen and Singh, 2006):
where e is the electron charge, Ω is the reciprocal space volume, ε is the carrier energy, f is the Fermi distribution function, μ is the chemical potential, and T is the absolute temperature. It is noted here that k is the electronic thermal conductivity.
On the other hand, the conductivity tensor [σαβ(ε)] as a function of energy is expressed as:
where N is the number of k-points in the reciprocal space.
The relaxation time τ depends, in principle, on both the wave vector and frequency. However, BoltzTraP treats the relaxation time to be a constant, which has been shown to be a reasonable assumption (Madsen and Singh, 2006). Our calculations for all TE properties were performed with a constant relaxation time approximation τ = 1.0 × 10−14 s, which is the value often chosen in similar calculations (Gao et al., 2005; Madsen and Singh, 2006; Yabuuchi et al., 2013; Ding et al., 2015).
To obtain the thermal conductivity, we calculate the harmonic force constants using the density functional perturbation theory as implemented in Quantum Espresso with a q-point grid size of 8 × 8 × 1. Then, a finite difference method based on supercell calculations (cell size of 4 × 4 × 1) is used to extract the cubic force constants. A cutoff radius of 5 Å is used for the cubic force constant calculation based on convergence test. These force constants are then fed into the ShengBTE program (Carrete et al., 2014) to calculate thermal conductivity based on an iterative solution of phonon BTE. A q-mesh of 30 × 30 × 1 is used for all thermal conductivity calculations.
We need to specially emphasize the choice of the thicknesses of the 2D materials used for calculating the electrical conductivity, electronic thermal conductivity, and lattice thermal conductivity. We used a thickness of 6.0 Å (the interlayer distance of bulk SnSe crystal) for all calculations to enable fair comparison of the properties among all the two materials. In 2D materials, thickness is not well defined, but the concept of electrical and thermal conductivity, which are 3D intensive property, require their quantities to be independent of the cross-sectional area of the material. However, since all electron and heat has to go through the single-layer structures, no matter how “thick” or “thin” the structure is, the same thickness should be used to remove any artifact in comparing the electron and thermal transport ability of different 2D materials when using the 3D property—electrical and thermal conductivity. Such a factor has been discussed in details in previous papers (Liu et al., 2017; Wu et al., 2017).
The 2D TE compounds simulated in this work have two kinds of crystal structures, including orthorhombic and hexagonal (Ding et al., 2015; Guo et al., 2015; Sun et al., 2015; Wang et al., 2015). Figure 2A shows the orthorhombic crystal structure for compounds such as SnSe, SnS, GeSe, and GeS in the Pnma-phase (#62) (Tritsaris et al., 2013; Ding et al., 2015; Guo et al., 2015; Wang et al., 2015), and Figure 2B shows the hexagonal crystal structure for compounds such as SnSe2 and SnS2 in the P3m1-phase (#164) (Sava et al., 2006; Bauer Pereira et al., 2013; Sun et al., 2015). For each simulation, only one layer was considered, where the number of atoms per primitive cell is 4 for the orthorhombic crystal structure and 3 for the hexagonal crystal structure.
Since SOC has been reported to have the possibility of influencing the electronic transport in TEs (Guan et al., 2015; Guo and Wang, 2017), we computed the electronic structures for GeS, GeSe, SnS, SnSe, SnS2, and SnSe2 without and with SOC. The band structures are shown in Figure 3. As expected, all materials are found to be semiconductors. The results without and with SOC both show that all materials have indirect band gaps, except for GeSe, which has a direct band gap. The indirect band gap of GeS, SnS, and SnSe is between the valence band maxima (VBM) located along the Γ − X path and the conduction band minima (CBM) along the Y − Γ path. For SnS2 and SnSe2, the VBM is located along the K − M path and the CBM at the K-point. For GeSe, the direct band gap is located along the Γ − X path. The band gaps values (with and without SOC) are shown in Table 2. All reference band gaps are from numerical simulation with exception of Butt et al. (2012). After applying SOC, we can notice very minor effects on the electronic structure, decreasing slightly the band gaps in all TE materials. The computed band gaps are seen to agree reasonably with the literature values.
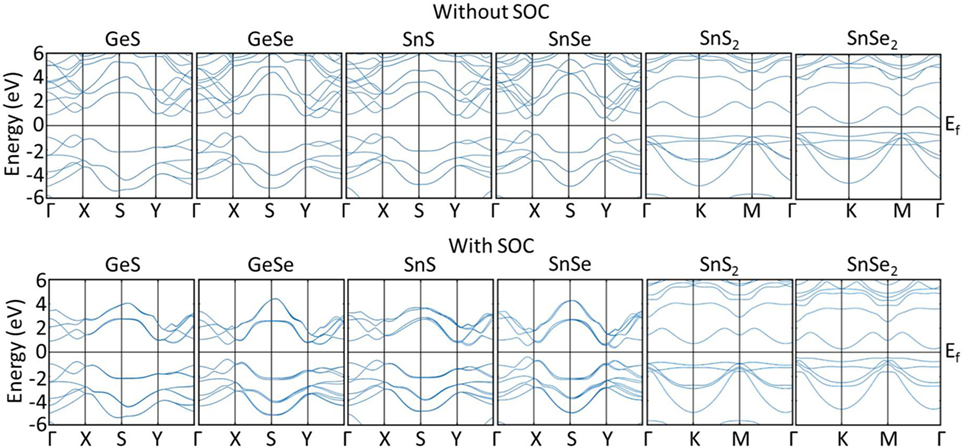
Figure 3. Band structures of TE materials (top row) without SOC and (bottom row) with SOC. TE, thermoelectric; SOC, spin orbit coupling.
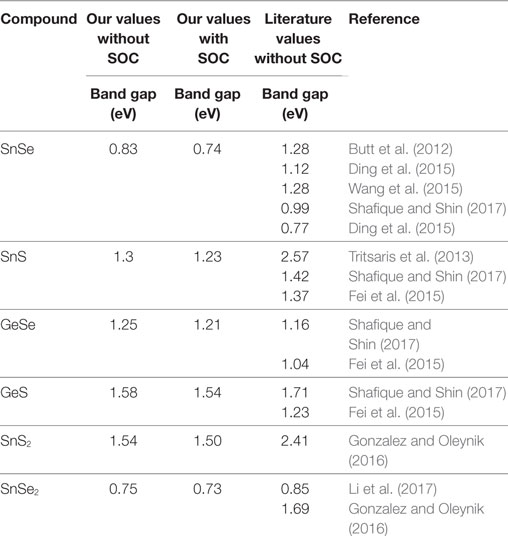
Table 2. Comparison of band gap energies (eV) with and without spin orbit coupling (SOC) for the 2D semiconductors.
We compute the TE properties of all materials considering three doping levels corresponding to 300 K carrier concentrations of 1018, 1019, and 1020 cm−3, respectively. The TE properties are plotted at a temperature range from 300 to 800 K. The electronic properties of TE materials are influenced by SOC, resulting in some cases with better TE properties such as Seebeck coefficient and electrical conductivity (Guo, 2016; Guo and Zhang, 2016; Guo and Wang, 2017). Figure 4 shows the calculated Seebeck coefficient without and with SOC at different doping levels. The signs of the Seebeck coefficients indicate that SnSe, SnS, SnSe2, and SnS2 are n-type, while GeS and GeSe are p-type semiconductors. We can notice that for all cases, the influences of SOC in Seebeck coefficients are small. As a result, for the following text, we use cases without SOC for further study.
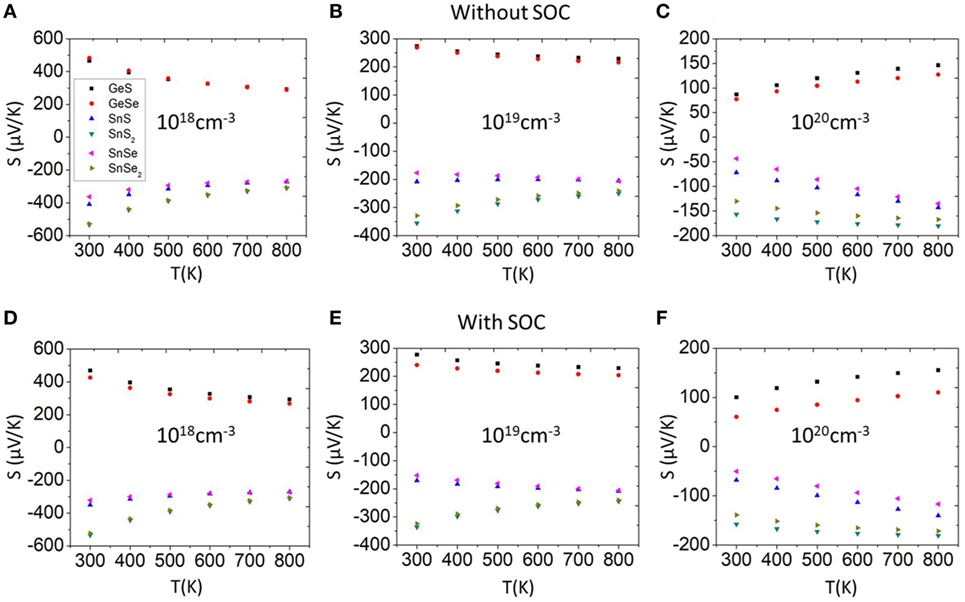
Figure 4. Seebeck coefficient as a function of temperature (A–C) without SOC and (D–F) with SOC at different doping levels. SOC, spin orbit coupling.
Figure 5 summarizes all the TE properties without SOC for the materials studied at the three levels of doping. The absolute values of Seebeck coefficients exhibit a decreasing trend with temperature at 1018 and 1019 cm−3, with the exception for SnS where the change is small, and for SnSe where the absolute values increase slightly at 1019 cm−3. At 1020, an increasing trend for all TE materials in the Seebeck coefficient in absolute values is observed. Due to the interrelationship between carrier concentration and Seebeck coefficient (Snyder and Toberer, 2008), we notice that as doping level increases, the Seebeck coefficient decreases dramatically. We can see that for SnS and SnSe, the Seebeck coefficient at 300 K decreases more than six times when the doping level increases from 1018 to 1020 cm−3. As shown in Figure 5 (second row), the electrical conductivity has the same increasing trend for all materials as a function temperature for all three doping levels. As temperature increase, more electrons are excited and thus the electrical conductivity increases.
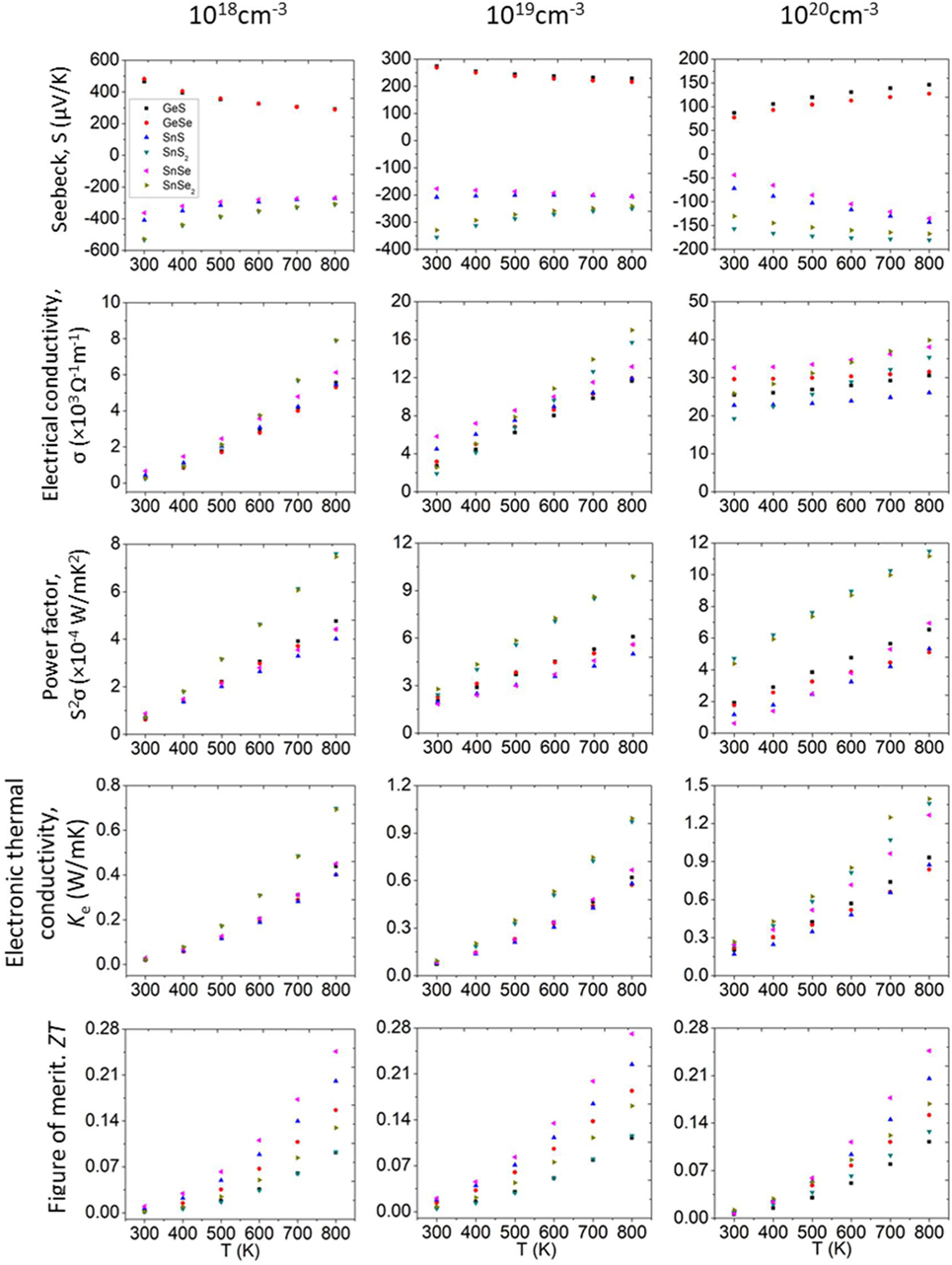
Figure 5. TE properties as a function of temperature without SOC at different doping levels. TE, thermoelectric; SOC, spin orbit coupling.
After the calculations of the Seebeck coefficient and electrical conductivity, we can calculate the power factor (PF = S2σ). The PF for all compounds at the three doping levels as a function of temperature are shown in Figure 5 (third row). We can notice clearly the temperature dependence of PF, indicating that as the temperature increases, the PF for both p- and n-type semiconductors increases monotonically.
The temperature dependence of the electrical thermal conductivity (ke) is shown to be relatively strong (Figure 5, fourth row). As the temperature increases, ke for both p- and n-type semiconductors increases monotonically. In contrast to the PF, where we seek for a maximum value, for ke we want to find a minimum value to maximize ZT. We can see that the minimum values of ke are obtained at 1018 cm−3 level of carrier concentration. GeSe has a minimum value of 0.019 (W mK−1) at lower temperature (300 K), and at higher temperature (800 K), GeSe and SnS both have a minimum value of 0.401 (W mK−1). To validate and compare our results, we consider the reported experimental values of SnSe, because it is one of the most studied materials due to its high reported TE properties. From theoretical reports, the number of studies has been consistently increasing in the last decade, and several studies of 2D materials related to this field and presented in this work have been recently reported. For both experimental and theoretical studies, we found a fairly reasonable agreement of electrical properties with our reported values (Kumar and Schwingenschlögl, 2015; Sun et al., 2015; Zhang et al., 2015; Morales Ferreiro et al., 2016; Tyagi et al., 2016; Ding et al., 2017; Guo and Wang, 2017; Li et al., 2017; Shafique and Shin, 2017).
The lattice thermal conductivity, as we mentioned previously, are calculated by solving the BTE for phonons using the iterative method. The values are shown in Figure 6. We can see that as temperature increases, lattice thermal conductivity decreases monotonically. This is because as temperature increases, anharmonic phonon–phonon scattering becomes more intensive, leading to a thermal conductivity inversely proportional to the temperature (Balandin and Wang, 1998; Gang, 2005). The high temperature dependencies are ~Tn, where n is −1.012, −1.003, −0.998, −1.036, −0.999, and −1.015 for GeS, GeSe, SnS, SnS2, SnSe, and SnSe2, respectively.
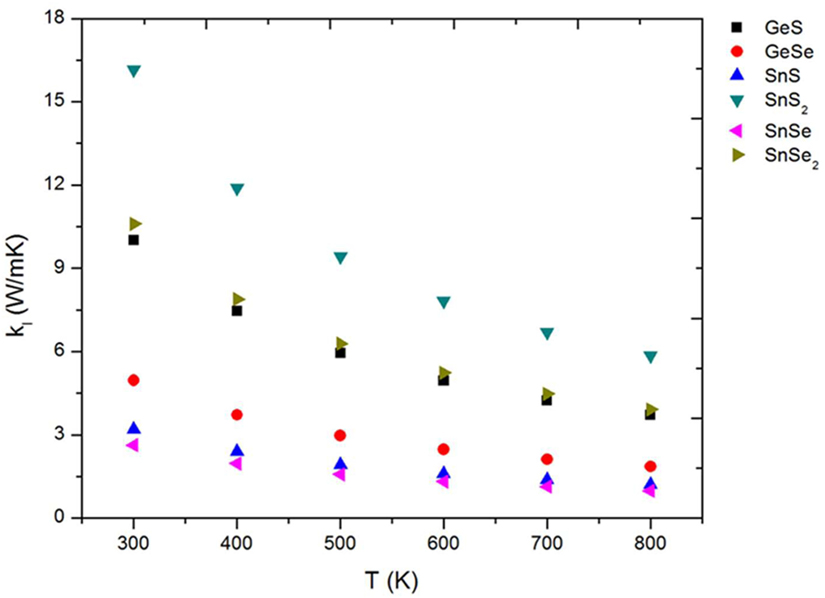
Figure 6. Lattice thermal conductivity of 2D TE materials as a function of temperature. TE, thermoelectric.
All the 2D materials studied here have relatively low lattice thermal conductivity compared with other 2D materials like graphene, MoSe2, BN, WS2, ZrS2, HfS2, and ZrSe2 (Wu et al., 2017) making them promising candidates to have higher ZT. The lattice thermal conductivity values obtained in the present work are in good agreement with recently reported results (Qin et al., 2016; Shafique and Shin, 2017). If we consider the lattice thermal conductivity as a good approach to obtain high efficiency (ZT) in TE materials, we can expect, from our results (Figure 6), that the monolayer SnSe should be one of the best candidate for TE applications as we can see in previously reports for this material (Carrete et al., 2014; Zhao et al., 2014, 2016; Guan et al., 2015; Guo et al., 2015; Hong et al., 2015; Kutorasinski et al., 2015; Sassi et al., 2015; Wang et al., 2015; Chere et al., 2016; Leng et al., 2016; Morales Ferreiro et al., 2016; Popuri et al., 2016; Li et al., 2017).
Combining the all the calculated TE properties so far, we obtained the dimensionless figure-of-merit (ZT) as a function of temperature for different doping levels (Figure 5, fifth row). We notice that the ZT value can be significantly influenced by temperature. For all materials, ZT increases with temperature. Among all the 2D materials studied from 300 to 800 K here, the best ZT values are all obtained from SnSe disregard of doping levels.
In this study, DFT and the Boltzmann transport model are used to calculate the TE properties of monolayer materials belonging to the group IV–VI compounds, including SnSe, GeSe, SnS, GeS, SnSe2, and SnS2. We determine the electronic bands and Seebeck coefficient without and with SOC. We notice a small effect of SOC over the band gaps for all materials. Indirect band gaps from calculations without SOC of 0.83, 1.3, 1.58, 0.75, and 1.54 eV are obtained for SnSe, SnS, GeS, SnSe2, and SnS2, respectively. A direct band gaps of 1.25 eV is found for GeSe. We also obtain indirect band gaps from calculations with SOC of 0.74, 1.23, 1.54, 0.73, and 1.5 eV for SnSe, SnS, GeS, SnSe2, and SnS2, respectively, and a direct band gap of 1.21 eV for GeSe. The TE properties are calculated at different doping levels, and it was found the SnSe has the largest ZT disregard the doping level, which is related to the low lattice thermal conductivity of this material.
The project was conceived by TL. The simulation was performed by JM-F. The data analysis was performed by JM-F and TL. The manuscript was written by JM-F and TL with editing and suggestions from DD-D and DC.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We wish to thank Mechanical and Metallurgical Engineering Department of Pontificia Universidad Católica de Chile, the Physics Institute, the Research Center on Nanotechnology and Advanced Materials, CIEN-UC of Pontificia Universidad Católica de Chile, and finally thanks the support provided by the Chilean Council for Scientific and Technological Research (CONICYT). We would also like to thank the U.S. National Science Foundation grant 1433490.
Adessi, C., Thebaud, S., Bouzerar, R., and Bouzerar, G. (2017). First principle investigation on thermoelectric properties of transition metal dichalcogenides: beyond the rigid band model. J. Phys. Chem. C 121, 12577–12584. doi: 10.1021/acs.jpcc.7b02570
Balandin, A., and Wang, K. L. (1998). Effect of phonon confinement on the thermoelectric figure of merit of quantum wells. J. Appl. Phys. 84, 6149. doi:10.1063/1.368928
Barma, M. C., Riaz, M., Saidur, R., and Long, B. D. (2015). Estimation of thermoelectric power generation by recovering waste heat from biomass fired thermal oil heater. Energy Convers. Manage. 98, 303–313. doi:10.1016/j.enconman.2015.03.103
Bauer Pereira, P., Sergueev, I., Gorsse, S., Dadda, J., Muller, E., and Hermann, R. P. (2013). Lattice dynamics and structure of GeTe, SnTe and PbTe. Phys. Status Solidi B 250, 1300–1307. doi:10.1002/pssb.201248412
Bernardi, M., Ataca, C., Palummo, M., and Grossman, J. C. (2017). Optical and electronic properties of two-dimensional layered materials. Nanophotonics 6, 479–493. doi:10.1515/nanoph-2015-0030
Britnell, L., Novoselov, K. S., Ribiro, R. M., Eckmann, A., Jalil, R., Mishchenko, A., et al. (2013). Strong light-matter interactions in heterostructures of atomically thin films. Science 340, 1311–1314. doi:10.1126/science.1235547
Butt, F. K., Chuanbao, C., Waheed, S. K., Zulfiqar, A., Ahmed, R., Idrees, F., et al. (2012). Synthesis of highly pure single crystalline SnSe nanostructures by thermal evaporation and condensation route. Mater. Chem. Phys. 137, 565–570. doi:10.1016/j.matchemphys.2012.09.059
Cahill, D. G., Braun, P. V., Chen, G., Clarke, D. R., Shanhui, F., Goodson, K. E., et al. (2014). Nanoscale thermal transport. II. 2003-2012. Appl. Phys. Rev. 1, 011305. doi:10.1063/1.4832615
Carrete, J., Mingo, N., Curtarolo, S., Mingo, N., and Curtarolo, S. (2014). Low thermal conductivity and triaxial phononic anisotropy of SnSe. Appl. Phys. Lett. 105, 101907. doi:10.1063/1.4895770
Chen, J., Klein, J., Yongjia, W., Shaoxu, X., Flammang, R., Heibel, M., et al. (2016). A thermoelectric energy harvesting system for powering wireless sensors in nuclear power plants. IEEE Trans. Nucl. Sci. 63, 2738–2746. doi:10.1109/TNS.2016.2606090
Chere, E. K., Zhang, Q., Dahal, K., Cao, F., Mao, J., and Ren, Z. (2016). Studies on thermoelectric figure of merit of Na-doped p-type polycrystalline SnSe. J. Mater. Chem. A 4, 1848–1854. doi:10.1039/C5TA08847J
Ding, G., Gao, G., and Yao, K. (2015). High-efficient thermoelectric materials: the case of orthorhombic IV-VI compounds. Sci. Rep. 5, 9567. doi:10.1038/srep09567
Ding, Y., Xiao, B., Tang, G., and Hong, J. (2017). Transport properties and high thermopower of SnSe2: a full Ab-initio investigation. J. Phys. Chem. C 121, 225–236. doi:10.1021/acs.jpcc.6b11467
Dresselhaus, M. S., Chen, G., Ming, Y. T., Ronggui, Y., Hohyun, L., Dezhi, W., et al. (2007). New directions for low-dimensional thermoelectric materials. Adv. Mater. 19, 1043–1053. doi:10.1002/adma.200600527
Du, Y., Cai, K., Chen, S., Wang, H., Shen, S. Z., Donelson, R., et al. (2015). Thermoelectric fabrics: toward power generating clothing. Sci. Rep. 5, 6411. doi:10.1038/srep06411
Fang, H., Chuang, S., Chang, T. C., Takei, K., Takahashi, T., and Javey, A. (2012). High-performance single layered WSe2 p-FETs with chemically doped contacts. Nano Lett. 12, 3788–3792. doi:10.1021/nl301702r
Favarel, C., Bédécarrats, J.-P., Kousksou, T., and Champier, D. (2015). Experimental analysis with numerical comparison for different thermoelectric generators configurations. Energy Convers. Manage. 107, 114–122. doi:10.1016/j.enconman.2015.06.040
Fei, R., Li, W., Li, J., and Yang, L. (2015). Giant piezoelectricity of monolayer group IV monochalcogenides: SnSe, SnS, GeSe, and GeS. Appl. Phys. Lett. 107, 173104. doi:10.1063/1.4934750
Fiori, G., Bonaccorso, F., Iannccone, G., Palacios, T., Neumaier, D., Seabaugh, A., et al. (2014). Electronics based on two-dimensional materials. Nat. Nanotechnol. 9, 768–779. doi:10.1038/nnano.2014.207
Gang, C. (2005). Nanoscale Energy Transport and Conversion. A Parallel Treatment of Electrons, Molecules, Phonons, and Photons. New York, NY: Oxford University Press, Inc.
Gao, X., Uehara, K., Klug, D. D., Patchkovskii, S., Tse, J. S., and Tritt, T. M. (2005). Theoretical studies on the thermopower of semiconductors and low-band-gap crystalline polymers. Phys. Rev. B 72, 1–7. doi:10.1103/PhysRevB.72.125202
Gayner, C., and Kar, K. K. (2016). Recent advances in thermoelectric materials. Prog. Mater. Sci. 83, 330–382. doi:10.1016/j.pmatsci.2016.07.002
Geim, A. K., and Novoselov, K. S. (2007). The rise of graphene. Nat. Mater. 6, 183–191. doi:10.1038/nmat1849
Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502. doi:10.1088/0953-8984/21/39/395502
Gonzalez, J. M., and Oleynik, I. I. (2016). Layer-dependent properties of SnS2 and SnSe2 novel two-dimensional materials. Phys. Rev. B 94, 125443. doi:10.1103/PhysRevB.94.125443
Gu, X. K., and Yang, R. G. (2014). Phonon transport in single-layer transition metal dichalcogenides: a first-principles study. Appl. Phys. Lett. 105, 5. doi:10.1063/1.4896685
Guan, X., Lu, P., Wu, L., Han, L., Liu, G., Song, Y., et al. (2015). Thermoelectric properties of SnSe compound. J. Alloys Compd. 643, 116–120. doi:10.1016/j.jallcom.2015.04.073
Guo, R., Wang, X., Kuang, Y., and Huang, B. (2015). First-principles study of anisotropic thermoelectric transport properties of IV-VI semiconductor compounds SnSe and SnS. Phys. Rev. B Condens. Matter Mater. Phys. 92, 1–42. doi:10.1103/PhysRevB.92.115202
Guo, S.-D. (2016). Strain effect on power factor in monolayer MoS2. Comput. Mater. Sci. 123, 8–13. doi:10.1016/j.commatsci.2016.06.011
Guo, S. D., and Wang, Y. H. (2017). Thermoelectric properties of orthorhombic group IV-VI monolayers from the first-principles calculations. J. Appl. Phys. 121, 0–7. doi:10.1063/1.4974200
Guo, S.-D., and Zhang, L. (2016). Biaxial strain tuned thermoelectric properties in monolayer PtSe2. J. Mater. Chem. C 4, 9366–9374. doi:10.1039/C6TC03074B
Heremans, J. P., Wiendlocha, B., and Chamoire, A. M. (2012). Resonant levels in bulk thermoelectric semiconductors. Energy Environ. Sci. 5, 5510–5530. doi:10.1039/C1EE02612G
Hong, A. J., Li, L., Zhu, H. X., Yan, Z. B., Liu, J.-M., and Ren, Z. F. (2015). Optimizing the thermoelectric performance of low-temperature SnSe compounds by electronic structure design. J. Mater. Chem. A 3, 13365–13370. doi:10.1039/C5TA01703C
Ioffe, A. F. (1957). Semiconductor Thermoelements, and Thermoelectric Cooling. London, England: Infosearch.
Jin, Z., Liao, Q., Fang, H., Liu, Z., Liu, W., Ding, Z., et al. (2015). A revisit to high thermoelectric performance of single-layer MoS2. Sci. Rep. 5, 18342. doi:10.1038/srep18342
Khan, A. A., Khan, I., Ahmad, I., and Ali, Z. (2016). Thermoelectric studies of IV-VI semiconductors for renewable energy resources. Mater. Sci. Semicond. Process. 48, 85–94. doi:10.1016/j.mssp.2016.03.012
Kim, J. Y., and Grossman, J. C. (2015). High-efficiency thermoelectrics with functionalized graphene. Nano Lett. 15, 2830–2835. doi:10.1021/nl504257q
Kim, S. J., We, J. H., and Cho, B. J. (2014). A wearable thermoelectric generator fabricated on a glass fabric. Energy Environ. Sci. 7, 1959. doi:10.1039/c4ee00242c
Kraemer, D., Poudel, B., Feng, H. P., Caylor, J. C., Yu, B., Yan, X., et al. (2011). High-performance flat-panel solar thermoelectric generators with high thermal concentration. Nat. Mater. 10, 532–538. doi:10.1038/nmat3013
Kumar, S., and Schwingenschlögl, U. (2015). Thermoelectric response of bulk and monolayer MoSe2 and WSe2. Chem. Mater. 27, 1278–1284. doi:10.1021/cm504244b
Kutorasinski, K., Wiendlocha, B., Kaprzyk, S., and Tobola, J. (2015). Electronic structure and thermoelectric properties of n- and p-type SnSe from first-principles calculations. Phys. Rev. B 91, 205201. doi:10.1103/PhysRevB.91.205201
Larentis, S., Fallahazad, B., and Tutuc, E. (2012). Field-effect transistors and intrinsic mobility in ultra-thin MoSe 2 layers. Appl. Phys. Lett. 101, 1–4. doi:10.1063/1.4768218
Leng, H.-Q., Zhou, M., Zhao, J., Han, Y.-M., and Li, L.-F. (2016). The thermoelectric performance of anisotropic SnSe doped with Na. RSC Adv. 6, 9112–9116. doi:10.1039/C5RA19469E
Leonov, V., and Vullers, R. J. M. (2009). Wearable thermoelectric generators for body-powered devices. J. Electron. Mater. 38, 1491–1498. doi:10.1007/s11664-008-0638-6
Li, G., Ding, G., and Gao, G. (2017). Thermoelectric properties of SnSe2 monolayer. J. Phys. Condens. Matter 29, 15001. doi:10.1088/0953-8984/29/1/015001
Li, H. M., Lee, D. Y., Choi, M. S., Qu, D., Liu, X., Ra, C. H., et al. (2014a). Metal-semiconductor barrier modulation for high photoresponse in transition metal dichalcogenide field effect transistors. Sci. Rep. 4, 4041. doi:10.1038/srep04041
Li, W., Carrete, J., Katcho, N. A., and Mingo, N. (2014b). ShengBTE: a solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015
Liao, B., and Chen, G. (2015). Nanocomposites for thermoelectrics and thermal engineering. MRS Bull. 40, 746–752. doi:10.1557/mrs.2015.197
Liu, W., Kang, J., Sarkar, D., Khatami, Y., Jena, D., and Banerjee, K. (2013). Role of metal contacts in designing high-performance monolayer n-type WSe2 field effect transistors. Nano Lett. 13, 1983–1990. doi:10.1021/nl304777e
Liu, Z., Wu, X., and Luo, T. (2017). The impact of hydrogenation on the thermal transport of silicene. 2D Mater. 4, 25002. doi:10.1088/2053-1583/aa533e
Løvvik, O. M., and Prytz, Ø (2004). Density-functional band-structure calculations for La-, Y-, and Sc-filled CoP3-based skutterudite structures. Phys. Rev. B 70, 195119. doi:10.1103/PhysRevB.70.195119
Madsen, G. K. H., and Singh, D. J. (2006). BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 175, 67–71. doi:10.1016/j.cpc.2006.03.007
Mahan, G. D., and Sofo, J. O. (1996). The best thermoelectric. Proc. Natl. Acad. Sci. U.S.A. 93, 7436–7439. doi:10.1073/pnas.93.15.7436
Mehdizadeh Dehkordi, A., Zebarjadi, M., He, J., and Tritt, T. M. (2015). Thermoelectric power factor: enhancement mechanisms and strategies for higher performance thermoelectric materials. Mater. Sci. Eng. R Rep. 97, 1–22. doi:10.1016/j.mser.2015.08.001
Moraes, F. S., Santos, L. C., Alencar, R. N., Sempels, E. V., Sandoval, J. C., and Lesage, F. J. (2015). Solar thermoelectric generator performance relative to air speed. Energy Convers. Manage. 99, 326–333. doi:10.1016/j.enconman.2015.04.049
Morales Ferreiro, J. O., Díaz-Droguett, D., Celentano, D., and Luo, T. (2016). Effect of the annealing on the power factor of un-doped cold-pressed SnSe. Appl. Therm. Eng. 111, 1426–1432. doi:10.1016/j.applthermaleng.2016.07.198
Nolas, G. S., Morelli, D. T., and Tritt, T. M. (1999). SKUTTERUDITES: a phonon-glass-electron crystal approach to advanced thermoelectric energy conversion applications. Annu. Rev. Mater. Sci. 29, 89–116. doi:10.1146/annurev.matsci.29.1.89
Novoselov, K. S., Geeim, A. K., Morozov, S. V., Jiang, D., Katsnelson, M. I., Grigorieva, I. V., et al. (2005). Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200. doi:10.1038/nature04233
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865
Popuri, S. R., Pollet, M., Decourt, R., Morrison, F. D., Bennett, N. S., and Bos, J. W. G. (2016). Large thermoelectric power factors and impact of texturing on the thermal conductivity in polycrystalline SnSe. J. Mater. Chem. C 4, 1685–1691. doi:10.1039/C6TC00204H
Pu, J., Kanahashi, K., Cuong, N. T., Chen, C. H., Li, L. J., Okada, S., et al. (2016). Enhanced thermoelectric power in two-dimensional transition metal dichalcogenide monolayers. Phys. Rev. B 94, 14312. doi:10.1103/PhysRevB.94.014312
Qin, G., Qin, Z., Fang, W., and Zhang, L. (2016). Diverse anisotropy of phonon transport in two-dimensional group IV-VI compounds: a comparative study. Nanoscale 8, 11306–11319. doi:10.1039/c6nr01349j
Rais, I., Lefevre, L., Orgerie, A. C., and Benoit, A. (2016). “An analysis of the feasibility of energy harvesting with thermoelectric generators on petascale and exascale systems,” in 2016 Int. Conf. High Perform. Comput. Simulation, HPCS 2016 (Innsbruck, Austria), 808–813.
Sassi, S., Candolfi, C., Vaney, J. B., Ohorodniichuk, V., Masschelein, P., Dausher, A., et al. (2015). Transport properties of polycrystalline p-type SnSe. Mater. Today Proc. 2, 690–698. doi:10.1016/j.matpr.2015.05.093
Sava, F., Lorinczi, A., Popescu, M., Socol, G., Axente, E., Mihailescu, I. N., et al. (2006). Amorphous SnSe2 films. J. Optoelectron. Adv. Mater. 8, 1367–1371.
Shafique, A., and Shin, Y. (2017). Thermoelectric and phonon transport properties of two-dimensional IV–VI compounds. Sci. Rep. 7, 1–10. doi:10.1038/s41598-017-00598-7
Singh, A. K., and Hennig, R. G. (2016). Computational prediction of two-dimensional group-IV mono-chalcogenides computational prediction of two-dimensional group-IV mono-chalcogenides. Appl. Phys. Lett. 105, 42103. doi:10.1063/1.4891230
Snyder, G. J., and Toberer, E. S. (2008). Complex thermoelectric materials. Nat. Mater. 7, 105–114. doi:10.1038/nmat2090
Sootsman, J. R., Chung, D. Y., and Kanatzidis, M. G. (2009). New and old concepts in thermoelectric materials. Angew. Chemie. Int. Ed. Engl. 48, 8616–8639. doi:10.1002/anie.200900598
Sun, B.-Z., Ma, Z., He, C., and Wu, K. (2015). Anisotropic thermoelectric properties of layered compounds in SnX2 (X = S, Se): a promising thermoelectric material. Phys. Chem. Chem. Phys. 17, 29844–29853. doi:10.1039/C5CP03700J
Tian, Z., Lee, S., and Chen, G. (2013). Heat transfer in thermoelectric materials and devices. J. Heat Transfer 135, 61605. doi:10.1115/1.4023585
Tritsaris, G. A., Malone, B. D., and Kaxiras, E. (2013). Optoelectronic properties of single-layer, double-layer, and bulk tin sulfide: a theoretical study. J. Appl. Phys. 113, 233507. doi:10.1063/1.4811455
Tyagi, K., Gahtori, B., Bathula, S., Singh, N. K., Bishnoi, S., Auluck, S., et al. (2016). Electrical transport and mechanical properties of thermoelectric tin selenide. RSC Adv. 6, 11562–11569. doi:10.1039/C5RA23742D
Vineis, C. J., Shakouri, A., Majumdar, A., and Kanatzidis, M. G. (2010). Nanostructured thermoelectrics: big efficiency gains from small features. Adv. Mater. 22, 3970–3980. doi:10.1002/adma.201000839
Wang, F. Q., Zhang, S., Yu, J., and Wang, Q. (2015). Thermoelectric properties of single-layered SnSe sheet. Nanoscale 7, 15962–15970. doi:10.1039/c5nr03813h
Wang, H., Schechtel, E., Pei, Y., and Snyder, G. J. (2013). High thermoelectric efficiency of n-type PbS. Adv. Energy Mater. 3, 488–495. doi:10.1002/aenm.201200683
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N., and Strano, M. S. (2012). Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712. doi:10.1038/nnano.2012.193
Wu, X., and Luo, T. (2014). The importance of anharmonicity in thermal transport across solid-solid interfaces. J. Appl. Phys. 115, 014901. doi:10.1063/1.4859555
Wu, X., Varshney, V., Lee, J., Pang, Y., Roy, A., and Luo, T. (2017). How to characterize thermal transport capability of 2D materials fairly? Sheet thermal conductance and the choice of thickness. Chem. Phys. Lett. 669, 233–237. doi:10.1016/j.cplett.2016.12.054
Yabuuchi, S., Okamoto, M., Nishide, A., Kurosaki, Y., and Hayakawa, J. (2013). Large Seebeck coefficients of Fe 2 TiSn and Fe 2 TiSi: first-principles study. Appl. Phys. Exp. 6, 25504. doi:10.7567/APEX.6.025504
Yan, R., Simpson, J. R., Bertolazzi, S., Brivio, J., Watson, M., Wu, X., et al. (2014). Thermal conductivity of monolayer molybdenum disulfide obtained from temperature-dependent Raman spectroscopy. ACS Nano 8, 986–993. doi:10.1021/nn405826k
Zhang, G., and Zhang, Y. W. (2015). Strain effects on thermoelectric properties of two-dimensional materials. Mech. Mater. 91, 382–398. doi:10.1016/j.mechmat.2015.03.009
Zhang, G., and Zhang, Y.-W. (2017). Thermoelectric properties of two-dimensional transition metal dichalcogenides. J. Mater. Chem. C 5, 7684–7698. doi:10.1039/C7TC01088E
Zhang, Q., Chere, E. K., Sun, J., Cao, F., Dahal, K., Chen, S., et al. (2015). Studies on thermoelectric properties of n-type polycrystalline SnSe1-xSx by iodine doping. Adv. Energy Mater. 5, 1–8. doi:10.1002/aenm.201500360
Zhao, L. D., Lo, S. H., Zhang, Y., Sun, H., Tan, G., Uher, C., et al. (2014). Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 508, 373–377. doi:10.1038/nature13184
Zhao, L. D., Tan, G., Hao, S., He, J., Pei, Y., Chi, H., et al. (2016). Ultrahigh power factor and thermoelectric performance in hole-doped single-crystal SnSe. Science 351, 141–144. doi:10.1126/science.aad3749
Keywords: ZT, Seebeck coefficient, electrical conductivity, electronic thermal conductivity, power factor, lattice thermal conductivity, figure-of-merit
Citation: Morales-Ferreiro JO, Diaz-Droguett DE, Celentano D and Luo T (2017) First-Principles Calculations of Thermoelectric Properties of IV–VI Chalcogenides 2D Materials. Front. Mech. Eng. 3:15. doi: 10.3389/fmech.2017.00015
Received: 21 August 2017; Accepted: 23 October 2017;
Published: 07 December 2017
Edited by:
Satish Kumar, Georgia Institute of Technology, United StatesReviewed by:
Liang Chen, Xi’an Jiaotong University, ChinaCopyright: © 2017 Morales-Ferreiro, Diaz-Droguett, Celentano and Luo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: J. O. Morales-Ferreiro, amZlcnJlaTJAbmQuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.