Study on mechanical properties of large deformation segmental cement-based honeycomb structure

Honeycomb structures provide a new means of controlling and supporting the tunnel envelope. However, traditional honeycomb structures have low strength and poor stability, and are prone to stress concentration and instability, further limiting their application in deep tunnel support projects. In this paper, a new type of segmental cementitious honeycomb structure is investigated, its performance under different loading rates is tested, and its application in deep large deformation tunnel support is discussed. Firstly, the honeycomb model was drawn and the honeycomb skeleton was prepared. Then, the cement suspension technique was optimised. Secondly, the effects of different loading rates on the performance of segmented cement-bonded honeycomb structures were investigated by laboratory experiments. The results show that when the loading rate is 3 mm/min, the structure has the maximum load capacity and the best energy absorption performance. It is worth noting that too fast or too slow loading rate will affect the performance of the structure. Finally, the damage mechanism of the segmented honeycomb structure was further investigated by using an acoustic emission system, and the acoustic emission characteristics showed that the segmented cementitious honeycomb structure firstly went through a relatively stable stage of microcrack development under the action of the loads in all bands, and then a large area of damage was observed in the top layer of the honeycomb skeleton when the peak load was reached, resulting in the collapse of the whole layer of the honeycomb structure, which led to the collapse of the whole layer of the honeycomb skeleton. This led to the collapse of the whole layer of the honeycomb structure and a significant decrease in the bearing capacity, which confirmed the layer-by-layer damage characteristics of segmental cementitious honeycomb structures. In addition, the RA-AF values show that the loading rate has little effect on the crack type, which is almost unchanged with the increase of loading rate. These studies verify the feasibility of using honeycomb structure to support roadway with fast deformation speed and large deformation. It is of great significance to guide the application of honeycomb structure in deep roadway support engineering.

1 Introduction

The surrounding rock in deep soft rock roadways is characterized by loose and fragmented conditions, exhibiting prolonged instability, rapid deterioration, and significant deformation. Due to the intense geostress at deeper levels, the soft rock exhibits diminished strength, leading to an expanded plastic damage zone and increased severity post-roadway excavation. This often leads to challenges such as roof subsidence, wall bulging, and structural deformation, impeding the effectiveness of roadway support and posing significant risks to mine safety (Wu et al., 2024). Consequently, effectively managing deformation during the operational lifespan of soft rock roadways has emerged as a critical issue demanding immediate attention (Wu et al., 2020). In soft rock roadway, bolt and grouting can effectively improve the overall stability of supporting structure and prevent rock collapse and collapse (Shi et al., 2023; Wu et al., 2023). However, under soft rock geological conditions, rock mass deformation is large, and the supporting effect of bolt and grouting is affected by rock mass deformation, which is difficult to be completely controlled (Wu et al., 2022; Shi et al., 2024). As coal mining progresses to greater depths, there is a growing requirement for enhanced energy absorption within the roadway support structures. The honeycomb structure was inspired by the nests of bees. It is arranged in a polygonal structure and has the advantages of high strength, light weight and high energy absorption (Zhang et al., 2015; Thomas and Tiwari, 2019). The traditional honeycomb structure is usually arranged in a regular hexagonal shape, which is characterized by high density, less material consumption, and large void space. In addition, studies have confirmed that honeycomb structures have high shear modulus and excellent energy absorption properties (Gupta et al., 2001; Velea and Lache, 2011; Rajaneesh et al., 2014; Siromani et al., 2014; Gaitanaros and Kyriakides, 2015; Mozafari et al., 2016). Since the 1980s, honeycomb structures have been widely used in engineering, such as hexagonal towers in buildings. In recent years, honeycomb structures have expanded into the nano and biomedical fields, covering applications such as nanopore arrays, microporous arrays, and activated carbon honeycomb (Masuda and Fukuda, 1995; Broeng et al., 1998; Gadkaree, 1998; Yabu et al., 2005; Allen et al., 2010). With the advancement of manufacturing technology, honeycomb structures are expanding into traditional engineering, micro and nano manufacturing, and biomedical applications (Sugiura et al., 1998; Kageyama et al., 1999; Connal and Qiao, 2006; Mukai et al., 2006; Pawin et al., 2006; Engelmayr et al., 2008; Mishchenko et al., 2010; Baggetto et al., 2011; Ng et al., 2011; Tejavibulya et al., 2011; Mao et al., 2012). Structural designers also incorporate units of different shapes, such as square (Wadley, 2005), triangular (Hohe and Becker, 1999), cylindrical (Sunami et al., 2006), and square and triangular configurations of square super monoliths (Saha et al., 2007) and Kagome units (Zhang and Zhang, 2013) to enhance the functionality of honeycomb structures. Honeycomb structures have evolved from basic shapes to various variants such as flexible cores (Bitzer, 1994), double bending (Kuo, 1991) and reinforced hexagonal cells to provide a wider range of applications as well as superior mechanical properties and formability. However, studies on the mechanical properties of traditional honeycomb structures show that there are defects in strength and stability under the action of out-of-plane loads. Similarly, limitations in load transfer can arise when facing in-plane loading, potentially leading to localized stress concentration or structural instability (Cahangirov et al., 2009; Wang and Bai, 2015; Zhang et al., 2017; Zhang et al., 2018; Wang, 2019; Qi et al., 2021). In addition, the construction of the honeycomb structure is relatively complex, not suitable for rapid implementation in a complex environment, and the traditional honeycomb structure requires a large number of steel bars as the skeleton, the cost is high, and it may be difficult to bear the cost in the soft rock alley. Therefore, the defects of the traditional honeycomb structure make it difficult to cope with the complex environment of deep soft rock roadway.

In response to the limitations of traditional honeycomb structures, researchers have devised innovative solutions, including gradient honeycombs, hierarchical honeycombs, composite honeycombs, and plasticized honeycombs. The gradient honeycomb structure improves the mechanical properties of the structure while maintaining the original density and mass (Liu et al., 2023). Compared with the traditional honeycomb structure, the layered honeycomb structure can exert better mechanical properties under dynamic load, and the energy absorption capacity is improved compared with the traditional honeycomb structure (Fan et al., 2008). The composite honeycomb has better mechanical properties, including shear strength, indentation resistance and fracture toughness. In addition to the above honeycomb structures, a lightweight honeycomb structural scaffold has been proposed (Wang et al., 2022), consisting of multiple hollow cell elements arranged adjacent to each other in the form of arrays to form a scaffold. When the scaffold is placed into the cement slurry, the cement slurry adheres to the inner and outer surfaces of the scaffold due to surface tension, and the openings in the scaffold enhance this adhesion. After the cement slurry is solidified, the segmental honeycomb structure is formed together with the original honeycomb support.

Deep soft rock roadway has become a difficult problem in support engineering because of its large deformation and fast deformation speed. In this paper, a new segmental cement-based honeycomb structure is designed, and its application in this roadway support engineering is simulated for the first time. The feasibility of support engineering has been verified successfully. Firstly, the segmental cementitious honeycomb structure was prepared based on high-precision 3D printing technology and submerged method. The mechanical properties, acoustic emission characteristics and energy absorption characteristics of cement-based honeycomb structures under different loading rates were studied by uniaxial out-of-plane compression experiments. The optimal loading rate for the structure is obtained, which reveals that the structure can maintain stability and high load capacity under large deformation or impact. This presents a new avenue for tackling issues related to substantial tunnel support deformation, rock blasting, impact pressure, and other catastrophic events by enhancing energy absorption and stability control. This discovery is anticipated to advance the utilization of honeycomb structures in tunnel support projects.

2 Materials and methods

2.1 Materials

The test was conducted using ordinary silicate 42.5 grade cement as the cementing material for the segmental cementitious honeycomb structure with a density of 3.1 g/cm³. As shown in Table 1, the chemical composition of the cement was obtained after X-ray diffraction test. The honeycomb skeleton structure is complex and requires unsupported 3D printing, and the photosensitive resin has moderate elastic modulus and high ultimate strength, which can be used for unsupported 3D printing. As shown in Table 2, the mechanical properties of the photosensitive resin material can be acquired through testing.

Table 1

Table 1. Chemical composition of cement (%).

Table 2

Table 2. Physical properties of photosensitive resins.

2.2 Sample preparation

2.2.1 Design and preparation of honeycomb skeleton

Using Rhino software to draw the basic model, the honeycomb support consists of hexagonal arc-shaped basic cells, so the drawing idea is to draw a single hexagonal arc-shaped cells, and then through the continuous copying and arraying to get the final structure. The basic shape is first drawn using the multi-circle intersection method, and then the offset command is used to offset inward and outward, remove the intermediate line and cut the edge to get the hexagonal surface element. Then it is divided into hexagonal units and columnar units. Finally, the two components are integrated and a complete cellular structure is built systematically using the array command.

The high height of each layer of the honeycomb skeleton means that the gap between the two layers is larger. Cement cannot fill the gap between the two layers. This results in sample preparation failure. The small height of each layer of honeycomb skeleton is also not conducive to sample preparation. This makes it difficult for the external cement to penetrate into the internal framework, resulting in uneven cement coating. For the above reasons, the height of each layer of the honeycomb skeleton is set at 2 mm.

After the modeling process is completed, a photosensitive resin is used for printing, and the honeycomb bracket is made by a light curing 3D printer. Subsequently, it was submerged in a 90% alcohol solution to eliminate surface adhesives. Finally, it underwent UV light exposure for 15–20 min to enhance its durability. Because of the thin side walls and low strength of the honeycomb bracket, the skeleton needs to be moved carefully with tool pliers.

2.2.2 Sample preparation of segmental cement-based honeycomb structure

The cement of grade 42.5 was used, and according to the proportion of water-cement ratio of 0.5, the constant speed mixer of the cement test equipment was used to fully mix the fresh cement paste until the cement paste was viscous and without obvious lumps, and in order to improve the cement paste’s ease of use, a polyacrylate-based high-efficiency water reducing agent was added. After the mixing process, a small slump test was conducted to assess the compatibility of the ordinary silicate cement paste and regulate consistency across different sample batches. Figure 1 shows the fabrication process of the segmented honeycomb bracket.

Figure 1

Figure 1. Cement slurry hanging process of segmental honeycomb support: (A) Honeycomb skeleton; (B) infiltration process; (C) Coating process; (D) Sample finished product (E) Curing and drying.

It is found that the uniformity of cement coating has a great influence on the mechanical properties of the honeycomb model. Therefore, the preparation process will be optimized in subsequent studies. For example, the orientation of the sample is adjusted, and the method of multiple wetting is used to ensure that the honeycomb skeleton is evenly coated with cement.

The honeycomb supports are moistened by immersion in cement slurry for approximately 2 min, ensuring the formation of a stable film on the vertical surfaces. Alternatively, specialized spraying equipment can be used to spray the cement slurry evenly onto the honeycomb skeleton. During the slurry hanging process, it is necessary to ensure that the cement slurry evenly covers each cell and joint of the honeycomb structure to ensure the uniformity and integrity of the structure. Use wire hooks to hook the bracket, slowly lift it up and place it on the perforated iron frame, so that the excess cement paste flows out under the effect of gravity, if the effect of hanging slurry is not satisfactory, repeat the above operation. The support is soaked with cement slurry several times to make the cement slurry fully cover the honeycomb skeleton to ensure that a stable cement layer is formed on the surface of the honeycomb wall. After the cement coating was completed, the sample was cured in a high humidity environment for 24 h. Due to the large surface area of the samples of segmental cementitious honeycomb structures, the samples were placed in saturated Ca(OH)₂ solution for 6 days after 24 h of curing in order to prevent the effects of rapid evaporation of water. After the curing of the samples at this stage, the samples were transferred to the curing box at a temperature of 20°C ± 1°C and a relative humidity of more than 95% for 21 days of curing. After curing, the surface moisture of the sample is dried in the oven, and then it can be used for subsequent mechanical property testing.

2.3 Mechanical testing

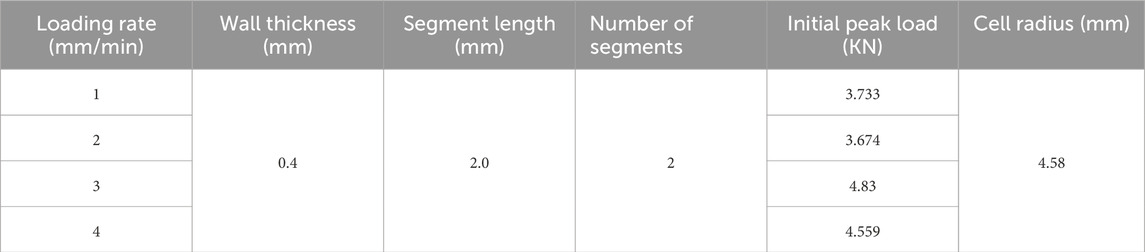
The mechanical testing system is an MTS 816 electro-hydraulic servo pressure tester with a maximum axial load of 459 kN, which can perform uniaxial compression tests on geotechnical materials, concrete and other materials. The uniaxial compression test is conducted at four different loading rates of 1, 2, 3 and 4 mm/min while keeping the parameters of the honeycomb structure constant. The same conditions of the honeycomb structure to prepare three for ensuring the accuracy of the results, a total of 12 uniaxial compression test, the specific operating parameters and the main test results are shown in Table 3. The Micro-II acoustic emission system is used to collect real-time acoustic emission data generated during mechanical testing. The monitoring system uses a piezoelectric ceramic acoustic emission transducer with a resonance frequency of 140 kHz, a gain and sum value of 35 db, an impact time of 50 μs, an impact interval of 300 μs, and an acquisition rate of 100 ms/time.

Table 3

Table 3. Experimental conditions of segmental cement-based honeycomb structure.

3 Results and discussion

3.1 Force-displacement characteristics

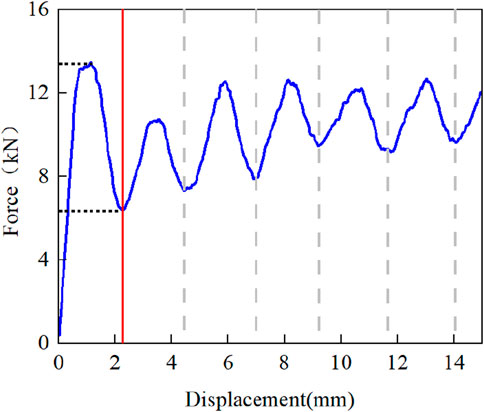
In order to explore the effect of loading rate on the mechanical properties of segmental cementitious honeycomb structures in out-of-face compression, it is first necessary to understand the force-displacement response characteristics in the out-of-face compression process. Figure 2 shows the force-displacement curve of a typical segmental cement-based honeycomb structure specimen. The loading process is divided into two stages.

Figure 2

Figure 2. Force-displacement curve of a typical specimen.

In the first stage, the left part of the red line in Figure 3 experienced the load rise process. With the increase of loading displacement, the load carrying capacity of the specimen rises until it reaches the first peak point, which is the initial peak load. Subsequently, the load falls down by about 50%. Because the typical curve is obtained at a slower loading rate. In this case, the failure of the honeycomb structure is relatively slow, and the indenter always maintains contact with the honeycomb structure, so the load drop is small. The force-displacement curve then enters the second phase, which is a wave-like cyclic phase. As the displacement increases, the load rises again to the next peak, and the displacement between the peaks is approximately equal to the section length (2 mm). At this stage, there are multiple peaks, and the sizes of each peak load are close to each other. The curve presents a cyclic change of first increasing and then decreasing, and the peak-valley difference gradually decreases, which is close to but slightly smaller than the initial peak load.

Figure 3

Figure 3. Force-displacement curves of honeycomb structures at different loading rates.

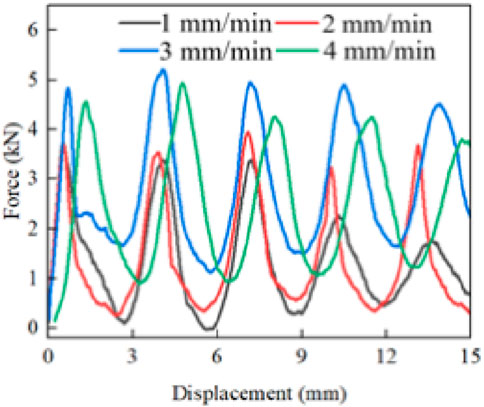
Under different loading rates, the force-displacement curves of segmental cement-based honeycomb specimens are shown in Figure 3. After reaching the peak value, the force-displacement curves of the honeycomb structures under different loading rates all show a large drop, and the shapes of the different peak cycles are also relatively similar. Because in the process of loading, the honeycomb bracket has a certain brittleness, and it breaks directly under pressure. At the same time, the cement coating also breaks and collapses instantaneously when subjected to pressure, so the contact force between the indenter and the specimen almost disappears at this moment, resulting in the force-displacement curve falling to almost zero.

3.2 Effect of loading rate on strength

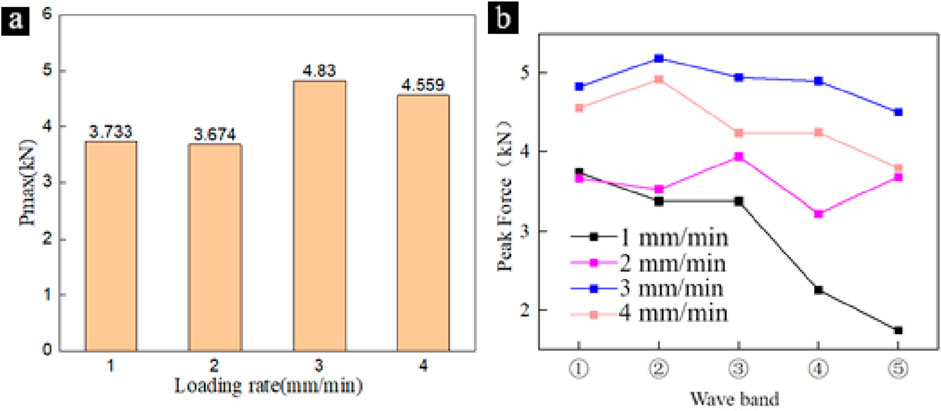
As shown in Figure 4A, the loading rate has a significant effect on the mechanical properties of segmental cement-based honeycomb structures. As the loading rate increases from 1 to 4 mm/min, the initial peak load of the sample increases from 3.73 to 4.56 KN. The initial peak load at 3 and 4 mm/min is significantly higher than that at 1 and 2 mm/min. The strength is close when the loading rate is 1 and 2 mm/min. The strength is similar when the loading rate is 3 and 4 mm/min. The increase in loading rate increases its initial peak load by nearly a third. The increase of loading rate cannot lead to the increase of initial peak load in time, but only when the loading rate increases to a certain extent will the initial peak load increase. This is because when the loading rate is high, the honeycomb skeleton of the same layer of segmental cement-based honeycomb structure may be partially destroyed first, resulting in the multi-layer honeycomb skeleton bearing the load at the same time, thus increasing the overall bearing capacity. When the loading rate is low, the internal stress distribution is more uniform, and the stress of the skeleton can be extended to the adjacent skeleton in time after the failure, so that the same layer of skeleton is nearly destroyed at the same time, thus reducing the phenomenon of multi-layer skeleton bearing at the same time, resulting in a low bearing capacity.

Figure 4

Figure 4. (A) Initial peak load; (B) Peak bearing capacity of each band.

According to the data in Figure 4B, it can be seen that the peak loads in different bands are basically equal, and the overall variation is small, which demonstrates the stability and continuity of the strength of segmental cementitious honeycomb structures. However, for the 1 mm/min specimen, the peak loads in the first three bands are relatively stable, while the peak loads in the fourth and fifth bands show a significant decrease, which may be attributed to the uneven coverage of the cement film during specimen preparation. This reveals the importance of the uniformity of the cement slurry for segmental cementitious honeycomb structures, and the uneven slurry coverage may seriously affect the structural strength, stability, and energy-absorbing effect. Under normal conditions, once the top skeleton is destroyed, the top of the honeycomb structure is no longer flat, the integrity of the specimen is damaged, and micro-damage begins to appear inside, resulting in the subsequent peak load decreasing, resulting in the peak load of the first frequency band of the specimen being higher than that of the subsequent frequency band.

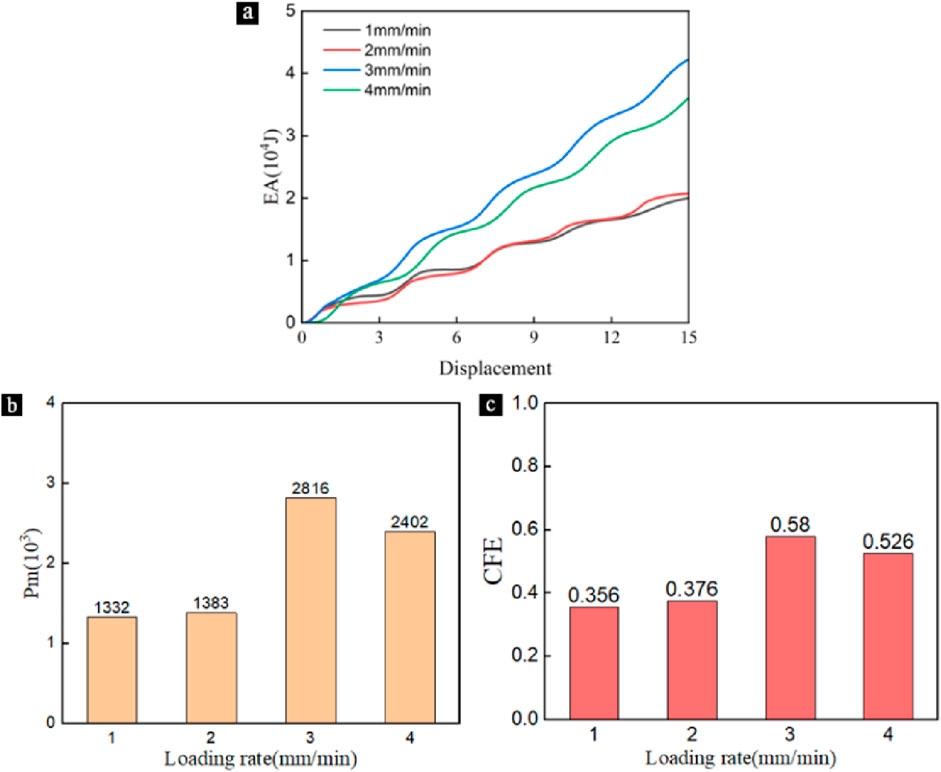
3.3 Energy absorption characteristic

EA characterizes the ability of a structure to dissipate energy through plastic deformation, and is the total energy absorbed by the structure throughout the compression collapse process, the larger the value of EA represents the stronger energy absorption capacity of the structure (Lu et al., 2017). It can be determined by the integral area under the corresponding force-displacement curve and can be calculated using Equation 1:

$EA={\int }_0^{d}F\left(x\right)dx(1)$

As can be seen from Figure 5A, the experimental results show that there are differences in the energy absorption properties of the segmental cementitious honeycomb structures under different loading rate conditions. When the loading rate is 3 mm/min, the energy absorption curve of the specimen is always above the other rate curves, showing the most excellent energy absorption performance. This may be due to the fact that under the faster loading rate, the stress concentration occurs inside the structure, which makes it easier for the local honeycomb skeleton to reach the energy-absorbing limit, thus reflecting a better energy-absorbing effect in the whole. On the other hand, the energy-absorption curves of the specimens with loading rates of 1 and 2 mm/min gradually intersect with increasing displacement, and the energy-absorption curves are close to and significantly lower than those of 3 and 4 mm/min. This is because when the loading rate is low, the phenomenon of multi-layer skeleton bearing at the same time does not occur, and the impact energy cannot be transferred effectively, thus limiting the overall energy absorption effect. When the loading speed is 4 mm/min, the energy absorption effect is different from that of 3 mm/min, because the loading speed is too fast, which may cause serious deformation and even instability inside the honeycomb structure. This will affect the energy absorption properties of the structure, making it unable to effectively absorb the impact energy.

Figure 5

Figure 5. (A) Total absorption energy; (B) Average crushing load; (C) Crushing force efficiency.

The average crush load P_m is defined as the ratio between the total energy absorption EA and the effective crush displacement (Tian et al., 2023), characterizing the level of loading on the structural specimen during the energy absorption process. It can be calculated using Equation 2:

$P_m=\frac{EA}{d}(2)$

As can be seen from Figure 5B, the average crushing load of the specimens showed a trend of increasing and then decreasing with the increase of loading rate. When the loading rate is 3 mm/min, the average crushing load increases from 1,332 kN to the maximum of 2,816 kN, and when the loading rate increases to 4 mm/min, the average crushing load decreases to 2,402 kN, indicating that there is a threshold value for the influence of loading rate on crushing load. When the loading rate is less than the threshold, the crushing load increases with the increase of the loading rate. When the loading rate is greater than the threshold value, the crushing load decreases with the increase of the loading rate.

The compressive collapse force efficiency CFE is defined as the ratio of the average compressive collapse load P_m to the initial peak load P_max. The higher the CFE value, the smaller the initial peak load generated by the sample while dissipating a large amount of energy. This shows that the better the load consistency of the structure, the higher the CFE value, the better the impact resistance of the structure. The calculation formula is as follows Equation 3:

$CFE=\frac{P_m}{P_{\max }}(3)$

It can be seen from Figure 5C that with the increase of loading rate, the crushing force efficiency of the specimen has a consistent change rule with the crushing load. In the interval of 1∼3 mm/min, the compressive collapse force efficiency increases with the increase of loading rate, and starts to decrease when the loading rate exceeds 3 mm/min, which is consistent with the change of the average compressive collapse load of the specimens in Figure 5B. The total absorbed energy, the average crushing load and the crushing force efficiency of the specimens with different loading rates show identical trends, which are all increasing and then decreasing with the increase of loading rate. The experimental results show that the segmented cementitious honeycomb structure can give the best performance at a loading rate of 3 mm/min.

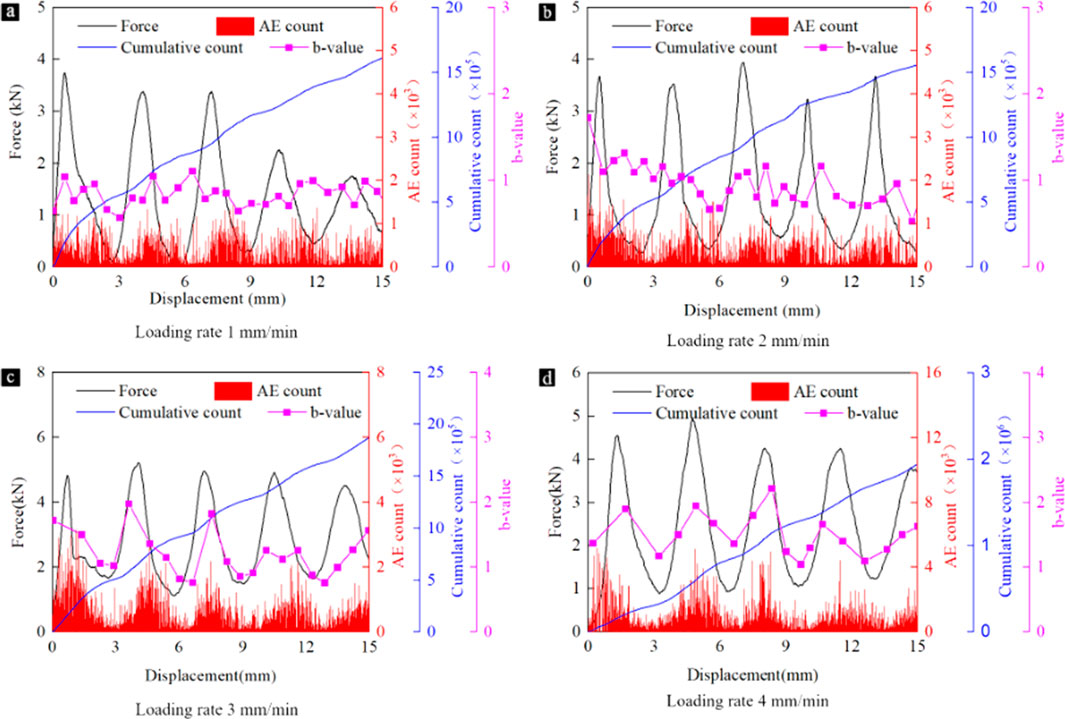
3.4 Acoustic emission parameter characteristics

The changes of load, acoustic emission count, cumulative count and b value of the specimen under different loading rates are shown in Figure 6. It can be seen from the figure that under different loading rates, the force-displacement curve is a stable wave-like curve, and the peak load and displacement distance of each cycle are roughly equal. Each curve consists of a number of approximately the same curve fluctuations, each segment represents a layer of the specimen destroyed, the four specimens experienced five fluctuations in the displacement are in the vicinity of 15 mm, is the height of the 5-layer honeycomb skeleton, showing a high degree of regularity, that is, each fluctuation in the force-displacement curve of the specimen represents a layer of the honeycomb skeleton was destroyed, the curve of each fluctuation traveled a distance equal to the height of a single layer of the skeleton.

Figure 6

Figure 6. Evolution characteristics of force and sound emission at different loading rates.

The characteristic parameters of acoustic emission have a good correspondence with the force-displacement curves. The acoustic emission signal is always generated during the whole loading process, which means that the uniaxial compression test is always accompanied by the closing, initiation, expansion and penetration of microcracks. Therefore, the cumulative AE count curve increases with the increase of loading time. The acoustic emission counts and the force-displacement curves have an obvious peak-to-peak relationship, and the peak of each force-displacement curve fluctuation corresponds to the peak region of the acoustic emission counts, which indicates that a large amount of damage occurs in the segmental cementitious honeycomb structure at the peak loading. The peak value of acoustic emission is slightly delayed compared with the peak value of load, because the damage inside the honeycomb sample is more intense after the peak value. Like the fluctuation of force-displacement curves in each segment, the peak counts and count distribution of acoustic emission counts in each segment are approximately the same, so that the cumulative acoustic emission counts rise slowly and steadily at a constant rate, and the shape of the cumulative counts curve is close to a straight line of the primary function. This result also confirms that the segmental cement-based honeycomb structure is destroyed layer by layer.

The b-value is derived from seismic studies and is used to express the relationship between the magnitude and frequency of earthquakes with the equation shown in Equation 4:

$\lg N=a-b{m}_{si}/20(4)$

where N is the frequency of earthquakes and m_si is the magnitude. a, b are constants.

In this experiment, the amount of acoustic emission data is determined by the test time. Under the same displacement size, the faster the loading rate and the shorter the experiment time, the less AE data is obtained. The slower the loading rate and the longer the experiment time, the more acoustic emission data can be obtained. The number of B-value points is determined by the number of AE data. The more AE data, the more B-value points, and the less AE data, the fewer B-value points. When the loading rate is 4 mm/min, although the number of B-value points is the least, it can still reflect the change trend of B-value.

In acoustic emission monitoring, the b-value is a function of the scale of crack extension inside the object, and the dynamic change of the b-value is characterized by direct physical significance. Theoretically, the b-value is negatively correlated with the degree of damage within the material. An increase in the b-value during the loading process implies an increase in the proportion of small-scale events, and the microcracks within the material are in a stable expansion state. The b value is constant or the fluctuation range is small, indicating that the damage state of the microcrack inside the material is relatively stable. The decrease of b value means that the proportion of large events increases, and the microcracks inside the material are mainly large-scale damage. When the B value fluctuates greatly, it indicates that the micro-crack state changes suddenly, indicating that sudden instability failure occurs.

Under uniaxial compression experiment, the change law of AE b value is obvious under the four loading rates. b value, AE count and load almost show the same change trend, and b value and load rise or fall together. When b value and load reach the extreme point, AE count also reaches the highest point. The change curve of b value is consistent with the change curve of load. The change of b value indirectly reflects the damage and crack development inside the specimen. At the initial stage of uniaxial loading, the b-value increases, which indicates that the microcracks inside the specimen are in a stable state of expansion at the beginning of loading, and the acoustic emission b-value fluctuates as the load comes to the peak and then falls down, and then there is a large decrease, at which time, the top layer of the honeycomb skeleton is greatly damaged, and the honeycomb structure of this layer is in an overall collapse. With the loading of the second wave band, the acoustic emission b-value fluctuates, which may be caused by the destruction of the remaining honeycomb skeleton in the first layer and the compression of the honeycomb skeleton in the lower layer at the same time, under which the destruction of microcracks inside the honeycomb specimen is relatively stable. The trend of “b value decreasing - b value increasing - decreasing - increasing” again verifies the progressive damage mode of the segmental cementitious honeycomb structure layer by layer. At the same time, the size of b-value is generally more stable, without obvious large-scale changes, indicating that the damage state of microcracks inside the material is generally slow, which reflects the stability of the segmental cementitious honeycomb structure.

The acoustic emission characteristics of the specimens at different loading rates are still different. When the loading rate is low, the size of the AE count is relatively average. As the loading rate increases, the difference between the high and low counts of the acoustic emission counts gradually increases, and the counts fluctuate significantly, indicating that the crack extension of the specimens is more stable at lower loading rates compared with higher loading rates, and at higher loading rates, the thin cement layer is more brittle, and collapses more rapidly under high-speed compression. At loading rates of 1 and 2 mm/min, the b-values of the specimens are more stable, and the b-values of the neighboring points are closer to each other, while the b-values of the specimens fluctuate relatively obviously at loading rates of 3 and 4 mm/min. This also indicates that the crack extension of the specimens at lower loading rates is more stable compared with higher loading rates, and the b-values of the specimens with higher loading rates are also larger, which again indicates that the higher the loading rate, the more intense the damage of the specimens. The effect of loading rate on b value is greater than that on cumulative AE count. The acoustic emission counts of the specimens under the four loading rates do not differ much, while the b-value changes and sizes are more obviously differentiated, which suggests that the b-value is more sensitive to the different loading rates, and is more responsive to the damage characteristics of the segmented cementitious honeycomb structure under the influence of the different loading rates.

3.5 Fracture crack type characteristics

In order to study the crack propagation of honeycomb structures under different loading rates and characterize the internal cracks and damage of materials. The scatter map is drawn by combining RA and AF parameters, and the distribution of AE RA-AF values under uniaxial compression is analyzed.

AF = count/duration, RA = rise time/amplitude.

It is usually considered that the corresponding acoustic emission RA-AF signals are characterized by “low AF and high RA” corresponding to the form of damage for shear damage, and on the contrary, “high AF and low RA” for tensile damage, so the diagonal line of the distribution of RA-AF values is used as the dividing line between tension cracks and shear cracks. Therefore, the diagonal line of the RA-AF value distribution graph is used as the dividing line between tension cracks and shear cracks, and the judgment method is shown in Figure 7A.

Figure 7

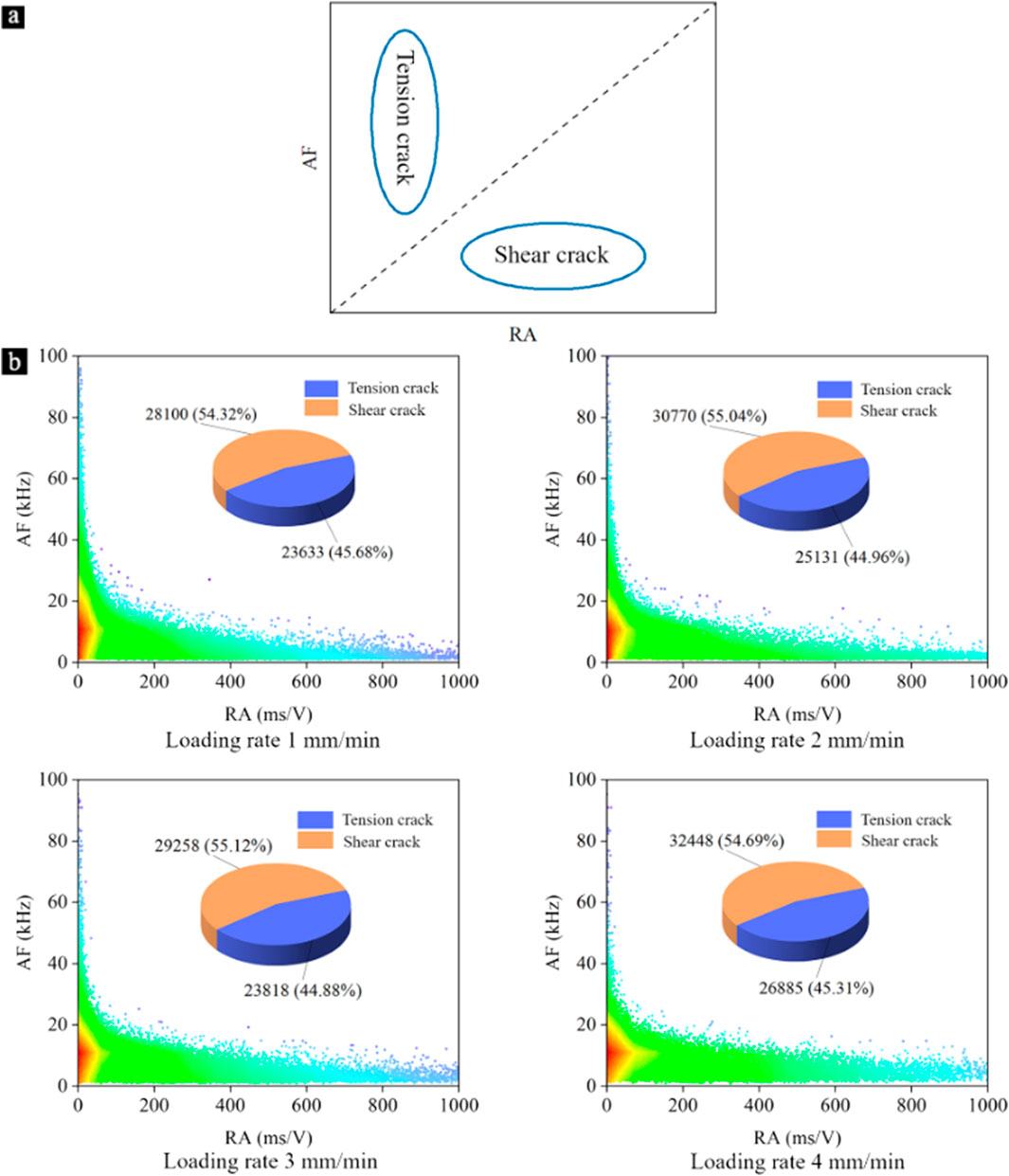
Figure 7. (A) Crack distribution diagram; (B) RA-AF distribution and crack type proportion of samples at different loading rates.

The RA-AF distributions of the specimens at different loading rates are shown in Figure 7B. The red part has the densest number of dots, followed by the green part, and the blue part has the sparsest number of dots. The scatter distributions are denser near the origin of the coordinates and sparser away from the origin of the coordinates. In the scatter plot, the RA value intercepts the part between 0 and 1,000 ms/V, and the AF value intercepts the part between 0 and 100 kHz.

It can be seen from the figure that AF values of honeycomb structures are small at each loading rate, and the scatter distribution is mainly concentrated in the vicinity of RA, mainly shear cracks. With the change of loading rate, the proportion of tension cracks and shear cracks is basically unchanged. The percentage of shear cracks in the four specimens is only slightly higher than that of tension cracks, and the shear cracks are less, which may be due to the fact that the cement layer is thin, and many places do not satisfy the conditions for shear crack generation. In conclusion, the change of loading rate has a minimal effect on the type of cracks in the segmental cementitious honeycomb structure.

4 Conclusion

In this paper, static uniaxial external compression experiments were carried out on segmental cementitious honeycomb structure, exploring the force-displacement curves, acoustic emission characteristics and the changing law of energy absorption characteristics of segmental cementitious honeycomb structure under different loading rates, which is a useful exploration for the large deformation of the tunnel support and rock explosion, impact pressure and other power disasters such as energy-absorbing stabilization control. The main conclusions are as follows:

(1) When the load was 1 mm/min, the peak load of the subsequent wave band showed a large decrease, which was caused by the uneven cement slurry on the honeycomb skeleton. When the cement of the honeycomb structure is uniformly grouted, the peak loads of each band are basically equal, and the overall change is small; while when the grout of the honeycomb structure is unevenly grouted, there is a large decrease in the peak load of a certain band, which in turn affects the stability of the structure. Therefore, future research on the use of honeycomb skeleton and cementitious materials to prepare composite honeycomb structures should further optimize the process preparation process, so that the outer cementitious material can evenly cover the inner skeleton, so as to ensure the strength and overall stability of the honeycomb structure.

(2) The variation of loading rate has little effect on the fluctuation of force-displacement curve of honeycomb structure, which mainly affects the peak load and energy absorption index of the honeycomb structure. When the loading rate was increased from 1 to 4 mm/min, the force-displacement curves showed obvious periodicity, and the initial peak load, total energy absorption, crushing load and crushing efficiency all increased and then decreased with the increase of loading rate, and the maximum values all appeared at 3 mm/min. Segmental cement-based honeycomb structures have good mechanical properties and energy absorption properties at high loading rates, but poor properties at low loading rates. Therefore, the actual working conditions should be fully considered when designing and selecting segmental cement-based honeycomb structures.

(3) The b-values and counts of acoustic emissions showed cyclic variations. The increasing and decreasing b-values and counts reveal that the honeycomb structure undergoes a stable stage of microcrack development under loading, and then suffers large-scale damage in the first layer of the honeycomb structure when it reaches the peak load; this cyclic process verifies the layer-by-layer damage of segmental cementitious honeycomb structures. The loading rate affects the b-value and the counts as well, and a faster loading rate leads to a more drastic change in the b-value, which indicates that the microcracks in the honeycomb structure develop faster and the damage is more severe; the increase in the total counts also indicates that the destruction of the honeycomb structure is more complete when the loading rate is faster. The RA-AF values show that the proportion of shear cracks in the honeycomb structure is higher than that of the tensile cracks, and the effect of the loading rate on the crack type is smaller, as the loading rate increases. has less effect and the crack type hardly changes as the loading rate increases.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

GS: Writing–original draft, Writing–review and editing. AW: Writing–original draft, Writing–review and editing. CH: Writing–original draft, Writing–review and editing. BZ: Writing–original draft, Writing–review and editing. HJ: Writing–original draft, Writing–review and editing. BM: Writing–original draft, Writing–review and editing. ZY: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (Nos. 52074259, 52174092) and the Yunlong Lake Laboratory of Deep Underground Science and Engineering Project (No. 104023002).

Acknowledgments

The authors gratefully appreciate this support.

Conflict of interest

Authors GS and BZ were employed by China Coal (Tianjin) Underground Engineering Intelligent Research Institute Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allen, M. J., Tung, V. C., and Kaner, R. B. (2010). Honeycomb carbon: a review of graphene. Chem. Rev. 110, 132–145. doi:10.1021/cr900070d

PubMed Abstract | CrossRef Full Text | Google Scholar

Baggetto, L., Danilov, D., and Notten, P. H. L. (2011). Honeycomb-structured silicon: remarkable morphological changes induced by electrochemical (de)lithiation. Adv. Mater 23, 1563–1566. doi:10.1002/adma.201003665

PubMed Abstract | CrossRef Full Text | Google Scholar

Bitzer, T. (1994). Honeycomb marine applications. J. Reinf. Plastics Compos. 13, 355–360. doi:10.1177/073168449401300406

CrossRef Full Text | Google Scholar

Broeng, J., Barkou, S. E., Bjarklev, A., Knight, J. C., Birks, T. A., and Russell, P.St. J. (1998). Highly increased photonic band gaps in silica/air structures. Opt. Commun. 156, 240–244. doi:10.1016/S0030-4018(98)00470-2

CrossRef Full Text | Google Scholar

Cahangirov, S., Topsakal, M., Aktürk, E., Şahin, H., and Ciraci, S. (2009). Two- and one-dimensional honeycomb structures of silicon and germanium. Phys. Rev. Lett. 102, 236804. doi:10.1103/PhysRevLett.102.236804

PubMed Abstract | CrossRef Full Text | Google Scholar

Connal, L. A., and Qiao, G. G. (2006). Preparation of porous poly(dimethylsiloxane)-based honeycomb materials with hierarchal surface features and their use as soft-lithography templates. Adv. Mater. 18, 3024–3028. doi:10.1002/adma.200600982

CrossRef Full Text | Google Scholar

Engelmayr, G. C., Cheng, M., Bettinger, C. J., Borenstein, J. T., Langer, R., and Freed, L. E. (2008). Accordion-like honeycombs for tissue engineering of cardiac anisotropy. Nat. Mater 7, 1003–1010. doi:10.1038/nmat2316

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, H. L., Jin, F. N., and Fang, D. N. (2008). Mechanical properties of hierarchical cellular materials. Part I: analysis. Compos. Sci. Technol. 68, 3380–3387. doi:10.1016/j.compscitech.2008.09.022

CrossRef Full Text | Google Scholar

Gadkaree, K. P. (1998). Carbon honeycomb structures for adsorption applications. Carbon 36, 981–989. doi:10.1016/S0008-6223(97)00230-3

CrossRef Full Text | Google Scholar

Gaitanaros, S., and Kyriakides, S. (2015). On the effect of relative density on the crushing and energy absorption of open-cell foams under impact. Int. J. Impact Eng. 82, 3–13. doi:10.1016/j.ijimpeng.2015.03.011

CrossRef Full Text | Google Scholar

Gupta, N. K., Sekhon, G. S., and Gupta, P. K. (2001). A study of lateral collapse of square and rectangular metallic tubes. Thin-Walled Struct. 39, 745–772. doi:10.1016/S0263-8231(01)00033-7

CrossRef Full Text | Google Scholar

Hohe, J., and Becker, W. (1999). Effective elastic properties of triangular grid structures. Compos. Struct. 45, 131–145. doi:10.1016/S0263-8223(99)00016-1

CrossRef Full Text | Google Scholar

Kageyama, K., Tamazawa, J., and Aida, T. (1999). Extrusion polymerization: catalyzed synthesis of crystalline linear polyethylene nanofibers within a mesoporous silica. Science 285, 2113–2115. doi:10.1126/science.285.5436.2113

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuo, C. (1991). “Adaptive optics - one meter deformable composite mirror,” in 32nd structures, structural dynamics, and materials conference (American Institute of Aeronautics and Astronautics). doi:10.2514/6.1991-907

CrossRef Full Text | Google Scholar

Liu, Z., Liu, J., Liu, J., Zeng, W., and Huang, W. (2023). The impact responses and failure mechanism of composite gradient reentrant honeycomb structure. Thin-Walled Struct. 182, 110228. doi:10.1016/j.tws.2022.110228

CrossRef Full Text | Google Scholar

Lu, D., Wang, G., Du, X., and Wang, Y. (2017). A nonlinear dynamic uniaxial strength criterion that considers the ultimate dynamic strength of concrete. Int. J. Impact Eng. 103, 124–137. doi:10.1016/j.ijimpeng.2017.01.011

CrossRef Full Text | Google Scholar

Mao, M., He, J., Liu, Y., Li, X., and Li, D. (2012). Ice-template-induced silk fibroin–chitosan scaffolds with predefined microfluidic channels and fully porous structures. Acta Biomater. 8, 2175–2184. doi:10.1016/j.actbio.2011.12.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Masuda, H., and Fukuda, K. (1995). Ordered metal nanohole arrays made by a two-step replication of honeycomb structures of anodic alumina. Science 268, 1466–1468. doi:10.1126/science.268.5216.1466

PubMed Abstract | CrossRef Full Text | Google Scholar

Mishchenko, L., Hatton, B., Bahadur, V., Taylor, J. A., Krupenkin, T., and Aizenberg, J. (2010). Design of ice-free nanostructured surfaces based on repulsion of impacting water droplets. ACS Nano 4, 7699–7707. doi:10.1021/nn102557p

PubMed Abstract | CrossRef Full Text | Google Scholar

Mozafari, H., Khatami, S., Molatefi, H., Crupi, V., Epasto, G., and Guglielmino, E. (2016). Finite element analysis of foam-filled honeycomb structures under impact loading and crashworthiness design. Int. J. Crashworthiness 21, 148–160. doi:10.1080/13588265.2016.1140710

CrossRef Full Text | Google Scholar

Mukai, S., Nishihara, H., and Tamon, H. (2006). Porous microfibers and microhoneycombs synthesized by ice templating. Catal. Surv. Asia 10, 161–171. doi:10.1007/s10563-006-9015-8

CrossRef Full Text | Google Scholar

Ng, K. Y., Lin, Y., and Ngan, A. H. W. (2011). Compression of micron-sized pillars of anodic aluminium oxide nano-honeycomb. J. Mech. Phys. Solids 59, 251–264. doi:10.1016/j.jmps.2010.10.008

CrossRef Full Text | Google Scholar

Pawin, G., Wong, K. L., Kwon, K.-Y., and Bartels, L. (2006). A homomolecular porous network at a Cu(111) surface. Science 313, 961–962. doi:10.1126/science.1129309

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, C., Jiang, F., and Yang, S. (2021). Advanced honeycomb designs for improving mechanical properties: a review. Compos. Part B Eng. 227, 109393. doi:10.1016/j.compositesb.2021.109393

CrossRef Full Text | Google Scholar

Rajaneesh, A., Sridhar, I., and Rajendran, S. (2014). Relative performance of metal and polymeric foam sandwich plates under low velocity impact. Int. J. Impact Eng. 65, 126–136. doi:10.1016/j.ijimpeng.2013.11.012

CrossRef Full Text | Google Scholar

Saha, G. C., Kalamkarov, A. L., and Georgiades, A. V. (2007). Asymptotic homogenization modeling and analysis of effective properties of smart composite reinforced and sandwich shells. Int. J. Mech. Sci. 49, 138–150. doi:10.1016/j.ijmecsci.2006.08.019

CrossRef Full Text | Google Scholar

Shi, H., Chen, W., Zhang, H., Song, L., Li, M., Wang, M., et al. (2023). Dynamic strength characteristics of fractured rock mass. Eng. Fract. Mech. 292, 109678. doi:10.1016/j.engfracmech.2023.109678

CrossRef Full Text | Google Scholar

Shi, H., Zhang, H., Chen, W., Song, L., and Li, M. (2024). Pull-out debonding characteristics of rockbolt with prefabricated cracks in rock: a numerical study based on particle flow code. Comput. Part. Mech. 11, 29–53. doi:10.1007/s40571-023-00607-9

CrossRef Full Text | Google Scholar

Siromani, D., Awerbuch, J., and Tan, T.-M. (2014). Finite element modeling of the crushing behavior of thin-walled CFRP tubes under axial compression. Compos. Part B Eng. 64, 50–58. doi:10.1016/j.compositesb.2014.04.008

CrossRef Full Text | Google Scholar

Sugiura, T., Yoshida, T., and Minoura, H. (1998). Designing a TiO2 nano-honeycomb structure using photoelectrochemical etching. Electrochem. Solid-State Lett. 1, 175. doi:10.1149/1.1390676

CrossRef Full Text | Google Scholar

Sunami, H., Ito, E., Tanaka, M., Yamamoto, S., and Shimomura, M. (2006). Effect of honeycomb film on protein adsorption, cell adhesion and proliferation. Colloids Surfaces A Physicochem. Eng. Aspects 284–285, 548–551. doi:10.1016/j.colsurfa.2005.11.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Tejavibulya, N., Youssef, J., Bao, B., Ferruccio, T.-M., and Morgan, J. R. (2011). Directed self-assembly of large scaffold-free multi-cellular honeycomb structures. Biofabrication 3, 034110. doi:10.1088/1758-5082/3/3/034110

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, T., and Tiwari, G. (2019). Crushing behavior of honeycomb structure: a review. Int. J. Crashworthiness 24, 555–579. doi:10.1080/13588265.2018.1480471

CrossRef Full Text | Google Scholar

Tian, R., Guan, H., Lu, X., Zhang, X., Hao, H., Feng, W., et al. (2023). Dynamic crushing behavior and energy absorption of hybrid auxetic metamaterial inspired by Islamic motif art. Appl. Math. Mech. Engl. 44, 345–362. doi:10.1007/s10483-023-2962-9

CrossRef Full Text | Google Scholar

Velea, M. N., and Lache, S. (2011). Numerical simulations of the mechanical behavior of various periodic cellular cores for sandwich panels. Proc. Eng. 10, 287–292. doi:10.1016/j.proeng.2011.04.050

CrossRef Full Text | Google Scholar

Wadley, H. N. G. (2005). Multifunctional periodic cellular metals. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 364, 31–68. doi:10.1098/rsta.2005.1697

CrossRef Full Text | Google Scholar

Wang, D., and Bai, Z. (2015). Mechanical property of paper honeycomb structure under dynamic compression. Mater. and Des. 77, 59–64. doi:10.1016/j.matdes.2015.03.037

CrossRef Full Text | Google Scholar

Wang, W., Chen, S. J., Sagoe-Crentsil, K., and Duan, W. (2022). Graphene oxide-reinforced thin shells for high-performance, lightweight cement composites. Compos. Part B Eng. 235, 109796. doi:10.1016/j.compositesb.2022.109796

CrossRef Full Text | Google Scholar

Wang, Z. (2019). Recent advances in novel metallic honeycomb structure. Compos. Part B Eng. 166, 731–741. doi:10.1016/j.compositesb.2019.02.011

CrossRef Full Text | Google Scholar

Wu, J., Jing, H., Gao, Y., Meng, Q., Yin, Q., and Du, Y. (2022). Effects of carbon nanotube dosage and aggregate size distribution on mechanical property and microstructure of cemented rockfill. Cem. Concr. Compos. 127, 104408. doi:10.1016/j.cemconcomp.2022.104408

CrossRef Full Text | Google Scholar

Wu, J., Jing, H., Yin, Q., Yu, L., Meng, B., and Li, S. (2020). Strength prediction model considering material, ultrasonic and stress of cemented waste rock backfill for recycling gangue. J. Clean. Prod. 276, 123189. doi:10.1016/j.jclepro.2020.123189

CrossRef Full Text | Google Scholar

Wu, J., Wong, H. S., Yin, Q., and Ma, D. (2023). Effects of aggregate strength and mass fraction on mesoscopic fracture characteristics of cemented rockfill from gangue as recycled aggregate. Compos. Struct. 311, 116851. doi:10.1016/j.compstruct.2023.116851

CrossRef Full Text | Google Scholar

Wu, J., Wong, H. S., Zhang, H., Yin, Q., Jing, H., and Ma, D. (2024). Improvement of cemented rockfill by premixing low-alkalinity activator and fly ash for recycling gangue and partially replacing cement. Cem. Concr. Compos. 145, 105345. doi:10.1016/j.cemconcomp.2023.105345

CrossRef Full Text | Google Scholar

Yabu, H., Takebayashi, M., Tanaka, M., and Shimomura, M. (2005). Superhydrophobic and lipophobic properties of self-organized honeycomb and pincushion structures. Langmuir 21, 3235–3237. doi:10.1021/la050013w

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, P., Arceneaux, D. J., and Khattab, A. (2018). Mechanical properties of 3D printed polycaprolactone honeycomb structure. J. Appl. Polym. Sci. 135, 46018. doi:10.1002/app.46018

CrossRef Full Text | Google Scholar

Zhang, Q., Yang, X., Li, P., Huang, G., Feng, S., Shen, C., et al. (2015). Bioinspired engineering of honeycomb structure – using nature to inspire human innovation. Prog. Mater. Sci. 74, 332–400. doi:10.1016/j.pmatsci.2015.05.001

CrossRef Full Text | Google Scholar

Zhang, X., and Zhang, H. (2013). Theoretical and numerical investigation on the crush resistance of rhombic and Kagome honeycombs. Compos. Struct. 96, 143–152. doi:10.1016/j.compstruct.2012.09.028

CrossRef Full Text | Google Scholar

Zhang, Z., Kutana, A., Yang, Y., Krainyukova, N. V., Penev, E. S., and Yakobson, B. I. (2017). Nanomechanics of carbon honeycomb cellular structures. Carbon 113, 26–32. doi:10.1016/j.carbon.2016.11.020

CrossRef Full Text | Google Scholar