- 1Lane Department of Computer Science and Electrical Engineering, West Virginia University, Morgantown, WV, United States
- 2Department of Physics and Astronomy, West Virginia University, Morgantown, WV, United States
Machine learning (ML) models have emerged as powerful tools for accelerating materials discovery and design by enabling accurate predictions of properties from compositional and structural data. These capabilities are vital for developing advanced technologies across fields such as energy, electronics, and biomedicine, potentially reducing the time and resources needed for new material exploration and promoting rapid innovation cycles. Recent efforts have focused on employing advanced ML algorithms, including deep learning-based graph neural networks, for property prediction. Additionally, ensemble models have proven to enhance the generalizability and robustness of ML and Deep Learning (DL). However, the use of such ensemble strategies in deep graph networks for material property prediction remains underexplored. Our research provides an in-depth evaluation of ensemble strategies in deep learning-based graph neural network, specifically targeting material property prediction tasks. By testing the Crystal Graph Convolutional Neural Network (CGCNN) and its multitask version, MT-CGCNN, we demonstrated that ensemble techniques, especially prediction averaging, substantially improve precision beyond traditional metrics for key properties like formation energy per atom
1 Introduction
Predicting material crystal properties involves forecasting the chemical and physical traits of crystalline materials based on their molecular and atomic structures. This task is vital for fields like electronics, medicine, aeronautics, and energy storage management Shen et al. (2022); Shahzad et al. (2024); Wei et al. (2019); Liu et al. (2017). Accurately predicting these properties from compositional and structural data is instrumental in the discovery of new materials for advanced technologies. Using computational methods and data-driven strategies, researchers can efficiently explore and optimize material designs, avoiding the slow and costly process of experimental trial-and-error Kauwe et al. (2020). Understanding how a material’s crystalline structure impacts its properties requires a blend of computational and experimental investigations. Although density functional theory (DFT) Kohn and Sham (1965); Hohenberg and Kohn (1964) is a well-established method, it is often perceived as computationally complex and time-intensive. Moreover, the quest for materials with specific properties within an extensive material search space poses challenges, and delays progress in swiftly evolving domains like medical science, aeronautics, and energy engineering, where accuracy and speed are paramount.
Machine learning (ML)-based models have emerged as a promising solution to this challenge. These models can match the accuracy of DFT calculations and support rapid material discovery, thanks to the growing material databases Jain et al. (2013); Choudhary et al. (2020); Kirklin et al. (2015). By harnessing the capabilities of ML algorithms and the growing abundance of data in material repositories, these models can effectively navigate the vast material landscape and pinpoint promising candidates with desired properties. This data-driven approach for predicting material crystal properties has shown promise and gained significant attention for its accuracy and unparalleled speed Choudhary and DeCost (2021).
However, the intricate atomic arrangements and the intrinsic correlations between structure and properties present formidable challenges for ML models to encode pertinent structural information accurately, mainly because of the number of atoms involved and the internal degrees of freedom within the crystal structures. Thus, effective representation capturing spatial relationships, and periodic boundary conditions within a crystal lattice become challenging. Furthermore, a model adept with one crystal structure might falter with another, given crystals’ inherent periodicity and symmetry. Also, traditional ML models often fail to incorporate the nuanced knowledge of unit cells and their repetitive nature, an essential aspect of crystallography Chen et al. (2019).
Moreover, for ML models the challenge of representing crystal systems, which vary widely in size, arises because these models typically require input data in the form of fixed-length vectors. To address this, researchers have developed two main approaches. The first involves manually creating fixed-length feature vectors based on basic material properties Isayev et al. (2017); Xue et al. (2016), which, though effective, necessitates tailored designs for each property being predicted. The second approach uses symmetry-invariant transformations Seko et al. (2017) of the atomic coordinates to standardize input data, which, while solving the issue of variable crystal sizes, complicates model interpretability due to the complexity of these transformations. Historically, AI-driven material science has focused on creating custom descriptors for predicting material properties, utilizing expert knowledge for specific applications. However, these custom descriptors often lack versatility beyond their initial scope.
To address these challenges in material property prediction, the recent adoption of deep learning (DL) has shown significant promise Cao et al. (2019). These networks are adept at learning data distributions as embeddings, serving as effective feature descriptors for predicting input data characteristics. Unlike traditional grid-like image representations, crystal structures—with their node-like atoms and bond-like edges—are ideally represented as graph-based structures. This has highlighted the suitability of graph neural networks (GNN) for modeling crystal structures, leveraging their natural composition and bonding structures. GNNs thus facilitate the automatic extraction of optimal representations from atoms and bonds by representing these materials in deep networks.
While current DL models, including advanced GNNs, have successfully integrated complex structural, geometrical, and topological features for predicting material properties, a critical aspect often overlooked is the comprehensive exploration of their training dynamics. Typically, the quest for the lowest validation loss serves as a proxy for identifying the optimal model. However, due to the highly non-convex nature of training deep neural networks, this lowest validation loss does not necessarily correspond to the true optimal point Gyawali et al. (2022); Garipov et al. (2018). Other regions within the loss landscape might capture the relationship between material structure and properties differently. There has been limited focus on understanding model behavior beyond the conventional point of lowest validation loss. This oversight suggests we might not fully grasp the potential and versatility of these models in capturing structure-to-property relationships.
In this research, we propose a critical yet often overlooked hypothesis: optimal model performance may not reside solely at the singular point of lowest validation loss. Instead, it could be spread across multiple valleys within the loss terrain. Our objective is to highlight these hidden, underexplored models that could offer more accurate predictions and a deeper understanding of material attributes. Furthermore, this approach may reveal models that provide a better balance between variance and bias, underscoring the necessity of examining the overall loss landscape to fully understand the adaptability and efficiency of deep learning models.
Thus, we investigate various regions within the loss landscape where models still perform satisfactorily. This exploration has yielded insights into models that are robust and generalize well to new data. We propose combining these different models to create a unified ensemble model. First, we analyze the property prediction performance of a prominent GNN-based material prediction model, CGCNN Xie and Grossman (2018), and its multi-task variant, MT-CGCNN Sanyal et al. (2018), focusing on six widely studied properties: formation energy per atom, bandgap, density, equivalent reaction energy per atom, energy per atom and atomic density. We then examine the impact of ensemble techniques on model performance, specifically the model average ensemble and prediction average ensemble methods, to support our hypothesis of identifying influential models within adjacent areas of the loss landscape. Finally, we conduct an extensive evaluation to understand the ensemble’s effect on prediction performance across the spectrum of properties. Overall, our contributions include:
1. We introduce ensemble techniques to improve the material property prediction capabilities of prominent GNN-based methods, including CGCNN Xie and Grossman (2018), and MT-CGCNN Sanyal et al. (2018).
2. We conduct comprehensive experiments on six widely studied properties: formation energy per atom, bandgap, density, equivalent reaction energy per atom, energy per atom and atomic density.
3. We assess the impact of ensemble models across a wide spectrum of material properties, highlighting the effectiveness of ensemble-based approaches in extreme test conditions.
2 Related work
Not having regular grid-like structures such as images or 1-D signals, CNN could not be the automatic choice for studying material structure from DL point of view. Rather its irregular structural shape made it a suitable candidate for graph representation and graph neural network (GNN), where atoms are considered nodes and atomic bonds edges. Therefore, convolving on the graph structure which is converted from the actual atomic structure of the material was a prominent choice for the researchers. Crystal Graph Convolutional Neural Network (CGCNN) Xie and Grossman (2018) and SchNet Schütt et al. (2018) first proposed this graph representation and utilized raw features like atom type and atomic bond distance to predict material properties comparable with DFT computed values. Although these models performed very well in terms of predicting material’s properties they also exhibit inevitable and notable challenges due to their reliance on distance-based message-passing mechanisms Gong et al. (2023). Firstly, neglecting many-body and directional information can overlook critical aspects important for understanding material properties. Secondly, the reliance on nearest neighbors to define graph edges could misrepresent key interactions due to the ambiguity of chemical bonding. Lastly, the models are limited by their receptive field, compounded by issues like over-smoothing and over-squashing, which restrict their ability to account for the long-range or global influence of structures on properties.
The more recent DL models for material property prediction such as Atomistic Line Graph Neural Network (ALIGNN) Choudhary and DeCost (2021), iCGCNN Park and Wolverton (2020),MatErials Graph Network (MEGNet) Chen et al. (2019), Orbital Graph Convolution Neural Network (OGCNN) Karamad et al. (2020), DimeNet Gasteiger et al. (2020), GemNet Gasteiger et al. (2021) and Geometric-information-enhanced Crystal Graph Neural Network (Geo-CGNN) Cheng et al. (2021) thus tried to incorporate more geometrical information like bond angle, orbital interaction, body order information, directional information, distance vector to outperform previously proposed distance-based models. Some models proposed attention mechanisms and self supervised learning (SSL) as well to choose the relative importance of features in predicting material properties like Matformer Yan et al. (2022), Equiformer Liao and Smidt (2022), GATGNN Louis et al. (2020), Crystal-Twins Magar et al. (2022) and DSSL Fu et al. (2024).
It is a well-known fact that Deep learning models for complicated tasks navigate a high-dimensional space to minimize a function that quantifies the “loss” or error between the actual data and the expected results. We refer to this optimization landscape as the “loss landscape” Li et al. (2018); Goodfellow et al. (2016); Garipov et al. (2018). It is frequently represented visually as a surface or landscape with hills and valleys. The loss landscapes of deep neural networks are extremely intricate and non-convex. This indicates that while the model may converge to numerous local minima (valleys), not all of them will result in the best solution (global minimum). The training epoch in which the model achieves the lowest validation loss is referred to as the “best-validated epoch.” Nevertheless, the model at this epoch may not truly represent the best generalizable model because of the complexity of the loss landscape and elements like overfitting and identical loss with differences in functional space Draxler et al. (2018); Fort and Jastrzebski (2019); Fort et al. (2019). Though they may have a little larger or the same loss, models from other epochs may perform better on unknown data or have superior generalization ability for having differences in loss dynamics. Therefore, our focus in this work is not on the GNN models or associating features with them to strengthen material property prediction but on creating a generalized framework of ensemble models based on the cross-validation loss trajectory that might yield better generalization of the prediction task with improved accuracy of prediction.
The comprehensive approach of any ensemble technique is to combine a set of models using an aggregation mechanism. It has been widely used to enhance the performance of ML models. Consequently, various data fusion methods, such as max-voting, average voting, weighted average voting, and meta-learning, have been proposed Mohammed and Kora (2023). Additionally, these ensemble techniques have been adopted in the literature, including bagging, boosting, stacking, and decision fusion Ganaie et al. (2022). Even within the materials science literature, the use of ML-based ensemble techniques has demonstrated improved results Mishra et al. (2022); Ghosh et al. (2022a); Hou et al. (2023); AlFaraj et al. (2023); Karande et al. (2022) compared to single models. For instance, Mishra et al. (2022) predicted the phase of high-entropy alloys with greater accuracy than SVM and random forest by utilizing a stacked ensemble model. Similarly, Ghosh et al. (2022a) proposed an ensemble of trees to classify cation ordering with a higher confidence level of prediction. Further, there have also been efforts to create ensembles from DL models, such as using an ensemble of neural networks to select features free of artifacts and to generate uncertainty maps for imaging data from materials Ghosh et al. (2021), as well as applying an ensemble of models to identify atomistic features in graphene Ghosh et al. (2022b). Compared to these existing works, our study is the first to consider ensembles for graph-based deep learning models, particularly since these architectures have demonstrated improved generalization performance in material property prediction. In general deep learning applications, the ensemble approach has shown improved performance across several domains, including speech recognition Li et al. (2017), healthcare Tanveer et al. (2021); Gyawali et al. (2022), natural language processing Elnagar et al. (2020), and computer vision Roshan et al. (2024). In contrast to these efforts, our work is the first to explore ensemble strategies for material property prediction tasks. Our ensemble framework is straightforward, focusing on model aggregation across different training stages.
3 Methodology
In this section, we first provide background details about the GCNN framework for material property prediction, and then introduce our ensemble framework to achieve enhanced predictions.
3.1 Preliminary: GCNN
Graph Convolutional Neural Networks (GCNNs) have emerged as a powerful tool in materials science, enabling researchers to analyze and predict the properties and behaviors of materials in a novel and efficient manner. Unlike traditional convolutional neural networks that process grid-like data (e.g., images), GCNNs are designed to handle graph-structured data, which is intrinsic to the representation of atomic and molecular structures in materials science. These models exploit the graph structure of materials, where nodes can represent atoms and edges can denote chemical bonds or spatial relationships. By doing so, GCNNs can capture both the local and global structural information of materials.
Crystal Graph Convolutional Neural Networks (CGCNN) Xie and Grossman (2018) and SchNet Schütt et al. (2018) represent the two most prominent graph neural network architectures tailored for material science applications. These models refine atom representations within a structure by considering the types and bond lengths of neighboring atoms. Subsequently, they aggregate these updated atom-level representations to form a comprehensive representation of the entire structure. In CGCNN, the crystal architecture is represented as a graph that accommodates the details of atoms and their bonds with neighbors, and a graph convolution network is constructed on such graph to attain the representations useful to material property prediction. The architecture can comprise of single-task head Xie and Grossman (2018) or multi-task Sanyal et al. (2018) head depending on the application. We present the overall diagram combining the single- and multi-task setup in Figure 1. In the presented network, the atom feature encoding vector can be noted as
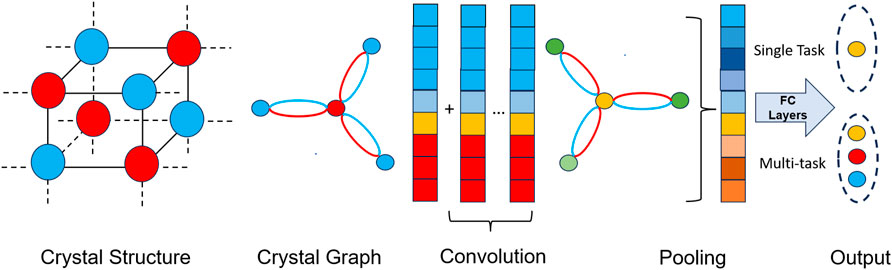
Figure 1. Overview of GCNN in material property prediction tasks. Initially, the crystal structure is created from information files. Then, the crystal graph is constructed from the structure. GCN layers and pooling layers are utilized to obtain crystal embeddings, after which fully connected (FC) layers are employed to predict properties. For a single-task head, a single FC layer is used, while for the prediction of multiple properties, multiple FC layers are utilized.
The training procedure involves minimizing a cost function
3.2 Ensemble models
In this section, we present an ensemble framework to enhance the results obtained from GCNN networks. Our central hypothesis is that in the training of deep neural networks, selecting a single model based solely on the lowest validation error may not always guarantee the most comprehensive learning of all features within the dataset. This limitation can be attributed to the highly non-convex nature of the loss landscape that characterizes neural network optimization Cooper (2018). In such a complex terrain, the path to minimizing loss involves numerous local minima and saddle points. This suggests that multiple models—each residing in different areas of the loss landscape—could perform similarly well on the validation set, albeit potentially capturing different aspects of the data Gyawali et al. (2022).
Toward this, we propose ensemble framework for achieving ensemble models from the training dynamics of GCNNs, that capitalizes on the temporal evolution of model parameters across training epochs. Consider the training process to span a fixed number of epochs,
where
3.3 Prediction-based ensemble modeling
For prediction-based ensemble modeling, we first calculate the prediction for each
and create prediction ensemble as in Equation 6:
3.4 Model-based ensemble modeling
Here, we first aggregate top-
The final prediction of the ensemble model for a new input
We present the overall schematic of our proposed ensemble-based framework in Figure 2. On the left, we illustrate the prediction ensemble, and on the right panel, the model ensemble framework is depicted.
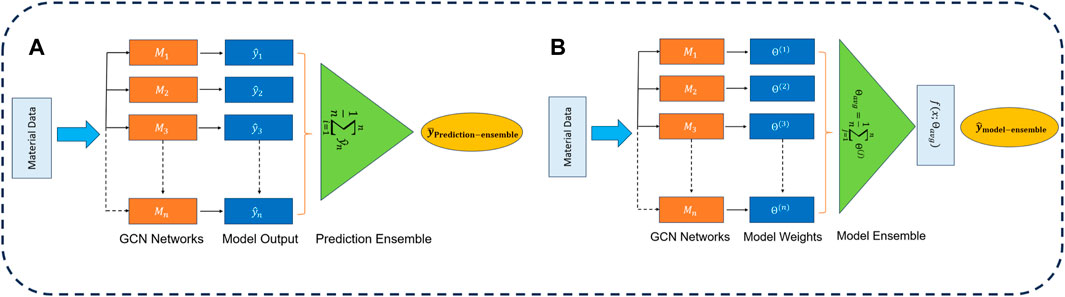
Figure 2. Overview of ensemble strategies: (A) prediction averaging ensemble technique and (B) the model averaging ensemble technique.
4 Experiment
In this section, we discuss the data we have used for experiments, the implications of choosing the properties we worked with, the outline of the experimental setup, and the results with their interpretation, significance, and implications.
4.1 Data
All the models in this study were trained on the dataset from the Materials Project Jain et al. (2013) (MP). The MP database uses the first-principles Density Functional Theory (DFT) calculations to derive the majority of the material properties. It is a multi-institutional, multinational effort to compute the properties of all inorganic materials and provide the data and associated analysis algorithms to every materials researcher free of charge. One of the largest and most popular three-dimensional (3D) materials datasets in the materials science field, the MP collection covers approximately 155,000 materials, including a wide variety of inorganic compounds. This broad coverage guarantees a representative and varied sampling of material kinds, extending the generalizability of our results. Moreover, the MP dataset has been successfully used in numerous studies to create and evaluate predictive models for a range of material properties. The trustworthiness of the dataset and the accomplishments of earlier studies employing MP data highlight its suitability for verifying our methods. For this study, we worked with 33,990 stable materials, which refers to the set of materials that, under standard conditions, have a low energy state and are hence thermodynamically favorable to exist in their current form. An indicator of stability is the “energy above hull” metric, which shows how much energy would be released by each atom in the event that the material changes into the most stable phase combination. For several reasons, it is critical for this work to concentrate on stable materials. Stable materials are more important for real-world applications because they are thermodynamically favored, meaning they occur naturally or can be created with less energy. Focusing on these materials allows the research to directly target materials that are useful in energy storage, electronics, and catalysis, among other real-world applications. To demonstrate the efficacy of the proposed ensemble framework, we focused on six distinct properties: Formation energy per atom (
Figure 3 shows the class-wise distribution of 33,990 stable material structures based on four distinct material classes—conductivity, direct band gap, metallic, and magnetic property. Each bar shows the percentage of the dataset’s elements that fall into each category within each property. In the first bar graph, the proportion of the dataset divided in terms of Conductor, Semiconductor, and Insulator is shown. This distribution shows that most of the materials in the dataset are conductive, with a significant portion also exhibiting semiconducting or insulating properties. In the case of the type of band gap, 16% exhibits direct and 84% indirect bandgap. The dataset is almost evenly split between metallic and non-metallic materials. This near-equal distribution indicates a balanced representation of metallic and non-metallic materials in the dataset. Furthermore, the relatively low proportion of magnetic materials highlights the prevalence of non-magnetic materials in the dataset.
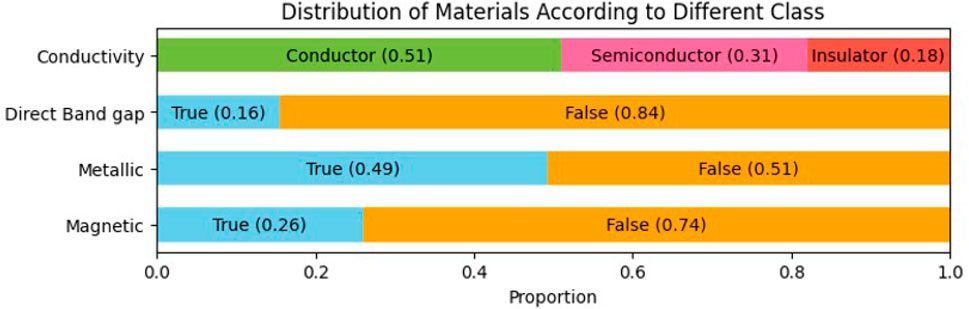
Figure 3. Class-wise distribution of 33,990 stable materials from the Materials Project Jain et al. (2013) used in our study, illustrating the proportional breakdown across key material properties: conductivity, direct band gap, metallic, and magnetic. Conductivity is categorized into conductor, semiconductor, and insulator, while the remaining properties are classified as either true or false.
We also analyze the frequency of different elements within the materials in the dataset. Figure 4 shows the frequency distribution of 88 unique elements. Each tile represents an element, with color indicating frequency, ranging from low (purple) to high (yellow). This visualization highlights the diversity of elements across the 33,990 material structures in the dataset. As seen in Figure 4, oxygen (O) is the most frequent element, appearing 64,331 times, reflecting its prominence in inorganic compounds and oxides, which are common in materials science. Neon (Ne), with just one occurrence, is the least frequent element, consistent with the chemically inert nature of noble gases, making them less prevalent in solid-state material compositions. The Shannon entropy of the element distribution in the dataset is 3.81, indicating a moderate level of diversity. A lower entropy would suggest dominance by a few elements, while a higher value would indicate a more even distribution. Although the dataset contains a wide range of elements, some, like oxygen, are far more common, as reflected in the entropy value.
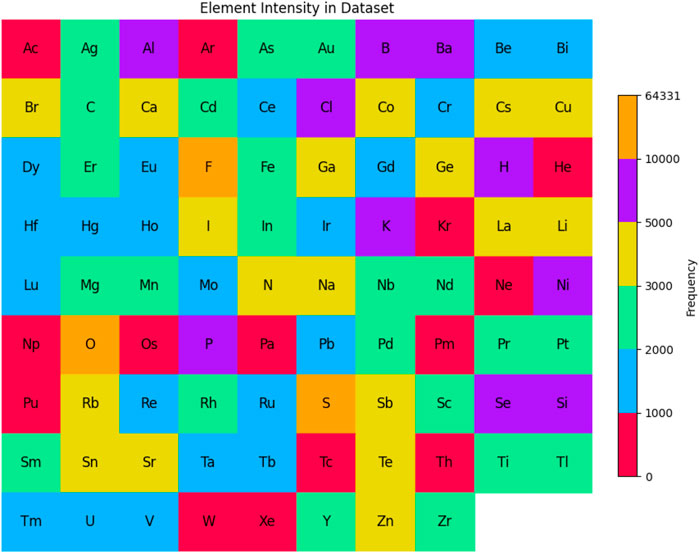
Figure 4. Element frequency distribution in the dataset that we use for experiments. Oxygen (O) is the most common element, while Neon (Ne) appears the least. The color scale reflects element frequency, with a Shannon entropy of 3.81 indicating moderate diversity.
4.2 Experimental setup
For exploring the efficacy of our proposed ensemble model, we primarily consider CGCNN Xie and Grossman (2018) and its multi-task extension, MT-CGCNN Sanyal et al. (2018), as base models, and apply our proposed ensembling to construct the ensemble framework. Furthermore, we vary the number of convolutional layers within CGCNN and MT-CGCNN to create two separate versions of the network for each category. Throughout our experiments and results, we refer to them as
Across all models, the length of the atom feature vector was set to 64, and the hidden feature vector to 128. For all experiments, MSE was used as the loss function, SGD as the optimizer, and a fixed learning rate of 0.01 was applied. We utilized an NVIDIA GeForce GTX TITAN X graphics processing unit (GPU) with 12 GB of memory for all model training and evaluation tasks. The training, validation, and test data were randomly selected from 33990 data points and were kept consistent across all experiments, employing a 70-10-20 distribution strategy, and the batch size was uniformly set at 256. This random selection ensures that our model is not biased towards any specific subset of data, thereby enhancing its ability to generalize to unseen data. Our sampling strategy did not follow any particular distribution, ensuring that the training, validation, and test sets were representative of the overall dataset. By not constraining the sampling process to a specific distribution, we mitigate the risk of overfitting to particular patterns in the training data, thus improving the model’s robustness. All models were run for 100 epochs, and up to 50 models were considered for the ensemble. To determine the best model among the baseline models, and to select several models for creating the ensemble, MSE loss on validation data was used. However, for reporting results, we used MAE on the test dataset to follow standard practice in the literature.
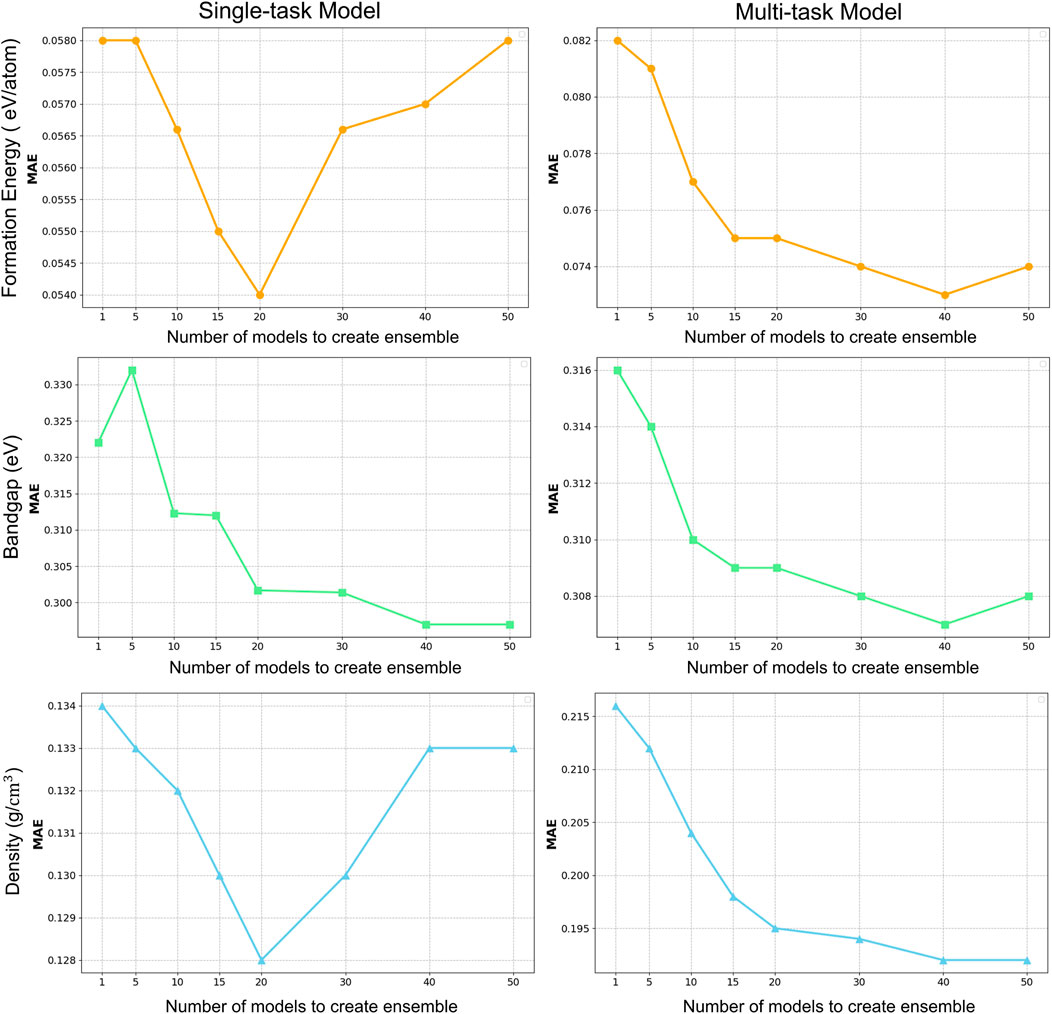
We progressively calculated the average prediction from subsets of the best-performing models, starting with smaller subsets and increasing the number, to find the ideal number of models to average for predictions. To maximize prediction performance, we used two different ensemble settings in our study: a single-tasking strategy (CGCNN) with an average of predictions from 20 models, and a multi-tasking approach (MT-CGCNN) with an average of predictions from 40 models. For the case of the CGCNN setup, based on empirical study, the best results were obtained by averaging the predictions from the first 20 models based on MSE, since this approach balanced model diversity and accuracy. Less than 20 models decreased the benefit of ensemble variety; more than 20 models included models with larger mean square error (MSE), which may adversely affect the prediction accuracy overall. We increased the ensemble size to 40 models for the multi-tasking strategy, where models were trained to predict three properties at the same time. To fully take advantage of the diversity and stability of the predictions, a more comprehensive ensemble was required, as multi-tasking models typically capture more complex interactions between properties. Upon assessing various ensemble sizes, we discovered that 40 models offered the best balance between computational economy and performance. Beyond this, more models introduced diminishing returns and did not enhance accuracy considerably. We customized each configuration by utilizing these two distinct ensemble sizes. While the multi-tasking setup benefitted from a bigger ensemble to reflect the broader complexity involved in predicting numerous properties simultaneously, the single-tasking setup did better with a smaller, more concentrated ensemble. In both situations, we were able to optimize prediction accuracy because of this flexible approach.
5 Result
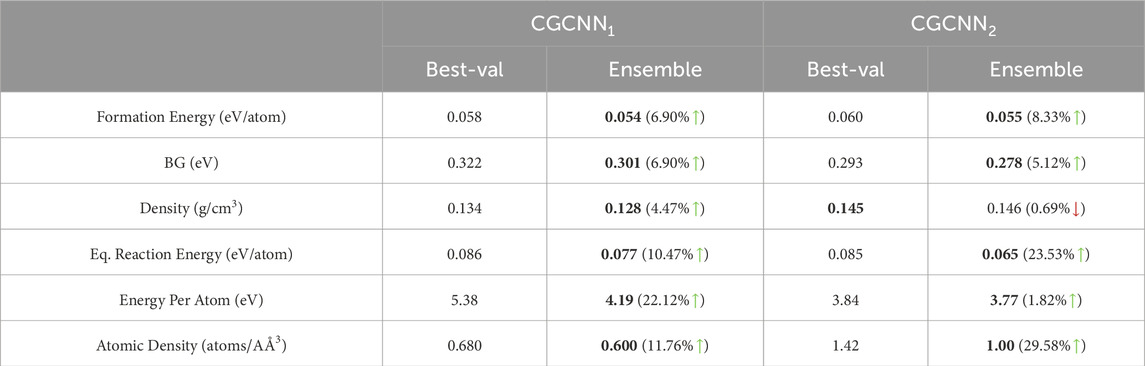
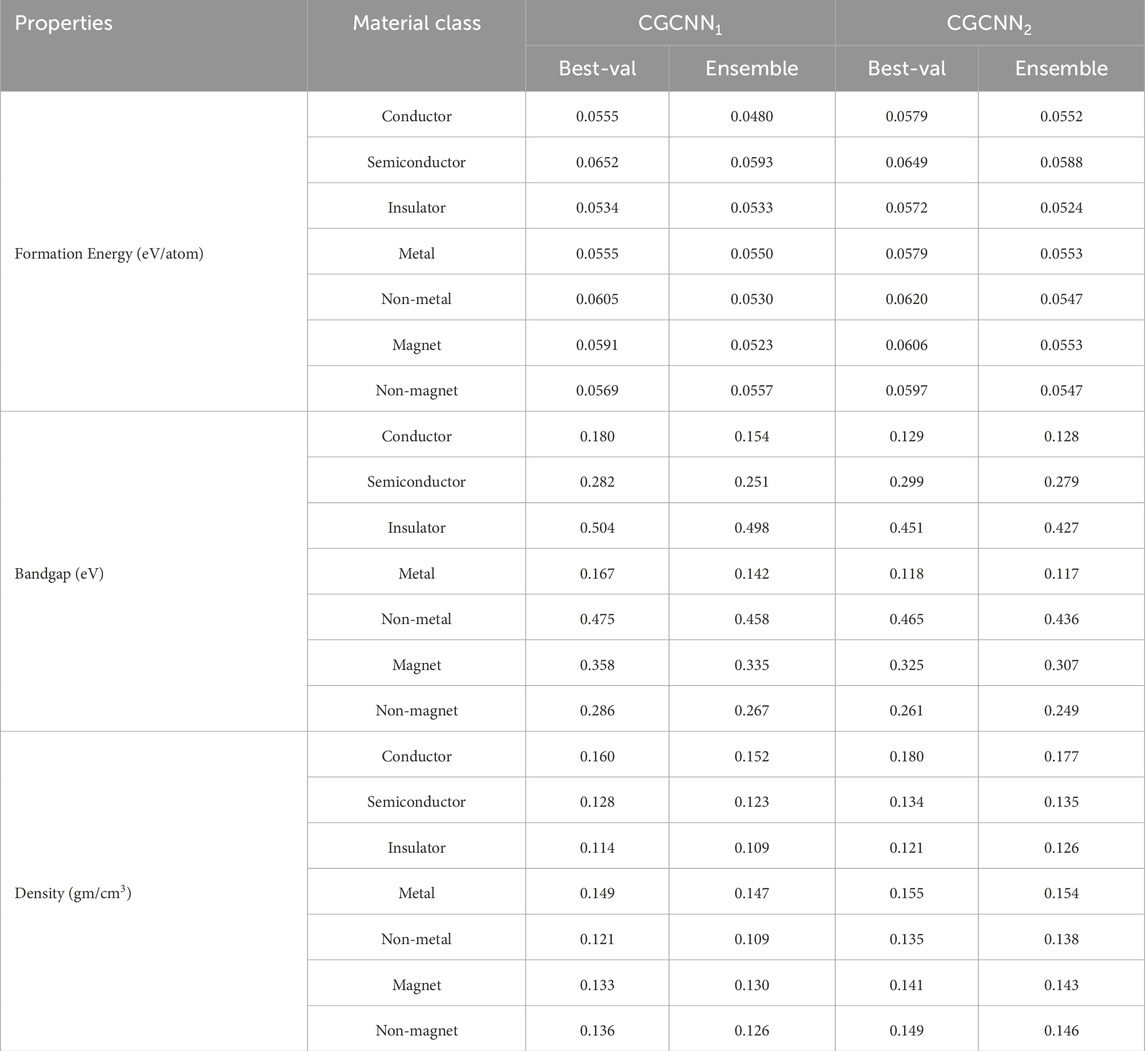
We present our main results in Table 1 to demonstrate the benefits of doing ensemble over its non-ensemble counterpart for six different properties. For other analyses, which we present in the remaining tables and figures, we used the three most studied properties in material property prediction literature: formation energy per atom, bandgap and density. Specifically, in Tables 1, 2 we present outcomes from the prediction ensemble for a fixed number of epochs (20 for single-task and 40 for multi-task) as determined by validation performance. In Table 3 we have shown the improvement of the performance of ensemble models (20 for
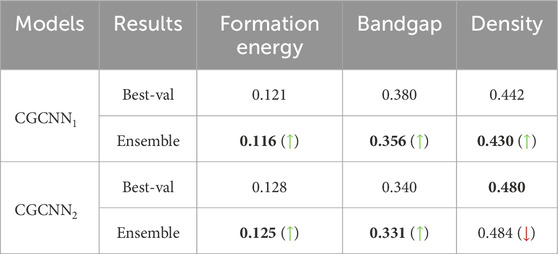
Table 4. Comparative results to evaluate the performance of prediction ensemble on noisy test dataset for
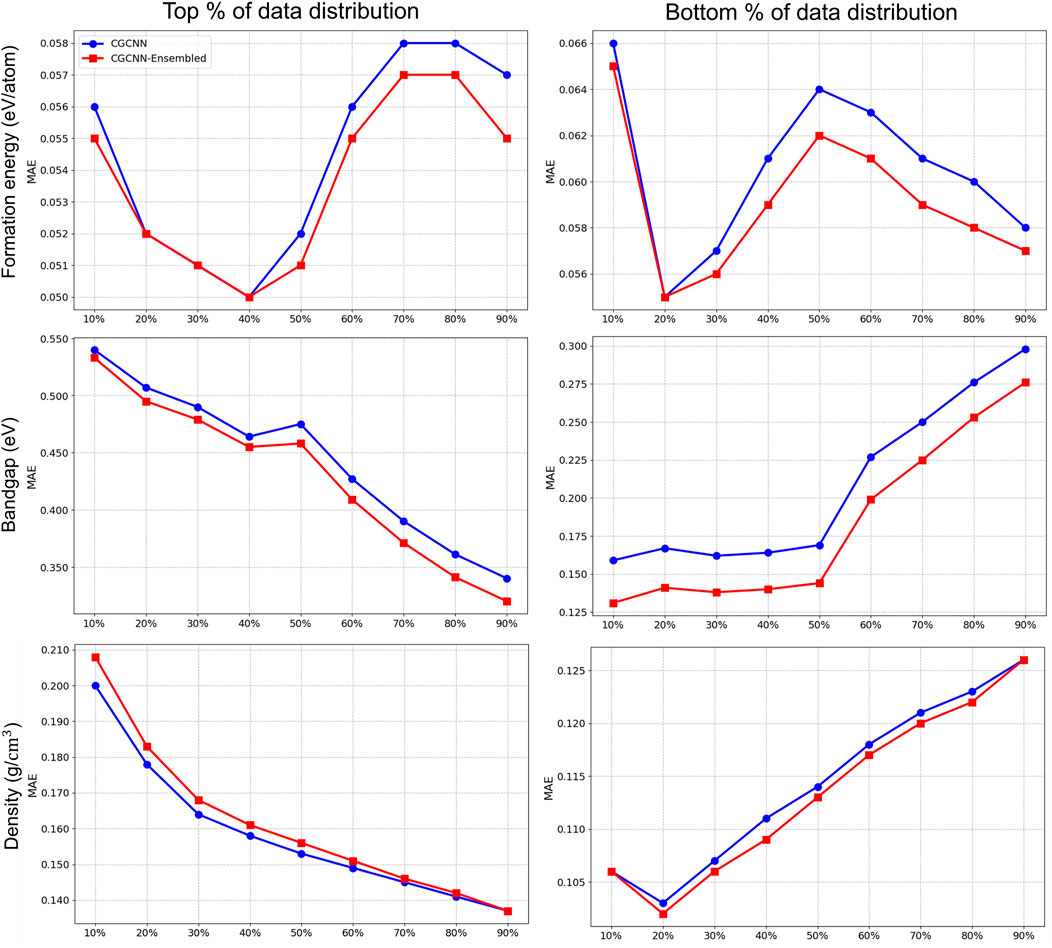
We also explore the impact of the ensemble-based framework across different regions of the material property spectrum. This analysis is crucial for a comprehensive understanding of the various properties involved in our study. For example, specific regions of the bandgap determine a material’s suitability as a conductor, semiconductor, or insulator. Grasping the range of formation energy per atom is vital, as it reflects the stability and synthesizability of materials. Materials that are thermodynamically stable, and therefore more likely to occur in nature or be successfully synthesized in the laboratory, are distinguished by lower formation energies. Additionally, pinpointing the extremes within density ranges aids in assessing the durability of high-density materials or the practicality of lightweight insulators with low density.
We present the results in Figures 6, 7, where we partitioned the test data from the 10th to the 90th percentile in both top-bottom (left panel) and bottom-top (right panel) distributions. This approach helps to identify performance differences across different regions of the property spectrum for
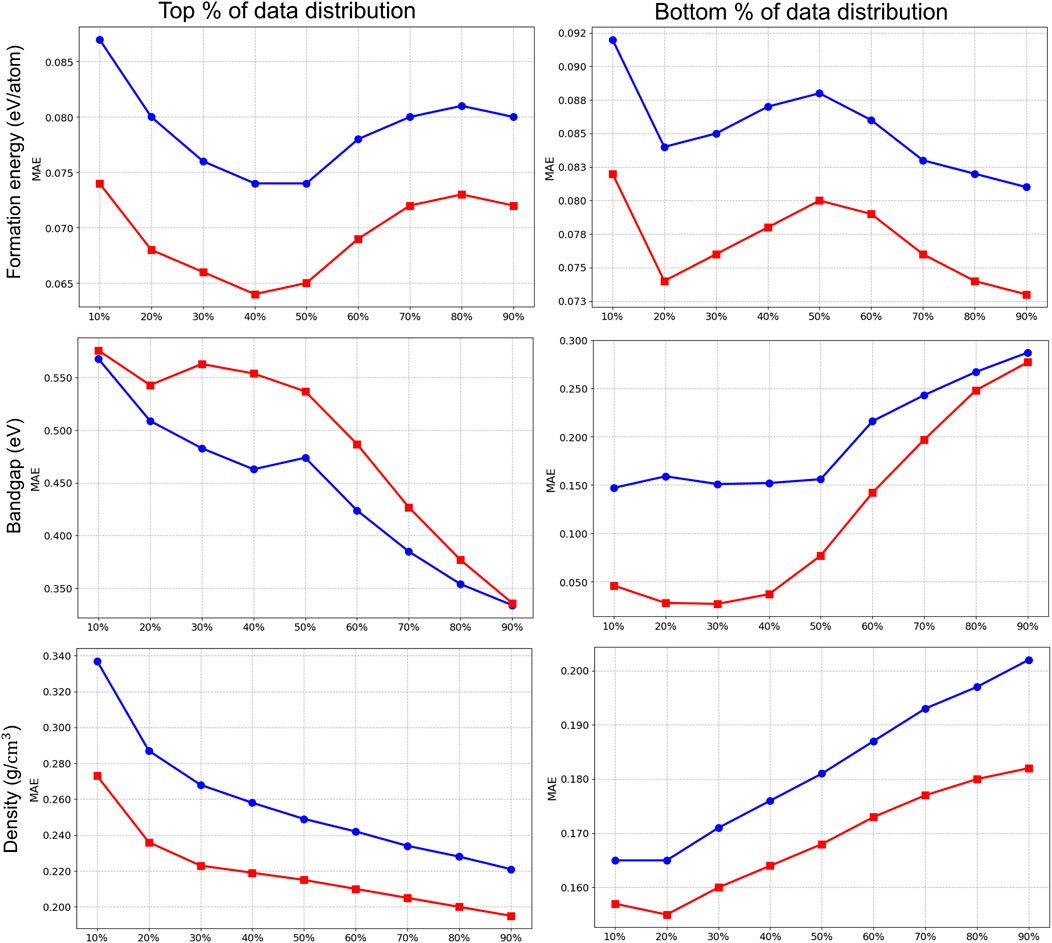
Figure 7. Prediction ensemble MT-
To check the generality, robustness, and applicability of the ensemble approach in effectively improving the prediction accuracy from the baseline, we also perform for the first time in material property prediction literature, a noise tolerance test for the ensemble models. In this test, we inject variation in the material structure by masking random atoms and edges and changing the structure making it noisy from the perspective of material construction. Therefore, we purposefully remove 5% random atoms and edges from each data point of the test dataset and then apply the prediction ensemble technique to calculate the MAE of the altered test dataset. It is to be mentioned that, the trained models used for the ensemble are the same models we used to compute the MAE for the un-altered test dataset and our goal is to establish the fact that, the ensemble improves the prediction accuracy even if the unseen data points are altered. The noise test results are depicted in Table 4, where it is evident that although the MAE values for prediction have aggravated, the ensemble improves the prediction accuracy for noisy data points for most of the cases. For
Finally, although our experiment clearly demonstrated the benefit of a prediction ensemble over a model ensemble, in Figure 8, we include an analysis in this paper that compares the performance between a prediction ensemble and a model ensemble for both single-task and multi-task frameworks for band gap. As shown in the figure, although the performances of both ensemble approaches appear similar in the multi-task settings (right panel), for the single-task model, we observe that the model ensemble resulted in the worst performance, even when compared to the single best validation model.
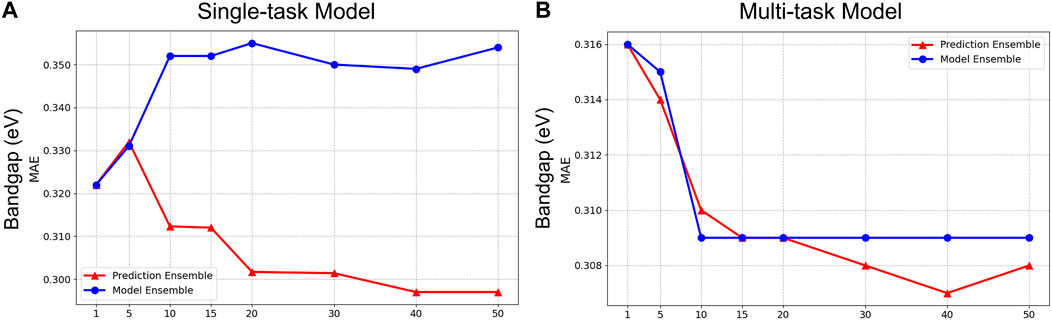
Figure 8. Result comparison for Prediction Ensemble and Model average Ensemble on Single-task
6 Conclusion
In this paper, we explore the impact of an ensemble framework on the task of material property prediction. Our proposed framework is both simple and effective, leveraging the loss landscape of deep neural network training without requiring computationally expensive ensemble strategies. We present two types of ensembles: prediction-based and model-based. The former involves aggregating predictions across different models to form the ensemble model, while the latter aggregates the models first, and then generates a single prediction as the ensemble result. Our analysis shows that the prediction ensemble consistently outperforms the model ensemble. As a result, we conducted a comprehensive analysis across various models (single-task vs. multi-task), architectures (variations in GCNN depth), and properties, finding that the prediction ensemble almost always improves the predictive performance overthe single best validation model. Moreover, to better understand the effect of the ensemble on material properties, we divided the test dataset into different broad classes based on electronic and magnetic characteristics and our analysis reveals that the ensemble invariably improves prediction accuracy for those sub-categories of materials. To test the noise tolerance of the ensemble approach we injected material defects in the test dataset and observed that although the prediction accuracy is affected by noise, the ensemble approach is still performing consistently well for noisy unseen data points for most of the cases. We also examined the efficacy of our proposed framework across different property spectra for test data distribution. Overall, our extensive analysis demonstrates the robustness of the proposed framework in generating enhanced predictive results. Future work will focus on investigating systematic approaches for calculating the number of models to select candidate models for the ensemble framework, extending the analysis to include other GNN models, and expanding our results to 2D datasets.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://next-gen.materialsproject.org/.
Author contributions
CR: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing. GB: Methodology, Software, Validation, Writing–review and editing. NN: Formal Analysis, Methodology, Supervision, Writing–review and editing. AR: Formal Analysis, Funding acquisition, Methodology, Writing–review and editing. PG: Funding acquisition, Project administration, Resources, Supervision, Validation, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research is partially supported by the West Virginia Higher Education Policy Commission’s Research Challenge Grant Program 2023 and the Center for Identification Technology Research and the National Science Foundation under Grant Nos 1650474 and 2413177.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
AlFaraj, Y. S., Mohapatra, S., Shieh, P., Husted, K. E., Ivanoff, D. G., Lloyd, E. M., et al. (2023). A model ensemble approach enables data-driven property prediction for chemically deconstructable thermosets in the low-data regime. ACS Central Sci. 9 1810–1819. doi:10.1021/acscentsci.3c00502
Cao, Z., Dan, Y., Xiong, Z., Niu, C., Li, X., Qian, S., et al. (2019). Convolutional neural networks for crystal material property prediction using hybrid orbital-field matrix and magpie descriptors. Crystals 9 191. doi:10.3390/cryst9040191
Chen, C., Ye, W., Zuo, Y., Zheng, C., and Ong, S. P. (2019). Graph networks as a universal machine learning framework for molecules and crystals. Chem. Mater. 31 3564–3572. doi:10.1021/acs.chemmater.9b01294
Cheng, J., Zhang, C., and Dong, L. (2021). A geometric-information-enhanced crystal graph network for predicting properties of materials. Commun. Mater. 2 92. doi:10.1038/s43246-021-00194-3
Choudhary, K., and DeCost, B. (2021). Atomistic line graph neural network for improved materials property predictions. Mater. 7 185. doi:10.1038/s41524-021-00650-1
Choudhary, K., Garrity, K. F., Reid, A. C., DeCost, B., Biacchi, A. J., Hight Walker, A. R., et al. (2020). The joint automated repository for various integrated simulations (Jarvis) for data-driven materials design. npj Comput. 6 173. doi:10.1038/s41524-020-00440-1
Cooper, Y. The loss landscape of overparameterized neural networks. arXiv preprint arXiv:1804.10200 (2018). doi:10.48550/arXiv.1804.10200
Draxler, F., Veschgini, K., Salmhofer, M., and Hamprecht, F. (2018) “Essentially no barriers in neural network energy landscape” in International conference on machine learning (PMLR) 1309–1318.
Elnagar, A., Al-Debsi, R., and Einea, O. (2020). Arabic text classification using deep learning models. Inf. Process. Manage. 57 102121. doi:10.1016/j.ipm.2019.102121
Fort, S., Hu, H., and Lakshminarayanan, B. (2019). Deep ensembles: a loss landscape perspective. arXiv Prepr. arXiv:1912.02757. doi:10.48550/arXiv.1912.02757
Fort, S., and Jastrzebski, S. (2019). Large scale structure of neural network loss landscapes. Adv. Neural Inf. Process. Syst. 32.
Fu, N., Wei, L., and Hu, J. (2024). Physics-guided dual self-supervised learning for structure-based material property prediction. J. Phys. Chem. Lett. 15 2841–2850. doi:10.1021/acs.jpclett.4c00100
Ganaie, M. A., Hu, M., Malik, A. K., Tanveer, M., and Suganthan, P. N. (2022). Ensemble deep learning: a review. Eng. Appl. Artif. Intell. 115 105151. doi:10.1016/j.engappai.2022.105151
Garipov, T., Izmailov, P., Podoprikhin, D., Vetrov, D. P., and Wilson, A. G. (2018). Loss surfaces, mode connectivity, and fast ensembling of dnns. Adv. neural Inf. Process. Syst. 31.
Gasteiger, J., Becker, F., and Günnemann, S. (2021). Genet: universal directional graph neural networks for molecules. Adv. Neural Inf. Process. Syst. 34 6790–6802.
Gasteiger, J., Groß, J., and Günnemann, S. (2020). Directional message passing for molecular graphs. arXiv Prepr. arXiv:2003.03123. doi:10.48550/arXiv.2003.03123
Ghosh, A., Palanichamy, G., Trujillo, D. P., Shaikh, M., and Ghosh, S. (2022a). Insights into cation ordering of double perovskite oxides from machine learning and causal relations. Chem. Mater. 34 7563–7578. doi:10.1021/acs.chemmater.2c00217
Ghosh, A., Sumpter, B. G., Dyck, O., Kalinin, S. V., and Ziatdinov, M. (2021). Ensemble learning-iterative training machine learning for uncertainty quantification and automated experiment in atom-resolved microscopy. npj Comput. Mater. 7 100. doi:10.1038/s41524-021-00569-7
Ghosh, A., Ziatdinov, M., Dyck, O., Sumpter, B. G., and Kalinin, S. V. (2022b). Bridging microscopy with molecular dynamics and quantum simulations: an atomai based pipeline. npj Comput. Mater. 8 74. doi:10.1038/s41524-022-00733-7
Gong, S., Yan, K., Xie, T., Shao-Horn, Y., Gomez-Bombarelli, R., Ji, S., et al. (2023). Examining graph neural networks for crystal structures: limitations and opportunities for capturing periodicity. Sci. Adv. 9 eadi3245. doi:10.1126/sciadv.adi3245
Gyawali, P. K., Liu, X., Zou, J., and He, Z. (2022). Ensembling improves stability and power of feature selection for deep learning models. Mach. Learn. Comput. Biol. (PMLR) 33–45.
Hohenberg, P., and Kohn, W. (1964). Inhomogeneous electron gas. Phys. Rev. 136 B864–B871. doi:10.1103/PhysRev.136.B864
Hou, H., Wang, J., Ye, L., Zhu, S., Wang, L., and Guan, S. (2023). Prediction of mechanical properties of biomedical magnesium alloys based on ensemble machine learning. Mater. Lett. 348 134605. doi:10.1016/j.matlet.2023.134605
Isayev, O., Oses, C., Toher, C., Gossett, E., Curtarolo, S., and Tropsha, A. (2017). Universal fragment descriptors for predicting properties of inorganic crystals. Nat. Commun. 8 15679. doi:10.1038/ncomms15679
Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: the materials project: a materials genome approach to accelerating materials innovation. Apl. Mater. 1. doi:10.1063/1.4812323
Karamad, M., Magar, R., Shi, Y., Siahrostami, S., Gates, I. D., and Farimani, A. B. (2020). Orbital graph convolutional neural network for material property prediction. Phys. Rev. Mater. 4 093801. doi:10.1103/PhysRevMaterials.4.093801
Karande, P., Gallagher, B., and Han, T. Y. J. (2022). A strategic approach to machine learning for material science: how to tackle real-world challenges and avoid pitfalls. Chem. Mater. 34 7650–7665. doi:10.1021/acs.chemmater.2c01333
Kauwe, S. K., Welker, T., and Sparks, T. D. (2020). Extracting knowledge from dft: experimental band gap predictions through ensemble learning. Integr. Mater Manuf. Innov. 9 213–220. doi:10.1007/s40192-020-00178-0
Kirklin, S., Saal, J. E., Meredig, B., Thompson, A., Doak, J. W., Aykol, M., et al. (2015). The open quantum materials database (oqmd): assessing the accuracy of dft formation energies. npj Comput. Mater. 1 15010–15015. doi:10.1038/npjcompumats.2015.10
Kohn, W., and Sham, L. J. (1965). Self-consistent equations including exchange and correlation effects. Phys. Rev. 140 A1133–A1138. doi:10.1103/PhysRev.140.A1133
Li, H., Xu, Z., Taylor, G., Studer, C., and Goldstein, T. (2018). Visualizing the loss landscape of neural nets. Adv. neural Inf. Process. Syst. 31.
Li, S., Lu, X., Sakai, S., Mimura, M., and Kawahara, T. (2017) “Semi-supervised ensemble dnn acoustic model training” in 2017 IEEE international Conference on acoustics, Speech and signal processing (ICASSP) IEEE 5-9 March 2017.
Liao, Y. L., and Smidt, T. (2022). Equiformer: equivariant graph attention transformer for 3d atomistic graphs. arXiv Prepr. arXiv:2206.11990. doi:10.48550/arXiv.2206.11990
Liu, Y., Zhao, T., Ju, W., and Shi, S. (2017). Materials discovery and design using machine learning. J. Materiomics 3 159–177. doi:10.1016/j.jmat.2017.08.002
Louis, S. Y., Zhao, Y., Nasiri, A., Wang, X., Song, Y., Liu, F., et al. (2020). Graph convolutional neural networks with global attention for improved materials property prediction. Phys. Chem. Chem. Phys. 22 18141–18148. doi:10.1039/D0CP01474E
Magar, R., Wang, Y., and Barati Farimani, A. (2022). Crystal twins: self-supervised learning for crystalline material property prediction. NPJ. Comput. Mater. 8 231. doi:10.1038/s41524-022-00921-5
Mishra, A., Kompella, L., Sanagavarapu, L. M., and Varam, S. (2022). Ensemble-based machine learning models for phase prediction in high entropy alloys. Comput. Mater. Sci. 210 111025. doi:10.1016/j.commatsci.2021.111025
Mohammed, A., and Kora, R. (2023). A comprehensive review on ensemble deep learning: opportunities and challenges. J. King Saud. Univ. Comput. Inf. Sci. 35 757–774. doi:10.1016/j.jksuci.2023.01.014
Park, C. W., and Wolverton, C. (2020). Developing an improved crystal graph convolutional neural network framework for accelerated materials discovery. Phys. Rev. Mater. 4 063801. doi:10.1103/PhysRevMaterials.4.063801
Roshan, S., Tanha, J., Zarrin, M., Babaei, A. F., Nikkhah, H., and Jafari, Z. (2024). A deep ensemble medical image segmentation with novel sampling method and loss function. Comput. Biol. Med. 172 108305. doi:10.1016/j.compbiomed.2024.108305
Sanyal, S., Balachandran, J., Yadati, N., Kumar, A., Rajagopalan, P., Sanyal, S., et al. (2018). Integrating crystal graph convolutional neural network with multitask learning for material property prediction. arXiv Prepr. arXiv:1811.05660. doi:10.48550/arXiv.1811.05660
Schütt, K. T., Sauceda, H. E., Kindermans, P. J., Tkatchenko, A., and Müller, K. R. (2018). Sachet–a deep learning architecture for molecules and materials. J. Chem. Phys. 148 241722. doi:10.1063/1.5019779
Seko, A., Hayashi, H., Nakayama, K., Takahashi, A., and Tanaka, I. (2017). Representation of compounds for machine-learning prediction of physical properties. Phys. Rev. B 95 144110. doi:10.1103/PhysRevB.95.144110
Shahzad, K., Mardare, A. I., and Hassel, A. W. (2024). Accelerating materials discovery: combinatorial synthesis, high-throughput characterization, and computational advances. Sci. Technol. Adv. Mater. Methods 4 2292486. doi:10.1080/27660400.2023.2292486
Shen, L., Zhou, J., Yang, T., Yang, M., and Feng, Y. P. (2022). High-throughput computational discovery and intelligent design of two-dimensional functional materials for various applications. Acc. Mater. Res. 3 572–583. doi:10.1021/accountsmr.1c00246
Tanveer, M., Rashid, A. H., Ganaie, M., Reza, M., Razzak, I., and Hua, K. L. (2021). Classification of alzheimer’s disease using ensemble of deep neural networks trained through transfer learning. IEEE J. Biomed. Health. Inf. 26 1453–1463. doi:10.1109/JBHI.2021.3083274
Wei, J., Chu, X., Sun, X. Y., Xu, K., Deng, H. X., Chen, J., et al. (2019). Machine learning in materials science. InfoMat 1 338–358. doi:10.1002/inf2.12028
Xie, T., and Grossman, J. C. (2018). Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120 145301. doi:10.1103/PhysRevLett.120.145301
Xue, D., Balachandran, P. V., Hogden, J., Theiler, J., Xue, D., and Lookman, T. (2016). Accelerated search for materials with targeted properties by adaptive design. Nat. Commun. 7 11241–11249. doi:10.1038/ncomms11241
Keywords: material property prediction, graph neural networks, ensemble model, prediction ensemble, model ensemble
Citation: Rahman CMA, Bhandari G, Nasrabadi NM, Romero AH and Gyawali PK (2024) Enhancing material property prediction with ensemble deep graph convolutional networks. Front. Mater. 11:1474609. doi: 10.3389/fmats.2024.1474609
Received: 01 August 2024; Accepted: 23 September 2024;
Published: 10 October 2024.
Edited by:
Yongfeng Zhang, University of Wisconsin-Madison, United StatesReviewed by:
Ayana Ghosh, Oak Ridge National Laboratory (DOE), United StatesBenjamin Afflerbach, University of Wisconsin-Madison, United States
Copyright © 2024 Rahman, Bhandari, Nasrabadi, Romero and Gyawali. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chowdhury Mohammad Abid Rahman, Y3IwMDA3MUBtaXgud3Z1LmVkdQ==
 Chowdhury Mohammad Abid Rahman
Chowdhury Mohammad Abid Rahman Ghadendra Bhandari
Ghadendra Bhandari Nasser M. Nasrabadi1
Nasser M. Nasrabadi1 Aldo H. Romero
Aldo H. Romero Prashnna K. Gyawali
Prashnna K. Gyawali