Nonlinear regression modeling of swelling characteristics in cracked expansive soil: integrating crack, moisture, density, and load effect

Expansive soils, known for their significant volume change with variations in moisture content, are widely distributed around the globe. Due to their swelling properties, expansive soils pose significant engineering challenges, especially in rapidly developing countries like China. This study aims to investigate the swelling mechanisms of expansive soils, focusing on the influence of crack characteristics on swelling behavior. The research methodology includes field investigations, laboratory experiments, and theoretical modeling. By comprehensively considering crack rate, dry density, initial moisture content, and overburden load, a nonlinear regression swelling model is proposed in this research. The degree of crack development in expansive soils is quantitatively characterized by the content of filling materials, leading to the establishment of a crack rate model for expansive soils. Swelling tests on expansive soils with different crack contents were conducted. The results show that the swelling rate is negatively correlated with the initial moisture content and positively correlated with dry density and crack rate. Additionally, the larger the crack rate, the more significant the change in the swelling rate. Furthermore, model validation confirms that this nonlinear regression model accurately describes the relationship between swelling rate and influencing factors. It offers a more precise prediction tool for infrastructure design and maintenance in expansive soil areas, advancing geotechnical engineering practices.

1 Introduction

Expansive soils, also known as swelling clays, are a type of soil that undergo significant volume changes with variations in moisture content (Dai et al., 2024a). These soils are primarily composed of hydrophilic clay minerals, such as montmorillonite, and are characterized by their unique swelling-shrinkage properties, crack features, and overconsolidation, which have garnered extensive attention in geotechnical engineering (Uppal and Chadda, 1967; Rui et al., 2017; Leng et al., 2018; Dai et al., 2020). The swelling and shrinkage properties of expansive soils pose severe challenges to infrastructure, such as buildings, roads, and foundations (Mokhtari and Dehghani, 2012). With the rapid expansion of infrastructure, including highways and railways, driven by China’s economic growth and the Yangtze River Economic Belt development plan (Chen et al., 2019), construction in expansive soil areas is inevitable (Shang et al., 2020). Consequently, the stability and deformation issues associated with expansive soils have become significant challenges in engineering practice (Su et al., 2020; Huang et al., 2023a). Understanding and accurately predicting the swelling behavior of expansive soils is crucial for designing safe and durable infrastructure (Dai et al., 2021; Huang et al., 2024).

The swelling mechanism of expansive soils is complex and influenced by multiple coupled factors (Robert, 1999). These factors include soil properties, environmental conditions (Bai et al., 2020), and soil stress states (Dai et al., 2024c). For example, once expansive soils reach certain engineering properties, their swelling potential is significantly affected by moisture content, dry density, and external loads (Rahimi and Baroothoob, 2002; Dai et al., 2023). When compacted at higher density or lower moisture content, expansive soils may generate higher swelling pressures, exhibiting notable swelling behavior; however, swelling deformation decreases under higher vertical pressures (Ömür et al., 2012). Current mature theories divide the swelling process into two stages: crystal layer swelling and double-layer swelling. The former is primarily controlled by the crystal layer swelling of clay minerals such as montmorillonite and illite (Jia, 2010). As moisture increases, the bonding forces between crystal layers weaken, and swelling behavior transitions to being controlled by the double layer, particularly changes in the thickness of the diffuse layer (Chijioke and Donald, 2019; Bai et al., 2023).

In recent decades, studies on expansive soils have involved extensive modeling work. Early models mainly relied on empirical correlations, using parameters such as initial moisture content, dry density, and overburden pressure to predict swelling potential. Among these, the loaded swelling model, widely applied in oedometers, considers the soil mass as a semi-infinite body, with no lateral deformation and only vertical one-dimensional swelling deformation. Although simple and easy to operate with a wide range of applications, this model exhibits certain discrepancies between fitting forms and experimental data (Huang et al., 2014; Liu et al., 2016).

As early as the 1970s, Huder-Amberg et al. conducted uniaxial swelling strain tests on marl using conventional oedometers, proposing an empirical formula for swelling models under confined conditions, indicating that axial swelling strain of soil samples is linearly related to the logarithm of pressure (Einstein, 1989). Weston (1980) proposed an exponential relationship linking linear swelling with initial moisture content and overburden pressure. Miao et al. (1999) obtained similar results when studying unsaturated expansive soils using a lightweight oedometer, suggesting a linear relationship between swelling rate and these factors. Xu and Lei (2003) studied the loaded swelling deformation test of weak expansive soils, proposing empirical relationships between swelling rate and the initial physical state and mechanical factors of the soil mass. Miao et al. (2008) further revealed that the swelling rate of expansive soils is linearly negatively correlated with initial moisture content and overburden pressure, and positively correlated with initial dry density. Zhang et al. (2010) proposed the concept of a normalization coefficient through loaded swelling tests to describe the relationship between sample compaction and loaded swelling rate, establishing empirical formulas. Huang et al. (2011) conducted loaded swelling rate tests on different types of expansive soils, finding a linear relationship between swelling rate and the logarithm of load. Shen et al. (2015) believed that compaction degree had little effect on swelling rate. Although these models are applicable under certain conditions, they often fail to comprehensively explain the complex interactions between different soil properties and environmental factors. In recent years, with the application of unsaturated soil mechanics and microstructure analysis techniques, researchers are adopting more sophisticated methods to deeply understand swelling mechanisms.

A crucial aspect of expansive soils is the presence of micropores and cracks, which have increasingly gained attention (Huang et al., 2023b). Although existing studies have revealed the deformation laws of expansive soils to some extent, most models have not fully considered the characteristics of cracks in expansive soils. The presence of cracks significantly impacts the moisture absorption and retention characteristics of the soil mass, thereby altering its swelling behavior (Dai et al., 2024b). Therefore, developing swelling models that accurately capture the influence of cracks is essential for improving prediction accuracy and reliability in engineering design.

This study proposes an improved nonlinear regression swelling model, predicting the swelling rate of expansive soils by comprehensively considering crack rate, dry density, initial moisture content, and overburden load. By incorporating crack characteristics, the model aims to enhance understanding of how crack networks interact with the soil matrix and affect overall swelling behavior. Compared to existing models, the proposed model offers the following advantages: it provides a more accurate representation of soil microstructure by considering crack effects, thereby improving the predictive capability of swelling models; it captures the nonlinear characteristics of swelling behavior, which traditional linear models struggle to represent; and it has been validated by experimental data, demonstrating its applicability and reliability under a wide range of expansive soil conditions. This research contributes to the design and maintenance of infrastructure in expansive soil regions by providing a more accurate prediction tool, advancing related geotechnical engineering practices.

2 Engineering geological characteristics of cracked expansive soils

The expansive soil samples used in this study were collected from the Nanyang Basin area in Henan Province, China (Figure 1). According to the Chinese standard (2013) GB 50112-2013 for the classification of expansive soil subgrade swelling-shrinkage grade, geological surveys indicate that the expansive soil in this region is characterized by strong expansive soil (90 ≤ δ_ef). The expansive soil has a moisture content of 27.5%, a density of 1.94 g/cm³, a liquid limit of 89%, and a plastic limit of 29%. The mineral content includes 8.5% montmorillonite and 12.8% illite-smectite mixed-layer. One of the most notable macroscopic features of these soils is the extensive development of cracks filled with various materials. These strong expansive soils, with their pronounced cracking, pose significant challenges for engineering design and construction.

Figure 1

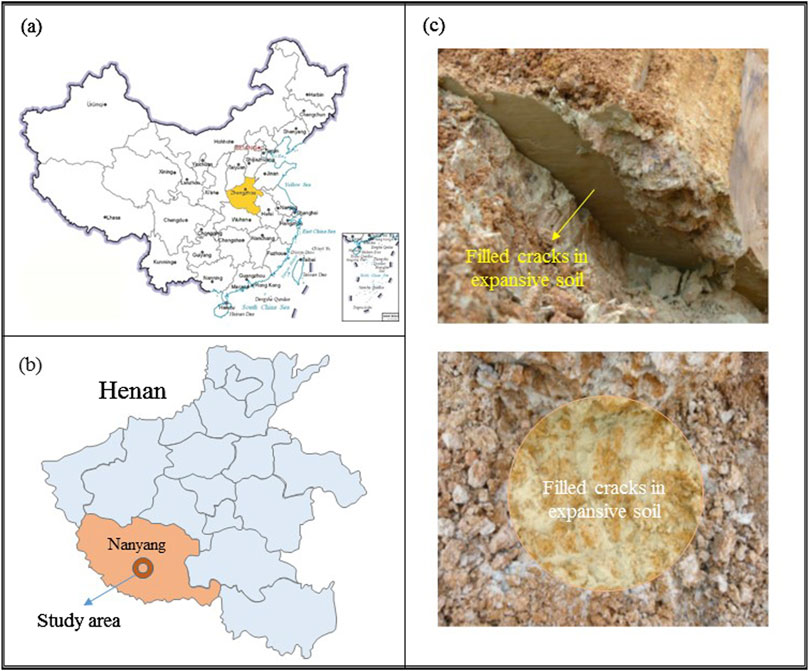
Figure 1. Study area and expansive soil filled cracks: (A) Geographical location, (B) Study area, (C) Expansive soil filled cracks.

Cracks in strong expansive soils are widespread. Based on their origin and morphological characteristics, cracks can be categorized into primary and secondary cracks. Primary cracks are inherent structural features formed due to uneven shrinkage stress within the soil mass. The magnitude of shrinkage stress is proportional to the degree of moisture loss, decreasing from the surface downwards, causing primary cracks to be wider at the top and narrower at the bottom, often filled with secondary clay. Secondary cracks, formed due to tensile or shear stresses, are more pervasive and denser. These cracks are typically smooth and filled with highly expansive gray-green or gray-white clay, which has poorer engineering properties than the primary clay (Figure 1C).

The cracks in strong expansive soils are primarily filled cracks. Even at depths exceeding 15 m in some excavation slopes, these cracks are fully developed and filled with gray-white or gray-green clay, rich in hydrophilic minerals and colloidal particles. These filling materials form through ion exchange or mineral deposition as groundwater moves through the cracks, interacting with clay minerals like montmorillonite and illite. The filling material often forms irregular, net-like patterns within the soil, with thicknesses typically ranging from 5 to 10 mm, though some can be as thin as 2 mm or exceed 10 mm in localized areas. The clay filling is extremely fine and has a high natural moisture content.

To analyze the swelling characteristics of expansive soils with numerous cracks, tests were conducted on both the soil matrix and the crack-filling materials. The filling material is usually gray-white clay, while the soil matrix is generally yellow-brown expansive soil. The physical properties of these materials are shown in Table 1. Groundwater activity is frequent in the Nanyang expansive soil area, significantly influencing the composition of the crack-filling materials, which are predominantly gray-green clay. Other filling materials include calcareous and iron-manganese compounds, with a minimal presence of unfilled cracks. Gray-green clay-filled cracks constitute 64.3%–83.9% of the total cracks in weak expansive soils. In moderately expansive soils, these cracks display vertical zoning characteristics, with about 80% occurring within a depth of 6 m. In strong expansive soils, which are found at greater depths, gray-green filled cracks are even more prominent, accounting for over 90% of the total cracks.

Table 1

Table 1. The physical properties of cracked expansive soil samples.

Considering the typical clay-filled cracks in strong expansive soils, this study proposes using the content of filling materials to assess the degree of crack development. Based on statistical results, we assume that cracks in strong expansive soils are completely filled with gray-green clay. The crack rate, K_r, defined as the volume of cracks to the volume of soil outside the cracks, can be indirectly described by the ratio of the content of gray-white clay filling to the yellow-brown matrix clay. This allows for the establishment of a quantitative indicator of crack content in strong expansive soils.

3 Swelling test of cracked expansive soil and influencing factors

Using the quantified indicator of crack rate as a key factor, the study incorporates crackiness into the deformation model of expansive soil due to moisture absorption. Indoor experiments were conducted using remolded expansive soil samples with varying proportions of gray-white and yellow-brown clays to simulate crack rates of 35%, 50%, and 65%. In this study, the crack rates were chosen based on typical field observations and empirical evidence from previous studies. This approach was chosen due to the practical difficulties associated with directly creating and controlling specific crack rates in soil samples. By using this rate, we can indirectly reflect the crack characteristics within the soil, allowing for a consistent and controlled examination of their effects on swelling behavior. This method provides an effective and accurate means of simulating and studying the impact of cracks on expansive soils. These samples were prepared with gray-white clay contents of 35%, 50%, and 65%, respectively. The study aimed to investigate the swelling deformation of expansive soils under different crack rates through moisture absorption tests under both unloaded and loaded conditions.

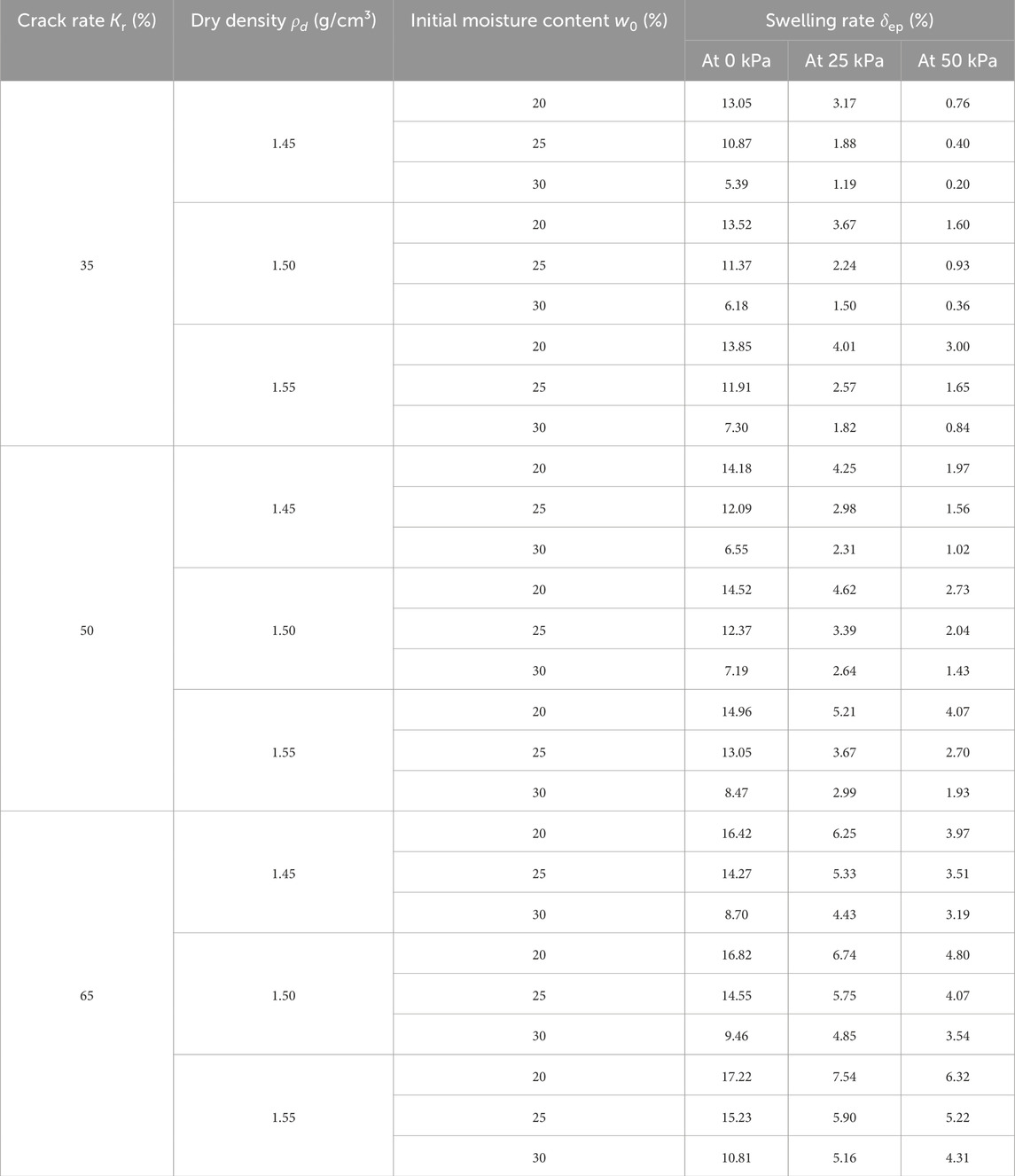
Three levels of dry density (1.45 g/cm³, 1.50 g/cm³, 1.55 g/cm³), three levels of initial moisture content (20%, 25%, 30%), and three levels of load (0 kPa, 25 kPa, 50 kPa) were applied to each crack rate sample. This experimental design allowed for the analysis of the swelling behavior and influencing factors of strong expansive soils under varying conditions. Results are shown in Table 2.

Table 2

Table 2. Test results of swelling rate for cracked expansive soil.

Numerous studies have demonstrated a logarithmic-linear relationship between swelling rate and overburden load. Here, the study specifically analyzes the correlation between swelling rate of strong expansive soils and crack rate, dry density, and initial moisture content.

3.1 Relationship between swelling rate and crack rate

The relationship between swelling rate and crack rate under varying loads, dry densities, and initial moisture contents is shown in Figure 2.

Figure 2

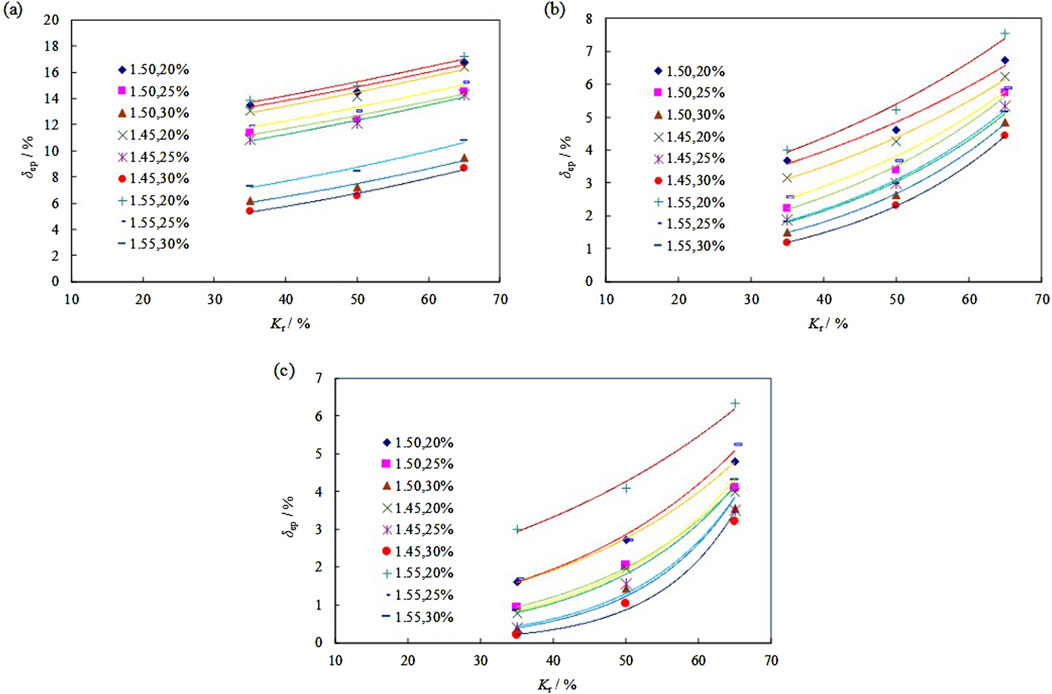
Figure 2. Correlation between swelling rate and crack rate (Legend “1.50,20%” stands for “dry density, initial moisture content”): (A) σ = 0 kPa, (B) σ = 25 kPa, (C) σ = 50 kPa.

Across different levels of initial moisture content, dry density, and load, the relationship between swelling rate and crack rate exhibits a consistent exponential trend, as depicted in the figure. Higher crack rates correspond to stronger crack development in expansive soils, characterized by higher proportions of crack fillings. Consequently, higher crack fillings lead to increased swelling rates, with greater variability in swelling rates observed as the number of filled cracks increases.

3.2 Relationship between swelling rate and dry density

The relationship between swelling rate and dry density under varying loads, crack rates, and initial moisture contents is shown in Figure 3.

Figure 3

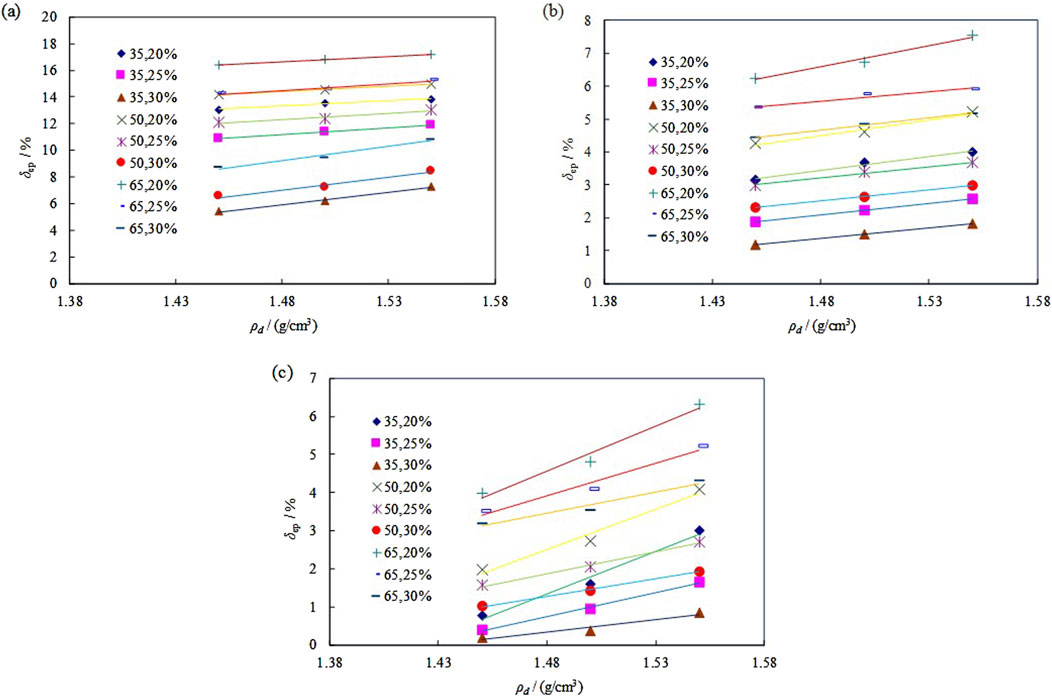
Figure 3. Correlation between swelling rate and dry density (Legend “35,20%” stands for “crack rate, initial moisture content”): (A) σ = 0 kPa, (B) σ = 25 kPa, (C) σ = 50 kPa.

Across different levels of initial moisture content, crack rate, and load, the relationship between swelling rate and dry density generally shows a linear correlation, as illustrated in Figure 3. Particularly at lower initial moisture contents, swelling rate is significantly influenced by dry density, showing faster growth with increasing dry density.

3.3 Relationship between swelling rate and initial moisture content

The relationship between swelling rate and initial moisture content under different loads, crack rates, and dry densities is shown in Figure 4.

Figure 4

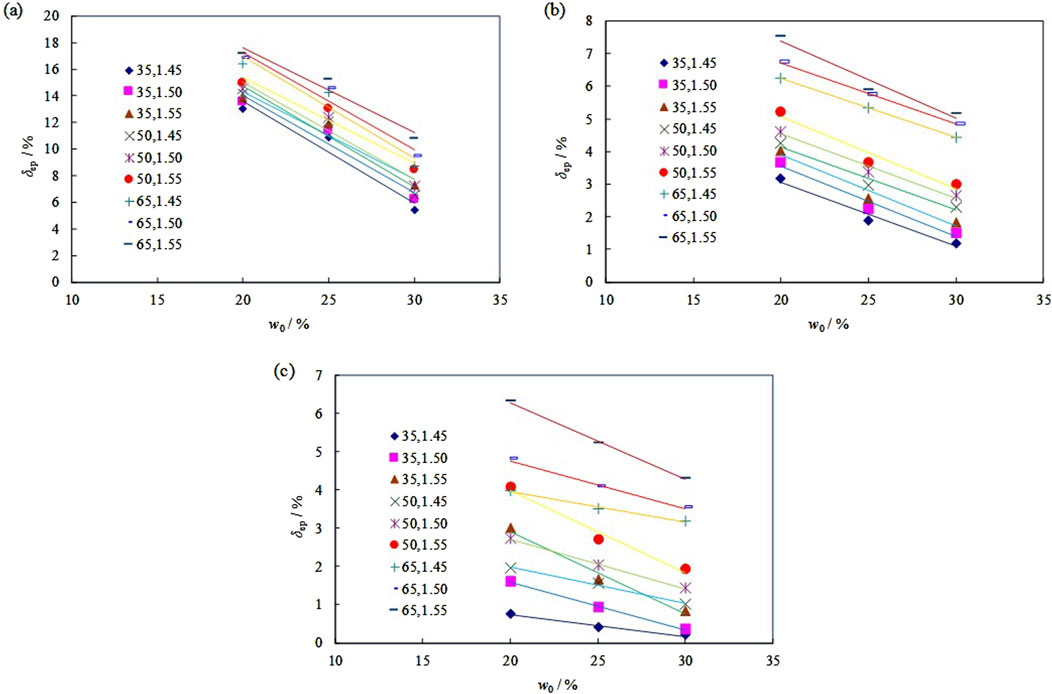
Figure 4. Correlation between swelling rate and initial moisture content (Legend “35,1.45”stands for “crack rate, dry density”): (A) σ = 0 kPa, (B) σ = 25 kPa, (C) σ = 50 kPa.

Across varying dry densities, crack rates, and loads, swelling rate exhibits a basic negative linear correlation with initial moisture content. When other conditions are constant and dry density is high, initial moisture content has a significant impact on swelling rate, decreasing noticeably as initial moisture content increases.

4 Swelling models and sensitivity analysis of different crack rate expansive soils

Based on the swelling test results, the swelling rate of expansive soils is jointly influenced by initial moisture content w₀, dry density ρ_d, load σ, and crack rate K_r. These factors exhibit linear relationships with swelling rate, where w₀, ρ_d, ln(1+σ) show linear relationships, while K_r demonstrates an exponential relationship. Statistical analysis using SPSS software was employed to conduct regression analysis on the swelling rate of strong expansive soils, establishing sensitivity analysis indices for each influencing factor, and subsequently developing multivariate linear and nonlinear swelling models.

Under constant crack rate K_r, the relationship between swelling rate and influencing factors w₀, ρ_d, ln(1+σ) is linear. Different multivariate linear regression models were considered for various crack rates K_r. Regression analysis methods in SPSS include forced entry, elimination, forward selection, backward elimination, and stepwise entry. In this analysis, swelling rate was taken as the dependent variable, with w₀, ρ_d, and ln(1+σ) as independent variables. The relationships and significant impacts of each independent variable on the dependent variable were theoretically analyzed. To ensure model integrity and comprehensiveness, forced entry was used for variable selection, where all selected independent variables were included in the regression model.

Significance testing of the multiple regression equation and regression coefficients is essential. The significance of the regression equation is typically assessed using goodness of fit and analysis of variance, considering the overall linear correlation between the dependent and independent variables. Goodness of fit tests were conducted using multiple correlation coefficients $\sqrt{R^2}$ and adjusted coefficients $\sqrt{{\overline{R}}^2}$ of determination. The null hypothesis was introduced into the analysis of variance (Equation 1):

$H_0:{\beta }_1={\beta }_2=...={\beta }_p=0(1)$

Using the F-test for verification (Equation 2):

$F=\frac{R^2}{1-R^2}\frac{n-p-1}{p}\sim F\left(p,n-p-1\right)(2)$

From the regression analysis, the obtained p-value is judged. If p < 0.05, the null hypothesis in the analysis of variance holds true, indicating the regression equation is significant. If p ≥ 0.05, the regression equation is not significant.

The significance testing of regression coefficients assesses the significance of each independent variable’s impact on the dependent variable. Initially, the null hypothesis is set for each independent variable X_j (Equation 3):

$H_0:{\beta }_j=0,j=1,2,...,p(3)$

Subsequently, the T-test is used for verification (Equation 4), with the test statistic:

$T_j=\frac{{\widehat{\beta }}_j/\sqrt{l_{\mathit{jj}}}}{\sqrt{{\displaystyle \sum _{t=1}^n}{\left(Y_t-{\widehat{Y}}_t\right)}^2/\left(n-p-1\right)}}\sim t\left(p,n-p-1\right)(4)$

Similarly, if the null hypothesis holds true, the regression coefficient is significant; otherwise, it is not significant.

Regression analysis is conducted accordingly. Firstly, for different crack rates K_r, multivariate linear regression analysis of swelling rate with initial moisture content w₀, dry density ρ_d, and load condition ln(1+σ) is performed.

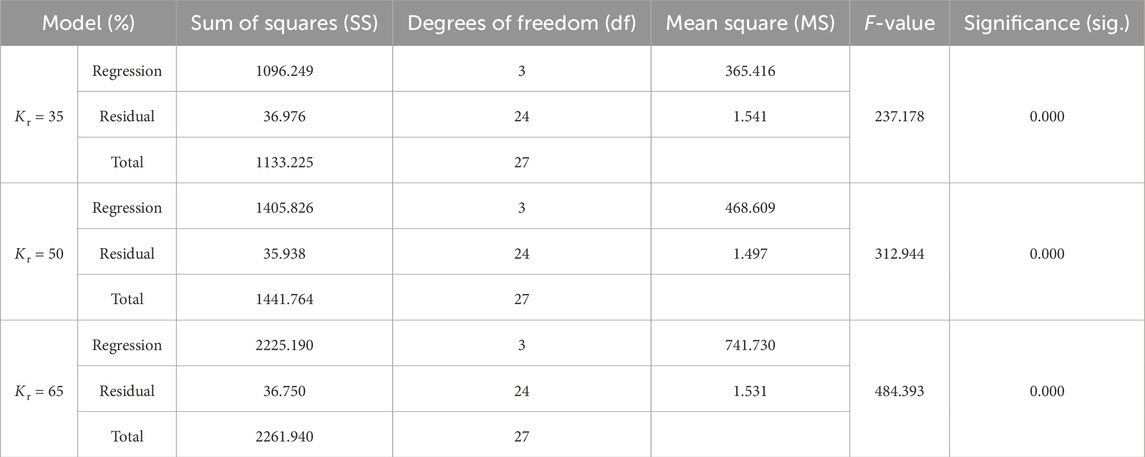
The results of the regression analysis are shown in Tables 3–5.

Table 3

Table 3. Summary of regression models.

Table 4

Table 4. Analysis of variance (ANOVA) table.

Table 5

Table 5. Regression coefficients.

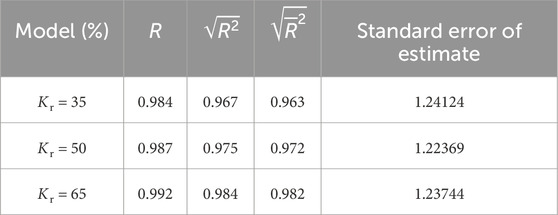
When K_r = 35%, the model’s coefficient of determination is the square root of 0.984, R² = 0.967, the adjusted R² is 0.963, and the standard error is 1.24. These values indicate a high covariance ratio between the independent variables w₀, ρ_d, ln(1+σ), and the dependent variable δ_ep, suggesting a good fit between the model and the data. The analysis of variance (ANOVA) table includes sources of variation, degrees of freedom, mean squares, F-values, and significance tests for F. With Sig. < 0.05, the regression equation is effective and highly significant.

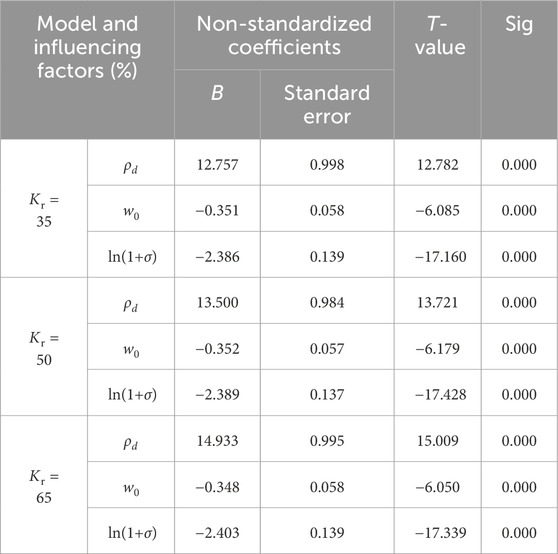
The regression coefficients table presents the values of the regression coefficients, with significance levels for w₀, ρ_d, ln(1+σ) all at Sig. = 0.000, indicating significance levels below 0.05. This implies that w₀, ρ_d, ln(1+σ) each have a significant impact on δ_ep.

Thus, for K_r = 35%, the regression Equation 5 of swelling rate δ_ep on initial moisture content w₀, dry density ρ_d, and load condition ln(1+σ) is:

${\delta }_{\text{ep}}=12.757{\rho }_{\mathrm{d}}-0.351w_0-2.386\ln \left(1+\sigma \right)(5)$

This indicates that dry density has the most significant impact on swelling rate, followed by load condition, with initial moisture content having the least influence.

When K_r = 50%, the model’s coefficient of determination is the square root of 0.987, R² = 0.975, the adjusted R² is 0.972, and the standard error is 1.22. With a high R value, the model exhibits a strong fit. The significance level of the regression equation, Sig.<0.05, indicates that the regression equation is effective. Additionally, the coefficients w₀, ρ_d, ln(1+σ) all have significance levels Sig. = 0.000, which are below 0.05, implying that w₀, ρ_d, ln(1+σ) each have a significant impact on δ_ep.

Therefore, for K_r = 50%, the regression Equation 6 of swelling rate δ_ep on initial moisture content w₀, dry density ρ_d, and load condition ln(1+σ) is:

${\delta }_{\text{ep}}=13.500{\rho }_{\mathrm{d}}-0.352w_0-2.389\ln \left(1+\sigma \right)(6)$

This indicates that dry density has the highest impact on swelling rate, followed by load condition, with initial moisture content having the least influence.

When K_r = 65%, similar to the cases of K_r = 35% and K_r = 50%, the regression equation shows a high R value, indicating a strong fit. The regression equation’s significance level with respect to the variables Sig.<0.05 confirms the effectiveness of the regression equation and the significant impact of the parameters.

For K_r = 65%, the sensitivity coefficients of swelling rate δ_ep to dry density ρ_d, initial moisture content w₀, and load condition ln(1+σ) are 14.933, −0.348, and −2.403 respectively. The regression Equation 7 is:

${\delta }_{\text{ep}}=14.933{\rho }_{\mathrm{d}}-0.348w_0-2.403\ln \left(1+\sigma \right)(7)$

Thus, the regression equation for swelling rate δ_ep with respect to dry density ρ_d, initial moisture content w₀, and load condition ln(1+σ) can be uniformly expressed as Equation 8:

${\delta }_{\text{ep}}=a{\rho }_{\mathrm{d}}-b{w}_0-c\ln \left(1+\sigma \right)(8)$

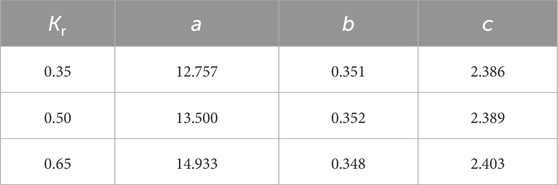
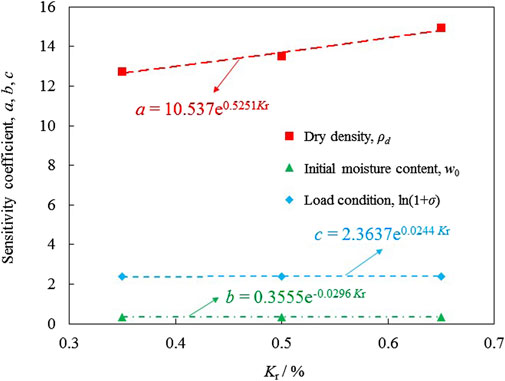
where a, b, and c are empirical parameters. The values of a, b, and c for different K_r are listed in Table 6, and their fitting is shown in Figure 5 using an exponential curve fitting approach.

Table 6

Table 6. Relationship between Crack Rate K_r and Parameters a, b, c.

Figure 5

Figure 5. Relationship curve between crack rate K_r and parameters a, b, c.

The relationship between the parameters a, b, c and the crack rate K_r is given by Equations 9, 10 and 11:

$a=10.537{\mathrm{e}}^{0.5251K\mathrm{r}}(9)$

$\mathit{b}=0.3555{\mathrm{e}}^{-0.0296Kr}(10)$

$c=2.3637{\mathrm{e}}^{0.0244K\mathrm{r}}(11)$

Therefore, the swelling rate model for cracked expansive soil based on crack rate K_r can be expressed as Equation 12:

${\delta }_{\text{ep}}=10.537{\mathrm{e}}^{0.5251K\mathrm{r}}{\rho }_{\mathrm{d}}-0.3555{\mathrm{e}}^{-0.0296K\mathrm{r}}{w}_0-2.3637{\mathrm{e}}^{0.0244K\mathrm{r}}\ln \left(1+\sigma \right)(12)$

This model describes how the swelling rate varies with dry density, initial moisture content, and load condition as functions of the crack rate K_r.

5 Nonlinear regression swelling model for cracked expansive soil

Due to the linear relationship between swelling rate in cracked expansive soil with initial moisture content, dry density, and load, and the exponential relationship with crack rate K_r, further coupling K_r directly into the model is conducted for nonlinear regression analysis of swelling rate with K_r, w₀, ρ_d, and ln(1+σ). The regression Equation 13 used is as follows:

${\delta }_{\text{ep}}=a{\mathrm{e}}^{bK\mathrm{r}}+c{\rho }_{\mathrm{d}}+d{w}_0+e\ln \left(1+\sigma \right)(13)$

Regression analysis results are shown in Tables 7–9.

Table 7

Table 7. Parameter estimates.

Table 8

Table 8. Analysis of variance for regression equation.

Table 9

Table 9. Parameter correlation.

The residual sum of squares (RSS) for the regression model is 109.247, and the total sum of squares (TSS) for the dependent variable is calculated as 1818.281. Therefore, the coefficient of determination R² for the nonlinear regression model is computed as R² = 1−RSS/TSS = 0.9399, indicating a high correlation. This high R² suggests a good fit of the regression equation to the data.

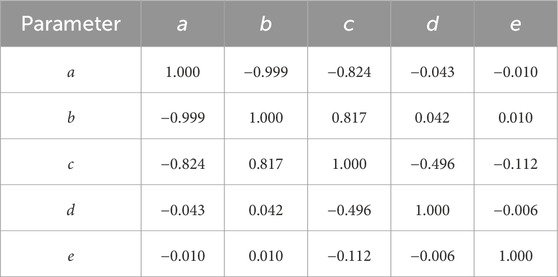
In terms of parameter correlations, a, b, and c show strong correlations, indicating that a change in any one of these parameters significantly affects the others. a has negative correlations with the other parameters, meaning an increase in a leads to decreases in the others, while b correlates positively with the other parameters. d, e, and c exhibit low correlations with each other and with b, indicating their effects are relatively independent.

Based on the parameter values, the nonlinear regression Equation 14 for swelling rate in relation to K_r, w₀, ρ_d, and ln(1+σ) is given by:

${\delta }_{\text{ep}}=0.225{\mathrm{e}}^{4.580K\mathrm{r}}+12.054{\rho }_{\mathrm{d}}-0.353w_0-2.394\ln \left(1+\sigma \right)(14)$

The typical regression surface derived from the nonlinear swelling model for cracked expansive soil is shown in Figure 6.

Figure 6

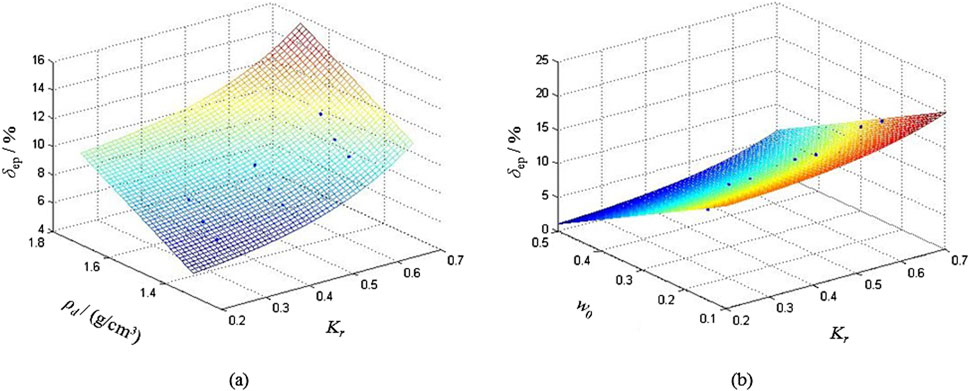
Figure 6. Typical regression surfaces of nonlinear expansion model: (A) w₀ = 30%, σ = 0 kPa, (B) ρ_d = 1.5 g/cm³, σ = 0 kPa.

A total of 81 samples were utilized for predicting the swelling rate of cracked expansive soils. The crack rates for these samples ranged from 10% to 65%, covering a broader range than that in this study. This extensive range allows for a more comprehensive evaluation of the swelling characteristics and enhances the robustness of the predictive model. The predictions of the swelling rate δ_ep1 for cracked expansive soil based on measured crack rate K_r, initial moisture content w₀, dry density ρ_d, and load ln(1+σ) were made. These predictions were compared with actual measurements δ_ep2 and shown in Figure 7. The results show a high degree of agreement between predicted and actual values, displaying a nearly linear relationship with a slope k approximating 1. Therefore, this nonlinear regression model effectively describes the relationship between swelling rate and crack rate, initial moisture content, dry density, and load. It serves well as a predictive model for the swelling characteristics of cracked expansive soils.

Figure 7

Figure 7. Comparison between predicted and measured swelling rates.

6 Conclusions

This study proposes a nonlinear regression swelling model that predicts the swelling rate of expansive soils by considering crack rate, dry density, initial moisture content, and overburden load comprehensively. By incorporating crack characteristics, the model aims to enhance understanding of how crack networks interact with soil matrix, thereby influencing overall swelling behavior. The conclusions of the paper are as follows.

(1) A crack rate model for expansive soils was established based on the ratio of gray-white filling clay to yellow-brown matrix clay content, serving as a quantitative indicator to determine the degree of crack development.

(2) The swelling rate decreases linearly with increasing initial moisture content, showing a negative correlation. Conversely, swelling rate significantly increases with increasing dry density, exhibiting a positive correlation. The relationship between swelling rate and crack rate is exponential: higher crack rates correspond to higher swelling rates, and greater variability in swelling rate is observed with more filled cracks.

(3) A nonlinear regression model for swelling rate was established based on crack rate, dry density, initial moisture content, and load. This nonlinear model effectively describes the relationship between swelling rate and crack rate, initial moisture content, dry density, and load, serving as a predictive model for the swelling characteristics of cracked expansive soils.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JY: Writing–original draft, Writing–review and editing, Conceptualization, Data curation, Funding acquisition. DC: Writing–review and editing, Investigation, Supervision. KS: Writing–original draft, Methodology, Validation. HY: Writing–review and editing, Methodology.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The work reported in this paper was financially supported by the Science and Technology Research and Development Program of China State Railway Group Co., Ltd. (No. J2022G002), Foundation of China Academy of Railway Sciences (No. 2023QT002) and Youth Talent Program Supported by China Railway Society.

Acknowledgments

We would like to acknowledge the reviewers and the editors for their comments and suggestions.

Conflict of interest

Authors JY, DC, KS, and HY were employed by China Academy of Railway Sciences Corporation Limited.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, B., Bai, F., Nie, Q., and Jia, X. (2023). A high-strength red mud–fly ash geopolymer and the implications of curing temperature. Powder Technol. 416, 118242. doi:10.1016/j.powtec.2023.118242

CrossRef Full Text | Google Scholar

Bai, B., Xu, T., Nie, Q., and Li, P. (2020). Temperature-driven migration of heavy metal Pb²⁺ along with moisture movement in unsaturated soils. Int. J. Heat Mass Transf. 153, 119573. doi:10.1016/j.ijheatmasstransfer.2020.119573

CrossRef Full Text | Google Scholar

Chen, Q., Peng, Y. L., Cao, Z. Z., and Wang, W. (2019). Experimental study on dynamic characteristics of expansive soil from Yanzhou-Shijiusuo railway roadbed under cyclic loading. J. Eng. Geol. 27 (4), 737–744. doi:10.13544/j.cnki.jeg.xq2019030

CrossRef Full Text | Google Scholar

Chijioke, C. I., and Donald, C. N. (2019). Emerging trends in expansive soil stabilisation: a review. J. Rock Mech. Geotechnical Eng. 11 (2), 423–440. doi:10.1016/j.jrmge.2018.08.013

CrossRef Full Text | Google Scholar

Chinese Standard (2013). Technical code for buildings in expansive soil regions. GB 50112-2013. Available at: http://www.codeofchina.com/standard/GB50112-2013.html.

Google Scholar

Dai, Z., Chen, S., and Li, J. (2020). Physical model test of seepage and deformation characteristics of shallow expansive soil slope. Bull. Eng. Geol. Environ. 79 (8), 4063–4078. doi:10.1007/s10064-020-01811-0

CrossRef Full Text | Google Scholar

Dai, Z., Guo, J., Chi, Z., and Chen, S. (2023). Three-dimensional soil–water characteristics model of expansive soil considering swelling effect. Int. J. Geomechanics 23 (8), 04023119. doi:10.1061/ijgnai.gmeng-8423

CrossRef Full Text | Google Scholar

Dai, Z., Guo, J., Yu, F., Zhou, Z., Li, J., and Chen, S. (2021). Long-term uplift of high-speed railway subgrade caused by swelling effect of red-bed mudstone: case study in Southwest China. Bull. Eng. Geol. Environ. 80 (6), 4855–4869. doi:10.1007/s10064-021-02220-7

CrossRef Full Text | Google Scholar

Dai, Z., Guo, J., Zhong, K., Tong, K., Li, S., Huang, K., et al. (2024a). Dynamic evolution of three-dimensional cracks in expansive soil under wet-dry cycles: insights from resistivity monitoring. Bull. Eng. Geol. Environ. 83 (8), 305. doi:10.1007/s10064-024-03812-9

CrossRef Full Text | Google Scholar

Dai, Z., Huang, K., Chi, Z., and Chen, S. (2024b). Model test study on the deformation and stability of rainfall-induced expansive soil slope with weak interlayer. Bull. Eng. Geol. Environ. 83 (3), 76. doi:10.1007/s10064-024-03576-2

CrossRef Full Text | Google Scholar

Dai, Z., Huang, K., Li, J., Chi, Z., and Chen, S. (2024c). Decoupling analysis method for rain-induced failure of shallow expansive soil slopes considering swelling and strength softening. Int. J. Geomechanics 24 (2), 04023280. doi:10.1061/ijgnai.gmeng-8837

CrossRef Full Text | Google Scholar

Einstein, H. H. (1989). Suggested methods for laboratory testing of arginaceous swelling rock. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 26 (5), 415–426.

Google Scholar

Huang, B., Cheng, Z. L., and Xu, H. (2014). Expansive model of expansion soil and its application to slope engineering. Rock Soil Mech. 35 (12), 3550–3555. doi:10.16285/j.rsm.2014.12.004

CrossRef Full Text | Google Scholar

Huang, B., He, X. M., and Tan, F. (2011). Experimental study on expansion model of expansive soil in state of K0 stress. Chin. J. Geotechnical Eng. 33 (S1), 442–447.

Google Scholar

Huang, K., Dai, Z., Yan, C., and Chen, S. (2023a). Numerical study on the swelling and failure of red-layer mudstone subgrade caused by humidity diffusion. Comput. Geotechnics 156, 105272. doi:10.1016/j.compgeo.2023.105272

CrossRef Full Text | Google Scholar

Huang, K., Dai, Z., Yan, C., Yu, F., Zhang, W., and Chen, S. (2024). Swelling behaviors of heterogeneous red-bed mudstone subjected to different vertical stresses. J. Rock Mech. Geotechnical Eng. 16 (5), 1847–1863. doi:10.1016/j.jrmge.2023.08.004

CrossRef Full Text | Google Scholar

Huang, K., Yu, F., Zhang, W., Tong, K., Guo, J., Li, S., et al. (2023b). Relationship between capillary water absorption mechanism and pore structure and microfracture of red-layer mudstone in central Sichuan. Bull. Eng. Geol. Environ. 82 (4), 100. doi:10.1007/s10064-023-03115-5

CrossRef Full Text | Google Scholar

Jia, J. C. (2010). Study on the swelling mechanism and mesomechanical swelling model of expansive soil. (Doctoral dissertation). Dalian, China: Dalian University of Technology.

Google Scholar

Leng, T., Tang, C. S., Xu, D., Li, Y. S., Zhang, Y., Wang, K., et al. (2018). Advance on the engineering geological characteristics of expansive soil. J. Eng. Geol. 26 (1), 112–128. doi:10.13544/j.cnki.jeg.2018.01.013

CrossRef Full Text | Google Scholar

Liu, Q. B., Wu, Y. G., Xiang, W., and Wang, R. (2016). Swelling model study of expansive soil at K0 and triaxial stress state. Rock Soil Mech. 37 (10), 2795–2802. doi:10.16285/j.rsm.2016.10.008

CrossRef Full Text | Google Scholar

Miao, L. C., Zhong, X. C., and Yin, Z. Z. (1999). Test research of unsaturated expansive soil strain laws. Dam Observation Geotechnical Test 23 (3), 36–39.

Google Scholar

Miao, P., Xiao, H. B., and Fan, Z. Q. (2008). Trial tests on the swell-shrink strain of Nanning expansive soil under different initial conditions. Highw. Eng. 33 (2), 38–41.

Google Scholar

Mokhtari, M., and Dehghani, M. (2012). Swell-shrink behavior of expansive soils, damage and control. Electron. J. Geotechnical Eng. 17, 2673–2682.

Google Scholar

Ömür, S. N. K., Hüseyin, Y., and Yıldırım, H. (2012). Prediction of swelling potential and pressure in compacted clay. Arabian J. Sci. Eng. 37 (6), 1535–1546. doi:10.1007/s13369-012-0268-4

CrossRef Full Text | Google Scholar

Rahimi, H., and Baroothoob, S. H. (2002). Concrete canal lining cracking in low to medium plastic soils. Irrig. Drain. 51, 141–153.

CrossRef Full Text | Google Scholar

Robert, L. L. (1999). Expansive soils problems and practice in foundation and pavement engineering john D. Nelson and debora J. Miller, wiley, New York, 1992, 259 pp. Int. J. Numer. Anal. Methods Geomechanics 23 (10), 1067. doi:10.1002/(sici)1096-9853(19990825)23:10<1067::aid-nag994>3.0.co;2-e

CrossRef Full Text | Google Scholar

Rui, S. J., Chen, X. L., Liu, Q. H., and Yang, Q. (2017). Study on the strength of expansive soil based on water content and dry-wet cyclic. Sci. Technol. Eng. 17 (25), 284–289.

Google Scholar

Shang, Y. H., Xu, L. R., Huang, Y. L., and Chen, Z. F. (2020). Laboratory tests on dynamic modulus and damping ratio of cement stabilized expansive soil as subgrade filling of heavy haul railway. J. Eng. Geol. 28 (1), 103–110. doi:10.13544/j.cnki.jeg.2017-511

CrossRef Full Text | Google Scholar

Shen, Y. B., Shao, X., Wu, J. J., Yao, H. Y., and Chen, Q. (2015). Study on swelling law of expansive soil in foundation pit of Hefei metro station under loading condition. Railw. Eng. (4), 122–126.

Google Scholar

Su, P. H., Chen, S. K., Zhao, X. Y., Ji, Y. M., Tian, Y., and Yang, Y. (2020). Model test on reinforcement mechanism of geogrid steel tube expansive soil retaining wall for slope stability of Nankun railway. J. Eng. Geol. 28 (3), 658–666. doi:10.13544/j.cnki.jeg.2019-213

CrossRef Full Text | Google Scholar

Uppal, H. L., and Chadda, L. R. (1967). Physico-chemical changes in the lime stabilization of black cotton soil (India). Eng. Geol. 2 (3), 179–189. doi:10.1016/0013-7952(67)90017-8

CrossRef Full Text | Google Scholar

Weston, D. J. (1980). Expansive roadbed treatment for southern africa. Proc. 4th Int. Conf. Expans. Soils 1, 339–360.

Google Scholar

Xu, Y., and Lei, S. Y. (2003). Analysis of variance affecting linear swelling ratio. J. Chang'an Univ. Archit. Environ. Sci. Ed. 20 (2), 6–9.

Google Scholar

Zhang, F. H., Wang, B. T., and Liu, H. L. (2010). Research on deformation disciplines of compacted expansive soils. Rock Soil Mech. 31 (1), 206–210. doi:10.16285/j.rsm.2010.01.015

CrossRef Full Text | Google Scholar