Exploring the dynamic mechanical response and mesoscopic characteristics of typical frozen rock in Yulong Copper Mine

Dynamic mechanical characteristic testing at low temperatures was conducted for the typical porphyry and sandstone specimens of Yulong Copper Mine in Tibet, China. The stress and strain characteristics of the specimens at different temperatures were analyzed. A dynamic constitutive model was developed by considering the initial damage. Furthermore, microscopic damage characteristics during the water-saturated rock freezing process were investigated using the PFC^3D software, revealing the mechanisms of frost heave damage to rocks. The results indicated that the water-ice phase transition either enhanced or deteriorated the specimen strength at low temperatures. Specifically, freezing at −10°C and −20°C enhanced the strength of sandstone. However, freezing at −10°C enhanced the porphyry specimens, and freezing at −20°C caused significant frost swelling injury. The new constitutive equation effectively fitted the dynamic stress and strain curves for both specimens, highlighting their differences. The maximum contact force and particle contact in the frozen rock PFC^3D model were affected by rock and water particle deformations. The frost swelling deformation of water particles had a more pronounced impact on specimen damage and was related to the temperature. A specific freezing temperature existed at which the increase in saturated rock strength corresponded to the maximum specimen strength at that temperature.

1 Introduction

In recent years, there has been a significant upsurge in construction projects in cold regions worldwide, with remarkable development in western China. The rock and soil masses in Western China experience perennial sub-zero temperatures. Therefore, conducting mechanical tests on frozen rock is essential for providing theoretical support for engineering excavations. Studies have indicated that the compressive tensile strength (Inada and Yokota, 1984), elastic modulus (Yamabea and Neaupane, 2001), and fracture toughness (Wang et al., 2022) of rocks can be significantly enhanced under specific negative temperatures. This enhancement is closely related to the shrinkage of rock particles. For water-saturated rocks, the rock particle shrinkage can be caused by freezing, with the defects in the rocks filled by ice bodies. This increases the “integrity” of the rocks. However, water icing generates a frost heave force, which can contribute to specimen breakage. This dual effect indicates that there is an equilibrium point between expansion and contraction within the rocks. Temperature can affect the ice content in rocks during the freezing process, thus influencing the frost heave force within the rock. Therefore, the mechanical characteristics of water-saturated freezing forces are influenced not only by the particle cementation properties and defect distribution of the rock, but also by the freezing temperature (Jia et al., 2019). As it is challenging to directly observe the frozen-water swelling process and frost-swelling damage within frozen specimens, particle flow analytical methods, such as PFC^3D (Feng et al., 2023), FLAC^3D (Guo et al., 2023) and Monte Carlo simulation (Li et al., 2023), are necessary. PFC^3D can record the position coordinates and stress states of the particles during the freezing process, facilitating the simulation of the microscopic characteristics of the frozen specimens (Zhou et al., 2021a; Wang et al., 2023; Huang et al., 2022) utilized PFC^2D to analyze the changes in uniaxial compressive strength and elastic modulus weakening with the number of freeze-thaw cycles, discussing the effects of porosity and initial uniaxial compressive strength on the attenuation coefficient (Lin et al., 2020). employed PFC^3D to simulate and analyze the distribution of frost heave forces in fractured rocks. Their findings revealed that the frost heave force within the joint remained stable, with a tension stress concentration area at the tip, whereas the frost heave force gradually decreased in the area farther from the joint.

The aforementioned studies of mechanical properties of frozen rock have primarily focused on the static mechanics. However, the excavation of frozen rock masses often involves dynamic rock-breaking procedures, including mechanical rock breaking and blasting rock breaking. In recent years, there has been growing interest in investigating the dynamic mechanical properties of frozen rock masses (Liu et al., 2021; Pu et al., 2020; Meng et al., 2023). It has been demonstrated that the dynamic compressive strength of water-saturated frozen sandstone increases as the freezing temperature decreases, exhibiting a significant rate-strengthening effect (Wen et al., 2017; Weng et al., 2019; Weng et al., 2020) suggested that both water-saturated and dry siltstone specimens exhibited their maximum dynamic modulus and dynamic strength at −30°C, with water-saturated specimens displaying greater susceptibility to breakage (Lin et al., 2021). conducted experiments to discover that the dynamic tensile strength of sandstone first increased and then decreased with decreasing freezing temperature. They also established a statistical model relating the temperature and loading rate to the change in the tensile strength of the sandstone (Zhou et al., 2021b). observed a substantial increase in the compressive strength and elastic modulus of dry sandstone samples at −60°C compared to room temperature. Conversely, the water-saturated frozen sandstone samples exhibited higher dependence on the strain rate (Ke et al., 2018). investigated the variation in the dynamic strength of sandstone after different freeze-thaw cycles, analyzing the change in DIF value. They proposed a new model to describe the relationship between the DIF and the strain rate of rock after freeze-thaw cycles (Yang and Yang, 2019). have suggested that low negative temperatures can lead to numerous cracks at the interface between internal components of red sandstone. These cracks have limited plastic deformation ability, making them prone to instability expansion and low-stress brittle failure under high-strain-rate loading. Furthermore (Ma et al., 2018), examined the impact of freeze-thaw cycles on the uniaxial compressive strength and energy distribution parameters, indicating that the dynamic freeze-thaw damage coefficient (K_df) of mudstone was higher than that of sandy mudstone. This presented varying responses to freezing among different rock types. In addition, the establishment of constitutive relationships has been a focal point in the study of mechanical properties of rock-like materials (Zhai et al., 2022; Luo et al., 2020; Wang et al., 2020a). For saturated siltstone (Weng et al., 2022), proposed a dynamic constitutive model that considered the strain rate and low-temperature effects based on the Z-W-T nonlinear viscoelastic model. They also developed dynamic constitutive equations for low-temperature sandstone and siltstone (Wang et al., 2020; Li et al., 2020) established a rock constitutive model that accounted for strain rate effects, damage softening effects, and low-temperature effects using the mechanical element combination theory (Renliang et al., 2019) implemented a constitutive model consisting of a damaged body, viscoelastic body, and spring body, revealing the changes in compressive strength and strain of frozen red sandstone at varying high strain rates.

The dynamic stress-strain relationship of frozen rock is intricately linked to factors such as water saturation, temperature, rock particle cementation characteristics, and pore crack distribution. As a combination of ice and rock, frozen rocks exhibit distinct dynamic mechanical properties compared with conventional rocks. This study focused on investigating these properties using typical porphyry and sandstone samples from the Yulong Copper Mine. Laboratory impact tests were conducted on these rock samples using a freezing device and Split Hopkinson Pressure Bar(SHPB) system to analyze their dynamic load failure characteristics and establish corresponding dynamic constitutive relationships. Additionally, PFC^3D numerical simulation software was employed to investigate the frost heave damage mechanisms affecting these two specimens.

2 Test plan overview

2.1 Specimen preparation and static load characteristics

The test utilized porphyry and sandstone specimens obtained from the Yulong Copper Mine in Tibet Autonomous Region, China, situated at altitudes ranging from 4,569 to 5,118 m. Standard specimens of Φ50 × 100 mm and Φ50 × 25 mm was prepared from the bulk rock specimens, as showing in Figure 1. The selection for the static load and SHPB tests was based on the similar wave velocities among the specimens. Table 1 presents the relevant physical and mechanical parameters of both specimens at normal temperatures. Given the annual temperature fluctuations at the Yulong Copper Mine site, ranging from a maximum of 17.5°C to a minimum of −19.4°C, the freezing temperatures of this experiment were set at normal temperature, including 20°C, −10°C, and −20°C. Additionally, the water conditions were categorized as dry and saturated. After the saturated water treatment, the experiment was conducted for 48 h.

Figure 1

Figure 1. Static and dynamic tests of porphyry and sandstone specimens. (A) Standard specimens, (B) Static loading tests, (C) SHPB tests at low temperature.

Table 1

Table 1. Related physical and mechanical parameters of porphyry and sandstone.

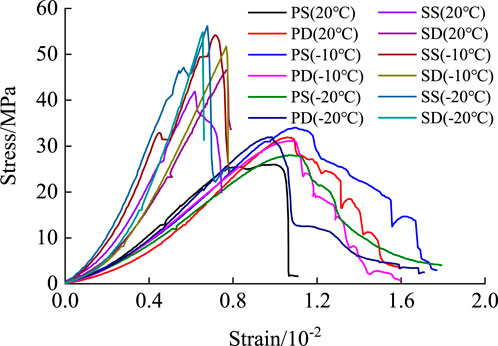
Figure 2 illustrates the static load stress-strain curves. In the figures, “PS” and “PD” denote water-saturated porphyry and dry porphyry, and “SS” and “SD” represent water-saturated sandstone and dry sandstone, respectively. A notable decline in strength was observed in both specimens when subjected to water saturation compared with dry conditions at normal temperatures. Freezing had an impact on the strength of the specimens. Although it minimally affected dry specimens, it significantly influenced the strength of water-saturated rocks. Specifically, the strength of sandstone specimens increased under the negative temperature conditions. Porphyry exhibited greater strength at −10°C than at −20°C, with a more substantial proportion beyond the peak. This indicated pronounced plastic characteristics. Moreover, the peak strain of the porphyry surpassed that of the sandstone specimens. Notably, frozen sandstone specimens exhibited brittleness in the loading elastic section due to sudden local stress drops.

Figure 2

Figure 2. Static stress-strain curves at different temperatures.

2.2 SHPB system and data processing method

Testing was conducted at the State Key Laboratory of Mining Response and Disaster Prevention in Deep Coal Mine, Anhui University of Science and Technology. The SHPB system employed an elastic rod with a diameter of 50 mm, density of 7,800 kg/m³, wave velocity of 5,190 m/s, and elastic modulus of 210 GPa. A cylindrical punch was utilized to generate a rectangular wave upon impact on an incident rod. This impact procedure maintained a nearly constant strain rate during the specimen deformation. The static load and test results, porphyry exhibited relatively low strength, with specimens experiencing significant fracturing at an impact strength of 0.3 MPa. As a result, only three impact pressures, 0.2, 0.25, and 0.30 MPa were applied. The sandstone specimens exhibited a significant level of strength with three different air pressure values established at 0.25, 0.30, and 0.4 MPa. To process the test data, the two-wave method was applied based on the one-dimensional stress wave theory after verifying the overall stress balance, as shown in Equations 1–3.

$\sigma \left(t\right)=\frac{A_b{E}_b}{A_s}{\epsilon }_T\left(t\right)(1)$

$\epsilon \left(t\right)=\frac{C_b}{L_s}{\int }_0^t-2{\epsilon }_R\left(t\right)dt(2)$

$\dot{\epsilon }\left(t\right)=\frac{C_b}{L_s}\left[-2{\epsilon }_R\left(t\right)\right]dt(3)$

where ${\epsilon }_T\left(t\right)$ and ${\epsilon }_R\left(t\right)$ are the transmitted and reflected strain pulses, respectively. $A_b$, $E_b$, and $C_b$ represent the cross-sectional area, Young’s modulus, and P-wave velocity of the pressure bars, respectively. $A_s$ and $L_s$ are the cross-sectional area and length of specimens, respectively.

3 Analysis of dynamic test results

3.1 Dynamic stress-strain characteristics

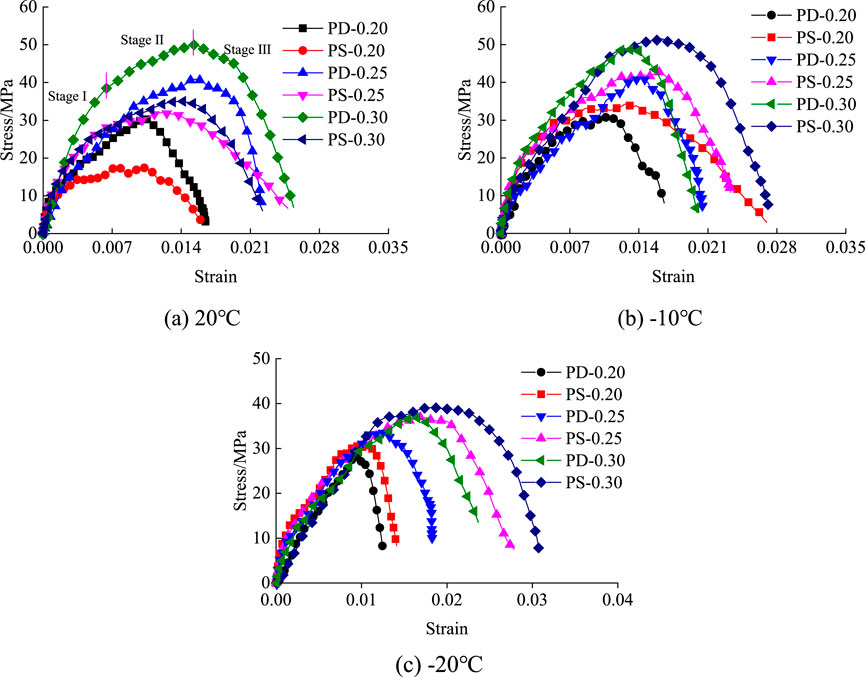
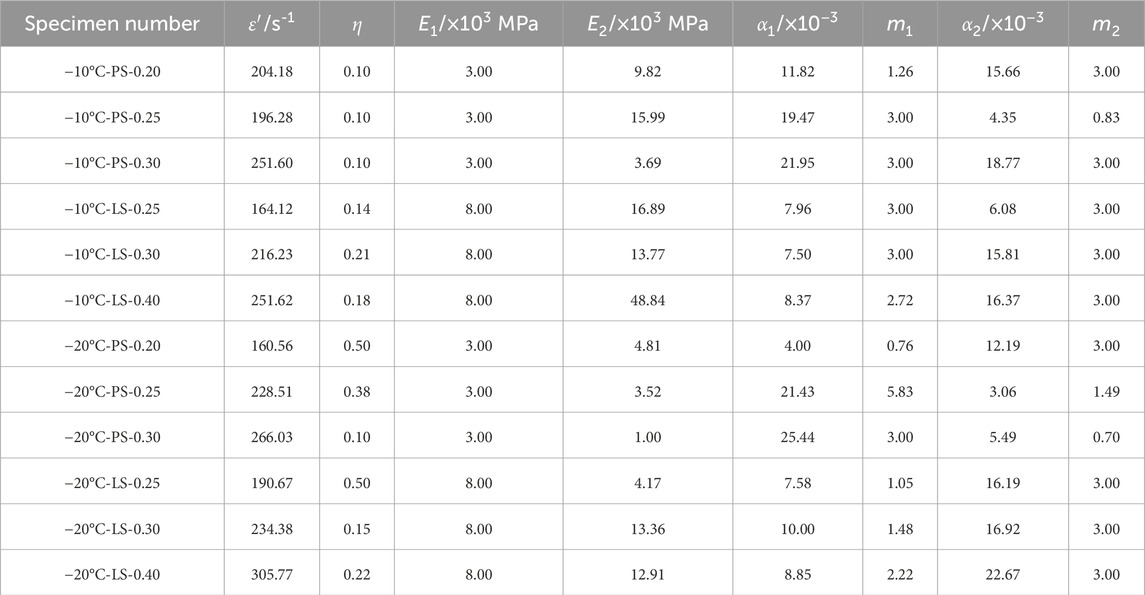
The dynamic stress-strain curves for the porphyry and sandstone specimens are shown in Figures 3, 4, respectively. In the figures, for example, “PS-0.30” represents the dynamic stress-strain curves of a water-saturated porphyry under an impact pressure of 0.30 MPa. The dynamic stress-strain curves for both specimen types exhibit three distinct stages: an initial elastic deformation (Stage I), plastic deformation leading to failure (Stage II), and a post-failure (Stage III). For the porphyry specimen, the strength of the water-saturated specimen at 20°C was notably lower than that of the dry specimen, with the peak strain of the water-saturated specimen being slightly lower. Conversely, at −10°C, the strength of the saturated frozen specimens was slightly higher than that of the dry specimens. At −20°C, the strength of the saturated frozen specimens was generally comparable to that of the dry specimens, with some saturated specimens exhibiting slightly lower strength. At both negative temperatures, the peak strain of the water-saturated specimen was slightly larger than that of the dry specimen, and the curve for the water-saturated frozen specimen in the plastic deformation to failure section appeared relatively gentle, whereas the curve for the dry specimen in this section was relatively steep.

Figure 3

Figure 3. Stress-strain characteristics of porphyry specimens. (A) 20°C, (B) −10°C, (C) −20°C.

Figure 4

Figure 4. Stress-strain characteristics of sandstone specimens. (A) 20°C, (B) −10°C, (C) −20°C.

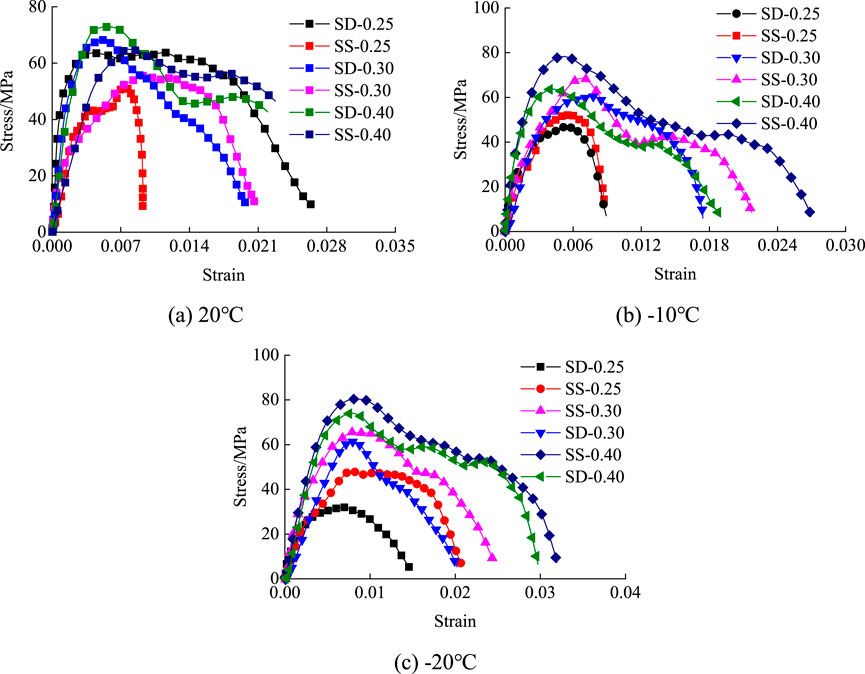
Compared to the porphyry specimens, the sandstone specimens exhibited distinct characteristics of linear elastic deformation. The peak stress observed in the sandstone specimens surpassed that of the porphyry specimens, whereas the peak strain was considerably smaller. The stress-strain curve for sandstone demonstrated a less pronounced plastic deformation in the failure phase, with a gradual reduction in the post-failure section, particularly under negative temperature conditions. At 20°C, similar to porphyry, the strength of the water-saturated sandstone specimens was lower than that of their dry counterparts, accompanied by a larger dynamic modulus and smaller peak strain. Conversely, at −10°C and −20°C, the peak strength of the water-saturated sandstone specimens significantly exceeded that of the dry specimens, and the post-failure section of the stress-strain curve became more significant. Notably, unlike porphyry, the strength of the water-saturated frozen sandstone at −20°C was slightly higher than that at −10°C.

Based on the static and dynamic stress-strain curves, the elastic modulus, dynamic peak strain and stress of the two types of specimens under different water-saturated freezing conditions were statistically obtained, as shown in Table 2. It can be observed that the values of these parameters exhibit some variability with changes in temperature and impact pressure. However, in general, the dynamic elastic modulus of the specimens is greater than the static modulus. The static and dynamic elastic modulus and dynamic peak stress of sandstone are greater than those of porphyry, while the dynamic peak strain of sandstone is smaller than that of porphyry.

Table 2

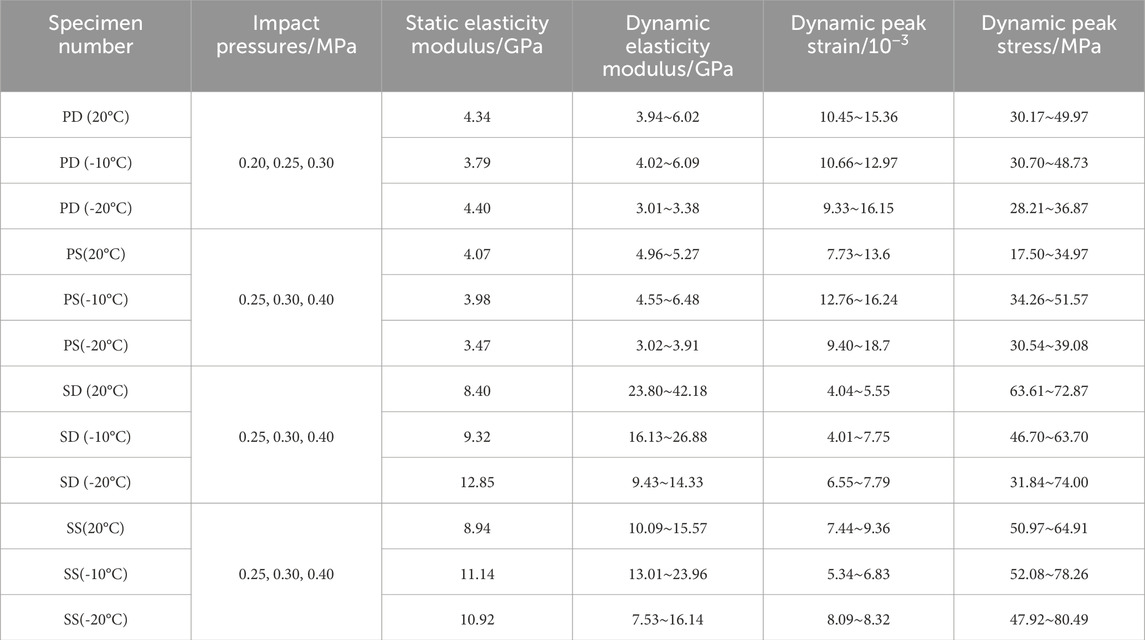
Table 2. Static and dynamic mechanical parameters of specimens under different water-saturated freezing conditions.

The dynamic stress intensity factor (SIF) was typically represented as the ratio of the dynamic and static strengths of the specimens. This ratio reflected the increase in the rock dynamic strength relative to its static strength. To compare variations in dynamic strength among specimens under varying strain rates, temperatures, and water content levels, the SIF for the two rocks was obtained by referencing the static strength of each specimen in the dry state. The calculation formula is shown in Equation 4:

$SIF={\sigma }_d/{\sigma }_s(4)$

where ${\sigma }_d$ and ${\sigma }_s$ are respectively the dynamic strength and static strength of frozen rock. The $SIF$ values obtained for the specimens are shown in Figure 5. At lower pressures, some samples remained intact, and only the $SIF$ values at the two higher pressures were discussed below. In the case of the porphyry specimens, the $SIF$ values for dry specimens at 20°C and −10°C were similar, and slightly lower than those of the saturated water-frozen specimens at −10°C, but higher than those at −20°C, with the lowest values observed for saturated water specimens at 20°C. Water saturation reduced the strength of sandstone at 20°C, with a lower $SIF$ value than that of dry specimens. However, at negative temperatures, the RDIF value of saturated sandstone was higher than that of dry specimens, indicating a more significant increase in the strength of water-saturated specimens after freezing. At −10°C and −20°C, the SIF values of the specimens were relatively close. Notably, at −20°C, frost heave caused significantly greater damage to the porphyry specimens than to the sandstone specimens.

Figure 5

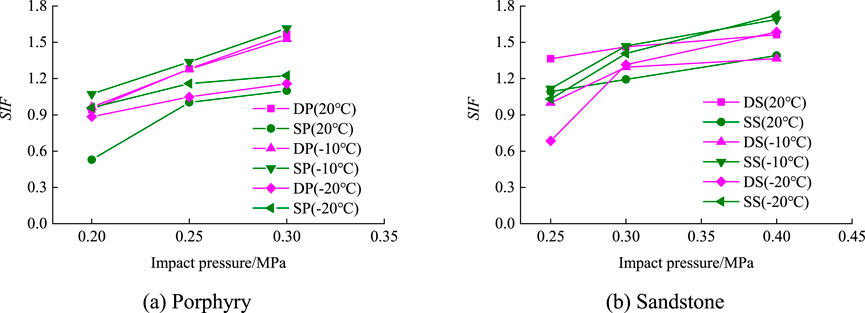
Figure 5. Variations in SIF values of porphyry and sandstone specimens. (A) Porphyry, (B) Sandstone.

Under constant temperature and saturation conditions, the strength and peak strain of the porphyry specimens decreased. This was attributed to the dissolution of the rock’s cementing components under water infiltration, and the particle bonding was weakened, which subsequently reduced the resistance of the rock particle frame. At lower temperatures, the water-ice phase transition can either enhance or deteriorate specimen strength. Water-saturated specimens exhibited increased strength at −10°C owing to the freezing-induced water-ice phase transition filling microcracks within the porphyry specimens, resulting in a strength increase that surpassed the strength reduction caused by the phase transition. As the temperature dropped to −20°C, the water-ice phase transition increased, significantly increasing specimen deterioration. Consequently, greater damage occurred compared to that at −10°C so the specimen strength decreased. However, the sandstone specimens did not experience significant damage from the two temperature-freezing effects. This was primarily due to the smaller porosity of sandstone, more compact particle cementation, and limited freezing expansion, resulting in minimal damage to the specimens.

3.2 Construction of dynamic damage constitutive model

3.2.1 Determination of constitutive relation

Based on the preceding analysis, the frozen porphyry and sandstone specimens displayed distinct characteristics of “freeze softening” or “freeze hardening”, indicating varying degrees of damage during the freezing process. To enhance the accuracy of the model, the incorporation of damage variables was proposed to quantify the freezing-induced damage effect. In this study, an improvement was achieved on the Bowedin-Thomson body model depicted in Figure 6A, which consisted of a linear elastomer and Maxwell body. The elastic constants for the linear elastomer and Maxwell body are denoted as $E_1$ and $E_2$, respectively, with the viscosity coefficient in the Maxwell body represented as ${\eta }_0$. In the enhanced model depicted in Figure 6B, two linear elastomers are substituted with damaged bodies. The elastic coefficients for damaged body I and combination II are $E_{D1}$ and $E_{D2}$, respectively, and the viscosity coefficient for combination II is $\eta$.

Figure 6

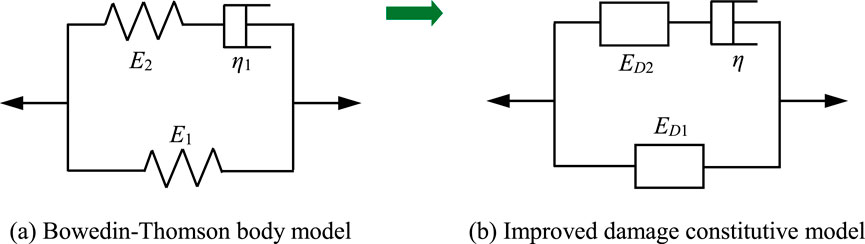
Figure 6. Establishment of the improved constitutive model. (A) Bowedin-Thomson body model, (B) Improved damage constitutive model.

Assuming that the specimen consisted of numerous micro-elements with evenly distributed original defects and the strength of these micro-elements followed a Weibull distribution (Yang et al., 2021) its probability density function can be expressed as Equation 5.

$\varphi \left(\epsilon \right)=\frac{m}{\alpha }{\epsilon }^{m-1}\exp \left(-{\left(\frac{\epsilon }{\alpha }\right)}^m\right)(5)$

where m and $\alpha$ are the distribution parameters, the size of which is related to the property and shape of the material. Damage variables D and $\varphi \left(\epsilon \right)$ have the following relationship, as shown in Equation 6.

$\frac{\mathrm{d}D}{\mathrm{d}\epsilon }=\varphi \left(\epsilon \right)(6)$

It can be gain by integration and obtain Equation 7.

$D=1-\exp \left(-\frac{{\epsilon }^m}{\alpha }\right)(7)$

3.2.2 Derivation of the constitutive equations

According to the improved damage model shown in Figure 4,

$\sigma ={\sigma }_1\left(t\right)+{\sigma }_2\left(t\right)(8)$

$\epsilon \left(t\right)={\epsilon }_1\left(t\right)={\epsilon }_2\left(t\right)(9)$

The constitutive relationship of the damaged body I is as follows:

${\sigma }_1\left(t\right)=E_{D1}\epsilon =\left(1-D_1\right)E_1{\epsilon }_1=E_1{\epsilon }_1\exp \left(-{\left(\frac{\epsilon }{{\alpha }_1}\right)}^{m_1}\right)(10)$

The stress-strain relationship between the viscous element and damaged element in combination II is as follows:

${\epsilon }_2\left(t\right)={\epsilon }_{21}\left(t\right)+{\epsilon }_{22}\left(t\right)(11)$

${\sigma }_2\left(t\right)={\sigma }_{21}\left(t\right)={\sigma }_{22}\left(t\right)(12)$

${\sigma }_{21}=E_{D2}{\epsilon }_{21}(13)$

${\sigma }_{22}=\eta {\epsilon }_{22}^{\prime }(14)$

Derivation of both sides of Equation 11 parallel vertical Equations 12–14 was conducted:

${\epsilon }_2^{\prime }\left(t\right)=\frac{{\sigma }_2^{\prime }\left(t\right)}{E_{D2}}+\frac{{\sigma }_2\left(t\right)}{\eta }(15)$

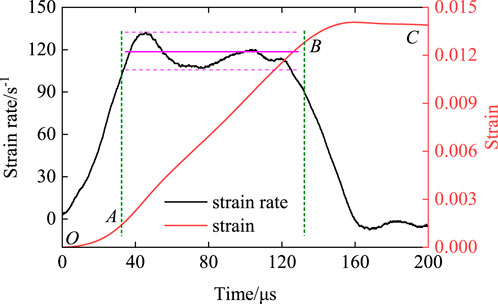
The data processing reveals the variation of the specimen’s strain rate and strain over time during the propagation of stress waves in the elastic rod and specimen. Taking the specimen SS-0.4 at −10°C as an example, as shown in Figure 7, it is evident that under the rectangular stress wave generated by the impact of the cylindrical punch, the deformation of the specimen in the AB segment increases approximately linearly, meaning the strain rate tends to stabilize. In this range, the specimen’s deformation has reached its limit, indicating that failure has occurred.

Figure 7

Figure 7. Variation of strain rate and strain over time during the failure process of the specimen.

Thus, taking the strain rate as a constant, the Laplace transform of Equation 15 can be obtained as shown in Equations 16, 17.

$L\left({\epsilon }_2^{\prime }\left(t\right)\right)=L\left(\frac{{\sigma }_2^{\prime }\left(t\right)}{E_{D2}}\right)+L\left(\frac{{\sigma }_2\left(t\right)}{\eta }\right)(16)$

$\frac{{\epsilon }_2^{\prime }\left(t\right)}{S}=\frac{S{\sigma }_2\left(S\right)-{\sigma }_2\left(0\right)}{E_{D2}}+\frac{{\sigma }_2\left(S\right)}{\eta }(17)$

By putting $\sigma \left(0\right)=0$ into Formula 17, we can obtain:

${\sigma }_2\left(S\right)=\eta {\epsilon }_2^{\prime }\left(\frac{1}{S}-\frac{1}{S+E_{D2}/\eta }\right)(18)$

The inverse Laplace transformation of Equation 18 are shown in Equations 19, 20.

$L^{-1}\left({\sigma }_2\left(S\right)\right)={\epsilon }_2^{\prime }\eta L^{-1}\left(\frac{1}{S}-\frac{1}{S+E_{D2}/\eta }\right)(19)$

${\sigma }_2\left(t\right)={\epsilon }_2^{\prime }\eta \left(1-\exp \left(-\frac{E_{D2}}{\eta }t\right)\right)(20)$

Substituting $t=\frac{{\epsilon }_2}{{\epsilon }_2^{\prime }}$ into Equation, we can obtain Equation 21.

${\sigma }_2\left(t\right)={\epsilon }_2^{\prime }\eta \left(1-\exp \left(-\frac{E_{D2}}{\eta }\frac{{\epsilon }_2}{{\epsilon }_2^{\prime }}\right)\right)(21)$

That is

${\sigma }_2\left(t\right)={\epsilon }_2^{\prime }\eta \left(1-\exp \left(-\frac{E_2{\epsilon }_2}{{\epsilon }_2^{\prime }\eta }\exp \left(-{\left(\frac{\epsilon }{{\alpha }_2}\right)}^{m_2}\right)\right)\right)(22)$

Therefore, the constitutive equation of the model can be obtained from Equations 8–10, 22 as follows:

$\sigma =E_{D1}\epsilon \exp \left(-{\left(\frac{\epsilon }{{\alpha }_1}\right)}^{m_1}\right)+{\epsilon }^{\prime }\eta \left(1-\exp \left(-\frac{E_2\epsilon }{{\epsilon }^{\prime }\eta }\exp \left(-{\left(\frac{\epsilon }{{\alpha }_2}\right)}^{m_2}\right)\right)\right)(23)$

Equation 23 is a dynamic constitutive equation intended to describe a frozen, damaged specimen.

3.2.3 Analysis of fitting results

Equation 23 involves six unknown parameters with the strain rate adjusted to its true value. Among these parameters, m represents the shape coefficient of the Weibull distribution curve, which typically ranges from 0.5 to 3. The parameter ${\alpha }_1$ generally varies near the peak strain and typically varies between 0.1 and 0.5. According to the method outlined in reference (Wang et al., 2020), a fixed value for $E_1$ was employed to determine the remaining five parameter values through trial calculations. During the fitting process, the fixed value of $E_1$ for porphyry was set at 3,000, with ${\alpha }_1$ ranging from 0.004 to 0.03, while $E_1$ of the sandstone specimen was 8,000, and the change range ${\alpha }_1$ was 0.004–0.01.

Figures 8, 9 illustrate the fitting curves for two types of water-saturated freezing specimens at −10°C and −20°C, and their respective fitting parameters are detailed in Table 3. The figures illustrate that the dynamic stress-strain behavior of both specimens aligned more effectively with the enhanced constitutive equation mentioned earlier. An examination of the table data confirmed the congruence between the obtained fitting parameters and the actual observations. Notably, the parameter $E_2$ for sandstone specimens surpassed that of porphyry specimens, while ${\alpha }_1$ was comparatively smaller for the former.

Figure 8

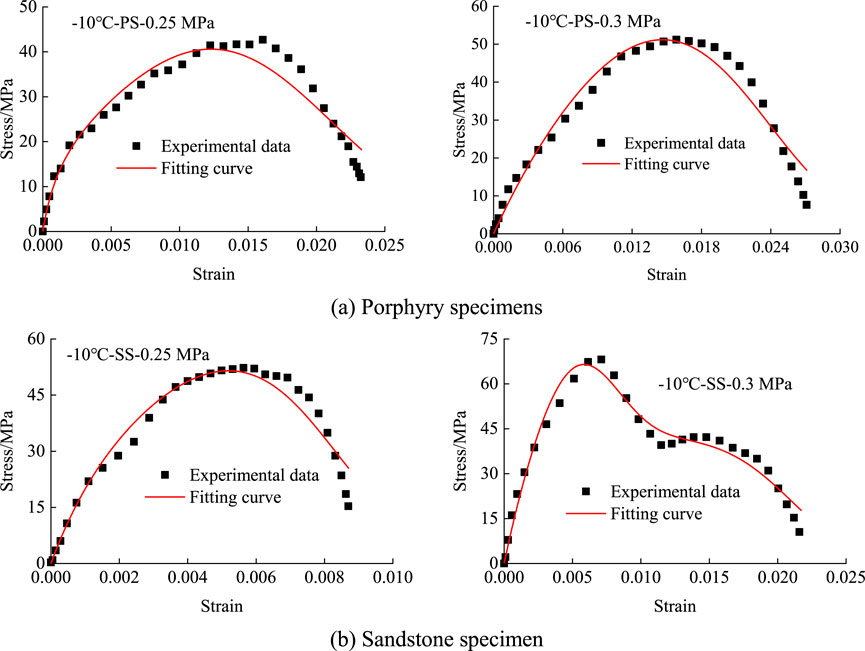
Figure 8. Fitting condition of two specimens at −10°C. (A) Porphyry specimens, (B) Sandstone specimen.

Figure 9

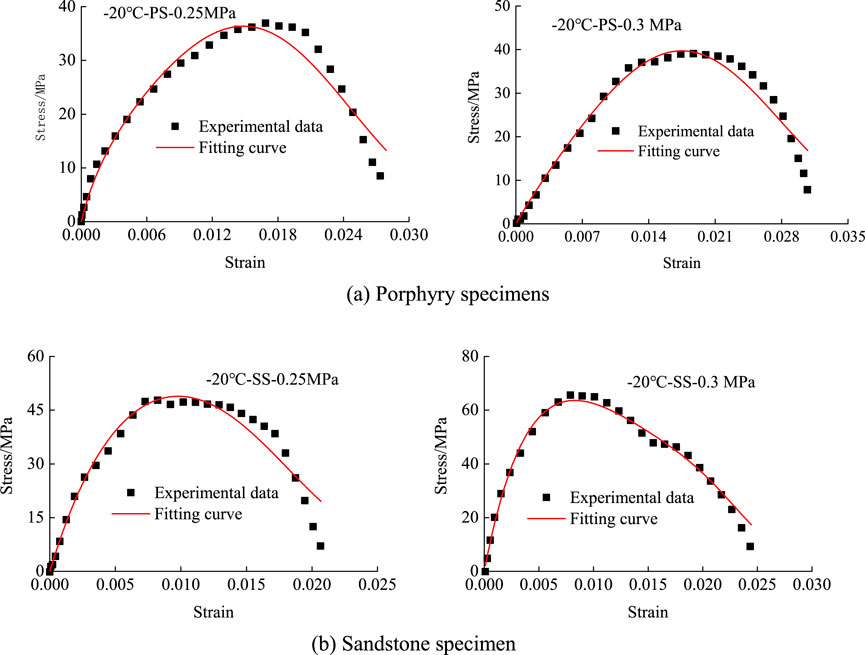
Figure 9. Fitting condition of two specimens at −20°C. (A) Porphyry specimens, (B) Sandstone specimen.

Table 3

Table 3. Fitting parameters of two specimens at subzero temperatures.

4 Microscopic characteristics of frost heave damage based on PFC^3D

The two frozen porphyry and sandstone specimens exhibited distinct dynamic mechanical responses, which could be reflected from their microscopic characteristics observed during the freezing process. Subsequent analysis employed PFC^3D software to examine alterations in the mesoscopic characteristics of both specimens throughout the freezing process. This analysis aimed to elucidate the disparate dynamic response results observed in the two types of rocks.

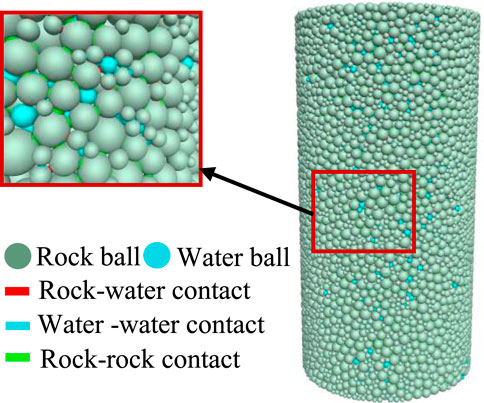
4.1 Freezing model construction and parameter setting

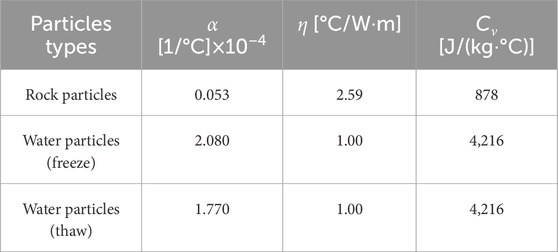
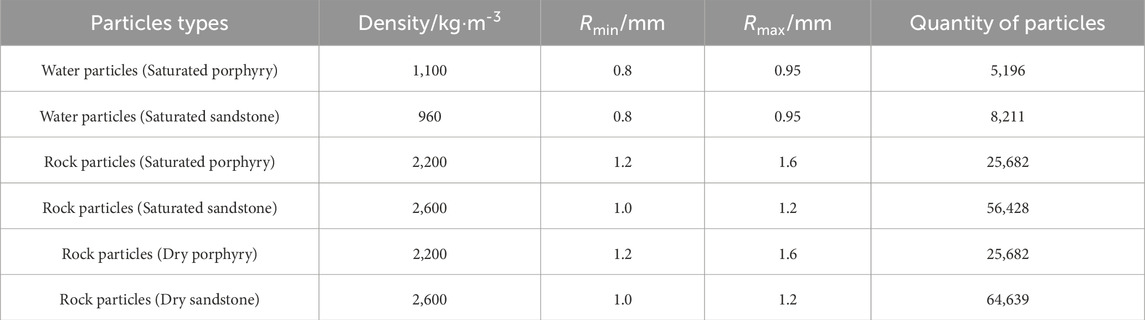
The model dimensions were established as Φ50 mm × 100 mm, with mesoscale parameters calibrated through trial and error, as illustrated in Figure 10. Within the PFC^3D, the expansion force of water particles was equal to the ice swelling force, with a crucial focus on determining the volume deformation of pore-water particles during frost heaving. First, the calibration process was applied to the unfreezing-thawing sandstone model, with the parameters necessary for freezing determined while maintaining consistent mesoscopic parameters. Subsequently, the simulation accuracy was enhanced by aligning the microparameters with the macromechanics. Tables 4, 5 present the mesoscopic parameters specific to both frozen rock types. Figure 11 illustrates the strong correspondence between the peak stress and peak strain observed in the testing and numerical simulation of porphyry and sandstone at various freezing temperatures. This suggested that the selected mesoscopic parameters were suitable for the freezing model, facilitating the prediction of the mechanical properties of freeze-thawed rocks. Furthermore, the damage mechanism of freeze-thaw on sandstone can be analyzed at the mesoscopic level.

Figure 10

Figure 10. Numerical model diagram.

Table 4

Table 4. Related parameters of rock freezing.

Table 5

Table 5. Frozen sandstone particle parameters.

Figure 11

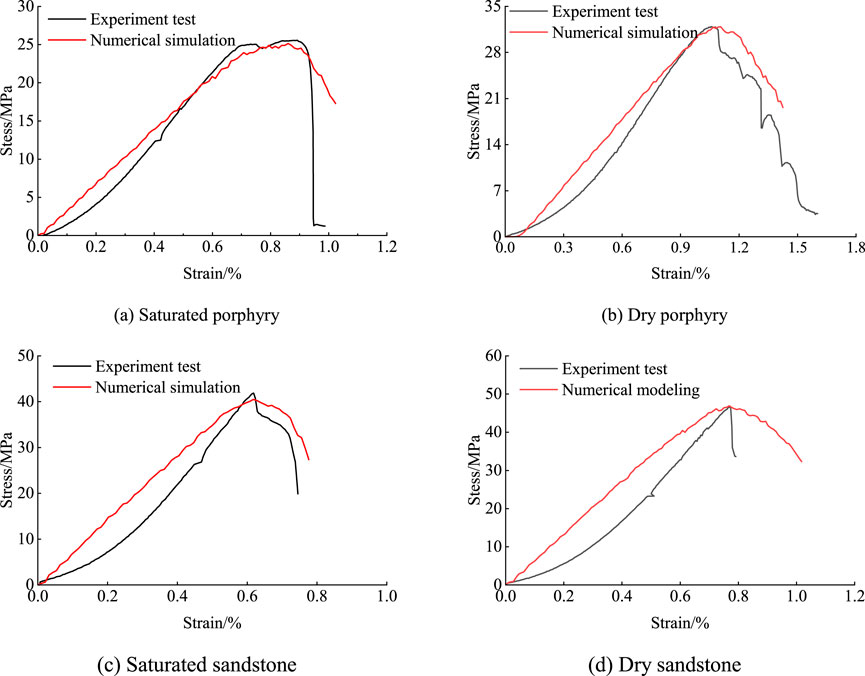
Figure 11. Comparison of stress-strain curves between laboratory test and numerical simulation. (A) Saturated porphyry, (B) Dry porphyry, (C) Saturated sandstone, (D) Dry sandstone.

4.2 Simulation analysis of mesoscopic characteristics of frozen rock

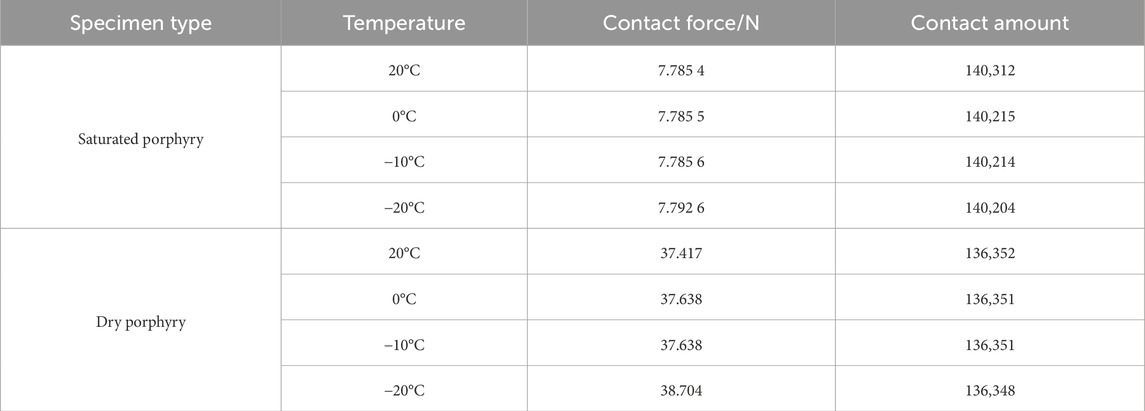
According to the established freezing model, when the particle contact force surpassed the tensile or shear strength of the bonding bond, the bond was fractured, and the contact area was reduced. Hence, the extent of damage to rocks during the freezing process can be quantitatively analyzed by examining the variations in the contact force and particle contact during freezing. Figure 12 demonstrates the variations in the contact force and contact levels during the freezing of fully saturated water and dry porphyry at various freezing temperatures. Further details of the specific particle contact force and contact dimensions can be found in Table 6.

Figure 12

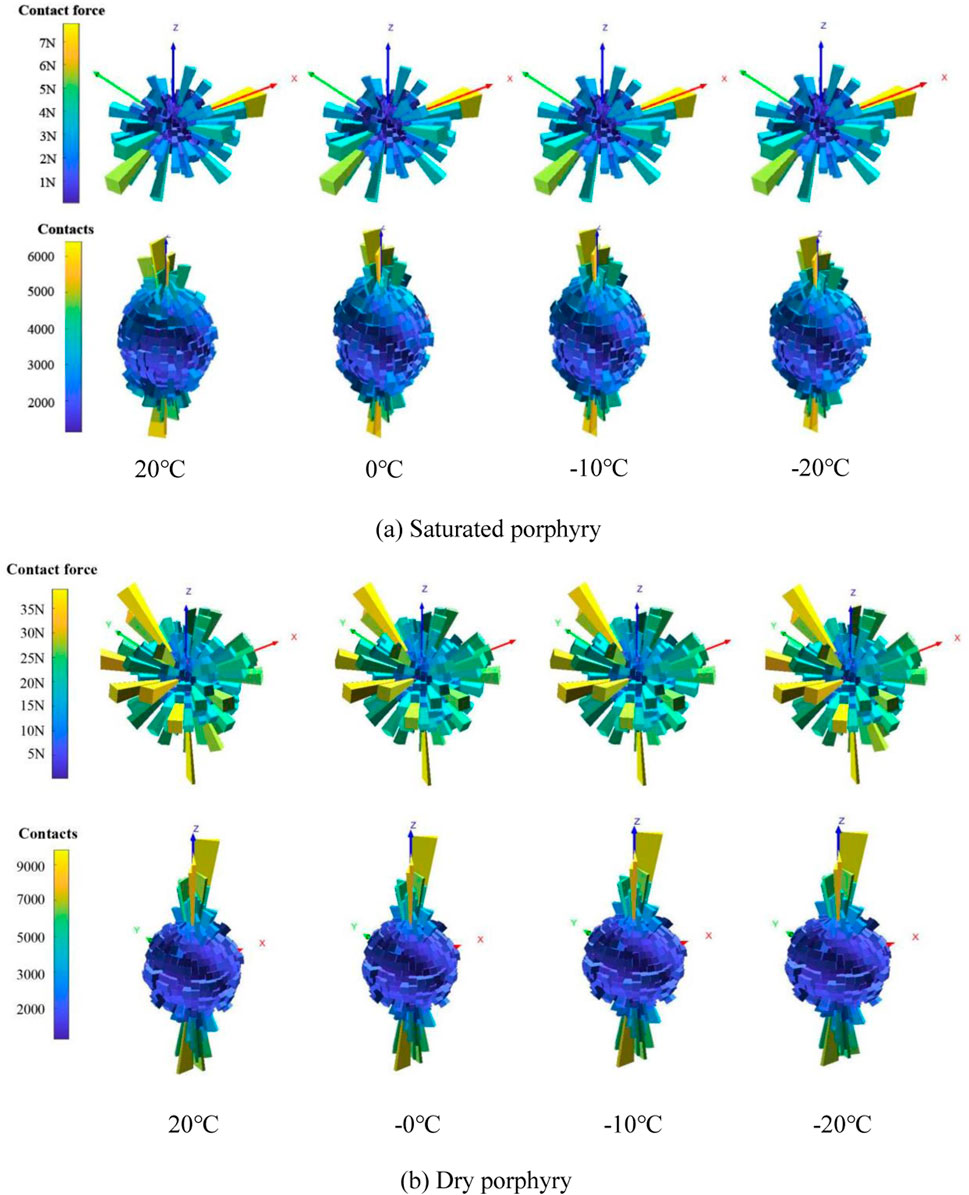
Figure 12. Contact force and contact amount between particle of porphyry during freezing process. (A) Saturated porphyry, (B) Dry porphyry.

Table 6

Table 6. Contact changes of porphyry specimens at different temperatures.

As shown in Figure 12 and Table 6, as the temperature decreased from 20°C to 0°C, there was an increase of 10⁻⁴ N in the maximum contact force between the particles, accompanied by a substantial decrease of 97 in the maximum contact quantity. When the temperature further decreased from 0°C to −10°C, the maximum contact force increased by 10⁻⁴ N, while the maximum contact quantity decreased by 98. When the temperature dropped from −10°C to −20°C, an increase of 6.5 × 10⁻³ N in the maximum contact force between particles and a reduction of 108 in the maximum contact quantity was observed. The maximum contact force in the saturated porphyry specimen gradually increased, and the particle contact quantity steadily decreased during the freezing process from 20°C to −20°C. Although the overall trend remained consistent, the variations at different freezing stages exhibited distinct patterns.

When the temperature decreased from 20°C to 0°C, there was no changes in the micromechanical parameters. The water-saturated porphyry model particles were filled water particles. Consequently, both the rock and water particles experienced a reduction in volume, contributing to a cessation of contact between the water particles and the rock particles due to a volume decrease. The extrusion dislocation among the particles amplifies the contact force during the shrinkage process, consequently increasing the maximum contact force. Upon further lowering the temperature from 0°C to −10°C, the water particles began to freeze into ice particles, expanding in volume by approximately 11%. Although the rock particles also experience volume reduction, the volume increase was significantly smaller than that of the water particles. As the volume of water particles increased, the maximum contact force between them and the adjacent rock particles became larger, causing the fracture of the adhesive bonds between particles and the formation of cracks. This reduced the contact between the rock and water particles. Furthermore, the expansion of water particles in contact with rock particles repelled other water particles. Although the contact force increased, the total contact decreased. As the temperature further decreased from −10°C to −20°C, intergranular bonds continued to break, further reducing the contact quantity while gradually increasing the maximum contact force. At −20°C, although not all water particles were transformed into ice particles, more ice particles were converted, and the extrusion of adjacent rock particles enhanced the contact force compared to −10°C. The continued breakage of bonds at −20°C, led to a further reduction in the contact quantity among the particles.

For the dry porphyry specimens, as the temperature decreased from 20°C to 0°C, only a volume reduction occurred in the rock particles. During this phase, the contact force between the particles increased, whereas the contact quantity remained largely unaffected. This was because the bonding between adjacent rock particles remained intact throughout the volume reduction of rock particles. The temperature decreases only increased contact force between the particles. This observation further indicated that the volume deformation of rock particles was significantly smaller than that of water particles. As the temperature decreased from 0°C to −10°C, the contact force and contact quantity of dry porphyry particles remained stable, which differed from the behavior observed in saturated porphyry. Despite the shrinkage of rock particles, the reduction in the contact quantity during the shrinking process was balanced with the damage-induced reduction in the contact quantity. When the temperature further decreased from −10°C to −20°C, the maximum contact force between particles experienced a notable increase, while the maximum contact quantity remained largely unchanged. In this temperature range, the volume shrinkage of rock particles was intensified, leading to closer particle contact, and the damage occurring between particles was considerably less than that in saturated porphyry.

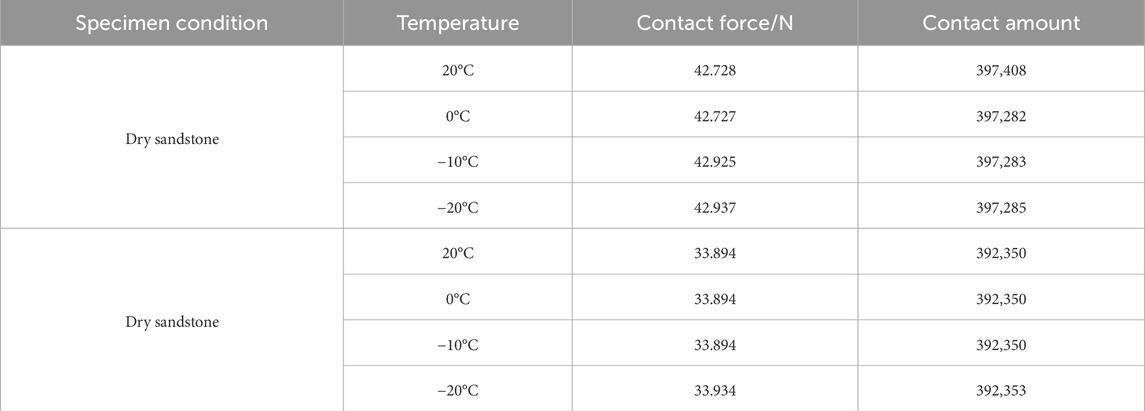
The changes in the interparticle contact force and contact quantity during the freezing process of saturated water and dry sandstone at various freezing temperatures are depicted in Figure 13 and summarized in Table 7. As the temperature of the saturated sandstone decreased from 20°C to 0°C, the maximum contact force remained essentially constant, and the maximum contact quantity decreased by 126. This was similar to that observed in the saturated porphyry. When the temperature continued to decrease from 0°C to −20°C, the primary factor contributing to the increase in the maximum contact force between particles was the expansion of ice particles. The contact quantity remained relatively stable because of more rock particles in the frozen model of saturated sandstone, which underwent minimal volume deformation, in contrast to the more significant deformation of water particles, albeit in smaller numbers. Different from saturated sandstone, the dry sandstone model lacked water particles, but contained more rock particles. Consequently, the contact force and quantity were primarily influenced by the volume shrinkage of the rock particles. Therefore, as the temperature decreased from 20°C to −20°C, both the maximum contact force and the contact quantity between particles remain essentially unchanged, with only a slight increase noted at −20°C in the maximum contact force.

Figure 13

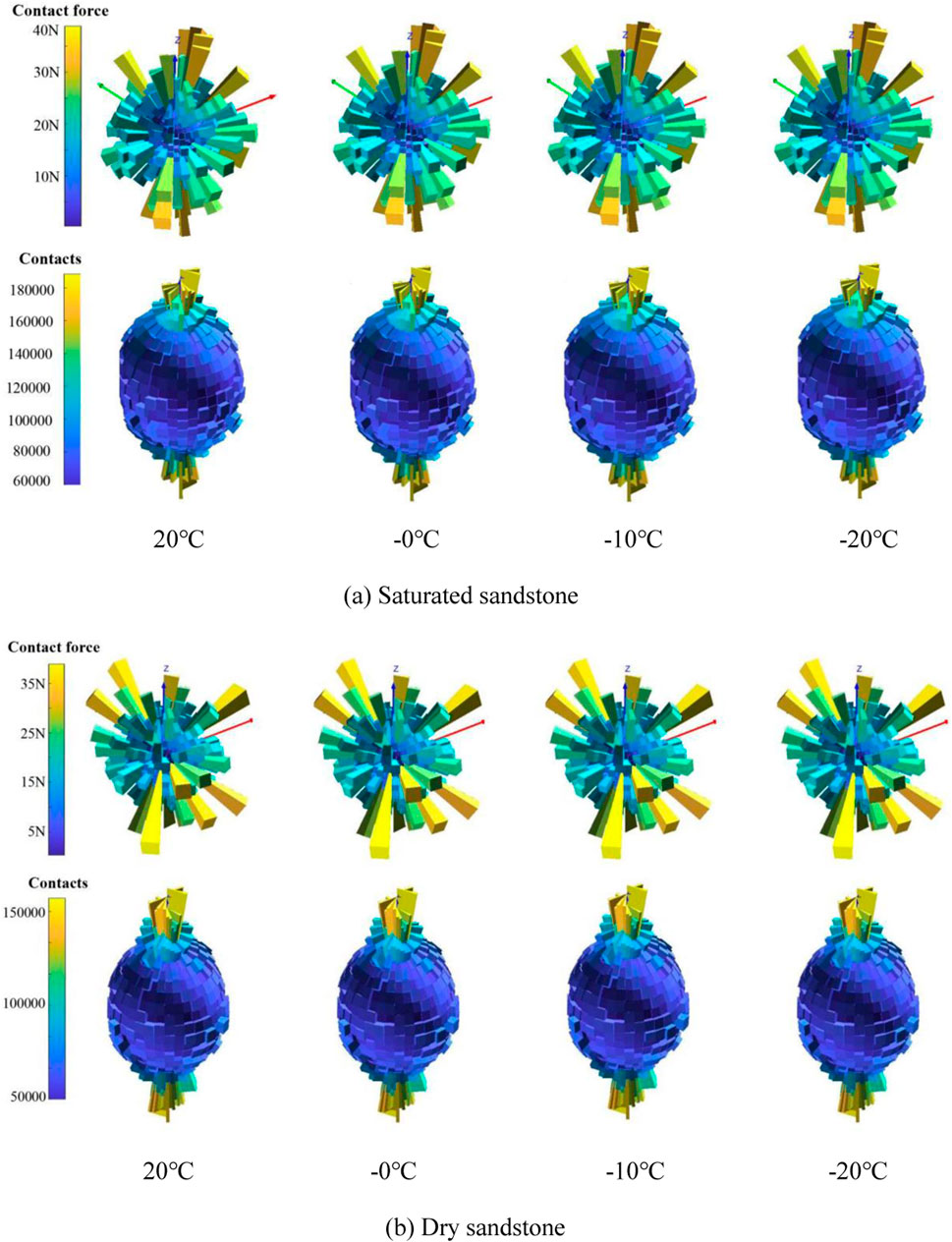
Figure 13. Distribution of contact force and contact amount between particles during sandstone freezing process. (A) Saturated sandstone, (B) Dry sandstone.

Table 7

Table 7. Contact force and contact amount between particles in the process of sandstone freezing.

In summary, within the temperature range of 20°C to −20°C, both types of rocks exhibited distinct variations in the maximum contact force and contact quantity. In different temperature ranges, varying effects on the deformation of rock and water particles were obtained, which affected the maximum contact force and contact quantity. Laboratory tests revealed that porphyry possessed larger internal pores, and more water particles were introduced into the models of both saturated porphyry and saturated sandstone. Conversely, the water-saturated sandstone involved dense particle, smaller pores, fewer water particles, and more rock particles. Consequently, the contact force and quantity between particles in the water-saturated sandstone were significantly higher than those in the saturated porphyry. The freezing effect on the two dry specimens was minimal, whereas it was more pronounced in the water-saturated specimens. This indicated the substantial impact of water particles on freeze damage during the freezing process of the two rock types, which could be further evident when comparing the changes in static and dynamic strengths between frozen specimens and those at normal temperatures. In addition, the extent of frost heave deformation varied among water-saturated rocks with different porosity levels. The freezing effect had a minimal impact on dense sandstone due to its limited water absorption ability. In contrast, porphyry specimens with higher porosity experienced a more pronounced influence. Moreover, the degree of freezing damage was temperature dependent. For instance, porphyry specimens exhibit increased strength at −10°C, while there was noticeable freezing damage at −20°C. However, sandstone specimens at −20°C did not exhibit evident freeze damage.

5 Conclusion

A frozen SHPB test was conducted on two representative rock specimens from Yulong Copper Mine. The analysis encompassed the evaluation of dynamic strength, stress-strain behavior, and the development of a dynamic constitutive model that incorporated the initial damage effect. Additionally, the microscopic damage features during the freezing process were investigated using the PFC3D software, leading to a discussion on the strength disparities between the two specimens. The primary conclusions are as follows.

(1) The impact of subzero temperatures was more significant in saturated specimens than in dry specimens, and there were distinct variations in the impacts on the dynamic strength of these two types of specimens. Frost heaving at −10°C resulted in an increase in the strength of both saturated specimens, with saturated sandstone specimens displaying a more noticeable strength enhancement than that of the dry specimens. Conversely, at −20°C, frost heave caused evident damage to the porphyry specimens, while its effect on sandstone was minimal. Notably, at this temperature, the R_DIF value for sandstone samples closely was similar to that observed at −10°C, whereas the R_DIF value for porphyry specimens decreased.

(2) The dynamic constitutive equation considering damage effectively reflected the stress-strain behaviors of sandstone and porphyry specimens. It also accurately represented the dynamic modulus and peak strain characteristics of both specimens. Furthermore, the fitting parameters of the dynamic constitutive equation aligned with the practical observations. Notably, the sandstone specimens exhibited a higher dynamic modulus and smaller peak strain in comparison.

(3) The established PFC^3D model for frozen rock effectively captured the variations in mesoscopic characteristics during the freezing process of both rock types. The maximum contact force and contact quantity between particles were affected by the deformation of both the rock and water particles and were related to temperature. Under negative temperatures, the rock strength was enhanced. Concurrently, frost heave deformation induced microscopic damage. Notably, the frost heave deformation of water particles significantly affected specimen damage. There emerged a critical frost heaving temperature at which the increase in freezing strength was counterbalanced by localized freezing damage, resulting in maximum specimen strength at that specific temperature.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

XS: Resources, Writing–original draft. LC: Data curation, Formal Analysis, Writing–original draft. XY: Funding acquisition, Writing–review and editing. ZZ: Software, Writing–review and editing. WM: Investigation, Methodology, Writing–review and editing. AQ: Investigation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was financially supported by Scientific Research Foundation for High-level Talents of Anhui University of Science and Technology (2021yjrc31), State Key Laboratory of Safety Intelligent Mining in Non-coal Open-pit Mines, National Mine Safety Administration (2024-K04) and Anhui Provincial Natural Science Foundation (2208085QE174).

Conflict of interest

Author XS was employed by Hongda Blasting Engineering Group Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Feng, Q., Hou, S., Liu, W., Zhang, S., Li, W., and Tian, M. (2023). Study on the simulation method and mesoscopic characteristics of rock freeze-thaw damage. Comput. Geotechnics 153, 105038. doi:10.1016/j.compgeo.2022.105038

CrossRef Full Text | Google Scholar

Guo, C., Zhang, Y., Zhang, Y., Wu, Z., Li, X., Wu, R., et al. (2023). Freeze-thaw cycle effects on granite and the formation mechanism of long-runout landslides: insights from the Luanshibao case study in the Tibetan Plateau, China. Bull. Eng. Geol. Environ. 82, 394. doi:10.1007/s10064-023-03427-6

CrossRef Full Text | Google Scholar

Huang, C., Zhu, C., Ma, Y., and Aluthgun Hewage, S. (2022). Investigating mechanical behaviors of rocks under freeze–thaw cycles using discrete element method. Rock Mech. Rock Eng. 55 (12), 7517–7534. doi:10.1007/s00603-022-03027-y

CrossRef Full Text | Google Scholar

Inada, Y., and Yokota, K. (1984). Some studies of low temperature rock strength. Int. J. rock Mech. Min. Sci. and geomechanics Abstr. 21 (3), 145–153. doi:10.1016/0148-9062(84)91532-8

CrossRef Full Text | Google Scholar

Jia, H., Ding, S., Wang, Y., Zi, F., Sun, Q., and Yang, G. (2019). An NMR-based investigation of pore water freezing process in sandstone. Cold Regions Sci. Technol. 168, 102893. doi:10.1016/j.coldregions.2019.102893

CrossRef Full Text | Google Scholar

Ke, B., Zhou, K., Xu, C., Deng, H., Li, J., and Bin, F. (2018). Dynamic mechanical property deterioration model of sandstone caused by freeze–thaw weathering. Rock Mech. Rock Eng. 51, 2791–2804. doi:10.1007/s00603-018-1495-0

CrossRef Full Text | Google Scholar

Li, J., Zhang, J., Yang, X., Zhang, A., and Yu, M. (2023). Monte Carlo simulations of deformation behaviour of unbound granular materials based on a real aggregate library. Int. J. Pavement Eng. 26 (1), 2165650. doi:10.1080/10298436.2023.2165650

CrossRef Full Text | Google Scholar

Li, J., Zhang, G., Liu, M., Hu, S., and Zhou, X. (2020). Constitutive model of water-saturated marble under coupling effects of uniaxial impact compressive loading and low-temperature. Acta Geodyn. Geomaterialia 17 (2), 157–168. doi:10.13168/AGG.2020.0011

CrossRef Full Text | Google Scholar

Lin, G., Li, M., Chen, Y., Zhang, J., Jiskani, I. M., Doan, D. V., et al. (2021). Dynamic tensile mechanical properties and fracture characteristics of water-saturated sandstone under the freezing effect. Int. J. Geomechanics 21 (5), 04021044. doi:10.1061/(ASCE)GM.1943-5622.0001999

CrossRef Full Text | Google Scholar

Lin, H., Lei, D., Yong, R., Jiang, C., and Du, S. (2020). Analytical and numerical analysis for frost heaving stress distribution within rock joints under freezing and thawing cycles. Environ. Earth Sci. 79, 305–317. doi:10.1007/s12665-020-09051-x

CrossRef Full Text | Google Scholar

Liu, C., Wang, D., Wang, Z., Ke, B., and Yu, S. (2021). Dynamic splitting tensile test of granite under freeze-thaw weathering. Soil Dyn. Earthq. Eng. 140, 106411. doi:10.1016/j.soildyn.2020.106411

CrossRef Full Text | Google Scholar

Luo, Y., Qu, D., Wang, G., Li, X., and Zhang, G. (2020). Degradation model of the dynamic mechanical properties and damage failure law of sandstone under freeze-thaw action. Soil Dyn. Earthq. Eng. 132, 106094. doi:10.1016/j.soildyn.2020.106094

CrossRef Full Text | Google Scholar

Ma, Q., Ma, D., and Yao, Z. (2018). Influence of freeze-thaw cycles on dynamic compressive strength and energy distribution of soft rock specimen. Cold Regions Sci. Technol. 153, 10–17. doi:10.1016/j.coldregions.2018.04.014

CrossRef Full Text | Google Scholar

Meng, F., Zhai, Y., Li, Y., Xie, Q., Gao, H., Li, Y., et al. (2023). Research on deterioration mechanism and dynamic triaxial compression characteristics of freeze–thaw sandstone. Rock Mech. Rock Eng. 56 (3), 2333–2355. doi:10.1007/s00603-022-03172-4

CrossRef Full Text | Google Scholar

Pu, Q., Huang, J., Zeng, F., Luo, Y., Li, X., Zhou, J., et al. (2020). Study on long-term dynamic mechanical properties and degradation law of sandstone under freeze-thaw cycle. Shock Vib. 2020, 1–10. doi:10.1155/2020/8827169

CrossRef Full Text | Google Scholar

Renliang, S., Yongwei, S., Liwei, S., and Yao, B. (2019). Dynamic property tests of frozen red sandstone using a split hopkinson pressure bar. Earthq. Eng. Eng. Vib. 18, 511–519. doi:10.1007/s11803-019-0518-5

CrossRef Full Text | Google Scholar

Wang, L., Su, H., Chen, S., and Qin, Y. (2020a). Nonlinear dynamic constitutive model of frozen sandstone based on Weibull distribution. Adv. Civ. Eng. 2020. doi:10.1155/2020/6439207

CrossRef Full Text | Google Scholar

Wang, L., Su, H., Qin, Y., and Chen, S. (2020b). Study on dynamic constitutive model of weakly consolidated soft rock in western China. Shock Vib. 2020, 1–13. doi:10.1155/2020/8865013

CrossRef Full Text | Google Scholar

Wang, T., Li, P., Tang, C., Zhang, B., and Yu, J. (2023). Finite element analysis for the mechanism of stress wave propagation and crack extension due to blasting of a frozen rock mass. Sustainability 15 (5), 4616. doi:10.3390/su15054616

CrossRef Full Text | Google Scholar

Wang, T., Sun, Q., Jia, H., Shen, Y., and Li, G. (2022). Fracture mechanical properties of frozen sandstone at different initial saturation degrees. Rock Mech. Rock Eng. 55, 3235–3252. doi:10.1007/s00603-022-02830-x

CrossRef Full Text | Google Scholar

Wen, M., Xu, J., Wang, H., Fang, X., and Zheng, G. (2017). Fractography analysis of sandstone failure under low temperature-dynamic loading coupling effects. Chin. J. Rock Mech. Eng. 36 (s2), 3822–3830. doi:10.13722/j.cnki.jrme.2017.0514

CrossRef Full Text | Google Scholar

Weng, L., Wu, Z., and Liu, Q. (2020). Dynamic mechanical properties of dry and water-saturated siltstones under sub-zero temperatures. Rock Mech. Rock Eng. 53, 4381–4401. doi:10.1007/s00603-019-02039-5

CrossRef Full Text | Google Scholar

Weng, L., Wu, Z., Liu, Q., and Wang, Z. (2019). Energy dissipation and dynamic fragmentation of dry and water-saturated siltstones under sub-zero temperatures. Eng. Fract. Mech. 220, 106659. doi:10.1016/j.engfracmech.2019.106659

CrossRef Full Text | Google Scholar

Weng, L., Zhang, H., and Zhang, Y. (2022). Dynamic mechanical properties and the constitutive models of the water-saturated siltstones under frozen conditions. Chin. J. Appl. Mech. 39 (06), 1096–1107+1134. (In Chinese). doi:10.11776/j.issn.1000-4939.2022.06.010

CrossRef Full Text | Google Scholar

Yamabea, T., and Neaupane, K. M. (2001). Determination of some thermo-me-chanical properties of Sirahama sandstone under subzero temperature condition. Int. J. Rock Mech. Min. 38 (7), 1029–1034. doi:10.1016/S1365-1609(01)00067-3

CrossRef Full Text | Google Scholar

Yang, B., Qin, S., Xue, L., and Chen, H. (2021). The reasonable range limit of the shape parameter in the Weibull distribution for describing the brittle failure behavior of rocks. Rock Mech. Rock Eng. 54, 3359–3367. doi:10.1007/s00603-021-02414-1

CrossRef Full Text | Google Scholar

Yang, Y., and Yang, R. (2019). “Frostbite effect”of red sandstone under high strain rates. Chin. J. Eng. 41 (10), 1249–1257. (In Chinese). doi:10.13374/j.issn2095-9389.2019.01.14.002

CrossRef Full Text | Google Scholar

Zhai, Y., Meng, F., Li, Y., Zhao, R., and Zhang, Y. (2022). Research on dynamic compression failure characteristics and damage constitutive model of sandstone after freeze–thaw cycles. Eng. Fail. Anal. 140, 106577. doi:10.1016/j.engfailanal.2022.106577

CrossRef Full Text | Google Scholar

Zhou, Y., Ma, W., Tan, X., Chen, W., Yang, D., Su, Z., et al. (2021a). Numerical simulation of fracture propagation in freezing rocks using the extended finite element method (XFEM). Int. J. Rock Mech. Min. Sci. 148, 104963. doi:10.1016/j.ijrmms.2021.104963

CrossRef Full Text | Google Scholar

Zhou, Z., E, Y., Cai, X., and Zhang, J. (2021b). Coupled effects of water and low temperature on quasistatic and dynamic mechanical behavior of sandstone. Geofluids 2021, 1–12. doi:10.1155/2021/9926063

CrossRef Full Text | Google Scholar