Room temperature magnetoelectric magnetic spirals by design

Frustrated magnets with ordered magnetic spiral phases that spontaneously break inversion symmetry have received significant attention from both fundamental and applied sciences communities due to the experimental demonstration that some of these materials can couple to the lattice and induce electric polarization. In these materials, the common origin of the electric and magnetic orders guarantees substantial coupling between them, which is highly desirable for applications. However, their low-magnetic ordering temperatures (typically $<$ 100 K) greatly restrict their fields of application. Recently, investigations on Cu/Fe-based layered perovskites uncovered an unexpected knob to control the stability range of a magnetic spiral-chemical disorder-, which has been successfully employed to stabilize magnetic spiral phases at temperatures as high as 400 K. These unexpected observations, which are hard to conciliate with traditional magnetic frustration mechanisms, were recently rationalized in terms of an original, local frustration model that explicitly accounts for the presence of disorder. In this mini-review, we summarize the main experimental observations on Cu/Fe layered perovskites, which show excellent agreement with the predictions of this novel magnetic frustration mechanism. We also present different strategies aimed at exploiting these experimental and theoretical developments for the design of materials featuring magnetoelectric spirals stable up to temperatures high enough for daily-life applications.

1 Introduction

The spiral is a common pattern in nature and can be found in items as diverse as snail shells, pea tendrils, galaxies, and DNA. One of the distinctive characteristics of spirals is the presence of chirality, a term introduced by Lord Kelvin for describing objects that cannot be superimposed on their mirror image (Thomson, 1894; Kelvin, 1904). Chirality is of enormous importance in biology, chemistry, and physics (Wagnière, 2007; Lee and Yang, 1956; Lee et al., 1957; Balents and Fisher, 1996; Emori et al., 2013; Everschor-Sitte et al., 2018; Taguchi et al., 2001; Tokura et al., 2014), with various definitions used across different (sub)disciplines (Simonet et al., 2012; Fecher et al., 2022; Cheong and Xu, 2022). In the context of spin networks, which includes the magnetic spirals discussed in this mini-review, the word chirality is usually employed as a synonym of helicity, a vector quantity (${\mathbf{S}}_i$ $\times$ ${\mathbf{S}}_j$) that indicates the direction of rotation of two consecutive spins ${\mathbf{S}}_i$ and ${\mathbf{S}}_j$ along an oriented link. Spin spirals are relatively uncommon among magnetically ordered phases, but they can be stabilized in certain materials as a result of the presence of competing magnetic interactions between magnetic moments that cannot be simultaneously satisfied (Herpin, 1968). Until very recently, the interest in these objects was limited to the scientific community working on frustrated magnetism. However, they are now also in the focus of applied sciences due to the experimental demonstration that, in insulators, certain magnetic spirals can couple to the lattice and induce electric polarization P in the absence of external electric (E) or magnetic (H) stimuli. This was first reported for TbMn${\text{O}}_3$, which develops spontaneous electric polarization P and gigantic dielectric anomalies when the M${\text{n}}^{3+}$ magnetic moments order into a cycloidal spiral below $T_{\text{spiral}}$ = 28 K (Kimura et al., 2003), and other materials exhibiting similar behavior followed soon after (Lawes et al., 2005; Kimura et al., 2006; Arkenbout et al., 2006; Kimura et al., 2008; Johnson et al., 2012). The control of the electric polarization orientation with magnetic fields (Kimura et al., 2005; Taniguchi et al., 2006) and the spiral’s sense of rotation with electric fields (Cabrera et al., 2009; Finger et al., 2010; Babkevich et al., 2012) were also demonstrated. These discoveries—particularly the possibility of using electric fields for controlling the magnetic state—raised great expectations regarding the possible use of magnetoelectric (ME) cross-control in a number of technological applications, and have been the subject of some excellent reviews (Kimura, 2007; Tokura et al., 2014). At the same time, a number of questions arose, including the origin of this phenomenon and possible strategies for designing materials featuring magnetoelectric spirals suitable for applications (Fiebig et al., 2016; Spaldin and Ramesh, 2019; Liang et al., 2021).

2 Status and challenges for magnetoelectric magnetic spirals

For a large number of insulating spiral magnets, the generation of polarization is believed to originate from spin-orbit (SO) splitting on the magnetic ions (Katsura et al., 2005; Mostovoy, 2006; Sergienko and Dagotto, 2006); this exchange coupling can result in polar charge displacements when the magnetic order exhibits non-vanishing torques ${\mathbf{S}}_i$ $\times$ ${\mathbf{S}}_j$ between neighboring magnetic moments ${\mathbf{S}}_i$ and ${\mathbf{S}}_j$, as found in spiral patterns (Figure 1A). A spin pair at (${\mathbf{r}}_i$, ${\mathbf{r}}_j$) contributes to the polarization by the double cross product P $\sim$ (${\mathbf{r}}_i$ − ${\mathbf{r}}_j$) $\times$ ${\mathbf{S}}_i$ x ${\mathbf{S}}_j$, a condition that requires the spins to rotate in a plane that is not perpendicular to the spiral propagation vector ${\mathbf{k}}_s$. The spirals satisfying this condition are known as cycloids, while those that do not are called proper spirals (Figure 1B). Proper spirals can also induce polarization in some particular cases, but this requires both SO coupling and a particular crystal lattice symmetry (Kimura et al., 2006; Kurumaji et al. (2011, 2013)). In the case of $S=\frac{1}{2}$ chain helical magnets, where quantum fluctuations are believed to influence the ME response, the details of the magnetic order and origin of the polarization are still under debate (Seki et al. (2008, 2010); Zhao et al., 2012).

Figure 1

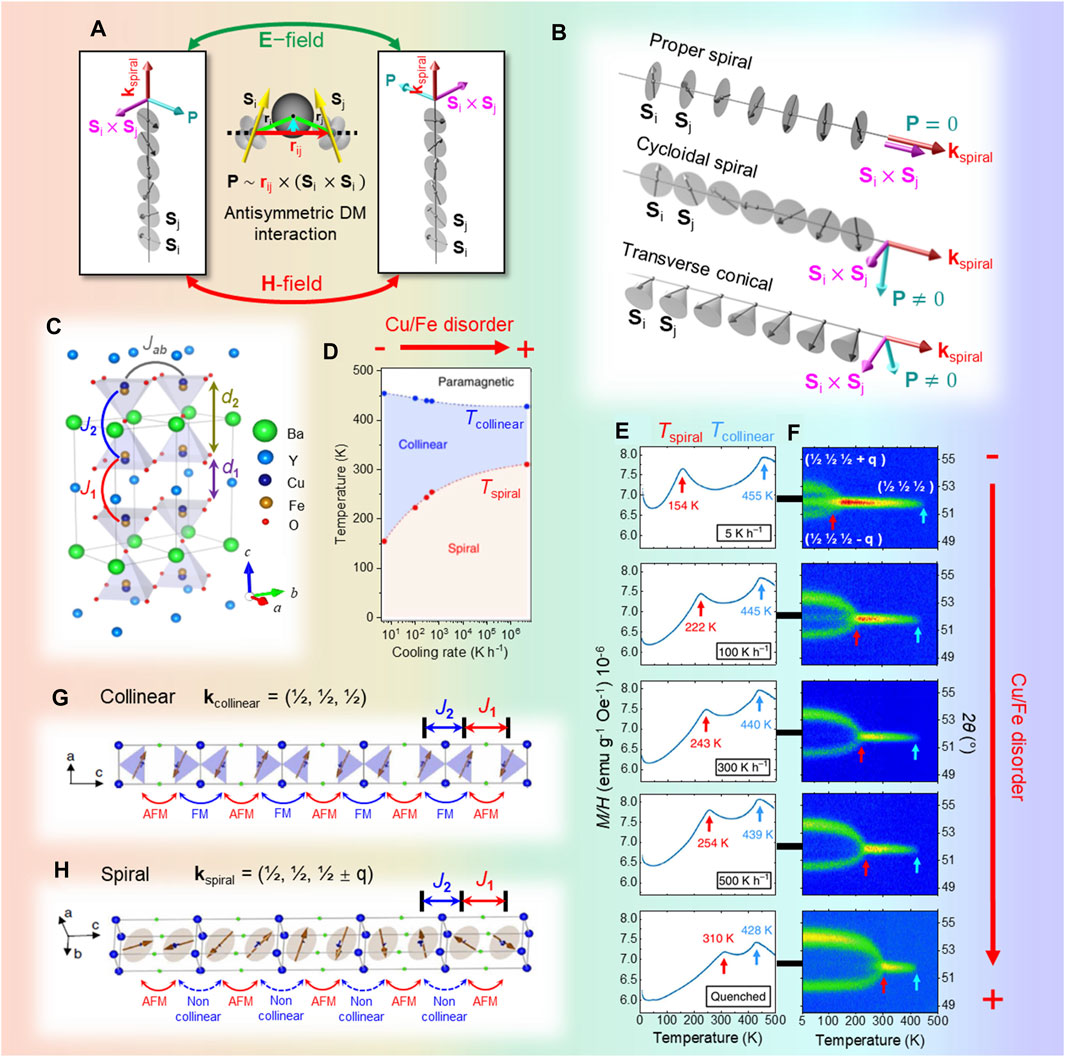
Figure 1. (A) Illustration of the coupling between magnetic chirality and electrical polarization driven by the antisymmetric Dzyaloshinskii–Moriya (DM) interaction under electric $(E)$ and magnetic $(H)$ fields. (B) Examples of magnetic spiral structures. Only spiral structures with a cycloidal component may give rise to polarization. (C) Crystal structure of YBaCuFeO₅ showing the Cu/Fe disorder in the bipyramidal layers, d₁ and d₂ interatomic distances, and nearest-neighbor magnetic couplings J₁, J₂ and J_ab. (D) Phase diagram showing temperature dependence of collinear and spiral phases with varying cooling rates (i.e., Cu/Fe disorder) (Morin et al., 2016). (E, F) Evolution of the collinear and spiral magnetic transitions in YBaCuFeO₅ with increasing Cu/Fe disorder, observed from the temperature dependence of the magnetic mass susceptibility (E) and the positions and intensities of the magnetic Bragg reflections (F): $\left(\frac{1}{2}\frac{1}{2}\frac{1}{2}\right)$ associated with the high-temperature collinear antiferromagnetic phase and $\left(\frac{1}{2}\frac{1}{2}\frac{1}{2}\pm q\right)$ satellites corresponding to the low-temperature magnetic spiral phase, as measured by powder neutron diffraction (Morin et al., 2016). (G, H) Magnetic structures in the commensurate collinear (G) and spiral (H) phases (Morin et al., 2016).

Despite their promising multifunctionalities, three main shortcomings have hindered the implementation of magnetic spirals able to create polarization (henceforth magnetoelectric spirals) in real devices. One of them is that they do not have a net magnetization M, a characteristic that makes the magnetic detection of the spiral rotation sense, directly related to P, more difficult than the M sense in ferromagnets. A more favorable situation is found in transverse conical cycloids, characterized by a ferromagnetic (FM) component perpendicular to the cycloid rotation plane that guarantees the simultaneous presence of spontaneous M and P (Figure 1B) (Yamasaki et al., 2006; White et al., 2012). Unfortunately, conical magnets are often not stable in the absence of a magnetic field (Murakawa et al., 2008; Kitagawa et al., 2010; Ramakrishnan et al., 2019). Another important drawback is the low polarization values reported for ME spirals, typically far below 1 $\mu$C/cm², which is considered the minimum limit for applications (Scott, 2013; Tokura et al., 2014). This is a consequence of (usually) rather weak SO interactions in these materials, which result in modest charge displacements. However, the main limitation is perhaps the very low magnetic ordering temperatures $T_{\text{spiral}}$ of most known spiral magnets, typically lower than 100 K. The underlying reason is that the spiral order requires the presence of magnetic frustration, characterized by magnetic interactions that cannot be satisfied simultaneously (Herpin, 1968). Such frustration can have a geometrical origin or arise from a competition between nearest-neighbor (NN) J and next-nearest neighbor (NNN) magnetic interactions J’. In the first case, the large degeneracy of the ground state drastically lowers the ordering temperature, even in the presence of large NN couplings. In the second case, J and J′ should have comparable strengths, but in insulators (metals cannot sustain P), J′ is usually much smaller than J. As a consequence, magnetic spirals generally appear in materials with small NN couplings, and this naturally leads to low $T_{\text{spiral}}$ values (Goodenough, 1963). The main challenge in magnetoelectric spiral magnet research is thus to identify design principles to obtain materials with magnetic spiral phases stable well above room temperature (RT) and spin-orbit coupling large enough to induce significant polarization.

3 Stabilizing magnetic spirals far beyond RT

3.1 Chemical disorder as a tool for $T_{\mathrm{spiral}}$ control

Recently, an unexpected knob for controlling both the ordering temperature and periodicity of a magnetic spiral has emerged: chemical disorder. The positive impact of this variable on $T_{\mathrm{spiral}}$ was first demonstrated in YBaCuFeO₅ (Morin et al., 2016), a simple layered perovskite whose crystal structure is shown in Figure 1C. This material was first synthesized in the 1980s (Er-Rakho et al., 1988) and was mostly investigated in connection with the structurally related high-temperature superconductor YBa₂Cu₃${\text{O}}_{6+\delta }$ (Meyer et al., 1990; Atanassova et al., 1993; Diko et al., 1993; Mombru et al., 1994). However, it has received renewed attention after the recent reports of spontaneous polarization, dielectric anomalies, and magnetoelectric effects linked to the presence of spiral magnetic order at temperatures as high as 230 K (Kundys et al., 2009; Kawamura et al., 2010; Morin et al., 2015). YBaCuFeO₅ is thus one of the rare insulating oxides where the spiral magnetic order can be stabilized at temperatures close to RT in the absence of a magnetic field. However, what makes this material truly exceptional compared with the other few exceptions [CuO (Kimura et al., 2008), and some hexaferrites if we also include transverse conical cycloids (Kimura, 2012)], is the extraordinary tunability of its spiral ordering temperature, which can be enhanced by more than 250 K upon a modest increase in the Cu/Fe chemical disorder (Morin et al., 2016; Romaguera et al., 2022). As shown in Figure 1C, the tetragonal unit cell (space group P4mm) contains two pseudocubic unit cells whose A-cations (Ba²⁺ and Y³⁺) order in layers perpendicular to the c crystal axis, owing to their large difference in ionic radii. Cu²⁺ and Fe³⁺, more similar in size, occupy the B-positions within the bipyramidal units, but contrary to the A-cations, they are usually disordered (Caignaert et al., 1995; Morin et al., 2015). This is illustrated by the splitting of the two cation positions within the pyramids, where Cu and Fe have slightly different $z$-coordinates. An important characteristic of the Cu/Fe disorder in YBaCuFeO₅ is that it is not random. Instead, the bipyramids are preferentially occupied by Cu–Fe pairs, and these Cu–Fe “dimers” are disordered in the structure (Caignaert et al., 1995; Morin et al., 2015). The degree of disorder is usually described in terms of the probabilities $n_{\text{Cu}}$ and $n_{\text{Fe}}$ of finding Cu and Fe within a pyramid ($n_{\text{Cu}}$ = $n_{\text{Fe}}$ = 50$\%$ for full disorder), which can be determined by diffraction techniques. The parameters $n_{\text{Cu}}$ and $n_{\text{Fe}}$ can be experimentally controlled by different methods, including adjusting the cooling speed of the sample after the last annealing (Figures 1D–F). Remarkably, modest changes in the degree of Cu/Fe disorder have a gigantic impact on $T_{\mathrm{spiral}}$, which can be increased up to 310 K by quenching the samples in liquid nitrogen (Morin et al., 2016) and up to 390 K by quenching them in water (Romaguera et al., 2022).

To understand this surprising behavior, it is worth mentioning that the magnetic order expected from the Goodenough–Kanamori–Anderson (GKA) superexchange rules, consistent with the NN exchanges calculated using density functional theory (DFT) (Morin et al., 2015), is not a spiral but a collinear antiferromagnetic (AFM) arrangement described by the propagation vector ${\mathbf{k}}_c$ = $\left(\frac{1}{2},\frac{1}{2},\frac{1}{2}\right)$ (Mombru et al., 1994). This magnetic structure, shown in Figure 1G, is indeed experimentally observed in YBaCuFeO₅ but only at high temperatures $(T_{\text{collinear}}>T>T_{\text{spiral}})$. At low temperatures $\left(T<T_{\text{spiral}}\right)$, the propagation vector changes to ${\mathbf{k}}_s$ = $\left(\frac{1}{2},\frac{1}{2},\frac{1}{2}\pm q\right)$ and the magnetic order transforms into an inclined spiral that is incommensurate with the crystal lattice along the c-axis (Caignaert et al., 1995; Mombru et al., 1998; Ruiz-Aragón et al., 1998; Morin et al. (2015, 2016); Lai et al., 2017; Romaguera et al., 2022; Lai et al., 2024). As shown in Figures 1H, 2D, this spiral is not a pure cycloid; however, it has a nonzero cycloidal component that can induce ferroelectricity.

Figure 2

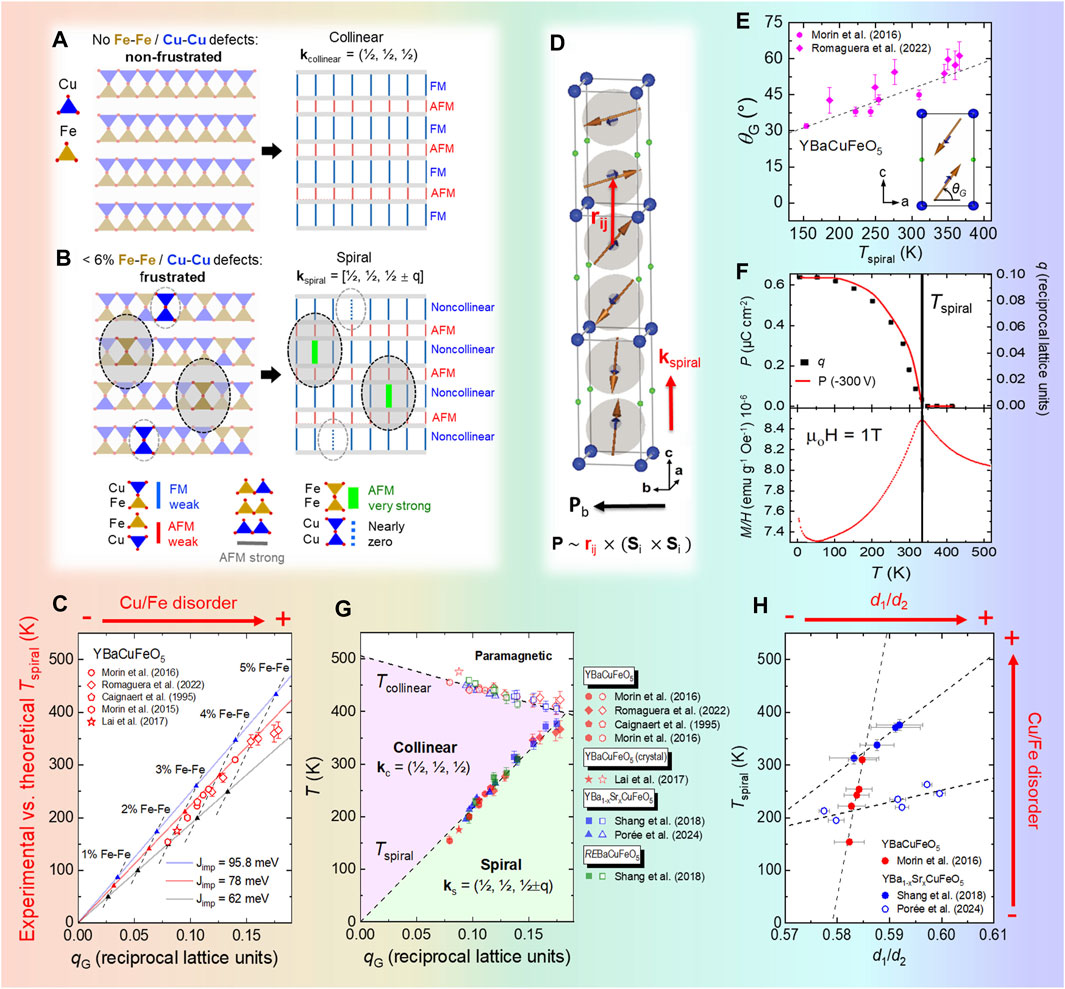
Figure 2. (A, B) Scheme of Cu/Fe disorder’s impact on the magnetic order in YBaCuFeO₅. Perfect Cu/Fe order (A) leads to collinear AFM order, while introducing AFM Fe–Fe “defects” (B) leads to frustrated exchanges, causing spiral order. (C) Linear correlation between $T_{\text{spiral}}$ and $q_{\text{G}}$ in YBaCuFeO₅ with increasing Cu/Fe disorder, compared to theoretical predictions for different Fe–Fe exchange strengths [adapted from Scaramucci et al. (2020)]. (D) Magnetic structure of the incommensurate spiral phase, showing the expected direction of the spin-induced electric polarization. (E) Positive correlation between spiral plane inclination $({\theta }_{\text{G}})$ and stability $(T_{\text{spiral}})$ with increasing Cu/Fe disorder. The inset shows the $\theta$ tilt relative to the a-axis. (F) Temperature dependence of electric polarization, magnetic susceptibility, and incommensurability $(q)$ of the spiral in YBaCuFeO₅ [adapted from Morin et al. (2015; 2016)]. (G) Magnetic phase diagram showing the linear relationship between the ($T_{\text{spiral}}$, $q_{\text{G}}$) points in three families of AA’CuFeO₅-layered perovskites: YBaCuFeO₅ with different disorders, ${\text{YBa}}_{1\text{x}}{\text{Sr}}_{\text{x}}$CuFeO₅ $(0\le x\le 0.5)$ and $RE$BaCuFeO₅ ($RE$ = Lu to Dy). Open symbols corresponding to $T_{\text{collinear}}$ illustrate its convergence with $T_{\text{spiral}}$ at ∼400 K and $q_{\text{G}}\sim 0.18$. (H) Dependence of $T_{\text{spiral}}$ as a function of the $d_1$/$d_2$ ratio for YBaCuFeO₅ with increasing disorder and two ${\text{YBa}}_{1\text{x}}{\text{Sr}}_{\text{x}}$CuFeO₅ series having a distinct, approximately constant disorder.

The emergence of a stable spiral phase in a material without any obvious source of magnetic frustration and the huge, positive impact of the Cu/Fe chemical disorder on the spiral ordering temperature were both puzzling and difficult to conciliate with traditional magnetic frustration mechanisms. Interestingly, both observations could be recently rationalized in terms of a novel, disorder-based frustration mechanism based on the gigantic impact of a few Fe–Fe “defects” occupying the bipyramidal units (Scaramucci et al. (2018, 2020)). Such defects are energetically very expensive, but their presence in small amounts (together with the same number of Cu–Cu defects to preserve electric neutrality) cannot be disregarded in real samples, in particular in those with large amounts of Cu/Fe disorder (Figures 2A, B). As mentioned previously, the bipyramidal units are preferentially occupied by Cu–Fe pairs, whose NN exchange $J_{\text{Cu–Fe}}$ is ferromagnetic (FM) and weak ($\sim$ 2 meV). The exchange $J_{\text{Cu–Cu}}$ within a Cu–Cu defect is also very weak ($\sim$ 0.1 meV). In contrast, the exchange $J_{\text{Fe}-\text{Fe}}$ between the two Fe³⁺ moments of a Fe–Fe defect is AFM and $\sim$ 40 times stronger ($\sim$ 80 meV). A tiny defect concentration thus constitutes a gigantic perturbation of the underlying collinear order that can extend over several unit cells (Figure 2B). Scaramucci et al. (2018, 2020) reported that this perturbation can become collective and stabilize long-range spiral order as long as the impurity concentration $n$ remains modest and the Fe–Fe defects avoid certain arrangements, such as clustering.

Within this model, both $T_{\text{spiral}}$ and the ground-state incommensurate part of the propagation vector $q_G$ are proportional to the Fe–Fe defect concentration $n$. Moreover, $T_{\text{spiral}}$ is a linear function of $q_G$ that crosses the origin. Given the difficulty of accessing $n$ experimentally, this is a very important prediction regarding model validation because it relies exclusively on variables—$T_{\text{spiral}}$ and $q_Q$—that can be determined by experimental methods (Figures 1E,F). As shown in Figure 2C, this prediction is verified by all the YBaCuFeO₅ samples reported in the literature to a very good approximation. Moreover, the highest values of both variables are observed for the samples with the largest degree of Cu/Fe disorder (i.e., those where $n$ is expected to be the highest). The slope of the experimental $T_{\text{spiral}}$ versus $q_{\text{G}}$ line, which in the framework of this theory depends exclusively on $J_{\text{Fe}-\text{Fe}}$ and the NN exchange constants ($J_1$, $J_2$, and $J_{ab}$, Figures 1C, 2B), also agrees very well with the slope calculated using the NN exchanges obtained from DFT. This allows us to estimate the defect concentration of a sample from its $T_{\text{spiral}}$ value, which can be easily measured by bulk magnetometry. Figure 2C shows that Fe–Fe defects with $J_{\text{Fe}-\text{Fe}}$ = 78 meV and concentrations between $\sim$ 2$\%$ and $\sim$ 6$\%$ are enough to stabilize magnetic spirals with ordering temperatures between $\sim$ 150 and $\sim$ 400 K (Scaramucci et al., 2020).

An important question, not addressed by this theoretical model, is the relationship between $T_{\text{spiral}}$ and the ground-state inclination angle of the spiral rotation plane ${\theta }_G$ with respect to the ab plane. As shown in Figures 2D, E, this angle is 0$°$ in a proper spiral and 90$°$ in a perfect cycloid, and it is directly related to P. Experimentally, it has been found that YBaCuFeO₅ samples with the largest ${\theta }_{\text{G}}$ angles (and hence the most sizable cycloidal components) are those with the highest spiral ordering temperatures (Morin et al., 2016; Romaguera et al., 2022) (Figure 2E). In other words, materials with the highest $T_{\text{spiral}}$ values are expected to also have the largest polarization. Given that the magnetic moment orientation is usually controlled by magnetic anisotropy, which is related to the orbital occupancies, this observation is unexpected for samples of identical chemical composition. Since the only difference between them is the degree of Cu/Fe disorder (and hence the Fe–Fe defect concentration), this finding suggests that the chemical disorder could impact magnetic anisotropy, but the precise mechanism remains to be investigated. Meanwhile, other attempts aiming to enhance the spin-orbit coupling through targeted partial B-cation replacements (such as Fe³⁺ with Mn³⁺) led to a substantial increase in the cycloidal component of the spiral, suggesting that this could be an interesting strategy to explore in the future (Zhang et al., 2021; Sharma and Maitra, 2023).

3.2 Adding A-cation substitutions

Although reaching high $T_{\text{spiral}}$ values in YBaCuFeO₅ requires “just” a synthesis procedure that can create large amounts of Fe–Fe defects, this can be experimentally challenging (Porée et al., 2024). As an alternative, the frustrating power of the defects can be enhanced through the modification of the $J_{\text{Fe}-\text{Fe}}$ strength. This can be achieved by reducing the size $d_2$ of the bipyramidal units (Figure 1C), which, due to the inverse relationship between exchange constants and interatomic distances, is expected to increase $J_{\text{Fe}-\text{Fe}}$. This strategy has been validated by the observation of a positive correlation between $T_{\text{spiral}}$ and the $d_1$/$d_2$ ratio, where $d_1$ is the separation between the bipyramids along the c-axis (Figure 1C) (Morin et al., 2016). This simple, purely empirical law turns out to be extremely useful. On one side, it opens the way to $T_{\text{spiral}}$ control with targeted A-cation substitutions, extending substantially the possibilities for magnetic spiral design. Moreover, if the substitutions are isovalent, $J_1$, $J_2$, and $J_{ab}$ do not change sign and their modifications are moderate, allowing the A-substituted materials to remain within the premises of the random frustrating exchanges model. This approach has been successfully employed in the YB${\text{a}}_{1-x}$S${\text{r}}_x$CuFeO₅ series, where the progressive replacement of Ba²⁺ with Sr²⁺ results in smaller $d_2$ values that increase both $d_1$/$d_2$ and $T_{\text{spiral}}$ (Shang et al., 2018). In the same study, large $d_1$/$d_2$ ratios were also engineered in $RE$BaCuFeO₅ series by replacing Y³⁺ with trivalent 4f cations (Lu³⁺ to Dy³⁺), whose growing ionic radii result in a continuous $d_1$ increase that increases both $d_1$/$d_2$ and $T_{\text{spiral}}$ (Figure 2G). Larger 4f cations (Tb³⁺ to La³⁺) could lead to even higher $T_{\mathit{spiral}}$ values, but their synthesis will require additional experimental work (reduction) due to their tendency to incorporate additional oxygen into the RE layers (Klyndyuk and Chizhova, 2006; Marelli et al., 2024).

A particularly interesting characteristic of the two spiral tuning mechanisms described in the previous sections—Cu/Fe disorder and $d_1$/$d_2$ control through A-cation isovalent substitutions—is that their impact on the spiral ordering temperature is additive: once the highest $T_{\text{spiral}}$ value is reached by tuning the $d_1$/$d_2$ ratio, it can be further increased by manipulating the Cu/Fe disorder. This is illustrated in Figure 2H, where we compare the evolution of $T_{\text{spiral}}$ with $d_1$/$d_2$ for two ${\text{YBa}}_{1-x}{\text{Sr}}_x$CuFeO₅ series with 0 $\le x<0.5$ prepared by quenching the samples after annealing at different temperatures (1,150$°$C and 980$°$C, respectively) (Shang et al., 2018; Porée et al., 2024). In both series, we observe a substantial increase in the $d_1$/$d_2$ ratio for growing Sr contents, which results in both cases in a monotonic $T_{\text{spiral}}$ growth. On the other side, the spiral ordering temperatures are more than 100 K higher for the samples quenched from 1,150$°$C, where the Cu/Fe disorder (and hence the density of Fe–Fe defects) is expected to be much higher. We can now compare these results with those reported for the YBaCuFeO₅ samples prepared with different cooling rates shown in Figures 1D–F (Morin et al., 2016). In this case, the $d_1$/$d_2$ ratio increases very little with the cooling rate, directly related to the degree of the Cu/Fe disorder. However, $T_{\text{spiral}}$ increases by more than 150 K, about two times more than in the ${\text{YBa}}_{1-x}{\text{Sr}}_x$ CuFeO₅ series ($\le$ 80 K), where the variation in the $d_1$/$d_2$ ratio is much more pronounced. These results highlight the exceptional efficiency of chemical disorder alone for $T_{\text{spiral}}$ tuning. On the other side, they also show that a good efficiency in terms of $T_{\text{spiral}}$ increase can also be reached by acting on the $d_1$/$d_2$ ratio. The combination of both mechanisms thus opens the possibility of tuning $T_{\text{spiral}}$ over unprecedentedly large temperature ranges, providing, at the same time, a versatile tool for stabilizing spin spirals at temperatures far beyond RT (Shang et al., 2018).

As shown in Figures 1D, E, the increase in $T_{\text{spiral}}$ is accompanied by a simultaneous decrease in the collinear order temperature. This is better appreciated in Figure 2G, showing the evolution of $T_{\text{spiral}}$ and $T_{\mathit{colinear}}$ with $q_G$ for all the AA’CuFeO₅ isovalent substitutions that, to our best knowledge, have been reported to date in the literature. Remarkably, all data points merge within two lines with very little dispersion. Within the theoretical model of references (Scaramucci et al. (2018, 2020)), the slopes of both lines depend exclusively on $J_{\text{FeFe}}$, $J_1$, $J_2$, and $J_{ab}$. Hence, this observation suggests that, for these samples, the model is robust against the variations in these constants associated with $d_1$/$d_2$ tuning. Another interesting observation is that both lines cross when $T_{\text{spiral}}$ = $T_{\text{collinear}}$ = $\sim$ 400 K. The region beyond the crossing point has not been investigated in detail, but both theory and the few available experimental studies suggest that the spiral state may not be stable beyond this point (Shang et al., 2018; Scaramucci et al., 2020; Romaguera et al., 2022; Porée et al., 2024). If this is confirmed, 400 K would be the highest $T_{\text{spiral}}$ value that can be reached in AA’CuFeO₅ layered perovskites by combining the Cu/Fe disorder with $d_1$/$d_2$ control through isovalent A-site substitutions.

3.3 Adding B-cation substitutions

Although 400 K is a value comfortably far from RT, a relevant question is whether magnetic spirals with higher $T_{\text{spiral}}$ upper limits could be stabilized in the layered perovskite structure. In particular, it will be interesting to know whether this can be accomplished through B-site substitutions. This strategy looks a priori less promising because depending on the electronic configuration of the chosen cations, both the sign and magnitude of the NN couplings can change substantially (Goodenough, 1963), eventually leading to a scenario that does not fit anymore the premises of the random frustrating exchanges model. An example of this situation is provided by the YBaCu${\text{Fe}}_{1-x}{\text{Mn}}_x$O₅ series reported by Zhang et al. (2021). Here, the partial replacement of Fe³⁺ with Mn³⁺ increases the $d_1$/$d_2$ ratio and even the cycloidal component of the spiral. However, it decreases $T_{\text{spiral}}$ due to the introduction of new, unfavorable exchanges within the bipyramids. Substituting the Jahn–Teller cation Cu²⁺ with other isovalent cations, preferably non-magnetic and non-Jahn–Teller (i.e., with shorter apical distances), may be more efficient. Low substitution levels of such cations can indeed substantially decrease the bipyramid size $d_2$ in such a way that the enhanced strength of the Fe–Fe defects compensates for the presence of new, non-favorable exchange couplings. This situation could be realized in the ${\text{YBaCu}}_{1-x}{\text{Mn}}_x$FeO₅, ${\text{YBaCu}}_{1-x}{\text{Ni}}_x$FeO₅, and ${\text{YBaCu}}_{1-x}{\text{Zn}}_x$FeO₅ series reported by Yasui et al. (2024), where magnetization data suggest a crossing of $T_{\text{spiral}}$ and $T_{\text{collinear}}$ close to 400 K for the three solid solutions. Neutron diffraction experiments, not reported in this work, will be necessary to confirm whether this is the case.

In the case of B-cation substitutions with a 1:1 B:B′ ratio, much easier to model theoretically than solid solutions, the theory developed by Scaramucci and co-workers provides some guidelines for material design. In addition to respecting electric neutrality, BB’-cation pair candidates should have comparable sizes in order to promote the presence of B-site disorder and display affinity for the square-pyramidal coordination. They should also comply with the premises of the random magnetic exchanges model, which requires having a single direction with weak, alternating FM and AFM exchanges, along with the experimental possibility of replacing the weak FM bonds with a small amount of strongly frustrating AFM defects. This scenario is realized in AA’CuFeO₅ layered perovskites, where the exchanges are very strong in the ab plane, weak FM $(J_2)$ and AFM $(J_2)$ bonds alternate along the c-axis, and $J_2$ can be replaced by small amounts of strongly frustrating AFM $J_{\mathit{defect}}$ = $J_{Fe-Fe}$ bonds (Figures 2A, B). Any other B-cation pair fulfilling these conditions could a priori be suitable for stabilizing a long-range magnetic spiral. Identifying such pairs, however, requires previous knowledge of the NN exchanges, whose sign and strength are strongly dependent on the B-cation electronic configuration. Since this information is usually not available and is difficult to obtain experimentally, DFT calculations could be a valuable alternative, which may allow screening a large number of material candidates with 3d, 4d, and even 5d cations in a fast, efficient way. We are not aware of any layered perovskite hosting 4d and/or 5d cations, but the presumably larger SO interactions in these materials could result in larger polarization values. For each potential candidate, $T_{\text{spiral}}$ and $T_{\text{collinear}}$ versus $q_G$ curves, whose crossing point defines the maximal value of the spiral ordering temperature, could be easily calculated because their slope depends exclusively on $J_1$, $J_2$, $J_{ab}$, and $J_{\mathit{defect}}$.

4 Next steps and perspectives

4.1 Polarization, magnetization, and magnetoelectric coupling

Despite the huge progress in $T_{\text{spiral}}$ tuning and material design made during the last 10 years, the ferroelectric and magnetoelectric properties of AA’CuFeO₅-layered perovskites have been barely investigated. As (nearly) all the reported materials feature spirals with cycloidal components, spontaneous polarization P is a priori expected to appear at the onset of the cycloidal order (Figure 2F). Observations in this regard have been reported for YBaCuFeO₅, YbBaCuFeO₅ and LuBaCuFeO₅ ceramic samples (Kundys et al., 2009; Kawamura et al., 2010; Morin et al., 2015) using the pyrocurrent method, although in some cases, the non-exact coincidence of $T_{\text{spiral}}$ with the polarization onset suggests the presence of leakage. Interestingly, some of the reported saturation polarization values reach 0.4–0.6 $\mu$C/cm², close to 1 $\mu$C/cm², considered the minimum for applications and much larger than the values reported for other spiral magnetoelectrics (Kimura, 2007; Scott, 2013; Tokura et al., 2014). Single crystals, less leaky than ceramics due to the absence of grain boundaries, will be necessary to confirm these results. Their growth, characterization, and $T_{\text{spiral}}$ control are unfortunately more difficult than those of polycrystalline samples. Large crystals synthesized using the floating zone method have been recently grown by two different groups (Lai et al., 2015; Zhang et al. (2021, 2022); Romaguera et al., 2023); so, progress in this area is expected in the near future. Single crystals should allow us to determine the polarization direction, presently unknown, which, according to the P $\sim$ (${\mathbf{r}}_i$ − ${\mathbf{r}}_j$) $\times$ ${\mathbf{S}}_i$ x ${\mathbf{S}}_j$ relationship, should lie in the ab plane (Figure 2D). They should also enable the use of techniques such as inelastic neutron scattering and 3D neutron polarimetry, which can provide direct information on the nature of the incommensurate magnetic order and the values of the exchange constants. They will also be crucial for investigating the magnetoelectric coupling, presently under debate (Dey et al., 2018), whose existence has been suggested by the changes in the polarization and the dielectric constant upon the application of magnetic fields on ceramic samples reported by Kundys et al. (2009); Luo and Wang (2018). Once these fundamental questions have been clarified, the next step will be to fabricate these materials as thin films, probably easier to grow than large single crystals due to the layered nature of these materials. Moreover, the similarity between their in-plane lattice parameters and those of many commercially available perovskite oxide substrates may allow a direct transfer of the material design strategies—Cu/Fe disorder and $d_1$/$d_2$ control—established for bulk materials, which could be combined with the usual strain control (Sando et al., 2013; Mukherjee et al., 2018).

Although AA’CuFeO₅-layered perovskites were believed to be purely AFM, the recent report of weak ferromagnetism (WFM) in YBaCuFeO₅ ceramic samples coexisting with the spiral modulation suggests that the ground-state magnetic order of these materials could be conical (Lyu et al., 2022). Since the measurements were performed on ceramic samples, the direction of the WFM component and its degree of coupling with the cycloid orientation, directly linked to P, are unknown. However, its appearance precisely at the onset of the spiral magnetic order strongly suggests the existence of some type of coupling between the spiral and WFM components. As ferromagnets respond strongly to external magnetic fields, this observation is extremely interesting because it could facilitate the detection and manipulation of the spiral rotation plane—and hence the polarization direction—with magnetic fields.

4.2 Beyond layered perovskites

The disorder-based local magnetic frustration mechanism proposed by Scaramucci and co-workers was initially developed for the layered perovskite YBaCuFeO₅. However, it could, with some modifications, also be relevant for other materials with different crystal structures. Possible material candidates could be identified among frustrated magnets with chemical disorders and incommensurate spiral phases stable up to medium-to-high temperatures whose origin is not understood. The hexaferrite ${\text{Ba}}_{1-x}{\text{Sr}}_x$Zn₂${\text{Fe}}_{12}$O₂₂ (Momozawa et al., 1985; Kimura, 2012) and ${\text{Cr}}_{1-x}{\text{Fe}}_x$O₃ (Cox et al., 1963) solid solutions, where both the ordering temperature of the spiral phase and its periodicity are doping-dependent, could belong to this category. Establishing whether or not the model can explain these observations will, however, require information about the relevant exchange constants and the possibility of creating the proper concentration of impurity bonds strong enough to produce frustration and stabilize long-range spiral order. An alternative possibility could be to up-scale the FM/AFM bond sequence along the c-axis in YBaCuFeO₅ (Figures 2A, B) through the fabrication of artificial magnetic multilayers, where the main difficulty will probably be being able to introduce frustrating impurities in the proper amounts.

5 Concluding remarks

To conclude, we believe that the results summarized in this mini-review will be of interest to the community interested in magnetoelectric material research. On one side, they demonstrate that magnetic spirals, a class of magnetic textures rarely stable above 100 K, where the magnetoelectric coupling can be very strong, can be engineered in AA’CuFeO₅-layered perovskites in such a way that they survive up to 400 K, i.e., safely far from RT. On the other hand, they provide a theoretical framework that rationalizes these experimental findings and a set of empirical rules to tune the spiral ordering temperature that can be used for the design of other materials with improved functional properties. This eliminates one of the main obstacles to the integration of spiral magnets in real-life devices and suggests that technological applications based on magnetoelectric spirals could become reality in the not-too-distant future.

Author contributions

AR: conceptualization, visualization, writing–original draft, and writing–review and editing. MM: conceptualization, supervision, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The previous work of the authors reported in this mini-review was supported by the following funding agencies: AR: Spanish Ministerio de Ciencia, Innovación y Universidades (project nos. MAT2015-68760-C2-2, RTI2018-098537-B-C21, PID2021-124734OB-C22, and FPI grant no. PRE2018-084769, co-funded by ERDF (from EU)), and Severo Ochoa Program for Centers of Excellence in R$\&$D (grant no. SEV-2015-0496 and FUNFUTURE grant no. CEX2019-000917-S). MM: Swiss National Science Foundation (grant nos. 200021-141334 and 206021-139082), PSI CROSS Program (grant 04-17), and MaMaself Erasmus Mundus Program (from EU). Open access funding was provided by the Paul Scherrer Institute (PSI).

Acknowledgments

The previous work of the authors reported in this mini-review benefited from fruitful discussions with A. Scaramucci, M. Müller, Ch. Mudry, N. Spaldin, M. Morin, T. Shang, V. Poree, E. Razzoli, H. Ueda, M. Ciomaga-Hatnean, J.L. García-Muñoz, and J. Herrero-Martín. The authors also acknowledge the allocation of beam time at several neutron and synchrotron X-ray large-scale facilities: SINQ and SLS (Villigen, Switzerland); ILL (Grenoble, France); Alba (Bellaterra, Spain), which was crucial for the above-mentioned work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arkenbout, A. H., Palstra, T. T. M., Siegrist, T., and Kimura, T. (2006). Ferroelectricity in the cycloidal spiral magnetic phase of MnWO₄. Phys. Rev. B 74, 184431–184438. doi:10.1103/PhysRevB.74.184431

CrossRef Full Text | Google Scholar

Atanassova, Y., Popov, V., Bogachev, G., Iliev, M., Mitros, C., Psycharis, V., et al. (1993). Raman-active and infrared-active phonons in YBaCuFeO₅ - experiment and lattice dynamics. Phys. Rev. B 47, 15201–15207. doi:10.1103/PhysRevB.47.15201

PubMed Abstract | CrossRef Full Text | Google Scholar

Babkevich, P., Poole, A., Johnson, R. D., Roessli, B., Prabhakaran, D., and Boothroyd, A. T. (2012). Electric field control of chiral magnetic domains in the high-temperature multiferroic CuO. Phys. Rev. B 85, 134428–134433. doi:10.1103/PhysRevB.85.134428

CrossRef Full Text | Google Scholar

Balents, L., and Fisher, M. A. (1996). Chiral surface states in the bulk quantum hall effect. Phys. Rev. Lett. 76, 2782–2785. doi:10.1103/PhysRevLett.76.2782

PubMed Abstract | CrossRef Full Text | Google Scholar

Cabrera, I., Kenzelmann, M., Lawes, G., Chen, Y., Chen, W. C., Erwin, R., et al. (2009). Coupled magnetic and ferroelectric domains in multiferroic ni₃v₂o8. Phys. Rev. Lett. 103, 087201–087204. doi:10.1103/PhysRevLett.103.087201

PubMed Abstract | CrossRef Full Text | Google Scholar

Caignaert, V., Mirebeau, I., Bourée, F., Nguyen, N., Ducouret, A., Greneche, J. M., et al. (1995). Crystal and magnetic structure of YBaCuFeO₅. J. Solid State Chem. 114, 24–35. doi:10.1006/jssc.1995.1004

CrossRef Full Text | Google Scholar

Cheong, S.-W., and Xu, X. (2022). Magnetic chirality. npj Quantum Mater. 7, 40–45. doi:10.1038/s41535-022-00447-5

CrossRef Full Text | Google Scholar

Cox, D., Takei, W., and Shirane, G. (1963). A magnetic and neutron diffraction study of the cr2o3-fe2o3 system. J. Phys. Chem. Solids 24, 405–423. doi:10.1016/0022-3697(63)90199-9

CrossRef Full Text | Google Scholar

Dey, D., Nandy, S., Maitra, T., Yadav, C., and Taraphder, A. (2018). Nature of spiral state and absence of electric polarisation in sr-doped YBaCuFeO₅ revealed by first-principle study. Sci. Rep. 8, 2404–2412. doi:10.1038/s41598-018-20774-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Diko, P., Duvignaud, P., Lanckbeen, A., Van Moer, A., Naessens, G., and Deltour, R. (1993). Influence of iron doping on the microstructure of YBa₂(Cu₁−_xFe_x)₃O_7−δ ceramics. J. Am. Ceram. Soc. 76, 2859–2864. doi:10.1111/j.1151-2916.1993.tb04027.x

CrossRef Full Text | Google Scholar

Emori, S., Bauer, U., Ahn, S.-M., Martinez, E., and Beach, G. S. D. (2013). Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Matter. 12, 611–616. doi:10.1038/NMAT3675

PubMed Abstract | CrossRef Full Text | Google Scholar

Er-Rakho, L., Michel, C., Lacorre, P., and Raveau, B. (1988). YBaCuFeO_5+δ: a novel oxygen-deficient perovskite with a layer structure. J. Solid State Chem. 73, 531–535. doi:10.1016/0022-4596(88)90141-7

CrossRef Full Text | Google Scholar

Everschor-Sitte, K., Masell, J., Reeve, R. M., and Kläui, M. (2018). Perspective: magnetic skyrmions—overview of recent progress in an active research field. J. Appl. Phys. 124, 240901–240918. doi:10.1063/1.5048972

CrossRef Full Text | Google Scholar

Fecher, G., Kübler, J., and Felser, C. (2022). Chirality in the solid state: chiral crystal structures in chiral and achiral space groups. Materials 15, 5812–5844. doi:10.3390/ma15175812

PubMed Abstract | CrossRef Full Text | Google Scholar

Fiebig, M., Lottermoser, T., Meier, D., and Trassin, M. (2016). The evolution of multiferroics. Nat. Rev. Mater. 1, 16046–16060. doi:10.1038/natrevmats.2016.46

CrossRef Full Text | Google Scholar

Finger, T., Senff, D., Schmalzl, K., Schmidt, W., Regnault, L. P., Becker, P., et al. (2010). Electric-field control of the chiral magnetism of multiferroic MnWO₄ as seen via polarized neutron diffraction. Phys. Rev. B 81, 054430–054435. doi:10.1103/PhysRevB.81.054430

CrossRef Full Text | Google Scholar

Goodenough, J. (1963). Magnetism and the chemical bond. Cambridge, MA: Wiley.

Google Scholar

Herpin, A. (1968). Théorie du magnétisme. Paris: Presses Universitaires de France.

Google Scholar

Johnson, R. D., Chapon, L. C., Khalyavin, D. D., Manuel, P., Radaelli, P. G., and Martin, C. (2012). Giant improper ferroelectricity in the ferroaxial magnet CaMn₇O₁₂. Phys. Rev. Lett. 108, 067201–067205. doi:10.1103/PhysRevLett.108.067201

PubMed Abstract | CrossRef Full Text | Google Scholar

Katsura, H., Nagaosa, N., and Balatsky, A. V. (2005). Spin current and magnetoelectric effect in noncollinear magnets. Phys. Rev. Lett. 95, 057205. doi:10.1103/PhysRevLett.95.057205

PubMed Abstract | CrossRef Full Text | Google Scholar

Kawamura, Y., Kai, T., Satomi, E., Yasui, Y., Kobayashi, Y., Sato, M., et al. (2010). High-temperature multiferroic state of RBaCuFeO₅ (R = Y, Lu, and Tm). J. Phys. Soc. Jpn. 79, 073705. doi:10.1143/JPSJ.79.073705

CrossRef Full Text | Google Scholar

Kelvin, L. (1904). Baltimore lectures on molecular dynamics and wave theory of light. Warehouse, London, UK: C. J. Clay and Sons, Cambridge University Press.

Google Scholar

Kimura, T. (2007). Spiral magnets as magnetoelectrics. Annu. Rev. Mater. Res. 37, 387–413. doi:10.1146/annurev.matsci.37.052506.084259

CrossRef Full Text | Google Scholar

Kimura, T. (2012). Magnetoelectric hexaferrites. Annu. Rev. Condens. Matter Phys. 3, 93–110. doi:10.1146/annurev-conmatphys-020911-125101

CrossRef Full Text | Google Scholar

Kimura, T., Goto, T., Shintani, H., Ishizaka, K., Arima, T.-h., and Tokura, Y. (2003). Magnetic control of ferroelectric polarization. Nature 426, 55–58. doi:10.1038/nature02018

PubMed Abstract | CrossRef Full Text | Google Scholar

Kimura, T., Lashley, J. C., and Ramirez, A. P. (2006). Inversion-symmetry breaking in the noncollinear magnetic phase of the triangular-lattice antiferromagnet CuFeO₂. Phys. Rev. B 73, 220401. doi:10.1103/PhysRevB.73.220401

CrossRef Full Text | Google Scholar

Kimura, T., Lawes, G., Goto, T., Tokura, Y., and Ramirez, A. P. (2005). Magnetoelectric phase diagrams of orthorhombic rMnO₃ (r = gd, tb, and dy). Phys. Rev. B 71, 224425. doi:10.1103/PhysRevB.71.224425

CrossRef Full Text | Google Scholar

Kimura, T., Sekio, Y., Nakamura, H., Siegrist, T., and Ramirez, A. P. (2008). Cupric oxide as an induced-multiferroic with high-T_C. Nature Mater. 7, 291–294. doi:10.1038/nmat2125

PubMed Abstract | CrossRef Full Text | Google Scholar

Kitagawa, Y., Hiraoka, Y., Honda, T., Ishikura, T., Nakamura, H., and Kimura, T. (2010). Low-field magnetoelectric effect at room temperature. Nat. Mater. 9, 797–802. doi:10.1038/nmat2826

PubMed Abstract | CrossRef Full Text | Google Scholar

Klyndyuk, A. I., and Chizhova, E. A. (2006). Properties of RBaCuFeO_5+δ (R = Y, La, Pr, Nd, Sm-Lu). Inorg. Mater 42, 550–561. doi:10.1134/S0020168506050189

CrossRef Full Text | Google Scholar

Kundys, B., Maignan, A., and Simon, C. (2009). Multiferroicity with high in ceramics of the YBaCuFeO₅ ordered perovskite. Appl. Phys. Lett. 94, 072506. doi:10.1063/1.3086309

CrossRef Full Text | Google Scholar

Kurumaji, T., Seki, S., Ishiwata, S., Murakawa, H., Kaneko, Y., and Tokura, Y. (2013). Magnetoelectric responses induced by domain rearrangement and spin structural change in triangular-lattice helimagnets NiI₂ and CoI₂. Phys. Rev. B 87, 014429. 014429–014437. doi:10.1103/PhysRevB.87.014429

CrossRef Full Text | Google Scholar

Kurumaji, T., Seki, S., Ishiwata, S., Murakawa, H., Tokunaga, Y., Kaneko, Y., et al. (2011). Magnetic-field induced competition of two multiferroic orders in a triangular-lattice helimagnet MnI₂. Phys. Rev. Lett. 106, 167206–167209. doi:10.1103/PhysRevLett.106.167206

PubMed Abstract | CrossRef Full Text | Google Scholar

Lai, C.-H., Wang, C.-W., Wu, H.-C., Liang, Y.-H., Studer, A. J., Chen, W.-T., et al. (2024). Tunable magnetic structures in the helimagnet YBa(Cu_2−xFe_x)₂O₅. Phys. Rev. Matter. 8, 054404. doi:10.1103/PhysRevMaterials.8.054404

CrossRef Full Text | Google Scholar

Lai, Y.-C., Du, C.-H., Lai, C.-H., Liang, Y.-H., Wang, C.-W., Rule, K. C., et al. (2017). Magnetic ordering and dielectric relaxation in the double perovskite YBaCuFeO₅. J. Phys. Condens. Matter 29, 145801. doi:10.1088/1361-648X/aa5708

PubMed Abstract | CrossRef Full Text | Google Scholar

Lai, Y.-C., Shu, G.-J., Chen, W.-T., Du, C.-H., and Chou, F.-C. (2015). Self-adjusted flux for the traveling solvent floating zone growth of YBaCuFeO₅ crystal. J. Cryst. Growth 413, 100–104. doi:10.1016/j.jcrysgro.2014.12.020

CrossRef Full Text | Google Scholar

Lawes, G., Harris, A. B., Kimura, T., Rogado, N., Cava, R. J., Aharony, A., et al. (2005). Magnetically driven ferroelectric order in ni₃v₂o₈. Phys. Rev. Lett. 95, 087205–087208. doi:10.1103/PhysRevLett.95.087205

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, T., Oehme, R., and Yang, C. (1957). Remarks on possible noninvariance under time reversal and charge conjugation. Phys. Rev. B 106, 340–345. doi:10.1103/PhysRev.106.340

CrossRef Full Text | Google Scholar

Lee, T., and Yang, C. (1956). Question of parity conservation in weak interactions. Phys. Rev. B 104, 254–258. doi:10.1103/PhysRev.104.254

CrossRef Full Text | Google Scholar

Liang, X., Matyushov, A., Hayes, P., Schell, V., Dong, C., Chen, H., et al. (2021). Roadmap on magnetoelectric materials and devices. IEEE Trans. Magnetics 57, 1–57. doi:10.1109/TMAG.2021.3086635

CrossRef Full Text | Google Scholar

Luo, S., and Wang, K. (2018). Giant dielectric permittivity and magneto-capacitance effect in YBaCuFeO₅. Scr. Mater. 146, 160–163. doi:10.1016/j.scriptamat.2017.11.032

CrossRef Full Text | Google Scholar

Lyu, J., Morin, M., Shang, T., Fernández-Díaz, M. T., and Medarde, M. (2022). Weak ferromagnetism linked to the high-temperature spiral phase of YBaCuFeO₅. Phys. Rev. Res. 4, 023008. doi:10.1103/PhysRevResearch.4.023008

CrossRef Full Text | Google Scholar

Marelli, E., Lyu, J., Morin, M., Leménager, M., Shang, T., Yüzbasi, N., et al. (2024). Cobalt-free layered perovskites RBaCuFeO_5+δ (R = 4f lanthanide) as electrocatalysts for the oxygen evolution reaction. EES. Catal. 2, 335–350. doi:10.1039/D3EY00142C

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyer, C., Hartmann-Boutron, F., Gros, Y., and Strobel, P. (1990). Mössbauer study of YBaCuFeO_5+δ -site assignments of the metallic ions. Solid State Comm. 76, 163–168. doi:10.1016/0038-1098(90)90535-J

CrossRef Full Text | Google Scholar

Mombru, A., Christides, C., Lappas, A., Prassides, K., Pissas, M., Mittros, C., et al. (1994). Magnetic structure of the oxygen-deficient perovskite YBaCuFeO_5+δ. Inorg. Chem. 33, 1255–1258. doi:10.1021/ic00085a008

CrossRef Full Text | Google Scholar

Mombru, A., Prassides, K., Christides, C., Erwin, R., Pissas, M., Mitros, C., et al. (1998). Neutron powder diffraction study (T = 4.2-300 K) and polarization analysis of YBaCuFeO_5+δ. J. Phys. Condes. Matter 10, 1247–1258. doi:10.1088/0953-8984/10/6/008

CrossRef Full Text | Google Scholar

Momozawa, N., Yamaguchi, Y., Takei, H., and Mita, M. (1985). Magnetic structure of (Ba₁−_xSr_x)₂Zn₂Fe₁₂O₂₂. J. Phys. Soc. Jpn. 54, 771–780. doi:10.1143/JPSJ.54.771

CrossRef Full Text | Google Scholar

Morin, M., Canévet, E., Raynaud, A., Bartkowiak, M., Sheptyakov, D., Ban, V., et al. (2016). Tuning magnetic spirals beyond room temperature with chemical disorder. Nat. Commun. 7, 13758–13764. doi:10.1038/ncomms13758

PubMed Abstract | CrossRef Full Text | Google Scholar

Morin, M., Scaramucci, A., Bartkowiak, M., Pomjakushina, E., Deng, G., Sheptyakov, D., et al. (2015). Incommensurate magnetic structure, Fe/Cu chemical disorder, and magnetic interactions in the high-temperature multiferroic YBaCuFeO₅. Phys. Rev. B 91, 064408. doi:10.1103/PhysRevB.91.064408

CrossRef Full Text | Google Scholar

Mostovoy, M. (2006). Ferroelectricity in spiral magnets. Phys. Rev. Lett. 96, 067601. doi:10.1103/PhysRevLett.96.067601

PubMed Abstract | CrossRef Full Text | Google Scholar

Mukherjee, S., Shimamoto, K., Windsor, Y. W., Ramakrishnan, M., Parchenko, S., Staub, U., et al. (2018). Multiferroic phase diagram of E-type RMnO₃ films studied by neutron and x-ray diffraction. Phys. Rev. B 98, 174416. doi:10.1103/PhysRevB.98.174416

CrossRef Full Text | Google Scholar

Murakawa, H., Onose, Y., Ohgushi, K., Ishiwata, S., and Tokura, Y. (2008). Generation of electric polarization with rotating magnetic field in helimagnet ZnCr₂Se₄. J. Phys. Soc. Jpn. 77, 043709. doi:10.1143/JPSJ.77.043709

CrossRef Full Text | Google Scholar

Porée, V., Gawryluk, D., Shang, T., Rodríguez-Velamazán, J., Casati, N., Sheptyakov, D., et al. (2024) “YBa₁−_xSr_xCuFeO₅ layered perovskites: exploring the magnetic order beyond the paramagnetic-collinear-spiral triple point. doi:10.48550/arXiv.2402.04816

CrossRef Full Text | Google Scholar

Ramakrishnan, M., Constable, E., Cano, A., Mostovoy, M., White, J., Gurung, N., et al. (2019). Advances in magnetoelectric multiferroics. Nat. Mater. 18, 203–212. doi:10.1038/s41563-018-0275-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Romaguera, A., Zhang, X., Fabelo, O., Fauth, F., Blasco, J., and García-Muñoz, J. (2022). Helimagnets by disorder: its role on the high-temperature magnetic spiral in the YBaCuFeO₅ perovskite. Phys. Rev. Res. 4, 043188. doi:10.1103/PhysRevResearch.4.043188

CrossRef Full Text | Google Scholar

Romaguera, A., Zhang, X., Fabelo, O., Fauth, F., Blasco, J., and García-Muñoz, J. (2023). Magnetic properties of highly ordered single crystals with layered YBaCuFeO₅ structure. EPJ Web Conf. 286, 05005. doi:10.1051/epjconf/202328605005

CrossRef Full Text | Google Scholar

Ruiz-Aragón, M. J., Morán, E., Amador, U., Martínez, J. L., Andersen, N. H., and Ehrenberg, H. (1998). Low-temperature magnetic structure of YBaCuFeO₅ and the effect of partial substitution of yttrium by calcium. Phys. Rev. B 58, 6291–6297. doi:10.1103/PhysRevB.58.6291

CrossRef Full Text | Google Scholar

Sando, D., Agbelele, A., Rahmedov, D., Liu, J., Rovillain, P., Toulouse, C., et al. (2013). Crafting the magnonic and spintronic response of BiFeO₃ films by epitaxial strain. Nat. Mater. 12, 641–646. doi:10.1038/NMAT3629

PubMed Abstract | CrossRef Full Text | Google Scholar

Scaramucci, A., Shinaoka, H., Mostovoy, M. V., Lin, R., Mudry, C., and Müller, M. (2020). Spiral order from orientationally correlated random bonds in classical XY models. Phys. Rev. Res. 2, 013273. doi:10.1103/PhysRevResearch.2.013273

CrossRef Full Text | Google Scholar

Scaramucci, A., Shinaoka, H., Mostovoy, M. V., Müller, M., Mudry, C., Troyer, M., et al. (2018). Multiferroic magnetic spirals induced by random magnetic exchanges. Phys. Rev. X 8, 011005. doi:10.1103/PhysRevX.8.011005

CrossRef Full Text | Google Scholar

Scott, J. (2013). Room-temperature multiferroic magnetoelectrics. NPG Asia Mater. 5, e72. doi:10.1038/am.2013.58

CrossRef Full Text | Google Scholar

Seki, S., Kurumaji, T., Ishiwata, S., Matsui, H., Murakawa, H., Tokunaga, Y., et al. (2010). Cupric chloride CuCl₂ as an S =1/2 chain multiferroic. Phys. Rev. B 82, 064424. doi:10.1103/PhysRevB.82.064424

CrossRef Full Text | Google Scholar

Seki, S., Yamasaki, Y., Soda, M., Matsuura, M., Hirota, K., and Tokura, Y. (2008). Correlation between spin helicity and an electric polarization vector in quantum-spin chain magnet LiCu₂O₂. Phys. Rev. Lett. 100, 127201. doi:10.1103/PhysRevLett.100.127201

PubMed Abstract | CrossRef Full Text | Google Scholar

Sergienko, I. A., and Dagotto, E. (2006). Role of the Dzyaloshinskii-Moriya interaction in multiferroic perovskites. Phys. Rev. B 73, 094434–094438. doi:10.1103/PhysRevB.73.094434

CrossRef Full Text | Google Scholar

Shang, T., Canévet, E., Morin, M., Sheptyakov, D., Fernández-Díaz, M. T., Pomjakushina, E., et al. (2018). Design of magnetic spirals in layered perovskites: extending the stability range far beyond room temperature. Sci. Adv. 4, eaau6386. doi:10.1126/sciadv.aau6386

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharma, M., and Maitra, T. (2023). Orbitally driven spin reorientation in Mn-doped YBaCuFeO₅. J. Phys. Chem. Solids 181, 111494. doi:10.1016/j.jpcs.2023.111494

CrossRef Full Text | Google Scholar

Simonet, V., Loire, M., and Ballou, R. (2012). Magnetic chirality as probed by neutron scattering. Eur. Phys. J. Spec. Top. 213, 5–36. doi:10.1140/epjst/e2012-01661-8

CrossRef Full Text | Google Scholar

Spaldin, N. A., and Ramesh, R. (2019). Advances in magnetoelectric multiferroics. Nat. Mater. 18, 203–212. doi:10.1038/s41563-018-0275-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Taguchi, Y., Oohara, Y., Yoshizawa, H., Nagaosa, N., and Tokura, Y. (2001). Spin chirality, berry phase, and anomalous hall effect in a frustrated ferromagnet. Science 291, 2573–2576. doi:10.1126/science.1058161

PubMed Abstract | CrossRef Full Text | Google Scholar

Taniguchi, K., Abe, N., Takenobu, T., Iwasa, Y., and Arima, T. (2006). Ferroelectric polarization flop in a frustrated magnet MnWO₄ induced by a magnetic field. Phys. Rev. Lett. 97, 097203. 097203–097206. doi:10.1103/PhysRevLett.97.097203

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomson (Lord Kelvin), W. (1894). The molecular tactics of a crystal. Oxford, UK: Clarendon Press.

Google Scholar

Tokura, Y., Seki, S., and Nagaosa, N. (2014). Multiferroics of spin origin. Rep. Prog. Phys. 77, 076501. doi:10.1088/0034-4885/77/7/076501

PubMed Abstract | CrossRef Full Text | Google Scholar

Wagnière, G. (2007). On chirality and the universal asymmetry: reflections on image and mirror image. Zürich, CH: Wiley.

Google Scholar

White, J. S., Honda, T., Kimura, K., Kimura, T., Niedermayer, C., Zaharko, O., et al. (2012). Coupling of magnetic and ferroelectric hysteresis by a multicomponent magnetic structure in Mn₂GeO₄. Phys. Rev. Lett. 108, 077204. doi:10.1103/PhysRevLett.108.077204

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamasaki, Y., Miyasaka, S., Kaneko, Y., He, J.-P., Arima, T., and Tokura, Y. (2006). Magnetic reversal of the ferroelectric polarization in a multiferroic spinel oxide. Phys. Rev. Lett. 96, 207204. doi:10.1103/PhysRevLett.96.207204

PubMed Abstract | CrossRef Full Text | Google Scholar

Yasui, Y., Kihara, S., Ikeda, K., and Banshodani, T. (2024). Doping effect on magnetic properties of high-temperature multiferroic compound YBaCuFeO₅. AIP Adv. 14. doi:10.1063/9.0000741

CrossRef Full Text | Google Scholar

Zhang, X., Romaguera, A., Falbelo, O., Fauth, F., Herrero-Martín, J., and García-Muñoz, J. L. (2021). Tuning the tilting of the spiral plane by Mn doping in YBaCuFeO₅ multiferroic. Acta Mater 206, 116608. doi:10.1016/j.actamat.2020.116608

CrossRef Full Text | Google Scholar

Zhang, X., Romaguera, A., Sandiumenge, F., Fabelo, O., Blasco, J., Herrero-Martín, J., et al. (2022). Magnetic properties of a highly ordered single crystal of the layered perovskite YBaCuFe_0.95Mn_0.05O₅. J. Magn. Magn. Mater. 551, 169165. doi:10.1016/j.jmmm.2022.169165

CrossRef Full Text | Google Scholar

Zhao, L., Hung, T.-L., Li, C.-C., Chen, Y.-Y., Wu, M.-K., Kremer, R. K., et al. (2012). CuBr₂-a new multiferroic material with high critical temperature. Adv. Mater. 24, 2469–2473. doi:10.1002/adma.201200734

PubMed Abstract | CrossRef Full Text | Google Scholar