
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 05 August 2024
Sec. Environmental Degradation of Materials
Volume 11 - 2024 | https://doi.org/10.3389/fmats.2024.1441220
 Jing Liu1,2*
Jing Liu1,2*The cracking of recycled aggregate concrete (RAC) is well known to promotes the chloride diffusion, accelerates the corrosion of reinforcement embedded in RAC. To reveal the mechanism of chloride diffusion in RAC under cracking, a multiphase mesoscopic model for chloride diffusion in RAC was proposed. It should be noted that RAC is regarded as eight-phase composite materials consisting of coarse aggregate, reinforcement, new and old mortar, new and old interface transition zones (ITZ), cracks, and damage zones. The effects of the width and depth of cracks and damage zones on chloride diffusion behavior in RAC after cracking were further investigated. The numerical simulation results show that the damage zones accelerate the chloride diffusion and exacerbates the accumulation effect of chloride at the crack tip. Compared to the crack depth, the crack width of RAC has a small effect on chloride diffusion behavior, especially, the crack width is less than 50 µm. More importantly, the chloride diffusion streamline generated by numerical simulation reveals the mechanism of cracks promoting chloride diffusion. The research in this paper provides new insights into the durability design of RAC by revealing the diffusion behavior of chloride ions in RAC.
Concrete is the most widely used building material, and Portland Cement is one of the important cementitious materials for preparing concrete. It is estimated that CO2 emissions from the manufacture of Portland Cement for 8%–10% of CO2 emissions worldwide (Krausmann et al., 2018; Xiao et al., 2021). Therefore, low-carbon and sustainable development are urgent issues to be addressed in the production process of concrete. Currently, the preparation of recycled aggregate concrete (RAC) by replacing natural aggregate (NA) with recycled coarse aggregate (RA) is one of the important methods to achieve carbon neutrality and sustainable development strategies (Reddy and Lahoti, 2023). However, compared to natural aggregate concrete (NAC), the weak old mortar and multiple interface transition zones (ITZ) caused by the replacement of RA are the main reasons for the deterioration of mechanical and durability properties of RAC (Silva et al., 2014; Algourdin et al., 2022; Liu et al., 2023; Wu et al., 2024). Hence, in recent decades, a large number of research reports (Algourdin et al., 2022; Kim, 2022; Lu et al., 2022; Liu et al., 2023; Ouyang et al., 2023; Rezaei et al., 2023; Wu et al., 2024) have been accumulated on the physical, chemical, mechanical, durability and improvement of RAC. Relevant research shows that adding various admixtures, RCA shaping, reducing the water cement ratio, and two-stage mixing can effectively improve the performance of RAC (Algourdin et al., 2022; Kim, 2022; Lu et al., 2022; Liu et al., 2023; Ouyang et al., 2023; Rezaei et al., 2023; Wu et al., 2024). In short, RAC as a sustainable green building material still has a good application prospect.
However, in marine or saline soils environments, various aggressive substances, including chloride ions, enter the concrete in various ways, which can damage the passivation film of the reinforcement steel in the concrete, reduce its protective effect on the reinforcement steel, and cause corrosion of the reinforcement steel in the presence of sufficient water and oxygen (Yi et al., 2020; Ye et al., 2023). Due to the expansion of corrosion products from corroded steel bars, the protective layer of the steel bars may crack, and then reduce the bearing capacity and service life of the structure (Yi et al., 2020; Ye et al., 2023). Thereby, a large number of researchers have conducted extensive research on improving the impermeability of concrete and the corrosion protection and repair techniques induced by chloride ions (Miranda et al., 2006; Ann et al., 2008; Ogunsanya et al., 2020; Yi et al., 2020; Shang et al., 2021; Ahmad et al., 2022; Algourdin et al., 2022; Lu et al., 2022; Liu et al., 2023; Rezaei et al., 2023; Ye et al., 2023; Wu et al., 2024). For example, extensive research work has shown that partial replacement of silicate cement by major auxiliary cementitious materials (e.g., fly ash, silica fume, slag, and a variety of other pozzolanic materials) improves the resistance of concrete to chloride-ion penetration (Ann et al., 2008; Yi et al., 2020; Ahmad et al., 2022; Algourdin et al., 2022; Lu et al., 2022; Liu et al., 2023; Rezaei et al., 2023; Ye et al., 2023; Wu et al., 2024). Similarly, in recent years, many scholars have proposed various methods for preventing and repairing steel corrosion in concrete, such as steel reinforcement coating, special replacement steel, corrosion inhibitors, concrete surface coating, electrochemical repair, etc. (Miranda et al., 2006; Ogunsanya et al., 2020; Shang et al., 2021; Ye et al., 2023).
Meanwhile, in the past few decades, many researchers have conducted extensive experimental and numerical studies on the mechanical properties and ion transport behavior of RAC (Xiao et al., 2014; Li et al., 2016; Nisreen et al., 2018; Bai et al., 2020; Bao et al., 2020; Sun et al., 2020; Rezaei et al., 2023), and important research results have been achieved. For instance, As the replacement rate of RAC increases, the mechanical properties and permeability of RAC are weaker. The effect of aggregate substitution rate on chloride transport in RAC has been revealed by Xiao et al. (2014) and Bao et al. (2020). Besides, related studies have revealed that ITZ (e.g., OITZ, NITZ) has a skeleton structure with higher porosity (Xue et al., 2019; Sun et al., 2020). Thus, the ITZ provides a fast channel for chloride ion transport and crack sprouting often sprouts here, deteriorating the mechanical properties and durability of concrete (Xue et al., 2019; Zhang et al., 2019). As is well known, RAC is a multiphase composite material at the meso-structure, and the comprehensive influence of each component on chloride diffusion forms the macroscopic physical phenomenon studied in the above experiments. Thus, it is particularly important to study the effects of each component on the chloride diffusion performance at a meso-structure level. However, it is difficult to ensure that each phase has a single and stable variable in the experiment (such as the depth and width of the damage zone, the thickness of the attached old mortar layer, etc.), making it difficult to accurately predict the chloride ion migration behavior in RAC. Numerical research can make up for the shortcomings in experimental research. For instance, Yu and Lin (2020) studied the effects of coarse aggregate shape, position, old mortar adhesion rate, and ITZ on chloride permeability behavior in RAC based on a micro finite element model, and established expressions for chloride diffusion coefficient and related factors. Xiao et al. (2012) and Hu et al. (2018) proposed a five-phase mesoscale numerical model and conducted parametric analysis. Numerical simulations by Wu and Xiao (2018) indicate that the randomness of microcracks may have an undeniable effect on the chloride ion diffusion rate. It should be noted that in the previous numerical studies, the randomness of the ITZ and the thickness of the attached old mortar layer is often overlooked in order to simplify the numerical model, and cannot truly reflect the microstructure of RAC. Hence, this paper constructs the adhesive old mortar layer and ITZ with random thickness by Monte Carlo metho at each aggregate boundary. In addition, due to the physical and chemical shrinkage, corrosive environment, and load effects, concrete inevitably works with cracks. Cracks can significantly increase the corrosion rate of chloride ions in RAC, accelerate the corrosion of reinforcement, and reduce the durability of RAC structures. Therefore, the study of chloride diffusion behavior in RAC under cracking has very important engineering value. However, previous research on the effect of cracking has mainly focused on NAC, while there have been few reports on RAC, and the time of cracking is often set at the time of concrete service, while the time of cracking occurrence is ignored. Many studies (Tuutti, 1979; Reale and O’Connor, 2012; Xu et al., 2019; CCES, 2004; Lu et al., 2011) have found that the cracking of concrete cover caused by chloride ion ingress in reinforced concrete structure (RC) is divided into two stages, namely the stage of corrosion initiation and the stage of crack initiation. a) The stage of corrosion initiation: During this stage, chloride ions enter the RAC by various means and accumulate on the surface of the reinforcement until reaching a critical concentration for corrosion of the reinforcement (Xu et al., 2019; CCES, 2004; Lu et al., 2011), destroying the passivation film around the reinforcement and causing corrosion in the presence of sufficient oxygen and water. b) The stage of crack initiation: during this stage, Corrosion products grow as the reinforcement rusts. Due to the volumetric expansion of the corrosion products, tensile stresses are generated in the concrete around the steel reinforcement. As the tensile stress reaches the tensile strength of the concrete cover, the concrete cover will crack (Bazant, 1979; Liu and Weyers, 1998; El Maaddawy and Soudki, 2007). However, relevant studies (Reale and O’Connor, 2012; Xu et al., 2019) have shown that the crack initiation accounts for a very small proportion of the total periods by comparing with the corrosion initiation period. Therefore, in order to simplify and ensure safety reserves, this paper ignores the crack initiation period and assumes that the criterion for cracking of the concrete cover is when the concentration of chloride ions on the surface of the reinforcement in the concrete reaches a critical value (CCES, 2004; Lu et al., 2011).
So, the purpose of this article is to establish a multiphase numerical model for the transport of chloride in RAC to reveal the transport mechanism of chloride in different components. Furthermore, the effects of factors such as crack width and depth, as well as the depth and width of the damage zone, on the transport of chloride in RAC were analyzed. In addition, the diffusion trajectory of chloride in RAC is depicted by diffusion streamlines.
To accurately reflect the meso-structure of RAC, a multiphase meso-structure model containing random old mortar and transition zones between new and old interfaces is developed, which based on the two-dimensional (2D) random aggregate model of concrete proposed by Gao and Liu (2003). The size of the RAC is 100 mm × 100 mm, the coarse aggregate adopts a continuous grading of 5–20 mm. The detailed process is as follows: 1) Firstly, use Fuller’s grading theory and Walraven’s plane transformation formula to obtain the content of recycled coarse aggregates at all levels (Walraven and Reinhardt, 1981). 2) According to the coarse aggregate placement method proposed by Gao and Liu (2003), polygonal recycled coarse aggregates without ITZ are randomly generated. 3) Then each vertex of the boundary of recycled coarse aggregate shrinks a certain distance along the radial direction, and connects each new vertex in turn to form the boundary of natural coarse aggregate. The closed area between the boundary of recycled coarse aggregate and the boundary of natural coarse aggregate forms the attached old mortar layer, which obeys the normal distribution. Please refer to reference (Liu et al., 2022) for the detailed process. 4) Similar to the previous method, the boundary of recycled coarse aggregate and natural aggregate are randomly extended outward by a certain distance, forming a transition zone between the new and old interfaces.
Furthermore, an eight-phase meso-structure model was further established, including coarse aggregate, reinforcement, new and old mortar, old ITZ, new ITZ, cracks, and damage zones. Figure 1 shows schematic diagram of numerical model for cracked recycled aggregate concrete, in which the crack phase is modeled as an equilateral triangle within the damage zone (DZ) as shown by the red color, and the DZ is modeled as a rectangle shape as shown by the yellow color. It should be noted that the true shape of cracks and damage zones is influenced by the distribution of aggregates and cannot be an ideal triangle or rectangle. However, relevant studies have found that when the crack is short, the curvature of the crack has little effect on the diffusion behavior of chloride ions (Peng et al., 2019). Hence, the crack phase in the present study has been simplified, and it is assumed to be located in the middle of the DZ. In Figure 1, WCr and WDZ are the width of the crack and the DZ, respectively, and, HCr and HDZ are the depth of the crack and the DZ, respectively. The cracked RAC finite element division is demonstrated in Figure 2.
In the marine environment, under the driving forces of concentration difference and convection, chloride continue to migrate into the interior of concrete through the pore structure of concrete. In this study, it is assumed that recycled concrete is in a saturated state, and the chloride transport behavior is only driven by concentration differences. In addition, the chlorides that diffuse into the concrete have both free and bound components (Tuutti, 1979; Reale and O’Connor, 2012; Xu et al., 2019; CCES, 2004; Lu et al., 2011; Bazant, 1979; Liu and Wayers, 1998; El Maaddawy and Soudki, 2007; Gao and Liu, 2003; Walraven and Reinhardt, 1981; Liu et al., 2022; Peng et al., 2019; Martin-Pe et al., 2001). The bound component is present in the pore walls as chloroaluminate and adsorbed phases, which prevent it from being freely transported. Hence, the diffusion behavior of chloride in concrete can be expressed as in Eqs 1, 2 (Martın-Pe et al., 2001; Ishida et al., 2008; Ishida et al., 2009),
where
where CS is the chloride concentration at the surface (% by mass of concrete), as shown in Figure 1.
RAC is regarded as eight-phase composite materials consisting of natural coarse aggregate, reinforcement, new and old mortar, new and old ITZ, cracks, and DZ. Each phase has an independent diffusivity property related to its microstructure. Due to the dense microstructure and poor pore connectivity of natural coarse aggregate, hence, natural aggregates are considered impermeable and chloride are not transported within the natural aggregates. Similarly, the reinforcement phase is also considered as impermeable. Several researchers (Jain and Gencturk, 2021; Zhang et al., 2021; Słomka-Słupik and Labus, 2022) have conducted extensive experimental studies on the diffusion coefficient of chloride in the transition zone between mortar and interface. And new cement mortar can be regarded as a composite material composed of pore structure and various cement hydration products, and its effective chloride diffusion coefficient can be expressed as a function of pore structure (Oh and Jang, 2004).
where DM, D0 (2.03 × 10−9 m2/s) are the diffusion coefficients of chloride in new cement mortar and water, respectively (Xie et al., 2022);
As the age of concrete increases, cement hydration becomes more complete, and the porosity of concrete decreases. Then, the age of concrete is negatively correlated with the diffusion coefficient (Mangat and Molloy, 1994; Boddy et al., 1999), which can be expressed as
where tref is the reference exposure time, usually taken as 28 days; m is the time decay index (Mangat and Molloy, 1994; Boddy et al., 1999).
Several researchers (Jain and Gencturk, 2021; Zhang et al., 2021; Słomka-Słupik and Labus, 2022) have conducted extensive experimental studies on the diffusion coefficient of chloride in mortar and ITZ. However, there is little research on the diffusion performance of hardened old mortar (DOM). According to existing literature (Sun et al., 2011), it can be seen that the ratio of chloride ion diffusion coefficients between new and old mortar is between 0.2 and 5. Hence, the DOM in this paper takes twice the value of DM. In addition, research by relevant scholars (Hu et al., 2018; Peng et al., 2019; Liu et al., 2022) has shown that the diffusion coefficients of the transition zone between the new and old interfaces are (DNITZ and DOITZ) are 10 times that of the new and old cement mortar (DM and DOM), respectively.
Furthermore, relevant experimental research (Djerbi et al., 2008; Du et al., 2015) shows that the diffusion performance of cracks is highly correlated with the crack width. On the basis of experimental data, the relationship equation between crack chloride ion diffusion coefficient and crack width was established, as shown in Eq. 9
where,
Peng et al. (2019) showed that the influence of damage zone on the diffusion behavior of chloride ions in concrete cannot be ignored. And existing literature (Peng et al., 2019) has shown that when the chloride ion diffusion coefficient in the damaged zoon is taken as 20 times of the new mortar, the numerical simulation results are in good agreement with the experimental results. Hence, in this paper, the chloride diffusion coefficient in the damaged zoon (DDZ) is simplified to 20 times that of the new mortar (DM).
To verify the reliability of chloride diffusion model in RAC proposed in this paper, experimental data from Algourdin et al. (2022) were selected for comparative analysis with the numerical simulation results in this paper. On the diffusion boundary of the numerical model, it was supposed that the top surface chloride concentration (Cs) was 0.46% (Algourdin et al., 2022), and the chloride concentration was taken to be zero at the left and right surfaces and at the bottom surface, as shown in Figure 1. Other parameters of the numerical model are shown in Table 1. Due to the consideration of the randomness of the microstructure of recycled concrete, three data lines were selected as references. It can be seen from Figure 3 that the distribution curve of chloride concentration with depth in the numerical simulation is in good agreement with the experimental curve. Therefore, the mesoscopic chloride diffusion model proposed in this paper for RAC has high reliability.
To study the diffusion mechanism of chloride ions in RAC after cracking, two numerical samples are selected for a comparative analysis, namely cracked and uncracked RAC. In the analysis the crack and damage zone width and length are respectively fixed as 0.01, 15, 1, and 25 mm. To consider the time of concrete crack cracking, this paper simplifies the cracking time and assumes that the judgment standard for cracking RAC is when the chloride ion concentration on the surface of the steel bar reaches the critical value of corrosion (i.e., 0.8% by mass of cementitious material) (CCES, 2004; Lu et al., 2011).
From Figure 4, it can be seen that at the same depth, the chloride concentration in the cracking mode is higher than that of the uncracked mode. Moreover, as the erosion depth increases, the concentration difference between the two mode increases first and then decreases. Among them, the turning point is the depth of the damage zone (i.e., 25 mm). This is mainly due to the significant difference in chloride ion diffusion rate between the damage zone and the surrounding area, a chloride ion aggregation effect is formed, resulting in the maximum increase in chloride ion concentration here.
From the diffusion trajectory of chloride in RAC as shown in Figure 5, it can be seen that the coarse aggregate increases the diffusion path of chloride, which has a certain hindrance effect. For example, A diffuses to B. In the cracking mode, higher concentrations of chloride ions accumulate in the damaged area, which diffuse around the coarse aggregate to the surrounding low concentration areas through ITZ, such as C diffusing to D and E. It is worth noting that the diffusion from C to D and E is not a straight line, but a curve, further confirming that ITZ is a fast channel for chloride ion diffusion (Yu and Lin, 2020). In summary, the cracking of RAC has a significant effect on the diffusion behavior of chloride ions, so it is necessary to further explore the effects of cracks and damage zones.
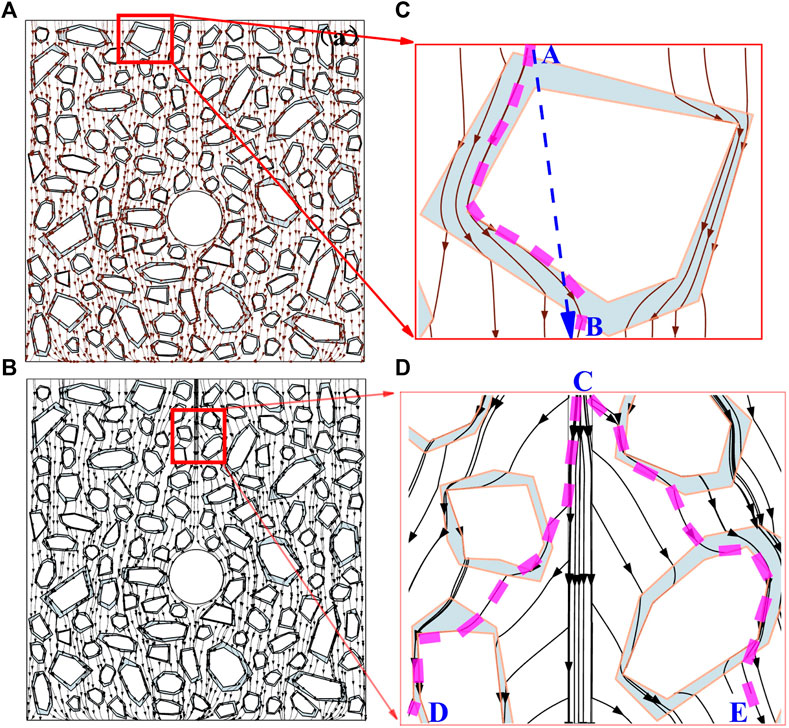
Figure 5. The diffusion trajectory line and partial enlarged view, (A) RAC without crack and, (B) RAC with crack, (C) Local amplification of Figure 5A, (D) Local amplification of Figure 5B.
To investigate the effect of damage zone width on chloride diffusion behavior, five numerical samples with different damage zone widths were designed, with a damage zone width range of 0–2 mm and a value taken at 0.5 mm intervals.
After 1 year of cracking of the RAC protective layer, the concentration curves and cloud charts of chloride ions along the depth direction under different damage zone widths were obtained as shown in Figures 6, 7. It is evident that as the width of the damage zone increases, the chloride concentration also gradually increases, as shown in Figures 6, 7. Moreover, at the tip of the damage, there is a turning point in the chloride concentration curve, mainly due to the significant difference in the chloride diffusion coefficient between the damaged zone and the mortar zone. Furthermore, as the width of the damaged zone increases, the range of influence of the damage on the distribution of chloride concentration also increases, as shown in Figure 7.
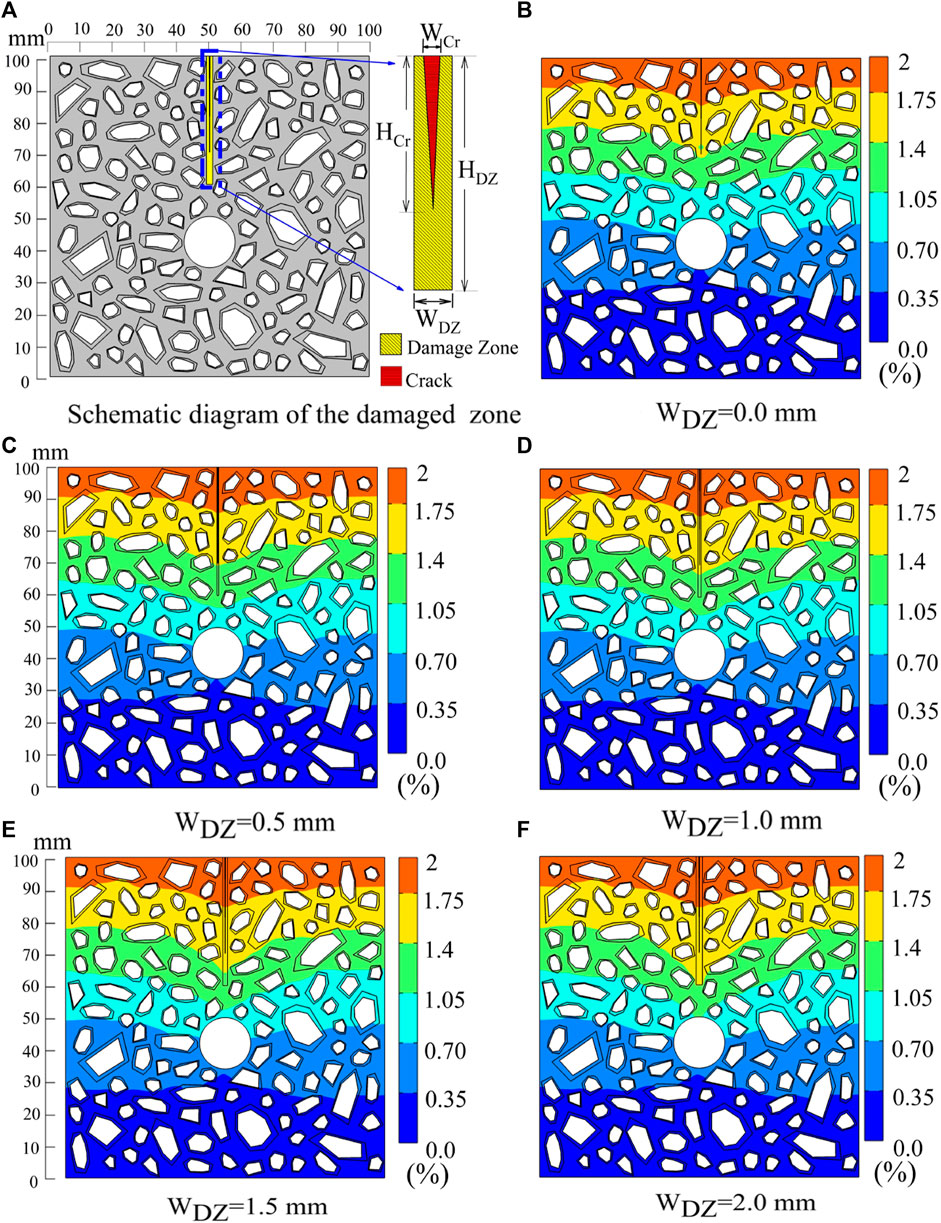
Figure 7. Spatial distribution of chloride concentration in RAC for different damage zone widths (WDZ). (A) Schematic diagram of the damages zone. (B) WDZ = 0.0 mm. (C) WDZ = 0.5 mm. (D) WDZ = 1.0 mm. (E) WDZ = 1.5 mm. (F) WDZ = 2.0 mm.
From the previous section, it can be seen that the presence of damage zones has an undeniable effect on chloride ion diffusion. Therefore, this section further studies the influence of damage zone depth on chloride ion diffusion performance, and designs eight numerical samples with different damage zone depths, namely damage zone depths of 0, 15, 20, 25, 30, 35, 40, and 45 mm.
It can be seen from Figure 8 that at the depth of the damage zone, all chloride ion distribution curves correspond to protruding positions, which is related to the accumulation effect at the end of the damage mentioned in the previous section. In addition, at different depths of the damage zone, there is a significant intersection of the chloride ion concentration curve along the depth direction. When the erosion depth is less than the intersection depth, the chloride ion concentration is negatively correlated with the depth of the damage zone. On the contrary, when the erosion depth exceeds the intersection depth, the chloride ion concentration is positively correlated with the depth of the damage zone. The main reason is that the length of the damage zone has a significant effect on the chloride ion diffusion rate. Moreover, It can be seen from Figure 9 that, as the depth of damage increases, the chloride concentration on the surface of the reinforcement increases nonlinearly, and the amplitude is increasing.
To investigate the effect of crack depth on the chloride concentration on the surface of reinforcement and compensate for the defects of large and dispersed experimental values, eight samples with different crack depths were designed, with a crack depth range of 0–35 mm and a value taken every 5 mm interval. It can be seen from Figure 10, that under the same exposure time, the chloride concentration on the surface of the reinforcement has significantly increased compared to the uncracked samples, indicating that cracks significantly accelerate the diffusion rate of chloride ions in RAC. After the thickness of the RAC protective layer cracks, as the crack depth increases, the chloride ion concentration on the surface of the steel bar first slowly increases, and then increases. The boundary point is HCr = 20 mm, which can also be confirmed from the concentration cloud map.

Figure 10. The chloride concentration (% by mass of cementitious material)in RAC for different crack depths (HCr = 0–30 mm). (A) Schematic diagram of the damages zone. (B) HCr = 0.0 mm. (C) HCr = 5 mm. (D) HCr = 10 mm. (E) HCr = 15 mm. (F) HCr = 20 mm. (G) HCr = 25 mm. (H) HCr = 30 mm.
As shown in Figure 11, the chlorine contour near the top of the crack and damage zone is significantly protruding downwards, indicating deeper diffusion in this area. The crack and damage zone provide a fast transport channel for chloride. As the depth of the crack increases, the closer it is to the upper surface of the steel bar, the greater the concentration of chloride ions on the upper surface of the steel bar. Therefore, the depth of cracks has a significant effect on chloride ion ingress of reinforcement. How to improve the crack resistance of concrete is of great significance in preventing steel corrosion and improving the durability of recycled concrete.
To investigate the effect of crack width on the chloride ion concentration on the surface of reinforcement, 10 samples with different crack widths were designed (e.g., 0–400 µm). The depth of the crack and the width and depth of the damage zone remain unchanged, at 30, 1, and 40 mm respectively. The distribution curve of chloride concentration in RAC under different crack widths after 1 year of cracking is obtained as shown in Figure 12. It can be seen that when the crack width is not greater than 50 μm, the difference of chloride concentration curve from uncracked is very small, mainly due to the relatively narrow cracks. When the crack width increases from 50 to 100 μm, there is a significant increase in chloride ion concentration. Afterwards, as the crack width increases, the concentration of chloride increases slightly and uniformly. Therefore, controlling the crack width below 50 µm could improve the chloride corrosion resistance of reinforcement in RAC.
By constructing a multiphase meso-structure model of RAC, including natural aggregates, recycled aggregates, new and old mortars, new and old ITZ, cracking and damage zones, a meso-structure numerical model for chloride transport in RAC was established. The influence of meso-structure characteristics and cracks induced by reinforcement corrosion on chloride transport behavior was analyzed. Moreover, the transport mechanism of chloride in RAC multi-components is revealed. The following conclusions can be drawn.
(a) Through the analysis of chloride diffusion flow lines, cracks and ITZ provide fast channels for chloride ion diffusion, revealing the mechanism of RAC promoting chloride transport.
(b) The presence of damaged zone accelerates the diffusion of chloride, especially the phenomenon of chloride aggregation at the end of the damaged zone. Consequently, the damage zone is a crucial factor that cannot be ignored. How to define the scope of damage zone in cracked RAC is a very meaningful work.
(c) As the depth of the crack increases, the concentration of chloride ions on the surface of the reinforcement increases sharply, and there is a non-linear relationship with the depth of the crack. Then, in practical engineering, attention should be paid to the repair of surface cracks and ITZ microcracks in RAC to suppress the diffusion of chloride in RAC and improve its durability.
(d) Compared to the depth of cracking, the crack width of recycled concrete has a relatively small effect on the chloride ion concentration on the surface of reinforcement, especially when the crack width is less than 50 µ m. Therefore, it is recommended to allow a crack width of less than 50 µ m in the design of recycled concrete structural components.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
JL: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the National Natural Science Foundation of China (grant No. 52268002 and No. 51968014), Guangxi Science and Technology Program (grant No. GuikeAD21238025) and Guangxi Universities Scientific Research Project (grant No. 2023KY0269).
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Ahmad, S., Baghabra Al-Amoudi, O. S., Khan, S. M. S., and Maslehuddin, M. (2022). Effect of silica fume inclusion on the strength, shrinkage and durability characteristics of natural pozzolan-based cement concrete. Case Stud. Constr. Mater. 17, e01255. doi:10.1016/j.cscm.2022.e01255
Algourdin, N., Pliya, P., Beaucour, A. L., Noumow´e, A., and di Coste, D. (2022). Effect of fine and coarse recycled aggregates on high-temperature behaviour and residual properties of concrete. Constr. Build. Mater. 341, 127847. doi:10.1016/j.conbuildmat.2022.127847
Ann, K. Y., Moon, H. Y., Kim, Y. B., and Ryou, J. (2008). Durability of recycled aggregate concrete using pozzolanic materials. Waste Manag. 28 (6), 993–999. doi:10.1016/j.wasman.2007.03.003
Bai, W., Li, W., Guan, J., Wang, J., and Yuan, C. (2020). Research on the mechanical properties of recycled aggregate concrete under uniaxial compression based on the statistical damage model. Materials 13, 3765. doi:10.3390/ma13173765
Bao, J. W., Li, S. G., Zhang, P., Ding, X., Xue, S., Cui, Y., et al. (2020). Influence of the incorporation of recycled coarse aggregate on water absorption and chloride penetration into concrete. Constr. Build. Mater 239, 117845. doi:10.1016/j.conbuildmat.2019.117845
Bazant, Z. P. (1979). Physical model for steel corrosion in concrete sea structures-theory. J. Struct. Div. 105 (6), 1137–1153. doi:10.1061/jsdeag.0005168
Boddy, A., Bentz, E., Thomas, M. D. A., and Hooton, R. D. (1999). An overview and sensitivity study of a multimechanistic chloride transport model. Cem. Concr. Res. 29, 827–837. doi:10.1016/s0008-8846(99)00045-9
CCES (2004). Guide to durability design and construction of reinforced structures. China: China Architecture and Building Press.
Djerbi, A., Bonnet, S., Khelidj, A., and Baroghel-bouny, V. (2008). Influence of traversing crack on chloride diffusion into concrete. Cem. Concr. Res. 38 (6), 877–883. doi:10.1016/j.cemconres.2007.10.007
Du, X., Jin, L., Zhang, R., and Li, Y. (2015). Effect of cracks on concrete diffusivity: a meso-scale numerical study. Ocean. Eng. 108, 539–551. doi:10.1016/j.oceaneng.2015.08.054
El Maaddawy, T., and Soudki, K. (2007). A model for prediction of time from corrosion initiation to corrosion cracking. Cem. Concr. Compos 29, 168–175. doi:10.1016/j.cemconcomp.2006.11.004
Gao, Z. G., and Liu, G. T. (2003). Two-dimensional random aggregate structure for concrete. J. Tsinghua Univ. Sci. Technol. 43 (5), 710–714. doi:10.16511/j.cnki.qhdxxb.2003.05.035
Hu, Z., Li-xuan, M., Jin, X., Liu, J., Gao, J., Yang, J., et al. (2018). Five-phase modelling for effective diffusion coefficient of chlorides in recycled concrete. Mag. Concr. Res. 70 (11), 583–594. doi:10.1680/jmacr.17.00194
Ishida, T., Iqbal, P. O. N., and Anh, H. T. L. (2009). Modeling of chloride diffusivity coupled with non-linear binding capacity in sound and cracked concrete. Cem. Concr. Res. 39 (10), 913–923. doi:10.1016/j.cemconres.2009.07.014
Ishida, T., Miyahara, S., and Maruya, T. (2008). Chloride binding capacity of mortars made with various Portland cements and mineral admixtures. J. Adv. Concr. Technol. 6 (2), 287–301. doi:10.3151/jact.6.287
Jain, A., and Gencturk, B. (2021). Multiphysics and multiscale modeling of coupled transport of chloride ions in concrete. Materials 14 (4), 885. doi:10.3390/ma14040885
Kim, J. (2022). Influence of quality of recycled aggregates on the mechanical properties of recycled aggregate concretes: an overview. Constr. Build. Mater. 188, 127071. doi:10.1016/j.conbuildmat.2022.127071
Krausmann, F., Lauk, C., Haas, W., and Wiedenhofer, D. (2018). From resource extraction to outflows of wastes and emissions: the socioeconomic metabolism of the global economy, 1900–2015. Glob. Environ. Change 52, 131–140. doi:10.1016/j.gloenvcha.2018.07.003
Li, L., Xiao, J., and Poon, C. S. (2016). Dynamic compressive behavior of recycled aggregate concrete. Mater. Struct. 49 (11), 4451–4462. doi:10.1617/s11527-016-0800-1
Liu, J., Chen, X., Rong, H., Yu, A., Ming, Y., and Li, K. (2022). Effect of interface transition zone and coarse aggregate on microscopic diffusion behavior of chloride ion. Materials 15, 4171. doi:10.3390/ma15124171
Liu, J., Ma, K., Shen, J., Zhu, J., Long, G., Xie, Y., et al. (2023). Influence of recycled concrete aggregate enhancement methods on the change of microstructure of ITZs in recycled aggregate concrete. Constr. Build. Mater. 371, 130772. doi:10.1016/j.conbuildmat.2023.130772
Liu, Y., and Weyers, R. E. (1998). Modeling the time-to-corrosion cracking in chloride contaminated reinforced concrete structures. ACI Mater J. 95 (6), 675–681. doi:10.14359/410
Lu, Z., Tan, Q., Lin, J., and Wang, D. (2022). Properties investigation of recycled aggregates and concrete modified by accelerated carbonation through increased temperature. Constr. Build. Mater. 341, 127813. doi:10.1016/j.conbuildmat.2022.127813
Lu, Z. H., Zhao, Y. G., Yu, Z. W., and Ding, F. X. (2011). Probabilistic evaluation of initiation time in RC bridge beams with load-induced cracks exposed to de-icing salts. Cem. Concr. Res. 41 (3), 365–372. doi:10.1016/j.cemconres.2010.12.003
Mangat, P. S., and Molloy, B. T. (1994). Prediction of long term chloride concentration in concrete. Mater Struct. 27, 338–346. doi:10.1007/bf02473426
Martın-Perez, B., Pantazopoulou, S. J., and Thomas, M. D. A. (2001). Numerical solution of mass transport equations in concrete structures. Comput. Struct. 79 (13), 1251–1264. doi:10.1016/S0045-7949(01)00018-9
Miranda, J. M., Gonzalez, J. A., Cobo, A., and Otero, E. (2006). Several questions about electrochemical rehabilitation methods for reinforced concrete structures. Corros. Sci. 48, 2172–2188. doi:10.1016/j.corsci.2005.08.014
Nakarai, K., Ishida, T., and Maekawa, K. (2006). Multi-scale physicochemical modeling of soil-cementitious material interaction. Soils Found. 46 (5), 653–663. doi:10.2208/jscej.2005.802_137
Nisreen, M., Kaiss, S., Mazin, H., et al. (2018). The influence of recycled concrete aggregate on the properties of concrete. MATEC Web Conf. 162, 02020. doi:10.1051/matecconf/201816202020
Ogunsanya, I. G., Strong, V., and Hansson, C. M. (2020). Corrosion behavior of austenitic 304L and 316LN stainless steel clad reinforcing bars in cracked concrete. Mater. Corrosion-Werkstoffe Und Korrosion 71 (7), 1066–1080. doi:10.1002/maco.201911221
Oh, B. H., and Jang, S. Y. (2004). Prediction of diffusivity of concrete based on simple analytic equations. Cem. Concr. Res. 34 (3), 463–480. doi:10.1016/j.cemconres.2003.08.026
Ouyang, K., Liu, J., Liu, S., Song, B., Guo, H., Li, G., et al. (2023). Influence of pre-treatment methods for recycled concrete aggregate on the performance of recycled concrete: a review. Resour. Conservation Recycl. 188, 106717. doi:10.1016/j.resconrec.2022.106717
Peng, J., Hu, S., Zhang, J., Cai, C. S., and Li, L.-Y. (2019). Influence of cracks on chloride diffusivity in concrete: a five-phase mesoscale model approach. Constr. Build. Mater. 197, 587–596. doi:10.1016/j.conbuildmat.2018.11.208
Powers, T. C. (1962). Physical properties of cement paste. Proc. Fourth Int. Conf. Chem. Cem. 43, 577–613.
Reale, T., and O’Connor, A. (2012). A review and comparative analysis of corrosion induced time to first crack models. Constr. Build. Mater. 36, 475–483. doi:10.1016/j.conbuildmat.2012.06.033
Reddy, N. S., and Lahoti, M. (2023). A succinct review on the durability of treated recycled concrete aggregates. Environ. Sci. Pollut. Res. 30, 25356–25366. doi:10.1007/s11356-021-18168-w
Rezaei, F., Memarzadeh, A., Davoodi, M.-R., Dashab, M.-A., and Nematzadeh, M. (2023). Mechanical features and durability of concrete incorporating recycled coarse aggregate and nano-silica: experimental study, prediction, and optimization. J. Build. Eng. 73, 106715. doi:10.1016/j.jobe.2023.106715
Shang, H., Shao, S., and Wang, W. (2021). Bond behavior between graphene modified epoxy coated steel bars and concrete. J. Build. Eng. 42, 102481. doi:10.1016/j.jobe.2021.102481
Silva, R. V., Brito, J., and Dhir, R. K. (2014). Properties and composition of recycled aggregates from construction and demolition waste suitable for concrete production. Constr. Build. Mater. 65 (2014), 201–217. doi:10.1016/j.conbuildmat.2014.04.117
Słomka-Słupik, B., and Labus, K. (2022). Laboratory test and geochemical modeling of cement paste degradation, in contact with ammonium chloride solution. Materials 15 (8), 2930. doi:10.3390/ma15082930
Sun, D., Shi, H., Wu, K., Miramini, S., Li, B., and Zhang, L. (2020). Influence of aggregate surface treatment on corrosion resistance of cement composite under chloride attack. Constr. Build. Mater. 248, 118636. doi:10.1016/j.conbuildmat.2020.118636
Sun, G., Zhang, Y., Sun, W., Liu, Z., and Wang, C. (2011). Multi-scale prediction of the effective chloride diffusion coefficient of concrete. Constr. Build. Mater. 25, 3820–3831. doi:10.1016/j.conbuildmat.2011.03.041
Tuutti, K. (1979). Service life of structures with regard to corrosion of embedded steel. Metal. Constr. 1, 293–301. doi:10.14359/6355
Walraven, J., and Reinhardt, H. W. (1981). Theory and experiments on the mechanical behaviour of cracks in plain and reinforced concrete subjected to shear loading. HERON 26 (1A), 1981.
Wu, L., Sun, Z., and Cao, Y. (2024). Modification of recycled aggregate and conservation and application of recycled aggregate concrete: a review. Constr. Build. Mater. 431, 136567. doi:10.1016/j.conbuildmat.2024.136567
Wu, Y., and Xiao, J. (2018). The effect of microscopic cracks on chloride diffusivity of recycled aggregate concrete. Constr. Build. Mater. 170, 326–346. doi:10.1016/j.conbuildmat.2018.03.045
Xiao, J., Ying, J., Tam, V. W. Y., and Gilbert, I. R. (2014). Test and prediction of chloride diffusion in recycled aggregate concrete. Sci. China Technol. Sci. 57, 2357–2370. doi:10.1007/s11431-014-5700-4
Xiao, J. Z., Xiao, Y., Liu, Y., and Ding, T. (2021). Carbon emission analyses of concretes made with recycled materials considering CO2 uptake through carbonation absorption. Struct. Concr. 22 (S1), E58–E73. doi:10.1002/suco.201900577
Xiao, J. Z., Ying, J. W., and Shen, L. (2012). FEM simulation of chloride diffusion in modeled recycled aggregate concrete. Constr. Build. Mater. 29, 12–23. doi:10.1016/j.conbuildmat.2011.08.073
Xie, J. H., Wang, J. J., Li, M. L., Xu, L., Xiang, D., Wang, Y., et al. (2022). Estimation of chloride diffusion coefficient from water permeability test of cementitious materials. Constr. Build. Mater. 340, 127816. doi:10.1016/j.conbuildmat.2022.127816
Xu, Q. H., Shi, D. D., and Shao, W. (2019). Service life prediction of RC square piles based on time-varying probability analysis. Constr. Build. Mater 227, 116824. doi:10.1016/j.conbuildmat.2019.116824
Xue, S., Zhang, P., Bao, J., He, L., Hu, Y., and Yang, S. (2019). Comparison of Mercury Intrusion Porosimetry and multi-scale X-ray CT on characterizing the microstructure of heat-treated cement mortar. Mater. Charact. 160, 110085. doi:10.1016/j.matchar.2019.110085matchar.2019.110085
Ye, T., Zhang, G., Ye, H., Zeng, Q., Zhang, Z., Tian, Z., et al. (2023). Corrosion of steel rebar in concrete induced by chloride ions under natural environments. Constr. Build. Mater. 369, 130504. doi:10.1016/j.conbuildmat.2023.130504
Yi, Y., Zhu, D., Guo, S., Zhang, Z., and Shi, C. (2020). A review on the deterioration and approaches to enhance the durability of concrete in the marine environment. Cem. Concr. Compos. 113, 103695. doi:10.1016/j.cemconcomp.2020.103695
Yu, Y., and Lin, L. (2020). Modeling and predicting chloride diffusion in recycled aggregate concrete. Constr. Build. Mater. 264, 120620. doi:10.1016/j.conbuildmat.2020.120620
Zhang, F., Hu, Z., Wei, F., Wen, X., Li, X., Dai, L., et al. (2021). Study on concrete deterioration in different NaCl-Na2SO4 solutions and the mechanism of Cl− diffusion. Materials 14 (17), 5054. doi:10.3390/ma14175054
Keywords: recycled aggregate concrete (RAC), multiphase mesoscopic model, chloride diffusion, numerical simulation, crack
Citation: Liu J (2024) Mesoscopic numerical simulation of chloride diffusion behavior in cracked recycled aggregate concrete. Front. Mater. 11:1441220. doi: 10.3389/fmats.2024.1441220
Received: 30 May 2024; Accepted: 15 July 2024;
Published: 05 August 2024.
Edited by:
Facundo Almeraya-Calderón, Autonomous University of Nuevo León, MexicoReviewed by:
Citlalli Gaona-Tiburcio, Autonomous University of Nuevo León, MexicoCopyright © 2024 Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jing Liu, NjYxNDA2MkBnbHV0LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.