Multiscale micromechanics modeling of viscoelastic natural plant fibers

Natural plant fibers are hierarchical structures with multi-level microstructures. With advances in composite material science, these fibers have been widely used in various polymer products. Therefore, it is crucial to quantitatively understand the relationship between their microstructures and mechanical behavior. This paper utilizes the Mori-Tanaka micromechanics model, viscoelasticity theory, and Zakian’s inversion method to study the impact of plant fiber microstructure on the viscoelastic behavior of multiscale structures. At the microscopic scale, the macromolecular polymer (matrix) and cellulose (fiber) are first homogenized. The second homogenization involves the cell wall microstructure, and the third homogenization considers the porosity of the cell wall and lumen to predict the effective modulus of fiber bundles. By applying the principle of elastic-viscoelastic correspondence, the viscoelastic mechanical parameters of plant fibers are calculated. The study examines the effects of cellulose crystallinity and lumen porosity on the structural stiffness and viscoelastic properties of fibers, identifying these factors as key influences on the mechanical behavior of plant fibers. Given their significant economic potential, the feasibility of using tobacco plant fibers as bio-based materials is also explored.

1 Introduction

With the continuing development of material science and emerging demand of biotechnology, natural plant fibers are extensively employed in the engineering and high-tech industries. It is demonstrated that natural fibers exhibit significantly high mechanical properties, such as bast fibers (flax/ramie) exhibit almost high Young’s modulus as the synthetic glass fibers (Dicker et al., 2014; Sathishkumar et al., 2013; Symington et al., 2009); while synthetic glass fibers possess tensile strength as 1,800 MPa.

The excellent performance of natural plant fibers is generally considered due to their hierarchical microstructures with constituents across several different scales. For instance, a typical plant fiber is composed of cellulose, hemicellulose and lignin, etc., (Jamir et al., 2018). With the continuing advancement of spectroscopic, scattering and imaging methods, more details about the microstructures of tissue or subcellular structures become available. The hierarchy of the microstructures generally guarantee their corresponding effective mechanical response under external stimuli or mechanical loading (Zhao et al., 2021; Chen et al., 2022a). Despite the variety of species, most natural fibers share a common hierarchy of microstructures (Alves Fidelis et al., 2013). A typical fiber consists of fiber cells, formed by central lumen that is surrounded by cell walls and connected by middle lamellae. What’s more, the cell wall is composed of a primary and several secondary layers. The S2 layer contains amorphous lignin and hemicellulose regions mixed with cellulose microfibrils with random distribution and rotary angle. It is also demonstrated that the microfibril angle plays a key role in affecting the mechanical properties of fibers (Bledzki and Gassan, 1999). Within these microfibrils it contains two areas, highly ordered fiber regions (crystalline) and disordered regions (amorphous-like) (Figure 1B) (Moon et al., 2011). Nanofiber (Figure 1C), the highly ordered crystalline regions, as the smallest fiber unit in plant fibers, the mechanical properties of plant fibers are largely influenced by it. At the molecular scale, cellulose nanofibers are composed of linear chains of dehydrated glucose rings. In individual glucose molecules, carbon atoms are bonded to oxygen atoms and hydroxyl groups. The extensive hydrogen bonding between hydroxyl groups of glucose units contributes to the high tensile strength and insolubility of cellulose, rendering it a crucial structural component in plant cell walls and a valuable material in diverse applications (Figure 1A). Higher plant nanofibers have a cross-sectional size of only 2-3 nm (Song et al., 2020; Newman et al., 2013; Thomas et al., 2013), whereas microfiber has a cross-sectional size in the range of 20–40 nm (Nishiyama et al., 2002; Nishiyama et al., 2003). A growing number of studies are beginning to embrace the 18-chain nanofiber model of plant microfibers, it is believed that microfibers are synthesized by enzyme complexes containing six groups of three synthase units (Nixon et al., 2016; Vandavasi et al., 2016), whereas crystalline and disordered fiber bundles coexist in every cross-section of the microfibers (Atalla and VanderHart, 1999; Sturcová et al., 2004). Nanofibers have very excellent mechanical properties, with a tensile stiffness of 140 GPa and a density of 1.56 (Sturcova et al., 2005). Most recent work has estimated the mechanical behavior of cellulose nanofibrils through molecular dynamic simulations (Tashiro and Kobayashi, 1985; Dri et al., 2014).

Figure 1

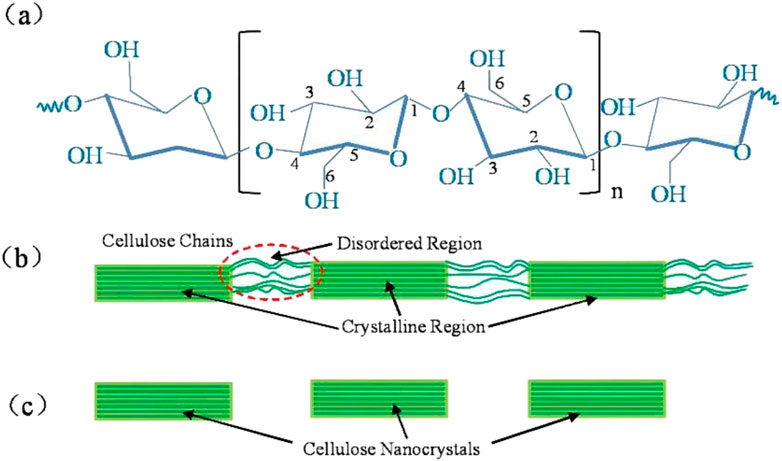
Figure 1. Structural illustration of celluloses. (A) The monomeric units and typical functional groups of celluloses, the numbers 1–6 represent the carbon atoms in the monomeric glucose molecule, (B) Idealized cellulose microfibril with a configuration of crystalline and amorphous regions, and (C) cellulose nanocrystals after dissolving the disordered regions by acid hydrolysis.

The most direct knowledge about the mechanical behavior of natural fibers is generally via experimental measurement. Shinichiro Iwamoto (Iwamoto et al., 2009) measured the elastic moduli of single microfibers from tunicate (Halocynthia papillosa) cellulose by atomic force microscopy (AFM). Šturcová et al. (2005) used Raman spectroscopic technique to measure the elastic modulus of tunicate cellulose. X-ray diffraction (XRD) and scanning electron microscopy (SEM) techniques have also been used in the study of the micromechanical properties of microfiber materials (Tabet and Abdul, 2013; William et al., 2016). To circumvent the laborious and costly AFM and XRD testing, researchers introduced mechanical models to quantitatively understand the microstructural hierarchy from a bottom-up perspective and several parameters that could be influential in determining the effective properties, such as lumens’ volume fraction, cellulose crystallinity, cell wall-related phase volume fractions, etc. From this point of view, multiscale micromechanics models happen to be suitable for this task, while the most classical micromechanics tools, such as Mori-Tanaka (M-T) model, composite cylinder assemblage (CCA), etc., Karin Hofstetter started to apply the continuum micromechanics approach to develop a multi-scale elastic model of wood, which can predict the macro elastic properties of wood (Hofstetter et al., 2005), afterwards the multiscale model was extended to predict the elastic limit state of wood (Hofstetter et al., 2008). At the microscopic scale, the acquisition of data on the mechanical parameters of materials is a great challenge, the inverse modeling approach to continuous media micromechanics provides a new solution idea to calculate nanoscale phase properties in reverse through higher length scales (Schwiedrzik et al., 2016). Elasticity-based continuous media micromechanics model has gradually been applied from wood to a variety of materials with hierarchical microstructures, such as bone materials (Fritsch et al., 2009; Chen et al., 2022b), crop stem materials (Gangwar et al., 2021), plant culm materials (Zhao et al., 2018), plant culm materials (Gangwar and Schillinger, 2019), etc. For example, tobacco, a crop of great economic value, contains cellulose in the leaf plates, ribs and stems, providing structural strength to ensure proper stem and leaf growth (Djafari, 2017). As shown in Figure 2, cellulose is mainly found in phloem cells and xylem cells (Yao and Chen, 2017). A deeper comprehension of the mechanical properties of plant fibers with high cellulose content, including jute, flax and cotton, will facilitate the breeding of plant varieties with enhanced mechanical properties. Furthermore, this understanding is crucial for augmenting the wind resistance, disease resistance and harvesting efficiency of plants.

Figure 2

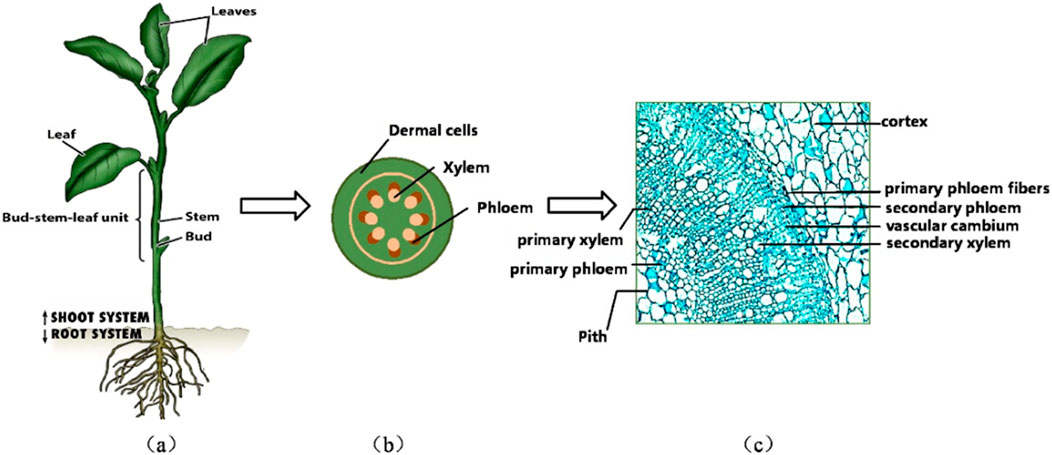
Figure 2. Multiscale modelling of tobacco plants. (A) Typical growing tobacco crop. (B) Cross-section of a typical stem of a tobacco plant, (C) Transverse SEM photographs of tobacco stems (Yao and Chen, 2017)

In addition to the existing literature, most papers consider the elastic properties of natural constituents, with fewer attention is focused on the elastoplastic behavior. However, there seems scarce literature paying attention to the viscoelastic properties of the natural fibers whose major constituents are natural viscoelastic organic materials. It is thus the purpose of this work to investigate the elastic-viscoelastic properties of natural fibers from micromechanics perspective. In order to facilitate the theoretical implementation, the recently developed Mori-Tanaka model is introduced to fulfill the micromechanics simulation and homogenization of natural microstructures, where plant fibers from several species are summarized and categorized. What’s more, the elasticity-viscoelasticity corresponding principle is introduced and implemented into the micromechanics model to study the viscoelastic behavior of heterogeneous biomaterials. The multiscale viscoelastic problem and homogenization are firstly solved and conducted in the Laplace domain and the solutions are then transferred into the time domain via analytical formulae proposed by Zakian in the 1960s.

The remainder of the paper is organized as follows: Section 2 provides details on the multiscale microscopic hierarchical model of plant fibers, the viscoelastic correspondence principle and M-T models. Section 3 describes the submicroscopic, microscopic, and macroscopic scales of plant fibers, the homogenization process, and lists the corresponding component and mechanical parameters. The predictions of the multiscale fine-scale mechanical model developed in this paper are compared with literature data to verify the correctness of the computational model. Section 4 analyzes the effects of cellulose content and lumen porosity on the mechanical properties of plant fibers. Section 5 concludes this manuscript.

2 Materials and methods

2.1 Multiscale framework and RVE characterization

Similar multi-scale microstructures exist between different plant fibers (Figures 3A, B). Jute fiber, for example, exists in its natural state as fiber bundles in the flax stem. The cellular fibers in jute fibers are thick walled hollow structures (Figures 3C, D), The cellular fibers in jute fibers consist of a primary wall, a secondary wall and a hollow lumen, cell fibers are tightly connected to each other by the middle laminae (Li et al., 2000; Bos, 2004). The plant secondary wall occupies most of the thickness of the cell wall and is divided into three layers from the outside to the inside, called s1, s2, and s3 layers, each of which possesses different thickness and microfibril helix angle (MFA), in which the S2 layer is the thickest (Gorshkova and Morvan, 2006). The S2 layer contains amorphous lignin and hemicellulose regions and is mixed with right-handed helical cellulose microfibers (Figure 1B) (Bledzki and Gassan, 1999).

Figure 3

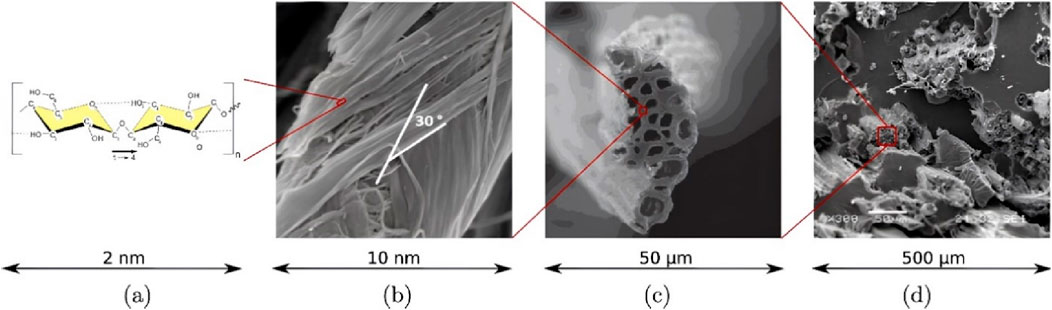
Figure 3. Biofibers with hierarchy across several scales, (A) Chemical structure of cellulose chains, (B) SEM images of microfibrils in bamboo fibers, (C) SEM images of jute fiber cross-section, (D) Hemp oil-based bio-composite with jute fiber reinforcements by Konigsberger is licensed under CC BY 4.0.

Based on the hierarchical nature of plant fibers, we primarily considered the S2 layer of plant cell walls. We simulated plant fibers using four types of representative volume elements (RVEs) across three observation scales. Differences between various plant fibers are mainly reflected in lumen volume fraction, cell wall thickness, and microstructural component content. While there are differences in the geometrical shapes of plant fibers, this study assumes all fiber geometries are cylindrical models to focus on other factors impacting mechanical properties. Assuming the fibers are transversely isotropic materials, we considered a uniform random distribution of microfibers in the plane. The “polymer network RVE” consists of four spherical phases: hemicellulose, lignin, pectin, and ash (including waxes, oils, fats, and inorganic fractions), as illustrated in Figure 4A. A “cellulose RVE” models nanocellulose as an infinitely long array of cylinders embedded in an amorphous cellulose matrix (Figure 4B). Crystalline cellulose nano protofibrils align with amorphous cellulose fibers oriented in the coordinate base r,t, and l.l being longitudinal along the axis of the protofibrils. At the single micron scale, we consider “the cell wall RVE” to consist of infinitely long cylindrical cellulose microfibrils embedded within a polymer network matrix (Figure 4C). “The fiber RVE” is modeled as a cell wall matrix phase containing infinitely long cylindrical inner cavity pores aligned with the longitudinal fiber direction (Figure 4D).

Figure 4

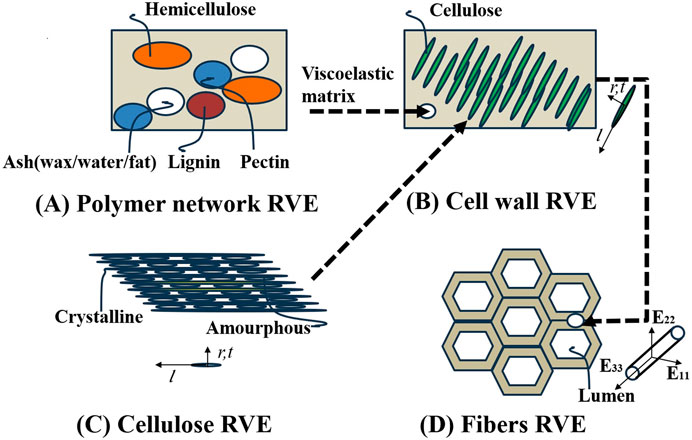
Figure 4. Multiscale micromechanics representation of plant fibers by means of four scale separated RVEs across three scales of observation. (A) Polymer network RVE, (B) Cellulose RVE, (C) Cell wall RVE, (D) Fibers RVE.

2.2 Elastic-viscoelastic correspondence principle

The elastic-viscoelastic correspondence principle is employed in this work to obtain the viscoelastic solution and effective properties in the time domain for hierarchical bio-microstructures. The basic idea is taking advantage of the similar patterns of strain-displacement and compatibility relations of elastic problem in time domain and viscoelastic problem in the Laplace domain. Through Laplace transformation, the stress-strain integral relationship in the time domain is simplified into an almost linear expression in the Laplace domain. Then the viscoelasticity in the Laplace domain is solved in a similar fashion as the linear elasticity in the time domain. Herein the problem is to obtain the effective moduli of natural fibers after establishing the microstructural RVE and corresponding solutions of localized problem. Finally, the effective moduli in the Laplace domain are transferred into the time domain through inverse methods, where an efficient inversion method proposed by Zakian (1969) is employed for the homogenized relaxation moduli and creep compliances in the time domain. The advantage of the correspondence principle is to circumvent the incremental integral step-by-step that is usually bothered by the divergence problem and large-scale computation.

Regarding transferred problem, the initial displacements, strains and stresses in the time domain is replaced by the corresponding quantities in the Laplace domain, e.g., and the elastic stiffness matrix elements by their corresponding Carson-Laplace transforms, where: $u_{ij}\to {\widehat{u}}_{ij}\left(s\right),{\epsilon }_{ij}\to {\widehat{\epsilon }}_{ij}\left(s\right),{\sigma }_{ij}\to {\widehat{\sigma }}_{ij}\left(s\right),{\mathbf{C}}_{ijkl}\to s{\widehat{\mathbf{C}}}_{ijkl}\left(s\right)$, in which s is denoted as the Laplace variable.

The solution of RVE at each level in the Laplace-transform domain finally yields the effective relaxation moduli that usually generating the averaging stress components under strain loading in six directions following the homogenization theory. It should be noted that the homogenized strain loading applied at a higher level $\overline{\epsilon }\left(t\right)={\overline{\epsilon }}^{0}H\left(t\right)$ is transferred to Laplace domain as $\widehat{\overline{\epsilon }}\left(s\right)={\overline{\epsilon }}^0/s$. The homogeneous stress-strain relationship in the Carson-Laplace domain is shown in Equation 2:

${\widehat{\overline{\sigma }}}_{ij}\left(s\right)=\frac{1}{\mathrm{V}}{\displaystyle \sum _{k=f,m}}\mathrm{s}{\widehat{\mathbf{C}}}_{ijkl}^{\left(k\right)}{\widehat{\epsilon }}_{kl}^{\left(k\right)}{\text{dV}}^{\left(k\right)}={\displaystyle \sum _{k=f,m}}{v}^{\left(k\right)}s{\widehat{\mathbf{C}}}_{ijkl}^{\left(k\right)}{\widehat{\overline{\epsilon }}}_{kl}^{\left(k\right)}(1)$

After obtaining the effective relaxation moduli in the Carson domain, the solution is further inversely transfer to the real domain, which is accomplished through the adopted inverse transformation technique proposed by Zakian. A few basic steps are followed:

1) The history time interval is divided into several increments $t=\left[t_1,t_2,t_3,...,t_N\right]$, at each time increment the Laplace parameter is assigned as Equation 2, where ${\alpha }_j$ is essentially complex value offered in Table 1 (Chen et al., 2017).

$s\left(j\right)={\alpha }_j/t_i\left(j=1,2,3,4,5\right)(2)$

2) The viscoelastic relaxation moduli at each time increment are then obtained by Equation 3, Where ${\mathrm{K}}_j$ is also complex coefficient whose values are listed in Table 1.

${\mathbf{C}}_{ijkl}^{*}\left(t_i\right)=\frac{2}{t_i}{\displaystyle \sum _{j=1}^5}\text{Re}\left[{\mathrm{K}}_j{\widehat{\mathbf{C}}}_{ijkl}^{*}\left({\alpha }_j/t_i\right)\right](3)$

Table 1

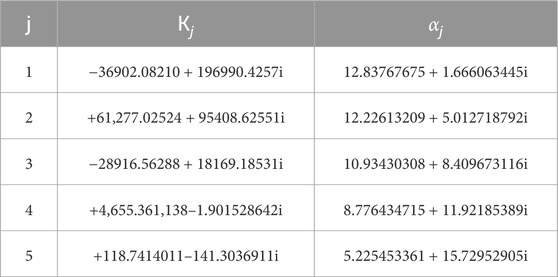
Table 1. Complex coefficients employed in Zakian’s inversion formula from Laplace transform to time domain (Chen et al., 2017).

The following subsection briefly review the micromechanics and homogenization theory that we employ in this work to predict the time-domain relaxation functions based on the aforementioned inverse technique.

2.3 Micromechanics Mori-Tanaka theory

In the 1970s, Mori and Tanaka introduced the M-T model for predicting the effective moduli of composite materials. The model is based on the premise of average stresses within the material and is grounded in the classical Eshelby solution. This solution describes the presence of inhomogeneities embedded in an infinitely large matrix and considers macroscopic loads sustained at infinity.

For typical plant layered materials, we consider layering inhomogeneities as fibers, especially cellulose and cell walls in this paper. The main theory of the M-T model is as follows: given the small size of the fibers in the infinite matrix domain, it is reasonable to assume that the average strain in the matrix is equal to the macroscopic applied strain ${\overline{\epsilon }}_m=\overline{\epsilon }$. The Eshelby-type strain concentration matrix establishes ${\mathrm{A}}_{m\infty }^{\left(f\right)}$ to link between the average fiber strain and the matrix ${\overline{\epsilon }}_f={\mathrm{A}}_{m\infty }^{\left(f\right)}{\overline{\epsilon }}_m$, where ${\mathrm{A}}_{m\infty }^{\left(f\right)}$ is a crucial parameter in the Eshelby model that describes a fiber embedded into an infinite matrix phase, used to transform the average strain in the matrix phase into the average strain in the fiber phase, it can be calculated using the Eshelby tensor and the elastic moduli of the matrix and the fibers (Chen et al., 2021; Gao et al., 2024). Thus, the following Equation 4 relation can be obtained for two-phase composites:

$\overline{\epsilon }=v_f{\overline{\epsilon }}_f+v_m{\overline{\epsilon }}_m\Rightarrow \overline{\epsilon }=\left[v_f{\mathrm{A}}_{m\infty }^{\left(f\right)}+v_m\mathrm{I}\right]{\overline{\epsilon }}_m(4)$

At a particular scale in the hierarchical structure, $v_f$ and $v_m$ represent the volume fractions of the fiber phase and matrix phase, respectively. The relationship between them is $v_f+v_m=1$.

Substitution of Equation 4 into ${\overline{\epsilon }}_f={\mathrm{A}}^{\left(f\right)}\overline{\epsilon }$ yields Equation 5:

${\overline{\epsilon }}_f={\mathrm{A}}^{\left(f\right)}\left[v_f{\mathrm{A}}_{m\infty }^{\left(f\right)}+v_m\mathrm{I}\right]{\overline{\epsilon }}_m(5)$

where ${\mathrm{A}}^{\left(f\right)}$ is the fiber’s strain concentration matrix relating the averaging fiber strain with the macroscopic strain concentration strain (Chen et al., 2021; Gao et al., 2024). Subsequently, The strain concentration matrix of the two-phase composite shown in Equation 6 can be calculated by substituting ${\overline{\epsilon }}_f={\mathrm{A}}_{m\infty }^{\left(f\right)}{\overline{\epsilon }}_m$ into Equation 5:

${\mathrm{A}}^{\left(f\right)}={\mathrm{A}}_{m\infty }^{\left(f\right)}{\left[v_f{\mathrm{A}}_{m\infty }^{\left(f\right)}+v_m\mathrm{I}\right]}^{-1}(6)$

Finally, using the homogenization equation, the homogenized stiffness matrix of the two-phase composite can be derived as Equation 7:

${\mathbf{C}}^{*}={\mathbf{C}}^{\left(m\right)}+v_f\left({\mathbf{C}}^{\left(f\right)}-{\mathbf{C}}^{\left(m\right)}\right){\mathrm{A}}_{m\infty }^{\left(f\right)}{\left[v_f{\mathrm{A}}_{m\infty }^{\left(f\right)}+v_m\mathrm{I}\right]}^{-1}(7)$

In this equation, ${\mathbf{C}}^{\left(f\right)}$ and ${\mathbf{C}}^{\left(m\right)}$ represent the elastic matrices of the fiber and matrix, respectively.

The elastic moduli of the composite can be calculated directly by using the strain concentration matrix ${\mathrm{A}}_{m\infty }^{\left(f\right)}$. In this study, the M-T model is applied using the simplified expression of Equation 7 to create and homogenize the multiscale microstructure of the plant tissue. The resulting effective properties can then be used as inputs in higher-level microstructural analyses.

3 Numerical validations of multiscale model

3.1 Multiscale elastic coefficients of plant fibers

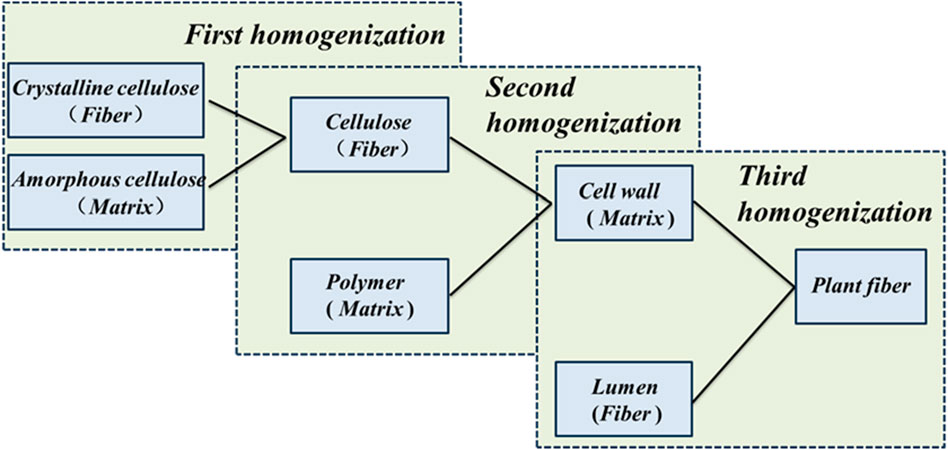
The mechanical and multifunctional behavior of plant fibers is closely related to the optimized multilevel fine structure at each scale. Based on the theory of fiber-matrix composites, a multi-scale structural model of the fine structure of plant fibers has been developed. The model begins at the microscopic level by considering cellulose filaments composed of crystalline and amorphous cellulose located in the S2 structural layer of the fibroblast wall. The cellulose filaments and surrounding polymer network at the microscopic scale form the microstructure of the plant cell wall, and the cell wall and surrounding lumen form the highest-level structure of the plant fiber. In this progressive multiscale framework, the homogenized effective stiffness matrix is passed as input data to higher level microstructures through the M-T model to finally obtain the macroscopic effective moduli, and the flow chart of plant fiber homogenization is shown in Figure 5. In this section, we explain the progressive homogenization mainly through the M - T model.

Figure 5

Figure 5. Flow chart of homogenization of plant fibers.

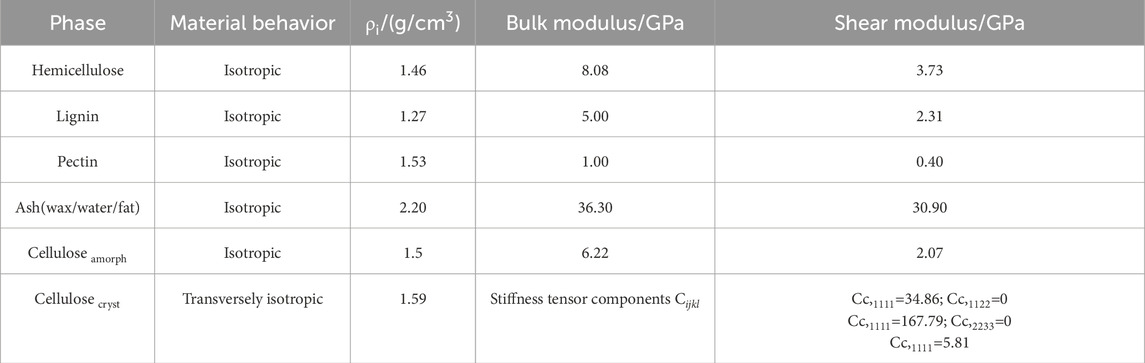
There are five main categories of different plant fibers in nature—bast, grass, leaf, fruit and straw, Konigsberger et al. (2023) collected and calculated the contents of the main components of 26 plant fibers from those five groups. To emphasize a conservative estimation and parametric analysis of fiber materials under non-ideal conditions, we selected the fiber fraction corresponding to the minimum homogeneous fiber stiffness/strength for modeling calculations, thereby avoiding the underestimation of material weakening effects under actual working conditions due to excessive fiber content. As shown in Table 2, it calculated cell wall-related phase volume fractions according to the minimum homogenized fiber stiffness/strength. These data were used as input parameters in our model to calculate the homogenized modulus of the fibers under different microstructures. In the polymer network’s RVE, we calculate the homogeneous moduli by taking a weighted average based on the volume fraction of each component. This approach ensures that each component’s contribution is accounted for in the final result. For the cellulose RVE, we consider amorphous cellulose as the matrix and crystalline cellulose as the dopant phase. By using the proposed multiscale M-T method, we can obtain a homogeneous modulus. For the cell wall RVE, we considered the polymer network as the matrix and cellulose as the inhomogeneity. We were able to use the M-T method obtain the homogeneous modulus of the cell wall RVE. For the fiber RVE, we consider the cell wall as the matrix and the pores as the inhomogeneity, and obtain the homogeneous modulus of cellular fiber RVE by the M-T method. The tissue-independent elastic phase mechanical properties of plant fiber cells are shown in Table 3.

Table 2

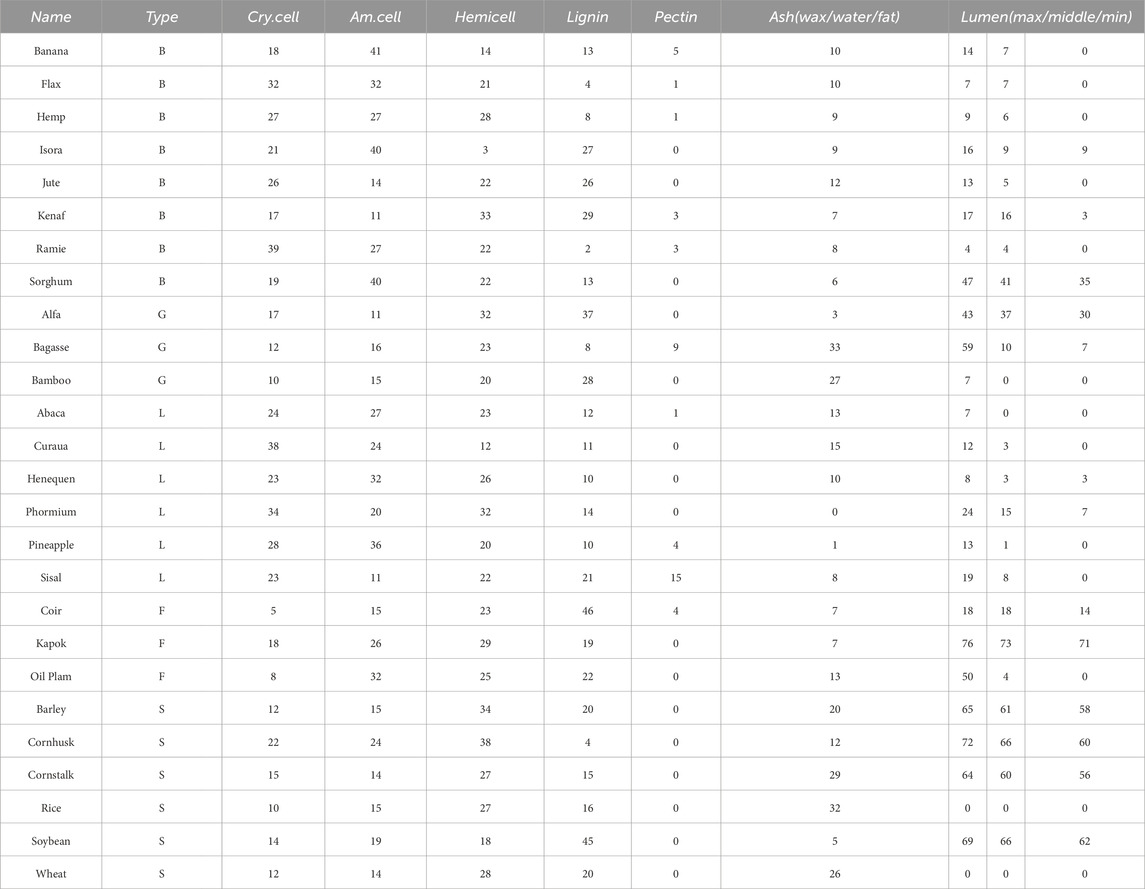
Table 2. Cell wall-related phase volume fractions in percent (Konigsberger et al., 2023).

Table 3

Table 3. Tissue-independent elastic phase properties.

Figure 6 displays the predicted results of the axial moduli of elasticity of the cellular fiber bundles in the literature. The red triangular markers represent the calculated results of the M-T model, which are in good agreement with the predicted results. This indicates the accuracy of the calculated results of the M-T model. The optimum range of the M-T model is smaller than the literature results, because only the variation in the eigenvalues of the lumen content of plant fibers is considered in the M-T multiscale computational model. In the polymer network calculations, the eigenvalues of the substance components are regard as their average values, whereas the range of eigenvalues of the substance components of plant fibers counted in the literature is somewhat larger.

Figure 6

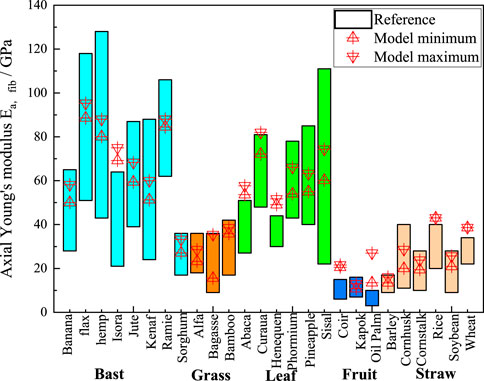
Figure 6. Comparison chart of axial elastic moduli. The cyan, orange, green, blue, and light orange boxes represent bast, grass, leaf, fruit, and straw plant fibers, respectively (The reference of Konigsberger et al. (2023) describes the moduli of elasticity of natural plant fibers calculated using numerical simulations).

Additionally, as shown in Table 4 we compared the calculated axial Young’s moduli of fibers with existing literature. Zhao numerically calculated the mechanical properties of bamboo fibers at varying fiber contents (0-1), obtaining a modulus of 32.55 GPa at a fiber content of 0.93 (Zhao et al., 2018). This value differed by only 3.29 GPa from our M-T model, resulting in a relative error of approximately 10%. The comparison demonstrates good agreement between the two results. Similarly, Nilsson tested the mechanical properties of flax fibers using tensile loading experiments (Nilsson, 2006). The cellulose content in the flax test fibers varied between 64% and 78%. The axial Young’s modulus of flax fibers measured by Nilsson was 67.1 GPa, while our M-T model yielded a modulus of 91.94 GPa with a cellulose content of 0.96. The slightly higher modulus from our model can be attributed to the higher cellulose content assumed in our calculations compared to the values reported in the literature.

Table 4

Table 4. Comparison of axial Young’s moduli of fibers with literature results.

In Figures 7–9, we present the ranges of homogenized transverse Young’s modulus, transverse shear modulus, and axial shear modulus of plant fibers calculated based on the data from Table 2. The minimum values are derived from the fibers’ minimum lumen content, and the maximum values are derived from the maximum lumen content. Since the minimum, intermediate, and maximum lumen content for rice and wheat are all zero, the model can only calculate a single modulus value, which is represented as a short black line in the figures. Specifically, Figure 7 shows the statistically predicted transverse elastic modulus of plant fibers using the M-T model. The mean modulus predicted by the model is connected by short black straight lines. Bast fibers exhibit transverse modulus of elasticity ranging from 3 GPa to 19 GPa. Grass fibers exhibit transverse moduli of elasticity ranging from 3 GPa to 16 GPa. Leaf fibers exhibit transverse moduli of elasticity ranging from 6 GPa to 18 GPa. Fruit fibers exhibit transverse moduli of elasticity ranging from 1 GPa to 10 GPa. Straw fibers exhibit transverse modulus of elasticity ranging from 1 GPa to 18 GPa.

Figure 7

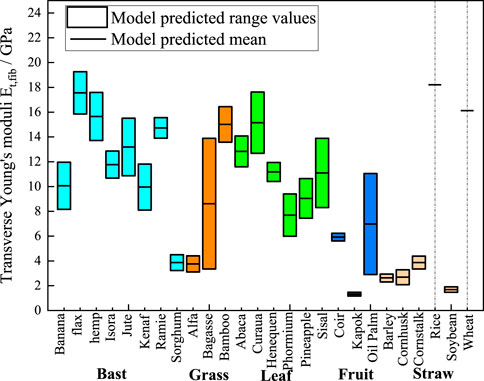
Figure 7. M-T model predictions chart of transverse elastic moduli. The cyan, orange, green, blue, and light orange boxes represent bast, grass, leaf, fruit, and straw plant fibers, respectively. The lumen content for rice and wheat is zero, so the model shows a single modulus value as a short black line.

Figure 8

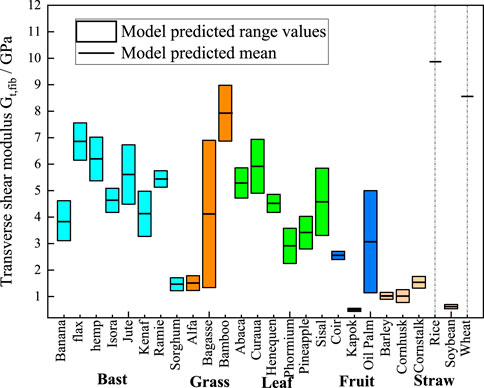
Figure 8. M-T model predictions chart of transverse shear moduli. The cyan, orange, green, blue, and light orange boxes represent bast, grass, leaf, fruit, and straw plant fibers, respectively. The lumen content for rice and wheat is zero, so the model shows a single modulus value as a short black line.

Figure 9

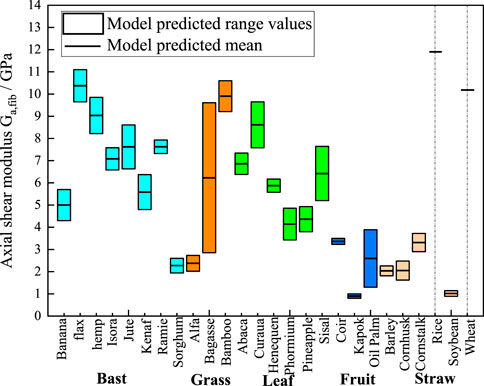
Figure 9. M-T model predictions chart of axial shear moduli. The cyan, orange, green, blue, and light orange boxes represent bast, grass, leaf, fruit, and straw plant fibers, respectively. The lumen content for rice and wheat is zero, so the model shows a single modulus value as a short black line.

Figure 8 presents the statistically predicted transverse shear moduli of the plant fibers using the M-T model. The mean modulus predicted by the model is connected by short black straight lines. Bast fibers exhibit transverse shear modulus ranging from 1 GPa to 7.5 GPa. Grass fibers exhibit transverse shear moduli ranging from 1 GPa to 9 GPa. Leaf fibers exhibit transverse shear modulus ranging from 2 GPa to 7 GPa. Fruit fibers exhibit transverse shear modulus ranging from 0.4 GPa to 4.5 GPa. Straw fibers exhibit transverse shear moduli ranging from 0.2 GPa to 9.5 GPa.

Figure 9 presents the statistically predicted axial shear moduli of the plant fibers using the M-T model. The mean modulus predicted by the model is connected by short black straight lines. Bast fibers exhibit axial shear modulus ranging from 2 GPa to 11 GPa. Grass fibers exhibit axial shear moduli ranging from 2 GPa to 10.5 GPa. Leaf fibers exhibit axial shear moduli ranging from 3.5 GPa to 9.5 GPa. Fruit fibers exhibit axial shear moduli ranging from 1 GPa to 3 GPa. Straw fibers exhibit axial shear moduli ranging from 1 GPa to 12 GPa.

The above findings demonstrate that plant fibers with varying polymer content, cellulose volume fraction and lumen content exhibit significant discrepancies in their mechanical properties. Conversely, plant fibers of the same species display relatively minor differences in polymer content, cellulose volume fraction and lumen content, with fluctuations in their mechanical properties being considerably less pronounced. The mechanical properties of the fibers are primarily determined by their component composition, cellulose content and crystallinity. In general, the tensile strength and Young’s modulus of plant fibers increase with the increase of cellulose content (Djafari, 2017). High cellulose content exhibits high Young’s modulus, while the relative polymer content shows a negative correlation with the tensile strength and Young’s modulus of plant fibers (Komuraiah et al., 2014). As illustrated in Figures 7, 8, flax fibers comprising 32% crystalline cellulose exhibit a transverse Young’s modulus of 19.26 GPa and a transverse shear modulus of 7.56 GPa. In comparison, sorghum fibres with a lower crystalline cellulose content (19%) display a transverse Young’s modulus of 4.5 GPa and a transverse shear modulus of 1.71 GPa. The lumen content exhibits a negative correlation with the Young’s modulus of plant fibers; as the lumen content increases, the Young’s modulus of the plant fibers tends to decrease.

3.2 Viscoelastic model validation of plant fibers

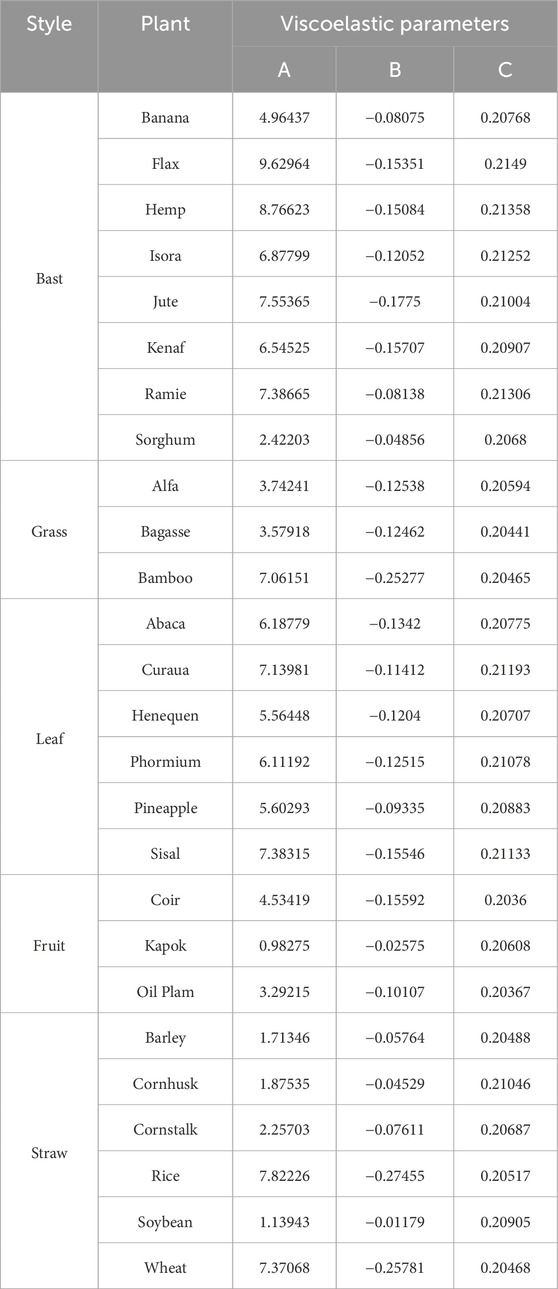
Viscoelasticity is the behavior of a material that exhibits strain accumulation (creep) under constant stress and/or stress reduction (relaxation) under constant stress. The power law model describing creep shows two mechanisms for the evolution of strain induced by a constant stress: (i) a transient elastic response followed by (ii) a degenerate creep response. The creep function expression can be expressed by the following three-parameter equation (Equation 8), where A is the instantaneous modulus of elasticity, B is the coefficient of flexibility associated with the material properties, and C is the dynamic properties associated with the material creep. In the absence of experimentally derived creep properties for each of the macromolecules such as lignin, hemicellulose, pectin, etc., these phases were treated together and calibrated to the results of the macroscopic normal creep experiments reported in the literature (Eitelberger et al., 2012) by fitting the model predictions to the following parameters of the normal creep softness function for the plant fiber specific samples, as shown in Table 5.

${{\mathrm{J}}_{\mathrm{T}}}^{\exp }=\mathrm{A}+\mathrm{B}{\left(\frac{\mathrm{t}}{1\min }\right)}^{\mathrm{C}}(8)$

Table 5

Table 5. Parameter list of creep function equations for specific plant fibers.

According to the predicted data in Figure 10, the viscous moduli of different types of plant fibers shows a decreasing trend and gradually stabilizes with increasing simulation time, and the magnitude of the out-of-plane viscous moduli of their plant fibers is influenced by the content of macromolecular polymer fractions, cellulose crystallinity and lumen porosity. The instantaneous modulus of elasticity of the plant fiber, which is the out-of-plane shear moduli of the plant fiber, can be derived from the curve at the instant of 0. It can be seen that the instantaneous modulus of elasticity of the five plant fibers predicted by the viscous model is close to the result of the out-of-plane shear moduli predicted by the M-T model, which indicates that the proposed multiscale viscous model can predict the viscoelastic mechanical properties of plant fibers very well. Although the modulus predicted by the viscous model is close to that of the M-T model, the differences mainly arise from the assumptions and inherent modeling approaches. The M-T model assumes homogeneity in material properties at each scale and simplifies the interactions between microstructures based on the material’s linear elastic behavior. In contrast, the viscous model accounts for the time-dependent behavior of materials, particularly considering the heterogeneity of microstructures and the influence of fiber porosity. These factors can lead to nonlinear viscoelastic responses, resulting in slight differences from the predictions of the M-T model.

Figure 10

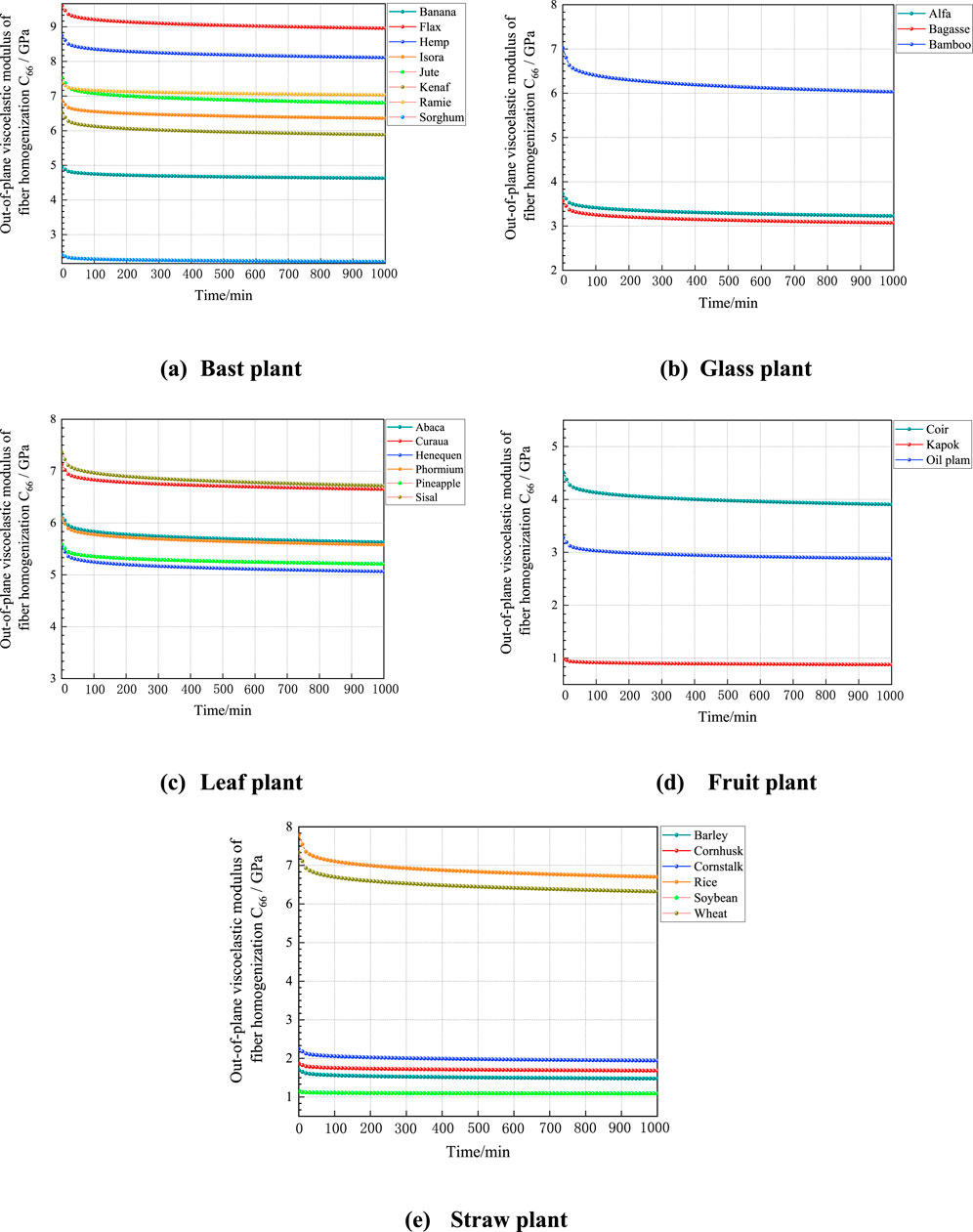
Figure 10. Relative creep curves of plant fibers. (A) Bast plant, (B) Glass plant, (C) Leaf plant, (D) Fruit plant, (E) Straw plant.

Agricultural technicians can develop more rational planting, support, and management strategies to prevent plant damage due to natural factors such as wind and rain by gaining an in-depth understanding of the mechanical properties of plant cells and tissues. This understanding can also serve as a reference for similar studies on other plants.

4 Parametric study

The fiber content of various plants varies significantly. The red dashed line in the figure indicates the maximum value of the axial modulus of elasticity predicted by the M-T model for each type of plant fiber, while the black dashed line indicates the minimum value of the axial modulus of elasticity predicted by the model for each type of plant fiber. Figure 11 shows that plants of the same species generally have a closely related cellulose content. The average cellulose content of bast plant fibers was about 0.64 and the average value of the in-plane modulus of elasticity was 70.75 GPa, the average cellulose content of grass plant fibers was about 0.31 and the average value of the in-plane modulus of elasticity was 34.17 GPa, and the average cellulose content of leaf plant fibers was about 0.62 and the average value of the in-plane modulus of elasticity was 65.8 GPa. The average cellulose content of fruit-type plant fibers was about 0.44 and the average value of in-plane modulus of elasticity was 20.5 GPa, and the average cellulose content of straw-type plant fibers was about 0.43 and the average value of in-plane modulus of elasticity was 29.3 GPa, which can be seen to basically follow the rule that the higher the cellulose content of plant fibers, the higher the axial modulus of elasticity of the fibers.

Figure 11

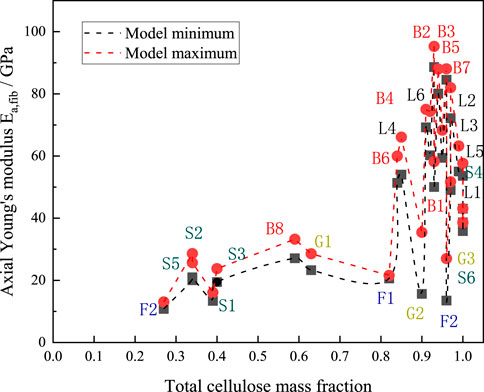
Figure 11. Axial elastic moduli plotted against cellulose content. B1-B8 denote Banana, Flax, Hemp, Isora, Jute, Kenaf, Ramie, and Sorghum, respectively; G1-G3 denote Alfa, Bagasse, and Bamboo, respectively; and L1-L6 denote Abaca, respectively, Curaua, Henequen, Phormium, Pineapple and Sisal, respectively; F1-F3 denote Coir, Kapok and Oil Plam, respectively; and S1-S6 denote Barley, Cornhusk, Cornstalk, Rice, Soybean and Wheat, respectively.

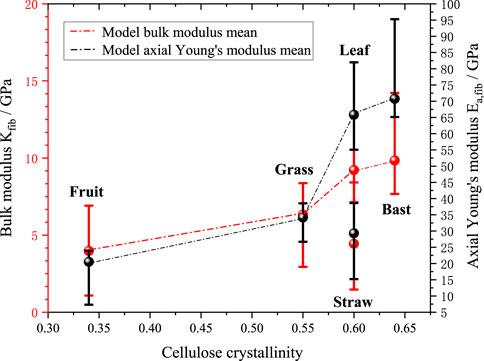
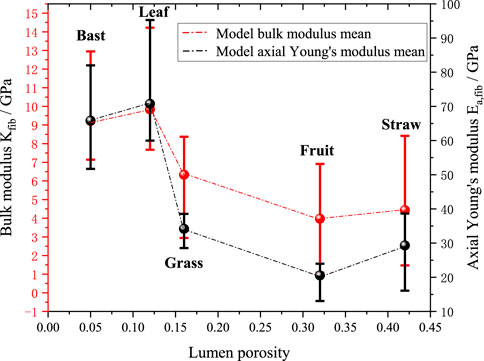
Figures 12, 13 further investigate the effects of cellulose crystallinity and lumen porosity on bulk moduli and axial young’s moduli. The model’s predicted data shows that the bulk moduli and axial moduli of elasticity exhibit a similar trend. The data shows that plant fibers with bast style have cellulose crystallinity of 0.64, lumen porosity of 0.12, and bulk moduli of 9.8 GPa. The plant fibers with grass style have cellulose crystallinity of 0.55, lumen porosity of 0.16, and bulk moduli of 6.3 GPa. The plant fibers with leaf style have cellulose crystallinity of 0.6, lumen porosity of 0.05, and bulk moduli of 9.2 GPa. The plant fibers with fruit style have cellulose crystallinity of 0.34, lumen porosity of 0.32, and bulk moduli of 4.0 GPa. The plant fibers with straw style have cellulose crystallinity of 0.6, lumen porosity of 0.42, and bulk moduli of 4.4 GPa. It can be seen that it basically follows the rule that the greater the cellulose crystallinity of the plant fiber, the higher the bulk moduli; at the same time the greater the lumen porosity, the smaller the bulk moduli.

Figure 12

Figure 12. Effect of average cellulose crystallinity on mechanical properties of fibers.

Figure 13

Figure 13. Effect of average lumen porosity on mechanical properties of fibers.

It has been demonstrated that the mechanical properties of plant fibres are influenced by two key factors: cellulose crystallinity and internal cavity porosity. These insights provide new avenues for innovation in composite fibre materials. Tobacco plants are a rich source of fibres, which could provide a viable resource for a range of bio-based applications. This spectrum of potential applications extends to but is not limited to, the development of biodegradable plastics, paper products, bio-composite materials, and even ventures into the energy sector, thereby underpinning the versatility and utility of tobacco fibres as a sustainable material resource.

The investigation delineates a pronounced correlation between the cellulose crystallinity and lumen porosity of plant fibers and their intrinsic mechanical properties, notably the bulk moduli and axial Young’s moduli. It has been observed that an augmentation in cellulose crystallinity correlates with an increase in bulk modulus, thereby indicating that materials endowed with higher cellulose crystallinity are characteristically more rigid and exhibit enhanced resistance to compressive forces. Conversely, an elevation in lumen porosity is indicative of a proliferation of void spaces within the fiber’s architecture, which consequentially leads to a diminished bulk modulus, signifying a decrement in the material’s rigidity and compressive resilience. This revelation holds substantial implications for the conceptualization and fabrication of bio-based composite materials, particularly within arenas keen on harnessing sustainable resources. The application of these findings is vast, spanning across numerous sectors including construction, automotive, packaging, and composite materials manufacturing, where leveraging these correlations can significantly aid in engineering materials tailored to possess bespoke mechanical attributes.

5 Conclusion and outlook

In this study, we examine the relationship between the multiscale microstructures of plant fibers and their viscoelastic properties, leveraging theoretical and computational analyses. We predict the elastic and creep moduli of plant fibers by homogenizing their structure across three scales: polymer and cellulose, cell wall, and fiber bundle cells. This approach integrates the Mori-Tanaka method with viscoelastic correspondence principles to accurately model the fibers’ behavior. Utilizing the elastic-viscoelastic correspondence principle, we transform homogenized elastic solutions into the Laplace domain, and through reverse engineering with empirical formulas, derive creep functions for each fiber type. The Zakian inversion method is then applied to obtain time-domain homogenized relaxation moduli.

Our model’s initial relaxation moduli predictions closely match those obtained from established viscoelastic models, confirming its accuracy against published data. By performing a triple homogenization of plant fibers, we systematically analyze the effects of cellulose content, crystallinity, and lumen porosity on the overall effective moduli. Our results indicate that increasing cellulose content and crystallinity enhances the moduli, whereas higher lumen porosity diminishes it. These findings highlight the crucial influence of microstructural characteristics on the mechanical properties of plant fibers.

The multiscale viscoelastic model presents opportunities for advancing bio composite materials. By integrating plant fibers with tailored matrices at the microscale, it is possible to develop composites with superior mechanical properties. This approach could facilitate the innovation of new and enhanced material formulations. Future research, bridging botany, materials science, and mechanics, should aim at predicting plant mechanical behaviors to breed varieties with improved mechanical characteristics, enhancing lodging resistance, disease resilience, and harvest efficiency. This direction promises wide-ranging applications and interdisciplinary collaboration potential.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

JL: Writing–review and editing, Visualization, Supervision, Project administration, Conceptualization. JW: Writing–original draft, Formal Analysis, Conceptualization. MW: Writing–original draft, Investigation. JT: Writing–original draft, Supervision, Resources, Project administration, Investigation, Funding acquisition. XG: Writing–original draft, Investigation. YW: Writing–original draft, Visualization, Resources. JS: Writing–review and editing, Resources. CX: Writing–original draft, Supervision, Project administration, Funding acquisition, Formal Analysis, Conceptualization.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors JL, MW, JT, XG, YW, JS, and CX were employed by China Tobacco Zhejiang Industrial Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alves Fidelis, M. E., Pereira, T. V. C., Gomes, ODFM, De Andrade Silva, F., and Toledo Filho, R. D. (2013). The effect of fiber morphology on the tensile strength of natural fibers. Mater Res. Technol. 2 (2), 149–157. doi:10.1016/j.jmrt.2013.02.003

CrossRef Full Text | Google Scholar

Atalla, R. H., and VanderHart, D. L. (1999). The role of solid state NMR spectroscopy in studies of the nature of native celluloses. Solid State Nucl. Magn. reson. 15, 1–19. doi:10.1016/s0926-2040(99)00042-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Bledzki, A. K., and Gassan, J. (1999). Composites reinforced with cellulose based fibers. Prog. Polym. Sci. 24 (2), 221–274. doi:10.1016/s0079-6700(98)00018-5

CrossRef Full Text | Google Scholar

Bos, H. L. (2004). Potential of flax fiber reinforced composites. Eindhoven: Technical University of Eindhoven, 157–173. doi:10.13140/RG.2.1.1540.4643

CrossRef Full Text | Google Scholar

Chen, Q., Chen, W., and Wang, G. (2021). Fully-coupled electro-magneto-elastic behavior of unidirectional multiphased composites via finite-volume homogenization. Mech. Mater. 154, 103553. doi:10.1016/j.mechmat.2020.103553

CrossRef Full Text | Google Scholar

Chen, Q., Wang, G., Chen, X., and Geng, J. (2017). Finite-volume homogenization of elastic/viscoelastic periodic materials. Compos. Struct. 182, 457–470. doi:10.1016/j.compstruct.2017.09.044

CrossRef Full Text | Google Scholar

Chen, Y., Wu, R., Shen, L., Wang, G., and Yang, B. (2022a). The multi-scale meso-mechanics model of viscoelastic dentin. J. Mech. Behav. Biomed. Mater. 136, 105525. doi:10.1016/j.jmbbm.2022.105525

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Wu, R., Yang, B., and Wang, G. (2022b). The multiscale meso-mechanics model of viscoelastic cortical bone. Biomechanics Model. Mechanobiol. 21 (6), 1713–1729. doi:10.1007/s10237-022-01615-z

CrossRef Full Text | Google Scholar

Dicker, M. P. M., Duckworth, P. F., Baker, A. B., Francois, G., Hazzard, M. K., and Weaver, P. M. (2014). Green composites: a review of material attributes and complementary applications. Compos. Part A Appl. Sci. Manuf. 56, 280–289. doi:10.1016/j.compositesa.2013.10.014

CrossRef Full Text | Google Scholar

Djafari, P. S. R. (2017). 3 - physical and mechanical properties of natural fibers. Adv. High Strength Nat. Fiber Compos. Constr., 59–83. doi:10.1016/B978-0-08-100411-1.00003-0

CrossRef Full Text | Google Scholar

Dri, F. L., Shang, S., Hector, L. G., Saxe, P., Liu, Z.-K., Moon, R. J., et al. (2014). Anisotropy and temperature dependence of structural, thermodynamic, and elastic properties of crystalline cellulose I_β: a first-principles investigation. Model. Simul. Mater. Sci. Eng. 22, 085012. doi:10.1088/0965-0393/22/8/085012

CrossRef Full Text | Google Scholar

Eitelberger, J., Bader, T., Borst, K., and Jäger, A. (2012). Multiscale prediction of viscoelastic properties of softwood under constant climatic conditions. Comput. Mater. Sci. 55, 303–312. doi:10.1016/j.commatsci.2011.11.033

CrossRef Full Text | Google Scholar

Fritsch, A., Hellmich, C., and Dormieux, L. (2009). Ductile sliding between mineral crystals followed by rupture of collagen crosslinks: experimentally supported micromechanical explanation of bone strength. Theor. Biol. 260 (2), 230–252. doi:10.1016/j.jtbi.2009.05.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Gangwar, T., Heuschele, D. J., Annor, G., Fok, A., Smith, K. P., and Schillinger, D. (2021). Multiscale characterization and micromechanical modeling of crop stem materials. Biomech. Model Mechanobiol. 20 (1), 69–91. doi:10.1007/s10237-020-01369-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Gangwar, T., and Schillinger, D. (2019). Microimaging-informed continuum micromechanics accurately predicts macroscopic stiffness and strength properties of hierarchical plant culm materials. Mech. Mater 130, 39–57. doi:10.1016/j.mechmat.2019.01.009

CrossRef Full Text | Google Scholar

Gao, M., He, Z., Lu, C., and Wang, G. (2024). Homogenized moduli and local multiphysics fields of unidirectional piezoelectric nanocomposites with energetic surfaces. Mech. Mater. 196, 105080. doi:10.1016/j.mechmat.2024.105080

CrossRef Full Text | Google Scholar

Gorshkova, T., and Morvan, C. (2006). Secondary cell-wall assembly in flax phloem fibres: role of galactans. Plant 223 (2), 149–158. doi:10.1007/s00425-005-0118-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Hofstetter, K., Hellmich, C., and Eberhard steiner, J. (2005). Development and experimental validation of a continuum micromechanics model for the elasticity of wood. Eur. J. Mech. A/Solids 24 (6), 1030–1053. doi:10.1016/j.euromechsol.2005.05.006

CrossRef Full Text | Google Scholar

Hofstetter, K., Hellmich, C., and Eberhard steiner, J. (2008). Mang Micromechanical estimates for elastic limit states in wood materials, revealing nano structural failure mechanisms. Mech. Adv. Mat. Struct. 15 (6), 474–484. doi:10.1080/15376490802142387

CrossRef Full Text | Google Scholar

Iwamoto, S., Kai, W., Isogai, A., and Iwata, T. (2009). Elastic modulus of single cellulose microfibrils from tunicate measured by atomic force microscopy. Biomacromolecules 10 (9), 2571–2576. doi:10.1021/bm900520n

PubMed Abstract | CrossRef Full Text | Google Scholar

Jamir, R. M., Majid, M. S. A., and Khasri, A. (2018). 8 - natural lightweight hybrid composites for aircraft structural applications. Woodhead Publishing Series in Composites Science and Engineering, 155–170. doi:10.1016/B978-0-08-102131-6.00008-6

CrossRef Full Text | Google Scholar

Komuraiah, A., ShyamKumar, N., and DurgaPrasad, B. (2014). Chemical composition of natural fibers and its influence on their mechanical properties. Mech. Compos. Mater. 50 (3), 359–376. doi:10.1007/s11029-014-9422-2

CrossRef Full Text | Google Scholar

Konigsberger, M., Lukacevic, M., and Fussl, J. (2023). Multiscale micromechanics modeling of plant fibers: upscaling of stiffness and elastic limits from cellulose nanofibrils to technical fibers. Mater. Struct. 56, 13. doi:10.1617/s11527-022-02097-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Mai, Y., and Ye, L. (2000). Sisal fibre and its composites: a review of recent developments. Compos. Sci. Technol. 60 (11), 2037–2055. doi:10.1016/s0266-3538(00)00101-9

CrossRef Full Text | Google Scholar

Moon, R. J., Martini, A., Nairn, J., Simonsen, J., and Youngblood, J. (2011). Cellulose nanomaterials review: structure, properties and nanocomposites. Chem. Soc. Rev. 40 (7), 3941–3994. doi:10.1039/c0cs00108b

PubMed Abstract | CrossRef Full Text | Google Scholar

Newman, R. H., Hill, S. J., and Harris, P. J. (2013). Wide-angle X-ray scattering and solid-state nuclear magnetic resonance data combined to test models for cellulose microfibrils in mung bean cell walls. Plant Physiol. 163, 1558–1567. doi:10.1104/pp.113.228262

PubMed Abstract | CrossRef Full Text | Google Scholar

Nilsson, T. (2006). “Micro mechanical modelling of natural fibres for composite materials,” in Licentiate thesis, structural mechanics. Structural mechanics (Lund University). doi:10.13140/RG.2.1.3003.2081

CrossRef Full Text | Google Scholar

Nishiyama, Y., Langan, P., and Chanzy, H. (2002). Crystal structure and hydrogen-bonding system in cellulose iβ from synchrotron X-ray and neutron fiber diffraction. J. Am. Chem. Soc. 124, 9074–9082. doi:10.1021/ja0257319

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishiyama, Y., Sugiyama, J., Chanzy, H., and Langan, P. (2003). Crystal structure and hydrogen bonding system in cellulose i_α from synchrotron X-ray and neutron fiber diffraction. J. Am. Chem. Soc. 125, 14300–14306. doi:10.1021/ja037055w

PubMed Abstract | CrossRef Full Text | Google Scholar

Nixon, B., Mansouri, K., Singh, A., Du, J., Davis, J. K., Lee, J. G., et al. (2016). Comparative structural and computational analysis supports eighteen cellulose synthases in the plant cellulose synthesis complex. Sci. Rep. 6, 28696. doi:10.1038/srep28696

PubMed Abstract | CrossRef Full Text | Google Scholar

Sathishkumar, T., Navaneethakrishnan, P., Shankar, S., Rajasekar, R., and Rajini, N. (2013). Characterization of natural fiber and composites – a review. J. Reinf. Plastics Compos. 32 (19), 1457–1476. doi:10.1177/0731684413495322

CrossRef Full Text | Google Scholar

Schwiedrzik, J., Raghavan, R., Rüggeberg, M., Hansen, S., Wehrs, J., Adusumalli, R. B., et al. (2016). Identification of polymer matrix yield stress in the wood cell wall based on micropillar compression and micromechanical modelling. Philos. Mag. 96 (32-34), 3461–3478. doi:10.1080/14786435.2016.1235292

CrossRef Full Text | Google Scholar

Song, B., Zhao, S., Shen, W., Collings, C., and Ding, S. (2020). Direct measurement of plant cellulose microfibril and bundles in native cell walls. Front. Plant Sci. 11, 479–462. doi:10.3389/fpls.2020.00479

PubMed Abstract | CrossRef Full Text | Google Scholar

Šturcová, A., Davies, G., and Eichhorn, S. (2005). Elastic modulus and stress-transfer properties of tunicate cellulose whiskers. Biomacromolecules 62, 1055–1061. doi:10.1021/bm049291k

CrossRef Full Text | Google Scholar

Sturcova, A., Davies, G. R., and Eichhorn, S. J. (2005). Elastic modulus and stress-transfer properties of tunicate cellulose whiskers. Biomacromolecules 6, 1055–1061. doi:10.1021/bm049291k

PubMed Abstract | CrossRef Full Text | Google Scholar

Sturcová, A., His, I., Apperley, D. C., Sugiyama, J., and Jarvis, M. C. (2004). Structural details of crystalline cellulose from higher plants. Biomacromolecules 5 (4), 1333–1339. doi:10.1021/bm034517p

PubMed Abstract | CrossRef Full Text | Google Scholar

Symington, M. C., Banks, W. M., Opukuro, D. W., and Pethrick, R. A. (2009). Tensile testing of cellulose based natural fibers for structural composite applications. J. Compos. Mater. 43, 1083–1108. doi:10.1177/0021998308097740

CrossRef Full Text | Google Scholar

Tamer, T. A., and Abdul, F. (2013). Cellulose microfibril angle in wood and its dynamic mechanical significance. Cellul. - Fundam. Asp. doi:10.5772/51105

CrossRef Full Text | Google Scholar

Tashiro, K., and Kobayashi, M. (1985). Calculation of crystallite modulus of native cellulose. Polym. Bull. 14 (3–4), 213–218. doi:10.1007/bf00254940

CrossRef Full Text | Google Scholar

Thomas, L. H., Forsyth, V. T., Sturcova, A., Kennedy, C. J., May, R. P., Altaner, C. M., et al. (2013). Structure of cellulose microfibrils in primary cell walls from collenchyma. Plant Physiol. 161, 465–476. doi:10.1104/pp.112.206359

PubMed Abstract | CrossRef Full Text | Google Scholar

Vandavasi, V. G., Putnam, D. K., Zhang, Q., Petridis, L., Heller, W. T., Nixon, B. T., et al. (2016). A structural study of CESA1 catalytic domain of arabidopsis cellulose synthesis complex: evidence for CESA trimers. Plant Physiol. Jan. 170 (1), 123–135. doi:10.1104/pp.15.01356

PubMed Abstract | CrossRef Full Text | Google Scholar

William, T. K., Wonsuk, K., Alan, A., Ellen, C. L., and Deborah, F. M. (2016). Finite element analysis and microscopy of natural fiber composites containing microcellular voids. Mater. and Des. 106, 285–294. doi:10.1016/j.matdes.2016.05.094

CrossRef Full Text | Google Scholar

Yao, J., Chen, W., et al. (2017). Plant tobacco science. Beijing: Science Press.

Google Scholar

Zhao, X., Tu, W., Chen, Q., and Wang, G. (2021). Progressive modeling of transverse thermal conductivity of unidirectional natural fiber composites. Int. J. Therm. Sci. 162, 106782. doi:10.1016/j.ijthermalsci.2020.106782

CrossRef Full Text | Google Scholar

Zhao, X., Wang, G., and Wang, Y. (2018). Micromechanical modeling in determining the transverse elastic moduli and stress distributions of bamboo. J. Mater. Sci. 53 (4), 2553–2565. doi:10.1007/s10853-017-1692-3

CrossRef Full Text | Google Scholar