Machine learning-based prediction of compressive strength in circular FRP-confined concrete columns

This research aims to evaluate the compressive strength of FRP-confined columns using machine learning models. By systematically organizing codes and models proposed by various researchers, significant indicators influencing compressive strength have been identified. A comprehensive database comprising 366 samples, including both CFRP and GFRP, has been assembled. Based on this database, a machine learning model was developed to accurately predict compressive strength. A thorough evaluation was conducted, comparing models proposed by codes and researchers. Additionally, a detailed parameter analysis was performed using the XGBoost model. The findings highlight the importance of both code-based and researcher-proposed models in enhancing our understanding of compressive strength. However, certain models show tendencies towards conservative or overestimated predictions, indicating the need for further accuracy enhancement. Among the models considered, the XGBoost model demonstrated the highest goodness of fit (0.97) and the lowest coefficient of variation (8%), making it a suitable choice for investigating compressive strength. Notable parameters significantly influencing compressive strength include FRP thickness, elastic modulus, and concrete strength.

1 Introduction

The lightweight, high-strength, and easily processable nature of Fibre Reinforced Polymer (FRP) materials make them extensively utilized for reinforcing concrete or reinforced concrete structures (Deifalla, 2022; Jedrzejko et al., 2023; Liao et al., 2023; Nadir et al., 2023; Sayed et al., 2023). Traditionally, steel cages or steel sleeves are externally applied to concrete columns to enhance ductility and load-bearing capacity (Richart et al., 1929; Ruiz-Pinilla et al., 2021; Salah et al., 2022; Truong et al., 2022). However, steel cages increase the self-weight and cross-sectional area of the structure, whereas steel sleeves have a comparatively lesser impact on self-weight and cross-sectional area. Additionally, steel structures are vulnerable to environmental factors and corrosion. Furthermore, both methods are time-consuming, require significant labor input, and are less economically viable (Saadatmanesh et al., 1994; Elsanadedy et al., 2012). In contrast, FRP materials exhibit outstanding corrosion resistance and weigh approximately 20% of steel while possessing equivalent tensile strength. Moreover, the thermal expansion coefficient of FRP closely matches that of concrete, allowing them to function harmoniously without inducing significant temperature-induced stresses amid environmental fluctuations. Consequently, incorporating FRP materials for structural reinforcement has the potential to substantially reduce maintenance expenditures and prolong the lifespan of the structure (Tafsirojjaman et al., 2022; Chole et al., 2023; Hu et al., 2023; Rafieizonooz et al., 2023).

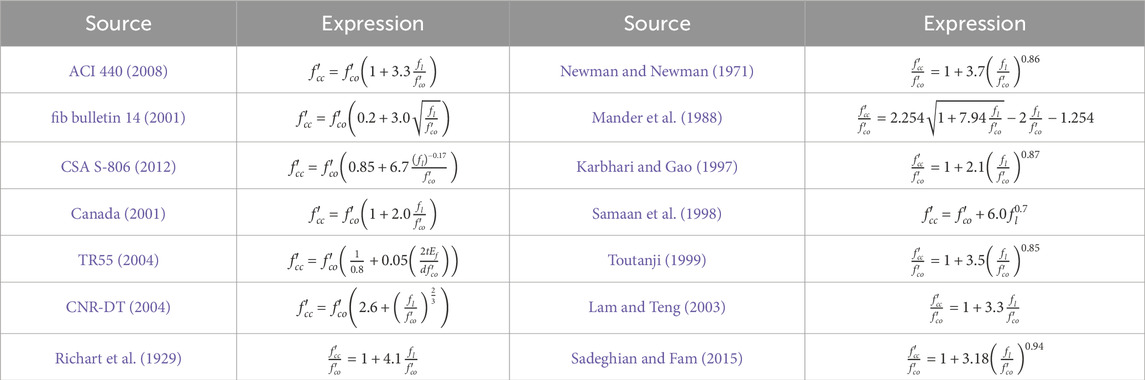
Since the 1990s, researchers and committees dedicated to code development have undertaken substantial endeavours to devise calculation models for the ultimate limit state analysis of FRP-confined columns. These models have predominantly focused on two fundamental aspects: compressive strength and ultimate axial strain. The current ACI440 guidelines endorse the model introduced by Lam and Teng in 2003, alongside the model presented by ISIS (ACI 440, 2008; Lam and Teng, 2003; Canada, 2001). These models are grounded on the concept of a linear correlation between the ratio of compressive strength to unconfined concrete strength and the ratio of ultimate axial strain. Conversely, alternative methodologies, including those proposed by fib, CSA S-806, TR55, CNR-DT, Newman, Mander, Karbhari, Toutanji, Sadeghian, and Fam, advocate for a power function relationship between the aforementioned ratios (fib bulletin 14, 2001; CSA S-806, 2012; TR55, 2004; CNR-DT, 2004; Newman and Newman, 1971; Mander et al., 1988; Karbhari and Gao, 1997; Toutanji, 1999; Sadeghian and Fam, 2015). Meanwhile, Samaan’s model proposes a linear correlation between the compressive strength of FRP-confined concrete columns and the concrete strength, while recognising a non-linear association with ultimate axial strain (Samaan et al., 1998). Research findings indicate that progress in comprehending the compressive strength of FRP-confined columns has been facilitated by models proposed by codes and researchers. Nevertheless, it is imperative to acknowledge that the compressive strength is influenced by a myriad of parameters, and the intricate interplay among these parameters presents significant challenges. The reliability and precision of existing models are not always assured. Consequently, this research paper presents a sophisticated machine learning model capable of addressing the complexities inherent in multi-parameter modelling to accurately predict compressive strength in FRP-restrained columns.

2 Research significance

Compared to existing published literature, this paper establishes a model for assessing the compressive strength of FRP-confined concrete structures based on ensemble learning method (XGBoost). It comprehensively considers the influence of material strength grades, structural dimensions, FRP thickness, and fracture strain on its compressive strength. The accuracy of the model is validated by comparing the predictive results of the ensemble learning model with models proposed by relevant codes and researchers. The aim of this study is to provide engineers and researchers with a novel method and perspective to better understand the evolution of mechanical properties of FRP-reinforced concrete structures. Additionally, a corresponding graphical interface will be developed in the later stages to offer reliable support for engineering design and maintenance work.

3 Methodology

This section outlines the methodology employed in this study. Firstly, data on the compressive strength of FRP-confined concrete columns under different conditions are collected from relevant literature and experiments, and divided into training and testing sets. Based on the training set data, an ensemble learning model (XGBoost) is utilized to predict the compressive strength of FRP-confined concrete columns. The proposed model incorporates input variables such as material dimensions, material strength, FRP thickness, and elasticity modulus, with the output parameter being the compressive strength of the concrete after FRP reinforcement. Additionally, the predictive results of the XGBoost ensemble learning model are compared with those of corresponding normative models and models proposed in the literature to further demonstrate the superiority of this model. Finally, the influence of each input variable on the compressive strength of FRP-confined concrete columns is analyzed.

4 Building an indicator system for prediction

4.1 Review of the existing models

Table 1 presents an overview of the models proposed by both codes concerning the compressive strength of FRP-confined concrete columns (Notes: The models listed in Table 1 mainly originate from relevant standards of different countries and have been widely accepted by the industry. Currently, these calculation models have not been updated. The prediction accuracy of newly developed theoretical models and machine learning models for this year has been demonstrated in Figure 5 of this paper).

Table 1

Table 1. Models proposed by codes and researchers.

The mathematical expression for the maximum confinement stress, f_l, is shown in Eq. 1.

$f_l=\frac{{\rho }_{frp}{f}_{frp}}{2}=\frac{2t{E}_{frp}{\epsilon }_{frp}}{d}(1)$

Where, t denotes the thickness of FRP, E_frp denotes the elasticity modulus of FRP, ɛ_frp denotes the FRP rupture strain, and d denotes the diameter of the column. Therefore, taking into consideration the models proposed by codes and researchers, as well as the collectability of the data, the initial parameters for this study are determined as follows: column diameter (D), FRP thickness (t), concrete strength (f^’_co), elasticity modulus of FRP (E_f), FRP fracture strain (ɛ_h,rup), and compressive strength of the confined column (f^’_cc). Among these parameters, f^’_cc is the dependent variable, i.e., the output feature, while the others are independent variables, i.e., the input features.

4.2 Establishment of database and indicator system

4.2.1 Established the database

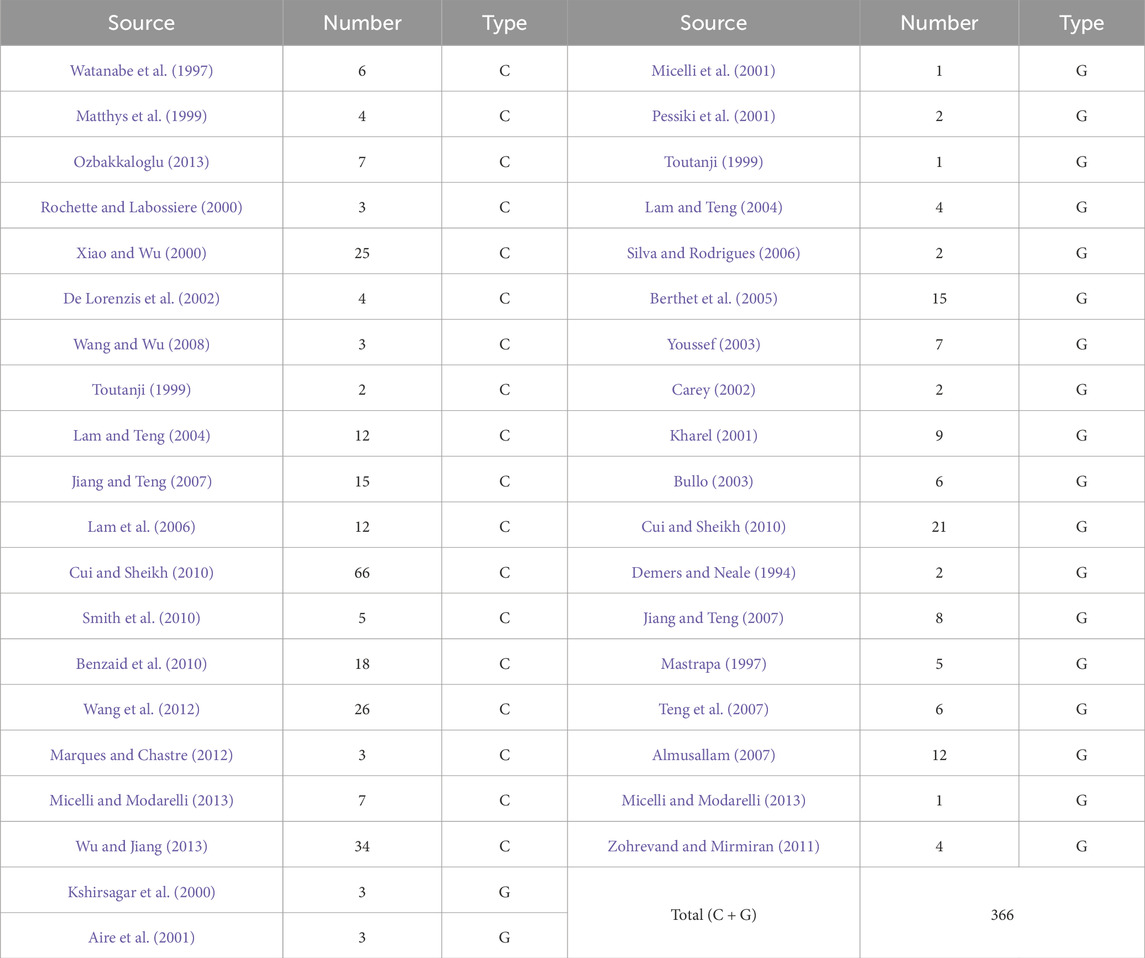
In this study, a comprehensive dataset comprising 366 entries was compiled, sourced from experiments conducted by 41 researchers. The origins of these data are delineated in Table 2, with the distribution of parameters illustrated in Figure 1. The criteria for selecting experimental data are as follows:

(1) This study exclusively focuses on investigating FRP-strengthened circular concrete columns, and the database has not yet been designed for related research on concrete beams.

(2) The selected concrete columns were not reinforced with steel bars; thus, only the influence of FRP on the load-bearing capacity of plain concrete was considered.

(3) The chosen samples consist of concrete columns entirely wrapped with FRP.

Table 2

Table 2. Experimental database.

Figure 1

Figure 1. Distribution of parameters.

In addition, this study primarily investigated the variation in load-bearing capacity of ordinary concrete columns reinforced with CFRP and GFRP. Due to limitations in experimental data availability, the data for BFRP (Basalt Fiber-Reinforced Polymer) reinforcement was relatively limited or insufficient, hence the assessment of load-bearing capacity of concrete columns reinforced with BFRP was not conducted at this time. Future research will be needed to conduct corresponding experiments to explore the variation in load-bearing capacity of concrete structures reinforced with BFRP.

Upon analysis of Table 2, it is apparent that the dataset comprises a significant total of 366 samples, sourced from a diverse array of origins. This comprehensive selection aids in mitigating the inherent variability encountered during subsequent model establishment endeavours. Through examination of Figure 1, it is evident that parameter D exhibits a predominant distribution within the range of 150–160 mm, while parameter t predominantly falls within the range of 0–2 mm. Additionally, f^’_co demonstrates a distribution pattern encompassing the interval of 25–60 MPa. Notably, ɛ reveals a higher occurrence of distribution within the intervals of 0–1 and 1–2.5. Similarly, E_f exhibits a higher frequency of distribution within the range of 0–300 GPa. It is worth noting that occurrences in other intervals are comparatively less frequent.

4.2.2 Establishment of indicator system

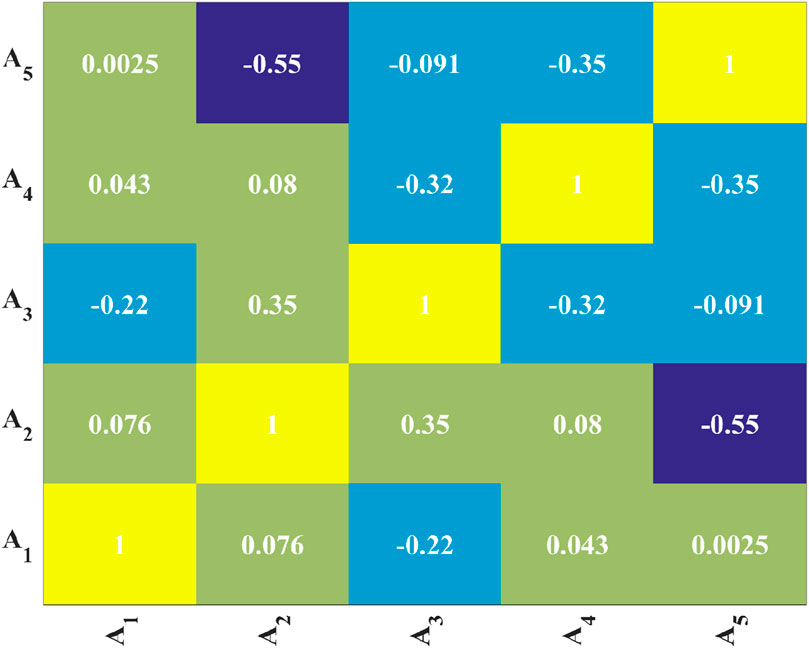
Initially, relying on the parameters delineated in Section 4.2.1: D, t, f^’_co, E_f, ɛ_h,rup, and the f^’_cc, an initial indicator system is devised. The correlation analysis of each indicator is shown in Figure 2. It is evident that, with the exception of a weak correlation between E_f and t, there exists no correlation among the other indicators.

Figure 2

Figure 2. Correlation among indicators.

5 Compression strength model based on machine learning

5.1 Selection of the optimal machine learning model

This section primarily investigates the suitability of both individual and ensemble machine learning models within this research context. The single machine learning models employed encompass linear regression (LR), ridge regression (RR), decision tree (DT), and artificial neural network (ANN). Additionally, ensemble machine learning models, including random forest (RF) and XGBoost, are utilised. The linear regression (LR) model is suitable for exploring linear relationships between dependent and one or more independent variables. It is simple, intuitive, and computationally efficient; however, its performance may degrade when data exhibits non-linear relationships. The ridge regression (RR) model is an improvement over linear regression, designed to handle multicollinearity (high correlation between independent variables). It still struggles with non-linear problems. The decision tree (DT) model is effective for handling non-linear datasets and can address classification and regression tasks, but it is prone to overfitting. Random forest (RF) consists of multiple decision tree models and is suitable for processing high-dimensional and large-scale datasets, effectively reducing overfitting risk. However, it is sensitive to data quality and feature selection. The artificial neural network (ANN) model can learn and capture complex patterns in data but is sensitive to hyperparameters, requires complex tuning, and its results are challenging to interpret. In contrast, the XGBoost model (Extreme Gradient Boosting) offers superior predictive performance compared to traditional linear regression, ridge regression, decision trees, and random forests. It achieves ensemble learning through gradient boosting, progressively enhancing the performance of multiple weak learners during training to achieve higher predictive accuracy. Additionally, XGBoost can effectively handle non-linear relationships and high-dimensional data, exhibiting strong fitting capabilities to capture complex patterns in the data. Moreover, XGBoost employs regularization and pruning strategies to control model complexity and mitigate overfitting risks (Vapnik, 1995; Breiman, 2001; Friedman et al., 2001; Chen and Guestrin, 2016).

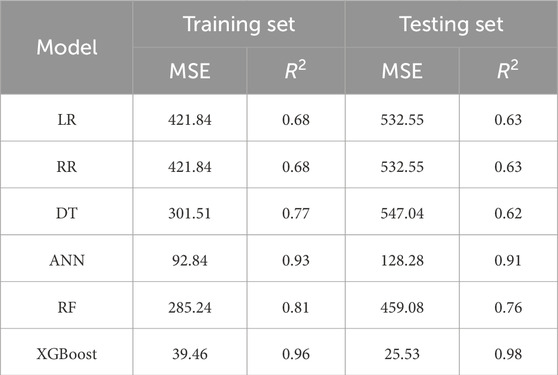
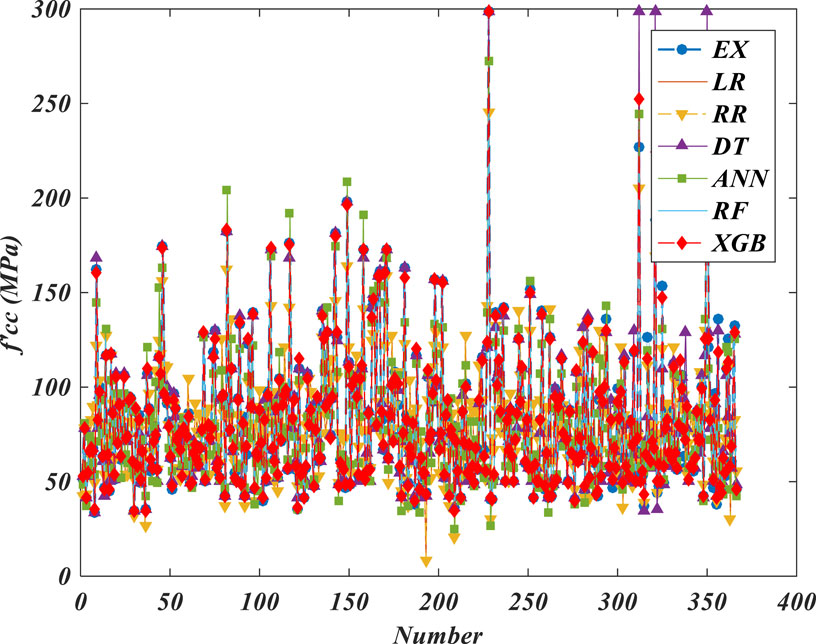
The data used to construct these models are sourced from the database established in Section 2.2.1. Among these samples, 70% are allocated for the training set, 10% for the validation set, and 20% for the testing set. The models’ performance is evaluated based on the mean squared error (MSE) and coefficient of determination (R²). The MSE assesses the model’s accuracy by quantifying the disparity between predicted and experimental values, with a smaller value indicating reduced error. Meanwhile, R² gauges the degree of correspondence between predicted and experimental values, with a value closer to 1 signifying a stronger alignment. The performance of each machine learning model on both the training and testing sets is detailed in Table 3.

Table 3

Table 3. Performance of the models.

Based on Table 3; Figure 3, it is apparent that linear regression and ridge regression manifest comparable performance across both the training and testing datasets. Random forest, overall, surpasses decision trees in performance. Particularly noteworthy is the markedly superior performance of neural networks and XGBoost in comparison to other models. Furthermore, both these model categories display comparable MSE and R² values across both the training and testing datasets.

Figure 3

Figure 3. Performance of the models after adding the labels.

5.2 Evaluation of models proposed by codes and researchers

This section assesses the performance of the models outlined in Section 4.2.1, utilising the database established in Section 2.2.1. The evaluation is conducted using measures of goodness of fit (R²), mean value ($\upsilon$), and coefficient of variation (Cov). The $\upsilon$ is employed to ascertain whether the models’ predictions tend towards conservatism or overestimation. Meanwhile, the Cov serves to gauge the precision or accuracy of a model. A smaller Cov indicates greater precision, suggesting that the model’s predictions closely align with actual or experimental values. Comparisons between the calculated values and experimental values for the model recommended by codes and researchers are illustrated in Figures 4, 5, respectively. Furthermore, Figure 6 presents a comparison between the predicted values and experimental values of the XGBoost model developed in Section 5.1.

Figure 4

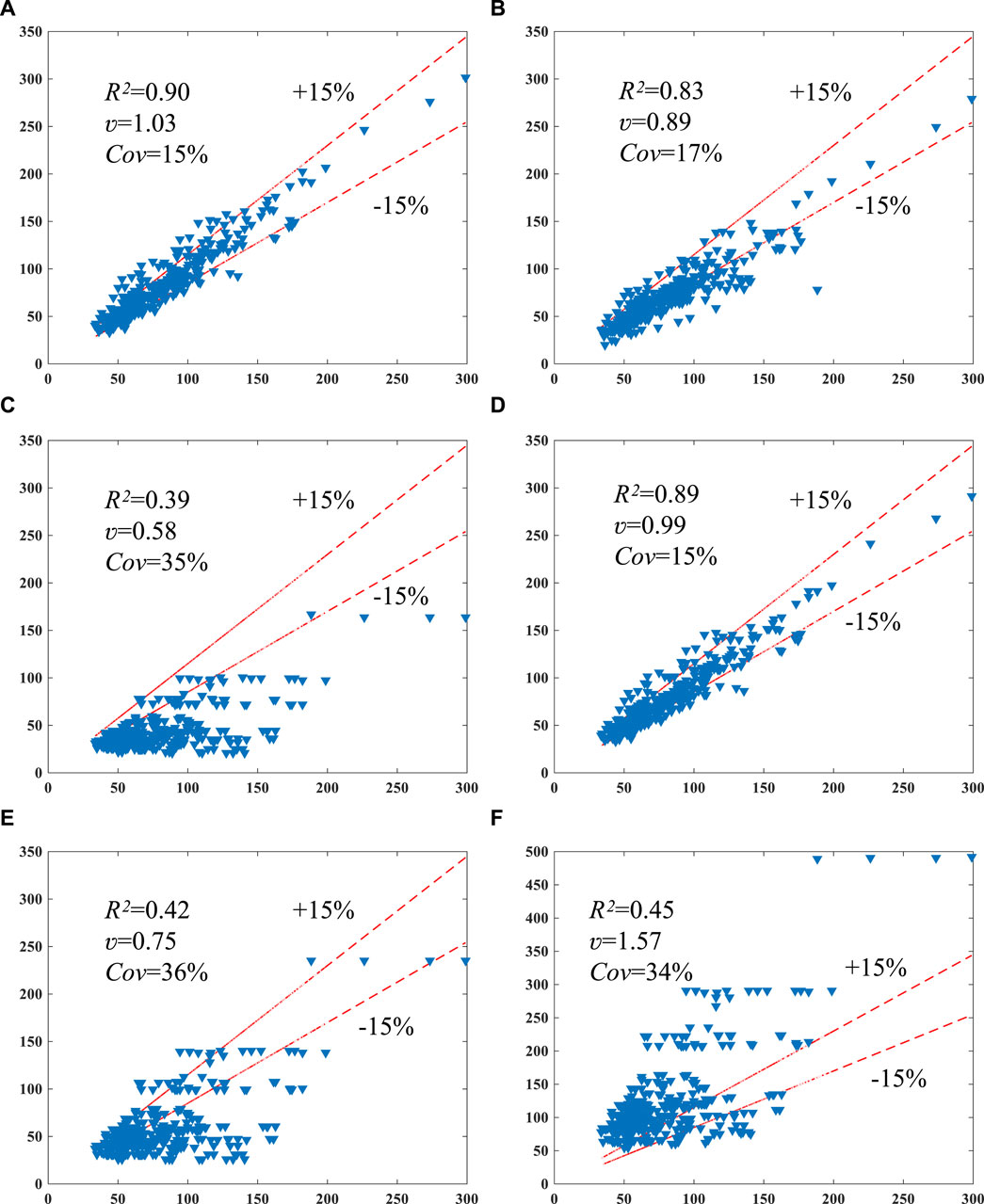
Figure 4. Evaluation of the codes’ models. (A) [ACI 440 (2008)], (B) [fib bulletin 14 (2001)], (C) [CSA S-806 (2012)], (D) ISIS Canada, ISIS (2001), (E) [TR55 (2004)], (F) [CNR-DT (2004)].

Figure 5

Figure 5. Evaluation of the researchers’ models. (A) (Richart et al., 1929), (B) Newman and Newman, 1971 (C) Mander et al., 1988, (D) Karbhari et al., 1997, (E) Samaan et al., 1998, (F) Toutanji et al., 1999, (G) Lam and Teng et al., 2003, (H) Sadeghian and Fam et al., 2015.

Figure 6

Figure 6. Performance of the XGboost model.

Based on Figure 4, it is evident that among all the codes, ACI demonstrates the highest R² value (0.90). Both ACI and ISIS exhibit the lowest Cov (15%), indicating high accuracy. On the contrary, the models recommended by CSA, TR55, and CNR have R² values below 0.5 and Cov values above 30%, indicating lower accuracy. Furthermore, the models recommended by fib, CSA, and TR55 demonstrate a conservative tendency with R² values below 0.90, while the CNR model ($\upsilon$ = 1.57) poses a risk of overestimating the f’_cc value. Referring to Figure 5, it can be concluded that the models suggested by researchers exhibit high R² values (above 0.8) and low Cov values (below 20%). Newman and Lam & Teng’s models have the highest R² values (0.90), while Sadeghian and Fam’s model exhibits the lowest Cov (14%). Additionally, the models of Richart et al., Newman, Mander, and Toutanji show a risk of overestimating the f’_cc value with $\upsilon$ above 1.1, whereas Karbhari’s model appears to be more conservative with a low $\upsilon$ (0.92).

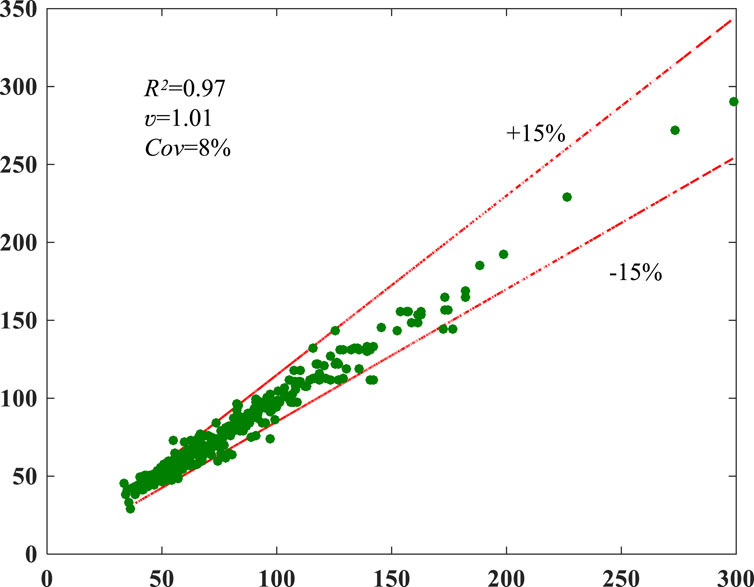
Figure 6 illustrates that the XGBoost model attains a commendable R² of 0.97 and a Cov of 8%. These findings highlight the superior accuracy of the XGBoost model in forecasting f’_cc values compared to models advocated by both codes and researchers. The XGBoost model excels in precisely predicting f’_cc values based on the dataset established in this study.

Based on the above analysis, it is evident that certain early models (such as CSA, TR55, CNR, etc.) face significant challenges in terms of predictive accuracy, with lower R² values and higher Cov values indicating considerable prediction bias and an inability to accurately predict the compressive strength of concrete columns. Specifically, certain models (such as the CNR model) exhibit a conservative tendency, tending to underestimate the compressive strength of concrete, which may lead to excessively conservative estimates of structural performance. These challenges likely stem from early models failing to account for key factors such as specific properties of concrete, geometric dimensions of Fibre Reinforced Polymer (FRP), and the interface characteristics between FRP and concrete. These factors significantly influence the mechanical properties of concrete columns but may have been overlooked or inadequately considered in early models.

In contrast, this study employs the XGBoost ensemble learning method, which excels in handling complex feature and data relationships, enabling a more comprehensive analysis and prediction of the mechanical properties of FRP-confined concrete columns. The XGBoost model leverages gradient boosting to progressively enhance the performance of multiple weak learners, thereby improving predictive accuracy and reliability. Furthermore, XGBoost is effective in handling nonlinear relationships and high-dimensional data, demonstrating strong fitting capabilities and the ability to capture complex patterns within the data, thereby providing more accurate and reliable predictive capabilities for concrete structural engineering.

6 Parameter study

6.1 Parameter importance analysis

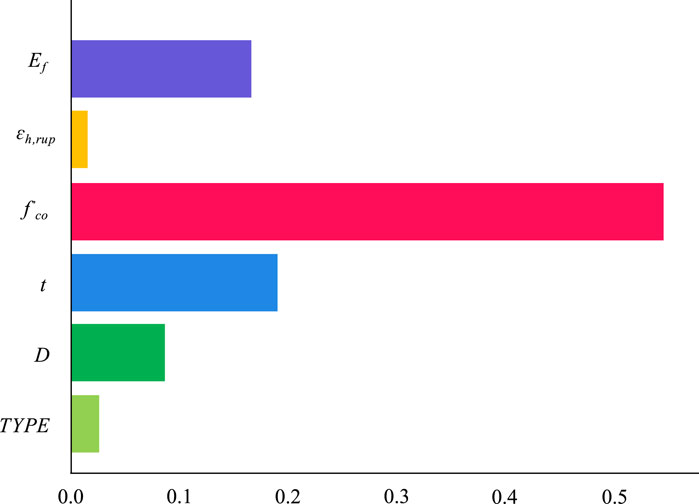
In accordance with Section 3.1, the XGBoost model in machine learning demonstrates superior performance in predicting the compressive strength of FRP-confined columns. Consequently, this section employs XGBoost for conducting model importance and sensitivity analysis. In XGBoost, feature importance is evaluated by computing the average gain for each feature across all decision tree nodes. Specifically, this process entails traversing through every decision tree node and computing the gain value associated with the respective feature at each node. The significance of each feature is then determined by averaging the gains across all nodes. These calculated feature importance values serve as valuable indicators of each feature’s impact on the overall model performance, facilitating a comprehensive assessment of their significance within the analysis framework. The outcomes of the parameter importance analysis are presented in Figure 7.

Figure 7

Figure 7. Feature importance based on XGBoost.

Figure 7 reveals the hierarchy of parameter influence on the compressive strength of FRP-confined columns as follows: concrete strength, FRP thickness, FRP elastic modulus, column diameter, FRP type, and FRP failure strain. Notably, concrete strength exerts a significantly greater influence on compressive strength compared to the other parameters.

6.2 Parameter sensitivity analysis

Furthermore, this study conducted parameter sensitivity analysis using XGBoost. To investigate the relationship between a specific feature and the compressive strength (f^’_cc), the analysis was performed considering four levels of the feature “t”: 0.5 mm, 1.5 mm, 2.5 mm, and 3.5 mm. Additionally, for the parameter “D”, four distinct levels were examined: 100 mm, 150 mm, 200 mm, and 250 mm. It is noteworthy that the average values from a dataset comprising 366 data points (as outlined in Table 2) were utilised for the remaining features. Specifically, values for “D” were fixed at 160 mm, “ f^’_co” (average compressive strength of concrete) at 46.5 MPa, “ε_frp” (FRP strain) at 1.21%, and “E_f ” (elastic modulus of FRP) at 165.6 GPa.

In Figure 8A, it is evident that f^’_cc and the diameter of the column are inversely proportional, although the diminishing trend of f^’_cc becomes less pronounced with increasing D. Figure 8B illustrates that f^’_cc is directly proportional to the thickness of the FRP. For t values below 1mm, there is a higher sensitivity between f^’_cc and t, whereas for t values above 1mm, the sensitivity is lower. Figure 8C reveals a positive correlation between f^’_cc and the concrete strength, although this correlation becomes less pronounced when f^’_co exceeds 100 MPa. From Figure 8D, it can be observed that f^’_cc and the fracture strain of FRP are directly proportional, albeit with a relatively modest increase in magnitude. Lastly, Figure 8E demonstrates that f^’_cc is directly proportional to the elastic modulus of FRP.

Figure 8

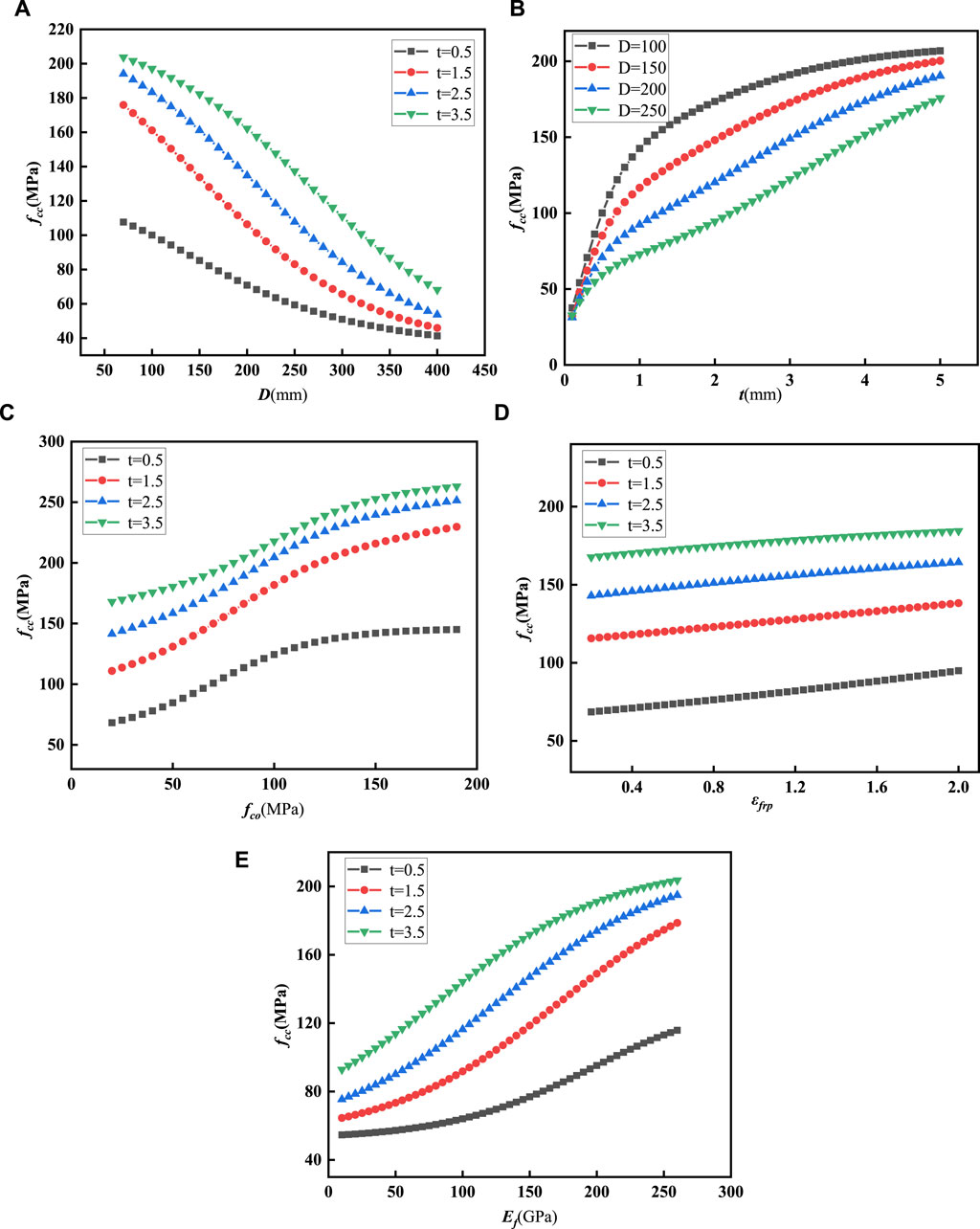
Figure 8. Feature sensitivity analysis based on XGBoost. (A) f_cc affected by D, (B) f_cc affected by t, (C) f_cc affected by f_co, (D) f_cc affected by εfrp, (E) f_cc affected by E_f.

7 Conclusion

This study utilized a comprehensive database along with machine learning models to predict the compressive strength of FRP-confined columns. It evaluated models recommended by both codes and researchers, conducting parameter analysis, leading to the following conclusion:

(1) Among the machine learning models, XGBoost demonstrated exceptional performance on both the training and testing datasets, showing the lowest MSE values of 39.46 and 25.53, respectively, along with the highest R2 scores of 0.96 and 0.98, respectively.

(2) The XGBoost model used in this study exhibits commendable accuracy and robustness. Among the models based on codes, ACI and ISIS performed well, while other models showed lower precision, insufficient robustness, and potential issues of conservatism or overestimation of compressive strength. Regarding models proposed by researchers, their percentage errors ranged from 0% to 20%. Notably, models by Lam and Teng, as well as Samaan, demonstrated higher precision, while there was a risk of overestimating compressive strength in models by Richart, Newman, Mander, Toutanji, and Sadeghian.

(3) The primary factor influencing the compressive strength of FRP-confined columns is concrete strength, with the impact of FRP rupture strain being relatively minimal. In the XGBoost model, compressive strength showed an inverse relationship with column diameter and a direct relationship with other parameters.

(4) This study focused on selecting data related to FRP-reinforced concrete cylinders to delve deeper into the impact of FRP reinforcement on circular concrete columns. In contrast, square columns exhibit unique geometric shapes and load-bearing characteristics, and currently, there is insufficient experimental data available for FRP-reinforced square columns. Therefore, this research opted to study circular columns, which have a richer and more reliable dataset. Future studies will endeavor to conduct experiments on FRP-reinforced concrete square columns and beams to address this research gap.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RC: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing–original draft. HY: Data curation, Investigation, Methodology, Visualization, Writing–original draft. JL: Conceptualization, Investigation, Methodology, Software, Validation, Visualization, Writing–review and editing. YX: Formal Analysis, Investigation, Visualization, Writing–review and editing. GY: Data curation, Methodology, Validation, Writing–review and editing. YY: Investigation, Software, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported in part by Open Fund of the State Key Laboratory of Bridge and Tunnel Engineering in Mountainous Areas (Chongqing Jiaotong University) jointly constructed by the province and the ministry (SKLBT- 2104), in part by 2021 Chongqing Municipal Education Commission Humanities and Social Sciences Research General Planning Project (21SKGH215), in part by Yongchuan District Natural Science Foundation Project (2021yc-jckx20010), in part by Yongchuan District Technology Innovation and Application Development Special General Project (2023yc-cxfz30002), in part by Chongqing Municipal Education Commission Science and Technology Research Plan Project (KJQN202301337), and in part by Chongqing Municipal Education Commission Science and Technology Project (KJQN202201313), in part by China railway 21st bureau group corporation limited Fifth Engineering Co., LTD.’s horizontal project (WLHX-2023-0102).

Conflict of interest

Author YX was employed by China Railway 21st Bureau Group Corporation Limited Fifth Engineering Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

ACI 440 (2008) Guide for the design and construction of externally bonded FRP systems for strengthening concrete structures. Farmington Hills, MI, USA: American Concrete Institute.

Google Scholar

Aire, C., Gettu, R., and Casas, J. R. (2001). “Study of the compressive behavior of concrete confifined by fifiber reinforced composites,” in Proc, international conference on composites in constructions. Lisse (The Netherlands: A.A. Balkema Publishers), 239–243.

Google Scholar

Almusallam, T. H. (2007). Behavior of normal and high-strength concrete cylinders confined with E-glass/epoxy composite laminates. Compos. Part B Eng. 38 (5-6), 629–639. doi:10.1016/j.compositesb.2006.06.021

CrossRef Full Text | Google Scholar

Benzaid, R., Habib, M., and Eddine Chikh, N. (2010). FRP-confined concrete cylinders: axial compression experiments and strength model. J. Reinf. plastics Compos. 29 (16), 2469–2488. doi:10.1177/0731684409355199

CrossRef Full Text | Google Scholar

Berthet, J. F., Ferrier, E., and Hamelin, P. (2005). Compressive behavior of concrete externally confined by composite jackets. Part A: experimental study. Constr. Build. Mater. 19 (3), 223–232. doi:10.1016/j.conbuildmat.2004.05.012

CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random forests. Mach. Learn. 45 (1), 5–32. doi:10.1023/a:1010933404324

CrossRef Full Text | Google Scholar

Bullo, S. (2003). “Experimental study of the effects of the ultimate strain of fiber reinforced plastic jackets on the behavior of confifined concrete,” in Proc, international conference on composites in construction, Cosenza, Italy, 18-20 February, 2003, 465–470.

Google Scholar

Canada, ISIS (2001) Strengthening reinforced concrete structures with externally-bonded ribre reinforced polymers. Manitoba, Canada: University of Manitoba.

Google Scholar

Carey, S. A. (2002) Behavior of variably confifined concrete. Columbia, SC: University of South Carolina. Honors thesis.

Google Scholar

Chen, T., and Guestrin, C. (2016). “XGBoost: a scalable tree boosting system,” in Proceedings of he 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, San Francisco, CA, USA, August 13-17, 2016, 785–794.

Google Scholar

Chole, A., Tembhurne, A., Bawanthade, A., Bhadade, H., Ali Khan, H., and Kumar Shaw, S. (2023). Strengthening of reinforced concrete beams by using FRPs-An overview. Mater. Today Proc. doi:10.1016/j.matpr.2023.05.149

CrossRef Full Text | Google Scholar

CNR-DT (2004) Guide for the design and construction of externally bonded FRP systems for strengthening existing structures. Rome, Italy: National Research Council, Advisory Committee on Technical Regulations for Constructions.

Google Scholar

CSA S-806 (2012) Design and construction of building components with fibre-reinforced polymers. Mississauga, Ontario, Canada: Canadian Standards Association.

Google Scholar

Cui, C., and Sheikh, S. A. (2010). Experimental study of normal-and high-strength concrete confined with fiber-reinforced polymers. J. Compos. Constr. 14 (5), 553–561. doi:10.1061/(asce)cc.1943-5614.0000116

CrossRef Full Text | Google Scholar

Deifalla, A. (2022). Punching shear strength and deformation for FRP-reinforced concrete slabs without shear reinforcements. Case Stud. Constr. Mater. 16, e00925. doi:10.1016/j.cscm.2022.e00925

CrossRef Full Text | Google Scholar

De Lorenzis, L., Micelli, F., and La Tegola, A. (2002). Influence of specimen size and resin type on the behaviour of FRP-confined concrete cylinders. Adv. Polym. Compos. Struct. Appl. Constr., 231–239.

CrossRef Full Text | Google Scholar

Demers, M., and Neale, K. W. (1994). “Strengthening of concrete columns with unidirectional composite sheets,” in Proc, 4th international conference on short and medium span bridges, Montreal, Canada, August 1994, 895–905.

Google Scholar

Elsanadedy, H. M., Al-Salloum, Y., Abbas, H., and Alsayed, S. (2012). Prediction of strength parameters of FRP-confined concrete. Compos. Part B 43 (2), 228–239. doi:10.1016/j.compositesb.2011.08.043

CrossRef Full Text | Google Scholar

fib bulletin 14 (2001) Externally bonded FRP reinforcement for RC structures. Lausanne, Switzerland: fédération internationale du béton fib, 165.

Google Scholar

Friedman, J., Hastie, T., and Tibshirani, R. (2001) The elements of statistical learning, springer series in statistics. Berlin: Springer.

Google Scholar

Hu, T., Zhang, H., and Zhou, J. (2023). Machine learning-based model for recognizing the failure modes of FRP-strengthened RC beams in flexure. Case Stud. Constr. Mater. 18, e02076. doi:10.1016/j.cscm.2023.e02076

CrossRef Full Text | Google Scholar

Jedrzejko, M. J., Tian, J., Zhang, S., Ke, Y., Nie, X., and Yang, Y. (2023). Strengthening of RC beams in shear with novel near-surface mounted (NSM) U-shaped fiber-reinforced polymer (FRP) composites. Eng. Struct. 292, 116479. doi:10.1016/j.engstruct.2023.116479

CrossRef Full Text | Google Scholar

Jiang, T., and Teng, J. G. (2007). Analysis-oriented stress–strain models for FRP–confined concrete. Eng. Struct. 29 (11), 2968–2986. doi:10.1016/j.engstruct.2007.01.010

CrossRef Full Text | Google Scholar

Karbhari, V. M., and Gao, Y. (1997). Composite jacketed concrete under uniaxial compression—verification of simple design equations. J. Mater. Civ. Eng. 9 (4), 185–193. doi:10.1061/(asce)0899-1561(1997)9:4(185)

CrossRef Full Text | Google Scholar

Kharel, G. (2001) Behavior and modeling of variably confifined concrete. Columbia, SC: University of South Carolina. MS thesis.

Google Scholar

Kshirsagar, S., Lopez-Anido, R. A., and Gupta, R. K. (2000). Environmental aging of fiber-reinforced polymer-wrapped concrete cylinders. Mater. J. 97 (6), 703–712.

Google Scholar

Lam, L., Teng, J., Cheung, C., and Xiao, Y. (2006). FRP-confined concrete under axial cyclic compression. Cem. Concr. Compos. 28 (10), 949–958. doi:10.1016/j.cemconcomp.2006.07.007

CrossRef Full Text | Google Scholar

Lam, L., and Teng, J. G. (2003). Design-oriented stress–strain model for FRP-confined concrete. Constr. Build. Mater. 17 (6-7), 471–489. doi:10.1016/s0950-0618(03)00045-x

CrossRef Full Text | Google Scholar

Lam, L., and Teng, J. G. (2004). Ultimate condition of fiber reinforced polymer-confined concrete. J. Compos. Constr. 8 (6), 539–548. doi:10.1061/(asce)1090-0268(2004)8:6(539)

CrossRef Full Text | Google Scholar

Liao, J. J., Zeng, J. J., Zhuge, Y., Zheng, Y., Ma, G., and Zhang, L. (2023). FRP-confined concrete columns with a stress reduction-recovery behavior: a state-of-the-art review, design recommendations and model assessments. Compos. Struct. 321, 117313. doi:10.1016/j.compstruct.2023.117313

CrossRef Full Text | Google Scholar

Mander, J. B., Priestley, M. J. N., and Park, R. (1988). Theoretical stress-strain model for confined concrete. J. Struct. Eng. 114 (8), 1804–1826. doi:10.1061/(asce)0733-9445(1988)114:8(1804)

CrossRef Full Text | Google Scholar

Marques, P. F., and Chastre, C. (2012). Performance analysis of load–strain models for circular columns confined with FRP composites. Compos. Struct. 94 (11), 3115–3131. doi:10.1016/j.compstruct.2012.04.036

CrossRef Full Text | Google Scholar

Mastrapa, J. C. (1997). The effect of construction bond on confifinement with FRP composites (Orlando, FL: University of Central Florida). MS thesis.

Matthys, S., Taerwe, L., and Audenaert, K. (1999). “Test on axially loaded concrete columns confifined by fifiber reinforced polymer sheet wrapping,” in Proc, 4th international symposium on fiber reinforced polymer reinforcement for reinforced concrete structures (FRPRCS-4), NO. SP-188 (Farmington, MI: American Concrete Institute), 217–229.

Google Scholar

Micelli, F., and Modarelli, R. (2013). Experimental and analytical study on properties affecting the behaviour of FRP-confined concrete. Compos. Part B Eng. 45 (1), 1420–1431. doi:10.1016/j.compositesb.2012.09.055

CrossRef Full Text | Google Scholar

Micelli, F., Myers, J. J., and Murthy, S. (2001). “Effect of environmental cycles on concrete cylinders confined with FRP,” in Proceedings of CCC2001 international conference on composites in construction, Porto, Portugal, 10-12 October 2001.

Google Scholar

Nadir, W., Kadhim, M. M., Jawdhari, A., Fam, A., and Majdi, A. (2023). RC beams strengthened in shear with FRP-Reinforced UHPC overlay: an experimental and numerical study. Structures 53, 693–715. Elsevier. doi:10.1016/j.istruc.2023.04.117

CrossRef Full Text | Google Scholar

Newman, K., and Newman, J. B. (1971). Failure theories and design criteria for plain concrete. Struct. solid Mech. Eng. Des., 963–995.

Google Scholar

Ozbakkaloglu, T. (2013). Compressive behavior of concrete-filled FRP tube columns: assessment of critical column parameters. Eng. Struct. 51, 188–199. doi:10.1016/j.engstruct.2013.01.017

CrossRef Full Text | Google Scholar

Pessiki, S., Harries, K. A., Kestner, J. T., Sause, R., and Ricles, J. M. (2001). Axial behavior of reinforced concrete columns confined with FRP jackets. J. Compos. Constr. 5 (4), 237–245. doi:10.1061/(asce)1090-0268(2001)5:4(237)

CrossRef Full Text | Google Scholar

Rafieizonooz, M., Kim, J. H. J., Varaee, H., Nam, Y., and Khankhaje, E. (2023). Testing methods and design specifications for FRP-prestressed concrete members: a review of current practices and case studies. J. Build. Eng. 73, 106723. doi:10.1016/j.jobe.2023.106723

CrossRef Full Text | Google Scholar

Richart, F. E., Brandtzæg, A., and Lenoi Brown, R. (1929). Failure of plain and spirally reinforced concrete in compression. Univ. Ill. Eng. Exp. Stn. Bull. 190.

Google Scholar

Rochette, P., and Labossiere, P. (2000). Axial testing of rectangular column models confined with composites. J. Compos. Constr. 4 (3), 129–136. doi:10.1061/(asce)1090-0268(2000)4:3(129)

CrossRef Full Text | Google Scholar

Ruiz-Pinilla, J. G., Cladera, A., Pallarés, F. J., Calderón, P. A., and Adam, J. M. (2021). RC columns strengthened by steel caging: cyclic loading tests on beam-column joints with non-ductile details. Constr. Build. Mater. 301, 124105. doi:10.1016/j.conbuildmat.2021.124105

CrossRef Full Text | Google Scholar

Saadatmanesh, H., Ehsani, M. R., and Li, M.-W. (1994). Strength and ductility of concrete columns externally reinforced with fiber composite straps. Struct. J. 91 (4), 434–447.

Google Scholar

Sadeghian, P., and Fam, A. (2015). Improved design-oriented confinement models for FRP-wrapped concrete cylinders based on statistical analyses. Eng. Struct. 87, 162–182. doi:10.1016/j.engstruct.2015.01.024

CrossRef Full Text | Google Scholar

Salah, A., Elsanadedy, H., Abbas, H., Almusallam, T., and Al-Salloum, Y. (2022). Behavior of axially loaded L-shaped RC columns strengthened using steel jacketing. J. Build. Eng. 47, 103870. doi:10.1016/j.jobe.2021.103870

CrossRef Full Text | Google Scholar

Samaan, M., Shahawy, M., and Mirmiran, A. (1998). Model of concrete confined by fiber composites. J. Struct. Eng. 9, 124.

CrossRef Full Text | Google Scholar

Sayed, Y. A. K., Ibrahim, A. A., Tamrazyan, A. G., and Fahmy, M. F. (2023). Machine-learning-based models versus design-oriented models for predicting the axial compressive load of FRP-confined rectangular RC columns. Eng. Struct. 285, 116030. doi:10.1016/j.engstruct.2023.116030

CrossRef Full Text | Google Scholar

Silva, M. A., and Rodrigues, C. C. (2006). Size and relative stiffness effects on compressive failure of concrete columns wrapped with glass FRP. J. Mater. Civ. Eng. 18 (3), 334–342. doi:10.1061/(asce)0899-1561(2006)18:3(334)

CrossRef Full Text | Google Scholar

Smith, S. T., Kim, S. J., and Zhang, H. (2010). Behavior and effectiveness of FRP wrap in the confinement of large concrete cylinders. J. Compos. Constr. 14 (5), 573–582. doi:10.1061/(asce)cc.1943-5614.0000119

CrossRef Full Text | Google Scholar

Tafsirojjaman, T., Ur Rahman Dogar, A., Liu, Y., Manalo, A., and Thambiratnam, D. P. (2022). Performance and design of steel structures reinforced with FRP composites: a state-of-the-art review. Eng. Fail. Anal. 138, 106371. doi:10.1016/j.engfailanal.2022.106371

CrossRef Full Text | Google Scholar

Teng, J. G., Yu, T., Wong, Y., and Dong, S. (2007). Hybrid FRP–concrete–steel tubular columns: concept and behavior. Constr. Build. Mater. 21 (4), 846–854. doi:10.1016/j.conbuildmat.2006.06.017

CrossRef Full Text | Google Scholar

Toutanji, H. A. (1999). Stress-strain characteristics of concrete columns externally confined with advanced fiber composite sheets. ACI Struct. J. 96 (3), 397–404.

Google Scholar

TR55 (2004) Design guidance for strengthening concrete structures using fibre composite materials. Century House, Berkshire, UK: Concrete Society.

Google Scholar

Truong, G. T., Hwang, H.-J., and Kim, C.-S. (2022). Assessment of punching shear strength of FRP-RC slab-column connections using machine learning algorithms. Eng. Struct. 255, 113898. doi:10.1016/j.engstruct.2022.113898

CrossRef Full Text | Google Scholar

Vapnik, V. (1995) The nature of statistical learning theory, springer-verlag. Springer.

Google Scholar

Wang, L.-M., and Wu, Y.-F. (2008). Effect of corner radius on the performance of CFRP-confined square concrete columns: test. Eng. Struct. 30 (2), 493–505. doi:10.1016/j.engstruct.2007.04.016

CrossRef Full Text | Google Scholar

Wang, Z., Wang, D., Smith, S. T., and Lu, D. (2012). Experimental testing and analytical modeling of CFRP-confined large circular RC columns subjected to cyclic axial compression. Eng. Struct. 40, 64–74. doi:10.1016/j.engstruct.2012.01.004

CrossRef Full Text | Google Scholar

Watanabe, K. (1997). Confinement effect of FRP sheet on strength and ductility of concrete cylinders under uniaxial compression. Non-Metallic (FRP) Reinforcement for Concrete Structures. Japan Concrete Institute. Proc. Third Int. Symposium 1.

Google Scholar

Wu, Y.-F., and Jiang, J.-F. (2013). Effective strain of FRP for confined circular concrete columns. Compos. Struct. 95, 479–491. doi:10.1016/j.compstruct.2012.08.021

CrossRef Full Text | Google Scholar

Xiao, Y., and Wu, H. (2000). Compressive behavior of concrete confined by carbon fiber composite jackets. J. Mater. Civ. Eng. 12 (2), 139–146. doi:10.1061/(asce)0899-1561(2000)12:2(139)

CrossRef Full Text | Google Scholar

Youssef, M. N. (2003) Stress strain model for concrete confifined by FRP composites. Irvine, Irvine, CA: University of California. Doctoral dissertation.

Google Scholar

Zohrevand, P., and Mirmiran, A. (2011). Behavior of ultrahigh-performance concrete confined by fiber-reinforced polymers. J. Mater. Civ. Eng. 23 (12), 1727–1734. doi:10.1061/(asce)mt.1943-5533.0000324

CrossRef Full Text | Google Scholar