Study on the vibration suppression mechanisms of the lightweight flexible metamaterial sticker with non-independent resonators

The working mechanism of an acoustic metamaterial (AM) for broadband elastic vibration suppression with non-independent local resonators is presented in this paper along with the general formulas for the effective mass (EM), dispersion relation, and transmission spectrum (TR) of this metamaterial unit. A kind of flexible metamaterial sticker that is lightweight and skillfully uses flexible materials is proposed based on a theoretical approach. The flexible metamaterial sticker has a surface density of only 2.22 kg/m² and an overall thickness of only 3 mm. It is made by depositing the flexible cylindrical supports in a square lattice pattern on the surface of the flexible plate. The finite element method (FEM) was used to systematically investigate the band structures, frequency response function (FRF), dynamic effective mass density (EMD), as well as the formation mechanisms of the flexural vibration bandgaps (FVBGs) of the metamaterial plates (composite structure after applying the metamaterial sticker). Additionally, a thorough analysis was conducted on the impacts of geometrical parameters (the rubber cylinder thickness, the flexible material plate thickness, the lattice constant, and the rubber cylinder radius) on the FVBGs. Finally, an overall vibration attenuation for the proposed metamaterials was estimated by using the spatial quadratic velocity and experiment. The findings confirmed that the AM caused multi-frequency negative EM, while the overall bandgap width was substantially wider than that of conventional metamaterials. Due to the numerous vibration modes of the flexible metamaterial, the suggested flexible lightweight metamaterial sticker can generate several observable local resonance FVBGs in the low-frequency range. Significantly broadening the bandwidth of FVBGs can be achieved by varying the rubber cylinder radius and thickness, as well as by adjusting the lattice constant and flexible material plate thickness. Within the FVBGs, the proposed lightweight flexible metamaterial sticker shows a good vibration-suppression performance, when compared with the traditional damping structure or metamaterials.

1 Introduction

The thin plate is widely used in as a common structure in engineering applications aerospace, automotive industry, and other fields (Mao and Pietrzko, 2013). However, the suppression of vibration and its radiated noise (especially low-frequency noise) for the thin plate indicates one of the key issues in the past decades. The traditional vibration reduction methods for plate structure mainly include: using damping materials, dynamic vibration absorbers or improving the equivalent stiffness of plate structure. However, the above-mentioned damping methods have some problems, such as narrow vibration-suppression band, poor low-frequency vibration reduction performance and excessive overall additional weight. Therefore, how to achieve broadband low-frequency vibration isolation using the lightweight materials for thin plate is a key problem in the current research (Benaroya et al., 2017).

As acoustic/elastic metamaterials have advanced, new concepts and techniques for addressing low-frequency vibration in thin plate structures have surfaced (Sigalas and Economou, 1992; Martínez-Sala et al., 1995; Sánchez-Pérez et al., 1998; Liu et al., 2000; Liu et al., 2002; Wang et al., 2004; Benchabane et al., 2006; Khelif et al., 2006; Hsu and Wu, 2007; Mohammadi et al., 2008; Pennec et al., 2008; Xiao et al., 2008; Oudich et al., 2010; Zhu et al., 2010; Croënne et al., 2011; Hsu, 2011; Wu et al., 2011; Hsu, 2012; Xiao et al., 2012; Zhang et al., 2012; Wang et al., 2013; Peng and Pai, 2015; Zhao et al., 2015; Zhao et al., 2016; Beli et al., 2018; Tian et al., 2019; Zhou et al., 2019; Lu et al., 2020; Oyelade and Oladimeji, 2021; Deng et al., 2023a). The initial research mainly focused on the research of Bragg scattering metamaterials, but these kinds of structures generally form a high bandgap and are greatly affected by the periodicity of the structure (Gao et al., 2021), which cannot be applied in practical vibration suppression (Sigalas and Economou, 1992; Martínez-Sala et al., 1995; Sánchez-Pérez et al., 1998). However, in 2000, with the development of local resonance AM, it became possible for metamaterials to be utilized for low-frequency vibration damping and noise isolation. A series of 2D locally resonant AM plates with low-frequency bandgaps were reported (Sánchez-Pérez et al., 1998; Liu et al., 2000; Liu et al., 2002; Wang et al., 2004; Benchabane et al., 2006; Khelif et al., 2006; Hsu and Wu, 2007; Mohammadi et al., 2008; Pennec et al., 2008; Xiao et al., 2008; Oudich et al., 2010; Zhu et al., 2010; Croënne et al., 2011; Hsu, 2011; Wu et al., 2011; Hsu, 2012; Xiao et al., 2012; Zhang et al., 2012), achieved either by creating perforations in the plate or by intermittently placing the pillar-like structures onto the plate’s surface. Furthermore, multi-degree-of-freedom local resonators were incorporated into the design of metamaterials to widen the low-frequency bandgaps, while the formation and related mechanisms of the bandgaps were thoroughly investigated (Wang et al., 2013; Peng and Pai, 2015; Zhao et al., 2015; Zhao et al., 2016; Beli et al., 2018; Tian et al., 2019; Lu et al., 2020; Oyelade and Oladimeji, 2021; Deng et al., 2023b). The above-mentioned metamaterials constructed based on hard materials (especially the matrix materials), which have certain limitations in practical use (cannot be made into any shape and cannot be completely pasted on the target structural plate). Therefore, pure flexible materials have been introduced into the design of metamaterials, and fruitful results have been achieved (Wang et al., 2019; Zhou et al., 2020; Ma et al., 2021). Zhou et al. (2019) and Zhou et al. (2020) systematically studied the design method and sound insulation mechanism of large-size flexible acoustic package, and perfectly verified the sound insulation performance through experiments. Because of the abundant vibration modes of the flexible materials, the sound insulation frequency band can be further broaden via the reasonable structural design.

This paper presents the impact of mutual coupling between the non-independent local resonators of AM on the dynamic EM and bandgaps. According to theoretical assessment, and inspired by the design idea of flexible acoustic packaging used in automobiles and the bandgap opening mechanism of local resonance, a lightweight flexible metamaterial sticker with low-frequency and broadband vibration suppression is proposed. The metamaterial sticker has the characteristics of simple structure, lightweight and easy processing. Furthermore, the vibration-suppression performance and formation mechanism of the bandgaps of the metamaterial sticker were systematically investigated via FEM and experiment.

2 Theoretical model analysis

As illustrated in Figure 1, consider an infinitely long one-dimensional lattice system composed of non-independent resonators. This model is comparable to the classic single-degree-of-freedom metamaterial mechanics model in that k₂ connects the resonance mass m₂ and outer matrix mass m₁, while spring k₁ connects the units. The biggest difference is that each local resonance mass is connected to each other by the spring K. The lattice constant is L. For ease of explanation, the EM of the non-independent AM is investigated using the unit cell of the lattice model with two resonators (Figure 1B). The outer mass m₁ as well as its displacement u₁, the inner mass m₂ as its displacement u₂ have been relabeled as m₃, u₃, m₄, and u₄, respectively.

Figure 1

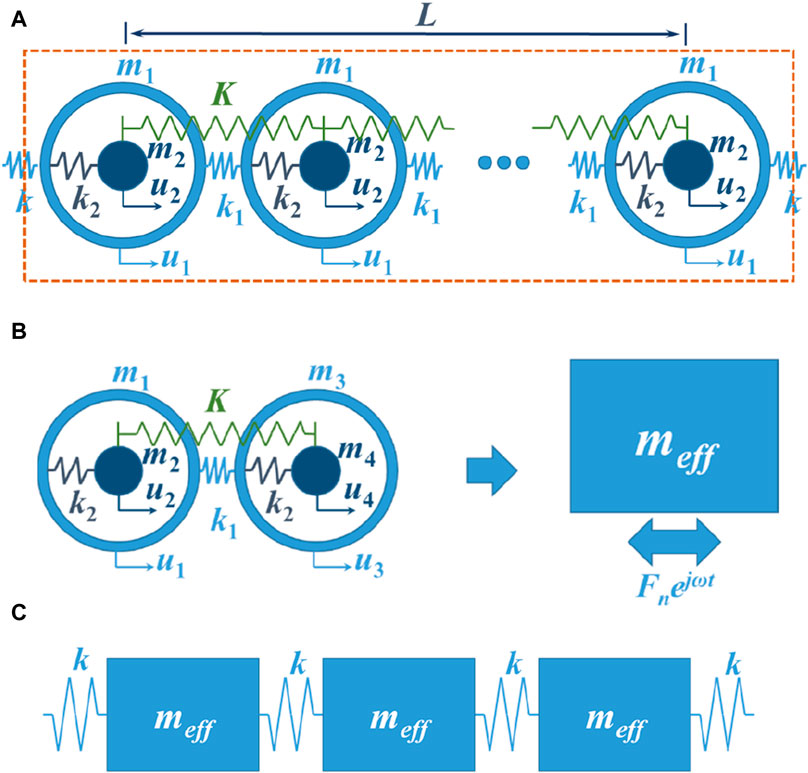
Figure 1. (A) The one-dimensional lattice system comprising non-independent resonators. (B) The unit cell with two linked lattice system resonators and its EM. (C) The n-period one-dimensional lattice meta-composite system with EM.

The unit cell motion equation with two resonators is expressed as:

$\begin{array}{c}\left[\begin{array}{llll}{m}_1& 0& 0& 0\\ 0& m_2& 0& 0\\ 0& 0& m_3& 0\\ 0& 0& 0& m_4\end{array}\right]\left[\begin{array}{c}{\ddot{u}}_1\\ {\ddot{u}}_2\\ {\ddot{u}}_3\\ {\ddot{u}}_4\end{array}\right]+\left[\begin{array}{cccc}{k}_1+k_2& -k_2& -k_1& 0\\ -k_2& K+k_2& 0& -K\\ -k_1& 0& k_1+k_2& -k_2\\ 0& -K& -k_2& K+k_2\end{array}\right]\\ \left[\begin{array}{c}{u}_1\\ u_2\\ u_3\\ u_4\end{array}\right]=\left[\begin{array}{c}F\\ 0\\ 0\\ 0\end{array}\right]\end{array}(1)$

wherein u_i = U_iexp(jωt) is the ith lump mass displacement, and F = F₀exp(jωt) is the external force on the unit cell.

Equation 1 can be further expressed as:

$\begin{array}{c}\left[\begin{array}{cccc}{k}_1+k_2-m_1{\omega }^2& -k_2& -k_1& 0\\ -k_2& K+k_2-m_2{\omega }^2& 0& -K\\ -k_1& 0& k_1+k_2-m_3{\omega }^2& -k_2\\ 0& -K& -k_2& K+k_2-m_4{\omega }^2\end{array}\right]\\ \left[\begin{array}{c}{U}_1\\ U_2\\ U_3\\ U_4\end{array}\right]=\left[\begin{array}{c}{F}_n\\ 0\\ 0\\ 0\end{array}\right]\end{array}(2)$

From Eq. 2, the expression of U₁ can be calculated, and then the EM of the unit cell was acquired as:

$m_{eff}=-\frac{F_n}{{\omega }^2{U}_1}(3)$

Furthermore, from Eq. 3, the dispersion relationship is expressed as Eq. 4

$2k\left(1-\cos qL\right)=m_{eff}{\omega }^2(4)$

Using the structure in Figure 1C, the motion equation of the simplified n-period system was expressed as:

$\left(2k-m_{eff}{\omega }^2\right)U_j-k\left(U_{j-1}+U_{j+1}\right)=0, j=1,2,\cdots ,n-1(5)$

$\left(k-m_{eff}{\omega }^2\right)U_n-k{U}_{n-1}=0(6)$

wherein U_j denotes the displacement amplitude of the jth equivalent unit cell.

The Eqs 7, 8 are obtained by combining Eqs 5, 6

$T_j=\frac{k}{k\left(2-T_{j+1}\right)-m_{eff}{\omega }^2}, j=1,2,\cdots ,n-1(7)$

$T_n=\frac{k}{k-m_{eff}{\omega }^2}(8)$

wherein T_n = U_j/U_j-1. Therefore, the one-dimensional lattice system TR was acquired as Eq. 9:

$\text{TR}=20\lg \left(\left|U_n/U_0\right|\right)=20\lg \left(\left|{\displaystyle \prod _{j=1}^n}{T}_j\right|\right)(9)$

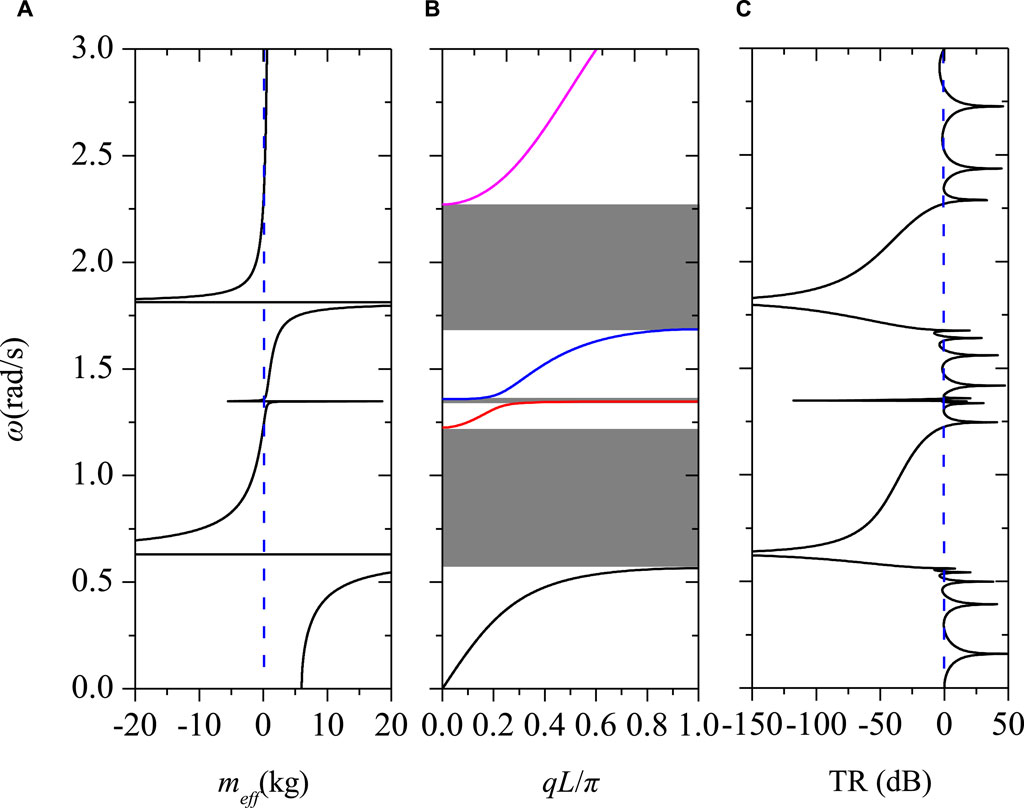
The EM, dispersion relation, and transmission spectrum of the lattice model are illustrated in Figure 2. In the calculation, the specific parameter settings included m₁ = m₃ = 1 kg, m₂ = m₄ = 2 kg, K = 1.5 N/m, k = k₁ = 2 N/m, k₂ = 1 N/m.

Figure 2

Figure 2. The calculated (A) EM, (B) dispersion relation, and (C) TR of the metamaterial model.

As shown in Figure 2A, the metamaterial model exhibited three negative EM regions for the metamaterial model: 0.631 ∼ 1.224 rad/s, 1.349 ∼ 1.357 rad/s and 1.813 ∼ 2.271 rad/s, respectively, and shows better low-frequency broadband characteristics. Figures 2B, C shows the mechanical model dispersion curve and transmission spectra, respectively. Compared with the traditional metamaterials, the mechanical model has obvious advantages in the number and width of bandgaps (only one negative EM region for the traditional model: $\sqrt{k_2/m_2}$ ∼ $\sqrt{k_2/m_1+k_2/m_2}$), which means that through a reasonable AM structure can achieve good vibration damping performance. Next, the flexible metamaterial sticker with a low-frequency broadband was designed for vibration suppression of thin plate materials, and the bandgap formation mechanism and vibration damping performance were further discussed in detail.

3 Overview of the continuum model

3.1 Model

Figure 3A illustrates the flexible metamaterial sticker structure. Construction involved depositing the flexible cylindrical supports (yellow part) in a square lattice arrangement on the flexible plate (gray part) surface. The flexible plate is made from ethylene-vinyl acetate (EVA) copolymer with a ρ_e = 2,050 kg/m³ static density, a Young’s modulus of E_e = 1.7 × 10⁸ Pa, and Poisson’s ratio of ν_e = 0.45. The flexible cylindrical support, as the roles stiffness, is a silicon rubber with mass density ρ_r = 1,300 kg/m³, the Young’s modulus is E_r = 6 × 10⁵ Pa and Poisson’s ratio is ν_r = 0.48, respectively. The dimensions of each metamaterial section included a = 30 mm, t_e = 1 mm, d = 10 mm, and t_r = 2 mm. The metamaterial composite surface density was 2.22 kg/m² with a 3 mm overall thickness. In practical engineering application, the side of the metamaterial with flexible support needs to be pasted on the surface of the thin plate that needs vibration reduction. Figure 3B shows an application status of the flexible metamaterial sticker pasted on the surface of the aluminum backplane. The density (ρ_a) of the aluminum backplane material is 2,730 kg/m³, with a Young’s modulus of E_a = 7.8 × 10¹⁰ Pa and a Poisson’s ratio of ν_a = 0.35.

Figure 3

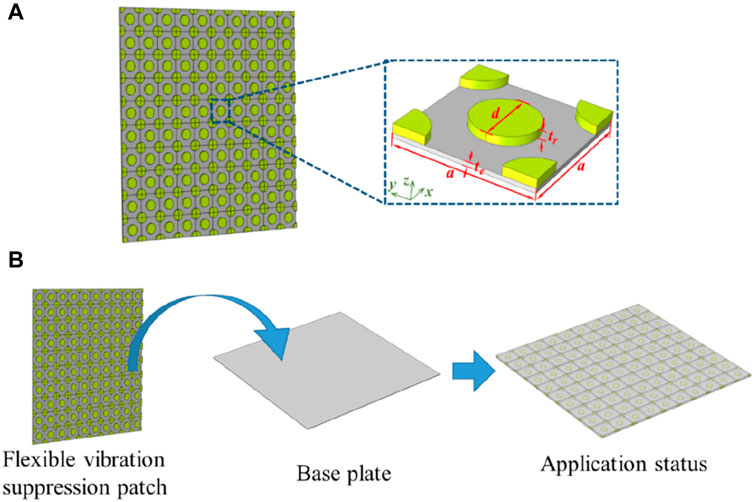
Figure 3. Schematics of (A) the flexible metamaterial sticker: overall structure (left) and unit cell (right), and (B) application status of the flexible metamaterial sticker for thin plate vibration suppression.

Compared with the traditional metamaterial (single-degree-of-freedom), the AM composed of metamaterial sticker and aluminum plate also still some differences: there is no obvious matrix and local resonators. However, combined with common sense and practical engineering experience, we can know that the flexible material and its flexible cylindrical support constitute the local resonance system, while the relatively hard aluminum plate is the matrix, which will be proved by later calculations. In fact, metamaterials designed based on a one-dimensional “spring-mass” mechanical model are a two-dimensional structure, and there are certain differences between the mechanical model and the metamaterial structure. The original intention of this paper is to use a one-dimensional mechanical model to verify that the interaction between non independent resonators can open multiple bandgaps, and based on this idea, design a metamaterial structure with simple structure and broadband characteristics.

3.2 Method

Due to the easier interaction of flexure waves (zero-order antisymmetric Lamb mode) with air media, the out-of-plane vibration has received much attention. FEM, an effective method in previous works (Mohammadi et al., 2008; Pennec et al., 2008; Zhu et al., 2010; Croënne et al., 2011; Hsu, 2011; Hsu, 2012; Xiao et al., 2012; Zhang et al., 2012; Wang et al., 2013; Peng and Pai, 2015; Zhao et al., 2015; Zhao et al., 2016; Beli et al., 2018; Tian et al., 2019; Wang et al., 2019; Zhou et al., 2019; Aladwani and Nouh, 2020; Lu et al., 2020; Zhou et al., 2020; Gao et al., 2021; Ma et al., 2021; Oyelade and Oladimeji, 2021; Deng et al., 2023a; Deng et al., 2023b), is used to calculate the composite structure dispersion relations depicted in Figure 3B to explore the vibration suppression features of the proposed flexible metamaterial. The governing equations of elastic wave propagation was characterized as Eq. 10 to compute the band structures:

${\displaystyle \sum _j^3}\frac{\partial }{\partial x_j}\left({\displaystyle \sum _{l=1}^3}{\displaystyle \sum _{k=1}^3}{c}_{ijkl}\frac{\partial u_k}{\partial x_l}\right)=\rho \frac{{\partial }^2{u}_i}{\partial t^2}\left(i=1,2,3\right)(10)$

wherein u_i, u_k, and u_l represent the displacements, c_ijkl refers to the elastic modulus tensor components, ρ signifies the mass density, t refers to time, and x_j denotes the x, y, and z coordinate variables, respectively. A periodic infinite system is evident in the x- and y-direction simultaneously. Therefore, only one unit cell was considered in the calculations. As shown in Figure 4A, the interfaces between the closest unit cells were determined using the stress-free boundary conditions based on the Bloch-Floquet theorem. The elastic displacement was denoted as Eq. 11:

$\mathit{u}\left(\mathit{r}\right)=e^{i\left(\mathit{k}\cdot \mathit{r}\right)}{\mathit{u}}_k\left(\mathit{r}\right)(11)$

wherein k = (k_x, k_y) represents the wave vector. Employing the Bloch computation involves varying the k value within the first irreducible Brillouin zone (Figure 4B), which in turn yields the eigenfrequencies and their corresponding eigenvectors. This procedure also elucidates the dispersion relations and eigenmodes.

Figure 4

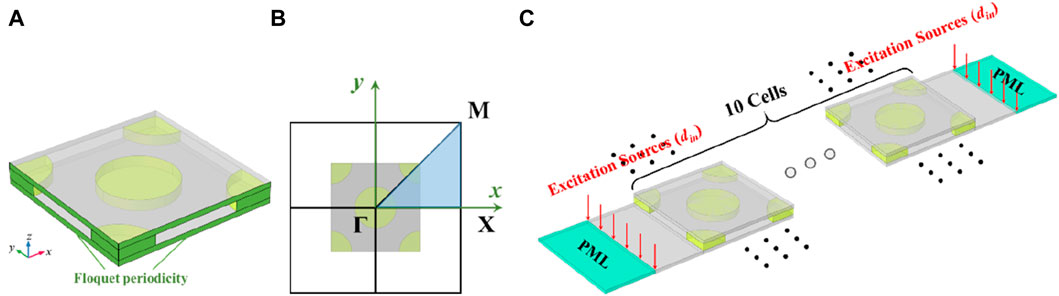
Figure 4. A schematic diagram of (A) the boundary conditions used in the calculations, (B) the first irreducible rectangular Brillouin zone, and (C) a calculation scheme for the TR.

The analysis involved computing the transmission spectrum across a confined arrangement made up of ten units along either the x- or y-axis, while in the orthogonal direction, Bloch periodic conditions are enforced at the boundaries. FEM was employed to verify the presence of FVBGs within the studied structure. Additionally, the examination revealed an average displacement response on the right side, indicating the application of harmonic displacement excitation on the plate surface located at the left side (Figure 4C). The TR is expressed as Eq. 12:

$\text{TR}=20\log \frac{\left|d_{out}\right|}{\left|d_{in}\right|}(12)$

wherein $\left|d_{in}\right|$ and $\left|d_{out}\right|$ represent the average input and output displacements of the plate, respectively. Perfectly matched layers were applied at the domain boundaries to stop reflections because the system domain had to be finite for FEM utilization (Zhu et al., 2010; Hsu, 2011; Hsu, 2012). COMSOL Multiphysics 5.4, a commercial program recognized for its efficacy in analyzing dispersion relations and transmission spectra of metamaterials across various studies and research (Zhu et al., 2010; Croënne et al., 2011; Hsu, 2011; Hsu, 2012; Xiao et al., 2012; Zhang et al., 2012; Wang et al., 2013; Peng and Pai, 2015; Zhao et al., 2015; Oyelade and Oladimeji, 2021), was employed for all numerical computations in this investigation. The solid grid cell dimensions must be less than one-sixth of the mesh partition material flexural wavelength.

4 Results and discussion

4.1 Band structures of the elastic metamaterial plates

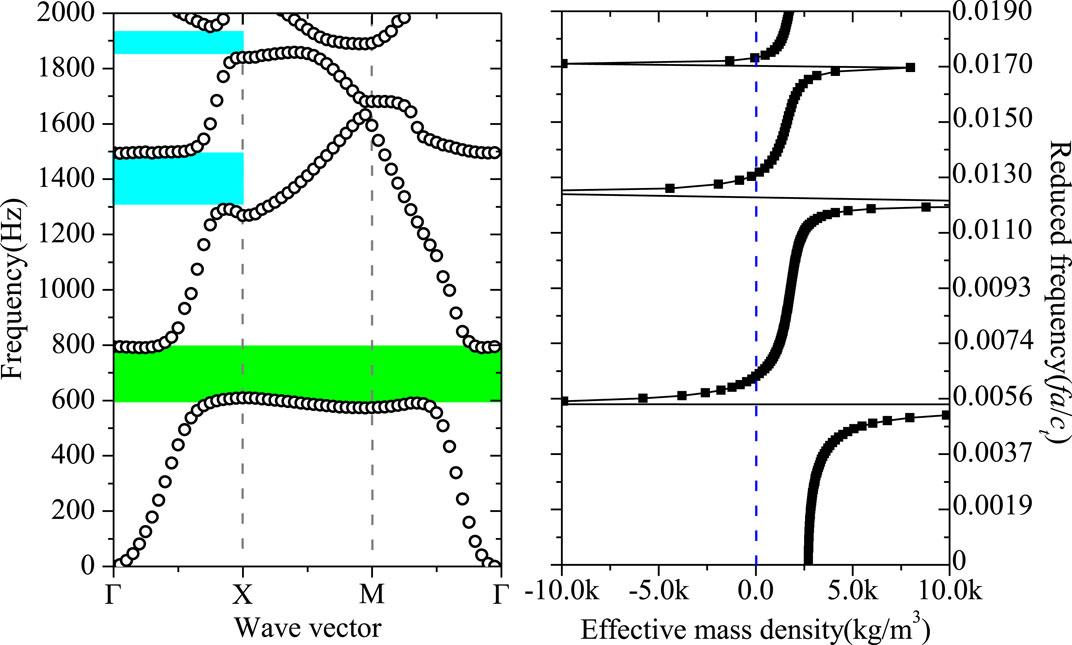
When the frequency is between 0 Hz and 2000 Hz, there are fifteen bands in the band structure (Figure 5A), where three FVBGs (one complete bandgap, green regions; two directional bandgaps, cyan regions) are involved. Between the first and fifth flexural wave bands, or 610.1 Hz–794.07 Hz, is the lowest frequency range of the bandwidth. The second directional FVBG lies between the fifth and ninth bands, spanning from 1,290.8 Hz with a 205.9 Hz width. The third directional FVBG spans 93.6 Hz in width and is located between the 11th and 15th bands, measuring between 1857.8 Hz and 1951.4 Hz. The total width of the bandgaps is 483.47 Hz. In order to conveniently and intuitively display the structure and position of the flexural wave bandgaps, the energy bands in the full-wave band are simplified and only the flexural wave energy bands are retained, as shown in Figure 5B. The TR depicting the flexural wave propagation in x- or y-direction are shown in Figure 5C. It is evident in the TR that three frequency ranges exhibiting significant obvious attenuation (highlighted in green and cyan) in flexural wave propagation in the respective directions are observed. Remarkably, these regions align closely with the bandgaps in Figure 5A. Nonetheless, prior research has discovered that periodic metamaterials can support both Bragg scattering and local resonances (Xiao et al., 2008; Oudich et al., 2010). The reduced frequency fa/c_t is shown in Figure 5B (right), where c_t represents the transverse velocity in the metamaterial and a is the lattice constant. This serves to validate the formation mechanism of the bandgaps. The transverse velocity in the metamaterial is expressed as $c_t=\sqrt{G/\rho }$. The effective shear modulus (G) and effective density (ρ) of the base plate correspond to the transverse velocity in the metamaterial, respectively. In the frequency regions, the bandgaps are situated roughly two to three orders below the Bragg scattering mechanism. This indicates that the local resonance mechanism is where the FVBGs originate.

Figure 5

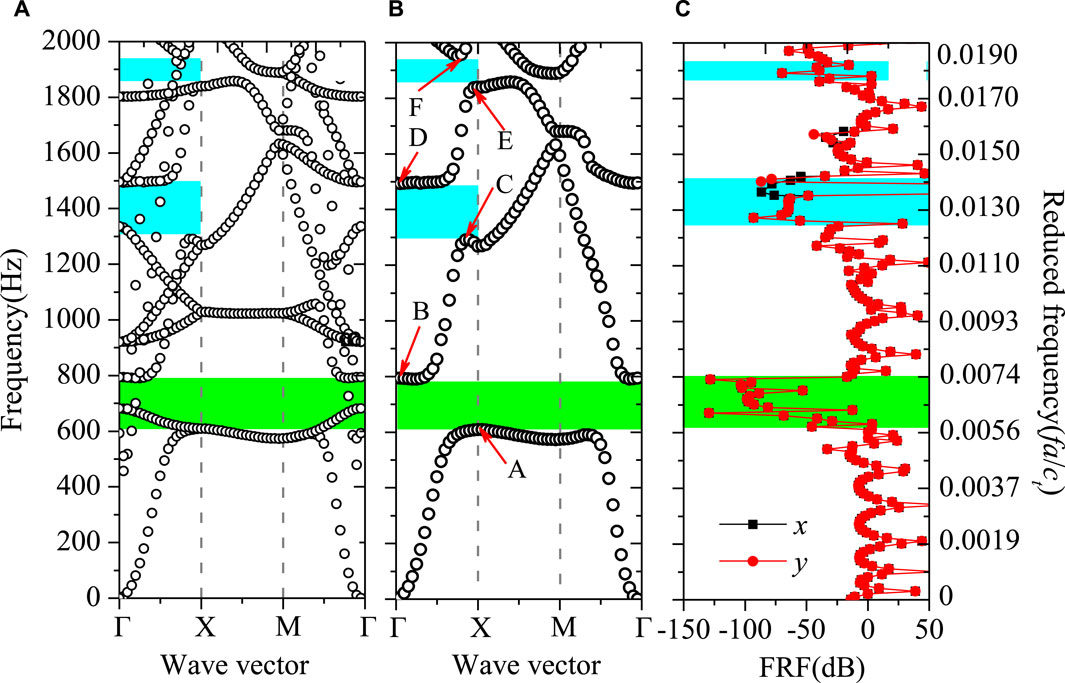
Figure 5. The computing results for the (A) band structures of full-wave, (B) band structures of flexural wave, and (C) TR of the flexural composite structure vibration.

4.2 Formation mechanisms of the three FVBGs

It has been established that the formation mechanism of FVBGs is attributed to local resonance. Local resonance occurs when the frequency of the incident elastic wave aligns with the natural frequency of the internal spring-mass system. However, the flexible metamaterial sticker introduced in this research does not exhibit a distinct local resonance resonator form. Despite this, three noticeable local resonance FVBGs were observed in the low-frequency spectrum. This observation was elucidated by presenting the eigenmode shapes and displacement vector fields of the labeled modes in Figure 5A within Figure 6. The colored map shows the displacement vector field magnitude, calculated via $\sqrt{\left(u_x^2+u_y^2+u_z^2\right)}$.

Figure 6

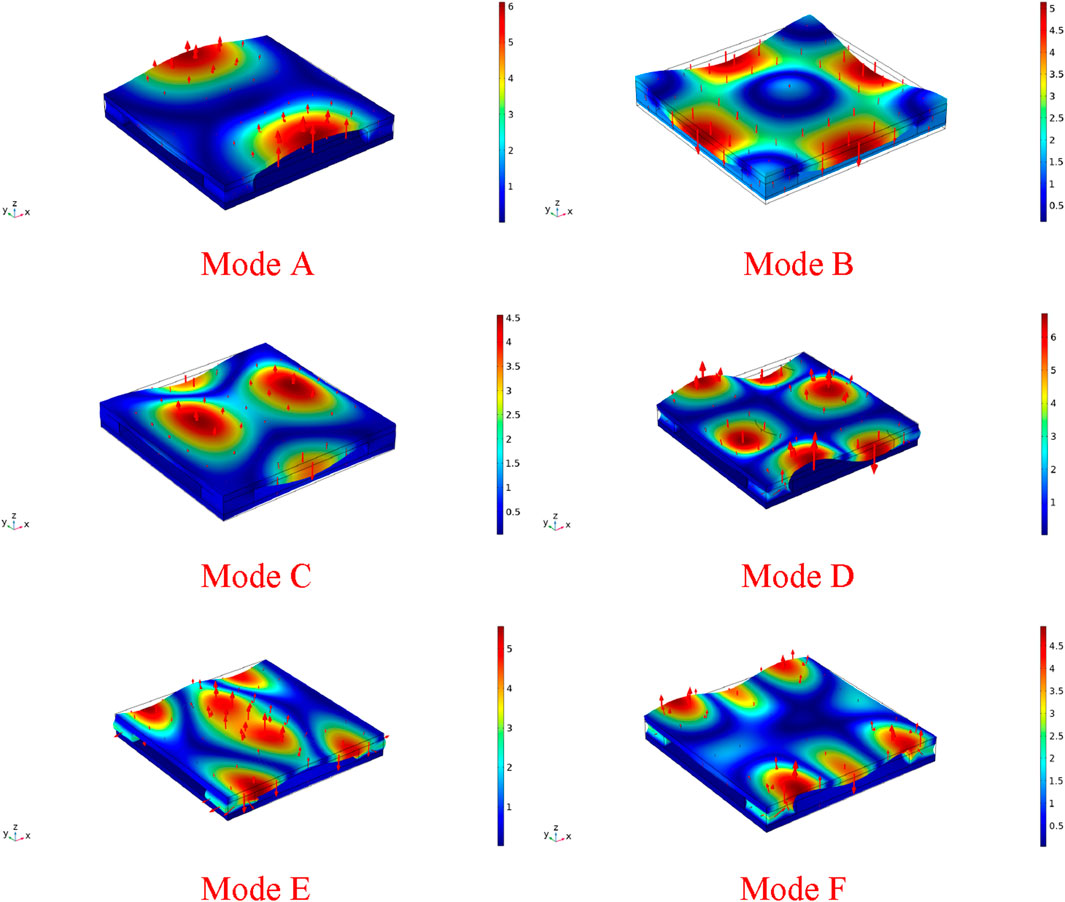
Figure 6. Eigenmode shapes and displacement vector field of the modes labeled in Figure 5.

For modes A, C, and E, representing the lower boundaries of the bandgaps, the flexible plate (EVA plate) exhibits vibration displacement primarily in the z-direction, while the base plate remains fixed. Owning to the abundant vibration modes of the flexible material, a local resonance system with multi-degree-of-freedom is formed between the flexible plate and rubber cylinder. The propagation of flexural waves is hindered because the reaction force generated from the local resonance system suppresses the vibration of the base plate, creating bandgaps at these frequencies. However, in modes B, D, and F, there is a dynamic balance between the base plate and the local resonance system, allowing elastic waves to propagate freely and closing the bandgaps.

Through the above analysis, it can be seen that the metamaterial sticker exhibits obvious local resonance characteristics: the flexible material EVA shows the functions of the local resonance mass and partial spring, the aluminum plate and flexible supports represent the matrix and spring, respectively. The maximum displacement occurs between the flexible cylindrical supports, that is, there is obvious mutual coupling between the resonators. And because the flexible material has abundant vibration modes at low-frequencies, multi bandgaps can be opened. Moreover, the position of the bandgaps (Figure 5C) demonstrates the effectiveness of the local resonance formation mechanism.

This section uses a numerical method to compute the composite structure dynamic EMD. The reaction forces at the four lateral boundaries were determined by surface integration following the application of a specific harmonic displacement A along the z-direction. The dynamic EMD was calculated using Eq. 13 (Lu et al., 2020),

${\rho }_{eff}=-\frac{1}{V}\frac{{\oint }_S{F}_z^{\left(r\right)}dS}{A{\omega }^2}(13)$

wherein $F_z^{\left(r\right)}$ is the reaction force z-component at the four boundaries, ω denotes the angular frequency, V signifies the unit cell volume, and S refers to the total region of the four vertical boundaries. Figure 7 shows the calculation results.

Figure 7

Figure 7. Dynamic EMD for the composite structure.

Figure 7 shows the three negative EMD regions when the frequency is lower than 2,000 Hz. As shown in Figure 5A, the negative EMD regions locates inside the FVBGs. Here, the internal local resonance mass vibration opposes the base vibration direction because of the negative EM, which lowers the matrix vibration. Therefore, the above research further shows that the designed metamaterial sticker opens the bandgaps and suppresses the vibration with the aid of local resonance mechanism.

4.3 The impact of the geometrical criteria on the FVBGs

The starting f_s and the cutoff frequency f_c are calculated using FEM to show the impact of the geometrical criteria on the complete or directional FVBGs. Figures 8A–D show the impact of the geometrical criteria of the rubber cylinder t_r thickness, the flexible material plate (EVA plate) t_e thickness, the lattice constant a, and the rubber cylinder radius d/2 on the FVBGs, respectively.

Figure 8

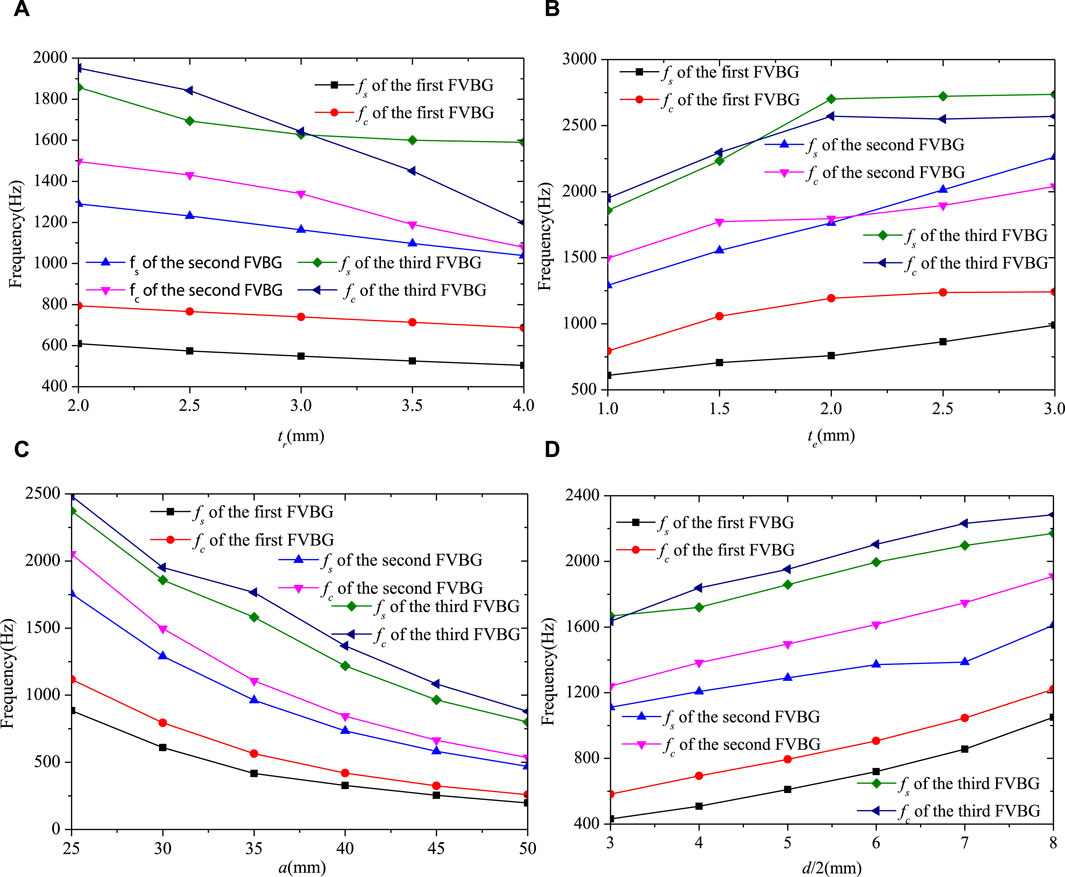
Figure 8. Effects of (A) the rubber cylinder t_r thickness, (B) the flexible material plate (EVA plate) t_e thickness, (C) the lattice constant a, and (D) the rubber cylinder radius d/2 on the FVBGs.

As shown in Figure 8A, the fs and fc of the three FVBGs declined as the rubber cylinder t_r thickness increased. Among them, the bandwidth of the first complete FVBG is almost invariable. While for the second directional FVBG, the decline rate of f_c exceeds that of f_s, narrowing the bandgap. For the third directional FVBG, the boundaries’ variations are the same as those of the second bandgap. Moreover, when t_r is equal to 3 mm, the third directional FVBG disappears. The equivalent rubber stiffness decreases with the increasing of the thickness of the rubber cylinder t_r, which greatly weakens the interactions between the traveling wave modes and local resonance. Thus, the total bandwidth of the FVBGs gradually become narrow.

Figure 8B shows that the f_c of the first complete FVBG stabilizes after an initial rapid ascent, while f_s shows the converse behavior. The width of the first complete FVBG initially increases, then decreases. f_s and f_c of the second and third directional FVBG all increase, while the increasing rate of the fc of the two FVBGs both are greater than that of f_s, which narrows the two FVBGs. When t_e equals 1.6 mm and 2.1 mm, respectively, the third and second directional FVBGs disappear successively. From the above analysis, it can be found that the flexible plate cannot be thickened infinitely. Because when the flexible plate is infinitely thickened, the overall stiffness of the flexible plate increases, it cannot produce abundant vibration modes at low-frequency, and the vibration of the plate also shows the overall vibration (only one bandgap opens at a low-frequency when t_e ≥ 2.5 mm).

Figure 8C shows the impact of the lattice constant a on the FVBGs. Here, f_s, f_c, and the bandwidth (except for bandwidth of the third directional FVBG) of three FVBGs all decrease with the increase of the lattice constant a. The bandwidth of the third directional FVBG initially increases, followed by a decline. When the lattice constant a increases, the EM provided by the flexible plate increase responsively, resulting in low-frequency bandgaps. The coupling between the traveling wave modes and the local resonance corresponded, opening narrower bandgaps.

Figure 8D displays the impact of the rubber cylinder radius d/2 on the FVBGs. f_s and f_c of the first complete FVBG were higher as the rubber cylinder radius increases, showing an almost invariable bandwidth. The f_s and f_c of the second directional FVBG move to a higher frequency when d/2 increases. However, the increasing rate of f_s exceeds that of f_c, broadening the bandgap, while and the bandwidth remains almost unchanged. However, when d/2 ≤ 3 mm, the third directional FVBG disappears. Increasing the rubber cylinder radius actually increases the equivalent rubber stiffness, and the change trend of bandgap is just opposite to that of increasing the thickness of the rubber cylinder.

In practical applications, one can select the ideal structure parameters to achieve the desired bandgap frequency ranges by analyzing the geometrical criteria associated with FVBGs.

4.4 Evaluation of overall vibration attenuation of the proposed metamaterials

4.4.1 Prediction of spatial quadratic velocity level

In engineering applications, for structures containing a large number of plate and shell elements (such as surface ships and underwater vehicles, etc.), the magnitude of normal vibration is of main concern. Therefore, the spatial quadratic velocity is usually used as an evaluation index for vibration magnitude, to reflect the overall vibration of the structure. Herein, the spatial quadratic velocity can be defined as Eq. 14

$〈v^2〉=\frac{1}{S}\underset{S}{\iint }{\left|V\right|}^2\mathrm{d}s(14)$

wherein S represents the area of vibrating surface, and V is the normal velocity distribution function of the vibrating surface.

Furthermore, the spatial quadratic velocity level can be defined as Eq. 15

$L_v=10\log \left(〈v^2〉/v_0^2\right)(15)$

wherein v₀ = 1 × 10⁻⁵ m/s is the reference speed.

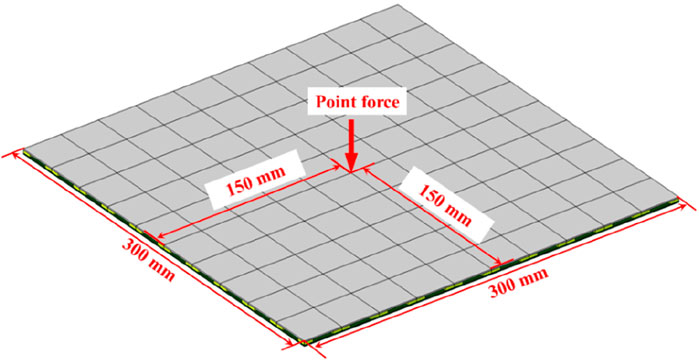
To demonstrate the effective low-frequency vibration-suppression capabilities of the suggested metamaterials, this study only used point force to predict spatial quadratic velocity. Besides, the position of the point force is highlighted in Figure 9, and the applied harmonic force magnitude is 1 N. The calculated results are presented in Figure 10. Additionally, to validate a good damping performance of metamaterials, the vibration of pure plate and plate coated with damping materials (the thickness of the damping material is 2 mm, and the loss factor is 0.2, the total mass of the additional damping material is heavier than that of metamaterials sticker) are also shown.

Figure 9

Figure 9. The position of the point force applied on metamaterial.

Figure 10

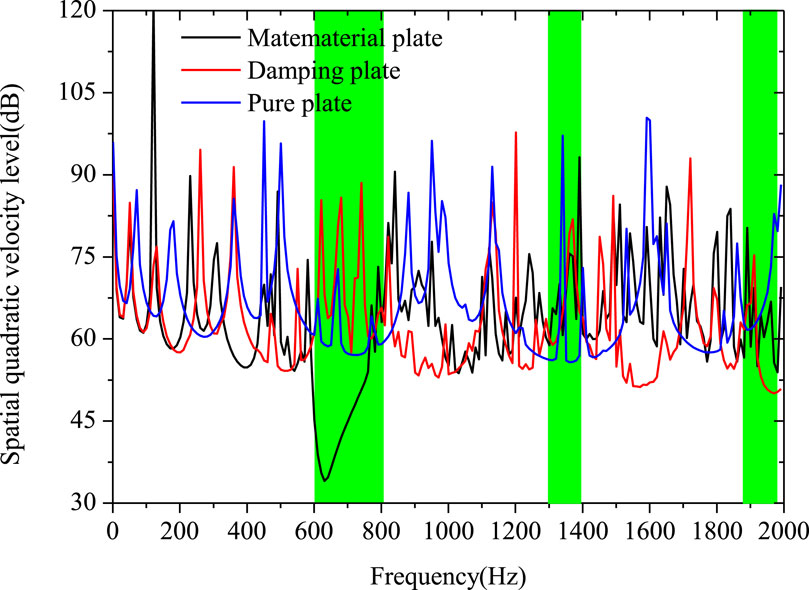
Figure 10. The prediction of spatial quadratic velocity level for the metamaterial (black curve), plate coated with damping materials (red curve), and pure plate (blue curve), respectively.

As can be found from the calculated results, for the studied frequency range, the vibration-suppression ability of metamaterials is the best, especially in the bandgap ranges (green area). Likewise, the vibration-suppression effect of damping materials on matrix plates is second to that of metamaterials, while the vibration of pure plates is most intense among all. It is worth noting that since the second and third bandgaps are directional bandgaps, this can only suppress the propagation of flexural waves in one direction (ΓX). The mean square velocity level is calculated using a single point excitation, which produces waves that travel in three directions. When the metamaterial structure is laid on the surface of the matrix, the flexural wave propagating along the diagonal of the matrix can not be effectively suppressed, so the vibration suppression of the second and third bandgaps will be slightly worse. In addition, relevant studies have also shown that the directional bandgaps will weaken the attenuation ability of vibration, but they are equally important for vibration and noise reduction (Zhang, 2016). Therefore, it can be concluded that the proposed metamaterial sticker can well realize the broadband vibration reduction of thin plate structure.

4.4.2 Experiment

As illustrated in Figure 11A, transmission-measuring experiments of a flexible metamaterial sticker with ten periodic units are performed to further confirm the good vibration suppression performance of the proposed structure. The flexible metamaterial sticker is pasted on the aluminum plate with a size of 300 mm × 300 mm × 1 mm by using rubber glue. Furthermore, in the experimental test, to realize the free flexural vibration, a soft rubber band is used to hang and install the test specimen (Figure 11B). In the experiment, the transmission characteristics of the sample are tested by hammering method, which is considered to be a very effective means (Figure 11C).

Figure 11

Figure 11. The test sample and the experimental measurement setup. Schematic illustration of (A) test sample, (B) sample installation, and (C) experimental setup.

The transmission spectrum was obtained and shown as the black solid curve in Figure 12. The experimental results show the obvious vibration attenuation in a range of 390 ∼ 2,000 Hz (the studied range), especially in the region corresponding to the bandgap, the transmission dips can be observed. From the comparison between the FEM and the experimental results, the metamaterial can achieve good vibration damping performance in a broadband frequency range, which verifies the good vibration-suppression performance of the flexible AM sticker.

Figure 12

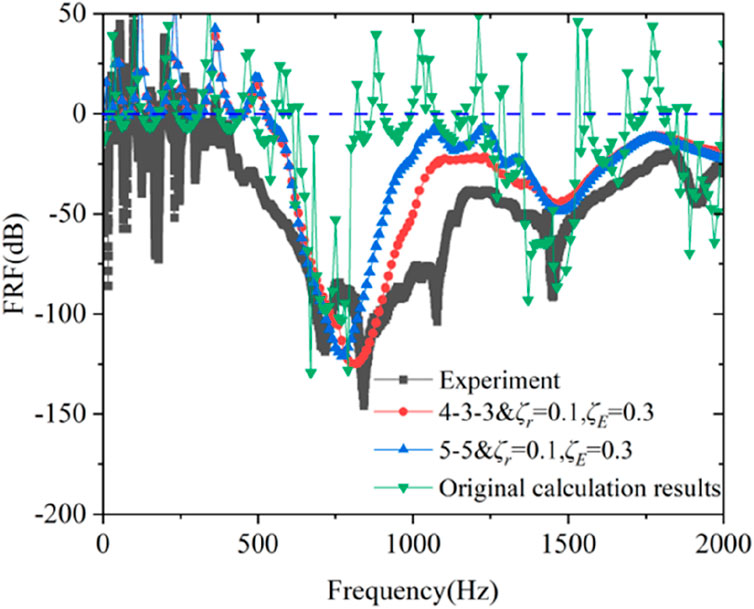
Figure 12. Comparisons of transmission rate data for composite models with the different parameters (black dotted lines represent experimental results, red dotted lines and blue dotted lines represent calculated results of the “4-3-3” and “5-5” configurations considering damping, respectively, and green dotted lines represent calculated results of the original model).

In addition, despite the fact that the results are generally consistent, some discrepancies remain. Moreover, the bandwidth of the attenuation region obtained from the experimental results is significantly larger than those of the FEM. There are two primary causes for the discrepancy between the calculated and experimental results: the dimensions of the rubber and EVA that were designed, those that were actually manufactured, and the simplification of the loss factor. An intrinsic material property called damping, which is primarily connected to soft polymeric materials like rubber and EVA in this study, is important for the structure’s response. Previous studies have proved that the existence of damping in polymer materials can broaden or even connect the multiple bandgaps (Aladwani and Nouh, 2020). The processing technology and equipment play a major role in the discrepancy between the manufactured dimensions and the designed dimensions, although these factors generally have minimal influence. In order to demonstrate the above issues more intuitively, the damping of rubber material is set to 0.1 (using homogeneous loss factors to characterize the material’s damping), and the damping of EVA is set to 0.3. At the same time, considering the influence of size errors, the transmission rates of the two composite metamaterials, “5–5” and “4-3-3,” were repeatedly calculated and compared, respectively. In Figure 12, “5–5” represents a diameter of 5 mm for the first 5 rubber cylinders and 6 mm for the last 5 (this model is referred to as the “5–5” configuration); “4-3-3” indicates that the diameter of the first four rubber cylinders is 4 mm, the middle three are 5 mm, and the last three are 6 mm (this model is called the “4-3-3” configuration). As can be seen from Figure 12, the gaps between the calculated transmission rate and its experimental value are gradually narrowed, which also confirms the previous conjecture. However, it is undeniable that there are still some gaps between the two, which is caused by the test environment and conditions.

5 Conclusion

A working mechanism for AM with non-independent local resonators is presented in this study. Based on the theoretical analysis of the EM, dispersion relation, and transmission characteristics, the lightweight flexible metamaterial sticker is proposed skillfully via using the flexible materials, which is used to realize the broadband vibration-suppression and low-frequency performance of thin the plate structure. The band structures, TR, dynamic EMD and the formation mechanisms of the FVBGs of the metamaterial plates were systematically investigated via FEM. Moreover, the impact of the geometrical criteria on the FVBGs were examined in detail. Lastly, an overall vibration attenuation for the proposed metamaterials was estimated by using the spatial quadratic velocity. Based on this analysis, the following conclusions can be drawn.

(1) The AM causes multi-frequency negative EM (multiple bandgaps) with significant wider total width of bandgaps than traditional metamaterials due to the mutual coupling between the local resonators.

(2) The metamaterial sticker surface density is 2.22 kg/m² while the thickness is 3 mm, which is beneficial to realize the lightweight of equipment design and engineering application potential. Moreover, the proposed flexible lightweight metamaterial sticker can produce multiple obvious local resonance FVBGs in a low-frequency range owning to the abundant vibration modes of the flexible material.

(3) By enhancing the coupling between flexible thin plate and matrix plate (increasing the rubber cylinder radius or decreasing the rubber cylinder thickness, the flexible material plate thickness, and the lattice constant), the bandwidth of FVBGs can be broadened significantly.

(4) The proposed lightweight flexible metamaterial sticker shows a good vibration-suppression performance for the thin plate, when compared with the traditional damping structure. Moreover, in practical use, due to the existence of damping of the material itself, the region of vibration attenuation can be further broadened.

The lightweight metamaterial sticker put forth in this work offers a fresh approach to the difficult issue of thin plate radiated noise and low-frequency vibration.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

GZ: Conceptualization, Funding acquisition, Investigation, Writing–original draft. KL: Data curation, Formal Analysis, Software, Writing–review and editing. ML: Funding acquisition, Project administration, Writing–review and editing. YL: Funding acquisition, Project administration, Writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Key R&D Plan Project under Grant No. 2021YFB3801804, the Key Project of Shanghai Zhangjiang National Independent Innovation Demonstration Zone under Grant No. ZJ2021-ZD-006, and the Fundamental Research Program of Shanxi Province under Grant No. 20210302124010.

Conflict of interest

Authors GZ and YL were employed by Shanghai Research Institute of Materials Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aladwani, A., and Nouh, M. (2020). Mechanics of metadamping in flexural dissipative metamaterials: analysis and design in frequency and time domains. Int. J. Mech. Sci. 173, 105459. doi:10.1016/j.ijmecsci.2020.105459

CrossRef Full Text | Google Scholar

Beli, D., Arruda, J. R. F., and Ruzzene, M. (2018). Wave propagation in elastic metamaterial beams and plates with interconnected resonators. Int. J. Solids Struct. 139, 105–120. doi:10.1016/j.ijsolstr.2018.01.027

CrossRef Full Text | Google Scholar

Benaroya, H., Nagurka, M., and Han, S. (2017) Mechanical vibration: analysis, uncertainties, and control[M]. Boca Raton, London, New York: CRC Press.

Google Scholar

Benchabane, S., Khelif, A., Rauch, J. Y., Robert, L., and Laude, V. (2006). Evidence for complete surface wave band gap in a piezoelectric phononic crystal. Phys. Rev. E 73 (6), 065601. doi:10.1103/physreve.73.065601

PubMed Abstract | CrossRef Full Text | Google Scholar

Croënne, C., Lee, E. J. S., Hu, H., and Page, J. H. (2011). Band gaps in phononic crystals: generation mechanisms and interaction effects. AIP Adv. 1 (4), 041401. doi:10.1063/1.3675797

CrossRef Full Text | Google Scholar

Deng, J., Gao, N., and Chen, X. (2023b). Ultrawide attenuation bands in gradient metabeams with acoustic black hole pillars. Thin-Walled Struct. 184, 110459. doi:10.1016/j.tws.2022.110459

CrossRef Full Text | Google Scholar

Deng, J., Gao, N., Chen, X., Pu, H., and Guo, J. (2023a). Underwater sound radiation from a Mindlin plate with an acoustic black hole. Ocean. Eng. 278, 114376. doi:10.1016/j.oceaneng.2023.114376

CrossRef Full Text | Google Scholar

Gao, N., Wang, B., Lu, K., and Hou, H. (2021). Complex band structure and evanescent Bloch wave propagation of periodic nested acoustic black hole phononic structure. Appl. Acoust. 177 (3), 107906. doi:10.1016/j.apacoust.2020.107906

CrossRef Full Text | Google Scholar

Hsu, J. C. (2011). Local resonances-induced low-frequency band gaps in two-dimensional phononic crystal slabs with periodic stepped resonators. J. Phys. D Appl. Phys. 44 (5), 055401. doi:10.1088/0022-3727/44/5/055401

CrossRef Full Text | Google Scholar

Hsu, J. C. (2012). Effects of elastic anisotropy in phononic band-gap plates with two-dimensional lattices. J. Phys. D Appl. Phys. 46 (1), 015301. doi:10.1088/0022-3727/46/1/015301

CrossRef Full Text | Google Scholar

Hsu, J. C., and Wu, T. T. (2007). Lamb waves in binary locally resonant phononic plates with two-dimensional lattices. Appl. Phys. Lett. 90 (20), 201904. doi:10.1063/1.2739369

CrossRef Full Text | Google Scholar

Khelif, A., Aoubiza, B., Mohammadi, S., Adibi, A., and Laude, V. (2006). Complete band gaps in two-dimensional phononic crystal slabs. Phys. Rev. E 74 (4), 046610. doi:10.1103/physreve.74.046610

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Chan, C. T., and Sheng, P. (2002). Three-component elastic wave band-gap material. Phys. Rev. B 65 (16), 165116. doi:10.1103/physrevb.65.165116

CrossRef Full Text | Google Scholar

Liu, Z., Zhang, X., Mao, Y., Zhu, Y. Y., Yang, Z., Chan, C. T., et al. (2000). Locally resonant sonic materials. science 289 (5485), 1734–1736. doi:10.1126/science.289.5485.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, K., Zhou, G., Gao, N., Li, L., Lei, H., and Yu, M. (2020). Flexural vibration bandgaps of the multiple local resonance elastic metamaterial plates with irregular resonators. Appl. Acoust. 159, 107115. doi:10.1016/j.apacoust.2019.107115

CrossRef Full Text | Google Scholar

Ma, F., Wang, C., Liu, C., and Wu, J. H. (2021). Structural designs, principles, and applications of thin-walled membrane and plate-type acoustic/elastic metamaterials. J. Appl. Phys. 129 (23), 231103. doi:10.1063/5.0042132

CrossRef Full Text | Google Scholar

Mao, Q., and Pietrzko, S. (2013) Control of noise and structural vibration[M]. New York, NY: Springer.

Google Scholar

Martínez-Sala, R., Sancho, J., Sánchez, J. V., Gómez, V., Llinares, J., and Meseguer, F. (1995). Sound attenuation by sculpture. nature 378 (6554), 241. doi:10.1038/378241a0

CrossRef Full Text | Google Scholar

Mohammadi, S., Eftekhar, A. A., Khelif, A., Hunt, W. D., and Adibi, A. (2008). Evidence of large high frequency complete phononic band gaps in silicon phononic crystal plates. Appl. Phys. Lett. 92 (22), 221905. doi:10.1063/1.2939097

CrossRef Full Text | Google Scholar

Oudich, M., Li, Y., Assouar, B. M., and Hou, Z. (2010). A sonic band gap based on the locally resonant phononic plates with stubs. New J. Phys. 12 (8), 083049. doi:10.1088/1367-2630/12/8/083049

CrossRef Full Text | Google Scholar

Oyelade, A. O., and Oladimeji, O. J. (2021). Coupled multiresonators acoustic metamaterial for vibration suppression in civil engineering structures. Forces Mech. 5, 100052. doi:10.1016/j.finmec.2021.100052

CrossRef Full Text | Google Scholar

Peng, H., and Pai, P. F. (2015). Design of multi-stopband metamaterial plates for absorption of broadband elastic waves and vibration[C]//Health Monitoring of Structural and Biological Systems 2015. Int. Soc. Opt. Photonics 9438, 94380X. doi:10.1117/12.2084197

CrossRef Full Text | Google Scholar

Pennec, Y., Djafari-Rouhani, B., Larabi, H., Vasseur, J. O., and Hladky-Hennion, A. C. (2008). Low-frequency gaps in a phononic crystal constituted of cylindrical dots deposited on a thin homogeneous plate. Phys. Rev. B 78 (10), 104105. doi:10.1103/physrevb.78.104105

CrossRef Full Text | Google Scholar

Sánchez-Pérez, J. V., Caballero, D., Mártinez-Sala, R., Rubio, C., Sánchez-Dehesa, J., Meseguer, F., et al. (1998). Sound attenuation by a two-dimensional array of rigid cylinders. Phys. Rev. Lett. 80 (24), 5325–5328. doi:10.1103/physrevlett.80.5325

CrossRef Full Text | Google Scholar

Sigalas, M. M., and Economou, E. N. (1992). Elastic and acoustic wave band structure. J. sound Vib. 158 (2), 377–382. doi:10.1016/0022-460x(92)90059-7

CrossRef Full Text | Google Scholar

Tian, Y., Wu, J. H., Li, H., Gu, C., Yang, Z., Zhao, Z., et al. (2019). Elastic wave propagation in the elastic metamaterials containing parallel multi-resonators. J. Phys. D Appl. Phys. 52 (39), 395301. doi:10.1088/1361-6463/ab2dba

CrossRef Full Text | Google Scholar

Wang, G., Wen, X., Wen, J., Shao, L., and Liu, Y. (2004). Two-dimensional locally resonant phononic crystals with binary structures. Phys. Rev. Lett. 93 (15), 154302. doi:10.1103/physrevlett.93.154302

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, P., Chen, T. N., Yu, K. P., and Wang, X. P. (2013). Lamb wave band gaps in a double-sided phononic plate. J. Appl. Phys. 113 (5), 053509. doi:10.1063/1.4790301

CrossRef Full Text | Google Scholar

Wang, X., Chen, Y., Zhou, G., Chen, T., and Ma, F. (2019). Synergetic coupling large-scale plate-type acoustic metamaterial panel for broadband sound insulation. J. Sound Vib. 459, 114867. doi:10.1016/j.jsv.2019.114867

CrossRef Full Text | Google Scholar

Wu, T. T., Hsu, J. C., and Sun, J. H. (2011). Phononic plate waves. IEEE Trans. ultrasonics, Ferroelectr. Freq. control 58 (10), 2146–2161. doi:10.1109/tuffc.2011.2064

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, W., Zeng, G. W., and Cheng, Y. S. (2008). Flexural vibration band gaps in a thin plate containing a periodic array of hemmed discs. Appl. Acoust. 69 (3), 255–261. doi:10.1016/j.apacoust.2006.09.003

CrossRef Full Text | Google Scholar

Xiao, Y., Wen, J., and Wen, X. (2012). Flexural wave band gaps in locally resonant thin plates with periodically attached spring-mass resonators. J. Phys. D Appl. Phys. 45 (19), 195401. doi:10.1088/0022-3727/45/19/195401

CrossRef Full Text | Google Scholar

Zhang, H. (2016) Study on the tunability of the band gaps and their vibration reduction performance of phononic crystal plates[D]. Hunan University.

Google Scholar

Zhang, H., Chen, J., and Han, X. (2012). Lamb wave band gaps in a homogenous plate with periodic tapered surface. J. Appl. Phys. 112 (5), 054503. doi:10.1063/1.4749400

CrossRef Full Text | Google Scholar

Zhao, H. J., Guo, H. W., Gao, M. X., Liu, R. Q., and Deng, Z. Q. (2016). Vibration band gaps in double-vibrator pillared phononic crystal plate. J. Appl. Phys. 119 (1), 014903. doi:10.1063/1.4939484

CrossRef Full Text | Google Scholar

Zhao, H. J., Guo, H. W., Li, B. Y., Deng, Z. Q., and Liu, R. Q. (2015). Flexural vibration band gaps in a double-side phononic crystal plate. J. Appl. Phys. 118 (4), 044906. doi:10.1063/1.4927627

CrossRef Full Text | Google Scholar

Zhou, G., Wu, J. H., Lu, K., Tian, X., Huang, W., and Zhu, K. (2020). Broadband low-frequency membrane-type acoustic metamaterials with multi-state anti-resonances. Appl. Acoust. 159, 107078. doi:10.1016/j.apacoust.2019.107078

CrossRef Full Text | Google Scholar

Zhou, G., Wu, J. H., Lu, K., Tian, X., Liang, X., Huang, W., et al. (2019). An approach to broaden the low-frequency bandwidth of sound insulation by regulating dynamic effective parameters of acoustic metamaterials. J. Phys. D Appl. Phys. 52 (21), 215102. doi:10.1088/1361-6463/ab07f9

CrossRef Full Text | Google Scholar

Zhu, X., Zou, X., Liang, B., and Cheng, J. (2010). One-way mode transmission in one-dimensional phononic crystal plates. J. Appl. Phys. 108 (12), 124909. doi:10.1063/1.3520491

CrossRef Full Text | Google Scholar